Abstract
Key message
Genome-wide association revealed that resistance to Striga hermonthica is influenced by multiple genomic regions with moderate effects. It is possible to increase genetic gains from selection for Striga resistance using genomic prediction.
Abstract
Striga hermonthica (Del.) Benth., commonly known as the purple witchweed or giant witchweed, is a serious problem for maize-dependent smallholder farmers in sub-Saharan Africa. Breeding for Striga resistance in maize is complicated due to limited genetic variation, complexity of resistance and challenges with phenotyping. This study was conducted to (i) evaluate a set of diverse tropical maize lines for their responses to Striga under artificial infestation in three environments in Kenya; (ii) detect quantitative trait loci associated with Striga resistance through genome-wide association study (GWAS); and (iii) evaluate the effectiveness of genomic prediction (GP) of Striga-related traits. An association mapping panel of 380 inbred lines was evaluated in three environments under artificial Striga infestation in replicated trials and genotyped with 278,810 single-nucleotide polymorphism (SNP) markers. Genotypic and genotype x environment variations were significant for measured traits associated with Striga resistance. Heritability estimates were moderate (0.42) to high (0.92) for measured traits. GWAS revealed 57 SNPs significantly associated with Striga resistance indicator traits and grain yield (GY) under artificial Striga infestation with low to moderate effect. A set of 32 candidate genes physically near the significant SNPs with roles in plant defense against biotic stresses were identified. GP with different cross-validations revealed that prediction of performance of lines in new environments is better than prediction of performance of new lines for all traits. Predictions across environments revealed high accuracy for all the traits, while inclusion of GWAS-detected SNPs led to slight increase in the accuracy. The item-based collaborative filtering approach that incorporates related traits evaluated in different environments to predict GY and Striga-related traits outperformed GP for Striga resistance indicator traits. The results demonstrated the polygenic nature of resistance to S. hermonthica, and that implementation of GP in Striga resistance breeding could potentially aid in increasing genetic gain for this important trait.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The purple witchweed or giant witchweed, Striga hermonthica (Del.) Benth., is the most widespread parasitic weed posing a serious threat to maize production in sub-Saharan Africa (SSA) (Berner et al. 1995; De Groote et al. 2008; Spallek et al. 2013). Striga hermonthica (hereafter referred to as Striga) lacks its own root system and survives by drawing water and nutrients from host plants like maize for its own growth and has a potent phytotoxic effect (Bebawi and Mutwali 1991). Maize plants infested with Striga become chlorotic, produce thin stalks with severe reduction in plant height, biomass and eventually grain yield (Menkir et al. 2012, 2020). Striga infestation is severe in areas with poor soil fertility and poorly managed but intensively cultivated farming systems (Ransom 2000). Many farmers experience total maize crop failure due to Striga infestation. Farmers who faced 100% yield loss usually move from one affected field to another, and abandoned fields become Striga seed banks. It is estimated that Striga infestation causes up to US$ 7 billion in crop losses (Berner et al. 1995), affecting the livelihoods of over 100 million people (Badu-Apraku and Akinwale 2011).
Striga infestation is extremely difficult to control since the parasite inflicts most of its damage when it is below the ground and emerges after most weeding operations are completed (Odhiambo and Ransom 1995). The emerged parasitic plants act as strong sink for host resources to support their own growth, flowering and seed production (Gurney et al. 1995, 1999). Several Striga plants attach to a single maize plant as parasites; thus, their impact on maize biomass and grain yield is often devastating and may lead to 100% yield loss (Ransom et al. 1990; Haussmann et al. 2000; Kim et al. 2002). Several methods have been proposed for Striga management, including host plant resistance, cultural, chemical and manual control options (Odhiambo and Ransom 1995; Kim et al. 2002). Integrated Striga management is a strategy involving a combination of two control methods, where the methods are used simultaneously to control Striga (Kanampiu et al. 2018). However, the use of host plant resistance is considered the most economical, environmentally viable and affordable for smallholder or resource-constrained farmers in SSA. Progress in breeding for native genetic resistance to Striga in maize has been reported in several studies (Menkir et al. 2005, 2012; Badu-Apraku and Lum 2007; Badu-Apraku et al. 2016; Menkir and Meseka 2019). Efforts to incorporate herbicide resistance in maize for Striga control have also been reported (Kanampiu et al. 2001; Makumbi et al. 2015).
Genome-wide association study (GWAS) enables genetic dissection of complex traits. GWAS offers high mapping resolution and could effectively identify favorable genomic regions associated with the trait of interest (Yu and Buckler 2006). Linkage disequilibrium (LD) decay is rapid in maize due to its extensive genetic diversity (Kump et al. 2011; Guo et al. 2013). Therefore, GWAS needs to be implemented with a large number of high-quality markers to ensure complete coverage of the genome. To date, GWAS has been successfully applied to identify the quantitative trait nucleotide (QTN) or haplotypes conferring resistance to several important diseases of maize, such as gray leaf spot (Shi et al. 2014), Southern corn leaf blight (Kump et al. 2011), Fusarium ear rot (Zila et al. 2013), maize lethal necrosis (Gowda et al. 2015; Nyaga et al. 2019; Sitonik et al. 2019) and sugarcane mosaic virus (Tao et al. 2013; Gustafson et al. 2018). Recently, Adewale et al. (2020) reported first GWAS on Striga resistance traits with small set of 132 early maturing inbred lines. On the other hand, in this study, we used GWAS panel with 380 lines for identifying genomic regions controlling resistance to Striga hermonthica.
Crop breeders need innovative methods that aid in selection for improvement of complex traits such as Striga resistance. Genomic prediction (GP) facilitates prediction of best-performing lines and can potentially accelerate the breeding cycle with optimal resources (Crossa et al. 2017). In a maize breeding program, GP-based selection is comparable to a traditional selection scheme; however, GP produces considerable savings in both time and resources (Combs and Bernardo 2013; Beyene et al. 2015, 2019). In general, results of random cross-validation with genomic best linear unbiased predictor (GBLUP) indicate that GP can significantly increase prediction accuracy for complex traits (Crossa et al. 2017). Further, GBLUP models could be extended to multi-environment settings where G × E effects are modeled to improve the prediction accuracy. Earlier studies on complex traits like grain yield (Burgueño et al. 2012; Jarquín et al. 2014; Juliana et al. 2018) clearly showed that by modeling G × E using both pedigree and markers, prediction accuracy could be increased substantially. Therefore, in this study, we ascertained the potential of GP for a complex trait like Striga resistance with and without modeling the G × E effects.
The trait of interest to be predicted could be affected by variability in the correlated traits; for instance, grain yield under artificial Striga infestation could be affected by other Striga resistance-related traits, disease and other agronomic traits. Therefore, these traits could be considered for inclusion in prediction models. Several statistical models which incorporate multiple traits in GP are available (Montesinos-López et al. 2016) but to fit these factors into models is complex and time-consuming. Recently, a new algorithm called ‘item-based collaborative filtering’ (IBCF) was reported to be competitive with respect to computing time and prediction accuracy (Montesinos-López et al. 2018a). IBCF is popularly used for recommending items/products in electronic commerce websites, where a list of recommended items/products is generated based on customer’s interests. The IBCF uses inputs about a customer’s interests to generate predictions. This algorithm has been implemented in GP and proved to be comparable and sometimes even superior to conventional whole-genome prediction models when the correlation between traits and environments was moderate or high (Montesinos-López et al. 2018b). Recently, the IBCF recommender system was applied for multivariate predictions of traits in maize and wheat breeding (Juliana et al. 2018, 2019; Montesinos-López et al. 2018b).
While several studies have reported the use of GWAS to understand the genetic architecture of some biotic stresses, e.g., (Zila et al. 2013; Ding et al. 2015; Gowda et al. 2015; Mammadov et al. 2015; Kuki et al. 2018; Nyaga et al. 2019; Sitonik et al. 2019) and abiotic stresses in maize, e.g., (Yuan et al. 2019; Ertiro et al. 2020), its application for identification of genomic regions associated with resistance to Striga has not been reported. Also, GP has been applied to several traits in maize (Burgueño et al. 2012; Gowda et al. 2015; Gustafson et al. 2018; Sitonik et al. 2019; Yuan et al. 2019) but not for Striga resistance. The overall aim of this study was to dissect the genetic basis underlying Striga resistance in maize under artificial infestation and to identify targets for knowledge-based improvement of Striga resistance in tropical maize germplasm. The specific objectives of the study were to: (i) evaluate the diverse array of 380 tropical maize inbred lines for response to Striga under artificial infestation; (ii) detect main-effect QTL and putative candidate genes associated with Striga resistance; (iii) assess the utility of GP for Striga resistance with different cross-validation methods in the tropical maize panel; and (iv) evaluate multivariate predictions of Striga resistance indicator traits using other correlated agronomic traits based on the IBCF approach. We evaluated the IBCF approach for predicting a given target trait (for example, GY and Striga resistance indicator traits) by incorporating information from other traits that can affect the target trait(s). In this study, users represent the target trait while items represent other related traits evaluated in different environments, that are expected to have some correlation with the target trait.
Materials and methods
Plant materials and field trials
This study used the Improved Maize for African Soils (IMAS) association mapping panel (Gowda et al. 2015) of 380 CIMMYT maize inbred lines. All the inbred lines were developed by International Maize and Wheat Improvement Center (CIMMYT) and International Institute for Tropical Agriculture (IITA) breeding programs for drought, low N, soil acidity (SA) and pest and disease resistance, through conventional breeding methods. The list of the inbred lines, the source germplasm and the method employed for the development of the lines can be found at http://www.data.cimmyt.org. This panel broadly represents tropical and subtropical maize genetic diversity, including germplasm derived from diverse breeding programs at CIMMYT (Wen et al. 2011).
Field evaluation, experimental design and artificial infestation with Striga hermonthica
The 380 inbred lines were evaluated in replicated trials in three environments (environment 1—Kibos2013, environment 2—Alupe2013 and environment 3—Alupe2014) under artificial Striga infestation during the long rainy seasons (March–August). Both Kibos [− 0.03861°S, 34.81596°E; 1,193 m above mean sea level (masl); 865 mm mean annual rainfall] and Alupe (0.503725°N, 34.12148°E; 1153 masl; 1400 mm mean annual rainfall) have a bimodal rainfall distribution. Striga seeds collected from sorghum fields were stored for few months which helps to break the seed dormancy which was later used for the infestation. Artificial infestation of the S. hermonthica trials at Kibos and Alupe was carried out by adding viable Striga seeds to each planting hole. Each maize plant was exposed to a minimum of 2000 viable S. hermonthica seeds. A standard scoop calibrated to deliver specified amount of germinable Striga seeds per hill was used for the artificial infestation (Kim 1991). Striga seeds collected earlier from farmers maize and sorghum fields around Kibos station, containing about 25% extraneous material and 25% viability in 10 g of soil/seed mixture, were added to an enlarged planting hole at a depth of 7–10 cm directly below the maize, as per the protocol optimized by Kanampiu et al. (2018) to ensure that each maize plant was exposed to Striga at germination. Two maize seeds were placed into the holes infested with sand–Striga seeds mixture and then covered with soil. The experimental design used was 5 by 76 simple alpha-lattice with two replications at both locations. Plot size was two rows, with a spacing of 0.75 m and 0.25 m between rows and plants, respectively. Plots were thinned to one plant per hill two weeks after planting to attain a population density of approximately 53,333 plants per hectare. The recommended fertilizer rate was reduced, and application was delayed up to three weeks after planting to induce the production of strigolactones which stimulate good germination of the Striga seeds and the attachment of the Striga plants to the roots of host plants (Adewale et al. 2020; Badu-Apraku et al. 2020a, b). Weeding was done by hand to remove all weeds from the field except S. hermonthica. IMAS panel was also evaluated in Striga-free environments, under Striga-free conditions as well as under low N (Ertiro et al. 2020) and under maize lethal necrosis conditions (Sitonik et al. 2019). However, in this study, we focused only on data collected under Striga infestation environments.
Data recording
Grain yield, host plant Striga damage syndrome rating and emerged Striga plant counts were recorded in the field trials. Host plant Striga damage syndrome rating (SDR) was visually rated for each plot at 10 and 12 weeks after planting (WAP) using a scale of 1–9, where 1 to 3 = no visible or mild damage symptoms; 4 to 5 = some leaf blotching, wilting and stunting; 6 to 8 = extensive leaf scorching, noticeable stunting and reduction in plant growth; and 9 = all leaves completely scorched and dead (Kim 1994). The number of emerged S. hermonthica plants was recorded at 8, 10 and 12 WAP. The emerged Striga plant counts at the three intervals were used to calculate the “area under the Striga number progress curve” (AUSNPC), using the formula for “area under the disease progress curve” (AUDPC) (Shaner and Finney 1977; Haussmann et al. 2000).
Other agronomic traits including days to anthesis (AD, days from planting to when 50% of the plants had shed pollen) and days to silking (SD, days from planting to when 50% of the plants had extruded silks) were recorded. Plant height (PH, measured in centimeters as the distance from the base of the plant to the height of the first tassel branch), ear height (EH, measured in centimeters), number of ears per plant (EPP, determined by dividing the total number of ears per plot by the number of plants harvested per plot), husk cover (HC, obtained by dividing the number of ears with poor husk cover by the number or plants harvested per plot), plant aspect (PASP, rated on a scale of 1–5, where 1 = excellent plant type and 5 = poor plant type) and grain moisture at the time of harvest were also recorded. All the ears harvested from each plot were weighed, and representative samples of ears were shelled to determine percentage moisture using a Dickey John moisture meter at all locations. Grain yield (GY, t ha−1) was calculated from ear weight and grain moisture, assuming a shelling percentage of 80% and adjusted to 12.5% grain moisture content. These agronomic traits data were collected to understand their correlations and their usefulness in the breeding for Striga resistance. Further other traits are also used in multivariate predictions for Striga-related traits and GY.
Phenotypic data analyses
All quantitative genetic parameters were estimated based on the performance of the 380 inbred lines in the IMAS association mapping panel. Residuals for all traits were normally distributed. Individual location analyses were performed, and data from locations with significant genotypic variation and good repeatability were selected for across location analyses. We removed the outliers and did the across location analyses. Analyses of variance within and across environments were undertaken by the restricted maximum likelihood method using the software ASREML-R (Gilmour et al. 2009). The following linear mixed model was used for analysis:
where Yijko is the phenotypic performance of the ith genotype at the jth environment in the kth replication of the oth incomplete block, µ is an intercept term, Gi is the genetic effect of the ith genotype, Ej is the effect of the jth environment, R(E)kj is the effect of the kth replication at the jth environment, B(R.E)ojk is the effect of the oth incomplete block in the kth replication at the jth environment and eijko is the residual. Environments and replications were treated as fixed effects and the other effects as random. Heritability on an entry-mean basis was estimated from the variance components on a progeny mean basis as described by Hallauer and Miranda (1981): \(h^{2} = \, \sigma^{2}_{G} / \, (\sigma^{2}_{G} + \, \sigma^{2}_{{{\text{GXE}}}} /E \, + \, \sigma^{2}_{e} /{\text{ER}}\)), where \(\sigma^{2}_{G} , \, \sigma^{2}_{{{\text{GXE}},}} \sigma^{2}_{e}\) refer to the genotypic, genotype X environment interaction and error variances, and E and R indicate the number of environments and replications, respectively. Best linear unbiased predictions (BLUPs) and best linear unbiased estimates (BLUEs) were calculated using META-R software (Alvarado et al. 2015) (https://hdl.handle.net/11529/10201). Pairwise Pearson’s correlation coefficients (r) among the traits were calculated using R software version 3.2.5 (https://www.r-project.org/).
Molecular data analyses
Detailed description of the IMAS panel and their genotyping with genotyping-by-sequencing (GBS) markers was described earlier (Gowda et al. 2015; Ertiro et al. 2020). In brief, DNA of all inbred lines extracted from 2–3 weeks old seedlings was genotyped using GBS (Elshire et al. 2011) at Cornell University, Ithaca, USA, as per the procedure described earlier (Elshire et al. 2011; Glaubitz et al. 2014). SNPs which were polymorphic, having minor allele frequency of > 0.05, with < 5% of missing data, and heterozygosity of < 5%, were reserved for final GWAS analysis. Applying these filtering metrics, 278,810 polymorphic SNPs were retained for GWAS in the IMAS panel.
BLUPs calculated for Striga count at 8, 10 and 12 WAP, AUSNPC, SDR and GY at each environment and across environments were used in GWAS. Trait data were corrected for population structure using the general linear model (GLM), as well as population structure and kinship (Q + K) using the mixed linear model (MLM) algorithm (Flint‐Garcia et al. 2005; Yu and Buckler 2006). GWAS and principal component (PC) analysis were performed using TASSEL ver 4.0 (Bradbury et al. 2007). Population structure was corrected by using the first three PCs which explained the maximum variation. For multiple testing correction to determine the significance threshold, instead of 278,810 independent tests, the total number of tests was estimated based on the average extent of LD at r2 = 0.1 (Cui et al. 2016, 2017). Based on this, significant associations were declared when the P values in independent tests were less than 2 × 10−06 for Striga resistance traits and P = 5.6 × 10–6 for GY. The total proportion of phenotypic variance explained by the detected QTL was calculated by fitting all significant SNPs simultaneously in a linear model to obtain R2adj. The proportion of the genotypic variance explained by all QTLs was calculated as the ratio of pG = R2adj/h2. Candidate genes containing or adjacent to the significant SNPs were obtained from the B73 gene set in Maize GDB (https://www.maizegdb.org/gene_center/gene).
Multivariate predictions of Striga-related traits and grain yield
We used the IBCF approach for multivariate prediction of GY and Striga-associated traits in individual environments using its similarity to other traits measured at different environments. The detailed steps involved in IBCF approach implementation are described in earlier studies (Juliana et al. 2017, 2018; Montesinos-López et al. 2018a). In brief, the basic idea of IBCF algorithm is building a database of users (lines) by preferences for items (trait-environment combination). Then, each column of this matrix (\(\left[ {z_{ij} = (y_{ij} - \mu_{j} } \right)\sigma_{j}^{ - 1} ]\)) is standardized, where \(i\) denotes the users (lines), \(j\) denotes the columns (trait-environment combinations), \({\mu }_{j}\) is the mean of column \(j\) and \({\sigma }_{j}\) denotes the standard deviation of column\(j\). Then, the Pearson correlation between the columns of the resulting standardized matrix (trait-environment combinations) is computed. Next with the following formula (Sarwar et al. 2001; Montesinos-López et al. 2018a), the predictions for the missing phenotypes of line \(i\) in item \(j\) are computed.
where \(\hat{z}_{ij} = \frac{{\sum\nolimits_{{j^{\prime } \int {N_{i} \left( j \right)} }} {z_{{ij^{\prime } }} w_{{jj^{\prime } }} } }}{{\sum\nolimits_{{j^{\prime } \int {N_{i} \left( j \right)} }} {w_{{jj^{\prime } }} } }}\) is the predicted scaled phenotype for user (line) \(i\) on item (trait-environment) \(j.\) \(N_{i}\)(j) denotes the items rated by user (line) \(i\) most similar to item j, \(w_{{jj^{\prime } }}\) is the weight between items \(j\) and \(j^{\prime }\) and the weights are obtained from an item-to-item similarity matrix built using the Pearson’s correlation, which provides information on how similar an item is to another item. We implemented IBCF to predict each trait from one environment using other traits from remaining environments in the complete set of lines using the ‘R’ package IBCF.MTME (Montesinos-López et al. 2018a).
Genomic prediction
High similarities have been reported among available GP models (Juliana et al. 2017). In this study, we used the whole-genome regression approach GBLUP which employed the genomic relationship matrix (G-matrix) calculated from markers (VanRaden 2008) and has been successfully applied to predict complex traits (Habier et al. 2013; Yang et al. 2017). The GBLUP model was implemented in the ‘R’ package BGLR (Pérez and de Los Campos 2014). The models include genomic effect within environment, and multi-environment including environment and genomic main effects and genomic × environment interaction (G × E). First, we provide the model used within each environment, with only the main effects of genotypes (genomic) in the predictor:
where \(y_{j}\) represents the normal response observed in the \(j\)-th line with \(j = 1,2, \ldots J.\) \(G_{j}\) represents the genotype effect of the \(j\)-th line and is assumed as a random effect distributed as \(G = \left( {G_{1} , \ldots , G_{J} } \right)^{T} \sim N\left( {0,G_{1} \sigma_{G}^{2} } \right)\), where \(G_{1}\) denotes the genomic relationship matrix calculated as suggested by (VanRaden 2008) and \(\sigma_{G}^{2}\) denotes the genomic variance. Finally, \({\varepsilon }_{j}\) is the random error term associated with the \(j\)-th line distributed \(N\left( {0,\sigma_{e}^{2} } \right)\), where \(\sigma_{e}^{2}\) denotes the residual variance. Next, the model containing environmental main effects and the genotype \(\times\) environment interaction is
where \({y}_{ij}\) represented the normal response observed in the \(j\)-th line at the \(i\)-th environment, where \(i = 1,2, \ldots ,I;\;j = 1,2, \ldots J.\) The main effect of environments \(E_{i} \sim\) \(N\left( {0,I\sigma_{E}^{2} } \right)\) (where I is the identity matrix and \(\sigma_{E}^{2}\) is the variance of environments) \({\text{EG}}_{ij}\) is the interaction between the genotype effect of the \(j\)-line with the \(i\)-th environment and is also assumed as a random effect distributed as \({\text{GE}} = \left( {{\text{EG}}_{11} , \ldots , {\text{EG}}_{IJ} } \right)^{T} \sim\)\(N\left( {0,G_{1} \otimes I_{I} \sigma_{{{\text{GE}}}}^{2} } \right)\), where \(\sigma_{{{\text{GE}}}}^{2}\) denotes the variance of the interaction of G × E. Finally, \(\varepsilon_{ij}\) is the random error term associated with the \(j\)-th line in the \(i\)-th environment distributed \(N\left( {0,\sigma_{e}^{2} } \right)\), where \(\sigma_{e}^{2}\) denotes the residual variance.
Evaluation of prediction performance
The IBCF was used only for one type of cross-validation (CV) scheme and was found very useful in breeding programs, this cross-validation called incomplete field trials (CV2) was the practical method when some lines were evaluated in some environments but not in others; the goal here was to predict the performance of these lines in environments where they had not been phenotyped (Crossa et al. 2017). However, the GBLUP model in addition to the CV2 cross-validation also evaluated the prediction of new lines (CV1) in an attempt to measure the predictive ability of new lines that had not been phenotyped in any environments, predictive ability between phenotyped and unphenotyped lines were primarily based on genetic similarities as the main source of information, and predicting already observed lines in unobserved environments (CV0; leaving one environment out). Here, the main interest was to predict the performance of lines in potentially new locations. For random cross-validation CV0, CV1 and CV2, the prediction accuracies were calculated by performing random fivefold cross-validation where 20% of the maize lines (testing set) were predicted and 80% were used as training set. For CV1, none of the 20% of the lines in the testing set was observed in any of the environments, whereas for CV2 (in both the GBLUP and IBCF), the 20% of the lines in the testing set were observed in some environments but not in the others. The prediction accuracy was computed as the correlations between the observed and predicted values. Additionally, one more CV was carried out where accuracies were predicted within IMAS association mapping panel by using BLUEs across environments. The GP was carried out with and without inclusion of significant markers detected in GWAS analyses for the respective traits. For each trait, the sampling of training and validation sets was repeated 100 times.
Results
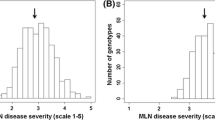
Severity of Striga hermonthica infestation was moderate to high at the phenotyping locations. The average Striga plant count at 8 WAP was 6.2 which gradually increased to 30 and 65 after 10 and 12 WAP, respectively (Table 1). Location means for AUNSPC ranged from 189 to 2457 with the mean of 970. SDR scored 12 WAP ranged between 2 and 7. The GY of the 380 lines under artificial Striga infestation ranged from 0.0 to 3.5 tons ha−1, with an average of 1.52 tons ha−1. All measured traits showed significant (P < 0.05) genotypic and genotype-by-environment (G × E) interaction variances (Table 1). For traits associated with Striga resistance, the ratio of genotypic variance to G × E interaction variance was highest for SDR with 8.1 and lowest for Striga count at 8 WAP with 0.7. Heritability estimates under artificial Striga infestation were moderate (0.51–0.68) for Striga plant counts and AUSNPC, and high for SDR (0.84) and GY (0.70). The distribution of phenotypic values was unimodal for the number of emerged Striga plants at different intervals, AUSNPC and SDR indicating the quantitative nature of Striga resistance (Fig. 1).
The strongest positive and significant correlations were observed between number of emerged Striga plants at 8, 10 and 12 WAP and AUNSPC (Fig. 2). SDR was positively and significantly correlated with number of emerged Striga plants at different intervals and AUSNPC. GY was significantly but negatively correlated with number of emerged Striga plants at different time intervals, AUSNPC and SDR. AD was positively correlated with number of emerged Striga plants at different time intervals, AUSNPC and SDR, and was negatively correlated with GY. HC was also negatively correlated with all Striga resistance indicator traits except for SDR. We observed significant correlations but of low magnitude between Striga resistance indicator traits and other agronomic traits. The correlation between GY and AUSNPC, as well as between GY and SDR, revealed many lines with good levels of resistance based on AUSNPC and SDR yielding > 2 tons per hectare of grain (Supplementary Figure S1).
Correlations among fourteen measured traits. The correlation level is color-coded according to the color key plotted on the extreme right. Correlation values with > 0.12 and > 0.16 were significant at P = 0.05 and P = 0.01 levels, respectively. Str8, Str10, Str12 = Striga emerged plant count at 8, 10 and 12 weeks after planting, respectively; AUSPC = Area under Striga number progress curve; SDR12 = Striga damage rating at 12 weeks after planting; GY = Grain yield; AD = days to anthesis; PH = plant height, EPO = ear position; EPP = number of ears per plant; HC = husk cover; GLS = gray leaf spot; TLB = Turcicum leaf blight; ER = Fusarium ear rot
The top 16 lines in terms of GY and their performance for other traits under Striga infestation are shown in Table 2. IMAS panel lines IMAS175 (DTPYC9-F46-1–2-1–2-B) and IMAS275 ((JL16.R119W)-1–1-#) had the highest GY coupled with low SDR. However, both IMAS175 (DTPYC9-F46-1–2-1–2-B) and IMAS275 ((JL16.R119W)-1–1-#) also supported a high number of Striga plants at 10 and 12 WAP. Inbred lines with high GY and supporting a low number of emerged Striga plants in addition to lower SDR were considered as resistant/tolerant to Striga.
GWAS was performed for the number of emerged Striga plants at 8, 10 and 12 WAP, AUSNPC, SDR and GY. The results for the six traits are shown in Manhattan and Q–Q plots of P values comparing the expected -log10p values to observed − log10p values (Fig. 3 and Supplementary Figure S3). GWAS detected 57 SNPs distributed across the genome that were significantly associated with the six different traits (Table 3; P = 2 × 10–6). Eleven, fourteen and six significant SNPs individually explained 8–10%, 8–11% and 8–10% of the total phenotypic variance for number of emerged Striga plants at 8, 10 and 12 WAP, respectively. For AUSNPC, SDR and GY, sets of 11, four and nine significant SNPs individually explaining 7–10%, 6–7% and 7–8% of the total phenotypic variance, respectively, were detected. The most significant SNP across the six traits was S5_56842787 on chromosome 5 which explained 10% of the total phenotypic variance for number of emerged Striga plants at 8 WAP. SNPs S5_56842787 on chromosome 5, S7_70368510, S7_7160192 and S7_144538472 on chromosome 7, S1_298988628 on chromosome 1 and S7_165944748 on chromosome 7 were found to be the most significantly associated for Striga count at 8, 10 and 12 WAP, AUSNPC, SDR and GY under Striga, respectively. A set of putative candidate genes associated with the significant markers was identified (Table 3). Additionally, the genome-wide linkage disequilibrium (LD) decay was plotted as LD (r2) between adjacent pair of markers and distance in kb (Figure S2). The average physical distance was 6.53 kb and 18.82 kb at a cut-off value of r2 = 0.2 and 0.1, respectively.
Manhattan plots of the GWAS for six different Striga-related traits in IMAS association mapping panel. The dashed horizontal line depicts the significance threshold (P = 2 × 10–6 for Striga resistance traits and P = 5.6 × 10–6 for GY). The X-axis indicates the SNP location along the 10 chromosomes, with chromosomes separated by different colors; Y-axis is the—log10(P observed) for each analysis
GP was applied to evaluate the accuracy with different cross-validation methods with individual locations as well as across locations. Average correlations between predictions and observed phenotypes in CV0, CV1 and CV2 for all the measured traits with and without G × E interaction effects are presented in Table 4 and Fig. 4. Among the three different cross-validations, CV1 performed poorly compared with CV0 and CV2 for measured traits, with CV0 and CV2 performing equally well. Prediction for one environment (Alupe 2014) showed better correlations for number of emerged Striga plants at 8, 10 and 12 WAP and AUSNPC compared with the other environments, whereas for SDR and GY, Alupe2013 performed better. There were slight increases in the prediction correlations for models with the G × E interaction in cross-validation scenarios for most traits and environments. Prediction correlations were also obtained for the measured traits using BLUEs across locations which showed values similar to those observed for CV0 and CV2 (Fig. 4). Inclusion of significant markers detected through GWAS in the prediction model showed slight increase in prediction correlations for all the Striga resistance indicator traits and GY. The prediction correlations were higher for all Striga resistance-related traits compared with GY. For GY in CV2, we observed a similar increase in the prediction correlations for two out of three environments. The two environments Alupe 2014 and Kibos 2013 had prediction correlations of 0.376 and 0.505 for a model without G × E and 0.411 and 0.518 for a model with G × E, respectively.
Distribution of the accuracy of genomic predictions for five different Striga related traits and grain yield under artificial Striga infestation. Prediction was based on random markers (white box) as well as combined prediction based on random markers and trait-associated markers (gray box) detected through GWAS with fivefold cross-validations in IMAS association panel of 380 inbred lines
We compared prediction accuracies from the GBLUP model with the IBCF approach with CV2 (Table 5). For IBCF, the training population included all the traits from any two environments while the prediction set included the target traits in the remaining third environment. GY was predicted with moderate accuracy with IBCF approach, with 0.010, and 0.013 increases in accuracy in location Alupe 2014 and Kibos 2013, respectively. However, in Alupe 2013, a decrease (-0.004) in accuracy compared with the GBLUP model was observed. For all Striga resistance indicator traits, the prediction accuracy was at least 15% higher with the IBCF approach compared with the GBLUP model in all locations (Table 5). Overall, with the IBCF approach, a maximum increase of 0.40 was observed for number of emerged Striga plants at 10 WAP and AUSNPC for Alupe2013 over the GBLUP model.
Discussion
The defense mechanisms of maize against Striga were grouped into resistance and tolerance (Kim 1994). The ability of the host plant to withstand the effects of the Striga plants that are already attached, regardless of their number was termed as tolerance. It is quantified by a host damage syndrome rating score using a 1–9 scale (Kim 1994). Ability of the host plant to prevent the parasite from attaching itself to the roots was referred to as resistance (Kim 1994). This is quantified by the number of emerged Striga plants around the base of the host plant. Resistance mechanisms were also further categorized as pre‐attachment and post‐attachment. Mechanisms that prevent or reduce Striga seed germination rates were categorized as pre‐attachment resistance, while those that prevent or reduce the success of root penetration or establishment of the vascular connection between host and parasite were called post‐attachment resistance (Yoder and Scholes 2010). Both host damage score and Striga emergence, along with GY under Striga infestation, were considered as the most appropriate criteria to use in breeding for Striga tolerance/resistance (Kim 1991; Kim et al. 1998; Badu-Apraku and Fakorede 1999; Badu-Apraku and Akinwale 2011).
Genetic variability is important in efficient selection for improved GY under stress environments such as Striga-infested conditions. The observed significant genotypic variance for the measured traits in the present study showed the potential for selection of improved GY under Striga-infested conditions. There was a wide range of responses to Striga infestation in terms of GY and Striga resistance parameters. The inbred lines used in this study were from diverse geographical regions with different breeding histories and this may have contributed to the variation observed. The lines showing good response to artificial Striga infestation should be utilized in more detailed studies to ascertain the resistance mechanisms involved. The significant G × E variances for the measured traits indicated that they are highly affected by the G × E interaction which could be attributed to variation in climatic and soil conditions across the two years. Previous studies have also reported significant G × E under Striga-infested conditions (Menkir et al. 2012; Makumbi et al. 2015; Kanampiu et al. 2018). Moderate to high heritability estimates were observed indicating the potential for these traits to be improved through recurrent selection. Broad-sense heritability is an estimate of the upper boundary of the narrow-sense heritability. High broad-sense heritability estimates for GY, AUSNPC, SDR and number of emerged Striga plants 12 WAP suggest that the actual narrow-sense heritability could be higher and that reasonable genetic gain for these traits could be expected. The high broad-sense heritability estimates for GY (0.70) and number of emerged Striga plants 12 WAP (0.68) observed in this study corroborate previous reports under artificial Striga infestation (Menkir et al. 2012; Makumbi et al. 2015; Adewale et al. 2020) and higher than the heritability observed in biparental populations (Badu-Apraku et al. 2020a, b).
The significant negative correlation between GY and number of emerged Striga plants indicated that increase in number of emerged Striga plants led to severe reduction in GY (Menkir et al. 2012; Adewale et al. 2020). For SDR, tolerance is associated with lower values in the 1–9 scale and thus significant negative correlation between SDR and GY implied that lower SDR values were associated with improved GY. The observed positive and significant correlations between number of emerged Striga plants, SDR and AUNSPC suggest that these traits can be combined into an index for selection under Striga infestation.
The detection power of GWAS depends on the LD between the QTL and the markers. Cross-pollinated crops like maize have more rapid LD decay compared with self-pollinated crops due to outcrossing and consequently high genetic diversity (Kaler et al. 2020). The results of the present study indicated that the LD decayed rapidly across the physical distance (18.82 kb and 6.53 kb at a cut-off value of r2 = 0.1 and 0.2; Supplementary Figure S2) indicating that the IMAS association mapping panel has significant diversity, mimicking a natural population, and thus was appropriate for conducting GWAS. Previous studies on the population structure of the IMAS panel used in this study showed confounding structure in the panel (Gowda et al. 2015; Ertiro et al. 2020).
Correcting for population structure is an important step in GWAS to reduce the false positives that could arise from it without overcorrecting and further causing false negatives (Jaiswal et al. 2019). Another factor that leads to false positives is the more recent common ancestry and family relatedness which is controlled by the inclusion of a kinship model through the identity by state approach (Loiselle et al. 1995). Therefore, we incorporated the population structure and kinship matrix as covariates (Q + K) in the mixed linear model. The Q–Q plots of the six traits showed proper distribution of the observed over the expected P values indicating that the model and the comparison method used were an appropriate fit in this GWAS approach (Supplementary Figure S3).
At a significant threshold p value (p = 2 × 10–6 for Striga resistance traits and P = 5.6 × 10–6 for GY), we identified a total of 57 marker trait associations distributed across the genome and controlled by few major and many minor effect QTL (6–11% of the total phenotypic variance) suggesting the complexity of resistance to Striga infestation. For SDR and number of emerged Striga plants at 8 WAP, we observed four and 11 SNPs and Adewale et al (2020) reported nine and one significantly associated SNPs, respectively. However, no overlapping SNPs were observed across the studies for both the traits possibly due to different timing of data scored and the different materials used in the study. On the other hand, one SNP S3_158421414 detected consistently for number of emerged Striga plants at 10 and 12 WAP and AUSNPC was overlapped with the QTL reported by Badu-Apraku et al (2020a) in biparental population. In this study, no overlapping of SNPs was detected between number of Striga-emerged plants and SDR, however five SNPs on chromosome 3 (S3_143803575, S3_143804650, S3_145603175, S3_145603187 and S3_158421414) detected for number of Striga-emerged plants were overlapped with four QTL detected for SDR in an earlier study (Badu-Apraku et al 2020b) which suggests this region might be carrying an important gene/s for resistance to Striga.
A set of putative candidate genes associated with the significant markers was identified; their functions indicated their direct or indirect involvement in plant defense responses (Table 3). These candidate genes may be useful after validation in breeding for Striga resistance through marker-assisted selection. Out of the nine, two candidate genes: GRMZM2G018508 and GRMZM2G015520 were most significantly associated with number of emerged Striga plants at 10 and 12 WAP, respectively. GRMZM2G018508 was identified to be involved in the ubiquitination processes (Zhou et al. 2017), while GRMZM2G015520 is involved in signal- and stress-related regulated pathways of the transcription factors (Niu et al. 2017) that play important roles in plant responses to stress.
The other seven candidate genes are involved in plant responses to stress through various mechanisms ranging from metabolism and biosynthesis of compounds to detoxification processes. In particular, GRMZM2G127230 is linked to chloroplast recognition particle (cpSRP) involved in the post-translational targeting of the nuclear encoding light harvesting chlorophyll-binding proteins (LHCPs) to the thylakoid membrane (Funke et al. 2005). The LHCPs members are positively involved in the abscisic acid (ABA) signaling in the stomata movement and plant responses to stress (Funke et al. 2005). GRMZM2G146034 is linked to the ABC transporters found in the plant cell membranes and is involved in the detoxification processes, response to abiotic stresses, pathogen resistance and interaction of the plant with its environment (Choi 2005). GRMZM2G074871 was found to be involved in the metabolism of a wide variety of exogenous and endogenous compounds, biosynthesis of pigments, volatiles, antioxidants, allelochemicals and defense compounds including phenolics and conjugates through the heme–thiolate proteins in specific, the cytochrome P450s (Chadha et al. 2018).
Two candidate genes were found to be involved in the degradation processes important in plant defense. GRMZM2G092112 is involved in protein degradation and autophagy processes that allow the plant to perceive and react to invading pathogens and thus are involved in plant immunity responses through the regulation of programmed cell death (Fujiki et al. 2007). Another candidate gene, GRMZM2G075368, is involved in the degradation of ethylene receptors and signal transduction (Chen et al. 2007). The production of ethylene is tightly regulated by internal stimuli during development and in response to environmental stimuli from biotic and abiotic stresses (Chen et al. 2007). The other candidate gene GRMZM2G164502 plays a role in plant stress responses through Leucine-Rich Repeats Receptor-Like Kinase which acts as mediators of cell-to-cell communication to relay environmental stimuli or to activate defense/resistance pathways against pathogens (Dufayard et al. 2017). Further studies on the candidate genes can pave the way for their potential use in breeding for Striga resistance.
GP has been widely applied in plant breeding to circumvent the drawbacks of marker-assisted selection by capturing all marker effects. GP that includes G × E interaction into the model substantially improves the accuracy (Guo et al. 2013). However, the presence of G × E negatively affects the heritability of traits thereby limiting the selection process (Roorkiwal et al. 2018). The assessment of GP correlations for measured traits with and without G × E using the three CVs revealed that CV1 performed relatively poor as compared to CV0 and CV2. The lower prediction correlations shown in CV1 corroborate the results from previous studies (Burgueño et al. 2012; Jarquín et al. 2014). Overall, CV1 scenario is more challenging than CV2, as in CV1, we are trying to predict the performance of newly developed lines (not tested in the field), whereas in CV2, we predict the performance of lines that have not been evaluated in some environments but which have been evaluated in different correlated environments. This is reflected in the results that showed CV‐correlations obtained in CV2 to be 12, 13, 15, 15, 27 and 25% greater than those obtained in CV1 for number of emerged Striga plants at 8WAP, 10WAP, 12WAP, AUSNPC, SDR and GY, respectively. This emphasizes the importance of having information from correlated environments when predicting performance. Selection of lines without field testing, as mimicked in CV1, allows the reduction of the breeding cycle interval, but the lower prediction accuracy might negatively affect the rate of genetic gain in a breeding program. Ultimately, the trade-off between desired prediction accuracy and generation interval depends on the structure of the breeding scheme.
For Striga resistance indicator traits, we observed an increase of up to 4% in the prediction accuracy with CV0 and CV2 but not much change was observed under CV1 after incorporating the G × E interaction in the model. Similar to observed prediction correlations for GY in CV2, Burgueño et al. (2012) and Jarquín et al. (2014) also reported prediction correlations of 0.439 and 0.475 (for a model without G × E) and of 0.556 and 0.514 (for a model with G × E), respectively, for GY in wheat. These results show the importance of incorporating the G × E interaction in the model. The observed slight differences in the prediction correlations between the studies are possibly due to model differences, the trait under study and the heritability. Overall, the prediction ability obtained in this study with CV0 and CV2, as well as observed accuracy based on BLUEs across locations, is high enough to warrant implementation of GP in practical breeding for Striga resistance in maize. The prediction accuracies based on BLUEs across locations, with and without inclusion of GWAS-detected markers, are moderately high. This is slightly overestimated since we fitted the markers detected with whole population-based GWAS rather training population alone. Nevertheless, we observed very small change in prediction accuracy by including GWAS-detected markers into the prediction model which supports Striga resistance indicator traits are governed by more of small to moderate effect genes/QTLs rather by major effect genes.
The IBCF approach was used to predict Striga resistance indicator traits and GY one at a time by integrating information from multiple traits evaluated in correlated environments. We observed an increase in accuracy for GY and Striga resistance indicator traits over the GBLUP model for all three locations. On the other hand, the GBLUP model outperformed the IBCF approach for all three locations for AD. The moderately low correlations obtained with the IBCF approach for GY compared with high prediction correlations for Striga resistance indicator traits might be due to the low magnitude of correlation of other traits with GY, as compared to each of the Striga-related traits. This indicates that changes in correlations of target trait with related traits will affect the predictive ability, especially when there is low correlation between selected locations and traits. While the ability of the IBCF approach resulted correlations higher than the GP correlations specifically for all Striga resistance indicator traits supports the utility of the method for improving Striga resistance breeding. This is also clearly supported by observed high correlations between Striga resistance indicator traits like number of emerged Striga plants at 8WAP, 10WAP, 12WAP and AUSNPC (Fig. 2). The observed prediction correlations are based on single-trait model and it is possible to improve further with multiple trait-based models. In rice for water usage trait data collected at different time intervals, multiple-trait regression models showed better prediction accuracy over single-trait regression model (Baba et al. 2020). Alternatively, from the perspective of traditional multiple-trait selection, we can also use the phenotype value of the closest related trait as the predicted value of the target trait. Overall, IBCF approach is very useful when the number of traits or environments, as well as correlations between them, is large. Moreover, its implementation is very fast as it can be used on very large data sets with limited computational power.
Conclusion
In this study, we evaluated an association mapping panel of 380 inbred lines in multiple locations in Western Kenya under artificial S. hermonthica infestation to understand the genetic architecture of traits related to resistance to Striga. GWAS results revealed the polygenic nature of Striga resistance indicator traits with moderate genetic effects and significant G × E. We demonstrated that GWAS together with GP could potentially increase the efficiency of breeding for Striga resistance by improving the prediction accuracy. We found a significant improvement in prediction performance of Striga resistance indicator traits when G \(\times\) E interaction was taken into account under the CV0 and CV2 cross-validation approaches where prediction is for the line’s performance in new environments. Results suggested that integration of GP in maize breeding even with diverse germplasm like this IMAS association mapping panel could effectively complement phenotypic selection to improve resistance to Striga, besides significantly reducing time and cost of breeding. Incorporation of the IBCF approach could further improve selection decisions in breeding for Striga resistance.
Data availability
All datasets generated for this study are included in the article/Supplementary material.
References
Adewale SA, Badu-Apraku B, Akinwale RO et al (2020) Genome-wide association study of Striga resistance in early maturing white tropical maize inbred lines. BMC Plant Biol 20:203. https://doi.org/10.1186/s12870-020-02360-0
Alvarado G, López M, Vargas M, Pacheco A, Rodríguez F, Burgueño J et al (2015) META-R (Multi environment trail analysis with R for windows) version 5.0-CIMMYT research software dataverse-CIMMYT dataverse network. https://data.cimmyt.org/dataset.xhtml?persistentId=hdl:11529/10201. Accessed 25 Mar 2020
Baba T, Momen M, Campbell MT, Walia H, Morota G (2020) Multi-trait random regression models increase genomic prediction accuracy for a temporal physiological trait derived from high-throughput phenotyping. PLoS ONE 15(2):e0228118
Badu-Apraku B, Akinwale RO (2011) Cultivar evaluation and trait analysis of tropical early maturing maize under Striga-infested and Striga-free environments. Field Crops Res 121:186–194
Badu-Apraku B, Fakorede MAB (1999) Progress in breeding for Striga hermonthica resistant early and extra-early maize varieties. In: Impact, challenges and prospects of maize research and development in West and Central Africa. Proceedings of a regional maize workshop. pp 4–7
Badu-Apraku B, Fakorede MAB, Oyekunle M, Akinwale RO (2016) Genetic gains in grain yield under nitrogen stress following three decades of breeding for drought tolerance and Striga resistance in early maturing maize. J Agric Sci 154:647–661
Badu-Apraku B, Lum AF (2007) Agronomic performance of Striga resistant early-maturing maize varieties and inbred lines in the savannas of West and Central Africa. Crop Sci 47:737–748
Badu-Apraku B, Adewale S, Paterne A, Gedil M, Asiedu R (2020a) Identification of QTLs controlling resistance/tolerance to Striga hermonthica in an extra-early maturing yellow maize population. Agronomy 10:1168
Badu-Apraku B, Adewale S, Paterne AA, Gedil M, Toyinbo J, Asiedu R (2020b) Identification of QTLs for grain yield and other traits in tropical maize under Striga infestation. PLoS ONE 15(9):e0239205. https://doi.org/10.1371/journal.pone.0239205
Bebawi FF, Mutwali EM (1991) Witchweed management by sorghum-sudangrass seed size and stage of harvest. Agron J 83:781–786
Berner DK, Kling JG, Singh BB (1995) Striga research and control. A perspective from Africa. Plant Dis 79:652–660
Beyene Y, Gowda M, Olsen MS et al (2019) Empirical comparison of tropical maize hybrids selected through genomic and phenotypic selections. Front Plant Sci 10:1502
Beyene Y, Semagn K, Mugo S et al (2015) Genetic gains in grain yield through genomic selection in eight bi-parental maize populations under drought stress. Crop Sci 55:154–163
Bradbury P, Zhang Z, Kroon E, D, et al (2007) TASSEL: software for association mapping of complex traits in diverse samples. Bioinformatics 23:2633–2635. https://doi.org/10.1093/bioinformatics/btm308
Burgueño J, Campos G, Weigel K, Crossa J (2012) Genomic prediction of breeding values when modeling genotype × environment interaction using pedigree and dense molecular markers. Crop Sci 52:707. https://doi.org/10.2135/cropsci2011.06.0299
Chadha S, Mehetre ST, Bansal R et al (2018) Genome-wide analysis of cytochrome P450s of Trichoderma spp.: annotation and evolutionary relationships. Fungal Biol Biotechnol 5:12. https://doi.org/10.1186/s40694-018-0056-3
Chen Y-F, Shakeel S, Bowers J et al (2007) Ligand-induced degradation of the ethylene receptor ETR2 through a proteasome-dependent pathway in arabidopsis. J Biol Chem 282:24752–24758. https://doi.org/10.1074/jbc.M704419200
Choi C-H (2005) ABC transporters as multidrug resistance mechanisms and the development of chemosensitizers for their reversal. Cancer Cell Int 5:30. https://doi.org/10.1186/1475-2867-5-30
Combs E, Bernardo R (2013) Accuracy of genomewide selection for different traits with constant population size, heritability, and number of markers. Plant Genome 6(1). https://doi.org/10.3835/plantgenome2012.11.0030
Crossa J, Pérez-Rodríguez P, Cuevas J et al (2017) Genomic selection in plant breeding: methods, models, and perspectives. Trends Plant Sci 22:961–975. https://doi.org/10.1016/j.tplants.2017.08.011
Cui C, Mei H, Liu Y et al (2017) genetic diversity, population structure, and linkage disequilibrium of an association-mapping panel revealed by genome-wide snp markers in sesame. Front Plant Sci 8:1–10. https://doi.org/10.3389/fpls.2017.01189
Cui Z, Luo J, Qi C et al (2016) Genome-wide association study (GWAS) reveals the genetic architecture of four husk traits in maize. BMC Gen 17:946. https://doi.org/10.1186/s12864-016-3229-6
De Groote H, Wangare L, Kanampiu F et al (2008) The potential of a herbicide resistant maize technology for Striga control in Africa. Agric Syst 97:83–94
Ding J, Ali F, Chen G et al (2015) Genome-wide association mapping reveals novel sources of resistance to northern corn leaf blight in maize. BMC Plant Biol 15:206
Dufayard J-F, Bettembourg M, Fischer I et al (2017) New insights on leucine-rich repeats receptor-like kinase orthologous relationships in angiosperms. Front Plant Sci 8:381. https://doi.org/10.3389/fpls.2017.00381
Elshire RJ, Glaubitz JC, Sun Q et al (2011) A robust, simple genotyping-by-sequencing (GBS) approach for high diversity species. PLoS ONE 6:1–10. https://doi.org/10.1371/journal.pone.0019379
Ertiro BT, Labuschagne M, Olsen M, Das B, Prasanna BM, Gowda M (2020) Genetic dissection of nitrogen use efficiency in tropical maize through genome-wide association and genomic prediction. Front Plant Sci 11:474. https://doi.org/10.3389/fpls.2020.00474
Flint-Garcia SA, Thuillet A, Yu J et al (2005) Maize association population: a high-resolution platform for quantitative trait locus dissection. Plant J 44:1054–1064
Fujiki Y, Yoshimoto K, Ohsumi Y (2007) An arabidopsis homolog of yeast ATG6/VPS30 is essential for pollen germination. Plant Physiol 143:1132–1139. https://doi.org/10.1104/pp.106.093864
Funke S, Knechten T, Ollesch J, Schünemann D (2005) A unique sequence motif in the 54-kDa subunit of the chloroplast signal recognition particle mediates binding to the 43-kDa subunit. J Biol Chem 280:8912–8917. https://doi.org/10.1074/jbc.M409992200
Gilmour AR, Gogel BJ, Cullis BR, Thompson R (2009) ASReml user guide release 3.0. VSN. International Ltd, Hemel Hemp-stead
Glaubitz JC, Casstevens TM, Lu F et al (2014) TASSEL-GBS: a high capacity genotyping by sequencing analysis pipeline. PLoS ONE 9:e90346
Gowda M, Das B, Makumbi D et al (2015) Genome-wide association and genomic prediction of resistance to maize lethal necrosis disease in tropical maize germplasm. Theor Appl Genet. https://doi.org/10.1007/s00122-015-2559-0
Guo Z, Tucker D, Wang D et al (2013) Accuracy of across-environment genome-wide prediction in maize nested association mapping populations. G3 (Bethesda) 3:263–272. https://doi.org/10.1534/g3.112.005066
Gurney AL, Press MC, Ransom JK (1995) The parasitic angiosperm Striga hermonthica can reduce photosynthesis of its sorghum and maize hosts in the field. J Exp Bot 46:1817–1823
Gurney AL, Press MC, Scholes JD (1999) Infection time and density influence the response of sorghum to the parasitic angiosperm Striga hermonthica. New Phytol 143:573–580
Gustafson TJ, de Leon N, Kaeppler SM, Tracy WF (2018) Genetic analysis of sugarcane mosaic virus resistance in the wisconsin diversity panel of maize. Crop Sci 58:1853–1865. https://doi.org/10.2135/cropsci2017.11.0675
Habier D, Fernando RL, Garrick DJ (2013) Genomic BLUP decoded: a look into the black box of genomic prediction. Genetics 194:597–607
Hallauer AR, Miranda JB (1981) Hereditary variance: mating designs. In: Quantitative genetics in maize breeding. IA State University Press, Ames
Haussmann BIG, Hess DE, Welz H-G, Geiger HH (2000) Improved methodologies for breeding Striga-resistant sorghums. F Crop Res 66:195–211
Jaiswal V, Gupta S, Gahlaut V et al (2019) Genome-wide association study of major agronomic traits in foxtail millet (Setaria italica L.) using ddRAD sequencing. Sci Rep. https://doi.org/10.1038/s41598-019-41602-6
Jarquín D, Crossa J, Lacaze X et al (2014) A reaction norm model for genomic selection using high-dimensional genomic and environmental data. Theor Appl Genet 127:595–607. https://doi.org/10.1007/s00122-013-2243-1
Juliana P, Montesinos-López OA, Crossa J et al (2019) Integrating genomic-enabled prediction and high-throughput phenotyping in breeding for climate-resilient bread wheat. Theor Appl Genet 132:177–194
Juliana P, Singh RP, Poland J et al (2018) Prospects and challenges of applied genomic selection—a new paradigm in breeding for grain yield in bread wheat. Plant Gen 11:1–17
Juliana P, Singh RP, Singh PK et al (2017) Genomic and pedigree-based prediction for leaf, stem, and stripe rust resistance in wheat. Theor Appl Genet 130:1415–1430
Kaler A, Gillman J, Beissinger T, Purcell L (2020) Comparing different statistical models and multiple testing corrections for association mapping in soybean and maize. Front Plant Sci 10:1794. https://doi.org/10.3389/fpls.2019.01794
Kanampiu F, Makumbi D, Mageto E et al (2018) Assessment of management options on striga infestation and maize grain yield in Kenya. Weed Sci 66:516–524
Kanampiu FK, Ransom JK, Gressel J (2001) Imazapyr seed dressings for Striga control on acetolactate synthase target-site resistant maize. Crop Prot 20:885–895
Kim S (1994) Genetics of maize tolerance of Striga hermonthica. Crop Sci 34:900–907
Kim SK (1991) Breeding maize for Striga tolerance and the development of a field infestation technique. In combating Striga in Africa, proceedings of the workshop by IITA, ICRISAT and IDRC, 22–24 August 1988; IITA: Ibadan, Nigeria, 1991; pp. 96–108
Kim SK, Adetimirin VO, The C, Dossou R (2002) Yield losses in maize due to Striga hermonthica in West and Central Africa. Int J Pest Manag 48:211–217
Kim SK, Fajemisin JM, Thé C et al (1998) Development of synthetic maize populations for resistance to Striga hermonthica. Plant Breed 117:203–209
Kuki MC, Scapim CA, Rossi ES et al (2018) Genome wide association study for gray leaf spot resistance in tropical maize core. PLoS ONE 13:e0199539
Kump KL, Bradbury PJ, Wisser RJ et al (2011) Genome-wide association study of quantitative resistance to southern leaf blight in the maize nested association mapping population. Nat Genet 43:163
Loiselle B, Sork V, Nason J, Graham C (1995) Spatial genetic structure of a tropical understory shrub. Am J Bot 82:1420–1425
Makumbi D, Diallo A, Kanampiu F et al (2015) Agronomic performance and genotype × environment interaction of herbicide-resistant maize varieties in eastern Africa. Crop Sci 55:540. https://doi.org/10.2135/cropsci2014.08.0593
Mammadov J, Sun X, Gao Y et al (2015) Combining powers of linkage and association mapping for precise dissection of QTL controlling resistance to gray leaf spot disease in maize (Zea mays L.). BMC Gen 16:916
Menkir A, Crossa J, Meseka S et al (2020) Staking tolerance to drought and resistance to a parasitic weed in tropical hybrid maize for enhancing resilience to stress combinations. Front Plant Sci 11:166
Menkir A, Kling JG, Badu-Apraku B, Ingelbrecht I (2005) Molecular marker-based genetic diversity assessment of Striga-resistant maize inbred lines. Theor Appl Genet 110:1145–1153
Menkir A, Makumbi D, Franco J (2012) Assessment of reaction patterns of hybrids to Striga hermonthica (Del.) Benth. under artificial infestation in Kenya and Nigeria. Crop Sci 52:2528–2537
Menkir A, Meseka S (2019) Genetic improvement in resistance to Striga in tropical maize hybrids. Crop Sci 59:2484–2497
Montesinos-López OA, Luna-Vázquez FJ, Montesinos-López A et al (2018a) An R package for multitrait and multienvironment data with the Item-based collaborative filtering algorithm. Plant Gen 11:1–16
Montesinos-López OA, Montesinos-López A, Crossa J et al (2016) A genomic Bayesian multi-trait and multi-environment model. G3 Genes. Gen, Genet 6:2725–2744
Montesinos-López OA, Montesinos-López A, Crossa J et al (2018b) Prediction of multiple-trait and multiple-environment genomic data using recommender systems. G3 Genes. Gen, Genet 8:131–147
Niu X, Guan Y, Chen S, Li H (2017) Genome-wide analysis of basic helix-loop-helix (bHLH) transcription factors in Brachypodium distachyon. BMC Gen 18:619. https://doi.org/10.1186/s12864-017-4044-4
Nyaga C, Gowda M, Beyene Y et al (2019) Genome-wide analyses and prediction of resistance to mln in large tropical maize germplasm. Genes (Basel) 11:16. https://doi.org/10.3390/genes11010016
Odhiambo G, Ransom JK (1995) Long term strategies for Striga control. In: Maize research for stress environments: proceedings of the fourth eastern and southern africa regional maize conference, Harare, Zimbabwe. pp 263–266
Pérez P, de Los CG (2014) Genome-wide regression and prediction with the BGLR statistical package. Genetics 198:483–495
Ransom JK (2000) Long-term approaches for the control of Striga in cereals: field management options. Crop Prot 19:759–763
Ransom JK, Eplee RE, Langston MA (1990) Genetic variability for resistance to Striga asiatica in maize. Cereal Res Commun 18:329–333
Roorkiwal M, Jarquin D, Singh MK et al (2018) Genomic-enabled prediction models using multi-environment trials to estimate the effect of genotype × environment interaction on prediction accuracy in chickpea. Sci Rep. https://doi.org/10.1038/s41598-018-30027-2
Sarwar B, Karypis G, Konstan J, Riedl J (2001) Item-based collaborative filtering recommendation algorithms. In: proceedings of the 10th international conference on world wide web. pp 285–295
Shaner G, Finney RE (1977) The effect of nitrogen fertilization on the expression of slow-mildewing resistance in Knox wheat. Phytopathology 67:1051–1056
Shi L, Lv X, Weng J et al (2014) Genetic characterization and linkage disequilibrium mapping of resistance to gray leaf spot in maize (Zea mays L.). Crop J 2:132–143. https://doi.org/10.1016/j.cj.2014.02.001
Sitonik C, Suresh LM, Beyene Y et al (2019) Genetic architecture of maize chlorotic mottle virus and maize lethal necrosis through GWAS, linkage analysis and genomic prediction in tropical maize germplasm. Theor Appl Genet. https://doi.org/10.1007/s00122-019-03360-x
Spallek T, Mutuku M, Shirasu K (2013) The genus S triga: a witch profile. Mol Plant Pathol 14:861–869
Tao Y, Jiang L, Liu Q et al (2013) Combined linkage and association mapping reveals candidates for Scmv1, a major locus involved in resistance to sugarcane mosaic virus (SCMV) in maize. BMC Plant Biol 13:162. https://doi.org/10.1186/1471-2229-13-162
VanRaden PM (2008) Efficient methods to compute genomic predictions. J Dairy Sci 91:4414–4423
Wen W, Araus JL, Shah T et al (2011) Molecular characterization of a diverse maize inbred line collection and its potential utilization for stress tolerance improvement. Crop Sci 51:2569–2581. https://doi.org/10.2135/cropsci2010.08.0465
Yang Q, Balint-Kurti P, Xu M (2017) Quantitative disease resistance: dissection and adoption in maize. Mol Plant. https://doi.org/10.1016/j.molp.2017.02.004
Yoder JI, Scholes JD (2010) Host plant resistance to parasitic weeds; recent progress and bottlenecks. Curr Opin Plant Biol 13:478–484
Yu J, Buckler ES (2006) Genetic association mapping and genome organization of maize. Curr Opin Biotechnol 17:155–160
Yuan Y, Cairns J, Babu R et al (2019) Genome-wide association mapping and genomic prediction analyses reveal the genetic architecture of grain yield and flowering time under drought and heat stress conditions in maize. Front Plant Sci. https://doi.org/10.3389/fpls.2018.01919
Zhou H, Zhao J, Cai J, Patil SB (2017) UBIQUITIN-specific proteases function in plant development and stress responses. Plant Mol Biol 94:565–576. https://doi.org/10.1007/s11103-017-0633-5
Zila CT, Samayoa LF, Santiago R et al (2013) A genome-wide association study reveals genes associated with Fusarium ear rot resistance in a maize core diversity panel. G3 Genes, Gen, Genet 3:2095–2104
Acknowledgements
Our sincere thanks to CIMMYT technicians Carolyne Odhiambo and Veronica Ogugo in Kenya; and we also thank Dr. Edward S Buckler and the Institute of Genomic Diversity, Cornell University for the high-density genotyping (GBS) and imputation service.
Funding
The research was supported by the Bill and Melinda Gates Foundation (B&MGF), and the United States Agency for International Development (USAID) through Stress Tolerant Maize for Africa (STMA, B&MGF Grant # OPP1134248) Project, AG2MW project (Accelerating Genetic Gains in Maize and Wheat for Improved Livelihoods, B&MGF Investment ID INV-003439), IMAS Project, and the CGIAR Research Program MAIZE. MAIZE receives W1&W2 support from the Governments of Australia, Belgium, Canada, China, France, India, Japan, Korea, Mexico, Netherlands, New Zealand, Norway, Sweden, Switzerland, the UK, the USA and the World Bank.
Author information
Authors and Affiliations
Contributions
BD, DM, TK, BMP and MG conceived the experiment; BD, MG, TK and DM conducted the field evaluations and phenotyping; MG, JC and OAML coordinated the GBS experiments; MG carried out the GWAS analyses; JC, MG, OAML undertook GP and IBCF analyses; MG, BD, DM, YB, MO, BMP, OAML, CN and JC interpreted the results and drafted the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Additional information
Communicated by Antonio Augusto Franco Garcia.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gowda, M., Makumbi, D., Das, B. et al. Genetic dissection of Striga hermonthica (Del.) Benth. resistance via genome-wide association and genomic prediction in tropical maize germplasm. Theor Appl Genet 134, 941–958 (2021). https://doi.org/10.1007/s00122-020-03744-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00122-020-03744-4