Dynamical analysis of an age-space structured malaria epidemic model

Abstract

In this paper, we will revisit the model studied in Lou and Zhao (J Math Biol 62:543–568, 2011), where the model takes the form of a nonlocal and time-delayed reaction–diffusion model arising from the fixed incubation period. We consider the infection age to be a continuous variable but without the limitation of the fixed incubation period, leading to an age-space structured malaria model in a bounded domain. By performing the elementary analysis, we investigate the well-posedness of the model by proving the global existence of the solution, define the explicit formula of basic reproduction number when all parameters remain constant. By analyzing the characteristic equations and designing suitable Lyapunov functions, we also establish the threshold dynamics of the constant disease-free and positive equilibria. Our theoretical results are also validated by numerical simulations for 1-dimensional and 2-dimensional domains.

1 Introduction

Human malaria, caused by the genus Plasmodium, belongs to a mosquito-borne disease. The main intermediary vector is female anopheles mosquitoes. Rapid spread and global distribution (especially in Africa, Asia and South America) of human malaria causes public health problems and kills over a million people a year [20]. Since the classical work of [19], a lot of mathematical models based on vector-borne diseases framework (see, e.g., [3, 7, 9, 13,14,15,16,17, 27, 30, 31]) have been devoted to investigating the temporal and spatial patterns of disease burden and control strategies, which provides useful insights into the malaria transmission dynamics. In recent years, more and more biologically factors affecting vector-borne diseases are incorporated into mathematical models, such as immunity and clinical death [1, 21], spatial heterogeneity [3, 14, 15, 27, 31], the mobility of human and mosquito populations, extrinsic incubation period (EIP), vector-bias mechanism and seasonality (see, e.g., [3, 9, 14, 15, 27, 30, 31]). Here, EIP is a time interval during which mosquitoes could not transmit the malaria parasite to humans, which varies from 10 to 14 days [12] and significantly affect the number of infected mosquitoes. Spatial heterogeneity reflects the distinct contact patterns in distinct geographic regions, demonstrating the diversity in habitats. It is widely accepted and well known that the environmental conditions vary spatially, affecting the biting patterns, so setting the disease transmission parameters depending the location variable is biologically reasonable. The reaction–diffusion model is one of the most common tool in describing the spatial evolution of an epidemic, generalizing the classical models [16, 17, 19].

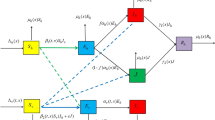
Let $\Omega \subset \mathbb {R}^n\ (n\ge 1)$ be a bounded domain equipped with a smooth boundary $\partial \Omega$. For $x\in \Omega$, we introduce the Laplacian operator $\Delta =\partial ^2/\partial x^2$ to represent the random mobility of human and mosquito populations in the domain. At time t and location x, we denote by $S_m:=S_m(t,x)$, $I_m:=I_m(t,x)$ and $I_h:=I_h(t,x)$ the density of susceptible mosquitoes, infected mosquitoes and infected humans, whose diffusion rates are given by $D_m$, $D_m$ and $D_h$, respectively. The model studied in [14] takes the following form,

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\partial S_m}{\partial t} -D_m\Delta S_m=\mu (x)-\frac{b\beta (x)}{H(x)}S_mI_h-d_mS_m, \\ \displaystyle \frac{\partial I_m}{\partial t} - D_m\Delta I_m=-d_m I_m+e^{-d_m\tau }\int \limits _{\Omega }\Gamma (D_m\tau , x, y)\frac{b\beta (y)}{H(y)}S_m(t-\tau ,y)I_h(t-\tau ,y)\textrm{d}y,\\ \displaystyle \frac{\partial I_h}{\partial t} - D_h\Delta I_h =\frac{c\beta (x)}{H(x)}(H(x)-I_h)I_m-(d_h+\rho ) I_h, \end{array}\right. \end{aligned}$$

(1.1)

for $x\in \Omega , t>0$ and

$$\begin{aligned} \frac{\partial S_m}{\partial n}=\frac{\partial I_m}{\partial n}=\frac{\partial I_h}{\partial n}=0,\ x\in \partial \Omega , t>0. \end{aligned}$$

(1.2)

Here, the density of total human population is assumed to be remained at H(x), $H(x) \in C^2(\Omega , (0, \infty )) \cap C^1(\overline{\Omega },(0,\infty ))$ and H(x) satisfies

$$\begin{aligned} -D_h \Delta H(x) = d_h H(x)\left( 1-\frac{H(x)}{K(x)}\right) , \ x \in \Omega ; \quad \frac{\partial H(x)}{\partial n} = 0, \ x \in \partial \Omega , \end{aligned}$$

(1.3)

where $K(x) \in C(\overline{\Omega }, (0,\infty ))$ is the carrying capacity dependent of location x and $d_h$ the birth rate of humans, so the density of susceptible humans is given by $H(x)-I_h$; The force of infection for human and mosquito populations is, respectively, characterized by $\frac{b\beta (x)}{H(x)}S_mI_h$ and $\frac{c\beta (x)}{H(x)}(H(x)-I_h)I_m$; $\mu (x)$ and $\beta (x)$, respectively, depict the space-dependent recruitment rate of adult female mosquitoes emerged from larval and biting rate; $d_m$ and $d_h$, respectively, stand for the natural death rate of mosquito and human populations; b and c describe the transmission probabilities per bite from infected humans to susceptible female mosquitoes and from infected female mosquitoes to susceptible humans; $\rho$ is the recovery rate of humans; $\Gamma (D_m\tau , x, y)$ is the Green function with respect to Laplace operator $D_m\Delta$ subject to (1.2); $\tau$ is a positive constant representing the fixed incubation period; $\frac{\partial }{\partial n}$ denotes the differentiation along the outward normal n to $\partial \Omega$. The basic assumptions on the parameters are as follows: $D_m, D_h, d_m, \rho , b, c \in (0,\infty )$; $\beta , \mu \in C(\overline{\Omega }, [0, \infty ) )$; $\beta _1 \in L^\infty (\mathbb {R}_+, [0, \infty ))$.

The main feature of (1.1) is the nonlocal and time-delayed term appeared in $I_m$ equation, which is obtained by the assumption that the incubation period is fixed at $\tau >0$ and the standard method on characterizing age structured population with spatial diffusion [10]. Let $i_m:=i_m(t,a,x)$ the density of the mosquitoes with infection age a at time t and location x, and $i_m(t,0,x)=\frac{b\beta (x)}{H(x)}S_mI_h$ be the newly infected mosquitoes, which comes from the contact of susceptible mosquitoes and infectious humans. Then, $i_m(t,a,x)$ fulfills

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \left( \frac{\partial }{\partial t} +\frac{\partial }{\partial a} - D_m\Delta \right) i_m=-d_m i_m,&{} x\in \Omega ,\ t>0, a\ge 0, \\ \displaystyle \frac{\partial i_m}{\partial n}=0,\ {} &{} x\in \partial \Omega ,\ a\ge 0, \end{array}\right. \end{aligned}$$

(1.4)

By the integration along characteristics, the nonlocal and time-delayed term in (1.1) is given by $i_m(t,\tau ,x)$.

Unlike in [14] where spatial movements in EIP will cause nonlocal infection, here we plan to ignore the fixed incubation period and view the infection age as a continuous variable. In this paper, adopting the same notations used in [14], we directly investigate the following malaria model with age and space structure:

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\partial S_m}{\partial t} -D_m\Delta S_m=\mu (x)-\frac{b\beta (x)}{H(x)}S_mI_h-d_mS_m,&{}{}x\in \Omega , \ t>0, \\ \displaystyle \left( \frac{\partial }{\partial t}+ \frac{\partial }{\partial a} - D_m\Delta \right) i_m =-d_m i_m,&{}{}x\in \Omega , \ t>0, \ a>0, \\ \displaystyle \frac{\partial I_h}{\partial t} - D_h\Delta I_h =\frac{c\beta (x)(H(x)-I_h)}{H(x)}\int \limits _0^\infty \beta _1(a)i_m\textrm{d}a-(d_h+\rho )I_h,&{}{}x\in \Omega ,\ t>0, \\ \displaystyle i_m(t,0,x)=\frac{b\beta (x)}{H(x)}S_mI_h,&{}{}x\in \overline{\Omega }, \ t>0, \end{array}\right. \end{aligned} \end{aligned}$$

(1.5)

where the initial condition for (1.5) is given by, for all $x \in \overline{\Omega }$ and $a \ge 0$,

$$\begin{aligned} S_m(0,x) = \phi _1(x), \quad i_m(0,a,x) = \phi _2(a,x), \quad I_h(0,x) = \phi _3(x), \end{aligned}$$

(1.6)

where $\phi _1,\phi _3 \in C_+(\Omega )$ and $\phi _2 \in L^1_+(\mathbb {R}_+, C(\Omega ))$. The boundary condition for (1.5) is the homogeneous Neumann condition, that is, for all $x \in \partial \Omega$, $t>0$ and $a>0$,

$$\begin{aligned} \frac{\partial S_m}{\partial n}=\frac{\partial i_m}{\partial n}=\frac{\partial I_h}{\partial n}=0. \end{aligned}$$

(1.7)

We also note that some studies on spatial Zika models [9, 15, 27] could be viewed as an extension of the classical models in [16, 17, 19]. Specifically, in a recent paper [33], the authors implemented the global attractivity of a positive constant equilibrium of model (1.1) in a homogeneous case by designing a suitable Lyapunov functional, where the same problem was partially solved in [14], but requiring a sufficient condition through the fluctuation method. Very recently, Wang and Wang in [28] attempted to solve the global threshold dynamics of the problem (1.5)–(1.7) with mass-action mechanism and a stabilized density of susceptible humans H(x), which is not altered by the epidemics as in [15].

Our main goal of this paper is to provide a rigorous analysis of (1.5), where (1.5) can be viewed as the one for the generalization version of model (1.1). Here, we use an age structured population with spatial diffusion reflecting the diffusion of the latent individuals. Following the main idea in [3, 14] but using different analysis method, we address in Sect. 3, the basic questions on the existence, uniqueness and positivity of solutions to problem (1.5)–(1.7). We first treat the local existence of solution on $[0,T] \times \overline{\Omega }$ for small $T>0$, where the method is different to that of [5, 6, 28, 29, 32]. The main reason is that we cannot construct a fixed point problem with one equation. To overcome this issue, we construct a fixed point problem with vector-valued functions. We also confirm that the solution never blows up in finite time and globally exists in a positive invariant set $\mathcal {D}$ for all $t > 0$. In Sect. 4, we derive the next-generation operator aiming to define the basic reproduction number $\Re _0$ through renewal equations. In general, $\Re _0$ cannot be directly calculated. However, in a spatially homogeneous case, the next-generation operator is compact. Thus, the Krein–Rutman theorem can be directly applied to get the explicit formula of $\Re _0$. Section 4 is devoted to investigating the local and global dynamics of the disease-free and positive steady states in a spatially homogeneous case. It should be highlighted here that it is not easy work to design suitable Lyapunov functions. The main results obtained in Sect. 4 are validated by numerical simulations in Sect. 5 for 1-dimensional and 2-dimensional domain.

2 Preliminaries

Throughout of the paper, for ease of notations, we set

$$\begin{aligned} \overline{\beta }_1:= \mathop {\mathrm {ess.sup}}_{a \ge 0} \beta _1(a), \quad f^*:= \sup _{x\in \Omega } f(x), \quad f_*:= \inf _{x \in \Omega } f(x), \end{aligned}$$

where $f \in \{ \mu , \beta , H, \Lambda \}$.

Let $\mathbb {Y}:= C(\overline{\Omega },\mathbb {R})$ and $\mathbb {X}:=L^1(\mathbb {R}_+,\mathbb {Y})$ equipped with norms

$$\begin{aligned} \Vert \varphi \Vert _\mathbb {Y}:= \sup _{x\in \Omega } | \varphi (x)|, \varphi \in \mathbb {Y}\ \text{ and }\ \Vert \varphi \Vert _\mathbb {X}:= \int \limits _0^\infty \Vert \varphi (a) \Vert _{\mathbb {Y}} \textrm{d}a,\ \varphi \in \mathbb {X},\end{aligned}$$

, respectively. Denote the positive cones of $\mathbb {X}$ and $\mathbb {Y}$ by $\mathbb {X}_+$ and $\mathbb {Y}_+$, respectively. It is a classical fact that the diffusion operators $D_m \Delta$ and $D_h\Delta$ with (1.7) generate the strongly continuous semigroups $\{ T_i(t)\}_{t\ge 0}:\mathbb {Y}_+ \rightarrow \mathbb {Y}_+$ ($i=1,2$) defined by, for $t > 0$,

$$\begin{aligned} (T_i(t)\varphi )(x) =\int \limits _{\Omega }\Gamma _i(t, x, y)\varphi (y)\textrm{d}y, \text{ and }\ T_i(0)\varphi = \varphi ,\ \varphi \in \mathbb {Y}_+, \end{aligned}$$

where $\Gamma _i(t, x, y)$ ($i=1,2$) denote the associated Green functions. Note that, for any $\varphi \in \mathbb {Y}_+$, $i=1,2$ and $t>0$,

$$\begin{aligned} \begin{aligned} \Vert T_i(t)\varphi \Vert _{\mathbb {Y}} \le \int \limits _\Omega \Gamma _i(t,x,y) \textrm{d}y \Vert \varphi \Vert _{\mathbb {Y}} = \Vert \varphi \Vert _{\mathbb {Y}}, \end{aligned} \end{aligned}$$

(2.1)

because $\int \limits _\Omega \Gamma _i(t,x,y)\textrm{d}y = 1$.

Let $\mathbb {\overline{X}}=\mathbb {Y}\times \mathbb {X}\times \mathbb {Y}$ and $\mathbb {\overline{X}}_+=\mathbb {Y}_+\times \mathbb {X}_+\times \mathbb {Y}_+$, equipped with norm

$$\begin{aligned} \Vert (\varphi _1,\varphi _2,\varphi _3) \Vert _{\mathbb {\overline{X}}}:= \Vert \varphi _1 \Vert _{\overline{\mathbb {Y}}} + \Vert \varphi _2 \Vert _{\overline{\mathbb {X}}} + \Vert \varphi _3 \Vert _{\overline{\mathbb {Y}}}, \quad (\varphi _1,\varphi _2,\varphi _3) \in \overline{\mathbb {X}}. \end{aligned}$$

The state space for our system is as follows:

$$\begin{aligned} \mathcal {D}:= \left\{ (\varphi _1, \varphi _2, \varphi _3) \in \overline{\mathbb {X}}_+: 0 \le \varphi _1(x) + \int \limits _0^\infty \varphi _2(a,x) \textrm{d}a \le \frac{\mu ^*}{d_m}, \ 0\le \varphi _3(x) \le H(x), \ x \in \overline{\Omega } \right\} . \end{aligned}$$

Our main result of this section reads as follows.

Theorem 2.1

There exists a solution semiflow $\{ \Phi (t) \}_{t\ge 0}: \overline{\mathbb {X}}_+ \rightarrow \overline{\mathbb {X}}_+$ such that, for any $\phi :=(\phi _1, \phi _2, \phi _3) \in \mathcal {D}$, $\Phi (0)\phi = \phi$ and

$$\begin{aligned} \Phi (t)\phi := (S_m(t, \cdot ), i_m(t, a, \cdot ), I_h(t, \cdot )) \in \mathcal {D}, \quad t > 0, \end{aligned}$$

gives a unique global solution to problem (1.5)–(1.7).

Before proving Theorem 2.1, we first introduce a lemma. For convenience, let us denote the newly infected mosquitoes by

$$\begin{aligned} \mathcal {B}(S_m,I_h)(t,x):=i_m(t,0,x)=\frac{b\beta (x)}{H(x)}S_mI_h, \quad t > 0, \ x \in \Omega . \end{aligned}$$

(2.2)

By appealing to the method of characteristics, one can easily get that, for all $x \in \Omega$,

$$\begin{aligned} i_m(t,a,x)= \left\{ \begin{array}{ll} \displaystyle (T_1(a) (\mathcal {B}(S_m,I_h)(t-a,\cdot ))) \Pi (a), &{}\ t>a, \\ \displaystyle (T_1(t) \phi _2(a-t,\cdot )) \Pi (t),&{}\ a\ge t, \end{array}\right. \end{aligned}$$

(2.3)

where $\Pi (a):=e^{-d_m a}$. Hence, we directly have

$$\begin{aligned} \begin{aligned} \int \limits _0^\infty \beta _1(a) i_m(t,a,x) \textrm{d}a =&\int \limits _0^t \beta _1(a) (T_1(a) (\mathcal {B}(S_m,I_h)(t-a,\cdot ))) \Pi (a) \textrm{d}a \\ {}&+ \int \limits _t^\infty \beta _1(a) (T_1(t) \phi _2(a-t,\cdot )) \Pi (t) \textrm{d}a. \end{aligned} \end{aligned}$$

We now show the local existence of the solution.

Lemma 2.2

For each $\phi \in \mathbb {\overline{X}}$, there exists a $T>0$ such that problem (1.5)–(1.7) has a unique solution for all $t \in (0,T)$.

Proof

Solving the equations of $S_m$ and $I_h$ in (1.5), we directly obtain: for $t>0$,

$$\begin{aligned}&S_m(t,\cdot ) = \mathbb {F}_1(t,\cdot ) + \int \limits _0^t e^{-d_m (t-s)} T_1(t-s)[\mu (\cdot )-\mathcal {B}(S_m,I_h)(s,\cdot )]\textrm{d}s =: \mathcal {F}_1(S_m,I_h)(t,\cdot ), \end{aligned}$$

(2.4)

$$\begin{aligned}&I_h(t,\cdot ) = \mathbb {F}_2(t,\cdot ) + \mathbb {F}_3(t,\cdot )+ \int \limits _0^t e^{-(d_h+\rho )(t-s)} T_2(t-s) [\mathcal {C}(S_m,I_h)(s,\cdot )] \textrm{d}s =: \mathcal {F}_2(S_m,I_h)(t,\cdot ), \end{aligned}$$

(2.5)

where

$$\begin{aligned} \begin{aligned}&\mathbb {F}_1(t,\cdot ) := e^{-d_m t} T_1(t) \phi _1, \quad \mathbb {F}_2(t,\cdot ) := e^{-(d_h+\rho ) t} T_2(t) \phi _3, \\ {}&\mathbb {F}_3(t,\cdot ) := \int \limits _0^t e^{-(d_h+\rho )(t-s)} T_2(t-s) \left[ c \beta (\cdot ) \int \limits _s^\infty \beta _1(a) T_1(s)\phi _2(a-s,\cdot ) \Pi (s) \textrm{d}a \right] \textrm{d}s, \end{aligned} \end{aligned}$$

(2.6)

and

$$\begin{aligned} \begin{aligned} \mathcal {C}(S_m,I_h)(s,\cdot ) :=&c\beta (\cdot ) \int \limits _0^s \beta _1(a) T_1(a)[\mathcal {B}(S_m,I_h)(s-a,\cdot )] \Pi (a)\text {d}a \\ {}&-\frac{c\beta (\cdot ) I_h(s,\cdot )}{H(\cdot )} \int \limits _0^s \beta _1(a) T_1(a) [\mathcal {B}(S_m,I_h)(s-a,\cdot )] \Pi (a)\text {d}a \\ {}&-\frac{c\beta (\cdot ) I_h(s,\cdot )}{H(\cdot )} \int \limits _s^\infty \beta _1(a) T_1(s)[\phi _2(a-s,\cdot )] \Pi (s) \textrm{d}a. \end{aligned} \end{aligned}$$

For $T>0$, we set

$$\begin{aligned}&\mathbb {Y}_T :=C([0,T], \mathbb {Y})\ \text{ with }\ \Vert \psi \Vert _{\mathbb {Y}_T} := \sup \limits _{0\le t\le T}\Vert \psi (t,\cdot )\Vert _\mathbb {Y},\ \psi \in \mathbb {Y}_T, \\&\mathbb {W}_T := \mathbb {Y}_T \times \mathbb {Y}_T \ \text{ with } \ \Vert (\psi _1,\psi _2)\Vert _{\mathbb {W}_T} := \Vert \psi _1 \Vert _{\mathbb {Y}_T} + \Vert \psi _2 \Vert _{\mathbb {Y}_T}, \ (\psi _1,\psi _2) \in \mathbb {W}_T. \end{aligned}$$

Let $\mathcal {F}$ be a nonlinear operator defined on $\mathbb {W}_T$ to itself,

$$\begin{aligned} \mathcal {F} \left( \begin{array}{c} \psi _1 \\ \psi _2 \end{array} \right) := \left( \begin{array}{c} \mathcal {F}_1(\psi _1,\psi _2) \\ \mathcal {F}_2(\psi _1, \psi _2) \end{array} \right) , \quad \psi _1,\psi _2 \in \mathbb {W}_T. \end{aligned}$$

Next, we show that $\mathcal {F}$ has a fixed point on $\mathbb {W}_T$, i.e., (1.5)–(1.7) has a unique solution on $[0,T] \times \overline{\Omega }$. For any $(S_m',I_h'), (S_m'',I_h'') \in \mathbb {W}_T$, we have

$$\begin{aligned} \Vert \mathcal {B}(S_m', I_h') - \mathcal {B}(S_m'',I_h'') \Vert _{\mathbb {Y}_T} \le&\frac{b \beta ^*}{H_*} \Vert S_m' I_h' - S_m'' I_h'' \Vert _{\mathbb {Y}_T} \\ \le&\frac{b \beta ^*}{H_*} \left( \Vert I_h' \Vert _{\mathbb {Y}_T} \Vert S_m'-S_m'' \Vert _{\mathbb {Y}_T} + \Vert S_m'' \Vert _{\mathbb {Y}_T} \Vert I_h'-I_h'' \Vert _{\mathbb {Y}_T} \right) . \end{aligned}$$

Hence, by virtue of (2.1), we obtain

$$\begin{aligned} \begin{aligned} \Vert \mathcal {F}_1(S_m', I_h') - \mathcal {F}_1(S_m'',I_h'') \Vert _{\mathbb {Y}_T} \le&\int \limits _0^t e^{-d_m(t-s)} \textrm{d}s \Vert \mathcal {B}(S_m', I_h') - \mathcal {B}(S_m'',I_h'') \Vert _{\mathbb {Y}_T} \\ \le&\frac{b \beta ^* (1-e^{-d_m t})}{d_m H_*} \left( \Vert I_h' \Vert _{\mathbb {Y}_T} \Vert S_m'-S_m'' \Vert _{\mathbb {Y}_T} + \Vert S_m'' \Vert _{\mathbb {Y}_T} \Vert I_h'-I_h'' \Vert _{\mathbb {Y}_T} \right) \\ \le&h_1(T) \left\| \left( \begin{array}{c} S_m' \\ I_h' \end{array} \right) - \left( \begin{array}{c} S_m'' \\ I_h'' \end{array} \right) \right\| _{\mathbb {W}_T}, \end{aligned}\end{aligned}$$

where

$$\begin{aligned} h_1(T):= \frac{b\beta ^* (1-e^{-d_m T})}{d_m H_*} \max \left( \Vert I_h'\Vert _{\mathbb {Y}_T}, \Vert S_m'' \Vert _{\mathbb {Y}_T} \right) . \end{aligned}$$

Note that for any $0<T_*<T$, we can regard $(S_m',I_h'), (S_m'',I_h'')$ as functions in $\mathbb {W}_{T_*}$, and

$$\begin{aligned} h_1(T_*) =&\frac{b\beta ^* (1-e^{-d_m T_*})}{d_m H_*} \max \left( \Vert I_h'\Vert _{\mathbb {Y}_{T_*}}, \Vert S_m'' \Vert _{\mathbb {Y}_{T_*}} \right) \\ \le&\frac{b\beta ^* (1-e^{-d_m T_*})}{d_m H_*} \max \left( \Vert I_h'\Vert _{\mathbb {Y}_{T}}, \Vert S_m'' \Vert _{\mathbb {Y}_{T}} \right) = \frac{1-e^{-d_mT_*}}{1-e^{-d_mT}} h_1(T), \end{aligned}$$

and thus, $h_1(T_*) \rightarrow 0$ as $T_* \rightarrow + 0$. Hence, we let T being sufficiently small that $h_1(T)<1$ (regarding $T_*$ such that $h(T_*)<1$ as a new T). Similarly, we obtain

$$\begin{aligned} \begin{aligned}&\Vert \mathcal {C}(S_m', I_h') - \mathcal {C}(S_m'',I_h'') \Vert _{\mathbb {Y}_T} \le \sup _{0\le s \le T} \left\{ c \beta ^* \overline{\beta }_1 \left( 1+ \frac{\Vert I_h' \Vert _{\mathbb {Y}_T}}{H_*} \right) \int \limits _0^s \Pi (a) \textrm{d}a \Vert \mathcal {B}(S_m', I_h') - \mathcal {B}(S_m'',I_h'') \Vert _{\mathbb {Y}_T} \right. \\ {}&\qquad + \frac{c\beta ^* \Vert I_h' - I_h'' \Vert _{\mathbb {Y}_T}}{H_*} \int \limits _0^s \beta _1(a) \Vert T_1(a) [\mathcal {B}(S_m'',I_h'')(s-a,\cdot )] \Vert _{\mathbb {Y}} \Pi (a) \textrm{d}a \\ {}&\qquad \left. + \frac{c\beta ^* \Vert I_h'-I_h''\Vert _{\mathbb {Y}_T}}{H_*} \int \limits _s^\infty \beta _1(a) \Vert T_1(s)[\phi _2(a-s,\cdot )] \Vert _{\mathbb {Y}} \Pi (s)\text {d}a \right\} \\ {}&\quad \le \frac{c \beta ^* \overline{\beta }_1}{d_m} \left( 1+ \frac{\Vert I_h' \Vert _{\mathbb {Y}_T}}{H_*} \right) \Vert \mathcal {B}(S_m', I_h') - \mathcal {B}(S_m'',I_h'') \Vert _{\mathbb {Y}_T} + \frac{c\beta ^* \overline{\beta }_1}{H_*} \left( \frac{b\beta ^* \Vert S_m'' I_h'' \Vert _{\mathbb {Y}_T}}{d_m H_*} + \Vert \phi _2 \Vert _{\mathbb {X}} \right) \Vert I_h'-I_h''\Vert _{\mathbb {Y}_T}, \end{aligned} \end{aligned}$$

and hence,

$$\begin{aligned} \begin{aligned}&\Vert \mathcal {F}_2(S_m', I_h') - \mathcal {F}_2(S_m'',I_h'') \Vert _{\mathbb {Y}_T} \le \int \limits _0^t e^{-(d_h+\rho ) (t-s)} \textrm{d}s \Vert \mathcal {C}(S_m', I_h') - \mathcal {C}(S_m'',I_h'') \Vert _{\mathbb {Y}_T} \\ {}&\le h_2(T) \left\| \left( \begin{array}{c} S_m' \\ I_h' \end{array} \right) - \left( \begin{array}{c} S_m'' \\ I_h'' \end{array} \right) \right\| _{\mathbb {W}_T}, \end{aligned} \end{aligned}$$

where

$$\begin{aligned}&h_2(T) := \frac{c\beta ^* \overline{\beta }_1 (1-e^{-(d_h+\rho )T})}{(d_h+\rho )} \max (g_1, g_2), \\&g_1 := \frac{b\beta ^*}{d_m H_*} \left( 1+ \frac{\Vert I_h' \Vert _{\mathbb {Y}_T}}{H_*} \right) \Vert I_h' \Vert _{\mathbb {Y}_T}, \\&g_2 := \frac{b\beta ^*}{d_m H_*} \left( 1+ \frac{\Vert I_h' \Vert _{\mathbb {Y}_T}}{H_*} \right) \Vert S_m'' \Vert _{\mathbb {Y}_T} + \frac{1}{H_*} \left( \frac{b\beta ^* \Vert S_m'' I_h'' \Vert _{\mathbb {Y}_T}}{d_m H_*} + \Vert \phi _2 \Vert _{\mathbb {X}} \right) . \end{aligned}$$

Similar to the case of $h_1$, we let T being sufficiently small that $h_2(T)<1$. Consequently, we obtain

$$\begin{aligned} \left\| \mathcal {F}\left( \begin{array}{c} S_m' \\ I_h' \\ \end{array} \right) -\mathcal {F}\left( \begin{array}{c} S_m'' \\ I_h'' \\ \end{array} \right) \right\| _{\mathbb {W}_T} \le \max (h_1(T),h_2(T)) \left\| \left( \begin{array}{c} S_m' \\ I_h' \end{array} \right) - \left( \begin{array}{c} S_m'' \\ I_h'' \end{array} \right) \right\| _{\mathbb {W}_T}. \end{aligned}$$

As $\max (h_1(T),h_2(T)) < 1$, the operator $\mathcal {F}$ is a strict contraction in $\mathbb {W}_T$. Consequently, $\mathcal {F}$ has a unique fixed point in $\mathbb {W}_T$. Hence, the local existence of $S_m$ and $I_h$ follows. The local existence of $i_m$ then follows from (2.2) and (2.3). The regularity of the solution directly follows because the right-hand sides of (2.4) and (2.5) are continuously differentiable with respect to t and twice continuously differentiable with respect to x by virtue of the Green functions in $\{ T_i(t) \}_{t\ge 0}$, $i=1,2$. This proves Lemma 2.2. $\square$

Using Lemma 2.2, we continue to show Theorem 2.1.

Proof of Theorem 2.1

Let $\phi =(\phi _1,\phi _2,\phi _3) \in \mathcal {D}$ and $\tilde{T} \in (0,T)$. We first show the positivity of $S_m$ on $(0,\tilde{T}) \times \overline{\Omega }$. Clearly, for $x \in \Omega , \ t \in (0,\tilde{T})$,

$$\begin{aligned} \frac{\partial S_m}{\partial t} - D_m \Delta S_m > - \left[ \frac{b\beta (x)}{H(x)} I_h + d_m \right] S_m. \end{aligned}$$

As $b\beta (x)I_h/H(x)+d_m$ is bounded and continuous on $(0,\tilde{T}) \times \overline{\Omega }$, a standard result for PDEs ensures that $S_m>0$ for all $(t,x) \in (0,\tilde{T}) \times \overline{\Omega }$.

We next show that, for all $(t,x) \in (0, \tilde{T}) \times \overline{\Omega }$,

$$\begin{aligned} \begin{aligned} 0< M(t,x):= S_m + \int \limits _0^\infty i_m \textrm{d}a \le \frac{\mu ^*}{d_m}. \end{aligned} \end{aligned}$$

(2.7)

By (1.5)–(1.7), we have

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\partial M}{\partial t} - D_m \Delta M =\mu (x) - d_m M \le \mu ^* - d_m M, &{} x \in \Omega , \ t \in (0,\tilde{T}), \\ \displaystyle M(0,x) = \phi _1(x) + \int \limits _0^\infty \phi _2(a,x)\textrm{d}a \le \frac{\mu ^*}{d_m}, &{} x \in \overline{\Omega }, \\ \displaystyle \frac{\partial M}{\partial n} = 0, &{} x \in \partial \Omega , \ t \in (0,\tilde{T}). \end{array} \right. \end{aligned}$$

One can then easily see from the maximum principle that the last inequality in (2.7) holds. In addition, we have

$$\begin{aligned} \frac{\partial M}{\partial t} - D_m \Delta M > - d_m M, \quad x \in \Omega , \ t \in (0,\tilde{T}). \end{aligned}$$

Hence, similar to the above, one can easily see that $M(t,x) > 0$ for all $(t,x) \in (0,\tilde{T}) \times \overline{\Omega }$.

We then show that $I_h < H(x)$ for all $(t,x) \in (0,\tilde{T}) \times \overline{\Omega }$. Let $Y_h:= H-I_h$. It then follows from (1.5)–(1.7) and (1.3) that

$$\begin{aligned} \begin{aligned}&\frac{\partial Y_h}{\partial t} - D_h\Delta Y_h \\ {}&= -\frac{c\beta (x) Y_h}{H(x)} \int \limits _0^\infty \beta _1(a)i_m \textrm{d}a + (d_h+\rho ) [H(x)-Y_h] -D_h\Delta H(x) \\ {}&= \Lambda (x) + \rho H(x) - \left[ \frac{c\beta (x)}{H(x)} \int \limits _0^\infty \beta _1(a) i_m \textrm{d}a +d_h + \rho \right] Y_h \\ {}&> - \left[ \frac{c\beta (x) \overline{\beta }_1}{H(x)} \int \limits _0^\infty i_m \textrm{d}a +d_h + \rho \right] Y_h, \quad x \in \Omega , \ t \in (0,\tilde{T}), \end{aligned} \end{aligned}$$

and

$$\begin{aligned} Y_h(0,x) =H(x) -\phi _3(x) \ge 0, \ x \in \overline{\Omega }; \quad \frac{\partial Y_h}{\partial n}=0, \ x \in \partial \Omega , \ t \in (0,\tilde{T}). \end{aligned}$$

Similar to the above, as $c\beta (x)\overline{\beta }_1\int \limits _0^\infty i_m \textrm{d}a/H(x) + d_h + \rho$ is bounded and continuous on $(0,\tilde{T}) \times \overline{\Omega }$, the standard result for PDEs yields that $Y_h > 0$, $(t,x) \in (0,\tilde{T}) \times \overline{\Omega }$. We then directly have $I_h < H(x)$ for all $(t,x) \in (0,\tilde{T}) \times \overline{\Omega }$.

We continue to prove that $I_h \ge 0$ for all $(t,x) \in (0,\tilde{T}) \times \overline{\Omega }$. The abstract equation (2.5) in $\mathbb {Y}$ can be rewritten as follows: for $t \in (0,\tilde{T})$,

$$\begin{aligned} \begin{aligned} I_h(t,\cdot ) = \mathbb {F}_2(t,\cdot ) + \mathbb {F}_4(t,\cdot )+ \int \limits _0^t e^{-(d_h+\rho )(t-s)} T_2(t-s) [\tilde{\mathcal {C}}(S_m,I_h)(s,\cdot )] \textrm{d}s, \end{aligned} \end{aligned}$$

(2.8)

where $\mathbb {F}_2$ is given as in (2.6) and

$$\begin{aligned} \begin{aligned}&\mathbb {F}_4(t,\cdot ) := \int \limits _0^t e^{-(d_h+\rho )(t-s)} T_2(t-s) \left[ \frac{c \beta (\cdot ) (H(\cdot )-I_h(s,\cdot ))}{H(\cdot )} \int \limits _s^\infty \beta _1(a) T_1(s)\phi _2(a-s,\cdot ) \Pi (s) \textrm{d}a \right] \textrm{d}s, \\ {}&\tilde{\mathcal {C}}(S_m,I_h)(s,\cdot ) := \frac{c\beta (\cdot ) (H(\cdot )-I_h(s,\cdot ))}{H(\cdot )} \int \limits _0^s \beta _1(a) T_1(a) [\mathcal {B}(S_m,I_h)(s-a,\cdot )] \Pi (a)\text {d}a. \end{aligned} \end{aligned}$$

By (2.2), we get

$$\begin{aligned} \begin{aligned} \mathcal {B}(S_m,I_h)(t,\cdot ) = \frac{b\beta }{H}S_m(t,\cdot ) \left[ \mathbb {F}_2(t,\cdot ) + \mathbb {F}_4(t,\cdot )+ \int \limits _0^t e^{-(d_h+\rho )(t-s)} T_2(t-s) [\tilde{\mathcal {C}}(S_m,I_h)(s,\cdot )] \textrm{d}s \right] . \end{aligned} \end{aligned}$$

(2.9)

This is a renewal equation and the solution can be written as $\mathcal {B}=\sum _{n=0}^\infty \mathcal {B}_n$, where

$$\begin{aligned} \begin{aligned}&\mathcal {B}_0(t,\cdot ) := \frac{b\beta }{H}S_m(t,\cdot ) \left[ \mathbb {F}_2(t,\cdot ) + \mathbb {F}_4(t,\cdot )\right] , \\ {}&\mathcal {B}_n(t,\cdot ) := \frac{b\beta }{H}S_m(t,\cdot ) \int \limits _0^t e^{-(d_h+\rho )(t-s)} T_2(t-s) \left[ \frac{c\beta (\cdot ) (H(\cdot )-I_h(s,\cdot ))}{H(\cdot )} \int \limits _0^s \beta _1(a) T_1(a) [\mathcal {B}_{n-1}(s-a,\cdot )] \Pi (a)\text {d}a \right] \textrm{d}s, \\ {}&n=1,2,\ldots . \end{aligned} \end{aligned}$$

Since $S_m$ and $H-I_h$ are positive, one can see that $\mathcal {B}_n$ is nonnegative for all $n \ge 0$. Hence, $\mathcal {B}=\sum _{n=0}^\infty \mathcal {B}_n$ is also nonnegative. From (2.8), one knows that $I_h\ge 0$ for all $(t,x) \in (0,\tilde{T}) \times \overline{\Omega }$. In addition, the nonnegativitiy of $i_m$ also follows from (2.3).

In conclusion, the solution remains in the bounded set $\mathcal {D}$ for all $t \in (0,\tilde{T})$, that is, $\mathcal {D}$ is positively invariant for system (1.5)–(1.7). Thus, the solution never blows up in finite time and globally exists in $\mathcal {D}$ for all $t > 0$. The existence of the solution semiflow $\{ \Phi (t) \}_{t\ge 0}$ is a simple consequence. This proves Theorem 2.1. $\square$

3 The basic reproduction number

The disease-free equilibrium of (1.5) with boundary condition (1.7) can be written as $E_0:= (S^0_m(x),0,0) \in \mathcal {D}$, where $S_m^0(x)$ satisfies

$$\begin{aligned} -D_m \Delta S_m^0(x) = \mu (x) - d_m S_m^0(x), \ x \in \Omega ; \quad \frac{\partial S_m^0(x)}{\partial n} = 0, \ x \in \partial \Omega . \end{aligned}$$

More precisely, using the Green function $\Gamma _1$, we can obtain the following explicit formulation of $S_m^0(x)$:

$$\begin{aligned} S_m^0 (x) = \int \limits _0^\infty e^{-d_m s} \int \limits _\Omega \Gamma _1(s,x,y) \mu (y) \textrm{d}y \textrm{d}s, \quad x \in \overline{\Omega }. \end{aligned}$$

Note that, if $\mu (x) \equiv \mu$, then $S_m^0 \equiv \mu /d_m$.

By appealing to the standard procedures as those in [8, 25], let us define the basic reproduction number $\Re _0$ of (1.5)–(1.7). The linearized system of (1.5)–(1.7) around $E_0$ is given by

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\partial i_m}{\partial t}+ \frac{\partial i_m}{\partial a} - D_m\Delta i_m =-d_m i_m, \\ \displaystyle \frac{\partial I_h}{\partial t} -D_h \triangle I_h= c\beta (x)\int \limits _0^\infty \beta _1(a)i_m\textrm{d}a - (d_h+\rho )I_h, \\ \displaystyle i_m(t,0,x) = \frac{b\beta (x)}{H(x)} S_m^0(x) I_h =: \widetilde{\mathcal {B}}(t,x), \\ \displaystyle i_m(0,a,x)=\phi _2(a,x), \ I_h(0,x)=\phi _3(x), \end{array}\right. \end{aligned}$$

(3.1)

for $x\in \Omega , \ t> 0, \ a> 0$ and

$$\begin{aligned} \begin{array}{ll} \displaystyle \displaystyle \frac{\partial i_m}{\partial n}=\frac{\partial I_h}{\partial n}=0,&\ x\in \partial \Omega , \ t>0, \ a > 0. \end{array} \end{aligned}$$

(3.2)

By integrating the equations of $I_h$ and $i_m$ in (3.1), we obtain the following abstract equations in $\mathbb {Y}$:

$$\begin{aligned} I_h(t,\cdot ) = e^{-(d_h+\rho ) t} T_2(t)\phi _3 +\int \limits _0^t e^{-(d_h+\rho )(t-s)} T_2(t-s) \left( c\beta (\cdot ) \int \limits _0^\infty \beta _1(a) i_m(s,a,\cdot ) \textrm{d}a \right) \textrm{d}s, \quad t>0, \end{aligned}$$

and

$$\begin{aligned} i_m(t,a,\cdot )= \left\{ \begin{array}{ll} \displaystyle T_1(a) \widetilde{\mathcal {B}}(t-a,\cdot ) \Pi (a), &{}\ t>a, \\ \displaystyle T_1(t)\phi _2(a-t,\cdot ) \Pi (t), &{}\ a\ge t, \end{array}\right. \quad t>0, \ a>0. \end{aligned}$$

(3.3)

Hence, we get the following abstract equation in $\mathbb {Y}$: for $t>0$,

$$\begin{aligned} \widetilde{\mathcal {B}}(t,\cdot ) =&\frac{b\beta }{H}S_m^0(x) I_h(t,\cdot ) \\ =&\mathbb {G}(t,\cdot ) + \frac{b\beta }{H}S_m^0(x) \int \limits _0^t e^{-(d_h+\rho )(t-s)} T_2(t-s) \left( c\beta (\cdot ) \int \limits _0^s \beta _1(a) T_1(a)\widetilde{\mathcal {B}}(s-a,\cdot ) \Pi (a) \textrm{d}a \right) \textrm{d}s, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} \mathbb {G}(t,\cdot ) :=&\ \frac{b\beta }{H}S_m^0(x) \Biggl [ e^{-(d_h+\rho ) t} T_2(t)\phi _3(\cdot )\\ {}&\ \hspace{1.8cm}+\int \limits _0^t e^{-(d_h+\rho )(t-s)} T_2(t-s) \left( c\beta (\cdot ) \int \limits _s^\infty \beta _1(a) T_1(s)\phi _2(a-s,\cdot )\Pi (s) \textrm{d}a \right) \text {d}s \Biggr ]. \end{aligned} \end{aligned}$$

Hence, the generational expression $\widetilde{\mathcal {B}} = \sum _{n=0}^\infty \widetilde{\mathcal {B}}_n$ can be obtained, where

$$\begin{aligned}&\widetilde{\mathcal {B}}_0(t,\cdot ) := \mathbb {G}(t,\cdot ), \\&\widetilde{\mathcal {B}}_n(t,\cdot ) := \frac{b\beta }{H}S_m^0(x) \int \limits _0^t e^{-(d_h+\rho )(t-s)} T_2(t-s) \left( c\beta (\cdot ) \int \limits _0^s \beta _1(a) T_1(a) \widetilde{\mathcal {B}}_{n-1}(s-a,\cdot ) \Pi (a)\textrm{d}a \right) \textrm{d}s, \\&n=1,2,\ldots . \end{aligned}$$

Note that $\widetilde{\mathcal {B}}_n$ denotes the newly infected population in the n-th generation. Let $\widehat{\mathcal {B}}_n:= \int \limits _0^\infty \widetilde{\mathcal {B}}_n(t,\cdot )\textrm{d}t$. We then have, by changing the order of integration,

$$\begin{aligned} \begin{aligned} \widehat{\mathcal {B}}_n =&\int \limits _0^\infty \frac{b\beta }{H}S_m^0(x) \int \limits _0^t e^{-(d_h+\rho )(t-s)} T_2(t-s) \left( c\beta (\cdot ) \int \limits _0^s \beta _1(a) T_1(a) \widetilde{\mathcal {B}}_{n-1}(s-a,\cdot ) \Pi (a)\text {d}a \right) \text {d}s \text {d}t \\ =&\frac{b\beta }{H}S_m^0(x) \int \limits _0^\infty \int \limits _s^\infty e^{-(d_h+\rho )(t-s)} T_2(t-s) \text {d}t \left( c\beta (\cdot ) \int \limits _0^s \beta _1(a) T_1(a) \widetilde{\mathcal {B}}_{n-1}(s-a,\cdot ) \Pi (a)\text {d}a \right) \text {d}s \\ =&\frac{b\beta }{H}S_m^0(x) \int \limits _0^\infty e^{-(d_h+\rho ) u} T_2(u) \textrm{d}u \left( c\beta (\cdot ) \int \limits _0^\infty \int \limits _0^s \beta _1(a) T_1(a) \widetilde{\mathcal {B}}_{n-1}(s-a,\cdot ) \Pi (a)\text {d}a ds \right) \\ =&\frac{b\beta }{H}S_m^0(x) \int \limits _0^\infty e^{-(d_h+\rho ) u} T_2(u) \textrm{d}u \left( c\beta (\cdot ) \int \limits _0^\infty \beta _1(a) \Pi (a) T_1(a) \int \limits _a^\infty \widetilde{\mathcal {B}}_{n-1}(s-a,\cdot ) \text {d}s \text {d}a \right) \\ =&\frac{b\beta }{H}S_m^0(x) \int \limits _0^\infty e^{-(d_h+\rho ) u} T_2(u) \textrm{d}u \left( c\beta (\cdot ) \int \limits _0^\infty \beta _1(a) \Pi (a) T_1(a) \widehat{\mathcal {B}}_{n-1} \textrm{d}a \right) . \end{aligned} \end{aligned}$$

Thus, the next-generation operator $\mathcal {K}:\mathbb {Y}_+ \rightarrow \mathbb {Y}_+$ can be defined by

$$\begin{aligned} \mathcal {K}\psi := \frac{b\beta }{H}S_m^0(x) \int \limits _0^\infty e^{-(d_h+\rho ) u} T_2(u) \textrm{d}u \left( c\beta (\cdot ) \int \limits _0^\infty \beta _1(a) \Pi (a) T_1(a) \psi \right) , \quad \psi \in \mathbb {Y}_+. \end{aligned}$$

More precisely, for $\psi \in \mathbb {Y}_+$ and $x \in \overline{\Omega }$,

$$\begin{aligned}&\mathcal {K}\psi (x) = \\&\frac{b\beta (x) S_m^0(x)}{H(x)} \int \limits _0^\infty e^{-(d_h+\rho ) u} \int \limits _\Omega \Gamma _2(u,x,y) c\beta (y) \int \limits _0^\infty \beta _1(a) \Pi (a) \int \limits _\Omega \Gamma _1(a,y,z) \psi (z) \textrm{d}z \textrm{d}a \textrm{d}y \textrm{d}u. \end{aligned}$$

One can easily see that $\mathcal {K}$ is strictly positive, i.e., if $\psi \in \mathbb {Y}_+ \setminus \{ 0 \}$, then $\mathcal {K}\psi (x)>0$ for all $x \in \overline{\Omega }$. According to [8, 25], $\Re _0:= r(\mathcal {K})$, the spectral radius of $\mathcal {K}$. In general, $\Re _0$ cannot be explicitly calculated. However, in a spatially homogeneous case that

$$\begin{aligned} \mu (x)\equiv \mu , \beta (x)\equiv \beta \ \text{ and }\ H(x) \equiv H, \end{aligned}$$

we can get that $S_m^0(x) \equiv \mu /d_m$ and $\mathcal {K}$ is compact. The Krein–Rutman theorem [2, Theorem 3.2] guarantees that $\Re _0$ is the only positive eigenvalue of $\mathcal {K}$ associated with a positive eigenvector. More precisely, we obtain

$$\begin{aligned}{}[\Re _0]=\frac{bc\beta ^2 \mu }{H d_m (d_h+\rho )} \int \limits _0^\infty \beta _1(a)\Pi (a)\textrm{d}a. \end{aligned}$$

(3.4)

4 Dynamical analysis in the spatially homogeneous case

In the spatially homogeneous case, problem (1.5)–(1.7) reduces to

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\partial S_m}{\partial t} - D_m\Delta S_m = \mu -\frac{b\beta }{H} S_mI_h-d_m S_m,&{}x\in \Omega ,\ t>0, \\ \displaystyle \frac{\partial i_m}{\partial t}+ \frac{\partial i_m}{\partial a} - D_m\Delta i_m =-d_m i_m,&{} x\in \Omega ,\ t>0,\ a> 0, \\ \displaystyle \frac{\partial I_h}{\partial t} - D_h\Delta I_h =\frac{c\beta (H-I_h)}{H}\int \limits _0^\infty \beta _1(a)i_m\textrm{d}a-(d_h+\rho )I_h,&{} x\in \Omega ,\ t>0, \\ \displaystyle i_m(t,0,x)=\frac{b\beta }{H} S_mI_h,&{} x\in \overline{\Omega },\ t>0, \end{array}\right. \end{aligned}$$

(4.1)

with the same initial and boundary conditions (1.6) and (1.7).

Corollary 4.1

The solution semiflow $\{ \Phi \}_{t\ge 0}$ of (4.1) admits a global attractor in $\mathcal {D}$.

Proof

With the help of Theorem 2.1, one knows that $\Phi$ is point dissipative and eventually bounded on bounded sets of $\mathcal {D}$. Moreover, one can easily confirm that $\Phi$ is asymptotically smooth in the spatially homogeneous case by using the method as in [18]. An application of [22, Theorem 2.33] confirms that (4.1) admits a global attractor. This proves Corollary 4.1. $\square$

System (4.1) has constant equilibria which are solutions to the following equations:

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle 0 = \mu - \frac{b\beta }{H} S_m I_h - d_m S_m, \quad (d_h +\rho ) I_h = \frac{c\beta (H-I_h)}{H} \int \limits _0^\infty \beta _1(a) i_m(a)\textrm{d}a, \\ \displaystyle \frac{\partial i_m}{\partial a} = - d_m i_m, \ a>0, \quad i_m(0) = \frac{b\beta }{H}S_m I_h. \end{array} \right. \end{aligned}$$

(4.2)

Obviously, there exists a constant disease-free equilibrium $\tilde{E}_0:= (S_m^0,0,0) \in \mathcal {D}$, where $S_m^0=\mu /d_m$. Moreover, rearranging (4.2), we have

$$\begin{aligned} S_m = \frac{H \mu }{b\beta I_h + H d_m}, \quad I_h = \frac{c \beta H K i_m(0)}{c\beta K i_m(0) + H(d_h + \rho )}, \quad i_m(a) = i_m(0) \Pi (a), \ a>0, \end{aligned}$$

where $K:= \int \limits _0^\infty \beta _1(a) \Pi (a) \textrm{d}a$. By the equation of $i_m(0)$ in (4.2), we have

$$\begin{aligned}&i_m(0) = \frac{\mu b\beta I_h}{b\beta I_h + H d_m} \ \ \Leftrightarrow \ \ [i_m(0) - \mu ] b \beta I_h + Hd_m i_m(0) = 0 \\&\Leftrightarrow \ \ \frac{[i_m(0) - \mu ] b c \beta ^2 H K i_m(0)}{c\beta K i_m(0) + H(d_h + \rho )} + Hd_m i_m(0) = 0 \\&\Leftrightarrow \ \ c\beta K (b\beta + d_m) i_m(0) \left[ i_m(0) - \frac{H(d_h+\rho )d_m}{c\beta K (b\beta + d_m)} \left( [\Re _0]- 1 \right) \right] = 0. \end{aligned}$$

Thus, we have the following proposition on the existence of constant equilibrium.

Proposition 4.2

Let $[\Re _0]$ is defined in (3.4). If $[\Re _0] > 1$, then (4.1) admits a constant equilibrium $E^*=(S^*_m, i^*_m(a), I_h^*) \in \mathcal {D}$, where

$$\begin{aligned} S_m^* = \frac{H \mu }{b\beta I_h^* + H d_m}, \quad I_h^* = \frac{c \beta H K i_m^*(0)}{c\beta K i_m^*(0) + H(d_h + \rho )}, \quad i_m^*(a) = i_m^*(0) \Pi (a), \ a>0, \end{aligned}$$

and

$$\begin{aligned} i_m^*(0) = \frac{H(d_h+\rho )d_m}{c\beta K (b\beta + d_m)} \left( [\Re _0]- 1 \right) > 0. \end{aligned}$$

4.1 Local asymptotic stability of equilibria

We shall prove that both $\tilde{E}_0$ and $E^*$ are locally asymptotically stable (LAS).

Theorem 4.3

Let $[\Re _0]$ be defined by (3.4).

• (i) If $[\Re _0]<1$, then $\tilde{E}_0$ is LAS;

• (ii) If $[\Re _0]>1$, then $E^*$ is LAS.

Proof

We first prove (i). The linearized system of (4.1) around $\tilde{E}_0$ is as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\partial S_m}{\partial t}- D_m\Delta S_m =-\frac{b\beta }{H}S_{m}^{0}I_h-d_m S_m, &{} x \in \Omega , \ t>0, \\ \displaystyle \frac{\partial i_m}{\partial t}+ \frac{\partial i_m}{\partial a} - D_m\Delta i_m =-d_m i_m, &{} x \in \Omega , \ t> 0, \ a> 0, \\ \displaystyle \frac{\partial I_h}{\partial t} - D_h\Delta I_h = c\beta \int \limits _0^\infty \beta _1(a)i_m\textrm{d}a - (d_h+\rho )I_h, &{} x \in \Omega , \ t> 0, \\ \displaystyle i_m(t,0,x)=\frac{b\beta }{H}S_{m}^{0}I_h, &{} x \in \overline{\Omega }, \ t > 0, \end{array}\right. \end{aligned}$$

(4.3)

with boundary condition (1.7). Let $\mu _j \ (j= 1,2,\ldots )$ be the eigenvalues of linear operator $-\Delta$ on $\Omega$ with homogeneous Neumann boundary condition corresponding to the eigenvectors $v_j\in C^2(\Omega ) \cap C^1(\overline{\Omega })$:

$$\begin{aligned} \Delta v_j = - \mu _j v_j, \ x \in \Omega ; \quad \frac{\partial v_j}{\partial n}=0, \ x \in \partial \Omega . \end{aligned}$$

From a well-known fact, we can assume that $0=\mu _0<\mu _1<\mu _2< \cdots$. Substituting $(S_m, i_m, I_h)=e^{\eta t} v_i(x) (u_1, u_2 (a), u_3) \ (\eta \in \mathbb {C})$ into (4.3) and dividing each side by $e^{\eta t}v_i(x)$, we have

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \eta u_1+D_m\mu _i u_1 = -\frac{b\beta }{H}S_{m}^{0} u_3-d_m u_1,\\ \displaystyle \eta u_2(a)+ \frac{\partial u_2(a)}{\partial a} +D_m\mu _i u_2(a)= -d_m u_2(a),\\ \displaystyle \eta u_3 + D_h\mu _i u_3 =c\beta \int \limits _0^\infty \beta _1(a) u_2(a) \textrm{d}a - (d_h+\rho )u_3,\\ \displaystyle u_2(0) = \frac{b\beta }{H}S_{m}^{0} u_3. \end{array}\right. \end{aligned}$$

(4.4)

It is easy checked from the second and fourth equations of (4.4) that

$$\begin{aligned} u_2(a)= \frac{b\beta }{H}S_m^0 u_3 e^{-\eta a}\tilde{\Pi }(a), \end{aligned}$$

where $\tilde{\Pi }(a)=e^{-D_m\mu _ia}\Pi (a)$. Rewriting (4.4) in terms of $(u_1,u_3)$, we obtain the following characteristic equation:

$$\begin{aligned}\left| \begin{array}{cc} \eta +D_m\mu _i+d_m &{} \frac{b\beta }{H}S_{m}^{0} \\ 0 &{} \eta +D_h\mu _i+d_h+\rho -\frac{bc\beta ^{2}}{H}S_{m}^{0}\int \limits _0^\infty \beta _1(a)e^{-\eta a}\tilde{\Pi }(a)\textrm{d}a \\ \end{array} \right| =\mathcal {K(\eta )}(\eta +D_m\mu _i+d_m)=0, \end{aligned}$$

where $\mathcal {K(\eta )}=\eta +D_h\mu _i+d_h+\rho -\frac{bc\beta ^{2}}{H}S_{m}^{0}\int \limits _0^\infty \beta _1(a)e^{-\eta a}\tilde{\Pi }(a)\textrm{d}a$. To show that $\tilde{E}_0$ is LAS, we suppose on the contrary that $\eta = m + ni \ (m,n \in \mathbb {R}, \ i^2=-1)$ with $m \ge 0$. We then see that $\eta +D_m\mu _i+d_m\ne 0$, and thus, we can only pay attention to the roots of $\mathcal {K(\eta )}=0$. This equation can be rewritten as

$$\begin{aligned} \begin{aligned} \frac{\frac{bc\beta ^{2}}{H}S_{m}^{0}\int \limits _0^\infty \beta _1(a)e^{-\eta a}\tilde{\Pi }(a)\text {d}a}{\eta +D_h\mu _i+d_h+\rho }=1.\\ \end{aligned} \end{aligned}$$

Taking the absolute value of both sides, we have

$$\begin{aligned} 1=\left| \frac{\frac{bc\beta ^{2}}{H}S_{m}^{0}\int \limits _0^\infty \beta _1(a)e^{-\eta a}\tilde{\Pi }(a)\textrm{d}a}{\eta +D_h\mu _i+d_h+\rho }\right| \\ \le \frac{\frac{bc\beta ^{2}}{H}S_{m}^{0}\int \limits _0^\infty \beta _1(a){\Pi }(a)\textrm{d}a}{d_h+\rho }=[\Re _0], \end{aligned}$$

which leads to a contradiction with $[\Re _0]<1$. Hence, $m \le 0$. This proves (i).

We next proceed to prove (ii). The linearized system of (4.1) around $E^{*}$ is as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\partial S_m}{\partial t}- D_m\Delta S_m =-\frac{b\beta }{H}S_{m}^{*}I_h-\frac{b\beta }{H}I_{h}^{*}S_m-d_m S_m, &{} x \in \Omega , \ t> 0, \\ \displaystyle \frac{\partial i_m}{\partial t}+ \frac{\partial i_m}{\partial a} - D_m\Delta i_m =-d_m i_m, &{} x \in \Omega , \ t>0, \ a> 0, \\ \displaystyle \frac{\partial I_h}{\partial t} - D_h\Delta I_h = c\beta \int \limits _0^\infty \beta _1(a)i_m\textrm{d}a-\frac{c\beta }{H}I_{h}^{*}\int \limits _0^\infty \beta _1(a)i_m\textrm{d}a\\ \hspace{2.8cm}\displaystyle -\frac{c\beta }{H}I_{h} \int \limits _0^\infty \beta _1(a)i_{m}^{*}(a)\textrm{d}a - (d_h+\rho )I_h, &{} x \in \Omega , \ t> 0, \\ \displaystyle i_m(t,0,x)=\frac{b\beta }{H}{S}_mI_h^{*}+\frac{b\beta }{H}{S}_m^{*}I_h, &{} x\in \overline{\Omega }, \ t > 0, \end{array}\right. \end{aligned}$$

(4.5)

with boundary condition (1.7). Substituting $(S_m, i_m, I_h)=e^{\eta t} v_i(x) (u_1, u_2(a), u_3)$ into (4.5) and dividing each side by $e^{\eta t}v_i(x)$, we have

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \eta u_1+D_m\mu _i u_1=-\frac{b\beta }{H}S_{m}^{*}u_3-\frac{b\beta }{H}I_{h}^{*}u_1-d_m u_1,\\ \displaystyle \eta u_2(a)+ \frac{\partial u_2(a)}{\partial a} +D_m\mu _i u_2(a)=-d_m u_2(a),\\ \displaystyle \eta u_3 + D_h\mu _i u_3 =c\beta \int \limits _0^\infty \beta _1(a)u_2(a)\textrm{d}a-\frac{c\beta }{H}I_{h}^{*}\int \limits _0^\infty \beta _1(a) u_2(a)\textrm{d}a\\ \displaystyle \hspace{2.8cm}-\frac{c\beta }{H}u_3 \int \limits _0^\infty \beta _1(a)i_{m}^{*}(a)\textrm{d}a - (d_h+\rho ) u_3,\\ \displaystyle u_2(0) = \frac{b\beta }{H}S_{m}^{*} u_3+\frac{b\beta }{H}I_{h}^{*}u_1. \end{array}\right. \end{aligned}$$

(4.6)

It is easily checked that

$$\begin{aligned} u_2(a)= \left( \frac{b\beta }{H}S_{m}^{*} u_3+\frac{b\beta }{H}I_{h}^{*}u_1 \right) e^{-\eta a}\tilde{\Pi }(a). \end{aligned}$$

Hence, rewriting (4.6) in terms of $(u_1,u_3)$, we obtain the following characteristic equation:

$$\begin{aligned}\left| \begin{array}{cc} \eta +D_m\mu _i+d_m+\frac{b\beta }{H}I_h^{*} &{} \frac{b\beta }{H}S_m^{*} \\ -\frac{bc\beta ^{2}(H-I_h^{*})}{H^{2}}I_h^{*} P &{} \eta +D_h\mu _i-\frac{bc\beta ^{2}(H-I_h^{*})}{H^{2}}S_m^{*}P+\frac{c\beta }{H}Q+(d_h+\rho ) \\ \end{array} \right| =0, \end{aligned}$$

where $P=\int \limits _0^\infty \beta _1(a)e^{-\eta a}\tilde{\Pi }(a)\textrm{d}a$ and $Q=\int \limits _0^\infty \beta _1(a)i_{m}^{*}(a)\textrm{d}a$. Rearranging this equation, we obtain

$$\begin{aligned} \eta +D_h\mu _i+d_h+\rho +\frac{c\beta }{H} Q = \frac{\eta +D_m\mu _i+d_m}{\eta +D_m\mu _i+d_m+\frac{b\beta }{H}I_h^{*}} \frac{bc\beta ^{2}(H-I_h^{*})}{H^{2}} S_m^{*}P. \end{aligned}$$

(4.7)

To show that $E^*$ is LAS, we suppose on the contrary that $\eta = m + ni \ (m,n \in \mathbb {R}, \ i^2=-1)$ with $m \ge 0$. By taking the absolute value of both sides of (4.7), we obtain

$$\begin{aligned} d_h+\rho<&\left| \eta +D_h\mu _i+d_h+\rho +\frac{c\beta }{H} Q \right| =\left| \frac{\eta +D_m\mu _i+d_m}{\eta +D_m\mu _i+d_m+\frac{b\beta }{H}I_h^{*}} \frac{bc\beta ^{2}(H-I_h^{*})}{H^{2}} S_m^{*}P \right| \\ <&\frac{bc\beta ^{2}(H-I_h^{*})}{H^{2}} S_m^{*} K. \end{aligned}$$

It then follows from the equilibrium equations that

$$\begin{aligned} 0 < \frac{bc\beta ^{2}(H-I_h^{*})}{H^{2}}S_m^{*}K -(d_h+\rho ) = 0, \end{aligned}$$

a contradiction. Hence, $m \le 0$. This proves (ii). $\square$

4.2 Global dynamics

We shall investigate the threshold dynamics of (4.1) in terms of $[\Re _0]$, that is, both $\tilde{E}_0$ and $E^*$ are globally attractive. This together with the related results in above subsection tells us that both $\tilde{E}_0$ and $E^*$ are globally asymptotically stable (GAS).

Theorem 4.4

Suppose that $[\Re _0]<1$. Then, $\tilde{E}_0$ is GAS in $\mathcal {D}$.

Proof

Note that, in $\mathcal {D}$, $S_m\le \mu /d_m = S_m^0$ for all $t>0$ and $x \in \overline{\Omega }$. Hence, an application of the comparison principle gives $0\le i_m \le \overline{i}_m$ and $0\le I_h \le \overline{I}_h$, where $(\overline{i}_m, \overline{I}_h)$ is the solution to the following auxiliary system:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\partial \overline{i}_m}{\partial t}+ \frac{\partial \overline{i}_m}{\partial a} - D_m\Delta \overline{i}_m =-d_m \overline{i}_m, \\ \displaystyle \frac{\partial \overline{I}_h}{\partial t} - D_h\Delta \overline{I}_h =\frac{c\beta (H-\overline{I}_h)}{H}\int \limits _0^\infty \beta _1(a)\overline{i}_m\textrm{d}a-(d_h+\rho )\overline{I}_h, \\ \displaystyle \overline{i}_m(t,0,x)=\frac{b\beta }{H} S_m^0 \overline{I}_h,\\ \overline{i}_m(0,a,x)=\phi _2(a,x), \quad \overline{I}_h(0,x)=\phi _3(x), \\ \end{array}\right. \end{aligned}$$

for $x\in \Omega ,\ t>0,\ a > 0$ and

$$\begin{aligned} \begin{array}{ll} \displaystyle \frac{\partial \overline{i}_m}{\partial n}=\frac{\partial \overline{I}_h}{\partial n}=0,&x\in \partial \Omega ,\ t>0, \ a>0. \end{array} \end{aligned}$$

It then suffices to show that $(\overline{i}_m, \overline{I}_h)$ converges to (0, 0) as time goes to infinity, which implies that $(i_m,I_h)$ convereges to (0, 0), and thus, $S_m$ converges to $S_m^0$ as time goes to infinity.

Let

$$\begin{aligned} \begin{aligned} \Psi _1(a):=\frac{c\beta }{\Pi (a)}\int \limits _a^\infty \beta _1(\theta )\Pi (\theta )\textrm{d}\theta . \end{aligned} \end{aligned}$$

One can then easily check that

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \Psi _1'(a) =-c \beta \beta _1(a)+d_m\Psi _1(a), \\ \displaystyle \Psi _1(0) = c\beta K. \end{array} \right. \end{aligned}$$

Let $V(t):=V_1(t) + V_2(t)$ be a Lyapunov function, where

$$\begin{aligned} \begin{aligned} V_1(t):= \int \limits _\Omega \int \limits _0^\infty \Psi _1(a) \overline{i}_m\text {d}a \text {d}x, \quad V_2(t):= \int \limits _\Omega \overline{I}_h \textrm{d}x. \end{aligned} \end{aligned}$$

We then have that

$$\begin{aligned} \begin{aligned} V_1'(t)=&\frac{\partial }{\partial t} \int \limits _\Omega \int \limits _0^\infty \Psi _1(a) \overline{i}_m\text {d}a \text {d}x =\int \limits _\Omega \int \limits _0^\infty \Psi _1(a) \left[ \frac{\partial \overline{i}_m}{\partial t} \right] \text {d}a \text {d}x \\ =&\int \limits _\Omega \int \limits _0^\infty \Psi _1(a) \left[ -\frac{\partial \overline{i}_m}{\partial a} + D_m \Delta \overline{i}_m - d_m \overline{i}_m \right] \text {d}a \text {d}x \\ =&\int \limits _\Omega \left\{ \Psi _1(0)\overline{i}_m(t,0,x) + \int \limits _0^\infty \left[ \Psi _1'(a) - d_m \Psi _1(a) \right] \overline{i}_m \textrm{d}a \right\} dx \\ =&\int \limits _\Omega \left[ \frac{bc\beta ^2 K}{H} S_m^0 \overline{I}_h - c\beta \int \limits _0^\infty \beta _1(a)\overline{i}_m \textrm{d}a \right] dx, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} V_2'(t) =&\int \limits _\Omega \left[ D_h \Delta \overline{I}_h + \frac{c\beta (H-\overline{I}_h)}{H} \int \limits _0^\infty \beta _1(a)\overline{i}_m \textrm{d}a - (d_h+\rho )\overline{I}_h \right] \textrm{d}x \\ =&\int \limits _\Omega \left[ \left( c\beta - \frac{\overline{I}_h}{H} \right) \int \limits _0^\infty \beta _1(a)\overline{i}_m \textrm{d}a - (d_h+\rho )\overline{I}_h \right] \textrm{d}x. \end{aligned} \end{aligned}$$

Hence, the derivative of V gives

$$\begin{aligned} V'(t) =&\int \limits _\Omega \left[ \frac{bc\beta ^2 K}{H} S_m^0 \overline{I}_h - (d_h+\rho ) \overline{I}_h - \frac{\overline{I}_h}{H} \int \limits _0^\infty \beta _1(a) \overline{i}_m da \right] dx \\ =&(d_h+\rho ) \left( [\Re _0]-1\right) \int \limits _\Omega \overline{I}_h dx - \frac{1}{H} \int \limits _\Omega \overline{I}_h \int \limits _0^\infty \beta _1(a) \overline{i}_m \textrm{d}a \textrm{d}x \le 0. \end{aligned}$$

Consequently, $\tilde{E}_0$ is globally attractive in $\mathcal {D}$ when $[\Re _0] < 1$ (see, for instance, [26, Theorem 4.2]). Combined with the results in Theorem 4.3, one knows that $\tilde{E}_0$ is GAS. This completes the proof of Theorem 4.4. $\square$

To define a Lyapunov function for $E^*$ when $[\Re _0] > 1$, we need a uniform persistence result. The following estimation for $S_m$ immediately follows.

Proposition 4.5

There exists an $\epsilon _0>0$ such that, for any $\phi \in \mathcal {D}$ and $x\in \overline{\Omega }$,

$$\begin{aligned} \liminf _{t \rightarrow \infty } S_m > \epsilon _0. \end{aligned}$$

(4.8)

Proof

By Theorem 2.1, and $I_h \le H$, one can get that $\frac{\partial S_m}{\partial t}\ge \ D_m\Delta S_m+\mu -( b\beta + d_m)S_m$. Again from the comparison principle, one can get that for any $x\in \overline{\Omega }$,

$$\begin{aligned} \liminf _{t\rightarrow \infty } S_m>\frac{\mu }{b\beta + d_m} =: \epsilon _0. \end{aligned}$$

This proves Proposition 4.5. $\square$

We next define the following subset of $\mathcal {D}$:

$$\begin{aligned} \mathcal {D}_0:= \left\{ \varphi =(\varphi _1, \varphi _2, \varphi _3) \in \mathcal {D}: \varphi _3 \not \equiv 0 \right\} . \end{aligned}$$

(4.9)

Epidemiologically, $\mathcal {D}_0$ is the set where the disease persists. The forthcoming lemma immediately follows.

Lemma 4.6

If $\phi \in \mathcal {D}_0$, then $I_h > 0$ for all $t>0$ and $x \in \overline{\Omega }$.

The following result indicates that $\{ \tilde{E}_0 \}$ is a uniform weak repeller in $\mathcal {D}$.

Lemma 4.7

If $[\Re _0] > 1$, then there exists an $\epsilon _1>0$ such that, for any $\phi \in \mathcal {D}_0$,

$$\begin{aligned} \limsup _{t\rightarrow \infty } \Vert \Phi (t)\phi - \tilde{E}_0 \Vert _{\overline{\mathbb {X}}} > \epsilon _1. \end{aligned}$$

Proof

We proceed it indirectly and assume that for any $\epsilon _1>0$, there exists a $\phi \in \mathcal {D}_0$ that

$$\begin{aligned} \limsup _{t\rightarrow \infty } \Vert \Phi (t)\phi - \tilde{E}_0 \Vert _{\overline{\mathbb {X}}} \le \epsilon _1. \end{aligned}$$

This inequality implies that there exists a $t_1>0$ such that, for any $t > t_1$ and $x \in \overline{\Omega }$,

$$\begin{aligned} \begin{aligned} S_m \ge S_m^0 - \epsilon _1, \quad \int \limits _0^\infty i_m \textrm{d}a \le \epsilon _1, \quad I_h \le \epsilon _1. \end{aligned} \end{aligned}$$

(4.10)

Without loss of generality, taking $\Phi (t_1)\phi$ be the new initial condition, we can assume that inequalities (4.10) hold for all $t>0$ and $x \in \overline{\Omega }$.

For simplicity, we write $\mathcal {B}(t)=\mathcal {B}(S_m,I_h)(t)$. By (2.9), we obtain the following abstract inequality in $\mathbb {Y}$:

$$\begin{aligned} \begin{aligned} \mathcal {B}(t) \ge&\frac{b\beta }{H} (S_m^0-\epsilon _1) \int \limits _0^t e^{-(d_h+\rho )(t-s)} T_2(t-s) \left[ \frac{c\beta (H-\epsilon _1)}{H} \int \limits _0^s \beta _1(a) T_1(a) [\mathcal {B}(s-a)] \Pi (a)\text {d}a \right] \textrm{d}s \\ =&\frac{b c \beta ^2}{H} (S_m^0-\epsilon _1) \left( 1-\frac{\epsilon _1}{H} \right) \int \limits _0^t e^{-(d_h+\rho )(t-s)} T_2(t-s) \left[ \int \limits _0^s \beta _1(a) T_1(a) [\mathcal {B}(s-a)] \Pi (a)\text {d}a \right] \textrm{d}s. \end{aligned} \end{aligned}$$

(4.11)

For any $\lambda > 0$, let $\hat{\mathcal {B}}(\lambda ): = \int \limits _0^\infty e^{-\lambda t} \int \limits _\Omega \mathcal {B}(t,x) \textrm{d}x \textrm{d}t$. By Lemma 4.6 and (2.2), we can easily confirm that $0< \hat{\mathcal {B}}(\lambda ) < +\infty$. Moreover, from (4.11), we have

$$\begin{aligned} \hat{\mathcal {B}}(\lambda ) \ge&\frac{b c \beta ^2}{H} (S_m^0-\epsilon _1) \left( 1-\frac{\epsilon _1}{H} \right) \int \limits _0^\infty e^{-\lambda t} \int \limits _0^t e^{-(d_h+\rho )(t-s)} \int \limits _0^s \beta _1(a) \int \limits _\Omega \mathcal {B}(s-a,x) \textrm{d}x \Pi (a)\textrm{d}a \textrm{d}s \textrm{d}t \nonumber \\ =&\frac{b c \beta ^2}{H} (S_m^0-\epsilon _1) \left( 1-\frac{\epsilon _1}{H} \right) \frac{1}{\lambda + d_h+\rho } \int \limits _0^\infty e^{-\lambda a}\beta _1(a) \Pi (a)\textrm{d}a \hat{\mathcal {B}}(\lambda ) \nonumber \\ =&[\Re _{\epsilon _1,\lambda }] \hat{\mathcal {B}}(\lambda ), \end{aligned}$$

(4.12)

where

$$\begin{aligned}{}[\Re _{\epsilon _1,\lambda }]:= \frac{b c \beta ^2}{H} (S_m^0-\epsilon _1) \left( 1-\frac{\epsilon _1}{H} \right) \frac{1}{\lambda + d_h+\rho } \int \limits _0^\infty e^{-\lambda a}\beta _1(a) \Pi (a)\textrm{d}a. \end{aligned}$$

One can easily see that $[\Re _{\epsilon _1,\lambda }] \rightarrow [\Re _0] > 1$ as $(\epsilon _1,\lambda )\rightarrow (0,0)$, which allow us to choose $\epsilon _1>0$ and $\lambda >0$ small enough such that $[\Re _{\epsilon _1,\lambda }] > 1$. We then have from (4.12) that $\hat{\mathcal {B}}(\lambda ) > \hat{\mathcal {B}}(\lambda )$, a contradiction. This proves Lemma 4.7. $\square$

Using Lemma 4.7, we now prove the following result.

Proposition 4.8

If $[\Re _0] > 1$, then there exists an $\epsilon _2>0$ such that, for any $\phi \in \mathcal {D}_0$ and $x \in \overline{\Omega }$,

$$\begin{aligned} \liminf _{t\rightarrow \infty } I_h(t,x) > \epsilon _2. \end{aligned}$$

(4.13)

Before the proof, we prepare some notations:

• $\partial \mathcal {D}_0: = \mathcal {D} \setminus \mathcal {D}_0 = \left\{ \varphi = (\varphi _1, \varphi _2, \varphi _3) \in \mathcal {D}: \varphi _3 \equiv 0 \right\}$.

• $M_\partial := \{ \varphi \in \partial \mathcal {D}_0: \Phi (t)\varphi \in \partial \mathcal {D}_0 \ \mathrm {for \ all} \ t > 0 \}$.

• $\omega (\varphi ):= \cap _{t\ge 0}\overline{\cup _{s\ge t} \Phi (s)\varphi }$: the omega limit set.

• $\delta (\varphi ):= \inf _{x\in \Omega } \varphi _3(x)$, $\rho :\mathcal {D}\rightarrow \mathbb {R}_+$: a generalized distance function.

• $W^s(\tilde{E}_0):= \{ \varphi \in \mathcal {D}: \lim _{t\rightarrow \infty } \Vert \Phi (t)\varphi - \tilde{E}_0 \Vert _{\overline{\mathbb {X}}} = 0 \}$: the stable set of $\tilde{E}_0$.

Proof

One can easily confirm that

• 1. $\cup _{\varphi \in M_\partial } \omega (\varphi ) = \{ \tilde{E}_0 \}$.

• 2. No subset of $\{ \tilde{E}_0\}$ forms a cycle in $\partial \mathcal {D}_0$.

• 3. $\{ \tilde{E}_0 \}$ is isolated in $\mathcal {D}$.

• 4. $W^s(\tilde{E}_0) \cap \delta ^{-1}(0,\infty ) = \emptyset$.

Moreover, by Corollary 4.1, $\Phi$ has a global attractor in $\mathcal {D}$. Thus, conditions in [23, Theorem 3] are satisfied and there exists an $\epsilon _2>0$ such that

$$\begin{aligned} \min _{\varphi \in \mathcal {L}}\delta (\varphi ) > \epsilon _2, \end{aligned}$$

where $\mathcal {L}$ is an arbitrary compact chain transitive set in $\mathcal {D} \setminus \{ \tilde{E}_0 \}$. Hence, for any $\phi \in \mathcal {D}_0$ and $x \in \overline{\Omega }$, (4.13) holds. This proves Proposition 4.8. $\square$

By Propositions 4.5 and 4.8, there exists $c_i>0, i=1,2$, such that, for any total trajectory in a persistence attractor (see, e.g., [18, Theorem 8.3]), the following inequalities hold:

$$\begin{aligned} c_1< \frac{i_m}{i_m^*(a)} = \frac{T_1(a)(\mathcal {B}(t-a,\cdot ))(x)}{i_m^*(0)} <c_2, \quad x\in \overline{\Omega }, \ t \in \mathbb {R}, \ a \ge 0. \end{aligned}$$

Thus, for any total trajectory in a persistence attractor, the following functions are finite for all $t \in \mathbb {R}$:

$$\begin{aligned}&W_1(t) := \int \limits _\Omega S_m^* g\left( \frac{S_m}{S_m^*}\right) \textrm{d}x, \quad W_2(t) := \int \limits _\Omega \int \limits _0^\infty \Psi _2 (a) i_m^*(a) g\left( \frac{i_m}{i_m^*(a)} \right) \textrm{d}a \textrm{d}x, \\&W_3(t) := \int \limits _\Omega I_h^* g\left( \frac{I_h}{I_h^*}\right) \textrm{d}x, \end{aligned}$$

where $g(u):= u-1-\ln u$ and

$$\begin{aligned} \Psi _2(a):=\frac{c\beta }{\Pi (a)} \left( 1-\frac{I_h^*}{H} \right) \int \limits _a^\infty \beta _1(\theta )\Pi (\theta )d\theta . \end{aligned}$$

Clearly, $g(u) > 0$ for each $u \in (0,\infty ) \setminus \{1 \}$ and $g(1)=0$. Using a Lyapunov function $W:=\kappa W_1+W_2+W_3$ with $\kappa >0$ to be determined below, we can obtain the following result.

Theorem 4.9

Suppose that $[\Re _0] > 1$. Then, $E^*$ is GAS in $\mathcal {D}_0$.

Proof

By appealing to [18, Theorem 9.5], we consider a total trajectory in the persistence attractor. Then, $W(t)=\kappa W_1(t)+W_2(t)+W_3(t)$ is finite for all $t \in \mathbb {R}$. Direct calculation gives

$$\begin{aligned} \begin{aligned} W_1'(t) =&\int \limits _\Omega \left[ \left( 1 - \frac{S_m^*}{S_m} \right) \left( D_m \Delta S_m + \mu - \frac{b\beta }{H} S_m I_h - d_m S_m \right) \right] \textrm{d}x \\ =&- D_m S_m^* \int \limits _\Omega \frac{|\nabla S_m|^2}{S_m^2}\textrm{d}x + d_m S_m^* \int \limits _\Omega \left( 2-\frac{S_m^*}{S_m} - \frac{S_m}{S_m^*} \right) \text {d}x \\ {}&+ \frac{b\beta }{H} S_m^* I_h^* \int \limits _\Omega \left( 1-\frac{S_m^*}{S_m} + \frac{I_h}{I_h^*} - \frac{S_m I_h}{S_m^* I_h^*} \right) \text {d}x \\ =&- D_m S_m^* \int \limits _\Omega \frac{|\nabla S_m|^2}{S_m^2}\textrm{d}x - d_m S_m^* \int \limits _\Omega \left[ g\left( \frac{S_m^*}{S_m} \right) + g\left( \frac{S_m}{S_m^*} \right) \right] \textrm{d}x \\ {}&+i_m^*(0) \int \limits _\Omega \left[ -g\left( \frac{S_m^*}{S_m}\right) + g\left( \frac{I_h}{I_h^*} \right) - g\left( \frac{S_m I_h}{S_m^* I_h^*} \right) \right] \textrm{d}x, \\ W_3'(t) =&\int \limits _\Omega \left[ \left( 1 - \frac{I_h^*}{I_h} \right) \left( D_h \Delta I_h + c\beta \left( 1 - \frac{I_h}{H} \right) \int \limits _0^\infty \beta _1(a) i_m \textrm{d}a - (d_h + \rho ) I_h \right) \right] \textrm{d}x \\ =&- D_h I_h^* \int \limits _\Omega \frac{|\nabla I_h|^2}{I_h^2}\textrm{d}x + c\beta \int \limits _\Omega \left( 1 - \frac{I_h^*}{I_h} \right) \left( 1 - \frac{I_h}{H} \right) \int \limits _0^\infty \beta _1(a) i_m \text {d}a \text {d}x \\ {}&+(d_h+\rho ) I_h^* \int \limits _\Omega \left( 1-\frac{I_h}{I_h^*} \right) \text {d}x \\ =&- D_h I_h^* \int \limits _\Omega \frac{|\nabla I_h|^2}{I_h^2} \textrm{d}x - c\beta \int \limits _\Omega \frac{(I_h-I_h^*)^2}{HI_h} \int \limits _0^\infty \beta _1(a) i_m \text {d}a \text {d}x \\ {}&+ c\beta \left( 1 - \frac{I_h^*}{H} \right) \int \limits _\Omega \int \limits _0^\infty \beta _1(a) i_m^* \left( 1-\frac{I_h}{I_h^*} + \frac{i_m}{i_m^*} - \frac{I_h^* i_m}{I_h i_m^*} \right) \text {d}a \text {d}x \\ =&- D_h I_h^* \int \limits _\Omega \frac{|\nabla I_h|^2}{I_h^2} \textrm{d}x - c\beta \int \limits _\Omega \frac{(I_h-I_h^*)^2}{HI_h} \int \limits _0^\infty \beta _1(a) i_m \text {d}a \text {d}x \\ {}&- c\beta \left( 1 - \frac{I_h^*}{H} \right) K i_m^*(0) \int \limits _\Omega g\left( \frac{I_h}{I_h^*} \right) \text {d}x \\ {}&+ c\beta \left( 1 - \frac{I_h^*}{H} \right) \int \limits _\Omega \int \limits _0^\infty \beta _1(a) i_m^* \left[ g\left( \frac{i_m}{i_m^*} \right) - g\left( \frac{I_h^* i_m}{I_h i_m^*} \right) \right] \text {d}a \text {d}x, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} W_2'(t) =&\int \limits _\Omega \int \limits _0^\infty \Psi _2(a) \left( 1-\frac{i_m^*}{i_m}\right) \left( D_m \Delta i_m -\frac{\partial i_m}{\partial a} - d_m i_m \right) \textrm{d}a \textrm{d}x \\ =&- D_m \int \limits _\Omega \int \limits _0^\infty \Psi _2(a) \frac{|\nabla i_m|^2}{i_m^2} \textrm{d}a \textrm{d}x -\int \limits _\Omega \int \limits _0^\infty \Psi _2(a) \left( 1-\frac{i_m^*}{i_m}\right) \left( \frac{\partial i_m}{\partial a} + d_m i_m \right) \textrm{d}a \textrm{d}x. \end{aligned}$$

Fig. 1

$\Omega =(0,1)$. The time evolution of susceptible mosquitoes $S_m(t,x)$, infected mosquitoes with $I(t,x)=\int \limits _0^{\infty }i_m(t,a,x)\textrm{d}a$) and infected humans $I_h(t,x)$ of system (4.1) with (5.1), $\beta _ =0.026$ and $\Omega =(0,1)$. The initial data is $\phi _1(x)=100,\ \phi _2(a,x)=e^{-d_m*a} (x-0.3)(0.7-x)$ and $\phi _3(x)=0.$

Fig. 2

The time evolution of susceptible mosquitoes $S_m(t,x)$, infected mosquitoes with $I(t,x)=\int \limits \limits _0^{\infty }i_m(t,a,x)\textrm{d}a$) and infected humans $I_h(t,x)$ of system (4.1) with (5.1), $\beta =0.036$ and $\Omega =(0,1)$. The initial data is $\phi _1(x)=100,\ \phi _2(a,x)=e^{-d_m*a} (x-0.3)(0.7-x)$ and $\phi _3(x)=0.$

Fig. 3

$t=280$. The time evolution of susceptible mosquitoes $S_m(t,x)$, infected mosquitoes with $I(t,x)=\int \limits _0^{\infty }i_m(t,a,x)\textrm{d}a$) and infected humans $I_h(t,x)$ of system (4.1) with (5.1), $\beta =0.26$ and $\Omega = (0, 1)\times (0,1)$. The initial data is $\phi _1(x,y)=100,\ \phi _2(a,x,y)=e^{-d_m*a}(x-0.3)(0.7-x)(y-0.3)(0.7-y)$ and $\phi _3(x,y)=0.$

Fig. 4

$t=350$. The time evolution of susceptible mosquitoes $S_m(t,x)$, infected mosquitoes with $I(t,x)=\int \limits _0^{\infty }i_m(t,a,x)\textrm{d}a$) and infected humans $I_h(t,x)$ of system (4.1) with (5.1), $\beta =0.36$ and $\Omega = (0, 1)\times (0,1)$. The initial data is $\phi _1(x,y)=100,\ \phi _2(a,x,y)=e^{-d_m*a}(x-0.3)(0.7-x)(y-0.3)(0.7-y)$ and $\phi _3(x,y)=0.$

Fig. 5

PRCC for $[\Re _0].$

Fig. 6

Sensitive analysis of the $[\Re _0]$ via parameters

Fig. 7

The influence of n on $[\Re _0].$

Here, note that

$$\begin{aligned} i_m^* \frac{\partial }{\partial a} g\left( \frac{i_m}{i_m^*} \right) =&i_m^* \left( 1 - \frac{i_m^*}{i_m} \right) \frac{\partial }{\partial a} \left( \frac{i_m}{i_m^*} \right) =\left( 1 - \frac{i_m^*}{i_m} \right) \left( \frac{\partial i_m}{\partial a} + d_m i_m \right) . \end{aligned}$$

Thus, we have

$$\begin{aligned} W_2'(t) =&- D_m \int \limits _\Omega \int \limits _0^\infty \Psi _2(a) \frac{|\nabla i_m|^2}{i_m^2} \textrm{d}a \textrm{d}x -\int \limits _\Omega \int \limits _0^\infty \Psi _2(a) i_m^* \frac{\partial }{\partial a} g\left( \frac{i_m}{i_m^*} \right) \textrm{d}a \textrm{d}x \\ =&- D_m \int \limits _\Omega \int \limits _0^\infty \Psi _2(a) \frac{|\nabla i_m|^2}{i_m^2} \textrm{d}a \textrm{d}x +\Psi _2(0) i_m^*(0) \int \limits _\Omega g\left( \frac{i_m(t,0,x)}{i_m^*(0)} \right) \textrm{d}x \\&- c\beta \left( 1-\frac{I_h^*}{H} \right) \int \limits _\Omega \int \limits _0^\infty \beta _1(a) i_m^* g \left( \frac{i_m}{i_m^*} \right) \textrm{d}a \textrm{d}x. \end{aligned}$$

Hence, letting $\kappa := c\beta (1-I_h^*/H) K$, we obtain

$$\begin{aligned} W'(t) =&\kappa W_1'(t) + W_2'(t) + W_3'(t) \\ =&- \kappa D_m S_m^* \int \limits _\Omega \frac{|\nabla S_m|^2}{S_m^2}\textrm{d}x - \kappa d_m S_m^* \int \limits _\Omega \left[ g\left( \frac{S_m^*}{S_m} \right) + g\left( \frac{S_m}{S_m^*} \right) \right] \textrm{d}x - \kappa i_m^*(0) \int \limits _\Omega g\left( \frac{S_m^*}{S_m}\right) \textrm{d}x \\&- D_h I_h^* \int \limits _\Omega \frac{|\nabla I_h|^2}{I_h^2}\textrm{d}x - c\beta \int \limits _\Omega \frac{(I_h-I_h^*)^2}{HI_h} \int \limits _0^\infty \beta _1(a) i_m \textrm{d}a \textrm{d}x \\&- c\beta \left( 1 - \frac{I_h^*}{H} \right) \int \limits _\Omega \int \limits _0^\infty \beta _1(a) i_m^* g\left( \frac{I_h^* i_m}{I_h i_m^*} \right) \textrm{d}a \textrm{d}x - D_m \int \limits _\Omega \int \limits _0^\infty \Psi _2(a) \frac{|\nabla i_m|^2}{i_m^2} \textrm{d}a \textrm{d}x\\ \le&0. \end{aligned}$$

One can easily see that $W'(t)=0$ iff $(S_m,i_m,I_h)=E^*$. As in the proof of [18, Theorem 9.5], we see that the singleton $\{E^*\}$ is indeed the persistence attractor. This gives the global attractivity of $E^*$. Together with Theorem 4.3, one can get $E^*$ is GAS. This proves Theorem 4.9. $\square$

5 Numerical simulations

5.1 Dynamical behaviors of system (4.1)

We perform numerical simulations to support the main results obtained in Sect. 4. Specifically, we shall carry out the simulations for 1-dimensional and 2-dimensional domain to validate Theorems 4.4 and 4.9, that is, both $\tilde{E}_0$ and $E^*$ are GAS.

For the case that $\Omega =(0,1)$, we set the following parameters:

$$\begin{aligned} \begin{aligned}{}&{} \mu = 20,\;d_{m} = 0.2,\;b = 0.5,\;c = 0.5,\;H = 100,d_{h} = 0.00004,\;\rho = 0.1, \\{}&{} \quad D_{m} = D_{h} = 0.000125,\;\beta _{1} = 1 . \end{aligned} \end{aligned}$$

(5.1)

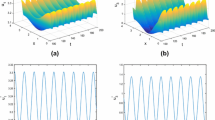
If we take $\beta =0.26$, we can compute $[\Re _0] = 0.844669$. From Theorem 4.4, we know that $\tilde{E}_0$ is GAS in $\mathcal {D}$. Figure 1a, b and c illustrates that the density of susceptible mosquitoes will attain a positive level and infected mosquitoes and infected humans decay to zero. We also know from Fig. 1d that the spatial distribution of infected mosquitoes gradually enlarges with higher prevalence but decays to zero.

If we take $\beta =0.36$ and the other parameters remain the same as in (5.1), then $[\Re _0] = 1.619366$. It is known from Theorem 4.9 that $E^*$ is GAS in $\mathcal {D}_0$. Figure 2a, b and c illustrates that the densities of susceptible mosquitoes, infected mosquitoes and infected humans will attain a positive level as time evolves. Figure 2d illustrates that the spatial distribution of infected mosquitoes gradually enlarge with higher prevalence.

For the case that $\Omega = (0, 1)\times (0,1)$. We set the same parameters as in Fig. 1 and 2. Figure 3a illustrates that the density of susceptible mosquitoes will attain a positive level. We can see from Fig. 3b, c that the densities of infected mosquitoes and infected humans decay to zero. Figure 4 demonstrates the densities of susceptible mosquitoes, infected mosquitoes and infected humans will attain a positive level.

5.2 The influence of parameters on [$\Re _0$]

To analyze the effects of the parameter values on $[\Re _0]$, we perform sensitivity analysis to check the effects of the parameter values on [$\Re _0$] by Latin Hypercube Sampling and partial rank correlation coefficient (PRCC) method (see, for example, [4, 11]). Under the setting that $\mu$, $d_m$, $\rho$ and $\beta _1$ are changed concomitantly, we can observe the dependence of $[\Re _0]$ on parameters $\mu$, $d_m$, $\rho$ and $\beta _1$, respectively. Specifically, numeric plots in Fig. 5 indicate that $[\Re _0]$ is a monotonically increasing function with respect to $\mu$ and $\beta _1$, while $[\Re _0]$ is a monotonically decreasing function of $d_m$ and $\rho$, respectively. Figure 6 demonstrates that $[\Re _0]$ is more sensitive to $\mu$ and $\beta _1$.

We next investigate the influence of $\beta _1(a)$ on $[\Re _0]$. As pointed in [24], the smaller the age of infection, the smaller transmission rate $\beta _1(a)$ of the disease. The rate of infection increases along with the infectious age. When the age of infection is very large, the infection rate is reduced to zero due to the loss of infectivity. Therefore, we artificially select the following form of $\beta _1$,

$$\begin{aligned} \beta _1(a) = 0.3 + 0.63ae^{-n(a-10)^2},\ n\in (0,1]. \end{aligned}$$

It can be observed from Fig. 7 that $[\Re _0]$ decreases monotonically as n increases.