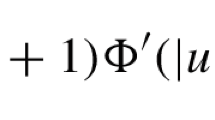Abstract
We consider the Cauchy problem of the focusing \(\dot{H}^{1/2}\)-critical Hartree equation
By adapting the methods in Dodson and Murphy (Proc Am Math Soc 145(11):4859–4867, 2017), we shall prove a scattering result for solutions both below and beyond the mass–energy threshold M(Q)E(Q) and uniformly describe both cases the boundary of the scattering region by the ground state’s mass and potential energy product.
Similar content being viewed by others
References
Bahouri, H., Chemin, J.-Y., Danchin, R.: Fourier Analysis and Nonlinear Partial Differential Equations. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 343. Springer, Heidelberg (2011)
Cazenave, T.: Semilinear Schrödinger Equations, Volume 10 of Courant Lecture Notes in Mathematics. New York University, Courant Institute of Mathematical Sciences, New York; American Mathematical Society, Providence, RI (2003)
Dodson, B., Murphy, J.: A new proof of scattering below the ground state for the 3D radial focusing cubic NLS. Proc. Am. Math. Soc. 145(11), 4859–4867 (2017)
Dodson, B., Murphy, J.: A new proof of scattering below the ground state for the non-radial focusing nls. Math. Res. Lett. 25(6), 1805–1825 (2018)
Duyckaerts, T., Roudenko, S.: Going beyond the threshold: scattering and blow-up in the focusing NLS equation. Commun. Math. Phys. 334(3), 1573–1615 (2015)
Fröhlich, J., Lenzmann, E.: Mean-field limit of quantum Bose gases and nonlinear Hartree equation. In: Séminaire: Équations aux Dérivées Partielles. 2003–2004, Sémin. Équ. Dériv. Partielles, pages Exp. No. XIX, 26. École Polytech., Palaiseau (2004)
Gao, Y., Wang, Z.: Scattering versus blow-up for the focusing \(L^2\) supercritical Hartree equation. Z. Angew. Math. Phys. 65(1), 179–202 (2014)
Guo, Z., Nakanishi, K.: The Zakharov system in 4D radial energy space below the ground state (2018). arXiv e-prints, arXiv:1810.05794
Holmer, J., Roudenko, S.: A sharp condition for scattering of the radial 3D cubic nonlinear Schrödinger equation. Commun. Math. Phys. 282(2), 435–467 (2008)
Kenig, C.E., Merle, F.: Global well-posedness, scattering and blow-up for the energy-critical, focusing, non-linear Schrödinger equation in the radial case. Invent. Math. 166(3), 645–675 (2006)
Killip, R., Visan, M.: The focusing energy-critical nonlinear Schrödinger equation in dimensions five and higher. Am. J. Math. 132(2), 361–424 (2010)
Li, D., Miao, C., Zhang, X.: The focusing energy-critical Hartree equation. J. Differ. Equ. 246(3), 1139–1163 (2009)
Moroz, V., Van Schaftingen, J.: A guide to the Choquard equation. J. Fixed Point Theory Appl. 19(1), 773–813 (2017)
Miao, C., Guixiang, X., Zhao, L.: The Cauchy problem of the Hartree equation. J. Partial Differ. Equ. 21(1), 22–44 (2008)
Miao, C., Guixiang, X., Zhao, L.: Global well-posedness and scattering for the mass-critical Hartree equation with radial data. J. Math. Pures Appl. (9) 91(1), 49–79 (2009)
Sun, C., Wang, H., Yao, X., Zheng, J.: Scattering below ground state of focusing fractional nonlinear Schrödinger equation with radial data. Discrete Contin. Dyn. Syst. 38(4), 2207–2228 (2018)
Tao, T.: On the asymptotic behavior of large radial data for a focusing non-linear Schrödinger equation. Dyn. Partial Differ. Equ. 1(1), 1–48 (2004)
Tao, T.: Nonlinear Dispersive Equations, Volume 106 of CBMS Regional Conference Series in Mathematics. Published for the Conference Board of the Mathematical Sciences, Washington, DC; by the American Mathematical Society, Providence, RI, Local and Global Analysis (2006)
Weinstein, M.I.: Nonlinear Schrödinger equations and sharp interpolation estimates. Commun. Math. Phys. 87(4), 567–576 (1982/83)
Yang, L., Li, X., Yonghong, W., Caccetta, L.: Global well-posedness and blow-up for the Hartree equation. Acta Math. Sci. Ser. B (Engl. Ed.) 37(4), 941–948 (2017)
Acknowledgements
The authors would like to thank Jiqiang Zheng for useful discussions. Y. Gao is supported in part by NSFC (Nos. 11501111 and 11771082). Y. Gao thanks the China Scholarship Council (CSC) (No. 201808350018) for fellowship support. Z. Wang is supported in part by NSFC (Nos. 11601082 and 11501111), the Foundation of the Science and Technology Department of Fujian Province (No. 2017J05002) and Foundation of the Education Department of Fujian Province (No. JA15110). Z. Wang thanks Fujian Normal University for fellowship support. Both authors would like to thank the referees for their useful comments and suggestions of the manuscript.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A: Construct a scattering solution with initial datum beyond the mass–energy threshold
Appendix A: Construct a scattering solution with initial datum beyond the mass–energy threshold
In appendix, we shall construct a scattering solution with initial datum beyond the mass–energy threshold in Corollary A.3 following the process used in [5, Corollary 1.12].
First, we introduce the virial quantity. Let u(t, x) be a solution of (1.1) and denote the virial quantity \(V(t) = \mathop {\int }\limits _{{\mathbb {R}}^{d}} |x|^{2}|u(t,x)|^{2}\,\mathrm {d}x.\) If \(V(0) < \infty \), a direct computation using the equation (1.1) yields
Yang et al. proved a general global well-posedness theorem in [20]. Here we summarize their results in the version that we need.
Theorem A.1
([20, Theorem 3.1 with \(s_{c} = 1/2\)]) Let u(t, x) be a solution of (1.1), assume \(u_{0} \in H^{1}(R^{d})\) and \(V(0) < \infty \). If
and
Then, u(t, x) exists globally, and
Remark A.2
Instead of (A.7), the authors in [20] proved that
which is the same as Theorem 1.4 in [5] for nonlinear Schrödinger equation. Reviewing the proof in [20], one finds that (A.7) can be also obtained.
Next, we shall construct a scattering solution with initial datum beyond the mass–energy threshold by Theorem A.1.
Corollary A.3
Let \(\gamma > 0\) and \(Q^{\gamma }(t,x)\) be the solution of (1.1) with initial datum
where Q is the ground state solution of (1.2), which is a real positive function. Then, there exists a small positive \(t_{0}\) such that
is a forward global solution with initial datum beyond the mass–energy threshold
and
Proof
We shall check the conditions in Theorem A.1 step by step.
By the local theory and the identity
we see that for \(\gamma > 0\),
Thus, by the formula (A.1), \(V'(0) > 0\) for the solution \(Q^{\gamma }_{t_{0}}(t,x)\). And (A.6) is satisfied.
Let \(P(t) = P(u(t))\). If \(u\) is a solution of (1.1), then by formal calculation,
Let \(u(t) = Q^{\gamma }(t)\). Since Q(x) is real, we have \({{\,\mathrm{Im}\,}}(\Delta u(0) \overline{u(0)}) = 2 \gamma (d Q^{2} + 2x Q \nabla Q) = 2 \gamma \nabla \cdot (x Q^{2})\).
An integral by parts and a change of variables yield
Thus, for small positive \(t_{0}\),
So for the solution \(Q^{\gamma }_{t_{0}}\), the condition (A.5) is fulfilled.
By the Pohozaev identities (2.1), \(E(Q) = \frac{1}{2}\mathop {\int }\limits _{{\mathbb {R}}^{d}}|Q|^{2}\,\mathrm {d}x > 0\). By conservation of mass and energy,
and
Thus, \(M(Q^{\gamma }_{t_{0}}) E(Q^{\gamma }_{t_{0}}) > M(Q)E(Q)\), which is (A.3).
To show that \(Q_{t_{0}}^{\gamma }\) obeys (A.4), we define
We claim that
Note that \(t=0\), \({{\,\mathrm{Im}\,}}\mathop {\int }\limits _{{\mathbb {R}}^{d}} x \cdot \nabla Q^{\gamma } (0) \overline{Q^{\gamma }} (0)\,\mathrm {d}x = 2 \gamma \mathop {\int }\limits _{{\mathbb {R}}^{d}} |xQ|^{2}\,\mathrm {d}x\). Therefore, \(F(0) = 0\) by (A.10). Let
F(t) can be rewritten as
By conservation of mass and energy, we have
and
By invoking (A.1), (A.2) and the Pohozaev identities \(\mathop {\int }\limits _{{\mathbb {R}}^{d}} |\nabla Q|^{2} \,\mathrm {d}x = 3\mathop {\int }\limits _{{\mathbb {R}}^{d}}|Q|^{2}\,\mathrm {d}x\) and \(P(Q) = 4 \mathop {\int }\limits _{{\mathbb {R}}^{d}}|Q|^{2}\,\mathrm {d}x\), we get
Then, we get for \(\gamma > 0\)
Thus,
and
where \({{\,\mathrm{sgn}\,}}(s) = \frac{s}{|s|}\) for \(s \ne 0\) and \({{\,\mathrm{sgn}\,}}(0) = 0\).
Since \(V(t) = (z(t))^{2}\), we have \(V_{ttt} = 6 z_{t}z_{tt} + 2 z z_{ttt}\), which together with \(z_{tt}(0) = 0\) and (A.12) implies that \({{\,\mathrm{sgn}\,}}(-V_{ttt}(0)) = {{\,\mathrm{sgn}\,}}(F''(0))\). Meanwhile, we get from (A.2) that
Thus, \(F''(0) < 0\) due to (A.9). The claim (A.11) is proved. As a consequence, there exists \(t_{0} > 0\) such that \(F(t_{0}) < 0\). Taking the initial datum \(u_{0}(x) = Q^{\gamma }(t_{0},x)\), which fulfills the assumptions of Theorem A.1, we get (A.8). \(\square \)
By (A.8) and Theorem 1.1, \(Q_{t_{0}}^{\gamma }(t,x)\) scatters forward in time.
Rights and permissions
About this article
Cite this article
Gao, Y., Wang, Z. Below and beyond the mass–energy threshold: scattering for the Hartree equation with radial data in \(\pmb {d \ge 5}\). Z. Angew. Math. Phys. 71, 52 (2020). https://doi.org/10.1007/s00033-020-1274-0
Received:
Revised:
Published:
DOI: https://doi.org/10.1007/s00033-020-1274-0