Gradient higher integrability for singular parabolic double-phase systems

Abstract

We prove a local higher integrability result for the gradient of a weak solution to parabolic double-phase systems of p-Laplace type when $\tfrac{2n}{n+2}< p\le 2$. The result is based on a reverse Hölder inequality in intrinsic cylinders combining p-intrinsic and (p, q)-intrinsic geometries. A singular scaling deficits affects the range of q.

1 Introduction

This paper discusses the local higher integrability of the spatial gradient of weak solutions $u=u(z)=u(x,t)$ to parabolic double-phase systems with the prototype

$$\begin{aligned} u_t-{{\,\textrm{div}\,}}(|\nabla u|^{p-2}\nabla u+a(z)|\nabla u|^{q-2}\nabla u)=-{{\,\textrm{div}\,}}(|F|^{p-2}F+a(z)|F|^{q-2}F) \end{aligned}$$

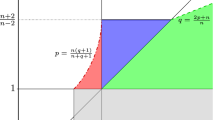
in $\Omega _T=\Omega \times (0,T)$, where $\Omega$ is a bounded domain in ${\mathbb {R}}^n$, $n\ge 2$, and $T>0$. The coefficient function $a\in C^{\alpha ,\alpha /2}(\Omega _T)$ is non-negative and Hölder continuous. The higher integrability result in Theorem 2.2 was obtained when $p\ge 2$ in [11] and here we extend this result to singular the parameter range. More precisely, in this paper we assume that

$$\begin{aligned} \frac{2n}{n+2}< p \le 2, \quad p<q\le p+\frac{\alpha \mu }{n+2},\quad \mu = \frac{p(n+2)-2n}{2}. \end{aligned}$$

(1.1)

When $p=\tfrac{2n}{n+2}$ we have $\mu = 0$, while at $p=2$ the range of q is the same as in [11]. Note that $\tfrac{\mu }{p}$ is the usual scaling deficit appearing in singular p-parabolic problems, cf. [7, Section VIII]. An upper bound for q in terms of $p, \alpha$ and n appears naturally in regularity properties of double-phase problems. Otherwise the solution may not be regular already in the elliptic case, see [8].

The method for showing the higher integrability result in this paper originates from [13] where the result was shown for parabolic p-Laplace systems. There a reverse Hölder inequality was shown in p-intrinsic cylinders as in (2.1). See also [2] for the gradient higher integrability of p(x, t)-Laplace systems. On the other hand, in [10] the same result was shown for the Orlicz setting including parabolic (p, q)-Laplace problems (corresponding to $a(z)=a_0$ for some constant $a_0>0$) in (p, q)-intrinsic cylinders. For the double-phase model $\inf a(z)$ may be zero and a priori neither the p-term nor the q-term dominates. Instead, the behaviour of the system varies locally between two distinct phases based on which of the terms is dominating. To incorporate this into the argument, we divide into cases at every point $z_0$ by comparing $a(z_0)$ to the level of the gradient. If $a(z_0)$ is sufficiently small, we show a reverse Hölder inequality in a p-intrinsic cylinder. In the complementary case, it follows that a(z) is comparable to $a(z_0)$ in a sufficiently large neighborhood of $z_0$ and the reverse Hölder inequality can be shown in a (p, q)-intrinsic cylinder.

To construct the intrinsic cylinders, we use a stopping time argument to find a p-intrinsic cylinder at every point in a suitable upper level set. Moreover, we obtain a decay estimate for the radius of a p-intrinsic cylinder in terms of the level. This estimate, stated in Lemma 3.1, gives the comparability of a(z) around (p, q)-intrinsic cylinders, see the property (p,q-2). Lemma 3.1 is also used in the p-intrinsic case to transform terms involving q into terms of a p-Laplace system, for example in the proof of Lemma 3.7. This argument gives the range of q in (1.1), see Remark 3.2. Note that (1.1) allows for the situation that $q>2$ while $p<2$. However, this case does not have to be considered separately and the division to p- and (p, q)-intrinsic cylinders is sufficient.

Stationary double-phase problems have been studied extensively in [1, 3,4,5,6]. Note that the double-phase model in these papers is not included in the (p, q)-problems studied for instance in [14]. For parabolic double-phase problems existence has been studied in [15] and [12] while many regularity questions remain open.

2 Notation and main result

2.1 Notation

We denote a point in ${\mathbb {R}}^{n+1}$ as $z=(x,t)$, where $x\in {\mathbb {R}}^n$ and $t\in {\mathbb {R}}$. A ball with center $x_0\in {\mathbb {R}}^n$ and radius $\rho >0$ is denoted as

$$\begin{aligned} B_\rho (x_0)=\{x\in {\mathbb {R}}^n:|x-x_0|<\rho \}. \end{aligned}$$

Parabolic cylinders with center $z_0=(x_0,t_0)$ and quadratic scaling in time are denoted as

$$\begin{aligned} Q_\rho (z_0)=B_\rho (x_0)\times I_\rho (t_0), \end{aligned}$$

where

$$\begin{aligned} I_\rho (t_0)=(t_0-\rho ^2,t_0+\rho ^2). \end{aligned}$$

We use the following notation for the double-phase functional. With the non-negative coefficient function $a(\cdot )$ being fixed, we define a function $H(z,s):\Omega _T\times {\mathbb {R}}^+\longrightarrow {\mathbb {R}}^+$ as

$$\begin{aligned} H(z,s)=s^p+a(z)s^q. \end{aligned}$$

We use two types of intrinsic cylinders. For $\lambda \ge 1$ and $\rho > 0$, a p-intrinsic cylinder centered at $z_0=(x_0,t_0)$ is

$$\begin{aligned} Q_\rho ^\lambda (z_0)= B^\lambda _\rho (x_0)\times I_{\rho }(t_0), \quad B^\lambda _\rho (x_0) = B_{\lambda ^\frac{p-2}{2}\rho }(x_0), \end{aligned}$$

(2.1)

and a (p, q)-intrinsic cylinders centered at $z_0=(x_0,t_0)$ is

$$\begin{aligned} \begin{aligned}&G_{\rho }^\lambda (z_0)=B^\lambda _{\rho }(x_0)\times J_{\rho }^\lambda (t_0),\\&J_\rho ^{\lambda }(t_0)=\biggl (t_0-\frac{\lambda ^p}{H(z_0,\lambda )}\rho ^2,t_0+\frac{\lambda ^p}{H(z_0,\lambda )}\rho ^2\biggr ). \end{aligned} \end{aligned}$$

(2.2)

Note that $\tfrac{\lambda ^p}{H(z_0,\lambda )}\rho ^2=\tfrac{\lambda ^2}{H(z_0,\lambda )}(\lambda ^\frac{p-2}{2}\rho )^2$ and thus $G_\rho ^\lambda (z_0)$ is the standard intrinsic cylinder for (p, q)-Laplace system. For $c>0$, we write

$$\begin{aligned} cQ_\rho ^\lambda (z_0)=Q_{c\rho }^\lambda (z_0) \quad \text {and}\quad cG_\rho ^\lambda (z_0)=G_{c\rho }^\lambda (z_0). \end{aligned}$$

We also consider parabolic cylinders with arbitrary scaling in time and denote

$$\begin{aligned} Q_{R,\ell }(z_0)=B_R(x_0)\times (t_0-\ell ,t_0+\ell ),\quad R,\ell >0. \end{aligned}$$

The $(n+1)$-dimensional Lebesgue measure of a set $E\subset {\mathbb {R}}^{n+1}$ is denoted as |E|. For $f\in L^1(\Omega _T,{\mathbb {R}}^N)$ and a measurable set $E\subset \Omega _T$ with $0<|E|<\infty$, we denote the integral average of f over E as

2.2 Main result

We consider weak solutions to the parabolic double-phase system

$$\begin{aligned} u_t-{{\,\textrm{div}\,}}{\mathcal {A}}(z,\nabla u)=-{{\,\textrm{div}\,}}(|F|^{p-2}F+a(z)|F|^{q-2}F) \end{aligned}$$

(2.3)

in $\Omega _T=\Omega \times (0,T)$, where $\Omega$ is a bounded domain in ${\mathbb {R}}^n$, $n\ge 2$, and $T>0$. Here ${\mathcal {A}}(z,\nabla u):\Omega _T\times {\mathbb {R}}^{Nn}\longrightarrow {\mathbb {R}}^{Nn}$ with $N\ge 1$ is a Carathéodory vector field satisfying the following structure assumptions: there exist constants $0<\nu \le L<\infty$ such that

$$\begin{aligned} {\mathcal {A}}(z,\xi )\cdot \xi \ge \nu (|\xi |^p+a(z)|\xi |^q)\quad \text {and}\quad |{\mathcal {A}}(z,\xi )|\le L(|\xi |^{p-1}+a(z)|\xi |^{q-1}) \end{aligned}$$

for almost every $z\in \Omega _T$ and every $\xi \in {\mathbb {R}}^{Nn}$. The source term $F:\Omega _T\longrightarrow {\mathbb {R}}^{Nn}$ satisfies

$$\begin{aligned} \iint _{\Omega _T} H(z,|F|)\ dz=\iint _{\Omega _T}(|F|^p+a(z)|F|^q)\,dz<\infty . \end{aligned}$$

We assume that $a \ge 0$ and $a\in C^{\alpha ,\frac{\alpha }{2}}(\Omega _T)$ for some $\alpha \in (0,1]$. Here $a\in C^{\alpha ,\frac{\alpha }{2}}(\Omega _T)$ means that $a\in L^{\infty }(\Omega _T)$ and there exists a constant $[a]_\alpha =[a]_{\alpha ,\alpha /2;\Omega _T}<\infty$, such that

$$\begin{aligned} \begin{aligned}&|a(x,t)-a(y,t)|\le [a]_\alpha |x-y|^\alpha \quad \text {and}\\&|a(x,t)-a(x,s)|\le [a]_\alpha |t-s|^\frac{\alpha }{2}, \end{aligned} \end{aligned}$$

(2.4)

for every $(x,y)\in \Omega$ and $(t,s)\in (0,T)$.

Definition 2.1

A map $u:\Omega _T\longrightarrow {\mathbb {R}}^N$ satisfying

$$\begin{aligned} u\in C(0,T;L^2(\Omega ,{\mathbb {R}}^N))\cap L^1(0,T;W^{1,1}(\Omega ,{\mathbb {R}}^N)) \end{aligned}$$

and

$$\begin{aligned} \iint _{\Omega _T} H(z,|\nabla u|)\, dz=\iint _{\Omega _T}(|\nabla u|^p+a(z)|\nabla u|^q)\,dz<\infty , \end{aligned}$$

is a weak solution to (2.3), if

$$\begin{aligned} \begin{aligned}&\iint _{\Omega _T}(-u\cdot \varphi _t+{\mathcal {A}}(z,\nabla u)\cdot \nabla \varphi )\,dz\\&\quad =\iint _{\Omega _T}(|F|^{p-2}F\cdot \nabla \varphi +a(z)|F|^{p-2}F\cdot \nabla \varphi )\,dz \end{aligned} \end{aligned}$$

for every $\varphi \in C_0^\infty (\Omega _T,{\mathbb {R}}^N)$.

The main result of this paper is the following higher integrability estimate for the gradient of a weak solution to (2.3). The constants depend on

$$\begin{aligned} \begin{aligned} data =&(n,N,p,q,\alpha ,\nu ,L,[a]_{\alpha },{{\,\textrm{diam}\,}}(\Omega ),\\&\Vert u\Vert _{L^\infty (0,T;L^2(\Omega ))},\Vert H(z,|\nabla u|)\Vert _{L^1(\Omega _T)},\Vert H(z,|F|)\Vert _{L^1(\Omega _T)}). \end{aligned} \end{aligned}$$

Theorem 2.2

Let u be a weak solution to (2.3). There exist constants $0<\epsilon _0=\epsilon _0( data )$ and $c=c( data ,\Vert a\Vert _{L^\infty (\Omega _T)})\ge 1$, such that

for every $Q_{2r}(z_0)\subset \Omega _T$ and $\epsilon \in (0,\epsilon _0)$.

2.3 Auxiliary lemmas

We start with two estimates derived from the weak formulation of (2.3). A priori Definition 2.1 does not guarantee that u can be used as a test function in the weak formulation and thus we do not immediately obtain the following Caccioppoli inequality. A Lipschitz truncation method could be used as in the degenerate case [12], but we omit the proof since it is beyond the scope of this paper.

Lemma 2.3

Let u be a weak solution to (2.3). There exists a constant $c=c(n,p,q,\nu ,L)$, such that

for every $Q_{R,\ell }(z_0)\subset \Omega _T$, with $R,\ell >0$, $r\in [R/2,R)$ and $\tau \in [\ell /2^2,\ell )$.

The following parabolic Poincaré inequality can be shown in the same way as in [11].

Lemma 2.4

Let u be a weak solution to (2.3). There exists a constant $c=c(n,N,m,L)$, such that

for every $Q_{R,\ell }(z_0\subset \Omega _T$ with $R,\ell >0$, $m\in (1,q]$ and $\theta \in (1/m,1]$.

Finally, we have two technical lemmas. The first lemma is a Gagliardo–Nirenberg inequality and the second one is a standard iteration lemma, see [9, Lemma 8.3].

Lemma 2.5

Let $B_{\rho }(x_0)\subset {\mathbb {R}}^n$, $\sigma ,s,r\in [1,\infty )$ and $\vartheta \in (0,1)$ such that

$$\begin{aligned} -\frac{n}{\sigma }\le \vartheta \left( 1-\frac{n}{s}\right) -(1-\vartheta )\frac{n}{r}. \end{aligned}$$

Then there exists a constant $c=c(n,\sigma )$, such that

for every $v\in W^{1,s}(B_{\rho }(x_0))$.

Lemma 2.6

Let $0<r<R<\infty$ and $h:[r,R]\longrightarrow {\mathbb {R}}$ be a non-negative and bounded function. Suppose there exist $\vartheta \in (0,1)$, $A,B\ge 0$ and $\gamma >0$ such that

$$\begin{aligned} h(r_1)\le \vartheta h(r_2)+\frac{A}{(r_2-r_1)^\gamma }+B \quad \text {for all}\quad 0<r\le r_1<r_2\le R. \end{aligned}$$

Then there exists a constant $c=c(\vartheta ,\gamma )$, such that

$$\begin{aligned} h(r)\le c\left( \frac{A}{(R-r)^\gamma }+B\right) . \end{aligned}$$

3 Reverse Hölder inequality

In this section we provide a reverse Hölder inequality for u, a weak solution to (2.3). The reverse Hölder inequality is used to show the higher integrability result in the next section. We consider the p-intrinsic and (p, q)-intrinsic cases in separate subsections. In both cases we show parabolic Sobolev–Poincaré inequalities and a series of estimates leading to the reverse Hölder inequality.

Throughout this section, let $z_0=(x_0,t_0)\in \Omega _T$, with $x_0\in \Omega$ and $t_0\in (0,T)$, be a Lebesgue point of $|\nabla u(z)|^p+a(z)|\nabla u(z)|^q$ satisfying

$$\begin{aligned} |\nabla u(z_0)|^p+a(z_0)|\nabla u(z_0)|^q>\Lambda \end{aligned}$$

for some $\Lambda >1+\Vert a\Vert _{L^\infty (\Omega _T)}$. Note that $H(z_0,s)$ is strictly increasing and continuous with

$$\begin{aligned} \lim _{s\rightarrow 0^+}H(z_0,s)=0 \quad \text {and}\quad \lim _{s\rightarrow \infty }H(z_0,s)=\infty . \end{aligned}$$

Therefore, by the intermediate value theorem for continuous functions, there exists $\lambda =\lambda (z_0)>1$, such that

$$\begin{aligned} \Lambda =\lambda ^p+a(z_0)\lambda ^q. \end{aligned}$$

We also use the constants

$$\begin{aligned} M_1=\frac{1}{2|B_1|}\iint _{\Omega _T}\left( H(z,|\nabla u|)+H(z,|F|)\right) \,dz \end{aligned}$$

(3.1)

and

$$\begin{aligned} M_2=\Vert u\Vert _{L^\infty (0,T;L^2(\Omega ))}, \quad K=2+40[a]_\alpha M_1^\frac{\alpha }{n+2}, \quad \kappa = 10K. \end{aligned}$$

In the p-intrinsic case we consider a cylinder $Q_\rho ^\lambda (z_0)$ defined as in (2.1) and assume the following:

• (p-1) p-intrinsic case: $K\lambda ^{p}\ge a(z_0)\lambda ^q$.

• (p-2) Stopping time argument for a p-intrinsic cylinder:

  • (p-i)

  • (p-ii) for every $s\in (\rho ,2\kappa \rho ]$.

In the (p, q)-intrinsic case we consider a cylinder $G_\rho ^\lambda (z_0)$ defined as in (2.2) and assume the following:

• (p,q-1) (p, q)-intrinsic case: $K\lambda ^{p}< a(z_0)\lambda ^q$.

• (p,q-2) $\tfrac{a(z_0)}{2}\le a(z)\le 2a(z_0)$ for every $z\in G_{4\rho }^\lambda (z_0).$

• (p,q-3) Stopping time argument for a (p, q)-intrinsic cylinder:

  • (p,q-i)

  • (p,q-ii) for every $s\in (\rho ,2\kappa \rho ]$.

The fact that these two cases are complementary will be shown in Sect. 4.1.

The following decay estimate will be used in this and the next section. Note that the estimate holds without assumption (p-1).

Lemma 3.1

Assumption (p-i) implies

$$\begin{aligned} \rho ^\alpha \le \frac{K}{40[a]_\alpha }\lambda ^{-\frac{\alpha \mu }{n+2}}\quad \text {and}\quad \rho ^\alpha \lambda ^q\le \frac{K}{40[a]_\alpha }\lambda ^p, \end{aligned}$$

(3.2)

where $\mu >0$ is defined in (1.1).

Proof

It follows from (p-i) and (3.1) that

$$\begin{aligned} \lambda ^p=\frac{\lambda ^{\frac{(2-p)n}{2}}}{2\rho ^{n+2}|B_1|}\iint _{Q_{\rho }^\lambda (z_0)}\left( H(z,|\nabla u|)+H(z,|F|)\right) \,dz\le \frac{\lambda ^{\frac{(2-p)n}{2}}}{\rho ^{n+2}}M_1. \end{aligned}$$

Therefore, we have by (1.1) that $\rho ^\alpha \le M_1^\frac{\alpha }{n+2}\lambda ^{-\frac{\alpha \mu }{n+2}}\le \tfrac{K}{40[a]_\alpha }\lambda ^{-\frac{\alpha \mu }{n+2}}$. Also $\rho ^\alpha \lambda ^q\le \tfrac{K}{40[a]_\alpha }\lambda ^p$ follows from (1.1). $\square$

Remark 3.2

The range of q is determined to satisfy the second inequality of (3.2) and this is where the intrinsic deficit appears in the range of q. Although it is not mentioned in [11], the same argument holds for the degenerate case.

3.1 The p-intrinsic case

In this subsection we show a reverse Hölder inequality in the p-intrinsic cylinder $Q_\rho ^\lambda (z_0)$ satisfying (p-1), (p-2) and $Q_{2\kappa \rho }^\lambda (z_0)\subset \Omega _T$. The scaling deficit $\mu$ defined in (1.1) plays a role throughout the argument. In particular, note that $0<p-1-\tfrac{\alpha \mu }{n+2}<1$. We begin by estimating the last term in Lemma 2.4.

Lemma 3.3

For $s\in [2\rho ,4\rho ]$ and $\theta \in ((q-1)/p,1]$, there exists a constant $c=c(n,p,q,\alpha ,L,[a]_{\alpha },M_1)$, such that

Proof

By (2.4) there exists a constant $c=c([a]_{\alpha })$, such that

(3.3)

We apply (p-1) to estimate the second term on the right-hand side of (3.3) and obtain

In order to estimate the last term on the right-hand side of (3.3), note that by (3.2) we have

$$\begin{aligned} s\le 4\rho \le c(M_1,n)\lambda ^\frac{-\mu }{n+2}. \end{aligned}$$

(3.4)

As $q-1<p$ by $\alpha \le 1$ and (1.1), it follows from Hölder’s inequality, (3.4) and (p-ii) that

where $c=c(n,p,\alpha ,M_1)$ and $\theta \in ((q-1)/p,1]$. It follows from (p-ii), $\lambda \ge 1$ and (1.1) that

where $c=c(n,p,q,\alpha )$. We conclude that

where $c=c(n,p,q,\alpha ,M_1)$. Similarly, replacing $|\nabla u|$ by |F| in the above argument, we have

This completes the proof. $\square$

Next, we provide a p-intrinsic parabolic Poincaré inequality.

Lemma 3.4

For $s\in [2\rho ,4\rho ]$ and $\theta \in ((q-1)/p,1]$, there exists a constant $c=c(n,N,p,q,\alpha ,L,[a]_{\alpha },M_1)$, such that

Proof

By Lemmas 2.4 and 3.3, there exists a constant $c=c(n,N,p,q, \alpha ,L,[a]_{\alpha },M_1)$, such that

(3.5)

To estimate the second term on the right-hand side of (3.5), we use Hölder’s inequality and (p-ii) to obtain

where $c=c(n,p)$. Similarly, the third term on the right-hand side of (3.5) is estimated by

where $c=c(n,N,p,q,\alpha ,L,[a]_{\alpha },M_1)$. This finishes the proof. $\square$

Lemma 3.5

For $s\in [2\rho ,4\rho ]$ and $\theta \in ((q-1)/p,1]$, there exists a constant $c=c(n,N,p,q,\alpha ,L,[a]_{\alpha },M_1)$, such that

Proof

By Lemmas 2.4 and 3.3, there exists a constant $c=c(n,N,p,q, \alpha ,L,[a]_{\alpha },M_1)$, such that

(3.6)

By (p-1) and (p-ii), we obtain for the second term on the right-hand side of (3.6) that

where $c=c(n,p,\alpha ,[a]_{\alpha },M_1)$. Similarly, the third and the fourth terms on the right-hand side of (3.6) can be estimated by

and

The conclusion follows from Hölder’s inequality. $\square$

In the following lemma we estimate the quadratic term

Lemma 3.6

There exists a constant $c=c( data )$, such that

Proof

Let $2\rho \le \rho _1<\rho _2\le 4\rho$. By Lemma 2.3, there exists a constant $c=c(n,p,q,\nu ,L)$, such that

(3.7)

We estimate the first term on the right-hand side of (3.7). From Lemma 3.4 and (p-ii), we obtain

(3.8)

where $c=c(n,N,p,q,\alpha ,L,[a]_{\alpha },M_1)$. On the other hand, we observe that

(3.9)

By Lemma 3.5 and (p-ii), we have

where $c=c(n,N,p,q,\alpha ,L,[a]_{\alpha },M_1)$. For the other term in (3.9), we obtain from Lemma 2.5 with $\sigma =q$, $s=p$, $r=2$ and $\vartheta =\tfrac{p}{q}$, that

where $c=c(n,q)$. We have by (3.8) and (p-ii) and (3.2) that

where the last inequality follows from (1.1) and $c=c(n,N,p,q,\alpha ,L,[a]_{\alpha },M_1)$. We conclude that

where $c=c(n,N,p,q,\alpha ,L,[a]_{\alpha },M_1)$.

Next, we estimate the second term on the right-hand side of (3.7). Using Lemma 2.5 with $\sigma =2, s=p, r=2, \vartheta =1/2$, and then (3.8) and (p-ii), we have

where $c=c(n,N,p,q,\alpha ,L,[a]_{\alpha },M_1)$. Observe that by $p> \tfrac{2n}{n+2}$ it was possible to use these parameters in Lemma 2.5 as

$$\begin{aligned} \frac{n}{2}+\frac{1}{2}-\frac{n}{2p}-\frac{n}{4}\ge \frac{n}{2}+\frac{1}{2}-\frac{n+2}{4}-\frac{n}{4}=0. \end{aligned}$$

For the last term on the right-hand side of (3.7) we obtain by (p-ii) that

Combining the estimates, we conclude from (3.7) that

$$\begin{aligned} \begin{aligned} S(u,Q_{\rho _1}^\lambda (z_0))&\le c\frac{\rho _2^q}{(\rho _2-\rho _1)^q}\lambda ^2+c\frac{\rho _2^q}{(\rho _2-\rho _1)^q}\lambda ^{p-q+2}\left( S(u,Q_{\rho _2}^\lambda (z_0))\right) ^\frac{q- p}{2}\\&\quad +c\frac{ \rho _2^2}{(\rho _2-\rho _1)^2}\lambda \ S(u,Q_{\rho _2}^\lambda (z_0))^\frac{1}{2}, \end{aligned} \end{aligned}$$

where $c=c(n,N,p,q,\alpha ,L,[a]_{\alpha },M_1)$. Finally, we apply Young’s inequality twice, with conjugate pairs (2, 2) and $(\tfrac{2}{q-p},\tfrac{2}{2-q+p})$, to obtain

$$\begin{aligned} \begin{aligned} S(u,Q_{\rho _1}^\lambda (z_0))&\le \frac{1}{2}S(u,Q_{\rho _2}^\lambda (z_0))\\&+ c\left( \frac{\rho _2^q}{(\rho _2-\rho _1)^q}+\frac{\rho _2^\frac{2q}{2-q+p}}{(\rho _2-\rho _1)^\frac{2q}{2-q+p}}+\frac{ \rho _2^4}{(\rho _2-\rho _1)^4}\right) \lambda ^2. \end{aligned} \end{aligned}$$

The proof is concluded by an application of Lemma 2.6. $\square$

Next, we prove an estimate for the first term on the right-hand side of the energy estimate in Lemma 2.3 by using Lemma 2.5.

Lemma 3.7

There exist constants $c=c( data )$ and $\theta _0=\theta _0(n,p,q)\in (0,1)$, such that for any $\theta \in (\theta _0,1)$ we have

Proof

By (2.4) we obtain

(3.10)

We begin with the first term on the right-hand side of (3.10). The condition in Lemma 2.5 with $\sigma =p$, $s=\theta p$, $r=2$ and $\vartheta = \theta$ is satisfied for $\theta \in (n/(n+2),1)$, and we obtain

where $c=c(n,p)$.

For the second term on the right-hand side of (3.10), we apply Lemma 2.5 with $\sigma =q$, $s=\theta q$, $\vartheta = \theta$ and $r=2$. Again the condition of the lemma holds for $\theta \in (n/(n+2),1)$. We obtain

where $c=c(n,q)$. By using (p-1), we have

Then we consider the last term on the right-hand side of (3.10). The assumptions in Lemma 2.5 with $\sigma =q$, $s=\theta p$, $r = 2$ and $\vartheta =\theta p/q$ are satisfied for $\theta \in (nq/((n+2)p),1)$, and we obtain

where $c=c(n,q)$. Note that

and that from (3.2) we obtain $\rho \le c(M_1,n)\lambda ^\frac{-\mu }{n+2}$. Therefore

where $c=c(n,p,q,\alpha ,{{\,\textrm{diam}\,}}(\Omega ),M_1,M_2)$. Observe that the last inequality follows from (1.1), as

$$\begin{aligned} \begin{aligned}&\frac{-\mu }{n+2}(\alpha -\frac{(q-p)(n+2)}{2})+\frac{(2-p)(q-p)(n+2)}{4}\\&\quad \le \frac{-\mu }{n+2}(\alpha -\frac{\alpha \mu }{2})+\frac{(2-p)\alpha \mu }{4}\\&\quad = \frac{\alpha \mu }{n+2}(-1+\frac{\mu }{2}+\frac{(2-p)(n+2)}{4})=0. \end{aligned} \end{aligned}$$

The claim follows by combining the estimates above. $\square$

Now we are ready to prove the reverse Hölder inequality in the p-intrinsic case.

Lemma 3.8

There exist constants $c=c( data )$ and $\theta _0=\theta _0(n,p,q)\in (0,1)$, such that for any $\theta \in (\theta _0,1)$ we have

Proof

Lemma 2.3 implies that

(3.11)

where $c=c(n,p,q,\nu ,L)$. To estimate the first term on the right-hand side of (3.11), we apply Lemmas 3.6 and 3.7 to conclude that there exist $\theta _0=\theta _0(n,p,q)\in (0,1)$ and $c=c( data )$, such that for any $\theta \in (\theta _0,1)$ we have

By Lemmas 3.4 and 3.5 we obtain

(3.12)

Note that $p-1-\tfrac{\alpha \mu }{n+2} > 0$ by (1.1). Letting

$$\begin{aligned} \beta =\min \left\{ p-1-\frac{\alpha \mu }{n+2},\frac{1}{2}\right\} , \end{aligned}$$

we obtain from (3.12) by (p-ii) that

To estimate the second term on the right-hand side of (3.11), we apply Lemma 2.5 with $\sigma = 2, s= \theta p, \vartheta = \tfrac{1}{2}$ and $r=2$, where $\theta \in (2n/((n+2)p),1)$. This and Lemma 3.6 gives

where $c=c( data )$. Applying Lemma 3.4 and (p-ii) to the right-hand side implies

Combining the estimates for the terms in (3.11) and applying (p-ii) gives

By applying Young’s inequality, we obtain

and using (p-i) to absorb $\tfrac{1}{2}\lambda ^p$ into the left hand side we conclude that

This completes the proof. $\square$

We finish this subsection with a corollary of the previous lemma which is used in the proof of higher integrability. The distribution sets are denoted as

$$\begin{aligned} \Psi (\Lambda )=\{ z\in \Omega _T: H(z,|\nabla u(z)|)>\Lambda \} \end{aligned}$$

(3.13)

and

$$\begin{aligned} \Phi (\Lambda )=\{ z\in \Omega _T: H(z,|F|)>\Lambda \}. \end{aligned}$$

(3.14)

Lemma 3.9

There exist constants $c=c( data )$ and $\theta _0=\theta _0(n,p,q)\in (0,1)$, such that for any $\theta \in (\theta _0,1)$ we have

$$\begin{aligned} \begin{aligned}&\iint _{Q_{2\kappa \rho }^\lambda (z_0)}H(z,|\nabla u|)\,dz \le c\Lambda ^{1-\theta }\iint _{Q_{2\rho }^\lambda (z_0)\cap \Psi (c^{-1}\Lambda )}H(z,|\nabla u|)^\theta \,dz\\&\quad +c\iint _{Q_{2\rho }^\lambda (z_0)\cap \Phi (c^{-1}\Lambda )}H(z,|F|)\,dz. \end{aligned} \end{aligned}$$

Proof

The condition (p-ii) implies that

By representing $Q_{2\rho }^\lambda (z_0)$ as a union of $Q_{2\rho }^\lambda (z_0)\cap \Psi ((4c)^{-1/\theta }\lambda ^p)$ and $Q_{2\rho }^\lambda (z_0)\setminus \Psi ((4c)^{-1/\theta }\lambda ^p)$ , we have

for any $c > 0$. A similar argument gives

It follows from Lemma 3.8 that

By recalling (p-2), we obtain

Thus, we have

$$\begin{aligned} \begin{aligned}&\iint _{Q_{2\kappa \rho }^\lambda (z_0)}H(z,|\nabla u|)\,dz\\&\quad \le 2c\lambda ^{p(1-\theta )}\iint _{Q_{2\rho }^\lambda (z_0)\cap \Psi ((4c)^{-1/\theta }\lambda ^p)}H(z,|\nabla u|)^{\theta }\,dz\\&\qquad +2c\iint _{Q_{2\rho }^\lambda (z_0)\cap \Phi ((4c)^{-1}\lambda ^p)}H(z,|F|)\,dz. \end{aligned} \end{aligned}$$

(3.15)

We note that

$$\begin{aligned} \frac{\lambda ^p}{4c}\ge \frac{\lambda ^p}{(4c)^{1/\theta }}\ge \frac{\lambda ^p}{(4c)^{1/\theta _0}}\ge \frac{\lambda ^p+a(z_0)\lambda ^q}{2K(4c)^{1/\theta _0}}=\frac{\Lambda }{2K(4c)^{1/\theta _0}}, \end{aligned}$$

where we applied (p-1). The estimate above implies that

$$\begin{aligned} \begin{aligned}&\Psi ((4c)^{-1/\theta }\lambda ^p)\subset \Psi ((2K(4c)^{1/\theta _0})^{-1}\Lambda ) \quad \text {and}\\&\quad \Phi ((4c)^{-1}\lambda ^p)\subset \Phi ((2K(4c)^{1/\theta _0})^{-1}\Lambda ). \end{aligned} \end{aligned}$$

Therefore, by replacing $2K(4c)^{1/\theta _0}$ with c, (3.15) can be written as

$$\begin{aligned} \begin{aligned}&\iint _{Q_{2\kappa \rho }^\lambda (z_0)}H(z,|\nabla u|)\,dz \le c\Lambda ^{1-\theta }\iint _{Q_{2\rho }^\lambda (z_0)\cap \Psi (c^{-1}\Lambda )}H(z,|\nabla u|)^{\theta }\,dz\\&\quad +c\iint _{Q_{2\rho }^\lambda (z_0)\cap \Phi (c^{-1}\Lambda )}H(z,|F|)\,dz. \end{aligned} \end{aligned}$$

This completes the proof. $\square$

3.2 The (p, q)-intrinsic case

In this subsection we show a reverse Hölder inequality in the (p, q)-intrinsic cylinder $G_\rho ^\lambda (z_0)$ satisfying (p,q-1), (p,q-2), (p,q-3) and $G_{2\kappa \rho }^\lambda (z_0)\subset \Omega _T$. Note that (p,q-2) and (p,q-ii) imply

It follows that

(3.16)

We start with a (p, q)-intrinsic parabolic Poincaré inequality.

Lemma 3.10

For $s\in [2\rho ,4\rho ]$ and $\theta \in ((q-1)/p,1]$, there exists a constant $c=c(n,N,p,q,L)$, such that

Proof

Note that

Therefore, by Lemma 2.4 and (p,q-2), there exists a constant $c=c(n,N,p,q,L)$, such that

(3.17)

To estimate the second term on the right-hand side of (3.17), we note that

By (3.16) and Hölder’s inequality, and the same argument for the term with $H(z_0,|F|)$, we have

where $c=c(p,q)$. We conclude that

(3.18)

where $c=c(p,q)$. In order to estimate the first term on the right-hand side of (3.18), we apply Hölder’s inequality and (3.16) to get

for any $\theta \in ((q-1)/p,1]$ with $c=c(n,p)$. Similarly, we have for any $\theta \in ((q-1)/q,1]$ that

where $c=c(n,p)$. Combining the above inequalities, we conclude that

which completes the proof. $\square$

Note that by replacing $H(z_0,s)^\theta$ with $s^{\theta p}$ in the proof of Lemma 3.10, we also get the following result. All necessary calculations are already contained in the proof of the previous lemma.

Lemma 3.11

For $s\in [2\rho ,4\rho ]$ and $\theta \in ((q-1)/p,1]$, there exists a constant $c=c(n,N,p,q,L)$, such that

As in the previous subsection, we estimate the term

Lemma 3.12

There exists a constant $c=c(n,N,p,q,\nu ,L)$, such that

Proof

Let $2\rho \le \rho _1<\rho _2\le 4\rho$. By Lemma 2.3, there exists a constant $c=c(n,p,q,\nu ,L)$, such that

(3.19)

For the first term on the right-hand side of (3.19), we apply Lemma 3.10, together with (p,q-2) and (p,q-ii), to obtain

where $c=c(n,N,p,q,L)$.

For the second term on the right-hand side of (3.19) we obtain by Lemma 2.5, as in the proof of Lemma 3.6, that

where $c=c(n,N,p)$. Using Lemma 3.11 and (3.16), we obtain

where $c=c(n,N,p,q,L)$. Combining the estimates and applying (p,q-ii) for the last term on the right-hand side of (3.19), we get

$$\begin{aligned} S(u,G_{\rho _1}^\lambda (z_0)) \le c\frac{\rho _2^q}{(\rho _2-\rho _1)^q}\lambda ^2+c\frac{ \rho _2^2}{(\rho _2-\rho _1)^2}\lambda \ S(u,Q_{\rho _2}^\lambda (z_0))^\frac{1}{2}. \end{aligned}$$

The claim follows by applying Young’s inequality and Lemma 2.6 as in the proof of Lemma 3.6. $\square$

Lemma 3.13

There exists a constant $c=c(n,p,q)$, such that for any $\theta \in (n/(n+2),1)$ we have

Proof

We obtain from (p,q-2) that

As in the proof of Lemma 3.7, by Lemma 2.5 there exists a constant $c=c(n,p,q)$, such that for any $\theta \in (n/(n+2),1)$ we have

and

We conclude that

This completes the proof. $\square$

Now we are ready to show the reverse Hölder inequality in (p, q)-intrinsic cylinders.

Lemma 3.14

There exist constants $c=c(n,N,p,q,\nu ,L)$ and $\theta _0=\theta _0(n,p,q)\in (0,1)$, such that for any $\theta \in (\theta _0,1)$ we have

Moreover, we have

$$\begin{aligned} \begin{aligned}&\iint _{G_{2\kappa \rho }^\lambda (z_0)}H(z,|\nabla u|)\,dz \le c\Lambda ^{1-\theta }\iint _{G_{2\rho }^\lambda (z_0)\cap \Psi (c^{-1}\Lambda )}H(z,|\nabla u|)^\theta \,dz\\&\quad +c\iint _{G_{2\rho }^\lambda (z_0)\cap \Phi (c^{-1}\Lambda )}H(z,|F|)\,dz, \end{aligned} \end{aligned}$$

where $\Psi (\Lambda )$ and $\Phi (\Lambda )$ are defined in (3.13) and (3.14).

Proof

Lemma 2.3 gives

(3.20)

Using Lemmas 3.13, 3.10 and 3.12 for the first term on the right-hand side of (3.20), we obtain

As in the proof of Lemma 3.8, we obtain from Lemmas 3.6 and 3.12 that

We conclude from Lemma 3.11 that

Therefore, we have for the second term on the right-hand side of (3.20) that

(3.21)

Note that by Hölder’s inequality

Using a similar argument for |F|, we conclude from (3.21) that

Collecting the estimates for the terms in (3.20) and applying Young’s inequality and (p,q-2), we obtain

We use (p,q-i) to absorb $\tfrac{1}{2}\Lambda$ into the left hand side. This completes the proof of the first statement.

To show the second statement, observe that as in the proof of Lemma 3.9, we obtain from the first statement that

It follows from (p,q-3) that

and we have

$$\begin{aligned} \begin{aligned} \iint _{G_{2\kappa \rho }^\lambda (z_0)}H(z,|\nabla u|)\,dz&\le c\Lambda ^{(1-\theta )}\iint _{G_{2\rho }^\lambda (z_0)\cap \Psi ((4c)^{-1/\theta }\Lambda )}H(z,|\nabla u|)^{\theta }\,dz\\&\quad +c\iint _{G_{2\rho }^\lambda (z_0)\cap \Phi ((4c)^{-1}\Lambda )}H(z,|F|)\,dz. \end{aligned} \end{aligned}$$

This completes the proof.

$\square$

4 Proof of the main result

In this section we complete the proof of Theorem 2.2. In the first subsection, we use a stopping time argument to construct intrinsic cylinders which are either p-intrinsic, as in (p-1)-(p-2), or (p, q)-intrinsic, as in (p,q-1)-(p,q-3). In the second subsection, we construct a Vitali type covering for this collection of intrinsic cylinders. Also here the decay estimate of Lemma 3.1 is needed to show the covering property of the intrinsic cylinders. In the last subsection, we complete the proof of the gradient estimate by applying Fubini’s theorem together with Lemma 2.6.

4.1 Stopping time argument

Let

(4.1)

Moreover, recalling the definition of $M_1$ in (3.1), let

$$\begin{aligned} K=2+40[a]_{\alpha } M_1^\frac{\alpha }{n+2}\text {and}\quad \kappa =10K. \end{aligned}$$

(4.2)

Recalling the notation in (3.13) and (3.14), for $\rho \in [r,2r]$ we denote

$$\begin{aligned} \Psi (\Lambda ,\rho )=\Psi (\Lambda )\cap Q_{\rho }(z_0)=\{ z\in Q_{\rho }(z_0): H(z,|\nabla u(z)|)>\Lambda \} \end{aligned}$$

and

$$\begin{aligned} \Phi (\Lambda ,\rho )=\Phi (\Lambda )\cap Q_{\rho }(z_0) =\{ z\in Q_{\rho }(z_0): H(z,|F(z)|)>\Lambda \}. \end{aligned}$$

Next, we apply a stopping time argument. Let $r\le r_1<r_2\le 2r$ and

$$\begin{aligned} \Lambda >\left( \frac{4\kappa r}{r_2-r_1}\right) ^\frac{2q(n+2)}{p(n+2)-2n}\Lambda _0, \end{aligned}$$

(4.3)

where $\kappa$ is as in (4.2). For every $w\in \Psi (\Lambda ,r_1)$, let $\lambda _w>0$ be such that

$$\begin{aligned} \Lambda =\lambda _w^p+a( w)\lambda _w^q. \end{aligned}$$

(4.4)

We claim that

$$\begin{aligned} \lambda _w>\left( \frac{4\kappa r}{r_2-r_1}\right) ^\frac{2(n+2)}{p(n+2)-2n}\lambda _0. \end{aligned}$$

(4.5)

For a contradiction, assume that the inequality above does not hold. Then

$$\begin{aligned} \begin{aligned} \Lambda&=\lambda _w^p+a(w)\lambda _w^q \\&\le \left( \frac{4\kappa r}{r_2-r_1}\right) ^\frac{2q(n+2)}{p(n+2)-2n}\left( \lambda _0^p+a( w)\lambda _0^q\right) \le \left( \frac{ 4\kappa r}{r_2-r_1}\right) ^\frac{2q(n+2)}{p(n+2)-2n}\Lambda _0, \end{aligned} \end{aligned}$$

which is a contradiction with (4.3). Therefore, (4.5) is true and we have for every $s\in [(r_2-r_1)/(2\kappa ),r_2-r_1)$ that

By (4.4) we have $w\in \Psi (\lambda _w^p,r_1)$. Therefore, by the Lebesgue differentiation theorem there exists $\rho _{ w}\in (0,(r_2-r_1)/(2\kappa ))$, such that

and

(4.6)

for every $s\in (\rho _{ w},r_2-r_1)$. This shows that at each point $w\in \Psi (\Lambda ,r_1)$ we have a p-intrinsic cylinder satisfying (p-2).

Next, we assume that

$$\begin{aligned} K\lambda _w^p< a( w)\lambda _w^q \end{aligned}$$

(4.7)

and show that in this case there exists a (p, q)-intrinsic cylinder satisfying (p,q-2) and (p,q-3). For every $s\in [\rho _{ w},r_2-r_1)$, we have by (2.1), (2.2), (4.4) and (4.6) that

Recall that $w\in \Psi (\Lambda ,r_1)$. Again by the Lebesgue differentiation theorem, we find $\varsigma _{w}\in (0,\rho _{w}]$ such that

and

for every $s\in (\varsigma _{w},r_2-r_1)$.

To show (p,q-2), we claim that

$$\begin{aligned} a( w)\ge 2[a]_{\alpha }(10\rho _{ w})^\alpha . \end{aligned}$$

(4.8)

Assume for contradiction that the opposite holds. By (4.7) and the negation of (4.8), we have

$$\begin{aligned} K\lambda _w^p< 20[a]_{\alpha }\rho _{ w}^{\alpha }\lambda _w^q. \end{aligned}$$

As (4.6) holds true also in this case, Lemma 3.1 gives

$$\begin{aligned} K\lambda _w^p\le 20[a]_{\alpha }\frac{K}{40[a]_\alpha }\lambda _w^p \le \frac{K}{2}\lambda _w^p. \end{aligned}$$

This is a contradiction and therefore (4.8) is true. It follows from (4.8), that

$$\begin{aligned} 2[a]_{\alpha }(10\rho _{ w})^\alpha \le a( w)\le \inf _{Q_{10\rho _{ w}}( w)}a(z)+[a]_{\alpha }(10\rho _{ w})^\alpha \end{aligned}$$

and

$$\begin{aligned} \sup _{Q_{10\rho _{ w}}( w)}a(z)\le \inf _{Q_{10\rho _{ w}}( w)}a(z)+[a]_{\alpha }(10\rho _{ w})^\alpha \le 2\inf _{Q_{10\rho _{ w}}( w)}a(z). \end{aligned}$$

Therefore, when (4.7) is true

$$\begin{aligned} \frac{a( w)}{2}\le a(z)\le 2a( w) \text { for every } z\in Q_{10\rho _{ w}}( w). \end{aligned}$$

As $\varsigma _w \le \rho _w$, we have shown the properties (p,q-1)-(p,q-3).

4.2 Vitali type covering argument

For each $w\in \Psi (\Lambda ,r_1)$, we consider

$$\begin{aligned} U( w)= {\left\{ \begin{array}{ll} Q_{2\rho _{ w}}^{\lambda _w}( w)&{}\text { in { p}-intrinsic case,}\\ G_{2\varsigma _{ w}}^{\lambda _w}( w)&{}\text { in ({ p},\,{ q})-intrinsic case.} \end{array}\right. } \end{aligned}$$

We prove a Vitali type covering lemma for this collection of intrinsic cylinders. We denote

$$\begin{aligned} {\mathcal {F}}=\left\{ U( w): w\in \Psi (\Lambda ,r_1)\right\} \quad \text {and}\quad l_{ w}= {\left\{ \begin{array}{ll} 2\rho _{w}&{}\text {in { p}-intrinsic case,}\\ 2\varsigma _{w}&{}\text {in ({ p},\,{ q})-intrinsic case.} \end{array}\right. } \end{aligned}$$

Recall that $l_{ w}\in (0,R)$ for every $w\in \Psi (\Lambda ,r_1)$, where $R=(r_2-r_1)/\kappa$ and $\kappa$ is as in (4.2). Let

$$\begin{aligned} {\mathcal {F}}_j=\left\{ U( w)\in {\mathcal {F}}: \frac{R}{2^j}<l_{ w}\le \frac{R}{2^{j-1}} \right\} ,\quad j\in {\mathbb {N}}. \end{aligned}$$

We construct subcollections ${\mathcal {G}}_j\subset {\mathcal {F}}_j$, $j\in {\mathbb {N}}$, recursively as follows. Let ${\mathcal {G}}_1$ be a maximal disjoint collection of cylinders in ${\mathcal {F}}_1$. Observe that for each $U(w)\in {\mathcal {F}}_j$ we have

$$\begin{aligned} \left( \frac{R}{2^j}\right) ^{n+2}\Lambda ^{-1}\le |U(w)|, \end{aligned}$$

which implies that the collection is finite. Suppose that we have selected ${\mathcal {G}}_1,\ldots ,{\mathcal {G}}_{k-1}$ with $k\ge 2$, and let

$$\begin{aligned} {\mathcal {G}}_k=\left\{ U( w)\in {\mathcal {F}}_k: U( w)\cap U( v)=\emptyset \text { for every }U( v)\in \bigcup _{j=1}^{k-1}{\mathcal {G}}_j\right\} \end{aligned}$$

be a maximal collection of pairwise disjoint cylinders. It follows that

$$\begin{aligned} {\mathcal {G}}=\bigcup _{j=1}^\infty {\mathcal {G}}_j, \end{aligned}$$

(4.9)

is a countable subcollection of pairwise disjoint cylinders in ${\mathcal {F}}$. We claim that for each $U( w)\in {\mathcal {F}}$, there exists $U( v)\in {\mathcal {G}}$ such that

$$\begin{aligned} U( w)\cap U( v)\ne \emptyset \quad \text {and}\quad U( w)\subset \kappa U( v). \end{aligned}$$

(4.10)

For every $U( w)\in {\mathcal {F}}$, there exists $j \in {\mathbb {N}}$ such that $U( w)\in {\mathcal {F}}_j$. By the construction of ${\mathcal {G}}_j$, there exists a cylinder $U( v)\in \cup _{i=1}^j {\mathcal {G}}_i$ for which the first condition in (4.10) holds true. Moreover, since $l_{ w}\le \tfrac{R}{2^{j-1}}$ and $l_{ v} \ge \tfrac{R}{2^j}$, we have

$$\begin{aligned} l_{ w}\le 2l_{ v}. \end{aligned}$$

(4.11)

In the remaining of this subsection, we prove the second claim in (4.10). First, we show the comparability of $\lambda _w$ and $\lambda _v$ using the following observations. For $i\in \{v,w\}$, there exist $2\rho _i\ge l_i>0$ and $\lambda _i>0$ such that

$$\begin{aligned} \Lambda =\lambda _i^p+a(z_i)\lambda _i^q \end{aligned}$$

(4.12)

and

(4.13)

It follows from (4.13) and (3.2) that

$$\begin{aligned} \rho _i^\alpha \lambda _i^q\le \frac{K}{40[a]_\alpha }\lambda _i^p. \end{aligned}$$

(4.14)

Moreover, the first condition in (4.10) and (4.11) imply that $Q_{l_{w}}(w) \cap Q_{l_{v}}(v) \ne \emptyset$ and

$$\begin{aligned} Q_{l_{w}}(w) \subset Q_{5l_{v}}(v)\subset Q_{10\rho _v}(v). \end{aligned}$$

Therefore, we have by (2.4) that

$$\begin{aligned} | a(w) - a(v) | \le [a]_\alpha (10 \rho _v)^\alpha . \end{aligned}$$

(4.15)

Now we show the comparability of $\lambda _w$ and $\lambda _v$. First, we claim that if $\lambda _w \le \lambda _v$, then

$$\begin{aligned} \lambda _v\le K^\frac{1}{p}\lambda _w. \end{aligned}$$

(4.16)

For a contradiction, assume that (4.16) does not hold. By (4.12) and (4.15), we have

$$\begin{aligned} \begin{aligned} \Lambda =\lambda _w^p+a(w)\lambda _w^q\le \lambda _w^p+a(v)\lambda _w^q+[a]_{\alpha }(10\rho _v)^{\alpha }\lambda _w^q. \end{aligned} \end{aligned}$$

From the negation of (4.16) and (4.14), we obtain

$$\begin{aligned} 10[a]_{\alpha }\rho _v^\alpha \lambda _w^q < \frac{1}{K^\frac{q}{p}}10[a]_{\alpha }\rho _v^\alpha \lambda _v^q \le \frac{1}{K^\frac{q}{p}}10[a]_{\alpha }\frac{K}{40[a]_\alpha }\lambda _v^p \le \frac{1}{2} \lambda _v^p. \end{aligned}$$

Negation of (4.16) and the above estimates lead to the contradiction

$$\begin{aligned} \Lambda < \frac{1}{2}\left( \lambda _v^p+a(v)\lambda _v^q\right) +\frac{1}{2}\lambda _v^p\le \Lambda , \end{aligned}$$

and thus (4.16) holds.

On the other hand, if $\lambda _v\le \lambda _w$, we claim that

$$\begin{aligned} \lambda _w\le K^\frac{1}{p}\lambda _v. \end{aligned}$$

Again, assume for contradiction that the opposite holds. It follows from (4.14) that

$$\begin{aligned} \begin{aligned} \Lambda&=\lambda _v^p+a(v)\lambda _v^q\le \lambda _v^p+a(w)\lambda _v^q+[a]_{\alpha }(10\rho _v)^\alpha \lambda _v^q\\&\le \lambda _v^p+a(w)\lambda _v^q+\frac{K}{4}\lambda _v^p\\&< \frac{1}{K}\lambda _w^p+\frac{1}{K^\frac{q}{p}}a(w)\lambda _w^q+\frac{1}{4}\lambda _w^p\le \Lambda , \end{aligned} \end{aligned}$$

which is a contradiction. We conclude that

$$\begin{aligned} K^{-\frac{1}{p}}\lambda _w\le \lambda _v \le K^\frac{1}{p} \lambda _w. \end{aligned}$$

(4.17)

We show that the second claim in (4.10) holds in all four possible cases that may occur:

• (i) $U(v)=Q_{l_v}^{\lambda _v}(v)$ and $U(w)=Q_{l_w}^{\lambda _w}(w)$,

• (ii) $U(v)=G_{l_v}^{\lambda _v}(v)$ and $U(w)=G_{l_w}^{\lambda _w}(w)$,

• (iii) $U(v)=G_{l_v}^{\lambda _v}(v)$ and $U(w)=Q^{\lambda _w}_{l_w}(w)$ or

• (iv) $U(v)=Q_{l_v}^{\lambda _v}(v)$ and $U(w)=G_{l_w}^{\lambda _w}(w)$.

Proof for the spatial inclusion is the same in all the cases. We denote $v=(x_v,t_v)$ and $w=(x_w,t_w)$, where $x_v,x_w\in {\mathbb {R}}^n$ and $t_v,t_w\in {\mathbb {R}}$, and recall the notation in (2.1) and (2.2). For any $\xi \in B_{l_w}^{\lambda _w}(w)$ we have by (4.11) and (4.17), that

$$\begin{aligned} \begin{aligned} |\xi -x_v|&\le |\xi -x_w|+|x_w-x_v|\le 2l_w\lambda _w^\frac{p-2}{2}+l_v\lambda _v^\frac{p-2}{2}\\&\le 4K^\frac{2-p}{2p} l_v\lambda _v^\frac{p-2}{2}+l_v\lambda _v^\frac{p-2}{2}\le 6Kl_v\lambda _v^\frac{p-2}{2}, \end{aligned} \end{aligned}$$

and therefore $B_{l_w}^{\lambda _w}(w) \subset 6KB_{l_v}^{\lambda _v}(v)$.

We show the inclusion in time direction in the four possible cases separately. In case (i), we have by (4.11) for any $\tau \in I_{l_w}(t_w)$ that

$$\begin{aligned} |\tau - t_v|\le |\tau - t_w| + |t_w - t_v|\le 2l_w^2+ l_v^2\le 9l_v^2, \end{aligned}$$

and therefore $I_{l_w}(t_w) \subset 9I_{l_v}(t_v)$.

In case (ii), we have by (4.11) and (4.17) for any $\tau \in J^{\lambda _w}_{l_w}(t_w)$ that

$$\begin{aligned} |\tau - t_v|\le |\tau - t_w| + |t_w - t_v|\le 2\frac{\lambda _w^p}{\Lambda }l_w^2+ \frac{\lambda _v^p}{\Lambda }l_v^2\le 9K\frac{\lambda _v^p}{\Lambda }l_v^2, \end{aligned}$$

and therefore $J^{\lambda _w}_{l_w}(t_w)\subset 9KJ^{\lambda _v}_{l_v}(t_v)$.

In case (iii) we have $K\lambda _w^p\ge a(w)\lambda _w^q$, which along with (4.17) and (4.12) gives

$$\begin{aligned} 1 = \frac{2\lambda _v^p}{2\lambda _v^p}\le \frac{2K\lambda _v^p}{2\lambda _w^p} \le \frac{2K\lambda _v^p}{\lambda _w^p+K^{-1}a(w)\lambda _w^q}\le \frac{2K^2\lambda _v^p}{\Lambda }. \end{aligned}$$

Therefore, we have for any $\tau \in I_{\rho _w}(t_w)$ that

$$\begin{aligned} |\tau - t_v| \le |\tau - t_w| + |t_w - t_v|\le 2 l_w^2 + \frac{\lambda _v^p}{\Lambda } l_v^2\le \frac{17K^2\lambda _v^p}{\Lambda } l_v^2. \end{aligned}$$

Together with the spatial inclusion this implies $Q_{l_w}^{\lambda _w}(w)\subset 6KG_{l_v}^{\lambda _v}(v)$.

Finally, in case (iv) we have by (4.11) and (4.12) for any $\tau \in J_{l_w}^{\lambda _w}(t_w)$ that

$$\begin{aligned} |\tau - t_v|\le |\tau - t_w| + |t_w - t_v|\le 2 \frac{\lambda _w^p}{\Lambda }l_w^2 + l_v^2 \le 9 l_v^2 , \end{aligned}$$

and therefore $J_{l_w}^{\lambda _w}(t_w) \subset 9KI_{l_v}(t_v)$. We have covered every case and conclude that (4.10) holds.

4.3 Final proof of the gradient estimate

We write the countable pairwise disjoint collection ${\mathcal {G}}$ defined in (4.9) as ${\mathcal {G}}=\cup _{j=1}^\infty U_j$, where $U_j=U( w_j)$ with $w_j \in \Psi (\Lambda ,r_1)$. By Lemma 3.9 and Lemma 3.14, there exist $c=c( data )$ and $\theta _0=\theta _0(n,p,q)\in (0,1)$, such that

$$\begin{aligned} \begin{aligned} \iint _{\kappa U_{j}}H(z,|\nabla u|)\,dz&\le c\Lambda ^{1-\theta }\iint _{U_j\cap \Psi (c^{-1}\Lambda )}H(z,|\nabla u|)^\theta \,dz\\&\quad +c\iint _{U_j\cap \Phi (c^{-1}\Lambda )}H(z,|F|)\,dz \end{aligned} \end{aligned}$$

for every $j\in {\mathbb {N}}$ with $\theta = (\theta _0+1)/2$. By summing over j and applying the fact that the cylinders in ${\mathcal {G}}$ are pairwise disjoint, we obtain

$$\begin{aligned} \begin{aligned}&\iint _{\Psi (\Lambda ,r_1)}H(z,|\nabla u|)\,dz \\&\quad \le \sum _{j=1}^\infty \iint _{\kappa U_{j}}H(z,|\nabla u|)\,dz \\&\quad \le c\Lambda ^{1-\theta }\sum _{j=1}^\infty \iint _{U_j\cap \Psi (c^{-1}\Lambda )}H(z,|\nabla u|)^\theta \,dz +c\sum _{j=1}^\infty \iint _{U_j\cap \Phi (c^{-1}\Lambda )}H(z,|F|)\,dz\\&\quad \le c\Lambda ^{1-\theta }\iint _{\Psi (c^{-1}\Lambda ,r_2)}H(z,|\nabla u|)^\theta \,dz +c\iint _{\Phi (c^{-1}\Lambda ,r_2)}H(z,|F|)\,dz. \end{aligned}\nonumber \\ \end{aligned}$$

(4.18)

Moreover, since

$$\begin{aligned} \iint _{\Psi (c^{-1}\Lambda ,r_1)\setminus \Psi (\Lambda ,r_1)}H(z,|\nabla u|)\,dz \le \Lambda ^{1-\theta }\iint _{\Psi (c^{-1}\Lambda ,r_2)}H(z,|\nabla u|)^{\theta }\,dz, \end{aligned}$$

we conclude from (4.18) that

$$\begin{aligned} \begin{aligned}&\iint _{\Psi (c^{-1}\Lambda ,r_1)}H(z,|\nabla u|)\,dz\\&\quad \le c\Lambda ^{1-\theta }\iint _{\Psi (c^{-1}\Lambda ,r_2)}H(z,|\nabla u|)^\theta \,dz +c\iint _{\Phi (c^{-1}\Lambda ,r_2)}H(z,|F|)\,dz. \end{aligned}\nonumber \\ \end{aligned}$$

(4.19)

For $k\in {\mathbb {N}}$, let

$$\begin{aligned} H(z,|\nabla u|)_k=\min \{H(z,|\nabla u|),k\} \end{aligned}$$

and

$$\begin{aligned} \Psi _k(\Lambda ,\rho )=\{z\in Q_{\rho }(z_0):H(z,|\nabla u(z)|)_k>\Lambda \}. \end{aligned}$$

It is easy to see that if $\Lambda >k$, then $\Psi _k(\Lambda ,\rho )=\emptyset$, and if $\Lambda \le k$, then $\Psi _k(\Lambda ,\rho )=\Psi (\Lambda ,\rho )$. Therefore, we deduce from (4.19) that

$$\begin{aligned} \begin{aligned}&\iint _{\Psi _k(c^{-1}\Lambda ,r_1)}\left( H(z,|\nabla u|)_k\right) ^{1-\theta }H(z,|\nabla u|)^\theta \,dz\\&\quad \le c\Lambda ^{1-\theta }\iint _{\Psi _k(c^{-1}\Lambda ,r_2)}H(z,|\nabla u|)^\theta \,dz+c\iint _{\Phi (c^{-1}\Lambda ,r_2)}H(z,|F|)\,dz. \end{aligned} \end{aligned}$$

Recalling (4.3), we denote

$$\begin{aligned} \Lambda _1=c^{-1}\left( \frac{4\kappa r}{r_2-r_1}\right) ^\frac{q(n+2)}{p(n+2)-2n}\Lambda _0. \end{aligned}$$

Then for any $\Lambda >\Lambda _1$, we obtain

$$\begin{aligned} \begin{aligned}&\iint _{\Psi _k(\Lambda ,r_1)}\left( H(z,|\nabla u|)_k\right) ^{1-\theta }H(z,|\nabla u|)^\theta \,dz\\&\quad \le c\Lambda ^{1-\theta }\iint _{\Psi _k(\Lambda ,r_2)}H(z,|\nabla u|)^\theta \,dz+c\iint _{\Phi (\Lambda ,r_2)}H(z,|F|)\,dz. \end{aligned} \end{aligned}$$

Let $\epsilon \in (0,1)$ to be chosen later. We multiply the inequality above by $\Lambda ^{\epsilon -1}$ and integrate each term over $(\Lambda _1,\infty )$, which implies

$$\begin{aligned} \begin{aligned} \textrm{I}&=\int _{\Lambda _1}^{\infty }\Lambda ^{\epsilon -1}\iint _{\Psi _k(\Lambda ,r_1)}\left( H(z,|\nabla u|)_k\right) ^{1-\theta }H(z,|\nabla u|)^\theta \,dz\,d\Lambda \\&\le c\int _{\Lambda _1}^{\infty }\Lambda ^{\epsilon -\theta }\iint _{\Psi _k(\Lambda ,r_2)}H(z,|\nabla u|)^\theta \,dz\,d\Lambda \\&\quad +c\int _{\Lambda _1}^{\infty }\Lambda ^{\epsilon -1}\iint _{\Phi (\Lambda ,r_2)}H(z,|F|)\,dz\,d\Lambda \\&= \textrm{II}+ \textrm{III}. \end{aligned} \end{aligned}$$

We apply Fubini’s theorem to estimate $\textrm{I}$ and obtain

$$\begin{aligned} \begin{aligned} \textrm{I}&=\frac{1}{\epsilon }\iint _{\Psi _k(\Lambda _1,r_1)}\left( H(z,|\nabla u|)_k\right) ^{1-\theta +\epsilon }H(z,|\nabla u|)^\theta \,dz\\&\quad -\frac{1}{\epsilon }\Lambda _1^\epsilon \iint _{\Psi _k(\Lambda _1,r_1)}\left( H(z,|\nabla u|)_k\right) ^{1-\theta }H(z,|\nabla u|)^\theta \,dz. \end{aligned} \end{aligned}$$

Since

$$\begin{aligned} \begin{aligned}&\iint _{Q_{r_1}(z_0)\setminus \Psi _k(\Lambda _1,r_1)}\left( H(z,|\nabla u|)_k\right) ^{1-\theta +\epsilon }H(z,|\nabla u|)^\theta \,dz\\&\quad \le \Lambda _1^{\epsilon }\iint _{Q_{2r}(z_0)}\left( H(z,|\nabla u|)_k\right) ^{1-\theta }H(z,|\nabla u|)^\theta \,dz, \end{aligned} \end{aligned}$$

we have

$$\begin{aligned} \begin{aligned} \textrm{I}\ge&\frac{1}{\epsilon }\iint _{Q_{r_1}(z_0)}\left( H(z,|\nabla u|)_k\right) ^{1-\theta +\epsilon }H(z,|\nabla u|)^\theta \,dz\\&-\frac{2}{\epsilon }\Lambda _1^\epsilon \iint _{Q_{2r}(z_0)}\left( H(z,|\nabla u|)_k\right) ^{1-\theta }H(z,|\nabla u|)^\theta \,dz. \end{aligned} \end{aligned}$$

Similarly, by Fubini’s theorem, we have

$$\begin{aligned} \textrm{II} \le \frac{1}{1-\theta +\epsilon }\iint _{Q_{r_2}(z_0)}\left( H(z,|\nabla u|)_k\right) ^{1-\theta +\epsilon }H(z,|\nabla u|)^\theta \,dz \end{aligned}$$

and

$$\begin{aligned} \textrm{III}\le \frac{1}{\epsilon }\iint _{Q_{2r}(z_0)}H(z,|F|)^{1+\epsilon }\,dz. \end{aligned}$$

By combining the estimates above, we obtain

$$\begin{aligned} \begin{aligned}&\iint _{Q_{r_1}(z_0)}\left( H(z,|\nabla u|)_k\right) ^{1-\theta +\epsilon }H(z,|\nabla u|)^\theta \,dz\\&\quad \le \frac{c\epsilon }{1-\theta +\epsilon }\iint _{Q_{r_2}(z_0)}\left( H(z,|\nabla u|)_k\right) ^{1-\theta +\epsilon }H(z,|\nabla u|)^\theta \,dz\\&\qquad +c\Lambda _1^\epsilon \iint _{Q_{2r}(z_0)}\left( H(z,|\nabla u|)_k\right) ^{1-\theta }H(z,|\nabla u|)^\theta \,dz\\&\qquad +c\iint _{Q_{2r}(z_0)}H(z,|F|)^{1+\epsilon }\,dz. \end{aligned} \end{aligned}$$

We choose $\epsilon _0=\epsilon _0( data )\in (0,1)$ so that for any $\epsilon \in (0,\epsilon _0)$,

$$\begin{aligned} \frac{c\epsilon }{1-\theta +\epsilon }\le \frac{1}{2}. \end{aligned}$$

Then, by applying Lemma 2.6 we get

$$\begin{aligned} \begin{aligned}&\iint _{Q_{r}(z_0)}\left( H(z,|\nabla u|)_k\right) ^{1-\theta +\epsilon }H(z,|\nabla u|)^\theta \,dz\\&\quad \le c\Lambda _0^\epsilon \iint _{Q_{2r}(z_0)}\left( H(z,|\nabla u|)_k\right) ^{1-\theta }H(z,|\nabla u|)^\theta \,dz\\&\qquad +c\iint _{Q_{2r}(z_0)}H(z,|F|)^{1+\epsilon }\,dz. \end{aligned} \end{aligned}$$

The claim follows by letting $k\longrightarrow \infty$ and recalling (4.1).