Translation-Like Isoptic Surfaces and Angle Sums of Translation Triangles in $\textbf{Nil}$ Geometry

Abstract

After having investigated the geodesic and translation triangles and their angle sums in $\textbf{Sol}$ and $\widetilde{{\textbf{S}}{\textbf{L}}_2{\textbf{R}}}$ geometries we consider the analogous problem in $\textbf{Nil}$ space that is one of the eight 3-dimensional Thurston geometries. We analyze the interior angle sums of translation triangles in $\textbf{Nil}$ geometry and we provide a new approach to prove that it can be larger than or equal to $\pi$. Moreover, for the first time in non-constant curvature Thurston geometries we have developed a procedure for determining the equations of $\textbf{Nil}$ isoptic surfaces of translation-like segments and as a special case of this we examine the $\textbf{Nil}$ translation-like Thales sphere, which we call Thaloid. In our work we will use the projective model of $\textbf{Nil}$ described by Molnár (Beitr Algebra Geom 38(2):261–288, 1997).

1 Introduction

In this paper we are interested in translation triangles and isoptic surfaces in $\textbf{Nil}$ space that is one of the eight Thurston geometries (see [26, 41]) derived by the Heisenberg matrix group [16, 19].

In the Thurston spaces translation curves can be introduced in a natural way (see [17, 35]) by translations mapping each point to any point. Consider a unit vector at the origin. Translations, postulated at the beginning carry this vector to any point by its tangent mapping. If a curve $t\rightarrow (x(t),y(t),z(t))$ has just the translated vector as tangent vector in each point, then the curve is called a translation curve. This assumption leads to a system of first order differential equations, thus translation curves are simpler than geodesics and differ from them in $\textbf{Nil}$, $\widetilde{{\textbf{S}}{\textbf{L}}_2{\textbf{R}}}$ and $\textbf{Sol}$ geometries. Moreover, they play an important role and often seem to be more natural in these geometries, than their geodesic lines.

In the remaining five Thurson geometries ${\textbf{E}}^3,$ ${\textbf{S}}^3,$ ${\textbf{H}}^3,$ ${\textbf{S}}^2\!\times \!{\textbf{R}}$ and ${\textbf{H}}^2\!\times \!{\textbf{R}},$ the translation and geodesic curves coincide with each other.

Internal angle sum for triangles in ${\textbf{S}}^2\!\times \!{\textbf{R}}$ and ${\textbf{H}}^2\!\times \!{\textbf{R}}$ had been studied in [36].

In [6] we investigated the angle sum of translation and geodesic triangles in $\widetilde{{\textbf{S}}{\textbf{L}}_2{\textbf{R}}}$ geometry and proved that the possible sum of the interior angles in a translation triangle must be greater than or equal to $\pi .$ However, in geodesic triangles this sum can be less than, greater than or equal to $\pi .$

In [34] interior angle sum of translation triangles had been studied in $\textbf{Sol}$ geometry to obtain that it must be greater than or equal to $\pi .$ To calculate this sum for geodesic curves needs further research.

In [1] Brodaczewska showed, that the sum of the interior angles of translation triangles of $\textbf{Nil}$ space is larger than or equal to $\pi ,$ which is also the aim of this study. However, our approach below seems generally effective to all three geometries, where geodesic and translation curves differ. In [33], we investigated the interior angle sum of geodesic triangles in $\textbf{Nil}$ space.

Remark 1.1

Of the Thurston geometries, those with constant curvature (Euclidean ${\textbf{E}}^3$, hyperbolic ${\textbf{H}}^3$, spherical ${\textbf{S}}^3$) have been extensively studied, but the other five geometries, ${\textbf{H}}^2\!\times \!{\textbf{R}}$, ${\textbf{S}}^2\!\times \!{\textbf{R}}$, $\textbf{Nil}$, $\widetilde{{\textbf{S}}{\textbf{L}}_2{\textbf{R}}}$, $\textbf{Sol}$ have been thoroughly studied only from a differential geometry and topological point of view. However, classical concepts highlighting the beauty and underlying structure of these geometries—such as geodesic curves and spheres, translation curves an spheres, the lattices, ball packing, the geodesic and translation triangles and their surfaces, their interior sum of angles, equidistant surfaces, locus of points in the plane or in the space from a segment subtends a given angle (isoptic curves or surfaces) and similar statements to those known in constant curvature geometries—can be formulated. These have not been in the focus of attention yet, but there are some results, e.g. [20, 23, 30,31,32, 37,38,39,40].

In this paper we consider some of these topics.

In Sect. 2 we describe the projective model of $\textbf{Nil}$ and we shall use its standard Riemannian metric obtained by pull back transform to the infinitesimal arc-length-square at the origin. We also recall the isometry group of $\textbf{Nil}$ and give an overview about translation curves.

In Sect. 3 we study the $\textbf{Nil}$ translation triangles and prove that the interior angle sum of a translation triangle in $\textbf{Nil}$ geometry can be larger than, or equal to $\pi .$ We also determine when this internal angle sum is exactly $\pi .$

In Sect. 4 we introduce isoptic curves with the usual Euclidean planar definition, then we define the basic idea of spatial visibility, i.e. the concept of isoptic surfaces. With the help of these, we can introduce the isoptic and orthoptic surfaces for any segment, which can then be defined for translation-like segments similarly in the $\textbf{Nil}$ geometry.

In the last Sect. 5, we examine the translation-like isoptic surfaces of a given translation-like segment. We give the definition of these surfaces and a procedure by which we can determine the translation-like isoptic surface of any translation-like segment. This procedure can perhaps be further developed, to determine translation-like isoptic surfaces to any given $\textbf{Nil}$ curve. We determine the implicit equation of these surfaces and visualize them. Thaloids are also analyzed as a special case. Similar investigations in this topic have only been carried out in spaces with constant curvature (see [4, 7, 8, 24, 25]).

2 $\textbf{Nil}$ Geometry and Its Translation Curves

$\textbf{Nil}$ geometry can be derived from the famous real matrix group $\mathbf {L({\mathbb {R}})}$ discovered by Werner Heisenberg. The left (row-column) multiplication of Heisenberg matrices

$$\begin{aligned} \begin{aligned} \begin{pmatrix} 1&{}\quad x&{}\quad z \\ 0&{}\quad 1\quad &{}y \\ 0&{}\quad 0&{}\quad 1 \\ \end{pmatrix} \begin{pmatrix} 1&{}\quad a&{}\quad c \\ 0&{}\quad 1&{}\quad b \\ 0&{}\quad 0&{}\quad 1 \\ \end{pmatrix} =\begin{pmatrix} 1&{}\quad a+x&{}\quad c+xb+z \\ 0&{}\quad 1&{}\quad b+y \\ 0&{}\quad 0&{}\quad 1 \\ \end{pmatrix} \end{aligned} \end{aligned}$$

(2.1)

defines “translations” ${\textbf{L}}({\mathbb {R}})= \{(x,y,z): x,~y,~z\in {\mathbb {R}} \}$ on the points of $\textbf{Nil}= \{(a,b,c):a,~b,~c \in {\mathbb {R}}\}$. These translations are not commutative in general. The matrices ${\textbf{K}}(z) \vartriangleleft {\textbf{L}}$ of the form

$$\begin{aligned} \begin{aligned} {\textbf{K}}(z) \ni \begin{pmatrix} 1&{}\quad 0&{}\quad z \\ 0&{}\quad 1&{}\quad 0 \\ 0&{}\quad 0&{}\quad 1 \\ \end{pmatrix} \mapsto (0,0,z) \end{aligned} \end{aligned}$$

(2.2)

constitute the one parametric centre, i.e. each of its elements commutes with all elements of ${\textbf{L}}$. The elements of ${\textbf{K}}$ are called fibre translations. $\textbf{Nil}$ geometry of the Heisenberg group can be projectively (affinely) interpreted by “right translations” on points as the matrix formula

$$\begin{aligned} \begin{aligned} (1;a,b,c) \rightarrow (1;a,b,c) \begin{pmatrix} 1&{}\quad x&{}\quad y&{}\quad z \\ 0&{}\quad 1&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 1&{}\quad x \\ 0&{}\quad 0&{}\quad 0&{}\quad 1 \\ \end{pmatrix} =(1;x+a,y+b,z+bx+c) \end{aligned}\qquad \end{aligned}$$

(2.3)

shows, according to (2.1). Here we consider ${\textbf{L}}$ as projective collineation group with right actions in homogeneous coordinates. We will use the Cartesian homogeneous coordinate simplex $E_0({\textbf{e}}_0)$,$E_1^{\infty }({\textbf{e}}_1)$, $E_2^{\infty }({\textbf{e}}_2)$, $E_3^{\infty }({\textbf{e}}_3), \ (\{{\textbf{e}}_i\}\subset {\textbf{V}}^4$$\text {with the unit point}$ $E({\textbf{e}}= {\textbf{e}}_0 + {\textbf{e}}_1 + {\textbf{e}}_2 + {\textbf{e}}_3 ))$ which is distinguished by an origin $E_0$ and by the ideal points of coordinate axes, respectively. Moreover, ${\textbf{y}}=c{\textbf{x}}$ with $0<c\in {\mathbb {R}}$ (or $c\in {\mathbb {R}}{\setminus }\{0\})$ defines a point $({\textbf{x}})=({\textbf{y}})$ of the projective 3-sphere ${\mathcal {P}} {\mathcal {S}}^3$ (or that of the projective space ${\mathcal {P}}^3$ where opposite rays $({\textbf{x}})$ and $(-{\textbf{x}})$ are identified). The dual system $\{({\varvec{e}}^i)\}, \ (\{{\varvec{e}}^i\}\subset {\varvec{V}}_4)$, with ${\textbf{e}}_i{\varvec{e}}^j=\delta _i^j$ (the Kronecker symbol), describes the simplex planes, especially the plane at infinity $({\varvec{e}}^0)=E_1^{\infty }E_2^{\infty }E_3^{\infty }$, and generally, ${\varvec{v}}={\varvec{u}}\frac{1}{c}$ defines a plane $({\varvec{u}})=({\varvec{v}})$ of ${\mathcal {P}}{\mathcal {S}}^3$ (or that of ${\mathcal {P}}^3$). Thus $0={\textbf{x}}{\varvec{u}}={\textbf{y}}{\varvec{v}}$ defines the incidence of point $({\textbf{x}})=({\textbf{y}})$ and plane $({\varvec{u}})=({\varvec{v}})$, as $({\textbf{x}}) \text {I} ({\varvec{u}})$ also denotes it. Thus Nil can be visualized in the affine 3-space ${\textbf{A}}^3$ (so in ${\textbf{E}}^3$) as well [21].

In this context Molnár [16] has derived the well-known infinitesimal arc-length square invariant under translations ${\textbf{L}}$ at any point of $\textbf{Nil}$ as follows

$$\begin{aligned} \begin{aligned} (dx)^2+(dy)^2+(-xdy+dz)^2&=(dx)^2+(1+x^2)(dy)^2 \\&\quad -2x(dy)(dz)+(dz)^2=:(ds)^2 \end{aligned} \end{aligned}$$

(2.4)

The translation group ${\textbf{L}}$ defined by formula (2.3) can be extended to a larger group ${\textbf{G}}$ of collineations, preserving the fibres, that will be equivalent to the (orientation preserving) isometry group of $\textbf{Nil}$.

In [18] Molnár has shown that a rotation through angle $\omega$ about the z-axis at the origin, as isometry of $\textbf{Nil}$, keeping invariant the Riemann metric everywhere, will be a quadratic mapping in x, y to z-image ${\overline{z}}$ as follows:

$$\begin{aligned} \begin{aligned} {\mathcal {M}}={\textbf{r}}(O,\omega ):(1;x,y,z) \rightarrow (1;{\overline{x}},{\overline{y}},{\overline{z}}); \\ {\overline{x}}=x\cos {\omega }-y\sin {\omega }, \ \ {\overline{y}}=x\sin {\omega }+y\cos {\omega }, \\ {\overline{z}}=z-\frac{1}{2}xy+\frac{1}{4}(x^2-y^2)\sin {2\omega }+\frac{1}{2}xy\cos {2\omega }. \end{aligned} \end{aligned}$$

(2.5)

This rotation formula ${\mathcal {M}}$, however, is conjugate by the quadratic mapping $\alpha$ to the linear rotation $\Omega$ as follows

$$\begin{aligned} \begin{aligned} \alpha ^{-1}: \ \ (1;x,y,z) {\mathop {\longrightarrow }\limits ^{\alpha ^{-1}}} (1; x',y',z')=\left( 1;x,y,z-\frac{1}{2}xy\right) \ \ \text {to} \\ \Omega : \ \ (1;x',y',z') {\mathop {\longrightarrow }\limits ^{\Omega }} (1;x'',y'',z'')=(1;x',y',z') \begin{pmatrix} 1&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad \cos {\omega }&{}\quad \sin {\omega }&{}\quad 0 \\ 0&{}\quad -\sin {\omega }&{}\quad \cos {\omega }&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 1 \\ \end{pmatrix}, \\ \text {with} \ \ \alpha : (1;x'',y'',z'') {\mathop {\longrightarrow }\limits ^{\alpha }} (1; {\overline{x}}, {\overline{y}},{\overline{z}})=\left( 1; x'',y'',z''+\frac{1}{2}x''y''\right) . \end{aligned}\nonumber \\ \end{aligned}$$

(2.6)

This quadratic conjugacy modifies the $\textbf{Nil}$ translations in (2.3), as well. Now a translation with (X, Y, Z) in (2.3) instead of (x, y, z) will be changed by the above conjugacy to the translation

$$\begin{aligned} \begin{aligned} (1;x,y,z) \longrightarrow (1; {\overline{x}}, {\overline{y}},{\overline{z}})=(1; x,y,z) \begin{pmatrix} 1&{}\quad X&{}\quad Y&{}\quad Z-\frac{1}{2}XY \\ 0&{}\quad 1&{}\quad 0&{}\quad -\frac{1}{2}Y \\ 0&{}\quad 0&{}\quad 1&{}\quad \frac{1}{2}X \\ 0&{}\quad 0&{}\quad 0&{}\quad 1 \\ \end{pmatrix}, \\ \end{aligned} \end{aligned}$$

(2.7)

that is again an affine collineation.

2.1 Translation Curve and Sphere

We consider a $\textbf{Nil}$ curve (1, x(t), y(t), z(t) ) with a given starting tangent vector at the origin $O=E_0=(1,0,0,0)$

$$\begin{aligned} \begin{aligned} u={\dot{x}}(0),\ v={\dot{y}}(0), \ w={\dot{z}}(0). \end{aligned} \end{aligned}$$

(2.8)

For a translation curve let its tangent vector at the point (1, x(t), y(t), z(t) ) be defined by the matrix (2.3) with the following equation:

$$\begin{aligned} \begin{aligned} (0,u,v,w) \begin{pmatrix} 1&{}\quad x(t)&{}\quad y(t)&{}\quad z(t) \\ 0&{}\quad 1&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 1&{}\quad x(t) \\ 0&{}\quad 0&{}\quad 0&{}\quad 1 \\ \end{pmatrix} =(0,{\dot{x}}(t),{\dot{y}}(t),{\dot{z}}(t)). \end{aligned} \end{aligned}$$

(2.9)

Thus, the translation curves in $\textbf{Nil}$ geometry (see [17, 21, 22]) are defined by the above first order differential equation system ${\dot{x}}(t)=u, \ {\dot{y}}(t)=v, \ {\dot{z}}(t)=v \cdot x(t)+w,$ whose solution is the following:

$$\begin{aligned} \begin{aligned} x(t)=u t, \ y(t)=v t, \ z(t)=\frac{1}{2}uvt^2+wt. \end{aligned} \end{aligned}$$

(2.10)

We assume that the starting point of a translation curve is the origin, because we can transform a curve into an arbitrary starting point by translation (2.3), moreover, unit initial velocity translation can be assumed by “geographic” parameters $\phi$ and $\theta$:

$$\begin{aligned} \begin{gathered} x(0)=y(0)=z(0)=0; \\ \ u={\dot{x}}(0)=\cos {\theta } \cos {\phi }, \ \ v={\dot{y}}(0)=\cos {\theta } \sin {\phi }, \ \ w={\dot{z}}(0)=\sin {\theta }; \\ - \pi \le \phi \le \pi , \ -\frac{\pi }{2} \le \theta \le \frac{\pi }{2}. \end{gathered}\nonumber \\ \end{aligned}$$

(2.11)

Definition 2.1

The translation distance $d^t(P_1,P_2)$ between the points $P_1$ and $P_2$ is defined by the arc length of the above translation curve from $P_1$ to $P_2$.

Definition 2.2

The sphere of radius $r >0$ with centre at the origin, (denoted by $S^t_O(r)$), with the usual longitude and altitude parameters $\phi$ and $\theta$, respectively by (2.11), is specified by the following equations:

$$\begin{aligned} \begin{gathered} S_O^t(r): \left\{ \begin{array}{ll} x(\phi ,\theta )=r \cos {\theta } \cos {\phi }, \\ y(\phi ,\theta )=r \cos {\theta } \sin {\phi }, \\ z(\phi ,\theta )=\frac{r^2}{2} \cos ^2{\theta } \cos {\phi } \sin {\phi }+ r \sin {\theta }. \end{array} \right. \end{gathered} \end{aligned}$$

(2.12)

Definition 2.3

The body of the translation sphere of centre O and of radius r in the $\textbf{Nil}$ space is called translation ball, denoted by $B^t_{O}(r)$, i.e. $Q \in B^t_{O}(r)$ iff $0 \le d^t(O,Q) \le r$.

The parametrization in (2.12) allows us, to create the implicit equation of $B^t_{O}(r)$:

$$\begin{aligned} \begin{gathered} x^2+y^2+\left( z-\dfrac{xy}{2}\right) ^2=r^2 \end{gathered} \end{aligned}$$

(2.13)

3 Translation Triangles

We consider 3 points $A_1$, $A_2$, $A_3$ in the projective model of $\textbf{Nil}$ space. The translation segments $a_k$ connecting the points $A_i$ and $A_j$ $(i<j,~i,j,k \in \{1,2,3\}, k \ne i,j$) are called sides of the translation triangle with vertices $A_1$, $A_2$, $A_3$.

In Riemannian geometries the metric tensor (or infinitesimal arc-lenght square (see 2.4) is used to define the angle $\theta$ between two curves. If their tangent vectors in their common point are ${\textbf{u}}$ and ${\textbf{v}}$ and $g_{ij}$ are the components of the metric tensor then

$$\begin{aligned} \cos (\theta )=\frac{u^i g_{ij} v^j}{\sqrt{u^i g_{ij} u^j~ v^i g_{ij} v^j}} \end{aligned}$$

(3.1)

It is clear by the above definition of the angles and by the infinitesimal arc-lenght square (2.4), that the angles are the same as the Euclidean ones at the origin of the projective model of $\textbf{Nil}$ geometry.

Considering a translation triangle $A_1A_2A_3$ we can assume by the homogeneity of the $\textbf{Nil}$ geometry that one of its vertex coincide with the origin $A_1=E_0=(1,0,0,0)$ and the other two vertices are $A_2(1,x^2,y^2,z^2)$ and $A_3(1,x^3,y^3,z^3)$.

We will consider the interior angles of translation triangles that are denoted at the vertex $A_i$ by $\omega _i$ $(i\in \{1,2,3\})$. We note here that the angle of two intersecting translation curves depends on the orientation of their tangent vectors.

In order to determine the interior angles of a translation triangle $A_1A_2A_3$ and its interior angle sum $\sum _{i=1}^3(\omega _i)$, we define translations ${\textbf{T}}_{A_i}$, $(i\in \{2,3\})$ as elements of the isometry group of $\textbf{Nil}$, that maps the origin $E_0$ onto $A_i$ (see Fig. 2).

E.g. the isometry ${\textbf{T}}_{A_2}$ and its inverse (up to a positive determinant factor) can be given by:

$$\begin{aligned} {\textbf{T}}_{A_2}= \begin{pmatrix} 1 &{}\quad x_2 &{}\quad y_2 &{}\quad z_2 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad x_2 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \end{pmatrix}, ~ ~ ~ {\textbf{T}}_{A_2}^{-1}= \begin{pmatrix} 1 &{}\quad -x_2 &{}\quad -y_2 &{}\quad x_2 y_2 - z_2 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad -x_2 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \end{pmatrix}, \nonumber \\ {\textbf{T}}_{A_3}= \begin{pmatrix} 1 &{}\quad x_3 &{}\quad y_3 &{}\quad z_3 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad x_3 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \end{pmatrix}, ~ ~ ~ {\textbf{T}}_{A_3}^{-1}= \begin{pmatrix} 1 &{} -x_3 &{} -y_3 &{} x_3 y_3 -z_3 \\ 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} -x_3 \\ 0 &{} 0 &{} 0 &{} 1, \end{pmatrix}, \end{aligned}$$

(3.2)

Fig. 1

Translation triangles with vertices $A_1=(1,0,0,0)$, $A_2=(1,-1,1,1)$, $A_3=(1,1/2,5,1/2)$ (left) and with vertices $A_1=(1,0,0,0)$, $A_2=(1,-1,1,1)$, $A_3=(1,1/2,-1,1/2)$ (right)

and the images ${\textbf{T}}^{-1}_{A_2}(A_i)$ of the vertices $A_i$ $(i \in \{1,2,3\})$ are the following (see also Fig. 2):

$$\begin{aligned} \begin{gathered} T^{-1}_{A_{2}}(A_{1})=A^{2}_{1}=(1,-x_2,-y_2,x_2 y_2-z_2); \text { } T^{-1}_{A_{2}}(A_2)=A^{2}_{2}=E_0=(1,0,0,0);\\ T^{-1}_{A_{2}}(A_3)=A^{2}_{3}=(1,-x_2+x_3,-y_2+y_3,x_2 y_2-x_2 y_3-z_2+z_3);\\ T^{-1}_{A_{3}}(A_{1})=A_{1}^{3}=(1,-x_3,-y_3,x_3 y_3 -z_3); \text { } T^{-1}_{A_{3}}(A_{3})=A_{3}^{3}=E_0=(1,0,0,0); \\ T^{-1}_{A_{3}}(A_2)=A_{2}^{3}=(1,x_2-x_3,y_2-y_3,-x_3 y_2+x_3 y_3 +z_2 -z_3). \end{gathered}\nonumber \\ \end{aligned}$$

(3.3)

Fig. 2

Translation triangle with vertices $A_1=(1,0,0,0)$, $A_2=(1,-1,1,1)$, $A_3=(1,1/2,3/2,1/2)$ and its translated copies $A_1^2A_3^2E_0$ and $A_1^3A_2^3E_0$

Our aim is to determine angle sum $\sum _{i=1}^3(\omega _i)$ of the interior angles of translation triangles $A_1A_2A_3$ (see Figs. 1 and 2). We have seen that $\omega _1$ and the angle of translation curves with common point at the origin $E_0$ is the same as the Euclidean one therefore can be determined by usual Euclidean sense.

The translations ${\textbf{T}}_{A_i}$ $(i=2,3)$ are isometries in $\textbf{Nil}$ geometry thus $\omega _i$ is equal to the angle $(t(A_i^i, A_1^i)t(A_i^i, A_j^i))\angle$ $(i,j=2,3$, $i \ne j)$ (see Fig. 2) where $t(A_i^i, A_1^i)$, $t(A_i^i, A_j^i)$ are oriented translation curves $(E_0=A_2^2=A_3^3)$ and $\omega _1$ is equal to the angle $(t(E_0, A_2)t(E_0, A_3)) \angle$ where $t(E_0, A_2)$, $t(E_0, A_3)$ are also oriented translation curves.

We denote the oriented unit tangent vectors of the oriented geodesic curves $t(E_0, A_i^j)$ with ${\textbf{t}}_i^j$ where $(i,j)\in \{(1,3),(1,2),(2,3),(3,2),(3,0),(2,0)\}$ and $A_3^0=A_3$, $A_2^0=A_2$. The Euclidean coordinates of ${\textbf{t}}_i^j$ are:

$$\begin{aligned} t_{i}^{j}=(\cos {\theta _{i}^{j}} \cos {\phi _{i}^{j}},\cos {\theta _{i}^{j}} \sin {\phi _{i}^{j}},\sin {\theta _{i}^{j}}). \end{aligned}$$

(3.4)

In order to obtain the angle of two translation curves $t_{E_0A_i^j}$ and $t_{E_0A_k^l}$ ($(i,j)\ne (k,l)$; $(i,j),(k,l)\in \{(1,3),(1,2),(2,3),(3,2),(3,0),(2,0)\})$ intersected at the origin $E_0$ we need to determine their tangent vectors ${\textbf{t}}_s^r$ $((s,r) \in \{(1,3),(1,2),$ $(2,3),(3,2),(3,0),(2,0)\})$ (see 3.4) at their starting point $E_0$. From (3.4) follows that a tangent vector at the origin is given by the parameters $\phi$ and $\theta$ of the corresponding translation curve (see 2.11) that can be determined from the homogeneous coordinates of the endpoint of the translation curve.

It can be assumed by the homogeneity of $\textbf{Nil}$ that the starting point of a given translation curve segment is $E_0=P_1=(1,0,0,0)$ and the other endpoint will be given by its homogeneous coordinates $P_2=(1,a,b,c)$. We consider the translation curve segment $t_{P_1P_2}$ and determine its parameters $(\phi ,\theta ,r)$ expressed by the real coordinates a, b, c of $P_2$. We obtain directly by equation system (2.11) the following:

Lemma 3.1

• 1. Let (1, a, b, c) $(a,b \in {\mathbb {R}} {\setminus } \{0\},~c\in {\mathbb {R}})$ be the homogeneous coordinates of the point $P \in \textbf{Nil}$. The parameters of the corresponding translation curve $t_{E_0P}$ are the following

  $$\begin{aligned} \begin{gathered} \phi =\textrm{arccot}\Big (\frac{a}{b}\Big ),~\text {or}~ \phi =\textrm{arccot}\Big (\frac{a}{b}\Big )-\pi , \\ \theta =\textrm{arctan}\Big ( \frac{c-\frac{ab}{2}}{\sqrt{a^{2}+b^{2}}}\Big ),~ r=\Big |\frac{c-\frac{ab}{2}}{\sin {\theta }}\Big |. \end{gathered} \end{aligned}$$

  (3.5)

• 2. Let (1, a, 0, c) $(a,c \in {\mathbb {R}} {\setminus } \{0\})$ be the homogeneous coordinates of the point $P \in \textbf{Nil}$. The parameters of the corresponding translation curve $t_{E_0P}$ are the following

  $$\begin{aligned} \begin{gathered} \phi =\pi \cdot n,~ (n\in \{0,1\}),~ \theta = \textrm{arctan}\Big (\frac{c}{a}\Big ),~ r=\Big |\frac{a}{\cos {\theta }}\Big |. \end{gathered} \end{aligned}$$

  (3.6)

• 3. Let (1, a, 0, 0) $(a \in {\mathbb {R}}{\setminus } \{0\})$ be the homogeneous coordinates of the point $P \in \textbf{Nil}$. The parameters of the corresponding translation curve $t_{E_0P}$ are the following

  $$\begin{aligned} \begin{gathered} \phi =\pi \cdot n,~ (n\in \{0,1\}),~ \theta =\pi \cdot n,~ (n\in \{0,1\}),~ r=|a|. \end{gathered} \end{aligned}$$

  (3.7)

• 4. Let (1, 0, b, 0) $(b \in {\mathbb {R}}{\setminus } \{0\})$ be the homogeneous coordinates of the point $P \in \textbf{Nil}$. The parameters of the corresponding translation curve $t_{E_0P}$ are the following

  $$\begin{aligned} \begin{gathered} \phi =\pm \frac{\pi }{2},~ \theta =\pi \cdot n,~ (n\in \{0,1\}),~ r=|b|. \end{gathered} \end{aligned}$$

  (3.8)

• 5. Let (1, 0, 0, c) $(c \in {\mathbb {R}}{\setminus } \{0\})$ be the homogeneous coordinates of the point $P \in \textbf{Nil}$. The parameters of the corresponding translation curve $t_{E_0P}$ are the following

  $$\begin{aligned} \begin{gathered} \theta =\pm \frac{\pi }{2},~ r=|c|.~ ~ \square \end{gathered} \end{aligned}$$

  (3.9)

Applying the above lemma we obtain the following

Theorem 3.2

The sum of the interior angles of a translation triangle is greater than or equal to $\pi$.

Proof

The translations ${\textbf{T}}_{A_2}^{-1}$ and ${\textbf{T}}_{A_3}^{-1}$ are isometries in $\textbf{Nil}$ geometry thus $\omega _2$ is equal to the angle $((A_2^2 A_1^2), (A_2^2 A_3^2)) \angle$ (see Fig. 2) of the oriented translation segments $t_{A_2^2 A_1^2}$, $t_{A_2^2A_3^2}$ and $\omega _3$ is equal to the angle $((A_3^3 A_1^3),(A_3^3 A_2^3)) \angle$ of the oriented translation segments $t_{A_3^3 A_1^3}$ and $t_{A_3^3 A_2^3}$ $(E_0=A_2^2=A_3^3$).

Substituting the coordinates of the points $A_i^j$ (see 3.3 and 3.4) $((i,j) \in \{(1,3),(1,2),$ $(2,3),(3,2),(3,0),(2,0)\})$ to the appropriate equations of Lemma 3.1, it is easy to see that

$$\begin{aligned} \begin{gathered} \theta _2^0=-\theta _1^2,~\phi _2^0-\phi _1^2=\pm \pi \Rightarrow {\textbf{t}}_2^0=-{\textbf{t}}_1^2,\\ \theta _3^0=-\theta _1^3,~\phi _3^0-\phi _1^3=\pm \pi \Rightarrow {\textbf{t}}_3^0=-{\textbf{t}}_1^3,\\ \theta _3^2=-\theta _2^3,~\phi _3^2-\phi _2^3=\pm \pi \Rightarrow {\textbf{t}}_3^2=-{\textbf{t}}_2^3. \end{gathered} \end{aligned}$$

(3.10)

The endpoints $T_i^j$ of the position vectors ${\textbf{t}}_i^j=\overrightarrow{E_0T_i^j}$ lie on the unit sphere centered at the origin. The measure of angle $\omega _i$ $(i\in \{1,2,3\})$ of the vectors ${\textbf{t}}_i^j$ and ${\textbf{t}}_r^s$ is equal to the spherical distance of the corresponding points $T_i^j$ and $T_r^s$ on the unit sphere (see Fig. 3). Moreover, a direct consequence of equations (3.9) that each point pair ($T_2$, $T_1^2$), $(T_3$,$T_1^3$), ($T_2^3$,$T_3^2$) contains antipodal points related to the unit sphere with centre $E_0$.

Due to the antipodality $\omega _1=T_2E_0T_3 \angle =T_1^2E_0T_1^3 \angle$, therefore their corresponding spherical distances are equal, as well (see Fig. 3). Now, the sum of the interior angles $\sum _{i=1}^3(\omega _i)$ can be considered as three consecutive spherical arcs $(T_3^2 T_1^2)$, $(T_1^2 T_1^3)$, $T_1^3 T_2^3)$. Since the triangle inequality holds on the sphere, the sum of these arc lengths is greater or equal to the half of the circumference of the main circle on the unit sphere i.e. $\pi$. $\square$

The following lemma is an immediate consequence of the above proof:

Fig. 3

Translation triangle with vertices $A_1=(1,0,0,0)$, $A_2=(1,-1,1,1)$, $A_3=(1,1/2,3/2,1/2)$, its translated copies $A_1^2A_3^2E_0$, $A_1^3A_2^3E_0$ with angles $\omega _i$ $(i\in \{1,2,3\}$

Lemma 3.3

The angle sum $\sum _{i=1}^3(\omega _i)$ of a $\textbf{Nil}$ translation triangle $A_1A_2A_3$ is $\pi$ if and only if the points $T_i^j$ $((i,j) \in \{(1,3),(1,2),$ $(2,3),(3,2),(3,0),(2,0)\})$ lie in an Euclidean plane (Fig. 4).

Now, we distinguish the cases, when the internal angle sum is exactly $\pi .$

Lemma 3.4

If the vertices of a translation triangle $A_1A_2A_3$ lie in a plane perpendicular to the base plane (coordinate plane [x, y]) of the model of $\textbf{Nil}$ geometry then the interior angle sum $\sum _{i=1}^3(\omega _i)=\pi$.

Proof

We get from the equation system (2.10) of the translation curves that the points of a translation curve $t_{E_0P}$ ($P\in \textbf{Nil}$) lie in an Euclidean plane that is perpendicular to [x, y] base plane, therefore, its tangent line also lies in this plane.

Moreover, a direct consequence of formulas (2.10) and (3.3) than if a translation triangle $A_1A_2A_3$ lies in this to base plane perpendicular $\alpha$ plane then its translated image by a translation lies also in a to the base plane perpendicular plane $\alpha '$ and each to the base plane orthogonal $\alpha '$ can be derived as a translated copy of $\alpha$. Thus, applying the Lemma 3.3 we proved this lemma. $\square$

Fig. 4

Translation triangle with vertices $A_1=(1,0,0,0)$, $A_2=(1,-1,1/2,2)$, $A_3=(1,3,-3/2,1)$. The translation curve segments $t_{A_1A_2}$, $t_{A_2A_3}$, $t_{A_3A_1}$ lie on a plane orthogonal to the [x, y] base plane. The interior angle sum of this translation triangle is $\sum _{i=1}^3(\omega _i)=\pi$

We can determine the interior angle sum of arbitrary translation triangle. In the following table we summarize some numerical data of interior angles of given translation triangles (Table 1):

Table 1 $A_2(1,-1,1,1),$ $A_3(1,1/2,y^3,1/2)$

4 Introduction to Isoptic Curves

It is well known that in the Euclidean plane the locus of points from a segment subtends a given angle $\alpha$ $(0<\alpha <\pi )$ is the union of two arcs except for the endpoints with the segment as common chord. If this $\alpha$ is equal to $\frac{\pi }{2}$ then we get the Thales circle. Replacing the segment to another general curve, we obtain the Euclidean definition of isoptic curve:

Definition 4.1

([45]). The locus of the intersection of tangents to a curve meeting at a constant angle $\alpha$ $(0<\alpha <\pi )$ is the $\alpha$—isoptic of the given curve. The isoptic curve with right angle called orthoptic curve.

Remark 4.2

Sometimes we consider the $\alpha$—and $\pi -\alpha$—isoptics together. Thus, in the case of the section, we get two circles with the segment as a common chord (endpoints of the segment are excluded). Hereafter, we call them $\alpha$—isoptic circles.

Although the name “isoptic curve” was suggested by Taylor in 1884 ([41]), reference to former results can be found in [45]. In the obscure history of isoptic curves, we can find the names of la Hire (cycloids 1704) and Chasles (conics and epitrochoids 1837) among the contributors of the subject. A very interesting table of isoptic and orthoptic curves is introduced in [45], unfortunately without any exact reference of its source. However, recent works are available on the topic, which shows its timeliness. In [2] and [3], the Euclidean isoptic curves of closed strictly convex curves are studied using their support function. Papers [11, 43, 44] deal with Euclidean curves having a circle or an ellipse for an isoptic curve. Further curves appearing as isoptic curves are well studied in Euclidean plane geometry ${\textbf{E}}^2$, see e.g. [12, 42]. Isoptic curves of conic sections have been studied in [9] and [27, 28]. There are results for Bezier curves by Kunkli et al. as well, see [10]. Many papers focus on the properties of isoptics, e.g. [13,14,15], and the references therein. There are some generalizations of the isoptics as well e.g. equioptic curves in [25] by Odehnal or secantopics in [24, 29] by Skrzypiec.

We can extend the very first question to the space: “What is the locus of points where a given segment subtends a given angle?” Or a question equivalent to the former: “For the given spatial points A and B, what is the locus of the points P for which the internal angle at P of the triangle $ABP\triangle$ is a given angle?” We use this to define the $\alpha$—isoptic surface of a Euclidean spatial segment.

Definition 4.3

The $\alpha$—isoptic surface of a Euclidean spatial segment $\overline{A_1A_2}$ is the locus of points P for which the internal angle at P in the triangle, formed by $A_1,$ $A_2$ and P is $\alpha .$ If $\alpha$ is the right angle, then it is called the Thaloid of $\overline{A_1A_2}.$

It is easy to see in the Euclidean space that:

Theorem 4.4

The locus of points in the Euclidean space from where a given segment subtends a given angle $\alpha$ $(0<\alpha <\pi )$ or $\pi -\alpha$ is a self-intersecting torus obtained by rotating the $\alpha$—isoptic circles drawn in any plane containing the section around the line of the section. $\square$

Remark 4.5

• 1. The torus in the above theorem contains both the isoptic surface for the given angle and the supplementary angle. In this case, we can easily separate the $\alpha$—and $\pi -\alpha$—isoptic surfaces along the self-intersection. Specifically, the orthoptic surface is a sphere whose diameter is the section. We can call this the Thaloid of the segment.

• 2. There is no point in examining the isoptic surface defined in the above way for other spatial curves, because if the curve is not of constant 0 curvature, then there is an external point from which the curve and the point cannot be fitted into a plane. In this case, the above definition needs to be generalized.

For further isoptic surfaces in Euclidean geometry, see [7, 8], where we extend the definition of isoptic surfaces to other spatial objects. The notion of isoptic curve can be extended to the other planes of constant curvature (hyperbolic plane ${\textbf{H}}^2$ and spherical plane ${\textbf{H}}^2$). We studied these questions in [4] and [5].

5 Translation-Like Isoptic Surfaces in $\textbf{Nil}$

In the rest of this study, we will focus on the isoptic surface of the translation-like segment in $\textbf{Nil}$ geometry, which in the projective model is far from straight, but a parametric curve described in (2.10). We can make the following definition along the lines of the Definition 4.3.

Definition 5.1

The $\textbf{Nil}$ translation-like $\alpha$—isoptic surface of a translation-like segment $\overline{A_1A_2}$ is the locus of points P for which the internal angle at P in the translation-like triangle, formed by $A_1,$ $A_2$ and P is $\alpha .$ If $\alpha$ is the right angle, then it is called the translation-like Thaloid of $\overline{A_1A_2}.$

We emphasize here that the section itself does not appear in our calculations, we only deal with the endpoints. An interesting question beyond this study is how the ruled surface, or more precisely in this case, how the triangular surface looks like generated by the curves drawn from the outer point to all points of the section. Thus the angle can really be considered planar in $\textbf{Nil}$ sense or any non desirable intersection occurs between the segment and the rays. The section itself and the rays can be translation-like or geodesic-like as well. Some of these questions arise in [37].

We can assume by the homogeneity of the $\textbf{Nil}$ geometry that one of its endpoints coincide with the origin $A_1=E_0=(1,0,0,0)$ and the other is $A_2(1,a,b,c)$. Considering a point P(1, x, y, z), we can determine the angle $A_1PA_2\angle$ along the procedure described in the previous section.

We apply ${\textbf{T}}_{P}^{-1}$ to all three points. This transformation preserves the angle $A_1PA_2\angle$ and pulls back P to the origin, hence the angle in question seems in real size. We get ${\textbf{T}}_{P}^{-1}$ by replacing $x_2,$ $y_2$ and $z_2$ in (3.2) with x,  y and z respectively:

$$\begin{aligned} {\textbf{T}}_{A_3}^{-1}= \begin{pmatrix} 1 &{}\quad -x &{}\quad -y &{}\quad xy -z \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad -x \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1, \end{pmatrix} \end{aligned}$$

(5.1)

$$\begin{aligned} \begin{aligned} {\textbf{T}}^{-1}_{P}(P)&=(1,0,0,0); \\ {\textbf{T}}^{-1}_{P}(A_1)&=(1,-x,-y,xy -z);\\ {\textbf{T}}^{-1}_{P}(A_2)&=(1,a-x,b-y,-bx +xy +c -z). \end{aligned} \end{aligned}$$

(5.2)

According to (2.10) and (2.11), the tangent of the translation curve between the origin and a point T(1, x, y, z) at the origin can be obtained by the following formulas:

$$\begin{aligned} {\textbf{t}}=(u,v,w)=\left( x,y,z-\dfrac{x y}{2}\right) \end{aligned}$$

(5.3)

Let us denote with ${\textbf{t}}_1$ and ${\textbf{t}}_2$ the tangents of the translation curves to ${\textbf{T}}_{P}^{-1}(A_1)$ and ${\textbf{T}}_{P}^{-1}(A_2)$ from the origin $E_0={\textbf{T}}_{P}^{-1}(P)$ at the origin. We can calculate these tangents by applying (5.3) to (5.2).

$$\begin{aligned} \begin{aligned} {\textbf{t}}_{1}&=\left( -x,-y,\dfrac{x y}{2}-z\right) \\ {\textbf{t}}_{2}&=\left( a-x,b-y,c-z+\dfrac{(x+a)(y-b)}{2}\right) \end{aligned} \end{aligned}$$

(5.4)

Finally, fixing the angle of the ${\textbf{t}}_1$ and ${\textbf{t}}_2$ to $\alpha ,$ we get the translation-like $\alpha$—isoptic surface of $\overline{A_1A_2}.$

Theorem 5.2

Given a translation-like segment in the $\textbf{Nil}$ geometry by its endpoints $A_1=(1,0,0,0)$ and $A_2=(1,a,b,c).$ Then the translation-like $\alpha$—isoptic surface of the translation-like segment $\overline{A_1A_2}$ have the implicit equation:

$$\begin{aligned} \cos (\alpha )=\displaystyle {\frac{x\left( x-a \right) + y\left( y-b \right) + \left( z- \frac{xy}{2} \right) \left( z-c-\dfrac{(x+a)(y-b)}{2}\right) }{ \sqrt{\left( {x}^{2}+{y}^{2}+ \left( z-\frac{xy}{2} \right) ^{2} \right) \left( \left( x-a \right) ^{2}+ \left( y-b \right) ^{2}+ \left( z-c-\dfrac{(x+a)(y-b)}{2}\right) ^{2} \right) }}}\nonumber \\ \end{aligned}$$

(5.5)

$\square$

Fig. 5

Isoptic surface with $A_2=(1,1,1,2)$ and $\alpha =\frac{\pi }{3}$ (left) and $\frac{\pi }{2}$ (right)

On Fig. 5, one can see some isoptic surfaces to a general translation-like segment in $\textbf{Nil}$ geometry. The left side shows the isoptic surface to an acute angle, the right side shows the translation-like Thaloid of the same segment.

Let us examine the special case when the endpoints of the segment are situated on the z axis, i.e. $A_1=(1,0,0,0)$ and $A_2=(1,0,0,c).$ In this case, the translation-like segment looks like a Euclidean segment in the model. Replacing in (5.5) a,  b and $\alpha$ with 0,  0 and $\frac{\pi }{2}$ we get the following equation:

$$\begin{aligned} x^2+y^2+\left( z-\dfrac{xy}{2}\right) \left( z-\dfrac{xy}{2}-c\right) =0 \end{aligned}$$

(5.6)

Or, after some transformation:

$$\begin{aligned} x^2+y^2+\left( z-\dfrac{xy}{2}-\frac{c}{2}\right) ^2=\dfrac{c^2}{4} \end{aligned}$$

(5.7)

Now, applying ${\textbf{T}}^{-1}_F$ to all points of this equation, where F(1, 0, 0, c/2),  we obtain

$$\begin{aligned} \begin{aligned} {\textbf{T}}^{-1}_F(P)=(1;x',y',z')=(1;x,y,z) \begin{pmatrix} 1&{}\quad 0&{}\quad 0&{}\quad -\frac{c}{2} \\ 0&{}\quad 1&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 1&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 1 \\ \end{pmatrix} =\left( 1;x,y,z-\frac{c}{2}\right) \end{aligned}\qquad \end{aligned}$$

(5.8)

$$\begin{aligned} (x')^2+(y')^2+\left( z'-\dfrac{xy}{2}\right) ^2=\dfrac{c^2}{4} \end{aligned}$$

(5.9)

Comparing (5.9) equation with (2.13), we can claim the following lemma:

Lemma 5.3

Given a translation-like segment in the $\textbf{Nil}$ geometry by its endpoints $A_1=(1,0,0,0)$ and $A_2=(1,a,b,c).$ Then the translation-like Thaloid of this line segment is a $\textbf{Nil}$ sphere without the endpoints of the segment if and only if $a=b=0.$ Then the center of the $\textbf{Nil}$ sphere is F(1, 0, 0, c/2) and its radius is $\dfrac{|c|}{2}.$

Proof

To prove Lemma 5.3, we need further consideration to the other direction, not covered by the calculations above. Due to lengthy calculations and formulas, we only present here the outline of the proof. First, we need to find the midpoint F of the translation section $\overline{A_1A_2}$ and its length, half of which will be the radius of the sphere. Then, using ${\textbf{T}}^{-1}_F$ and (2.13), we write the equation of the translation sphere whose diameter is $\overline{A_1A_2}.$ We compare this to the numerator of the right side in equation (5.5) (substituting $\alpha =\pi /2$). Finally, considering the difference of the two equations, we get that it will be 0 if and only if $ay-bx=0,$ or $ay-bx=2ab-4c$ which is equivalent to $a=b=0.$ $\square$

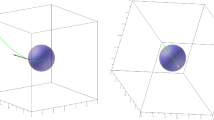
On Fig. 6 we can see the translation-like Thaloid related to the translation segment $A_1=(1,0,0,0)$ and $A_2=(1,0,0,4),$ as well as a sphere with center $F=(1,0,0,2)$ and radius 2.

Fig. 6

Isoptic surface (translation-like Thaloid) of translation segment $\overline{A_1A_2}$ where $A_1=(1,0,0,0)$, $A_2=(1,0,0,4)$ and $\alpha =\frac{\pi }{2}.$