Discrete Fault Models

Abstract

Fault surfaces are characterized by an inhomogeneous friction distribution, that can be represented with asperity models. Fault mechanics is dominated by asperities, so that a fruitful approach is to use discrete models, where asperities are the basic elements and the state of the fault is described by the average values of stress, friction and slip on each asperity. Under reasonable assumptions, the equations of motion can be solved analytically, with a deeper understanding of the behavior of the system. Fault dynamics has a sticking mode, where asperities are stationary, and a number of slipping modes, corresponding to the separate or simultaneous motion of asperities. Any seismic event is a sequence of slipping modes and a large variety of source functions is possible. Many large earthquakes are observed to be the consequence of the failure of two asperities: a discrete two-asperity model shows a rich dynamics and allows a detailed study of interaction between asperities. In this framework, fault evolution during coseismic and interseismic intervals can be calculated in terms of fault slip, stress state, energy release and seismic spectrum, including viscoelastic relaxation, fault creep and stress perturbations from other faults. Discrete models may include interaction between neighboring faults, allowing to assess conditions for the occurrence of seismic sequences in a fault system. A review of recent work on this subject is presented with applications to real earthquakes.

1 Introduction

Fault surfaces usually present a strongly nonuniform friction distribution, producing a remarkable complication in fault mechanics. An important achievement of seismic source theory is that friction distribution can be represented by asperity models (Lay et al., 1982; Ruff, 1983; Ruff & Kanamori 1983; Scholz, 1990). Such models assume that earthquakes result from slip of a small number of fault patches, characterized by high static friction and velocity-weakening dynamic friction.

An inhomogeneous friction distribution entails a nonuniform distribution of coseismic slip. Seismic source functions retrieved from seismometric data show that fault slip usually takes place irregularly and suggest a complex interaction between different fault patches, resulting from a continuous stress transfer between them. One of the first events for which this behavior was observed is the 1992 Landers, California, earthquake (Kanamori et al., 1992; Wald & Heaton, 1994).

Heterogeneous fault models have been proposed by many authors. Models with nonuniform friction distributions under a uniform shear stress were considered by Mikumo and Miyatake (1978, 1995) and Beroza and Mikumo (1996). Somerville et al. (1999) showed that in most cases the slip distribution can be represented in terms of a small number of asperities. Pisarenko (2002) suggested that velocity weakening friction is a consequence of the dynamical failure of asperities. A stochastic model of fault slip complexity was developed by Mai and Beroza (2002). The case of nonuniform initial stress was considered by Cochard and Madariaga (1994), Ripperger et al. (2007) and Bizzarri et al. (2010). A multiple-asperity model was considered by Johnson (2010). Zielke et al. (2017) considered friction deriving from geometrical roughness of the fault surface. Numerical solutions were obtained in most of these studies.

A different approach is suggested by the evidence that asperities play a crucial role in fault mechanics. Processes controlling fault mechanics are stress accumulation on asperities, asperity strength and slip, as well as stress transfer between asperities. Therefore, the fault can be considered as a discrete dynamical system where asperities are the basic elements (Ruff, 1992; Rice 1993; Turcotte, 1997). Fault dynamics coincides with asperity dynamics and the state of the fault can be described by a finite number of variables characterizing asperities.

In fact, fault mechanics is controlled by a small number of asperities, so that models with a small number of degrees of freedom can be employed. Discrete fault models reproduce the essential features of the seismic source, but avoid the more complicated description based on continuum mechanics. The small number of degrees of freedom allows visualization of the state of the fault and of its evolution by inspection of orbits of the representative point in the phase space.

It should be noticed that discrete models considered here are different from models made of a large number of blocks discretizing the fault, such as those originally proposed by Burridge and Knopoff (1967). Those models approximate a continuous system with a system made of a finite, but very large number of degrees of freedom. On the contrary, models considered here are devised to study those aspects of fault mechanics resulting from a structure made of few strong patches, i.e. asperities. Average values of stress, friction and slip on each asperity are considered.

Early papers adopting this approach were Nussbaum and Ruina (1987), Huang and Turcotte (1990) and Ruff (1992). The instability properties of discrete fault models and their possible chaotic behavior were investigated by McCloskey and Bean (1992), de Sousa Vieira (1995), Turcotte (1997), Wang (2000), He (2003) and Galvanetto (2004). Wang (2008) gave a review of previous studies.

Originally, these models were conceived as low-order analogues of real faults, with asperities described as blocks sliding on a rough plane. However, equations governing these systems can be viewed as approximations of continuum mechanical equations, with a correspondence between model parameters and continuum mechanical quantities (Dragoni & Santini, 2012). In this formulation, an asperity is assumed to be a compact and simply connected subset of the fault surface and asperity failure can reproduce any kind of source mechanism.

In this framework, a fault with n asperities is a nonlinear, dissipative, piecewise smooth dynamical system with n degrees of freedom (di Bernardo et al., 2008). The evolution of such systems in the phase space is characterized by smooth intervals separated by rapid transitions, that can be considered as instantaneous events. Smooth intervals are the dynamic modes of the system and each mode is associated with a different set of differential equations. Such systems are named Filippov systems (Filippov, 1988).

A fault with n asperities has $2^n$ dynamic modes: a sticking mode, corresponding to stationary asperities, and $2^n - 1$ slipping modes, corresponding to individual or simultaneous asperity motion. If asperities are labeled with integers from 1 to n, each mode can be indicated by a string of n digits $i_1 i_2 \dots i_n$, that may assume values 0 or 1, where 0 denotes that the asperity is stationary and 1 that the asperity is slipping. A seismic event generated by the fault is a sequence of slipping modes.

Seismological data show that several large earthquakes occurred in the last decades can be ascribed to the failure of two asperities, from the 1964 Great Alaska Earthquake (Christensen & Beck, 1994) to the 2010 Maule earthquake (Delouis et al., 2010). A discrete fault model with two asperities has two degrees of freedom and four dynamic modes, and exhibits a very rich dynamics. Its evolution can be studied in detail during coseismic slip and interseismic intervals. Complex seismic events, that are sequences of several slipping modes, can be generated and initial conditions producing such events can be determined. Slip rates and shear stresses on asperities can be calculated as functions of time and their relationships can be investigated. Energy release, seismic moments and seismic wave spectra can be also calculated as functions of initial conditions.

The present paper summarizes the results obtained in a number of papers published on this subject in the last decade. Section 2 presents the model: a plane fault with two asperities subject to uniform strain rate from the motion of tectonic plates. The system variables and parameters are defined and the dynamic modes of the system are introduced. The general formulae for slip rates, moment rates, shear stress, seismic efficiency, seismic moments and spectra are given.

Section 3 illustrates the dynamics of the two-asperity fault, starting from the simplest case of identical asperities. The properties of long-term behavior and the conditions for the occurrence of large earthquakes are investigated. The case of two asperities with equal areas, but different strengths is then considered and the variety of possible source functions that it can generate is illustrated. Effects of wave radiation are highlighted by calculation of seismic energy and spectrum as functions of model parameters. The more general case of asperities with different areas and strengths is then considered and the role of stress perturbations in controlling fault evolution is examined. Finally, the effect of viscoelastic relaxation of the lithosphere during interseismic intervals is treated. Section 4 considers particular aspects of fault mechanics, such as the effect of variable strain rate, fault creep and afterslip, fault interaction and the occurrence of seismic sequences in a fault system. Section 5 gives a summary of the main results.

Fig. 1

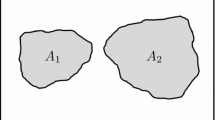
Adapted from Lorenzano and Dragoni (2018a)

The two-asperity fault model. A rectangular fault surface with two asperities of areas $A_1$ and $A_2$ is shown. Asperities may have different strengths. The fault is subject to uniform strain rate, but shear stress is typically nonuniform on the fault.

2 The Asperity Model

A plane fault with two asperities is considered. The asperities are named 1 and 2 respectively: they are disjoint subsets of the fault surface, with areas $A_1$ and $A_2$ (Fig. 1). It is assumed that the fault lies in a shear zone that is a homogeneous and isotropic Poisson solid with rigidity $\mu$. The shear zone has thickness d and is subject to a uniform strain rate $\dot{e}$ imposed by the motion of two tectonic plates at constant relative velocity v.

2.1 The Dynamical System

The state of an asperity at any time t is described by its slip deficit, defined as the slip that the asperity should undergo in order to recover the relative plate displacement occurred up to that time (Dragoni & Santini, 2015). The reason for using slip deficit is that it changes continuously even during interseismic intervals, when asperities are stationary. Accordingly, the state of the fault is described by slip deficits x(t) and y(t) of asperities 1 and 2, respectively. The model assumes the no-overshooting conditions

$$\begin{aligned} x\ge 0, \quad y \ge 0 \end{aligned}$$

(1)

implying that asperity slip does not exceed the plate displacement accumulated up to that time.

Since it is assumed that asperities move as rigid surfaces, their dynamics can be described by forces instead of tractions. Asperity slip is induced by forces exerted by the surrounding medium and is controlled by friction. Let $f_1$ and $f_2$ be the tangential forces applied to asperities in the slip direction. They can be written as (Lorenzano & Dragoni, 2018a)

$$\begin{aligned} f_1 = - K_1 x - K_c (x - y) - \iota _1 \dot{x} \end{aligned}$$

(2)

$$\begin{aligned} f_2 = - K_2 y - K_c (y - x) - \iota _2 \dot{y} \end{aligned}$$

(3)

where terms $-K_1 x$ and $-K_2 y$ are the effect of tectonic loading, with

$$\begin{aligned} K_1 = {2\mu \dot{e} A_1 \over v}, \quad K_2 = {2\mu \dot{e} A_2 \over v} \end{aligned}$$

(4)

Terms $\pm K_c (x - y)$ are contributions of stress transfer between asperities, with a coupling constant

$$\begin{aligned} K_c = \mu A_1 A_2 s \end{aligned}$$

(5)

where s is the shear traction (per unit seismic moment) that the slip of one asperity imposes to the other, calculated at the asperity centroid (Lorenzano & Dragoni, 2018a).

Let a be the distance between the asperity centroids. At distances $a >1.5 \sqrt{A}$, the traction produced by a finite dislocation source of area A is indistinguishable from that of a point-like double-couple source (Dragoni & Lorenzano, 2016). Accordingly, shear tractions are

$$\begin{aligned} s = {5 \over 12 \pi a^3} \end{aligned}$$

(6)

for a strike-slip mechanism and

$$\begin{aligned} s = {1 \over 6 \pi a^3} \end{aligned}$$

(7)

for a dip-slip mechanism (Love, 1944). Finally, terms $-\iota _1 \dot{x}$ and $-\iota _2 \dot{y}$ in (2) and (3) are due to radiation damping, where $\iota _1$ and $\iota _2$ are impedances, and contribute only during fault slip (Rice, 1993).

It is assumed that asperities obey a velocity-weakening frictional law, with static frictions $f_{s1}$ and $f_{s2}$ and dynamic frictions $f_{d1}$ and $f_{d2}$ (Dragoni & Santini, 2012), that can be considered a simplified version of the more general rate and state-dependent law (Ruina, 1983; Dieterich, 1994; Scholz, 1998). Accordingly, conditions for failure of asperities 1 and 2 are, respectively

$$\begin{aligned} f_1 = - f_{s1}, \qquad f_2 = - f_{s2} \end{aligned}$$

(8)

The fault has four dynamic modes: a sticking mode (indicated by the string 00), where asperities are stationary, and three slipping modes, corresponding to slip of asperity 1 (10), slip of asperity 2 (01) and simultaneous slip (11). Each mode is described by a system of two differential equations. Equations for the sticking mode are

$$\begin{aligned} {\ddot{x}} = 0 \end{aligned}$$

(9)

$$\begin{aligned} {\ddot{y}} = 0 \end{aligned}$$

(10)

and equations for the slipping modes are

$$\begin{aligned} m_1 \ddot{x} + \iota _1 \dot{x} + K_1 x + K_c (x - y) - f_{d1} = 0 \end{aligned}$$

(11)

$$\begin{aligned} m_2 \ddot{y} + \iota _1 \dot{y} + K_2 y + K_c (y - x) - f_{d2} = 0 \end{aligned}$$

(12)

where $m_1$ and $m_2$ are masses associated with the asperities (Lorenzano & Dragoni, 2018a). Hence, the evolution of the system is described by (9) and (10) in mode 00, by (11) and (10) in mode 10, by (9) and (12) in mode 01 and by (11) and (12) in mode 11.

Fig. 2

Adapted from Dragoni and Tallarico (2016)

The sticking region Q of the system in the plane XY. The sides of Q are defined by conditions on the forces $F_1$ and $F_2$ acting on asperities. The dashed line is $Y = X + p_0$, separating initial conditions leading to failure of asperity 1 or 2 respectively. The region is drawn for $\alpha =1$, $\beta =0.5$, $\gamma =0.5$, $\epsilon =0.7$, $\xi =1$.

2.2 Nondimensional Formulation

It is useful to express the model variables and parameters in nondimensional form. To this aim, nondimensional variables and time are introduced (Lorenzano & Dragoni, 2018a):

$$\begin{aligned} X = {K_1 x \over f_{s1}}, \quad Y = {K_1 y \over f_{s1}}, \quad T = \sqrt{K_1 \over m_1} \,t \end{aligned}$$

(13)

Accordingly, the state of the fault is described by nondimensional slip deficits X(T) and Y(T). The following nondimensional parameters are also introduced:

$$\begin{aligned} \alpha = {K_c \over K_1}, \quad \beta = {f_{s2} A_1 \over f_{s1} A_2} = {f_{d2} A_1 \over f_{d1} A_2}, \quad \gamma = {\iota _1 \over \sqrt{K_1 m_1}} \end{aligned}$$

(14)

$$\begin{aligned} \epsilon = {f_{d1} \over f_{s1}} = {f_{d2} \over f_{s2}}, \quad \xi = {A_2 \over A_1}, \quad V = {\sqrt{K_1 m_1} \over f_{s1}} \,v \end{aligned}$$

(15)

where $\alpha$ is a coupling parameter for asperities; $\beta$ is the ratio between the frictional stresses of asperity 2 and the same quantities of asperity 1; $\gamma$ is a measure of impedance associated with asperity 1; $\epsilon$ is the ratio between dynamic and static friction for both asperities; $\xi$ is the ratio between asperity areas; V is the nondimensional velocity of tectonic plates.

It is assumed that masses $m_1$ and $m_2$ are proportional to the respective asperity areas and that the impedance per unit area is the same for both asperities, so that

$$\begin{aligned} \xi = {m_2 \over m_1} = {\iota _2 \over \iota _1} \end{aligned}$$

(16)

Nondimensional forces are defined as

$$\begin{aligned} F_1 = {f_1\over f_{s1}}, \quad F_2 = {f_2\over f_{s1}} \end{aligned}$$

(17)

Thanks to (2), (3) and (14), they can be written in terms of slip deficits as

$$\begin{aligned} F_1 = - X - \alpha (X - Y) - \gamma \dot{X}, \qquad F_2 = - Y - \alpha (Y - X) - \gamma \dot{Y} \end{aligned}$$

(18)

where dots indicate differentiation with respect to time T. Therefore, the evolution equations for the sticking mode become

$$\begin{aligned} {\ddot{X}} = 0 \end{aligned}$$

(19)

$$\begin{aligned} {\ddot{Y}} = 0 \end{aligned}$$

(20)

and those for the slipping modes become

$$\begin{aligned} {\ddot{X}} + \gamma \dot{X} + (1 + \alpha ) X - \alpha Y - \epsilon = 0 \end{aligned}$$

(21)

$$\begin{aligned} {\ddot{Y}} + \gamma \dot{Y} + (1 + \alpha ^\prime ) Y - \alpha X - \beta \epsilon = 0 \end{aligned}$$

(22)

where

$$\begin{aligned} \alpha^\prime = {\alpha \over \xi } \end{aligned}$$

(23)

Since the system has two degrees of freedom, its phase space is a 4-manifold S. The evolution of the system can be described by the orbit of its representative point (X, Y, $\dot{X}$, $\dot{Y}$) in S.

The effect of radiation on fault dynamics is expressed by parameters (Dragoni & Santini, 2015; Lorenzano & Dragoni, 2018a)

$$\begin{aligned} \kappa _1 = {1\over 2} \biggl (1 + e^{-{\pi \gamma \over 2\omega _1}} \biggr ), \quad \kappa _2 = {1\over 2} \biggl (1 + e^{-{\pi \gamma \over 2\omega _2}} \biggr ) \end{aligned}$$

(24)

where

$$\begin{aligned} \omega _1 = \sqrt{1 + \alpha - {\gamma ^2\over 4}}, \quad \omega _2 = \sqrt{1 + \alpha ^\prime - {\gamma ^2\over 4}} \end{aligned}$$

(25)

If m(t) is the seismic moment produced in a seismic event as a function of time, the nondimensional moment is

$$\begin{aligned} M = {K_1 m\over f_{s1}^2} \end{aligned}$$

(26)

Let w(t) be the energy of the system at time t and r(t) be the radiation produced by asperity slip after a time t from the beginning of the event. The corresponding nondimensional quantities are

$$\begin{aligned} W = {K_1 w\over f_{s1}^2}, \quad R = {K_1 r\over f_{s1}^2} \end{aligned}$$

(27)

Finally, if $\omega$ is the angular frequency of seismic waves, the nondimensional frequency is

$$\begin{aligned} \Omega = \sqrt{m_1 \over K_1} \,\omega \end{aligned}$$

(28)

2.3 Initial Conditions

For most time, the system is in the sticking mode 00, where $\dot{X}$ and $\dot{Y}$ are equal to the velocity V of tectonic plates, hence extremely small with respect to the values they assume in slipping modes. Therefore, the representative point of the system in mode 00 can be assumed as belonging to the plane XY. The onset of seismic events is controlled by forces

$$\begin{aligned} F_1 = - X - \alpha (X - Y), \quad F_2 = - Y - \alpha (Y - X) \end{aligned}$$

(29)

that are applied to asperities in mode 00. The no-overshooting condition (1) implies that both $F_1$ and $F_2$ are in the direction of velocity v, or

$$\begin{aligned} F_1 \le 0, \quad F_2 \le 0 \end{aligned}$$

(30)

From (8), the conditions for failure of asperities 1 and 2 are respectively

$$\begin{aligned} F_1 = - 1, \quad F_2 = -\beta \xi \end{aligned}$$

(31)

Therefore, the state of the system in mode 00 is constrained to a subset of the plane XY, whose borders are defined by conditions

$$\begin{aligned} F_1 = 0, \quad F_2 = 0, \quad F_1 = - 1, \quad F_2 = -\beta \xi \end{aligned}$$

(32)

In terms of slip deficits, Eq. (32) can be written as

$$\begin{aligned} Y= & {} {1 + \alpha \over \alpha } X, \quad Y = {\alpha \over \alpha + \xi } X \end{aligned}$$

(33)

$$\begin{aligned} Y= & {} {1 + \alpha \over \alpha } X - {1 \over \alpha }, \quad Y = {\alpha \over \alpha + \xi } X + {\beta \xi \over \alpha + \xi } \end{aligned}$$

(34)

that are the equations of four lines defining a parallelogram Q (Fig. 2). The subset Q, corresponding to stationary asperities, is called the sticking region (di Bernardo et al., 2008). Vertices of Q are the origin O and points $P_a$, $P_b$ and P with coordinates (Lorenzano & Dragoni, 2018a)

$$\begin{aligned} X_a = {\alpha + \xi \over \alpha + \alpha \xi + \xi }, \quad Y_a = {\alpha \over \alpha + \alpha \xi + \xi } \end{aligned}$$

(35)

$$\begin{aligned} X_b = {\alpha \beta \xi \over \alpha + \alpha \xi + \xi }, \quad Y_b = {(1 + \alpha ) \beta \xi \over \alpha + \alpha \xi + \xi } \end{aligned}$$

(36)

$$\begin{aligned} X_P = X_a + X_b, \quad \quad Y_P = Y_a + Y_b \end{aligned}$$

(37)

If we consider an initial point $P_0 = (X_0, Y_0) \in \mathbf{Q}$, the evolution of the system from $P_0$ is given by solutions of (19) and (20), or

$$\begin{aligned} X(T) = X_0 + VT \end{aligned}$$

(38)

$$\begin{aligned} Y(T) = Y_0 + VT \end{aligned}$$

(39)

These are the parametric equations of a line

$$\begin{aligned} Y = X + p \end{aligned}$$

(40)

where

$$\begin{aligned} p = Y_0 - X_0 \end{aligned}$$

(41)

If one calculates the difference $F_1 - F_2$ at $P_0$ from (29), one obtains

$$\begin{aligned} F_1 - F_2 = (1 + 2\alpha ) p \end{aligned}$$

(42)

so that p is proportional to the difference between forces acting on asperities: hence it expresses the degree of stress inhomogeneity on the fault (Dragoni & Santini, 2010).

A seismic event occurs when the representative point of the system, moving along line (40), intersects one of lines (34). The subsequent evolution depends on the value of p, expressing the initial condition for the seismic event. Values of p range in the interval $[p_a, p_b]$, where

$$\begin{aligned} p_a = Y_a - X_a, \quad p_b = Y_b - X_b \end{aligned}$$

(43)

Different initial conditions may produce very different seismic events. In particular, an event begins with mode 10 when $p<p_0$ and with mode 01 when $p>p_0$, where

$$\begin{aligned} p_0 = Y_P - X_P \end{aligned}$$

(44)

In many cases, a 1-mode seismic event, involving motion of a single asperity, is produced. More complex events are generated if p belongs to the narrower interval $[p_1, p_2]$, where (Lorenzano & Dragoni, 2018a)

$$\begin{aligned} p_1 = p_0 - {\alpha \kappa _1 U \over \alpha + \alpha \xi + \xi }, \quad p_2 = p_0 + {\alpha \beta \xi \kappa _2 U^\prime \over \alpha + \alpha \xi + \xi } \end{aligned}$$

(45)

where

$$\begin{aligned} U = 2\, {1 - \epsilon \over 1 + \alpha }, \quad U^\prime = 2\, {1 - \epsilon \over 1 + \alpha ^\prime } \end{aligned}$$

(46)

In this case, the motion of an asperity triggers the motion of the other one, originating a stress interchange between them: events that are sequences of three or more slipping modes are produced. In the particular case $p = p_0$, a 2-mode event 11-01 takes place: this is the largest event produced by the 2-asperity fault.

Fig. 3

Adapted from Dragoni and Santini (2010)

A limit cycle of the two-asperity fault, projected on the plane XY. Segments $P_1 P_2$ and $P_3 P_4$ represent 1-mode seismic events 10 and 01 respectively. Segments $P_2 P_3$ and $P_4 P_1$ represent interseismic intervals of different durations. The cycle can be run in both senses depending on the initial value of the variable p ($-0.17$ or 0.13), expressing stress distribution on the fault. Model parameters are $\alpha =1$, $\beta =1$, $\gamma =0$, $\epsilon =0.7$, $\xi =1$.

2.4 Seismic Events

During a seismic event, a continuous change in slip deficits X and Y, as well as in slip rates $\dot{X}$ and $\dot{Y}$, takes place. Therefore, the event is represented by an orbit in the 4-manifold S. However, a seismic event can be more easily characterized by drawing the projection of its orbit on the plane XY, where the system dwells for most of its lifetime.

Each event is a sequence of m slipping modes and a segment of curve in the plane XY is associated with each mode. The functions X(T) and Y(T) relative to that mode are the parametric equations of the segment. If one introduces normal coordinates

$$\begin{aligned} H_1 = {Y + X\over \sqrt{2}}, \qquad H_2 = {Y - X\over \sqrt{2}} \end{aligned}$$

(47)

the solution for a generic mode starting at $T=0$ can be written as (Dragoni & Tallarico, 2016)

$$\begin{aligned} H_1(T) = h_1 + (a_1 \sin \Omega _1 T + b_1 \cos \Omega _1 T) \,e ^{-{\gamma \over 2}T} \end{aligned}$$

(48)

$$\begin{aligned} H_2(T) = h_2 + (a_2 \sin \Omega _2 T + b_2 \cos \Omega _2 T) \,e ^{-{\gamma \over 2}T} \end{aligned}$$

(49)

where $h_1$, $h_2$, $a_1$, $a_2$, $b_1$ and $b_2$ are constants depending on the particular mode and on initial conditions, while $\Omega _1$ and $\Omega _2$ depend on model parameters. These are the parametric equations of a damped Lissajous curve (Lawrence, 1972). The orbit representing an m-mode event is the union of m segments of such curves, separated by singular points. The sequence of modes in the event and the associated slip amplitudes are evident from inspection of orbits in the plane XY.

Let $T_i$ ($i = 1, 2, \dots m$) be the instant of time when the system enters the i-th mode and $T_{m+1}$ be the end time of the event. The duration of an m-mode seismic event is then

$$\begin{aligned} \Delta T = T_{m+1} - T_1 \end{aligned}$$

(50)

The duration of each mode, as well as the total duration of the event, may vary sensibly from one event to the other (Dragoni & Tallarico, 2016).

Let $X_i$ and $Y_i$ be the slip deficits at time $T_i$. The slip amplitudes in the i-th mode are then

$$\begin{aligned} \Delta X_i = X_i - X_{i+1}, \quad \Delta Y_i = Y_i - Y_{i+1} \end{aligned}$$

(51)

and the total slip amplitudes are respectively

$$\begin{aligned} U_1 = X_1 - X_{m+1}, \quad U_2 = Y_1 - Y_{m+1} \end{aligned}$$

(52)

The dynamics of a seismic event is evident if we consider the slip rates of asperities and the moment rate of the event. In each slipping mode, slip rates are given by different functions for each asperity. Let $X_i(T)$ and $Y_i(T)$ be the slip deficits in the i-th mode. The slip rates of asperities are

$$\begin{aligned} \Delta \dot{X}_i(T) = - \dot{X}_i(T)\end{aligned}$$

(53)

$$\begin{aligned} \Delta \dot{Y}_i(T) = - \dot{Y}_i(T) \end{aligned}$$

(54)

The slip rates in an m-mode seismic event are then

$$\begin{aligned} \Delta \dot{X}(T)= & {} \sum _{i=1}^m \Delta \dot{X}_i(T)\, [H(T - T_i) - H(T - T_{i+1})] \end{aligned}$$

(55)

$$\begin{aligned} \Delta \dot{Y}(T)= & {} \sum _{i=1}^m \Delta \dot{Y}_i(T)\, [H(T - T_i) - H(T - T_{i+1})] \end{aligned}$$

(56)

where H(T) is the Heaviside function. For each event, the moment rate can be calculated from (55) and (56). Let $M_1$ be the seismic moment of a 1-mode event 10 in the absence of radiation ($\gamma =0$), corresponding to the slip amplitude U defined in (46). The moment rate of a generic m-mode event is then

$$\begin{aligned} \dot{M}(T) = {M_1 \over U} \sum _{i=1}^m (\Delta \dot{X}_i + \Delta \dot{Y}_i) [H(T -T_i) - H(T - T_{i+1})] \end{aligned}$$

(57)

or

$$\begin{aligned} \dot{M}(T) = M_1 {\Delta \dot{X} + \Delta \dot{Y} \over U} \end{aligned}$$

(58)

Very different moment rates result depending on initial conditions (Dragoni & Tallarico, 2016). The total seismic moment of an m-mode event is

$$\begin{aligned} M_0 = M_1 {U_1 + U_2 \over U} \end{aligned}$$

(59)

The moment rate spectrum S of a seismic event is defined as the magnitude of the Fourier transform of $\dot{M}(T)$:

$$\begin{aligned} S(\Omega) = \left| \, \int_{T_i}^{T_{m+1}} \dot{M}(T) \,e^{-i \Omega T} dT \,\right| \end{aligned}$$

(60)

The energy of the system at a point $(X, Y) \in \mathbf{Q}$ is (Dragoni & Santini, 2015)

$$\begin{aligned} E(X,Y) = {1\over 2} (X^2 + Y^2) + {1\over 2}\alpha (X - Y)^2 \end{aligned}$$

(61)

Let $E_i$ be the energy at the beginning of the ith mode. The energy change in the ith mode is then

$$\begin{aligned} \Delta E_i = E_{i+1} - E_i \end{aligned}$$

(62)

and the total energy change is

$$\begin{aligned} \Delta E = E_{m+1} - E_1 \end{aligned}$$

(63)

or, thanks to (52),

$$\begin{aligned} \Delta E = E(X_1 - U_1, Y_1 - U_2) - E(X_1, Y_1) \end{aligned}$$

(64)

In the ith mode, seismic energy is released at a rate (Dragoni & Santini, 2015)

$$\begin{aligned} \dot{R}_i = - \gamma (\dot{X}_i^2 + \dot{Y}_i^2) \end{aligned}$$

(65)

and the energy released in the ith mode is

$$\begin{aligned} \Delta R_i = \int _{T_i}^{T_{i+1}} \dot{R}_i(T) \, dT \end{aligned}$$

(66)

The total seismic energy released in the event is

$$\begin{aligned} \Delta R = \sum _{i=1}^m \Delta R_i \end{aligned}$$

(67)

Finally, the seismic efficiency can be defined as

$$\begin{aligned} \eta = {\Delta R \over \Delta E} \end{aligned}$$

(68)

Fig. 4

Adapted from Dragoni and Tallarico (2016)

An example of orbit for a 3-mode seismic event 01-11-01, projected on the plane XY. Initial condition is $p=-0.15$. In this case $p \in [p_1, p_2]$, so that the event includes mode 11. Each segment of the orbit is labeled with the string indicating the slipping mode. The dashed line is $Y=X+p_0$, where $p_0 \simeq -0.17$. Model parameters are $\alpha =1$, $\beta =0.5$, $\gamma =0.5$, $\epsilon =0.7$, $\xi =1$.

3 Dynamics of a Two-Asperity Fault

The dynamics of a two-asperity fault can be highlighted by considering a number of cases of increasing complexity. In all cases, analytical solutions for the dynamic modes of the system can be obtained.

According to Turcotte (1997), chaotic behavior is attained for higher values of the coupling parameter $\alpha$. From (14), (4), (5) and (6) or (7), it results that $\alpha$ is proportional to the ratio $A/a^3$, where $A=A_1$ or $A_2$. Since asperities are disjoint subsets of the fault surface, larger areas imply larger values of distance a. Therefore the high values of $\alpha$ required for chaotic behavior are hardly attained and this kind of behavior is not considered here. Analysis of seismological data is not conclusive in this regard (e.g. Marzocchi et al., 1997).

3.1 Identical Asperities

The simplest case is a fault with two identical asperities (Dragoni & Santini, 2010). In this case $A_1 = A_2$, $f_{s1} = f_{s2}$ and $f_{d1} = f_{d2}$. Then the parameters $\beta$ and $\xi$ are equal to 1. For the sake of simplicity, wave radiation is neglected, a reasonable assumption in view of the low seismic efficiency of faults (Kanamori, 2001): hence $\gamma =0$. Therefore, Eqs. (21) and (22) reduce to

$$\begin{aligned} {\ddot{X}} + (1 + \alpha ) X - \alpha Y - \epsilon = 0 \end{aligned}$$

(69)

$$\begin{aligned} {\ddot{Y}} + (1 + \alpha ) Y - \alpha X - \epsilon = 0 \end{aligned}$$

(70)

The system has a rich variety of behaviors even in this simpler case. An analysis of orbits in the phase space shows that the system has an infinite number of limit cycles, each one characterized by the variable p defined in (41). An initial value $p+U$ gives rise to the same cycle, but run in the opposite way (Fig. 3). An interesting aspect is that the recurrence pattern of seismic events depends on the initial stress distribution on the fault (Dragoni & Santini, 2010).

Each cycle is made of two 1-mode events 10 and 01, separated by interseismic periods of variable duration. The slip amplitude U given in (46) is associated with each event. From (59) with $U_1=U$ and $U_2=0$ or $U_1=0$ and $U_2=U$, the seismic moment of each event is

$$\begin{aligned} M_0 = M_1 \end{aligned}$$

(71)

In the particular case when one interseismic period is equal to zero, a single 2-mode event 10-01 or 01-10, with seismic moment $2M_1$ takes place in the cycle. There is no simultaneous slip of asperities.

Orbits reach a limit cycle only after entering a particular subset L of the sticking region Q. This means that only a subset of initial stress distributions on the fault allows the system to enter a limit cycle. In this case, the behavior is periodic, with alternate asperity slip.

When the representative point of the system is outside L, the motion of one asperity can trigger the motion of the other one and simultaneous motion takes place (mode 11). This happens because, while an asperity is slipping, the condition for slip of the other asperity is attained. In this case, (69) and (70) must be solved simultaneously (Dragoni & Santini 2011). When simultaneous slip takes place, asperity 1 may trigger the failure of asperity 2 or vice versa: the two cases produce earthquakes with similar seismic moments, but different epicentres. The seismic moment of events including mode 11 is always larger than the maximum value $2M_1$ produced in a limit cycle. Events including simultaneous slip of asperities are the largest earthquakes that can be generated by the fault.

In the long term, the representative point reaches in any case the subset L and enters a limit cycle, with periodic behavior. Of course, this contrasts with observation, showing that the seismic activity of a fault is aperiodic and produces earthquakes of different magnitudes. This behavior can easily result from the model if one assumes that the fault is not isolated, but may receive stress transfers from the seismic activity of neighboring faults.

The system is sensitive to small perturbations, because the sticking region $\mathbf{Q}$ can be divided into narrow stripes leading to different evolutions (Dragoni & Santini, 2011). If the system is in L, a small stress perturbation can shift the system from one limit cycle to another having a different recurrence pattern. The system may also be shifted outside L: in this case, one or more larger events, with simultaneous asperity motion, will be produced, until a stress distribution leading to periodic behavior is restored. Therefore periodicity could not be observed.

Fig. 5

Adapted from Dragoni and Tallarico (2016)

Moment rate $\dot{M}$ of the 3-mode seismic event 01-11-01 represented in Fig. 4. Moment rate is normalized to the nondimensional seismic moment $M_1$ of a 1-mode event 10 in the absence of radiation. Nondimensional event duration is $\Delta T = 4.47$.

3.2 Asperities with Different Strengths

In the case of a fault with two asperities with equal areas, but different strengths, we have still $\xi =1$ but $\beta \ne 1$. The equations for slipping modes are

$$\begin{aligned} {\ddot{X}} + (1 + \alpha ) X - \alpha Y - \epsilon = 0 \end{aligned}$$

(72)

$$\begin{aligned} {\ddot{Y}} + (1 + \alpha ) Y - \alpha X - \beta \epsilon = 0 \end{aligned}$$

(73)

Solution of these equations shows that the system has a greater range of possible behaviors (Dragoni & Santini 2012). As in the case of equal strengths, the fault can produce earthquakes from the failure of one asperity or may involve failure of both asperities, but the symmetry of section 3.1 is lost. When one asperity is involved in a seismic event, the following event is originated in most cases by the failure of the other asperity, but in some cases failure of the same asperity may occur. In particular cases (Fig. 4), an earthquake may be due to slip of one asperity followed by slip of the other one and again by slip of the first one (Dragoni & Santini, 2012).

At any instant of time, the evolution of the fault depends on the variable p, that is proportional to the difference between forces $F_1$ and $F_2$ according to (42). For the largest part of the interval $[p_a, p_b]$, the difference is remarkable. It is concluded that the initial stress distribution on the fault is not uniform in most cases.

As an example, Dragoni and Santini (2012) considered the 1964 Great Alaska Earthquake, one of the largest events in the last century, with magnitude 9.2. Seismological, geodetic and tsunami data show that the earthquake was due to the failure of two large asperities (Christensen & Beck, 1994; Holdahl & Sauber 1994; Johnson et al., 1996; Santini et al. 2003; Zweck et al., 2002). On the basis of data, a coupling parameter $\alpha =0.1$ was assumed. Friction distribution was estimated from the ratio of maximum slip amplitudes for the two asperities, yielding $\beta =0.75$. With an appropriate value of p, the event can be modelled as a mode sequence 10-01.

If one assumes that after an earthquake the state of stress is controlled only by tectonic loading, the model predicts that next earthquakes will involve only one asperity: hence they will be smaller than the 1964 one, until conditions for a new large event are attained. This prediction leans on simplifying assumptions and approximate data, but it shows that discrete fault models, focusing on large-scale properties, may disclose mechanisms controlling the long-term evolution of faults (Dragoni & Santini, 2012).

The source function of a seismic event is usually expressed by the moment rate $\dot{M}$ as a function of time. A study of the moment rate of events produced by a two-asperity fault shows how the moment rate changes as a function of initial conditions and model parameters (Dragoni & Santini, 2014). For given values of parameters, the moment rate function depends on the sequence of slipping modes in the event, which is controlled by the value of p. The graph of moment rate appears as a sequence of humps, each one corresponding to a slipping mode, that may partially overlap in connection with simultaneous slip (Fig. 5).

A seismic event including simultaneous asperity slip was the 2010 Maule earthquake, a magnitude 8.8 thrust event occurred in central Chile (Delouis et al., 2010; Lay et al., 2010a; Vigny et al., 2010). Slip concentrated on two main asperities located south and north of the epicentre. According to observations, the event can be modeled as a mode sequence 10-11-01, involving asperities with similar strengths ($\beta =1$). The model provides a good fit of the observed moment rate and an estimate of stress distribution on the fault before and after the earthquake (Dragoni & Santini, 2014).

A consequence of friction heterogeneity on faults is that complex events can be produced (Dragoni & Tallarico, 2016). With the exception of the case $p=p_0$, all events start with the motion of one asperity. The initial mode is 10 or 01 according to whether p is smaller or greater than the value $p_0$ given in (44). After some time, the asperity motion triggers the motion of the other asperity and the system passes to mode 11. When asperities slip simultaneously, they never stop at the same time, so that mode 11 is followed by mode 10 or 01.

When p has the smallest values in the interval $[p_a, p_b]$, the mode sequence is 10-11-01. As p increases, mode 11 becomes prevailing over modes 10 and 01, until an inversion in the order of arrest takes place in mode 11: asperity 2 stops earlier than asperity 1, so that the sequence is 10-11-10.

When $p=p_0$, the initial mode 10 disappears and asperities slip simultaneously from the onset of the event. Asperity 1 stops earlier, so that a 2-mode sequence 11-01 results. For $p>p_0$, the event starts with mode 01 and the sequence is 01-11-01. A greater complication results for the largest values of p, such as a 5-mode sequence 01-11-10-11-01. Different sequences are possible depending on the values of model parameters (Dragoni & Tallarico 2016).

The evolution of stress on the fault is described by forces $F_1$ and $F_2$ on asperities, given in (18). They increase with time on both asperities in the sticking mode, but oscillate in the slipping modes, owing to two processes: stress drops on asperities and stress transfers between them (Fig. 6). These processes determine the state of stress at the end of the event. Depending on the initial stress distribution and on the mode sequence, the final stress can be more or less heterogeneous than the initial one.

An example of complex event is 1992 Landers, California, earthquake, a magnitude 7.3 event originated by strike-slip faulting (Kanamori et al., 1992; Olsen et al., 1997; Peyrat et al., 2001; Wald & Heaton, 1994). The observed slip distribution is very heterogeneous, but can be modelled in terms of a friction distribution made of two asperities with different strengths ($\beta =0.5$). The model shows that the initial stress distribution was strongly heterogeneous, with a reduced heterogeneity at the end. With an appropriate choice of model parameters, the moment rate for a 2-mode event fits the observed function (Dragoni & Tallarico, 2016).

Fig. 6

Adapted from Dragoni and Tallarico (2016)

Evolution of forces on asperities during the 3-mode seismic event 01-11-01 represented in Fig. 4. The magnitudes of forces $F_1$ (upper curve) and $F_2$ (lower curve) are shown as functions of time, ranging from $T_1=0$ to $T_4=4.47$. Nondimensional frictional strengths of asperity 1 and 2 are 1 and $\beta$, respectively.

3.3 Seismic Energy and Spectrum

Consideration of wave radiation introduces further effects. Radiation during slipping modes can be taken into account by addition of a term proportional to slip rate (Rice, 1993). If asperities are assumed to have the same area ($\xi =1$), equations for slipping modes are

$$\begin{aligned} {\ddot{X}} + \gamma \dot{X} + (1 + \alpha ) X - \alpha Y - \epsilon = 0 \end{aligned}$$

(74)

$$\begin{aligned} {\ddot{Y}} + \gamma \dot{Y} + (1 + \alpha ) Y - \alpha X - \beta \epsilon = 0 \end{aligned}$$

(75)

In the presence of radiation, fault dynamics changes both in the sticking and in the slipping modes, in a measure that depends on the impedance $\gamma$ (Dragoni & Santini, 2015). Emission of radiation changes the evolution of the system from a given state, because it shifts the boundaries between different subsets of the sticking region Q. In particular, the presence of radiation changes the width of the interval $[p_1, p_2]$ leading to simultaneous asperity slip. In the presence of radiation, slip amplitude is smaller, while slip duration is longer. The moment rate depends on seismic efficiency $\eta$ and has its maximum in the first half of source duration $\Delta T$.

The smaller value of slip implies a smaller seismic moment $M_0$, that decreases with increasing $\eta$, at constant radiated energy. It is found that (Dragoni & Tallarico, 2016)

$$\begin{aligned} M_0 = \kappa _1 M_1 \end{aligned}$$

(76)

for a 1-mode event 10 and

$$\begin{aligned} M_0 = \beta \kappa _1 M_1 \end{aligned}$$

(77)

for a 1-mode event 01, where $\kappa _1$ is given in (24). Events including mode 11 have a moment

$$\begin{aligned} M_0 = M_1 f(p),\quad p_1 \le p \le p_2 \end{aligned}$$

(78)

where f(p) must be evaluated numerically (Fig. 7). The greatest values of $M_0$ are achieved by these events, with a maximum at $p=p_0$.

The seismic spectrum $S(\Omega )$ defined in (60) exhibits the classical Brune (1970) shape (Fig. 8). It has an infinite number of relative minima, their positions and values depending on $\beta$. They are zeroes only in the case of homogeneous friction ($\beta =1$). The corner frequency is (Dragoni & Santini, 2015)

$$\begin{aligned} \Omega _c = \sqrt{1 + \alpha } {\pi \over \omega _1 \Delta T} \end{aligned}$$

(79)

where $\omega _1$ is defined in (25) and $\Delta T$ is the source duration. It depends on parameters $\alpha$, $\beta$ and $\gamma$ and can sensibly change as a function of initial conditions.

If one considers again the 1964 Great Alaska Earthquake, mode durations, slip distribution, moment rate and seismic moment can be calculated in the presence of radiation (Dragoni & Santini 2015): they are consistent with observed values (Ichinose et al., 2007) provided an appropriate value of p is chosen. The state of the fault after the earthquake is different from that obtained in the absence of radiation, implying that the long-term evolution is different.

During fault slip, elastic strain energy is partly dissipated into heat and partly radiated in the surrounding medium (Kanamori & Heaton 2000; Kanamori & Rivera 2006; Rudnicki & Freund, 1981). The model shows that the energy release $\Delta E$ decreases, while the radiated energy $\Delta R$ increases with increasing impedance $\gamma$. Accordingly, seismic efficiency $\eta$ given by (68) increases with increasing $\gamma$, its maximum value depending only on the ratio $\epsilon$ between dynamic and static friction (Dragoni & Santini, 2015).

The effect of friction heterogeneity on seismic energy and spectrum can be studied by considering events produced by the failure of asperities with different strengths (Dragoni & Santini 2017). As underlined above, the stress distribution on the fault, expressed by $\beta$, is in general strongly heterogeneous at the onset of a seismic event. Seismic energy $\Delta R$ decreases with increasing $\beta$, while seismic efficiency $\eta$ is constant. An equation relating $\eta$ to the parameters of the friction law can be obtained, showing that $\eta$ is maximum for smaller values of $\epsilon$. The model provides a relation between $\Delta R$ and the seismic moment $M_0$, that is consistent with the empirical relation between the two quantities (Kanamori, 2001). It results that heterogeneity introduces a correction to the value of energy radiated by a homogeneous fault (Dragoni & Santini, 2017).

As an example, the 1965 Rat Islands, Alaska, earthquake, was considered, a magnitude 8.7 event occurred at the Alaska-Aleutinian Trench (Beck & Christensen 1991; Johnson & Satake, 1996; Wu & Kanamori, 1973). The event can be modeled as due to the separate failure of two asperities with different strengths, with $\beta =0.67$. For this event, moment rate, stress evolution, radiated energy and seismic spectrum can be calculated on the basis of the model, showing how friction heterogeneity controls the characteristics of a seismic event (Dragoni & Santini, 2017).

Fig. 7

Adapted from Dragoni and Tallarico (2016)

Seismic moment $M_0$ as a function of the variable p expressing initial conditions of the event. Allowed values of p are in the interval $[p_a, p_b]$. Values in the interval $[p_1, p_2]$ produce simultaneous asperity slip. Moment is normalized to the seismic moment $M_1$ produced by a 1-mode event 10 in the absence of radiation. Values of model parameters are as in Fig. 4.

3.4 Asperities with Different Areas and Strengths

In the case of a fault with two asperities of different areas and strengths, the equations for slipping modes have the general forms given in (21) and (22). There are remarkable differences with the case of asperities with equal areas (Lorenzano & Dragoni, 2018a).

Force rates on asperities are not equal to each other and their difference is not constant during interseismic intervals. The sticking region Q grows with the total asperity area, while the probability that the fault produces events involving simultaneous asperity slip decreases. If one considers events produced by the failure of a single asperity, slip duration and amplitude increase with asperity size, while corner frequency decreases. In 2-mode events involving consecutive failure of asperities, seismic efficiency $\eta$ depends on the total asperity area.

As an application of the model, Lorenzano and Dragoni (2018a) considered the 2007 Pisco, Peru, earthquake, a magnitude 8.0 event at the border between the Nazca and South American plates (Lay et al., 2010b). Seismological and geodetic data indicate the presence of two asperities (Sladen et al., 2010). By an appropriate choice of initial conditions, the event can be modelled as a 2-mode sequence 01-10, starting with slip of the weaker asperity and followed by slip of the stronger one, with $\beta =0.5$ and $\xi = 0.6$. The moment rate fits reasonably well the observed function.

The case of simultaneous asperity motion was considered by Santini and Dragoni (2020). The aim was to model the observed moment rate and seismic moment of the 2018 Gulf of Alaska earthquake, a magnitude 7.9 event originated by strike-slip faulting (Krabbenhoeft et al., 2018; Lay et al., 2018; Ruppert et al., 2018). Observations indicate that the earthquake was due to the failure of two main asperities and suggest an intermediate phase of simultaneous slip. Accordingly, the earthquake can be ascribed to a 3-mode sequence 10-11-01. Asperity sizes are very different from each other, with $\xi =0.25$. An estimate of frictional strengths yields $\beta =0.45$. The moment rate calculated from the model fits observations reasonably well.

Fig. 8

Adapted from Dragoni and Tallarico (2016)

Moment rate spectrum S as a function of angular frequency $\Omega$ for the 3-mode seismic event 01-11-01 represented in Fig. 4. The spectrum is normalized to the nondimensional seismic moment $M_0$ produced by the event. Nondimensional corner frequency is $\Omega _c=1.01$.

3.5 Effects of Stress Perturbations

In a fault system, any fault is subject to stress perturbations due to earthquakes generated by neighboring faults. The stress redistribution produced by each earthquake affects occurrence times and magnitudes of following earthquakes. Therefore, stress transfer between faults plays an important role in fault systems (Stein et al., 1992; Harris, 1998; Stein, 1999; Steacy et al., 2005; Tallarico et al., 2005).

Belardinelli et al. (2003) discussed the effects of stress perturbations in the case of a homogeneous fault. Dragoni and Piombo (2015) considered the case of a fault containing two asperities. Fault heterogeneity produces effects that are not present in the case of a homogeneous fault. This occurs because the stress field of a dislocation is inhomogeneous, so that asperities belonging to a fault are subject to different stress changes. As a consequence, a stress perturbation may not only advance or delay the next earthquake, but it may change the sequence of dynamic modes in the event, thus changing the hypocentre position, source duration and seismic moment.

The proximity of a fault to failure can be expressed by its Coulomb stress. If $\sigma _t$ is shear stress in the direction of fault slip and $\tau _s$ is static friction on the fault surface, the Coulomb stress is (Gomberg et al., 2000; Stein, 1999)

$$\begin{aligned} \sigma _C = \sigma _t - \tau _s \end{aligned}$$

(80)

Accordingly, $\sigma _C$ is negative during interseismic intervals and seismic events occur when $\sigma _C$ vanishes. Since there are two asperities, a value of Coulomb stress must be assigned to each of them. If forces are used instead of stresses, nondimensional Coulomb forces on the two asperities are

$$\begin{aligned} F_1^C = - F_1 - 1, \qquad F_2^C = - F_2 - \beta \end{aligned}$$

(81)

where $F_1$ and $F_2$ are given by (2) and (3) and $\xi =1$ is assumed for the sake of simplicity. While $F_1^C$ and $F_2^C$ measure the proximity of asperities to the respective failure conditions, the difference $F_2^C - F_1^C$ indicates the proximity to the condition of simultaneous slip.

When the fault is subject to a stress perturbation, the changes $\Delta F_1^C$ and $\Delta F_2^C$ in Coulomb forces are different from each other, so that the evolution of the fault is controlled by the difference

$$\begin{aligned} \Delta F^C = \Delta F_2^C - \Delta F_1^C \end{aligned}$$

(82)

expressing the change in the asymmetry degree of stress and friction on the fault.

These results explain why earthquakes generated by a fault are not only aperiodic, but are different from each other as to hypocenter position, slip amplitude and involved area. Differences are connected with the kind of stress perturbations occurring during interseismic intervals (Dragoni & Piombo, 2015).

The model has been applied to the fault of the 2010 Maule earthquake, that was considered in Sect. 3.2, in order to investigate the effect of the perturbation produced by the 1960 Great Chilean Earthquake (Dragoni & Piombo, 2015). As noted above, the stresses imposed on the asperities of the Maule fault were necessarily different from each other: this altered the stress distribution on the fault, with important consequences for its evolution.

The model predicts that, in the absence of the 1960 earthquake, the Maule earthquake would have occurred several decades later, with a different sequence of dynamic modes and a different seismic moment. The 1960 earthquake increased stress inhomogeneity on the Maule fault, preparing the conditions for the 2010 earthquake.

Fig. 9

Adapted from Dragoni and Lorenzano (2015)

The sticking region T of the two-asperity fault in the presence of viscoelastic relaxation. T is a tetrahedron ABCD in the space XYZ. Seismic events take place when the representative point of the system reaches face ACD or BCD. Model parameters are $\alpha =1$, $\beta =1$, $\gamma =0$, $\xi =1$.

3.6 Effects of Viscoelasticity

An important role in seismic activity is played by rheological properties of the lithosphere. Due to anelasticity of lithospheric rocks (Carter, 1976; Kirby, 1983; Kirby & Kronenberg, 1987; Nishimura & Thatcher, 2003), stress fields produced by fault slip are partially relaxed during interseismic intervals (Chen & Molnar, 1983; Dragoni et al., 1986; Kusznir, 1991). In the long term, this changes the stress distribution on faults, controlling the occurrence times of seismic events (Lynch et al., 2003; Piombo et al., 2007; Smith & Sandwell, 2006).

The effects of viscoelastic relaxation on a two-asperity fault were considered by Amendola and Dragoni (2013) in the case of identical asperities and by Dragoni and Lorenzano (2015) in the case of asperities with different strengths. As reported in Sect. 3.1, in the case of purely elastic coupling the long-term behavior of the system is a limit cycle with a recurrence pattern of earthquakes depending on the degree of stress inhomogeneity on the fault. In the presence of viscoelastic relaxation, this simple behavior is modified, because stress transferred from one asperity to the other partially relaxes during interseismic intervals.

In order to take into account viscoelasticity, a third variable z, expressing viscoelastic deformation, is introduced in the model. In nondimensional form

$$\begin{aligned} Z = {K_1 z\over f_{s1}} \end{aligned}$$

(83)

Hence the system has three degrees of freedom and phase space S is 6-dimensional. In the sticking mode, tangential forces on asperities are

$$\begin{aligned} F_1 = - X + \alpha Z \quad F_2 = - Y - \alpha Z \end{aligned}$$

(84)

where terms $\pm \alpha Z$ are contributions of stress transfer between asperities in the presence of viscoelastic deformation. If asperities with equal areas are considered for the sake of simplicity ($\xi =1$), conditions for the onset of slip are from (31)

$$\begin{aligned} F_1 = -1, \quad F_2 = -\beta \end{aligned}$$

(85)

or, thanks to (84),

$$\begin{aligned} X - \alpha Z - 1 = 0, \quad Y + \alpha Z - \beta = 0 \end{aligned}$$

(86)

that are the equations of two planes in the space XYZ. If one considers the no-overshooting condition (30), the sticking region is defined from the six inequations

$$\begin{aligned} 0 \le X \le 1, \quad 0 \le Y \le 1, \quad {X - 1 \over \alpha } \le Z \le {\beta - Y \over \alpha } \end{aligned}$$

(87)

that define a convex tetrahedron T (Fig. 9). A seismic event takes place when the representative point of the system reaches face ACD or BCD, entering mode 10 or 01. If it reaches the edge CD, the system enters mode 11.

The simplest viscoelastic model describing long-term behavior of lithospheric rocks is the Maxwell body (e.g. Ranalli, 1995), characterized by a relaxation time $\tau$, that is expressed in nondimensional form as

$$\begin{aligned} \Theta = \sqrt{K_1 \over m_1}\, \tau \end{aligned}$$

(88)

The evolution equations in mode 00 are then

$$\begin{aligned} {\ddot{X}} = 0, \qquad {\ddot{Y}} = 0, \qquad {\ddot{Z}} = {Z \over \Theta ^2} \end{aligned}$$

(89)

where Z is determined by the Maxwell constitutive equation. Hence

$$\begin{aligned} X(T) = X_0 + VT, \quad Y(T) = Y_0 + VT, \quad Z(T) = Z_0 e^{-T/ \Theta } \end{aligned}$$

(90)

where $X_0$, $Y_0$ and $Z_0$ are the coordinates of the system at $T=0$. From (86) and (90), the time $T_1$ required for the fault to reach the condition for slip of asperity 1 is

$$\begin{aligned} T_1 = \Theta W(\gamma _1) + {1 - X_0 \over V} \end{aligned}$$

(91)

where W is the Lambert function with argument

$$\begin{aligned} \gamma _1 = {\alpha Z_0 \over V\Theta } e^{-{1 - X_0 \over V\Theta }} \end{aligned}$$

(92)

An analogous formula holds for asperity 2, with

$$\begin{aligned} T_2 = \Theta W(\gamma _2) + {\beta - Y_0 \over V} \end{aligned}$$

(93)

where

$$\begin{aligned} \gamma _2 = -{\alpha Z_0 \over V\Theta } e^{-{\beta - Y_0 \over V\Theta }} \end{aligned}$$

(94)

From (91) and (93), it is easy to find that initial states belonging to T lead to mode 10 or to mode 01 according to whether they are below or above the surface

$$\begin{aligned} V \Theta \,[W(\gamma _1) - W(\gamma _2)] + Y - X + 1 - \beta = 0 \end{aligned}$$

(95)

From (84) and (90), forces applied to asperities in mode 00 are

$$\begin{aligned} F_1(T) = - X_0 - VT + \alpha Z_0 e^{-T/ \Theta } \end{aligned}$$

(96)

$$\begin{aligned} F_2(T) = - Y_0 - VT - \alpha Z_0 e^{-T/ \Theta } \end{aligned}$$

(97)

A comparison with the purely elastic case shows that there are additional nonlinear terms, so that forces change non-monotonically during the interseismic interval. Additionally, the difference $F_1 - F_2$ changes in time, entailing a change in stress distribution on asperities. In summary, seismic events are anticipated or delayed with respect to the elastic case, the importance of viscoelastic relaxation being controlled by the product $V\Theta$ (Dragoni & Lorenzano, 2015).

In order to illustrate this effect, the fault that originated the 1964 Great Alaska Earthquake can be considered again. Being a large-size event, the earthquake was followed by a remarkable post-seismic deformation (Zweck et al., 2002). As reported in Sect. 3.2, the earthquake source can be represented as a 2-mode event 10-01. Consideration of viscoelastic effects shows that stress relaxation controls the occurrence times of earthquakes produced by that fault (Amendola & Dragoni, 2013).

Fault evolution depends on the state from which the 1964 event originated, that is inferred from the observed moment rate. This constrains the evolution of the system to a subset of phase space. Knowledge of the moment rate of the next earthquake would further constrain the orbit, and so on (Dragoni & Lorenzano, 2015).

There is a complex interplay between stress perturbations and viscoelastic relaxation. Following a stress perturbation, the change in Coulomb stress on a given asperity determines the anticipation or delay of slip of that asperity, if a purely elastic behavior is assumed. This property no longer holds in the presence of viscoelastic relaxation (Lorenzano & Dragoni 2018b). In the latter case, from (81) and (84), Coulomb forces on asperities are

$$\begin{aligned} F_1^C = X - \alpha Z - 1, \quad F_2^C = X + \alpha Z - \beta \end{aligned}$$

(98)

Following a perturbation in normal stress, static frictions on asperities are modified. If $f_{s1}^\prime$ and $f_{s2}^\prime$ are the new static frictions on asperity 1 and 2, respectively, the following parameters are defined

$$\begin{aligned} \beta _1 = {f_{s1}^\prime \over f_{s1}}, \qquad \beta _2 = {f_{s2}^\prime \over f_{s1}} \end{aligned}$$

(99)

Changes in static friction imply that conditions (85) for the onset of asperity slip become

$$\begin{aligned} F_1 = - \beta _1, \quad F_2 = - \beta _2 \end{aligned}$$

(100)

meaning that changes in normal stress change the sticking region. Then the changes in frictions can be written as

$$\begin{aligned} \Delta \beta _1 = \beta _1 - 1, \quad \Delta \beta _2 = \beta _2 - \beta \end{aligned}$$

(101)

If $\Delta F_1$ and $\Delta F_2$ are the changes in tangential forces due to the perturbation, the changes in Coulomb forces are

$$\begin{aligned} \Delta F_1^C = \Delta F_1 - \Delta \beta _1, \quad \Delta F_2^C = \Delta F_2 - \Delta \beta _2 \end{aligned}$$

(102)

The signs of $\Delta F_1^C$ and $\Delta F_1^C$ determine whether the perturbation takes an asperity closer to or farther from failure conditions. However, there is not a direct connection between the signs of the two quantities and the anticipation or delay. The effect depends on the state of the fault immediately before and after the stress perturbation (Lorenzano & Dragoni 2018b).

An interesting case is the stress perturbation produced by the 1999 Hector Mine, California, earthquake on the fault originating the 1992 Landers earthquake, the latter being followed by a remarkable viscoelastic relaxation (Lorenzano & Dragoni 2018b). The 1999 Hector Mine earthquake was a magnitude 7.1 event generated by strike-slip faulting located about 20 km from the Landers fault (Jónsson et al. 2002; Salichon et al., 2004). As reported in Sect. 3.2, the Landers earthquake source can be modelled as a 2-mode 01-10 event. The stress transfer produced by the 1999 Hector Mine earthquake can be calculated and the complex effects of the stress perturbation on the future activity of the Landers fault can be explored.

4 Other Aspects of Fault Mechanics

The model developed in previous sections can be adjusted in order to investigate other aspects of fault mechanics, such as the effects of variable strain rate, the presence of fault creep and the occurrence of seismic sequences in fault systems.

4.1 Variable Strain Rate

In the study of fault behavior it is generally assumed that faults are subject to a constant strain rate. However, velocities of tectonic plates may change in the very long term, probably due to changes in the rate of mantle convection (e.g. Iaffaldano & Bunge, 2009; King et al., 2002). Therefore strain rates controlling seismic activity are also bound to change in the long term.

Studies of long-term correlations of earthquakes have been based on different approaches: addition of Brownian perturbations to steady tectonic motion (Matthews et al., 2002; Zöller & Hainzl, 2007), use of the concept of self-organized criticality (Abaimov et al., 2007; Baiesi, 2009) or study of stress evolution in discrete fault models (Ben-Zion et al., 2003; Zöller et al., 2007).

Dragoni and Piombo (2011) considered the effect of a slowly variable strain rate on the activity of a fault with a single asperity. The state of the fault is described by slip deficit X(T) and can assume two dynamic modes, denoted by 0 and 1 respectively. Two cases were considered: a sinusoidal oscillation in velocity of tectonic plates and a slow transition between two velocity values. It was assumed that such oscillations or transitions have small amplitudes with respect to the average velocity and longer periods and durations than recurrence times of earthquakes.

In the case of constant plate velocity V, equations governing fault dynamics in the two modes are respectively (19) and (69) with $\alpha =0$ (radiation is neglected):

$$\begin{aligned} {\ddot{X}} = 0, \quad {\ddot{X}} + X - \epsilon = 0 \end{aligned}$$

(103)

In this case, the fault produces seismic events with a recurrence period

$$\begin{aligned} \Delta T_0 = {U \over V} \end{aligned}$$

(104)

where

$$\begin{aligned} U = 2 (1-\epsilon ) \end{aligned}$$

(105)

In the case of variable plate velocity, slip deficit changes with a variable rate $\dot{X}(T)$ in mode 0. Since interest is focused on the interseismic intervals, seismic events can be considered as instantaneous.

In the case of sinusoidal oscillation with frequency $\Omega$, fault activity is made of cycles including several seismic events and repeating periodically with a period that is a multiple of $2\pi /\Omega$ (Dragoni & Piombo, 2011). Within each cycle, recurrence times of events oscillate about an average value equal to $\Delta T_0$ and the oscillation amplitude is proportional to that of strain rate oscillations. The number of events in a cycle depends on the ratio between $\Omega$ and $2\pi /\Delta T_0$. In the case of monotonic transition between different values of strain rate, recurrence times change gradually from an initial to a final value.

If the fault is subject to stress perturbations, the subsequent earthquake is anticipated or delayed. In the case of sinusoidal oscillations in strain rate, the perturbation will interrupt the current seismic cycle and will start a new one. Hence the pattern of seismic cycles determined by strain rate oscillations is destroyed by frequent stress perturbations, as may occur in systems made of several faults. In the case of a monotonic transition in strain rate, perturbations similarly alter the pattern of recurrence times and the number of events occurring during the transition (Dragoni & Piombo, 2011).

Therefore, even though slow variations in strain rate are difficult to observe in seismicity records, they significantly contribute to the aperiodicity of seismic events in the long term.

4.2 Fault Creep and Afterslip

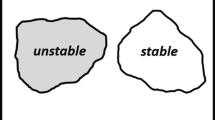
It is often observed that fault slip continues for some time after an earthquake, although at a decreasing rate, a phenomenon called afterslip. Afterslip is interpreted as aseismic slip of a velocity-strengthening region of the fault (Belardinelli & Bonafede, 1995; Marone et al., 1991; Scholz, 1990). This is confirmed by seismic and geodetic observations, indicating that faults can accommodate tectonic motion with stable, quasi-static slip or with fast slip and production of seismic waves. Such observations can be accounted for if one considers two kinds of regions on the fault surface: stable regions, which mostly creep, and unstable regions, producing earthquakes (Johnson, 2010).

The time dependence of aseismic slip has been mostly described by empirical relationships. An exponential function approaching a constant value was proposed by Nason and Weertman (1973). Later, observations and theoretical considerations suggested a logarithmic function (Marone et al., 1991). A review of different time functions was given by Barbot et al. (2004).

The interaction between two fault segments due to aseismic slip was studied by Dragoni and Tallarico (1992) and Tallarico et al. (2002) in the framework of continuum mechanics. A discrete fault model with two mechanically different regions was considered in Dragoni and Lorenzano (2017). The two regions are an asperity and a weak region and the state of the fault is described by their slip deficits x and y.

In this section, quantities referring to the asperity and to the weak region are denoted by indices 1 and 2, respectively. Let $f_1^\prime$ and $f_2^\prime$ be the frictional resistances of the two regions. For the asperity, a velocity-weakening law is assumed as above, characterized by a static friction $f_s$ and a dynamic friction $f_d$. For the weak region, a velocity-strengthening law is assumed

$$\begin{aligned} f_2^\prime = f_0 + \Lambda \dot{y} \end{aligned}$$

(106)

where $f_0$ is the steady-state dynamic friction and $\Lambda$ is a constant. Nondimensional slip deficits are

$$\begin{aligned} X = {K_1 x \over f_s}, \quad Y = {K_1 y \over f_s} \end{aligned}$$

(107)

where $K_1$ is defined as in (24). Nondimensional parameters are defined as

$$\begin{aligned} \alpha = {K_c \over K_1}, \quad \beta = {f_0 \over f_s}, \quad \gamma = {\iota _1 \over \sqrt{K_1 m_1}}, \quad \epsilon = {f_d \over f_s} \end{aligned}$$

(108)

$$\begin{aligned} \lambda = {\Lambda \over \sqrt{K_1 m_1}}, \quad \xi = {A_2 \over A_1}, \quad V = {\sqrt{K_1 m_1} \over f_s} \,v \end{aligned}$$

(109)

where a new parameter $\lambda$ has been intoduced and the others have the same meaning as in two-asperity models. The evolution equations in the interseismic intervals are

$$\begin{aligned} {\ddot{X}} = 0 \end{aligned}$$

(110)

$$\begin{aligned} (\alpha + \xi ) Y - \alpha X = 0 \end{aligned}$$

(111)

When the two regions slip, the evolution equations are respectively

$$\begin{aligned} {\ddot{X}} + \gamma \dot{X} + (1 + \alpha ) X - \alpha Y - \epsilon = 0 \end{aligned}$$

(112)

$$\begin{aligned} {\ddot{Y}} + \lambda \dot{Y} + (\alpha + \xi ) Y - \alpha X - \beta \epsilon = 0 \end{aligned}$$

(113)

The equations are solved analytically for interseismic intervals, asperity slip and afterslip in the weak region (Fig. 10). During interseismic intervals, the asperity is stationary, while the weak region is creeping. Stress accumulates on the asperity, until it is released when frictional threshold $f_s$ is exceeded. Asperity slip transfers stress to the weak region and afterslip takes place. In turn, afterslip transfers stress back to the asperity, determining the conditions for the next earthquake (Dragoni & Lorenzano, 2017).

According to the model, afterslip is a dynamic mode of the fault and its time dependence can be approximated by a function

$$\begin{aligned} \Delta Y(T) = U_a (1 - e^{-kT}) \end{aligned}$$

(114)

where k is a function of $\alpha$, $\lambda$ and $\xi$. In the long term, afterslip approaches an asymptotic value $U_a$ and may have any duration, depending on the intensity of velocity strengthening. The amount of afterslip $U_a$ is proportional to seismic slip of the asperity, in agreement with observations (Dragoni & Lorenzano, 2017).

The model was applied to the fault of the 2011 Tohoku-Oki earthquake (Ide et al., 2011; Maercklin et al., 2012; Simons et al., 2011), that was followed by a prolonged afterslip episode (Ozawa et al., 2011). According to observations, seismic slip concentrated at shallow depth, while afterslip took place downdip (Lay et al., 2012; Silverii et al., 2014; Wei et al., 2012).

On these grounds, a fault with a single shallow asperity and a downdip weak region was considered (Dragoni & Lorenzano, 2017). With a suitable choice of model parameters, a good fit of the seismic moment rate is obtained. The model suggests that afterslip dominated the first months after the event, while later postseismic deformation was due to bulk viscoelastic relaxation (Sun et al., 2014; Yamagiwa et al., 2015).

Fig. 10

Adapted from Dragoni and Lorenzano (2017)

Representation of the cycle made of seismic slip, afterslip and interseismic creep in the space XY. The dashed and dotted lines represent conditions for asperity failure and fault creep, respectively. Points $P_1$, $P_2$ and $P_3$ represent the state of the fault at the beginning of the seismic event, at the end of the event and at the end of afterslip, respectively. Segments $P_1 P_2$ and $P_2 P_3$ give the amplitudes $U_s$ and $U_a$ of seismic slip and afterslip, respectively. From $P_3$ to $P_1$, the fault is subject to creep.

4.3 Seismic Sequences

A typical manifestation of seismic activity is the occurrence of seismic sequences. This term is used to mean a series of earthquakes produced by sources located in a relatively small region and occurring in a time interval much shorter than the intervals between sequences (Dragoni & Lorenzano, 2016). Sequences take place in fault systems producing earthquakes with similar mechanisms and magnitudes. A sequence is typically made of a small number of larger events having medium magnitudes, accompanied by a greater number of smaller events.

Since the faults of the system are close to each other, fault interaction plays a major role, concentrating the events in a shorter time interval. The distribution in time of seismic sequences has been investigated by multifractal analysis (e.g. Telesca et al., 2004; Telesca & Lapenna, 2006).

If we consider a system made of n faults, the state of the system can be described by n variables that are the Coulomb stresses of the faults (Dragoni & Lorenzano, 2016). If faults are ordered according to the magnitude of their Coulomb stresses, each state of the system can be expressed by a permutation of the first n integers, such as

$$\begin{aligned} \theta = \begin{pmatrix} 1 &{} 2 &{} \dots &{} n\\ i_1 &{} i_2 &{} \dots &{} i_n \end{pmatrix} \end{aligned}$$

(115)

where fault $i_1$ has the maximum value of Coulomb stress and fault $i_n$ has the minimum. This permutation changes whenever a fault produces a seismic event, so that the evolution of the system can be described as a sequence of permutations.

When a seismic sequence of n events takes place, the order of fault activation is a consequence of initial stress state of the fault system and of fault interaction. One may conceive an order implicit in the initial state, that is modified due to changes in Coulomb stresses occurring whenever an event takes place. There are n! possible sequences, differing for the order of fault activation, and a sequence itself can be expressed as permutation

$$\begin{aligned} \theta ^*= \begin{pmatrix} 1 &{} 2 &{} \dots &{} n \\ i_1 &{} j_1 &{} \dots &{} k_1 \end{pmatrix} \end{aligned}$$

(116)

where faults $i_1$, $j_1$...$k_1$ are in the order of activation (Dragoni & Lorenzano, 2016).

Thanks to the model, the stress state of a fault system as a function of time can be retrieved from observation of the order of fault activation in a seismic sequence. It results that consecutive seismic sequences originated by a fault system are necessarily different from each other, because the state of the system at the end of a sequence is always different from the initial one.

The model has been applied to the 2012 Emilia (Italy) seismic sequence, that was made of seven events with magnitudes between 5 and 6 (Castro et al., 2013; Pezzo et al., 2013; Scognamiglio et al., 2012). According to the model, stress evolution in the fault system was conditioned by the first and fourth events, that were greater than the others, and produced a greater stress heterogeneity at the end of the sequence. The model predicts that, in the absence of external perturbations, the next sequence will take place after a few centuries and will be different from the 2012 one (Dragoni & Lorenzano, 2016).

5 Conclusions

Discrete fault models based on the concept of asperity have proven to be a useful tool in the study of fault mechanics. In such models, the state of the fault is described by few variables expressing the state of asperities, so that the dynamical system is characterized by few degrees of freedom.

The present review has focused on the dynamics of a fault surface with two asperities. This is a common case, because many large earthquakes can be interpreted as due to the failure of two asperities. A two-asperity model is apparently simple, but reveals an unexpected richness of complicated behaviors.

Due to the presence of friction, the system is nonlinear and evolves as a sequence of dynamic modes, where each mode is described by a different set of differential equations. Analytical solutions can be obtained and the evolution of the system can be visualized in a low-dimensional phase space.

The main conclusions are:

• 1. The fault can produce very different seismic events according to initial conditions, expressed by the stress distribution on the fault. Events are sequences of slipping modes, involving the separate or simultaneous slip of asperities, with durations ranging over a wide time interval.

• 2. The system is sensitive to small changes in initial conditions and to small stress perturbations. Hence its evolution is unpredictable in the long term, even if there is no chaotic behavior.

• 3. Most initial conditions of seismic events correspond to strongly nonuniform stress distributions on the fault. This should be considered the typical case in fault activity.

• 4. The moment rate of seismic events may have very different shapes, according to initial conditions. Observation of the moment rate of a real event allows to constrain initial conditions to a subset of the larger set of possible conditions.

• 5. Interaction between asperities plays a crucial role during fault slip: continuous stress transfer between asperities controls the sequence of dynamic modes in a seismic event.

• 6. The stress distribution on the fault after a seismic event is always different from that before the event: hence the next event will be different from the previous one.

• 7. Radiation of seismic waves has an influence on fault dynamics and the frequency spectrum of emitted waves exhibits remarkable variations as a function of initial conditions.

• 8. Viscoelastic stress relaxation occurring during interseismic intervals plays an important role, because it changes the stress distribution on the fault and may lead to a completely different evolution.

• 9. If one of the asperities is replaced with a velocity strengthening region, the latter is subject to afterslip as a consequence of coseismic slip of the asperity. Afterslip is a possible dynamic mode of the fault.

• 10. Generalization of the model to a fault system shows that the order of events in a seismic sequence is a consequence of initial stress state and of interaction between faults. The stress states of the system can be retrieved from observation of the order of fault activation in the sequence.

Discrete models are of course a simplification of real faults. Their strength is to catch the essential features of fault dynamics and to provide analytical solutions, enlightening the details of processes occurring both in coseismic and interseismic intervals. The possibility of visualizing the evolution in the phase space adds a long-term overview that is precluded to models based on continuum mechanics.