Introduction

It is a common observation that fault slip following an earthquake may continue for some time, at a decreasing rate. This phenomenon is known as afterslip and may last up to several months. It is expected to be the consequence of aseismic slip of a velocity-strengthening region of the fault, which has been loaded by the coseismic slip of a velocity-weakening region (Scholz 1990).

In fact, seismic and geodetic observations have shown that faults can accommodate tectonic motion in different ways. Some fault regions respond with stable, quasi-static motion, with slip rates comparable to tectonic rates; other regions remain locked for decades or centuries and then experience fast slip with emission of seismic waves. Typically, the amount of afterslip is proportional to that of seismic slip. For instance, afterslip can account for a part of the postseismic deformation following the 1906 San Francisco earthquake (Kenner and Segall 2000).

One way to account for such observations is to separate the fault surface into two kinds of regions: stable regions, which mostly creep, and unstable regions, which produce earthquakes (e.g. Johnson 2010). In studying a thrust earthquake at the Japan Trench, Heki et al. (1997) found that the afterslip distribution was relatively even throughout the fault surface, while the coseismic slip was concentrated in a small central part corresponding to an asperity. Yagi and Kikuchi (2002) acknowledged that afterslip following the 1994 Sanriku-Haruka-Oki earthquake took place in a region adjacent to the asperity whose failure generated the mainshock. However, it has been suggested that in some cases the two regions may not be spatially separated (Noda and Lapusta 2013).

There is obviously an interaction between the two fault regions. The interaction between seismic and aseismic fault slip was studied by Dragoni and Tallarico (1992) and Tallarico et al. (2002). Kato (2004, 2014) discussed the interplay between velocity-weakening and velocity-strengthening patches on a fault plane and the conditions for seismic and aseismic slip events. Dublanchet et al. (2013) and Yabe and Ide (2017) considered a fault with a large number of asperities and pointed out that asperity concentration remarkably affects the slip behaviour of heterogeneous faults containing both velocity-weakening and velocity-strengthening regions: specifically, the entire fault may slip seismically if the asperity concentration exceeds a critical threshold. Bulk relaxation of the crust and the effect of pore fluid diffusion may also play a role. Belardinelli and Bonafede (1995) modelled afterslip as driven by viscous flow in the asthenosphere. A study of the effects of viscoelastic relaxation on a complex fault was made by Amendola and Dragoni (2013) and Dragoni and Lorenzano (2015).

Several empirical relationships have been proposed in order to describe aseismic slip. Nason and Weertman (1973) proposed an exponential function approaching a constant value. More recently, observations and theoretical considerations suggested that afterslip can be represented as a logarithmic function of time (Marone et al. 1991). Even though this function represents well the observations in many cases, it yields a slip that increases indefinitely with time and must be truncated ad hoc. A discussion of different time functions was presented by Barbot et al. (2009).

Seismic and aseismic slip in a two-degree-of-freedom spring-block model was studied by Yoshida and Kato (2003). Friction on the blocks was described by means of a rate- and state-dependent friction law. Under the condition of velocity-weakening for one block and velocity-strengthening for the other, afterslip was found as a result of the relaxation of the stress imposed on the latter by the sudden slip of the former. The model was further investigated by Abe and Kato (2013) employing a different expression for the friction law and assuming a velocity-weakening behaviour for both blocks. Numerical simulations were carried out using different initial conditions for the stiffnesses of the coupling springs, and several slip patterns were acknowledged accordingly, including stable sliding, seismic and aseismic slip. In both papers, the evolution equations were solved numerically.

The aim of the present study is to obtain afterslip as a dynamic mode of a fault containing two regions with different mechanical behaviours: a strong, velocity-weakening region (asperity) and a weak, velocity-strengthening region. The two regions may have different areas and seismic wave radiation associated with asperity slip is considered. We base on a model developed by Dragoni and Santini (2015) and Dragoni and Tallarico (2016), where the average values of stress, friction and slip are considered for each region, so that the fault is described as a discrete dynamical system (Ruff 1992; Rice 1993; Turcotte 1997). Such an approach has the advantage of reducing the number of degrees of freedom required to describe the dynamics of the fault; furthermore, it allows the study of the evolution of the system by means of orbits in the phase space, making it possible to better visualize the different aspects of the dynamics. On the whole, models with a finite number of degrees of freedom allow to focus on the main features of the seismic source, while avoiding the more complicated characterization based on continuum mechanics.

We describe the different stages of fault behaviour, including the interaction between the weak region and the asperity responsible for earthquakes. During the interseismic intervals, the asperity accumulates stress that is released by asperity slip in seismic events. When the asperity slips, it transfers stress to the weak region, triggering the afterslip. In the same way, we expect that afterslip transfers stress back to the asperity, thus changing its state and subsequent evolution. An analytical solution for the evolution equations of the system will be obtained.

As an example, we apply the model to the fault of the 2011 Tohoku-Oki earthquake. The moment rate function associated with this event was dominated by one single hump (Wei et al. 2012), making it appropriate to ascribe the seismic slip to a large unstable region on the fault plane; what is more, this earthquake was followed by a prolonged afterslip episode (Ozawa et al. 2011). Observations show that seismic slip concentrated in a compact area at shallow depth, while afterslip occurred on a similar area downslip (Lay et al. 2012; Silverii et al. 2014). A part of postseismic deformation was certainly due to viscoelastic relaxation in the asthenosphere (Sun et al. 2014; Yamagiwa et al. 2015), and an attempt will be made to discriminate between the two mechanisms.

The model

We consider a plane fault embedded in a shear zone between two tectonic plates moving at constant relative velocity v. The shear zone is assumed to be a homogeneous and isotropic Hooke solid with rigidity \(\mu\). As a consequence of plate motion, the fault is subject to a tangential strain rate \({\dot{e}}\).

The fault contains two regions with different mechanical behaviours: a strong region (asperity) with a high static friction and a velocity-weakening dynamic friction and a weak region with a negligible static friction and a velocity-strengthening dynamic friction. Henceforth, symbols with an index 1 refer to the asperity and symbols with an index 2 refer to the weak region.

Fig. 1
figure 1

Sketch of the fault model. An asperity with area \(A_1\) and a weak region with area \(A_2\) are shown. The rectangular frame is the fault border. The state of the fault is described by the slip deficits x(t) and y(t) of the two regions

Full size image

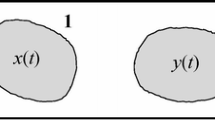
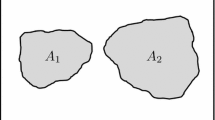
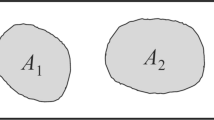
The two regions have areas \(A_1\) and \(A_2\) , respectively and the distance between their centres is a (Fig. 1). They are allowed to slip in the direction of the tangential traction imposed by the motion of tectonic plates. Their slip is controlled by their constitutive equations and by the forces exerted by the surrounding medium. We introduce a discrete fault model where the average values of stress, friction and slip on each region are considered. The state of the fault is described by two variables: the slip deficits x(t) and y(t) of the asperity and of the weak region, respectively, as functions of time t. At a certain instant t in time, the slip deficit of a fault region is defined as the slip that such region should undergo in order to recover the relative plate displacement occurred up to time t.

Of course, this is a simplification of fault mechanics. Considering only the average values of stress, friction and slip on a fault region entails that the region moves as a rigid surface and slip propagation within the region is not allowed. However, we are mostly interested in the effect of asperity slip on the weak region. Since asperity slip is very fast with respect to afterslip, the final asperity dislocation is more relevant than the detailed space-time history of slip. In the case of afterslip, the model does not describe the possible propagation of slip on the weak region, but assumes that slip involves the final area since the beginning. Since the two regions move as rigid surfaces, it is simpler to use forces instead of tractions. Let \(f_1\) and \(f_2\) be the tangential forces applied to the asperity and to the weak region in the slip direction and let \(f_1^\prime\) and \(f_2^\prime\) be the frictional resistances. The evolution equations for the two regions can be written as

$$\begin{aligned} \mu _1 {\ddot{x}}= f_1 + f_1^\prime \end{aligned}$$
(1)
$$\begin{aligned} \mu _2 {\ddot{y}}= f_2 + f_2^\prime \end{aligned}$$
(2)

where \(\mu _1\) and \(\mu _2\) are the masses associated with the two regions and dots indicate differentiation with respect to t. The force \(f_1\) applied to the asperity includes three terms: the elastic force due to plate motion, the elastic force due to a difference in the slip deficits of the two regions and a rate-dependent force due to radiation damping (e.g. Rice 1993). It can be written as

$$\begin{aligned} f_1 = -\, K_1 x - K_c (x - y) - \varGamma {\dot{x}} \end{aligned}$$
(3)

where \(K_1\) and \(K_c\) are coupling constants and \(\varGamma\) is the impedance of the medium. The force \(f_2\) applied to the weak region includes only the first two terms:

$$\begin{aligned} f_2 = - \,K_2 y - K_c (y - x) \end{aligned}$$
(4)

where \(K_2\) is a coupling constant. The coupling constants can be expressed as

$$\begin{aligned} K_1= {2 \mu {\dot{e}} A_1 \over v}, \qquad K_2 = {2 \mu {\dot{e}} A_2 \over v} \end{aligned}$$
(5)
$$\begin{aligned} K_c= \mu A_1 A_2 s \end{aligned}$$
(6)

where s is the average tangential traction (per unit moment) that the dislocation of one region imposes to the other one. According to (3) and (4), the forces applied to each region depend on x and y, so that a change in x or y entails a change in both forces, hence a change in the stress distribution on the fault. The interaction between the two regions is controlled by the constant \(K_c\).

The gravity force is neglected. In fact, it has a role only when movements have a vertical component, so it intervenes only in dip-slip faulting. However, the variables x and y express the relative motion of fault walls. The effect of gravity on the motion of one wall is opposite to the effect on the other one. There is not exact compensation, but this suffices to render gravity a second-order effect that can be ignored in a first approximation. Neglecting gravity has the effect to slightly overestimate or underestimate dynamic friction. As to friction, we use simplified versions of the general rate and state-dependent law. For the asperity, we assume a velocity-weakening law, characterized by a static friction \(f_{\mathrm{s}}\) and an average dynamic friction \(f_{\mathrm{d}}\):

$$\begin{aligned} f_1^\prime = \left\{ \begin{array}{ll}f_{\mathrm{s}}, & \quad {\dot{x}}=0\\ f_{\mathrm{d}}, &\quad {\dot{x}} \ne 0 \end{array}\right. \end{aligned}$$
(7)

For the weak region, we assume a velocity-strengthening law

$$\begin{aligned} f_2^\prime = f_0 - \varLambda {\dot{y}} \end{aligned}$$
(8)

where \(f_0\) is the steady-state dynamic friction and \(\varLambda\) is a constant. The minus sign is due to the fact that \({\dot{y}} <0\) during fault slip. The evolution equations for the two regions are then

$$\begin{aligned}&\mu _1 {\ddot{x}} + \varGamma {\dot{x}} + (K_1 + K_c) x - K_c y - f_{\mathrm{d}} = 0 \end{aligned}$$
(9)
$$\begin{aligned}&\mu _2 {\ddot{y}} + \varLambda {\dot{y}} + (K_2 + K_c) y - K_c x - f_0 = 0 \end{aligned}$$
(10)

Hence, the evolution of the fault is governed by a system of two coupled ordinary differential equations. We exclude simultaneous slip of the two regions (e.g. Dublanchet et al. 2013; Yabe and Ide 2017), even though it could be easily treated by models describing the dynamics of faults with two asperities (e.g. Dragoni and Santini 2015; Dragoni and Tallarico 2016). Accordingly, the system has three dynamic modes, corresponding to evolution in the interseismic interval, seismic slip of the asperity and afterslip in the weak region. We now specialize Eqs. (9) and (10) for the three modes.

  1. 1.

    During interseismic intervals, \(f_1 < f_{\mathrm{s}}\) by definition, so that the asperity is stationary. However, its slip deficit x increases due to tectonic loading. As to the weak region, we allow a steady-state creep at constant stress, so that its slip deficit y increases with time, but slower than x. Equations (9) and (10) become

    $$\begin{aligned} {\ddot{x}}= 0 \end{aligned}$$
    (11)
    $$\begin{aligned} (K_2 + K_c) y - K_c x= f_0 \end{aligned}$$
    (12)
  2. 2.

    During asperity slip, both tectonic loading and steady-state creep can be neglected, because they give negligible contributions in such a short time. Equations (9) and (10) become

    $$\begin{aligned}&\mu _1 {\ddot{x}} + \varGamma {\dot{x}} + (K_1 + K_c) x - K_c y - f_{\mathrm{d}} = 0 \end{aligned}$$
    (13)
    $$\begin{aligned}&{\dot{y}} = 0 \end{aligned}$$
    (14)
  3. 3.

    During afterslip in the weak region, the asperity is stationary. Afterslip has a much shorter duration than typical interseismic intervals; therefore, we neglect tectonic loading also in this case. Equations (9) and (10) become

    $$\begin{aligned}&{\dot{x}} = 0 \end{aligned}$$
    (15)
    $$\begin{aligned}&\mu _2 {\ddot{y}} + \varLambda {\dot{y}} + (K_2 + K_c) y - K_c x - f_0 = 0 \end{aligned}$$
    (16)

Solutions

In order to solve the evolution equations, we employ a dimensionless formulation. We introduce nondimensional variables and time

$$\begin{aligned} X = {K_1 x \over f_{\mathrm{s}}}, \quad Y = {K_1 y \over f_{\mathrm{s}}}, \quad T = \sqrt{K_1\over \mu _1} \,t \end{aligned}$$
(17)

and nondimensional forces

$$\begin{aligned} F_1 = {f_1 \over f_{\mathrm{s}}}, \qquad F_2 = {f_2 \over f_{\mathrm{s}}} \end{aligned}$$
(18)

We also introduce the following nondimensional parameters:

$$\begin{aligned} \alpha= {K_c \over K_1}, \quad \beta = {f_0 \over f_{\mathrm{s}}}, \quad \gamma = {\varGamma \over \sqrt{K_1 \mu _1}} \end{aligned}$$
(19)
$$\begin{aligned} \epsilon= {f_{\mathrm{d}} \over f_{\mathrm{s}}}, \quad \lambda = {\varLambda \over \sqrt{K_1 \mu _1}}, \quad \xi = {A_2 \over A_1}, \quad V = {\sqrt{K_1 \mu _1} \over f_{\mathrm{s}}} \,v \end{aligned}$$
(20)

where \(\alpha\) expresses the coupling between the asperity and the weak region; \(\beta\) is the ratio between the steady-state frictional stress of the weak region and the static frictional stress of the asperity; \(\gamma\) is a function of the seismic efficiency of the asperity; \(\epsilon\) is the ratio between the dynamic and the static frictions of the asperity; \(\lambda\) measures the intensity of velocity strengthening; \(\xi\) is the ratio between the areas of the two regions; V is the nondimensional velocity of tectonic plates. The parameter values have the following ranges: \(\alpha \ge 0, 0< \beta< 1, \gamma \ge 0, \lambda> 0, 0<\epsilon <1, \xi>0, V>0.\) We also assume that the masses associated with the two regions are proportional to their areas: accordingly,

$$\begin{aligned} {\mu _2 \over \mu _1} = {K_2 \over K_1} = \xi \end{aligned}$$
(21)

where (5) was employed. Hence, the forces (3) and (4) become

$$\begin{aligned} F_1= -\, (1 + \alpha ) X + \alpha Y - \gamma {\dot{X}} \end{aligned}$$
(22)
$$\begin{aligned} F_2= -\, (\alpha + \xi ) Y + \alpha X \end{aligned}$$
(23)

We next express the evolution equations for the three dynamic modes in nondimensional form and give their solutions.

Interseismic intervals

The evolution Eqs. (11) and (12) become

$$\begin{aligned} {\ddot{X}}= 0 \end{aligned}$$
(24)
$$\begin{aligned} (\alpha + \xi ) Y - \alpha X= \beta \end{aligned}$$
(25)

where dots indicate differentiation with respect to T. With initial conditions

$$\begin{aligned} X(0) = X_0, \quad {\dot{X}}(0) = V, \quad Y(0) = Y_0 \end{aligned}$$
(26)

their solution is

$$\begin{aligned} X(T)= X_0 + VT \end{aligned}$$
(27)
$$\begin{aligned} Y(T)= Y_0 + {\alpha \over \alpha + \xi } VT \end{aligned}$$
(28)

where, according to (25),

$$\begin{aligned} Y_0 = {\alpha X_0 + \beta \over \alpha + \xi } \end{aligned}$$
(29)

The solution shows that the slip deficit X of the asperity increases in time with the velocity V of tectonic plates, so that the asperity is stationary. The slip deficit Y of the weak region also increases in time, but with a lower rate

$$\begin{aligned} {\dot{Y}} = {\alpha \over \alpha + \xi } V \end{aligned}$$
(30)

implying a steady creep \(\Delta Y(T)\) with constant rate

$$\begin{aligned} \Delta {\dot{Y}} = V - {\dot{Y}} = {\xi \over \alpha + \xi } V \end{aligned}$$
(31)

that is smaller than plate velocity. From (22) and (23), the forces on the two regions are

$$\begin{aligned} F_1(T)= -\, (1 + \alpha ) X(T) + \alpha Y(T) \end{aligned}$$
(32)
$$\begin{aligned} F_2(T)= -\, (\alpha + \xi ) Y(T) + \alpha X(T) \end{aligned}$$
(33)

Thanks to (27) and (28), they become

$$\begin{aligned} F_1(T)= F_1(0) - {\alpha + \alpha \xi + \xi \over \alpha + \xi } VT \end{aligned}$$
(34)
$$\begin{aligned} F_2= - \beta \end{aligned}$$
(35)

where

$$\begin{aligned} F_1(0) = - (1 + \alpha ) X_0 + \alpha Y_0 \end{aligned}$$
(36)

showing that stress increases linearly with time on the asperity, while it remains constant on the weak region.

Seismic slip

We suppose that asperity slip starts at \(T=T_1\), when the forces have the values

$$\begin{aligned} F_1 = -\,1, \qquad F_2 = - \beta \end{aligned}$$
(37)

Thanks to (32) and (33), they can be written as

$$\begin{aligned} (1 + \alpha ) X - \alpha Y= 1 \end{aligned}$$
(38)
$$\begin{aligned} (\alpha + \xi ) Y - \alpha X= \beta \end{aligned}$$
(39)

The system of the two equations yields the state of the fault at the beginning of the seismic event:

$$\begin{aligned} X_1 = {\alpha + \alpha \beta + \xi \over \alpha + \alpha \xi + \xi }, \quad \quad Y_1 = {\alpha + \alpha \beta + \beta \over \alpha + \alpha \xi + \xi } \end{aligned}$$
(40)

The evolution Eqs. (13) and (14) become

$$\begin{aligned}&{\ddot{X}} + \gamma {\dot{X}} + (1 + \alpha ) X - \alpha Y_1 - \epsilon = 0 \end{aligned}$$
(41)
$$\begin{aligned}&{\dot{Y}} = 0 \end{aligned}$$
(42)

We solve (41) in the case of weak damping, implying that the rate-dependent term is small with respect to the other forces: this choice is suggested by the fact that the seismic efficiency of faults is small (e.g. Kanamori 2001). If we set \(T_1=0\) for the sake of simplicity, the initial conditions are

$$\begin{aligned} X(0) = X_1, \quad {\dot{X}}(0) = 0, \quad Y(0) = Y_1 \end{aligned}$$
(43)

and the solution is

$$\begin{aligned} X(T)= X_1 - {U\over 2} \left[ 1 -\left( \cos \omega _1 T + {\gamma \over 2 \omega _1} \sin \omega _1 T \right) \,{\hbox {e}}^{-{\gamma \over 2} T}\right] \end{aligned}$$
(44)
$$\begin{aligned} Y= Y_1 \end{aligned}$$
(45)

where

$$\begin{aligned} U = 2\, {1 - \epsilon \over 1 + \alpha } \end{aligned}$$
(46)

and

$$\begin{aligned} \omega _1 = \sqrt{1 + \alpha - {\gamma ^2\over 4}} \end{aligned}$$
(47)

The duration of the seismic event, calculated by setting \({\dot{X}} =0\), is

$$\begin{aligned} T_{\mathrm{s}} = {\pi \over \omega _1} \end{aligned}$$
(48)

The slip amplitude of the asperity is defined as

$$\begin{aligned} \Delta X(T) = X_1 - X(T) \end{aligned}$$
(49)

and the final amplitude is

$$\begin{aligned} U_{\mathrm{s}} = \kappa U \end{aligned}$$
(50)

where

$$\begin{aligned} \kappa = {1\over 2} \left( 1 + {\hbox {e}}^{-{\gamma \over 2} T_{\mathrm{s}}}\right) \end{aligned}$$
(51)

The moment rate of the seismic event can be calculated as

$$\begin{aligned} \dot{M}_{\mathrm{s}}(T) = M_1 {\Delta {\dot{X}}(T) \over U} \end{aligned}$$
(52)

where \(M_1\) is a reference seismic moment, corresponding to slip U. From (49) and (44), we obtain

$$\begin{aligned} \dot{M}_{\mathrm{s}}(T) = M_1 {1 + \alpha \over 2\omega _1} \sin \omega _1 T \,{\hbox {e}}^{-{\gamma \over 2} T} \end{aligned}$$
(53)

The final seismic moment is

$$\begin{aligned} M_{\mathrm{s}} = \kappa M_1 \end{aligned}$$
(54)

From (22) and (23), the forces on the asperity and on the weak region during the event are

$$\begin{aligned} F_1(T)= -\, (1 + \alpha ) X(T) + \alpha Y_1 - \gamma {\dot{X}}(T) \end{aligned}$$
(55)
$$\begin{aligned} F_2(T)= -\, (\alpha + \xi ) Y_1 + \alpha X(T) \end{aligned}$$
(56)

At the end of the event (\(T=T_2\)), the slip deficits of the two regions are

$$\begin{aligned} X_2 = X_1 - \kappa U, \qquad Y_2 = Y_1 \end{aligned}$$
(57)

Introducing (57) into (55) and (56), we obtain the forces

$$\begin{aligned} F_1(T_2)= - \,1 + (1 + \alpha ) U_{\mathrm{s}} \end{aligned}$$
(58)
$$\begin{aligned} F_2(T_2)= -\,\beta - \alpha U_{\mathrm{s}} \end{aligned}$$
(59)

The force \(F_1\) on the asperity has decreased in magnitude, with a force drop

$$\begin{aligned} \Delta F_1 = (1 + \alpha ) U_{\mathrm{s}} \end{aligned}$$
(60)

At the same time, the force \(F_2\) on the weak region has increased in magnitude by an amount \(\alpha U_{\mathrm{s}}\): this drives the region out of the steady-state creep and starts the afterslip.

Afterslip

In dimensionless form, the evolution Eqs. (15) and (16) become

$$\begin{aligned}&{\dot{X}} = 0 \end{aligned}$$
(61)
$$\begin{aligned}&\xi {\ddot{Y}} + \lambda {\dot{Y}} + (\alpha + \xi ) Y - \alpha X_2 - \beta = 0 \end{aligned}$$
(62)

Since afterslip has a long duration with respect to seismic slip, a high value of \(\lambda\) is expected; hence, we consider the overdamped solution of (62). If we set \(T_2=0\) for the sake of simplicity, initial conditions are

$$\begin{aligned} X(0) = X_2, \quad Y(0) = Y_2, \quad {\dot{Y}}(0) = 0 \end{aligned}$$
(63)

and the solution is

$$\begin{aligned} X= X_2 \end{aligned}$$
(64)
$$\begin{aligned} Y(T)= {\bar{Y}} - ({\bar{Y}} - Y_1) \left( \cosh \omega _2 T + {\lambda \over 2\xi \omega _2} \sinh \omega _2 T \right) {\hbox {e}}^{-{\lambda \over 2\xi }T} \end{aligned}$$
(65)

where

$$\begin{aligned} {\bar{Y}} = {\alpha X_2 + \beta \over \alpha + \xi } \end{aligned}$$
(66)

and

$$\begin{aligned} \omega _2 = \sqrt{{\lambda ^2 \over 4\xi ^2} - 1 - {\alpha \over \xi }} \end{aligned}$$
(67)

The afterslip amplitude is

$$\begin{aligned} \Delta Y (T) = Y_1 - Y(T) \end{aligned}$$
(68)

or

$$\begin{aligned} \Delta Y(T) = U_{\mathrm{a}} \left[ 1 - \left( \cosh \omega _2 T + {\lambda \over 2\xi \omega _2} \sinh \omega _2 T \right) {\hbox {e}}^{-{\lambda \over 2\xi }T} \right] \end{aligned}$$
(69)

with a final value

$$\begin{aligned} U_{\mathrm{a}} = Y_1 - {\bar{Y}} \end{aligned}$$
(70)

Thanks to (40), (50), (57) and (66), we obtain

$$\begin{aligned} U_{\mathrm{a}} = {\alpha \over \alpha + \xi } \,U_{\mathrm{s}} \end{aligned}$$
(71)

showing that afterslip in the weak region is proportional to the seismic slip of the asperity, in agreement with observations (e.g. Scholz 1990). The state of the fault at the end of afterslip is then

$$\begin{aligned} X_3 = X_2, \quad Y_3 = {\bar{Y}} \end{aligned}$$
(72)

It is noteworthy that \(X_3\) and \(Y_3\) satisfy (24) and (25), i.e. the evolution equations for interseismic intervals. Hence, the system can go through a cycle made of a sequence of its three dynamic modes.

From (69) and (71), the afterslip rate is

$$\begin{aligned} \Delta {\dot{Y}}(T) = {\alpha U_{\mathrm{s}} \over \xi \omega _2} \sinh \omega _2 T \, {\hbox {e}}^{-{\lambda \over 2\xi }T} \end{aligned}$$
(73)

The geodetic moment rate associated with afterslip is

$$\begin{aligned} \dot{M}_{\mathrm{a}}(T) = \xi M_1 {\Delta {\dot{Y}}(T) \over U} \end{aligned}$$
(74)

whence

$$\begin{aligned} \dot{M}_{\mathrm{a}}(T) = M_1 {\alpha \kappa \over \omega _2} \sinh \omega _2 T \, {\hbox {e}}^{-{\lambda \over 2\xi }T} \end{aligned}$$
(75)

and the final moment is

$$\begin{aligned} M_{\mathrm{a}} = {\alpha \xi \over \alpha + \xi } \,\kappa M_1 \end{aligned}$$
(76)

differing from the seismic moment (54) by a factor \(\alpha \xi / (\alpha + \xi )\). According to (69), the final value \(U_{\mathrm{a}}\) of afterslip is reached only for \(T\rightarrow \infty\). However, the slip rate \(\Delta {\dot{Y}}\) is exponentially decreasing and, after some time, afterslip becomes indistinguishable from the steady-state creep typical of interseismic intervals. Therefore, we can assign afterslip a finite duration, defined as the time interval \(T_{\mathrm{a}}\) after which the afterslip rate (73) lowers below the creep rate (31):

$$\begin{aligned} \Delta {\dot{Y}}(T_{\mathrm{a}}) = {\xi \over \alpha + \xi } V \end{aligned}$$
(77)

The equation can be easily solved for \(T_{\mathrm{a}}\) if we note that, for large values of T, we can write to a very good approximation

$$\begin{aligned} \Delta {\dot{Y}}(T) = {\alpha U_{\mathrm{s}} \over 2 \xi \omega _2} {\hbox {e}}^{-T/\varTheta } \end{aligned}$$
(78)

where

$$\begin{aligned} \varTheta = \left( {\lambda \over 2\xi } - \omega _2 \right) ^{-1} \end{aligned}$$
(79)

Then (77) yields

$$\begin{aligned} T_{\mathrm{a}} = \varTheta \ln {\alpha U_{\mathrm{s}} (\alpha + \xi ) \over 2\xi ^2 \omega _2 V} \end{aligned}$$
(80)

Afterslip duration \(T_{\mathrm{a}}\) is remarkably affected by the degree of coupling between the two regions of the fault. This is illustrated in Fig. 2, where \(T_{\mathrm{a}}\) is shown as a function of the coupling parameter \(\alpha\) for different values of the parameter \(\xi\). The graph shows an initial steep growth for smaller values of \(\alpha\), reaching a maximum value that depends on the particular combination of the parameters of the system; finally, it decreases for higher values of \(\alpha\). From (22) and (23), the forces acting on the asperity and on the weak region during afterslip are, respectively,

$$\begin{aligned} F_1(T)= -\,(1 + \alpha ) X_2 + \alpha Y(T) \end{aligned}$$
(81)
$$\begin{aligned} F_2(T)= - \,(\alpha + \xi ) Y(T) + \alpha X_2 \end{aligned}$$
(82)

If we introduce expressions (72) for \(X_3\) and \(Y_3\), we obtain the forces at the end of afterslip (\(T=T_3\))

$$\begin{aligned} F_1(T_3)= -\,1 + {\alpha + \alpha \xi + \xi \over \alpha + \xi } \,U_{\mathrm{s}} \end{aligned}$$
(83)
$$\begin{aligned} F_2(T_3)= - \,\beta \end{aligned}$$
(84)

The force \(F_1\) on the asperity has increased (in magnitude) with respect to its value at \(T=T_2\), because afterslip transfers stress to the asperity. A comparison with (58) shows that \(F_1\) has increased by an amount \(\alpha U_{\mathrm{a}}\); hence, it is closer to the condition for asperity failure. The amount of stress transferred to the asperity significantly increases with the coupling parameter \(\alpha\); however, \(F_1(T_3) > -1\), which guarantees that afterslip never triggers asperity failure. Nevertheless, the amount of stress that afterslip transfers to the asperity will produce a time advance of the next earthquake. This is illustrated in Fig. 3, where \(F_1(T_3)\) is shown as a function of \(\alpha\) for different values of the parameter \(\xi\). The force \(F_2\) on the weak region shows that the condition for steady-state creep has been recovered.

Fig. 2
figure 2

Afterslip duration. The afterslip duration (80) is plotted as a function of the coupling parameter \(\alpha\) for different values of the parameter \(\xi\). Other parameters are \(\epsilon = 0.7, \gamma = 1, \lambda = 10^5\) and \(V = 10^{-9}\)

Full size image
Fig. 3
figure 3

Tangential force on the asperity at the end of afterslip. The tangential force (83) is plotted as a function of the coupling parameter \(\alpha\) for different values of the parameter \(\xi\). Other parameters are \(\epsilon = 0.7\) and \(\gamma = 1\)

Full size image

Subsequent evolution

We can now calculate the duration \(T_{i{\mathrm{s}}}\) of the next interseismic interval. We see from (83) that, in order to reach the unit value, \(F_1\) must increase in magnitude by an amount

$$\begin{aligned} \Delta F_1 = {\alpha + \alpha \xi + \xi \over \alpha + \xi } \,U_{\mathrm{s}} \end{aligned}$$
(85)

This requires a time

$$\begin{aligned} T_{i{\mathrm{s}}} = {\Delta F_1 \over |\dot{F}_1|} \end{aligned}$$
(86)

where \(\dot{F}_1\) is the rate of increase of \(F_1\) that can be calculated from (34). We obtain

$$\begin{aligned} T_{i{\mathrm{s}}} = {U_{\mathrm{s}} \over V} \end{aligned}$$
(87)

In order to enlighten the role of afterslip, we calculate the interseismic interval \(T_{i{\mathrm{s}}}^\prime\) in the absence of afterslip. In this case, according to (58), \(F_1\) must increase in magnitude by an amount

$$\begin{aligned} \Delta F_1^\prime = (1 + \alpha ) \,U_{\mathrm{s}} \end{aligned}$$
(88)

so that

$$\begin{aligned} T_{i{\mathrm{s}}}^\prime = {(1 + \alpha ) (\alpha + \xi ) \over \alpha + \alpha \xi + \xi } \, {U_{\mathrm{s}} \over V} \end{aligned}$$
(89)

The ratio between the two times is

$$\begin{aligned} {T_{i{\mathrm{s}}} \over T_{i{\mathrm{s}}}^\prime } = 1 - {\alpha ^2 \over (1 + \alpha ) (\alpha + \xi )} \end{aligned}$$
(90)

Since \(\alpha\) and \(\xi\) are positive, the ratio is always smaller than 1, meaning that the following earthquake is anticipated by the occurrence of afterslip.

From (31) and (87), the cumulative creep in the interseismic interval is

$$\begin{aligned} U_{i{\mathrm{s}}} = {\xi \over \alpha + \xi } \,U_{\mathrm{s}} \end{aligned}$$
(91)

corresponding to a geodetic moment

$$\begin{aligned} M_{i{\mathrm{s}}} = {\xi ^2 \over \alpha + \xi } \,M_{\mathrm{s}} \end{aligned}$$
(92)

Comparing (92) with (54) and (76), we see that, in a cycle including the three dynamic modes, the total geodetic moment is a fraction \(\xi\) of the seismic moment and the total moment release is

$$\begin{aligned} M = (1 + \xi ) M_{\mathrm{s}}{.} \end{aligned}$$
(93)

Discussion

In order to test the model, it is necessary to assign appropriate values to the parameters. They will be chosen within the allowed ranges, but do not pertain to any real case. A different set of parameters would imply different values of the quantities characterizing the seismic cycle, but would not alter the general conclusions of this section.

As an example, we consider a fault zone with rigidity \(\mu =30\) GPa, in the presence of a relative plate velocity \(v = 3\) cm a\(^{-1}\) and a tangential strain rate \({\dot{e}} = 10^{-14}\, \hbox {s}^{-1}\). We consider a medium-size earthquake produced by a fault with \(A_1 = A_2 = 500 \,\mathrm{km^2}, a = 25\) km and a strike-slip mechanism. We assume that the seismic event has a duration \(t_{\mathrm{s}} = 10\) s and a slip amplitude \(u_{\mathrm{s}} = 1\) m. The seismic moment is then \(m_{\mathrm{s}} = 1.5 \times 10^{19}\) N m.

The parameter \(\alpha\) can be evaluated from the values of the quantities \(A_2, v, {\dot{e}}, a\) and the kind of source mechanism. In fact, from (5) and (6), we have

$$\begin{aligned} \alpha = {A_2 v s \over 2 {\dot{e}}} \end{aligned}$$
(94)

For nonoverlapping regions, it is a good approximation to use tractions produced by pointlike dislocations (e.g. Dragoni and Lorenzano 2016)

$$\begin{aligned} s = k a^{-3} \end{aligned}$$
(95)

where \(k=5/(12\pi )\) for strike slip and \(k=1/(6\pi )\) for dip slip.

It is evident that the value of the distance a may have a strong influence on \(\alpha\). In fact, if we increase \(a, \alpha\) becomes smaller and smaller. But we cannot decrease a below a certain value without decreasing the area \(A_2\); otherwise, the two regions would overlap. It follows that \(\alpha\) is always much smaller than 1 (in the present example, \(\alpha =0.2\)). From the solutions of the governing equations, it can be seen that \(\alpha\) is always summed to unity or to the parameter \(\xi\), which is in the order of unity. Therefore, the results are moderately sensible to the value of \(\alpha\) and the sensitivity decreases with decreasing \(\alpha\). The parameter \(\beta\) is by definition smaller than 1. Since asperity models assume that weak regions may slip at a much lower stress level than asperities, a value \(\beta\) = 0.1 is reasonable, meaning that the force on the weak region is one-tenth of the force on the asperity at the onset of seismic slip. In applications to real cases, the value can be chosen in order that the model gives the best fit with observations. The parameter \(\epsilon\) is by definition smaller than 1. Experiments on rock samples suggest values ranging between 0.5 and 1 (Jaeger and Cook 1976). We take \(\epsilon =0.7\). Small variations do not have important consequences.

The parameter \(\gamma\) is a function of \(\alpha , \epsilon\) and the seismic efficiency \(\eta\) (Dragoni and Santini 2015). A straightforward calculation yields

$$\begin{aligned} \gamma = {2 \sqrt{1 + \alpha } \ln \psi \over \sqrt{\pi ^2 + \ln ^2 \psi }} \end{aligned}$$
(96)

where

$$\begin{aligned} \psi = {(1 - \epsilon ) (1 - \eta ) \over 1 - \epsilon - \eta (1 + \epsilon )} \end{aligned}$$
(97)

The seismic efficiency of faults is relatively small, ranging in many cases from 0.1 to 0.3 (e.g. Kanamori 2001). The value 0.15 is in this range and corresponds to \(\gamma =1\). According to the previous choice, we consider the value \(\xi = 1\) for the ratio between the areas of the two regions.

The parameter V can be calculated from the observed plate velocity v, the duration \(t_{\mathrm{s}}\) and the slip amplitude \(u_{\mathrm{s}}\) of the seismic event. From the definitions, we obtain

$$\begin{aligned} V = {U_{\mathrm{s}} \over u_{\mathrm{s}}} {t_{\mathrm{s}} \over T_{\mathrm{s}}} \,v \end{aligned}$$
(98)

With the values assumed above, \(V = 10^{-9}\).

Fig. 4
figure 4

Seismic slip. The graphs show a the slip amplitude \(\Delta X\); b the associated moment rate \(M_{\mathrm{s}}\); c the forces \(F_1\) (solid) and \(F_2\) (dashed) on the asperity and on the weak region, respectively, as functions of nondimensional time T

Full size image

With these values of the model parameters, Fig. 4 shows the main features of the seismic event. The slip amplitude \(\Delta X\), the moment rate \(\dot{M}_{\mathrm{s}}\) and the forces \(F_1\) and \(F_2\) are shown as functions of time in the interval \(0 \le T \le T_{\mathrm{s}}\). The event duration is \(T_{\mathrm{s}} \simeq 3.2\), with a final slip amplitude \(U_{\mathrm{s}} =0.30\) and a seismic moment \(M_{\mathrm{s}}/M_1=0.60\). In Fig. 4c, we note a decrease (in magnitude) of the force \(F_1\) on the asperity and a corresponding increase of the force \(F_2\) on the weak zone. At the end of the event, the force drop on the asperity is \((1+\alpha )U_{\mathrm{s}} =0.36\), while \(F_2\) has received a contribution \(-\,\alpha U_{\mathrm{s}} = -\,0.06\) from the asperity, reaching the value \(-\,0.16\).

Calculation of afterslip requires the parameter \(\lambda\). Its value controls the afterslip duration \(T_{\mathrm{a}}\) and may have large variations. We take \(\lambda = 10^5\), implying an afterslip duration \(t_{\mathrm{a}} \simeq 20\) days, if the duration of seismic slip is \(t_{\mathrm{s}}=10\) s and \(\xi =1\). Since \(\lambda\) is much greater than \(1 - \alpha /\xi\), formula (69) for \(\Delta Y\) can be written in a simpler form. Expressing the hyperbolic functions by exponentials, one easily finds

$$\begin{aligned} \Delta Y(T) = U_{\mathrm{a}} \left( 1 - {\hbox {e}}^{-T/\varTheta }\right) \end{aligned}$$
(99)

to a very good approximation.

Fig. 5
figure 5

Afterslip. The graphs show a the afterslip amplitude \(\Delta Y\); b the associated moment rate \(M_{\mathrm{a}}\); c the forces \(F_1\) (solid) and \(F_2\) (dashed) on the asperity and on the weak region, respectively, as functions of nondimensional time T

Full size image

Figure 5 shows the main features of afterslip. The slip amplitude \(\Delta Y\), the moment rate \(\dot{M}_{\mathrm{a}}\) and the forces \(F_1\) and \(F_2\) are plotted as functions of time in the interval \(0 \le T \le T_{\mathrm{a}}\). The final slip amplitude is \(U_{\mathrm{a}} =0.05\) and the geodetic moment is \(M_{\mathrm{a}}/M_1=0.10\). According to (71), the total afterslip is about 17% of seismic slip and the same is for the moment release. At the beginning of afterslip, the force \(F_2\) is equal to \(-\,0.16\). Then, it decreases in magnitude, approaching the value \(-\,\beta\) at the end of afterslip. At the same time, \(F_1\) increases in magnitude by an amount \(\alpha U_{\mathrm{a}} = 0.01\).

Fig. 6
figure 6

Geometrical illustration of the cycle made of seismic slip, afterslip and interseismic creep. The dashed line is given by (38), representing the condition for asperity failure. The dotted line is given by (39), representing the condition for interseismic fault creep. The state of the fault is \(P_1\) at the beginning of the seismic event, \(P_2\) at the end of the event and \(P_3\) at the end of afterslip. The lengths of the catheti are the amplitudes \(U_{\mathrm{s}}\) of seismic slip and \(U_{\mathrm{a}}\) of afterslip, respectively. From \(P_3\) to \(P_1\), the fault is subject to tectonic loading and creep. Arrows indicate the motion of the representative point of the system during the cycle

Full size image

The sequence of three dynamic modes (seismic slip, afterslip, interseismic evolution) makes a cycle that can be represented in the plane XY (Fig. 6). The coordinates of points \(P_1, P_2, P_3\) are given in (40), (57) and (72), respectively. During the interseismic interval, the representative point of the system moves on line (39). When it reaches \(P_1\), the seismic event takes place. The point moves by a quantity \(U_{\mathrm{s}}\) given by (50), reducing the value of X and reaching \(P_2\). Here, afterslip begins and lowers the value of Y by a quantity \(U_{\mathrm{a}}\) given by (71), driving the point to \(P_3\): this is again on line (39) and a new interseismic interval begins. The orbit is independent of \(\lambda\).

Of course, this cycle represents an ideal situation. There are several factors that may change this scheme. Often the seismic source is not made of a single asperity, but of two or more asperities that introduce complexity in the dynamics (Dragoni and Tallarico 2016). Secondly, the fault is not an isolated system, but is subject to stress perturbations from the slipping of neighbouring faults (Dragoni and Piombo 2015). These complexities may be introduced without difficulty in the model and would break the periodicity of the cycle.

In addition, bulk viscoelastic relaxation of the asthenosphere may add to afterslip as a source of postseismic deformation. The surface displacement associated with postseismic deformation has been often modelled as a function

$$\begin{aligned} s(t) = b \ln \left( 1 + {t\over \tau } \right) \end{aligned}$$
(100)

where b is a constant and \(\tau\) is a characteristic time (Scholz 1990; Marone et al. 1991; Heki et al. 1997; Barbot et al. 2009). This function becomes arbitrarily large for \(t\rightarrow \infty\), even though its derivative tends to zero. In many cases, it fits reasonably well the postseismic deformation data in finite time intervals. On the contrary, (99) yields an afterslip approaching a maximum value \(U_{\mathrm{a}}\) and the surface displacement would be

$$\begin{aligned} s_{\mathrm{a}}(t) = {\bar{s}}_{\mathrm{a}} \left( 1 - {\hbox {e}}^{-t/\theta }\right) \end{aligned}$$
(101)

where \({\bar{s}}_{\mathrm{a}}\) is the asymptotic value and

$$\begin{aligned} \theta = {t_{\mathrm{a}}\over T_{\mathrm{a}}} \varTheta \end{aligned}$$
(102)

If we suppose that the asthenosphere is a Maxwell body with a characteristic time \(\theta ^\prime\), the surface displacement produced by viscoelastic relaxation can be written as

$$\begin{aligned} s_v(t) = {\bar{s}}_v \left( 1 - {\hbox {e}}^{-t/\theta ^\prime }\right) \end{aligned}$$
(103)

where \({\bar{s}}_v\) is the asymptotic value. Due to the high value of the asthenosphere viscosity, the timescale of viscoelastic relaxation is typically much longer than that of afterslip, i.e. \(\theta ^\prime \gg \theta\). Then, if we consider the time interval \(0 \le t \le t_{\mathrm{a}}\), during which afterslip is observed, we have \(t \ll \theta ^\prime\) and the total displacement is given by

$$\begin{aligned} s(t) = s_{\mathrm{a}} \left( 1 - {\hbox {e}}^{-t/\theta }\right) + ct \end{aligned}$$
(104)

with \(c= {\bar{s}}_v/\theta ^\prime\). This function has a slope that decreases much slower than \(s_{\mathrm{a}}(t)\), thus resembling the logarithmic function (100).

An application: the 2011 Tohoku-Oki earthquake

The 2011 Tohoku-Oki earthquake was a very large event, with \(M_w= 9.0\) (Ide et al. 2011; Simons et al. 2011; Maercklin et al. 2012). The coseismic slip distribution extended approximately 400 km along the Japan trench, with a maximum slip ranging between 27 m (Ozawa et al. 2011) and 80 m (Iinuma et al. 2012). The data reveal a compact area of large slip, extending from the trench to about 50 km of depth (Bletery et al. 2014). Afterslip was mostly distributed in an area located downdip of the coseismic slip and extending to a depth of about 100 km (Lay et al. 2012; Silverii et al. 2014). A major role of viscoelastic relaxation was also suggested (Sun et al. 2014; Yamagiwa et al. 2015).

Fig. 7
figure 7

Fault model of the 2011 Tohoku-Oki earthquake. \(A_1\) and \(A_2\) are the areas of the asperity and of the weak region, respectively, and z is depth. The model is a simplified version of the tectonic settings suggested by Lay et al. (2012) and Silverii et al. (2014)

Full size image

The relevant data are given in Table 1. We take an average rigidity of the lithosphere \(\mu = 40\) GPa (Ozawa et al. 2011), a velocity of subduction \(v = 8\hbox { cm}\hbox { a}^{-1}\) (Simons et al. 2011) and a surface strain rate \({\dot{e}}_{\mathrm{s}} = 10^{-14}\hbox { s}^{-1}\) (Kato et al. 1998). We assume that the fault is made of a velocity-weakening and a velocity-strengthening region (Fig. 7). The two regions are rectangles with sides 400 and 150 km long, so that their areas are \(A_1 = A_2 = 60{,}000\hbox { km}^2\), with a distance \(a = 150\) km between their centres. We assume an average dip angle \(\delta = 20^\circ\) (Lay et al. 2012). The strain rate on the fault is then (Dragoni and Lorenzano 2016)

$$\begin{aligned} {\dot{e}} = {\sin 2\delta \over 2(1 - \nu )} {\dot{e}}_{\mathrm{s}} \end{aligned}$$
(105)

where \(\nu\) is the Poisson modulus, which we take equal to 0.25. Accordingly, we get \({\dot{e}} \simeq 4 \times 10^{-15}\hbox { s}^{-1}\).

Table 1 Data for the 2011 Tohoku-Oki earthquake
Full size table

The duration of the seismic event was about 160 s, with a moment rate concentrated in a time interval \(t_{\mathrm{s}}=80\) s and a seismic moment \(m_{\mathrm{s}} = 3.5 \times 10^{22}\) N m (Maercklin et al. 2012; Wei et al. 2012; Bletery et al. 2014). Accordingly, the average seismic slip was \(u_{\mathrm{s}} = 15\) m.

From these data, we evaluate the values of the model parameters \(\alpha , \xi\) and V. The value of \(\epsilon\) is taken as in the previous section. The value of \(\gamma\), corresponding to a seismic efficiency \(\eta = 0.17\), is chosen in order to obtain the best fit for the moment rate. The value of \(\lambda\) will be evaluated on the basis of the assumed afterslip duration. The values are given in Table 2. Notice that we aim to investigate only the seismic slip and afterslip phases associated with the event, whose evolutions are independent of \(\beta\) (as shown in “Seismic slip” and “Afterslip” sections); therefore, we do not need to assign a value to this parameter.

Table 2 Values of model parameters for the 2011 Tohoku-Oki fault
Full size table

We reproduce the observed seismic moment rate in a time interval \(t_1 \le t \le t_2\), where the dominant contribution to seismic moment is produced. In dimensional form, the moment rate (53) becomes

$$\begin{aligned} {\dot{m}}_{\mathrm{s}}(t) = m_1 {1 + \alpha \over 2\omega _1} \chi \sin \omega _1 \chi (t-t_1) \,{\hbox {e}}^{-{\gamma \over 2} \chi (t-t_1)} \end{aligned}$$
(106)

where

$$\begin{aligned} \chi = {T_{\mathrm{s}} \over t_2 - t_1} \end{aligned}$$
(107)

and

$$\begin{aligned} m_1 = \mu A_1 u \end{aligned}$$
(108)

where u is the slip that would be observed in the case \(\gamma =0\). Hence,

$$\begin{aligned} u = {u_{\mathrm{s}} \over \kappa } \end{aligned}$$
(109)

The final seismic moment is

$$\begin{aligned} m_{\mathrm{s}} = \kappa m_1 \end{aligned}$$
(110)

The moment rate \({\dot{m}}_{\mathrm{s}}(t)\), calculated from (106) with \(t_1=50\) s and \(t_2=130\) s, is shown in Fig. 8a. It is superimposed to the observed moment rate given by Wei et al. (2012) and fits well the central peak. The seismic moment calculated from (110) is \(m_{\mathrm{s}} = 3.6 \times 10^{22}\) N m, in agreement with observation. Figure 8b shows the evolution of forces on the asperity and on the weak region during the earthquake, calculated from (55) and (56). The magnitude of \(F_1\) has a decrease of 32%, while that of \(F_2\) has an increase of 26% with respect to the initial value. The stress drop on the asperity can be calculated as

$$\begin{aligned} \Delta \sigma = {f_{\mathrm{s}} \over A_1} \,\Delta F_1 \end{aligned}$$
(111)

where \(\Delta F_1\) is given by (60) and \(f_{\mathrm{s}}\) can be estimated as

$$\begin{aligned} f_{\mathrm{s}} = {K_1 u \over U} \end{aligned}$$
(112)

where we used (17). Accordingly, we have

$$\begin{aligned} \Delta \sigma = {(1 + \alpha ) K_1 u_{\mathrm{s}} \over A_1} \end{aligned}$$
(113)

It results \(\Delta \sigma \simeq 3\) MPa, which has the same order of magnitude as the values given by Bletery et al. (2014).

With regard to postseismic deformation, (71) predicts that the average afterslip amplitude on the weak region is \(u_{\mathrm{a}} = 0.23 \, u_{\mathrm{s}}\) or 3.5 m. From (76), the geodetic moment associated with afterslip is \(m_{\mathrm{a}} = 0.23 \, m_{\mathrm{s}}\) or \(8.3 \times 10^{21} \, \mathrm{N \, m}\).

Fig. 8
figure 8

Coseismic phase of the 2011 Tohoku-Oki earthquake. a Moment rate \({\dot{m}}_{\mathrm{s}}\) (solid) as a function of time, calculated according to (106), compared with the observed moment rate (dashed) reported by Wei et al. (2012). b Evolution of forces \(F_1\) on the asperity (solid) and \(F_2\) on the weak region (dashed), in units of the static friction \(f_{\mathrm{s}}\) of the asperity

Full size image

Let \(s_{\mathrm{s}}\) be the coseismic ground displacement. According to Ozawa et al. (2011), a postseismic displacement \(s_{\mathrm{a}}^\prime = 0.09 \, s_{\mathrm{s}}\) was reached at a time \(t_{\mathrm{a}}^\prime = 15\) days after the seismic event. We can ascribe \(s_{\mathrm{a}}^\prime\) entirely to afterslip, because viscoelastic relaxation takes place over much longer times. With a viscosity equal to \(10^{19}\) Pa s (Wang et al. 2012; Sun et al. 2014), the Maxwell time is \(\theta ^\prime = 8\) a. By means of (101) and taking into account that surface displacement is proportional to fault slip, we find \(\theta \simeq 30\) days. Hence, \(\theta ^\prime \gg \theta\), as anticipated.

Fig. 9
figure 9

Surface displacement generated by afterslip following the 2011 Tohoku-Oki earthquake, according to the model. The surface displacement is estimated over a time interval of 120 days. It is normalized to the coseismic surface displacement \(s_{\mathrm{s}}\)

Full size image

The surface displacement generated by afterslip is shown as a function of time in Fig. 9. The curve is consistent with data from Diao et al. (2013) and Silverii et al. (2014), according to whom postseismic ground displacement reached the value \({\bar{s}}_{\mathrm{a}}\) after a time from 120 to 150 days from the event. We conclude that afterslip reached the asymptotic value \(u_{\mathrm{a}}\) after a time \(t_{\mathrm{a}}\) of about four months. Further postseismic deformation should be ascribed to viscoelastic relaxation. Finally, by means of (80) and the relation

$$\begin{aligned} T_{\mathrm{a}} = {t_{\mathrm{a}}\over t_{\mathrm{s}}} T_{\mathrm{s}} \end{aligned}$$
(114)

we find \(\lambda \simeq 10^5\).

Fig. 10
figure 10

Ground displacement produced by afterslip following the 2011 Tohoku-Oki earthquake, according to the model. a Horizontal component; b vertical component \(u_3\). The rectangle is the projection of the weak fault region on the Earth’s surface, and the dashed segment is the fault trace. The \(x_1\) and \(x_2\) axes are parallel to the strike direction of the fault and to the direction normal to strike, respectively. Distances are measured in units of the half-side of the fault along the strike direction, namely \(L = 200\) km

Full size image

The ground displacement produced by afterslip has been calculated making use of Okada’s (1985) formulae. The graphs of the horizontal and vertical displacement components are shown in Fig. 10. The direction and magnitude of the calculated displacement are broadly comparable with displacements obtained from GPS data over a time interval comparable with \(t_{\mathrm{a}}\). For instance, Silverii et al. (2014) reported a maximum horizontal displacement of the order of 1 m at the eastern coasts of the Iwate/Miyagi prefectures of Japan and a maximum vertical displacement of about 20 cm in the same area. These figures are in good agreement with the results shown in Fig. 10, where the eastern coasts of the Iwate/Miyagi prefectures approximately correspond with the projection of the lower margin of the weak fault region on the Earth’s surface.

Of course, the present model cannot reproduce the details of the Tohoku-Oki earthquake nor of any other seismic event, but its aim is rather to investigate the basic mechanical processes occurring on the fault surface and to enlighten the relationships between them.

Conclusions

We presented a model that describes in a unique frame both seismic and aseismic slip on a fault, taking into account the interaction between the two processes. This has been achieved by considering a fault containing two regions with different mechanical behaviours: a strong, velocity-weakening region (asperity) and a weak, velocity-strengthening region.

During the interseismic intervals, the asperity is locked, while the weak region is subject to a very slow creep. Consequently, the slip deficit of the asperity increases in time with the velocity of tectonic plates, while the slip deficit of the weak region increases much slower. The asperity accumulates stress and eventually releases it, producing an earthquake, when a frictional threshold is exceeded. As a consequence of coseismic stress imposed by the asperity failure, the weak region is then subject to aseismic slip (afterslip).

The evolution equations of the system have been solved analytically for the interseismic intervals, the asperity slip and the afterslip in the weak region. The amount of afterslip is found to be proportional to the seismic slip of the asperity, in agreement with observations. The proportionality factor depends on the geometry of the fault and on the velocity of tectonic motion.

The model shows that afterslip is a natural consequence of seismic slip in a fault containing a velocity-strengthening region. Afterslip may have any duration, according to the intensity of velocity strengthening, thus accounting for the wide range of observed durations. According to the model, afterslip approaches an asymptotic value as time increases. We have shown that the higher rate that is often observed in postseismic deformation may be due to the superposition of the effects of afterslip and viscoelastic relaxation in the asthenosphere.

The model has been applied to the fault of the 2011 Tohoku-Oki earthquake. On the basis of data, the fault has been considered as made of a single large asperity, extending from the Japan trench to about 50 km of depth, and a weak region located downdip of the asperity to a depth of about 100 km. With the appropriate values of the model parameters, the dominant part of the seismic moment rate has been reproduced. The stress transfer from the slipping asperity produces a substantial increase of shear stress on the weak region, which is responsible for afterslip. The results suggest that the first four months after the event were dominated by afterslip, while the subsequent postseismic deformation was probably due to viscoelastic relaxation in the asthenosphere. Of course, the model presents a simplified description of real fault dynamics. It necessarily disregards complicated physical processes that may be dealt with via a numerical approach. However, a discrete model as the one we presented offers an alternative insight on the essential dynamics of the seismic source in an analytical framework.