1 Introduction

The theory of micropolar media, also called Cosserat’s theory (Cosserat & Cosserat, 1909), is a theory of elastic continua that includes, compared to the theory of linear elasticity, additional rotational degrees of freedom at each spatial location (Eringen & Kafadar, 1976; Nowacki, 1986). The theory accounts for the existence of an independent rotation of each particle of the elastic medium that can be different from the continuum rotation.

Micropolar theory is today widely applied to the design of seismic (elastic) metamaterials (Frenzel et al., 2017; Fernandez-Corbaton et al., 2019; Ha et al., 2016; Liu et al., 2012; Wu et al., 2019; Chen et al., 2014a, 2014b; Frenzel et al., 2019). The theory allows to describe materials with microstructure as continuous materials. In this sense, the properties of the micro-structure can be mapped onto simple effective-medium parameters (Reinbold et al., 2019). Working further with these effective-medium models helps to design elastic metamaterials by easing the way one deals with micro or nano-structures of the whole system.

Applications of micropolar theory also exist in the Earth’s sciences, in particular in the domain of earthquake source and fault dynamics (Teisseyre, 1973; Teisseyre et al., 2006; Teisseyre, 2011; Teisseyre et al., 2006; Teisseyre, 2008; Teisseyre et al., 2008; Teisseyre, 2011; Nagahama & Teisseyre, 2000b; Abreu et al., 2018; Abreu & Durand, 2021). Specifically, Twiss et al. (1991, 1993) adapted the kinematics of micropolar continuum theory (Eringen, 1966a, 1966b) to the analysis of fault-slip data (Twiss et al., 1991), and earthquake focal mechanisms (Twiss et al., 1993). With the use of micropolar theory, Twiss et al. (1991, 1993) describe brittle deformation in the Earth’s crust as a granular material, where the grains are represented by rigid and rotating fault blocks. These rigid fault blocks rotate around their centroids in a manner dictated by the local geometry of the blocks and their interactions with neighboring blocks. Using this description, permanent effects of rotational motions during seismogenic deformation have been observed and it has been shown that the deformation is better described by the micropolar theory compared to the linear elastic theory (Twiss, 2009; Twiss et al., 1993; Unruh et al., 2003; Lewis et al., 2008; Twiss et al., 1991; Schemmann et al., 2008; Wojtal 2001; Unruh et al., 1996; Gade & Raghukanth, 2016; Teisseyre et al., 2006; Twiss & Unruh, 1998, 2007).

The next step would be to apply dynamic micropolar equations to the study of the Earth, however, applications remain limited. This is mainly due to the lack of understanding of the required elastic material parameters present in the theory, namely the Cosserat couple modulus \(\mu _c\) and eigenfrequency \(\omega _r\). The question of the relevance of the micropolar theory to the study of the interior of the Earth is thus still open and deserves further investigation. Abreu et al. (2017a) studied the predicted seismic waveforms using the micropolar theory and included an analysis of the material elastic parameters. In their study, the authors analyzed the complexity of wave propagation showing its unusual frequency dependent behavior, unlike in conventional linear elasticity. Despite their effort, the authors could not conclude whether the dynamic micropolar behavior could be observed in seismological data and failed to give a detail procedure to find the required elastic parameters, mainly the understanding of the eigenfrequency \(\omega _r\). In another study, Abreu et al. (2017b) the authors provide a catalogue of Cosserat couple modulus \(\mu _c\) values required by the micropolar theory for mineralogical applications, however the extrapolations to these values to macroscopic observations does not seem trivial.

In this paper, we propose to go further by giving a clear understanding of the mathematics as well as of the elastic parameters appearing in the equations of motion in the context of macroscopic Earth’s sciences applications, providing solutions for the current encountered problems. To do so, we propose an analogy of the micropolar theory with the beam theory providing an understanding of the material elastic parameters. In particular, we show that the well known Timoshenko beam theory (Timoshenko & Woinowsky-Krieger, 1959) is equivalent to micropolar theory in the 1D case. We then propose a modified micropolar theory suitable for Earth’s sciences applications that overcomes the certain limitations of the original theory, in particular the existence of a division by zero at \(\omega =\omega _r\), and we test this theory making comparisons with real seismic data. We finally discuss the results obtained in this contribution.

2 From Linear Elasticity to Micropolar Theory

2.1 Linear Elasticity

Let first recall basics of linear elasticity. To find equations of motion that govern the elastic deformation produced by earthquakes, different approaches can be taken. A common one in seismology is to start by the definition of stress and strain and later consider the balance of linear and angular momentum (Slawinski, 2010; Aki & Richards, 2002). However, this is not the standard formulation for finding general equations of motion in complex media for engineering applications. Instead, the Langrangian formulation (also called the variational formalism of minimum action) is preferred. The Lagrangian formulation looks for minimizing the action integral I of the form (Whitham, 1973)

$$\begin{aligned} I = \int _0^t \int _{\Omega } {\mathcal {L}}\mathrm{d}\,^3 {\varvec{x}} \mathrm{d}t = \int _0^t \int _{\Omega } (K - {\mathcal {E}}) \mathrm{d}\,^3 {\varvec{x}} \mathrm{d}t , \end{aligned}$$
(1)

where \(\Omega \) denotes the volume of the continuum, \({\mathcal {L}}\) is the Lagrangian defined as the difference between the kinetic energy K and the potential energy (also called internal elastic free energy) \({\mathcal {E}}\).

The Lagrangian formulation solves the minimization problem \(\delta I = 0\), which yields the governing equations of motion. In linear elastic media the potential energy \({\mathcal {E}}\) is defined as follows

$$\begin{aligned} {\mathcal {E}} (\varepsilon ) = \frac{1}{2} \varepsilon _{ij} \, {\mathbb {C}}_{ijkl} \, \varepsilon _{kl}, \quad \text {with} \quad \varepsilon _{ij} = \frac{1}{2} (\partial _i u_j + \partial _j u_i) , \end{aligned}$$
(2)

where \( {\mathbb {C}}_{ijkl}\) is the fourth-order elastic tensor, u the displacement vector and \(\varepsilon _{ij}\) is a second-order symmetric tensor known as the strain tensor or Cauchy’s strain tensor. Because the strain tensor is symmetric \((\varepsilon _{ij}=\varepsilon _{ji})\), and because the energy is quadratic in the strain, the elements of the elastic tensor \({\mathbb {C}}\) exhibit the following symmetries

$$\begin{aligned} {\mathbb {C}}_{ijkl} = {\mathbb {C}}_{jikl} = {\mathbb {C}}_{ijlk} = {\mathbb {C}}_{klij} . \end{aligned}$$
(3)

The kinetic energy is defined as follows

$$\begin{aligned} K = \frac{1}{2} \rho \, \partial _t u \cdot \partial _t u , \end{aligned}$$
(4)

where \(\rho \) is the material density.

Using Eqs. (2) and (4) and assuming a homogeneous isotropic elastic tensor \({\mathbb {C}}\), the minimization problem \((\delta I=0)\) for the functional Eq. (1) gives the well known linear elastic equations of motion (Slawinski, 2010; Aki & Richards, 2002)

$$\begin{aligned} \rho \partial ^2_t u_j&= \partial _i \tau _{ij}\nonumber \\ \tau _{ij}&= \lambda \, \delta _{ij} \partial _k u_k + \mu (\partial _i u_j + \partial _j u_i), \end{aligned}$$
(5)

where \(\tau _{ij}\) is called the second-order stress tensor, which is simply a generalization of Hooke’s law. The parameters \(\lambda ,\mu \, [\text {MPa}]\) are the classical Lamé parameters. The free surface boundary conditions are given by

$$\begin{aligned} {\hat{n}} \cdot \tau&= 0 \quad \text{ on } \quad \partial \, \Omega , \end{aligned}$$
(6)

where \({\hat{n}}\) refers to the direction normal to the surface \(\partial \, \Omega \).

In the case of a 1D medium one can find that the equations of motion for shear displacements is given by the following expression

$$\begin{aligned} \rho \partial ^2_t u = \mu \partial ^2_x u , \end{aligned}$$
(7)

and assuming plane wave motion \(u=A e^{\mathbf{i }(k x \pm \omega t)}\), where A is the amplitude, k is the wavenumber and \(\omega \) the frequency, one can write the expression for the frequency \(\omega \) and phase velocity \(c=\omega /k\), respectively as follows

$$\begin{aligned} \omega ^2 = \frac{\mu }{\rho } k^2, \qquad c^2=\frac{\omega ^2}{k^2} = \frac{\mu }{\rho }. \end{aligned}$$
(8)

One can note that the phase velocity is frequency independent in conventional linear elastic media, which we will see is no longer true using micropolar theory.

2.2 Micropolar Theory

In order to find the dynamic micropolar equations of motion using the Lagrangian formulation we first define the internal energy \({\mathcal {E}}\) contributions, related to the displacement u and independent rotation \(\theta \) fields, given by the following expression (Eringen, 1999)

$$\begin{aligned} {\mathcal {E}} (e,\varpi ) = \underbrace{\frac{1}{2} e_{ij} \, {\mathbb {C}}_{ijkl} \,e_{kl}}_{\text {elastic free energy}} + \underbrace{\frac{1}{2} \varpi _{ij} \,{\mathbb {H}}_{ijkl} \, \varpi _{kl}}_{\text {rotational elastic free energy}}, \end{aligned}$$
(9)

where the strain measures are defined as follows

$$\begin{aligned} \begin{aligned} e_{ij}&= \underbrace{\frac{1}{2} (\partial _i u_j + \partial _j u_i)}_{\text {symmetric part}} + \underbrace{\epsilon _{ijk} \left( \frac{1}{2} \epsilon _{kab} \partial _a u_b - \theta _k\right) }_{\text {antisymmetric part}}, \\&\quad \text {Cosserat strain tensor} \\ \varpi _{ij}&= \frac{1}{2} (\partial _i \theta _j + \partial _j \theta _i) + \frac{1}{2} (\partial _i \theta _j - \partial _j \theta _i), \quad \text {curvature tensor} , \end{aligned} \end{aligned}$$
(10)

where u is the vector displacement and \(\theta \) is the micro rotational vector of motion.

Note that the micropolar strain tensor e assumed in Eq. (10) is given by the sum of the conventional linear strain (Eq. (2)) and an antisymmetric part given by the difference between the curl \(\frac{1}{2} \, \epsilon _{kab} \partial _a u_b\) and the independent rotation \(\theta \). This means that the difference between the macroscopic rotation and independent local rotation produce deformation within the continuum. Note also that the strain measure related to the independent rotation is called the curvature tensor. This can be easily understood in the 1D case because the spatial derivative of the independent rotation \(\theta \) scales the second derivative (curvature) of the displacement, i.e., \(\partial _x \theta = \alpha \partial ^2_x u\), where \(\alpha \) is a constant.

Having defined the total potential energy in Eq. (9) and the strain measures in Eq. (10), the total micropolar kinetic energy is defined as follows

$$\begin{aligned} K = \frac{1}{2} \rho \partial _t u \cdot \partial _t u + \frac{1}{2} I \cdot \partial _t \theta \cdot \partial _t \theta , \end{aligned}$$
(11)

where the \(\rho \) is the mass density and I the rotational inertia density.

Using Eqs. (9, 10, 11) and solving the minimization problem \((\delta I=0)\) for the functional Eq. (1) one can find the linear elastic micropolar equations of motion given by the following expressions

$$\begin{aligned} \begin{aligned} \rho \partial ^2_t u_j&= \partial _i \sigma _{ij}, \qquad \text {balance of linear momentum} \\ I \partial ^2_t \theta _j&= \partial _i m_{ij} + \epsilon _{jkl} \sigma _{kl}, \qquad \text {balance of angular momentum} \end{aligned} \end{aligned}$$
(12)

where \(\sigma \) is called the stress tensor and m is the couple-stress tensor or moment-stress tensor (Eringen, 1999) and \(\epsilon \) is the Levi-Civita symbol. The second-order tensor \(\sigma \) is the asymmetric stress and m the moment stress. The free surface boundary conditions are given by

$$\begin{aligned} {\hat{n}} \cdot \sigma&= {\hat{n}} \cdot m = 0 \quad \text{ on } \quad \partial \, \Omega , \end{aligned}$$
(13)

where \({\hat{n}}\) refers to the direction normal to the surface \(\partial \, \Omega \).

In a homogeneous isotropic media, we can write the linear micropolar stress tensor \(\sigma \) and the couple-stress tensor m as follows (Eringen, 1999)

$$\begin{aligned} \begin{aligned} \sigma _{ij}&= \underbrace{\mu (\partial _i u_j + \partial _j u_i) + \lambda \, \delta _{ij} \sum _{k=1}^3 \partial _k u_k}_{\text {symmetric part}}\\&\quad + \underbrace{2 \mu _c \epsilon _{ijk} \left( \frac{1}{2} \epsilon _{kab} \partial _a u_b - \theta _k\right) }_{\text {antisymmetric part}} , \\ m_{ij}&= \alpha \delta _{ij} \sum _{k=1}^3 \partial _k \theta _k + \beta (\partial _i \theta _j + \partial _j \theta _i) + \gamma (\partial _i \theta _j - \partial _j \theta _i) , \end{aligned} \end{aligned}$$
(14)

where the parameters \(\lambda ,\mu \, [\text {MPa}]\) are the classical Lamé parameters. A new elastic constant \(\mu _c \ge 0 \, [\text {MPa}]\) is introduced. It is called the Cosserat couple modulus (Neff & Jeong, 2009; Neff et al., 2010) and it is poorly constrained for Earth sciences applications. Other elastic parameters are defined, \(\alpha ,\beta ,\gamma \, [\text {MPa} \cdot m^2]\). They are related to the couple (or moment) stress m and very little is known about their values.

In a 1D homogeneous isotropic medium, the micropolar equations of motion are given by the following expression (Eringen, 1999; Abreu et al., 2017a)

$$\begin{aligned} \begin{aligned} \rho \partial _t ^2 u&= (\mu + \mu _c) \partial _x ^2 u- 2 \mu _c \partial _x \theta , \\ I \partial _t ^2 \theta&= (\beta + \gamma ) \partial _x ^2 \theta + 2 \mu _c \partial _x u - 4 \mu _c \theta , \end{aligned} \end{aligned}$$
(15)

where u is the transverse displacement field in the y direction and \(\theta \) is the micro-rotational field in the z direction. The displacement u and the micro rotation \(\theta \) can be decoupled from eq. (15) as follows (Grekova, 2016; Abreu et al., 2017a)

$$\begin{aligned}&\left[ \partial _t ^4 - \left( \frac{\mu + \mu _c}{\rho } + \frac{\beta +\gamma }{I}\right) \partial _t ^2 \partial _x ^2 + \left( \frac{\mu + \mu _c}{\rho }\right) \right. \nonumber \\&\quad \left. \left( \frac{\beta +\gamma }{I}\right) \partial _x ^4 - \frac{4 \mu \mu _c}{\rho I} \partial _x^2 + \frac{4\mu _c}{I} \partial _t ^2 \right] (u,\theta ) = 0, \end{aligned}$$
(16)

where both fields u and \(\theta \) can be modeled as independent variables.

Applying the micropolar theory thus requires to get relevant values for the new elastic parameters as well as the eigenfrequency \(\omega _r\). To do so, we need to better understand the micropolar theory and this is possible by making an analogy with the beam theory.

3 How Can we Understand Micropolar Theory in Earth’s Sciences?

3.1 Beam Theory

In many geological situations we are concerned with loads of a certain shape that act on the surface or inside the crust due to different factors like the presence of magmatic material, mountains, ice sheets (see Fig. 1). In order to model such deformations the conventional equations of linear elasticity presented in Sect. 2.1 cannot be applied. This is because linear elasticity cannot reproduce the correct curvature of the bending. Instead, beam as well as plate theories, have been developed and widely applied (Watts ,2015; Turcotte & Schubert, 2002; Watts, 2001; Burov, 2011; Watts & Burov, 2003; Gunn, 1943; Bott, 1993; Chase & Wallace, 1988; Steinberg et al., 2014; Kearey et al., 2009; Jaeger, 2012; Mavko, 1981; Artemieva, 2011; Walcott, 1970).

Fig. 1
figure 1

Cartoons representing the bending of the lithosphere in different scenarios: a due to a volcanic load of the Canary Islands (after Watts (2001)), b due to a mountain which exerts a force pointing down shown by the black arrow and c due to ice sheets, i.e., postglacial uplift scenarios

Full size image

Plates are defined as plane structural elements with a small thickness compared to the plane dimensions (Timoshenko and Woinowsky-Krieger, 1959). Plate theory thus has the advantage of reducing the full 3D problem to a 2D one. Beams, on the other hand, are 3D dimensional structural elements capable to tolerate load primarily by resisting to the bending, where the forces are understood to act perpendicular to the longitudinal axis (Watts, 2001). However, the deflection of beams is modeled in 1D, in other words, beam theory reduces the 3D problem to a 1D one. In realistic 3D scenarios, the lithosphere responds to surface and subsurface loads by bending. In order to model the resulting flexure, the solution of the plate equation is appropriate only if the dimensions of the plate in the horizontal direction are much larger in the vertical direction (Burov, 2011; Ventsel et al., 2002; Arnaiz-Rodríguez & Audemard, 2014; Van Wees & Cloetingh, 1994; Garcia et al., 2015; Sanford, 1959; Wessel, 1996; Braun et al., 2013; Stüwe, 2002; Judge & McNutt, 1991; Zhang et al., 2018; Manríquez et al., 2014; Contreras-Reyes & Osses, 2010). However, in many situations, the distortion of the plate during the bending is limited by the extreme edges of the plate. In this case, a beam of unit width as a part of a larger plate provides a better model and thus imply to use the beam theory (Watts, 2001).

Beam theory is founded on the classical Euler-Bernoulli equation and it is given by the following expression (Weaver et al., 1990)

$$\begin{aligned} \partial ^2_x \left( E I_z \partial ^2_x u \right) + \rho A \partial ^2_t u = 0, \end{aligned}$$
(17)

where E is the Young modulus \([\text {Pa}]\), \(I_z\) is the second moment of area \([m^4]\) and it must be calculated with respect to the axis which passes through the centroid of the cross-section and which is perpendicular to the applied loading, u is the transverse displacement [m] describing the deflection of the beam in the z direction at some location x, \(\rho \) is the material density \([kg/m^3]\) and A is the cross-sectional area of the beam \([m^2]\) (see Fig 2). The product \(EI_z\) \([\text {Pa} \cdot m^4]\) is known as the flexural rigidity and it is often considered constant.

Fig. 2
figure 2

Cartoon representing a beam of length L, height h and cross-sectional area A

Full size image

Note that Eq. (17) shows a fourth-order derivative in space, unlike conventional linear elasticity which shows a second-order derivative (see Eq. (7)). If we assume plane wave solution, one finds that the phase velocity \((c=\omega /k)\) is given by

$$\begin{aligned} \frac{\omega ^2}{k^2} = \sqrt{\frac{E I_z}{\rho A }} \omega . \end{aligned}$$
(18)

Note that the phase velocity in Eq. (18) is proportional to the frequency unlike in conventional elasticity (Eq. (8)). This means that, even in homogeneous media, small wavelengths will move faster than larger wavelengths. Therefore, unlike linear conventional elasticity, an arbitrary waveform will move with a variable speed and will then suffer a change in shape or be dispersed.

In many geological scenarios, the static form of the Euler-Bernoulli equations, Eq. (17), is solved considering a constant product \(EI_z\), yielding the following relationship between the beam’s deflection and the applied load (Watts, 2001; Steinberg et al., 2014)

$$\begin{aligned} D \partial ^4_x u = q(x), \end{aligned}$$
(19)

where D is the flexural rigidity \([\text {Pa} \cdot m^4]\) and q(x) is the sum of the external loading force and the isostatic restoring force: it is the net force per unit area \([\text {Pa}]\) acting on the plate, the so-called hydrostatic restoring force or vertical load. Its value depends on the physical configuration of the problem as illustrated in Fig. 3. When modeling the lithosphere, the flexural rigidity is commonly expressed in terms of the effective elastic thickness \(T_e\) of the plate [m] as follows

$$\begin{aligned} D^{\text{plate}}=\frac{ET_e^3}{12(1-\nu ^2)}, \end{aligned}$$
(20)

where E is the Young modulus \([\text {Pa}]\) and \(\nu \) the Poisson ratio. Note that the units of \(D^{\text{plate}}\) in eq. (20) are \(\text {Pa}\cdot m^3\)and it refers to the moment per unit length per unit of curvature.

Fig. 3
figure 3

Cartoons representing four types of different loads that can be incorporated into the flexure of plates (after Steinberg et al. (2014)). The hydrostatic restoring force or vertical load is denoted by q(x), \(\rho _m\) the density of the mantle, \(\rho _w\) the density of sea water, \(\rho _s\) the density of the sediments, g the gravitational acceleration, \(h_s\) the sediment thickness, \(h_w\) water level and u is the deflection of the lithosphere

Full size image

However, Eq. (19) does not include the presence of shear forces. In order to overcome this limitation Eq. (19) must include a force balance that relates the bending moments and the vertical load q to any applied horizontal shear forces F such that (Stüwe, 2002; Turcotte & Schubert, 2002)

$$\begin{aligned} D \partial ^4_x u + F \partial ^2_x u = q(x) . \end{aligned}$$
(21)

If the distribution of loads q is known, Eq. (21) can be solved for either the deflection of the plate u or the flexural rigidity D. Usually, the deflection is known from bathymetric or topographic observations and Eq. (21) is used to obtain the stiffness of the plate (Stüwe, 2002).

Equation (21) is a static equation, i.e., it does not include the time variable. In order to include the time dependence of the initial Euler-Bernoulli eq. (17) Rayleigh (1896) included the rotatory inertia of the beam cross-section as follows

$$\begin{aligned} E I _z \partial ^4_x u + \rho A \partial ^2_t u - \rho I_z \left( 1+ \frac{E}{M\mu }\right) \partial ^2_x \partial ^2_t u = 0. \end{aligned}$$
(22)

Timoshenko (Timoshenko, 1921) extended Rayleigh’s equation by incorporating the effect of shear deformation as follows (Timoshenko, 1921; Weaver et al., 1990)

$$\begin{aligned} E I_z \partial ^4_x u + \rho A \partial ^2_t u - \rho I_z \left( 1+ \frac{E}{M\mu }\right) \partial ^2_x \partial ^2_t u + \frac{\rho ^2 I_z}{M\mu }\partial ^4_t u = 0, \end{aligned}$$
(23)

where M is called the shear correction factor (Hutchinson, 2001; Gruttmann & Wagner, 2001), \(\mu \) is the shear modulus \([\text {Pa}]\).

If we include applied horizontal forces \(F_T\) and the shear forces to Timoshenko’s Eq. (23), as it was done in Eq. (21), we find

$$\begin{aligned}&EI_z\partial ^4_x u + \rho A\partial ^2_t u + F_T \partial ^2_x u - \rho I_z \left( 1+ \frac{E}{M\mu }\right) \partial ^2_x \partial ^2_t u\nonumber \\&\quad + \frac{\rho ^2 I_z}{M\mu }\partial ^4_t u = 0, \end{aligned}$$
(24)

where \(F_T\) denotes an additional temperature dependent axial force \(F_T=\alpha EA T\), where \(\alpha \) is the thermal expansion coefficient (Hsu et al. 2008; Avsec & Oblak, 2007).

On geological time scales, the lithosphere is often modeled statically, i.e., using the Euler-Bernoulli time independent Eq. (21). Additionally, Timoshenko Eq. (24) is a well known equation used for engineering applications and it includes the effects of the static version of Euler-Bernoulli Eq. (21).

3.2 Equivalence Between Micropolar and Beam Theories

At this point it becomes visible that Timoshenko’s beam theory Eq. (24) and micropolar theory Eq. (15) represent the same equation with the following equivalences in material parameters

$$\begin{aligned}&\frac{E M\mu }{\rho ^2} = \frac{\mu + \mu _c}{\rho }\frac{\beta +\gamma }{I}, \qquad \frac{M\mu + E}{\rho } = \frac{\mu + \mu _c}{\rho } + \frac{\beta +\gamma }{I},\nonumber \\&\quad \frac{4 \mu _c}{I} = \frac{M \mu A}{\rho I_z}, \qquad \frac{4 \mu \mu _c}{\rho I} = - \frac{F_T M \mu }{\rho ^2 I_z}. \end{aligned}$$
(25)

From the first two expressions in Eqs. (25) we can write the following quadratic equation for the term \((\mu + \mu _c)\)

$$\begin{aligned} (\mu + \mu _c)^2 -(\kappa \mu + E) (\mu +\mu _c) + E \kappa \mu =0, \end{aligned}$$
(26)

from which we can obtain two roots for the Cosserat Couple modulus

$$\begin{aligned} \mu _c = \mu (M-1), \qquad \text {and} \qquad \mu _c = E-\mu . \end{aligned}$$
(27)

Taking into account that Hutchinson (2001), Gruttmann and Wagner (2001), Vlachoutsis (1992) have reported that in general \(M< 1\) and that the Cosserat couple modulus must be positive \((\mu _c>0,\) Eringen (1999), we therefore discard the first solution in Eq. (27) for having non-physical significance.

We thus show the Cosserat couple modulus \(\mu _c\) becomes a measurable quantity that depends on the Young modulus E and shear modulus \(\mu \). In terms of the bulk modulus \(\kappa \) we can write the Cosserat couple modulus \(\mu _c\) as follows

$$\begin{aligned} \mu _c = \mu \left[ \frac{9\kappa }{3\kappa +\mu } - 1\right] . \end{aligned}$$
(28)

Since seismology often refer to the compressional \((v_p)\) and shear wave \((v_s)\) velocities in the interior of the Earth, the Cosserat couple modulus \(\mu _c\) can also be written as follows

$$\begin{aligned} \mu _c = \mu \left[ \frac{2v_p^2 - 3 v_s^2}{v_p^2-v_s^2} \right] , \qquad \text {the condition} \quad \mu _c>0 \quad \text {implies} \quad v_p>\sqrt{3/2} v_s. \end{aligned}$$
(29)

Using the second solution of eq. (27) an expression for the inertia density I is given by

$$\begin{aligned} I = \frac{4(E-\mu )\rho I_z}{M\mu A} . \end{aligned}$$
(30)

An illustration of the interpretation of the two theories is shown in Fig. 4, where we can observe that the difference between Euler-Bernoulli and Timoshenko beam or micropolar theories is the curvature induced in the model (Fig. 4a). This can be explained by the mathematical introduction of the difference between the macro-rotation \((0.5 \, \partial u/\partial x)\) and the local angle of rotation \((\theta )\) (Fig. 4b). The existence of a difference between the macro-rotation and the local angle of rotation is the basic assumption of the micropolar theory (Fig. 4c).

Fig. 4
figure 4

a Cartoon representing the bending of a beam: a the difference between the conventional Euler-Bernoulli and the Timoshenko (and Cosserat) theories and b the difference between the macro-rotation \((0.5 \, \partial u/\partial x)\) and the local rotation \((\theta )\) which is the basic assumption of the micropolar model. c Continuum deformation showing the existence of micro-rotation without the presence of a rupture in the material

Full size image

3.3 Understanding the Eigenfrequency \(\omega _r\)

Assuming plane wave propagation in the micropolar equations of motion, Eq. (15),

$$\begin{aligned} u = A e^{\mathbf{i }(-kx+\omega t)}, \qquad \theta = B e^{\mathbf{i }(-kx+\omega t)}, \end{aligned}$$
(31)

where A, B are wave amplitudes, we can write an expression for the frequency \(\omega \) in terms of the wavenumber k as follows

$$\begin{aligned} \omega ^4 - (c_2^2+c_4^2)\omega ^2k^2 + c_2^2 c_4^2 k^4 + k^2 c_T^2 \omega _r^2 - \omega _r^2 \omega ^2 = 0, \end{aligned}$$
(32)

where for simplification purposes, we have written the different velocities \(c_T,c_2,c_4\) and eigen frequency \(\omega _r\) as follows

$$\begin{aligned} c_T^2 =&\frac{\mu }{\rho }, \qquad c_2^2= \frac{\mu +\mu _c}{\rho },\nonumber \\ c_4^2=&\frac{\beta +\gamma }{I}, \qquad \omega _r^2 = \frac{4 \mu _c}{I}. \end{aligned}$$
(33)

The expressions for the phase velocity \((\omega /k)\) derived from Eqs. (15) and (16) and are equivalent and given by the following expression for the phase velocity \(c_f\) (Abreu et al., 2017a)

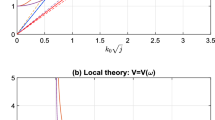
$$\begin{aligned} c_f^2 =&\frac{\displaystyle c_T^2/2}{1-\frac{\omega _r^2}{\omega ^2}} \left( X+\frac{2c_4^2}{c_T^2}\pm \sqrt{X^2+4\frac{\omega _r^2}{\omega ^2}\frac{c_4^2(c_2^2-c_T^2)}{c_T^4}}\right) , \qquad \text {with} \qquad \nonumber \\ X=&1-\frac{\omega _r^2}{\omega ^2}+\frac{c_2^2-c_T^2-c_4^2}{c_T^2} . \end{aligned}$$
(34)

We can observe two branches of the phase velocity \(c_f\) in Eq. (34), which are both related to the displacement u and the micro-rotation \(\theta \) (Fig. 5). We can also observe the presence of an eigenfrequency \(\omega _r\) at which \(c_f\) is not defined. It is here where we find one of the most controversial aspects of the micropolar theory for seismological applications: the presence of two phase velocities and the eigenfrequency \(\omega _r\).

For simplicity, we show in Fig. 5 the non-dimensional phase velocity plot of Eq. (34) (see Eqs. (33)). The most evident aspect that we can observe is that one of the roots \(c_f^-\) is the same as the conventional shear phase velocity \(c_T\). However, the other root \(c_f^+\) shows a very peculiar behavior: it possesses positive real and imaginary parts and it is non defined at \(\omega =\omega _r\). This, from the physical point of view, seems very similar to the behavior of a forced harmonic oscillator. The interpretation of this eigenfrequency is thus related to the rupture of the material. A detailed examination of the values of \(c_f^{\pm }\) for different parameter configuration can be found in Abreu et al. (2017a). From the theoretical point of view, many studies refer to this as a rotational eigenmode related to the independent rotation \(\theta \). However, we have shown that the equations for the displacement u and independent rotation \(\theta \) can be decoupled (see Eq. (16)). This means that one can observe the behavior of u independent of \(\theta \) and both are ruled by the same partial differential Eq. (16). Therefore, we can conclude that both phase velocities \(c_f^{\pm }\) are related to both u and \(\theta \). However, depending on the frequency domain, the translational or the rotational motions will prevail. This can be illustrated when examining the situation \(\omega =\omega _r\), where the system (15) gives the solution \(\theta =\theta _0e^{\mathbf{i }\omega _r t}, \quad u=0\), meaning that translations are zero and do not propagate, while rotations are equal everywhere. Everything occurs like a quasi-rigid motion, the phase is the same everywhere although no real signal propagates, the group velocity is zero at this frequency. This is usually true for any cutoff frequency.

From the experimental point of view, seismologists do not expect frequency dependent seismic wave velocities in a homogeneous medium and the presence of the second root of the phase velocity is unusual. From the seismological point of view, this can be considered as the most important questions to answer when one attempts to apply the dynamic micropolar equations of motion. It is needed to understand the meaning of \(\omega _r\) and \(c_f^+\) and how it can be determined from the use of seismic data. We discuss the experimental evidence of this eigenfrequency \((w_r)\) in the next Sect. 3.4.

Fig. 5
figure 5

Non-dimensional phase velocity plot for the micropolar model (Eq. (34))

Full size image

3.4 How Can we Obtain the Eigenfrequency \(\omega _r\)?

Understanding the physics and calculation of the eigenfrequency \(\omega _r\) in Eq. (33) is of primary importance when aiming at applying micropolar theory to realistic geological scenarios. Combining Eqs. (33, 25 and 27) we can write

$$\begin{aligned} \omega _r^2 = \frac{4\mu _c}{I} = \frac{4(E-\mu )}{I}= \frac{M \mu A}{\rho I_z} . \end{aligned}$$
(35)

Equation (35) shows that, by having information of the Young E modulus and shear \(\mu \) modulus and the micro inertia density I, we should be able to obtain the eigenfrequency \(\omega _r\) in order to make predictions of wave propagation in microstructured materials with micropolar theory. We can also observe that the eigenfrequency \(\omega _r\) can be written in terms of the shear correction factor M, among other physical measurable quantities. Timoshenko defines the shear correction factor M as a correction constant that depends upon the shape of the cross-section of the beam (Timoshenko, 1921). This factor increases with a decrease in the wavelength. There are several ways to define this correction factor (Kaneko, 1975; Timoshenko, 1922), but the general meaning is that the factor allows the shear stress to be nonuniform over the cross-section of the beam. It can be defined as follows (Kaneko, 1975)

$$\begin{aligned} M = \tau \mu \gamma _{\text {eff}} , \end{aligned}$$
(36)

where \(\tau \) is the average shear stress on the cross-section and \(\gamma _{\text {eff}}\) is the effective transverse shear strain.

Numerous attempts have been made to evaluate M theoretically and experimentally, and it seems that the best theoretical results are given by Timoshenko’s equation Eq. (36) when considering rectangular cross-sections (Kaneko, 1975; Rosinger & Ritchie, 1977). It can be suspected that when considering more general cross-sections, this value could be obtained numerically (Hutchinson, 2001).

There have been successful attempts to experimentally verify the presence of the eigenfrequency \(\omega _r\) in Timoshenko’s theory that is absent in the Euler-Bernoulli and Rayleigh theories. It has also been shown that Timoshenko’s theory gives only a rough approximation to the aforementioned second spectrum and fails to predict all other spectral characteristic of a 3D cylindrical waveguide (Abbas and Thomas 1977; Moreles et al., 2005). Despite some authors claim that the eigenfrequency \(\omega _r\) should be regarded as the inevitable,meaningless and being a consequence of an otherwise remarkable approximate engineering theory (Stephen 1997), the study made by Bhaskar (2009) concludes that this eigenfrequency must not be disregarded and experiments made by Chan et al. (2002), Mindlin (1951), Ellis and Smith (1967), Díaz-de Anda et al. (2012) have revealed that it is measurable.

4 An Alternative Micropolar Model Including Gradient Micro-Inertia

4.1 Presentation of the New Model

Despite having a way to experimentally obtain the eigenfrequency \(\omega _r\), the fact that the phase velocity in Eq. (34) is not defined at \(\omega =\omega _r\) seems to be unphysical for seismological applications. This, as an analogy to the forced harmonic oscillator where the same type of behavior appears, can in principle be solved by considering dissipation. However, the question of what represents \(\omega _r\) in the Earth still remains. Since micropolar theory has been related to the earthquake rupture, we can argue that \(\omega _r\) represents the frequency of rupture of the material. Despite being physically sound, this is, however, not observable from seismological records. In addition, the fact of having two phase velocities raises complications such as for example, which one fits the seismological observations. For these reasons, we develop a new version of the micropolar model based on seismological observable assumptions.

Following Twiss et al. (1993), we first define a physical observable variable: the effective rotational motion or net vorticity vector \(\Psi \) as the difference between the curl \((\frac{1}{2}\, \epsilon _{kab} \partial _a u_b)\) and the independent rotation \(\theta \) as follows

$$\begin{aligned} \Psi _k = \left( \frac{1}{2} \epsilon _{kab} \partial _a u_b - \theta _k \right) . \end{aligned}$$
(37)

It has been shown that the net vorticity vector \(\Psi \) is an objective variable (Twiss et al., 1993). This means that it is an intrinsic characteristic of the deformation and not simply the effect of rigid rotations of the micro-material. The net vorticity vector \(\Psi \) can be used to identify the antisymmetric part of the global micropolar seismic moment tensor and it can be observed in fault-slip data (Twiss et al., 1993). This allows us to write equivalent micropolar strain tensors e and \(\varpi \) as follows

$$\begin{aligned} \begin{aligned} e_{ij}&= \frac{1}{2} \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i}\right) + \epsilon _{ijk} \Psi _k ,\\ \varpi _{ij}&= \partial _i \left( \frac{1}{2} \epsilon _{jlm} \partial _l u_m - \Psi _j\right) . \end{aligned} \end{aligned}$$
(38)

The potential energy is defined by keeping Eq. (9), since we do not consider any cross-coupling. The total kinetic energy is defined as follows

$$\begin{aligned} K = \frac{1}{2} \rho \partial _t u \cdot \partial _t u + \frac{1}{2} I \cdot \partial _t \Psi \cdot \partial _t \Psi , \end{aligned}$$
(39)

where the \(\rho \) is the mass density and I the rotational inertia density. This kinetic energy is a particular case of the kinetic energy of the relaxed micromorphic model with gradient micro-inertia introduced in Owczarek et al. (2019) (see Sect. 3). For enriched theories of wave propagation with additional gradient micro-inertia terms we refer the reader to Askes and Aifantis (2011); Madeo et al. (2017), Owczarek et al. (2019).

Using Eqs. (38) and (39) and solving the minimization problem \((\delta I=0)\) for the functional Eq. (1) one can find the new linear elastic micropolar equations of motion given by the following expressions

$$\begin{aligned} \begin{aligned} \rho \partial ^2_t u_j&= \partial _i {\overline{\sigma }}_{ij}, \qquad \text {balance of linear momentum} \\ I \partial ^2_t \Psi _j&= \partial _i {\overline{m}}_{ij} + \epsilon _{jkl} {\overline{\sigma }}_{kl}. \qquad \text {balance of angular momentum} \end{aligned} \end{aligned}$$
(40)

The free surface boundary conditions are given by

$$\begin{aligned} {\hat{n}} \cdot {\overline{\sigma }}&= {\hat{n}} \cdot {\overline{m}} = 0 \quad \text{ on } \quad \partial \, \Omega , \end{aligned}$$
(41)

where \({\hat{n}}\) refers to the direction normal to the surface \(\partial \, \Omega \).

The stress and curvature tensors are given by the following expressions

$$\begin{aligned} \begin{aligned} {\overline{\sigma }}_{ij}&= {\mathbb {C}}_{ijkl} e_{kl}, \\ {\overline{m}}_{ij}&= {\mathbb {D}}_{ijkl} \varpi _{kl}, \end{aligned} \end{aligned}$$
(42)

where \({\mathbb {C}},{\mathbb {D}}\) are fourth-order tensors of elastic constants. In isotropic media we can write \({\mathbb {C}},{\mathbb {D}}\) as follows

$$\begin{aligned} \begin{aligned}&{\mathbb {C}}_{ijkl} = \lambda \delta _{ij} \delta _{kl} + (\mu +\mu _c) \delta _{ik} \delta _{jl} + (\mu -\mu _c) \delta _{il} \delta _{jk} , \\&{\mathbb {D}}_{ijkl} = \lambda ^c \delta _{ij} \delta _{kl} + (\mu ^c+\mu _c^c) \delta _{ik} \delta _{jl} + (\mu ^c-\mu _c^c) \delta _{il} \delta _{jk}. \end{aligned} \end{aligned}$$
(43)

Therefore, the stress \({\overline{\sigma }}\) and the couple-stress tensors \({\overline{m}}\) can be written as follows

$$\begin{aligned} \begin{aligned} {\overline{\sigma }}_{ij}&= \lambda \delta _{ij} \partial _k u_k + \mu (\partial _i u_j + \partial _j u_i) + 2 \mu _c \epsilon _{ijk} \Psi _k , \\ {\overline{m}}_{ij}&= \mu L_c^2 \left[ \frac{1}{2} \partial _i \epsilon _{jlm} \partial _l u_m - \alpha \partial _i \Psi _j \right] , \end{aligned} \end{aligned}$$
(44)

where we have assumed \(\lambda ^c=\mu ^c-\mu _c^c=0\) and \(\mu ^c+\mu _c^c=\mu L_c^2\), where \(L_c\) is a characteristic length related to the material in study. Following the concept of effective stress introduced by Nur and Byerlee (1971) we have introduced a parameter \(\alpha \) with \(0\le \alpha \le 1\). In poroelastic theory, the parameter \(\alpha \) is called the Biot’s parameter and it is defined as follows (Zoback, 2010)

$$\begin{aligned} \alpha =1-\frac{K_d}{K_g} , \end{aligned}$$
(45)

where \(K_d\) is the drained bulk modulus of the rock or aggregate and \(K_g\) is the bulk modulus of the rock’s individual solid grains. Note that we can write the couple-stress tensor \({\overline{m}}\) as follows

$$\begin{aligned} \begin{aligned} {\overline{m}}&= \mu L_c^2 \partial _i \left( \frac{1}{2} \epsilon _{jlm} \partial _l u_m - \alpha \Psi _j \right) , \\&= \mu L_c^2 \partial _i \left( \frac{1}{2} \epsilon _{jlm} \partial _l u_m - \Psi _j - (\alpha -1) \Psi _j \right) , \\&= \mu L_c^2 \partial _i \theta _j + (1-\alpha ) \mu L_c^2 \partial _i \left( \frac{1}{2} \epsilon _{kab} \partial _a u_b - \theta _k \right) . \end{aligned} \end{aligned}$$
(46)

Thus the model assumed for the couple-stress tensor \({\overline{m}}\) can be understood as a gradient theory for couple stresses. This form of the constitutive equation for the couple stresses makes clear that the requirement of the frame indifference is satisfied in the linear sense. Indeed, \(\nabla \theta \) and \(\Psi \) are frame indifferent in the linear approximation. It is easy to show then that \(\nabla \Psi \) also satisfies this requirement.

In a 1D isotropic medium we can write the following wave equation

$$\begin{aligned} \begin{aligned} \rho \partial _t ^2 u&= \mu \partial _x ^2 u + 2 \mu _c \partial _x \Psi , \\ I \partial _t ^2 \Psi&= \mu L_c^2 \left( \partial _x ^3 u - \alpha \partial _x^2 \Psi \right) + 4\mu _c \Psi . \end{aligned} \end{aligned}$$
(47)

The displacement u and the net rotation \(\Psi \) can be decoupled from Eq. (47) as follows

$$\begin{aligned}&\left[ \partial ^4_t - \alpha L_c^2 \frac{\mu }{\rho } \frac{\mu }{I} \partial _x^4 -\frac{2 \mu _c}{I} L_c^2 \frac{\mu }{\rho } \partial _x^4\right. \nonumber \\&\quad \left. + \alpha L_c^2 \frac{\mu }{I} \partial _t^2 \partial _x^2 - \frac{\mu }{\rho } \partial _t^2 \partial _x^2 - \frac{4 \mu _c}{I} \partial _t^2 + \frac{4 \mu _c}{I} \frac{\mu }{\rho } \partial _x^2 \right] (u,\Psi ) = 0, \end{aligned}$$
(48)

where both fields u and \(\Psi \) can be modeled as independent variables. Assuming plane wave solutions of the form of Eq. (31) we can write expressions for the frequency \(\omega \) and the phase velocity \(\omega /k\) as follows

$$\begin{aligned} \begin{aligned} \omega ^2&= \frac{-\left( \alpha \frac{\mu L_c^2}{I} k^2 - k^2 \frac{\mu }{\rho } + \omega _r^2\right) \pm \sqrt{\left( \alpha \frac{\mu L_c^2}{I} k^2 - k^2 \frac{\mu }{\rho } + \omega _r^2\right) ^2 + 4 \left[ k^4 \left( \alpha \frac{\mu L_c^2}{I} \frac{\mu }{\rho } + \frac{\omega _r^2}{2} L_c^2 \frac{\mu }{\rho } \right) + \omega _r^2 k^2 \frac{\mu }{\rho } \right] }}{2} , \\ c_f^2&= \frac{\omega ^2}{k^2} = \frac{\frac{\mu }{\rho } \left( {1+\frac{\omega _r^2}{\omega ^2}}\right) - \alpha L_c^2 \frac{\mu }{I} \pm \sqrt{\left( \frac{\mu }{\rho } \left( {1+\frac{\omega _r^2}{\omega ^2}}\right) - L_c^2 \frac{\mu }{I} \right) ^2+4\left( {1+\frac{\omega _r^2}{\omega ^2}}\right) L_c^2 \frac{\mu }{\rho } \left( \alpha \frac{\mu }{I} + \frac{\omega _r^2 }{2} \right) } }{2\left( {1+\frac{\omega _r^2}{\omega ^2}}\right) } . \end{aligned} \end{aligned}$$
(49)

In the limiting case when \(\alpha \rightarrow 0\) we can write the equations of motion as follows

$$\begin{aligned} \begin{aligned} \rho \partial _t ^2 u&= \mu \partial _x ^2 u + 2 \mu _c \partial _x \Psi , \\ I \partial _t ^2 \Psi&= \mu L_c^2 \partial _x ^3 u + 4\mu _c \Psi . \end{aligned} \end{aligned}$$
(50)

The displacement u and the net rotation \(\Psi \) can be decoupled from Eq. (50) as follows

$$\begin{aligned}&\left[ \partial _t ^4 - \frac{\mu }{\rho } \partial _x ^2 \partial _t ^2 - \frac{4\mu _c}{I} \frac{\mu }{\rho } \frac{L_c^2}{2} \partial _x ^4\right. \nonumber \\&\quad \left. + \frac{4\mu _c}{I} \frac{\mu }{\rho } \partial _x ^2 - \frac{4\mu _c}{I} \partial _t ^2\right] (u,\Psi ) = 0, \end{aligned}$$
(51)

where both fields u and \(\Psi \) can be modeled as independent variables. Assuming plane wave solutions of the form of eqs. (31) we can write expressions for the frequency \(\omega \) and the phase velocity \(\omega /k\) as follows

$$\begin{aligned} \begin{aligned} \omega ^2&= \frac{ \frac{\mu }{\rho } k^2 - \omega _r^2 \pm \sqrt{\left( \omega _r^2 - \frac{\mu }{\rho } k^2\right) ^2+2\frac{\mu }{\rho } \omega _r^2 k^2 \left( 2+L_c^2 k^2\right) }}{2}, \\ c_f^2&= \frac{\omega ^2}{k^2} = \frac{1}{2} \left[ \frac{\mu }{\rho } \pm \sqrt{\frac{\mu }{\rho }\left( \frac{\mu }{\rho } +2L_c^2 \frac{\omega ^2}{\left( 1+\frac{\omega ^2}{\omega _r^2}\right) }\right) }\right] . \end{aligned} \end{aligned}$$
(52)

Figure 6 shows the frequency and phase velocity predicted by the gradient micro-inertia micropolar model. We can observe that the frequency behavior for the positive root \(\omega ^+\) is similar to the conventional linear behavior which has an imaginary part zero and the real part grows linear with wavenumber (Fig. 6a). For the negative root \(\omega ^-\) we can observe that the real part is zero and the imaginary part exists only for \(\omega >\omega _r\). We can also observe that the phase velocity has no longer an indetermination at \(\omega =\omega _r\) (Fig. 6b). It can be shown that depending on the choice of the characteristic length \(L_c\) the positive solution \(c_f^+\) shows dispersion effects and for \(L_c\rightarrow 0\) it becomes frequency independent as predicted by conventional elasticity (eq. (7)). Figure 6b shows the existence of two waves, one which is somewhat similar to the classical wave, and another one localized (\(\mathfrak {Re}(c_f)=0\), \(\mathfrak {Im}(c_f)\ne 0\), \(|\mathfrak {Im}(c_f)|\) increases in \(\omega \)). For the real wave, we see from eq. (52) that at low frequencies the wave velocity square equals \(\mu /\rho \), and in the limit of high frequencies it is \(\mu /\rho \sqrt{(1+(2L_c^2\omega _r^2)\rho /\mu )}\), i.e., unlike the classical linear elastic case, the phase velocity at high frequencies is larger.

Fig. 6
figure 6

a Normalized angular frequency \(\omega /\omega _r\) as a function of the wavenumber k for the gradient micro-inertia micropolar model (Eq. (49)). b Non-dimensional phase velocity plots for the same model (Eq. (49))

Full size image

This means that the microstructure (higher frequencies) possesses greater velocities compared to the surrounding medium. For the case when \(\alpha \rightarrow 0\) the model (Eq. (52)) shows similar behavior.

It is important to note that we found two solutions for the phase velocity in both micropolar cases that we introduced and both have one of the solution being imaginary only. This can be interpreted as an standing wave that does not propagate in the medium. This second wave can be generated by the source of motion (rupture mechanism) and will oscillate while the second wave will propagate through the medium.

4.2 Comparison with Seismic Experiments

We now test the theory on seismic experiments. We use shear wave dispersion measurements done on water-saturated silica sand with a grain diameter of 0.113 mm and grain density of \(2659\, [kg/m^3]\) (Kimura, 2013). We fit the phase velocity of the micropolar model of eq. (52). The parameters of the model that match the observations are presented in Table 1 (see Fig. 7c). Our calculated shear wave velocities at \(f=0\) and \(f=\infty \) are 200 m/s and 333 m/s respectively. These results are consistent with those found by Kimura (2013) of 195.1 m/s and 297.4 m/s respectively.

Assuming that the micro-inertia of the sand grains can be approximated by \(I\approx \rho r^2\), where r is the radius of the grains, and assuming a value of the eigenfrequency \(\omega _r\) from the experimental data, i.e., a chosen frequency value where the curve bends (see Fig. 7), we can obtain the value of the Cosserat couple modulus \(\mu _c\) (see Table 1). The value of \(\mu _c\) compared to the value of the shear modulus at zero frequency \(\mu _{f=0}=106.36 \, [\text {MPa}]\) is small, which means that the sand grains are able to freely rotate. This confirms that micropolar models are the most relevant ones in order to properly describe wave propagation phenomena in granular material and wave localization (Sulem et al., 2011; Veveakis et al., 2012; Stefanou et al., 2017; Veveakis et al., 2013; Regenauer-Lieb et al., 2013).

Fig. 7
figure 7

Fitting results from Kimura (2013) using the phase velocity predicted in eq. (52)

Full size image
Table 1 Gradient micro-inertia micropolar parameter values
Full size table

5 Discussion and Conclusions

We have shown that micropolar (Eringen, 1999) and Timoshenko’s (Timoshenko & Woinowsky-Krieger, 1959) theories possess the same mathematical structure in 1D problems. This means that for the correct parameter selection, one can model the same physical event with both theories. There is, however, the fundamental difference that Timoshenko’s is a 1D theory while micropolar is a 3D theory. This does not affect the fundamental similarity of both theories for the phase velocity, meaning that if one aims to model a 3D problem with micropolar theory, the phase velocity of shear waves will show the same dispersion properties as it is in the 1D case. In the 1D case also, we can compare the micropolar (or Timoshenko) theory and the original Euler-Bernoulli for beams (Weaver et al., 1990). In the Euler-Bernoulli theory, the cross-section of the beam is perpendicular to the bending line. Timoshenko’s theory allows a rotation between the cross-section and the bending line. This rotation comes from a shear deformation, which is not included in the Euler-Bernoulli theory. This means that the Euler-Bernoulli beam is stiffer. However, if the relation between length and thickness is large enough the error between both models is small, meaning that the Timoshenko (or micropolar) theory works for shorter beam structures.

The application of beam theories for modeling a lithospheric flexure has been mainly done in the static case (Eq. (19)). Plate tectonics assumes that the lithosphere behaves as a thin elastic (plastic) plate overlying an inviscid fluid (asthenosphere) that flexes in response to applied stresses at geological time (i.e. \(>10^6\)yr) (Manríquez et al., 2014). When considering the dynamic equations of motion for micropolar or beams the problem becomes richer in the sense that more effects can be modeled such as the rotatory inertia (Rayleigh 1896). The static case can also be modeled using the dynamic equations. This process is called the quasi-static behavior. It can be done by considering slowly varying boundary conditions of the problem. The numerical simulations of quasi-static behavior will allow us to determine the differences when using the Timoshenko and micropolar theories to model the lithosphere.

For the dynamic modeling of physical phenomena using micropolar theory it is required to properly understand and identify the elastic parameters appearing in the equations. Of particular importance is the Cosserat couple modulus \(\mu _c\) since it allows the coupling between linear elastic and micropolar behaviors. Unlike other studies of shear localization, where the value of the Cosserat couple modulus \(\mu _c\) is assumed to be half the shear modulus \(\mu _c=0.5\mu \) (Sulem et al., 2011; Addessi, 2014), here we connect this value to physically measurable quantities. The physical understanding of the Cosserat couple modulus \(\mu _c\) allows us to find values of the eigenfrequency \(\omega _r\). This eigenfrequency has been observed in experiments for plates however it is laking in seismological data. For this reason we have presented a alternative micropolar model that, based on the same physical concepts as the original model, circumvents the problem of the eigenfrequency \(\omega _r\) laking in seismological data.

From the geodynamical point of view, the lithospheric deformation and delamination are numerically simulated by solving the governing equations of conservation of mass, momentum, and energy (Gerya, 2019). However, from the point of view of this study, modeling the lithospheric deformation and delamination with the micropolar model may help to answer the question of when the lithosphere breaks and delamination appears. When modeling layered materials where the slip between the layers is permitted, the independent bending of layers introduces another degree of freedom associated with the field of rotations of central axes of the layers independent of macroscopic displacement field. Such materials can be modeled as micropolar (Pasternak et al., 2002). In this case, the independent Cosserat rotation corresponds to the gradient of deflection, while the moment stress corresponds to the bending moment per unit area in the layer cross-section (Pasternak et al., 2002).

The oceanic lithosphere undergoes permanent deformation during subduction once the stresses exceed the elastic limit. As a consequence brittle failure occurs in the shallow lithosphere generating earthquakes (Willemann & Davies, 1982; Buffett & Becker, 2012). The connection between generalizations of micropolar theory, namely micromorphic, and the fracturing of the lithosphere and earthquake generation has been previously proposed (Nagahama & Teisseyre, 2000a, 2000b; Teisseyre, 2008; Teisseyre et al., 2008; Nagahama & Teisseyre, 2000b). However, experimental evidence and physical justification of the micromorphic parameters is still lacking in the literature.

From the mathematical point of view, following the pioneering study by Ericksen and Truesdell (1957), micropolar shell and plate theories are an active area of research and they have found room in several engineering applications (Altenbach & Eremeyev, 2012; Neff, 2004; Noor, 1990; Riahi & Curran, 2009; Perić et al., 1994; Selmi et al., 2014; Chandraseker et al., 2009; Chiroiu et al., 2010; Kumar et al., 2011; Fang et al., 2011). The present work is intended to push further these applications for the Earth sciences.