Abstract
The Indus Canyon in the northwestern Indian Ocean has been reported to be the site of numerous submarine mass failures in the past. This study is the first to investigate potential tsunami hazards associated with such mass failures in this region. We employed statistical emulation, i.e. surrogate modelling, to efficiently quantify uncertainties associated with slump-generated tsunamis at the slopes of the canyon. We simulated 60 slump scenarios with thickness of 100–300 m, width of 6–10.5 km, travel distances of 500–2000 m and submergence depth of 250–450 m. These scenarios were then used to train the emulator and predict 500,000 trial scenarios in order to study probabilistically the tsunami hazard over the near field. Due to narrow–deep canyon walls and the shallow continental shelf in the adjacent regions (\(<100\) m water depth), the tsunami propagation has a unique pattern as an ellipse stretched in the NE–SW direction. The results show that the most likely tsunami amplitudes and velocities are approximately 0.2–1.0 m and 2.5–13 m/s, respectively, which can potentially impact vessels and maritime facilities. We demonstrate that the emulator-based approach is an important tool for probabilistic hazard analysis since it can generate thousands of tsunami scenarios in few seconds, compared to days of computations on High Performance Computing facilities for a single run of the dispersive tsunami solver that we use here.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Tsunamigenic submarine landslides may occur in different geological settings around the world, from the gentle slopes of continental margins to steep slopes along volcano-tectonic islands (Harbitz et al. 2014). Such landslides have been the sources of catastrophic tsunamis worldwide. Some examples are the 1929 Grand Banks (Canada) (Fine et al. 2005; Løvholt et al. 2018) and the 1998 Papua New Guinea (more than 2100 deaths) tsunami events (Synolakis et al. 2002; Tappin et al. 2008; Heidarzadeh and Satake 2015). The Storegga Slide, 8 ka BP, generated tsunami waves with run-up heights reaching elevations of ca. 20 m at the Shetland islands (Bondevik et al. 2005). Landslide-induced tsunamis can be destructive in the near field but they tend to lose energy during propagation due to their relatively shorter wavelengths; their far field catastrophic potential, therefore, tends to be small (Fritz et al. 2003; Glimsdal et al. 2013; Heidarzadeh and Satake 2017). The complexity of the source mechanism and the lack of data render the study of landslide tsunamis cumbersome. As in-situ observations of the submarine sliding process are rare, physical and numerical experiments are often utilised to shed light on these events. Various numerical approaches have been employed up to date for landslide tsunami propagation, such as 3D Navier Stokes equation solvers for the generation process and shallow water equation solvers, often including a dispersive term (Boussinesq approximation) for tsunami propagation (Heidarzadeh et al. 2014; Løvholt et al. 2015; Yavari-Ramshe and Ataie-Ashtiani 2016).
Submarine canyons can be found all over the world; at many cases their morphology results from continuous episodes of sediment collapse (Normark and Carlson 2003). Canyons located in the vicinity of shorelines can pose a risk to populated areas when flank collapse gives way to tsunami generation. For example, submarine collapse in the Cook Strait Canyon could lead to tsunami inundation on the coasts of Wellington, in New Zealand (Lane et al. 2016). The steep slopes and narrow widths of submarine canyons are capable of producing destructive tsunamis. Tsunamigenesis by sliding on open continental margins differs from those in submarine canyons (Power et al. 2016). The abrupt depth changes between the canyon and the shelf have an effect on the wave speed; refraction and reflection may also occur when the waves propagate over the canyon walls (Power et al. 2016). Tsunami propagation is sensitive to the canyon size, with the width and length being the most critical parameters; the canyon depth and the distance between the shore and the canyon head play also an important role (Aranguiz and Shibayama 2013). Tsunami run-up and arrival are affected by the geomorphology of the canyon: smaller but faster approaching waves are observed in the locations adjacent to the canyon head, whereas wave amplitude magnification occurs at the sides of the canyon (Aranguiz and Shibayama 2013; Iglesias et al. 2014).
In this work, we assess the potential of submarine collapses in the Indus Canyon, NW Indian Ocean (Fig. 1), to generate tsunami in the near field and quantify the associated uncertainties of future events. The Indus Canyon is approximately 120 km long, 12–17 km wide and its maximum water depth is at the range of 700–1000 m (Fig. 1). Slump deposits and gullies, indicative of submarine mass wasting, have been identified at several locations along the canyon thanks to past bathymetric surveys (von Rad and Tahir 1997; Clift et al. 2014). We use these previously-identified slope failures as landslide tsunami sources to account for a realistic representation of the slump’s geomorphological characteristics. Due to the limited knowledge of these events, we do not attempt to reconstruct past collapse episodes but we quantify the uncertainty of potential tsunamigenic scenarios. To do so, we build a statistical emulator that predicts probabilistic maximum tsunami amplitudes and velocities at specific locations.
a The Indus Canyon. The red and grey stars denote locations of slumping described in von Rad and Tahir (1997) and Clift et al. (2014). The black rectangle and the red star show the location of the slope region in this study (b, c). The colorscale shows the depth in meters. b 2D view of the slope region. The grey dashed lines indicate the bathymetric profile A–A\('\) [which follows closely the seismic profile described in Clift et al. (2014)] and the profile B–B\('\) (d). c 3D view of the slope region. d Bathymetric profiles across the section A–A\('\) and B–B\('\) in the Indus Canyon
2 The Indus Canyon: Geological Setting and Past Slumping Activities
The Indus Canyon is a submarine canyon cutting the Indus shelf on the passive continental margin of India and Pakistan (Figs. 1, 2a). The head of the canyon is located in front of the delta of the Indus River, one of the longest rivers in Asia. The upper and middle parts of the Indus Canyon are characterised by steep erosional walls which gradually give way to an extensive channel-levee system at the lower part of the canyon (von Rad and Tahir 1997). The channel-levee system feeds with sediment the Indus Fan, the second largest deep-sea fan in the world, possibly being active since the late Eocene (Clift et al. 2001). Several canyon systems on the Indus shelf, that contributed to the sediment supply of the Indus Fan, have progressively become inactive and were filled with sediments (Kolla and Coumes 1987; Bourget et al. 2013). The Indus Canyon forms the most recently active canyon at the shelf. Large volumes of sediment from the Indus River basin are being stored in the form of submarine clinoforms at the continental shelf east and west of the canyon (Clift et al. 2014). Among the scientific expeditions that took place in the region, the cruise with R.V. Sonne in 1993 and the most recent expedition (winter 2008/2009) on board R.V. Pelagia have studied the morphology of the Indus Canyon collecting swath bathymetry and seismic reflection data.
The data from the R. V. Pelagia survey provided with a high resolution bathymetric map of the canyon (Clift et al. 2014). One of the major findings of the R. V. Pelagia cruise was that the head of the canyon acts as a depositional area with rapid sediment accumulation rates (Clift et al. 2014). Discharged sediments from the Indus River are accumulating on the head of the canyon. They are then transported towards the lowest parts of the canyon without, however, evidence of significant sedimentation inside the canyon in the last 7 ka (Clift et al. 2014). Changes in the sedimentation rates are possibly linked with falling sea-levels or heavy monsoon periods (Clift et al. 2014). In-situ observations, seismic profiles and sedimentary cores obtained during the 1995 and 2008/2009 scientific expeditions provide evidence for slumping in different parts of the Indus Canyon (von Rad and Tahir 1997; Clift et al. 2014). von Rad and Tahir (1997) linked mass wasting processes on the continental shelf and the steep walls of the canyon with the low sea levels during the Last Glacial Maximum.
Four plausible failure locations discussed in Clift et al. (2014) and von Rad and Tahir (1997) are shown in Fig. 2a by red/grey stars. Slump terraces were observed in the middle part of the canyon (von Rad and Tahir 1997). Scarps at depths of 325 and 620 m, but also as shallow as 200 m, and slump masses have been identified by von Rad and Tahir (1997). At the head of the canyon, erosional features observed at seismic reflection profiles provide evidence of major reworking through slumping (Clift et al. 2014). A seismic profile across the axis of the upper part of the canyon revealed slump deposits on the seabed (Clift et al. 2014). The study area and a bathymetric profile across the axis of the canyon are shown in Fig. 2b–d. The 1D profile A–A\('\) is similar to the seismic profile collected by R.V. Pelagia (Fig. 2b, d). Some thick sedimentary deposits can be observed at the bottom of the slope, NE of the profile (Fig. 2b), that may constitute the slump deposits observed by Clift et al. (2014).
3 Numerical and Statistical Methods
3.1 Numerical Modelling of Tsunami and Slump Sources
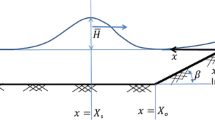
Tsunami generation is strongly affected by the shape parameters and the landslide kinematics (Watts et al. 2005). The rheological properties of the sliding material play an important role during the depositional process (Salmanidou et al. 2018). In this work, we consider the effect of variance of the shape parameters in tsunami generation. We use a slump model based on the empirical formulas developed by Grilli and Watts (2005) and Watts et al. (2005) to compute the tsunami waves induced by rotational slumping or translational sliding. The initial slump model is a simultaneous dipole Gaussian (Fig. 3) with varying length, width and height depending on the source scenario characteristics. This model has been used in several studies of landslide tsunamis in the past (Tappin et al. 2001, 2014; Synolakis et al. 2002; Heidarzadeh and Satake 2015, 2017; Løvholt et al. 2018).
Map showing the location and 3D projection of one of the landslide scenarios (scenario 42 in Table 2) considered in this study
For modelling tsunami propagation, the numerical code JAGURS is used (Baba et al. 2015, 2016). The code solves the nonlinear dispersive long-wave equations using a leapfrog (staggered-grid) scheme on Finite Differences (Baba et al. 2015). A domain-decomposition method was implemented for the parallelisation of the code (Baba et al. 2015). Dispersion of landslide tsunami propagation can be accounted by adding a dispersive term in the long wave equations (Boussinesq approach) (Baba et al. 2015). The use of nested grids allows the refinement of the regions of interest in the computational domain (Baba et al. 2015, 2016). Four grids are used in the numerical experiments with spatial resolutions varying from \(dx=dy=0.0045^\circ\) down to \(0.0005^\circ\) (Fig. 4). The largest domain (grid A) has the coarsest resolution and grid B has a spatial resolution of \(dx=dy=0.0015 ^\circ\). Grids C1 and C2 have the finest resolution (Table 1). Grid B acts as the transition between grids A and C1–C2; a grid ratio of 1 : 3 is chosen in accordance with other numerical studies with JAGURS (Baba et al. 2015, 2016).
Each grid is split into 32 subdomains to run the code in parallel. The time step used for tsunami simulation is \(dt=0.1\) seconds with a total simulation time of \(t_{fin} = 150\) min. A tsunami propagation scenario of 150 min may take roughly 85 h of KNL (KNights Landing) time on the computer cluster used in this study (32 processors on the Cambridge Service for Data Driven Discovery, CSD3, facility). Thirty-four artificial wave gauges measure the free surface elevation and velocity at various locations within the computational domain (Fig. 4). To study wave propagation toward the shoreline, we show here the records of three gauges located at lon. 68.129E, lat. 23.105N in water depth of – 19.22 m (G24 in Fig. 7); lon. 67.97E, lat. 23.508N in water depth of – 15.27 m (G30 in Fig. 7); and lon. 68.347E, lat. 22.711N in water depth of – 30.28 m (G31 in Fig. 7).
We make use of the Global Multi-Resolution Topography (GMRT) synthesis for the bathymetry and elevation data used in the modelling (Ryan et al. 2009). The GMRT synthesis is a product of different sources at multiple resolutions, multibeam sonar data assembled by scientists and institutions have been used to compile the dataset. Thanks to the scientific survey on board R.V. Pelagia (Clift et al. 2014), the Indus Canyon has been mapped in detail with a resolution of \(0.000125^\circ\). These data in combination with lower resolution data (GEBCO 2014, 30 arc-second resolution) have been used to compile the GMRT data used in this study.
The challenge for the design of computer experiments is to minimize the number of runs, considering the high computational cost of each run. A Latin Hypercube Sampling (LHS) approach was taken for its suitable coverage and space filling properties (Morris 1991). It is a random design used to build the emulator over the whole input ranges, irrespective of the subsequent chosen distributions of input parameters that will represent the subset of realistic cases within these ranges. The LHS is only based on the sensitivity of the tsunami response to the landslide uncertain inputs. As a rule of thumb, the minimum sampling size n for an experiment can be chosen as \(n=10p\) where p is the number of input parameters (Loeppky et al. 2009). For this study, we run 60 numerical experiments (Table 2) for the four input parameters: the initial maximum thickness of the material, h; the initial slump width, w; the initial depth of submergence, d; and the characteristic travel distance of the sliding mass, \(s_0\). The ranges of the parameters are selected in close agreement with the observations and the range of validity of the empirical equations (Grilli and Watts 2005; Watts et al. 2005). The range of the aforesaid four parameters are shown in Table 3.
The thickness of the material has a range of [100–300 m] which suggests that a substantial part of the slope may have failed and is in agreement with a reference threshold of \(h<0.2L\) (Watts et al. 2005). From observations of the collapsed slope width geometry, we select a slump width range of [6–10.5 km], where 10.5 km corresponds to the maximum possible width from the one edge of the slope to another (B–B\('\) profile, Fig. 2d). The higher scarp in the canyon is observed at a depth of 200 m (von Rad and Tahir 1997). The lower boundary of the initial depth range is considered to be relatively shallow with a total range of \([250-450 \hbox { m}]\). Yielding a minimum factor of \(d/L=0.005\), this value comes in close agreement with the reference threshold (\(d/L=0.006\)) and the studies of real events (Løvholt et al. 2018). The characteristic distance travelled by the slump \(s_0\) is estimated by: \(2s_0=Rd\phi\) where R is the radius of curvature and \(d\phi\) is the angular displacement (Watts et al. 2005). The distance that the mass travels is often smaller than half of the length of the slump (Watts et al. 2005); here we assume a range of [500–2000 m] for \(s_0\).
The initial length of the slump, the slope angle and the density of the material are kept constant for all the simulation scenarios. As the width of the Indus Canyon is narrow (12–17 km, Fig. 1), a length of \(L=5\) km is considered for the pre-failure slump length. The length is fixed for all the landslide scenarios. The slope angle of the failure plane is roughly \(11.3 ^\circ\). Submarine landslides can occur in both steep and gentle slopes, with the largest occurrences in slopes that can be as small as \(1^\circ\) (Masson et al. 2006; Harbitz et al. 2014). The slump orientation was taken in rough agreement with the slope orientation. Considering that the y-axis has a North–South alignment, the direction of the slump movement was \(225^\circ\) counter-clockwise. The density of the slumping materials is considered to be 2000 kg/m\(^3\).
3.2 Statistical Emulation
Probabilistic Hazard Tsunami Assessment (PTHA) quantify the uncertainty in tsunami hazard and thus risks and impacts (Grezio et al. 2017). Novel stochastic tsunami inversion methods rely on a breadth of observational data (Gopinathan et al. 2017). Statistical emulators form a prominent tool in these forward and inverse problems, as they can be used to assess the results of numerous scenarios in a fast and efficient way. Emulators are stochastic approximations of a computer model (also known as simulator) and thus can help compute the probabilistic distributions of tsunami hazards. In the past few years, novel statistical emulation methods have gained ground (Sarri et al. 2012; Beck and Guillas 2016; Liu and Guillas 2017). Statistical emulators have been used to study earthquake and landslide-induced tsunami hazards in the past (Sraj et al. 2014; Salmanidou et al. 2017; Guillas et al. 2018). For instance, Guillas et al. (2018) used an emulator to predict entire time series of wave heights over the Cascadia subduction zone whereas de Baar and Roberts (2017) used a multi-fidelity approach for the Hokkaido Nansei-oki Tsunami.
Here, we build a Gaussian Process emulator to compute probabilistic results of slumping in the Indus Canyon and quantify the uncertainty of such events. Statistical emulation using Gaussian Process regression is a highly flexible and non-linear interpolation approach. It assumes that the uncertainty in the interpolation follows a multivariate Gaussian distribution in between points in the multidimensional design, so the overall uncertainty distribution can be very complex. We employ here the squared exponential covariance function as it is a standard choice, but the choice of covariance structure usually has a very limited effect, particularly here compared to the overall levels of uncertainties in the hazard itself.
We use 60 tsunami simulation scenarios to train the emulator, a statistical approximation of the tsunami model. Then, 5000 scenarios will be generated using the emulator to enable a more complete (and fast) propagation of the uncertainties from the model parameters (submergence depth, width, thickness and travel distance of the slumps) to the outputs. To predict with the emulator, we use Kriging (Lophaven et al. 2002) and follow an approach similar to the one used in Salmanidou et al. (2017). The emulator approximates the deterministic input–output relationship between the response y(x) and the input parameters \(x=\left( x_1,\cdots ,x_p \right)\) through a stochastic relationship written down as:
It means that the predictor is the sum of a linear regression part—the mean of the Gaussian Process (GP)—and a more complex zero-mean GP z; see for instance Beck and Guillas (2016) for more details on the fitting and predictive abilities of GPs for computer experiments. The number of input parameters is denoted by p (here \(p=4\)). The \(\beta _i\)’s are the coefficients of the linear regression on all the inputs, used as a mean, and z is a Gaussian Process (GP) representing the non-linear part of the variations, unexplained by the mean, which employs another set of coefficients associated with the covariance structure of the GP. Formally, a Gaussian Process is a continuous stochastic process over the input space (hence an uncertain function), for which each marginal distribution of a finite set of unobserved outputs at selected inputs, constrained by the set of observed inputs–outputs, is multivariate normal. For more general details about GPs, see Rasmussen and Williams (2005).
Since there is a limited amount of information about the potential landslide characteristics in the Indus Canyon, we create probability distributions of these inputs that reflect our uncertain knowledge. Since these ranges are finite, we employ a standard beta distribution \(Be(\alpha ,c)\), where \(\alpha\) and c values refer to the shape (skewness) of the distribution (see also Fig. 5), which is commonly used in the literature for such efforts (Sarri et al. 2012; Guillas et al. 2018). We show samples from these distributions for 5000 scenarios in Fig. 5. We chose distributions that spread over the initially attributed ranges exactly. Hence, we selected Be(4, 3) for the maximum thickness and the distance travelled, Be(2, 2) for the width of the slump and Be(3, 4) for the depth above the slump centre (Fig. 5). The distributions present some skewness that reflects possible values taken by these parameters. For example, the input depths in this case have values between 250 and 450 m (as in Table 3) but due to the shape of the distribution (Be(3, 4), Fig. 5c) the most likely values are in the upper part of the slope between 300–350 m, in agreement also with slump scars observations in the canyon (von Rad and Tahir 1997; Clift et al. 2014). Using the emulator, we propagate the uncertainty from these distributions for the 5000 scenarios.
The free surface elevation (a, c and e) and wave velocities (b, d and f) recorded at the three gauges G24, G30 and G31. See also Fig. 7 for gauge locations
Snapshots of the tsunami propagation at t = 10 min (a), 30 min (b), 1 h (c) and 2 h (d) for scenario 42 (see Table 2 for details of this scenario)
Probabilistic predictions of the maximum free surface elevation (a, c, e) and maximum wave velocities (b, d, f) at three gauges. Histograms H1 & H2 show the predictions with (H2-500,000) and without (H1-5000) incorporating uncertainty of the emulator. The purple colour of the histograms results from the overlapping of H1 and H2
4 Probabilistic Landslide Tsunami Analysis
The results of the tsunami simulations for our initial 60 slump scenarios and statistical emulation are shown in this section. The simulation results demonstrate a large variability in the tsunami amplitudes and velocities (Fig. 6). We present here the tsunami waveforms and velocities at three gauges (see locations of gauges G24, G30 and G31 in Fig. 7). Each panel of Fig. 7 includes a snapshot from one simulation (scenario 42), but a similar pattern appears across all simulations. As it has been observed in several other tsunamis (Rabinovich et al. 2006), the first wave is not always the largest in all gauges shown in Fig. 6. Unlike tectonic tsunamis whose energetic waves persist for long times (Rabinovich and Thomson 2007), the waves generated by our slump scenarios generally lose in amplitude and velocity rapidly, mostly after a few cycles; except for G30 which could potentially be due to some wave resonance. The waves reach the northern part of the shelf at approximately 2 h from the generation time, such slow tsunami propagation speed can be attributed to the shallow depth of the area (a depth of 50–100 m, Fig. 1) which yields a tsunami phase velocity of approximately 100 km/h. The maximum tsunami amplitudes are in the range of 0.4–1.5 m in these three coastal gauges while the wave velocities vary from 2 to 12 m/s (neglecting a single peak velocity at 22 m/s).
Tsunami snapshots in Fig. 7 reveal a unique pattern for tsunami propagation in the Indus Canyon. These snapshots belong to Scenario 42 (Table 2) which is a worst-case scenario with maximum free surface elevation of ca. 20 m in the generation region (Fig. 7). The snapshots show that tsunami wave fronts approximately form an ellipse with its major axis in the NE–SW direction while the minor axis strikes NW–SE. Such a shape is controlled by the deeper water depth of the canyon’s axis (NE–SW direction) which provides faster propagation speed along the canyon’s axis. Several secondary and tertiary wave fronts are seen in the snapshots which are the reflected or refracted waves by the canyon’s walls.
Trained by the results of 60 tsunami simulations, the emulator can now be built and used for prediction. Histogram H1 in Fig. 8 represents the predictions of the probability of maximum tsunami amplitudes and maximum velocities at gauges 24, 30, and 31 drawn from 5000 slump scenarios (Fig. 5) According to Fig. 8, the most likely amplitude at G30 is approximately 0.5 m with most likely velocity of approximately 6 m/s out of 5000 tsunami trials.
To incorporate uncertainty from the predictions of the emulator itself, we compute 100 additional predictions for each prediction resulting in \(5000 \times 100= 500,000\) trials. The predictions are sampled from the normal distributions that characterise uncertainties in GP predictions, i.e. the part z(x) in (1). These new predictions are shown as H2 in Fig. 8. It can be seen in Fig. 8 that the two histograms H1 and H2 are very close to each other indicating that the results are robust to the uncertainty of the predictive GP distributions: our sample of 60 initial simulations was informative enough to obtain reliable emulations. Naturally, the spread of H2 is slightly larger than the spread of H1 due to this additional level of uncertainty incorporated.
Having as guidance the probabilistic distributions of the maximum free surface elevation and maximum wave velocities, we can produce hazard maps as shown in Fig. 9. The 34 gauges show the distributions of maximum elevation and velocity over the domain. To make these maps, we consider the 50th and 90th percentiles of the probabilistic predictions at the gauges (i.e. partial summaries of the histograms in Fig. 8). The results shown in Fig. 9 are the outcomes of 5000 and 500,000 trials for tsunami amplitude and velocity, respectively. We note that these results are indicative of variations of tsunami amplitude and velocity depending on the variations of input parameters as shown in Fig. 5. The percentiles show that as the waves propagate toward the coastal areas, the maximum tsunami amplitude is up to 1 m and the tsunami velocity achieves a maximum value of approximately 7 m/s (Fig. 9). These values are not the result of a single simulation, but they are the outcomes of 500,000 trials. The most likely amplitude and velocity overall in all three gauges is approximately in the range 0.2–1.0 m and 2.5–13 m/s, respectively. Our results once more demonstrate the applicability of the statistical emulator for probabilistic predictions of landslide tsunamis, as thousands of scenarios were computed in few seconds and the parameter space was explored fully. The emulator-based probabilistic approach in this study computes 500,000 predictions in ca. 2–3 s per gauge as opposed to around 85 h of computation on a state-of-the art cluster of the numerical code when the dispersive simulation is carried out. It can thus be a prominent solution to replace the numerical runs when fully exploring the parameter space.
5 Conclusions
We produced the first realistic landslide-generated tsunami waves in the Indus Canyon, NW Indian Ocean by dispersive modelling of 60 slump scenarios. We also introduced statistical emulation to this context, in order to create 500,000 scenarios for probabilistic analysis. The slump scenarios had thickness of 100–300 m, width of 6–10.5 km, travel distances of 500–2000 m, and submergence depth of 250–450 m. An uncommon propagation pattern, having an ellipse-shaped feature stretched in the NE–SW direction, was observed including several wave fronts resulting from reflections/refractions from the walls of the canyon and propagation over the shallow shelf.
From our probabilistic analysis, the most likely amplitude and velocity at the study locations is approximately 0.2–1.0 m and 2.5–13 m/s, respectively. Hazards maps based on the emulator’s predictions compute maximum tsunami amplitudes and velocities of approximately 1 m and 7 m/s, respectively, at close to shore locations. The emulator-based probabilistic approach used in this study for landslide tsunami is a powerful tool for probabilistic hazard studies capable of generating hundreds of thousands of tsunami scenarios in few seconds. A major extension of this work would be to produce a more complete hazard mapping at the coast, given more detailed bathymetry and topography data as well as considering (probabilistically) all possible slump locations along the Indus Canyon through enhanced geophysical surveys.
References
Aranguiz, R., & Shibayama, T. (2013). Effect of submarine canyons on tsunami propagation: A case study of the Biobio canyon, Chile. Coastal Engineering Journal, 55, 1350016. https://doi.org/10.1142/S0578563413500162.
Baba, T., Ando, K., Matsuoka, D., Hyodo, M., Hori, T., Takahashi, N., et al. (2016). Large-scale, high-speed tsunami prediction for the Great Nankai Trough Earthquake on the K computer. The International Journal of High Performance Computing Applications, 30(1), 71–84. https://doi.org/10.1177/1094342015584090.
Baba, T., Takahashi, N., Kaneda, Y., Ando, K., Matsuoka, D., & Kato, T. (2015). Parallel implementation of dispersive tsunami wave modeling with a nesting algorithm for the 2011 Tohoku Tsunami. Pure and Applied Geophysics, 172(12), 3455–3472. https://doi.org/10.1007/s00024-015-1049-2.
Beck, J., & Guillas, S. (2016). Sequential design with mutual information for computer experiments (MICE): Emulation of a tsunami model. SIAM/ASA Journal on Uncertainty Quantification, 4(1), 739–766. https://doi.org/10.1137/140989613.
Bondevik, S., Løvholt, F., Harbitz, C., Mangerud, J., Dawson, A., & Svendsen, J. I. (2005). The storegga slide tsunami-comparing field observations with numerical simulations. Marine and Petroleum Geology, 22(1), 195–208. https://doi.org/10.1016/j.marpetgeo.2004.10.003.
Bourget, J., Zaragosi, S., Rodriguez, M., Fournier, M., Garlan, T., & Chamot - Rooke, N. (2013). Late quaternary megaturbidites of the Indus fan: Origin and stratigraphic significance. Marine Geology, 336, 10–23. https://doi.org/10.1016/j.margeo.2012.11.011.
Clift, P. D., Giosan, L., Henstock, T. J., & Tabrez, A. R. (2014). Sediment storage and reworking on the shelf and in the Canyon of the Indus River—Fan system since the last glacial maximum. Basin Research, 26(1), 183–202. https://doi.org/10.1111/bre.12041.
Clift, P., Shimizu, N., Layne, G., Blusztajn, J., Gaedicke, C., Schlüter, H. U., et al. (2001). Development of the Indus Fan and its significance for the erosional history of the Western Himalaya and Karakoram. GSA Bulletin, 113(8), 1039.https://doi.org/10.1130/0016-7606(2001)113<1039:DOTIFA>2.0.CO;2
de Baar, J. H. S., & Roberts, S. G. (2017). Multifidelity sparse-grid-based uncertainty quantification for the Hokkaido Nansei-oki Tsunami. Pure and Applied Geophysics, 174(8), 3107–3121. https://doi.org/10.1007/s00024-017-1606-y.
Fine, I., Rabinovich, A., Bornhold, B., Thomson, R., & Kulikov, E. (2005). The Grand Banks landslide-generated tsunami of November 18, 1929: Preliminary analysis and numerical modeling. Marine Geology, 215(1–2), 45–57.
Fritz, H. M., Hager, W. H., & Minor, H. E. (2003). Landslide generated impulse waves. Experiments in Fluids, 35(6), 505–519.
Glimsdal, S., Pedersen, G. K., Harbitz, C. B., & Løvholt, F. (2013). Dispersion of tsunamis: Does it really matter? Natural Hazards and Earth System Sciences, 13(6), 1507–1526. https://doi.org/10.5194/nhess-13-1507-2013.
Gopinathan, D., Venugopal, M., Roy, D., Rajendran, K., Guillas, S., & Dias, F. (2017). Uncertainties in the 2004 Sumatra-Andaman source through nonlinear stochastic inversion of tsunami waves. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 473(2205), 20170353. https://doi.org/10.1098/rspa.2017.0353.
Grezio, A., Babeyko, A., Baptista, M. A., Behrens, J., Costa, A., Davies, G., et al. (2017). Probabilistic tsunami hazard analysis: Multiple sources and global applications. Reviews of Geophysics, 55(4), 1158–1198. https://doi.org/10.1002/2017RG000579.
Grilli, S. T., & Watts, P. (2005). Tsunami generation by submarine mass failure. I: Modeling, experimental validation, and sensitivity analyses. Journal of Waterway, Port, Coastal, and Ocean Engineering, 131(6), 283–297. https://doi.org/10.1061/(ASCE)0733-950X(2005)131:6(283).
Guillas, S., Sarri, A., Day, S., Liu, X., & Frederic, D. (2018). Functional emulation of the high resolution tsunami modelling over Cascadia. Annals of Applied Statistics, 12(4), 2023–2053. https://doi.org/10.1214/18-AOAS1142.
Harbitz, C., Løvholt, F., & Bungum, H. (2014). Submarine landslide tsunamis: How extreme and how likely? Natural Hazards, 72, 1341–1374.
Heidarzadeh M., Krastel S., & Yalciner A. C. (2014) The state-of-the-art numerical tools for modeling landslide Tsunamis: a short review. In: S. Krastel et al. (Eds.), Submarine mass movements and their consequences, Chap. 43. Advances in natural and technological hazards research (pp. 483–495), vol. 37. Cham: Springer (ISBN: 978-3-319-00971-1).
Heidarzadeh, M., & Satake, K. (2015). Source properties of the 1998 July 17 Papua New Guinea tsunami based on tide gauge records. Geophysical Journal International, 202(1), 361–369.
Heidarzadeh, M., & Satake, K. (2017). A Combined earthquake–landslide source model for the tsunami from the 27 November 1945 Mw 8.1 Makran earthquake. Bulletin of the Seismological Society of America, 107(2), 1033–1040.
Iglesias, O., Lastras, G., Souto, C., Costa, S., & Canals, M. (2014). Effects of coastal submarine canyons on tsunami propagation and impact. Marine Geology, 350, 39–51.
Kolla, V., & Coumes, F. (1987). Morphology, internal structure, seismic stratigraphy, and sedimentation of Indus Fan. American Association of Petroleum Geologists Bulletin, 71, 650–677.
Lane, E., Mountjoy, J., Power, W., & Mueller, C. (2016). Probabilistic hazard of tsunamis generated by submarine landslides in the Cook Strait Canyon (New Zealand). In: Pure and Applied Geophysics, pp. 3757–3774
Liu, X., & Guillas, S. (2017). Dimension reduction for Gaussian process emulation: An application to the influence of bathymetry on tsunami heights. SIAM/ASA Journal on Uncertainty Quantification, 5(1), 787–812. https://doi.org/10.1137/16M1090648.
Loeppky, J. L., Sacks, J., & Welch, W. J. (2009). Choosing the sample size of a computer experiment: A practical guide. Technometrics, 51(4), 366–376. https://doi.org/10.1198/TECH.2009.08040.
Lophaven, S., Nielsen, H., & Sondergaard, J. (2002). DACE—A MATLAB kriging toolbox, version 2.0. IMM-REP, Technical Report
Løvholt, F., Pedersen, G., Harbitz, C. B., Glimsdal, S., & Kim, J. (2015). On the characteristics of landslide tsunamis. Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 373(2053), 20140376. https://doi.org/10.1098/rsta.2014.0376.
Løvholt, F., Schulten, I., Mosher, D., Harbitz, C., & Krastel, S. (2018). Modelling the 1929 Grand Banks slump and landslide tsunami. Geological Society, London, Special Publications, 477, S477-28. https://doi.org/10.1144/SP477.28.
Masson, D., Harbitz, C., Wynn, R., Pedersen, G., & Løvholt, F. (2006). Submarine landslides: Processes, triggers and hazard prediction. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 364(1845), 2009–2039. https://doi.org/10.1098/rsta.2006.1810.
Morris, M. D. (1991). Factorial sampling plans for preliminary computational experiments. Technometrics, 33(2), 161–174.
Normark, W. R., & Carlson, P. R. (2003). Giant submarine canyons: Is size any clue to their importance in the rock record? Special Paper of the Geological Society of America, 370, 175–190.
Power, W., Mountjoy, J., Lane, E., Popinet, S., & Wang, X. (2016). Assessing landslide-tsunami hazard in submarine canyons, using the Cook strait canyon system as an example. Science of Tsunami Hazards, 35, 145–166.
Rabinovich, A.B., & Thomson, R.E. (2007). The 26 December 2004 Sumatra tsunami: Analysis of tide gauge data from the world ocean Part 1. Indian Ocean and South Africa. In: Tsunami and Its Hazards in the Indian and Pacific Oceans, Springer, pp 261–308
Rabinovich, A. B., Thomson, R. E., & Stephenson, F. E. (2006). The Sumatra tsunami of 26 december 2004 as observed in the North Pacific and North Atlantic oceans. Surveys in Geophysics, 27(6), 647–677.
Rasmussen, C. E., & Williams, C. K. I. (2005). Gaussian processes for machine learning (Adaptive Computation and Machine Learning). Cambridge, Massachusetts: The MIT Press (ISBN: 026218253X).
Ryan, W., Carbotte, S., Coplan, J., O’Hara, S., Melkonian, A., Arko, R., Weissel, R., Ferrini, V., Goodwillie, A., Nitsche, F., Bonczkowski, J., & Zemsky, R. (2009). Global multi-resolution topography synthesis. Geochem Geophys Geosyst, 10(Q03014), https://doi.org/10.1029/2008GC002332
Salmanidou, D. M., Georgiopoulou, A., Guillas, S., & Dias, F. (2018). Rheological considerations for the modelling of submarine sliding at Rockall Bank, NE Atlantic Ocean. Physics of Fluids, 30(3), 030705. https://doi.org/10.1063/1.5009552.
Salmanidou, D. M., Guillas, S., Georgiopoulou, A., & Dias, F. (2017). Statistical emulation of landslide-induced tsunamis at the Rockall Bank, NE Atlantic. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 473(2200), 20170026. https://doi.org/10.1098/rspa.2017.0026.
Sarri, A., Guillas, S., & Dias, F. (2012). Statistical emulation of a tsunami model for sensitivity analysis and uncertainty quantification. Natural Hazards and Earth System Sciences, 12(6), 2003–2018. https://doi.org/10.5194/nhess-12-2003-2012.
Sraj, I., Mandli, K. T., Knio, O. M., Dawson, C. N., & Hoteit, I. (2014). Uncertainty quantification and inference of Manning’s friction coefficients using DART buoy data during the Tōhoku tsunami. Ocean Modelling, 83, 82–97. https://doi.org/10.1016/j.ocemod.2014.09.001.
Synolakis, C. E., Bardet, J. P., Borrero, J. C., Davies, H. L., Okal, E. A., Silver, E. A., et al. (2002). The slump origin of the 1998 Papua New Guinea tsunami. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 458(2020), 763–789.
Tappin, D. R., Grilli, S. T., Harris, J. C., Geller, R. J., Masterlark, T., Kirby, J. T., et al. (2014). Did a submarine landslide contribute to the 2011 Tohoku tsunami? Marine Geology, 357, 344–361. https://doi.org/10.1016/j.margeo.2014.09.043.
Tappin, D. R., Watts, P., & Grilli, S. T. (2008). The Papua New Guinea tsunami of 17 July 1998: Anatomy of a catastrophic event. Natural Hazards and Earth System Sciences, 8(2), 243–266. https://doi.org/10.5194/nhess-8-243-2008.
Tappin, D., Watts, P., McMurtry, G., Lafoy, Y., & Matsumoto, T. (2001). The Sissano, Papua New Guinea tsunami of July 1998—offshore evidence on the source mechanism. Marine Geology, 175(1–4), 1–23.
von Rad, U., & Tahir, M. (1997). Late Quaternary sedimentation on the outer Indus shelf and slope (Pakistan): Evidence from high-resolution seismic data and coring. Marine Geology, 138, 193–236.
Watts, P., Grilli, S. T., Tappin, D. R., & Fryer, G. J. (2005). Tsunami generation by submarine mass failure. II: Predictive equations and case studies. Journal of Waterway, Port, Coastal, and Ocean Engineering, 131(6), 298–310. https://doi.org/10.1061/(ASCE)0733-950X(2005)131:6(298).
Wessel, P., & Smith, W. H. (1998). New, improved version of generic mapping tools released. Eos, Transactions American Geophysical Union, 79(47), 579–579.
Yavari-Ramshe, S., & Ataie-Ashtiani, B. (2016). Numerical modeling of subaerial and submarine landslide-generated tsunami waves–recent advances and future challenges. Landslides, 13(6), 1325–1368. https://doi.org/10.1007/s10346-016-0734-2.
Acknowledgements
This research was supported by the EPSRC (EP/P016774/1) network M2D (Models-to-Decisions): Decision making under uncertainty, and the EPSRC Impact Acceleration Account Grant (EP/R51163811). SG and MH acknowledge support from the NERC project (NE/P016367/1) “Tsunami risk for the Western Indian Ocean: steps toward the integration of science into policy and practice” under the Global Challenges Research Fund: Building Resilience programme. SG also acknowledges support from the Alan Turing Institute project “Uncertainty Quantification of multi-scale and multiphysics computer models: applications to hazard and climate models”. This work has been performed using resources provided by the Cambridge Tier-2 system operated by the University of Cambridge Research Computing Service (http://www.hpc.cam.ac.uk) funded by EPSRC Tier-2 capital grant EP/P020259/1. Some of the figures are drafted using the open-source code GMT, (Wessel and Smith 1998). The bathymetry and topography data are derived from the Global Multi-Resolution Topography (GMRT) dataset (Ryan et al. 2009). The authors would like to thank Dr Devaraj Gopinathan for the fruitful discussions and Dr Toshitaka Baba for his advice and help with the numerical simulations.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations'.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Salmanidou, D.M., Heidarzadeh, M. & Guillas, S. Probabilistic Landslide-Generated Tsunamis in the Indus Canyon, NW Indian Ocean, Using Statistical Emulation. Pure Appl. Geophys. 176, 3099–3114 (2019). https://doi.org/10.1007/s00024-019-02187-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00024-019-02187-3