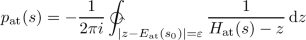Abstract
We consider Hamiltonians of models describing non-relativistic quantum mechanical matter coupled to a relativistic field of bosons. If the free Hamiltonian has an eigenvalue, we show that this eigenvalue persists also for nonzero coupling. The eigenvalue of the free Hamiltonian may be degenerate provided there exists a symmetry group acting irreducibly on the eigenspace. Furthermore, if the Hamiltonian depends analytically on external parameters then so does the eigenvalue and eigenvector. Our result applies to the ground state as well as resonance states. For our results, we assume a mild infrared condition. The proof is based on operator theoretic renormalization. It generalizes the method used in Griesemer and Hasler (Ann Henri Poincaré 10(3):577–621, 2009) to non-degenerate situations, where the degeneracy is protected by a symmetry group, and utilizes Schur’s lemma from representation theory.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We consider mathematical models describing non-relativistic quantum mechanical matter interacting with a quantized field consisting of infinitely many bosons. Such models are used to describe atoms or molecules interacting with the surrounding electromagnetic field or particles in solids interacting with lattice excitation, so-called phonons.
In this paper, we will focus on models describing interaction with the electromagnetic field. In that case, the bosons are photons and have a massless relativistic dispersion relation but the electrons and nuclei are treated as non-relativistic quantum mechanical particles. Such type of models are often referred to as non-relativistic qed.
The dynamics as well as the energy of these models is determined by a self-adjoint operator called the Hamiltonian. For these models, the Hamiltonian is typically bounded from below and the infimum of its spectrum is called ground-state energy. If the ground-state energy is an eigenvalue, the corresponding eigenvector is called ground state. As a consequence of the massless nature of photons, the ground-state energy is not isolated from the rest of the spectrum of the Hamiltonian. The question of existence of a ground state is nontrivial. It has been shown that for models of non-relativistic qed a ground state exists [7, 14, 18, 29, 35] under natural assumptions.
In this paper, we consider models for which the existence of a ground state has been established. We address the question, how the ground state as well as the ground-state energy, E, depend on parameters of the system. For example, one is interested on its dependence on the coupling constant, on the positions of static nuclei for molecules, or on analytic extensions of dilations and translations. The regularity of E as a function of such parameters is of fundamental importance for Born–Oppenheimer approximation, scattering theory, adiabatic theory, cf. [17].
If E were an isolated eigenvalue, like it is in quantum mechanical description of molecules without radiation, then analyticity of E with respect to any of the aforementioned parameters would follow from regular perturbation theory. But in models of qed describing photons, the energy E is not isolated and the analysis of its regularity is a difficult mathematical problem.
The aforementioned question has been addressed in [17]. In that paper, it was shown that if the Hamiltonian of the model depends analytically on some parameter, s, then also the ground state as well as E depend analytically on s. For the proof of the result in [17], a mild infrared regularization was needed. In the special case of the classical spin-boson model, analyticity of the ground state and the ground state energy as a function of the coupling constant could be established without the necessity of an infrared regularization [21]. Analyticity of ground states and ground-state energies as a function of the coupling parameter has been shown in [20] for atoms in the framework of non-relativistic qed. For models of non-relativistic qed and the spin boson model, analytic extensions of dilations have been studied in connection with resonances [5, 6, 8].
Furthermore, we want to mention related results about translation invariant models of quantum field theory, where the Hamiltonian commutes with the generators of translations. In such a situation, one can restrict the Hamiltonian to the generalized eigenspaces corresponding to the eigenvalues \(p \in {\mathord {\mathbb R}}^3\) of the generators of translations. This restriction, H(p), is called fiber Hamiltonian. Motivated by the construction of scattering states, regularity of the infimum of the spectrum for these fiber Hamiltonians H(p) as a function of p has been intensively investigated for various models [1, 4, 9, 10, 12] with results ranging from Hölder continuity up to real analyticity.
A common assumption of the aforementioned analyticity results in [5, 6, 8, 17, 20, 21] is that the ground-state energy of the Hamiltonian describing the massive non-relativistic matter is non-degenerate. However, in many situations this assumption is not met. For example, for almost all atoms, except the noble atoms, the valence shell is not fully occupied and therefore by common physical folklore the ground-state energy is degenerate by rotation symmetry (we have not found a rigorous proof of this fact but there is almost certain physical evidence corroborating it). Even for molecules, where rotation invariance is broken, degeneracy may occur by the spinorial degrees of freedom.
If an eigenvalue of the Hamiltonian describing the non-relativistic quantum mechanical matter is degenerate, the coupling to the quantized field can lift the degeneracy. It may be lifted completely or there might remain some degeneracy of possibly smaller multiplicity.
The lifting of the degeneracy of an eigenvalue of an atomic Hamiltonian due to the coupling of the electromagnetic field is usually referred to as the Lamb shift. The most prominent example is the splitting of the first excited energy level in the hydrogen atom [27]. For a mathematical discussion of such a phenomenon in the framework of non-relativistic qed, see for example [2] and references therein. The Lamb shift was studied in [22] in a situation where the degeneracy of the ground state energy is lifted at second-order formal perturbation theory. It was shown under a mild infrared condition that the ground state as well as the ground-state energy are analytic functions of the coupling constant in a sectorial region around the origin. This is in contrast to perturbation theory of isolated eigenvalues, where by general principles analyticity holds on a whole ball around the origin, cf. [31] and references therein.
In [9], the ground-state energy of the fiber Hamiltonian H(p) for an electron with spin interacting with the quantized electromagnetic field was studied and its regularity properties as a function of p in a neighborhood of zero were investigated. In this case, the coupling to the quantized electromagnetic field does not lift the spin degeneracy, which can be seen using time reversal symmetry and Kramer’s degeneracy theorem [38].
In this paper, we consider the situation where the so-called atomic Hamiltonian, describing the non-relativistic matter, has a discrete eigenvalue. This eigenvalue may be degenerate, but we assume that there exists an underlying symmetry of the full Hamiltonian, which acts irreducibly on the corresponding eigenspace. In that case, the interaction does not lift nor decrease the degeneracy, which turns out to be protected by the symmetry. In particular, we show the existence of an eigenvalue for small but nonzero coupling. Moreover, the main result states that if the Hamiltonian depends analytically on a parameter s, then also the eigenvalue as well as the eigenstate depend analytically on s.
The result is formulated analogously to the main result in [17]. We generalize the main result in that paper to degenerate situations, i.e., we relax the non-degeneracy condition to an irreducibility condition with respect to a symmetry group. Furthermore, we generalize the result in [17] to include general eigenvalues, which may be different from the ground-state energy. This allows the treatment of resonance states, by which we understand eigenvectors of an analytically dilated Hamiltonian.
As in [17] we assume that the interaction is linear in the field operator of the quantized field and that there is a mild infrared regularization. In fact, the main part of the proof also applies to situations arising for the standard model of non-relativistic qed, which is quadratic in the field operators. We isolate the part of the proof which applies to general situations as a corollary of the proof in separate theorem within the last section.
The proof of the main result is based on operator theoretic renormalization [6]. This method is based on an iterated application of the Schur complement also called Feshbach map. One can show that this procedure leads to a fix point, provided infrared behavior of the original operator is not to singular. Using this fixed point, one can construct the ground state as the limit of a convergent sequence. If the original Hamiltonian is analytic, one can show, as in [17], that this approximating sequence is analytic. Analyticity of the eigenvalue as well as the eigenvector will then follow from uniform convergence.
The main difficulty posed by the degeneracy is the iteration procedure of the renormalization analysis. To prove that an iteration step is contracting, one has to control the relevant direction. For this, one adjusts the spectral parameter to make vacuum expectations of the n-th renormalized Hamilton operator small. However, in a degenerate situation the vacuum expectation is a matrix. The key idea is to use the symmetry to conclude that this matrix is in fact a multiple of the identity, using irreducibility and Schur’s lemma. This will then turn the analysis of the relevant direction essentially into a one-dimensional problem, which can then be handled with the methods in [17]. Thus, our result is based on results from [17] as well as from [3]. To this end, we need to show that the symmetry property as well as the irreducibility property are preserved at each iteration step.
Let us give an outline of the paper. In Sect. 2, we introduce the model and state the main result. In Sect. 3, we give a simple but concrete example of a model in which all assumptions of the main result hold. In Sect. 4, we discuss the analysis related to the symmetry which we will need in the proof of the main theorem. In Sect. 5, we perform a first Feshbach map. Note that details about the Feshbach map can be found in Appendix D. We show that the assumptions needed for the Feshbach map to be applicable are satisfied. In Sect. 6, we introduce Banach spaces of matrix valued integral kernels, which describe operators on Fock space. Polydiscs in these spaces will later be needed to show that the iteration procedure of the renormalization analysis converges to a fixed point. In Sect. 7, we show that the first Feshbach map maps the original Hamiltonian into initial polydisc. In Sect. 8, we give an explicit definition of the renormalization transformation, as a composition of the Feshbach map and a rescaling of the energy. In Sect. 9, we show that the renormalization transformation preserves analyticity and symmetry. In Sect. 10, we derive conditions under which an iterated application of the renormalization transformation is possible and converges to a fixed point. Moreover, we show how one can construct the eigenvector, provided the renormalization analysis converges. In Sect. 11, we provide the proof of the main theorem by combining the results which are discussed in previous sections. In this section, we isolate in Theorem 11.1 the part of the renormalization analysis which is not model dependent and can be applied to larger class of Hamiltonians including for example the standard model of non-relativistic qed.
In Appendix A, we review basic properties of antilinear maps. In Appendix B, we collect properties of eigenprojections of isolated eigenvalues. In Sect. C, we review formal definitions of creation and annihilation operators and collect identities and estimates of these operators. We plan do consider applications of the main result in a forthcoming paper elaborating on examples discussed in [28].
2 Model and Statement of Results
We consider the following model. Let the atomic Hilbert space, \({\mathcal {H}}_{\textrm{at}}\), be a separable complex Hilbert space. Let \(\mathfrak {h}= L^2({\mathord {\mathbb R}}^3 \times {\mathord {\mathbb Z}}_2 )\) and let
denote the Fock space, which is used to describe quantum states of the field. Here \(S_0({\mathfrak {h}}^{\otimes 0}):={\mathord {\mathbb C}}\) and for \(n\ge 1\), \(S_n\in \mathcal {L}( {\mathfrak {h}}^{\otimes n})\) denotes the orthogonal projection onto the subspace left invariant by all permutation of the n factors of \({\mathfrak {h}}\). We call \(\mathcal {F}_n\) the space of n-particle subspace. A vector \(\psi \in \mathcal {F}\) can be identified with a sequences \((\psi _n)_{n \in {\mathord {\mathbb N}}_0 }\) such that \(\psi _n \in \mathcal {F}_n\). The vector \(\Omega := (1,0,0,\ldots ) \in {\mathcal {F}}\) is called the Fock vacuum. Furthermore, we shall use the following identification
where the subscript s indicates that the elements are symmetric with respect to interchange of coordinates. For details, we refer the reader to [32] or Appendix C.
A unitary operator \(U \in {\mathcal {L}}(\mathfrak {h})\) can be naturally extended to the linear operator \(\Gamma (U)\) in \({\mathcal {F}}\) by
respectively. An easy calculation shows that \(\Gamma (U)\) is unitary again. For \(\rho > 0\) and \(f \in \mathfrak {h}\), define
It is straight forward to see that \(U_\rho \) is a unitary operator on \(\mathfrak {h}\). The so-called dilation operator on \(\mathcal {F}\) is then given by
For a vector \(z \in {\mathord {\mathbb C}}^N\), we write \(| z | = \left( \sum _{j=1}^N |z_j|^2 \right) ^{1/2}\). To simplify our notation, we define for \(({\varvec{k}},\lambda ) \in {\mathord {\mathbb R}}^3 \times {\mathord {\mathbb Z}}_2\)
We will identify the tensor product of the Fock space \(\mathcal {F}\) with a separable Hilbert space \(\mathcal {H}'\) using the canonical identification
cf. [32]. For \(G \in L^2({\mathord {\mathbb R}}^3\times {\mathord {\mathbb Z}}_2; {\mathcal {L}}(\mathcal {H}'))\), one associates an annihilation operator a(G) as follows. For \(\psi = (\psi _n)_{n =0}^\infty \in \mathcal {H}' \otimes \mathcal {F}\) with the property that \(\psi _n = 0\) for all but finitely many n, we define \(a(G) \psi \) as a sequence of \(\mathcal {H}'\)-valued measurable functions such that the n-th term satisfies a.e.
where the integral on the right-hand side is defined as a Bochner integral. Equation (2.2) defines a closable operator a(G) whose closure is also denoted by a(G). The creation operator \(a^*(G)\) is defined to be the adjoint of a(G) with respect to the natural scalar product in \(\mathcal {F}\). In Appendix C, further properties about creation and annihilation operators can be found.
In this paper, we are interested in the dynamics of bosonic particles of mass zero. The energy, \(\omega (k)\), of such a particle with wave vector k is
We define the free-field Hamiltonian, \(H_{\textrm{f}}\), on a vector \(\psi \in \mathcal {H}' \otimes \mathcal {F}\) as the sequence of \(\mathcal {H}'\) -valued functions whose n-th term is defined by
The domain of \(H_{\textrm{f}}\), denoted by \(D(H_{\textrm{f}})\), is the set of all \(\psi \in \mathcal {H}' \otimes \mathcal {F}\) such that (2.3) is an element of \(\mathcal {H}' \otimes \mathcal {F}\). One verifies that \(H_{\textrm{f}}\) with this domain defines a positive, self-adjoint linear operator on \(\mathcal {H}' \otimes \mathcal {F}\) with purely absolutely continuous spectrum, except for an eigenvalue at 0, with eigenspace consisting of all vectors of the form \((v,0,0,\ldots )\) with \(v \in \mathcal {H}'\).
Let us now fix an atomic Hilbert space \(\mathcal {H}_{\textrm{at}}\). The Hilbert space, describing the atomic degrees of freedom and the quantized field, is given by the tensor product
Let X be an open subset of \({\mathord {\mathbb C}}^\nu \), where \(\nu \in {\mathord {\mathbb N}}\). For each \(s \in X\) let \(H_{\textrm{at}}(s)\) be a densely defined closed operator in \(\mathcal {H}_{\textrm{at}}\). For \(g \ge 0\) and \(s \in X\), we study the operator
where the interaction operator is given by
and \(k\mapsto G_{i,s}(k)\) is an element of \(L^2({\mathord {\mathbb R}}^3\times {\mathord {\mathbb Z}}_2;{\mathcal {L}}(\mathcal {H}_{\textrm{at}}))\) for each \(s \in X\). Note that the operator (2.4) does not need to be self-adjoint, however, under Hypothesis IV (2.4) will be self-adjoint for real s. For \(\mu > 0\) and \(G \in L^2({\mathord {\mathbb R}}^3\times {\mathord {\mathbb Z}}_2;{\mathcal {L}}(\mathcal {H}_{\textrm{at}}))\) we define
which possibly may be infinite.
In the following, we formulate Hypotheses, which will be used in the statements of the main results Theorem 2.10.
Hypothesis I
For \(s \in X\) and \(j=1,2\) the mapping \(s \mapsto G_{j,s}\) is a bounded analytic function that has values in \(L^2({\mathord {\mathbb R}}^3\times {\mathord {\mathbb Z}}_2;{\mathcal {L}}(\mathcal {H}_{\textrm{at}}))\). Moreover, there exists a \(\mu >0\) such that
A consequence of this Hypothesis is that the interaction operator W(s) and its adjoint \(W(s)^*\) are well-defined operators on \(\mathcal {H}_{\textrm{at}} \otimes D(H_{\textrm{f}})\) which are infinitesimally bounded with respect to \(H_{\textrm{f}}\) for all \(s \in X\), cf. Lemma C.1. Hence, the operator \(H_g(s)\) is defined on \(D\big (H_{\textrm{at}}(s)\big ) \otimes D(H_{\textrm{f}})\). Since \(H_\textrm{at}(s)\) is closed, this space is dense in \(\mathcal {H}\) and \(H_g(s)\) is densely defined. Thus, the adjoint \(H_g(s)^*\) exists and is closed. Moreover, \(D\big (H_{\textrm{at}}(s)\big ) \otimes D(H_{\textrm{f}})\) is contained in the domain of \(H_g(s)^*\). Hence, the map \(H_g(s): D\big (H_{\textrm{at}}(s)\big ) \otimes D(H_{\textrm{f}}) \subset \mathcal {H}\rightarrow \mathcal {H}\) has a densely defined adjoint and is therefore closable [25, Theorem 5.28]. Let us now introduce the notation of a symmetry of an operator. Details can be found in Appendix A.
Definition 2.1
Let \(\mathcal {H}\) be a Hilbert space and T an operator in \(\mathcal {H}\) (possibly unbounded). A unitary or antiunitary operator S in \(\mathcal {H}\) is called symmetry of the operator T, if
In that case, we say that T is symmetric or invariant with respect to S. If T is symmetric with respect to all elements of a set \({\mathcal {S}}\) of symmetries, we say T is symmetric or invariant with respect to \({\mathcal {S}}\).
Remark 2.2
We note that the set of symmetries of an operator form a group. More precisely, if \(S_1\) and \(S_2\) are symmetries, then so are \(S_1 S_2\) and \(S_1^{-1}\). Thus, without loss of generality we can assume that we are given a group of symmetries.
To formulate the second Hypothesis, we need the notion of a discrete point in the spectrum of a closed operator. We use the definition as given in [31]. To state it, let us first recall the following theorem. We shall make use of the following notation for open balls in the complex plane
where \(a \in {\mathord {\mathbb C}}\) and \(r > 0\).
Theorem 2.3
([31] Theorems XII.5 (a) & (b)). Suppose that A is a closed operator and let \(\lambda \) be an isolated point of \(\sigma (A)\). Then \(B_\epsilon (\lambda ) \cap \sigma (A) = \{ \lambda \}\) for some \(\epsilon > 0\), and for any \(r \in (0,\epsilon )\) the integral

exists and is independent of r. Moreover, \(P_\lambda \) is a projection, i.e., \(P_\lambda ^2 = P_\lambda \).
Definition 2.4
Let A be a closed operator. A point \(\lambda \in \sigma (A)\) is called discrete if \(\lambda \) is isolated and \(P_\lambda \), given by Theorem 2.3, is finite dimensional. If \(P_\lambda \) is one dimensional, we say \(\lambda \) is a nondegenerate eigenvalue. The dimension of \(P_\lambda \) is called the algebraic multiplicity. The dimension of \(\textrm{Ker}(A - \lambda )\) is called the geometric multiplicity. If algebraic and geometric multiplicity agree and are finite, we say \(\lambda \) is non-defective.
We can now state the second Hypothesis.
Hypothesis II
-
(i)
The mapping \(s \mapsto H_{\textrm{at}}(s)\) is an analytic family in the sense of Kato.
-
(ii)
There exists \(s_0 \in X\) such that \(E_{\textrm{at}}(s_0)\) is a non-defective, discrete element of the spectrum of \(H_{\textrm{at}}(s_0)\).
-
(iii)
If \(E_{\textrm{at}}(s_0)\) is degenerate, there exists a group of symmetries, \({\mathcal {S}}\), such that \(H_\textrm{at}(s) \otimes \mathbb {1}_{\mathcal {F}}\), \(H_{\textrm{f}}\), and W(s) are symmetric with respect to \({\mathcal {S}}\) for all \(s \in X\). Each element of \({\mathcal {S}}\) can be written in the form \(S_1 \otimes S_2\), where \(S_1\) is a symmetry in \(\mathcal {H}_{\textrm{at}}\) and \(S_2\) is a symmetry in \(\mathcal {F}\). Furthermore, the set of symmetries in \(\mathcal {H}_{\textrm{at}}\)
$$\begin{aligned} {\mathcal {S}}_1:= \{ S_1: S_1 \otimes S_2 \in {\mathcal {S}} \} \end{aligned}$$acts irreducibly on the eigenspace of \(H_{\textrm{at}}(s_0)\) with eigenvalue \(E_{\textrm{at}}(s_0)\). Each element of \({\mathcal {S}}_2:= \{ S_2: S_1 \otimes S_2 \in {\mathcal {S}} \}\) leaves the Fock vacuum as well as the one particle subspace invariant and commutes with the operator of dilations, cf. (2.1).
By Hypothesis II and the Kato–Rellich theorem of analytic perturbation theory, [31], together with a symmetry argument one can show the following lemma, which will be needed to formulate the third hypothesis. We note that parts (a) and (b) are well-known results and can be found in [31]. The proof of (c) will require a symmetry argument. We will provide a proof in Sect. 4.
Lemma 2.5
Suppose the situation is as in Hypothesis II. Then there exists an \(\epsilon > 0\) sufficiently small and a neighborhood \(N \subset X\) of \(s_0\), such that the following holds.
-
(a)
\(\{ z \in {\mathord {\mathbb C}}: |z - E_{\textrm{at}}(s_0) | = \varepsilon \} \subset \rho (H_{\textrm{at}}(s))\) for all \( s \in N\).
-
(b)
For all \(s \in N\)
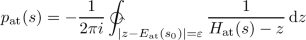 (2.7)
(2.7)defines a projection valued analytic function and the dimension of the range is finite and constant. In particular, \(p_{\textrm{at}}(s_0)\) projects onto the eigenspace of \(E_{\textrm{at}}(s_0)\).
-
(c)
There exists an analytic function \(e_{\textrm{at}}: N \rightarrow {\mathord {\mathbb C}}\) such that for all \(s \in N\)
$$\begin{aligned} H_{\textrm{at}}(s) \upharpoonright \textrm{Ran}\, p_{\textrm{at}}(s) = e_{\textrm{at}}(s) \upharpoonright \textrm{Ran}\, p_{\textrm{at}}(s)\,. \end{aligned}$$For \(s \in N\), the point \(e_{\textrm{at}}(s) \in {\mathord {\mathbb C}}\) is the only point in the spectrum of \(H_{\textrm{at}}(s)\) in a neighborhood of \(E_\textrm{at}(s_0)\). The number \(e_{\textrm{at}}(s)\) is a non-defective, discrete element of the spectrum of \(H_{\textrm{at}}(s)\). Furthermore, \(e_\textrm{at}(s_0) = E_{\textrm{at}}(s_0)\).
If Hypothesis II holds, it follows from a repeated application of Lemma 2.5, that there exists a connected open neighborhood \(X_1 \subset X\) of \(s_0\), an analytic projection valued function \(P_{\textrm{at}}\) on \(X_1\), and an analytic function \(E_{\textrm{at}}\) on \(X_1\) extending \(E_{\textrm{at}}(s_0)\) such that the following holds. For all \(s \in X_1\), the number \(E_{\textrm{at}}(s)\) is in the discrete spectrum of \(H_{\textrm{at}}(s)\) and it is non-defective; moreover,
For any \(s_1 \in X_1\), there exists an \(\epsilon _1 > 0\) and a neighborhood \(N_{1} \subset X_1\) of \(s_1\) such that for all \(s \in N_1\)
and

Henceforth, we denote by \(P_{\textrm{at}}\) and \(E_{\textrm{at}}\) any mappings having the properties stated above on an open connected neighborhood \(X_1 \subset X\) of \(s_0\).
Remark 2.6
In principle, one could use Lemma 2.5 to obtain a maximal analytic extension of \(P_{\textrm{at}}\) and \(E_{\textrm{at}}\). This will not be needed as it does not necessarily improve the main result.
To formulate the third Hypothesis, we use the notion of a reduced resolvent, which is introduced in Remark 2.7.
Remark 2.7
Let \(A:D(A) \subset X \rightarrow X\) be a densely defined closed linear operator and let P be a bounded projection in X such that for \({\overline{P}} = 1 - P\)
Then it is reasonable to study the densely defined operator \(A |_{\textrm{Ran}{\overline{P}} \cap D(A)}\) in \(\textrm{Ran}{\overline{P}}\). If \(z \in \rho (A|_{\textrm{Ran}{\overline{P}} \cap D(A)})\), we shall use the notation \((A-z)^{-1} {\overline{P}}:= ((A-z)|_{\textrm{Ran}{\overline{P}} \cap D(A)})^{-1} {\overline{P}}\), and refer to this expression as the reduced resolvent.
The third Hypothesis will be used to invert for z close to \(E_{\textrm{at}}(s_0)\) the operator \(H_{\textrm{at}}(s)-z\) when restricted to the range of
Aforementioned we formulate this in terms of the reduced resolvent. For this, we note that it follows from well-known properties of projections (2.6), c.f. [31] or Part (a) of Theorem B.1 in the appendix, that the assumptions (2.9), i.e.,
are satisfied for \(s \in X_1\). Thus, the reduced operator \(H_\textrm{at}(s)|_{{\overline{P}}_{\textrm{at}}(s) \cap D(H_{\textrm{at}}(s)))}\) is a densely defined operator in \(\textrm{Ran}{\overline{P}}_{\textrm{at}}(s)\).
Hypothesis III
Hypothesis II holds and there exists a neighborhood \({\mathcal {U}} \subset X_1 \times {\mathord {\mathbb C}}\) of \((s_0,E_{\textrm{at}}(s_0))\) such that for all \((s,z) \in {\mathcal {U}}\) we have \(|E_{\textrm{at}}(s) - z | < 1/2\), \(\sup _{(s,z) \in {\mathcal {U}} } \Vert P_{\textrm{at}}(s) \Vert < \infty \), and
Remark 2.8
We note that one can show that Hypothesis III follows from Hypothesis I and II and the additional assumption that \(H_g(s)\) is an analytic family of type (A) and that a semiboundedness condition holds, see [17].
When dealing with the ground state, we can assume the following additional Hypothesis. It will ensure that in the limit, as the interaction strength tends to zero, the ground state of the interacting system converges to the ground state of the non-interacting system. For a subset \(\Omega \subset {\mathord {\mathbb C}}^n\), we write \(\Omega ^*:= \{ {\overline{z}}: z \in \Omega \}\).
Hypothesis IV
The following holds.
-
(i)
We have \(X = X^*\) and for all \(s \in X\) the identities \(G_{1,s} = G_{2,s}\) and \(H_{\textrm{at}}(s)^* = H_{\textrm{at}}({\overline{s}})\) hold.
-
(ii)
We have \(s_0 \in X \cap {\mathord {\mathbb R}}^\nu \) and \(E_{\textrm{at}}(s_0) = \textrm{inf}\,\sigma (H_{\textrm{at }}(s_0))\).
Definition 2.9
Let \(\mathcal {H}_0\) be a Hilbert space and let \(X \subset {\mathord {\mathbb C}}^d\) with \(X^* = X\). For each \(x \in X\), let a densely defined operator T(x) in the Hilbert space \(\mathcal {H}_0\) be given. We say that T is reflection symmetric if \(T(x)^* = T({\overline{x}})\).
With theses Hypotheses at hand, we can now state the main result.
Theorem 2.10
Suppose Hypotheses I, II, III hold and let
Then there exists a neighborhood \(X_b \subset X\) of \(s_0\) and a positive constant \(g_b\) such that for all \(s \in X_b\) and all \(g \in [0, g_b]\) the operator \(H_g(s)\) has an eigenvalue \(E_g(s)\) with \(\text {d}\) linearly independent eigenvectors \(\psi _{g,j}(s)\), \(j=1,\ldots ,\text {d}\), with the following properties.
-
(i)
The functions \(s \mapsto E_g(s)\) and \(s \mapsto \psi _{g,j}(s)\) for \(j=1,\ldots ,\text {d}\) are analytic functions on \(X_b\).
-
(ii)
Uniformly in \(s \in X_b\), we have \(\lim _{g \rightarrow 0} E_g(s) = E_{\textrm{at}}(s)\) and \(\lim _{g \rightarrow 0} \psi _{g,j}(s) = \varphi _{\textrm{at},j}(s) \otimes \Omega \) for some \(\varphi _{\textrm{at},j}(s) \in \textrm{Ran}P_{\textrm{at}}(s)\).
If in addition Hypothesis IV holds, then \(X_{\textrm{b}} = X_{\textrm{b}}^*\) and
-
(iii)
for all \(s \in X_b \cap {\mathord {\mathbb R}}^\nu \) it holds that \(E_g(s) = \textrm{inf}\,\sigma (H_g(s)).\)
-
(iv)
for all \(s \in X_b \) it holds that \({\overline{E}}_g(s) = E_g({\overline{s}})\).
Remark 2.11
In case that the irreducibility assumptions of Hypothesis II (iii) are not satisfied, the eigenspace of the ground-state eigenvalue is expected to split at higher order in perturbation theory. This phenomenon is known as the Lamb shift and has been considered in the literature [19, 26]. It is natural to assume that degeneracies of eigenvalues are lifted at some order in perturbation theory until a residual degeneracy remains which is protected by a set of symmetries. Analyticity questions for degenerate ground-state eigenvalues, whos degeneracy is lifted in second-order perturbation theory, were investigated in [22] in the framework of generalized Spin–Boson models.
We note that the above result can be used to obtain analyticity in the coupling constant. We note that this will immediately improve the continuity statement, Part (ii), in Theorem 2.10. This will be the content of the following corollary. To state the result first recall that W(s) is infinitesimally \(H_{\textrm{f}}\) bounded, cf. Lemma C.1. Thus, for each \(s \in X\) the map on \({\mathord {\mathbb C}}\)
is an analytic family of type (A). It follows that \((g,s) \mapsto H_g(s)\) is an analytic family, since the weak analyticity of the resolvent implies strong analyticity of the resolvent and to show jointly weak analyticity we can use Hartog’s theorem, cf. [24].
Corollary 2.12
Suppose Hypotheses I, II, III hold and let \(d = \dim \textrm{ker} ( H_{\textrm{at}}(s_0) - E_{\textrm{at}}(s_0) ) \). Then there exists a neighborhood \(X_b \subset X\) of \(s_0\) and a positive constant \(g_b\) such that for all \(s \in X_b\) and all \(g \in B_{g_b}(0)\) the operator \(H_g(s)\) has an eigenvalue \(E_g(s)\) with \(\text {d}\) linearly independent eigenvectors \(\psi _{g,j}(s)\), \(j=1,\ldots ,\text {d}\), with the following property.
-
The functions \((s,g) \mapsto E_g(s)\) and \((s,g) \mapsto \psi _{g,j}(s)\) for \(j=1,\ldots ,\text {d}\) are analytic functions on \(X_b \times B_{g_{\textrm{b}}}(0)\).
Proof
First we extend the parameter space \({\hat{X}} = X \times B_{1}(0)\) and define for \((s,s') \in {\hat{X}}\) and \(g \ge 0\)
Now one easily verifies that \((s,s') \mapsto {\hat{H}}_{g}(s,s') \) satisfies the assumptions I, II, III. Thus, it follows from Theorem 2.10 that there exists a \(g_{\textrm{b}} > 0\) such that \({\hat{H}}_{g_{\textrm{b}}}(s,s')\) has an eigenvalue \(E_{g_{\textrm{b}}}(s,s')\) and an eigenvector \(\psi _{g_{\textrm{b}}}(s,s')\) both depending analytically on \((s,s')\). Now in view of (2.10), we see that they are also eigenvalue and eigenvector of \(H_{(s'g_{\textrm{b}})}(s) \). This shows the corollary. \(\square \)
We note that one can formulate the result in Theorem 2.10 in terms of so-called eigenprojections.
A densely defined operator H in a Hilbert space with the property that
for some antiunitary operator \({\mathcal {J}}\) is called complex-selfadjoint with respect to \({\mathcal {J}}\). To formulate the next corollary, we make another hypothesis.
Hypothesis V
Hypothesis II holds. For all \(g \ge 0\) and \(s \in X\), the operator \(H_g(s)\) is complex-selfadjoint with respect to a antiunitary operator \({\mathcal {J}}\). The bilinear form \(J: V \times V \rightarrow {\mathord {\mathbb C}}\) on \(V:= \textrm{Ran}( P_{\textrm{at}}(s_0) ) \otimes \Omega \) defined by \( J(v_1,v_2 ) = \langle { v_1, {\mathcal {J}} v_2 } \rangle \) is non-degenerate.
Corollary 2.13
Suppose Hypotheses I, II, III hold and let \(d = \dim \textrm{ker} ( H_{\textrm{at}}(s_0) - E_{\textrm{at}}(s_0) ) \). Assume that Hypothesis IV or Hypothesis V holds. Then there exists a neighborhood \(X_b \subset X\) of \(s_0\) and a positive constant \(g_b\) such that for all \(s \in X_b\) and all \(g \in [0, g_b]\) there exists a complex number \(E_g(s)\) and a projection \(P_g(s)\) with rank d such that
with the following properties.
-
(i)
\(s \mapsto P_g(s)\) and \(s \mapsto E_g(s) \) are analytic on \(X_b\).
-
(ii)
\( \lim _{g \downarrow 0} P_g(s) = P_{\textrm{at}}(s) \otimes P_\Omega \) uniformly on \(X_b\).
Proof
Let the situation be as in Theorem 2.10. First we assume that Hypothesis IV holds. By possibly restricting to the intersection of \(X_b\) and \(X_b^*\), we can assume without loss that these sets are equal and nonzero, since both contain \(s_0 \in {\mathord {\mathbb R}}^\nu \). Define the matrix \(M_{a,b}(s) = \langle { \psi _{g,a}({\overline{s}}), \psi _{g,b}(s) } \rangle \), \(a,b=1,\ldots ,d\), for \(s \in X_{\textrm{b}} \cap X_{\textrm{b}}^*\). By linear independence of the \(\psi _{g,j}(s) \) and continuity, we can assume without loss that M is invertible for all \(s \in X_b\) (by possible making \(X_b\) smaller, by intersecting it with a neighborhood of the real line). We define
It is straightforward to verify that this is a projection
Furthermore, since \(\psi _{g,a}\) are eigenvectors we find \(H_g(s) P_g(s) = E_g(s) P_g(s)\) and with Theorem 2.10 (iv)
It is now straight forward using Parts (i) and (ii) of Theorem 2.10 that Parts (i) and (ii) of Corollary 2.13 hold.
Now assume that Hypothesis V holds. In that case, we argue analogously. Define the matrix \(N_{a,b}(s) = \langle { {\mathcal {J}} \psi _a({s}), \psi _b(s) } \rangle \), \(a,b=1,\ldots ,d\), for \(s \in X_{\textrm{b}}\). Again by linear independence of the \(\psi _{g,j}(s) \) and Hypothesis V we find that \(N_{a,b}(s)\) is invertible for \(s=s_0\) and \(g=0\). Now by continuity in s and (ii) of Theorem 2.10, we can assume without loss that N is invertible for all \(s \in X_b\) (by possible making \(X_b\) as well as \(g_{\textrm{b}} > 0\) smaller). It is now again straightforward to verify using (i) and (ii) of Theorem 2.10 that
has the claimed properties. To show the first relation in (2.12), we observe that using (2.11) we find
\(\square \)
3 An Elementary Example
In this section, we give an elementary example for which the conditions of Theorem 2.10 can be easily verified. Resonances and systems involving several non-relativistic massive particles will be treated in a forthcoming paper.
We consider the ground state of the Hamiltonian describing a single charged particle with spin in an attracting potential and interacting with the quantized electromagnetic field in a dipole approximation, see [11, 15, 17] and references therein. Let \(\mathcal {H}_{\textrm{el}} = L^2({\mathord {\mathbb R}}^3; {\mathord {\mathbb C}}^2)\) and let
where \(V: {\mathord {\mathbb R}}^3 \rightarrow {\mathord {\mathbb R}}\) is measurable function such that \(H_\textrm{el}\) is selfadjoint and \(E_{\textrm{el}} = \textrm{inf}\,\sigma (H_{\textrm{el}}) \) is below the essential spectrum of \(H_{\textrm{el}}\). Note that since the Hamiltonian \(H_{\textrm{el}} \) does not affect the spin degrees of freedom, each discrete eigenvalue has even multiplicity. Let us assume that the ground-state energy of \(H_{\textrm{at}}\) is twice degenerate, i.e.,
Thus, there exists a normalized vector \(\phi _{\textrm{el}} \in L^2({\mathord {\mathbb R}}^3)\) such that \(\varphi _{\textrm{el},1} = (\phi _{\textrm{el}},0)\) and \(\varphi _{\textrm{el},2} = (0,\phi _{\textrm{el}})\) are two linearly independent eigenvectors of \(H_{\textrm{el}}\) with eigenvalue \(E_\textrm{el}\). To introduce the interaction with the quantized electromagnetic field, we define
where
is a measurable function describing the so-called photon polarization vectors, which satisfy \(\varepsilon (k,j)= \varepsilon (k/|k|,j)\), \(j=1,2\), and for which the vectors \(\varepsilon (k,1)\), \(\varepsilon (k,2)\), and k/|k| form an orthonormal basis of \({\mathord {\mathbb R}}^3\). The function \(\rho : {\mathord {\mathbb R}}^3 \rightarrow {\mathord {\mathbb R}}\) in (3.2) is a cutoff function, which we choose as \(\rho (k) = \exp (- ( k/\Lambda )^2)\) for some \(\Lambda > 0\). The function \(\chi \in C({\mathord {\mathbb R}}^3)\) in (3.2) serves as a spacial-cutoff and is a function for which we assume that
for some \(\lambda > 0\). Moreover, we introduced the spin matrices
with \(\sigma _1, \sigma _2, \sigma _3\) denoting the Pauli matrices. The interaction is given by
and the Hamiltonian is
Thus, for the Hamiltonian (3.3) we obtain the following result.
Corollary 3.1
Suppose (3.1) holds. Then there exists a positive constant \(g_b\) such that for all \(s \in B_1(0) =: B_1\) and all \(g \in [0, g_b]\) the operator \(H_{\textrm{dip},g}(s)\) has an eigenvalue \(E_{\textrm{dip},g}(s)\) with 2 linearly independent eigenvectors \(\psi _{\textrm{dip},g,j}(s)\), \(j=1,2\), with the following properties.
-
(i)
The functions \(s \mapsto E_g(s)\) and \(s \mapsto \psi _{g,j}(s)\) for \(j=1,2\) are analytic functions on \(B_1\).
-
(ii)
Uniformly in \(s \in B_1\) we have \(\lim _{g \rightarrow 0} E_{\textrm{dip},g}(s) = E_{\textrm{el}}\) and \(\lim _{g \rightarrow 0} \psi _{\textrm{dip}, g,j}(s) = \varphi _{\textrm{el},j} \otimes \Omega \) for some \(\varphi _{\textrm{at},j}(s) \in \textrm{Ran}P_\textrm{at}(s)\).
-
(iii)
for all \(s \in B_1 \cap {\mathord {\mathbb R}}\) it holds that \(E_{\textrm{dip},g}(s) = \textrm{inf}\,\sigma (H_g(s)).\)
-
(iv)
for all \(s \in B_1 \) it holds that \({\overline{E}}_{\textrm{dip},g}(s) = E_{\textrm{dip },g}({\overline{s}})\).
To prove Corollary 3.1, we apply Theorem 2.10. Thus, we need to verify Hypothesis I–IV. First observe that Hypothesis I holds, since for any \(\mu >0\) and \(s \in {\mathord {\mathbb C}}\) we find using (2.5)
Verifying Part (i) of Hypothesis II is trivial, since \(H_{\textrm{el}}\) does not depend on s. Part (ii) of Hypothesis II holds, since \(E_{\textrm{el}}\) is in the discrete spectrum of the self-adjoint operator \(H_{\textrm{el}}\). Since \(E_{\textrm{el}}(s_0)\) is degenerate, we need to find a symmetry group to verify Part (iii) of Hypothesis II. There are two candidates for symmetries:
-
(A)
rotation invariance,
-
(B)
time reversal symmetry.
If the potential V is rotationally invariant, it is natural to use rotation invariance. Otherwise, time reversal symmetry can always be applied. Despite that the proof using time reversal symmetry also works in the rotation invariant case, for expository purposes we discuss both methods below.
(A) Suppose the potential V is rotationally invariant. Thus, assume that
for some function v. Then it is natural to use rotation symmetry or more precisely SU(2) symmetry. To define the SU(2) symmetry we introduce the so-called canonical double covering homomorphism
where \(\pi (U)\) is the unique element of SO(3) such that for \(l = 1,2,3\),
On the one electron Hilbert space \(L^2({\mathord {\mathbb R}}^3;{\mathord {\mathbb C}}^2)\), we define \( (\mathcal {U}_{\textrm{el}}(U) \psi )(x) = U \psi (\pi (U)^{-1} x), \) for \(U \in SU(2)\). We define on \(\mathfrak {h}= L^2({\mathord {\mathbb R}}^3 \times {\mathord {\mathbb Z}}_2 )\), the transformation
with
It is straight forward to see that this is a unitary representation of SO(3) on \(\mathfrak {h}\) and \(\mathcal {U}_\mathcal {F}(R):= \Gamma (\mathcal {U}_{\mathfrak {h}}(R) )\) gives a unitary representation of SO(3) on \(\mathcal {F}\), cf. [23]. Thus, \(\mathcal {U}(U):= \mathcal {U}_{\textrm{el}} \otimes \mathcal {U}_\mathcal {F}(\pi (U))\) yields a unitary representation of SU(2) on \(\mathcal {H}_{\textrm{el}} \otimes \mathcal {F}\). Let \({\mathcal {S}}_{SU(2)} = \{ \mathcal {U}(U): U \in SU(2) \}\). From the transformation properties in [23][Proposition 4.8], it follows that \(H_{\textrm{el}} \otimes \mathbb {1}_\mathcal {F}\), \(H_{\textrm{f}}\), and \(W_\textrm{dip}(s)\) are symmetric with respect to all elements of \({\mathcal {S}}_{SU(2)}\) for every \(s \in B_1\). To show that \({\mathcal {U}}_{\textrm{el}}\) acts irreducibly on
the eigenspace of \(H_{\textrm{el}}\) to the eigenvalue \(E_{\textrm{el}}\), we observe that \(\phi _{\textrm{el}}\) is rotationally invariant as a vector of a one-dimensional subspace of the group of rotations (one dimensional representations of non-commutative groups are trivial [34]). Thus, it follows that
Since the identity representation of SU(2) is irreducible, it follows that \({\mathcal {U}}_{\textrm{el}}(U)\) acts irreducibly on Y. Furthermore, it follows as an immediate consequence of the definition that for each \(U \in SU(2)\) the unitary transformation \(\mathcal {U}_\mathcal {F}(\pi (U))\) leaves the Fock vacuum as well as the one particle subspace invariant and commutes with the operator of dilations. We conclude that also Part (iii) of Hypothesis II holds in case (A).
(B) On \(\mathcal {H}_{\textrm{el}}= L^2({\mathord {\mathbb R}}^3;{\mathord {\mathbb C}}^2)\) time reversal is defined by \( {\mathcal {T}}_{\textrm{mat}}:= K \sigma _2, \) where K denotes complex conjugation in \(\mathcal {H}_{\textrm{el}} \). To define operator of time reversal on the Fock space, we first define it on the one particle space as follows. We define the antiunitary operator \({\mathcal {K}}_\mathfrak {h}\) on \(\mathfrak {h}\) by setting for \(h \in \mathfrak {h}\)
for \(({k},\lambda ) \in {\mathord {\mathbb R}}^3 \times \{1,2\}\). Time reversal symmetry on Fock space is defined by \( {\mathcal {T}}_{\textrm{f}}:= \Gamma (- {\mathcal {K}}_{\mathfrak {h}}), \) cf. [23] (here \( \Gamma (- {\mathcal {K}}_{\mathfrak {h}}) |_{\mathcal {F}_n} = (- {\mathcal {K}}_{\mathfrak {h}})^{\otimes n}\), \(n \in {\mathord {\mathbb N}}\) and \( \Gamma (- {\mathcal {K}}_{\mathfrak {h}}) |_{\mathcal {F}_0}\) is complex conjugation). Time reversal symmetry on the full space \(\mathcal {H}_{\textrm{el}} \otimes \mathcal {F}\) is defined by
A calculation shows, cf. [23, Proposition 4.16], that \({\mathcal {T}}\) is a antiunitary and \(H_{\textrm{el}} \otimes \mathcal {F}\), \(H_{\textrm{f}}\), and \(W_{\textrm{dip}}(s)\) are symmetric with respect to \({\mathcal {T}}\) for all \(s \in B_1\). Since \({\mathcal {T}}_{\textrm{mat}}\) is a symmetry of the self-adjoint operator \(H_{\textrm{el}}\), it follows that \({\mathcal {T}}_{\textrm{mat}}\) leaves the eigenspace Y defined in (3.4) invariant. We will show that \({\mathcal {T}}_\textrm{f}\) acts irreducibly on Y. Suppose \(v \in Y\). Then using \({\mathcal {T}}_{\textrm{f}}^2 = - 1\) and the antiunitarity of \({\mathcal {T}}_{\textrm{f}}\), we find using a Kramer’s degeneracy argument, cf. [23, 30]
Thus, \(\langle v, {\mathcal {T}}_{\textrm{f}} v \rangle = 0\) and Y cannot have a one-dimensional subspace, which is invariant w.r.t. \({\mathcal {T}}_{\textrm{f}}\). Since Y has dimension two, the only subspaces of Y which are invariant with respect to \({\mathcal {T}}_{\textrm{f}}\) are trivial. Thus, \({\mathcal {T}}_{\textrm{f}}\) acts irreducibly on Y. By definition, it is straight forward to see that \({\mathcal {T}}_{\textrm{f}}\) leaves the Fock vacuum as well as the one particle subspace invariant. We conclude that also Part (iii) of Hypothesis II holds in case (B).
To verify Hypothesis III, we want to use the spectral theorem. To achieve this, we assume without loss that the distance between \(E_{\textrm{el}}\) and the rest of the spectrum is greater or equal to one, i.e.,
Otherwise apply Theorem 2.10 to the rescaled operators \({\hat{H}}_{\textrm{el}} = c H_{\textrm{el}}\) and \({\hat{H}}_{\textrm{dip},g}(s) = c {H}_{\textrm{dip},g}(s)\) for some \(c > 0\), such that assumption (3.5) holds. It now follows from the spectral theorem that
Thus, Hypothesis III is verified.
To verify Hypothesis IV, we observe that \(B_1^* = B_1\) and from the definition we see that \(G_{1,s} = G_s^{\textrm{dip}} = G_{2,s}\). The remaining properties of Hypothesis IV follow from the fact that \(H_{\textrm{el}}\) is self-adjoint and does not depend on s.
Thus all assumptions of Theorem 2.10 are verified and Corollary 3.1 now follows.
4 Symmetry Considerations
In this section, we consider consequences of the symmetries which will be used for the renormalization analysis. Elementary definitions and properties are collected in Appendix A. First we discuss Schur’s Lemma for symmetries of an operator. This will be needed to show that certain matrix valued vacuum expectations, occurring in the renormalization analysis, are multiples of the identity. Then we consider general properties of symmetries of analytic family of operators. We will apply these properties to the Hamiltonian defined in Sect. 2. As a main result, see Lemma 4.6, we will be able to assume without loss of generality that \(P_{\textrm{at}}(s)\) is a constant function of s. Moreover, in Lemma 4.8 at the end of this section we prove a crucial property of the Feshbach operator which will be important later during the renormalization procedure.
Definition 4.1
Let V be a subspace of a Hilbert space \(\mathcal {H}\) and let \({\mathcal {S}}\) be a set whose elements are unitary or antiunitary operators on \(\mathcal {H}\). We say that \(S \in {\mathcal {S}}\) acts irreducibly on V if for any subspace W of V with \(S W \subset W\) we have \(W = \{ 0 \}\) or \(W = V\).
The next two lemmas are versions of the well-known Lemma of Schur [33]. The first lemma is for self-adjoint operators. Since analytic continuations of the Hamiltonian are in general non-self-adjoint we need a second lemma for ordinary linear operators, as well.
Lemma 4.2
Let \({\mathcal {S}}\) be a set containing unitary and antiunitary operators which act irreducibly on a complex finite-dimensional Hilbert space V. Let T be a self-adjoint linear operator on V such that
Then there exists a number \(\lambda \in {\mathord {\mathbb R}}\) such that \(T = \lambda \, \mathbb {1}_V\).
Proof
First observe that T has a real eigenvalue, say \(\lambda \). Thus \(T - \lambda \) has a non vanishing kernel. Now S leaves the space \(\textrm{Ker}(T-\lambda )\) invariant since \(\lambda \) is real. Thus, by irreducibility we see that \(\textrm{Ker}(T - \lambda ) = V\). This yields the claim. \(\square \)
Now we want to extend the above lemma to non-self-adjoint operators.
Lemma 4.3
Let \({\mathcal {S}}\) be a set containing unitary and antiunitary operators which act irreducibly on a complex finite-dimensional Hilbert space V. Let T be a linear operator on V such that
Then there exists a number \(\lambda \in {\mathord {\mathbb C}}\) such that \(T = \lambda \, \mathbb {1}_V\).
Proof
Note that there exits a unique decomposition
with Y and Z self-adjoint operators on V. Then it follows from Eq. (4.1) that for S unitary/antiunitary
The uniqueness of the decomposition (4.2) and Lemma A.2 (c) implies
for all \(S \in {\mathcal {S}}\). Thus, Z and Y are multiples of the identity by Lemma 4.2. \(\square \)
The next theorem will allow us to work with the constant projection \(P_{\textrm{at}}(s_0)\) instead of the s dependent projection \(P_{\textrm{at}}(s)\), by means of an invertible analytic family. This is a standard method used in analytic perturbation theory. The theorem below is a version of Theorem XII.12 in [31] incorporating in addition a symmetry property.
Theorem 4.4
Let \(\mathcal {H}\) be a Hilbert space. Let \(P(s) \in {\mathcal {L}}(\mathcal {H})\) be a projection-valued analytic function on a connected, simple connected region of the complex plane X. For \(s_0 \in X\), there exists an analytic family U(s) of bounded and invertible operators on X with the following properties:
-
(a)
\(U(s)\, P(s_0)\, U(s)^{-1} = P(s)\).
-
(b)
If \(s_0\) is real and P(s) is self-adjoint for real s, then we can choose U(s) unitary for real s. Furthermore, \(U({\overline{s}})^* = U(s)^{-1}\) for all \(s \in X \cap X^*\).
-
(c)
If S is a symmetry of P(s), then one can choose U(s) to satisfy
$$\begin{aligned}&S U(s) S^* = U(s) , \qquad \text { if } S \text { is unitary} , \\&S U(s) S^* = (U(s)^{-1})^* , \qquad \text { if } S \text { is antiunitary} . \end{aligned}$$
For the proof, we use as in [31] the following lemma.
Lemma 4.5
Let R be a connected, simply connected subset of \({\mathord {\mathbb C}}\) with \(\beta _0 \in R\) and let \(A(\beta )\) be an analytic function on R with values in the bounded operators on some Banach space \({\mathcal {X}}\). Then for any \(x_0 \in {\mathcal {X}}\), there is a unique function \(f(\beta )\), analytic in R, with values in X obeying
For a proof of the lemma, we refer the reader to [31].
Proof of Theorem 4.4
The detailed proofs of (a) and (b) can be found in Theorem XII.12 of [31]. Here we merely give a sketch. Let \(Q(s) = P'(s)P(s) - P(s) P'(s)\), where \(P'(s) = \frac{\text{ d }}{\text{ d } s} P(s)\). Then a calculation shows that
We now use Lemma 4.5 with \({\mathcal {X}} = {\mathcal {L}}(\mathcal {H})\). Let U(s) be the unique solution of the initial value problem
and let V(s) be the unique solution of the initial value problem
Since
it follows that
On the other hand if \(F = U V\), then F solves the differential equation \(F' = [Q,F]\) with initial condition \(F(s_0)=1\). Since \(F=1\) solves the same initial value problem, it follows by uniqueness that
It follows that U is invertible. Furthermore, a calculation shows that \({\tilde{P}} = U P(s_0) V\) satisfies the initial value problem \({\tilde{P}}' = [Q,{\tilde{P}}]\) with initial condition \({\tilde{P}}(s_0)=P(s_0)\). Thus, from (4.3) we see that \({\tilde{P}}\) and P satisfy the same initial value problem and hence agree. This shows (a). To show (b) let us suppose that \(P(s) = P(s)^*\) for \(s= {\overline{s}}\). By the Schwarz reflection principle, it follows that \(P(s)^* = P({\overline{s}})\) for all \(s \in X \cap X^*\). By the definition of Q, \(Q(s)^* = - Q({\overline{s}})\). Let \({\tilde{V}}(s) = U({\overline{s}})^*\). Then \({\tilde{V}}\) obeys \(\hbox {d} {\tilde{V}} / \text{ d }s = - {\tilde{V}}(s) Q(s)\); \({\tilde{V}}(s_0) = I\). By the uniqueness of solutions of differential equations, \({\tilde{V}}(s) = V(s)\). Thus, \(U({\overline{s}})^*= {\tilde{V}}(s) = V(s) = U(s)^{-1}\), and if s is real, \(U(s)^* = U(s)^{-1}\) and so U(s) is unitary.
It remains to show (c). Suppose first that S is a unitary symmetry of P(s). Then we have by assumption \(S P(s) S^* = P(s)\) and hence \(\frac{\text{ d }}{\text{ d }s} P(s)= S \frac{\text{ d }}{\text{ d } s} P (s) S^*\). It follows that \(S Q(s) S^* = Q(s)\). Using (4.4), we thus obtain
By uniqueness of the initial value problem, Lemma 4.5, we conclude
Now let us suppose that S is an antiunitary symmetry of P(s). Then we have by assumption \(S P(s) S^* = P(s)^*\), and hence taking the adjoint we find \(S P(s)^* S^* = P(s)\). Differentiating we find \(\frac{\text{ d }}{\text{ d } s} P(s) = S \left( \frac{\text{ d }}{\text{ d }s} P (s) \right) ^* S^*\). A calculation now shows that
By (4.4), we have \( ( S U(s_0) S^*)^* = 1 \) and
where we used (4.8) in the last identity. Now from (4.5) we conclude
by uniqueness of the initial value problem, Lemma 4.5. Since \(V(s) = U(s)^{-1}\), by (4.6) and (4.7), the identity in (c) for antiunitary symmetries is now also shown. \(\square \)
Next we shall give a proof of Lemma 2.5 about the eigenprojection of \(P_{\textrm{at}}\) stated in the introduction.
Proof of Lemma 2.5
By Hypothesis II(ii), we can pick \(\epsilon > 0\) such that the only point of \(\sigma (H_{\textrm{at}}(s_0))\) within \( \{ z \in {\mathord {\mathbb C}}: |z-E_{\textrm{at}}(s_0)| \le \epsilon \}\) is \(E_{\textrm{at}}(s_0)\). Since the circle \(\{ z: |z-E_{\textrm{at}}(s_0)| = \epsilon \}\) is compact and the set
is open (Theorem XII.7 in [31]), we can find a \(\delta > 0\) so that \(z \in \rho (H_{\textrm{at}}(s))\) if \( |z-E_{\textrm{at}}(s_0)| = \epsilon \) and \(|s - s_0| \le \delta \). Thus, (a) holds for the set
(b) It follows from (a) that \(p_{\textrm{at}}(s)\), defined in (2.7), exists for all \(s \in N\). By Theorem 2.3, it is a projection. The analyticity of \(p_{\textrm{at}}\) on N now follows from expression (2.7) and Hypothesis II (i). That \(p_{\textrm{at}}(s_0)\) projects onto the eigenspace of \(E_{\textrm{at}}(s_0)\), follows from the non-defectivity assumption of Hypothesis II (ii). The range of \(p_{\textrm{at}}(s_0)\) is finite by assumption. The statement about the dimension of the range of \(p_{\textrm{at}}\) follows, since the rank of continuous projection-valued functions of a connected topological space is constant, cf., Lemma on page 14 in [31].
(c) Observe that \(H_{\textrm{at}}(s)\) leaves the range of \(p_{\textrm{at}}(s)\) invariant by Theorem B.1 (a). First we show that there exist a number \(e_{\textrm{at}}(s) \) such that for all \(s \in N\)
In case \(\dim \textrm{Ran}p_{\textrm{at}}(s_0)=1\), we can use that the dimension of the projection is constant, i.e., \(\dim \textrm{Ran}p_{\textrm{at}} (s) = \dim \textrm{Ran}p_{\textrm{at}}(s_0) = 1\). In that case (4.9) now follows since \(H_{\textrm{at}}(s)\) leaves the range of \(p_{\textrm{at}}(s)\) invariant. In case \(\dim \textrm{Ran}p_\textrm{at}(s_0) > 1\), we will use the symmetry property of Hypothesis II (iii). Since \({\mathcal {S}}_1\) is a symmetry of \(H_{\textrm{at}}(s)\), it follows from the integral representation (2.7) that it is also a symmetry of \(p_\textrm{at}(s)\). By Theorem 4.4, there exists an analytic family U(s) for \(s \in N\) of bounded invertible operators satisfying the assertions of Theorem 4.4 for the projection \(p_{\textrm{at}}(s)\). In particular,
Recall that by Theorem B.1 (a) the operator \(H_{\textrm{at}}(s)\) leaves the range of \(p_{\textrm{at}}(s)\) invariant. Thus by (4.10), the operator
leaves the range of \(p_{\textrm{at}}(s_0)\) invariant. By Theorem 4.4 (c), we have for unitary \(S \in {\mathcal {S}}_1\) that
and for antiunitary \(S \in {\mathcal {S}}_1\) that
Thus, by the lemma of Schur and the irreducibility condition of Hypothesis II (iii), there exists a function \(e_{\textrm{at}}:N \rightarrow {\mathord {\mathbb C}}\) such that
By (4.10), this implies
for all \(s \in N\), i.e., (4.9). Now the analyticity of \(e_{\textrm{at}}(s)\) follows from the analyticity of \(p_{\textrm{at}}(s)\) and \(H_{\textrm{at}}(s)\) and by calculating an inner product with a nonzero vector in the range of \(p_{\textrm{at}}(s)\). Furthermore, it follows from (a) and Theorem B.1 (c) that for all \(s \in N\) we have
This and (4.9) imply that for \(s \in N\) the point \(e_{\textrm{at}}(s) \in {\mathord {\mathbb C}}\) is the only point in the spectrum of \(H_{\textrm{at}}(s)\) in \(B_\epsilon (E_{\textrm{at}}(s_0))\). Thus, \(e_{\textrm{at}}(s)\) is isolated from the rest of the spectrum. Furthermore, it follows, by deforming the contour and Cauchy’s theorem that for \(s \in N\) with \(r(s) = \varepsilon - E_\textrm{at}(s_0) - e_{\textrm{at}}(s)\)

Thus, (4.9) implies that the number \(e_\textrm{at}(s)\) is a non-defective, discrete element of the spectrum of \(H_{\textrm{at}}(s)\). Finally, it follows for \(s=s_0\) from the definition of \(p_{\textrm{at}}(s)\) and (4.9) that \(e_\textrm{at}(s_0) = E_{\textrm{at}}(s_0)\). \(\square \)
In Lemma 4.6, we show that in the proof of the main theorem, Theorem 2.10, we can assume without loss of generality that the following Hypothesis holds.
Hypothesis VI
Hypothesis II holds and \(P_{\textrm{at}}(s) = P_{\textrm{at}}(s_0) \) for all \(s \in X\).
Lemma 4.6
Theorem 2.10 holds, if its assertion holds under the additional Assumption of Hypothesis VI.
Proof
Suppose that Hypotheses I, II, and III hold for some \(s_0 \in X\) and some symmetry group \({\mathcal {S}}\). By restricting to a smaller neighborhood of \(s_0\) we can assume without loss of generality that X is open, connected, simply connected. Then by Theorem 4.4 there exists an analytic family U(s) of bounded invertible operators on X such that
We now define
Then
where
Thus, if \(G_{j,s}\) satisfy Hypothesis I, then also \({\hat{G}}_{j,s}\) satisfies Hypothesis I on any subset \(X_0 \subset X\) on which U(s) and its inverse are uniformly bounded operator-valued functions (by continuity any bounded open \(X_0\) with closure contained in X will work). By analyticity of U(s), it follows that \({\hat{H}}_{\textrm{at}}(s)\) is an analytic family in the sense of Kato, and hence Part (i) of Hypothesis II holds. Now \({\hat{H}}_{\textrm{at}}(s)\) satisfies Part (ii) of Hypothesis II by the invertibility of U(s). Next we consider Part (iii) of Hypothesis II. Since by assumption \({\mathcal {S}}_1\) is a symmetry group for \(H_{\textrm{at}}(s)\) it follows from the integral representation of \(P_{\textrm{at}}(s)\), cf. (2.8), that it is also a symmetry of the latter. Thus, we can assume by Part (c) of Theorem 4.4 that for all symmetries \(S \in {\mathcal {S}}_1\)
If follows for unitary \(S \in {\mathcal {S}}_1\) that
and for antiunitary \(S \in {\mathcal {S}}_1\) that
Thus, \( {\hat{H}}_{\textrm{at}}(s)\) satisfies also Part (iii) of Hypothesis II. Similarly one shows that \({\hat{W}}(s)\) satisfies Part (iii) of Hypothesis II. Finally, if \(H_\textrm{at}(s)\) satisfies Hypothesis III, then by invertibility of U(s) also \({\hat{H}}_{\textrm{at}}\) satisfies Hypothesis III on any subset \(X_0 \subset X\) on which U(s) and its inverse are uniformly bounded operator-valued functions. Thus, we have shown that \({\hat{H}}_g(s)\) satisfies Hypothesis I, II, and III on an open set \(X_0\) containing \(s_0\).
Furthermore, Hypothesis VI holds for \({\hat{H}}_g(s)\) by construction. Thus, by assumption the assertion of the main result, Theorem 2.10, holds for the operator \({\hat{H}}_g(s)\). We conclude that there exists a neighborhood \(X_b \subset X_0\) of \(s_0\) and a positive constant \(g_b\) such that for all \(g \in [0,g_{\textrm{b}})\) and \(s \in X_{\textrm{b}}\) the operator \({\hat{H}}_g(s)\) has an eigenvalue \({\hat{E}}_g(s)\) with \(\text {d}:= \dim \textrm{ker} ( {\hat{H}}_{\textrm{at}}(s_0) - E_{\textrm{at}}(s_0) ) = \dim \textrm{ker} ( {H}_{\textrm{at}}(s_0) - E_{\textrm{at}}(s_0) ) \) linearly independent eigenvectors \({\hat{\psi }}_{g,j}(s)\), \(j=1,\ldots ,\text {d}\), all depending analytically on \(s \in X_{\textrm{b}}\). By the invertibility of U(s) we see that the operator \(H_g(s)\) has the eigenvalue \({E}_g(s):= {\hat{E}}_g(s)\) with \(\text {d}\) linearly independent eigenvectors \(\psi _{g,j}(s):= ( U(s) \otimes \mathbb {1}) {\hat{\psi }}_{g,j}(s) \), \(j=1,\ldots ,\text {d}\). They also depend analytically on s, since U(s) and its inverse depend by Theorem 4.4 analytically on s. This shows (i) of Theorem 2.10. Similarly one verifies (ii) of Theorem 2.10 by using the uniform boundedness of U(s) and \(U(s)^{-1}\). Finally, suppose that the operator \(H_g(s)\) satisfies Hypothesis IV. Then by Theorem 4.4 (b) we can choose the family of invertible operators U(s) to be unitary for real s such that \(U({\overline{s}})^* = U(s)^{-1}\) for all \(s \in X\). Thus, also \({\hat{H}}_g(s)\) satisfies Hypothesis IV and moreover it is isospectral to \(H_g(s)\) for real s. In that case, we have for real \(s \in {\mathord {\mathbb R}}^\nu \cap X_{\textrm{b}}\) that
This implies (iii) of Theorem 2.10.
Thus, we have shown that the assertion of Theorem 2.10 also holds for the original operator \(H_g(s)\). \(\square \)
The next lemma will be used to show that the so-called relevant direction in the renormalization analysis is one dimensional. For this, let us introduce the following definition. For V, a finite dimensional complex vector space, and a bounded operator \(T \in {\mathcal {B}}(V \otimes \mathcal {F})\) define \( \langle T \rangle _\Omega \) as the unique operator on V such that
for all \(v_1, v_2 \in V\). Note that it is straight forward to see that
which follows since for all \(v_1, v_2 \in V\) we have
Lemma 4.7
Let V be a finite-dimensional complex vector space and let \(T \in {\mathcal {B}}(V \otimes \mathcal {F})\). Assume that T is symmetric with respect to a set of symmetries \({\mathcal {S}}\) such that every element can be written in the form \(S_1 \otimes S_2\), where \(S_1\) is a symmetry in V and \(S_2\) is a symmetry in \(\mathcal {F}\) leaving the Fock vacuum invariant. Assume that \({\mathcal {S}}_1:= \{ S_1: S_1 \otimes S_2 \in {\mathcal {S}} \}\) acts irreducibly on V. Then there exists a number \(c \in {\mathord {\mathbb C}}\) such that
Proof
For all \(S_1 \otimes S_2 \in {\mathcal {S}}\), we have the following symmetry property. For A an operator or a number let \(A^\#\) stand for A or \(A^{*}\) whether the symmetry \(S_1 \otimes S_2 \) is unitary or antiunitary, respectively. Moreover, we write \(c^* = {\overline{c}}\) if \(c \in {\mathord {\mathbb C}}\). For all \(v_1, v_2 \in V\), we have
where in the last line we used (4.12). Thus,
The claim now follows from Schur’s Lemma 4.3 and the irreducibility assumption. \(\square \)
To conclude this section, we show that the Feshbach transformation preserves symmetry properties. A detailed review of the properties of the Feshbach–Schur map, which was introduced in [3], is given in Appendix D.
Lemma 4.8
Let (H, T) be a Feshbach pair for \(\chi \). Assume that there exists a group of symmetries \({\mathcal {S}}\) of the operator H, T and \(\chi \). Then \({\mathcal {S}}\) is also a group of symmetries for the Feshbach operator \(F_\chi (H,T)\).
Proof
This follows from the definition of the Feshbach operator given in Eq. (D.1). Let \(S \in {\mathcal {S}}\) be a symmetry and let \(A^\#\) stands for A or \(A^{*}\) if S is unitary or antiunitary, respectively. Then inserting \(S^* S = \mathbb {1}\), we find
\(\square \)
5 The Initial Hamiltonian
The first step of the operator-theoretic renormalization analysis is to prove that \(H_g(s)\) and \(H_0(s)\) are a Feshbach pair for a suitable choice for the projection operator, see (5.3). This is the content of Theorem 5.1. For a definition as well as the properties of Feshbach pairs, we refer to Appendix D. Moreover, we will show in this section, that the associated Feshbach operator, cf. (D.1), is an analytic function of s and the spectral parameter z and that it inherits the symmetry property of the original operator. This will be shown in Theorem 5.7.
We choose smooth functions \(\chi , {\overline{\chi }} \in C^\infty ({\mathord {\mathbb R}}; [0,1] )\) such that \(\chi ^2 + {\overline{\chi }}^2 = 1\) and
For \(\rho > 0\), we then define
and set \(\chi _\rho := \chi (H_{\textrm{f}} / \rho )\), \({\overline{\chi }}_\rho := {\overline{\chi }}(H_{\textrm{f}} / \rho )\). Next we define
Note that (5.1) and (5.2) are commuting, non-zero, bounded operators satisfying \( \overline{\varvec{\chi }}_\rho (s)^2 + \varvec{\chi }_\rho (s)^2 = 1, \) which are not necessarily self-adjoint. Moreover, we set
The following theorem gives us the conditions for which we can define the so-called first Feshbach operator.
Proposition 5.1
Suppose Hypothesis I, II, and III hold, and let \({\mathcal {U}} \subset X_1 \times {\mathord {\mathbb C}}\) be given by Hypothesis III. Then there is a \(g_{\textrm{b}} > 0 \) such that for all \(g \in [0,g_{\textrm{b}})\) and all \((s,z) \in {\mathcal {U}}\), the pair \((H_g(s)-z,H_0(s)-z)\) is a Feshbach pair for \(\varvec{\chi }(s)\). Furthermore, one has the absolutely convergent expansion on \({\mathcal {U}}\)
For the proof of this proposition, we make use the following lemma.
Lemma 5.2
Suppose Hypothesis II and III hold. Then
and
Proof
We recall that by definition, cf. Eqs. (5.2) and (5.3), \(\overline{\varvec{\chi }}(s) = {\overline{P}}_{\textrm{at}}(s) \otimes \mathbb {1}+ P_{\textrm{at}}(s) \otimes {\overline{\chi }}(H_{\textrm{f}} )\). First we estimate (5.6). Applying the triangle inequality, we obtain
We estimate (5.8) by the spectral theorem and find
where the right-hand side is finite by Hypothesis III. To estimate (5.7), we use again the spectral theorem and find
where the last bound follows from Hypothesis III. This shows (5.6).
Next we similarly show (5.5). Using the triangle inequality, we find
We obtain for the second term in (5.9) by the spectral theorem
where the right-hand side is again finite by Hypothesis III. To estimate the first term in (5.9), we use again the spectral theorem and find from Hypothesis III
This completes the proof. \(\square \)
Lemma 5.3
Let Hypothesis I hold. Then
Proof
This follows from Eq. (C.4) in Appendix C and Hypothesis I. \(\square \)
Lemma 5.4
Suppose Hypothesis I, II, and III hold. Then
Proof
Follows from Lemma 5.2, and (5.10) respective (5.11). \(\square \)
Now we are ready to prove Proposition 5.1. We will use the following notation.
Proof of Proposition 5.1
Let \({\mathcal {U}} \subset X \times {\mathord {\mathbb C}}\) be given by Hypothesis III. First we show the Feshbach property. For this, we need to show that \(H_g(s)\) and \(H_0(s)\) are closed operators on the same domain such that the assumptions (a’), (b’) and (c’) of Lemma D.3 hold.
Suppose \((s,z) \in {\mathcal {U}}\). To prove that \(H_g(s) = H_0(s) + g W(s)\) is closed on \(D(H_0(s))\) for all \(g > 0\), it suffices to prove that W(s) is infinitesimally bounded with respect to \(H_0(s)\), cf. [37, Theorem 5.5].
Note that \(H_{\textrm{at}}(s)\) leaves the ranges of \(P_{\textrm{at}}(s)\) and \({\overline{P}}_{\textrm{at}}(s)\) invariant, cf. Theorem B.1. Thus, by the spectral theorem \(H_0(s)\) leaves the range of \(P_{\textrm{at}}(s) \otimes \mathbb {1}\) invariant. Moreover, for \(w = z - 1\) we have \(w \in \rho ( H_0(s) |_{\textrm{Ran}P_{\textrm{at}}(s) \otimes D(H_{\textrm{f}})})\), since \(\sup _{r \ge 0}|E_{\textrm{at}}(s) - w + r |^{-1} \le \sup _{r \ge 0}(1 -| E_{\textrm{at}}(s) - z | + r )^{-1} \le 2\), and
where we used that by Hypothesis III we have \(|E_\textrm{at}(s) - z| < 1/2\) and the last inequality of (5.12). On the other hand by the spectral theorem and Hypothesis III, we find
In particular, for normalized \(\varphi \in D(H_{\textrm{at}}(s)) \otimes D(H_{\textrm{f}})\) we obtain using the triangle inequality together with (5.12) and (5.13)
Combining (5.10) and (5.14) we see that, for all \(\phi \in D(H_{\textrm{at}}(s))\otimes D(H_{\textrm{f}})\) and \(\epsilon > 0\)
with constants \(C_0,C_1,C_2\). This shows that W(s) is infinitesimally bounded with respect to \(H_0(s)\) and thus we have shown that \(H_g(s) = H_0(s) + g W(s)\) is closed on \(D(H_0(s))\) for all \(g > 0\).
Next we verify the criteria for Feshbach pairs from Lemma D.3. On \(D(H_{0}(s))\), we have by definition
Since this is valid on every core of \(H_0(s)\), we get that Condition \((a')\) of that Lemma D.3 is satisfied. By Lemma 5.2, \(H_0(s)-z\) is bounded invertible on \(\textrm{Ran}\overline{\varvec{\chi }}(s)\). Moreover, by Lemma 5.4 we get that there exists a \(g_b > 0\) such that
for all \(g \in [0, g_b)\). This proves (b’) and (c’) of Lemma D.3 and hence completes the proof that \((H_g(s)-z, H_0(s) - z)\) is a Feshbach pair for \(\varvec{\chi }(s)\). By choosing \(g_b > 0\) sufficiently small it follows that the Neumann series
converges uniformly for \((s,z)\in \mathcal {U}\). \(\square \)
Remark 5.5
We note that if Hypothesis II holds, then it is straight forward to see using (2.8) that \(\varvec{\chi }_\rho \) and \(\overline{\varvec{\chi }}_\rho \) commute with the group of symmetries \({\mathcal {S}}\) given by Hypothesis II (iii).
Provided the right-hand side exists, i.e., the Feshbach pair property holds, cf. Proposition 5.1, we define the so-called first Feshbach operator
where
Note that by the choice of the projection \(\varvec{\chi }(s)\) it follows that (5.15) and (5.16) leave the range of \(P_{\textrm{at}}(s) \otimes 1_{H_{\textrm{f}} \le 1} \) invariant. Furthermore, we define the following restrictions, which are for the isospectrality property sufficient to study, cf. Theorem D.2,
Note that as operators acting on the range of \(P_{\textrm{at}}(s) \otimes 1_{H_{\textrm{f}} \le 1}\) we have
We shall refer to (5.19) as the first Feshbach operator as well. Henceforth, we shall assume Hypothesis VI and so \(H_g^{(0)}(s,z)\) acts on the Hilbert space
Remark 5.6
Note that the notation introduced in (5.15)–(5.18) is similar to the one in [17] but not exactly the same.
In the following theorem, we show that the first Feshbach operator \({H}_g^{(0)}[s,z]\) is analytic on a suitable subset of \(X \times {\mathord {\mathbb C}}\). Moreover, we show that this operator is isospectral to \(H_g(s) - z\), in the sense of Theorem D.2. Furthermore, the first Feshbach operator commutes with the set of symmetries \({\mathcal {S}}\) from Hypothesis II. Note that in the theorem below, we make use of the auxiliary operator \(Q_{\chi }\) defined in Eq. (D.2).
Theorem 5.7
Suppose Hypothesis I, II, and III hold, and let \({\mathcal {U}} \subset X_1 \times {\mathord {\mathbb C}}\) be given by Hypothesis III. Then there is a \(g_{\textrm{b}} > 0 \) such that for all \(g \in [0,g_{\textrm{b}})\) and all \((s,z) \in {\mathcal {U}}\), the pair \((H_g(s)-z,H_0(s)-z)\) is a Feshbach pair for \(\varvec{\chi }(s)\) and the following holds on \({\mathcal {U}}\).
-
(a)
The map \((s,z) \mapsto H_g^{(0)}[s,z]\) is analytic. The map \((s,z) \mapsto Q_{\varvec{\chi }}(s,z)\) is analytic.
-
(b)
\(H_g(s)-z: D(H_0(s)) \subset \mathcal {H}\rightarrow \mathcal {H}\) is bounded invertible if and only if \({H}_g^{(0)}[s,z]\) is bounded invertible.
-
(c)
The following maps are linear isomorphisms and inverses of each other:
$$\begin{aligned}&\varvec{\chi }(s) : \textrm{Ker}\,(H_g(s) - z ) \rightarrow \textrm{Ker}\, {H}_g^{(0)}[s,z]\, , \\&Q_{\varvec{\chi }}(s,z) : \textrm{Ker}\, {H}_g^{(0)}[s,z] \rightarrow \textrm{Ker}\, (H_g(s) - z )\,. \end{aligned}$$
Furthermore, let \({\mathcal {S}}\) be the set of symmetries given in Hypothesis II, then
-
(d)
\(S {H}_g^{(0)}[s,z] \, S^* = {H}_g^{(0)}[s,z]\), for all unitary \(S \in {\mathcal {S}}\).
-
(e)
\(S {H}_g^{(0)}[s,z] \, S^* = \left( H_g^{(0)}[s,z]\right) ^*\) , for all antiunitary \(S \in {\mathcal {S}}\).
In addition, if Hypothesis IV is valid, we have for \((s,z) \in {\mathcal {U}} \cap {\mathcal {U}}^*\) that
-
(f)
\({H}_g^{(0)}[s,z]^* = {H}_g^{(0)}[{\overline{s}}, {\overline{z}}].\)
Lemma 5.8
Let Hypothesis I hold. Then the mapping \(s \mapsto W(s) (H_{\textrm{f}} + 1 )^{-1/2}\) is analytic on X.
Proof
[17, Lemma 12] \(\square \)
Proof of Theorem 5.7
Let \(g_{\textrm{b}} > 0\) be such that the assertion of Proposition 5.1 holds. Then the Feshbach pair property holds by Proposition 5.1.
(a) From (5.19) and the analyticity of \(s \mapsto E_{\textrm{at}}(s)\), the analyticity of \((s,z) \mapsto H_g^{(0)}(s,z)\) will follow provided \((s,z) \mapsto W_g^{(0)}(s,z)\) is analytic. Since that function can be obtained by a restriction to a subspace of the function \((s,z) \mapsto {\tilde{W}}_g^{(0)}(s,z)\) the analyticity of the former will follow from the analyticity of the latter. To show that the latter is analytic, we use the absolutely convergent expansion given in (5.4), which is granted by Proposition 5.1. Since absolutely convergent sequences of analytic functions have an analytic limit, it remains to show that each summand in the following series is analytic in s and z
where in the last equality we used associativity of composition and that \(H_{\textrm{f}}\) commutes with \(\varvec{\chi }(s)\) and \(\overline{\varvec{\chi }}(s)\). First observe that by Lemma 5.8, \(W(s) (H_{\textrm{f}} + 1)^{-1}\) is analytic. Hence to establish analyticity of (5.20), it remains to prove analyticity of
To this end, we observe that from the definition of \(\overline{\varvec{\chi }}(s)\) we can write
The analyticity of the second term in (5.21) follows by means of the spectral theorem from the fact that for every \(r \ge 0\) the function \((s,z) \mapsto (r + 1 )(E_{\textrm{at}}(s) + r - z)^{-1} {\overline{\chi }}_1(r)\) is analytic on \({\mathcal {U}}\) (by Hypothesis III we have on \({\mathcal {U}}\) that \(|E_{\textrm{at}}(s) - z | <1/2\) and so the denominator does not vanish for \(r \ge 0\) for which \({\overline{\chi }}_1(r) \ne 0\)) and is uniformly bounded in \(r \ge 0\). The analyticity of the first term on the r.h.s of (5.21) follows by means of the spectral theorem from the fact that the function \((s,z) \mapsto (r + 1 )(H_{\textrm{at}}(s) + r - z)^{-1} {\overline{P}}_{\textrm{at}}(s)\) is bounded uniformly in \(r \ge 0\) by the estimate in Hypothesis III and for every \(r \ge 0\) the function is analytic on \({\mathcal {U}}\) by Proposition B.2 and Hartog’s theorem, cf. [24]. This concludes the proof that \({H}_g^{(0)}(s,z)\) is analytic on \({\mathcal {U}}\). From Eq. (D.2), we see that the analyticity of \(Q_{\varvec{\chi }}(s,z)\) is established analogously as the analyticity of (5.20).
Part (b) follows in view of Hypothesis VI from Theorem D.2 (a) by making the choice \(Y = \mathcal {H}_{\textrm{red}} = \textrm{Ran}\big (P_{\textrm{at}}(s_0) \otimes 1_{H_{\textrm{f}} \le 1 } \big )\). Part (c) follows from Theorem D.2 (b). Statements (d) and (e) follow from Lemma 4.8 and the properties of the symmetry group given by Hypothesis II (iii).
Let us now show Part (f). First observe that without loss the neighborhood \(X_1 \subset X\) of \(s_0\) on which \(P_{\textrm{at}}\) is defined satisfies \(X_1^* = X_1\) (otherwise take the intersection of the two sets). Now for \(s \in {\mathord {\mathbb R}}\cap X_1\) close to \(s_0\) we find from (2.8) with \(s_1 = s_0\) and \(E_\textrm{at}(s_0) \in {\mathord {\mathbb R}}\) using Hypothesis IV (i), that
Since both sides of (5.22) are analytic functions of s on \(X_1\), we conclude that (5.22) holds for all \(s \in X_1\) (cf. the unique continuation property of analytic functions, e.g., [24]). Furthermore, it follows from Hypothesis IV (i) and (2.4) that
for all \(s \in X\). Now we recall that for any densely defined, closed operator A in \(\mathcal {H}\) and \(z \in \rho (A)\) we find \({\overline{z}} \in \rho (A^*)\) and
This follows directly from [37, Theorem 4.17(b)] as is shown in the proof of Theorem 5.12 in [37]. Using the fact that \({\tilde{H}}_g(s,z)\) leaves the range of \(P_{\textrm{at}}(s_0) \otimes 1_{H_{\textrm{f}} \le 1}\) invariant we find for \((s,z) \in {\mathcal {U}} \cap {\mathcal {U}}^*\) that
where the second to last identity can be seen by taking the adjoint of (5.4) and using (5.22), (5.23), and (5.24). \(\square \)
6 Banach Space of Hamiltonians
To control the renormalization transformation, in particular proving its convergence, it is convenient to introduce suitable Banach spaces of integral kernels, cf. [3, 17]. A generalization to matrix-valued integral kernels is a canonical choice to accommodate degenerate situations. In this section, we follow closely the definition and notation given in [17].
The renormalization transformation is defined on a subset of \(\mathcal {L}(\mathcal {H}_{\textrm{red}})\) that will be parameterized by vectors of a Banach space. We begin with the definition of this Banach space.
Let \({\mathcal {L}}({\mathord {\mathbb C}}^d)\) denote the space of linear maps A from \({\mathord {\mathbb C}}^d\) to \({\mathord {\mathbb C}}^d\) equipped with the operator norm \(\Vert A \Vert _{\textrm{op}}:= \sup \{ |A x |: |x| \le 1 \}\). The Banach space \(\mathcal {W}_{0,0}\) is the space of continuously differentiable functions
where \(w'(r):=\partial _r w(r)\). For \(m,n\in {\mathord {\mathbb N}}\) with \(m+n\ge 1\) and \(\mu >0\), we set
where \(B:=\{k\in {\mathord {\mathbb R}}^3\times \{1,2\}:|k| < 1\}\) and we defined
and
That is, \(\mathcal {W}_{m,n}\) is the space of measurable functions \(w_{m,n}:B^{m+n}\rightarrow \mathcal {W}_{0,0}\) that are symmetric with respect to all permutations of the m arguments from \(B^{m}\) and the n arguments from \(B^{n}\), respectively, such that \(\Vert w_{m,n}\Vert _{\mu }\) is finite. We note that the notation \(\Vert \cdot \Vert _\mu \) introduced in (6.2) also appears in (2.5). Which of the definitions is meant should be clear from the context.
For given \(\xi \in (0,1)\) and \(\mu >0\), we define a Banach space
\(\Vert w_{0,0}\Vert _{\mu }:=\Vert w_{0,0}\Vert _{(1,\infty )}\), as the completion of the linear space of finite sequences \(w=(w_{m,n})_{m,n\in {\mathord {\mathbb N}}_0}\in \bigoplus _{m,n\in {\mathord {\mathbb N}}_0} \mathcal {W}_{m,n}\) with respect to the norm \(\Vert w\Vert _{\mu ,\xi }\). The spaces \(\mathcal {W}_{m,n}\) will often be identified with the corresponding subspaces of \(\mathcal {W}_{\xi }\).
Next we define a linear mapping \(H:\mathcal {W}_{\xi }\rightarrow \mathcal {L}(\mathcal {H}_{\textrm{red}})\). For finite sequences \(w=(w_{m,n})\in \mathcal {W}_{\xi }\) the operator H(w) is the sum
of operators \(H_{m,n}(w)\) on \(\mathcal {H}_{\textrm{red}}\), defined by \(H_{0,0}(w):= w_{0,0}(H_{\textrm{f}}),\) and, for \(m+n\ge 1\),
where \(P_{\textrm{red}}:=P_{[0,1]}(H_{\textrm{f}})\) and
The formal definition of the operator valued distributions \(a^*(k)\) and a(k) in (6.3) can be found in Appendix C. By the continuity established in the following proposition, the mapping \(w\mapsto H(w)\) has a unique extension to a bounded linear transformation on \(\mathcal {W}_{\xi }\).
Proposition 6.1
([3, Theorem 3.1, Theorem 3.3])
-
(i)
For all \(\mu >0\), \(m,n\in {\mathord {\mathbb N}}\), with \(m+n\ge 1\), and \(w\in \mathcal {W}_{m,n}\),
$$\begin{aligned} \Vert H_{m,n}(w) \Vert \le \Vert P^\perp _\Omega H_{\textrm{f}}^{-m/2} H(w_{m,n}) P^\perp _\Omega H_{\textrm{f}}^{-n/2} \Vert \le \frac{1}{\sqrt{m^m n^n}} \Vert w_{m,n}\Vert _\mu , \end{aligned}$$where we denoted the orthogonal projection in \(\mathcal {F}\) onto the subspace \(\{ \Omega \}^\perp \) by \(P_\Omega ^\perp \).
-
(ii)
For all \(\mu >0\) and all \(w\in \mathcal {W}_{\xi }\)
$$\begin{aligned} \Vert H(w)\Vert\le & {} \Vert w\Vert _{\mu ,\xi } \\ \Vert H(w)\Vert\le & {} \xi \Vert w\Vert _{\mu ,\xi },\qquad \text {if}\ w_{0,0}=0. \end{aligned}$$In particular, the mapping \(w\mapsto H(w)\) is continuous.
-
(iii)
When restricted to
$$\begin{aligned} \{ w \in {\mathcal {W}}_\xi : w_{m,n}({k}^{(m)}, \tilde{{k}}^{(n)})(r) 1_{r + \max (\sum _{j=1}^m |{k}_j|, \sum _{l=1}^n |\tilde{{k}}_l | ) \ge 1 } = 0, \, m +n \ge 1 \} \end{aligned}$$the map \(H(\cdot )\) is injective.
Proof
Statement (ii) follows immediately from the triangle inequality and (i) since \(\xi \le 1\). For (i), we refer to the proof of [3, Theorem 3.1], which generalizes trivially to \({\mathord {\mathbb C}}^d\) with \(d \ge 1\) from \(d=1\).
(iii) For a proof, see the proof of [21, Theorem 5.4], which generalizes straight forward to \({\mathord {\mathbb C}}^d\). \(\square \)
Given \(\alpha ,\beta ,\gamma \in {\mathord {\mathbb R}}_{+}\) we define polydiscs, \(\mathcal {B}(\alpha ,\beta ,\gamma )\subset H(\mathcal {W}_{\xi })\) centered around \(P_{\textrm{red}}H_{\textrm{f}} P_{\textrm{red}}\in \mathcal {L}(\mathcal {H}_{\textrm{red}})\) by
Note that \(w_{0,0}(0) \in {\mathcal {L}}({\mathord {\mathbb C}}^d)\) is uniquely determined by the identity
which holds for all \(v_1, v_2 \in {\mathord {\mathbb C}}^d\). The definition of \(\mathcal {B}(\alpha ,\beta ,\gamma )\) is motivated by Lemma 8.1 and by Theorem 8.2.
7 First Transformation
In the following, we denote by
the dimension of the eigenspace corresponding to the eigenvalue \(E_{\textrm{at}}(s_0)\) of \(H_{\textrm{at}}(s_0)\).
Theorem 7.1
Suppose Hypothesis I holds for some \(\mu > 0\), Hypothesis II holds, Hypothesis III holds for some \({\mathcal {U}} \subset {\mathord {\mathbb C}}^{\nu } \times {\mathord {\mathbb C}}\), and Hypothesis VI holds. Then, for all \(\xi \in (0,1)\) and arbitrarily positive constants \(\alpha _0\), \(\beta _0\) and \(\gamma _0\), there exits a positive constant \(g_1\) such that for all \(g \in [0,g_1)\) and all \((s,z) \in {\mathcal {U}}\), \((H_g(s)-z, H_0(s)-z)\) is a Feshbach pair for \(\varvec{\chi }(s)\), and
Proof
Using Proposition 5.1, we directly obtain that the Feshbach property is satisfied for sufficiently small g. Hence to prove the theorem it remains to construct a sequence of integral kernels \(w \in \mathcal {W}_\xi \) such that \({H}_g^{(0)}(s,z) = H(w)\). By the definition of the space \({\mathcal {B}}(\alpha _0,\beta _0,\gamma _0)\), the validity of Hypotheses I, II, III, and \({d}= \dim \big (\textrm{Ran}P_{\textrm{at}}(s_0)\big )\) (by Hypothesis VI) this construction is equal to the one in [17, Theorem 23] where a sequence of integral kernels with values in \(C^1([0,1])\) was constructed. \(\square \)
Remark 7.2
We note that a result for matrix-valued integral kernels similar as in Theorem 7.1 can be found with a detailed proof in [22].
8 RG Transformation
By abuse of notation, we shall denote the following operators on \(\mathcal {H}_{\textrm{red}}\)
again by \(\chi _\rho \) and \(\overline{\chi }_\rho \), respectively, recalling the notation (7.1). It should be clear from the context which of the expressions is considered.
Lemma 8.1
Suppose \(\rho ,\xi \in (0,1)\) and \(\mu > 0\). If \(H(w) \in \mathcal {B}(\rho /2, \rho /8, \rho /8)\), then \((H(w), H_{0,0}(w))\) is a Feshbach pair for \(\chi _\rho \).
The proof of the lemma follows from a straight forward generalization of the proof given in Lemma 15 in [17]. Moreover, a similar proof can be found in [13].
Proof
The assumption \(H(w) \in \mathcal {B}(\rho /2, \rho /8, \rho /8)\) implies, by Proposition 6.1, that
For \(r \in [\frac{3}{4} \rho , 1 ]\), and for \(v\in {\mathord {\mathbb C}}^d\) a normalized vector we have by triangle inequality
Thus, for \(r \in [\frac{3}{4} \rho , 1]\) the linear map \(w_{0,0}(r)\) is invertible and \(\Vert w_{0,0}(r)^{-1} \Vert _{\textrm{op}} \le 8/\rho \). From this and the spectral theorem,
Since \(\Vert \overline{\chi }_\rho \Vert \le 1 \), it follows from the estimates above that
This implies the bounded invertibility of
The other conditions on a Feshbach pair are now also satisfied, since \(H(w) - H_{0,0}(w)\) is bounded on \(\mathcal {H}_{\textrm{red}}\). \(\square \)
The renormalization transformation we use is a composition of a Feshbach transformation and a unitary scaling that puts the operator back on the original Hilbert space \(\mathcal {H}_{\textrm{red}}\). Unlike the renormalization transformation of Bach et al [3], there is no analytic transformation of the spectral parameter.
Given \(\rho \in (0,1)\), let \(\mathcal {H}_{\rho }=1_{{\mathord {\mathbb C}}^d} \otimes \textrm{Ran}\chi (H_{\textrm{f}}\le \rho )\). Let \(w\in \mathcal {W}_{\xi }\) and suppose \((H(w),H_{0,0}(w))\) is a Feshbach pair for \(\chi _{\rho }\). Then
is isospectral with H(w) in the sense of Theorem D.2. In order to get a isospectral operator on \(\mathcal {H}_{\textrm{red}}\), rather than \(\mathcal {H}_{\rho }\), we use the linear isomorphism
introduced in (2.1). Note that \(\Gamma _{\rho }H_{\textrm{f}} \Gamma _{\rho }^{*}=\rho H_{\textrm{f}}\), and hence \(\Gamma _{\rho }\chi _{\rho } \Gamma _{\rho }^{*}=\chi _1\). The renormalization transformation \(\mathcal {R}_{\rho }\) maps bounded operators on \(\mathcal {H}_{\textrm{red}}\) to bounded linear operators on \(\mathcal {H}_{\textrm{red}}\) and is defined on those operators H(w) for which \((H(w), H_{0,0}(w))\) is a Feshbach pair with respect to \(\chi _{\rho }\). Explicitly,
which is a bounded linear operator on \(\mathcal {H}_{\textrm{red}}\).
The following theorem describes the action of the renormalization transformation on the polydiscs \({\mathcal {B}}(\alpha ,\beta ,\gamma )\). For its statement, we recall the notation (4.11).
Theorem 8.2
(BCFS [3]) There exists a constant \(C_\chi \ge 1\) depending only on \(\chi \), such that the following holds. If \(\mu > 0\), \(\rho \in (0,1)\), \(\xi = \sqrt{\rho }/(4C_\chi )\), and \(\beta , \gamma \le \rho /(8C_\chi )\), then
where
with \(C_\beta := \frac{3}{2} C_\chi \), \(C_\gamma := 128 C_\chi ^2\).
Theorem 8.2 is a variant of Theorem 3.8 of [3], with additional information from the proof of that theorem, in particular from Equations (3.104), (3.107) and (3.109). Another difference is due to our different definition of the renormalization transformation, i.e., without analytic deformation of the spectral parameter. We note that versions of Theorem 8.2 have been used in the literature in [17, Theorem 16] as well as in [13, Appendix 1], where a detailed proof was presented.
9 Renormalization Preserves Analyticity and Symmetry
In this section, we show that the renormalization transformation preserves analyticity, symmetry with respect to a group of symmetries \({\mathcal {S}}\) and reflection symmetry. We study these properties on the level of the operators. In principle, one could also study the symmetry property on the level of the integral kernels.
In [17, Proposition 17], Griesemer and Hasler proved that analyticity is preserved under renormalization. The following proposition is a straight forward generalization of their result.
Proposition 9.1
(Proposition 17, [17]) Let X be an open subset of \({\mathord {\mathbb C}}^{\nu + 1 }\) with \(\nu \ge 0\). Suppose that the map \(\sigma ~\mapsto ~H(w_{(\sigma )}) \in {\mathcal {L}}(\mathcal {H}_{\textrm{red}})\), where \(w_{(\sigma )} \in \bigoplus _{m,n\in {\mathord {\mathbb N}}_0} {\mathcal {W}}_{m,n}\), is analytic on X, and that \(H(w_{(\sigma )})\) belongs to some polydisc \({\mathcal {B}}(\alpha , \beta , \gamma )\) for all \(\sigma \in X\). Then
-
(a)
\(H_{0,0}(w_{(\sigma )})\) is analytic on X.
-
(b)
If for all \(\sigma \in X\), \((H(w_{(\sigma )}), H_{0,0}(w_{(\sigma )}))\) is a Feshbach pair for \(\chi _\rho \), then \(F_{\chi _\rho }(H(w_{(\sigma )},H_{0,0}(w_{(\sigma )}))\) is analytic on X.
Proof
Follows from [17, Proposition 17] and an obvious change of notation to accommodate the matrix-valued integral kernels. \(\square \)
The property in Proposition 9.1 together with Proposition 9.2 will be one of the main ingredients in the proof of Part (i) of Theorem 2.10.
Proposition 9.2
Let X be an open subset of \({\mathord {\mathbb C}}^{\nu + 1 }\) with \(\nu \ge 0\). Assume that for each \(\sigma \in X\) we are given an operator \(H(w_{(\sigma )})\) in the polydisc \({\mathcal {B}}(\alpha , \beta , \gamma )\).
-
(a)
Let \({\mathcal {S}}\) be a group of symmetries acting on \(\mathcal {H}_{\textrm{red}}\) leaving the Fock vacuum and the one particle subspace invariant. Assume that it commutes with \(\Gamma _\rho \) and \(H_{\textrm{f}}\). Let \(\sigma \in X\). Suppose that \( H(w_{(\sigma )}) \) is symmetric with respect to \({\mathcal {S}}\).
-
(i)
Then \(H_{0,0}(w_{(\sigma )})\) is symmetric with respect to \({\mathcal {S}}\).
-
(ii)
If \((H(w_{(\sigma )}), H_{0,0}(w_{(\sigma )}))\) is a Feshbach pair for \(\chi _\rho \), then \(F_{\chi _\rho }(H(w_{(\sigma )}),H_{0,0}(w_{(\sigma )}))\) and \({\mathcal {R}}_\rho (H(w_{(\sigma )}))\) are symmetric with respect to \({\mathcal {S}}\).
-
(i)
-
(b)
Suppose \(X = {X}^*\) and \(\sigma \mapsto H(w_{(\sigma )})\) is reflection symmetric.
-
(i)
Then \(H_{0,0}(w_{(\sigma )})\) is reflection symmetric.
-
(ii)
If \((H(w_{(\sigma )}), H_{0,0}(w_{(\sigma )}))\) is a Feshbach pair for \(\chi _\rho \), then \(F_{\chi _\rho }(H(w_{(\sigma )}),H_{0,0}(w_{(\sigma )}))\) and \({\mathcal {R}}_\rho (H(w_{(\sigma )}))\) are reflection symmetric.
-
(i)
Proof
We first show how one can recover \(w_{0,0}(r)\) from H(w). We follow the argument in [3]. Let \(w \in \mathcal {W}_\xi \). Let \(v_1,v_2 \in {\mathord {\mathbb C}}^d\). For \(f, g \in \mathfrak {h}\), we have
A simple calculation shows that
and
We pick a function \(f \in C_c^\infty (B_1;[0,\infty ))\) with \(\int |f(x)|^2 \hbox {d}x = 1\), and define \(f_{\epsilon ,k}:= \epsilon ^{-3/2} f(\epsilon ^{-1}(x-k))\). Then we find from (9.2)
This term tends to \(\langle { v_1, w_{0,0}(|k|) v_2} \rangle \) since
On the other hand, we find from (9.3)
This term tends to 0, because \(f_{\epsilon ,k} \rightarrow 0\), weakly in \(L^2(B_1)\). Thus, from (9.1) – (9.6), we conclude using that \(w_{0,0}\) is continuous that
(a) Since this part does not depend on \(\sigma \), we drop it in the notation. Now since \(S \in {\mathcal {S}}_2\) leaves the one photon space invariant, there is a map \(p_1(S)\) such that
If S is unitary or antiunitary, it follows that \(p_1(S) \) is unitary or antiunitary, respectively. Now let \(S = S_1 \otimes S_2 \in {\mathcal {S}}\) by a symmetry. If S is unitary, we write \(( \cdot )^\# = ( \cdot )\) and if it is antiunitary we write \(( \cdot )^\# = ( \cdot )^*\). Thus, we find from (9.7) that
where in (9.8) we made use of (9.1), (9.3) and the fact that \(p_2(S^*) f_{k,\epsilon }\) converges to zero. In (9.9), we used that \(H_{\textrm{f}}\) is symmetric with respect to \(S_2\). In the last line, we used (9.6) and (9.5). We conclude that \( S_1 w_{0,0}(r)S_1^* = w_{0,0}(r)\) for all \(r \in [0,1]\). This shows Part (i) of (a). This shows (i).
(ii) Then from (i) we know that \(H_{0,0}(w)\) is symmetric with respect to \({\mathcal {S}}\). Thus, it follows that also \(W:= H(w) - H_{0,0}(w)\) is symmetric. Now the claim for the Feshbach operator follows from Lemma 4.8. Since the symmetry commutes with dilations the claim follows also for the renormalized expression.
(b) Suppose now \(X = {X}^*\) and \(\sigma \mapsto H(w_{(\sigma )})\) is reflection symmetric. Then by (9.7) it follows that
Thus for \(r \in [0,1]\) we find \(w_{({\overline{\sigma }}) \,0,0}(r) = w_{(\sigma ) \, 0,0}(r)^*\). This shows Part (i) of (b). To show (ii) we write \(T_{(\sigma )} = H_{0,0}(w_{(\sigma )})\) and observe that \(W_{(\sigma )} = H(w_{(\sigma )}) - T_{(\sigma )}\) is also reflection symmetric as well as \(\chi = \chi _\rho \). We find
This shows the claim for the Feshbach operator. Since the symmetry commutes with dilation the claim follows also for the renormalized expression. \(\square \)
10 Iterating the Renormalization Transformation
In this section we follow closely, Sect. 8 in [17], and generalize the results given there to the non-degenerate situation. In particular the two lemmas stated below are almost identical to the main results stated in Lemma 18, Lemma 19, Corollary 20, and Proposition 21 of [17].
In Part (c) of Theorem 5.7 we have reduced, for small |g|, the problem of finding an eigenvalue of \(H_g(s)\) in the neighborhood
of \(E_\textrm{at}(s)\) to finding an \(z\in {\mathord {\mathbb C}}\) such that \(H^{(0)}[s,z]\) has a non-trivial kernel. We now use the renormalization map to define a sequence
of operators on \(\mathcal {H}_{\textrm{red}}\), which, by Theorem D.2, are isospectral in the sense that \(\textrm{Ker}H^{(n+1)}[s,z]\) is isomorphic to \(\textrm{Ker}H^{(n)}[s,z]\). The main purpose of the present section is to show that for every \(n \in {\mathord {\mathbb N}}\) the operator \(H^{(n)}[s,z]\) is well-defined for all z in a non-empty set \(U_n(s)\) with the following properties. We have \(U_{n+1}(s) \subset U_n(s)\) and
In Sect. 10, we will show that \(H^{(n)}[s,z_{\infty }(s)]\) has a non-trivial kernel and hence \(z_{\infty }(s)\) is an eigenvalue of \(H_g(s)\). The construction of the sets \(U_n(s)\) is based on Theorem 5.7 and Theorem 7.1, but not on the explicit form of \(H^{(0)}[s,z]\) as given by (5.17).
Moreover, this construction is pointwise in s and g, all estimates being uniform in \(s\in X\) and \(|g|<g_{\textrm{b}}\) for some \(g_{\textrm{b}}>0\). We therefore drop these parameters from our notations and we now explain the construction of \(H^{(n)}[z]\) making only the following assumption:
- (A):
-
\(U_0(s)\) is an open subset of \({\mathord {\mathbb C}}\) and for every \(z\in U_0\),
$$\begin{aligned} H^{(0)}[z] \in \mathcal {B}(\infty ,\rho /8,\rho /8). \end{aligned}$$If \( d \ge 1\) there is a group of symmetries \({\mathcal {S}}\) of \(H_{\textrm{f}}\) such that \(H^{(0)}[z]\) is symmetric with respect to each element of \({\mathcal {S}}\) and \({\mathcal {S}}_1:= \{ S_1: S_1 \otimes S_2 \in {\mathcal {S}} \}\) acts irreducibly on \({\mathord {\mathbb C}}^d\). Each element of \({\mathcal {S}}_2:= \{ S_2: S_1 \otimes S_2 \in {\mathcal {S}} \}\) leaves the Fock vacuum as well as the one particle subspace invariant and commutes with the operator of dilations.
The polydisc \(\mathcal {B}(\infty ,\rho /8,\rho /8)\subset H(\mathcal {W}_{\xi })\) is defined in terms of \(\xi := \sqrt{\rho }/(4 C_\chi )\) and \(\mu >0\), where \(\rho \in (0,1)\) and \(C_\chi \) is given by Theorem 8.2.
By Lemma 8.1, we may define \(H^{(1)}[z],\dots ,H^{(N)}[z]\), recursively by
provided that \(H^{(0)}[z],\ldots , H^{(N-1)}[z]\) belong to \(\mathcal {B}(\rho /2,\rho /8,\rho /8)\). Theorem 8.2 gives us sufficient conditions for this to occur: by iterating the map \((\beta ,\gamma )\mapsto (\beta ',\gamma ')\), cf. (8.1), starting with \((\beta _0,\gamma _0)\), we find the conditions
for \(n=0,\ldots , N-1\). They are obviously satisfied for all \(n\in {\mathord {\mathbb N}}\) if \(C_\gamma \rho ^\mu <1\) and if \(\beta _0,\gamma _0\) are sufficiently small. If this is the case, we define
Since the renormalization transformation \({\mathcal {R}}_\rho \) preserves the symmetry by Proposition 9.2, it follows by induction from Assumption (A) that each \(H^{(n)}[z]\) is symmetric with respect to the elements of \({\mathcal {S}}\). Since the symmetries leave the vacuum invariant it follows from Lemma 4.7 that the linear map \(T_0^{(n)}(z) \) is multiple of the identity. That is, there exists a function \(E^{(n)}: U_n \rightarrow {\mathord {\mathbb C}}\) such that
Now it remains to make sure that
for \(n=0,\ldots , N-1\). Since \(| E^{(n)}(z) | = \Vert T_0^{(n)}(z)\Vert _{\textrm{op}} \) this is achieved by adjusting the admissible values of z step by step. We define recursively, for all \(n\ge 1\),
If \(z\in U_N\), \(H^{(0)}(z)\in \mathcal {B}(\infty ,\beta _{0},\gamma _{0})\), and \(\rho ,\beta _0,\gamma _0\) are small enough, as explained above, then the operators \(H^{(n)}(z)\) for \(n=1,\ldots ,N\) are well defined by (10.1). In addition we know from Theorem 8.2 that \(H^{(n)}(z)\in \mathcal {B}(\infty ,\beta _n,\gamma _n)\), and that
This latter information will be used in the proof of Lemma 10.2 to show that the sets \(U_n\) are not empty.
The subsequent lemma is a summary of the above construction.
Lemma 10.1
Suppose that (A) holds with \(\rho \in (0,1)\) so small, that \(C_\gamma \rho ^\mu <1\). Suppose \(\beta _0, \gamma _0 \le \rho /(8C_\chi )\) and, in addition,
If \(H^{(0)}[z]\in \mathcal {B}(\infty ,\beta _0,\gamma _0)\) for all \(z\in U_0\), then \(H^{(n)}[z]\) is well defined for \(z\in U_n\), symmetric with respect to the elements of \({\mathcal {S}}\), and satisfies
with \(\alpha _n\), \(\beta _n\), and \(\gamma _n\) as in (10.4), (10.3), and (10.2).
The next lemma establishes conditions under which the set \(U_0\) and \(U_n\) are non-empty. We introduce the discs
and note that \(U_n={E^{(n-1)}}^{-1}(D_{\rho /2})\).
Remark
We call a function \(f:A\rightarrow B\) conformal if it is the restriction of an analytic bijection \(f:U\rightarrow V\) between open sets \(U\supset A\) and \(V\supset B\), and \(f(A)=B\).
Lemma 10.2
Suppose that (A) holds with \(U_0\ni E_\textrm{at}\) and \(\rho \in (0,4/5)\) so small that \(C_\gamma \rho ^\mu <1\) and \(\overline{B_\rho (E_\textrm{at})}\subset U_0\). Suppose that \(\alpha _0 < \rho /2\), \(\beta _0, \gamma _0 \le \rho /(8C_\chi )\) and that (10.5) holds. If \(z\mapsto H^{(0)}[z]\in \mathcal {L}(\mathcal {H}_{\textrm{at}})\) is analytic in \(U_0\) and
for all \(z\in U_0\), then the following is true.
-
(a)
For \(n \ge 0\), \(E^{(n)}:U_n \rightarrow {\mathord {\mathbb C}}\) is analytic in \(U_n^{\circ }\) and a conformal map from \(U_{n+1}\) onto \(D_{\rho /2}\). In particular, \(E^{(n)}\) has a unique zero, \(z_n\), in \(U_n\). Moreover,
$$\begin{aligned} B_\rho (E_{\textrm{at}}) \supset U_1 \supset U_2 \supset U_{3} \supset \cdots \;. \end{aligned}$$ -
(b)
The limit \(z_\infty := \lim _{n\rightarrow \infty } z_n\) exists and for \(\epsilon := 1/2 - \rho /2 - \alpha _1 > 0\),
$$\begin{aligned} | z_n - z_\infty | \le {\rho ^{n}} \exp \left( \frac{1}{2 \rho \epsilon ^2} \sum _{k=0}^\infty \alpha _k \right) \;. \end{aligned}$$ -
(c)
Let \(E_{\textrm{at}} \in {\mathord {\mathbb R}}\) and \(H^{(0)}[z]^* = H^{(0)}[{\overline{z}}]\) for all \(z \in B_\rho (E_\textrm{at})\). Then for all \(n\ge 0\), \( U_{n+1} \cap {\mathord {\mathbb R}}\) is an interval and \(\partial _x E^{(n)}(x) < 0\) on \(U_{n+1} \cap {\mathord {\mathbb R}}\). Then there exists an \(a < z_\infty \) such that \(H^{(0)}[x]\) has a bounded inverse for all \(x \in (a,z_\infty )\).
Proof of Lemma 10.2
The Lemma follows as a consequence of Lemma 10.1 and the property of the Feshbach map, cf. Theorem D.2. The details of the proof are the same as the proofs of Lemma 19, Corollary 20, and Proposition 21 in [17]. \(\square \)
Let us now discuss the construction of an eigenvector \(\varphi ^{(0)}\) such that \(H^{(0)}[z_\infty ] \varphi ^{(0)}= 0\). The same construction has been used in [3, 5, 6, 17]. The result which we use is from [17]. In order to formulate the result we define the following auxiliary operator for \(z \in U_n\)
where \(W^{(n)}[z]\) and \(H_{0,0}^{(n)}[z]\) are given as follows. By construction of \(H^{(n)}[z]\) there exists by Proposition 6.1 a unique \(w^{(n)}[z] \in {\mathcal {W}}_\xi \) such that \(H^{(n)}[z] = H(w^{(n)}[z])\). Then we set \(H_{0,0}^{(n)}:= H_{0,0}(w^{(n)}[z])\) and \(W^{(n)}[z]:= H^{(n)} [z]- H_{0,0}^{(n)}[z]\).
Theorem 10.3
(Theorem 22, [17]) Suppose the assumptions of Lemma 10.2 hold. Then for any nonzero vector \(v \in {\mathord {\mathbb C}}^d\)
exists, \(\varphi _v^{(0)} \ne 0\) and \(H^{(0)}[z_\infty ] \,\varphi _v^{(0)} = 0\). Moreover,
where
Proof
The proof follows from Lemma 10.2 with the help of Lemma 8.1 and Theorem D.2. The details of the proof carry over from the proof of Theorem 22 in [17] by merely replacing \(\Omega \) by \(v \otimes \Omega \). \(\square \)
Remark 10.4
Let the assumptions and notations be as in Theorem 10.3. It follows immediately from (10.6) that the map \({\mathord {\mathbb C}}^d \rightarrow \mathcal {H}_{\textrm{red}}\), \(v \mapsto \varphi _v^{(0)}\) is linear. Since by Theorem 10.3 that map has kernel \(\{ 0 \}\), it is injective.
11 Analyticity of Eigenvalues and Eigenvectors
This section is devoted to the proof of Theorem 2.10. It is essential for this proof, that a neighborhood \(V_0\subset V\) of \(s_0\) and a positive bound, \(g_1\), on g can be determined in such a way that the renormalization analysis of Sect. 10, and in particular the choices of \(\rho \) and \(\xi \) are independent of \(s\in V_0\) and \(g\le g_1\). Once \(V_0\) and \(g_1\) are found, the assertions of Theorem 2.10 are derived from Proposition 9.1 and 9.2 as well as the uniform bounds of Sect. 10.
Proof of Theorem 2.10
First let us recall that by Lemma 4.6 we can assume without loss that Hypothesis VI holds and \(P_{\textrm{at}}(s) = P_{\textrm{at}}(s_0) \) for all \(s \in X\). Furthermore by choosing a suitable basis we can assume that \(\textrm{Ran}P_{\textrm{at}}(s_0) = {\mathord {\mathbb C}}^d\).
Let \(\mu >0\) and \(\mathcal {U}\subset {\mathord {\mathbb C}}^{\nu + 1}\) be given by Hypothesis I and Hypothesis III, respectively. For the renormalization procedure to work, we first choose \(\rho \in (0,4/5)\) and a open neighborhood \(X_{\textrm{b}} \subset X_1\) of \(s_0\), both small enough, so that \(C_{\gamma }\rho ^{\mu }<1\) and
which is possible since \(s \mapsto E_{\textrm{at}}(s)\) is continuous. Here, and below we use the constants \(C_{\gamma }, C_{\chi }\) and \(C_{\beta }\) from Theorem 8.2. Let \(\xi =\sqrt{\rho }/(4C_{\chi })\). Next we pick small positive constants \(\alpha _0\), \(\beta _0\), and \(\gamma _0\) such that
and in addition
By Proposition 5.1 and Theorem 7.1, there exists a \(g_1>0\) such that for \(0 \le g \le g_1\)
where \(H_g^{(0)}[s,z]\) is analytic on \(\mathcal {U}\), by Theorem 5.7. We define
and
Then, by (11.2), (11.3), and (11.1) the assumptions of Lemma 10.2 are satisfied for \(s\in X_\textrm{b}\) and \(U_0=U_{0}(s)\). It follows that, for all \(n\in {\mathord {\mathbb N}}\), \(H_g^{(n)}[s,z]=\mathcal {R}^n H_g^{(0)}[s,z]\) is well-defined for \((s,z)\in \mathcal {U}_n\), and that \(U_n(s)\ne \emptyset \). By Proposition 9.1, \(H_g^{(n)}[s,z]\) is analytic in \( \mathcal {U}_n^{\circ }\).
Step 1: \(z_\infty (s)=\lim _{n\rightarrow \infty }z_n(s)\) exists and is analytic on \(X_{\textrm{b}}\).
Since \(H_g^{(n)}[s,z]\) is analytic on \(\mathcal {U}_n^{\circ }\), so is \(E_g^{(n)}(s,z)\). Let \(z_{n}(s)\) denote the unique zero of the function \(z\mapsto E_g^{(n)}(s,z)\) on \(U_n(s)\) as determined by Lemma 10.2. That is,
By the implicit function theorem \(z_n(s)\) is analytic in s. The application of the implicit function theorem is justified since \(z \mapsto E^{(n)}_g(s,z)\) is bijective in a neighborhood of \(z_n(s)\), and thus in this neighborhood \(\partial _z E_g^{(n)}(s,z)\ne 0\). By Lemma 10.2(b), \(z_n(s)\) converges to \(z_\infty (s)\) uniformly in \(s \in X_{\textrm{b}}\). This implies the analyticity of \(z_\infty (s)\) on \(X_{\textrm{b}}\), by the Weierstrass approximation theorem of complex analysis.
Step 2: For \(s \in X_{\textrm{b}}\), there exist d linearly independent eigenvectors \(\psi _{g,j}(s)\), \(j=1,\ldots ,d\), of \(H_g(s)\) with eigenvalue \(z_\infty (s)\), such that \(\psi _{g,j}(s)\) depends analytically on s.
Since \(H_g^{(n)}[s,z]\) is analytic on \(\mathcal {U}_n^{\circ }\), it follows, by Proposition 9.1, that
is analytic on \(\mathcal {U}_n^{\circ }\), where \(W_g^{(n)}:= H_g^{(n)} - H^{(n)}_{g,0,0}\). Hence, by Step 1, \(s \mapsto Q_{g,n}[s,z_\infty (s)]\) is analytic on \(X_{\textrm{b}}\). Let \(e_1,\ldots ,e_d\) be a basis of \({\mathord {\mathbb C}}^d\). It follows that
is analytic on \(X_{\textrm{b}}\). From Theorem 10.3 we know that these vectors converge uniformly on \(X_{\textrm{b}}\) to a vector \( \varphi _{g,j}^{(0)}(s)\ne 0\) and that \(H_g^{(0)}[s,z_{\infty }(s)] \varphi _{g,j}^{(0)}(s)= 0\). Hence \(\varphi ^{(0)}_{g,j}(s)\) is analytic on \(X_{\textrm{b}}\) and, by the Feshbach property (Theorem 5.7 (c)), the vector
is an eigenvector of \(H_g(s)\) with eigenvalue \(z_\infty (s)\). Using Theorem 5.7 (a) and again by Step 1 we see that \(s \mapsto Q_{\varvec{\chi }}(s,z_\infty (s))\) is analytic on \(X_{\textrm{b}}\). We conclude that \(\psi _{g,j}\) is analytic on \(X_\textrm{b}\) as well. The linear independence of \(\psi _{g,j}(s)\), \(j=1,\ldots ,d\), follows from Remark 10.4 and Theorem 5.7 (c).
Step 3: In the limit \(g \rightarrow 0 \), we have uniformly in \(s \in X_{\textrm{b}}\) that \(|z_\infty (s) - E_{\textrm{at}}(s)| = o(1)\) and that \(\Vert \psi _{g,j}(s) - \varphi _{\textrm{at},j}(s) \otimes \Omega \Vert = o(1)\) for some \(\varphi _{\textrm{at},j}(s) \in \textrm{Ran}P_{\textrm{at}}(s)\).
From Lemma 10.2 we know that \(z_\infty (s) \in B_\rho (E_{\textrm{at}}(s))\). Now by Theorem 7.1 we can make \(\alpha _0,\beta _0,\gamma _0\) arbitrarily small by choosing \(g_{\textrm{b}} > 0\) sufficiently small. Thus from (11.2) we see that we can choose \(\rho \in (0,1)\) arbitrarily small by choosing \(g_{\textrm{b}} > 0\) sufficiently small. This shows \(|z_\infty (s) - E_{\textrm{at}}(s)| = o(1)\) uniformly in \(X_{\textrm{b}}\). From (10.7) of Theorem 10.3 we find \(\Vert \psi _{g,j}(s) - e_j \otimes \Omega \Vert \le C \sum _{l=0}^\infty \gamma _l \) with C given in (10.8). Now from Eq. (10.2) of Lemma 10.1 we see that the right hand side can be made arbitrarily small if \(\gamma _0 > 0\) is sufficiently small. But by Theorem 7.1 the latter can be made small by choosing \(g_{\textrm{b}} > 0\) sufficiently small. This shows that \(\Vert \psi _{g,j}(s) - e_j \otimes \Omega \Vert = o(1)\) uniformly in s.
Step 4: If in addition Hypothesis IV holds, then
- (\(\alpha \)):
-
for all \(s \in X_b \cap {\mathord {\mathbb R}}^\nu \) it holds that \(z_\infty (s) = \textrm{inf}\,\sigma (H_g(s)),\)
- (\(\beta \)):
-
for all \(s \in X_b \cap X_b^*\) it holds that \({\overline{z}}_\infty (s) = z_\infty ({\overline{s}})\).
Let \(s \in X_{\textrm{b}}\cap {\mathord {\mathbb R}}^{\nu }\). Then by Hypothesis IV the operator \(H_g(s)\) is self-adjoint and its spectrum is a half line \([\Sigma _g(s),\infty )\) (cf. [36] ), where \(\Sigma _g(s):= \textrm{inf}\,\sigma (H_g(s))\). By Step 2, \(z_{\infty }(s)\ge \Sigma _g(s)\). We use Proposition 10.2 (c) to show that \(z_{\infty }(s)>\Sigma _g(s)\) is impossible. Clearly \(E_\textrm{at}(s)\in {\mathord {\mathbb R}}\), and \(H_g^{(0)}[s,z]^* = H_g^{(0)}[s,{\overline{z}}]\) for \(z \in B_\rho (E_{\textrm{at}}(s))\) is a direct consequence of the definition of \(H_g^{(0)}\) and the self-adjointness of \(H_g(s)\). Hence there exists a number \(a(s) < z_\infty (s)\) such that \(H^{(0)}_g[s,x]\) has a bounded inverse for all \(x \in (a(s),z_\infty (s))\). It follows, by Theorem D.2, that \((a(s),z_\infty (s))\cap \sigma (H_g(s))=\emptyset \). Therefore \(z_{\infty }(s)=\Sigma _g(s)\). This shows (\(\alpha \)). Now (\(\beta \)) is a consequence of Schwarz reflection principle.
The Theorem now follows for \(E_g(s) = z_{\infty }(s)\). \(\square \)
If we neglect the first Feshbach map in the above proof, we obtain the following theorem, which is independent of the explicit structure of the Hamiltonian.
Theorem 11.1
Suppose \(\mathcal {H}_{\textrm{red}} = {\mathord {\mathbb C}}^d \otimes \mathcal {F}\) with \( d \in {\mathord {\mathbb N}}\). Let \({\mathcal {S}}\) be a group of symmetries acting on \(\mathcal {H}_{\textrm{red}}\) commuting with dilations and \(H_{\textrm{f}}\) and \({\mathcal {S}}_1\) acts irreducibly on \({\mathord {\mathbb C}}^d\). For \(\mu > 0\) and \(\rho \in (0,1/2) \), there exist positive numbers \(\alpha _0, \beta _0, \gamma _0\) with the following properties. Let X be a nonempty subset of \({\mathord {\mathbb C}}^d\), \(e: X \rightarrow {\mathord {\mathbb C}}\) a function, and \({\mathcal {U}} \subset X \times {\mathord {\mathbb C}}\) a set such that
Suppose for each \((s,z) \in {\mathcal {U}}\) an operator H(w[s, z]) on \(\mathcal {H}_{\textrm{red}}\), with \(w[s,z] \in {\mathcal {W}}_\xi \) is given which is symmetric with respect to \({\mathcal {S}}\) such that
Then for each \(s \in X\) there exists an element \(z_\infty (s) \in \overline{B_\rho (e(s))} \) and linearly independent functions \(\varphi _j(s)\), \(j=1,\ldots ,d\), such that
-
(i)
There exists an \(e_j \in {\mathord {\mathbb C}}^d\). So that for any \(\epsilon > 0\) there exists \((\alpha _1,\beta _1,\gamma _1) \in (0,\alpha _0] \times (0,\beta _0] \times (0,\gamma _0] \) such that \(|z_\infty (s) - e(s) | < \epsilon \) and \(\Vert \varphi _j(s) - e_j \otimes \Omega \Vert < \epsilon \) whenever \( H(w[s,z]) - ( e(s) - z ) \in {\mathcal {B}}(\alpha _1,\beta _1,\gamma _1) \).
-
(ii)
If X and \({\mathcal {U}}\) are open and e and H(w) analytic on X and \({\mathcal {U}}\), respectively, then also \(z_\infty (s)\) and \(\varphi _j(s)\) depend analytically on s.
Proof
This follows from the same Proof as Theorem 2.10 by neglecting the first step. \(\square \)
References
Abdesselam, A., Hasler, D.: Analyticity of the ground state energy for massless Nelson models. Commun. Math. Phys. 310(2), 511–536 (2012)
Amour, L., Faupin, J.: Hyperfine splitting in non-relativistic QED: uniqueness of the dressed hydrogen atom ground state. Commun. Math. Phys. 319(2), 425–450 (2013)
Bach, V., Chen, T., Fröhlich, J., Sigal, I.M.: Smooth Feshbach map and operator-theoretic renormalization group methods. J. Funct. Anal. 203(1), 44–92 (2003)
Bach, V., Chen, T., Fröhlich, J., Sigal, I.M.: The renormalized electron mass in non-relativistic quantum electrodynamics. J. Funct. Anal. 243(2), 426–535 (2007)
Bach, V., Fröhlich, J., Sigal, I.M.: Quantum electrodynamics of confined nonrelativistic particles. Adv. Math. 137(2), 299–395 (1998)
Bach, V., Fröhlich, J., Sigal, I.M.: Renormalization group analysis of spectral problems in quantum field theory. Adv. Math. 137(2), 205–298 (1998)
Bach, V., Fröhlich, J., Sigal, I.M.: Spectral analysis for systems of atoms and molecules coupled to the quantized radiation field. Commun. Math. Phys. 207(2), 249–290 (1999)
Ballesteros, M., Deckert, D.-A., Hänle, F.: Analyticity of resonances and eigenvalues and spectral properties of the massless spin-boson model. J. Funct. Anal. 276(8), 2524–2581 (2019)
Chen, T.: Infrared renormalization in non-relativistic QED and scaling criticality. J. Funct. Anal. 254(10), 2555–2647 (2008)
Chen, T., Fröhlich, J., Pizzo, A.: Infraparticle scattering states in nonrelativistic quantum electrodynamics. II. Mass shell properties. J. Math. Phys. 50(1), 012103, 34 (2009)
Cohen-Tannoudji, C., Dupont-Roc, J., Grynberg, G.: Photons andAtoms. Wiley (1997)
Fröhlich, J.: On the infrared problem in a model of scalar electrons and massless, scalar bosons. Ann. Inst. H. Poincaré Sect. A (N.S.) 19, 1–103 (1973)
Fröhlich, J., Griesemer, M., Sigal, I.M.: On spectral renormalization group. Rev. Math. Phys. 21(4), 511–548 (2009)
Gérard, C.: On the existence of ground states for massless Pauli–Fierz Hamiltonians. Ann. Henri Poincaré 1(3), 443–459 (2000)
Griesemer, M.: Non-relativistic Matter and Quantized Radiation, Large Coulomb systems, Lecture Notes in Physics, vol. 695, pp. 217–248. Springer, Berlin (2006)
Griesemer, M., Hasler, D.: On the smooth Feshbach–Schur map. J. Funct. Anal. 254(9), 2329–2335 (2008)
Griesemer, M., Hasler, D.: Analytic perturbation theory and renormalization analysis of matter coupled to quantized radiation. Ann. Henri Poincaré 10(3), 577–621 (2009)
Griesemer, M., Lieb, E.H., Loss, M.: Ground states in non-relativistic quantum electrodynamics. Invent. Math. 145(3), 557–595 (2001)
Hainzl, C., Seiringer, R.: Mass renormalization and energy level shift in non-relativistic QED. Adv. Theor. Math. Phys. 6(5), 847–871 (2002)
Hasler, D., Herbst, I.: Convergent expansions in non-relativistic QED: analyticity of the ground state. J. Funct. Anal. 261(11), 3119–3154 (2011)
Hasler, D., Herbst, I.: Ground states in the spin boson model. Ann. Henri Poincaré 12(4), 621–677 (2011)
Hasler, D., Lange, M.: Renormalization analysis for degenerate ground states. J. Funct. Anal. 275(1), 103–148 (2018)
Hasler, D., Lange, M.: Symmetries in non-relativistic quantum electrodynamics. Rev. Math. Phys. 35, 39 (2023)
Hörmander, L.: An Introduction to Complex Analysis in Several Variables, North-Holland Mathematical Library, vol. 7, 3rd edn. North-Holland Publishing Co., Amsterdam (1990)
Kato, T.: Perturbation Theory for Linear Operators, Classics in Mathematics. Springer, Berlin (1995). (Reprint of the 1980 edition)
Kroll, N.M., Lamb, W.E.: On the self-energy of a bound electron. Phys. Rev. 75, 388–398 (1949)
Lamb, W.E., Retherford, R.C.: Fine structure of the hydrogen atom by a microwave method. Phys. Rev. 72, 241–243 (1947)
Lange, M.: Ground states and spectral properties in quantum field theories, Ph.D.-thesis, Friedrich-Schiller University Jena, Jena, Sep 2018, Dissertation, Friedrich-Schiller-Universität Jena (2018)
Lieb, E.H., Loss, M.: Existence of atoms and molecules in non-relativistic quantum electrodynamics. Adv. Theor. Math. Phys. 7(4), 667–710 (2003)
Loss, M., Miyao, T., Spohn, H.: Time reversal symmetries and properties of ground states in nonrelativistic QED, Applications of renormalization group methods in mathematical sciences, RIMS Kôkyûroku Bessatsu, B21, Res. Inst. Math. Sci. (RIMS), Kyoto, pp. 35–44 (2010)
Reed, M., Simon, B.: Methods of Modern Mathematical Physics. IV. Analysis of Operators, Academic Press [Harcourt Brace Jovanovich, Publishers], New York-London (1978)
Reed, M., Simon, B.: Methods of Modern Mathematical Physics. I, second ed., Academic Press, Inc. [Harcourt Brace Jovanovich, Publishers], New York, 1980, Functional analysis
Schur, I.: Neue Begründung der Theorie der Gruppencharaktere, Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin. Jan-Juni 1905, 26 (1905)
Simon, B.: Representations of Finite and Compact Groups, Graduate Studies in Mathematics. American Mathematical Society (1996)
Spohn, H.: Ground state of a quantum particle coupled to a scalar Bose field. Lett. Math. Phys. 44(1), 9–16 (1998)
Spohn, H.: Dynamics of Charged Particles and their Radiation Field. Cambridge University Press, Cambridge (2004)
Weidmann, J.: Linear Operators in Hilbert Spaces, Graduate Texts in Mathematics, vol. 68, Springer, New York (1980), Translated from the German by Joseph Szücs
Wigner, E.: Ueber die operation der zeitumkehr in der quantenmechanik. Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse 1932, 546–559 (1932)
Acknowledgements
Both authors acknowledge financial support by the Research Training Group (1523/2) “Quantum and Gravitational Fields” when this project was initiated. D. Hasler wants to thank M. Griesemer and I. Herbst for valuable discussions on the subject. M. Lange also acknowledges financial support from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (ERC StG MaMBoQ, grant agreement n.802901).
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Christoph Kopper.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Symmetries
In this section we introduce anti-linear operators and symmetries in a Hilbert space \(\mathcal {H}\).
Definition A.1
Let \(\mathcal {H}\) be a complex Hilbert space.
-
(a)
A mapping \(T: \mathcal {H}\rightarrow \mathcal {H}\) is called anti-linear operator in \(\mathcal {H}\) if
$$\begin{aligned} T(\alpha x + \beta y) = {\overline{\alpha }} T x + {\overline{\beta }}T y, \end{aligned}$$for all \(\alpha , \beta \in {\mathord {\mathbb C}}\) and \(x,y \in \mathcal {H}\). An anti-linear operator T is called bounded if
$$\begin{aligned} \sup _{x: \Vert x \Vert \le 1 } \Vert Tx \Vert < \infty . \end{aligned}$$ -
(b)
The adjoint of a bounded anti-linear operator, \(T: \mathcal {H}\rightarrow \mathcal {H}\), is defined to be the anti-linear operator \(T^*: \mathcal {H}\rightarrow \mathcal {H}\) such that
$$\begin{aligned} \langle x, T y \rangle = \overline{ \langle T^* x, y \rangle } \end{aligned}$$for all \(x, y \in \mathcal {H}\).
-
(c)
An anti-linear operator V in \(\mathcal {H}\) is called antiunitary if it is surjective and satisfies
$$\begin{aligned} \langle V x, V y \rangle = \overline{ \langle x, y \rangle } \end{aligned}$$for all \(x, y \in \mathcal {H}\).
In the following lemma we collect a few properties of anti-linear and antiunitary operators.
Lemma A.2
Let \(\mathcal {H}\) be a complex Hilbert space. Then the following holds.
-
(a)
Let S and T be a linear or an anti-linear operator in \(\mathcal {H}\). Then ST is linear if either both S and T are linear or both S and T are anti-linear. The operator ST is anti-linear if one of the two operators S and T is linear and the other is anti-linear.
-
(b)
Let S and T be anti-linear. Then \((\alpha S + \beta T)^* = {\overline{\alpha }} S^* + {\overline{\beta }} T^*\).
-
(c)
Let S and T be linear or anti-linear. Then we have \((ST)^* = T^* S^*\).
-
(d)
A bounded anti-linear operator T is antiunitary if and only if it satisfies \(T^* T = 1 \) and \(T T^* = 1\).
-
(e)
Let S and T be unitary or antiunitary. Then ST is unitary if either both S and T are unitary or both S and T are antiunitary. The operator ST is antiunitary if one of the two operators S and T is unitary and the other is antiunitary.
Proof
(a) and (b) are elementary to show.
(c) If S and T are linear, this is a well known identity. If S is linear and T is antilinear, then for all \(x, y \in \mathcal {H}\)
and so \((S T)^* = T^* S^*\) by the nondegeneracy of the inner product. If S and T are antilinear, then ST is linear by (a) and for all \(x, y \in \mathcal {H}\)
and so \((S T)^* = T^* S^*\) by the nondegeneracy of the inner product.
(d) and (e) are elementary to show. \(\square \)
Definition A.3
Let \(\mathcal {H}\) be a complex Hilbert space.
-
(a)
A symmetry in \(\mathcal {H}\) is a unitary or antiunitary operator in \(\mathcal {H}\).
-
(b)
We say that S is a symmetry of a linear operator T in \(\mathcal {H}\) (possibly unbounded) if
$$\begin{aligned} S^* D(T) \subset D(T) \quad \text { and }\quad S T S^*&= T , \quad \text {if } S \text { is unitary }, \\ S^* D(T^*) \subset D(T)\quad \text { and }\quad S T S^*&= T^* , \quad \text {if } S \text { is antiunitary }. \end{aligned}$$In that case, we also say that T is symmetric or invariant with respect to S.
We note that it is elementary to show that the set of symmetries of an operator form a group.
Lemma A.4
Let \(\mathcal {H}\) be a complex Hilbert space. Then the set of symmetries of an operator in \(\mathcal {H}\) form a group.
Proof
If \(S_1\) and \(S_2\) are symmetries, then we see from Lemma A.2 (c), (d), and (e) that also \(S_1 S_2\) and \(S_1^{-1}\) are symmetries. \(\square \)
Appendix B: Eigenprojections and their Properties
In this appendix we recall well-known properties about isolated points of the spectrum. For a detailed treatment we refer the reader to the discussion in [31] surrounding Theorems XII.4 and XII.5.
Theorem B.1
Suppose that A is a closed operator with \(\{ z \in {\mathord {\mathbb C}}: |z- \lambda | = r \} \subset \rho (A)\) for some \(r> 0\). Then

and \({\overline{P}}:=1 - P\) are bounded projections with the following properties.
-
(a)
The ranges of P and \({\overline{P}}\) are complementary closed subspaces, that is \( \textrm{Ran}P + \textrm{Ran}{\overline{P}} = \mathcal {H}\) and \(\textrm{Ran}P \cap \textrm{Ran}{\overline{P}} = \{ 0 \}\). Moreover, A leaves these subspaces invariant. More precisely, \(\textrm{Ran}P \subset D(A)\), \(A \textrm{Ran}P \subset \textrm{Ran}P\), \(\textrm{Ran}{\overline{P}} \cap D(A)\) is dense in \(\textrm{Ran}{\overline{P}}\), and \(A \left[ \textrm{Ran}{\overline{P}} \cap D(A) \right] \subset \textrm{Ran}{\overline{P}}\).
-
(b)
For \(|z - \lambda | \ne r\)

exists and we have the following two cases.
-
(i)
If \(|z-\lambda |< r\), then \((A-z)|_{\textrm{Ran}{\overline{P}} \cap D(A)}\) is invertible and
$$\begin{aligned} {\hat{R}}_z = ((A-z)|_{\textrm{Ran}{\overline{P}} \cap D(A)})^{-1} {\overline{P}}, \end{aligned}$$i.e., \({\hat{R}}_z P = P {\hat{R}}_z = 0\), \((A-z) {\hat{R}}_z = {\overline{P}}\), and \({\hat{R}}_z (A-z) = {\overline{P}}\).
-
(ii)
If \(|z-\lambda | > r\), then \((A-z)|_{\textrm{Ran}{P}}\) is invertible and
$$\begin{aligned} {\hat{R}}_z = ((A-z)|_{\textrm{Ran}{P}})^{-1} {P}, \end{aligned}$$i.e., \({\hat{R}}_z {\overline{P}} = {\overline{P}} {\hat{R}}_z = 0\), \((A-z) {\hat{R}}_z = -P\), and \({\hat{R}}_z (A-z) = -P\).
-
(i)
-
(c)
We have \(\sigma (A) \cap B_r(\lambda ) = \sigma (A|_{\textrm{Ran}P})\) and \(\sigma (A) {\setminus } B_r(\lambda ) = \sigma (A|_{\textrm{Ran}{\overline{P}} \cap D(A)})\) where \(B_r(a) = \{ z \in {\mathord {\mathbb C}}: |z-a|< r \}\).
-
(d)
If \(\lambda \) is an isolated element of the spectrum \(\sigma (A)\) its algebraic multiplicity is greater or equal to its geometric multiplicity.
Sketch of Proof
(a) \(\textrm{Ran}P \subset D(A)\) follows by expressing the integral as a limit of Riemann sums, using that A is closed and the identity \(A (A-\mu )^{-1} = 1 + \mu (A-\mu )^{-1}\). The remaining properties are elementary to verify, for details see [31] Theorem XII.6 (or more precisely [31, Theorems XII.5 (b)] whose proof carries through without change).
(b) The algebraic identities are straight forward to verify. They then imply the property about the invertibility.
(c) For all \(z \in \rho (A)\) it follows from (a) that \((A-z)^{-1} = (A-z)^{-1} P + (A-z)^{-1} {\overline{P}} = ((A-z)|_{\textrm{Ran}P})^{-1} P + ( (A-z)|_{\textrm{Ran}{\overline{P}} \cap D(A)})^{-1} {\overline{P}} \). In view of this identity the claim now follows from (b).
(d) Let \(\lambda \) be an isolated element of the spectrum. As in Theorem 2.3 choose \(\epsilon > 0\) such that \(\{ \lambda \} = \sigma (A) \cap B_\epsilon (\lambda )\). Let \((A - \lambda ) v = 0\). Then for every \(r \in (0,\epsilon )\)

and so \(v \in \textrm{Ran}P_\lambda \). \(\square \)
Proposition B.2
Let R be a complex domain. Let \(R \ni s \mapsto T(s)\) be an analytic family. Suppose there is a non-defective eigenvalue E(s) isolated from the rest of the spectrum with analytic projection operator P(s). Let \({\overline{P}}(s) = 1 - P(s)\) and let
Then \(\Gamma \) is open and \((s,z) \mapsto (T(s) - z)^{-1} {\overline{P}}(s)\) is analytic on \(\Gamma \).
Proof
Let \((s_0,z_0) \in \Gamma \). There exists in a neighborhood of \(s_0\) a bijective operator \(U(s): \mathcal {H}\rightarrow \mathcal {H}\), analytic in s, such that \(U(s) P(s) U(s)^{-1} = P(s_0)\) and hence \(U(s) {\overline{P}}(s) U(s)^{-1} = {\overline{P}}(s_0)\), (cf. [31, Thm. XII.12]). The operator \({\widetilde{T}}(s) = U(s) T(s) U(s)^{-1}\) is an analytic family. It leaves the closed space \(\textrm{Ran}{\overline{P}}(s_0)\) invariant and thus \({\widetilde{T}}(s) |_{ \textrm{Ran}{\overline{P}}(s_0)}: \textrm{Ran}{\overline{P}}(s_0) \cap D({\widetilde{T}}(s)) \rightarrow \textrm{Ran}{\overline{P}}(s_0)\) is an analytic family as well. By this and the fact that \(({\widetilde{T}}(s_0) - z_0 ) |_{ \textrm{Ran}{\overline{P}}(s_0)}\) is bijective since \((s_0,z_0) \in \Gamma \), it follows by [31, Thm. XII.7] that in a neighborhood of \((s_0,z_0)\), the operator \(({\widetilde{T}}(s) - z ) |_{ \textrm{Ran}{\overline{P}}(s_0)}\) is bijective and \(({\widetilde{T}}(s) - z )^{-1} {\overline{P}}(s_0)\) is analytic in both variables. Thus in this neighborhood also the linear operator \((T(s) - z ) |_{ \textrm{Ran}{\overline{P}}(s)} = U(s)^{-1} ({\tilde{T}}(s) - z ) U(s) |_{ \textrm{Ran}{\overline{P}}(s)} \) is bijective and \((T(s)-z)^{-1} {\overline{P}}(s) = U(s)^{-1} ({\widetilde{T}}(s) - z )^{-1} {\overline{P}}(s_0) U(s)\) is an analytic function of two variables. \(\square \)
Appendix C: Field Operators, Elementary Estimates and Identities
We consider the Hilbert space \(\mathcal {H}= \mathcal {H}' \otimes \mathcal {F}\) consisting of a separable Hilbert space \(\mathcal {H}'\) and the bosonic Fock Space \(\mathcal {F}\).
Let \({X}:= {\mathord {\mathbb R}}^3 \times {\mathord {\mathbb Z}}_2\). For a separable Hilbert space \(\mathcal {H}'\) we define for \(n \ge 1\)
where \({\mathfrak {S}}_n \) denotes the set of permutations of \(\{1,\ldots ,n\}\). We set \(L^2_s( X^0; \mathcal {H}' ):= \mathcal {H}'\). We shall use the canonical identification [32]
For \(G \in L^2({\mathord {\mathbb R}}^3\times {\mathord {\mathbb Z}}_2; {\mathcal {L}}(\mathcal {H}'))\) the creation operator \(a^*(G)\) is by definition the adjoint of a(G), cf. (2.2). The domain of the creation operator contains the so called finite particle vectors \(\psi = (\psi _n)_{n =0}^\infty \in \mathcal {H}' \otimes \mathcal {F}\) with the property that \(\psi _n = 0\) for all but finitely many n, and \(a^*(G) \psi \) is a sequence of \(\mathcal {H}'\)-valued measurable functions such for n-th term
where \(\widetilde{ \ }\) means that this variable is to be omitted and the integral on the right hand side is defined as a Bochner integral. A straight forward calculation using (2.2) and (C.1) shows that on finite particle vectors we have the commutation relations
which extend to their natural domains.
Next we express the creation and annihilation operator in terms of so called operator valued distributions, \(a^*(k)\) and a(k). For an element \(\psi \in \mathcal {H}' \otimes {\mathcal {F}}\) we define \(a(k) \psi \) for a.e. \(k \in {\mathord {\mathbb R}}^3 \times {\mathord {\mathbb Z}}_2\) as the sequence of \(\mathcal {H}'\)-valued measurable functions such that the n-th term satisfies a.e.
Moreover, using Fubini’s theorem [32, Theorem I.21], it is elementary to see that the vector-valued map \(k \mapsto a(k) \psi \) is an element of \(L^2(X; \mathcal {H}' \otimes \mathcal {F})\). For \(G \in L^2({\mathord {\mathbb R}}^3\times {\mathord {\mathbb Z}}_2; {\mathcal {L}}(\mathcal {H}'))\) we obtain the following identity
which holds on finite particle vectors. The creation operator valued distribution \(a^*(k)\) is defined as the adjoint of a(k) in the sense of forms, i.e., we define the form \(\langle { \varphi , a^*(k) \psi } \rangle := \langle { a(k) \varphi , \psi } \rangle \) for smooth finite particle vectors \(\varphi ,\psi \). On such vectors one obtains the following identity in the sense of forms and weak integrals
Using (C.2) we can express the free field energy in terms of the following identity on vectors \(\varphi , \psi \in D(H_{\textrm{f}})\)
We use the following estimates on multiple occasions in this paper. They establish well known elementary estimates for the annihilation and creation operators introduced following Eq. (2.2).
Lemma C.1
For \(G \in L^{2}({\mathord {\mathbb R}}^3 \times {\mathord {\mathbb Z}}_2; {\mathcal {L}}(\mathcal {H}'))\) we have
Proof
By density it suffices to show the identities for smooth finite particle vectors \(\psi \in \mathcal {H}' \otimes \mathcal {F}\). In order to prove the first inequality we estimate
To prove the second inequality we use the commutation relations
\(\square \)
The subsequent lemma states the well-known Pull-Through Formula. It can be proved using Eq. (C.2). For a detailed proof we refer the reader to [6, 21].
Lemma C.2
Let \(f: {\mathord {\mathbb R}}_+ \rightarrow {\mathord {\mathbb C}}\) be a bounded measurable function. Then for all \(k \in {\mathord {\mathbb R}}^3 \times {\mathord {\mathbb Z}}_2\)
In order to define field operators that depend on the free field energy we consider measurable functions \(w_{m,n}\) on \({\mathord {\mathbb R}}_+ \times {X}^{n+m}\) with values in the bounded linear operators of \(\mathcal {H}'\). To such a function we associate the sesquilinear form
defined for all \(\varphi \) and \(\psi \) in \(\mathcal {H}' \otimes \mathcal {F}\), for which the integrand on the right hand side is integrable. Here the r.h.s. of (C.5) is defined by means of an iterated application of (C.2). If the integral kernel \(w_{m,n}\) has sufficient regularity and decay, one can show that the sesquilinear form (C.5) defines a closed linear operator which we denote by
In particular, in the case where \(w_{m,n} \in {\mathcal {W}}_{m,n}\), cf. (6.1), it follows from a simple application of Lemma C.3 that (C.6) is bounded operator. To formulate the next lemma we denote by \(B([0,\infty );{\mathcal {L}}(\mathcal {H}'))\) the Banach space of all bounded measurable functions on \([0,\infty )\) with values in the bounded linear operators of \(\mathcal {H}'\).
Lemma C.3
For measurable \(w: X^{m+n} \rightarrow B([0,\infty ); {\mathcal {L}}(\mathcal {H}'))\), we define
Then for all finitely many particle vectors \(\varphi , \psi \in \mathcal {H}' \otimes \mathcal {F}\)
If \(\Vert w_{m,n} \Vert _\sharp < \infty \), the form \(q_{w_{m,n}}\) determines uniquely a bounded linear operator \({h}_{w_{m,n}}\) such that
for all \(\varphi , \psi \) in \(\mathcal {H}' \otimes \mathcal {F}\) and \(\Vert h_{w_{m,n}} \Vert _{} \le \Vert w_{m,n} \Vert _\sharp \).
Proof
Let us first introduce the number operator N, which is the linear operator on \(\mathcal {H}' \otimes \mathcal {F}\) such that \(N |_{\mathcal {H}' \otimes \mathcal {F}_n} = n\). It is straight forward to verify that N is self-adjoint. First observe that \(q_{w_{m,n}}(\varphi ,\psi ) = q_{w_{m,n}}(1_{N \ge m} \varphi , 1_{N \ge n} \psi ) \). For \(n \in {\mathord {\mathbb N}}\) we set \(P[k^{(n)}]:= \prod _{l=1}^n ( H_{\textrm{f}} + \sum _{j=1}^l | k_j | )^{1/2}\) and insert \(\mathbb {1}\)’s into the left hand side of Eq. (C.7) to obtain the trivial identity
The lemma now follows using the Cauchy–Schwarz inequality and the following identities. Note that a proof of these identities can also be found in [3, Theorem 3.1] and [21, Appendix A]. First let \(\phi \in \textrm{Ran}1_{N \ge 1}\). Then by the pull-through formula, cf. Lemma C.2, and the relation in Eq. (C.3) satisfied by \(H_{\textrm{f}}\) we obtain
Note that the expressions in (C.8) are well defined for all nonzero integration variables k in view of Lemma C.1. Now suppose \(n \ge 2\) and \(\phi \in \textrm{Ran}1_{N \ge n}\). Then using analogous identities as in (C.8) we obtain by the definitions introduced in Sect. 6
where in (C.9) we relabeled the coordinates, and then proceeded analogously until in (C.10) we have pulled through all n annihilation operators.
The last statement of the lemma follows from the first and the Riesz lemma [32, Theorem II.4]. \(\square \)
Appendix D: The Smooth Feshbach–Schur Map
In this section we review properties of the Feshbach-Schur map, introduced in [3]. The presentation follows [16]. Let \(\chi \) and \({\overline{\chi }}\) be commuting non-zero bounded operators, acting on a separable Hilbert space \(\mathcal {H}\) satisfying \(\chi ^2 + {\overline{\chi }}^2 = 1\).
Definition D.1
A Feshbach pair (H, T) for \(\chi \) is a pair of closed operators with the same domain
such that \(H, T, W:= H - T\), and the operators
defined on D(T) satisfy the following assumptions
-
(a)
\(\chi T \subset T \chi \) and \({\overline{\chi }} T \subset T {\overline{\chi }}\).
-
(b)
\(T, H_{{\overline{\chi }}}: D(T) \cap \textrm{Ran}{\overline{\chi }} \rightarrow \textrm{Ran}{\overline{\chi }}\) are bijections with bounded inverse.
-
(c)
\({\overline{\chi }} H_{{\overline{\chi }}}^{-1} {\overline{\chi }} W \chi : D(T) \subset \mathcal {H}\rightarrow \mathcal {H}\) is a bounded operator.
Given a Feshbach pair (H, T) for \(\chi \), the operator
on D(T) is called Feshbach operator. The mapping \((H,T) \mapsto F_\chi (H,T)\) is called Feshbach map. We say that an operator \(A: D(A) \subset \mathcal {H}\rightarrow \mathcal {H}\) is bounded invertible in a subspace \(Y \subset \mathcal {H}\), if \(A: D(A) \cap Y \rightarrow Y\) is a bijection with bounded inverse. Note that Y does not necessarily need to be closed. If (H, T) is a Feshbach pair for \(\chi \), we define the following auxiliary operators
By conditions (a) and (c) \(Q_\chi \) and \(Q_\chi ^\#\) are bounded operators on D(T) and \(Q_\chi \) leaves D(T) invariant.
Theorem D.2
(Theorem 1, [16]) Let (H, T) be a Feshbach pair for \(\chi \) on a separable Hilbert space \(\mathcal {H}\). Then the following holds
-
(a)
Let Y be a subspace with \(\textrm{Ran}\chi \subset Y \subset \mathcal {H}\),
$$\begin{aligned} T : D(T) \cap Y \rightarrow Y, \quad \text { and } \quad {\overline{\chi }}T^{-1}{\overline{\chi }}Y \subset Y. \end{aligned}$$Then \(H: D(H) \subset \mathcal {H}\rightarrow \mathcal {H}\) is bounded invertible if and only if \(F_\chi (H,T): D(T) \cap Y \rightarrow Y\) is bounded invertible in Y. Moreover,
$$\begin{aligned} H^{-1}&= Q_\chi F_\chi (H,T)^{-1}Q_\chi ^\# + {\overline{\chi }}H_{{\overline{\chi }}}^{-1} {\overline{\chi }}\,, \\ F_\chi (H,T)^{-1}&= \chi H^{-1} \chi + {\overline{\chi }} T^{-1} {\overline{\chi }}\,. \end{aligned}$$ -
(b)
\(\chi \textrm{Ker}H \subset \textrm{Ker}F_\chi (H,T)\) and \(Q_\chi \textrm{Ker}F_\chi (H,T) \subset \textrm{Ker}H\). The mappings
$$\begin{aligned}&\chi : \textrm{Ker}H \rightarrow \textrm{Ker}F_\chi (H,T)\,,&Q_\chi : \textrm{Ker}F_\chi (H,T) \rightarrow \textrm{Ker}H \,, \end{aligned}$$are linear isomorphisms and inverse to each other.
Lemma D.3
(Lemma 3, [16]) Conditions (a), (b) and (c) on Feshbach pairs are satisfied if
-
(a’)
\(\chi T \subset T \chi \text { and } {\overline{\chi }}T \subset T{\overline{\chi }}\).
-
(b’)
T is bounded invertible on \(\textrm{Ran}{\overline{\chi }}\).
-
(c’)
\(\Vert T^{-1}{\overline{\chi }}W{\overline{\chi }}\Vert< 1 \quad \text { and } \quad \Vert {\overline{\chi }}WT^{-1}{\overline{\chi }}\Vert < 1\).
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Hasler, D., Lange, M. Degenerate Perturbation Theory for Models of Quantum Field Theory with Symmetries. Ann. Henri Poincaré 25, 2489–2545 (2024). https://doi.org/10.1007/s00023-023-01359-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00023-023-01359-1