Trapped Surface Formation for Spherically Symmetric Einstein–Maxwell-Charged Scalar Field System with Double Null Foliation

Abstract

In this paper, we generalize a method introduced by Christodoulou for studying the Einstein-scalar field to prove a trapped surface formation criterion for the Einstein–Maxwell-charged scalar field system under spherical symmetry. If we further require the initial charge to be sufficiently small, we obtain an almost-scale-critical result in the perturbative regime. In the “Appendix”, we also include a proof of Christodoulou’s result on trapped surface formation for the Einstein-scalar field using double null coordinates, as well as a strengthed scale-critical criterion in the case of Minkowskian incoming characteristic initial data.

Appendix

1.1 Trapped Surface Formation for the Einstein Scalar Field

Here, we provide a proof of Christodolou’s sharp trapped surface formation criterion as in [6]. In the case for the real scalar field, the system of Eqs. (2.4) to (2.12) is reduced to

$$\begin{aligned}&r\partial _v\partial _ur+\partial _vr\partial _ur=-\frac{\Omega ^2}{4}, \end{aligned}$$

(4.1)

$$\begin{aligned}&\partial _u(\Omega ^{-2}\partial _ur) = -4\pi r\Omega ^{-2}|\partial _u\phi |^2,\end{aligned}$$

(4.2)

$$\begin{aligned}&\partial _v(\Omega ^{-2}\partial _vr) = -4\pi r\Omega ^{-2}|\partial _v\phi |^2,\end{aligned}$$

(4.3)

$$\begin{aligned}&r\partial _u\partial _v\phi +\partial _ur\partial _v\phi +\partial _vr\partial _u\phi =0. \end{aligned}$$

(4.4)

Also, the derivatives of the Hawking mass become:

$$\begin{aligned}&\partial _um= =-8\pi r^2\Omega ^{-2}\partial _vr|\partial _u\phi |^2, \end{aligned}$$

(4.5)

$$\begin{aligned}&\partial _vm = -8\pi r^2\Omega ^{-2}\partial _ur|\partial _v\phi |^2. \end{aligned}$$

(4.6)

For convenience, we restate theorem 1.1 here.

Theorem 1.1. Define the function

$$\begin{aligned} E(x):=\frac{x}{(1+x)^2}\bigg [\ln \bigg (\frac{1}{2x}\bigg )+5-x\bigg ]. \end{aligned}$$

Consider the system (1.1) with characteristic initial data along $u=u_0$ and $v=v_1$. For initial mass input $\eta _0$ along $u=u_0$, if the following lower bound holds:

$$\begin{aligned} \eta _0>E(\delta _0), \end{aligned}$$

then a trapped surface $S_{u,v}$, with properties $\partial _v r(u,v)<0$ and $\partial _u r(u,v)< 0$, forms in the region $[u_0,u_*]\times [v_1,v_2]\subset \mathcal {R}$.

In this section, we will first give a few technical estimates to the dynamical quantities in the strip $[u_0,0]\times [v_1,v_2]$. These will be used in the proof for Theorem 1.1. We start off by showing that $\partial _ur$ is negative and bounded away from 0.

Lemma 4.1

$\partial _ur\le -\frac{1}{2}\Omega ^2$ everywhere in $\mathcal {D}(0,v_1)\cup \big ([u_0,0]\times [v_1,\infty )\big )$

Proof

Rewrite (4.1) as

$$\begin{aligned} \partial _v\big (r\partial _ur\big )=-\frac{\Omega ^2}{4}. \end{aligned}$$

Note that $\Omega ^2=1$ along C. Integrating both sides from 0 to v and dividing by r:

$$\begin{aligned} -\frac{v}{4r(u_0,v)} = \partial _ur(u_0,v). \end{aligned}$$

(4.7)

Setting $v = 0$ in the above gives us

$$\begin{aligned} -\frac{1}{4\partial _vr(u_0,0)}=\partial _ur(u_0,0) = -\partial _vr(u_0,0)\implies \partial _vr(u_0,0)=\frac{1}{2}. \end{aligned}$$

(4.8)

Since $\Omega ^2 = 1$ on C as well, (4.3) gives us that $\partial _v\partial _vr\le 0$, i.e., r is concave with respect to v. Combining this with the fact that $r(u_0,0) = v(u_0,0) = 0$, we have:

$$\begin{aligned} \frac{r}{v}(u_0,v)\le \partial _vr(u_0,0). \end{aligned}$$

Hence,

$$\begin{aligned} \frac{r}{v}(u_0,v)\le \frac{1}{2}. \end{aligned}$$

Substitute this into (4.7), we get

$$\begin{aligned} \partial _ur(u_0,v)\le -\frac{1}{2}. \end{aligned}$$

By (4.3), $\Omega ^{-2}\partial _ur$ is decreasing along incoming null geodesics. Hence for a general point in $\mathcal {D}(0,v_1)\cup \big ([u_0,0]\times [v_1,\infty )\big )$, we have $\Omega ^{-2}\partial _ur\le -\frac{1}{2}$. $\square$

Remark 4.2

$m(u,v)\ge 0$ for all $(u,v)\in \mathcal {D}(0,v_1)\cup \big ([u_0,0]\times [v_1,\infty )\big )$

Proof

Given any point $(u,v)\in \mathcal {R}$, we can extend the outgoing null geodesic backwards until it intersects $\Gamma$ at some coordinate $(u,v_c)$, so that $r(u,v_c) = 0$. Using (4.6), we have

$$\begin{aligned} \partial _vm = -8\pi r^2\Omega ^{-2}\partial _ur|\partial _v\phi |^2, \end{aligned}$$

and since $\partial _ur\le 0$ by Lemma 4.1, we get that $\partial _vm\ge 0$. Combining with the fact that $m(u,v_c) = 0$, we obtain the desired result. $\square$

Next, we show that the mixed derivative of r is always negative. This places a upper bound on the growth on the ratio $\frac{r_2}{r_1}$.

Proposition 4.3

Assume that $\mathcal {D}(0,v_1)\cup \mathcal {R}$ is free of trapped surfaces. Then, i) $\partial _u\partial _vr \le 0$ in $\mathcal {R}$ and ii) $\delta (x):=\frac{r_2}{r_1}-1\le \frac{1}{2}$ for $u\in [u_0,u_*]$.

Proof

We rewrite (4.1) into the following equivalent form:

$$\begin{aligned} \partial _u\partial _vr=-\frac{\Omega ^2}{{2}}\frac{m}{r^2}. \end{aligned}$$

(4.9)

Since $m\ge 0$, the right side of the above equation is non-positive. This proves the first part of the lemma.

Integrating with respect to u, we get:

$$\begin{aligned} \partial _vr(u)-\partial _vr(u_0){\le 0}\implies \partial _vr(u)\le \partial _vr(u_0). \end{aligned}$$

Integrating the above inequality with respect to v,

$$\begin{aligned} r_2(u)-r_1(u)\le r_2(u_0)-r_1(u_0), \text {for all } u\in [u_0,u_*]. \end{aligned}$$

Hence, we can use the above inequality to compute a bound for $\delta (u)$:

$$\begin{aligned} \begin{aligned} \delta (u) = \frac{r_2}{r_1}-1&=\frac{r_2-r_1}{r_2-(r_2-r_1)}\le \frac{r_2(u_0)-r_1(u_0)}{r_2(u)-(r_2(u_0)-r_1(u_0))}\\&\le \frac{\delta _0}{\frac{r_2(u)}{r_1(u_0)}-\delta _0}=\frac{\delta _0}{x(u)(1+\delta _0)-\delta _0},\text { for all }u\in [u_0,u_*], \end{aligned} \end{aligned}$$

(4.10)

where $x(u):=r_2(u)/r_2(u_0)$. Recall $r_2(u_*):=\frac{3\delta _0}{1+\delta _0}\cdot r_2(u_0)$ and since x(u) is monotonically decreasing, we have

$$\begin{aligned} x(u)\ge x(u_*) = \frac{3\delta _0}{1+\delta _0} \text { for }u\in [u_0,u_*], \end{aligned}$$

and hence

$$\begin{aligned} \delta (u)\le \frac{\delta _0}{2\delta _0} = \frac{1}{2}\text { for all }u\in [u_0,u_*]. \end{aligned}$$

$\square$

Next we prove two key lemmas. In the first one, we bound the difference in $r\partial _u\phi$ between $v=v_1$ and $v=v_2$. Then in the second, we bound the ratio of $\partial _vr$ between $v=v_1$ and $v=v_2$.

Lemma 4.4

Define $\Theta :=r_2\partial _u\phi _2-r_1\partial _u\phi _1$. Suppose that $\mathcal {D}(0,v_1)\cup \mathcal {R}$ is free of trapped surfaces. Then,

$$\begin{aligned} \Theta (u)^2\le \frac{\partial _ur_2}{8\pi \Omega _2^{-2}\partial _vr_2}(m_2-m_1)\bigg (\frac{1}{r_2}-\frac{1}{r_1}\bigg )(u) \end{aligned}$$

for all $u\in [u_0,u_*]$.

Proof

We can write the wave Eq. (4.4) as

$$\begin{aligned} \partial _v(r\partial _u\phi ) = -\partial _ur\partial _v\phi . \end{aligned}$$

By integrating the above equation, we get

$$\begin{aligned} \Theta ^2&= \big (r_2\partial _u\phi _2-r_1\partial _u\phi _1\big )^2\nonumber \\ {}&=\bigg |\int _{v_1}^{v_2}-\partial _ur\partial _v\phi \mathrm{d}v\bigg |^2\nonumber \le \bigg (\int _{v_1}^{v_2}-\partial _ur|\partial _v\phi | \mathrm{d}v\bigg )^2\nonumber \\&\le \frac{1}{8\pi }\int _{v_1}^{v_2}-8\pi r^2\partial _ur\Omega ^{-2}|\partial _v\phi |^2\mathrm{d}v\cdot \int _{v_1}^{v_2}-\frac{\partial _ur}{r^2\Omega ^{-2}}\mathrm{d}v \end{aligned}$$

(4.11)

where we have applied Holder’s inequality for the last inequality.

The first integral can be written in terms of the hawking mass:

$$\begin{aligned} \int _{v_1}^{v_2}-8\pi r^2\partial _ur\Omega ^{-2}|\partial _v\phi |^2\mathrm{d}v&=\int _{v_1}^{v_2}\partial _vm\,\mathrm{d}v\nonumber \\&=m_2-m_1. \end{aligned}$$

(4.12)

To bound the second integral, we apply Proposition 4.3 to get $\partial _v\partial _ur\le 0$, and hence $\partial _ur\ge \partial _ur_2$. Also, Eq. (4.3) implies that $\Omega _2^{-2}\partial _vr_2\le \Omega ^{-2}\partial _vr$. Combining these two pieces of information, we have

$$\begin{aligned} \int _{v_1}^{v_2}-\frac{\partial _ur}{r^2\Omega ^{-2}}\mathrm{d}v&=\int _{r_1}^{r_2}-\frac{\partial _ur}{r^2\Omega ^{-2}\partial _vr}\mathrm{d}r\nonumber \le -\partial _ur_2\int _{r_1}^{r_2}\frac{1}{r^2\Omega ^{-2}\partial _vr}\mathrm{d}r\nonumber \\&\le \frac{-\partial _ur_2}{\Omega _2^{-2}\partial _vr_2}\int _{r_1}^{r_2}\frac{1}{r^2}\mathrm{d}r=\frac{\partial _ur_2}{\Omega _2^{-2}\partial _vr_2}\big (\frac{1}{r_2}-\frac{1}{r_1}\big ) \end{aligned}$$

(4.13)

Substituting (4.12) and (4.13) back into (4.11) gives us the desired result. $\square$

Lemma 4.5

Assume that $\mathcal {D}(0,v_1)\cup \mathcal {R}$ is free of trapped surfaces. Then

$$\begin{aligned} \frac{\Omega _2^{-2}\partial _vr_2}{\Omega _1^{-2}\partial _vr_1}(u)\le e^{-\eta (u)} \end{aligned}$$

for all $u\in [u_0,u_*]$.

Proof

Dividing both sides of Eq. (4.3) by $\Omega ^{-2}\partial _vr$ and integrating from $v_1$ to $v_2$, we get

$$\begin{aligned} \ln |\Omega _2^{-2}\partial _vr_2|-\ln |\Omega _1^{-2}\partial _vr_1| = \ln \bigg (\frac{\Omega _2^{-2}\partial _vr_2}{\Omega _1^{-2}\partial _vr_1}\bigg )=-4\pi \int _{v_1}^{v_2}\frac{r|\partial _v\phi |^2}{\partial _vr}\mathrm{d}v. \end{aligned}$$

By Eq. (4.6) and the definition of the Hawking mass, we have

$$\begin{aligned} \frac{\partial _vm}{r-2m}=\frac{-8\pi r^2\Omega ^{-2}\partial _ur|\partial _v\phi |^2}{-4r\Omega ^{-2}\partial _ur\partial _vr}=\frac{2\pi r|\partial _v\phi |^2}{\partial _vr}. \end{aligned}$$

Hence for any $u\in [u_0,u_*]$

$$\begin{aligned}&\ln \bigg (\frac{\Omega _2^{-2}\partial _vr_2}{\Omega _1^{-2}\partial _vr_1}\bigg )\\&\quad =-2\int _{v_1}^{v_2}\frac{\partial _vm}{r-2m}\mathrm{d}v\le -2\int _{v_1}^{v_2}\frac{1}{r}\partial _vm\,\mathrm{d}v\\&\quad \le \frac{-2}{r_2}\int _{v_1}^{v_2}\partial _vm\text { }\mathrm{d}v=-\frac{2(m_2-m_1)}{r_2}=-\eta \end{aligned}$$

Exponentiating both sides of the above inequality gives us the desired result. $\square$

Now we are ready to prove Theorem 1.1.

Proof

(Theorem 1.1) We consider the dimensionless length scale $x(u):=\frac{r_2(u)}{r_2(u_0)}$. Note that x decreases as u increases and $x(u_0) = 1$. We will show that $\frac{\mathrm{d}\eta }{\mathrm{d}x}$ is bounded from above, i.e., $\frac{\mathrm{d}\eta }{\mathrm{d}u}$ is bounded from below, and hence obtain a lower bound for $\eta (u_*)$. If this lower bound is greater than 1, this implies $S(u_*,v_2)$ is a trapped surface, for

$$\begin{aligned} \eta (u_*)= \frac{2(m_2-m_1)}{r_2}(u_*)>1&\implies \frac{2m_2}{r_2}(u_*)>1\\&\implies S(u_*,v) \text { is a trapped surface.} \end{aligned}$$

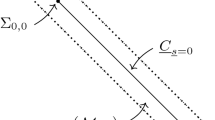
See Fig. 4 for an illustration.

Fig. 4

Idea of Proof of Theorem 1.1

To be precise, we prove a Gronwall-like inequality under the assumption that there is no trapped surface formed before $u_*$. In particular, we assume that $\partial _vr_2(u)>0$ for all $u\in [u_0,u_*]$. We show that this assumption will lead to a contradiction.

Assuming that $\partial _vr_2(u)>0$ for all $u\in [u_0,u_*]$, the following chain of identities hold in the region $[u_0,u_*]\times [v_1,v_2]$:

$$\begin{aligned} \frac{\mathrm{d}\eta }{\mathrm{d}x}&= \frac{\mathrm{d}\eta }{\mathrm{d}u}\bigg /\frac{\mathrm{d}x}{\mathrm{d}u} = \frac{r_2(u_0)}{\partial _ur_2}\bigg (-\frac{2\partial _ur_2}{r_2^2}(m_2-m_1)+\frac{2}{r_2}\partial _u(m_2-m_1)\bigg )\nonumber \\&=-\frac{\eta }{x}+\frac{2}{x\partial _ur_2}(-8\pi r_2^2\Omega _2^{-2}\partial _vr_2|\partial _u\phi _2|^2+8\pi r_1^2\Omega _1^{-2}\partial _vr_1|\partial _u\phi _1|^2)\nonumber \\&=-\frac{\eta }{x}-\frac{16\pi \partial _vr_2\Omega _2^{-2}}{x\partial _ur_2}\bigg (r_2^2|\partial _u\phi _2|^2-\frac{\Omega _1^{-2}\partial _vr_1}{\Omega _2^{-2}\partial _vr_2}r_1^2|\partial _u\phi _1|^2\bigg ). \end{aligned}$$

(4.14)

Using Lemma 4.5, we can bound the factor in the second term:

$$\begin{aligned} r_2^2|\partial _u\phi _2|^2-\frac{\Omega _1^{-2}\partial _vr_1}{\Omega _2^{-2}\partial _vr_2}r_1^2|\partial _u\phi _1|^2&\le r_2^2|\partial _u\phi _2|^2-e^\eta {r_1^2}|\partial _u\phi _1|^2\\&=\Theta ^2+2\Theta \partial _u\phi _1r_1+(1-e^\eta )r_1^2|\partial _u\phi _1|^2. \end{aligned}$$

The last expression, being a quadratic in $\Theta$, can be bounded by a monic quadratic polynomial in $\Theta$:

$$\begin{aligned} \Theta ^2+2\Theta \partial _u\phi _1r_1+(1-e^\eta )r_1^2|\partial _u\phi _1|^2&\le \bigg (1+\frac{1}{e^\eta -1}\bigg )\Theta ^2\le \bigg (1+\frac{1}{\eta }\bigg )\Theta ^2, \end{aligned}$$

since $\eta \ge 0$. This last inequality combines with (4.14) to give:

$$\begin{aligned} \frac{\mathrm{d}\eta }{\mathrm{d}x}\le -\frac{\eta }{x}-\frac{16\pi \partial _vr_2\Omega _2^{-2}}{x\partial _ur_2}\bigg (1+\frac{1}{\eta }\bigg )\Theta ^2. \end{aligned}$$

Applying Lemma 4.4, we have

$$\begin{aligned} \frac{\mathrm{d}\eta }{\mathrm{d}x}&\le -\frac{\eta }{x}-\frac{2}{x}\bigg (1+\frac{1}{\eta }\bigg )\bigg (\frac{1}{r_2}-\frac{1}{r_1}\bigg )(m_2-m_1)\nonumber \\&=-\frac{\eta }{x}+\frac{\eta }{x}\bigg (1+\frac{1}{\eta }\bigg )\bigg (\frac{r_2}{r_1}-1\bigg ). \end{aligned}$$

(4.15)

Using (4.10), we get

$$\begin{aligned} \delta = \frac{r_2-r_1}{r_2-(r_2-r_1)}\le \frac{r_2(u_0)-r_1(u_0)}{r_2(u)-(r_2(u_0)-r_1(u_0))}=\frac{\delta _0}{x(1+\delta _0)-\delta _0}. \end{aligned}$$

Combining the above with (4.15), we obtain

$$\begin{aligned} \frac{\mathrm{d}\eta }{\mathrm{d}x}\le \eta \bigg (\frac{\delta _0}{x^{{2}}(1+\delta _0)-{x}\delta _0}-\frac{1}{x}\bigg )+\frac{\delta _0}{x^{{2}}(1+\delta _0)-{x}\delta _0}. \end{aligned}$$

Defining $g(x):=1-\frac{\delta _0}{x(1+\delta _0)-\delta _0}$ and $f(x):=\frac{\delta _0}{x(1+\delta _0)-\delta _0}$, we obtain the following differential inequality:

$$\begin{aligned} \frac{\mathrm{d}\eta }{\mathrm{d}x}+\eta \frac{g(x)}{x}-\frac{f(x)}{x}\le 0. \end{aligned}$$

To solve this differential inequality, we multiply by an integrating factor then integrate with respect to x:

$$\begin{aligned}&\frac{\mathrm{d}}{\mathrm{d}x}\bigg (e^{-\int _x^1\frac{g(s)}{s}ds}\eta (x)\bigg )-e^{-\int _x^1\frac{g(s)}{s}ds}\frac{f(x)}{x}\le 0\\&\quad \implies \bigg [e^{-\int _{{x'}}^1\frac{g(s)}{s}ds}\eta (x')\bigg ]_{x'=x}^{x'=1}\le \int _x^1e^{-\int _{x'}^1\frac{g(s)}{s}ds}\frac{f}{x'}\mathrm{d}x'. \end{aligned}$$

We denote $G(x):= \int _x^1\frac{g(s)}{s}ds$ and $F(x):=\int _x^1e^{-G(x')}\frac{f}{x'}\mathrm{d}x'$. In this notation, we get

$$\begin{aligned} \eta _0-e^{-G(x)}\eta (x)\le F(x) \implies \eta (x)\ge e^{G(x)}\big (-F(x)+\eta _0\big ). \end{aligned}$$

Hence, in the region $[u_0,u_*]\times [v_1,v_2]$ free of trapped surfaces, we conclude that the following inequality holds:

$$\begin{aligned} \eta (x)\ge e^{G(x)}(-F(x)+\eta _0). \end{aligned}$$

(4.16)

Now, we compute explicit expressions for G(x) and F(x):

$$\begin{aligned} G(x)&= \int _x^1\frac{1}{s}-\frac{1}{s}\frac{\delta _0}{s(1+\delta _0)-\delta _0}ds\\&=\int _x^1\frac{1}{s}+\frac{1}{s}-\frac{1+\delta _0}{s(1+\delta _0)-\delta _0}ds\\&=\ln \bigg (\frac{s^2}{s(1+\delta _0)-\delta _0}\bigg )\bigg |^1_x = \ln \bigg (\frac{x(1+\delta _0)-\delta _0}{x^2}\bigg )\\ F(x)&= \int _x^1\frac{s^2}{s(1+\delta _0)-\delta _0}\frac{f}{s}ds = \int _x^1\frac{\delta _0s}{(s(1+\delta _0)-\delta _0)^2}ds\\&=\frac{\delta _0}{1+\delta _0}\int _x^1\frac{1}{s(1+\delta _0)-\delta _0}+\frac{\delta _0}{(s(1+\delta _0)-\delta _0)^2}ds\\&=\frac{\delta _0}{(1+\delta _0)^2}\ln \bigg (s(1+\delta _0)-\delta _0\bigg )\bigg |_x^1 - \frac{\delta _0^{{2}}}{(1+\delta _0)^2}\frac{1}{s(1+\delta _0)-\delta _0}\bigg |_x^1\\&=\frac{\delta _0}{(1+\delta _0)^2}\bigg (\ln \big (\frac{1}{x(1+\delta _0)-\delta _0}\big )+\delta _0\big (\frac{1}{x(1+\delta _0)-\delta _0}-1\big )\bigg ). \end{aligned}$$

Using the assumption that there is no trapped surface or MOTS, we have $\eta (x)=\frac{2(m_2-m_1)}{r_2}\le \frac{2m_2}{r_2}<1$ for $x\in [\frac{3\delta _0}{1+\delta _0},1]$. Rearranging (4.16) results in

$$\begin{aligned} \eta _0\le e^{-G(x)}\eta (x)+F(x)<e^{-G(x)}+F(x),\text { for all }x\in \bigg [\frac{3\delta _0}{1+\delta _0},1\bigg ]. \end{aligned}$$

In particular, we can substitute $x = \frac{3\delta _0}{1+\delta _0}$ into the above equation and get

$$\begin{aligned} \eta _0< E(\delta _0) = \frac{\delta _0}{(1+\delta _0)^2}\bigg [\log \big (\frac{1}{2\delta _0}\big )+5-\delta _0\bigg ]. \end{aligned}$$

This gives us the desired contradiction. $\square$

1.2 A Special Case of Minkowskian Incoming Characteristic Initial Data

Prescribe Minkowskian data along $v=v_1$, we can improve the lower bound required on $\eta _0$ in Theorem 1.1.

Theorem 1.2. Assume that Minkowskian data are prescribed along $v=v_1$ and require $\phi (u,v_1)=0$. Suppose that the following lower bound on $\eta _0$ holds:

$$\begin{aligned} \eta _0>\frac{9}{2}\delta _0, \end{aligned}$$

then there exist a MOTS or a trapped surface in $[u_0,u_*]\times [v_1,v_2]\subset \mathcal {R}$, i.e., $\partial _vr\le 0$ at some point in $[u_0,u_*]\times [v_1,v_2]$.

Proof

(Theorem 1.3) In this special case, we have $\phi _1\equiv 0$ and $m_1 \equiv 0$. Equation (4.14) now reads:

$$\begin{aligned} \frac{\mathrm{d}\eta }{\mathrm{d}x} = -\frac{\eta }{x}-\frac{16\pi \partial _vr_2\Omega _2^{-2}}{x\partial _ur_2}r_2^2|\partial _u\phi _2|^2, \end{aligned}$$

and we also have

$$\begin{aligned} \Theta ^2 = r_2^2|\partial _u\phi _2|^2. \end{aligned}$$

Combining the above equations, followed by applying Lemma 4.4, we get:

$$\begin{aligned} \frac{\mathrm{d}\eta }{\mathrm{d}x}&= -\frac{\eta }{x}-\frac{16\pi \partial _vr_2\Omega _2^{-2}}{x\partial _ur_2}\Theta ^2 \le -\frac{\eta }{x}-\frac{2}{x}\bigg (\frac{1}{r_2}-\frac{1}{r_1}\bigg )(m_2-m_1)\\&=-\frac{\eta }{x}+\frac{\eta }{x}\bigg (\frac{r_2}{r_1}-1\bigg )\le -\frac{\eta }{x}+\frac{\eta }{x}\frac{\delta _0}{x(1+\delta _0)-\delta _0}. \end{aligned}$$

Integrating the above inequality:

$$\begin{aligned}&\int _x^1\frac{1}{\eta }\mathrm{d}\eta \le \int _x^1-\frac{1}{s}+\frac{1}{s}\frac{\delta _0}{s(1+\delta _0)-\delta _0}ds=\int _x^1-\frac{2}{s}+\frac{1+\delta _0}{s(1+\delta _0)-\delta _0}ds\\&\quad \implies \ln \bigg (\frac{\eta _0}{\eta (x)}\bigg )\le \ln \bigg (\frac{x^2}{x(1+\delta _0)-\delta _0}\bigg )\\&\quad \implies \eta _0\le \eta (x)\frac{x^2}{x(1+\delta _0)-\delta _0}. \end{aligned}$$

Under the assumption of no trapped surfaces or MOTS, we have $\eta (x)<1$ for all $x\in [\frac{3\delta _0}{1+\delta _0},1]$, hence

$$\begin{aligned} \eta _0\le \frac{x^2}{x(1+\delta _0)-\delta _0}{\text {, for all }x\in \bigg [\frac{3\delta _0}{1+\delta _0},1\bigg ].} \end{aligned}$$

In particular, choosing $x=\frac{3\delta _0}{1+\delta _0}$ we have

$$\begin{aligned} \eta _0\le \frac{9}{2}\delta _0. \end{aligned}$$

This gives us the desired contradiction to the hypothesis. $\square$