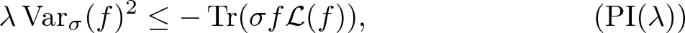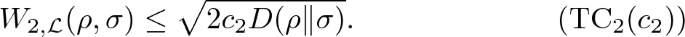Relating Relative Entropy, Optimal Transport and Fisher Information: A Quantum HWI Inequality

Abstract

Quantum Markov semigroups characterize the time evolution of an important class of open quantum systems. Studying convergence properties of such a semigroup and determining concentration properties of its invariant state have been the focus of much research. Quantum versions of functional inequalities (like the modified logarithmic Sobolev and Poincaré inequalities) and the so-called transportation cost inequalities have proved to be essential for this purpose. Classical functional and transportation cost inequalities are seen to arise from a single geometric inequality, called the Ricci lower bound, via an inequality which interpolates between them. The latter is called the HWI inequality, where the letters I, W and H are, respectively, acronyms for the Fisher information (arising in the modified logarithmic Sobolev inequality), the so-called Wasserstein distance (arising in the transportation cost inequality) and the relative entropy (or Boltzmann H function) arising in both. Hence, classically, the above inequalities and the implications between them form a remarkable picture which relates elements from diverse mathematical fields, such as Riemannian geometry, information theory, optimal transport theory, Markov processes, concentration of measure and convexity theory. Here, we consider a quantum version of the Ricci lower bound introduced by Carlen and Maas and prove that it implies a quantum HWI inequality from which the quantum functional and transportation cost inequalities follow. Our results hence establish that the unifying picture of the classical setting carries over to the quantum one.

1 Introduction

Realistic physical systems that are relevant for quantum information processing are inherently open. They undergo unwanted but unavoidable interactions with the surrounding environment and are hence subject to noise and decoherence. Under the Markovian approximation, which is valid when the system is only weakly coupled to its environment, the resulting dissipative dynamics of the system is described by a quantum Markov semigroup (QMS), whose generator we denote by ${{\mathcal {L}}}$. The analysis of quantum Markov semigroups is hence a key component of the theory of open quantum systems and quantum information. An important problem in the study of a QMS is the analysis of its convergence properties, in particular its mixing time, which is the time taken by any state evolving under the action of the QMS to come close to its invariant state.¹

1.1 Functional and Transportation Cost Inequalities

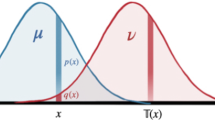
Classically, given a measure $\mu$, functional inequalities, e.g. the Poincaré inequality (usually denoted as PI($\lambda$)) [29] and the (modified) logarithmic Sobolev inequality (or log-Sobolev in short), denoted as MLSI($\alpha$) [22], constitute a powerful tool for deriving mixing times of a Markov semigroup with invariant measure $\mu$ and determining concentration properties of $\mu$. They are also related to the so-called transportation cost inequalities denoted by TC$_1(c_1)$ and TC$_2(c_2)$. Here $\alpha$, $c_1$ and $c_2$ denote constants appearing in the respective inequalities. Consider a compact manifold ${\mathcal {M}}$, and let ${{\mathcal {P}}}({\mathcal {M}})$ be the set of probability measures on ${\mathcal {M}}$. Given a measure $\mu \in {{\mathcal {P}}}({\mathcal {M}})$, the inequality TC$_1(c_1)$ (resp. TC$_2(c_2)$) provides an upper bound on the so-called Wasserstein distance $W_1$ (resp. $W_2$), between any probability measure $\nu \in {{\mathcal {P}}}({\mathcal {M}})$ and the given measure $\mu$, in terms of the square root of the relative entropy of $\nu$ with respect to $\mu$. Since $\mu$ is fixed, this relative entropy is simply a functional of $\nu$ and, due to its close links with the Boltzmann H-functional, is often denoted by the letter H in the literature. The notion of Wasserstein distances first appeared in the theory of optimal transport, which was initiated by Monge [21] and later analysed by Kantorovich [15]. In its original formulation by Monge, the problem of optimal transport concerns finding the optimal way, in the sense of minimal transportation cost, of moving a sand pile between two locations (see also [30]). In 1986, Marton [20] showed that transportation cost inequalities are also useful for deriving concentration of measure properties of the given measure $\mu$.²

The classical inequalities discussed above can be shown to be obtainable from a single geometric inequality, involving a quantity called the Ricci curvature of the manifold ${{\mathcal {M}}}$, and referred to as the Ricci lower bound. In fact, there is an inherent relation between the geometry of the manifold and a diffusion process (whose associated Markov semigroup has generator ${\mathcal {L}}$, say) defined on it: the diffusion process can be used to explore the geometry of ${{\mathcal {M}}}$, and conversely, the latter determines the mixing time of the diffusion process. Finding a quantum analogue of this appealing geometric inequality is hence a problem of fundamental interest and is considered in this paper. Before we present our results on this problem, we first need to explain the statement of the Ricci lower bound in the classical setting. In fact, it is instructive to start from the very definition of curvature which generalizes to the Ricci curvature for the case of a Riemannian manifold.

1.2 Ricci Curvature and Ricci Lower Bound (Classical Setting)

Given a surface $\mathcal {S}$ embedded in the Euclidean space $\mathbb {R}^3$, the Gauss curvature$\kappa$ of $\mathcal {S}$ is a measure of its local boundedness. More precisely, given a point $x\in \mathcal {S}$ and any two mutually orthogonal unit tangent vectors u, v at x, the distance between two geodesics $\gamma _u$ and $\gamma _v$, starting at x, with respective directions u and v, obeys the following Taylor expansions:

$$\begin{aligned} d_\mathrm{g}(\gamma _\mathbf {u}(t),\gamma _\mathbf {v}(t))=\sqrt{2}t\left( 1-\frac{\kappa (x)}{12}t^2+\mathcal {O}_{t\rightarrow 0}(t^3)\right) , \quad t \ge 0, \end{aligned}$$

(1.1)

where $d_\mathrm{g}$ is the geodesic distance defined with respect to the metric g induced on $\mathcal {S}$ by the Euclidean metric. In the case when $\kappa =0$ uniformly on the surface, the latter is flat, and we recover the Pythagoras theorem from Eq. (1.1). More generally, let x be a point on a d-dimensional compact Riemannian manifold $\mathcal {M}$, let u belong to the tangent space $T_x\mathcal {M}$ at the point x of $\mathcal {M}$, and complete the vector u into an orthonormal basis $(u,v_2,\ldots ,v_d)$ of $T_x\mathcal {M}$. Then, the Ricci curvature of ${\mathcal {M}}$, evaluated at u, is the averaged Gauss curvature over orthogonal surfaces defined by all the geodesics starting at x with direction given by the unit vectors belonging to the vector subspace spanned by u and any other vector $v_i$, $i=2,\ldots ,d$. The expression for the Ricci curvature [30] is given in terms of the Laplace–Beltrami operator (denoted simply as $\Delta$), and hence, the curvature is usually denoted as ${\text {Ric}}(\Delta )$. Since $\Delta$ is the generator of the heat semigroup, the curvature provides a bridge between the geometry of the manifold and the evolution on it induced by heat diffusion. There is an important inequality, known as the Ricci lower bound, which is denoted by ${\text {Ric}}(\Delta )\ge \kappa$ [3], and is the property that the Ricci curvature is uniformly bounded below by a real parameter $\kappa \ge 0$. Intuitively, the inequality is related to concentration of the uniform measure on ${\mathcal {M}}$, which is known to be the unique invariant measure of heat diffusion. For example, in the case of the sphere, which has constant Ricci curvature given in terms of its radius, the Haar measure can be shown to concentrate around any great circle. One can relax the condition of uniformity of the measure in order to allow for the study of concentration of measure phenomena for different measures $\mu$, invariant for other diffusions processes on $\mathcal {M}$. In this more general framework, the Ricci lower bound is denoted by ${\text {Ric}}(\mathcal {L})\ge \kappa$, where $\mathcal {L}$ denotes the generator of the diffusion semigroup associated with $\mu$ (Fig. 1).

Fig. 1

The Gauss curvature

More recently, Sturm [27, 28] and Lott–Villani [18] showed that ${\text {Ric}}(\mathcal {L})\ge \kappa$ can be viewed as a (refined) convexity property (called the $\kappa$-displacement convexity) of H along geodesics on the Riemannian manifold obtained by endowing the set of probability measures $\mathcal {P}(\mathcal {M})$ on $\mathcal {M}$ with the Wasserstein distance $W_2$ [31]. This discovery led to a more robust notion of a Ricci lower bound, which does not explicitly depend on the expression of the Ricci curvature, and hence can be extended to more general metric spaces. Starting from this convexity property, one can then construct a diffusion semigroup for which H decreases the most along the direction of evolution induced by the semigroup. In this case, the path on the Riemannian manifold $({{\mathcal {P}}}({{\mathcal {M}}}), W_2)$, which corresponds to the actual evolution under the diffusion, is said to be gradient flow for H. It is a striking fact that this diffusion coincides with the one whose generator appears in the Bakry–Émery condition (see [10, 14]).

In [23], the authors introduced the so-called HWI$(\kappa )$-interpolation inequality, using which they reproved the so-called Bakry–Émery theorem, which states that for $\kappa >0$, ${\text {Ric}}(\mathcal {L})\ge \kappa$ implies MLSI($\alpha$) (for diffusions on $\mathbb {R}^n$ with associated generator ${\mathcal {L}}$). The letters W, I and H are, respectively, acronyms for the Wasserstein distance $W_2$ (appearing in TC$_2(c_2)$), the Fisher information (which arises in MLSI($\alpha$)) and the relative entropy (also called the Boltzmann H-functional, as mentioned above) which appears in both these inequalities. They also showed that MLSI($\alpha$) implies TC$_2(c_2)$. The term interpolation here comes from the fact that in the case $\kappa =0$ and $c>0$, TC$_2$(c) together with HWI(0) gives back MLSI($\alpha$).

In [11, 12, 19], a modified version of the Ricci lower bound was defined for Markov processes on finite sets, which led to the unification of the previously discussed functional and concentration inequalities in this discrete framework. In particular, it was proved in [11] that one can recover the Poincaré and modified log-Sobolev inequalities from the Ricci lower bound, provided the diameter of ${{\mathcal {P}}}({{\mathcal {M}}})$, with respect to the Wasserstein distance, $W_2$, is bounded.

1.3 Ricci Lower Bound (Quantum Setting)

In the case of a quantum system with a finite-dimensional Hilbert space ${{\mathcal {H}}}$, the set $\mathcal {P}(\mathcal {M})$ is replaced by the set ${{\mathcal {D}}}({{\mathcal {H}}})$ of quantum states (i.e. density matrices) on ${{\mathcal {H}}}$. Then, in analogy with the classical case, starting with a primitive QMS with generator ${{\mathcal {L}}}$, Carlen and Maas [6, 7] defined a quantum Wasserstein distance $W_{2,\mathcal {L}}$ which renders ${{\mathcal {D}}}({{\mathcal {H}}})$ with a Riemannian structure, and for which the master equation associated with the QMS is gradient flow for the quantum relative entropy.

In [7], the authors proved that a quantum MLSI$(\alpha )$, first introduced in [16], holds provided the quantum relative entropy (between a state on a geodesic on this manifold and the invariant state of the QMS) satisfies a quantum analogue of the $\kappa$-displacement convexity property along geodesics, for $\alpha =\kappa >0$. This is denoted below by Ric$(\mathcal {L})\ge \kappa$ in analogy with the classical case, with ${\mathcal {L}}$ being the generator of the QMS.

The quantum versions of the Ricci lower bound, the HWI inequality, and the functional and transportation cost inequalities, all fit into a unifying picture which is analogous to the classical setting. It is given in Fig. 2.

Fig. 2

Chain of quantum functional- and Talagrand inequalities and related concentrations for a primitive semigroup $(\Lambda _t)_{t\ge 0}$ with generator $\mathcal {L}$ defined on a Hilbert space of dimension d. The implication MLSI$(\alpha )$$\Rightarrow$ PI$(\lambda )$ was proved in [16]. Here, “Exp.” refers to the notion of exponential concentration, whereas “Gauss.” refers to the stronger notion of Gaussian concentration. The implications MLSI($\alpha$)$\Rightarrow$TC$_2$($c_2$)$\Rightarrow$PI($\lambda$)$\Rightarrow$Exp., as well as TC$_2$($c_2$)$\Rightarrow$TC$_1$($c_1$)$\Rightarrow$Gauss. were proved in [24]

Our Contribution:

In this paper, we analyse the quantum version of the Ricci lower bound introduced by Carlen and Maas [7] and derive various implications of it in Theorem 3. Moreover, we show that ${\text {Ric}}(\mathcal {L})\ge \kappa$ implies a quantum version of the celebrated ${\text {HWI}}(\kappa )$ inequality which interpolates between the modified logarithmic Sobolev inequality and the transportation cost inequality (Theorem 5). We show that, in the case of $\kappa >0$, ${\text {HWI}}(\kappa )\Rightarrow {\text {MLSI}}(\kappa )$ (Corollary 2), recovering the result of [7]. On the other hand, in Corollary 3, we establish that in the case when $\kappa \in \mathbb {R}$, Ric($\mathcal {L}\ge \kappa$) together with TC$_2(c_2)$ implies MLSI$(\alpha )$. Moreover, in the case when $\kappa = 0$, we show that, under the assumption of boundedness of the diameter D of the set of states with respect to the quantum Wasserstein distance $W_{2,\mathcal {L}}$,  ${\text {Ric}}(\mathcal {L})\ge 0$ implies PI$(c_1D^{-2})$ for some universal constant $c_1$ (Theorem 6). Moreover, in the case of a unital QMS (i.e. one which has the completely mixed state as its unique invariant state), we show that it also implies MLSI$(c_2D^{-2})$ for some universal positive constant $c_2$ (Theorem 7). We hence extend the results of [11] to the quantum regime.

1.4 Layout of the Paper

In Sect. 2, we introduce the necessary notations and definitions, including quantum Markov semigroups, the quantum Wasserstein distance and quantum functional inequalities. The quantum version of $\kappa$-displacement convexity is studied in Sect. 3. In Sect. 4, we prove the quantum HWI$(\kappa )$ inequality, show that it implies ${\text {MLSI}}(\kappa )$ in the case when $\kappa >0$ and derive interpolation results between ${\text {MLSI}}(\kappa )$ and ${\text {TC}}_2(c_2)$ from it. In Sect. 5, we show that in the case in which $\kappa =0$, ${\text {PI}}(\lambda )$ holds with a constant $\lambda$ proportional to $D^{-2}$, where D stands for the diameter of the set of states. In Sect. 6, we show that under the further assumption of the QMS being unital, ${\text {MLSI}}(\alpha _1)$ holds with a constant $\alpha _1$ also proportional to $D^{-2}$.

2 Notations and Preliminaries

2.1 Operators, States and Entropic Quantities

In this paper, we denote by $({{\mathcal {H}}},\langle .|.\rangle )$ a finite-dimensional Hilbert space of dimension d with associated inner product $\langle .|.\rangle$, by ${{\mathcal {B}}}({{\mathcal {H}}})$ the algebra of linear operators acting on ${{\mathcal {H}}}$, and by ${{\mathcal {B}}}_{sa}({{\mathcal {H}}}) \subset {{\mathcal {B}}}({{\mathcal {H}}})$ the subspace of self-adjoint operators. Moreover, the Hilbert–Schmidt inner product $\langle .,.\rangle$, where $\langle A,B\rangle =\mathop {{\hbox {Tr}}}\nolimits (A^*B)$$\forall A,B\in {{\mathcal {B}}}({{\mathcal {H}}})$, provides ${{\mathcal {B}}}({{\mathcal {H}}})$ with a Hilbert space structure. Here, the trace $\mathop {{\hbox {Tr}}}\nolimits$ is unnormalized, adopting the uses of the community of quantum information theory, so that $\mathop {{\hbox {Tr}}}\nolimits (\mathbb {I})=d$. Let $\mathcal {P}({{\mathcal {H}}})$ be the cone of positive semi-definite operators on ${{\mathcal {H}}}$ and $\mathcal {P}_{+}({{\mathcal {H}}}) \subset \mathcal {P}({{\mathcal {H}}})$ the set of (strictly) positive operators. Further, let ${{\mathcal {D}}}({{\mathcal {H}}}):=\lbrace \rho \in \mathcal {P}({{\mathcal {H}}})\mid \mathop {{\hbox {Tr}}}\nolimits \rho =1\rbrace$ denote the set of density operators (or states) on ${{\mathcal {H}}}$, and ${{\mathcal {D}}}_+({{\mathcal {H}}}):={{\mathcal {D}}}({{\mathcal {H}}})\cap \mathcal {P}_+({{\mathcal {H}}})$ denote the subset of faithful states. We denote the support of an operator A by ${\mathrm {supp}}(A)$. Let $\mathbb {I}\in \mathcal {P}({{\mathcal {H}}})$ be the identity operator on ${{\mathcal {H}}}$, and $\mathrm{id}:{{\mathcal {B}}}({{\mathcal {H}}})\mapsto {{\mathcal {B}}}({{\mathcal {H}}})$ the identity map on operators on ${{\mathcal {H}}}$. For $p,q\ge 1$, the p-Schatten norm of an operator $A\in {{\mathcal {B}}}({{\mathcal {H}}})$ is denoted by $\Vert A\Vert _p:=(\mathop {{\hbox {Tr}}}\nolimits |A|^p)^{1/p}$, and the $p\rightarrow q$-norm of a superoperator $\Lambda :{{\mathcal {B}}}({{\mathcal {H}}})\rightarrow {{\mathcal {B}}}({{\mathcal {H}}})$ by $\Vert \Lambda \Vert _{p\rightarrow q}$. Such a linear map is said to be unital if $\Lambda (\mathbb {I})=\mathbb {I}$. Given two states $\rho ,\sigma \in {{\mathcal {D}}}({{\mathcal {H}}})$, the quantum relative entropy between $\rho$ and $\sigma$ is defined as:

$$\begin{aligned} {D}(\rho \Vert \sigma ):= \left\{ \begin{array}{ll} \mathop {{\hbox {Tr}}}\nolimits (\rho (\log \rho -\log \sigma )) &{}\quad {\text {if}}\,{\text {supp}}(\rho )\subseteq \mathop {\hbox {supp}}\nolimits (\sigma ),\\ +\infty &{}\quad {\text {else}}. \end{array} \right. \end{aligned}$$

2.2 Quantum Markov Semigroups and the Detailed Balance Condition

In the Heisenberg picture, a quantum Markov semigroup (QMS) on a finite-dimensional Hilbert space $\mathcal {H}$ is given by a one-parameter family $\left( \Lambda _t\right) _{t \ge 0}$ of linear, completely positive, unital maps on ${{\mathcal {B}}}({\mathcal {H}})$ satisfying the following properties

• $\Lambda _0 = {\mathrm{id}}$;

• $\Lambda _t\circ \Lambda _s = \Lambda _{t+s}$—semigroup property;

• $\forall X\in {{\mathcal {B}}}({{\mathcal {H}}}), \underset{t\rightarrow 0}{\lim } || \Lambda _t(X) - X||_\infty = 0$—strong continuity.

The parameter t plays the role of time. For each quantum Markov semigroup, there exists an operator $\mathcal {L}$ called the generator, or Lindbladian, of the semigroup, such that

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}\Lambda _t=\Lambda _t\circ \mathcal {L}=\mathcal {L}\circ \Lambda _t. \end{aligned}$$

(2.1)

In the Schrödinger picture, the dual of $\Lambda _t$ is written $\Lambda _{*t}$, for any $t\ge 0$. Similarly, we denote by ${{\mathcal {L}}}_*$ the dual of ${{\mathcal {L}}}$. The QMS is said to be primitive (or ergodic) if there exists a unique invariant state $\sigma$, i.e. such that $\Lambda _{*t}(\sigma )=\sigma$. Such a QMS is said to satisfy the detailed balance condition if the following holds:

$$\begin{aligned} \mathop {{\hbox {Tr}}}\nolimits (\sigma \mathcal {L}(X)^*Y)=\mathop {{\hbox {Tr}}}\nolimits ( \sigma X^*\mathcal {L}(Y)), \quad X,Y\in {{\mathcal {B}}}({{\mathcal {H}}}). \end{aligned}$$

(2.2)

In the context of quantum logarithmic Sobolev inequalities (introduced later), the quantum Fisher information of $\rho$ with respect to the state $\sigma$, first defined in [25], is particularly useful:

$$\begin{aligned} {\text {I}}_\sigma (\rho ):=\left\{ \begin{array}{ll} -\mathop {{\hbox {Tr}}}\nolimits (\mathcal {L}_*(\rho )(\log \rho -\log \sigma ) ), &{}\quad \rho \in {{\mathcal {D}}}_+({{\mathcal {H}}})\\ +\infty ,&{}\quad \text {otherwise}. \end{array}\right. \end{aligned}$$

This quantity is also referred to as entropy production and denoted by ${\text {EP}}_\sigma$ in the literature. We will use both notations in what follows. The following theorem provides a structure for the generators of primitive QMS satisfying the detailed balance condition:

Theorem 1

([1, 7]). Let $\sigma \in {{\mathcal {D}}}_+({{\mathcal {H}}})$, and let $(\Lambda _t)_{t\ge 0}$ be a quantum Markov semigroup on ${{\mathcal {B}}}({{\mathcal {H}}})$. Suppose that the generator $\mathcal {L}$ of $(\Lambda _t)_{t\ge 0}$ satisfies the detailed balance condition with respect to a full-rank invariant state $\sigma$. Then there exists an index set $\mathcal {J}$ of cardinality $|\mathcal {J}|\le d^2-1$, where $d=\dim ({{\mathcal {H}}})$, such that $\mathcal {L}$ takes the following form for any $f\in {{\mathcal {B}}}({{\mathcal {H}}})$:

$$\begin{aligned} \mathcal {L}(f)&=\sum _{j\in \mathcal {J}}c_j\left( \mathrm {e}^{-\omega _j/2}{\tilde{L}}_j^*[f,{\tilde{L}}_j]+\mathrm {e}^{\omega _j/2}[{\tilde{L}}_j,f]{\tilde{L}}_j^*\right) \end{aligned}$$

(2.3)

where $\omega _j\in \mathbb {R}$ and $c_j>0$ for all $j\in \mathcal {J}$, and $\{{\tilde{L}}_j\}_{j\in \mathcal {J}}$ is a set of operators in ${{\mathcal {B}}}({{\mathcal {H}}})$ with the properties:

• 1. $\frac{1}{\dim ({{\mathcal {H}}})} \mathrm{Tr}({\tilde{L}}_j^*{\tilde{L}}_k)=\delta _{k,j}$ for all $j,k\in \mathcal {J}$

• 2. $\mathrm{Tr}({\tilde{L}}_j)=0$ for all $j\in \mathcal {J}$

• 3. $\{{\tilde{L}}_j\}_{j\in \mathcal {J}}=\{{\tilde{L}}_j^*\}_{j\in \mathcal {J}}$

• 4. $\{{\tilde{L}}_j\}_{j\in \mathcal {J}}$ consists of eigenvectors of the modular operator $\Delta _\rho :f\mapsto \rho f \rho ^{-1}$ with

  $$\begin{aligned} \Delta _\sigma ({\tilde{L}}_j)=\mathrm {e}^{-\omega _j}{\tilde{L}}_j. \end{aligned}$$

Finally for each $j\in \mathcal {J}$

$$\begin{aligned} c_j=c_{j'}, \text { and }~ \omega _j=-\omega _{j'}~\text { when }{\tilde{L}}_j^*={\tilde{L}}_{j'}. \end{aligned}$$

(2.4)

Conversely, given any faithful (full-rank) state $\sigma$, any set $\{{\tilde{L}}_j\}_{j\in \mathcal {J}}$ satisfying the above four conditions for some $\{\omega _j\}_{j\in \mathcal {J}}\subset \mathbb {R}$ and any set $\{c_j\}_{j\in \mathcal {J}}$ of positive numbers satisfying the symmetry condition (2.4), the operator $\mathcal {L}$ given by Eq. (2.3) is the generator of a quantum Markov semigroup $(\Lambda _t)_{t\ge 0}$ which satisfies the detailed balance condition.

2.3 The Wasserstein Distance $W_{2,\mathcal {L}}$

In this section, we recall the construction of the Wasserstein metric $W_{2,\mathcal {L}}$ first defined in [7]. Assume given a generator $\mathcal {L}$ of a primitive QMS, with invariant state $\sigma$, of the form of (2.3). Given an operator $X\in {{\mathcal {B}}}({{\mathcal {H}}})$, its non-commutative gradient is defined as:

$$\begin{aligned} \nabla X:=(\partial _1X,\ldots ,\partial _{\mathcal {J}}X), \quad X\in {{\mathcal {B}}}({{\mathcal {H}}}), \end{aligned}$$

where $\partial _j X=[{\tilde{L}}_j,X]$ for all $j\in \mathcal {J}$. Similarly, given a vector $\mathbf {A}\equiv (A_1,\ldots ,A_{|{{\mathcal {J}}}|})\in \bigoplus _{j\in {{\mathcal {J}}}}{{\mathcal {B}}}({{\mathcal {H}}})$, the divergence of $\mathbf {A}$ is defined as

$$\begin{aligned} {\text {div}}(\mathbf {A}):=\sum _{j\in \mathcal {J}} c_j[A_j,{\tilde{L}}_j^*]\equiv - \sum _{j\in {{\mathcal {J}}}}c_j \partial ^*_j A_j, \end{aligned}$$

where $\partial _j^*X:=[{\tilde{L}}_j^*,X]$. For $\vec {\omega }:=(\omega _1,\ldots ,\omega _{|\mathcal {J}|})$, define the linear operator $[\rho ]_{\vec {\omega }}$ on $\bigoplus _{j\in \mathcal {J}}{{\mathcal {B}}}({{\mathcal {H}}})$ through

$$\begin{aligned} {[}\rho ]_{\vec {\omega }}\mathbf {A}:=([\rho ]_{\omega _1}A_1,\ldots ,[\rho ]_{\omega _{|\mathcal {J}|}}A_{|\mathcal {J}|}),~~~~~~~~\mathbf {A}\equiv (A_1,\ldots ,A_{|\mathcal {J}|}), \end{aligned}$$

where for any $\omega \in \mathbb {R}$,

$$\begin{aligned}{}[\rho ]_\omega :=R_\rho \circ f_\omega (\Delta _{\rho }),~~~~f_\omega (t):=\mathrm {e}^{\omega /2}\frac{t-\mathrm {e}^{-\omega }}{\log t+\omega },~~~~t\in \mathbb {R}, \end{aligned}$$

(2.5)

where $R_\rho :{{\mathcal {B}}}({{\mathcal {H}}})\rightarrow {{\mathcal {B}}}({{\mathcal {H}}})$ denotes the operator of left multiplication by $\rho$. Intuitively, $[\rho ]_\omega$ can be understood as a non-commutative way of multiplying by $\rho$:

Lemma 1

(see Lemma 5.8 of [7]). For any $\omega \in \mathbb {R}$, and $\rho \in {{\mathcal {D}}}_+({{\mathcal {H}}})$,

$$\begin{aligned} {[}\rho ]_{\omega }(A)=\int _0^1 \mathrm {e}^{\omega (1/2-s)}\rho ^s A\rho ^{1-s}\mathrm{d}s. \end{aligned}$$

Let $(\gamma (s))_{s\in (-\varepsilon ,\varepsilon )}$ be a differential path in ${{\mathcal {D}}}_+({{\mathcal {H}}})$ for some $\varepsilon >0$ and denote $\rho :=\gamma (0)$. Then $\mathop {{\hbox {Tr}}}\nolimits (\dot{\gamma }(0))=\left. \frac{\mathrm{d}}{\mathrm{d}s}\right| _{s=0}\mathop {{\hbox {Tr}}}\nolimits (\gamma (s))=0$. Carlen and Maas proved that there is a unique vector field $\mathbf {V}\in \bigoplus _{j\in \mathcal {J}} {{\mathcal {B}}}({{\mathcal {H}}})$ of the form $\mathbf {V}=\nabla U$, where $U\in {{\mathcal {B}}}({{\mathcal {H}}})$ is traceless and self-adjoint, for which the following non-commutative continuity equation holds:

$$\begin{aligned} \dot{\gamma }(0)=-{\text {div}}([\rho ]_{\vec {\omega }}\nabla U). \end{aligned}$$

(2.6)

Define the inner product $\langle .,. \rangle _{\mathcal {L},\rho }$ on $\bigoplus _{j\in \mathcal {J}}{{\mathcal {B}}}({{\mathcal {H}}})$ through:

$$\begin{aligned} \langle \mathbf {W},\mathbf {V}\rangle _{\mathcal {L},\rho }:=\sum _{j\in \mathcal {J}} c_j \langle W_j,[\rho ]_{\omega _j}{V}_j\rangle , \end{aligned}$$

(2.7)

where $\langle A,B\rangle :=\mathop {{\hbox {Tr}}}\nolimits (A^* B)$ denotes the usual Hilbert–Schmidt inner product on ${{\mathcal {B}}}({{\mathcal {H}}})$. Hence, looking upon ${{\mathcal {D}}}_+({{\mathcal {H}}})$ as a manifold, for each $\rho \in {{\mathcal {D}}}_+({{\mathcal {H}}})$, we can identify the tangent space $T_\rho$ at $\rho$ with the set of gradient vector fields $\{\nabla U:~U\in {{\mathcal {B}}}({{\mathcal {H}}}),~ U=U^*\}$ through the correspondence provided by the continuity equation (2.6). Defining the metric $g_\mathcal {L}$ through the relation

$$\begin{aligned} \Vert \dot{\gamma }(0)\Vert _{g_{\mathcal {L},\rho }}^2:= \Vert \mathbf {V}(0)\Vert ^2_{\mathcal {L},\rho }, \end{aligned}$$

(2.8)

this endows the manifold ${{\mathcal {D}}}_+({{\mathcal {H}}})$ with a smooth Riemannian structure. In this framework, Carlen and Maas then defined the modified non-commutative Wasserstein distance$W_{2,\mathcal {L}}$ to be the energy associated with the metric $g_{\mathcal {L}}$, i.e.:

$$\begin{aligned} W_{2,\mathcal {L}}(\rho ,\sigma ):=\inf _{\gamma }\left\{ \left( \int _0^1 \Vert \mathbf {V}(s)\Vert ^2_{\mathcal {L},\gamma (s)} \mathrm{d}s\right) ^{1/2}:\gamma (0)=\rho , \gamma (1)=\sigma \right\} , \end{aligned}$$

(2.9)

where the infimum is taken over smooth paths $\gamma :[0,1]\rightarrow {{\mathcal {D}}}_+({{\mathcal {H}}})$, and $\mathbf {V}:[0,1]\rightarrow \bigoplus _{i\in {{\mathcal {J}}}}{{\mathcal {B}}}({{\mathcal {H}}})$ is related to $\gamma$ through the continuity equation (2.6). The paths achieving the infimum, if they exist, are the minimizing geodesics with respect to the metric $g_\mathcal {L}$. The following lemma, proved in [24], follows from a standard argument:

Lemma 2

With the above notations, the Wasserstein distance between two faithful states $\rho ,\sigma$ is equal to the minimal length over the smooth paths joining $\rho$ and $\sigma$:

$$\begin{aligned} W_{2,\mathcal {L}}(\rho ,\sigma )=\inf _{\gamma (s)\text { const. speed}}\left\{ \int _0^1 \Vert \dot{\gamma }(s)\Vert _{g_{\mathcal {L},\gamma (s)}}\mathrm{d}s:~\gamma (0)=\rho ,~\gamma (1)=\sigma \right\} , \end{aligned}$$

(2.10)

where the infimum is taken over curves $\gamma$ of constant speed, i.e. such that $s\mapsto \Vert \dot{\gamma }(s)\Vert _{g_{\mathcal {L},\gamma (s)}}$ is constant on [0, 1].

This definition for the quantum Wasserstein distance, $W_{2,\mathcal {L}}$, is natural in the sense that the master equation

$$\begin{aligned} \dot{\rho }_t=\mathcal {L}_*\rho _t, \end{aligned}$$

is gradient flow for $D(.\Vert \sigma )$, where $\sigma$ is the invariant state associated with $\mathcal {L}$. This means that $\mathcal {L}_* \rho =-{\text {grad}}_\mathcal {L}D(\rho \Vert \sigma )$, where the gradient ${\text {grad}}_{\mathcal {L}}$ of a differentiable functional $\mathcal {F}:{{\mathcal {D}}}_+({{\mathcal {H}}})\rightarrow \mathbb {R}$ is defined as the unique element in the tangent space at $\rho$ so that

$$\begin{aligned} \left. \frac{\mathrm{d}}{\mathrm{d}t}\mathcal {F}(\gamma (t))\right| _{t=0}=g_{\mathcal {L},\rho }(\dot{\gamma },{\text {grad}}_{g_{\mathcal {L},\rho }}\mathcal {F}(\rho )) \end{aligned}$$

(2.11)

for all smooth paths $\gamma (t)$ defined on $(-\varepsilon ,\varepsilon )$ for some $\varepsilon >0$ with $\gamma (0)=\rho$. In particular, for $\gamma (t)=\rho _t\equiv \Lambda _{*t}(\rho )$,

$$\begin{aligned} \left. \frac{\mathrm{d}}{\mathrm{d}t}D(\rho _t\Vert \sigma )\right| _{t=0}=-g_{\mathcal {L},\rho }(\mathcal {L}_*(\rho ),\mathcal {L}_*(\rho ))=-\Vert \mathcal {L}_*(\rho )\Vert _{g_{\mathcal {L},\rho }}^2. \end{aligned}$$

(2.12)

The following lemma is going to play a crucial role in the rest of this paper:

Lemma 3

For any $\rho \in {{\mathcal {D}}}_+({{\mathcal {H}}})$, the map $D_{\vec {\omega }}(\rho ): U\mapsto -{\text {div}}([\rho ]_{\vec {\omega }} \nabla U)$ is invertible and positive in the sense of Loewner order on the Hilbert space of self-adjoint, traceless operators. Moreover, if $\rho \ge \varepsilon \mathbb {I}$ for some $\varepsilon >0$, then:

$$\begin{aligned} D_{\vec {\omega }}(\rho )^{-1} \le K_\mathcal {L}~ \varepsilon ^{-1} ~\mathrm{id}, \end{aligned}$$

where $K_\mathcal {L}:=\sup _{j\in {{\mathcal {J}}}} \frac{\omega _j}{\mathrm {e}^{\omega _j/2}-\mathrm {e}^{-\omega _j/2}}\Vert (-{\text {div}}\circ \nabla (.))^{-1}\Vert _{2\rightarrow 2}>0$.

Proof

Let $\mathcal {W}$ be the space of self-adjoint, traceless operators on ${{\mathcal {H}}}$. From Theorem 7.3 of [7], for any $C^1$ path $(\gamma (t))_{t\in (-\varepsilon ,\varepsilon )}$, with $\gamma (0)=\rho$, there exists a unique vector field of the form $\nabla U$ for which the continuity equation $\dot{\gamma }(0)= -{\text {div}} ([\rho ]_{\vec {\omega }}(\nabla U))$ holds. Moreover, by ergodicity of $(\Lambda _t)_{t\ge 0}$, $\ker (\nabla )$ consists of multiples of the identity. Therefore, there exists a unique $U\in \mathcal {W}$ such that $\dot{\gamma }(0)= -{\text {div}} ([\rho ]_{\vec {\omega }}(\nabla U))$. Now, for any $U,V\in \mathcal {W}$:

$$\begin{aligned} \langle U,D_{\vec {\omega }}(\rho )[V]\rangle&=\sum _{j\in {{\mathcal {J}}}} c_j \langle \partial _jU,[\rho ]_{\omega _j} \partial _j V\rangle \\&= \sum _{j\in {{\mathcal {J}}}} c_j\langle [\rho ]_{\omega _j}\partial _j U, \partial _j V\rangle \\&=\sum _{j\in {{\mathcal {J}}}} c_j \langle \partial _j^*([\rho ]_{\omega _j} \partial _j U), V\rangle \\&=-\langle {\text {div}}([\rho ]_{\vec {\omega }}\nabla U),V\rangle \\&= \langle D_{\vec {\omega }}(\rho )[U],V\rangle , \end{aligned}$$

which means that $D_{\vec {\omega }}(\rho )$ is indeed self-adjoint. By the same argument, we can show that the superoperators $\nabla : {{\mathcal {B}}}({{\mathcal {H}}})\rightarrow \oplus _{j\in {{\mathcal {J}}}}{{\mathcal {B}}}({{\mathcal {H}}})$ and $-{\text {div}}:\oplus _{j\in {{\mathcal {J}}}}{{\mathcal {B}}}({{\mathcal {H}}})\rightarrow {{\mathcal {B}}}({{\mathcal {H}}})$ are adjoint to each other, where ${{\mathcal {B}}}({{\mathcal {H}}})$ and $\oplus _{j\in {{\mathcal {J}}}}{{\mathcal {B}}}({{\mathcal {H}}})$ are provided with the inner products $\langle .,. \rangle$ and $\sum _{j\in {{\mathcal {J}}}} c_j\, \langle .,.\rangle$, respectively. Indeed for any $U\in {{\mathcal {B}}}({{\mathcal {H}}})$ and $\mathbf {V}=(V_1,\ldots ,V_{|{{\mathcal {J}}}|})\in \oplus _{j\in {{\mathcal {J}}}} {{\mathcal {B}}}({{\mathcal {H}}})$:

$$\begin{aligned} \sum _{j\in {{\mathcal {J}}}} c_j \langle V_j ,\partial _j U\rangle&= \sum _{j\in {{\mathcal {J}}}} c_j \mathop {{\hbox {Tr}}}\nolimits ((V_j)^* [{\tilde{L}}_j,U] )\\&= \sum _{j\in {{\mathcal {J}}}} c_j \mathop {{\hbox {Tr}}}\nolimits ( [V_j^* ,{\tilde{L}}_j] U )\\&= - \sum _{j\in {{\mathcal {J}}}} c_j \mathop {{\hbox {Tr}}}\nolimits ( [V_j ,{\tilde{L}}_j^*]^* U )\\&=\langle -{\text {div}}(\mathbf {V}),U\rangle . \end{aligned}$$

Assume now that $\rho \ge \varepsilon \mathbb {I}$ for some $\varepsilon >0$, so that for any $j\in {{\mathcal {J}}}$:

$$\begin{aligned}{}[\rho ]_{\omega _j}=\int _0^1 \mathrm {e}^{\omega _j(1/2-\alpha )}L_\rho ^\alpha R_\rho ^{1-\alpha }\mathrm{d}\alpha \ge \varepsilon \frac{\mathrm {e}^{\omega _j/2}-\mathrm {e}^{-\omega _j/2}}{\omega _j}\mathrm{id}>0. \end{aligned}$$

Hence, $-{\text {div}} \circ [\rho ]_{\vec {\omega }}\circ \nabla ( .)$ is positive and

$$\begin{aligned} ( -{\text {div}} \circ [\rho ]_{\vec {\omega }}\circ \nabla ( .) )^{-1}\le \varepsilon ^{-1}\sup _{j\in {{\mathcal {J}}}} \frac{\omega _j}{\mathrm {e}^{\omega _j/2}-\mathrm {e}^{-\omega _j/2}} (-{\text {div}}\circ \nabla (.))^{-1}, \end{aligned}$$

and the result follows. $\square$

The above lemma allows us to extend the definition of the Wasserstein distance to non-faithful states:

Proposition 1

(Extension of the metric to ${{\mathcal {D}}}({{\mathcal {H}}})$). Let $\rho ,\omega \in {{\mathcal {D}}}({{\mathcal {H}}})$ and let $\{\rho _n\}_{n\in \mathbb {N}}$ and $\{\omega _n\}_{n\in \mathbb {N}}$ be sequences of faithful states satisfying

$$\begin{aligned} \mathrm{Tr}[(\rho -\rho _n)^2]\rightarrow 0,~~~~~\mathrm{Tr}[(\omega -\omega _n)^2]\rightarrow 0, \end{aligned}$$

(2.13)

as $n\rightarrow \infty$. Then the sequence $\{W_{2,\mathcal {L}}(\rho _n,\omega _n)\}_{n\in \mathbb {N}}$ converges. Moreover, the limit does not depend on the choice of the approximating sequences $\{\rho _n\}_{n\in \mathbb {N}}$ and $\{\omega _n\}_{n\in \mathbb {N}}$.

Proof

The proof is similar to the one given in Proposition 4.5 of [6]. It is enough to show that $\{W_{2,\mathcal {L}}(\rho _n,\omega _n)\}_{n\in \mathbb {N}}$ is Cauchy. By the triangle inequality, it is even enough to prove that $W_{2,\mathcal {L}}(\rho _n,\rho _m)\rightarrow 0$ as $m,n\rightarrow \infty$. Let $\varepsilon \in (0,1)$ and set $\bar{\rho }:=(1-\varepsilon )\rho +\varepsilon \frac{\mathbb {I}}{d}$. Let $N\in \mathbb {N}$ be such that for any $n\ge N$, $\mathop {{\hbox {Tr}}}\nolimits [(\rho -\rho _n)^2]\le \varepsilon ^2$. For $n\ge N$, consider the convex interpolation $\gamma (s):= (1-s) \rho _n + s\bar{\rho }$. Since $\gamma (s) \ge \varepsilon s\frac{\mathbb {I}}{d}$ for $s\in [0,1]$, we find from Eq. 2.10 that

$$\begin{aligned} W_{2\mathcal {L}}(\rho _n,\bar{\rho })&\le \int _0^1 \Vert \dot{\gamma }(s)\Vert _{g_{\mathcal {L},\gamma (s)}}\mathrm{d}s\\&=\int _0^1 \left[ \sum _{j\in {{\mathcal {J}}}} c_j \langle \partial _j (-{\text {div}}\circ [\gamma (s)]_{\vec {\omega }}\circ \nabla )^{-1} (\dot{\gamma }(s)),\right. \\&\left. \quad [\gamma (s)]_{\omega _j} \partial _j (-{\text {div}}\circ [\gamma (s)]_{\vec {\omega }}\circ \nabla )^{-1} (\dot{\gamma }(s)) \rangle \right] ^{\frac{1}{2}}\mathrm{d}s \\&= \int _0^1 \sqrt{\langle \dot{\gamma }(s), ( -{\text {div}}([\gamma (s)]_{\vec {\omega }} \nabla (.)) )^{-1}~ \dot{\gamma }(s)\rangle } \mathrm{d}s \\&\le \sqrt{\frac{d\,K_\mathcal {L}}{\varepsilon }}\int _0^1 s^{-1/2} \sqrt{\mathop {{\hbox {Tr}}}\nolimits [(\dot{\gamma }(s))^2]} \mathrm{d}s, \end{aligned}$$

where we used Lemma 3 in the second, third and fourth lines above. Now

$$\begin{aligned} \mathop {{\hbox {Tr}}}\nolimits [(\dot{\gamma }(s))^2]&=\mathop {{\hbox {Tr}}}\nolimits [ (\rho -\rho _n +\varepsilon ({\mathbb {I}}/{d} -\rho ))^2 ]\\&\le 2\mathop {{\hbox {Tr}}}\nolimits [ ( \rho -\rho _n )^2 ]+2\varepsilon ^2 \mathop {{\hbox {Tr}}}\nolimits [(\mathbb {I}/d -\rho )^2]\\&\le 2\left( 1+\mathop {{\hbox {Tr}}}\nolimits [(\mathbb {I}/d-\rho )^2]\right) \varepsilon ^2. \end{aligned}$$

Hence, $W_{2,\mathcal {L}}(\rho _n,\bar{\rho })\le \sqrt{K(\mathcal {L},\rho ) \varepsilon }$, for some constant $K(\mathcal {L},\rho )$ depending on $\rho$ and $\mathcal {L}$. Since $\varepsilon$ is arbitrary, we conclude by triangle inequality that $W_{2,\mathcal {L}}(\rho _m,\rho _n)\le W_{2,\mathcal {L}}(\rho _m,\bar{\rho })+ W_{2,\mathcal {L}}(\bar{\rho },\rho _n) \rightarrow 0$. $\square$

The above proposition justifies the following definition: The modified Wasserstein distance $W_{2,\mathcal {L}}$ between two states $\rho ,\omega \in {{\mathcal {D}}}({{\mathcal {H}}})$ is defined as

$$\begin{aligned} W_{2,\mathcal {L}}(\rho ,\omega ):=\lim _{n\rightarrow \infty } W_{2,\mathcal {L}}(\rho _n,\omega _n), \end{aligned}$$

where $\{\rho _n\}_{n\in \mathbb {N}}$ and $\{\omega _n\}_{n\in \mathbb {N}}$ are arbitrary sequences in ${{\mathcal {D}}}_+({{\mathcal {H}}})$ satisfying (2.13). It can be shown that $({{\mathcal {D}}}({{\mathcal {H}}}),W_{2,\mathcal {L}})$ forms a complete metric space as follows:

Lemma 4

For any $\rho ,\omega \in {{\mathcal {D}}}({{\mathcal {H}}})$,

$$\begin{aligned} \Vert \rho -\omega \Vert _1\le 2 \left( \sum _{j\in \mathcal {J}} c_j (\mathrm {e}^{-\omega _j/2}+\mathrm {e}^{\omega _j/2})\Vert {\tilde{L}}_j\Vert ^2_\infty \right) ^{1/2} ~W_{2,{\mathcal {L}}}(\rho ,\omega ). \end{aligned}$$

Proof

The proof follows from a direct application of inequality (2.39) of Lemma 6 of [24]: for any $X\in {{\mathcal {B}}}_{sa}({{\mathcal {H}}})$:

$$\begin{aligned} |\mathop {{\hbox {Tr}}}\nolimits (X(\rho -\omega ))|\le \sqrt{d}~\Vert X\Vert _{{\text {Lip}}}W_{2,\mathcal {L}}(\rho ,\omega ), \end{aligned}$$

where

$$\begin{aligned} \Vert X\Vert _{{\text {Lip}}}&:= \left( \frac{1}{d} \sum _{j\in \mathcal {J}} c_j (\mathrm {e}^{-\omega _j/2}+\mathrm {e}^{\omega _j/2})\Vert \partial _jX\Vert _{\infty }^2\right) ^{1/2}\\&\le \frac{2}{\sqrt{d}}\left( \sum _{j\in \mathcal {J}} c_j (\mathrm {e}^{-\omega _j/2}+\mathrm {e}^{\omega _j/2})\Vert {\tilde{L}}_j\Vert ^2_\infty \right) ^{1/2}\Vert X\Vert _\infty . \end{aligned}$$

The result follows from the duality relation between the norms $\Vert .\Vert _\infty$ and

$\Vert .\Vert _1$. $\square$

Proposition 2

The metric space $({{\mathcal {D}}}({{\mathcal {H}}}),W_{2,\mathcal {L}})$ is complete.

Proof

This directly follows from Lemma 4 and Proposition 1: assume that $\{\rho _n\}_{n\in \mathbb {N}}$ is a Cauchy sequence in $({{\mathcal {D}}}({{\mathcal {H}}}),W_{2,\mathcal {L}})$, that is $W_{2,\mathcal {L}}(\rho _n,\rho _m)\rightarrow 0$ as $m,n\rightarrow \infty$. Then, by Lemma 4, $\{\rho _n\}_{n\in \mathbb {N}}$ is also Cauchy with respect to the trace norm $\Vert .\Vert _1$. By completeness of the normed vector space $({{\mathcal {B}}}({{\mathcal {H}}}),\Vert .\Vert _1)$, this implies existence of $\rho _\infty \in {{\mathcal {B}}}({{\mathcal {H}}})$ such that $\Vert \rho _n-\rho _\infty \Vert _1\rightarrow 0$ as $n\rightarrow \infty$. Moreover, $\rho _\infty \in {{\mathcal {D}}}({{\mathcal {H}}})$: indeed, for any $\psi \in ({{\mathcal {H}}},\langle .|.\rangle )$,

$$\begin{aligned} \langle \psi | \rho _\infty \psi \rangle&=\langle \psi | (\rho _\infty -\rho _n)\psi \rangle +\langle \psi |\rho _n\,\psi \rangle , \end{aligned}$$

which implies the positivity of $\rho _\infty$, since $|\langle \psi | (\rho _\infty -\rho _n)\psi \rangle |\le \Vert \rho _\infty -\rho _n\Vert _1\langle \psi |\psi \rangle \rightarrow 0$ as $n\rightarrow \infty$, and $\langle \psi |\rho _n\psi \rangle \ge 0$ for all n. Moreover

$$\begin{aligned} |\mathop {{\hbox {Tr}}}\nolimits (\rho _n-\rho _\infty )|\le \Vert \rho _n-\rho _\infty \Vert _1\rightarrow 0, ~~~n\rightarrow \infty , \end{aligned}$$

which implies $\mathop {{\hbox {Tr}}}\nolimits \rho _\infty =1$. We conclude that $W_{2,\mathcal {L}}(\rho _n,\rho _\infty )\rightarrow W_{2,\mathcal {L}}(\rho _\infty ,\rho _\infty )=0$ by Proposition 1. $\square$

2.4 Quantum Functional and Transportation Cost Inequalities

A primitive QMS $(\Lambda _t)_{t\ge 0}$ with unique invariant state $\sigma$ is said to satisfy:

• 1. a Poincaré inequality with constant $\lambda >0$, if for all $f\in {{\mathcal {B}}}_{sa}({{\mathcal {H}}})$ with $\mathop {{\hbox {Tr}}}\nolimits (\sigma f)=0$,

  

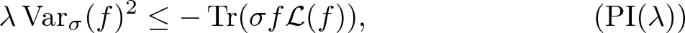
  where ${\text {Var}}_\sigma (f):=\mathop {{\hbox {Tr}}}\nolimits (\sigma f^2)-\mathop {{\hbox {Tr}}}\nolimits (\sigma f)^2$.

• 2. a modified logarithmic Sobolev inequality with constant $\alpha _1>0$ if for all $\rho \in {{\mathcal {D}}}_+({{\mathcal {H}}})$,

  

• 3. a transportation cost inequality of order 2 with constant $c_2>0$ if for all $\rho \in {{\mathcal {D}}}_+({{\mathcal {H}}})$,

  

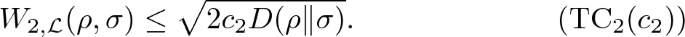
• 4. MLSI+TC$_2$(c) inequality with constant $c>0$ if for all $\rho \in {{\mathcal {D}}}_+({{\mathcal {H}}})$,

  

That (${\text {MLSI}}(\alpha _1)$) implies (TC$_2$($c_2$)) for $c_2=\alpha _1^{-1}$ was proved in [24]. Hence, the following corollary easily follows:

Corollary 1

Assume that $(\Lambda _t)_{t\ge 0}$ satisfies (${\text {MLSI}}(\alpha _1)$) for some $\alpha _1>0$. Then it also satisfies (MLSI+TC$_2$(c)) with $c=\alpha _1^{-1}$.

3 Quantum Ricci Lower Bound and $\kappa$-Displacement Convexity

In their celebrated paper [3] (see also [2]), Bakry and Emery found an elegant criterion which implies the logarithmic Sobolev inequality in the setting of diffusions. In this case of Markov semigroups defined on a Riemannian manifold $\mathcal {M}$, this criterion, called the Ricci lower bound, which is a special case of the Bakry–Emery condition, was shown later on to be equivalent to the so-called $\kappa$-displacement convexity of the relative entropy along geodesics in the Wasserstein space of probability measures on $\mathcal {M}$ in [26]. This notion of $\kappa$-displacement convexity was extended to the framework of (necessarily non-diffusive) finite Markov chains by Maas in [19]. Carlen and Maas generalized this notion to the quantum regime in [7] and proved that it implies the modified logarithmic Sobolev inequality as well as the contractivity of the Wasserstein metric under the flow associated with the underlying quantum semigroup $(\Lambda _t)_{t\ge 0}$. In their previous article [6], the same authors had already studied this quantum extension of the notion of $\kappa$-displacement convexity in the particular case of the fermionic Fokker–Planck equation. In this section, we provide a systematic analysis of the $\kappa$-displacement convexity, including a study of the geodesic equations on the Riemannian manifold $({{\mathcal {D}}}_+({{\mathcal {H}}}),g_{\mathcal {L}})$.

3.1 Geodesic Equations

Similarly to Theorem 2.4 of [12], Carlen and Maas provided in [7] the set of faithful states ${{\mathcal {D}}}_+({{\mathcal {H}}})$ with a Riemannian structure with associated Riemannian distance given by $W_{2,\mathcal {L}}$. Therefore, the local existence and uniqueness of constant speed geodesics is guaranteed by standard Riemannian geometry. We first recall that a constant speed geodesic $(\gamma (s),U(s))_{s\in [0,1]}$, where U is related to $\gamma$ through Eq. (2.6), satisfies a Euler–Lagrange equation that we derive in Theorem 2. This result is a direct generalization of Theorem 5.3 in [6]. We start by recalling the abstract framework. Let $(\mathcal {V},\langle .,.\rangle )$ be a finite-dimensional real Hilbert space. Let $\mathcal {W}\subset \mathcal {V}$ be a subspace of $\mathcal {V}$, and $z\in \mathcal {V}\backslash \mathcal {W}$. Consider the affine subspace $\mathcal {W}_z:=z+\mathcal {W}$, and let $\mathcal {M}\subset \mathcal {W}_z$ be a relatively open subset. Let $D:\mathcal {M}\rightarrow {{\mathcal {B}}}(\mathcal {W})$ be a smooth function such that D(x) is self-adjoint and invertible for all $x\in \mathcal {M}$. We shall write $C(x):=D(x)^{-1}$. Consider the Lagrangian $L:\mathcal {W}\times \mathcal {M}\rightarrow \mathbb {R}$ defined by $L(p,x)=\langle C(x) p,p\rangle$ and the associated minimization problem:

$$\begin{aligned} \inf _{u(.)\in C^1([0,1],\mathcal {M})}\left( \int _0^1 L(u'(t),u(t))dt:~~ u(0)=u_0,~ u(1)=u_1\right) , \end{aligned}$$

where $u_0, u_1\in \mathcal {M}$ are given boundary values. Then, the Euler–Lagrange equations are equivalent to the following system of equations:

$$\begin{aligned} \left\{ \begin{aligned}&u'(t)-D(u(t))v(t)=0,\\&v'(t)+\frac{1}{2}\langle \partial _x D(u(t))v(t),v(t)\rangle =0. \end{aligned} \right. \end{aligned}$$

(3.1)

Here, we apply this abstract result to the case where $\mathcal {V}={{\mathcal {B}}}_{sa}({{\mathcal {H}}})$, with inner product $\langle .,. \rangle$ the usual Hilbert–Schmidt inner product, $\mathcal {W}=\{A\in \mathcal {V}:~ \mathop {{\hbox {Tr}}}\nolimits (A)=0\}$, $z:=\mathbb {I}/\dim ({{\mathcal {H}}})$, and $\mathcal {M}={{\mathcal {D}}}_+({{\mathcal {H}}})$. Indeed, any density operator $\rho$ can be written as $\rho =\mathbb {I}/\dim {{{\mathcal {H}}}}+K$, for some self-adjoint and traceless operator K. For any $\rho \in {{\mathcal {D}}}_+({{\mathcal {H}}})$, we already proved in Lemma 3 that $D_{\vec {\omega }}(\rho ): U\mapsto -{\text {div}}([\rho ]_{\vec {\omega }}\nabla U)$ is invertible and self-adjoint. Now we use the following identity (see [6] p. 21):

$$\begin{aligned} \left. \frac{\mathrm{d}}{\mathrm{d}t} (\rho +t A)^{\alpha }\right| _{t=0}=\int _0^1 \int _0^\alpha \frac{\rho ^{\alpha -\beta }}{(1-s)\mathbb {I}+s\rho } A \frac{\rho ^\beta }{(1-s)\mathbb {I}+s \rho }\mathrm{d}\beta \mathrm{d}s \end{aligned}$$

(3.2)

for any $0<\alpha <1$, $\rho \in {{\mathcal {D}}}_+({{\mathcal {H}}})$ and $A \in \mathcal {W}$. Hence for all $A,U\in \mathcal {W}$,

$$\begin{aligned} \left. \frac{\mathrm{d}}{\mathrm{d}t}\right| _{t=0} \langle D_{\vec {\omega }}(\rho +tA)[U],U\rangle&=\left. \frac{\mathrm{d}}{\mathrm{d}t}\right| _{t=0} \sum _{j\in {{\mathcal {J}}}} c_j \langle \partial _j U,[\rho +tA]_{\omega _j} \partial _j U\rangle \nonumber \\&=\left. \frac{\mathrm{d}}{\mathrm{d}t}\right| _{t=0}\sum _{j\in {{\mathcal {J}}}} c_j \langle \partial _j U,\int _0^1\mathrm {e}^{\omega _j(1/2-\alpha )} (\rho +t A)^\alpha \nonumber \\&\quad \partial _j U(\rho + tA)^{1-\alpha }\rangle \mathrm{d}\alpha \nonumber \\&=\langle A,\nabla U._\rho \nabla U\rangle , \end{aligned}$$

(3.3)

where for two vectors $\vec {V}_1, \vec {V}_2$ in $\bigoplus _j {{\mathcal {B}}}({{\mathcal {H}}})$,

$$\begin{aligned} \vec {V}_1._\rho \vec {V}_2&:= \sum _{j\in {{\mathcal {J}}}}c_j \int _0^1\int _0^1\mathrm {e}^{\omega _j(1/2-\alpha )}( \chi _j(\vec {V}_1,\vec {V}_2^*,\rho ,\alpha ,s)\nonumber \\&\quad +\chi _j(\vec {V}_1^*,\vec {V}_2,\rho ,1-\alpha ,s)) \mathrm{d}\alpha \mathrm{d}s, \end{aligned}$$

(3.4)

where

$$\begin{aligned} \chi _j(\vec {V}_1,\vec {V}_2,\rho ,\alpha ,s):= \int _0^\alpha \frac{\rho ^\beta }{(1-s)\mathbb {I}+s\rho }(V_1)_j~\rho ^{1-\alpha }~(V_2)_j\frac{\rho ^{\alpha -\beta }}{(1-s)\mathbb {I}+s\rho }\mathrm{d}\beta . \end{aligned}$$

Therefore, in our context the Euler–Lagrange equations (3.1) reduce to the following:

Theorem 2

The geodesic equations in the Riemannian manifold $({{\mathcal {D}}}_+({{\mathcal {H}}}),W_{2,\mathcal {L}})$ are given by

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\mathrm{d}}{\mathrm{d}s}\gamma (s)+{\text {div}}([\gamma (s)]_{\vec {\omega }} \nabla U(s))=0,\\[2mm]&\frac{\mathrm{d}U(s)}{\mathrm{d}s}+\frac{1}{2} \nabla U(s)._{\gamma (s)} \nabla U(s)=0. \end{aligned} \right. \end{aligned}$$

(3.5)

3.2 Different Formulations of Quantum $\kappa$-Displacement Convexity

In analogy with [12], we say that a primitive quantum Markov semigroup $(\Lambda _t)_{t\ge 0}$ with associated invariant state $\sigma$ and generator $\mathcal {L}$ of the form of Eq. (2.3) has Ricci curvature bounded from below by a constant $\kappa \in \mathbb {R}$ if the following inequality holds:

where $(\gamma (s),U(s))_{s\in (-\varepsilon ,\varepsilon )}$ is the unique solution to the geodesic equation (3.5) such that ${{\mathcal {D}}}_+({{\mathcal {H}}})\ni \rho :=\gamma (0)$ and $U(0)=U$. We also refer to the above inequality as the quantum Ricci lower bound. Theorem 2 is useful to derive an expression for the second derivative of the relative entropy $D(\gamma (s)\Vert \sigma )$ with respect to s, where $(\gamma (s))_{s\in (-\varepsilon ,\varepsilon )}$ is a constant speed geodesic with associated tangent vector $\nabla U(s)$ at each s. We already know from the gradient flow equation (2.12) that

$$\begin{aligned}&\frac{\mathrm{d}}{\mathrm{d}s} D(\gamma (s)\Vert \sigma )\\&\quad =-g_{\mathcal {L},\gamma (s)}(\dot{\gamma }(s),\mathcal {L}_*(\gamma (s)))\\&\quad = \sum _{j\in {{\mathcal {J}}}} c_j \langle \partial _j U(s),[\gamma (s)]_{\omega _j}\partial _j(\log \gamma (s)-\log \sigma )\rangle \\&\quad =\sum _{j\in {{\mathcal {J}}}} c_j \langle \partial _j U(s),[\gamma (s)]_{\omega _j} ({\tilde{L}}_j\log (\mathrm {e}^{-\omega _j/2}\gamma (s))-\log (\mathrm {e}^{\omega _j/2}\gamma (s)){\tilde{L}}_j)\rangle , \end{aligned}$$

where the second line comes from Theorem 5.10 in [7], and the last identity comes from Lemma 5.9 of [7]. Now by identity (5.6) of the same paper,

$$\begin{aligned}{}[\gamma (s)]_{\omega _j} ({\tilde{L}}_j\log (\mathrm {e}^{-\omega _j/2}\gamma (s))-\log (\mathrm {e}^{\omega _j/2}\gamma (s)){\tilde{L}}_j)=\mathrm {e}^{-\omega _j/2}{\tilde{L}}_j\gamma (s)-\mathrm {e}^{\omega _j/2}\gamma (s){\tilde{L}}_j, \end{aligned}$$

so that we finally get

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}s}D(\gamma (s)\Vert \sigma )=\sum _{j\in {{\mathcal {J}}}} c_j \langle \partial _j U(s),\mathrm {e}^{-\omega _j/2}{\tilde{L}}_j\gamma (s)-\mathrm {e}^{\omega _j/2}\gamma (s){\tilde{L}}_j\rangle . \end{aligned}$$

Differentiating once more, we get:

$$\begin{aligned} \left. \frac{\mathrm{d}^2}{\mathrm{d}s^2}D(\gamma (s)\Vert \sigma )\right| _{s=0}=&\sum _{j\in {{\mathcal {J}}}} c_j ~\left\{ \langle \partial _j \left. \frac{\mathrm{d}}{\mathrm{d}s}U(s)\right| _{s=0},\mathrm {e}^{-\omega _j/2} {\tilde{L}}_j\rho -\mathrm {e}^{\omega _j/2}\rho {\tilde{L}}_j\rangle \right. \nonumber \\&\left. +\langle \partial _j U,\mathrm {e}^{-\omega _j/2}{\tilde{L}}_j \dot{\gamma }(0)-\mathrm {e}^{\omega _j/2}\dot{\gamma }(0) {\tilde{L}}_j\rangle \right\} . \end{aligned}$$

(3.6)

We first take care of the second line of Eq. (3.6). Using Theorem 2 as well as Eq. (2.3), we find

$$\begin{aligned}&\langle \partial _j U,\mathrm {e}^{-\omega _j/2}{\tilde{L}}_j \dot{\gamma }(0)-\mathrm {e}^{\omega _j/2}\dot{\gamma }(0) {\tilde{L}}_j\rangle \\&\quad = -\langle \partial _j U,\mathrm {e}^{-\omega _j/2}{\tilde{L}}_j {\text {div}}([\rho ]_{\vec {\omega }} \nabla U)-\mathrm {e}^{\omega _j/2}{\text {div}}([\rho ]_{\vec {\omega }} \nabla U){\tilde{L}}_j\rangle \\&\quad = -\langle \partial _j U,\mathrm {e}^{-\omega _j/2}{\tilde{L}}_j\sum _{k\in {{\mathcal {J}}}} c_k[[\rho ]_{\omega _k} \partial _k U, {\tilde{L}}_k^* ]-\mathrm {e}^{\omega _j/2} \sum _{k\in {{\mathcal {J}}}} c_k [[\rho ]_{\omega _k} \partial _k U,{\tilde{L}}_k^* ]{\tilde{L}}_j\rangle \\&\quad =\sum _{k\in {{\mathcal {J}}}} c_k \left( \mathrm {e}^{-\omega _j/2}\langle \partial _k ({\tilde{L}}_j^* \partial _j U),[\rho ]_{\omega _k}\partial _k U\rangle -\mathrm {e}^{\omega _j/2}\langle \partial _k ( \partial _j U {\tilde{L}}_j^*),[\rho ]_{\omega _k}\partial _k U\rangle \right) \\&\quad = \sum _{k\in {{\mathcal {J}}}} c_k \langle \partial _k \left( \mathrm {e}^{-\omega _j/2} {\tilde{L}}_j^* \partial _j U-\mathrm {e}^{\omega _j/2} \partial _j U {\tilde{L}}_j^*\right) ,[\rho ]_{\omega _k}\partial _k U\rangle . \end{aligned}$$

Hence by (2.3),

$$\begin{aligned} \sum _{j\in {{\mathcal {J}}}} c_j \langle \partial _j U,\mathrm {e}^{-\omega _j/2}{\tilde{L}}_j \dot{\gamma }(0)-\mathrm {e}^{\omega _j/2}\dot{\gamma }(0) {\tilde{L}}_j\rangle&= -\sum _k c_k \langle \partial _k \mathcal {L}(U),[\rho ]_{\omega _k}\partial _k U\rangle \nonumber \\&=-\langle \nabla \mathcal {L}(U),\nabla U\rangle _{\mathcal {L},\rho }. \end{aligned}$$

(3.7)

By (3.5), the first line of (3.6) is equal to

$$\begin{aligned}&\frac{1}{2} \sum _{j\in {{\mathcal {J}}}} c_j \langle \partial _j (\nabla U._{\rho }\nabla U),\mathrm {e}^{\omega _j/2} \rho {\tilde{L}}_j-\mathrm {e}^{-\omega _j/2} {\tilde{L}}_j\rho \rangle \nonumber \\&\quad =\frac{1}{2} \sum _{j\in {{\mathcal {J}}}} c_j \langle \nabla U._\rho \nabla U,[{\tilde{L}}_j^*,\rho {\tilde{L}}_j]\mathrm {e}^{\omega _j/2}-\mathrm {e}^{-\omega _j/2} [{\tilde{L}}_j^*,{\tilde{L}}_j\rho ]\rangle \nonumber \\&\quad = \frac{1}{2} \langle \nabla U._{\rho } \nabla U, \mathcal {L}_*(\rho )\rangle , \end{aligned}$$

(3.8)

where we used that, replacing ${\tilde{L}}_j$ by ${\tilde{L}}_j^*$ so that $\omega _j\rightarrow -\omega _j$ and $c_j\rightarrow c_j$,

$$\begin{aligned} \mathcal {L}_*(\rho )&=\sum _{j\in {{\mathcal {J}}}} c_j \left( \mathrm {e}^{\omega _j/2} [{\tilde{L}}_j^*\rho ,{\tilde{L}}_j]+\mathrm {e}^{-\omega _j/2}[{\tilde{L}}_j,\rho {\tilde{L}}_j^*] \right) \\&= \sum _{j\in {{\mathcal {J}}}} c_j \left( \mathrm {e}^{-\omega _j/2} [{\tilde{L}}_j\rho ,{\tilde{L}}_j^*]+\mathrm {e}^{\omega _j/2} [{\tilde{L}}_j^*,\rho {\tilde{L}}_j]\right) , \end{aligned}$$

Hence, using (3.7) and (3.8), (3.6) reduces to

$$\begin{aligned} \left. \frac{\mathrm{d}^2}{\mathrm{d}s^2}D(\gamma (s)\Vert \sigma )\right| _{s=0}&=\frac{1}{2} \langle \nabla U._{\rho }\nabla U,\mathcal {L}_*(\rho )\rangle -\langle \nabla \mathcal {L}(U),\nabla U\rangle _{\mathcal {L},\rho }. \end{aligned}$$

(3.9)

One can compare this expression with the one derived in Proposition 4.3 of [12]. To make this analogy more clear, we denote the quantity on the right-hand side of Eq. (3.9) by $B(\rho ,U)$ so that

$$\begin{aligned} \left. \frac{\mathrm{d}^2}{\mathrm{d}s^2}D(\gamma (s)\Vert \sigma )\right| _{s=0}= B(\rho ,U). \end{aligned}$$

(3.10)

The following lemma extends Lemma 4.6 of [12] to the quantum regime, as well as part of the proof of Proposition 5.11 of [6], and is proven to be useful in what follows:

Lemma 5

Let $(\gamma (s))_{s\in [0,1]}$ be a smooth curve in ${{\mathcal {D}}}_+({{\mathcal {H}}})$. For each $t\ge 0$, set $\gamma (s,t):=\Lambda _{*st}(\gamma (s))$, and let $(U(s,t))_{s\in [0,1]}$ be a smooth curve satisfying the continuity equation

$$\begin{aligned} \partial _s(\gamma (s,t))+{\text {div}} ([\gamma (s,t)]_{\vec {\omega }}\nabla U(s,t))=0,~~~~~~~s\in [0,1]. \end{aligned}$$

(3.11)

Therefore,

$$\begin{aligned} \frac{1}{2}\partial _t\Vert \partial _s\gamma (s,t)\Vert ^2_{g_{\mathcal {L},\gamma (s,t)}}+\partial _s D(\gamma (s,t)\Vert \sigma )=-s B(\gamma (s,t),U(s,t)). \end{aligned}$$

Proof

Start by noticing that

$$\begin{aligned} \partial _s D(\gamma (s,t)\Vert \sigma )&=\partial _s \mathop {{\hbox {Tr}}}\nolimits (\gamma (s,t) (\log \gamma (s,t)-\log \sigma ))\\&=\mathop {{\hbox {Tr}}}\nolimits (\partial _s \gamma (s,t) (\log \gamma (s,t)- \log \sigma ))\\&=-\mathop {{\hbox {Tr}}}\nolimits ( (\log \gamma (s,t) -\log \sigma ) {\text {div}} ([\gamma (s,t)]_{\vec {\omega }} \nabla U(s,t)) )\\&= -\langle \log \gamma (s,t) -\log \sigma ,{\text {div}} ([\gamma (s,t)]_{\vec {\omega }} \nabla U(s,t))\rangle \\&=-\sum _{j\in {{\mathcal {J}}}} c_j \langle \log \gamma (s,t)-\log \sigma ,[ [\gamma (s,t)]_{\omega _j}(\partial _j U(s,t)) ,{\tilde{L}}_j^*]\rangle \\&=\sum _{j\in {{\mathcal {J}}}} c_j\langle \partial _j (\log \gamma (s,t)-\log \sigma ),[\gamma (s,t)]_{\omega _j}(\partial _jU(s,t))\rangle \\&=\sum _{j\in {{\mathcal {J}}}} c_j \langle [\gamma (s,t)]_{\omega _j}(\partial _j (\log \gamma (s,t) -\log \sigma )),\partial _j U(s,t)\rangle \\&=\sum _{j\in {{\mathcal {J}}}} c_j \langle \partial _j^*[\gamma (s,t)]_{\omega _j}(\partial _j (\log \gamma (s,t)-\log \sigma )),U(s,t)\rangle \\&=-\langle \mathcal {L}_*(\gamma (s,t)),U(s,t)\rangle , \end{aligned}$$

where in the third line we used (3.11), in the last line we used Theorem 5.10 of [7], and in the second line we used that

$$\begin{aligned} \mathop {{\hbox {Tr}}}\nolimits (\gamma (s,t) \partial _s \log \gamma (s,t) )&= \mathop {{\hbox {Tr}}}\nolimits \left( \gamma (s,t) \partial _s \int _0^\infty \frac{1}{(1+u)\mathbb {I}} -\frac{1}{\gamma (s,t)+u\mathbb {I}} ~\mathrm{d}u \right) \\&= \mathop {{\hbox {Tr}}}\nolimits \gamma (s,t) \int _0^\infty \frac{1}{\gamma (s,t) +u \mathbb {I}}\partial _s \gamma (s,t) \frac{1}{\gamma (s,t) +u \mathbb {I}}~\mathrm{d}u\\&= \mathop {{\hbox {Tr}}}\nolimits \partial _s \gamma (s,t)\\&=0. \end{aligned}$$

Moreover, by definition of the metric $g_{\mathcal {L}}$ through Eqs. (2.8) and (2.7),

$$\begin{aligned}&\frac{1}{2} \partial _t \Vert \partial _s \gamma (s,t)\Vert _{g_{\mathcal {L},\gamma (s,t)}}^2\nonumber \\&\quad =\frac{1}{2}\partial _t\sum _{j\in {{\mathcal {J}}}}c_j \langle \partial _j U(s,t),[\gamma (s,t)]_{\omega _j} \partial _j U(s,t)\rangle \nonumber \\&\quad =\sum _{j\in {{\mathcal {J}}}} c_j\Big ( \langle \partial _t (\partial _j U(s,t)),[\gamma (s,t)]_{\omega _j}\partial _j U(s,t)\rangle \nonumber \\&\qquad +\frac{1}{2}\langle \partial _j U(s,t),\partial _t ([\gamma (s,t)]_{\omega _j} )\partial _j U(s,t)\rangle \Big ). \end{aligned}$$

(3.12)

From (3.3),

$$\begin{aligned}&\sum _{j\in {{\mathcal {J}}}} c_j \langle \partial _j U(s,t),\partial _t( [\gamma (s,t)]_{\omega _j})\partial _j U(s,t)\rangle \nonumber \\&\quad = \langle \partial _t \gamma (s,t),\nabla U(s,t)._{\gamma (s,t)} \nabla U(s,t)\rangle \nonumber \\&\quad =s \langle \mathcal {L}_*(\gamma (s,t)),\nabla U(s,t)._{\gamma (s,t)} \nabla U(s,t)\rangle . \end{aligned}$$

(3.13)

Moreover,

$$\begin{aligned}&\sum _{j\in {{\mathcal {J}}}} c_j \langle \partial _t (\partial _j U(s,t)), [\gamma (s,t)]_{\omega _j}\partial _j U(s,t)\rangle \nonumber \\&\quad =-\sum _{j\in {{\mathcal {J}}}} c_j \langle \partial _t U(s,t), [ [\gamma (s,t)]_{\omega _j} (\partial _j U(s,t)),{\tilde{L}}_j^*]\rangle \nonumber \\&\quad = -\langle \partial _t U(s,t),{\text {div}}([\gamma (s,t)]_{\vec {\omega }}(\nabla U(s,t)) )\rangle \nonumber \\&\quad = \langle \partial _t U(s,t),\partial _s \gamma (s,t)\rangle \nonumber \\&\quad = \partial _t (\langle U(s,t),\partial _s \gamma (s,t)\rangle ) -\langle U(s,t),\partial _s\partial _t \gamma (s,t)\rangle \nonumber \\&\quad = \partial _t\Vert \partial _s\gamma (s,t)\Vert _{g_{\mathcal {L},\gamma (s,t)}}^2-\langle U(s,t),\partial _s\partial _t \gamma (s,t)\rangle \nonumber \\&\quad =\partial _t\Vert \partial _s\gamma (s,t)\Vert _{g_{\mathcal {L},\gamma (s,t)}}^2- \langle U(s,t),\partial _s(s\mathcal {L}_*(\gamma (s,t)))\rangle , \end{aligned}$$

(3.14)

where we used once again (3.11) in the third and fifth lines above. Therefore, using (3.13) and (3.14), the right-hand side of (3.12) reduces to

$$\begin{aligned} \frac{1}{2}\partial _t \Vert \partial _s\gamma (s,t)\Vert _{g_{\mathcal {L},\gamma (s,t)}}^2&=\langle U(s,t),\partial _s(s\mathcal {L}_*(\gamma (s,t)))\rangle \\&\quad -\frac{1}{2}s\langle \mathcal {L}_*(\gamma (s,t)),\nabla U(s,t)._{\gamma (s,t)}\nabla U(s,t)\rangle . \end{aligned}$$

Hence,

$$\begin{aligned} \frac{1}{2}\partial _t \Vert&\partial _s\gamma (s,t)\Vert _{g_{\mathcal {L},\gamma (s,t)}}^2 +\partial _s D(\gamma (s,t)\Vert \sigma )\\&=s \langle U(s,t),\mathcal {L}_*\partial _s (\gamma (s,t))\rangle -\frac{1}{2}s \langle \mathcal {L}_*\gamma (s,t),\,\nabla U(s,t)._{\gamma (s,t)}\nabla U(s,t)\rangle \\&= -s \langle \mathcal {L}(U(s,t)),{\text {div}}([\gamma (s,t)]_{\vec {\omega }} \nabla U(s,t) )\rangle \\&\quad -\frac{1}{2} s \langle \mathcal {L}_*\gamma (s,t),\nabla U(s,t)._{\gamma (s,t)}\nabla U(s,t)\rangle \\&=s \langle \nabla \mathcal {L}(U(s,t)),\nabla U(s,t)\rangle _{\mathcal {L},\gamma (s,t)}\\&\quad -\frac{1}{2}s\langle \mathcal {L}_*(\gamma (s,t)),\nabla U(s,t)._{\gamma (s,t)}\nabla U(s,t)\rangle \\&=-s B(\gamma (s,t),U(s,t)), \end{aligned}$$

which is what needed to be proved. $\square$

Theorem 3

Let $\mathcal {L}$ be the generator of an ergodic QMS $(\Lambda _t)_{t\ge 0}$, with unique invariant state $\sigma$, of the form of Eq. 2.3). Then, for $\kappa \in \mathbb {R}$, the following are equivalent:

• (i) ${\text {Ric}}(\mathcal {L})\ge \kappa$

• (ii) For all $\rho \in {{\mathcal {D}}}_+({{\mathcal {H}}})$, and $U\in \mathcal {W}$, the space of self-adjoint, traceless operators on ${{\mathcal {H}}}$,

  $$\begin{aligned} B(\rho , U)\ge \kappa \Vert \nabla U\Vert _{\mathcal {L},\rho }^2\,. \end{aligned}$$

• (iii) For all $\rho ,\omega \in {{\mathcal {D}}}_+({{\mathcal {H}}})$ and all $t\ge 0$, writing $\rho _t:=\Lambda _{*t}(\rho )$:

  $$\begin{aligned} \frac{1}{2}\left. \frac{\mathrm{d}}{\mathrm{d}t}\right| _{t^+} \left( W_{2,\mathcal {L}}(\rho _t,\omega )\right) ^2+\frac{\kappa }{2} W_{2,\mathcal {L}}(\rho _t,\omega )^2\le D(\omega \Vert \sigma )-D(\rho _t\Vert \sigma ). \end{aligned}$$

  (3.15)

• (iv) Equation (3.15) holds for any $\rho ,\omega \in {{\mathcal {D}}}({{\mathcal {H}}})$.

• (v) $\kappa$-displacement convexity of the relative entropy: given any constant speed geodesic $(\gamma (s))_{s\in [0,1]}$ in ${{\mathcal {D}}}({{\mathcal {H}}})$,

  $$\begin{aligned} D(\gamma (s)\Vert \sigma )\le (1-s)D(\gamma (0)\Vert \sigma )+s D(\gamma (1)\Vert \sigma )-\frac{\kappa }{2}s(1-s) W_{2,\mathcal {L}}(\gamma (0),\gamma (1))^2. \end{aligned}$$

  (3.16)

Proof

The proof is inspired by the one of Theorem 4.5 of [12]. That $(i)\Leftrightarrow (ii)$ follows from Eq. (3.10). We use Lemma 5 to show that $(ii)\Rightarrow (iii)$: Take a smooth path $(\gamma (s),U(s))_{s\in [0,1]}$ such that $\gamma (0)=\omega$, $\gamma (1)=\rho$ and

$$\begin{aligned} \int _0^1 \Vert \dot{\gamma }(s)\Vert _{g_{\mathcal {L},\gamma (s)}}^2\mathrm{d}s\le W_{2,\mathcal {L}}(\rho ,\omega )^2+\varepsilon . \end{aligned}$$

(3.17)

With the notations of Lemma 5,

$$\begin{aligned} \frac{1}{2}\partial _t \left( \mathrm {e}^{2\kappa s t}\Vert \partial _s \gamma (s,t) \Vert _{g_{\mathcal {L},\gamma (s,t)}}^2 \right) +\partial _s \left( \mathrm {e}^{2\kappa s t}D(\gamma (s,t)\Vert \sigma ) \right) \le 2\kappa t\mathrm {e}^{2\kappa s t }D(\gamma (s,t)\Vert \sigma ). \end{aligned}$$

Integrating with respect to $t\in [0,h]$, for some $h>0$, and $s\in [0,1]$,

$$\begin{aligned}&\frac{1}{2}\int _0^1 \left( \mathrm {e}^{2\kappa s h}\Vert \partial _s \gamma (s,h) \Vert _{g_{\mathcal {L},\gamma (s,h)}}^2 -\Vert \partial _s \gamma (s,0)\Vert _{g_{\mathcal {L},\gamma (s,0)}}^2 \right) \mathrm{d}s \end{aligned}$$

(3.18)

$$\begin{aligned}&\qquad +\int _0^h \left( \mathrm {e}^{2\kappa t} D(\gamma (1,t)\Vert \sigma )- D(\gamma (0,t)\Vert \sigma ) \right) \mathrm{d}t\nonumber \\&\quad \le 2\kappa \int _0^1\mathrm{d}s\int _0^h \mathrm{d}t~ t\,\mathrm {e}^{2\kappa st} D(\gamma (s,t)\Vert \sigma ). \end{aligned}$$

(3.19)

The following inequality, for which a classical equivalent is given in the proof of Theorem 4.5 of [12], can be derived similarly to Lemma 5.1 of [9]:

$$\begin{aligned} m(\kappa h)W_{2,\mathcal {L}}(\rho _h,\omega )^2\le \int _0^1 \mathrm {e}^{2\kappa s h} \Vert \partial _s \gamma (s,h) \Vert _{g_{\mathcal {L},\gamma (s,h)}}^2 \mathrm{d}s, \end{aligned}$$

(3.20)

where $m(x):= x\mathrm {e}^x/\sinh (x)$. Indeed, define $f:s\mapsto \mathrm {e}^{2\kappa s h}$ and denote $L_{f}:=\int _0^1 \frac{1}{f(s)}\mathrm{d}s$. Then, let $g:[0,1]\mapsto [0,1]$ be the smooth increasing map defined as $g(s)=L_{f}^{-1}\int _0^s\frac{1}{f(u)}\mathrm{d}u$ and denote its inverse k such that $k'(g(s))=L_{f}f(s).$ Then define the reparametrized curve $(\gamma (k(r),h ),\,k'(r)\,U(k(r),h) )_{r\in [0,1]}$ which satisfies the continuity equation:

$$\begin{aligned} \partial _r \gamma (k(r),h)&=k'(r) \partial _1 \gamma (k(r),h)\\&=-k'(r) {\text {div}}([\gamma (k(r),h)]_{\vec {\omega }}\nabla U(k(r),h) ), \end{aligned}$$

where we used Eq. (3.11) in order to establish the second line. This curve satisfies $\gamma (k(0),h)=\omega$ and $\gamma (k(1),h)=\rho _h$, so that

$$\begin{aligned} W_{2,\mathcal {L}}(\rho _h,\omega )^2&\le \int _0^1 \Vert \partial _r \gamma (k(r),h)\Vert ^2_{g_{\mathcal {L},\gamma (k(r),h)}}\mathrm{d}r\\&= \int _0^1 k'(r)^2 \Vert \nabla U(k(r),h)\Vert ^2_{\mathcal {L},\gamma (k(r),h)}\mathrm{d}r\\&= \int _0^1 k'(g(s)) \Vert \nabla U(s,h)\Vert _{\mathcal {L},\gamma (s,h)}^2\mathrm{d}s\\&= L_f \int _0^1 f(s)\Vert \partial _s \gamma (s,h)\Vert _{g_{\mathcal {L},\gamma (s,h)}}^2\mathrm{d}s, \end{aligned}$$

which directly leads to (3.20). This inequality, together with (3.17), implies

$$\begin{aligned}&\frac{m(h\kappa )}{2}W_{2,\mathcal {L}}(\rho _h,\omega )^2-\frac{1}{2}W_{2,\mathcal {L}}(\rho ,\omega )^2-\varepsilon +\int _0^h\mathrm {e}^{2\kappa t} \mathrm{d}t~D(\rho _h\Vert \sigma )-hD(\omega \Vert \sigma )\\&\quad \le \frac{1}{2}\int _0^1 \mathrm {e}^{2\kappa s h}\Vert \partial _s \gamma (s,t)\Vert _{g_{\mathcal {L},\gamma (s,t)}}^2 \mathrm{d}s-\frac{1}{2}\int _0^1 \Vert \dot{\gamma }(s)\Vert _{g_{\mathcal {L},\gamma (s)}}^2\mathrm{d}s\\&\qquad +\int _0^h \mathrm {e}^{2\kappa t} D(\rho _t\Vert \sigma )~\mathrm{d}t-hD(\omega \Vert \sigma )\\&\quad \le 2\kappa \int _0^1\int _0^h ~t\mathrm {e}^{2\kappa st }D(\gamma (s,t)\Vert \sigma )\,\mathrm{d}t\,\mathrm{d}s. \end{aligned}$$

where, in the first inequality, we also used the monotonicity of the relative entropy so that $D(\rho _h\Vert \sigma )=D(\rho _h\Vert \Lambda _{*h}\sigma )\le D(\rho _t\Vert \Lambda _{*t}\sigma )=D(\rho _t\Vert \sigma )$, and in the second one that for all $t>0$, $\gamma (1,t)=\rho _t$, $\gamma (0,t)=\omega$, as well as (3.19). Since for all $s\in [0,1]$, $t\mapsto D(\gamma (s,t)\Vert \sigma )$ is bounded,

$$\begin{aligned} \lim _{h\rightarrow 0} \frac{1}{h}\int _0^1\int _0^h ~t\mathrm {e}^{2\kappa st} D(\gamma (s,t)\Vert \sigma )\mathrm{d}t~\mathrm{d}s=0. \end{aligned}$$

Moreover,

$$\begin{aligned} \lim _{h\rightarrow 0}\frac{1}{h}\left( \int _0^h \mathrm {e}^{2\kappa t}\mathrm{d}t~D(\rho _h\Vert \sigma )-hD(\omega \Vert \sigma )\right) =D(\rho \Vert \sigma )-D(\omega \Vert \sigma ) \end{aligned}$$

Since $\varepsilon >0$ is arbitrary, we arrive at

$$\begin{aligned} \left. \frac{\mathrm{d}}{\mathrm{d}h}\right| _{h=0^+}\left( \frac{m(\kappa h)}{2}W_{2,\mathcal {L}}(\rho _h,\omega )^2\right) +D(\rho \Vert \sigma )-D(\omega \Vert \sigma )\le 0. \end{aligned}$$

The result for $t=0$ follows from the fact that the first term in the left-hand side above is equal to $\frac{\kappa }{2} W_{2,\mathcal {L}}(\rho _h,\omega )^2+\frac{1}{2}\left. \frac{\mathrm{d}}{\mathrm{d}h}\right| _{h=0^+}W_{2,\mathcal {L}}(\rho _h,\omega )^2$. The case $t\ge 0$ directly follows from the case $t=0$.

$(iii)\Rightarrow (iv)$ follows from Theorem 3.3 of [9] together with the fact that $({{\mathcal {D}}}({{\mathcal {H}}}),W_{2,\mathcal {L}})$ is complete (cf. Proposition 2).

$(iv)\Rightarrow (v)$ follows directly from Theorem 3.2 of [9].

$(v)\Rightarrow (i)$ can easily be proved as follows: let $0<\varepsilon <\varepsilon '$, and without loss of generality, let $\gamma :(-\varepsilon ',\varepsilon ')\rightarrow {{\mathcal {D}}}_+({{\mathcal {H}}})$ be speed 1 geodesic, and that $\gamma (0)=\rho$. Then, construct the following constant speed geodesic $\tilde{\gamma }:[0,1]\rightarrow {{\mathcal {D}}}_+({{\mathcal {H}}})$ as follows: for any $s\in [0,1]$, $\tilde{\gamma }(s):= \gamma (2\varepsilon s-\varepsilon )$. It then follows that $W_{2,\mathcal {L}}(\tilde{\gamma }(0),\tilde{\gamma }(1))=2\varepsilon$. Moreover, by applying (3.16) to $\tilde{\gamma }$, we find, after a suitable rearrangement of the terms:

$$\begin{aligned} \frac{D(\gamma (\varepsilon )\Vert \sigma )-2D(\rho \Vert \sigma )+D(\gamma (-\varepsilon )\Vert \sigma )}{\varepsilon ^2}\ge \kappa . \end{aligned}$$

The result follows after taking the limit $\varepsilon \rightarrow 0$. $\square$

3.3 Other Equivalent Formulations of Displacement Convexity

Here, we provide other characterizations of the Ricci curvature lower bound in terms of some contraction properties of the Wasserstein metric along the semigroup $(\mathcal {P}_t)_{t\ge 0}$. In the next theorem, the characterization of displacement convexity in terms of gradient estimates can be interpreted as a non-commutative version of Bakry–Émery’s original gradient bound (see Theorem 4.7.2 of [4]): in particular they showed that the Ricci curvature lower bound is equivalent to the following pointwise inequality for smooth enough functions:

$$\begin{aligned} \varGamma (P_t(f),P_t(f))\le \mathrm {e}^{-2\kappa t}P_t(\varGamma (f,f))\,, \end{aligned}$$

(3.21)

where $\varGamma$ stands for the carré du champ operator:

$$\begin{aligned} \varGamma (f,g):=\nabla f.\nabla g\,. \end{aligned}$$

Proposition 3

(Gradient estimate). ${\text {Ric}}(\mathcal {L})\ge \kappa$ is equivalent to the following gradient estimate: for any $\rho \in {{\mathcal {D}}}_+({{\mathcal {H}}})$, any $U\in {{\mathcal {B}}}_{sa}({{\mathcal {H}}})$ with $\mathrm{Tr}(U)=0$, and all $t>0$:

$$\begin{aligned} \Vert \nabla (\Lambda _t(U))\Vert _{\mathcal {L},\rho }^2\le \mathrm {e}^{-2\kappa t} \Vert \nabla U\Vert _{\mathcal {L},\Lambda _{*t}(\rho )}^2. \end{aligned}$$

(3.22)

Proof

Define for $u\in [0,t]$$\rho _u\equiv \Lambda _{*u}(\rho )$ and $U_{u}\equiv \Lambda _{u}(U)$. Then,

$$\begin{aligned} \varPhi (s):=\mathrm {e}^{-2\kappa s}\Vert \nabla U_{t-s}\Vert _{\mathcal {L},\rho _s}^2\equiv \mathrm {e}^{-2\kappa s}\sum _{j\in {{\mathcal {J}}}} c_j \langle \partial _j( U_{t-s}),[\rho _s]_{\omega _j} \partial _j( U_{t-s})\rangle . \end{aligned}$$

Then, $\varPhi (0) = \Vert \nabla U_t\Vert _{\mathcal {L},\rho }^2$ and $\varPhi (t)= \mathrm {e}^{-2\kappa t}\Vert \nabla U\Vert _{\mathcal {L},\rho _t}^2$. It is then enough to prove that $\varPhi$ has non-negative derivative to prove the claim. But:

$$\begin{aligned} \varPhi '(s)&=2\mathrm {e}^{-2\kappa s} \Big [ -\kappa \Vert \nabla U_{t-s}\Vert _{\mathcal {L},\rho _s}^2 + \frac{1}{2}\frac{\partial }{\partial s} \Vert \nabla U_{t-s}\Vert _{\mathcal {L},\rho _s}^2 \Big ]\\&=2\mathrm {e}^{-2\kappa s} \Big [ -\kappa \Vert \nabla U_{t-s}\Vert _{\mathcal {L},\rho _s}^2 + \sum _{j\in {{\mathcal {J}}}} c_j \langle \partial _j\partial _s U_{t-s},[\rho _s]_{\omega _j}\partial _jU_{t-s}\rangle \\&\quad +\frac{1}{2} \sum _{j\in {{\mathcal {J}}}} c_j\langle \partial _j U_{t-s},\partial _s([\rho _s]_{\omega _j})\partial _jU_{t-s}\rangle \Big ]\\&=2\mathrm {e}^{-2\kappa s} \Big [ -\kappa \Vert \nabla U_{t-s}\Vert _{\mathcal {L},\rho _s}^2 - \langle \nabla \mathcal {L}(U_{t-s}),\nabla U_{t-s}\rangle _{\mathcal {L},\rho _s}\\&\quad + \frac{1}{2} \langle \mathcal {L}_*(\rho _s),\nabla U_{t-s}._{\rho _s}\nabla U_{t-s} \rangle \Big ]\\&=2\mathrm {e}^{-2\kappa s} \Big [ -\kappa \Vert \nabla U_{t-s}\Vert _{\mathcal {L},\rho _s}^2+ B(\rho _s,U_{t-s})\Big ] \end{aligned}$$

where we used Eq. (3.3) in the second line. We conclude by a use of (ii) of Theorem 3. For the reverse implication, assume that Eq. (3.22) holds. Then,

$$\begin{aligned} 0&\le \mathrm {e}^{-2\kappa \,t}\Vert \nabla U\Vert ^2_{{{\mathcal {L}}},\rho _t}-\Vert \nabla \,(\Lambda _t U )\Vert ^2_{{{\mathcal {L}}},\rho }\\&=(\mathrm {e}^{-2\kappa t}-1)\Vert \nabla U\Vert ^2_{{{\mathcal {L}}},\rho }+\mathrm {e}^{-2\kappa t}(\Vert \nabla U\Vert ^2_{{{\mathcal {L}}},\rho _t}-\Vert \nabla U\Vert ^2_{{{\mathcal {L}}},\rho })\\&-\Vert \nabla (\Lambda _t(U))\Vert ^2_{{{\mathcal {L}}},\rho }+\Vert \nabla U\Vert ^2_{{{\mathcal {L}}},\rho }\,. \end{aligned}$$

By dividing by t and letting $t\rightarrow 0$, we once again obtain that $-\kappa \Vert \nabla U\Vert ^2_{{{\mathcal {L}}},\rho }+B(\rho ,U)\ge 0$. $\square$

In the commutative diffusive setting, the Ricci curvature lower bound is also known to be equivalent to the contraction of the Wasserstein distance along the semigroup $(P_t)_{t\ge 0}$ (see Theorem 9.7.2 of [4]):

$$\begin{aligned} W_2(P_{t*}(\nu ),\,P_{t*}(\nu '))\le \mathrm {e}^{-\kappa t}W_2(\nu ,\nu ')\,. \end{aligned}$$

This still holds true in the non-commutative, finite-dimensional setting:

Proposition 4

For any $\kappa \in \mathbb {R}$, ${\text {Ric}}(\mathcal {L})\ge \kappa$ is equivalent to the contraction of the Wasserstein distance along the flow generated by $(\Lambda _t)_{t\ge 0}$: for any $\rho ,\omega \in {{\mathcal {D}}}_+({{\mathcal {H}}})$

$$\begin{aligned} W_{2,{{\mathcal {L}}}}(\Lambda _{t*}(\rho ),\Lambda _{t*}(\omega ))\le \mathrm {e}^{-\kappa t}W_{2,{{\mathcal {L}}}}(\rho ,\omega )\,. \end{aligned}$$

(3.23)

Proof

The direct implication follows from Proposition 3.1 of [9] and Theorem 3(iii). The reverse implication is proved as in inequality (2.12) of [9], using the smooth Riemannian structure provided by $({{\mathcal {D}}}_+({{\mathcal {H}}}),W_{2,{{\mathcal {L}}}})$ in the finite-dimensional case. $\square$

In the commutative diffusive setting, the contraction of (3.21) is actually known to be equivalent to its “square root” version, usually referred to as the strong gradient bound:

$$\begin{aligned} \sqrt{ \varGamma (P_t(f),P_t(f))}\le \mathrm {e}^{-\kappa t}P_t(\sqrt{\varGamma (f,f)})\,. \end{aligned}$$

(3.24)

The proof of (3.24)$\Rightarrow$(3.21) follows by a simple use of Jensen’s inequality, the converse being the content of Theorem 3.3.18 of [4]. The advantage of this formulation arises from the fact that some canonical semigroups (e.g. the quantum Ornstein–Uhlenbeck semigroup on $\mathbb {R}^n$) saturate the inequality, or equivalently:

$$\begin{aligned} \left[ L,\,\nabla \right] =\kappa \nabla \,. \end{aligned}$$

Therefore, the Ricci lower bound is equivalent to comparing the commutation of a semigroup with the gradient to the one of a canonical semigroup. A similar reasoning recently lead [13] to formulate a Bakry–Émery condition for birth and death processes on $\mathbb {N}$ in terms of a comparison to the Poisson process. Going back to our non-commutative setting, [7] showed that the quantum Ornstein–Uhlenbeck semigroup, as well as its fermionic version on the Clifford algebra, does satisfy such a commutation relation. They used this fact to derive the modified logarithmic Sobolev constant for these QMS via the contraction (3.23). In the next proposition, we recall their argument:

Proposition 5

Assume that the following equalities hold: there exists $\kappa \in \mathbb {R}$ such that, for any $j\in {{\mathcal {J}}}$ and any $t\ge 0$,

$$\begin{aligned} \partial _{j}\circ \Lambda _t= \mathrm {e}^{-\kappa t} \Lambda _t\circ \partial _{j}\,. \end{aligned}$$

(3.25)

Then, ${\text {Ric}}(\mathcal {L})\ge \kappa$ holds.

Proof

From Proposition 4, it is enough to prove that (3.23) holds. Assume that $(\gamma (s))_{s\in [0,1]}$ is a minimal geodesic relating $\rho$ to $\sigma$ and denote by $(\mathbf {A}(s))_{s\in [0,1]}$ the unique solution of the continuity equation

$$\begin{aligned} \dot{\gamma }(s)={\text {div}}\mathbf {A}(s)\,. \end{aligned}$$

By duality, Eq. (3.25) implies that $\Lambda _{t*}\dot{\gamma }(s)=\mathrm {e}^{-\kappa t}{\text {div}}\vec {\Lambda }_{t*}\mathbf {A}(s)$, where $\vec {\Lambda }_{t*}\mathbf {A}:=(\Lambda _{t*}A_j)_{j\in {{\mathcal {J}}}}$. Then, denoting $\gamma (s,t):=\Lambda _{t*}(\gamma (s))$,

$$\begin{aligned} g_{{{\mathcal {L}}},\gamma (s,t)}(\dot{\gamma }(s,t),\dot{\gamma }(s,t))&=\mathrm {e}^{-2\kappa t}\sum _{j\in {{\mathcal {J}}}}\,\langle \mathcal {P}_{*t}(A_j(s)),\,[\gamma (s,t)]^{-1}_{\omega _j}(\mathcal {P}_{t*}(A_j(s)))\rangle \\&\le \mathrm {e}^{-2\kappa t}\sum _{j\in {{\mathcal {J}}}}\,\langle A_j(s),\,[\gamma (s)]^{-1}_{\omega _j}A_j(s))\rangle \\&=\mathrm {e}^{-2\kappa t} g_{{{\mathcal {L}}},\gamma (s)}(\dot{\gamma }(s),\dot{\gamma }(s))\,, \end{aligned}$$

where the inequality arises from the property of monotonicity of Fisher information metrics (cf. [17]). The result follows after taking the integral over the geodesic path. $\square$

3.4 Example: The Quantum Depolarizing Semigroup

In this section, we derive a Ricci curvature lower bound on perhaps the simplest possible QMS: the depolarizing semigroup: define $(\Lambda _t^\mathrm{dep})_{t\ge 0}$ on ${{\mathcal {B}}}(\mathbb {C}^d)$ as follows,

$$\begin{aligned} \Lambda ^\mathrm{dep}_t(X)=\mathrm {e}^{-t}X\,+(1-\mathrm {e}^{-t})\frac{1}{d}\mathop {{\hbox {Tr}}}\nolimits (X)\,\mathbb {I}\,. \end{aligned}$$

Theorem 4

The quantum depolarizing semigroup $(\Lambda ^\mathrm{dep}_t)_{t\ge 0}$ satisfies ${\text {Ric}}({{\mathcal {L}}}^\mathrm{dep})\ge \frac{1}{2}$.

Proof

In the Schrödinger picture, the generator ${{\mathcal {L}}}^\mathrm{dep}_*$ can be written as

$$\begin{aligned} {{\mathcal {L}}}^\mathrm{dep}_*(\rho )=\frac{\mathbb {I}}{d}\mathop {{\hbox {Tr}}}\nolimits (\rho )-\rho =\frac{1}{d^2}\sum _{j=1}^{d^2} (U_j\,\rho \,U_j-\rho ),~~~~~\rho \in {{\mathcal {D}}}(\mathbb {C}^d), \end{aligned}$$

where the operators $U_j$ can be chosen to be self-adjoint (e.g. generalized Pauli matrices [32]). In this case, $c_j=\frac{1}{2d^2}$, ${\tilde{L}}_j=U_j$ and $\omega _j=0$, $j=1,\ldots ,d^2$. Now, given a vector $\vec {V}=(V_1,\ldots ,V_{d^2})\in \bigoplus _j\,{{\mathcal {B}}}(\mathbb {C}^d)$ and $\rho \in {{\mathcal {D}}}_+(\mathbb {C}^d)$,

$$\begin{aligned} \langle \vec {V},\vec {V}\rangle _{{{\mathcal {L}}}^\mathrm{dep},\,\rho }&=\frac{1}{2d^2}\sum _{j=1}^{d^2}\langle V_j,\,[\rho ]_0(V_j)\rangle \\&=\frac{1}{2d^2}\sum _{j=1}^{d^2}\int _0^1\,\langle V_j,\,\rho ^s\,V_j\rho ^{1-s}\rangle \,\mathrm{d}s\\&=\frac{1}{2d^2}\sum _{j=1}^{d^2}\int _0^1\,\mathop {{\hbox {Tr}}}\nolimits ( V_j^*\,\rho ^s\,V_j\rho ^{1-s})\,\mathrm{d}s \end{aligned}$$

Now, given $U\in {{\mathcal {B}}}_{sa}(\mathbb {C}^d)$ and $\rho \in {{\mathcal {D}}}_+(\mathbb {C}^d)$, the following holds:

$$\begin{aligned}&\nabla U._{\rho }\nabla U\\&=-\frac{1}{2d^2}\sum _{j=1}^{d^2}\int _0^1\int _0^1\int _0^\alpha \frac{\rho ^{\beta }}{(1-s)\mathbb {I}+s\rho }\,\partial _j U\,\rho ^{1-\alpha }\partial _j U\frac{\rho ^{\alpha -\beta }}{(1-s)\mathbb {I}+s\rho }\mathrm{d}\beta \mathrm{d}s\mathrm{d}\alpha \\&\quad +\int _0^1\int _0^1\int _0^{1-\alpha }\frac{\rho ^{\beta }}{(1-s)\mathbb {I}+s\rho }\,\partial _j U\,\rho ^{\alpha }\partial _j U\frac{\rho ^{1-\alpha -\beta }}{(1-s)\mathbb {I}+s\rho }\mathrm{d}\beta \mathrm{d}s\mathrm{d}\alpha , \end{aligned}$$

where we used that, since $U_j=U_j^*$, $(\nabla U)^*=-\nabla U$. Then:

$$\begin{aligned} \frac{1}{2}\langle&\nabla U._{\rho }\nabla U,\,{{\mathcal {L}}}^\mathrm{dep}_*(\rho )\rangle \\&=-\frac{1}{4d^2}\sum _{j=1}^{d^2}\int _0^1\int _0^1\mathrm{d}s\mathrm{d}\alpha \left\{ \int _0^\alpha \mathop {{\hbox {Tr}}}\nolimits \left( \frac{\mathbb {I}}{d}-\rho \right) \right. \\&\left. \quad \frac{\rho ^{\beta }}{(1-s)\mathbb {I}+s\rho }\,\partial _j U\,\rho ^{1-\alpha }\partial _j U\frac{\rho ^{\alpha -\beta }}{(1-s)\mathbb {I}+s\rho } \mathrm{d}\beta \right. \\&\quad \left. +\int _0^{1-\alpha }\mathop {{\hbox {Tr}}}\nolimits \left( \frac{\mathbb {I}}{d}-\rho \right) \,\frac{\rho ^{\beta }}{(1-s)\mathbb {I}+s\rho }\,\partial _j U\,\rho ^{\alpha }\partial _j U\frac{\rho ^{1-\alpha -\beta }}{(1-s)\mathbb {I}+s\rho }\mathrm{d}\beta \right\} . \end{aligned}$$

By cyclicity of the trace, and since $\int _0^1\frac{1}{((1-s)\mathbb {I}+s\rho )^2}\mathrm{d}s=\rho ^{-1}$, forgetting about the positive contributions coming from the terms in $d^{-1}\mathbb {I}$, the above expression can be lower bounded as follows:

$$\begin{aligned}&\frac{1}{2}\langle \nabla U._{\rho }\nabla U,\,{{\mathcal {L}}}^\mathrm{dep}_*(\rho )\rangle \\&\quad \ge \frac{1}{4d^2}\sum _{j=1}^{d^2}\int _0^1\,\left\{ \int _0^\alpha \mathop {{\hbox {Tr}}}\nolimits (\rho ^{\beta }\partial _j U\rho ^{1-\alpha }\partial _j U\rho ^{\alpha -\beta })\mathrm{d}\beta \right. \\&\left. \qquad +\int _0^{1-\alpha }\mathop {{\hbox {Tr}}}\nolimits (\rho ^{\beta }\partial _j U\rho ^{\alpha }\partial _j U\rho ^{1-\alpha -\beta }) \mathrm{d}\beta \right\} \,\mathrm{d}\alpha \\&\quad =\frac{1}{4d^2}\sum _{j=1}^{d^2}\int _0^1\,\left\{ \alpha \mathop {{\hbox {Tr}}}\nolimits (\partial _j U \rho ^{1-\alpha } \partial _j U\rho ^\alpha )+(1-\alpha )\mathop {{\hbox {Tr}}}\nolimits (\partial _j U\,\rho ^\alpha \partial _j U\rho ^{1-\alpha }) \right\} \,\mathrm{d}\alpha \\&\quad =\frac{1}{4d^2}\sum _{j=1}^{d^2}\int _0^1\,\mathop {{\hbox {Tr}}}\nolimits (\partial _j U\,\rho ^\alpha \partial _j U\rho ^{1-\alpha })\,\mathrm{d}\alpha . \end{aligned}$$

On the other hand,

$$\begin{aligned} \langle \nabla {{\mathcal {L}}}^\mathrm{dep}(U),\,\nabla U\rangle _{{{\mathcal {L}}}^\mathrm{dep},\,\rho }&=\frac{1}{2d^2}\sum _{j=1}^{d^2}\int _0^1\mathop {{\hbox {Tr}}}\nolimits \left[ \partial _j\left( \frac{\mathbb {I}}{d}\mathop {{\hbox {Tr}}}\nolimits (U)-U\right) ^*\rho ^s\,\partial _j U\,\rho ^{1-s}\right] \,\mathrm{d}s\\&=\frac{1}{2d^2}\,\sum _{j=1}^{d^2}\int _0^1\,\mathop {{\hbox {Tr}}}\nolimits [\,\partial _j U\,\rho ^s\partial _j U \,\rho ^{1-s}\,]\,\mathrm{d}s \end{aligned}$$

Therefore,

$$\begin{aligned} B(\rho ,U)\ge -\frac{1}{4d^2}\,\sum _{j=1}^{d^2}\int _0^1\,\mathop {{\hbox {Tr}}}\nolimits [\,\partial _j U\,\rho ^s\partial _j U \,\rho ^{1-s}\,]\,\mathrm{d}s=\frac{1}{2}\Vert \nabla U\Vert _{{{\mathcal {L}}}^\mathrm{dep},\rho }^2, \end{aligned}$$

and the result follows. $\square$

Remark 1

This result was independently found in [8].

4 A Quantum HWI Inequality

In [7] it was proved that, in the case when $\kappa >0$, ${\text {Ric}}(\mathcal {L})\ge \kappa$ implies ${\text {MLSI}}(\alpha _1)$ for $\kappa =\alpha _1$. This is, for example, the case of the classical and quantum Ornstein–Uhlenbeck processes. Here, we study the case of $\kappa \in \mathbb {R}$. In [12], the authors proved that, in the classical discrete framework, ${\text {Ric}}(\mathcal {L})\ge \kappa$ for $\kappa \in \mathbb {R}$ implies an HWI-like inequality (see Theorem 7.3). Here, we provide a quantum generalization of their result.

Theorem 5

Assume that ${\text {Ric}}(\mathcal {L})\ge \kappa$, for some $\kappa \in \mathbb {R}$. Then $\mathcal {L}$ satisfies the following inequality

Proof

By Theorem 3, for any $\rho ,\omega \in {{\mathcal {D}}}_+({{\mathcal {H}}})$

$$\begin{aligned} \frac{1}{2}\left. \frac{\mathrm{d}}{\mathrm{d}t}\right| _{t=0^+}W_{2,\mathcal {L}}(\rho _t,\omega )^2+\frac{\kappa }{2}W_{2,\mathcal {L}}(\rho ,\omega )^2\le D(\omega \Vert \sigma )-D(\rho \Vert \sigma ). \end{aligned}$$

Taking $\omega :=\sigma$, this implies that

$$\begin{aligned} D(\rho \Vert \sigma )\le -\frac{1}{2}\left. \frac{\mathrm{d}}{\mathrm{d}t}\right| _{t=0^+} W_{2,\mathcal {L}}(\rho _t\Vert \sigma )^2-\frac{\kappa }{2}W_{2,\mathcal {L}}(\rho ,\sigma )^2. \end{aligned}$$

(4.1)

Then,

$$\begin{aligned} -\frac{1}{2}\left. \frac{\mathrm{d}}{\mathrm{d}t}\right| _{t=0^+} W_{2,\mathcal {L}}(\rho _t,\sigma )^2&=\liminf _{s\rightarrow 0^+}\frac{1}{2s}(W_{2,\mathcal {L}}(\rho ,\sigma )^2 -W_{2,\mathcal {L}}(\rho _s,\sigma )^2 )\\&\le \limsup _{s\rightarrow 0^+}\frac{1}{2s}(W_{2,\mathcal {L}}(\rho ,\rho _s)^2 +2W_{2,\mathcal {L}}(\rho ,\rho _s)W_{2,\mathcal {L}}(\rho _s,\sigma ) )\\&\le \limsup _{s\rightarrow 0^+}\frac{1}{2s}W_{2,\mathcal {L}}(\rho ,\rho _s)^2+W_{2,\mathcal {L}}(\rho ,\sigma )\sqrt{{\text {I}}_\sigma (\rho )}\\&=W_{2,\mathcal {L}}(\rho ,\sigma )\sqrt{{\text {I}}_\sigma (\rho )}. \end{aligned}$$

where the second inequality follows from Lemma 7 of [24]. The result follows from inserting this back into (4.1). $\square$

In the case when $\kappa >0$, we recover the result of [7]:

Corollary 2

(Quantum Bakry–Émery theorem). Assume that ${\text {Ric}}(\mathcal {L})\ge \kappa$, for some $\kappa >0$. Then $\mathcal {L}$ satisfies ${\text {MLSI}}(\kappa )$.

Proof

By Theorem 5, $\mathcal {L}$ satisfies ${\text {HWI}}(\kappa )$. ${\text {MLSI}}(\kappa )$ follows from an application of Young’s inequality:

$$\begin{aligned} xy\le cx^2+\frac{1}{4c}y^2,~~~~~\forall x,y\in \mathbb {R}, c>0, \end{aligned}$$

(4.2)

in which we set $x=W_{2,\mathcal {L}}(\rho ,\sigma )$, $y=\sqrt{{\text {I}}_\sigma (\rho )}$, and $c=\frac{\kappa }{2}$. $\square$

In the case ${\text {Ric}}(\mathcal {L})\ge \kappa$ for $\kappa \in \mathbb {R}$, HWI$(\kappa )$ still implies a modified log-Sobolev inequality under the further condition that a transportation cost inequality holds. This is a direct quantum generalization of Theorem 7.8 of [12] (see also Corollary 3.1 of [23])

Corollary 3

Assume that ${\text {Ric}}(\mathcal {L})\ge \kappa$, $\kappa \in \mathbb {R}$, and that ${\text {TC}}_2(c_2)$ holds with $c_2^{-1}\ge \max ( 0,-\kappa )$. Then ${\text {MLSI}}(\alpha _1)$ holds for

$$\begin{aligned} \alpha _1=\max \left[ \frac{1}{4c_2}\left( 1+c_2\kappa \right) ^2 ,\,\kappa \right] \end{aligned}$$

Proof

The proof is identical to the one of Corollary 3.1 of [23]. $\square$

Similarly, we can show that ${\text {Ric}}(\mathcal {L})\ge \kappa$ for $\kappa \in \mathbb {R}$ implies MLSI as long as MLSI+TC$_2$ holds.

Corollary 4

Assume that ${\text {Ric}}(\mathcal {L})\ge \kappa$, $\kappa \in \mathbb {R}$, and that the inequality ${\text {MLSI}}+{\text {TC}}_2(c)$ (defined in Sect. 2.4) holds with $c^{-1}\ge \max (\kappa ,0)$, then ${\text {MLSI}}(\alpha _1)$ holds, with

$$\begin{aligned} \alpha _1=\frac{1}{c\,(2-\kappa c)}. \end{aligned}$$

Proof

See Corollary 3.2 of [23]. $\square$

The diameter of ${{\mathcal {D}}}({{\mathcal {H}}})$ in the Wasserstein distance $W_{2,\mathcal {L}}$ is defined as follows:

$$\begin{aligned} {\text {Diam}}_{\mathcal {L}}({{\mathcal {D}}}({{\mathcal {H}}}))=\sup _{\rho ,\omega \in {{\mathcal {D}}}({{\mathcal {H}}})} W_{2,\mathcal {L}}(\rho ,\omega ). \end{aligned}$$

Another straightforward consequence of the $\kappa$-displacement convexity of the quantum relative entropy for $\kappa >0$ is the following estimate on the diameter ${\text {Diam}}_{\mathcal {L}}({{\mathcal {D}}}({{\mathcal {H}}}))$, which is a quantum analogue of the Bonnet–Myers theorem (see Proposition 7.3 of [11]).

Proposition 6

Assume that ${\text {Ric}}(\mathcal {L})\ge \kappa$ holds for $\kappa >0$. Then for any two states $\rho ,\omega \in {{\mathcal {D}}}({{\mathcal {H}}})$,

$$\begin{aligned} W_{2,\mathcal {L}}(\rho ,\omega )^2\le \frac{4}{\kappa } (D(\rho \Vert \sigma )+D(\omega \Vert \sigma )). \end{aligned}$$

Therefore,

$$\begin{aligned} {\text {Diam}}_{\mathcal {L}}({{\mathcal {D}}}({{\mathcal {H}}}))\le \sup _{\rho \in {{\mathcal {D}}}({{\mathcal {H}}})}\sqrt{\frac{8}{\kappa } D(\rho \Vert \sigma )}. \end{aligned}$$

Proof

The result follows directly from the convexity of the quantum relative entropy (cf. (v) of Theorem 3):

$$\begin{aligned} 0\le D(\gamma (1/2)\Vert \sigma )\le \frac{1}{2}D(\rho \Vert \sigma )+\frac{1}{2} D(\omega \Vert \sigma )-\frac{\kappa }{8} W_{2,\mathcal {L}}(\rho ,\omega )^2. \end{aligned}$$

for a given constant speed geodesic $(\gamma (s))_{s\in [0,1]}$ relating $\rho$ and $\omega$. $\square$

5 From Ricci Lower Bound to the Poincaré Inequality

In this section, we show that ${\text {Ric}}(\mathcal {L})\ge 0$ together with a condition of finiteness of the diameter of ${{\mathcal {D}}}({{\mathcal {H}}})$ with respect to the distance $W_{2,\mathcal {L}}$ implies the Poincaré inequality, hence extending Proposition 5.9 of [11] to our non-commutative setting. Throughout this section, we fix $(\mathcal {P}_t)_{t\ge 0}$ to be a primitive QMS on ${{\mathcal {B}}}({{\mathcal {H}}})$, ${{\mathcal {H}}}$ finite dimensional, with unique invariant state $\sigma$ and associated generator $\mathcal {L}$, satisfying $\sigma$-DBC. The next result is a non-commutative extension of the fourth equivalent statement in Theorem 4.7.2 of [4]:

Proposition 7

(Reverse quantum Poincaré inequality) Assume that ${\text {Ric}}(\mathcal {L})\ge \kappa$ holds. Then for any $\rho \in {{\mathcal {D}}}_+({{\mathcal {H}}})$, any $U\in {{\mathcal {B}}}_{sa}({{\mathcal {H}}})$ and all $t>0$:

$$\begin{aligned} \mathrm{Tr}(\Lambda _{*t}(\rho ) U^2)-\mathrm{Tr}(\rho (\Lambda _t(U))^2)\ge \frac{\mathrm {e}^{2\kappa t}-1}{2\kappa } \Vert \nabla \Lambda _t(U) \Vert _{\mathcal {L},\rho }^2 \end{aligned}$$

(5.1)

Proof

The proof is similar to the one of Theorem 3.5 of [11]. For $u\ge 0$, let $\rho _u\equiv \Lambda _{*u}(\rho )$ and $U_u\equiv \Lambda _u (U)$. Then, from Proposition 3,

$$\begin{aligned}&2\mathrm {e}^{2\kappa s} \Vert \nabla U_t\Vert _{\mathcal {L},\rho }^2\\&\quad =2 \mathrm {e}^{2\kappa s} \Vert \nabla (\Lambda _{s}U_{t-s})\Vert _{\mathcal {L},\rho }^2 \\&\quad \le 2 \Vert \nabla U_{t-s}\Vert _{\mathcal {L},\rho _s}^2\\&\quad = 2\sum _{j\in {{\mathcal {J}}}} c_j \langle \partial _j U_{t-s},[\rho _s]_{\omega _j}\partial _j U_{t-s}\rangle \\&\quad \le \sum _{j\in {{\mathcal {J}}}} c_j \langle \partial _j U_{t-s}, ( \mathrm {e}^{-\omega _j/2} R_{\rho _s} +\mathrm {e}^{\omega _j/2} L_{\rho _s})\partial _j U_{t-s}\rangle \\&\quad = \sum _{j\in {{\mathcal {J}}}} c_j \left( \mathrm {e}^{\omega _j/2}\mathop {{\hbox {Tr}}}\nolimits [\rho _s \partial _j U_{t-s} (\partial _j U_{t-s} )^*] +\mathrm {e}^{-\omega _j/2}\mathop {{\hbox {Tr}}}\nolimits [\rho _s (\partial _j U_{t-s} )^*\partial _j U_{t-s} ] \right) \\&\quad = \sum _{j\in {{\mathcal {J}}}} c_j \left( \mathrm {e}^{\omega _j/2} \mathop {{\hbox {Tr}}}\nolimits (\rho _s [{\tilde{L}}_j,U_{t-s}][U_{t-s},{\tilde{L}}_j^*]) + \mathrm {e}^{-\omega _j/2} \mathop {{\hbox {Tr}}}\nolimits (\rho _s [U_{t-s},{\tilde{L}}_j^*][{\tilde{L}}_j,U_{t-s}]) \right) \\&\quad = \sum _{j\in {{\mathcal {J}}}} c_j \left( \mathop {{\hbox {Tr}}}\nolimits (\rho _s ({\tilde{L}}_j U_{t-s}^2 {\tilde{L}}_j^* \mathrm {e}^{\omega _j/2} + \mathrm {e}^{-\omega _j/2} {\tilde{L}}_j^* U_{t-s}^2 {\tilde{L}}_j ) ) \right. \\&\qquad \left. +\mathrm {e}^{\omega _j/2} \mathop {{\hbox {Tr}}}\nolimits (\rho _s (-{\tilde{L}}_jU_{t-s}{\tilde{L}}_j^* U_{t-s} -U_{t-s} {\tilde{L}}_j U_{t-s} {\tilde{L}}_j^* + U_{t-s} {\tilde{L}}_j{\tilde{L}}_j^* U_{t-s} ) ) \right. \\&\qquad \left. + \mathrm {e}^{-\omega _j/2} \mathop {{\hbox {Tr}}}\nolimits (\rho _s (U_{t-s} {\tilde{L}}_j^*{\tilde{L}}_j U_{t-s} -{\tilde{L}}_j^* U_{t-s} {\tilde{L}}_j U_{t-s} -U_{t-s} {\tilde{L}}_j^*U_{t-s} {\tilde{L}}_j ) ) \right) \\&\quad =\mathop {{\hbox {Tr}}}\nolimits (\rho _s\mathcal {L}(U_{t-s}^2)) \\&\qquad \,+\sum _{j\in {{\mathcal {J}}}} c_j \left( \mathrm {e}^{\omega _j/2} \mathop {{\hbox {Tr}}}\nolimits (\rho _s (-{\tilde{L}}_jU_{t-s}{\tilde{L}}_j^* U_{t-s} -U_{t-s} {\tilde{L}}_j U_{t-s} {\tilde{L}}_j^* \right. \\&\left. \qquad + U_{t-s} {\tilde{L}}_j{\tilde{L}}_j^* U_{t-s} +U_{t-s}^2 {\tilde{L}}_j {\tilde{L}}_j^* ) ) \right. \\&\qquad \,+\left. \mathrm {e}^{-\omega _j/2} \mathop {{\hbox {Tr}}}\nolimits (\rho _s (U_{t-s} {\tilde{L}}_j^*{\tilde{L}}_j U_{t-s} -{\tilde{L}}_j^* U_{t-s} {\tilde{L}}_j U_{t-s} \right. \\&\left. \qquad -U_{t-s} {\tilde{L}}_j^* U_{t-s} {\tilde{L}}_j +{\tilde{L}}_j^* {\tilde{L}}_j U_{t-s}^2 ) ) \right) \\&\quad = \mathop {{\hbox {Tr}}}\nolimits (\rho _s \mathcal {L}(U_{t-s}^2)) -\mathop {{\hbox {Tr}}}\nolimits (\rho _s U_{t-s}\mathcal {L}(U_{t-s}) )-\mathop {{\hbox {Tr}}}\nolimits (\rho _s \mathcal {L}(U_{t-s}) U_{t-s} ) \\&\quad =\frac{\partial }{\partial s}\mathop {{\hbox {Tr}}}\nolimits (\rho _s U^2_{t-s}) \end{aligned}$$

where we used (2.38) of [24], with $R_\rho (A)\equiv A\rho$ and $L_{\rho }(A)\equiv \rho A$, in the fourth line. The claim follows after integrating the above inequality from 0 to t. $\square$

Theorem 6

${\text {Ric}}(\mathcal {L})\ge 0 ~+~{\text {Diam}}_{\mathcal {L}}({{\mathcal {D}}}({{\mathcal {H}}}))\le D$ $\Rightarrow$ ${\text {PI}}(\frac{1}{\mathrm {e}D^2}).$

Proof

Let $f\in {{\mathcal {B}}}_{sa}({{\mathcal {H}}})$ be an eigenvector of $\mathcal {L}$ with associated eigenvalue opposite to the spectral gap $\lambda$ of $\mathcal {L}$. Without loss of generality, $\Vert f\Vert _\infty =1$, and by primitivity of $(\Lambda _t)_{t\ge 0}$, $\mathop {{\hbox {Tr}}}\nolimits (\sigma f)=0$. Now, note that $\Lambda _t(f)=\mathrm {e}^{-\lambda t}f$. Therefore, the reverse Poincaré inequality (5.1) in the case when $\kappa =0$ implies that for any $\rho \in {{\mathcal {D}}}_+({{\mathcal {H}}})$,

$$\begin{aligned} \Vert \nabla f\Vert _{\mathcal {L},\rho }^2\le \frac{\mathrm {e}^{2\lambda t}}{2t}\Vert f\Vert _\infty ^2. \end{aligned}$$

Optimizing over t and using $\Vert f\Vert _\infty =1$, we find

$$\begin{aligned} \Vert \nabla f\Vert _{\mathcal {L},\rho }^2\le \mathrm {e}\lambda \Vert f\Vert _\infty ^2. \end{aligned}$$

Given the following spectral decomposition of $f=\sum _\mu \mu P_\mu$, since $\mathop {{\hbox {Tr}}}\nolimits (\sigma f)=0$, the minimum and maximum eigenvalues of f, respectively, denoted by $\mu _{\min }$ and $\mu _{\max }$, obey $\mu _{\min }<0<\mu _{\max }$. Since we assumed $\Vert f\Vert _\infty =1$, this implies that given a path $(\gamma (s),U(s))_{s\in [0,1]}$ in ${{\mathcal {D}}}({{\mathcal {H}}})$ joining the states $\gamma (0)=\frac{P_{\mu _{\max }}}{\mathop {{\hbox {Tr}}}\nolimits (P_{\mu _{\max }})}$ and $\gamma (1)= \frac{P_{\mu _{\min }}}{\mathop {{\hbox {Tr}}}\nolimits (P_{\mu _{\min }} )}$ such that $\int _{0}^1 \Vert \dot{\gamma }(s)\Vert _{g_{\mathcal {L},\gamma (s)}}^2 \mathrm{d}s\le W_{2,\mathcal {L}}(\gamma (0),\gamma (1))^2+\varepsilon$,

$$\begin{aligned} 1\le |\mu _{\max } - \mu _{\min }|&=\left| \mathop {{\hbox {Tr}}}\nolimits f\left( \frac{P_{\mu _{\min }}}{\mathop {{\hbox {Tr}}}\nolimits (P_{\mu _{\min }} )} - \frac{P_{\mu _{\max }}}{\mathop {{\hbox {Tr}}}\nolimits (P_{\mu _{\max }} )} \right) \right| \\&= \left| \mathop {{\hbox {Tr}}}\nolimits \left( f\int _0^1 \dot{\gamma }(s) \mathrm{d}s\right) \right| \\&=\left| \int _0^1 \sum _{j\in {{\mathcal {J}}}} c_j \langle \partial _j f,[\gamma (s)]_{\omega _j}\partial _j U(s)\rangle \mathrm{d}s \right| \\&\quad \le \sqrt{( D^2+\varepsilon )}\left( \int _0^1 \Vert \nabla f\Vert ^2_{\mathcal {L},\gamma (s)}\mathrm{d}s\right) ^{1/2}\le \sqrt{(D^2+\varepsilon ) \lambda \mathrm {e}}, \end{aligned}$$

where in the last line we used the Cauchy–Schwarz inequality with respect to the inner product $\sum _{j\in {{\mathcal {J}}}}c_j\langle .~,\int _0^1[\gamma (s)]_{\omega _j}\mathrm{d}s~.\rangle$, and the result directlyfollows. $\square$

6 From Ricci Lower Bound to Modified Log-Sobolev Inequality

In [11], a modified logarithmic Sobolev inequality was proved to hold under the conditions that ${\text {Ric}}(\mathcal {L})\ge 0$ and that the diameter of the underlying space, in terms of the modified Wasserstein distance, is bounded. Here, we extend their results to the quantum regime under the further assumption that the semigroup $(\Lambda _t)_{t\ge 0}$ is unital, leaving the study of the general case to later. The idea of the proof is to get a non-tight logarithmic Sobolev inequality from ${\text {HWI}}(0)$ and then to tighten it using ideas borrowed from [5]. In what follows, we denote by d the dimension of ${{\mathcal {H}}}$.

Given two states $\rho ,\omega \in {{\mathcal {D}}}({{\mathcal {H}}})$, with associated spectral decompositions $\rho =\sum _{i\in \mathcal {A}} \lambda _i P_i$, $\omega =\sum _{j\in \mathcal {B}} \mu _jQ_j$, where ${{\mathcal {A}}}$ and ${{\mathcal {B}}}$ are two finite index sets, a coupling of $\rho$ and $\omega$ is a probability distribution q on ${{\mathcal {A}}}\times {{\mathcal {B}}}$ such that

$$\begin{aligned} \sum _{i\in {{\mathcal {A}}}} q(i,j)&=\mu _j\mathop {{\hbox {Tr}}}\nolimits (Q_j)\\ \sum _{j\in {{\mathcal {B}}}}q(i,j)&=\lambda _i \mathop {{\hbox {Tr}}}\nolimits (P_i). \end{aligned}$$

The set of couplings between $\rho$ and $\omega$ is denoted by $\Pi (\rho ,\omega )$. In analogy with the classical literature (see, for example, [12]), given an ergodic semigroup $(\Lambda _t)_{t\ge 0}$ with associated generator $\mathcal {L}$, the coupling Wasserstein distance of order two between $\rho$ and $\omega$ is defined as follows:

$$\begin{aligned} W_{2,\mathcal {L},c}(\rho ,\omega )^2:=\inf _{q\in \Pi (\rho ,\sigma )} \sum _{i\in {{\mathcal {A}}},~j\in {{\mathcal {B}}}} q(i,j) W_{2,\mathcal {L}} (\rho _i,\omega _j)^2, \end{aligned}$$

where

$$\begin{aligned} \rho _i:= \frac{P_i}{\mathop {{\hbox {Tr}}}\nolimits P_i},~~~~~~~~~~\omega _j:=\frac{Q_j}{\mathop {{\hbox {Tr}}}\nolimits (Q_j)},~~~~~~~~~i\in {{\mathcal {A}}},~j\in {{\mathcal {B}}}. \end{aligned}$$

The following result is a quantum generalization of Proposition 2.14 of [12]:

Proposition 8

Let $(\Lambda _t)_{t\ge 0}$ be a primitive QMS, with unique invariant state $\sigma$ and associated generator $\mathcal {L}$, satisfying the detailed balance condition. Then, for any $\rho ,\omega \in {{\mathcal {D}}}_+({{\mathcal {H}}})$,

$$\begin{aligned} W_{2,\mathcal {L}}(\rho ,\omega )\le W_{2,\mathcal {L},c}(\rho ,\omega ). \end{aligned}$$

Proof

Let $\rho =\sum _{i\in \mathcal {A}} \lambda _i P_i$, $\omega =\sum _{j\in \mathcal {B}} \mu _jQ_j$ the spectral decompositions of the states $\rho$ and $\omega$. For $(i,j)\in {{\mathcal {A}}}\times {{\mathcal {B}}}$, define $\rho _i:= \frac{P_i}{\mathop {{\hbox {Tr}}}\nolimits ( P_i)}$, $\omega _j:=\frac{Q_j}{\mathop {{\hbox {Tr}}}\nolimits (Q_j)}$, and let $\varepsilon >0$. By definition of the Wasserstein distance $W_{2,\mathcal {L}}$, there exists a curve $\gamma _{ij}:[0,1]\mapsto {{\mathcal {D}}}({{\mathcal {H}}})$ from $\rho _i$ to $\omega _j$ such that

$$\begin{aligned} \int _0^1 \Vert \dot{\gamma }_{ij}(s)\Vert _{g_{\mathcal {L},\gamma _{ij}(s)}}^2 \mathrm{d}s\le W_{2,\mathcal {L}}(\rho _i,\omega _j)^2+\varepsilon . \end{aligned}$$

For any coupling $q:{{\mathcal {A}}}\times {{\mathcal {B}}}\rightarrow \mathbb {R}_+$ of the states $\rho$ and $\omega$, define the path $(\gamma (s))_{s\in [0,1]}$ on ${{\mathcal {D}}}({{\mathcal {H}}})$ as

$$\begin{aligned} \gamma (s)=\sum _{i\in {{\mathcal {A}}},~j\in {{\mathcal {B}}}}q(i,j) \,\gamma _{ij}(s). \end{aligned}$$

Therefore, $\gamma (0)=\rho$ and $\gamma (1)=\omega$. Now,

$$\begin{aligned} W_{2,\mathcal {L}}(\rho ,\omega )^2&\le \int _0^1 \Vert \dot{\gamma }(s)\Vert _{g_{\mathcal {L},\gamma (s)}}^2\mathrm{d}s\\&\le \sum _{i\in {{\mathcal {A}}},~j\in {{\mathcal {B}}}} q(i,j) \int _0^1 \Vert \dot{\gamma }_{ij}(s)\Vert _{g_{\mathcal {L},\gamma (s)}}^2\mathrm{d}s\\&\le \sum _{i\in {{\mathcal {A}}},~j\in {{\mathcal {B}}}} q(i,j) ~W_{2,\mathcal {L}}(\rho _i,\omega _j)^2+\varepsilon . \end{aligned}$$

where we used the convexity of $g_{\mathcal {L}}$ in the second line (see equation (8.15) of [7]). As $\varepsilon$ is arbitrary, the result follows after optimizing over thecouplings q. $\square$

In what follows, we restrict our analysis to the case of a primitive QMS $(\Lambda _t)_{t\ge 0}$ with unique invariant state $\mathbb {I}/d$ that satisfies the detailed balance condition. In order to prove the main result of this section, we need the following two lemmas that are extensions of Lemmas 6.2 and 6.3 of [11]:

Lemma 6

Assume that ${\text {Ric}}(\mathcal {L})\ge 0$ and ${\text {Diam}}_{\mathcal {L}}({{\mathcal {D}}}({{\mathcal {H}}}))\le D$. Then for any $\delta >0$ and $f\in {{\mathcal {B}}}_{sa}({{\mathcal {H}}})$ such that $\mathrm{Tr} (f^2)=d$:

$$\begin{aligned} D\left( f^2/d\Vert \mathbb {I}/d \right) \le \delta D^2 {\text {I}}_{\mathbb {I}/d}(f^2/d)+\frac{1}{4d\,\delta } \mathrm{Tr} (f^2 \mathbf {1}_{[1,\infty )}(f^2)) \end{aligned}$$

Proof

The case when f is not of full support is trivial, as then ${\text {I}}_\sigma (f^2/d)=\infty$. Without loss of generality, we assume that f has full support, so that $f^2/d\in {{\mathcal {D}}}_+({{\mathcal {H}}})$. Write $f=\sum _{i\in {{\mathcal {A}}}}\varphi (i) P_i$ the spectral decomposition of f, for some index set ${{\mathcal {A}}}$. From ${\text {HWI}}(0)$, and Young’s inequality (4.2) with $c=\delta D^2$, $x=\sqrt{{\text {I}}_\sigma (f^2/d)}$, and $y=W_{2,\mathcal {L}}(f^2/d,\mathbb {I}/d)$:

$$\begin{aligned} D(f^2/d\Vert \mathbb {I}/d)\le \delta D^2 {\text {I}}_{\mathbb {I}/d}(f^2/d)+\frac{1}{4\delta D^2} W_{2,\mathcal {L}}(f^2/d,\mathbb {I}/d)^2. \end{aligned}$$

From Proposition 8, for any coupling $q:{{\mathcal {A}}}\times {{\mathcal {B}}}\rightarrow \mathbb {R}_+$ between $f^2/d$ and $\mathbb {I}/d$ such that $q(i,j)=0$ for all $j\ne i$ whenever $\varphi (i)^2\le 1$,

$$\begin{aligned} D(f^2/d\Vert \mathbb {I}/d)&\le \delta D^2{\text {I}}_{\mathbb {I}/d}(f^2/d) +\frac{1}{4\delta D^2}\\&\quad \sum _{i,j:~\varphi (i)^2>1} q(i,j) W_{2,\mathcal {L}}\left( \frac{P_i}{\mathop {{\hbox {Tr}}}\nolimits (P_i)},\frac{P_j}{\mathop {{\hbox {Tr}}}\nolimits (P_j)}\right) ^2, \\&\le \delta D^2{\text {I}}_{\mathbb {I}/d}(f^2/d) +\frac{1}{4d\,\delta } \mathop {{\hbox {Tr}}}\nolimits (f^2 \mathbf {1}_{(1,\infty )}(f^2)). \end{aligned}$$

We recall that such a coupling q exists due to Strassen’s theorem. $\square$

Lemma 7

For any $A>1$, there exists $\gamma >0$ such that for any $f\in {{\mathcal {B}}}_{sa}({{\mathcal {H}}})$ with $\mathrm{Tr}(f^2)=d$,

$$\begin{aligned}&\frac{1}{d}\mathrm{Tr} ( f^2 \mathbf {1}_{[A^2,\infty )}(f^2) )\le \left( \frac{A}{A-1}\right) ^2 {\text {Var}}_{\mathbb {I}/d}(f), \end{aligned}$$

(6.1)

$$\begin{aligned}&D(f^2/d\Vert \mathbb {I}/d)\le \gamma {\text {Var}}_{\mathbb {I}/d}(f)+\frac{1}{d}\mathrm{Tr}(f^2 \log f^2 \mathbf {1}_{[A^2,\infty )}(f^2)). \end{aligned}$$

(6.2)

Proof

This is a direct rewriting of Lemma 2.5 of [5]. $\square$

Theorem 7

Let $(\Lambda _t)_{t\ge 0}$ be a primitive semigroup with unique invariant state $\mathbb {I}/d$ and associated generator $\mathcal {L}$. Assume that ${\text {Ric}}(\mathcal {L})\ge 0$ and that ${\text {Diam}}_{\mathcal {L}}({{\mathcal {D}}}({{\mathcal {H}}}))\le D$. Then ${\text {MLSI}}(cD^{-2})$ holds, for some universal constant c.

Proof

Let $A>1$ and $f\in {{\mathcal {B}}}_{sa}({{\mathcal {H}}})$ of spectral decomposition $f=\sum _{i\in {{\mathcal {A}}}}\varphi (i) P_i$, with $\mathop {{\hbox {Tr}}}\nolimits ( f^2 )=d$. Without loss of generality, we can assume f positive definite. Then, set $f_A:= f\vee A\equiv \sum _{i:~\varphi (i) \ge A}\varphi (i) P_i + A \,\mathbf {1}_{(-\infty , A)}(f)$. Define the state $\rho _A=f_A^2/\mathop {{\hbox {Tr}}}\nolimits (f_A^2)$. By (6.2),

$$\begin{aligned} D(f^2/d\Vert \mathbb {I}/d)\le \gamma {\text {Var}}_{\mathbb {I}/d}(f)+ \frac{1}{d}\mathop {{\hbox {Tr}}}\nolimits (f^2 \log f^2 \mathbf {1}_{[ A^2,\infty )}(f^2)). \end{aligned}$$

(6.3)

By Theorem 6,

$$\begin{aligned} \gamma {\text {Var}}_{\mathbb {I}/d} (f)\le - 2\mathrm {e}D^2 \gamma \frac{1}{d}\langle f,\mathcal {L}(f)\rangle \le \frac{\gamma \mathrm {e}D^2}{2} {\text {I}}_{\mathbb {I}/d}(f^2/d), \end{aligned}$$

(6.4)

where in the last inequality, we used the strong regularity of Dirichlet forms of unital semigroups (see [16]). Moreover,

$$\begin{aligned}&\frac{1}{d}\mathop {{\hbox {Tr}}}\nolimits (f^2\log f^2 \mathbf {1}_{[A^2,\infty )}(f^2)) = \frac{1}{d} \mathop {{\hbox {Tr}}}\nolimits (f_A^2\log f_A^2)-\frac{1}{d} A^2\log A^2 \mathop {{\hbox {Tr}}}\nolimits (\mathbf {1}_{(-\infty , A)}(f))\nonumber \\&\quad \le (1+A^2)D(\rho _A\Vert \mathbb {I}/d) + \frac{ \mathop {{\hbox {Tr}}}\nolimits (f_A^2)}{d}\log \left( \frac{\mathop {{\hbox {Tr}}}\nolimits f_A^2}{d} \right) -\frac{A^2\log A^2}{d} \mathop {{\hbox {Tr}}}\nolimits (\mathbf {1}_{(-\infty , A)}(f)), \end{aligned}$$

(6.5)

where in the last line we used that $\frac{1}{d}\mathop {{\hbox {Tr}}}\nolimits (f_A^2)\le 1+A^2$. However, from Lemma 6 applied to $f_A$, since ${\text {I}}_{\mathbb {I}/d}(\rho _A)\le \frac{d}{\mathop {{\hbox {Tr}}}\nolimits (f_A^2)} {\text {I}}_{\mathbb {I}/d}(f^2/d)$ by convexity of monotone Riemannian metrics (see, for example, equation (8.16) of [7]),

$$\begin{aligned} D(\rho _A \Vert \mathbb {I}/d)&\le \frac{d\,\delta \, D^2}{\mathop {{\hbox {Tr}}}\nolimits (f_A^2)}{\text {I}}_{\mathbb {I}/d}(f^2/d)+\frac{1}{4\mathop {{\hbox {Tr}}}\nolimits (f_A^2 )\delta }\mathop {{\hbox {Tr}}}\nolimits (f_A^2\mathbf {1}_{[\frac{1}{d}\mathop {{\hbox {Tr}}}\nolimits (f_A^2) , \infty )}(f_A^2))\nonumber \\&\le \frac{\delta D^2}{A^2}{\text {I}}_{\mathbb {I}/d}(f^2/d)+\frac{1}{4d\,\delta A^2}\mathop {{\hbox {Tr}}}\nolimits (f^2\mathbf {1}_{[A^2 , \infty )}(f^2)), \end{aligned}$$

(6.6)

where in the last line we used that $A^2\le \frac{1}{d}\mathop {{\hbox {Tr}}}\nolimits (f_A^2)$. Using (6.1) and (6.4) together with Theorem 6,

$$\begin{aligned} D(\rho _A\Vert \mathbb {I}/d)&\le \frac{\delta D^2}{A^2}{\text {I}}_{\mathbb {I}/d}(f^2/d) +\frac{1}{4\delta (A-1)^2}{\text {Var}}_{\mathbb {I}/d}(f)\\&\le \frac{\delta D^2}{A^2} {\text {I}}_{\mathbb {I}/d}(f^2/d) -\frac{ \mathrm {e}D^2 }{2\delta (A-1)^2} \frac{1}{d}\langle f,\mathcal {L}(f)\rangle \\&\le \left( \frac{\delta D^2}{A^2} +\frac{ \mathrm {e}D^2 }{8\delta (A-1)^2} \right) {\text {I}}_{\mathbb {I}/d}(f^2/d)\\ \end{aligned}$$

Now,

$$\begin{aligned}&\frac{\mathop {{\hbox {Tr}}}\nolimits (f_A^2)}{d}\log \left( \frac{\mathop {{\hbox {Tr}}}\nolimits (f_A^2)}{d}\right) -\frac{A^2\log (A^2)}{d}\mathop {{\hbox {Tr}}}\nolimits (\mathbf {1}_{(-\infty ,A)}(f))\\&\quad \le \frac{1}{d}\Big ({A^2}\mathop {{\hbox {Tr}}}\nolimits (\mathbf {1}_{(-\infty ,A)}(f)) + \mathop {{\hbox {Tr}}}\nolimits ( f^2 \mathbf {1}_{[A^2,\infty )}(f^2) ) \Big )\\&\qquad \log \Big [ \frac{1}{d}\Big ( {A^2}\mathop {{\hbox {Tr}}}\nolimits (\mathbf {1}_{(-\infty ,A)}(f)) + \mathop {{\hbox {Tr}}}\nolimits ( f^2 \mathbf {1}_{[A^2,\infty )}(f^2) ) \Big )\Big ]\\&\qquad -\frac{A^2\log (A^2)}{d}\mathop {{\hbox {Tr}}}\nolimits (\mathbf {1}_{(-\infty ,A)}(f)) \\&\quad = A^2 \frac{1}{d}\mathop {{\hbox {Tr}}}\nolimits (\mathbf {1}_{(-\infty ,A)}(f))\log \left( \frac{1}{d} \mathop {{\hbox {Tr}}}\nolimits (\mathbf {1}_{(-\infty ,A)}(f)) +\frac{\mathop {{\hbox {Tr}}}\nolimits (f^2 \mathbf {1}_{[A^2,\infty )}(f^2) )}{dA^2} \right) \\&\qquad + \frac{1}{d}\mathop {{\hbox {Tr}}}\nolimits ( f^2 \mathbf {1}_{[ A^2,\infty )}(f^2) )\log \left( A^2 \frac{1}{d}\mathop {{\hbox {Tr}}}\nolimits ( \mathbf {1}_{(-\infty ,A]}(f) )+\frac{1}{d}\mathop {{\hbox {Tr}}}\nolimits ( f^2\mathbf {1}_{[ A^2,\infty )}(f^2) ) \right) \\&\quad \le A^2 \log \left( 1+ \frac{\mathop {{\hbox {Tr}}}\nolimits ( f^2\mathbf {1}_{[ A^2,\infty )} (f^2) )}{dA^2} \right) +\frac{1}{d}\mathop {{\hbox {Tr}}}\nolimits (f^2\mathbf {1}_{[ A^2,\infty )}(f^2)) \log (1+A^2)\\&\quad \le (1+\log (1+A^2))\frac{1}{d}\mathop {{\hbox {Tr}}}\nolimits (f^2\mathbf {1}_{[ A^2,\infty )}(f^2) ), \end{aligned}$$

where in the fourth line we used that $\frac{1}{d}\mathop {{\hbox {Tr}}}\nolimits (f^2)=1$. Using once more (6.1) and (6.4) together with Theorem 6, we find

$$\begin{aligned}&\frac{\mathop {{\hbox {Tr}}}\nolimits (f_A^2)}{d}\log \left( \frac{\mathop {{\hbox {Tr}}}\nolimits (f_A^2)}{d}\right) -\frac{A^2\log (A^2)}{d}\mathop {{\hbox {Tr}}}\nolimits (\mathbf {1}_{(-\infty ,A]}(f))\nonumber \\&\quad \le \frac{\mathrm {e}D^2 A^2(1+\log (1+A^2))}{2(1-A)^2} {\text {I}}_{\mathbb {I}/d}(f^2/d) \end{aligned}$$

(6.7)

The result follows after combining (6.7), (6.3), (6.4), (6.5) and (6.6). $\square$

7 Conclusion

In this paper, we prove that a classical picture, relating various inequalities which are useful in the analysis of Markov semigroups, carries over to the quantum setting. Classically, a key element of this picture is a geometric inequality called the Ricci lower bound. Functional and transportation cost inequalities, which play an important role in the study of mixing times of a primitive Markov semigroup and concentration properties of its invariant measure, can be obtained from this geometric inequality. The connection between them is provided by an interpolating inequality called the HWI inequality. In this paper, we analyse a quantum version of the Ricci lower bound (due to Carlen and Maas [7]) and show that it implies a quantum HWI inequality, from which quantum versions of the functional and transportation cost inequalities (which are relevant for the analysis of quantum Markov semigroups) follow.