Mean-Field Dynamics for the Nelson Model with Fermions

Abstract

We consider the Nelson model with ultraviolet cutoff, which describes the interaction between non-relativistic particles and a positive or zero mass quantized scalar field. We take the non-relativistic particles to obey Fermi statistics and discuss the time evolution in a mean-field limit of many fermions. In this case, the limit is known to be also a semiclassical limit. We prove convergence in terms of reduced density matrices of the many-body state to a tensor product of a Slater determinant with semiclassical structure and a coherent state, which evolve according to a fermionic version of the Schrödinger–Klein–Gordon equations.

1 Introduction

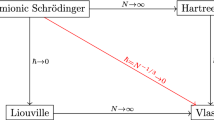
Interacting many-body systems are very difficult to analyze, and analytic or numerical solutions are usually not feasible. Therefore, simpler effective equations are used to analyze these systems throughout the sciences. These approximations work very well in many settings and can be derived with heuristic arguments and good intuition. In mathematical physics, the question of a rigorous justification of such effective equations is an active field of research, starting in the 1970s with works such as [12, 24, 25, 27, 29, 46] (see [45] for an excellent overview). Sparked by the 2001 Nobel Prize for the experimental realization of a Bose–Einstein condensate, there has been great interest in the derivation of effective equations for bosonic systems. (We refer to [10, 33] for references and an overview of the topic.) More recently, there has been an increasing interest in the evolution of many fermion systems. This started already in the 1980s with the works [34, 46], which introduce the mean-field limit for fermions and prove convergence to the classical Vlasov equation. Convergence to the Hartree–Fock equations was proved in 2004 in [17], where the authors consider short times and analytic interaction potentials, and in particular highlight the importance of the semiclassical structure in the derivation. The generalization to arbitrary times and a larger class of bounded interaction potentials was achieved in [8, 9]; see also [37] for a slightly different proof. The more recent work [40] extended the results to Coulomb interaction (see also [43] for weaker singularities), assuming a property of the Hartree–Fock dynamics that the authors only prove for the special situation of translation invariant initial data. The article [6] covers mixed initial states. Several other results for different timescales (without semiclassical structure) were obtained in [3,4,5] for a coupling constant $N^{-1}$, in [22] for a coupling constant $N^{-1}$ and Coulomb interaction, and in [2, 37, 38] for a coupling constant $N^{-2/3}$ and singular interactions potentials. In particular, in [38] convergence to the fermionic Hartree equations is proved for Coulomb interaction with a convergence rate that distinguishes the mean-field equation from the free equation. Let us also mention the article [11], where the authors discuss the Bogoliubov–de Gennes equations for fermions, which is an approximation more precise than Hartree–Fock theory. In particular, they derive these equations assuming that the states are quasifree for all times. These works show that many aspects of the mean-field regime of weakly correlated bosons and fermions that interact via a pair potential are well understood by now. However, less attention has been paid to systems in which the interaction between the particles is mediated by a second quantized radiation field. Also here effective equations are of great importance because quantized radiation fields are described on Fock space, i.e., a Hilbert space for an arbitrary number of particles. The complexity of such systems is reduced tremendously when the quantized field is approximated by a pair potential or a classical radiation field. The articles [16, 28, 49] show that the quantized radiation field can sometimes be replaced by a two-particle interaction if the particles are much slower than the bosons of the radiation field. Moreover, it is possible to derive classical field equations from second quantized models [1, 14, 15, 19,20,21, 23, 26, 31, 32]. While these works focus on bosonic systems or systems with a small number of fermions, the present paper seems to be the first that considers a many-particle limit of fermions which interact by means of a quantized radiation field. The scaling, which will be explained in the following, can been seen as a fermionic mean-field limit because it is chosen such that the source term of the radiation field can effectively be replaced by its mean value. Moreover, it can be viewed as a second quantized analogue of the fermionic mean-field model of [9].

We consider N identical fermions that interact by means of a quantized scalar field. The state of the radiation field is represented by elements of the bosonic Fock space $\mathcal {F}_\mathrm{s} :=\bigoplus _{n \ge 0} L^2(\mathbb {R}^3)^{\otimes _\mathrm{s} n}$, where the subscript s indicates symmetry under interchange of variables. The Hilbert space of the whole system is

$$\begin{aligned} \mathcal {H}^{(N)} :=L^2_{\mathrm {as}}\left( \mathbb {R}^{3N} \right) \otimes \mathcal {F}_\mathrm{s}. \end{aligned}$$

(1)

Here the subscript “$\mathrm {as}$” indicates antisymmetry under exchange of variables. An element $\Psi _N \in \mathcal {H}^{(N)}$ is a vector $\big ( \Psi _N^{(n)} \big )_{n \in \mathbb {N}_0}$ with $\Psi _N^{(n)} \in L^2_{\mathrm {as}}(\mathbb {R}^{3N}) \otimes L^2_\mathrm{s}(\mathbb {R}^{3n})$ and

$$\begin{aligned} \left\| \Psi _N \right\| ^2 = \sum _{n=0}^{\infty } \int \mathrm{d}^{3N}x \, \mathrm{d}^{3n}k \, \left| \Psi _{N}^{(n)}(X_N,K_n) \right| ^2 < \infty , \end{aligned}$$

(2)

where we use the shorthand notation $X_N = (x_1, \ldots , x_N)$ and $K_n = (k_1, \ldots k_n)$. We define the annihilation and creation operators by

$$\begin{aligned} \begin{aligned}&\left( a(k) \Psi _N \right) ^{(n)} (X_N,K_n) = ( n + 1)^{1/2} \Psi _N^{(n+1)}(X_N,k,K_n), \\&\left( a^*(k) \Psi _N \right) ^{(n)} (X_N,K_n) = n^{-1/2} \sum _{j=1}^n \delta (k- k_j) \Psi _N^{(n-1)}(X_N, k_1, \ldots , \hat{k}_j, \ldots , k_n), \end{aligned} \end{aligned}$$

(3)

where $\hat{k}_j$ means that $k_j$ is left out in the argument of the function. They satisfy the commutation relations

$$\begin{aligned} {[}a(k), a^*(l) ] = \delta (k-l), \quad [a(k), a(l) ] = [a^*(k), a^*(l) ] = 0. \end{aligned}$$

(4)

We choose units such that $\hbar =1=c$. The dispersion relation is then given by $\omega (k) = ( \left| k \right| ^2 + m^2 )^{1/2}$ with mass $m \ge 0$. We define the form factor of the radiation field by

$$\begin{aligned} \tilde{\eta }(k) = \frac{(2 \pi )^{-3/2}}{\sqrt{2 \omega (k)}} \mathbb {1}_{\left| k \right| \le \Lambda }(k), \quad \text {with} \; \mathbb {1}_{\left| k \right| \le \Lambda }(k) = {\left\{ \begin{array}{ll} 1 &{}\quad \text {if}\,\,\left| k \right| \le \Lambda , \\ 0 &{}\quad \text {otherwise}. \end{array}\right. } \end{aligned}$$

(5)

Here, $\Lambda$ is a momentum cutoff and we assume $\Lambda \ge 1$. The field operator is given by

$$\begin{aligned} \widehat{\Phi }_{\Lambda }(x) = \int \mathrm{d}^3k \, \tilde{\eta }(k) \left( e^{ikx} a(k) + e^{-ikx} a^*(k) \right) , \end{aligned}$$

(6)

and the free Hamiltonian of the scalar field is the self-adjoint operator

$$\begin{aligned} H_f&= \int \mathrm{d}^3k \, \omega (k) a^*(k) a(k) \end{aligned}$$

(7)

with

$$\begin{aligned} \mathcal {D}(H_f) = \left\{ \Psi _N \in \mathcal {H}^{(N)}{:}\,\sum _{n=1}^{\infty } \int \mathrm{d}^{3N}x \, \mathrm{d}^{3n}k \, \Bigg |\sum _{j=1}^n \omega (k_j) \Psi _N^{(n)}(X_N, K_n)\Bigg |^2 < \infty \right\} . \end{aligned}$$

(8)

The full system is described by the Nelson Hamiltonian

$$\begin{aligned} H_N = \sum _{j=1}^N \left( - \Delta _j + \widehat{\Phi }_{\Lambda }(x_j) \right) + \delta _N H_f. \end{aligned}$$

(9)

The factor $\delta _N$ is an arbitrary particle number-dependent scaling parameter that allows to scale the field energy. The Nelson Hamiltonian is self-adjoint on the domain $\mathcal {D}\left( H_N \right) = \big (H^2(\mathbb {R}^{3N})\otimes \mathcal {F}_\mathrm{s}\big ) \cap \mathcal {D}(H_f)$, where $H^2$ denotes the second Sobolev space. This can be shown by applying Kato’s theorem as in [35, 47]. The time evolution of the wave function $\Psi _{N,t}$ is governed by the Schrödinger equation

$$\begin{aligned} i \partial _t \Psi _{N,t} = N^{-1/3} H_N \Psi _{N,t}. \end{aligned}$$

(10)

The appearance of $N^{-1/3}$ in (10) stems from the fact that we are interested in initial conditions which are localized in a volume of order one. Then, due to the Fermi statistics, the average kinetic energy per fermion is of order $N^{2/3}$ and the average momentum per fermion of order $N^{1/3}$. Therefore, we rescale time so we track the particles only, while they move in the volume of order one, i.e., we go to timescales $N^{-1/3}$. This gives rise to a factor $N^{1/3}$ in front of the time derivative.

If we use the Schrödinger equation (10) to compute the Ehrenfest equation for the field operator, we obtain

$$\begin{aligned}&\big [ \partial _t^2 + N^{-2/3} \delta _N^2 (- \Delta _x + m^2) \big ] \left\langle \Psi _{N,t}, \widehat{\Phi }_{\Lambda }(x) \Psi _{N,t} \right\rangle \nonumber \\&\quad = - N^{1/3} \delta _N (2 \pi )^{-3} \int \mathrm{d}^3k e^{-ikx} \mathbb {1}_{\left| k \right| \le \Lambda }(k) \frac{1}{N} \left\langle {\Psi _{N,t},}{\sum _{j=1}^N e^{ik x_j} \Psi _{N,t}}\right\rangle , \end{aligned}$$

(11)

where $\left\langle \cdot , \cdot \right\rangle$ is the scalar product on $\mathcal {H}^{(N)}$ and the $x_j$’s on the right-hand side refer to the variables in $L^2_{\mathrm {as}}\left( \mathbb {R}^{3N} \right)$ that are integrated. Note that the integral on the right-hand side is proportional to $N^{-1}$ times the smeared out electron density (i.e., for $\Lambda \rightarrow \infty$ the electron density). Thus, for our initial conditions, the integral is a function of order one in a volume of order one. Equation (11) also shows that not only the coupling constant in front of the radiation field (which we set equal to one) but also $\delta _N$ determines the variation of the mean of the field operator. While our main result Theorem 2.3 holds for arbitrary $\delta _N$, we believe that two choices are of particular interest.

• 1. For $\delta _N = N^{1/3}$, the velocities of the electrons and the bosons scale equally. Moreover, it ensures that the right-hand side of (11) and hence the variation of the mean of the field operator are of order $N^{2/3}$. This gives rise to the interesting effective evolution equations (16) which capture the effect of the interaction.

• 2. If we set $\delta _N =1$, our model corresponds to an unscaled system whose dynamics is studied for timescales of order $N^{-1/3}$. This is interesting because usually mean-field results for systems with two-particle interaction require a scaling of the coupling constant. It should be noted that most of the electrons travel on a distance of order one and hence could interact with the other electrons. However, a look at (11) shows that the group velocity of the bosons is too slow to mediate an interaction between the electrons. This implies (see Theorem 2.7) that the electrons effectively evolve like free particles in an external potential.

Further insight concerning the scaling can be gained if we set $\varepsilon _N = N^{-1/3}$ and multiply (10) by $\varepsilon _N$. This gives

$$\begin{aligned} i \varepsilon _N \partial _t \Psi _{N,t} = \Bigg [ \sum _{j=1}^N \Big ( - \varepsilon _N^2 \Delta _j + N^{-1/2} \varepsilon _N^{1/2} \widehat{\Phi }_{\Lambda }(x_j) \Big ) + \varepsilon _N N^{-1/3} \delta _N H_f \Bigg ] \Psi _{N,t}. \end{aligned}$$

(12)

Here, the factor $\varepsilon _N$ appears exactly where the physical constant $\hbar$ appears in the Schrödinger equation. Thus, for $\delta _N = N^{1/3}$, our limit can be viewed as a combined weak coupling (the $N^{-1/2}$ in front of the interaction term) and semiclassical limit. Moreover, it displays a connection to the fermionic mean-field scaling considered in [9], i.e., to the model

$$\begin{aligned} i \varepsilon _N \partial _t \chi _{N,t} = \Bigg [ - \sum _{j=1}^N \varepsilon _N^2 \Delta _j + \frac{1}{N} \sum _{i<j}^N V(x_i - x_j) \Bigg ] \chi _{N,t} \end{aligned}$$

(13)

with $\chi _{N,t} \in L^2_{\mathrm {as}}(\mathbb {R}^{3N})$ and some $V{:}\,\mathbb {R}^3\rightarrow \mathbb {R}$. Like in [9], it will be crucial for us to consider initial data with a semiclassical structure, meaning that the kernel of the one-particle reduced density matrix is concentrated along its diagonal (see Remark 2.5 for more details).

We assume the initial states to be approximately of product form

$$\begin{aligned} \bigwedge _{j=1}^N \varphi _j^0 \otimes W( N^{2/3} \alpha ^0) \Omega . \end{aligned}$$

(14)

Here, $\alpha ^0 \in L^2(\mathbb {R}^3)$, $\bigwedge _{j=1}^N \varphi _j^0$ denotes the antisymmetrized tensor product (wedge product) of orthonormal $\varphi _1^0,\ldots ,\varphi _N^0 \in L^2(\mathbb {R}^3)$, $\Omega$ denotes the vacuum in $\mathcal {F}_\mathrm{s}$ and W is the Weyl operator

$$\begin{aligned} W(f) :=\exp \left( \int \mathrm{d}^3k \, \Big ( f(k) a^*(k) - \overline{f(k)} a(k) \Big ) \right) \end{aligned}$$

(15)

for all $f \in L^2(\mathbb {R}^3)$ ($\overline{f(k)}$ denotes the complex conjugate of f(k)). In such a state, the only correlations are due to the antisymmetry of the electron wave function. During the time evolution, correlations emerge, but the product structure (as will be shown) is preserved in the limit $N \rightarrow \infty$ on the level of reduced density matrices. This suggests to approximate the action of the scaled field operator $N^{-2/3} \widehat{\Phi }_{\Lambda }$ on $\Psi _{N,t}$ by a classical radiation field $\Phi _{\Lambda }(x,t)$ and replace the right-hand side of (11) by a coupling to the mean electron density. In fact, Theorem 2.3 says that $\Psi _{N,t}$ can be approximated by $\bigwedge _{j=1}^N \varphi _j^t \otimes W( N^{2/3} \alpha ^t) \Omega$, where $(\varphi _1^t, \ldots , \varphi _N^t,\alpha ^t)$ solves the Schrödinger–Klein–Gordon equations

$$\begin{aligned} \left\{ \begin{array}{ll} N^{-1/3} i \partial _t \varphi _j^t(x) = \left( -N^{-2/3} \Delta + \Phi _{\Lambda }(x,t) \right) \varphi _j^t(x), &{}\quad \text {for~} j = 1, \ldots , N, \\ i \partial _t \alpha ^t(k) = N^{-1/3} \delta _N \omega (k) \alpha ^t(k) + N^{-1} (2 \pi )^{3/2} \tilde{\eta }(k) \mathcal {F}\left[ \rho ^t \right] (k), &{}\\ \Phi _{\Lambda }(x,t) = \int \mathrm{d}^3k \, \tilde{\eta }(k) \big ( e^{ikx} \alpha ^t(k) + e^{-ikx} \overline{\alpha ^t(k)} \big ),&{} \end{array}\right. \end{aligned}$$

(16)

with $\rho ^t = \sum _{i=1}^N \left| \varphi _i^t \right| ^2$, $(\varphi _1^0, \ldots , \varphi _N^0,\alpha ^0) \in (L^2(\mathbb {R}^3))^{N+1}$, $\varphi _1^0,\ldots ,\varphi _N^0$ orthonormal, and where $\mathcal {F}[f](k) := (2\pi )^{-3/2}\int \mathrm{d}^3x e^{-ikx} f(x)$ denotes the Fourier transform of $f\in L^2(\mathbb {R}^3)$. This system of equations is formally equivalent to

$$\begin{aligned}&i N^{-1/3} \partial _t \varphi _j^t(x) = \left[ -N^{-2/3} \Delta + \Phi _{\Lambda }(x,t) \right] \varphi _j^t(x), \quad \text {for~} j = 1, \ldots , N, \nonumber \\&\big [ \partial _t^2 + N^{-2/3} \delta _N^2 (- \Delta + m^2) \big ] \Phi _{\Lambda }(x,t) \nonumber \\&\quad = - N^{-1/3} \delta _N (2 \pi )^{-3/2} \int \mathrm{d}^3k \, e^{ikx} \mathbb {1}_{\left| k \right| \le \Lambda }(k) \frac{1}{N} \mathcal {F}[\rho ^t](k). \end{aligned}$$

(17)

Its solutions have nice regularity properties because of the ultraviolet cutoff in the radiation field. For $m \in \mathbb {N}$, let $H^m(\mathbb {R}^3)$ denote the Sobolev space of order m and $L_m^2(\mathbb {R}^3)$ a weighted $L^2$-space with norm $\left\| \alpha \right\| _{L^2_m(\mathbb {R}^3)} = \big \Vert ( 1 + \left| \cdot \right| ^2 )^{m/2} \alpha \big \Vert _{L^2(\mathbb {R}^3)}$. Throughout this paper, we use

Proposition 1.1

Let $(\varphi _1^0, \ldots , \varphi _N^0, \alpha ^0) \in \bigoplus _{n=1}^N H^2(\mathbb {R}^3) \oplus L_1^2(\mathbb {R}^3)$. Then there is a strongly differentiable $\bigoplus _{n=1}^N H^2(\mathbb {R}^3) \oplus L_1^2(\mathbb {R}^3)$-valued function $(\varphi _1^t, \ldots , \varphi _N^t, \alpha ^t)$ on $[0, \infty )$ that satisfies (16). Moreover, if $\varphi _1^0,\ldots ,\varphi _N^0$ are orthonormal, then so are $\varphi _1^t,\ldots ,\varphi _N^t$ for all $t\in [0,\infty )$.

Proof

The proposition can be shown by a standard fixed point argument because of the ultraviolet cutoff. A proof is given in “Appendix B”. $\square$

For global well-posedness results of the Schrödinger–Klein–Gordon system without UV cutoff, i.e., (17) with $j=1$, $m=1$ and $\Lambda = \infty$, we refer to [13, 36].

In order to see that the effective equations are indeed non-trivial and to make the connection to the Coulomb potential, it is instructive to write them explicitly with physical constants. For $m=0$, fermion mass $m_\mathrm{F} > 0$ and for $\Lambda = \infty$, (17) is

$$\begin{aligned} \begin{aligned} i(N^{-1/3} \hbar ) \partial _t \varphi _j^t(x)&= \left[ -\frac{(N^{-1/3}\hbar )^2}{2m_\mathrm{F}} \Delta + \Phi (x,t) \right] \varphi _j^t(x), \\ \left[ \frac{1}{c^2} \partial _t^2 - (N^{-1/3}\delta _N)^2\Delta \right] \Phi (x,t)&= - (N^{-1/3}\delta _N) \frac{e^2}{\varepsilon _0} N^{-1} \rho ^t(x). \end{aligned} \end{aligned}$$

(18)

For $\delta _N=N^{1/3}$ and in the limit $c\rightarrow \infty$, this becomes the Poisson equation with solution $\Phi (x,t) = - N^{-1} \frac{e^2}{4\pi \varepsilon _0} (|\cdot |^{-1} * \rho ^t)(x)$. Finally, note that in (16) one can write the equation for $\alpha ^t(k)$ in integral form and plug it into the equations for the electrons. For $m=0$, $m_\mathrm{F} > 0$ and $\Lambda = \infty$, this yields

(19)

where $\Phi _{\Lambda }^{\mathrm {free}}(x,t) = e^{-i c \delta _N N^{-1/3} |\nabla | t} \Phi _{\Lambda }(x,0)$. For $\Phi _{\Lambda }(x,0)=0$, $\delta _N=N^{1/3}$ and in the formal limit $c\rightarrow \infty$, this becomes the Hartree equation with attractive mean-field Coulomb potential.

2 Main Result

As mentioned above, our goal is to show that $\Psi _{N,t} \approx \bigwedge _{j=1}^N \varphi _j^t \otimes W( N^{2/3} \alpha ^t) \Omega$ holds during the time evolution. In the following, this will be proved in the trace norm distance of reduced density matrices. Let us introduce the number operator

$$\begin{aligned} \mathcal {N} :=\int \mathrm{d}^3k \, a^*(k) a(k) \end{aligned}$$

(20)

with domain

$$\begin{aligned} \mathcal {D}(\mathcal {N}) = \left\{ \Psi _N \in \mathcal {H}^{(N)}{:}\,\sum _{n=1}^{\infty } n^2 \int \mathrm{d}^{3N}x \, \mathrm{d}^{3n}k \, \left| \Psi _N^{(n)}(X_N, K_n) \right| ^2 < \infty \right\} . \end{aligned}$$

(21)

Moreover, we choose $\left\| \Psi _{N,0} \right\| =1$ and $\Psi _{N,0} \in \mathcal {H}^{(N)} \cap \mathcal {D}(\mathcal {N}) \cap \mathcal {D}(\mathcal {N}H_N)$. (Note that for the definition of the reduced density matrix below we only need $\Psi _{N,0} \in \mathcal {H}^{(N)} \cap \mathcal {D}(\mathcal {N}^{1/2})$.) By unitarity, also $\left\| \Psi _{N,t} \right\| =1$ and the following lemma holds.

Lemma 2.1

Let $\Psi _{N,0} \in \mathcal {H}^{(N)} \cap \mathcal {D}(\mathcal {N}) \cap \mathcal {D}(\mathcal {N}H_N)$ and let $\Psi _{N,t}$ be the solution to (10) with initial condition $\Psi _{N,0}$. Then also $\Psi _{N,t} \in \mathcal {H}^{(N)} \cap \mathcal {D}(\mathcal {N}) \cap \mathcal {D}(\mathcal {N}H_N)$ for all $t\in [0,\infty )$.

Proof

A proof has been given before in [18, 19] and [30, Appendix 2.11]. $\square$

For $k\in \mathbb {N}$, we define the k-particle reduced density matrices of the fermions (as operators on $L^2(\mathbb {R}^{3k})$) by

$$\begin{aligned} \gamma _{N,t}^{(k,0)} :=\mathrm {Tr}_{k+1,\ldots , N} \mathrm {Tr}_{\mathcal {F}_\mathrm{s}} | \Psi _{N,t} \rangle \langle \Psi _{N,t} |, \end{aligned}$$

(22)

where $\mathrm {Tr}_{k+1,\ldots , N}$ denotes the partial trace over the coordinates $x_{k+1},\ldots , x_N$ and $\mathrm {Tr}_{\mathcal {F}_\mathrm{s}}$ the trace over Fock space. Additionally, we consider on $L^2(\mathbb {R}^3)$ the one-particle reduced density matrix of the bosons with kernel

$$\begin{aligned} \gamma _{N,t}^{(0,1)}(k,k') :=N^{-4/3} \left\langle \Psi _{N,t}, a^*(k') a(k) \Psi _{N,t} \right\rangle . \end{aligned}$$

(23)

The operator $\gamma _{N,t}^{(0,1)}$ is trace class with $\mathrm {Tr}\, \gamma _{N,t}^{(0,1)} = N^{-4/3} \left\langle \Psi _{N,t}, \mathcal {N} \Psi _{N,t} \right\rangle$. It is worth noting that (23) differs from the usual definition $\left\langle \Psi _{N,t}, \mathcal {N} \Psi _{N,t} \right\rangle ^{-1} \left\langle \Psi _{N,t}, a^*(k') a(k) \Psi _{N,t} \right\rangle$, which has trace one. In our choice, we only measure deviations from the classical mode function that are at least of order $N^{4/3}$. This is important if one starts initially with no bosons and examines the one-particle reduced density matrix after short times when only a few bosons have been created. Then, the state of the bosons might not be coherent and the usual definition of the one-particle reduced density matrix may not converge to the classical mode function. However, such mismatches are not important for the dynamics (and hence neglected in our definition) because the field operator is rescaled by a factor of $N^{-2/3}$; see (12).

Let us now state the main result of this article. We summarize the conditions on our initial data in the following assumption. We denote the trace norm of an operator A by $\left\| A \right\| _{\mathrm {Tr}} := \mathrm {Tr}\left| A \right|$.

Assumption 2.2

We have $\alpha ^0 \in L_1^2(\mathbb {R}^3)$ and $\varphi _1^0, \ldots , \varphi _N^0 \in H^2(\mathbb {R}^3)$ orthonormal and such that

$$\begin{aligned} \left\| p^0 e^{ikx} q^0 \right\| _{\mathrm {Tr}} \le C (1 + \left| k \right| ) N^{2/3}~\forall k\in \mathbb {R}^3 \quad \text {and} \quad \left\| p^0 \nabla q^0 \right\| _{\mathrm {Tr}} \le C N \end{aligned}$$

(24)

for some $C>0$, where $p^t = \sum _{j=1}^N | \varphi _j^t \rangle \langle \varphi _j^t |$ and $q^t=1-p^t$ for any $t\in \mathbb {R}$ (see also Definition 3.1). Moreover, $\Psi _{N,0} \in \mathcal {H}^{(N)} \cap \mathcal {D}(\mathcal {N}) \cap \mathcal {D}(\mathcal {N}H_N)$ with $\left\| \Psi _{N,0} \right\| =1$.

Our main theorem is the following.

Theorem 2.3

Let Assumption 2.2 hold, and let $\Psi _{N,t}$ be the solution to (10) with initial condition $\Psi _{N,0}$ and $\varphi _1^t,\ldots ,\varphi _N^t,\alpha ^t$ the solution to (16) with initial condition $\varphi _1^0,\ldots ,\varphi _N^0,\alpha ^0$. We define

$$\begin{aligned}&a_N = \left\| \gamma _{N,0}^{(1,0)} - N^{-1}p^0 \right\| _{\mathrm {Tr}}, \end{aligned}$$

(25)

$$\begin{aligned}&b_N = N^{1/3} \, \mathrm {Tr}\big ( \gamma _{N,0}^{(2,0)} q^0 \otimes q^0 \big ), \end{aligned}$$

(26)

$$\begin{aligned}&c_N = N^{-1} \left\langle W^{-1}(N^{2/3} \alpha ^0) \Psi _{N,0}, \mathcal {N} W^{-1}( N^{2/3} \alpha ^0) \Psi _{N,0} \right\rangle . \end{aligned}$$

(27)

Then there exists $C>0$ (independent of N, $\delta _N$, $\Lambda$ and t) such that for any $t \ge 0$,

$$\begin{aligned} \left\| \gamma _{N,t}^{(1,0)} - N^{-1} p^t \right\| _{\mathrm {Tr}}&\le \sqrt{a_N + b_N + c_N + N^{-1}} \, e^{e^{C \Lambda ^4 (1 + \Vert \alpha ^0\Vert _2)(1 + t^2)}}. \end{aligned}$$

(28)

If additionally $c_N \le \tilde{C}N^{1/3}$ for some $\tilde{C}>0$, then

$$\begin{aligned} \left\| \gamma _{N,t}^{(0,1)} - | \alpha ^t \rangle \langle \alpha ^t | \right\| _{\mathrm {Tr}}&\le \sqrt{ N^{-1/3} (a_N + b_N + c_N) + N^{-4/3}} \, e^{e^{C \Lambda ^4 ( 1 + \Vert \alpha ^0\Vert _2) ( 1 + t^2)}}. \end{aligned}$$

(29)

In particular, for $\Psi _{N,0} = \bigwedge _{j=1}^N \varphi _j^0 \otimes W( N^{2/3} \alpha ^0) \Omega$ we have $a_N=b_N=c_N=0$ and one obtains

$$\begin{aligned} \left\| \gamma _{N,t}^{(1,0)} - N^{-1} p^t \right\| _{\mathrm {Tr}}&\le N^{-1/2} e^{e^{C \Lambda ^4 (1 + \Vert \alpha ^0\Vert _2)(1 + t^2)}}, \end{aligned}$$

(30)

$$\begin{aligned} \left\| \gamma _{N,t}^{(0,1)} - | \alpha ^t \rangle \langle \alpha ^t | \right\| _{\mathrm {Tr}}&\le N^{-2/3} e^{e^{C \Lambda ^4 (1 + \Vert \alpha ^0\Vert _2)(1 + t^2)}}. \end{aligned}$$

(31)

The theorem is proved in Sect. 6.

Remark 2.4

In [9, 17], a similar limit was considered for fermions that interact by means of a pair potential. From these works, we learned the importance of the semiclassical structure. The most related works from a technical point of view are [19, 31, 32, 37].

Remark 2.5

For initial states without semiclassical structure, i.e., without assuming (24), the result only holds true for times of order $N^{-1/3}$. More precisely, Equations (28)–(31) hold with the double exponential replaced by $e^{C(\Lambda ,\left\| \alpha ^0 \right\| )N^{1/3}t}$.

The first inequality in (24) means that the kernel $p^0(x,y)$ is localized around a distance smaller than of order $N^{-1/3}$ around the diagonal $x=y$. The second inequality means that the density varies on scales of order one. In fact, these conditions should imply that the time evolution of $p^0$ (or, say, its Wigner transform) is close to a classical evolution equation, which here is the Vlasov equation. This has indeed been shown in the two-body interaction case; let us refer to [7] and references therein. Note also that for simple cases like plane waves in a box of volume of order one, (24) indeed holds; see [40]. For a more thorough discussion of these conditions, we refer to [9, 40].

Remark 2.6

Let us give a bit more intuition about $c_N$. We first note that the Weyl operator, defined in (15), is unitary, and thus, $W^{-1}(f) = W^*(f) = W(-f)$. One of its well-known properties (see, e.g., [42] for a nice exposition) is

$$\begin{aligned} W^*(f) a(k) W(f) = a(k) + f(k), \quad W^*(f) a^*(k) W(f) = a^*(k) + \overline{f(k)}. \end{aligned}$$

(32)

With that in hand, we can write $c_N$ as

$$\begin{aligned} c_N&= N^{1/3} \int \mathrm{d}^3k\, \left\| N^{-2/3} a(k) W^{-1}(N^{2/3} \alpha ^0) \Psi _{N,0} \right\| ^2 \nonumber \\&= N^{1/3} \int \mathrm{d}^3k\, \left\| \left( N^{-2/3} a(k) - \alpha ^0(k) \right) \Psi _{N,0} \right\| ^2, \end{aligned}$$

(33)

from which it might become more clear that $c_N$ measures the initial deviations around the classical radiation field $\alpha ^0$.

In the case of $\delta _N = N^{1/3 - \epsilon }$ with $\epsilon > 0$, the group velocity of the bosons is of lower order than the average speed of the electrons. This implies that the electrons effectively experience a stationary scalar field and evolve according to

$$\begin{aligned} N^{-1/3} i \partial _t \varphi _j^t(x) = \left( - N^{-2/3} \Delta + \Phi _{\Lambda }(x,0) \right) \varphi _j^t(x) \quad \text {for} \; j=1, \ldots , N. \end{aligned}$$

(34)

The precise statement is the following.

Theorem 2.7

Let Assumption 2.2 hold, let $(\varphi _1^t, \ldots , \varphi _N^t, \alpha ^t)$ be the solution to (16) with initial condition $(\varphi _1^0, \ldots , \varphi _N^0, \alpha ^0)$ and let $(\tilde{\varphi }_1^t, \ldots , \tilde{\varphi }_N^t)$ be the solution to (34) with initial condition $(\varphi _1^0, \ldots , \varphi _N^0)$. We define $\tilde{p}^t = \sum _{j=1}^N | \tilde{\varphi }_j^t \rangle \langle \tilde{\varphi }_j^t |$ and $p^t$ as in Assumption 2.2. Then there exists $C >0$ (independent of N, $\delta _N$, $\Lambda$ and t) such that

$$\begin{aligned} N^{-1} \left\| p^t - \tilde{p}^t \right\| _{\mathrm {Tr}} \le N^{-1/3} \delta _N e^{C \Lambda ^4 (1 + \left\| \alpha ^0 \right\| _2) ( 1 + t^2)}. \end{aligned}$$

(35)

Furthermore, let $\Psi _{N,t}$ be the solution to (10) with initial condition $\Psi _{N,0}$, and let $a_N$, $b_N$ and $c_N$ be defined as in Theorem 2.3. Then there exists $C>0$ (independent of N, $\delta _N$, $\Lambda$ and t) such that for all $t \ge 0$,

$$\begin{aligned} \left\| \gamma _{N,t}^{(1,0)} {-} N^{-1} \tilde{p}^t \right\| _{\mathrm {Tr}}&\le \Big ( N^{-1/3} \delta _N {+} \sqrt{a_N + b_N + c_N + N^{-1}} \Big ) \, e^{e^{C \Lambda ^4 (1 + \Vert \alpha ^0\Vert _2)(1 + t^2)}}. \end{aligned}$$

(36)

The theorem is proved in “Appendix A”.

3 Structure of the Proof

In order to prove Theorem 2.3, it is important to define and control the right macroscopic variables. For that, we adapt techniques that are based on the method from [39] and that were further developed in [31, 32, 37]. In addition, it is crucial to find the right measure for the correlations between the electrons and to consider only initial states with semiclassical structure. The key idea of the proof is to define a suitable functional $\beta (\Psi _N,\varphi _1, \ldots , \varphi _N, \alpha )$ which measures if the fermions are close to an antisymmetrized product state $\bigwedge _{j=1}^N \varphi _j$ with $\varphi _1, \ldots , \varphi _N$ orthonormal and if the state of the radiation field is approximately coherent. To this end, we introduce the following operators.

Definition 3.1

For $N \in \mathbb {N}$, $m, j \in \{1,2, \ldots , N \}$ and $\varphi _1, \ldots , \varphi _N \in L^2(\mathbb {R}^3)$ orthonormal, we define the projectors $p_m^{\varphi _j}{:}\,L^2(\mathbb {R}^{3N}) \rightarrow L^2(\mathbb {R}^{3N})$ by

$$\begin{aligned} p_m^{\varphi _j} f(x_1, \ldots , x_N) :=\varphi _j(x_m) \int \mathrm{d}^3x_m \, \overline{\varphi _j(x_m)} f(x_1, \ldots , x_N) \quad \forall \, f \in L^2(\mathbb {R}^{3N}). \end{aligned}$$

(37)

Moreover, we define the projectors $p_m^{\varphi _1, \ldots , \varphi _N}{:}\,L^2(\mathbb {R}^{3N}) \rightarrow L^2(\mathbb {R}^{3N})$ and $q_m^{\varphi _1, \ldots , \varphi _N}: L^2(\mathbb {R}^{3N}) \rightarrow L^2(\mathbb {R}^{3N})$ by

$$\begin{aligned} p_m^{\varphi _1, \ldots , \varphi _N} :=\sum _{j=1}^N p_m^{\varphi _j} \quad \text {and} \quad q_m^{\varphi _1, \ldots , \varphi _N} :=1 - p_m^{\varphi _1, \ldots , \varphi _N}. \end{aligned}$$

(38)

The correlations between the electrons are controlled by means of two functionals.

Definition 3.2

Let $N \in \mathbb {N}$, $\varphi _1, \ldots , \varphi _N \in L^2(\mathbb {R}^3)$ orthonormal and $\Psi _{N} \in \mathcal {H}^{(N)}$. Then, $\beta ^{a,1}{:}\,\mathcal {H}^{(N)} \times L^2(\mathbb {R}^3)^{N} \rightarrow [0, \infty )$ and $\beta ^{a,2}{:}\,\mathcal {H}^{(N)} \times L^2(\mathbb {R}^3)^N \rightarrow [0, \infty )$ are given by

$$\begin{aligned} \beta ^{a,1}(\Psi _{N}, \varphi _1, \ldots , \varphi _N)&:=\left\langle \Psi _{N}, q_1^{\varphi _1, \ldots , \varphi _N} \otimes \mathbb {1}_{\mathcal {F}_\mathrm{s}} \Psi _{N,t} \right\rangle \quad \text {and} \end{aligned}$$

(39)

$$\begin{aligned} \beta ^{a,2}(\Psi _{N}, \varphi _1, \ldots , \varphi _N)&:=N^{1/3} \left\langle \Psi _{N}, q_1^{\varphi _1, \ldots , \varphi _N} q_2^{\varphi _1, \ldots , \varphi _N} \otimes \mathbb {1}_{\mathcal {F}_\mathrm{s}} \Psi _{N} \right\rangle . \end{aligned}$$

(40)

We note that $\beta ^{a,1}(\Psi _{N}, \varphi _1, \ldots , \varphi _N)$ corresponds to the expectation value of the relative number of fermions outside the antisymmetric product $\bigwedge _{j=1}^N\varphi _j$ (i.e., the number of excitations around the state $\bigwedge _{j=1}^N\varphi _j$ divided by N). The functional $N^{-1/3}\beta ^{a,2}(\Psi _{N}, \varphi _1, \ldots , \varphi _N)$ corresponds (up to a small error) to the expectation value of the square of this number. More details about the technical relevance of $\beta ^{a,2}$ are given at the beginning of Sect. 5.

In order to determine whether the state of the radiation field is coherent, we define $\beta ^b$, which measures the fluctuations of the field modes around the complex function $\alpha$.

Definition 3.3

Let $\alpha \in L^2(\mathbb {R}^3)$ and $\Psi _{N} \in \mathcal {H}^{(N)} \cap \mathcal {D}\left( \mathcal {N} \right)$. Then $\beta ^b{:}\,\mathcal {H}^{(N)} \cap \mathcal {D}\left( \mathcal {N} \right) \times L^2(\mathbb {R}^3) \rightarrow [0,\infty )$ is given by

$$\begin{aligned} \beta ^b\left( \Psi _{N}, \alpha \right) :=N^{1/3} \int \mathrm{d}^3k \, \left\langle {\left( N^{-2/3} a(k) - \alpha (k) \right) \Psi _{N},}{ \left( N^{-2/3} a(k) - \alpha (k) \right) \Psi _{N}}\right\rangle . \end{aligned}$$

(41)

Note that $\beta ^b(\Psi _{N,0},\alpha ^0) = c_N$ as we showed in (33). Let us also remark that when $\Psi _{N,t}$ is a solution to (10) and $\varphi _1^t,\ldots ,\varphi _N^t,\alpha ^t$ a solution to (16), then the functional $\beta ^b\left( \Psi _{N,t}, \alpha ^t \right)$ coincides (up to scaling) with the one used in the coherent states approach; see, e.g., [10, Chapter 3]. Finally, the functional $\beta$ is defined by

Definition 3.4

Let $N \in \mathbb {N}$, $\varphi _1, \ldots , \varphi _N \in L^2(\mathbb {R}^3)$ orthonormal, $\alpha \in L^2(\mathbb {R}^3)$ and $\Psi _{N} \in \mathcal {H}^{(N)} \cap \mathcal {D}\left( \mathcal {N} \right)$. Then $\beta {:}\,\mathcal {H}^{(N)} \cap \mathcal {D}\left( \mathcal {N} \right) \times L^2(\mathbb {R}^3)^N \times L^2(\mathbb {R}^3) \rightarrow [0, \infty )$ is defined by

$$\begin{aligned} \beta \left( \Psi _{N}, \varphi _1, \ldots , \varphi _N, \alpha \right)&:=\beta ^{a,1}(\Psi _{N}, \varphi _1, \ldots , \varphi _N) \nonumber \\&\quad +\,\beta ^{a,2}(\Psi _{N}, \varphi _1, \ldots , \varphi _N) + \beta ^b\left( \Psi _{N}, \alpha \right) . \end{aligned}$$

(42)

In the following, we are interested in the value of $\beta \left( \Psi _{N,t}, \varphi _1^t, \ldots , \varphi _N^t, \alpha ^t \right)$, where $(\varphi _1^t, \ldots , \varphi _N^t, \alpha ^t)$ is a solution to the Schrödinger–Klein–Gordon equations (16) and $\Psi _{N,t}$ evolves according to the Schrödinger equation (10). In this case, we apply the shorthand notations $\beta (t)$, $\beta ^{a,1}(t)$, $\beta ^{a,2}(t)$ and $\beta ^b(t)$. Moreover, we use the abbreviations $p_m^{\varphi _1^t, \ldots , \varphi _N^t} = p_m^t$, $q_m^{\varphi _1^t, \ldots , \varphi _N^t} = q_m^t$ and write $p_m^{\varphi _j^t}$ occasionally as $| \varphi _j^t \rangle \langle \varphi _j^t |_m$.

For the proof of Theorem 2.3, we pursue the following strategy.

• (A) We choose initial data $(\varphi _1^0, \ldots , \varphi _N^0, \alpha ^0)$ of the Schrödinger–Klein–Gordon system (16) and a many-body wave function $\Psi _{N,0}$ that satisfy our Assumption 2.2. Proposition 1.1 and Lemma 2.1 make sure that the solutions at any time $t\ge 0$ are regular enough, and in Sect. 4, we show that the solutions still have the semiclassical structure.

• (B) After that, we control the change of $\beta (t)$ in time. For this, we use the semiclassical structure to estimate $\left| \frac{\mathrm{d}}{\mathrm{d}t} \beta (t) \right| \le e^{Ct} ( \beta (t) + N^{-1} )$ for some $C>0$ at each time $t \ge 0$. Gronwall’s lemma then yields $\beta (t) {\le } e^{e^{Ct}} \left( \beta (0) + N^{-1} \right)$.

• (C) Finally, we relate the initial states of Theorem 2.3 and the trace norm convergence of the reduced density matrices to $\beta (t)$.

Notation 3.5

In the rest of this article, the letter C denotes a generic positive constant and its value might change from line to line for notational convenience.

4 Semiclassical Structure

We first prove that the semiclassical structure from Eq. (24) can be propagated in time. The Hilbert–Schmidt norm of an operator A is denoted by $\left\| A \right\| _{\mathrm {HS}} := \sqrt{\mathrm {Tr}\, A^*A}$.

Lemma 4.1

Let $(\varphi _1^0, \ldots , \varphi _N^0, \alpha ^0) \in H^2(\mathbb {R}^3)^N \times L_1^2(\mathbb {R}^3)$ with orthonormal $\varphi _1^0,\ldots ,\varphi _N^0$ and let $(\varphi _1^t, \ldots , \varphi _N^t, \alpha ^t)$ be solutions of (16). We assume that

$$\begin{aligned} \left\| p^0e^{ikx}q^0 \right\| _{\mathrm {Tr}} \le \tilde{C} (1+\left| k \right| ) N^{2/3} \end{aligned}$$

(43)

for all $k\in \mathbb {R}^3$ and

$$\begin{aligned} \left\| p^0\nabla q^0 \right\| _{\mathrm {Tr}} \le \tilde{C} N \end{aligned}$$

(44)

for some $\tilde{C}>0$. Then there exists some $C>0$ (independent of N, $\Lambda$ and t) such that

$$\begin{aligned} \left\| p^te^{ikx}q^t \right\| _{\mathrm {HS}}^2 \le \left\| p^te^{ikx}q^t \right\| _{\mathrm {Tr}} \le 2\tilde{C} (1+\left| k \right| ) N^{2/3} e^{C \Lambda ^4 ( 1 + \left\| \alpha ^0 \right\| _{2}) (1 + t^2)} \end{aligned}$$

(45)

for all $k\in \mathbb {R}^3$ and

$$\begin{aligned} \left\| p^t\nabla q^t \right\| _{\mathrm {Tr}} \le 2\tilde{C} N e^{C \Lambda ^4 ( 1 + \left\| \alpha ^0 \right\| _{2}) (1 + t^2)} \end{aligned}$$

(46)

for all $t\in \mathbb {R}$.

Remark 4.2

We could formulate Lemma 4.1 likewise in terms of $\left\| \left[ p^t, e^{ikx} \right] \right\| _{\mathrm {Tr}}$ and $\left\| \left[ p^t, \nabla \right] \right\| _{\mathrm {Tr}}$ as it was done in [9], because

$$\begin{aligned} \begin{aligned} \left\| p^t e^{ikx} q^t \right\| _{\mathrm {Tr}}&= \left\| \left[ p^t, e^{ikx}\right] q^t \right\| _{\mathrm {Tr}}\\&\le \left\| \left[ p^t, e^{ikx} \right] \right\| _{\mathrm {Tr}} \le \left\| p^t e^{ikx} q^t \right\| _{\mathrm {Tr}} + \left\| p^t e^{-ikx} q^t \right\| _{\mathrm {Tr}}, \\ \left\| p^t \nabla q^t \right\| _{\mathrm {Tr}}&= \left\| \left[ p^t, \nabla \right] q^t \right\| _{\mathrm {Tr}} \le \left\| \left[ p^t, \nabla \right] \right\| _{\mathrm {Tr}} \le 2 \left\| p^t \nabla q^t \right\| _{\mathrm {Tr}}. \end{aligned} \end{aligned}$$

(47)

These inequalities hold since $p^t q^t = 0$, $\left\| AB \right\| _{\mathrm {Tr}} \le \left\| A \right\| \left\| B \right\| _{\mathrm {Tr}}$ and $\left\| BA \right\| _{\mathrm {Tr}} \le \left\| A \right\| \left\| B \right\| _{\mathrm {Tr}}$ for A bounded and B trace class, $\left\| q^t \right\| =1$, and $\left\| B \right\| _{\mathrm {Tr}} = \left\| B^* \right\| _{\mathrm {Tr}}$ for B trace class.

Proof of Lemma 4.1

The propagation of the semiclassical structure is shown in a similar way as in [9, Section 5]. Recall that due to Proposition 1.1 the solution $(\varphi _1^t, \ldots , \varphi _N^t, \alpha ^t)$ is in $\bigoplus _{n=1}^N H^2(\mathbb {R}^3) \oplus L_1^2(\mathbb {R}^3)$ and strongly continuous. If we define $h^t = - \Delta + N^{2/3} \Phi _{\Lambda }(\cdot ,t)$, the time derivative of the projector $iN^{1/3}\partial _t p^t = [h^t,p^t]$. Then¹

$$\begin{aligned} i N^{1/3} \partial _t \big ( q^te^{ikx}p^t \big )&= [h^t,q^t]e^{ikx}p^t + q^te^{ikx}[h^t,p^t]\nonumber \\&= [h^t,q^te^{ikx}p^t] - q^t[h^t,e^{ikx}]p^t. \end{aligned}$$

(48)

From

$$\begin{aligned} {[}h^t,e^{ikx}] = [- \Delta , e^{ikx}]&= - ik \Big (\nabla e^{ikx} + e^{ikx}\nabla \Big ) \end{aligned}$$

(49)

and using $p^t+ q^t = 1$, we conclude

$$\begin{aligned} i N^{1/3} \partial _t \big (q^te^{ikx}p^t\big )&= [h^t,q^te^{ikx}p^t] +ik q^t\Big (\nabla e^{ikx} + e^{ikx}\nabla \Big )p^t \nonumber \\&= [h^t,q^te^{ikx}p^t] + ik \nabla q^te^{ikx}p^t + ik q^te^{ikx}p^t \nabla \nonumber \\&\quad +\,ik \Big ( q^t\nabla p^t e^{ikx}p^t - p^t\nabla q^te^{ikx}p^t\nonumber \\&\quad -\,q^te^{ikx} p^t\nabla q^t + q^te^{ikx}q^t\nabla p^t \Big ) \nonumber \\&= \Big (h^t + ik\nabla \Big ) q^te^{ikx}p^t - q^te^{ikx}p^t \Big (h^t - ik\nabla \Big ) \nonumber \\&\quad +\,ik \Big ( \big (q^t\nabla p^t - p^t\nabla q^t\big ) e^{ikx}p^t + q^te^{ikx} \big (q^t\nabla p^t - p^t\nabla q^t\big ) \Big ). \end{aligned}$$

(50)

Next, we define the time-dependent self-adjoint operators

$$\begin{aligned} A_{+k}(t) = h^t + ik \nabla \quad \text {and} \quad A_{-k}(t) = h^t - ik \nabla \end{aligned}$$

(51)

and their respective unitary propagators $U_{+k}(t;s)$ and $U_{-k}(t;s)$. These are indeed well defined, which follows from [41, Theorem X.71] adapted to $H_0 = -\Delta \pm i\nabla k$, or, more conveniently, from [44, Theorem 2.5] and the fact that $\Phi _{\Lambda }(\cdot ,t)$ is continuously differentiable in $L^{\infty }(\mathbb {R}^3)$, a direct consequence of Proposition 1.1. The unitary propagators (with rescaled time) satisfy

$$\begin{aligned}&i N^{1/3} \partial _t U_{+k}(t;s)\varphi = A_{+k}(t) U_{+k}(t;s) \varphi \quad \text {and} \nonumber \\&i N^{1/3} \partial _t U_{-k}(t;s)\varphi = A_{-k}(t) U_{-k}(t;s) \varphi \end{aligned}$$

(52)

for all $\varphi \in H^2(\mathbb {R}^3)$, with initial conditions $U_{+k}(s;s)= U_{-k}(s;s) = 1$. This gives

$$\begin{aligned}&i N^{1/3} \partial _t \big (U_{+k}^*(t;0) q^te^{ikx}p^t U_{-k}(t;0)\big ) \nonumber \\&\quad = U_{+k}^*(t;0) \Big ( - A_{+k}(t) q^te^{ikx}p^t {+} q^te^{ikx}p^t A_{-k} {+} i N^{1/3} \partial _t \big ( q^te^{ikx}p^t \big )\Big ) U_{-k}(t;0) \nonumber \\&\quad = ik U_{+k}^*(t;0) \Big ( \big (q^t\nabla p^t - p^t\nabla q^t\big )e^{ikx}p^t +q^te^{ikx}\big ( q^t\nabla p^t p^t\nabla q^t \big ) \Big ) U_{-k}(t;0), \end{aligned}$$

(53)

which leads to

$$\begin{aligned}&U_{+k}^*(t;0) q^te^{ikx}p^t U_{-k}(t;0) \nonumber \\&\quad = q^0e^{ikx}p^0+\,N^{-1/3} k \int _0^t\,\mathrm{d}s \, U_{+k}^*(s;0) \bigg ( \big (q^s\nabla p^s - p^s\nabla q^s\big ) e^{ikx}p^s \nonumber \\&\qquad -\,q^se^{ikx}\big (p^s\nabla q^s - q^s\nabla p^s\big )\bigg ) U_{-k}(s;0), \end{aligned}$$

(54)

and thus,

$$\begin{aligned} q^te^{ikx}p^t&= U_{+k}(t;0) q^0e^{ikx}p^0 U_{-k}^*(t;0) \nonumber \\&\quad +\,N^{-1/3} k \int _0^t\,\mathrm{d}s \, U_{+k}(t;s) \bigg ( \big (q^s\nabla p^s -p^s\nabla q^s\big ) e^{ikx}p^s\nonumber \\&\quad - q^se^{ikx}\big (p^s\nabla q^s - q^s\nabla p^s\big )\bigg ) U_{-k}(s;t). \end{aligned}$$

(55)

For the trace norm, we then obtain the estimate

$$\begin{aligned} \left\| q^te^{ikx}p^t \right\| _{\mathrm {Tr}} \le \left\| q^0e^{ikx}p^0 \right\| _{\mathrm {Tr}} + 4 N^{-1/3} (1+ \left| k \right| ) \int _0^t \mathrm{d}s \, \left\| q^s\nabla p^s \right\| _{\mathrm {Tr}}, \end{aligned}$$

(56)

where we used that $\left\| AB \right\| _{\mathrm {Tr}} \le \left\| A \right\| \left\| B \right\| _{\mathrm {Tr}}$ and $\left\| BA \right\| _{\mathrm {Tr}} \le \left\| A \right\| \left\| B \right\| _{\mathrm {Tr}}$ for A bounded and B trace class. Thus,

$$\begin{aligned} \sup _{k \in \mathbb {R}^3} \left( (1 + \left| k \right| )^{-1} \left\| q^te^{ikx}p^t \right\| _{\mathrm {Tr}} \right)&\le \sup _{k \in \mathbb {R}^3} \left( (1 + \left| k \right| )^{-1} \left\| q^0e^{ikx}p^0 \right\| _{\mathrm {Tr}} \right) \nonumber \\&\quad +\,4 \int _0^t\,\mathrm{d}s \, N^{-1/3} \left\| q^s\nabla p^s \right\| _{\mathrm {Tr}}. \end{aligned}$$

(57)

In order to control the latter term, we calculate the time derivative of $q^t\nabla p^t$. We find

$$\begin{aligned} i N^{1/3} \partial _t \big (q^t\nabla p^t\big )&= [h^t,q^t]\nabla p^t + q^t \nabla [h^t,p^t] \nonumber \\&= [h^t,q^t\nabla p^t] - q^t [h^t,\nabla ]p^t \nonumber \\&= [h^t,q^t\nabla p^t] + N^{2/3} q^t (\nabla \Phi _{\Lambda })(t) p^t. \end{aligned}$$

(58)

In analogy to the previous calculation, we define the two-parameter group $U_h(t;s)$ satisfying

$$\begin{aligned} i N^{1/3} \partial _t U_h(t;s)\varphi = h^t U_h(t;s) \varphi \end{aligned}$$

(59)

for all $\varphi \in H^2(\mathbb {R}^3)$ and $U_h(s;s)=1$. Then, we calculate

$$\begin{aligned}&i N^{1/3} \partial _t \big ( U_h^*(t;0)q^t\nabla p^t U_h(t;0)\big ) \nonumber \\&\quad = U_h^*(t;0) \bigg ( -h^t q^t\nabla p^t + q^t\nabla p^t h^t + i N^{1/3}\partial _t \big (q^t \nabla p_t\big ) \bigg ) U_h(t;0) \nonumber \\&\quad = N^{2/3} U_h^*(t;0) q^t (\nabla \Phi _{\Lambda })(t) p^t U_h(t;0), \end{aligned}$$

(60)

which implies

$$\begin{aligned} q^t \nabla p^t&= U_h(t;0) q^0\nabla p^0 U^*_h(t;0) - i N^{1/3} \int _0^t\,\mathrm{d}s \, U_h(t;s) \Big (q^s (\nabla \Phi _{\Lambda })(s)p^s\Big ) U_h(s,t). \end{aligned}$$

(61)

Using the same inequalities as for (56), this leads to

$$\begin{aligned} \left\| q^t\nabla p^t \right\| _{\mathrm {Tr}} \le \left\| q^0\nabla p^0 \right\| _{\mathrm {Tr}} + N^{1/3} \int _0^t\,\mathrm{d}s \, \left\| q^s(\nabla \Phi _{\Lambda })(s)p^s \right\| _{\mathrm {Tr}}. \end{aligned}$$

(62)

By Lemma B.2, which says that $\left\| \alpha ^t \right\| _2 \le \left\| \alpha ^0 \right\| _2 + \left\| \tilde{\eta } \right\| _2 \left| t \right|$, we can estimate

$$\begin{aligned}&\left\| q^s(\nabla \Phi _{\Lambda })(s)p^s \right\| _{\mathrm {Tr}}\nonumber \\&\quad = \left\| \int \mathrm{d}^3k \, \tilde{\eta }(k) k \big ( \alpha ^s(k) q^se^{ikx}p^s - \overline{\alpha ^s(k)} q^se^{-ikx}p^s \big ) \right\| _{\mathrm {Tr}} \nonumber \\&\quad \le \int \mathrm{d}^3k \, \tilde{\eta }(k) \left| k \right| \left( \left| \alpha ^s(k) \right| \left\| q^se^{ikx}p^s \right\| _{\mathrm {Tr}} + \left| \alpha ^s(k) \right| \left\| q^se^{-ikx}p^s \right\| _{\mathrm {Tr}} \right) \nonumber \\&\quad \le 2 \left\| (1 + \left| \cdot \right| )^2 \tilde{\eta } \right\| _2 \left\| \alpha ^s \right\| _2 \sup _{k \in \mathbb {R}^3} \Big ((1 + \left| k \right| )^{-1} \left\| q^se^{ikx}p^s \right\| _{\mathrm {Tr}} \Big ) \nonumber \\&\quad \le 2 \left\| (1 +\left| \cdot \right| )^2 \tilde{\eta } \right\| _2 \Big ( \left\| \alpha ^0 \right\| _2 + \left\| \tilde{\eta } \right\| _2 \left| s \right| \Big )\sup _{k \in \mathbb {R}^3} \Big ((1 + \left| k \right| )^{-1} \left\| q^se^{ikx}p^s \right\| _{\mathrm {Tr}} \Big ) \end{aligned}$$

(63)

and obtain

$$\begin{aligned}&N^{-1/3} \left\| q^t\nabla p^t \right\| _{\mathrm {Tr}}\nonumber \\&\le N^{-1/3} \left\| q^0\nabla p^0 \right\| _{\mathrm {Tr}} +2 \left\| (1 + \left| \cdot \right| )^2 \tilde{\eta } \right\| _2 \int _0^t\,\mathrm{d}s \, \Big ( \left\| \alpha ^0 \right\| _2 + \left\| \tilde{\eta } \right\| _2 \left| s \right| \Big )\nonumber \\&\quad \times \sup _{k \in \mathbb {R}^3} \Big ((1 + \left| k \right| )^{-1} \left\| q^se^{ikx}p^s \right\| _{\mathrm {Tr}} \Big ). \end{aligned}$$

(64)

Together with the estimate (57), this gives

$$\begin{aligned}&\sup _{k \in \mathbb {R}^3} \Big ((1 + \left| k \right| )^{-1} \left\| q^te^{ikx}p^t \right\| _{\mathrm {Tr}} \Big ) + N^{-1/3} \left\| q^t\nabla p^t \right\| _{\mathrm {Tr}} \nonumber \\&\quad \le \sup _{k \in \mathbb {R}^3} \Big ((1 + \left| k \right| )^{-1} \left\| q^0e^{ikx}p^0 \right\| _{\mathrm {Tr}} \Big ) + N^{-1/3} \left\| q^0\nabla p^0 \right\| _{\mathrm {Tr}} \nonumber \\&\qquad +\,\int _0^t\,\mathrm{d}s \, C(\Lambda ,s,\left\| \alpha ^0 \right\| _2) \left( \sup _{k \in \mathbb {R}^3} \Big ((1 + \left| k \right| )^{-1} \left\| q^se^{ikx}p^s \right\| _{\mathrm {Tr}} \Big ) \right. \nonumber \\&\qquad \left. +\,N^{-1/3} \left\| q^s\nabla p^s \right\| _{\mathrm {Tr}} \right) , \end{aligned}$$

(65)

where $C(\Lambda ,s,\left\| \alpha ^0 \right\| _2) :=4 + 2 \left\| ( 1 + \left| \cdot \right| )^2 \tilde{\eta } \right\| _2 \big ( \left\| \alpha ^0 \right\| _2 + \left\| \tilde{\eta } \right\| _2 \left| s \right| \big )$. By means of Gronwall’s lemma and the chosen initial conditions, we obtain

$$\begin{aligned}&\sup _{k \in \mathbb {R}^3} \Big ((1 + \left| k \right| )^{-1} \left\| q^te^{ikx}p^t \right\| _{\mathrm {Tr}} \Big ) + N^{-1/3} \left\| q^t\nabla p^t \right\| _{\mathrm {Tr}} \nonumber \\&\quad \le 2\tilde{C} N^{2/3} \exp \Big [4 \left| t \right| \big ( 1 + \left\| ( 1 + \left| \cdot \right| ^2) \tilde{\eta } \right\| _2 \big ( \left\| \alpha ^0 \right\| _2 + \left\| \tilde{\eta } \right\| _2 \left| t \right| \big ) \Big ] \nonumber \\&\quad \le 2\tilde{C} N^{2/3} \exp \Big [ C \Lambda ^4 \big ( 1 + \left\| \alpha ^0 \right\| _2 \big ) \big ( 1 + t^2 \big ) \Big ]. \end{aligned}$$

(66)

Finally, note that

$$\begin{aligned} \left\| p^te^{ikx}q^t \right\| _{\mathrm {HS}}^2 = \left\| q^te^{-ikx}p^te^{ikx}q^t \right\| _{\mathrm {Tr}} \le \left\| p^te^{ikx}q^t \right\| _{\mathrm {Tr}}. \end{aligned}$$

(67)

$\square$

5 Estimates on the Time Derivative

In this section, we control the change of $\beta (t)$ in time by separately estimating the time derivatives of $\beta ^{a,1}(t)$, $\beta ^{a,2}(t)$ and $\beta ^b(t)$. Note that the time derivative of $\beta ^{a,1}(t)$ can be controlled in terms of $\beta ^{a,1}(t)$ itself, $\beta ^{b}(t)$ and an error of order $N^{-1}$. The time derivative of $\beta ^{b}(t)$, however, is controlled in terms of $\beta ^{a,1}(t)$, $\beta ^{a,2}(t)$, $\beta ^{b}(t)$ itself and an error of order $N^{-1}$. This is why, we also introduced $\beta ^{a,2}(t)$. It allows us to close the Gronwall argument, since its time derivative can be bounded in terms of $\beta ^{a,1}(t)$, $\beta ^{a,2}(t)$ itself, $\beta ^{b}(t)$ and an error of order $N^{-5/3}$. We first compute the corresponding time derivatives. Then, in the following subsections, we bound these expressions as explained above.

Lemma 5.1

Let $\alpha ^0 \in L_1^2(\mathbb {R}^3)$, $\varphi _1^0, \ldots , \varphi _N^0 \in H^2(\mathbb {R}^3)$ orthonormal and $\Psi _{N,0} \in \mathcal {H}^{(N)} \cap \mathcal {D}(\mathcal {N}) \cap \mathcal {D}(\mathcal {N}H_N)$ with $\left\| \Psi _{N,0} \right\| =1$. Let $\Psi _{N,t}$ be the solution to (10) with initial condition $\Psi _{N,0}$ and $\varphi _1^t,\ldots ,\varphi _N^t,\alpha ^t$ the solution to (16) with initial condition $\varphi _1^0,\ldots ,\varphi _N^0,\alpha ^0$. Then

$$\begin{aligned}&\frac{\mathrm{d}}{\mathrm{d}t} \beta ^{a,1}(t) = -2 N^{1/3} \mathrm {Im}\left\langle {\Psi _{N,t},}{p_1^t\Big ( N^{-2/3} \widehat{\Phi }_{\Lambda }(x_1) - \Phi _{\Lambda }(x_1,t) \Big ) q^t_1 \Psi _{N,t}}\right\rangle , \end{aligned}$$

(68)

$$\begin{aligned}&\frac{\mathrm{d}}{\mathrm{d}t} \beta ^{a,2}(t) = -4 N^{2/3}\mathrm {Im}\left\langle {\Psi _{N,t},}{p_1^t\Big ( N^{-2/3} \widehat{\Phi }_{\Lambda }(x_1) - \Phi _{\Lambda }(x_1,t) \Big ) q^t_1 q^t_2 \Psi _{N,t}}\right\rangle , \end{aligned}$$

(69)

$$\begin{aligned}&\frac{\mathrm{d}}{\mathrm{d}t} \beta ^b(t) = 2 N^{-2/3} \int \mathrm{d}^3k \, \tilde{\eta }(k)\mathrm {Im}\left\langle {\Big (N^{-2/3} a(k) - \alpha ^t(k) \Big ) \Psi _{N,t},}{N e^{-ikx_1} \Psi _{N,t}}\right\rangle \nonumber \\&\quad \qquad \qquad \!\!-\, 2 N^{-2/3} \int \mathrm{d}^3k \, \tilde{\eta }(k)\mathrm {Im}\left\langle {\Big (N^{-2/3} a(k) - \alpha ^t(k) \Big ) \Psi _{N,t},}{ (2 \pi )^{3/2} \mathcal {F}[\rho ^t](k) \Psi _{N,t}}\right\rangle . \end{aligned}$$

(70)

Proof

The functional $\beta ^{a,1}(t)$ is time-dependent, because $\Psi _{N,t}$ and $(\varphi _1^t, \ldots , \varphi _N^t, \alpha ^t)$ evolve according to (10) and (16), respectively. The time derivative of the projector $q_m^t:=q_m^{\varphi _1^t, \ldots , \varphi _N^t}$ with $m \in \{1, \ldots ,N \}$ is given by

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} q_m^t = - i N^{-1/3} \Big [ h_m^t, q_m^t \Big ], \end{aligned}$$

(71)

where $h_m^t = - \Delta _m + N^{2/3} \Phi _{\Lambda }(x_m,t)$ is the effective Hamiltonian acting on the mth variable. This leads to

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} \beta ^{a,1}(t)&= \frac{\mathrm{d}}{\mathrm{d}t} \left\langle \Psi _{N,t}, q^t_1 \Psi _{N,t} \right\rangle \nonumber \\&= i N^{-1/3} \left\langle \Psi _{N,t}, \Big [ H_N - h_1^t, q^t_1 \Big ] \Psi _{N,t} \right\rangle \nonumber \\&= i N^{-1/3} \left\langle \Psi _{N,t}, \Big [ -\Delta _1 + \widehat{\Phi }_{\Lambda }(x_1) - h_1^t, q^t_1 \Big ] \Psi _{N,t} \right\rangle \nonumber \\&= i N^{-1/3} \left\langle \Psi _{N,t}, \Big [ \widehat{\Phi }_{\Lambda }(x_1) - N^{2/3} \Phi _{\Lambda }(x_1,t), q^t_1 \Big ] \Psi _{N,t} \right\rangle \nonumber \\&= -2 N^{1/3} \mathrm {Im}\, \left\langle \Psi _{N,t}, \Big ( N^{-2/3} \widehat{\Phi }_{\Lambda }(x_1) - \Phi _{\Lambda }(x_1,t) \Big ) q^t_1 \Psi _{N,t} \right\rangle , \end{aligned}$$

(72)

where we used the self-adjointness of $\widehat{\Phi }_{\Lambda }$, $\Phi _{\Lambda }$ and $q^t_1$ in the last step. Inserting $1=p^t_1+q^t_1$, we find

(73)

since the scalar product with the two $q^t_1$ projectors is real. Analogously, one derives

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} \beta ^{a,2}(t)&= N^{1/3} \frac{\mathrm{d}}{\mathrm{d}t} \left\langle \Psi _{N,t}, q^t_1 q^t_2 \Psi _{N,t} \right\rangle \nonumber \\&= -4 \mathrm {Im}\, \left\langle \Psi _{N,t}, p_1^t\Big ( \widehat{\Phi }_{\Lambda }(x_1) - N^{2/3} \Phi _{\Lambda }(x_1,t) \Big ) q^t_1 q^t_2 \Psi _{N,t} \right\rangle . \end{aligned}$$

(74)

The time derivative of $\beta ^b(t)$ is obtained by the following calculations. Note that the expressions in the calculations are all indeed well defined, since the domain $\mathcal {D} \left( \mathcal {N} \right) \cap \mathcal {D} \left( \mathcal {N} H_N \right)$ is invariant under the time evolution; see Lemma 2.1. Then

$$\begin{aligned}&\frac{\mathrm{d}}{\mathrm{d}t} \beta ^{b}(t)\nonumber \\&\quad = N^{1/3} \int \mathrm{d}^3k \, \frac{\mathrm{d}}{\mathrm{d}t} \left\langle \Big ( N^{-2/3} a(k) - \alpha ^t(k) \Big ) \Psi _{N,t}, \Big ( N^{-2/3} a(k) - \alpha ^t(k) \Big ) \Psi _{N,t} \right\rangle \nonumber \\&\quad = -2 \int \mathrm{d}^3k \, \mathrm {Im}\left\langle \Big ( N^{-2/3} a(k) - \alpha ^t(k) \Big ) \Psi _{N,t}, \left[ H_N, \Big ( N^{-2/3} a(k) - \alpha ^t(k) \Big ) \right] \Psi _{N,t} \right\rangle \nonumber \\&\qquad -\,2 \int \mathrm{d}^3k \,\mathrm {Im}\left\langle \Big ( N^{-2/3} a(k) - \alpha ^t(k) \Big ) \Psi _{N,t}, iN^{1/3}(\partial _t\alpha ^t(k)) \Psi _{N,t} \right\rangle . \end{aligned}$$

(75)

For the commutator, we find

$$\begin{aligned} \Big [ H_N, \big ( N^{-2/3} a(k) - \alpha ^t(k) \big ) \Big ]&= N^{-2/3} \delta _N \Big [ H_f, a(k)\Big ] + N^{-2/3} \left[ \sum _{j=1}^N \widehat{\Phi }_{\Lambda }(x_j), a(k)\right] \nonumber \\&= - N^{-2/3} \left( \delta _N \omega (k) a(k)+ \tilde{\eta }(k) \sum _{j=1}^N e^{-ikx_j} \right) . \end{aligned}$$

(76)

Using (16), it follows that

$$\begin{aligned}&\frac{\mathrm{d}}{\mathrm{d}t}\beta ^{b}(t)\nonumber \\&\quad = 2 \int \mathrm{d}^3k \,\mathrm {Im}\Bigg [ \left\langle \Big ( N^{-2/3} a(k) - \alpha ^t(k) \Big )\Psi _{N,t}, \delta _N \omega (k) \Big ( N^{-2/3} a(k) - \alpha ^t(k) \Big ) \Psi _{N,t} \right\rangle \nonumber \\&\qquad +\,\left\langle {\Big ( N^{-2/3} a(k) {-} \alpha ^t(k) \Big )\Psi _{N,t}}, \tilde{\eta }(k)N^{-2/3}\left( \sum _{j=1}^N e^{-ikx_j} {-} (2 \pi )^{3/2} \mathcal {F}\left[ \rho ^t \right] (k) \right) \Psi _{N,t}\right\rangle \Bigg ] \nonumber \\&\quad = 2 N^{-2/3} \int \mathrm{d}^3k \, \tilde{\eta }(k)\mathrm {Im}\left\langle \Big ( N^{-2/3} a(k) - \alpha ^t(k) \Big )\Psi _{N,t}, N e^{-ikx_1} \Psi _{N,t} \right\rangle \nonumber \\&\qquad -\,2 N^{-2/3} \int \mathrm{d}^3k \, \tilde{\eta }(k)\mathrm {Im}\left\langle \Big ( N^{-2/3} a(k) - \alpha ^t(k) \Big )\Psi _{N,t}, (2 \pi )^{3/2} \mathcal {F}\left[ \rho ^t \right] (k) \Psi _{N,t} \right\rangle , \end{aligned}$$

(77)

since the scalar product in the first line is real. $\square$

Before we prove appropriate estimates for the time derivative of $\beta (t)$, let us state a technical lemma which was already proved, e.g., in [2, 37]; we give a proof here for convenience. Note that this is an important point where the antisymmetry of the wave function is used.

Lemma 5.2

Let $A_1 = A \otimes \mathbb {1}_{L^2(\mathbb {R}^{3(N-1)})} \otimes \mathbb {1}_{\mathcal {F}_\mathrm{s}}$ with $A{:}\,L^2({\mathbb {R}^3}) \rightarrow L^2(\mathbb {R}^3)$ trace class and $\Psi _{N}, \Psi _{N}' \in L^2(\mathbb {R}^{3N}) \otimes \mathcal {F}_\mathrm{s}$ antisymmetric in $x_1$ and all other electron variables except $x_{l_1}, \ldots , x_{l_j}$. Then

$$\begin{aligned} \left| \left\langle \Psi _{N}, A_1 \Psi _{N}' \right\rangle \right|&\le (N-j)^{-1} \left\| A \right\| _{\mathrm {Tr}} \big \Vert \Psi _{N}\big \Vert \big \Vert \Psi _{N}'\big \Vert . \end{aligned}$$

(78)

Proof

In order to prove the inequality, it is convenient to use the singular value decomposition $A = \sum _{i \in \mathbb {N}} \mu _i | \chi '_i \rangle \langle \chi _i |$ with $(\chi '_i)_{i \in \mathbb {N}}, (\chi _i)_{i \in \mathbb {N}}$ orthonormal bases in $L^2(\mathbb {R}^3)$ and $\mu _i \ge 0 \, \forall i \in \mathbb {N}$. Using Cauchy–Schwarz, this allows us to estimate

$$\begin{aligned}&\left| \left\langle \Psi _N, A_1 \Psi _N' \right\rangle \right| \nonumber \\&\quad = \left| \sum _{i \in \mathbb {N}} \mu _i \left\langle \Psi _N, | \chi '_i \rangle \langle \chi _i |_1 \Psi _N' \right\rangle \right| \nonumber \\&\quad \le \sum _{i \in \mathbb {N}} \mu _i \left\langle \Psi _N, | \chi '_i \rangle \langle \chi '_i |_1 \Psi _N \right\rangle ^{1/2} \, \left\langle \Psi '_N, | \chi _i \rangle \langle \chi _i |_1 \Psi '_N \right\rangle ^{1/2} \nonumber \\&\quad = (N{-}j)^{-1} \sum _{i \in \mathbb {N}} \mu _i \left\langle \Psi _N, \sum _{\begin{array}{c} k=1 \\ k\ne l_1,\ldots ,l_j \end{array}}^N | \chi '_i \rangle \langle \chi '_i |_k \Psi _N \right\rangle ^{1/2} \, \left\langle \Psi '_N, \sum _{\begin{array}{c} l=1 \\ l\ne l_1,\ldots ,l_j \end{array}}^N | \chi _i \rangle \langle \chi _i |_l \Psi '_N \right\rangle ^{1/2}. \end{aligned}$$

(79)

Note that $\sum _{k\in K} | \chi _i \rangle \langle \chi _i |_k$ is for all $i\in \mathbb {N}$ and $K \subset \{1,\ldots ,N\}$ a projector on functions antisymmetric in all K-variables, since

$$\begin{aligned} \left( \sum _{k\in K} | \chi _i \rangle \langle \chi _i |_k \right) ^2 \Psi _N&= \sum _{k\in K} \sum _{l \in K} | \chi _i \rangle \langle \chi _i |_k \, | \chi _i \rangle \langle \chi _i |_l \Psi _N = \sum _{k\in K} | \chi _i \rangle \langle \chi _i |_k \Psi _N, \end{aligned}$$

(80)

where the last step is true because the non-diagonal terms vanish due to the antisymmetry. It follows that

$$\begin{aligned} \left| \left\langle \Psi _N, A_1 \Psi _N' \right\rangle \right|&\le (N-j)^{-1} \sum _{i \in \mathbb {N}} \mu _i \left\| \Psi _N \right\| \left\| \Psi _N' \right\| \nonumber \\&= (N-j)^{-1} \left\| A \right\| _{\mathrm {Tr}} \left\| \Psi _N \right\| \left\| \Psi _N' \right\| . \end{aligned}$$

(81)

$\square$

5.1 Estimate on the Time Derivative of $\beta ^{a,1}(t)$

Lemma 5.3

Let Assumption 2.2 hold, and let $\Psi _{N,t}$ be the solution to (10) with initial condition $\Psi _{N,0}$ and $\varphi _1^t,\ldots ,\varphi _N^t,\alpha ^t$ the solution to (16) with initial condition $\varphi _1^0,\ldots ,\varphi _N^0,\alpha ^0$. Then there is a $C>0$ (independent of N, $\delta _N$, $\Lambda$ and t) such that for all $t>0$,

$$\begin{aligned} \left| \frac{\mathrm{d}}{\mathrm{d}t} \beta ^{a,1}(t) \right| \le e^{C \Lambda ^4 (1 + \Vert \alpha ^0\Vert _2)(1 + t^2)} \Big ( \beta (t) + N^{-1} \Big ). \end{aligned}$$

(82)

Proof

Using the Fourier expansion of the radiation field, we write

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} \beta ^{a,1}(t)&= 2 N^{1/3} \int \mathrm{d}^3k \, \tilde{\eta }(k) \mathrm {Im}\left\langle \Big ( N^{-2/3} a(k) - \alpha ^t(k) \Big )\Psi _{N,t}, q^t_1 e^{-ikx_1}p^t_1 \Psi _{N,t} \right\rangle \end{aligned}$$

(83a)

$$\begin{aligned}&\quad -\,2 N^{1/3} \int \mathrm{d}^3k \, \tilde{\eta }(k) \mathrm {Im}\left\langle \Big ( N^{-2/3} a(k) - \alpha ^t(k) \Big )\Psi _{N,t}, p^t_1 e^{-ikx_1} q^t_1 \Psi _{N,t} \right\rangle . \end{aligned}$$

(83b)

Since $\Psi _{N,t}$ is antisymmetric in the x variables, we find for the first summand

$$\begin{aligned}&\left| (83\mathrm{a}) \right| \nonumber \\&\quad \le 2 N^{1/3} \int \mathrm{d}^3k \, \left| \tilde{\eta }(k) \right| \left| \left\langle \Big ( N^{-2/3} a(k) - \alpha ^t(k) \Big )\Psi _{N,t}, N^{-1} \sum _{m=1}^N q_m e^{-ikx_m} p_m \Psi _{N,t} \right\rangle \right| \nonumber \\&\quad \le 2 \Bigg [ N^{1/3} \int \mathrm{d}^3k \, \left\| \Big ( N^{-2/3} a(k) - \alpha ^t(k) \Big )\Psi _{N,t} \right\| ^2 \Bigg ]^{1/2} \nonumber \\&\quad \quad \times \Bigg [ N^{1/3} \int \mathrm{d}^3k \, \left| \tilde{\eta }(k) \right| ^2 N^{-2} \left\| \sum _{m=1}^N q_m e^{-ikx_m} p_m \Psi _{N,t} \right\| ^2 \Bigg ]^{1/2}. \end{aligned}$$

(84)

We now use that by Lemma 5.2, $\left\| A_1B_2\Psi _{N} \right\| ^2 \le (N-1)^{-1} \left\| A \right\| _{\mathrm {HS}}^2 \left\| B_2\Psi _N \right\| ^2$ and $\left\| A_1\Psi _{N} \right\| ^2 \le N^{-1} \left\| A \right\| _{\mathrm {HS}}^2 \left\| \Psi _N \right\| ^2$ for all antisymmetric $\Psi _N$, Hilbert–Schmidt operators A and bounded operators B. In the end, we use the semiclassical structure, i.e., Lemma 4.1, and find

$$\begin{aligned}&N^{-2} \left\| \sum _{m=1}^N q_m^t e^{-ikx_m} p_m^t \Psi _{N,t} \right\| ^2 \nonumber \\&\quad = N^{-2} \bigg ( N(N-1) \left\langle \Psi _{N,t}, p_1^t e^{ikx_1}q_1^t q_2^t e^{-ikx_2} p_2^t \Psi _{N,t} \right\rangle \nonumber \\&\qquad +\,N \left\langle \Psi _{N,t}, p_1^t e^{ikx_1}q_1^t e^{-ikx_1} p_1^t \Psi _{N,t} \right\rangle \bigg ) \nonumber \\&\quad = N^{-1}(N-1) \left\langle q_1^t e^{-ikx_1} p_1^t q_2^t \Psi _{N,t}, q_2^t e^{-ikx_2} p_2^t q_1^t \Psi _{N,t} \right\rangle \nonumber \\&\qquad +\,N^{-1} \left\| q_1^t e^{-ikx_1} p_1^t \Psi _{N,t} \right\| ^2 \nonumber \\&\quad \le N^{-1} (N-1) \left\| q_1^t e^{-ikx_1} p_1^t q_2^t \Psi _{N,t} \right\| ^2 + N^{-1} \left\| q_1^t e^{-ikx_1} p_1^t \Psi _{N,t} \right\| ^2 \nonumber \\&\quad \le N^{-1} \left\| q^t e^{-ikx} p^t \right\| _{\mathrm {HS}}^2 \left\| q_2^t \Psi _{N,t} \right\| ^2 + N^{-2} \left\| q^t e^{-ikx} p^t \right\| _{\mathrm {HS}}^2 \left\| \Psi _{N,t} \right\| ^2 \nonumber \\&\quad \le N^{-1/3} C (1 + \left| k \right| ) e^{C \Lambda ^4 (1 + \left\| \alpha ^0 \right\| _2)(1 + t^2)} \left( \beta ^{a,1}(t) + N^{-1} \right) . \end{aligned}$$

(85)

Thus,

$$\begin{aligned} \left| (83\mathrm{a}) \right|&\le 2 \sqrt{\beta ^b(t)} \left( C e^{C \Lambda ^4 (1 + \left\| \alpha ^0 \right\| _2)(1 + t^2)} \left( \beta ^{a,1}(t) + N^{-1} \right) \left\| \tilde{\eta } (1 {+} \left| \cdot \right| )^{1/2} \right\| _2^2 \right) ^{1/2} \nonumber \\&= C e^{C \Lambda ^4 (1 + \left\| \alpha ^0 \right\| _2)(1 + t^2)} \left\| (1 + \left| \cdot \right| )^{1/2} \tilde{\eta } \right\| _2 \sqrt{\beta ^b(t)} \sqrt{\beta ^{a,1}(t) + N^{-1}}. \end{aligned}$$

(86)

For (83b), we can directly use Cauchy–Schwarz. We use again $\left\| A_1\Psi _{N} \right\| ^2 \le N^{-1} \left\| A \right\| _{\mathrm {HS}}^2 \left\| \Psi _N \right\| ^2$ and Lemma 4.1 in the end and find

$$\begin{aligned}&\left| (83\mathrm{b}) \right| \nonumber \\&\le 2 N^{1/3} \int \mathrm{d}^3k \, \left| \tilde{\eta }(k) \right| \left| \left\langle q_1^t e^{ikx_1} p_1^t \Big ( N^{-2/3} a(k) - \alpha ^t(k) \Big )\Psi _{N,t}, q^t_1 \Psi _{N,t} \right\rangle \right| \nonumber \\&\le 2 N^{-1/6} \int \mathrm{d}^3k \, \left| \tilde{\eta }(k) \right| \left\| q^t e^{ikx} p^t \right\| _{\mathrm {HS}} \left\| \Big ( N^{-2/3} a(k) - \alpha ^t(k) \Big )\Psi _{N,t} \right\| \left\| q^t_1 \Psi _{N,t} \right\| \nonumber \\&\le C e^{C \Lambda ^4 (1 + \left\| \alpha ^0 \right\| _2)(1 + t^2)} \left\| (1 + \left| \cdot \right| )^{1/2}\tilde{\eta } \right\| _2 \sqrt{\beta ^{b}(t)} \sqrt{\beta ^{a,1}(t)}. \end{aligned}$$

(87)

To summarize, we have

$$\begin{aligned} \left| \frac{\mathrm{d}}{\mathrm{d}t} \beta ^{a,1}(t) \right|&\le C e^{C \Lambda ^4 (1 + \left\| \alpha ^0 \right\| _2)(1 + t^2)} \left\| (1 + \left| \cdot \right| )^{1/2} \tilde{\eta } \right\| _2 \left( \beta ^{a,1}(t) + \beta ^b(t) + N^{-1} \right) . \end{aligned}$$

(88)

Since $\left\| (1 + \left| \cdot \right| )^{1/2} \tilde{\eta } \right\| _2 \le C \Lambda ^{3/2}$ and using for ease of notation $\left| x \right| \le \exp (\left| x \right| )$, this gives

$$\begin{aligned} \left| \frac{\mathrm{d}}{\mathrm{d}t} \beta ^{a,1}(t) \right| \le e^{C \Lambda ^4 (1 + \left\| \alpha ^0 \right\| _2)(1 + t^2)} \left( \beta ^{a,1}(t) + \beta ^b(t) + N^{-1} \right) . \end{aligned}$$

(89)

$\square$

5.2 Estimate on the Time Derivative of $\beta ^{a,2}(t)$

Lemma 5.4

Let Assumption 2.2 hold, and let $\Psi _{N,t}$ be the solution to (10) with initial condition $\Psi _{N,0}$ and $\varphi _1^t,\ldots ,\varphi _N^t,\alpha ^t$ the solution to (16) with initial condition $\varphi _1^0,\ldots ,\varphi _N^0,\alpha ^0$. Then there is a $C>0$ (independent of N, $\delta _N$, $\Lambda$ and t) such that for all $t>0$,

$$\begin{aligned} \left| \frac{\mathrm{d}}{\mathrm{d}t} \beta ^{a,2}(t) \right| \le e^{C \Lambda ^4 (1 + \Vert \alpha ^0\Vert _2)(1 + t^2)} \left( \beta (t) + N^{-1} \right) . \end{aligned}$$

(90)

Proof

We write the time derivative of $\beta ^{a,2}(t)$ as

$$\begin{aligned}&\frac{\mathrm{d}}{\mathrm{d}t} \beta ^{a,2}(t)\nonumber \\&= -4 N^{2/3} \int \mathrm{d}^3k \, \tilde{\eta }(k) \mathrm {Im}\left\langle \Psi _{N,t}, \Big ( N^{-2/3} a(k) - \alpha ^t(k) \Big ) \Big ( p^t_1 e^{ikx_1}q^t_1 - q^t_1 e^{ikx_1}p^t_1 \Big ) q^t_2 \Psi _{N,t} \right\rangle \nonumber \\&= -4 N^{2/3} \int \mathrm{d}^3k \, \tilde{\eta }(k) \mathrm {Im}\left\langle q^t_2 \Psi _{N,t}, \Big [ p^t_1, e^{ikx_1} \Big ] \Big ( N^{-2/3} a(k) - \alpha ^t(k) \Big ) \Psi _{N,t} \right\rangle \nonumber \\&= -4 N^{2/3} (N{-}1)^{-1} \int \mathrm{d}^3k \, \tilde{\eta }(k)\mathrm {Im}\left\langle \sum _{m=1}^N q_m^t \Psi _{N,t}, \Big [ p^t_1, e^{ikx_1} \Big ] \Big ( N^{-2/3} a(k) {-} \alpha ^t(k) \Big ) \Psi _{N,t} \right\rangle \nonumber \\&\qquad +\,4 N^{2/3} (N-1)^{-1} \int \mathrm{d}^3k \, \tilde{\eta }(k) \mathrm {Im}\left\langle \Psi _{N,t}, q_1^t \Big [ p^t_1, e^{ikx_1} \Big ] \Big ( N^{-2/3} a(k) - \alpha ^t(k) \Big ) \Psi _{N,t} \right\rangle . \end{aligned}$$

(91)

Here, we have symmetrized the $q_2^t$ so that we can bound the time derivative appropriately in terms of $\beta ^{a,2}(t)$. Note that

$$\begin{aligned} \left\| \sum _{m=1}^N q_m^t \Psi _{N,t} \right\| ^2&\le N \left\langle \Psi _{N,t}, q_1^t \Psi _{N,t} \right\rangle + N^2 \left\langle \Psi _{N,t}, q_1^t q_2^t \Psi _{N,t} \right\rangle \nonumber \\&\le N \beta ^{a,1}(t) + N^{5/3} \beta ^{a,2}(t). \end{aligned}$$

(92)

We can then use Lemma 5.2 as well as

$$\begin{aligned} \left\| q^t\left[ p^t, e^{ikx} \right] \right\| _{\mathrm {Tr}} \le \left\| \left[ p^t, e^{ikx} \right] \right\| _{\mathrm {Tr}} \le \left\| p^t e^{ikx} q^t \right\| _{\mathrm {Tr}} + \left\| p^t e^{-ikx} q^t \right\| _{\mathrm {Tr}} \end{aligned}$$

(93)

together with Lemma 4.1 and find

$$\begin{aligned}&\left| \frac{\mathrm{d}}{\mathrm{d}t} \beta ^{a,2}(t) \right| \nonumber \\&\quad \le C N^{-4/3} \int \mathrm{d}^3k \, \left| \tilde{\eta }(k) \right| \left\| \Big [ p^t, e^{ikx} \Big ] \right\| _{\mathrm {Tr}} \left\| \left( N^{-2/3} a(k) {-} \alpha ^t(k) \right) \Psi _{N,t} \right\| \bigg ( \bigg \Vert \sum _{j=1}^N q_j^t \Psi _{N,t} \bigg \Vert + 1 \bigg ) \nonumber \\&\quad \le C e^{C(t)} N^{-2/3} \int \mathrm{d}^3k \, (1 + \left| k \right| ) \left| \tilde{\eta }(k) \right| \left\| \left( N^{-2/3} a(k) - \alpha ^t(k) \right) \Psi _{N,t} \right\| \bigg ( \bigg \Vert \sum _{j=1}^N q_j^t \Psi _{N,t} \bigg \Vert + 1 \bigg ) \nonumber \\&\quad \le C e^{C(t)} N^{-5/6} \left\| (1 + \left| \cdot \right| )\tilde{\eta } \right\| _2 \sqrt{\beta ^b(t)} \bigg ( \sqrt{N} \sqrt{\beta ^{a,1}(t)} + N^{5/6}\sqrt{\beta ^{a,2}(t)} + 1 \bigg ) \nonumber \\&\quad \le C e^{C(t)} \left\| (1 + \left| \cdot \right| )\tilde{\eta } \right\| _2 \bigg ( \beta ^b(t) + \beta ^{a,1}(t) + \beta ^{a,2}(t) + N^{-5/3} \bigg ), \end{aligned}$$

(94)

where we abbreviated $C(t) := C \Lambda ^4 (1 + \left\| \alpha ^0 \right\| _2)(1 + t^2)$. Since $\left\| (1 + \left| \cdot \right| ) \tilde{\eta } \right\| _2 \le C \Lambda ^2$, we arrive at

$$\begin{aligned} \left| \frac{\mathrm{d}}{\mathrm{d}t}\beta ^{a,2}(t) \right| \le e^{C \Lambda ^4 (1 + \Vert \alpha ^0\Vert _2)(1 + t^2)} \Big ( \beta (t) + N^{-5/3} \Big ). \end{aligned}$$

(95)

$\square$

5.3 Estimate on the Time Derivative of $\beta ^b(t)$

The crucial terms in the time derivative of $\beta ^b(t)$ can be estimated with a diagonalization trick similar to the one used in [37]. For the following estimates, we introduce the operators

$$\begin{aligned} P^{\varphi } = \sum _{m=1}^N | \varphi \rangle \langle \varphi |_m = \sum _{m=1}^N p_m^{\varphi } \quad \text {and} \quad Q^{\varphi } = 1 - P^{\varphi }, \end{aligned}$$

(96)

where $\varphi \in L^2(\mathbb {R}^3)$. They have the following properties.

Lemma 5.5

The operators $P^{\varphi }$ and $Q^{\varphi }$ as defined in (96) are projectors on $\mathcal {H}^{(N)}$ for all $\varphi \in L^2(\mathbb {R}^3)$. Moreover, let $\chi _1, \ldots , \chi _N \in L^2(\mathbb {R}^3)$ and $\varphi _1,\ldots ,\varphi _N\in L^2(\mathbb {R}^3)$ each be orthonormal, such that ${{\,\mathrm{span}\,}}\{ \chi _1, \ldots , \chi _N \} = {{\,\mathrm{span}\,}}\{ \varphi _1, \ldots , \varphi _N \}$. Then

$$\begin{aligned} \Big [ Q^{\chi _j}, Q^{\chi _k} \Big ] = 0 ~\forall j,k=1,\ldots ,N \quad \text {and} \quad \sum _{j=1}^N Q^{\chi _j}&= \sum _{m=1}^N q_m^{\varphi _1,\ldots ,\varphi _N}. \end{aligned}$$

(97)

Proof

The lemma follows from a direct computation using the antisymmetry in the fermion variables. $\square$

Lemma 5.6

Let Assumption 2.2 hold, and let $\Psi _{N,t}$ be the solution to (10) with initial condition $\Psi _{N,0}$ and $\varphi _1^t,\ldots ,\varphi _N^t,\alpha ^t$ the solution to (16) with initial condition $\varphi _1^0,\ldots ,\varphi _N^0,\alpha ^0$. Then there is a $C>0$ (independent of N, $\delta _N$, $\Lambda$ and t) such that for all $t>0$,

$$\begin{aligned} \left| \frac{\mathrm{d}}{\mathrm{d}t} \beta ^b(t) \right| \le e^{C \Lambda ^4 (1 + \Vert \alpha ^0\Vert _2)(1 + t^2)} \left( \beta (t) + N^{-1} \right) . \end{aligned}$$

(98)

Proof

If we insert the identity $p_1^t + q_1^t = 1$ twice, (70) can be written as

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} \beta ^b(t) = pp{-}\mathrm {Term}+ qp{-}\mathrm {Term}+ pq{-}\mathrm {Term}+ {qq}{-}\mathrm {Term}\end{aligned}$$

(99)

with

$$\begin{aligned}&pp{-}\mathrm {Term}\nonumber \\&\quad = 2 N^{-2/3} \int \mathrm{d}^3k \, \tilde{\eta }(k)\mathrm {Im}\left\langle \Big ( N^{-2/3} a(k) - \alpha ^t(k) \Big )\Psi _{N,t}, \sum _{i=1}^N p_i^t e^{-ikx_i}p_i^t \Psi _{N,t} \right\rangle \nonumber \\&\qquad -\,2 N^{-2/3} \int \mathrm{d}^3k \, \tilde{\eta }(k)\mathrm {Im}\left\langle \Big ( N^{-2/3} a(k) {-} \alpha ^t(k) \Big )\Psi _{N,t}, \int \mathrm{d}^3y\, e^{-iky} \rho ^t(y) \Psi _{N,t} \right\rangle , \end{aligned}$$

(100)

$$\begin{aligned}&qp{-}\mathrm {Term}= 2 N^{1/3} \int \mathrm{d}^3k \, \tilde{\eta }(k)\mathrm {Im}\left\langle \Big ( N^{-2/3} a(k) - \alpha ^t(k) \Big )\Psi _{N,t}, q_1^t e^{-ikx_1}p_1^t \Psi _{N,t} \right\rangle , \end{aligned}$$

(101)

$$\begin{aligned}&pq{-}\mathrm {Term}= 2 N^{1/3} \int \mathrm{d}^3k \, \tilde{\eta }(k)\mathrm {Im}\left\langle \Big ( N^{-2/3} a(k) - \alpha ^t(k) \Big )\Psi _{N,t}, p_1^t e^{-ikx_1}q_1^t \Psi _{N,t} \right\rangle , \end{aligned}$$

(102)

$$\begin{aligned}&qq{-}\mathrm {Term}= 2 N^{1/3} \int \mathrm{d}^3k \, \tilde{\eta }(k)\mathrm {Im}\left\langle \Big ( N^{-2/3} a(k) - \alpha ^t(k) \Big )\Psi _{N,t}, q_1^t e^{-ikx_1}q_1^t \Psi _{N,t} \right\rangle . \end{aligned}$$

(103)

To estimate the $pp{-}\mathrm {Term}$, we split $e^{-ikx} = \cos (kx) - i \sin (kx)$ into its real and imaginary parts. Subsequently we only estimate the $\cos$ terms $pp{-}\mathrm {Term}_{\cos }$; the $\sin$ terms are estimated in exactly the same manner. Note that for each fixed $t > 0$ and $k\in \mathbb {R}^3$, we can regard $p^t\cos (kx)p^t$ as a Hermitian $N\times N$ matrix on ${{\,\mathrm{span}\,}}\{\varphi _1^t,\ldots ,\varphi _N^t\}$. By the spectral theorem, we can find orthonormal $\chi _1^{t,k}, \ldots , \chi _N^{t,k} \in {{\,\mathrm{span}\,}}\{\varphi _1^t,\ldots ,\varphi _N^t\}$ (i.e., $p^t = \sum _{j=1}^N | \varphi _j^t \rangle \langle \varphi _j^t | {=} \sum _{j=1}^N | \chi _j^{t,k} \rangle \langle \chi _j^{t,k} |$) and real $\lambda _1^{t,k},\ldots ,\lambda _N^{t,k}$ such that $p^t \cos (kx_1)p^t = \sum _{j=1}^N \lambda _j^{t,k} | \chi _j^{t,k} \rangle \langle \chi _j^{t,k} |$. In particular, this implies

$$\begin{aligned} \left| \lambda _j^{t,k} \right|&= \left| \left\langle \chi _j^{t,k}, \cos (kx)\chi _j^{t,k} \right\rangle \right| \le 1, \end{aligned}$$

(104)

$$\begin{aligned} \sum _{j=1}^N \lambda _j^{t,k}&= \mathrm {Tr}\Big (p^t\cos (kx)p^t\Big ) = \int \mathrm{d}^3y \, \cos (ky) \rho ^t(y), \end{aligned}$$

(105)

$$\begin{aligned} \sum _{i=1}^N p_i^t \cos (k x_i) p_i^t&= \sum _{i=1}^N \sum _{j=1}^N \lambda _j^{t,k} | \chi _j^{t,k} \rangle \langle \chi _j^{t,k} |_i = \sum _{j=1}^N \lambda _j^{t,k} P^{\chi _j^{t,k}}. \end{aligned}$$

(106)

Using (105) and (106), the $\cos$-part of the $pp{-}\mathrm {Term}$ can be written as

$$\begin{aligned}&pp{-}\mathrm {Term}_{\cos } \nonumber \\&\quad = 2 N^{-2/3} \int \mathrm{d}^3k \, \tilde{\eta }(k)\mathrm {Im}\left\langle \Big ( N^{-2/3} a(k) - \alpha ^t(k) \Big )\Psi _{N,t}, \sum _{j=1}^N \lambda _j^{t,k} \Big ( P^{\chi _j^{t,k}} - 1 \Big ) \Psi _{N,t} \right\rangle \nonumber \\&\quad = 2 N^{-2/3} \int \mathrm{d}^3k \, \tilde{\eta }(k) \mathrm {Im}\left\langle \Big ( N^{-2/3} a(k) - \alpha ^t(k) \Big )\Psi _{N,t}, \sum _{j=1}^N \lambda _j^{t,k} Q^{\chi _j^{t,k}} \Psi _{N,t} \right\rangle \end{aligned}$$

(107)

and be estimated by

$$\begin{aligned}&\left| pp{-}\mathrm {Term}_{\cos } \right| \nonumber \\&\quad \le 2 N^{-2/3} \int \mathrm{d}^3k \, \left\| \Big ( N^{-2/3} a(k) - \alpha ^t(k) \Big )\Psi _{N,t} \right\| \left| \tilde{\eta }(k) \right| \bigg \Vert \sum _{j=1}^N \lambda _j^{t,k} Q^{\chi _j^{t,k}} \Psi _{N,t} \bigg \Vert \nonumber \\&\quad \le 2 \left( \int \mathrm{d}^3k \, N^{1/3} \left\| \Big ( N^{-2/3} a(k) - \alpha ^t(k) \Big )\Psi _{N,t} \right\| ^2 \right) ^{1/2} \nonumber \\&\qquad \times \left( \int \mathrm{d}^3k \, N^{-5/3} \left| \tilde{\eta }(k) \right| ^2 \bigg \Vert \sum _{j=1}^N \lambda _j^{t,k} Q^{\chi _j^{t,k}} \Psi _{N,t} \bigg \Vert ^2 \right) ^{1/2} \nonumber \\&\quad = 2 \sqrt{\beta ^b(t)} \left( \int \mathrm{d}^3k \, N^{-5/3} \left| \tilde{\eta }(k) \right| ^2 \bigg \Vert \sum _{j=1}^N \lambda _j^{t,k} Q^{\chi _j^{t,k}} \Psi _{N,t} \bigg \Vert ^2 \right) ^{1/2}. \end{aligned}$$

(108)

If one makes use of (104) and Lemma 5.5, one finds

$$\begin{aligned} \bigg \Vert \sum _{j=1}^N \lambda _j^{t,k} Q^{\chi _j^{t,k}} \Psi _{N,t} \bigg \Vert ^2&= \sum _{i,j=1}^N \overline{\lambda _i^{t,k}} \lambda _j^{t,k} \left\langle Q^{\chi _i^{t,k}} \Psi _{N,t}, Q^{\chi _j^{t,k}} \Psi _{N,t} \right\rangle \nonumber \\&\le \sum _{i,j=1}^N \left| \left\langle Q^{\chi _i^{t,k}} \Psi _{N,t}, Q^{\chi _j^{t,k}} \Psi _{N,t} \right\rangle \right| \nonumber \\&= \sum _{i,j=1}^N \left\langle Q^{\chi _i^{t,k}} \Psi _{N,t}, Q^{\chi _j^{t,k}} \Psi _{N,t} \right\rangle \nonumber \\&= \left\langle \Psi _{N,t}, \sum _{i=1}^N q_i^t \sum _{j=1}^N q_j^t \Psi _{N,t} \right\rangle \nonumber \\&= N(N-1) \left\langle \Psi _{N,t}, q_1^t q_2^t \Psi _{N,t} \right\rangle + N \left\langle \Psi _{N,t}, q_1^t \Psi _{N,t} \right\rangle \nonumber \\&\le N \beta ^{a,1}(t) + N^{5/3} \beta ^{a,2}(t) \end{aligned}$$

(109)

and obtains

$$\begin{aligned} \left| pp{-}\mathrm {Term}_{\cos } \right|&\le 2 \left\| \tilde{\eta } \right\| _2 \sqrt{\beta ^b(t)} \sqrt{\beta ^{a,1}(t) + \beta ^{a,2}(t)}\nonumber \\&\le C \Lambda \left( \beta ^{a,1}(t) + \beta ^{a,2}(t) + \beta ^b(t) \right) . \end{aligned}$$

(110)

In exactly the same manner, one estimates $pp{-}\mathrm {Term}_{\sin }$ and obtains $\left| pp{-}\mathrm {Term} \right| \le C \Lambda \beta (t)$. From the observation that $qp{-}\mathrm {Term}=$ (83a) and $pq{-}\mathrm {Term}= -$ (83b), we immediately get

$$\begin{aligned} \left| qp{-}\mathrm {Term}+ pq{-}\mathrm {Term} \right|&\le e^{C \Lambda ^4 (1 + \left\| \alpha ^0 \right\| _2)(1 + t^2)} \left( \beta ^{a,1}(t) + \beta ^b(t) + N^{-1} \right) . \end{aligned}$$

(111)

Similar to (108), we estimate

$$\begin{aligned} \left| qq{-}\mathrm {Term} \right|&= 2 N^{-2/3} \left| \int \mathrm{d}^3k \, \tilde{\eta }(k) \left\langle \Big ( N^{-2/3} a(k) - \alpha ^t(k) \Big )\Psi _{N,t}, \sum _{m=1} q_m^t e^{-ikx_m}q_m^t \Psi _{N,t} \right\rangle \right| \nonumber \\&\le 2 \sqrt{\beta ^b(t)} \left( \int \mathrm{d}^3k \, N^{-5/3} \left| \tilde{\eta }(k) \right| ^2 \bigg \Vert \sum _{m=1}^N q_m^t e^{-ikx_m} q_m^t \Psi _{N,t} \bigg \Vert ^2 \right) ^{1/2}. \end{aligned}$$

(112)

By means of

$$\begin{aligned}&\bigg \Vert \sum _{m=1}^N q_m^t e^{-ikx_m} q_m^t \Psi _{N,t} \bigg \Vert ^2 \nonumber \\&\quad = N (N-1) \left\langle q_1^t e^{-ikx_1} q_1^t \Psi _{N,t}, q_2^t e^{-ikx_2} q_2^t \Psi _{N,t} \right\rangle + N \left\| q_1^t e^{-ikx_1} q_1^t \Psi _{N,t} \right\| ^2 \nonumber \\&\quad \le N^2 \left\langle e^{-ikx_1} q_1^t q_2^t \Psi _{N,t}, e^{-ikx_2} q_1^t q_2^t \Psi _{N,t} \right\rangle + N \left\| q_1^t e^{-ikx_1} q_1^t \Psi _{N,t} \right\| ^2 \nonumber \\&\quad \le N^2 \left\| q_1^t q_2^t \Psi _{N,t} \right\| ^2 + N \left\| q_1^t \Psi _{N,t} \right\| ^2 \nonumber \\&\quad = N \beta ^{a,1}(t) + N^{5/3} \beta ^{a,2}(t), \end{aligned}$$

(113)

this becomes

$$\begin{aligned} \left| qq{-}\mathrm {Term} \right|&\le 2 \left\| \tilde{\eta } \right\| _2 \sqrt{\beta ^b(t)} \sqrt{\beta ^{a,1}(t) + \beta ^{a,2}(t)} \le C \Lambda \beta (t). \end{aligned}$$

(114)

Summing all terms up then shows Lemma 5.6. $\square$

5.4 The Gronwall Estimate

Lemma 5.7

Let Assumption 2.2 hold, and let $\Psi _{N,t}$ be the solution to (10) with initial condition $\Psi _{N,0}$ and $\varphi _1^t,\ldots ,\varphi _N^t,\alpha ^t$ the solution to (16) with initial condition $\varphi _1^0,\ldots ,\varphi _N^0,\alpha ^0$. Then there is a $C>0$ (independent of N, $\delta _N$, $\Lambda$ and t) such that for all $t>0$,

$$\begin{aligned} \beta (t) \le e^{e^{C \Lambda ^4 (1 + \Vert \alpha ^0\Vert _2)(1 + t^2)}} \left( \beta (0) + N^{-1} \right) . \end{aligned}$$

(115)

Proof

If we use Lemmas 5.3, 5.4 and 5.6, we get

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} \beta (t)&\le \left| \frac{\mathrm{d}}{\mathrm{d}t} \beta ^{a,1}(t) \right| + \left| \frac{\mathrm{d}}{\mathrm{d}t} \beta ^{a,2}(t) \right| + \left| \frac{\mathrm{d}}{\mathrm{d}t} \beta ^b(t) \right| \nonumber \\&\le e^{C \Lambda ^4 (1 + \Vert \alpha ^0\Vert _2)(1 + t^2)} \left( \beta (t) + N^{-1} \right) . \end{aligned}$$

(116)

Applying Gronwall’s lemma, we obtain

$$\begin{aligned} \beta (t)&\le e^{\int _0^t\,\mathrm{d}s \, e^{C \Lambda ^4 (1 + \Vert \alpha ^0\Vert _2)(1 + s^2)}} \beta (0) + \Big ( e^{\int _0^t\,\mathrm{d}s \, e^{ C \Lambda ^4 (1 + \Vert \alpha ^0\Vert _2)(1 + s^2)}} - 1 \Big ) N^{-1} \nonumber \\&\le e^{\int _0^t\,\mathrm{d}s \, e^{C \Lambda ^4 (1 + \Vert \alpha ^0\Vert _2)(1 + s^2)}} \left( \beta (0) + N^{-1} \right) . \end{aligned}$$

(117)

Using $\int _0^t\,\mathrm{d}s \; e^{C \Lambda ^4 (1 + \Vert \alpha ^0\Vert _2)(1 + s^2)} \le e^{\tilde{C} \Lambda ^4 (1 + \Vert \alpha ^0\Vert _2)(1 + t^2)}$ for some $\tilde{C}>0$ shows the claim. $\square$

6 Proof of Theorem 2.3

In order to state our main result in terms of the trace norm difference of reduced density matrices, let us add the following lemma.

Lemma 6.1

Let $\varphi _1, \ldots , \varphi _N \in L^2(\mathbb {R}^3)$ be orthonormal, $\alpha \in L^2(\mathbb {R}^3)$ and $\Psi _{N} \in \mathcal {H}^{(N)} \cap \mathcal {D}\left( \mathcal {N} \right)$ with $\left\| \Psi _N \right\| =1$. Then

$$\begin{aligned} 2 \beta ^{a,1}(\Psi _{N}, \varphi _1, \ldots , \varphi _N)&\le \left\| \gamma ^{(1,0)}_{N} - N^{-1} p \right\| _{\mathrm {Tr}} \le \sqrt{8 \beta ^{a,1}(\Psi _N, \varphi _1, \ldots , \varphi _N)}, \end{aligned}$$

(118)

$$\begin{aligned} \left\| \gamma _{N}^{(0,1)} - | \alpha \rangle \langle \alpha | \right\| _{\mathrm {Tr}}&\le 3 N^{-1/3} \beta ^b(\Psi _N,\alpha ) + 6 \left\| \alpha \right\| _2 \sqrt{ N^{-1/3} \beta ^b(\Psi _N,\alpha )}. \end{aligned}$$

(119)

Proof

This is a standard result. For example, a proof of (118) can be found in [37, Section 3.1] and a proof of (119) in [32, Section VII]. $\square$

Let us now summarize all estimates and put them together for a proof of our main result.

Proof of Theorem 2.3

Let us first note that from Lemma 2.1 we have that $\Psi _{N,t} \in \mathcal {H}^{(N)} \cap \mathcal {D}(\mathcal {N}) \cap \mathcal {D}(\mathcal {N}H_N)$ for all $t\ge 0$ and from Proposition 1.1 that $(\varphi _1^t, \ldots , \varphi _N^t, \alpha ^t) \in H^2(\mathbb {R}^3)^N \times L_1^2(\mathbb {R}^3)$ for all $t\ge 0$. From Lemma 5.7, we obtain the Gronwall estimate

$$\begin{aligned} \beta (t) \le e^{e^{C \Lambda ^4 (1 + \Vert \alpha ^0\Vert _2)(1 + t^2)}} \left( \beta (0) + N^{-1} \right) . \end{aligned}$$

(120)

Recall that $\beta = \beta ^{a,1} + \beta ^{a,2} + \beta ^b$. From the first inequality of Lemma 6.1 and from (33), we get

$$\begin{aligned} \beta (0) \le a_N + b_N + c_N, \end{aligned}$$

(121)

so that

$$\begin{aligned} \beta (t) \le e^{e^{C \Lambda ^4 (1 + \Vert \alpha ^0\Vert _2)(1 + t^2)}} I_N, \end{aligned}$$

(122)

where we abbreviated $I_N=a_N + b_N + c_N + N^{-1}$. Since $\beta ^{a,1}$, $\beta ^{a,2}$ and $\beta ^b$ are all positive, we then get with Lemma 6.1 that

$$\begin{aligned} \left\| \gamma _{N,t}^{(1,0)} - N^{-1} p^t \right\| _{\mathrm {Tr}} \le \sqrt{8\beta (t)} \le e^{e^{C \Lambda ^4 (1 + \Vert \alpha ^0\Vert _2)(1 + t^2)}} \sqrt{I_N} \end{aligned}$$

(123)

for some $C>0$. From Lemma B.2, we know that $\left\| \alpha ^t \right\| _2 \le \left\| \alpha ^0 \right\| _2 + \left\| \tilde{\eta } \right\| _2 \left| t \right|$ and thus

$$\begin{aligned} \left\| \gamma _{N,t}^{(0,1)} - | \alpha ^t \rangle \langle \alpha ^t | \right\| _{\mathrm {Tr}}&\le 3 N^{-1/3} \beta ^b(t) + 6 \left\| \alpha ^t \right\| _2 \sqrt{ N^{-1/3} \beta ^b(t)} \nonumber \\&\le e^{e^{C \Lambda ^4 (1 + \Vert \alpha ^0\Vert _2)(1 + t^2)}} \left( N^{-1/3}I_N + \sqrt{N^{-1/3}I_N} \right) , \end{aligned}$$

(124)

which gives (29) for some $C > 0$, if $c_N \le \tilde{C}N^{1/3}$ for some $\tilde{C}>0$ is assumed.

In the theorem, we also provide bounds for the specific initial state $\bigwedge _{j=1}^N \varphi _j^0 \otimes W(N^{2/3} \alpha ^0) \Omega$. Since for this state $\gamma _{N,0}^{(1,0)} = N^{-1}p^0$, we have $a_N=0$, $b_N=0$ because $q_1 \bigwedge _{j=1}^N \varphi _j^0 \otimes W(N^{2/3} \alpha ^0) \Omega = 0$, and also,

$$\begin{aligned} c_N= & {} N^{-1} \left\langle W^{-1}(N^{2/3} \alpha ^0) W(N^{2/3} \alpha ^0) \Omega , \mathcal {N} W^{-1}(N^{2/3} \alpha ^0) W(N^{2/3} \alpha ^0) \Omega \right\rangle \nonumber \\= & {} N^{-1} \left\langle \Omega , \mathcal {N} \Omega \right\rangle = 0. \end{aligned}$$

(125)

Furthermore, we have

$$\begin{aligned} \bigwedge _{j=1}^N \varphi _j^0 \otimes W(N^{2/3} \alpha ^0) \Omega \in \left( L_{as}^2(\mathbb {R}^{3N}) \otimes \mathcal {F}_\mathrm{s} \right) \cap \mathcal {D} \left( \mathcal {N} \right) \cap \mathcal {D} \left( \mathcal {N} H_N \right) , \end{aligned}$$

(126)

which can be checked by direct calculation as in [32, Section IX]. $\square$

Appendices

Appendix: Convergence to the Free Evolution

In this section, we prove Theorem 2.7.

Proof of Theorem 2.7

We recall that $h^0 = - \Delta + N^{2/3} \Phi _{\Lambda }(\cdot ,0)$ and define a family of unitary operators by $i N^{1/3} \partial _t U(t) = h^0 U(t)$ and $U(0) = \mathbb {1}$, i.e., such that

$$\begin{aligned} i N^{1/3} \partial _t \big ( U^*(t) \tilde{p}^t U(t) \big )&= - U^*(t) h^0 \tilde{p}^t U(t) \nonumber \\&\quad +\,U^*(t) \Big [ h^0, \tilde{p}^t \Big ] U(t) + U^*(t) \tilde{p}^t h^0 U(t) = 0. \end{aligned}$$

(127)

Similarly, we obtain

$$\begin{aligned} i N^{1/3} \partial _t \big ( U^*(t) p^t U(t) \big )&= U^*(t) \Big [ h^t - h^0, p^t \Big ] U(t) \nonumber \\&= N^{2/3} U^*(t) \Big [ \Phi _{\Lambda }(\cdot ,t) - \Phi _{\Lambda }(\cdot ,0), p^t \Big ] U(t). \end{aligned}$$

(128)

With Duhamel’s formula, we conclude

$$\begin{aligned} p^t = U(t) p^0 U^*(t) - i N^{1/3} \int _0^t\,\mathrm{d}s \, U(t-s) \Big [ \Phi _{\Lambda }(\cdot ,s) - \Phi _{\Lambda }(\cdot ,0), p^s \Big ] U(s-t). \end{aligned}$$

(129)

Thus, if we use that $\tilde{p}^t = U(t) \tilde{p}^0 U^*(t) = U(t) p^0 U^*(t)$ we get

$$\begin{aligned} \left\| p^t - \tilde{p}^t \right\| _{\mathrm {Tr}}&\le N^{1/3} \left\| \int _0^t\,\mathrm{d}s \, U(t-s) \Big [ \Phi _{\Lambda }(\cdot ,s) - \Phi _{\Lambda }(\cdot ,0), p^s \Big ] U(s-t) \right\| _{\mathrm {Tr}} \nonumber \\&\le N^{1/3} \int _0^t\,\mathrm{d}s \, \left\| \Big [ \Phi _{\Lambda }(\cdot ,s) - \Phi _{\Lambda }(\cdot ,0), p^s \Big ] \right\| _{\mathrm {Tr}}. \end{aligned}$$

(130)

By means of the Duhamel expansion of Eq. (16) for $\alpha ^s$,

$$\begin{aligned} \alpha ^s(k)&= e^{- i N^{-1/3} \delta _N \omega (k) s} \alpha ^0(k) \nonumber \\&\quad - i N^{-1} (2 \pi )^{3/2} \tilde{\eta }(k) \int _0^s\,\mathrm{d}u \, e^{- i N^{-1/3} \delta _N \omega (k) (s-u)} \mathcal {F}[\rho ^u](k) \end{aligned}$$

(131)

and $\overline{\mathcal {F}[\rho ^u](k)} = \mathcal {F}[\rho ^u](-k)$, one obtains

$$\begin{aligned}&\Phi _{\Lambda }(x,s)\nonumber \\&\quad = \int \mathrm{d}^3k \, \tilde{\eta }(k) \big ( e^{ikx} e^{- i N^{-1/3} \delta _N \omega (k) s} \alpha ^0(k) + e^{-ikx} e^{i N^{-1/3} \delta _N \omega (k) s} \overline{\alpha ^0(k)} \big ) \nonumber \\&\qquad -\,2 N^{-1} (2 \pi )^{3/2} \int \mathrm{d}^3k \, \left| \tilde{\eta }(k) \right| ^2 e^{ikx}\int _0^s\,\mathrm{d}u \, \sin \big ( N^{-1/3} \delta _N \omega (k) (s-u) \big ) \mathcal {F}[\rho ^u](k). \end{aligned}$$

(132)

We continue the previous inequality and get

$$\begin{aligned}&\left\| p^t - \tilde{p}^t \right\| _{\mathrm {Tr}} \le 2 N^{1/3} \int _0^t\,\mathrm{d}s \left\| \int \mathrm{d}^3k \, \tilde{\eta }(k) \big ( e^{i N^{-1/3} \delta _N \omega (k) s} {-} 1 \big ) \overline{\alpha ^0(k)} \big [ e^{-ikx}, p^s \big ] \right\| _{\mathrm {Tr}} \end{aligned}$$

(133a)

$$\begin{aligned}&+\,C N^{-2/3} \int _0^t\,\mathrm{d}s \left\| \int \mathrm{d}^3k \, \left| \tilde{\eta }(k) \right| ^2 \int _0^s\,\mathrm{d}u \, \sin \big ( N^{-1/3} \delta _N \omega (k) (s{-}u) \big ) \mathcal {F}[\rho ^u](k) \big [ e^{ikx}, p^s \big ] \right\| _{\mathrm {Tr}}. \end{aligned}$$

(133b)

In the following, we use (45), $\left| e^{ix} -1 \right| \le 2 \left| x \right|$ and $\left| x \right| \le e^{\left| x \right| }$ to bound the first line by

(134)

where $C(s) = C \Lambda ^4 (1 + \left\| \alpha ^0 \right\| _2) ( 1 + s^2)$. Then, we notice that $\left| \mathcal {F}[\rho ^u](k) \right| \le (2 \pi )^{-3/2} \left\| \rho ^u \right\| _1 = (2 \pi )^{-3/2} N$ and use $\left| \sin (x) \right| \le \left| x \right|$ to estimate

(135)

Collecting the estimates and using $C (1 + \Lambda )^4 \int _0^t\,\mathrm{d}s \, e^{ C(s)} \le e^{ C(t)}$ proves (35). Then (36) follows from (28) and the triangle inequality. $\square$

Appendix: The Fermionic Schrödinger–Klein–Gordon Equations

Subsequently, we prove the existence and uniqueness of solutions of the effective equations (16). To shorten the notation, we introduce

$$\begin{aligned} \begin{aligned} \mathscr {H}&= \bigoplus _{n=1}^{N+1} L^2(\mathbb {R}^3), \quad \vec {\varphi } = (\varphi _1, \ldots , \varphi _N), \quad \rho _{\vec {\varphi }}(x) = \sum _{j=1}^N \left| \varphi _j(x) \right| ^2, \\ \Phi _{\Lambda }^{\alpha }(x)&= \int \mathrm{d}^3k \, \tilde{\eta }(k) \big (e^{ikx} \alpha (k) + e^{-ikx} \overline{\alpha (k)} \big ). \end{aligned} \end{aligned}$$

(136)

Then, we define the operator $A{:}\,\mathcal {D}(A) \rightarrow \mathscr {H}$ as the orthogonal sum

$$\begin{aligned} A {=} A_1 \oplus A_2 \oplus \cdots \oplus A_{N+1}, ~\text {with}~ A_j {=} {\left\{ \begin{array}{ll} 1 - N^{-1/3} \Delta &{}\text {for}~ j \in \{1, 2, \ldots , N \}, \\ 1 + N^{-1/3} \delta _N \omega &{}\text {for}~ j=N+1. \end{array}\right. } \end{aligned}$$

(137)

Moreover, we define $J{:}\,\mathcal {D}(A) \rightarrow \mathscr {H}$ by

$$\begin{aligned} J_j [(\varphi _1, \ldots , \varphi _N, \alpha )] = {\left\{ \begin{array}{ll} - i (N^{1/3} \Phi _{\Lambda }^{\alpha } - 1) \varphi _j &{}\quad \text {if} \; j \in \{1, \ldots , N \}, \\ - i (- \alpha + N^{-1} (2 \pi )^{3/2} \tilde{\eta } \mathcal {F}[\rho _{\vec {\varphi }}]) &{}\quad \text {if} \; j= N+1. \end{array}\right. } \end{aligned}$$

(138)

The fermionic Schrödinger–Klein–Gordon equations (16) can then be written as

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} \begin{pmatrix} \vec {\varphi }^{\,t} \\ \alpha ^t \end{pmatrix}&= - i A \begin{pmatrix} \vec {\varphi }^{\,t} \\ \alpha ^t \end{pmatrix} + J [(\vec {\varphi }^{\,t}, \alpha ^t)]. \end{aligned}$$

(139)

The goal of this section is to show

Lemma B.1

Let $N \in \mathbb {N} {\setminus } \{0 \}, \Lambda \in [1,\infty )$, $m\in [0,\infty )$ and $\delta _N \in (0, \infty )$. Then

• (a) A is a self-adjoint operator on $\mathscr {H}$ with $\mathcal {D}(A) = \big ( \bigoplus _{n=1}^{N} H^2(\mathbb {R}^3) \big ) \oplus L_1^2(\mathbb {R}^3)$,

• (b) J is a mapping which takes $\mathcal {D}(A)$ into $\mathcal {D}(A)$,

• (c) $\Vert J[(\vec {\varphi },\alpha )] - J[(\vec {\psi },\beta )] \Vert _{\mathscr {H}} \le C_{N,\Lambda }\big ( \Vert (\vec {\varphi }, \alpha )\Vert _{\mathscr {H}}, \Vert (\vec {\psi }, \beta )\Vert _{\mathscr {H}} \big ) \, \Vert (\vec {\varphi }, \alpha ) - (\vec {\psi }, \beta ) \Vert _{\mathscr {H}}$,

• (d) $\Vert A J[(\vec {\varphi },\alpha )] \Vert _{\mathscr {H}} \le C_{N,\Lambda ,m} \big ( \Vert (\vec {\varphi }, \alpha )\Vert _{\mathscr {H}}\big ) \, \Vert A (\vec {\varphi }, \alpha ) \Vert _{\mathscr {H}}$,

• (e)
  $$\begin{aligned}&\Vert A J[(\vec {\varphi },\alpha )] - A J[(\vec {\psi },\beta )] \Vert _{\mathscr {H}}\\&\quad \le C_{N,\Lambda ,m, \delta _N }\big ( \Vert (\vec {\varphi }, \alpha )\Vert _{\mathscr {H}}, \Vert (\vec {\psi }, \beta )\Vert _{\mathscr {H}}, \Vert A(\vec {\psi }, \beta )\Vert _{\mathscr {H}} \big ) \Vert A(\vec {\varphi }, \alpha ) {-} A (\vec {\psi }, \beta ) \Vert _{\mathscr {H}}, \end{aligned}$$

where each C is a monotone increasing (everywhere finite) function of all its variables. Moreover, let $(\vec {\varphi }^{\,0},\alpha ^0) \in \mathcal {D}(A)$ and assume there is a $T >0$ so that (139) has a unique continuously differentiable solution for $t \in [0,T)$. Then, $\Vert (\vec {\varphi }^{\,t},\alpha ^t)\Vert _{\mathscr {H}}$ is bounded from above for all $t \in [0,T)$.

We give the proof of the lemma below. In order to prove Proposition 1.1, we use [41, Theorem X.74] with $n=1$.

Proof of Proposition 1.1

From the statements in parts (a)–(e) in Lemma B.1, we have that all conditions of part (a) of Theorem X.73 in [41] are satisfied. This implies the existence of a $T >0$ and a unique continuously differentiable solution to (139) for $t\in [0,T)$ and for all $(\vec {\varphi }^{\, 0},\alpha ^0) \in \mathcal {D}(A)$. By the second part of Lemma B.1, this solution is bounded in norm for all $t\in [0,T)$. Proposition 1.1 then follows from Lemma B.1 and [41, Theorem X.74] with $n=1$. The $\varphi _1^t,\ldots ,\varphi _N^t$ are orthonormal for all $t\in [0,\infty )$ because $- \Delta + N^{2/3} \Phi _{\Lambda }(\cdot ,t)$ is a symmetric operator. $\square$

Before we prove Lemma B.1, let us show that on the chosen timescale $\left\| \alpha ^t \right\| _2$ remains of order one during the time evolution.

Lemma B.2

Let $(\varphi _1^t, \ldots , \varphi _N^t, \alpha ^t)$ be the solution to (16) with $(\varphi _1^0, \ldots , \varphi _N^0,\alpha ^0) \in H^2(\mathbb {R}^3) \oplus L_1^2(\mathbb {R}^3)$ and orthonormal $\varphi _1^0, \ldots , \varphi _N^0$, and let $\tilde{\eta }$ be defined as in (5). Then

$$\begin{aligned} \left\| \alpha ^t \right\| _2 \le \left\| \alpha ^0 \right\| _2 + \left\| \tilde{\eta } \right\| _2 \left| t \right| . \end{aligned}$$

(140)

Proof

We define $U_{\omega }(t) = e^{-iN^{-1/3}\delta _N\omega (k)t}$. Then the Duhamel expansion of Eq. (16) for $\alpha ^t$ can be written as

$$\begin{aligned} \alpha ^t = U_{\omega }(t)\alpha ^0 - i \int _0^t\,\mathrm{d}s \, U_{\omega }(t-s) N^{-1} (2\pi )^{3/2} \, \tilde{\eta } \, \mathcal {F}[\rho _{\vec {\varphi }^{\,s}}]. \end{aligned}$$

(141)

Then, since $\left\| \mathcal {F}[\rho _{\vec {\varphi }^{\,s}}] \right\| _{\infty } \le (2 \pi )^{-3/2} \left\| \rho _{\vec {\varphi }^{\,s}} \right\| _1 = (2 \pi )^{-3/2} N$ for all $s\in \mathbb {R}$, we have

$$\begin{aligned} \left\| \alpha ^t \right\| _2&\le \left\| U_{\omega }(t)\alpha ^0 \right\| _2 + N^{-1} (2\pi )^{3/2} \int _0^t\,\mathrm{d}s\, \left\| U_{\omega }(t-s) \, \tilde{\eta } \mathcal {F}[\rho _{\vec {\varphi }^{\,s}}] \right\| _2 \nonumber \\&\le \left\| \alpha ^0 \right\| _2 + N^{-1} (2\pi )^{3/2} \left\| \tilde{\eta } \right\| _2 \int _0^t\,\mathrm{d}s\, \left\| \mathcal {F}[\rho _{\vec {\varphi }^{\,s}}] \right\| _\infty \nonumber \\&\le \left\| \alpha ^0 \right\| _2 + \left\| \tilde{\eta } \right\| _2 \left| t \right| . \end{aligned}$$

(142)

$\square$

Proof of Lemma B.1

Part (a)

The operators $A_j = (1 - N^{-1/3} \Delta )$ with $\mathcal {D}(A_j) = H^2(\mathbb {R}^3)$ and $j \in \{1, 2, \ldots , N \}$ as well as $A_{N+1} = 1 + N^{-1/3} \delta _N \omega$ with $\mathcal {D}(A_{N+1}) =\{ \alpha \in L^2(\mathbb {R}^3) | A_{N+1} \alpha \in L^2(\mathbb {R}^3) \} = L_1^2(\mathbb {R}^3)$ are clearly self-adjoint. The fact that direct sums of self-adjoint operators are self-adjoint (see, e.g., [48, Theorem 2.24]) proves part (a) of Lemma B.1. Part (b)

Let $(\vec {\varphi }, \alpha ) \in \mathcal {D}(A)$ and $j \in \{1, 2, \ldots , N \}$. Then,

$$\begin{aligned} \left\| \Delta J_{j}[(\vec {\varphi }, \alpha )] \right\| _{L^2(\mathbb {R}^3)}&= \Vert \Delta (N^{1/3} \Phi _{\Lambda }^{\alpha } - 1) \varphi _j \Vert _2 \le \left\| \Delta \varphi _j \right\| _2 + N^{1/3} \left\| \Delta \Phi _{\Lambda }^{\alpha } \varphi _j \right\| _2. \end{aligned}$$

(143)

To bound the second summand, we note that $\Vert \tilde{\eta } \Vert _{L_2^2(\mathbb {R}^3)} \le (1 + \Lambda ^2 ) \Vert \tilde{\eta } \Vert _2 \le \Lambda ^3$ and estimate

$$\begin{aligned} \begin{aligned} \left\| \Phi _{\Lambda }^{\alpha } \right\| _{\infty }&\le 2 \int \mathrm{d}^3k \, \left| \tilde{\eta }(k) \right| \, \left| \alpha (k) \right| \le 2 \left\| \tilde{\eta } \right\| _2 \left\| \alpha \right\| _2 \le 2 \Lambda ^3 \left\| \alpha \right\| _2, \\ \left\| \nabla \Phi _{\Lambda }^{\alpha } \right\| _{\infty }&\le 2 \int \mathrm{d}^3k \, \left| k \right| \, \left| \tilde{\eta }(k) \right| \, \left| \alpha (k) \right| \le 2 \left\| \left| \cdot \right| \tilde{\eta } \right\| _2 \left\| \alpha \right\| _2 \le 2 \Lambda ^3 \left\| \alpha \right\| _2, \\ \left\| \Delta \Phi _{\Lambda }^{\alpha } \right\| _{\infty }&\le 2 \int \mathrm{d}^3k \, \left| k \right| ^2 \, \left| \tilde{\eta }(k) \right| \, \left| \alpha (k) \right| \le 2 \left\| \left| \cdot \right| ^2 \tilde{\eta } \right\| _2 \left\| \alpha \right\| _2 \le 2 \Lambda ^3 \left\| \alpha \right\| _2. \end{aligned} \end{aligned}$$

(144)

Thus,

$$\begin{aligned} \left\| \Delta \Phi _{\Lambda }^{\alpha } \varphi _j \right\| _2&\le \left\| \Phi _{\Lambda }^{\alpha } \right\| _{\infty } \left\| \Delta \varphi _j \right\| _2 + \left\| \Delta \Phi _{\Lambda }^{\alpha } \right\| _{\infty } \left\| \varphi _j \right\| _2 + 2 \left\| \nabla \Phi _{\Lambda }^{\alpha } \right\| _{\infty } \left\| \nabla \varphi _j \right\| _2 \nonumber \\&\le C \Lambda ^3 \left\| \alpha \right\| _2 \left\| \varphi _j \right\| _{H^2(\mathbb {R}^3)} \end{aligned}$$

(145)

and $\left\| \Delta J_{j}[(\vec {\varphi }, \alpha )] \right\| _{L^2(\mathbb {R}^3)} \le \big ( 1 + C N^{1/3} \Lambda ^3 \left\| \alpha \right\| _2 \big ) \left\| \varphi _j \right\| _{H^2(\mathbb {R}^3)}$. This shows that $J_{j}[(\vec {\varphi }, \alpha )] \in H^2(\mathbb {R}^3)$ for $j \in \{ 1, 2, \ldots , N \}$. The last component of J is estimated by $\left\| J_{N+1}[(\vec {\varphi }, \alpha )] \right\| _{L_1^2(\mathbb {R}^3)} \le \left\| \alpha \right\| _{L_1^2(\mathbb {R}^3)} + (2 \pi )^{3/2} N^{-1} \left\| \mathcal {F}[\rho _{\vec {\varphi }}] \right\| _{L^{\infty }(\mathbb {R}^3)} \left\| \tilde{\eta } \right\| _{L_1^2(\mathbb {R}^3)}$. So if we use

$$\begin{aligned} \left\| \mathcal {F}[\rho _{\vec {\varphi }}] \right\| _{L^{\infty }(\mathbb {R}^3)} \le (2 \pi )^{-3/2} \left\| \rho _{\vec {\varphi }} \right\| _{L^1(\mathbb {R}^3)} = (2 \pi )^{-3/2} \sum _{j=1}^N \left\| \varphi _j \right\| _2^2 \end{aligned}$$

(146)

and $\left\| \tilde{\eta } \right\| _{L_1^2(\mathbb {R}^3)} \le \Lambda ^2$, we get $\left\| J_{N+1}[(\vec {\varphi }, \alpha )] \right\| _{L_1^2(\mathbb {R}^3)} \le \left\| \alpha \right\| _{L_1^2(\mathbb {R}^3)} + \Lambda ^2 N^{-1}\sum _{j=1}^N \left\| \varphi _j \right\| _2^2$. Hence, $J_{N+1}[(\vec {\varphi }, \alpha )] \in L_1^2(\mathbb {R}^3)$, and thus, $J[(\vec {\varphi }, \alpha )] \in \mathcal {D}(A)$.

Part (c)

To show part (c) of Lemma B.1, we note that the classical radiation field $\Phi _{\Lambda }^{\alpha }$ is linear in $\alpha$, i.e.,

$$\begin{aligned} \Phi _{\Lambda }^{\alpha } + \Phi _{\Lambda }^{\beta } = \Phi _{\Lambda }^{\alpha + \beta } \quad \text {and} \quad \Phi _{\Lambda }^{\lambda \alpha } = \lambda \Phi _{\Lambda }^{\alpha } ~\forall \lambda \in \mathbb {R}. \end{aligned}$$

(147)

For $j \in \{ 1, \ldots , N \}$, we can write

$$\begin{aligned} i \big ( J[(\vec {\varphi }, \alpha )] - J[(\vec {\psi }, \beta )] \big )_j&= (N^{1/3} \Phi _{\Lambda }^{\alpha } -1) \varphi _j - (N^{1/3} \Phi _{\Lambda }^{\beta } -1) \psi _j \nonumber \\&= - (\varphi _j - \psi _j) + N^{1/3} \Phi _{\Lambda }^{\alpha } ( \varphi _j - \psi _j ) + N^{1/3} \Phi _{\Lambda }^{\alpha - \beta } \psi _j \end{aligned}$$

(148)

and estimate

$$\begin{aligned} \left\| \big ( J[(\vec {\varphi }, \alpha )] - J[(\vec {\psi }, \beta )] \big )_j \right\| _{L^2(\mathbb {R}^3)}&\le (1 + N^{1/3} \Lambda \left\| \alpha \right\| _2) \left\| \varphi _j - \psi _j \right\| _2 \nonumber \\&\quad +\,N^{1/3} \Lambda \left\| \psi _j \right\| _2 \left\| \alpha - \beta \right\| _2 \end{aligned}$$

(149)

by means of (144) and $\left\| \tilde{\eta } \right\| \le \Lambda$. Hence,

$$\begin{aligned}&\sum _{j=1}^N \left\| \big ( J[(\vec {\varphi }, \alpha )] - J[(\vec {\psi }, \beta )] \big )_j \right\| _{L^2(\mathbb {R}^3)}^2 \nonumber \\&\quad \le 2 (1 + N^{1/3} \Lambda \left\| \alpha \right\| _2)^2 \sum _{j=1}^N \left\| \varphi _j - \psi _j \right\| _2^{2} + 2 N^{2/3} \Lambda ^2 \sum _{j=1}^N \left\| \psi _j \right\| _2^2 \left\| \alpha - \beta \right\| _2^2 \nonumber \\&\quad \le 4 \Big ( 1 + N^{2/3} \Lambda ^2 \big ( \Vert (\vec {\varphi }, \alpha )\Vert _{\mathscr {H}}^2 + \Vert (\vec {\psi }, \beta )\Vert _{\mathscr {H}}^2 \big ) \Big ) \Vert (\vec {\varphi }, \alpha ) - (\vec {\psi }, \beta )\Vert _{\mathscr {H}}^2. \end{aligned}$$

(150)

In order to estimate the difference of $J[(\vec {\varphi },\alpha )]_{N+1}$ and $J[(\vec {\psi },\beta )]_{N+1}$, we note that

$$\begin{aligned} \rho _{\vec {\varphi }}(x) - \rho _{\vec {\psi }}(x)&= \sum _{j=1}^N \overline{\varphi _j(x)} (\varphi _j(x) - \psi _j(x)) + \sum _{j=1}^N \psi _j(x) ( \overline{\varphi _j(x)} - \overline{\psi _j(x)}). \end{aligned}$$

(151)

Thus,

$$\begin{aligned} \left\| \rho _{\vec {\varphi }} - \rho _{\vec {\psi }} \right\| _{L^1(\mathbb {R}^3)}&\le \sum _{j=1}^N \left\| \varphi _j \right\| _2 \left\| \varphi _j - \psi _j \right\| _2 + \sum _{j=1}^N \left\| \psi _j \right\| _2 \left\| \varphi _j - \psi _j \right\| _2 \nonumber \\&\le \left( \Vert (\vec {\varphi }, \alpha )\Vert _{\mathscr {H}} + \Vert (\vec {\psi }, \beta )\Vert _{\mathscr {H}} \right) \Vert (\vec {\varphi }, \alpha ) - (\vec {\psi }, \beta )\Vert _{\mathscr {H}}. \end{aligned}$$

(152)

So if we use the linearity of the Fourier transform, we obtain

$$\begin{aligned}&\left\| \big ( J[(\vec {\varphi }, \alpha )] - J[(\vec {\psi }, \beta )] \big )_{N+1} \right\| _{L^2(\mathbb {R}^3)} \nonumber \\&\quad \le \left\| \alpha - \beta \right\| _2 + N^{-1} (2 \pi )^{3/2} \left\| \tilde{\eta } \big (\mathcal {F}[\rho _{\vec {\varphi }}] - \mathcal {F}[\rho _{\vec {\psi }}] \big ) \right\| _2 \nonumber \\&\quad \le \left\| \alpha - \beta \right\| _2 + N^{-1} (2 \pi )^{3/2} \left\| \tilde{\eta } \right\| _2 \left\| \mathcal {F}[\rho _{\vec {\varphi }}] - \mathcal {F}[\rho _{\vec {\psi }}] \right\| _{\infty } \nonumber \\&\quad \le \left\| \alpha - \beta \right\| _2 + N^{-1} \Lambda \left\| \rho _{\vec {\varphi }} - \rho _{\vec {\psi }} \right\| _{L^1(\mathbb {R}^3)} \nonumber \\&\quad \le \left( 1 + N^{-1} \Lambda \left( \Vert (\vec {\varphi }, \alpha )\Vert _{\mathscr {H}} + \Vert (\vec {\psi }, \beta )\Vert _{\mathscr {H}} \right) \right) \Vert (\vec {\varphi }, \alpha ) - (\vec {\psi }, \beta )\Vert _{\mathscr {H}}. \end{aligned}$$

(153)

In total, we get

$$\begin{aligned} \left\| J[(\vec {\varphi }, \alpha )] - J[(\vec {\psi }, \beta )] \right\| _{\mathscr {H}}^2&\le 8 \Lambda ^2 N^{2/3} \Big ( 1 + \Vert (\vec {\varphi }, \alpha )\Vert _{\mathscr {H}}^2 \nonumber \\&\quad +\,\Vert (\vec {\psi }, \beta )\Vert _{\mathscr {H}}^2 \Big ) \Vert (\vec {\varphi }, \alpha ) - (\vec {\psi }, \beta )\Vert _{\mathscr {H}}^2. \end{aligned}$$

(154)

Part (d)

For $j \in \{1, \ldots , N \}$, we consider

$$\begin{aligned} \left\| (A J[(\vec {\varphi }, \alpha )])_j \right\| _{L^2(\mathbb {R}^3)}&= \left\| (1 - N^{-1/3} \Delta )(N^{1/3} \Phi _{\Lambda }^{\alpha } -1 )\varphi _j \right\| _{2} \nonumber \\&\le \left\| (1 - N^{-1/3} \Delta ) \varphi _j \right\| _2 \nonumber \\&\quad +\,C \Lambda ^3 \left\| \alpha \right\| _2 \big ( N^{1/3} \left\| \varphi _j \right\| _2 + \left\| \varphi _j \right\| _{H^2(\mathbb {R}^3)} \big ), \end{aligned}$$

(155)

where we made use of (144) and (145). By means of

$$\begin{aligned} \begin{aligned} \left\| \varphi \right\| _2&\le \left\| (1 - N^{-1/3} \Delta ) \varphi \right\| _2, \quad \left\| \Delta \varphi \right\| _2 \le N^{1/3} \left\| (1 - N^{-1/3} \Delta ) \varphi \right\| _2, \\ \left\| \varphi \right\| _{H^2(\mathbb {R}^3)}&\le 2 N^{1/3} \left\| (1 - N^{-1/3} \Delta ) \varphi \right\| _2, \end{aligned} \end{aligned}$$

(156)

we get

$$\begin{aligned}&\left\| (A J[(\vec {\varphi }, \alpha )])_j \right\| _{L^2(\mathbb {R}^3)} \le (1 + C N^{1/3} \Lambda ^3 \left\| \alpha \right\| _2) \left\| (1 - N^{-1/3} \Delta ) \varphi _j \right\| _2. \end{aligned}$$

(157)

Similarly, we have $\left\| \alpha \right\| _2 \le \left\| \left( 1 + N^{-1/3} \delta _N \omega \right) \alpha \right\| _2$ and obtain

$$\begin{aligned} \left\| (\vec {\varphi },\alpha ) \right\| _{\mathscr {H}}&\le \bigg ( \sum _{j=1}^N \left\| (1 - N^{-1/3} \Delta ) \varphi _j \right\| _2^{2} + \left\| (1 + N^{-1/3} \delta _N \omega ) \alpha \right\| _2^{2} \bigg )^{1/2} \nonumber \\&= \left\| A(\vec {\varphi },\alpha ) \right\| _{\mathscr {H}}. \end{aligned}$$

(158)

With (146), we estimate

$$\begin{aligned} \left\| (A J[(\vec {\varphi }, \alpha )])_{N+1} \right\| _{L^2(\mathbb {R}^3)}&\le \left\| (1 + N^{-1/3} \delta _N \omega ) \alpha \right\| _2 \nonumber \\&\quad +\,N^{-1} (2 \pi )^{3/2} \left( \left\| \tilde{\eta } \right\| _2 + N^{-1/3}\delta _N \left\| \omega \tilde{\eta } \right\| _2 \right) \left\| \mathcal {F}[\rho _{\vec {\varphi }}] \right\| _{\infty } \nonumber \\&\le \left\| A_{N+1}\alpha \right\| _2 + 2N^{-1} \Lambda ^2(1+\sqrt{m}) \sum _{j=1}^N \left\| \varphi _j \right\| _2^2 \nonumber \\&\le \Big ( 1 + 2N^{-1} \Lambda ^2(1+\sqrt{m}) \Big ) \left\| A(\vec {\varphi },\alpha ) \right\| _{\mathscr {H}}. \end{aligned}$$

(159)

Altogether, this yields

$$\begin{aligned} \left\| A J[(\vec {\varphi }, \alpha )] \right\| ^2_{\mathscr {H}}&\le C N^{2/3} \Lambda ^{6} (1+\sqrt{m})^2\big ( 1 + \left\| (\varphi , \alpha ) \right\| _{\mathscr {H}} \big )^2 \left\| A(\vec {\varphi },\alpha ) \right\| _{\mathscr {H}}^2. \end{aligned}$$

(160)

Part (e)

Note that

$$\begin{aligned}&\sum _{j=1} ^N \left\| (A J[(\vec {\varphi }, \alpha )] - A J[(\vec {\psi }, \beta )])_j \right\| _{L^2(\mathbb {R}^3)}^2 \nonumber \\&\quad = \sum _{j=1}^N \left\| (1 - N^{-1/3} \Delta ) ( J[(\vec {\varphi }, \alpha )] - J[(\vec {\psi }, \beta )])_j \right\| _2^2 \nonumber \\&\quad \le 2 \left( \left\| ( J[(\vec {\varphi }, \alpha )] - J[(\vec {\psi }, \beta )]) \right\| _{\mathscr {H}}^2 \right. \nonumber \\&\left. \qquad +\,N^{-2/3} \sum _{j=1}^N \left\| (- \Delta ) ( J[(\vec {\varphi }, \alpha )] - J[(\vec {\psi }, \beta )])_j \right\| _2^2 \right) . \end{aligned}$$

(161)

So if we recall (148) and (154), we get

$$\begin{aligned}&\sum _{j=1} ^N \left\| (A J[(\vec {\varphi }, \alpha )] - A J[(\vec {\psi }, \beta )])_j \right\| _{L^2(\mathbb {R}^3)}^2 \nonumber \\&\quad \le 8 N^{2/3} \Lambda ^2 \big ( 1 + \big ( \Vert (\vec {\varphi }, \alpha )\Vert _{\mathscr {H}}^2 + \Vert (\vec {\psi }, \beta )\Vert _{\mathscr {H}}^2 \big ) \big ) \Vert (\vec {\varphi }, \alpha ) - (\vec {\psi }, \beta )\Vert _{\mathscr {H}}^2 \nonumber \\&\qquad +\,N^{-2/3} \sum _{j=1}^N \left\| (- \Delta ) (\varphi _j - \psi _j) \right\| _2^2 + \sum _{j=1}^N \left\| (- \Delta ) \Phi _{\Lambda }^{\alpha } (\varphi _j - \psi _j) \right\| _2^2 \nonumber \\&\qquad +\,\sum _{j=1}^N \left\| (- \Delta ) \Phi _{\Lambda }^{\alpha - \beta } \psi _j \right\| _2^2. \end{aligned}$$

(162)

By means of (145), (156) and (158), we get

$$\begin{aligned} \begin{aligned} N^{-2/3} \sum _{j=1}^N \left\| ( - \Delta ) (\varphi _j - \psi _j) \right\| _2^2&\le \left\| A(\vec {\varphi },\alpha ) - A(\vec {\psi },\beta ) \right\| _{\mathscr {H}}^2, \\ \sum _{j=1}^N \left\| ( - \Delta ) \Phi _{\Lambda }^{\alpha } (\varphi _j - \psi _j) \right\| _2^2&\le C N^{2/3} \Lambda ^6 \left\| (\vec {\varphi },\alpha ) \right\| _{\mathscr {H}}^2 \left\| A(\vec {\varphi },\alpha ) - A(\vec {\psi },\beta ) \right\| _{\mathscr {H}}^2, \\ \sum _{j=1}^N \left\| (- \Delta ) \Phi _{\Lambda }^{\alpha - \beta } \psi _j \right\| _2^2&\le C N^{2/3} \Lambda ^6 \left\| A(\vec {\psi },\beta ) \right\| _{\mathscr {H}}^2 \left\| A(\vec {\varphi },\alpha ) - A(\vec {\psi },\beta ) \right\| _{\mathscr {H}}^2. \end{aligned} \end{aligned}$$

(163)

Thus,

$$\begin{aligned}&\sum _{j=1} ^N \left\| (A J[(\vec {\varphi }, \alpha )] - A J[(\vec {\psi }, \beta )])_j \right\| _{L^2(\mathbb {R}^3)}^2 \nonumber \\&\quad \le C N^{2/3} \Lambda ^6 \Bigg ( 1 + \left\| (\vec {\varphi },\alpha ) \right\| _{\mathscr {H}}^2 + \Vert (\vec {\psi },\beta )\Vert _{\mathscr {H}}^2 +\,\left\| A(\vec {\psi },\beta ) \right\| _{\mathscr {H}}^2 \Bigg )\nonumber \\&\qquad \times \left\| A(\vec {\varphi },\alpha ) - A(\vec {\psi },\beta ) \right\| _{\mathscr {H}}^2. \end{aligned}$$

(164)

On the other hand, we have

$$\begin{aligned}&\left\| (A J[(\vec {\varphi }, \alpha )] - A J[(\vec {\psi }, \beta )])_{N+1} \right\| _{L^2(\mathbb {R}^3)}^2 \nonumber \\&\quad \le 2 \left\| (1 + N^{-1/3} \delta _N \omega ) (\alpha - \beta ) \right\| _2^2\nonumber \\&\qquad +\,2 N^{-2} (2 \pi )^3 \left\| (1 + N^{-1/3} \delta _N \omega ) \tilde{\eta } \big ( \mathcal {F}[\rho _{\vec {\varphi }}] - \mathcal {F}[\rho _{\vec {\psi }}] \big ) \right\| _2^2 \nonumber \\&\quad \le 2 \left\| A (\vec {\varphi },\alpha ) - A(\vec {\psi },\beta ) \right\| _{\mathscr {H}}^2 \nonumber \\&\qquad +\,2 N^{-1} \big ( \Vert (\vec {\varphi }, \alpha )\Vert _{\mathscr {H}} + \Vert (\vec {\psi }, \beta )\Vert _{\mathscr {H}} \big )^2 \left\| (1 + N^{-1/3} \delta _N \omega ) \tilde{\eta } \right\| _2^2 \left\| (\vec {\varphi }, \alpha ) - (\vec {\psi }, \beta ) \right\| _{\mathscr {H}}^2 \nonumber \\&\quad \le 2 \Big ( 1 + N^{-1} \big ( \Vert (\vec {\varphi }, \alpha )\Vert _{\mathscr {H}} + \Vert (\vec {\psi }, \beta )\Vert _{\mathscr {H}} \big )^2\nonumber \\&\qquad \times \big ( 1 + N^{-1/3} \delta _N \sqrt{\Lambda ^2 + m^2} \big )^2 \Lambda ^2 \Big ) \left\| A (\vec {\varphi },\alpha ) - A(\vec {\psi },\beta ) \right\| _{\mathscr {H}}^2 \nonumber \\&\quad \le 8 \Lambda ^4 \Big ( 1 + \big ( \Vert (\vec {\varphi }, \alpha )\Vert ^2_{\mathscr {H}} + \Vert (\vec {\psi }, \beta )\Vert ^2_{\mathscr {H}} \big )\nonumber \\&\qquad \times \big ( 1 + N^{-1/3} \delta _N \sqrt{1 + m^2} \big )^2 \Big ) \left\| A (\vec {\varphi },\alpha ) - A(\vec {\psi },\beta ) \right\| _{\mathscr {H}}^2. \end{aligned}$$

(165)

In total, we get

$$\begin{aligned}&\left\| A J[(\vec {\varphi }, \alpha )] - A J[(\vec {\psi }, \beta )] \right\| _{\mathscr {H}}^2 \nonumber \\&\quad \le C N^{2/3} \Lambda ^6 \left( 1 + \left\| (\vec {\varphi },\alpha ) \right\| _{\mathscr {H}}^2 + \Vert (\vec {\psi },\beta )\Vert _{\mathscr {H}}^2 + \left\| A(\vec {\psi },\beta ) \right\| _{\mathscr {H}}^2 \right) \nonumber \\&\qquad \times \,\big ( 1 + N^{-1/3} \delta _N \sqrt{1 + m^2} \big )^2 \left\| A(\vec {\psi },\alpha ) - A(\vec {\psi },\beta ) \right\| _{\mathscr {H}}^2. \end{aligned}$$

(166)

Final Statement of the Lemma

Let $(\vec {\varphi }^{\,0},\alpha ^0) \in \mathcal {D}(A)$ and assume there is a $T >0$ so that (139) has a unique continuously differentiable solution for $t \in [0,T)$. Then,

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} \left\| \varphi _j^t \right\| _2^2&= \frac{\mathrm{d}}{\mathrm{d}t} \left\langle \varphi _j^t, \varphi _j^t \right\rangle = 2 \mathrm {Im}\left\langle \varphi _j^t, \big (- N^{-1/3} \Delta + \Phi _{\Lambda }^{\alpha ^t} \big )\varphi _j^t \right\rangle =0 \end{aligned}$$

(167)

because $\Phi _{\Lambda }^{\alpha ^t} \in \mathbb {R}$. Moreover, we can apply Lemma B.2 locally and conclude $\left\| \alpha ^t \right\| _2 \le \left\| \alpha ^0 \right\| _2 + C \Lambda t \le \left\| \alpha ^0 \right\| _2 + C \Lambda T$. For all $t \in [0,T)$, this shows

$$\begin{aligned} \left\| (\vec {\varphi }^{\,t}, \alpha ^t) \right\| _{\mathscr {H}}&\le \left\| (\vec {\varphi }^{\,0}, \alpha ^0) \right\| _{\mathscr {H}} + \left\| \alpha ^0 \right\| _2 + C \Lambda T. \end{aligned}$$

(168)

$\square$