Semiclassical Limit for Almost Fermionic Anyons

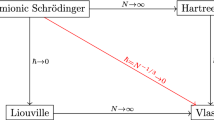
Abstract

In two-dimensional space there are possibilities for quantum statistics continuously interpolating between the bosonic and the fermionic one. Quasi-particles obeying such statistics can be described as ordinary bosons and fermions with magnetic interactions. We study a limit situation where the statistics/magnetic interaction is seen as a “perturbation from the fermionic end”. We vindicate a mean-field approximation, proving that the ground state of a gas of anyons is described to leading order by a semi-classical, Vlasov-like, energy functional. The ground state of the latter displays anyonic behavior in its momentum distribution. Our proof is based on coherent states, Husimi functions, the Diaconis–Freedman theorem and a quantitative version of a semi-classical Pauli pinciple.

Appendices

Appendix A: Properties of the Vlasov Functional

In this “Appendix” we etablish some of the fundamental properties of the functional $\mathcal {E}_{V}$ and some useful bounds on the vector potential $\mathbf {A}^{R}[\rho ]$ associated to a measure $\rho$.

Lemma A.1

(Lower semicontinuity of $\mathcal {E}_{V})$.

Let $(\mu _n)_{n\ge 0}$ be a sequence of positive measures on $\mathbb {R}^4$ satisfying

$$\begin{aligned} 0\le \mu _{n}\le \left( 2\pi \right) ^{-2}, \quad \int _{\mathbb {R}^4} \mu _n \le C \end{aligned}$$

with C independent of N. If $\mu _n$ converges to $\mu$ as measures we have

$$\begin{aligned} \liminf _{n\rightarrow \infty }\mathcal {E}_{V}\left[ \mu _{n}\right] \ge \mathcal {E}_{V}\left[ \mu \right] . \end{aligned}$$

(A.1)

Proof

We recall that the marginal in p of $\mu _{n}$ is

$$\begin{aligned} \rho _{n} (x)=\int _{\mathbb {R}^{2}}\mu _{n} (x,p)\mathrm{d}p. \end{aligned}$$

(A.2)

It follows from applying the bathtub principle [36, Theorem 1.14] in the p variable that

$$\begin{aligned} \mathcal {E}_{V}\left[ \mu _n \right] \ge \mathcal {E}_{V}^{\mathrm {TF}}\left[ \rho _n \right] :=2\pi \int _{\mathbb {R}^{2}}\rho _n ^{2}(x)\mathrm{d}x+\int _{\mathbb {R}^{2}}V(x)\rho _n(x)\mathrm{d}x. \end{aligned}$$

Hence we may assume that $\left\Vert \rho _n \right\Vert _{L^{2}}$ is uniformly bounded and that $\rho _{n} \rightharpoonup \rho$ weakly in $L^{2}\left( \mathbb {R}^{2}\right)$. We then deduce from the weak Young inequality [36, Chapter 4] that

$$\begin{aligned} \left\Vert \mathbf {A}^{2}[\rho _{n}]\rho _{n} \right\Vert _{L^{1}}\le C \left\Vert \nabla ^{\perp }w*\rho _{n} \right\Vert ^{2}_{L^{\infty }}\le C \left\Vert \rho _{n} \right\Vert ^{2}_{L^{2}}\left\Vert \nabla ^{\perp }w \right\Vert ^{2}_{L^{2,w}}\le C. \end{aligned}$$

We recall that the weak $L^{p}(\mathbb {R}^{d})$ space is the set of functions

$$\begin{aligned} L^{w,2}=\left\{ f\;|\; \mathrm {Leb}\left( \left\{ x\in \mathbb {R}^{d}:|f(x)|>\lambda \right\} \right) \le \left( \frac{C}{\lambda }\right) ^{p} \right\} \end{aligned}$$

with the associated norm

$$\begin{aligned} \left\Vert f \right\Vert _{L^{w,2}}=\sup _{\lambda>0}\lambda \;\mathrm {Leb}\left( x\in \mathbb {R}^{d},\;\left|f(x)\right|>\lambda \right) ^{1/2} \end{aligned}$$

where $\mathrm {Leb}$ is the Lebesgue measure. We expand the energy

$$\begin{aligned} \mathcal {E}_{V}\left[ \mu _{n} \right] =\int _{\mathbb {R}^{4}}\left( \left( p^{\mathbf {A}}\right) ^{2}+2\beta p^{\mathbf {A}}\cdot \mathbf {A}[\rho _{n}]+\beta ^{2}\mathbf {A}^{2}[\rho _{n}]+V\right) \mu _{n}(x,p)\mathrm{d}x\mathrm{d}p \end{aligned}$$

(A.3)

and use that $ab\le \frac{a^{2}}{2\sigma }+\frac{\sigma b^{2}}{2}$ to get

$$\begin{aligned} 2\left( p^{\mathbf {A}}\right) \cdot \mathbf {A}\left[ \rho _{n}\right] \ge -\sigma |p^{\mathbf {A}}|^{2}-\frac{1}{\sigma }\left|\mathbf {A}\left[ \rho _{n}\right] \right|^{2} \end{aligned}$$

and hence

$$\begin{aligned} \mathcal {E}_{V}\left[ \mu _{n}\right] +C\left\Vert \mathbf {A}^{2}\left[ \rho _{n}\right] \rho _{n} \right\Vert _{L^{1}}\ge C\int _{\mathbb {R}^{4}}\left( |p^{\mathbf {A}} |^{2}+V\right) \mathrm{d}\mu _{n}. \end{aligned}$$

Thus $(\mu _{n})$ is tight and, up to extraction, converges strongly in $L^{1}\left( \mathbb {R}^{4}\right)$. In order to obtain the convergence of $\mathbf {A}^{2}[\rho _{n}]\mu _{n}$ we write

$$\begin{aligned} \rho _{n}(x_{1})\rho _{n}(x_{2})\mu _{n}(x_{3},p_{3})- \rho (x_{1})\rho (x_{2})\mu (x_{3},p_{3})&=\left( \rho _{n}(x_{1})- \rho (x_{1})\right) \left( \rho _{n}(x_{2})\right. \nonumber \\&\quad \left. - \rho (x_{2})\right) \mu _{n}(x_{3},p_{3})\nonumber \\&\quad +\left( \rho _{n}(x_{1})- \rho (x_{1})\right) \rho (x_{2})\mu _{n}(x_{3},p_{3})\nonumber \\&\quad + \rho (x_{1})\left( \rho _{n}(x_{2})- \rho (x_{2})\right) \mu _{n}(x_{3},p_{3})\nonumber \\&\quad -\rho (x_{1})\rho (x_{2})\left( \mu _{n}(x_{3},p_{3})-\mu (x_{3},p_{3})\right) \end{aligned}$$

(A.4)

and treat each resulting term separately. The first term yields

$$\begin{aligned} \left\Vert \mathbf {A}^{2}[\rho _{n}-\rho ]\mu _{n} \right\Vert _{L^{1}} \le \left\Vert \mu _{n} \right\Vert _{L^1}\left\Vert \nabla ^{\perp }w*\left( \rho _{n}-\rho \right) \right\Vert ^{2}_{L^{\infty }}\le \left\Vert \rho _{n}-\rho \right\Vert ^{2}_{L^{2}}\left\Vert \nabla ^{\perp }w \right\Vert ^{2}_{L^{2,w}} \end{aligned}$$

using that $||\mu _{n}||_{L^1}\le C$ and the weak Young inequality. For the second term of (A.4)

$$\begin{aligned} \left\Vert \mathbf {A}[\rho _{n}-\rho ]\mathbf {A}[\rho ]\mu _{n} \right\Vert _{L^{1}}\le \left\Vert \mathbf {A}[\rho ] \right\Vert _{L^{\infty }}\left\Vert \nabla ^{\perp }w*(\rho _{n}-\rho ) \right\Vert _{L^{\infty }}\le \left\Vert \rho \right\Vert _{L^{2}}\left\Vert \rho _{n}-\rho \right\Vert _{L^{2}}\left\Vert \nabla ^{\perp }w \right\Vert ^{2}_{L^{2,w}} \end{aligned}$$

and for the last one

$$\begin{aligned} \left\Vert \mathbf {A}^{2}[\rho ](\mu _{n}-\mu ) \right\Vert _{L^{1}}\le \left\Vert \mu _{n}-\mu \right\Vert _{L^{1}}\left\Vert \mathbf {A}^{2}[\rho ] \right\Vert _{L^{\infty }}\le \left\Vert \mu _{n}-\mu \right\Vert _{L^1}\left\Vert \nabla ^{\perp }w \right\Vert ^{2}_{L^{2,w}}\left\Vert \rho \right\Vert _{L^2} \end{aligned}$$

For the cross term of (A.3), $p^{\mathbf {A}}.\mathbf {A}\left[ \rho _{n}\right] \mu _{n}$ we observe that

$$\begin{aligned} \left\Vert \mathbf {A}[\rho -\rho _{n}] \right\Vert _{L^2}\le \left\Vert \rho -\rho _{n} \right\Vert _{L^1}\left\Vert \nabla ^{\perp }w \right\Vert _{L^{2,w}} \end{aligned}$$

so $\mathbf {A}[\rho _{n}]$ converges strongly in $L^{2}$. We have $||\left( p^{\mathbf {A}}\right) ^{2}\mu _{n}||_{L^{1}}\le C$ so $p^{\mathbf {A}}\mu _{n}$ converges weakly in $L^{2}$ and by weak-strong convergence we deduce that the cross term converges. We conclude using Fatou’s lemma for V and the kinetic term

$$\begin{aligned} \liminf _{n\rightarrow \infty }\int _{\mathbb {R}^{4}}|p+\mathbf {A}_{e}(x)|^{2}\mu _{n}(x,p)\mathrm{d}x\mathrm{d}p&\ge \int _{\mathbb {R}^{4}}|p+\mathbf {A}_{e}(x)|^{2}\mu (x,p)\mathrm{d}x\mathrm{d}p\\ \liminf _{n\rightarrow \infty }\int _{\mathbb {R}^{2}}V(x)\rho _{n}(x)\mathrm{d}x&\ge \int _{\mathbb {R}^{2}}V(x)\rho (x)\mathrm{d}x \end{aligned}$$

$\square$

Lemma A.2

(Existence of minimizers).

There exists a minimizer for the problem

$$\begin{aligned} e^{\mathrm {TF}}=\inf \left\{ \mathcal {E}_{V}[\mu ]\;|\; 0\le \mu \le \left( 2\pi \right) ^{-2}\;|\; \int _{\mathbb {R}^{4}}\mu = 1 \right\} \end{aligned}$$

Proof

We consider a minimizing sequence $\left( \mu _{n}\right) _{n}$ converging to a candidate minimizer $\mu _{\infty }$. By Lemma (A.1) we have

$$\begin{aligned} e^\mathrm{TF} = \inf _{n\rightarrow \infty }\mathcal {E}_{V}\left[ \mu _{n}\right] \ge \mathcal {E}_{V}\left[ \mu _{\infty }\right] . \end{aligned}$$

We also found during the previous proof that $\left( \mu _{n}\right) _{n}$ must be tight, hence

$$\begin{aligned} \int _{\mathbb {R}^{4}}\mu _\infty = 1. \end{aligned}$$

$\square$

Lemma A.3

(Convergence to $\mathcal {E}_{V}$ when $R\rightarrow 0)$.

For any measure $\mu \le \left( 2\pi \right) ^{-2}$ such that $\int _{\mathbb {R}^{4}}\mu \le C$ we have that

$$\begin{aligned} \left|\mathcal {E}^{R}_{V}[\mu ]-\mathcal {E}^{0}_{V}[\mu ]\right|\le CR \left( \mathcal {E}^{0}_{V}[\mu ]+\mathcal {E}^{R}_{V}[\mu ]\right) \end{aligned}$$

where

$$\begin{aligned} \mathcal {E}^{R}_{V}[\mu ]=\int _{\mathbb {R}^{4}}\left( p^{\mathbf {A}}+\beta \mathbf {A}^{R}\left[ \mu \right] (x)\right) ^{2}+V(x) \mathrm{d}\mu \end{aligned}$$

Proof

$$\begin{aligned} \left|\mathcal {E}^{R}_{V}[\mu ]-\mathcal {E}^{0}_{V}[\mu ]\right|&= \left|\left\Vert \left( p^{\mathbf {A}}+_beta\mathbf {A}^{R}\left[ \mu \right] (x)\right) \sqrt{\mu } \right\Vert _{L^2}^{2}-\left\Vert \left( p^{\mathbf {A}}+\beta \mathbf {A}^{0}\left[ \mu \right] (x)\right) \sqrt{\mu } \right\Vert _{L^2}^{2}\right|\\&\le \left|\left\Vert \left( p^{\mathbf {A}}+_beta\mathbf {A}^{R}\left[ \mu \right] (x)\right) \sqrt{\mu } \right\Vert _{L^2}-\left\Vert \left( p^{\mathbf {A}}+\beta \mathbf {A}^{0}\left[ \mu \right] (x)\right) \sqrt{\mu } \right\Vert _{L^2}\right|\\&\;\;\;\;\;\;\;\;\;\cdot \left( \mathcal {E}_{V}^{R}\left[ \mu \right] ^{1/2}+\mathcal {E}_{V}\left[ \mu \right] ^{1/2}\right) \\&\le \left\Vert \left( \mathbf {A}^{R}\left[ \mu \right] -\mathbf {A}\left[ \mu \right] \right) \sqrt{\mu } \right\Vert _{L^2} \left( \mathcal {E}_{V}^{R}\left[ \mu \right] ^{1/2}+\mathcal {E}_{V}\left[ \mu \right] ^{1/2}\right) \end{aligned}$$

where we have used the triangle inequality. Moreover we have that

$$\begin{aligned} \left\Vert \left( \mathbf {A}^{R}\left[ \mu \right] -\mathbf {A}\left[ \mu \right] \right) ^{2}\rho \right\Vert ^{1/2}_{L^1}&\le \left\Vert \rho \right\Vert _{L^1}^{1/2}\left\Vert \left( \nabla ^{\perp }w_{R}-\nabla ^{\perp }w_{0}\right) *\rho \right\Vert _{L^\infty }\\&\le \left\Vert \rho \right\Vert _{L^2}\left\Vert \nabla ^{\perp }w_{R}-\nabla ^{\perp }w_{0} \right\Vert _{L^{2,w}} \end{aligned}$$

by the weak Young inequality and because

$$\begin{aligned} \int _{\mathbb {R}^{2}}\left( \int _{\mathbb {R}^{2}}\frac{1}{|x|}\chi (u) \mathrm{d}u-\int _{B(0,R)}\frac{1}{|x|}\chi (u)\mathrm{d}u\right) \mathrm{d}x\le \int _{B(0,2R)}\frac{1}{|x|}\mathrm{d}x =CR \end{aligned}$$

Using that the minimizer in p

$$\begin{aligned} \mu ^{\mathrm {TF}}=\left( 2\pi \right) ^{-2}11\left( |p^{\mathbf {A}}+\mathbf {A}[\rho ]|\le \sqrt{4\pi \rho }\right) \end{aligned}$$

is explicit we have

$$\begin{aligned} \mathcal {E}_{V}[\mu ]\ge \mathcal {E}_{\mathrm {TF}}(\rho )=2\pi \int _{\mathbb {R}^{2}}\rho ^{2}(x)\mathrm{d}x+\int _{\mathbb {R}^{2}}V(x)\rho (x)\mathrm{d}x \end{aligned}$$

and the minimization problem is now formulated in terms of

$$\begin{aligned} \rho (x)=\int _{\mathbb {R}^{2}}\mu (x,p)\mathrm{d}p. \end{aligned}$$

This gives

$$\begin{aligned} \mathcal {E}_{V}[\mu ]\ge C\left\Vert \rho \right\Vert _{L^2}^{2} \end{aligned}$$

and concludes the proof. $\quad \square$

Lemma A.4

(Dependence on the upper perturbed constraint).

The infimum of $\mathcal {E}_{V}$ does not depend on $\varepsilon$ nor $\gamma$ at first order

$$\begin{aligned} \inf \left\{ \mathcal {E}_{V}[\mu ]\;|\;0\le \mu \le \frac{1+\varepsilon }{\left( 2\pi \right) ^{2}},\;\int \mu = 1-\gamma \right\} \ge \left( 1-2\varepsilon \right) \left( 1-\gamma \right) e_{\mathrm {TF}} \end{aligned}$$

Proof

We calculate the infimum with the Bathtub principle [36, Theorem 1.14]. This infimum is achieved for

$$\begin{aligned} \mu =\mu _{\varepsilon }^{\mathrm {TF}}=\left( 2\pi \right) ^{-2}(1+\varepsilon )11\left( |p^{\mathbf {A}}+\beta \mathbf {A}[\rho ]|^{2}\le s(x)\right) \end{aligned}$$

where $s(x)=\frac{4\pi \rho }{1+\varepsilon }$ because

$$\begin{aligned} \int _{\mathbb {R}^{2}}\mu ^{\mathrm {TF}} (x,p)\mathrm{d}p=\rho (x)=\int _{\mathbb {R}^{2}}(1+\varepsilon )11\left( |p^{\mathbf {A}}+\beta \mathbf {A}[\rho ]|\le s(x)\right) \mathrm{d}p = \pi (1+\varepsilon )s(x) \end{aligned}$$

So, evaluating the energy

$$\begin{aligned} \mathcal {E}_{V}[\mu _{\varepsilon }^{\mathrm {TF}} ]=\mathcal {E}^{\varepsilon }_{\mathrm {TF}}[\rho ]=2\pi \int _{\mathbb {R}^{2}}\frac{\rho ^{2}\left( x\right) }{\left( 1+\varepsilon \right) ^{2}}\mathrm{d}x+\int _{\mathbb {R}^{2}}\frac{V(x)\rho (x)}{\left( 1+\varepsilon \right) }\mathrm{d}x \end{aligned}$$

(.5)

but we can see that

$$\begin{aligned} \mathcal {E}^{\varepsilon }_{\mathrm {TF}}[\rho ]\ge \mathcal {E}_{\mathrm {TF}}[\rho ]\left( 1-2\varepsilon \right) \end{aligned}$$

(.6)

where $\mathcal {E}_{\mathrm {TF}}[\rho ]$ is given in (1.21). $\quad \square$

Appendix B: Bounds for $\mathbf {A}^{R}$

Lemma B.1

(Bounds linked to $\mathbf {A}^{R})$.

All second-order directional derivative of the function

$$\begin{aligned} w_{R}(u_{1},u_{2}): \mathbb {R}^{2}\rightarrow \mathbb {R}^{2} \end{aligned}$$

are bounded in absolute value by the radial derivative:

$$\begin{aligned} \left|\partial _{u_{i}}\partial _{u_{j}} w_{R}(\mathbf {u})\right|\le C\left|\partial _{u}^{2}w_{R}(u)\right| \end{aligned}$$

(B.1)

for any $(i,j)\in \left\{ 1,2\right\} ^{2}$. We also have the estimates

$$\begin{aligned}&\left\Vert \Delta \nabla ^{\perp }w_{R} \right\Vert _{L^{\infty }}\le \frac{C}{R^{3}} \end{aligned}$$

(B.2)

$$\begin{aligned}&\left\Vert \nabla ^{\perp }w_{R} \right\Vert _{L^\infty }\le \frac{C}{R} \end{aligned}$$

(B.3)

$$\begin{aligned}&\left\Vert \Delta \nabla ^{\perp }w_{R} \right\Vert _{2}\le \frac{C}{R^{2}} \end{aligned}$$

(B.4)

$$\begin{aligned}&\left\Vert \nabla \left( \nabla ^{\perp }w_{R}(u)\right) ^{i} \right\Vert _{L^\infty }\le \frac{C}{R^{2}} \end{aligned}$$

(B.5)

$$\begin{aligned}&\left\Vert \nabla \left( \nabla ^{\perp }w_{R}(u).\nabla ^{\perp }w_{R}(v)\right) \right\Vert _{L^\infty }\le \frac{C}{R^{3}} \end{aligned}$$

(B.6)

Proof

Recall that

$$\begin{aligned} w_{R}(x)=\left( \log |\;.\;|*\chi _{R}\right) (x) \end{aligned}$$

with $\chi _{R}$ defined as in (1.8). We call $u_{1}$ and $u_{2}$ the two components of the vector $\mathbf {u}$ and u its norm. Using Newton’s theorem [36, Theorem 9.7] we write

$$\begin{aligned} w_{R}(u)=\int _{\mathbb {R}^{2}}\log |\mathbf {u}-\mathbf {v}|\chi _{R}(v)\mathrm {d}v&=2\pi \log (u)\int _{0}^{u}\chi _{R}(r)r\mathrm{d}r + 2\pi \int _{u}^{+\infty }r\log (r)\chi _{R}(r)\mathrm{d}r \end{aligned}$$

hence

$$\begin{aligned}&\partial _{u}w_{R}(u)=\frac{1}{u}\int _{B(0,u)}\chi _{R}(v) \mathrm{d}v\nonumber \\&\partial ^{2}_{u}w_{R}(u)=-\frac{1}{u^{2}}\int _{B(0,u)}\chi _{R}(v) \mathrm{d}v +2\pi \chi _{R}(u) \end{aligned}$$

(B.7)

$$\begin{aligned}&\partial ^{3}_{u}w_{R}(u)=\frac{1}{u^{3}}\int _{B(0,u)}\chi _{R}(v) \mathrm{d}v +C\frac{\chi _{R}(u)}{u}+C\phi _{R}(u) \end{aligned}$$

(B.8)

where $\phi _{R}(u)=\partial _{u}\chi _{R}(u)$ is bounded with compact support. We observe that regardless of whether u is smaller or greater than 2R we have

$$\begin{aligned} \left|\partial _{u}w_{R}(u)\right|\le \frac{C}{R}\;\;\text {and}\;\; \left|\partial ^{2}_{u}w_{R}(u)\right|\le \frac{C}{R^{2}} \end{aligned}$$

(B.9)

and get (B.3). Moreover

$$\begin{aligned} \nabla ^{\perp }w_{R}(u_{1},u_{2})=\nabla ^{\perp }w_{R}(u)=\frac{\partial _{u}w_{R}(u)}{u}\mathbf {u}^{\perp } \end{aligned}$$

(B.10)

We compute the two derivatives of the second component of (B.10)

$$\begin{aligned} \left|\partial _{u_{1}}(\frac{u_{1}}{u}\partial _{u}w_{R})\right|&=\left|\frac{\partial _{u}w_{R}}{u}+\frac{u_{1}^{2}}{u^{2}}\partial ^{2}_{u}w_{R}-\frac{u_{1}^{2}}{u^{3}}\partial _{u}w_{R}\right|\le \frac{C}{u^{2}}\int _{B(0,u)}\chi _{R}(v) \mathrm{d}v +C\chi _{R}(u) \end{aligned}$$

(B.11)

$$\begin{aligned} \left|\partial _{u_{2}}(\frac{u_{1}}{u}\partial _{u}w_{R})\right|&=\left|-\frac{u_{1}u_{2}}{u^{3}}\partial _{u}w_{R}(u)+\frac{u_{1}u_{2}}{u^{2}}\partial ^{2}_{u}w_{R}(u)\right|\le \frac{C}{u^{2}}\int _{B(0,u)}\chi _{R}(v) \mathrm{d}v +C\chi _{R}(u) \end{aligned}$$

(B.12)

we do the same with the first component of $\nabla ^{\perp }w_{R}$ and get (B.1). If we differentiate once again we get

$$\begin{aligned} \left|\partial ^{2}_{u_{1}}(\frac{u_{1}}{u}\partial _{u}w_{R})\right|&|\le \frac{C}{u^{3}}\int _{B(0,u)}\chi _{R}(v) \mathrm{d}v +C\frac{\chi _{R}(u)}{u}+C\phi _{R}(u) \end{aligned}$$

which is also the case for the other component and derivative. We deduce

$$\begin{aligned} \left\Vert \Delta \nabla ^{\perp }w_{R} \right\Vert _{L^{\infty }}\le \frac{C}{R^{3}} \end{aligned}$$

We can also compute

$$\begin{aligned} \left\Vert \Delta \nabla ^{\perp }w_{R} \right\Vert _{L^2}^{2}\le \frac{C}{R^{4}} \end{aligned}$$

which gives (B.4). To get (B.5) we combine (B.9) and (B.12). For the third inequality (B.6) we expand a little bit our first expression

$$\begin{aligned} \nabla ^{\perp }w_{R}(u).\nabla ^{\perp }w_{R}(v)&=(u_{1}v_{1}+u_{2}v_{2})\frac{\partial _{u}w_{R}(u)\partial _{v}w_{R}(v)}{uv} \end{aligned}$$

so the first component of the gradient is

$$\begin{aligned} \partial _{u_{1}}\nabla ^{\perp }w_{R}(u).\nabla ^{\perp }w_{R}(v)&=v_{1}\frac{\partial _{u}w_{R}(u)\partial _{v}w_{R}(v)}{uv}+\frac{u_{1}}{u}\partial _{u}\left[ \frac{\partial _{u}w_{R}(u)\partial _{v}w_{R}(v)}{uv}\right] (u_{1}v_{1}+u_{2}v_{2}) \end{aligned}$$

Now

$$\begin{aligned} \left\Vert \nabla \left( \nabla ^{\perp }w_{R}(u).\nabla ^{\perp }w_{R}(v)\right) \right\Vert ^{2}_{L^\infty }&=\sum _{x=u_{1},u_{2},v_{1},v_{2}}\left( \partial _{x}\nabla ^{\perp }w_{R}(u).\nabla ^{\perp }w_{R}(v)\right) ^{2} \end{aligned}$$

The rest of the proof consists of the computation of the above term using basic inequalities. $\quad \square$

Appendix C: Computations for Squeezed Coherent States

We give for completeness three proofs that we skipped in the main text.

Proof of Lemma 1.3

For any $u\in L^{2}(\mathbb {R}^{2})$,

$$\begin{aligned} \left\langle F_{x,p},u \right\rangle&=\int _{\mathbb {R}^{2}}F_{\hbar _{x}}(y-x)u(y)e^{-\mathrm {i}\frac{p.y}{\hbar }}\mathrm{d}y\nonumber \\&=2\pi \hbar \mathcal {F}_{\hbar }\left[ F_{\hbar _{x}}(\cdot -x)u(\cdot )\right] (p)=2\pi \hbar \left( \mathcal {F}_{\hbar }\left[ F_{\hbar _{x}}(\cdot -x)\right] *\mathcal {F}_{\hbar }\left[ u(\cdot )\right] \right) (p) \end{aligned}$$

(C.1)

$$\begin{aligned}&=\int _{\mathbb {R}^{2}}G_{\hbar _{p}}(k-p)\mathcal {F}_{\hbar } [u](k)e^{-\mathrm {i}\frac{k.x}{\hbar }}\mathrm{d}k=2\pi \hbar \mathcal {F}_{\hbar }\left[ G_{\hbar _{p}}(\cdot -p)\mathcal {F}_{\hbar } [u]\right] (x). \end{aligned}$$

(C.2)

It follows that

$$\begin{aligned} \frac{1}{(2\pi \hbar )^{2}}\int _{\mathbb {R}^{2}}\int _{\mathbb {R}^{2}}\left\langle \psi , P_{x,p}\psi \right\rangle \;\mathrm{d}x\mathrm{d}p&=\frac{1}{(2\pi \hbar )^{2}}\int _{\mathbb {R}^{2}}\int _{\mathbb {R}^{2}}|\left\langle F_{x,p},u \right\rangle |^{2}\mathrm{d}x\mathrm{d}p\\&=\int _{\mathbb {R}^{2}}\left( \int _{\mathbb {R}^{2}}\left|\mathcal {F}_{\hbar }\left[ F_{\hbar _{x}}(\cdot -x)u(\cdot )\right] (p)\right|^{2}\mathrm{d}p\right) \mathrm{d}x\\&=\int _{\mathbb {R}^{2}}\left( \int _{\mathbb {R}^{2}}\left|F_{\hbar _{x}}(y -x)u(y)\right|^{2}\mathrm{d}y\right) \mathrm{d}x\\&=||F_{\hbar _{x}}||^{2}_{L^{2}(\mathbb {R}^{2})}||u||^{2}_{L^{2}(\mathbb {R}^{2})}=||u||^{2}_{L^{2}(\mathbb {R}^{2})}. \end{aligned}$$

$\square$

Fourier transform of F

We need to calculate the Fourier Transform of the Gaussian

$$\begin{aligned} G_{\hbar _{p}}(p)=\frac{1}{2\pi \hbar }\frac{\sqrt{\hbar _{x}}^{2}}{\sqrt{\hbar _{x}}}\frac{1}{\sqrt{\pi }}\left( \int _{\mathbb {R}}e^{-\frac{u^{2}}{2}-\frac{\mathrm {i}pu}{\sqrt{\hbar _{p}}}}\mathrm{d}u\right) ^{2}=\frac{1}{2\pi \sqrt{\hbar _{p}}}\frac{1}{\sqrt{\pi }}G_{1}^{2}(p) \end{aligned}$$

with

$$\begin{aligned} G_{1}(p)=\int _{\mathbb {R}}e^{-\frac{u^{2}}{2}-\frac{\mathrm {i}pu}{\sqrt{\hbar _{p}}}}\mathrm{d}u \end{aligned}$$

but we also have

$$\begin{aligned} \frac{\mathrm{d}G_{1}(p)}{\mathrm{d}p}=-\frac{p}{\hbar _{p}}G_{1}(p) \end{aligned}$$

which gives the result. $\quad \square$

Proof of Lemma 3.2

We use (C.2) and write for every fixed $y\in \mathbb {R}^{2(N-k)}$

$$\begin{aligned}&\Big < F_{x_{1},p_{1}}(\cdot )\otimes ...\otimes F_{x_{k},p_{k}}(\cdot ),\Psi _{N}(\cdot ,z) \Big >_{L^{2}(\mathbb {R}^{2k})}\\&\quad =(2\pi \hbar )^{2k}\mathcal {F}_{\hbar }\left[ F_{x_{1},0}(\cdot )\otimes ...\otimes F_{x_{k},0}(\cdot )\Psi _{N}(\cdot , z)\right] (p_{1},...,p_{k})\\&\quad =(2\pi \hbar )^{2k}\mathcal {F}_{\hbar }\left[ G_{0,p_{1}}(\cdot )\otimes ...\otimes G_{0,p_{k}}(\cdot )\mathcal {F}_{\hbar } \left[ \Psi _{N}\right] (\cdot , z)\right] (x_{1},...,x_{k}). \end{aligned}$$

Next we sum over the $p_{j}$’s using (1.32):

$$\begin{aligned}&\frac{1}{(2\pi )^{2k}}\int _{\mathbb {R}^{2k}}m_{\Psi _{N}}^{(k)}(x_{1},p_{1},...,x_{k},p_{k})\mathrm{d}p_{1}...\mathrm{d}p_{k}\\&\quad =\frac{k!}{(2\pi )^{2k}}\begin{pmatrix} N \\ k \end{pmatrix}\int _{\mathbb {R}^{2k}}\mathrm{d}p_{1}...\mathrm{d}p_{k}\int _{\mathbb {R}^{2(N-k}}\left|\Big < F_{x_{1},p_{1}}(\cdot )\otimes ...\otimes F_{x_{k},p_{k}}(\cdot ),\Psi _{N}(\cdot ,z) \Big >\right|^{2}\mathrm{d}z\\&\quad =k!\begin{pmatrix} N \\ k \end{pmatrix}\int _{\mathbb {R}^{2k}}\mathrm{d}p_{1}...\mathrm{d}p_{k}\int _{\mathbb {R}^{2(N-k)}}\left|\mathcal {F}_{\hbar }\left[ F_{x_{1},0}(\cdot )\otimes ...\otimes F_{x_{k},0}(\cdot )\Psi _{N}(\cdot , z)\right] (p_{1},...,p_{k})\right|^{2}\mathrm{d}z\\&\quad =k!\begin{pmatrix} N \\ k \end{pmatrix}\int _{\mathbb {R}^{2k}}\left|F_{\hbar _{x}}(y_{1}-x_{1})...F_{\hbar _{x}}(y_{k}-x_{k})\Psi _{N}(y)\right|^{2}\mathrm{d}y_{1}...\mathrm{d}y_{N}\\&\quad =k!\hbar ^{2k}\rho ^{(k)}_{\Psi _{N}}*\left( |F_{\hbar _{x}}|^{2}\right) ^{\otimes k}(x_{1},...,x_{k}). \end{aligned}$$

which gives (3.4). The proof of (3.5) is similar. $\quad \square$