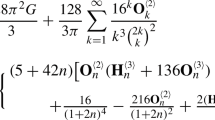Abstract
We use bounds on bilinear forms with Kloosterman fractions and improve the error term in the asymptotic formula of Balazard and Martin (Bull Sci Math 187:Art. 103305, 2023) on the average value of the smallest denominators of rational numbers in short intervals.
Similar content being viewed by others
1 Introduction
Given an integer \(N \geqslant 1,\) and \(j =1, \ldots , N,\) we denote by \(q_j(N)\) the smallest integer q such that, for some a, we have
Next, we consider the average value
Recently, Balazard and Martin [2] have confirmed the conjecture of Kruyswijk and Meijer [10] that
and in fact established the following much more precise asymptotic formula
see [2, Equation (1)]. Note that the asymptotic formula (1.1) improves on previous upper and lower bounds of Kruyswijk and Meijer [10] and Stewart [13], for example on the previous inequalities
in [13] (note that \(16/\pi ^2 = 1.6211 \ldots \)). For other related results, see [1, 4, 5, 7, 11, 12] and references therein.
The bound on the error term in (1.1) is based on the classical bound of Kloosterman sums, see, for example, [9, Corollary 11.12].
Here, we use bounds on bilinear forms with Kloosterman fractions due to Duke et al. [6], and improve the error term in the asymptotic formula (1.1) as follows.
Theorem 1.1
We have
as \(N\rightarrow \infty .\)
2 Preliminary reductions
As usual, we use the expressions \(U \ll V\) and \(U=O(V)\) to mean \(|U|\le c V\) for some constant \(c>0\) which throughout this paper is absolute.
We have
where by [2, Equations (19), (20), and (21)], we can write
for some quantities \(T_{11}(N),\) \(T_{12}(N),\) and \(T_{2}(N)\) which are estimated in [2] separately. In particular, by [2, Equations (23) and (26)], we have
Therefore, the error term in (1.1) comes from the bound
given by [2, Equation (22)].
We now see from (2.1), (2.2), and (2.3) that in order to establish Theorem 1.1 we only need to improve (2.4) as
We first recall the following expression for \(T_{11}(N)\) given in [2, Section 5.3]:
with the Bernoulli function
where \(\{u\}\) is the fractional part of a real u, the inversion \( r^{-1}\) in the fractional part \(\{N r^{-1}/s\}\) is computed modulo s, and \(R_s\) is a certain sequence of positive integers, satisfying
(we refer to [2] for an exact definition, which is not important for our argument).
It is more convenient for us to work with the function
which coincides with \(B_1(u) \) for all \(u \not \in {{\mathbb {Z}}}.\)
In particular,
unless \(s \mid N.\)
Using the classical bound on the divisor function
for a positive integer \(k \rightarrow \infty \) (see, for example, [9, Equation (1.81)]), we infer from (2.6) that
where
and, using (2.7),
3 Vaaler polynomials
For a real z, let \(\mathbf {\,e}(z) = \exp (2 \pi z)\). By a result of Vaaler [14], see also [8, Theorem A.6], we have the following approximation of \(\psi (u).\)
Lemma 3.1
For any integer \(H\geqslant 1,\) there is a trigonometric polynomial
for coefficients \(a_h\in [0,1]\) and such that
4 Bilinear forms with Kloosterman fractions
Here we collect some estimates on bilinear forms with exponentials \( \mathbf {\,e}\left( hr^{-1}/s\right) \) where, as before, \( r^{-1}\) in the argument is computed modulo s.
For \(U\geqslant 1,\) we also use \(u \sim U\) to indicate \(U \leqslant u < 2U.\)
We start with recalling the following bound of Duke et al. [6, Theorem 1].
Lemma 4.1
For sequences \({\varvec{\alpha }}= \{\alpha _r\}_{r=1}^\infty ,\) \({\varvec{\beta }}= \{\beta _s\}_{s=1}^\infty \) of complex numbers, a nonzero integer K, and real positive R and S, we have
where
Next, given two sequences of complex numbers
a sequence of positive integers
and an integer h, for \(S \geqslant 1,\) we define the bilinear form
Note that in the sums \({\mathscr {B}}_K(S; {{\mathcal {R}}}, {\varvec{\alpha }}, {\varvec{\beta }})\) the range of summation over r depends on s and hence Lemma 4.1 does not directly apply.
We observe that for
the argument in [2, Section 3] (in which we also inject the bound (2.8)) immediately implies that for
we have
Note that one can also derive (4.2) via [6, Lemma 8] and partial summation.
In fact, using the bound (4.2) for \(S \leqslant N^{2/3}\) and the trivial bound
in our argument below, one recovers the asymptotic formula (1.1). However, using some other bounds, we achieve a stronger result.
We also remark that for us only the choice of \({\varvec{\alpha }}= \{\alpha _r\}_{r=1}^\infty \) satisfying (4.1) matters. However we present the below results for a more general \({\varvec{\alpha }}\) (but still they admit even more general forms).
Using Lemma 4.1 together with the standard completing technique, see, for example, [9, Section 12.2], we derive our main technical tool.
Lemma 4.2
For sequences \({\varvec{\alpha }}= \{\alpha _r\}_{r=1}^\infty ,\) \({\varvec{\beta }}= \{\beta _s\}_{s=1}^\infty \), and \({{\mathcal {R}}}= \{R_s\}_{s=1}^\infty ,\) a nonzero integer K and real S with
and
we have
where
Proof
Note that
Using the orthogonality of exponential functions, we write
Using that
see [9, Equation (8.6)], we derive
It remains to observe that, for each \(u = 0, \ldots , R-1,\) the bound of Lemma 4.1 applies to the inner sum and implies
Recalling (4.3), this now simplifies as
which concludes the proof. \(\square \)
Remark 4.3
Instead of using Lemma 4.1, that is, essentially [6, Theorem 1], one can also derive a version of Lemma 4.2 from [6, Theorem 2], or from a stronger result due to Bettin and Chandee [3, Theorem 1]. However these bounds do not seem to improve our main result.
5 Proof of Theorem 1.1
As we have noticed in Section 2, it is enough to only estimate \(T_{11}(N),\) as we borrow the bounds on \(T_{12}(N)\) and \(T_{2}(N)\) from [2]. Furthermore, we see from (2.9) and (2.11) that it is enough to estimate U(N) given by (2.10).
We note that it is important to observe that the sum defining \(\psi _H(u)\) in Lemma 3.1 does not contain the term with \(h=0,\) while the sum on the right hand side of (3.1) does. Hence, for any integer \(H\geqslant 1,\) by Lemma 3.1, we have

Note that \(R_s\geqslant 1\) implies \(s \ll N.\) Therefore, partitioning the corresponding summation over s into dyadic intervals, we see that there is some integer S with
and such that
where
Now, if \(S \leqslant H^{1/5} N^{3/5},\) then we use the bound (4.2) and easily derive
On the other hand, for \(S > H^{1/5} N^{3/5},\) Lemma 4.2 (used with \(A\ll N/S\) and \(B \ll 1\)), after recalling that \(R \ll N/S,\) implies the same bound:
Therefore, recalling that \(S > H^{1/5} N^{3/5},\) we obtain
Therefore, the bound (5.2) holds for any S. Substituting (5.2) in (5.1) yields
and choosing

to optimise the bound, we obtain
Finally, recalling (2.9) and (2.11), we derive (2.5) and conclude the proof.
References
Artiles, A.: The minimal denominator function and geometric generalizations. arXiv:2308.08076 (2023)
Balazard, M., Martin, B.: Démonstration d’une conjecture de Kruyswijk et Meijer sur le plus petit dénominateur des nombres rationnels d’un intervalle. Bull. Sci. Math. 187, Paper No. 103305, 22 pp. (2023)
Bettin, S., Chandee, V.: Trilinear forms with Kloosterman fractions. Adv. Math. 328, 1234–1262 (2018)
Burrin, C., Shapira, U., Yu, S.: Translates of rational points along expanding closed horocycles on the modular surface. Math. Ann. 382, 655–717 (2022)
Chen, H., Haynes, A.: Expected value of the smallest denominator in a random interval of fixed radius. Int. J. Number Theory 19, 1405–1413 (2023)
Duke, W., Friedlander, J., Iwaniec, H.: Bilinear forms with Kloosterman fractions. Invent. Math 128, 23–43 (1997)
El-Baz, D., Lee, M., Strömbergsson, A.: Effective equidistribution of primitive rational points on expanding horospheres. arXiv:2212.07408 (2022)
Graham, S.W., Kolesnik, G.: Van der Corput’s Method of Exponential Sums. Cambridge University Press, Cambridge (1991)
Iwaniec, H., Kowalski, E.: Analytic Number Theory. American Mathematical Society, Providence (2004)
Kruyswijk, D., Meijer, H. G.: On small denominators and Farey sequences. Ned. Akad. Wet. Proc. Ser. A 80, 332–337 (1977)
Marklof, J.: Fine-scale statistics for the multidimensional Farey sequence. In: Limit Theorems in Probability, Statistics and Number Theory, pp. 49–57. Springer Proc. Math. Stat., 42. Springer, Berlin (2013)
Marklof, J.: Smallest denominators. Bull. London Math. Soc., to appear (2024)
Stewart, C.L.: On the distribution of small denominators in the Farey series of order \(N\). In: Kotsireas, I.S., Zima, E.V. (eds.) Advances in Combinatorics, pp. 275–286. Springer, Berlin (2013)
Vaaler, J.D.: Some extremal functions in Fourier analysis. Bull. Amer. Math. Soc. 12, 183–215 (1985)
Acknowledgements
The author is very grateful to Michel Balazard, Bruno Martin, and Jens Marklof for encouragement and very stimulating discussions and comments. The author also would like to thank the referee for a careful reading, which revealed some inaccuracies in the original version of the paper. During the preparation of this work, the author was supported in part by the Australian Research Council Grant DP230100534.
Funding
Open Access funding enabled and organized by CAUL and its Member Institutions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Shparlinski, I.E. Rational numbers with small denominators in short intervals. Arch. Math. (2024). https://doi.org/10.1007/s00013-024-01993-z
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00013-024-01993-z