1 Introduction

Transition metal mononitrides (TMMN) of 3d TM are an interesting class of compounds known to exhibit several interesting properties such as refractory nature, high electrical conductivity and chemical stability, applications as catalysis, energy storage and conversion and more recently in plasmonics [1,2,3,4,5]. Most of these properties are exhibited by early TMMN, viz. ScN, TiN, VN and CrN. In recent years, late TMMN, in particular CoN, have also been explored as an emerging material in renewable and sustainable energy. Though initial experimental research works on CoN were more curiosity driven [6,7,8,9], in recent years, it has been shown that CoN can be used as a high capacity anode in Li-ion batteries [10, 11], as a non-aqueous supercapacitor [12], as a low-cost catalyst for oxygen and hydrogen evolution reaction (OER and HER) required for electrocatalysis and water splitting [13,14,15,16,17] and for mesoscopic and perovskite solar cells [18].

Table 1 Lattice parameter (LP) and structure of CoN thin films grown using different methods and using different calculation methods [full-potential local density approximation(FP-LDA), generalized gradient approximation by Perdew–Burke–Ernzerhof (GGA-PBE)]
Full size table

Therefore, it is essential to have a deeper understanding of the structural and the magnetic properties of cobalt nitrides (Co–N). Co–N compounds are known to form in a variety of compositions and structures. Major Co–N phases that have been identified are: Co\(_{16}\)N\(_2\)(bct), Co4N(fcc), Co\(_3\)N(hcp), Co\(_2\)N (orthorhombic), CoN(fcc), CoN\(_2\)(marcasite—type). Among these, the Co\(_{16}\)N\(_2\) phase is being explored recently [24], Co\(_2\)N and Co\(_3\)N have been studied by several co-workers  [25,26,27,28,29]. The N-rich CoN\(_2\) phase was recently synthesized under high pressure high temperature (30 GPa, 1600 K) [30]. In this work, we will focus on the cobalt mononitride (CoN) phase only.

Though early TMMN are known to crystalize in a common rock-salt (RS)-type structure [31], late TMMN such as FeN and CoN exhibit a different behaviour as they are debated to crystalize in a zinc-blende (ZB) and a RS-type structure [21]. In the ZB-type structure, both FeN and CoN are non-magnetic. The RS-type FeN is expected to possess a nonzero magnetic moment, but in the RS-type CoN, a finite magnetic moment is expected only under a lattice expansion [21]. Among the late TMMN, FeN is the most studied compound yet its structural and magnetic ground state is still debated [32, 33].

From recent experimental works, it can be observed that FeN crystalizes in the ZB-type structure only (under ambient pressure and temperature) and the existence of the RS-type FeN has been questioned in several recent works [34,35,36]. Though theoretical works predict both ZB- and RS-type structures for FeN and CoN, but under ambient temperature and pressure, the ZB-type structure is preferred [21]. The energy minima in the total energy-volume plots is lower in ZB, as compared to that in RS CoN [21, 22, 37,38,39,40]. Under high pressure, a phase transition from ZB- to RS-type phase is expected at about 50 GPa in FeN [33] and about 40 GPa in CoN [22].

From a brief review of CoN compounds (see Table 1), it can be seen that the assignment to the RS- or ZB-type structure and associated lattice parameter (LP) is random. In early works, Dumont and Kron [19] obtained CoN by thermal decomposition of the cobalt amide—Co (NH\(_2\))\(_3\) and found RS-type structure with a LP = 4.27 Å from X-ray diffraction (XRD) measurements. Subsequently, Taylor et al. [23] prepared CoN by thermal decomposition of cobalt ammine azide [Co (NH\(_3\))\(_6\)](N\(_3\))\(_3\) and reported ZB-type CoN with LP = 4.28 Å. More recently, in a pioneering work seeking the structural and magnetic properties of CoN, Suzuki et al. [6] deposited CoN thin films on a Cu substrate using reactive dc sputtering of Co with a mixture of Ar + N\(_2\) gases. The film was stripped from the substrate and treated with nitric acid and annealed at 410 K for 6 h in vacuum. Thereafter, powdered samples were measured using XRD. By comparing the experimental data with theory for the ZB- and RS-type structures, they confirmed ZB-type CoN with LP = 4.297 Å. From detailed low-temperature measurements, they reported that CoN exhibits a Pauli paramagnetic character [6].

In recent years, Das et al. performed nitridation of cobalt tetraoxide Co\(_3\)O\(_4\) and NiCo\(_2\)O\(_4\) in the presence of NH\(_3\) + N\(_2\) and claimed RS-type CoN in Ni-doped CoN nanoparticles with LP = 4.295 Å from XRD and Co K-edge XANES measurements [10, 11]. Liu et al. [20] prepared epitaxial CoN thin films on SrTiO\(_3\) and sapphire substrates using laser ablation method, and from XRD measurements they found that the LP of their CoN samples was 4.27 Å. They also performed low-temperature magnetization measurements and claimed RS-type CoN due to appearance of a para-to-antiferromagnetic transition \(\approx\) 310 K. Very recently, Kang et al. [18] prepared CoN samples by rf sputtering on fluorine-doped tin oxide (FTO)-coated glass and indium tin oxide (ITO)/polyethylene naphthalate (PEN) substrates. They found a strong pre-edge feature in Co K-edge XANES spectra indicating that Co atom has tetrahedral symmetry which is expected in ZB-type CoN. A summary of these experimental works is shown in Table 1 and compared with recent theoretical predictions. CoN samples have also been prepared in some other works, but structural information (RS or ZB) was not provided [7,8,9, 14, 41].

It is to be noted that in most of the experimental works performed so far, the structure of CoN was identified using XRD only. The LP of CoN in RS- and ZB-type structures was found to be almost similar around 4.29±0.02 Å, the only difference between the ZB and RS structures is arrangements of N atoms—tetrahedral in ZB and octahedral in RS. Therefore, the difference in the structure factor leads to a variation in relative intensities, e.g. in ZB-type structure, the intensity of (111) reflection would be highest, whereas in RS-type structure (200) reflection would become most intense. In the case of powdered samples, this analogy holds good (as demonstrated by Suzuki et al. [6]) but in the case of epitaxial or polycrystalline films with a preferred orientation such analogy about relative intensity would not work and alternative ways should be explored to establish the structure of CoN thin films. This can be easily achieved utilizing X-ray absorption fine structure (XAFS) techniques—XANES and EXAFS measurements at a synchrotron radiation source [42].

In the present work, we performed reactive dcMS (dc magnetron sputtering) of a Co target using N\(_2\) alone as the process gas (no Ar) at room temperature (300 K) to get polycrystalline CoN thin films on Si (100) and amorphous quartz substrates. The synthesis of CoN using chemical route involves expensive and toxic cobalt-based compounds [11]. Reactive sputtering on the other hand is a clean, reproducible and industry-friendly method to synthesize CoN from the metal Co target. We employed various techniques to investigate the structural and magnetic properties of CoN thin films. Moreover, to probe the local structure in CoN thin films, XAFS measurements performed both at Co and N K-edge are also presented.

2 Experimental and theoretical procedures

Thin films of CoN were deposited using a home-made sputtering system, and a Co (\(\phi\) 2 in., purity 99.95\(\%\)) target was sputtered from a magnetron source (Angstrom Sciences) in N\(_2\) (purity 99.9995\(\%\)) environments. The sputtering power was fixed at about 45 W (2.2 Wcm\(^{-2}\)), and samples were deposited at ambient temperature (300 K) without any intentional heating. As shown recently, that N diffuse out from CoN even when the substrate temperature is raised marginally, it is essential to keep substrates at room temperature to grow the desired CoN phase [43]. With a base pressure of about 1\(\times\)10\(^{-7}\) hPa, the pressure during deposition was about 5\(\times\)10\(^{-3}\) hPa due to the flow of N\(_2\) gas at 50 sccm. Samples were deposited on a high-quality amorphous quartz and Si (100) (both from Matsurf-Tech) substrates simultaneously. Substrates were continuously rotated at a speed of 30 rpm, and film thickness of about 100 nm was achieved in 1 h. Prior to deposition of final samples, several samples were deposited to achieve optimum growth conditions to attain the CoN phase [44]. Samples of size typically 5 cm\(^2\) were deposited on Si and amorphous quartz substrates simultaneously and small samples (about 1 cm\(^2\)) cut from these were subject to different measurements that are reported in this work.

The structure of samples deposited on amorphous quartz substrates was determined using X-ray diffraction (XRD) using a standard diffractometer (Bruker D8 Advance) and using Cu-\(K_{\alpha }\) X-rays in \(\theta\)–2\(\theta\) mode. X-ray absorption near-edge spectroscopy (XANES) measurements at N K-edge were performed at the soft X-ray absorption spectroscopy (SXAS) beamline BL01 of Indus 2 synchrotron radiation (SR) source at RRCAT, Indore, India [45]. They were performed in the total electron yield (TEY) mode under ultra-high vacuum conditions.

XANES and extended X-ray absorption fine structure (EXAFS) measurements at Co K-edge were carried out under ambient conditions at the P64 beamline [46] of Petra III, DESY, Hamburg, Germany. These measurements were performed in the fluorescence geometry, and the integrated fluorescence (I\(_{\mathrm {f}}\)) from the sample was measured with a passivated implanted planar silicon detector. The upstream beam intensity (I\(_{\mathrm {0}}\)) was measured with a gas ionization detector filled with pure nitrogen. The normalized absorption was obtained using the expression I\(_{\mathrm {f}}\)/I\(_{\mathrm {0}}\). The incident flux on the sample was about 10\(^{12}\) photons/sec, and absorption in the upstream ionization chamber was 8% at 7000 eV, which is in the range where the beamline detector operates linearly. The dark current is properly offset, and no counts in the I\(_{\mathrm {0}}\) or I\(_{\mathrm {f}}\) were observed in the absence of X-ray beam. Energy calibration of a Si(111) monochromator was performed using an iron foil. The first inflection point in the absorption spectrum of iron foil was assigned to 7112 eV. Frequent measurement on iron foil was carried out to check the monochromator calibration, which was found to be stable during the entire experiment with nearly identical edge positions found for all the measurements. For the XANES and EXAFS measurements, samples of 10 mm\(\times\)10 mm were sliced from the 50 mm\(\times\)50 mm sample. The beam size on the samples was about 1 mm\(\times\)1 mm. Radiation damage on the samples was checked by measuring the spectrum at a different spot. Since no variation in the near-edge feature and EXAFS oscillation could be observed, any damage due to radiation can be ruled out. Multiple XAFS scans (six/twelve) were performed on each sample at a fixed beam spot, and the total measurement time was about 30 minutes. Lousy data points occurred in the spectrum due to the monochromator glitches were removed, and the polynomial interpolation was used to connect the stripped region.

Standard procedure was employed to carry out pre-edge and post-edge background subtraction [47]. The normalization of the data was performed by simulating a Victoreen polynomial function obtained from the regression of the absorption spectrum in the pre-edge region. The polynomial was then extrapolated to the end of the absorption spectrum and subtracted from the data. For the extraction of the EXAFS signal, an atomic-like background was calculated in the post-edge region using a polynomial spline of third order with three knots. The positions of knots were then optimized to remove the low-frequency background between 0-1 Å. The EXAFS fits were performed in the k-space in the range 3-13 Å\(^{-1},\) and five shells were used to fit the spectrum in the R-range between 1.1–4.5 Å  covering first three shells of ZnS-type CoN, respectively, for Co–N (1.87 Å), Co–Co (3.03 Å), and Co–Co (4.25 Å). The number of independent fitting parameters for this range is about 21. The EXAFS fitting was performed to derive metrical parameters for each shell, such as atomic pair distance (R), root–mean–square relative displacement (\(\sigma\)), coordination number(N), and relative change in \(E_0\) (\(\Delta E_0\)). For the five shells, it gives a total number of parameters 20, among which the parameter \(\Delta E_0\) for the first shell is varied independently, and its value for all the shell was kept constrained to vary between ±1 relative to the value obtained from the fits for the first shell. In the absence of a bulk CoN sample, the value of passive electron reduction factor (\(S_0^2\)) cannot be estimated, which usually varies between 0.8–0.9. Therefore, it was fixed at an average value of 0.9, which may give some errors in the estimation of the actual coordination number. However, it does not influence the results obtained in this work. The EXAFS fitting and background subtraction of the data was performed using the software written by Conradson et al. [48]. The photoelectron backscattering amplitude and phase-shift for different Co–N and Co–Co shells on ZB-type CoN and Co\(_2\)N phases were theoretically calculated using the FEFF9 code [49].

XANES spectra at Co K-edge and N K-edge were theoretically calculated using real-space multiple-scattering formalism using FDMNES code [50]. The lattice parameters for ZB- and RS-type structure of CoN were kept at 4.32 Å which is obtained from the XRD. Self-consistent calculations were performed to determine the Fermi energy. Hedin–Lundqvist exchange correlation potential was used for the simulation. The convolution of XANES spectra was performed using theoretically determined core hole width. The simulation is carried out for the atomic cluster with the radius of 9 Å.

Magnetization measurements were performed using a Quantum Design made SQUID-VSM (S-VSM) magnetometer and polarized neutron reflectivity (PNR) at AMOR, SINQ, PSI, Switzerland, in time of flight mode using Selene optics [51, 52]. Thermal stability of samples was studied by using an ultra-high vacuum (base pressure 1\(\times\)10\(^{-9}\) hPa) rapid thermal annealing system, and they were annealed for 1 h at each temperature. XRD and N K-edge XANES measurements were carried out in annealed samples.

3 Results and discussion

XRD measurements carried out on pristine and vacuum annealed samples are shown in Fig. 1. In the pristine sample, a broad peak appears around 35.95\(^{\circ }\) and it can be assigned to CoN (111) (JCPDS No. 830831), yielding lattice parameter (LP) = 4.32(\(\,\pm\)0.01) Å. The LP of our sample has been compared to CoN samples grown using different methods and also with theoretical calculations as shown in Table 1. Here, it can be seen that the theoretical value LP in RS- and ZB-type structure is around 4.0 and 4.27 Å, respectively, and experimental values 4.29(\(\,\pm\)0.03) Å are much more closer to the ZB-type rather than to the RS-type CoN. Therefore, assignment to RS-type structure on the basis of LP appears dubious.

The crystallite size calculated using Scherrer formula comes out to be \(\approx\) 8 nm. It may be noted that samples were deposited at ambient temperature and their thickness was only about 100 nm; this may lead to the formation of a nanocrystalline structure in the sample. Further, the peak profile appears somewhat asymmetric which may be due to some defects or vacancies. Similar defects or vacancies were also observed in FeN samples and characterized using Mössbauer spectroscopy measurements [34, 36]. Unlike FeN, the absence of Mössbauer nuclei in CoN makes it difficult to probe such defects or vacancies. After annealing the pristine sample at 473 K, the peak shifts marginally to 2\(\theta\) \(\approx\) 36.10\(^{\circ }\), reducing LP to 4.30(\(\,\pm\)0.01) Å. Such reduction in LP can be due to relaxation of quenched-in voids that get generated during thin film growth. After annealing at 523 K, the peak corresponding to CoN (111) almost disappears and peaks corresponding to hcp Co start to appear and they get more intense when annealing temperature was further raised to 573 K. Thermal stability of our CoN thin films is in agreement with previous works [6, 41, 53].

The thermal stability behaviour can be understood comparing the enthalpy of formation energy (\(\Delta H_f^{\circ }\)) of CoN together with other metal nitrides. For several nitrides \(\Delta H_f^{\circ }\) (in eV/atom) is negative, \(-\,0.5\) for FeN [54], \(-\,1.2\) for CrN [55], \(-\,3.5\) for TiN [56] but for CoN it is \(\approx\) 0 [57]. Therefore, early TMMN such as CrN and TiN are easy to form but difficult to decompose but CoN would be difficult to synthesize but gets decomposed easily upon heating. The decomposition temperature for early TMMN exceeds 1000 K [58], whereas for FeN it is about 600 K [36, 59] and for CoN even less (450–500 K) [6]. In fact as shown in a recent work, when Co–N films are deposited using reactive sputtering at 523 K, resulting films resemble pure Co rather than any Co–N phase [53]. Though poor thermal stability of CoN is a concern, it is a boon as well for its usage in catalytic reactions [60].

Fig. 1
figure 1

X-ray diffraction pattern CoN thin film grown at 300 K (pristine). The inset compares XRD patterns of pristine and vacuum annealed samples. They were annealed at different temperatures for 1 h in a vacuum furnace

Full size image

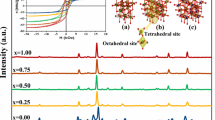
In order to further explore the local structure, we did N K-edge XANES and Co K-edge XANES and EXAFS measurements. Figure 2 shows N K-edge XANES of CoN thin films in the pristine state and after annealing at 523 K. In the pristine state, prominent N K-edge can be seen and features present there are marked as a, b, c and d. Features a and b correspond to transition from N 1s to hybridized states of Co 3d and N 2p, and features c and d appear due to due to electronic transition from N 1s to hybridized N 2p and Co 4sp states. The N K-edge features in our case are similar to those in ZB-FeN [59]. In a octahedral symmetry (RS) due to crystal-field splitting, the edge features split into two—t\(_{2g}\) and e\(_g\) states, whereas as in tetrahedral (ZB) symmetry, the crystal-field splitting is reversed and they are denoted by e and t\(_2\) (the gerade—g label is removed as symmetry is non-centrosymmetric). Such features have been clearly resolved in the case of early TMMN such as TiN [61] and CrN [55, 62]. The absence of any significant splitting around feature a is a clear indication of tetrahedral coordination of Co atoms surrounding N atoms. It may be noted that though N K-edge features have been studied in several works for early TMMN [63], for CoN they have not been reported hitherto. After annealing at 523 K, all N features disappear which can happen only if N is diffusing out from CoN leaving behind Co.

Fig. 2
figure 2

N K-edge XANES of CoN thin film in the pristine state and after annealing at 523 K. The inset shows simulated N K-edge XANES of CoN in RS- and ZB-type structures along with their schematic representations

Full size image

N K-edge was also generated using FDMNES code for CoN in ZB- and RS-type structures as shown in the inset of Fig. 2. Analogous to the experimental case, prominent features in simulated spectrum are also assigned as a, b, c and d. It can be seen that the feature b is more pronounced in RS and weaker in ZB-type CoN. Qualitatively, theoretically simulated N K-edge features resemble with experiment, but their energy difference with respect to a does not match. The separation between the first two features (a and b), i.e. 10Dq, comes out to be about 1.5 eV from simulations but experimentally, it is much larger at about 4 eV. Such difference between theory and experiments can also be observed in other nitrides, e.g. in CrN, VN and NbN theoretical values of 10Dq are 0.8, 1.1 and 2 eV [63, 64], respectively, whereas experimental values were about 3 eV for CrN [55, 65], 2.7 eV for VN [66] and 3.5 eV for NbN [67]. Therefore, combing the resemblance of our N K-edge spectra in CoN together with that of ZB-FeN and to the simulated spectra for ZB-CoN, it appears that the structure of CoN in our samples is closer to ZB-type.

Fig. 3
figure 3

Co K-edge XANES of CoN thin film sample in the pristine state compared with a bulk Co reference. The inset shows simulated Co K-edge XANES of CoN in RS- and ZB-type structures. Here, Co (ref.) corresponds to a Co foil with hcp structure

Full size image

We also did Co K-edge XANES and EXAFS measurements to further confirm the structure of our sample as shown in Fig. 3. The presence of an intense pre-edge feature can be clearly seen in the near-edge region and is indicative of tetrahedral coordination expected in ZB-type CoN. The inset of Fig. 3 compares experimental XANES spectrum together with theoretically simulated spectra for CoN in RS- and ZB-type structures. Clearly, our experimental data resembles well with ZB-type CoN. It must be noted that the intensity of pre-edge features in the experimental spectrum is lower compared to the theoretically calculated spectra. The smearing of pre-edge features is the cumulative effect of broadening due to instrumental resolution, and nanocrystalline structure of the sample, as also observed in other metallic nanoparticles [68,69,70].

To get quantitative information, EXAFS pattern (of the same sample as shown in Fig. 3) was fitted and is shown in Fig. 4; and obtained metrical fitting parameters are listed in Table 2. At the starting model, the EXAFS fitting was performed with the first three shells in the ZB-type CoN. The value of \(\sigma\) for the higher-order shells is constrained to vary between ±0.02 relative to the previous shell, and other parameters were kept free to vary except the \(\Delta\)E\(_0\) and the \(S_0^2\) as discussed in the experimental section. In the ZB-type CoN, Co atoms are tetrahedrally coordinated with N atoms. The bond lengths for Co–N bond were found to be about 1.87 Å and for the Co–Co bond it was about 3.0 Å and 4.25 Å for the second and third coordination shells. The first peak around 1.6 Å in the FT spectra is attributed to the Co–N shell, and the EXAFS fitting shows the Co–N bond distance is about 1.87 Å. The FT peak between 2–3 Å can be attributed to the Co–Co shell. However, it was observed that in this region, the FT peak is quite broad and slightly different on comparing it with the spectrum reported by Kang et al. [18] on relatively thick ZB-type CoN films. Further, it can be seen from Fig. 4 that the peak shoulder between 2–2.6 Å has a significantly higher amplitude. It results in the presence of a significant residual component between 2–2.6 Å, and 3–3.5 Å. The inclusion of Co–Co shell at 2.57 Å and 3.54 Å significantly improves the quality of the fit. The amplitude and phases of additional shells were obtained by performing the FEFF calculation on Co\(_2\)N having Co–Co shells at similar distances. With this approach, the value of the coordination number for the higher Co–Co shells was found to be smaller relative to the bulk. It is interesting to note that the value of N for the first Co–N shell is slightly smaller compared with the ideal tetrahedral geometry. For lower Co–N phases or RS-type CoN, the value of N is six due to octahedral geometry. Slightly lower coordination number from the ideal tetrahedral geometry can be attributed to the atomic defects and nanometre-sized particles [71].

Fig. 4
figure 4

Fourier-transform moduli of the Co K-edge EXAFS (\(|\chi (R)|\)) and real component (Re\([\chi (R)]\)) of the data and fit. Lower inset shows individual components of the fit which are inverted for clarity. Upper inset shows \(\chi (k) \times k^3\) data and fit. \(R-\phi\) is phase-shift-uncorrected atomic pair distance

Full size image
Table 2 EXAFS metrical parameters derived from nonlinear least-square fits for CoN thin films measured at Co K-edge
Full size table

Alternatively, we have also modelled the EXAFS fitting by constraining the N for Co–Co shell of ZB-type structure to vary between ±0.5 relative to thrice the value of N for the first Co–N shell and half the value of this shell, respectively, for Co–Co shells at 3.0 Å and 4.25 Å (see electronic supplementary malarial [72], fig. S1; table ST1). With this approach, we observed that the value of coordination number for higher Co–Co shell comes close to the bulk; however, the value of \(\sigma\) inflated to twice the value observed for the first Co–N shell. Moreover, the coordination number for the additional shell at 3.54 Å  is found to be extremely small, and the shell distance at 2.57 Å is shifted to 2.63 Å. A four shell fitting to the data excluding second extra shell was also tried (see electronic supplementary malarial [72] fig. S2; table ST1). This fitting approach indicates that a strong correlation exists between the EXAFS parameters, such as N and \(\sigma\). Therefore, additional fitting constraints are required to obtain the absolute value of the coordination number. Moreover, in the thin films, various parameters such as particle size distribution, defects and disorder can correlate with the EXAFS amplitude, and hence accurate estimation of coordination number is challenging [71, 73, 74].

The EXAFS fitting was also modelled by incorporating the higher-order cumulants for the additional shell at 2.57 Å(see electronic supplementary malarial [72] fig. S3; table ST1) [74, 75]. It was observed that the fitting improved significantly with the inclusion of the third cumulant. However, due to its correlation with the phase, the shell distance was found at 2.82 Å. The multiple EXAFS modelling suggests that the absolute value of the coordination number is difficult to obtain. Besides, the additional shell is highly disordered and may have an anharmonic distribution of atomic pair distance. Therefore, it cannot be attributed to any Co–N phases. Such highly disordered Co–Co atomic pairs can be observed around the defects and vacancies sites. The local region around these defects can adopt the local structure of lower (than CoN) concentration nitride phases to minimize the energy and can give similar pair distances.

The above analysis implies that the CoN crystallizes in the ZB-type structure. However, deposition condition can influence the defects and disorder in the sample. It can give distinct local structure; however they are localized in the proximity of defects sites. These findings corroborate with the XANES, XRD and magnetization results discussed as follows. The absence of additional XRD peaks suggests that the extra Co–Co shell is not the part of any crystalline domains and remains as a disordered or non-crystalline phase. Moreover, the magnetization measurements show absence of any magnetic component which ruled out the possibility of any lower (magnetic) Co–N phases. It is to be emphasized that the use of pure nitrogen as the sputtering gas will preclude the formation of isolated metallic clusters of Co with 1–2 nm particle size. Such nanoparticle clusters will be highly reactive in the nitrogen plasma. Therefore, its presence in the sample can be ruled out.

Magnetization and the magnetic ground state of mononitrides of Fe and Co, i.e. FeN and CoN, have been a long-standing concern and have been often correlated with the structure. For FeN, it is anticipated that it will be paramagnetic (PM) in the ZB-type structure but would have some magnetic ordering, i.e. ferromagnetic (FM) or antiferromagnetic (AFM) in the RS-type structure [76]. However, CoN is expected to remain PM even in the RS-type structure unless it is forced to adopt an expanded lattice [21, 76]. Therefore, recent experimental results show a PM-to-AFM transition around 310 K, and based on such transitions claiming the structure to be RS-type needs to be investigated further [20]. Anticipating the complexity of this issue, we not only used bulk magnetization methods (S-VSM) but polarized neutron reflectivity (PNR) technique as well to probe magnetism in our CoN samples. As a reference, a Co thin film sample that was prepared under identical conditions (but using Ar instead of N\(_2\)) was also measured.

PNR is a well-known technique to probe magnetization and magnetic depth profiles of thin film sample. In this technique, substrate magnetization (often diamagnetic as in present case for Si substrate) does not interfere with sample magnetization. Neutrons are spin \(\frac{1}{2}\) particles and possess quantization states that are aligned parallel or antiparallel (denoted by ‘+’ or ‘−’ ) with respect to the direction of applied external field (H). A dipolar interaction takes places between neutron magnetic moment and the magnetic field generated by unpaired spins [77]. The interaction potential is given by \(V_m=-\mu _n\cdot {\mathbf {B}}\), where magnetic induction \({\mathbf {B}} =H+4\pi M\), \(\mu _n\) is neutron magnetic moment and M is sample magnetization[78].

Fig. 5
figure 5

Polarized neutron reflectivity (PNR) measurements of CoN and Co thin film samples measured at 300 K (a). The inset of (a) compares the spin-asymmetry (SA = (R\(^+-R^-\))/(R\(^+\) + R\(^-\))) of experimental PNR data of CoN and Co samples. The zero field cooled (ZFC) and field cooled (FC) at H = 100 Oe magnetization (M)-temperature (T) plots of CoN thin film compared with M of Co measured at 300 K (b). The inset of b compares M–H loops of CoN and Co samples measured at 300 K

Full size image

The information about sample magnetization can be directly inferred by just observing the separation between spin-up (R\(^{+}\)) and spin-down (R\(^{-}\)) reflectivities at the critical value of wave vector transfer (\(q_c\)), given by \(q_c{^\pm } = \sqrt{(16\pi N(b_n\pm b_m)}\), where N is the number density, \(b_n\) and \(b_m\) are the nuclear and magnetic scattering lengths for neutrons [79]. As can be seen from Fig. 5a, the PNR pattern of the reference Co thin film sample exhibits well-separated R\(^{+}\) and R\(^{-}\) at \(q_c\), confirming the FM ordering in Co and yielding M = 1.6 \({\upmu _{\text{B}}}\) per Co atom which is expected in bulk Co [41]. But such separation cannot be seen in the CoN sample. In the PM state, \(b_m\) = 0, and therefore, R\(^{+}\) = R\(^{-}\). Thus, from our PNR measurements it can be directly seen that CoN sample adopts a PM state which is expected for CoN in ZB-type structure at 300 K [6]. This also becomes evident by comparing the spin-asymmetry (SA = (R\(^+-R^-\))/(R\(^+\) + R\(^-\))) of CoN and Co samples as shown in the inset of Fig. 5a. For CoN since R\(^{+}\) = R\(^{-}\), SA \(\approx\) 0, whereas for Co large separation between R\(^{+}\) and R\(^{-}\) is large near the critical q\(_{\mathrm {z}}\) due to large ferromagnetic moment of Co.

PNR patterns were fitted using SimulReflec [80] software and obtained fitting parameters are: thickness of CoN film = 95 nm, roughness \(\approx\)1 nm, film density \(\approx\) 6 g cm\(^{-3}\) and M = 0. The thickness, roughness and density of the film were also obtained from X-ray reflectivity measurements (not shown) and match well with PNR results.

Magnetization measurements were also performed using bulk magnetization method (S-VSM). The M-H hysteresis loops (taken at 300 K) for CoN and Co samples are compared in the inset of Fig. 5b. The saturation magnetization of Co sample comes out to be about 1100 emu cm\(^{-3}\) matching well with bulk Co, but for CoN, we can see that M \(\approx\) 0, which is in agreement with PNR results. We also did magnetization measurements by lowering the sample temperature down to 5 K under zero field cooled (ZFC) and field cooled (FC) conditions (at 100 Oe) and such M-T data are shown in Fig. 5b and again compared with Co magnetization value obtained at 300 K. As can be seen, the M of CoN remains at almost zero both in FC and ZFC cases. Therefore, it can be concluded from our magnetization data that CoN sample exhibited a paramagnetic behaviour down to 5 K.

4 Conclusions

The present study shows the systematic investigation of reactively sputtered CoN thin films grown at the ambient temperature. XRD analysis on the pristine film shows single diffraction peak that was attributed to the ZB-type CoN phase. The XRD peak was found to have an asymmetric shape which was assigned to the intrinsic defects introduced during the sputtering. Magnetization measurement does not show any signature of ferromagnetism. Experimental XANES spectra measured at N K-edge and Co K-edge were compared with the theoretically simulated spectra on the ZB- and RS-type CoN. It was observed that the near-edge features in the experimentally measured spectra are closely associated with the theoretically simulated spectra on ZB-type CoN. An intense pre-edge peak in the Co K-edge spectrum provides further evidence of tetrahedral coordination of Co in the sample. The local structure of Co was further investigated by performing the least-square fitting on the EXAFS data. The EXAFS fitting reveals that apart from the presence of Co–N and Co–Co atomic pairs similar to those found in the ZB-type CoN, additional Co–Co atomic pairs were observed. These extra Co–Co atomic pairs are attributed to the defects in the sample around which the Co has adopted local structure similar to the lower nitride phases.