Abstract
We present a statistical analysis of solar coronal mass ejections (CMEs) based on 23 years of quasi-continuous observations with the LASCO coronagraph, thus covering two complete Solar Cycles (23 and 24). We make use of five catalogs, one manual (CDAW) and four automated (ARTEMIS, CACTus, SEEDS, and CORIMP), to characterize the temporal evolutions and distributions of their properties: occurrence and mass rates, waiting times, periodicities, angular width, latitude, speed, acceleration and kinetic energy. Our analysis points to inevitable discrepancies between catalogs due to the complex nature of CMEs and to the different techniques implemented to detect them, but also to large areas of convergence that are critically important to ascertain the reliability of the results. The temporal variations of these properties are compared to four indices/proxies of solar activity: the radio flux at 10.7 cm (F10.7), the international sunspot number (SSN), the sunspot area (SSA), and the total magnetic field (TMF), either globally or separately in the northern and southern hemispheres in the case of the last three. We investigate the association of CMEs with flares, erupting prominences, active regions and streamers. We find that the CME occurrence and mass rates globally track the indices/proxies of solar activity with no time lag, prominently the radio flux F10.7, but the linear relationships were different during the two solar cycles, implying that the CME rates were relatively larger during SC 24 than during SC 23. However, there exists a pronounced divergence of the CME rates in the northern hemisphere during SC 24 as these rates were substantially larger than predicted by the temporal variation of the sunspot number. The distribution of kinetic energy follows a log-normal law and that of angular width follows an exponential law implying that they are random and independent. The distribution of waiting time (WTD) has a long power-law tail extending from 3 to 100 hr with a power-law index which varies with the solar cycle, thus reflecting the temporal variability of the process of CME formation. There is very limited evidence for periodicities in the occurrence and mass rates of CMEs, a striking feature being the dichotomy between the two hemispheres. Rather weak correlations are present among the various CME parameters and particularly none between speed and acceleration. The association of CMEs with flares and erupting prominences involves only a few percents of the overall population of CMEs but the associated CMEs have distinctly larger mass, speed, kinetic energy and angular width. A more pronounced association is found with active regions but the overwhelming one is with streamers further confirmed by the similarity between the heliolatitudinal distribution of CMEs and that of the electron density reconstructed from time-dependent tomographic inversion. We find no evidence of bimodality in the distributions of physical parameters that would support the existence of two classes, particularly that based on speed and acceleration, the distributions thus favoring a continuum of properties. There exists an excess of narrows CMEs which however does not define a special class. These narrow CMEs are likely associated with the ubiquitous mini-filaments eruptions and with mini flux ropes originating from small magnetic bipoles, the disruption mechanisms being similar to those launching larger CMEs. This supports the concept that CMEs at large arise from closed-field coronal regions at both large and small scales.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
No consensus has yet been achieved on a clear definition of coronal mass ejections (CMEs) formerly known as “transients” after their discovery in 1971. First attempts date back to 1984. Hundhausen et al. (1984) proposed a definition based on observations i.e., “an observable change in coronal structure that (1) occurs on a time scale of a few minutes and several hours and (2) involves the appearance of a new, discrete, bright, white-light feature in the coronagraph field of view”. In the first review on CMEs, Wagner (1984a) proposed a more physical description as “sudden expulsions of dense clouds of plasma from the outer atmosphere of the Sun” adding that “CMEs are a type of coronal transient, the general name given to the disruption of coronal structure” to make the link to the initial name. In his essay on terminology, Schwenn (1996) favored the definition of Hundhausen et al. (1984) simply suggesting to add “appearance and outward motion” to be more specific, “since it underlines the observational aspect, it stresses the transient event character, and it does not imply an interpretation of the feature and its potential origin”. Surprisingly, he ignored the proposal of Wagner (1984a) not even quoting it, and went on preferring the terminology “Solar Mass Ejections” (SMEs) following an early suggestion by Gosling et al. (1975). Schwenn (1996) also ignored another alternative definition of a CME as “a new, discrete brightening over a time-scale of tens of minutes which is always observed to move outward” (e.g., Webb and Hundhausen 1987; Webb and Howard 2012) which is implicitly connected to their visual appearance in the coronagraph field of view, but has the merit of being more concise and of mentioning the outward motion, but may be too restrictive as we now know that there exists very slow CMEs. The preference of the present authors would go to a physical definition along the lines of that proposed by Wagner (1984a), perhaps adding the presence of frozen-in magnetic fields (Howard and Simnett 2008) as a relevant feature. As a closing remark, none of the above definitions implies a size or a brightness so that attributes like “giant” or “spectacular” often found in the CME literature are irrelevant.
On the positive side, there is a consensus on the initiation of CMEs by a loss of equilibrium of a magnetic configuration in the solar corona (Priest 1988) and the conversion of magnetic free energy to radiative energy and kinetic energy that accelerates and propels the plasma cloud into the heliosphere. The process in which magnetic reconnection is though to play a fundamental role ends up in a reconfiguration of the disrupted magnetic fields. Several models have been proposed to explain the initial phase of eruption, notably the “mass-loading model” (Low 1996), the “catastrophe model” (Forbes 2000), the “breakout model” (Antiochos et al. 1999), and the “shearing arcade” model (Mikic and Linker 1994), see for instance Zhang and Low (2005) for a review.
CMEs attract considerable attention as they have far reaching consequences in solar, coronal, interplanetary, and planetary physics. From the viewpoint of solar and coronal physics, CMEs are fundamental to the understanding of how magnetic energy is built up, stored, and released in magnetic flux systems; they further provide mechanisms for removing large amounts of magnetic flux and helicity from the Sun (Low 1996) thus making room for the new solar cycle. In fact, CMEs may play a crucial role in the solar dynamo precisely by shedding magnetic helicity (Low 2001). From the viewpoint of the physics of interplanetary space, CMEs create heliospheric disturbances, driving shocks and accelerating electrons and protons evidenced by radio bursts and solar energetic particles (SEPs). They therefore play a major role in space weather whose forecast activities have considerably developed in the past decade. In addition, they contribute to the solar wind mass flux especially near solar maxima (Webb and Howard 1994; Lamy et al. 2017). From the viewpoint of planetary physics, their impact with planets with a magnetosphere leads to magnetic storms causing enhancement of ring currents and aurora. Resulting damaging effects at Earth such as disruption of electric power grids and telecommunication facilities and on artificial satellites are well known.
Consequently, there has been a rapid explosion of investigations of CMEs over the past four decades. According to Aschwanden (2017), there exist over 2000 refereed publications and at least 80 review articles for instance, Wagner (1984a), Kahler (1987), Low (1996), St. Cyr et al. (2000), Chen (2011), Webb and Howard (2012), and Gopalswamy et al. (2015c). The most extensive contribution to our knowledge of CMEs come from the white-light observations obtained with the Large-Angle and Spectroscopic COronagraph experiment (LASCO; Brueckner et al. 1995) onboard the Solar and Heliosphere Observatory (SoHO) with documented information provided by five different catalogs: CDAW, CACTus, SEEDS, ARTEMIS, and CORIMP. This knowledge can be fostered by investigating the temporal evolution of the physical properties of CMEs derived from the observations, by studying statistical distributions, and by inferring physical scaling laws, all of which require ample statistics. Whereas many CME studies concentrate on a single or on a small number of events, large statistical studies are still rare and their scopes usually focus on a limited number of physical parameters. Those dating before 2011 are limited to at most the full duration of Solar Cycle (hereafter abbreviated to SC) 23, notably Gopalswamy et al. (2003a), Cremades and St. Cyr (2007), Yashiro et al. (2008), Robbrecht et al. (2009), Ma et al. (2010), Vourlidas et al. (2010). Only two recent analysis extend over parts of SC 24, until 2013 for Gopalswamy et al. (2015c) and until 2014 for Compagnino et al. (2017). In most cases, these statistical analysis were based on a single catalog, namely CDAW, and only a few made use of CACTus.
The purpose of this article is to present a review of observations of coronal mass ejections over 23 years [1996–2018] encompassing SC 23 and 24 and a statistical analysis of their properties over the longest continuous record to date, well beyond what has been achieved from relatively short-lived past coronagraphic observations of OSO-7, Skylab, Solwind, Solar Maximum Mission, and even STEREO. Our study is based on white-light observations obtained with LASCO/SoHO and the resulting five catalogs: CDAW, CACTus, SEEDs, ARTEMIS, and CORIMP. An in-depth comparison of these catalogs is performed so as to assess the reliability of the reported parameters. It is structured as follows. Section 2 presents an overview of past observations of CMEs, of the LASCO observations, of the catalogs of CMEs, their limitations and problems, with particular attention to the ARTEMIS catalog since it has not been used so far for statistical analysis. In Sect. 3, we discuss the various observational biases—duty cycle, visibility function, projection effects—that affect coronagraphic observations of CMEs and their corrections. Section 4 is devoted to the occurrence, mass, and intensity rates reported by the catalogs, as well as mass and intensity distributions. The question of the waiting-time distribution, that is the distribution of time interval between successive CMEs is considered in Sect. 5 and that of periodicities in Sect. 6. The distributions of angular width and of apparent latitude are dealt with in Sects. 7 and 8. Section 9 is devoted to the kinematics of CMEs encompassing speed, acceleration, and kinetic energy. The correlations between the various physical parameters and between these parameters and the solar activity cycle are studied in Sects. 11 and 12. In Sect. 13, we consider halo and stealth CMEs. Section 14 extensively investigate the question of the physical relationship between CMEs and other manifestations of transient solar activity—flares, eruptive prominences and filaments—as well as with active regions and streamers. We finally discuss and summarize our results in Sect. 15 and then conclude.
2 LASCO Observations and Catalogs of CMEs
2.1 Overview of Observations of CMEs
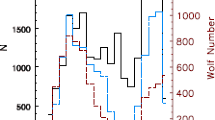
Although many space missions are relevant to the study of CMEs (see Fig. 1 of Webb and Howard 2012 for a timeline), the major contributions to our knowledge of their properties, in particular the statistical ones, come from the white-light coronagraphs flown since 1971. The very first CME was unambiguously observed from space with the coronagraph onboard the seventh Orbiting Solar Observatory (OSO-7) on 14 December 1971 as a bright transient traveling through its field of view (Tousey et al. 1973). Subsequent observations were performed by the following space-borne coronagraphs: Skylab-ATM (MacQueen et al. 1974), P78-1 Solwind (Howard et al. 1985), and the Coronagraph/Polarimeter (C/P) on the Solar Maximum Mission (SMM) (MacQueen et al. 1980). Figure 1 displays the yearly-averaged occurrence rate derived from these 17 years of observation supplemented by the Helios 1 and 2 spacecraft; although not equipped with coronagraphs, their zodiacal light photometers detected hundreds of CMEs in the heliosphere (Jackson 1985). Fortunately filling the gap of seven years before the following solar mission, Fig. 1 includes data from the ground-based Mauna Loa Solar Observatory (MLSO) Mark III K-coronameter as reported by St. Cyr et al. (2015). In January 1996, the Large Angle Spectrometric Coronagraph (LASCO; Brueckner et al. 1995) onboard the Solar and Heliosphere Observatory (SoHO) started its still on-going saga of CME detection giving birth to five catalogs: CDAW (Yashiro et al. 2004), CACTus (Robbrecht and Berghmans 2004), SEEDS (Olmedo et al. 2005), ARTEMIS (Boursier et al. 2009; Floyd et al. 2013), and CORIMP (Byrne et al. 2009). The COR2 A and B coronagraphs (Howard et al. 2008) onboard the STEREO twin spacecraft performed routine stereoscopic observation of CMEs from March 2007 to the end of dual-viewpoint observations in September 2014. To complete the picture, we mention the observations of CMEs in the heliosphere (strictly speaking ICMEs) by the all-sky Solar Mass Ejection Imager onboard the Coriolis spacecraft (Jackson et al. 2004) and by the Heliospheric Imagers HI-1 onboard STEREO (Harrison et al. 2018). When constructing Fig. 1, the occurrence rates of incomplete years were scaled according to the number of months of effective operation. This was also the case of the CORIMP data where several months have zero event.
Yearly-averaged daily occurrence rate of CMEs in comparison with the monthly smoothed sunspot number (dotted line). The plus symbols combine data from the Skylab, Helios, Solwind and SMM missions as compiled by Webb and Howard (1994). The MLSO data (star symbols) come from St. Cyr et al. (2015). The SoHO data come from the five catalogs of LASCO CMEs: ARTEMIS, CACTus, CDAW, CORIMP, and SEEDS. The STEREO data come from the MVC catalog of Vourlidas et al. (2017). See text for more detail
With observations now extending over four solar cycles (21 to 24), we have a clear confirmation that the frequency of occurrence of CMEs tracks the solar activity cycle, a trend already highlighted by Webb and Howard (1994) based on the data obtained during SC 21. A first striking feature is the much larger number of detections recorded after 1995 correctly attributed to the superior performances of the LASCO and SECCHI coronagraphs (the CORIMP data is somewhat at odd with this result). A second striking feature is the large differences in the occurrence rates reported by the different catalogs with factors of 2 to 3 and a third one is the apparent increase of the rates during SC 24 in comparison with SC 23 whereas the sunspot number follows the opposite trend. These features, together with the peculiar behaviour of the CORIMP data are extensively discussed in the following sections.
To complete our overview of observations of CMEs, Table 1 adapted from Table 1 of Webb and Howard (2012) summarizes the average statistical properties of CMEs as derived from the above sources when available. Note the impressive number of detections by LASCO resulting in part from its unsurpassed longevity. Except for SECCHI, the values of the apparent width are fairly consistent, lying in a narrow range of \(36\mbox{--}47^{\circ}\). This is less so for the values of the speed which ranges from 349 to \(470~\mbox{km}\,\mbox{s}^{-1}\) but this is possibly caused by the different methods of measurement. Much more puzzling is the range of masses from 1.2 to \(6.6 \times 10^{15}~\mbox{g}\). The largest values come from the early, pre-LASCO era coronagraphs and may be a consequence of their poor radiometric performances hampered by their Secondary Electron Conduction (SEC) vidicon detector and of their higher levels of stray light.
2.2 LASCO Observations of CMEs
The Solar and Heliosphere Observatory (SoHO, Domingo et al. 1995) was launched on 2 December 1995 and injected into a transfer trajectory towards the L1 Lagrangian point. The halo-orbit injection maneuver took place on 14 February 1996 followed by a small trim on 20 March 1996 and the observatory was formally transferred to the scientific community on 16 April 1996. In the meantime, the LASCO instrument, a suite of three coronagraphs C1, C2, and C3, had completed its check-out activities and had performed intermittent observations of the solar corona. However, the regular synoptic program relevant to CME observations really commenced in early May 1996.
The two externally occulted telescopes C2 and C3 having respective field of view of \(2.2\mbox{--}6.5~\mbox{R}_{\odot}\) and \(3.8\mbox{--}30~\mbox{R}_{\odot}\) have been and are still the workhorses of CME observations providing the inputs for several catalogs and many statistical studies. As a side note, C1 detected some CMEs during its short (2.5 year) lifetime (Plunkett et al. 1997; Schwenn et al. 1997). The routine synoptic observations are performed through broadband filters, an “orange” filter for C2 (bandpass of 540–640 nm) and a “clear” filter (bandpass of 420–860 nm) for C3 and images are acquired in the full CCD format of \(1024 \times 1024\) pixels. However, prior to September 1997, the north and south polar regions of the C2 and C3 image frames were often truncated into an equatorial band as a trade-off between field of view and cadence given the telemetry constraint. It was relaxed thereafter thus allowing the transmission of full-frame images. However, \(\approx50\%\) of the images recorded between 10 and 22 January 2008 were half-frame of \(512 \times 1024\) pixels covering the eastern hemisphere and this introduced a problem for the generation of the synoptic map for CR2065.
The operation of LASCO experienced minor interruptions since 1996 for various instrumental and spacecraft reasons except when an accidental loss of SoHO during a roll maneuver on 25 June 1998 resulted in a long data gap until recovery on 22 October 1998. Subsequent failure of the gyroscopes caused another long interruption from 21 December 1998 to 6 February 1999 when nominal operation resumed. Following the failure of the motor steering its antenna, SoHO was periodically (every three months) rolled by \(180^{\circ}\) starting in June 2003 to maximize telemetry transmission to Earth. Until 29 October 2010, the reference axis of SoHO was aligned along the sky-projected direction of the solar rotational axis resulting in solar north being up or down (in case of rolled images) on the LASCO images. To simplify operation, this was abandoned and the reference orientation was fixed to the perpendicular to the ecliptic plane causing the projected direction of the solar rotational axis to oscillate around the vertical direction on the LASCO images. These two last events had fortunately little impact on the CME observations unlike other scientific programs which suffers from changing stray light patterns.
More important for the CME program, the rate at which the C2 and C3 images were taken varied considerably throughout the first 3 years of the mission progressively increasing to stabilize at a cadence of \(\approx67\) images per day for C2 as illustrated in Fig. 2. This figure further highlights the rates of the two truncated formats used prior to September 1997. From 10 May 1996 to 24 January 2017, 4638 images were taken in the reduced format of \(1024 \times 576\) pixels and 971 images in the full format of \(1024 \times 1024\) pixels. From 1 January to 25 August 1997, 3959 images were taken in the reduced format of \(1024 \times 768\) pixels and 3452 images in the full format. Marginally, in February 1999, \(\approx30\) images were taken in the above reduced format. In September 2010, LASCO received additional telemetry resulting from the decommissioning of several SoHO instruments and the cadence of C2 was increased to \(\approx117\) images per day.
Apart from the loss of a few months of observation, the LASCO CME program is extraordinarily successful allowing giant steps in our understanding of CMEs. This stems from a combination of factors.
-
The intrinsic qualities of the instruments in terms of spatial resolution and unsurpassed low level of stray light;
-
Their photometric performances, notably sensitivity and dynamical range, offered by their CCD cameras;
-
Their image cadence and record longevity, 23 years at the end of 2018;
-
The benefit of observing from the L1 Lagrangian point procuring uninterrupted observations and a stable thermal environment;
-
The remarkable pointing capability and stability of the SoHO spacecraft, these last two factors insuring minimal variations of instrumental stray light.
As an illustration, let us finally mention that, after initial pointing of the C2 optical axis to the center of the Sun and adjustment of its inner occulter in January 1996, no correction was required thereafter and that its re-focusing device was never activated as its image quality remains nominal since the beginning of the mission.
2.3 Catalogs of LASCO CMEs and Their Problems
CMEs exhibit a variety of very different forms, sometime quite complex and this presents a major challenge for their detection when having to cope with thousands of them in order to build a robust catalog. As an illustration, Vourlidas et al. (2013) classified LASCO CMEs into six morphological categories which they slightly revised in their recent analysis of the STEREO COR2 observations (Vourlidas et al. 2017). Figure 3 displays typical examples of well-defined morphologies, the “flux rope CME” with its classical three-part structure (i.e., a circular front, a cavity, and a bright core), a “loop CME” (i.e., lacking a cavity and/or a core), and a “jet CME” (i.e., narrow and lacking the attributes of the aforementioned types). Other prominent classes are “Other” and “Unknown” which altogether amounts to nearly 50% of the COR2 CMEs. Morphology is determined not only by the intrinsic geometry of the CME itself (controlled by the process of its ejection) but also by the extrinsic viewing geometry (the vantage point) so that any identification based on morphology is inherently biased. Whatever the case, the variety of the visual appearance of the CMEs is a serious hurdle and this partly explains the existence of several catalogs of LASCO CMEs, each one implementing its own technique of detection and characterization.
The very first attempt was performed by St. Cyr et al. (2000) who reported the properties of 841 CMEs observed from January 1996 to June 1998, specifically annual and cumulative statistics of the rate, apparent latitude, apparent size, and apparent speed of these CMEs (their Table 2). The next efforts concentrated on the production of catalogs and, apart from the ARTEMIS catalog presented in the next sub-section, four other catalogs of LASCO CMEs are currently available. Let us briefly review their technique of detection, their products, and their possible shortcomings. More extended comparative descriptions can be found in Byrne (2015) and in Hess and Colaninno (2017).
-
The Coordinated Data Analysis Workshop catalog (CDAWFootnote 1) developed at the CDAW Data Center (Yashiro et al. 2004; Gopalswamy et al. 2009) relies on visual tracking of bright structures on series of LASCO-C2 and C3 images by human operators. It covers the period January 1996–March 2018 and appears to have been terminated thereafter. According to Webb and Howard (2012), this catalog is affected by observer bias since it has been compiled by at least four different observers. A decision to include narrow CMEs which were previously disregarded until 2004 has further artificially distorted the temporal variation of the occurrence rate which, unlike the other catalogs, does not track the solar cycle as will be illustrated later. In spite of these inherent limitations, the CDAW catalog has been used for several investigations of CME properties, for instance by Gopalswamy et al. (2004), Cremades and St. Cyr (2007), Vourlidas et al. (2010), Webb and Howard (2012), and Gopalswamy et al. (2015a). Following this first catalog, the next generation implemented automatic detection.
-
The Computer Aided CME Tracking catalog (CACTusFootnote 2) developed at the Royal Observatory of Belgium (Robbrecht and Berghmans 2004) relies on the Hough transform to automatically track CMEs on polar transformed LASCO-C2 and C3 images. CACTus encompasses in fact two different catalogs. The first (original) version covers the time interval April 1997–March 2007 and peaks at \(\approx360~\mbox{CME/month}\) (\(\approx12~\mbox{CME/day}\)) during the maximum of SC 23. It has been used for statistical analysis (in particular the characterization of the temporal variation of the CME rate) by Robbrecht et al. (2009) and by Webb and Howard (2012). The second version covers the time interval from April 1997 until present and displays a much lower occurrence rate, for instance peaking at \(\approx180~\mbox{CME/month}\) (\(\approx6~\mbox{CME/day}\)) during the above maximum. It has been used for the analysis of the temporal rate of CMEs for instance by Petrie (2013). The difference in peak rates suggests that some threshold has been changed resulting in a reduced rate by a factor of \(\approx2\) in the second version, possibly to put it more in line with the CDAW occurrence rate. Unfortunately the two versions are not clearly distinguished (and the second version is not documented) thus introducing a confusion when the CACTus catalog is used. The second catalog further presents three lists labeled “CMEs”, “Flows”, and their combination. According to the website, “Flows” are “suspicious detections” generally being faint, narrow events. From April 1997 to April 2018, the data set comprises 19608 CMEs and 7693 flows; in broad terms, the former have larger speeds (\(\langle \mbox{V}\rangle = 480~\mbox{km}\,\mbox{s}^{-1}\)) and larger widths (\(\langle \mbox{W}\rangle = 39^{\circ}\)) than the flows (\(\langle \mbox{V}\rangle = 370~\mbox{km}\,\mbox{s}^{-1}\), \(\langle \mbox{W}\rangle = 18^{\circ}\)).
-
The Solar Eruptive Event Detection System catalog (SEEDSFootnote 3) developed at the George Mason University (Olmedo et al. 2005, 2008) relies on an automated threshold-segmentation technique to detect CMEs in polar transformed running difference images constructed from the LASCO-C2 images. It covers the time interval from January 1996 until present.
-
The CORonal Image Processing (CORIMPFootnote 4) catalog developed at the University of Hawaii (Byrne et al. 2012; Byrne 2015) implements dynamic background separation technique and multiscale edge detection to isolate and characterize CME structures in LASCO-C2 and C3 images. Detection masks are generated to isolate the CME structure and a sequence of observations then reveals the changing CME kinematics and morphology. It extends from January 2000 to January 2016 and lists far less CMEs than all other catalogs as conspicuously illustrated in Fig. 1. Several months (three in 2014 and three in 2015) have no reported events as already mentioned and the temporal variation of the occurrence rate during SC 23 is at odd with that of the other catalogs. In view of these problems, CORIMP was found unsuited for comparative statistical studies but better suited to the detailed studies of individual CMEs as performed for instance by Byrne (2015). We however made two exceptions for the mass and the acceleration to enlarge the comparison which would have been otherwise limited to CDAW and ARTEMIS for the mass and to CDAW and SEEDS for the acceleration.
Table 2 summarizes the methods implemented by these catalogs (plus ARTEMIS) and Table 3 presents their main characteristics and specifies the listed parameters among: date of CMEs first appearance in C2, central position angle, angular width, speed(s), acceleration, mass, and kinetic energy.
2.4 The ARTEMIS Catalogs of CMEs
Unlike all other catalogs which use the LASCO images themselves, the automated detection and characterization of CMEs developed to generate the ARTEMIS catalogs are performed on synoptic Carrington maps of the K-corona radiance. They are built from time-series of LASCO-C2 “orange” images first corrected for instrumental effects, calibrated in units of the radiance of the mean solar disk, and re-sized to a common format of \(512 \times 512\) pixels. These tasks as well as the separation of the K-corona and the generation of the synoptic maps are performed by the pipeline processing developed by the LASCO team at the Laboratoire d’Astrophysique de Marseille as described in Lamy et al. (2014) and summarized in the appendix of Barlyaeva et al. (2015). These non-standard synoptic maps first introduced by Lamy et al. (2002) simultaneously display both east and west limbs and are particularly adapted to the detection of CMEs. Circular profiles are extracted at different radial distances from the center of the Sun, stacked and resampled uniformly with time by linear interpolation (to remove the effect of irregular image acquisition) in a frame where the horizontal or x-axis represents time running from left to right (this is equivalent to the longitude of the central meridian of the Sun). The vertical or y-axis represents the solar polar angle running from \(0{^{\circ}}\) to \(360{^{\circ}}\) starting from the north pole and increasing counterclockwise (instead of the latitude running from \(-90{^{\circ}}\) to \(+90{^{\circ}}\) in the standard synoptic maps). Our synoptic maps are generated at radial distances in multiples of \(0.5~\mbox{R}_{\odot}\) inside the field of view of LASCO-C2 and range from 3 to \(5.5~\mbox{R}_{\odot}\).
A first generation of synoptic maps used to generate the ARTEMIS-I catalog were constructed with an angular step of \(1{^{\circ}}\) and a uniform resampling with a time step of \(27.3~\mbox{days}/1000 = 39.3~\mbox{minutes}\) (Boursier et al. 2009). A second generation of synoptic maps used to generate the ARTEMIS-II catalog (Floyd et al. 2013) were subsequently produced to optimally take advantage of the spatial and temporal resolutions of the C2 images. First, two different angular steps were implemented: \(0.4{^{\circ}}\) for radial distances of 3 and \(3.5~\mbox{R}_{\odot}\) and \(0.25{^{\circ}}\) beyond. Second, the time step of the uniform linear resampling was decreased to \(27.3~\mbox{days}/1440 = 27.3~\mbox{minutes}\) comparable to the average temporal cadence (\(\approx21\) minutes) of the C2 images during 12 years (1999–2010), corresponding to \(\approx67\) images per day. In September 2010, the cadence was increased to \(\approx118\) images per day but the temporal resolution of the synoptic maps was kept at 27.3 minutes to avoid introducing a bias in the detection rate of CMEs. These maps have therefore a format of \(1440 \times 900\) pixels at radial distances of 3 and \(3.5~\mbox{R}_{\odot}\) and of \(1440 \times 1440\) pixels at larger distances.
Synoptic maps offer a clearly defined signature of CMEs in the form of vertical streaks expressing sudden and short disruptions in the corona well in line with the early terminology of “transients” which was commonly used in early investigations. These unambiguous signatures are therefore much easier to detect than CMEs of very different shapes as they appear on the LASCO images. The automated method developed by Boursier et al. (2009) and updated by Floyd et al. (2013) aimed at detecting these streaks and implement four successive operations, filtering, thresholding, segmentation, and merging with high-level knowledge (Fig. 4). At the end of the process, masks are produced where every CME is represented by a vertical segment whose center defines its central position angle (and thus its apparent latitude) and whose vertical extent defines its angular width; a lower limit of \(7{^{\circ}}\) is imposed to register the detected event in the catalog. Masks obtained at different radial distances are used to determine three velocities provided that the CME is detected on at least three masks (\(\approx60\%\) of the whole set of detected CMEs). A parameter called “Intensity” quantifies the total radiance of a CME at \(3~\mbox{R}_{\odot}\) as the excess radiance over the background and is calculated by summing the pixel values of the filtered synoptic maps limited by the masks resulting from the segmentation and merging operations. As pointed out by Floyd et al. (2013), it does not strictly correspond to its total radiance as recorded on the original C2 images because of the incomplete sampling introduced by the synoptic maps and, when comparing CMEs, it is furthermore biased by their respective velocities. However, it does provide an approximate estimate of the CME strength.
Illustration of the four steps of the procedure applied to the original synoptic maps (left panel). From left to right: filtering, thresholding, segmentation, and merging with high level knowledge. The effect of this final step is highlighted on three events by the red ellipses. The rightmost image is the detection mask used when computing the propagation velocity. Each subimage extends over five days (\(x\)-axis) and \(360{^{\circ}}\) (\(y\)-axis)
The calculation of the mass of each CME from the radiance recorded by the synoptic maps required a specific procedure developed by Floyd et al. (2013) and is inherently limited to those CMEs whose speeds are determined (\(\approx60\%\) of the whole set of detected CMEs). The mass calculation classically assumes that CMEs are composed of fully ionized hydrogen atoms with 10% helium. As always the case for observations from a single vantage point, the procedure further assumes that the CME lies close to the plane of the sky (“limb event”), since we have no longitudinal information from the images. Colaninno and Vourlidas (2009) and Bein et al. (2013) have exploited the two independent views offered by the SECCHI coronagraphs of the STEREO mission to determine the direction of propagation of CMEs by imposing the constraint that the same mass should be derived from the two stereoscopic views thus leading to more robust results. Floyd et al. (2013) and Lamy et al. (2017) compared the ARTEMIS and SECCHI masses for respectively 7 and 25 CMEs and found excellent general agreement between the two results except for those CMEs far out the LASCO sky plane, the ARTEMIS masses being underestimated as expected.
In summary, the ARTEMIS-II catalog lists the CMEs detected since March 1996 and characterized by: time of detection at \(3~\mbox{R}_{\odot}\), central apparent latitude, angular width, and for a large fraction of them (\(\approx60\%\)), three different velocities (“propagation”, “global”, and “median”), intensity, mass, and kinetic energy. The propagation velocity is determined by shifting the successive masks at each radial distance of the synoptic maps and retaining the values that maximizes the number of matches. The two other velocities are obtained by cross-correlating the detected CMEs on the original synoptic maps at 3 and \(5.5~\mbox{R}_{\odot}\). A global cross-correlation yields the global velocity whereas a line by line cross-correlation produces a distribution of velocities whose median value is taken as the median velocity.
For the time interval considered in this study, from March 1996 to September 2018 inclusive, the ARTEMIS-II (thereafter called ARTEMIS for simplicity) catalog lists a total of 39188 CMEs, of which 22894 have their velocities, mass, and kinetic energy determined. The ARTEMIS catalog is part of the LASCO-C2 Legacy ArchiveFootnote 5 hosted at the Integrated Data and Operation Center (formerly MEDOC) of Institut d’Astrophysique Spatiale.
We conclude this presentation by an excerpt of the article of Wang and Colaninno (2014) concerning the ARTEMIS catalog: “In our view, the use of synoptic maps, which provide a relatively simple and clearly defined signature of CMEs in the form of vertical streaks, is more likely to yield consistent estimates of the long-term variation of CME rates than attempts to identify and distinguish outward-propagating ejections in individual images, even with the aid of automated techniques. We therefore consider the ARTEMIS results for the intra- and inter-cycle variation of the CME rates to be the most reliable among the different catalogs”.
3 Observational Biases and Corrections
Real observations inherently suffer from various problems and limitations which must be accounted for to remove biases that could distort statistical properties. We present below the different problems which affect the LASCO-C2 observations and the methods used to correct them.
3.1 Duty Cycle
In general terms, the duty cycle of an instrument is defined as the fraction of useful observing time during a given time interval (e.g., day, month, Carrington rotation). In the case of CMEs, the question boils down to estimate how many CMEs have been missed because of interruptions in the observations (data gaps). Hundhausen et al. (1984) for the SMM observations and Howard et al. (1985) for the Solwind observations presented similar methods to estimate the duty cycle for CME detection. First, a typical CME is considered assuming a mean speed to define a time interval such as two views of that CME are obtained while traveling throughout the field of view of the instrument (for instance, 4.5 hours for Solwind). The fraction of a given time period not interrupted for times exceeding this value then defines the duty cycle for that period. This procedure has been widely implemented in the past, for instance by Webb and Howard (1994) for Skylab, Helios, Solwind, and SMM, St. Cyr et al. (2000) and Cremades and St. Cyr (2007) for LASCO-C2 and C3, Vourlidas et al. (2010) for LASCO-C3, St. Cyr et al. (2015) for MLSO Mk3, and Vourlidas et al. (2017) for SECCHI-COR2. Considering a typical CME traveling at a speed of \(\sim 300~\mbox{km}\,\mbox{s}^{-1}\) in the C2 field of view, we adopted 3 hours as a threshold for declaring a data gap in the C2 observations. Figure 5 displays the derived monthly-averaged duty cycle from 1996 to 2018. If we exclude the interval during which SoHO was lost, the duty cycle generally remained in the range 0.8–1 and occasionally decreased to 0.7 with a couple of extreme values of \(\approx0.6\). However, starting in October 2012, the duty cycle became very stable at a value of nearly 1 with a couple of exceptions in 2016 and in 2018.
3.2 Visibility Function
The visibility function attempts to correct for the decreased sensitivity of visible light coronagraphs in detecting mass ejections away from the plane of the sky because of the dependence of the efficiency of Thomson scattered light on the viewing angle of the CME with respect to the line-of-sight. A detailed formulation of the problem was given by Hundhausen (1993). It prominently affects faint halo CMEs propagating along or near the Sun-observer direction whose number may consequently be underestimated. A method to determine the visibility function was developed by Webb and Howard (1994) and applied to Skylab, Solwind, and SMM data. It relies on the association (although not one-to-one) of CMEs with metric type II radio bursts identified with \(\mbox{H}\alpha \) flares. These authors derived correction factors of 1.3 (Solwind) and 1.4 (Skylab and SMM) which they applied to the CME rates already corrected for duty cycle. This method was applied to the first 2.5 years of LASCO data by St. Cyr et al. (2000) relying on the work of Cliver et al. (1998) and they established that 95% of the metric Type II bursts were associated with LASCO CMEs thus indicating that little, if any, correction is required for the visibility of LASCO CMEs”. We are not aware of any extension of this kind of analysis beyond these first 2.5 years. In their study of EUV post-eruptive arcades as tracers of coronal mass ejection source regions during the [1997–2002] interval, Tripathi et al. (2004) found that 92% of these events were associated with a CME based on close space and time relationships and they suggested that the discrepancy could be caused by sensitivity limitation of LASCO. Howard and Simnett (2008) considered interplanetary coronal mass ejections (ICMEs) detected by the Solar Mass Ejection Imager (SMEI) from February 2003 to September 2005 and searched for possible progenitors among the LASCO CMEs. They found that 17% of the ICMEs had a weak or unlikely LASCO counterpart, and 7% had none. Rather than invoking a sensitivity limitation of LASCO, they investigated several physical mechanisms which could explain the discrepancy and finally proposed “erupting magnetic structures” that had not sufficient mass to be detected by LASCO. Regarding these last two works, two remarks can be put forward: (i) they made use of the CDAW catalog which roughly detect twice less CMEs than the ARTEMIS and SEEDS catalogs and (ii) they did not exclusively involve halo CMEs which are potentially the most affected by sensitivity limitations. It would be of interest to see whether their conclusions still hold when reconsidering their investigations on the ground of the above remarks. Vourlidas et al. (2017) recently addressed the issue of undetected CMEs by comparing the numbers of CMEs detected by COR2-A and -B during their simultaneous operation and found visibility functions of 96.5% for COR2-A and 86.7% for COR2-B, this smaller value resulting from a larger stray light background in the latter instrument.
In view of the above remarks, of the results of Vourlidas et al. (2017), and of the extremely large number of CMEs reported in the automated catalogs notably SEEDS and ARTEMIS, we can safely conclude that the visibility function is not an issue for LASCO CMEs and that any possible correction would be very small, probably at the level of a few percents with no impact on statistical aspects except possibly for halo CMEs.
3.3 Reduced Field of View
As mentioned in Sect. 2.2, during 1996 some C2 and C3 frames were truncated into an equatorial bands to reduce telemetry requirements and increase image cadence. However during this year of low solar activity, CMEs were confined to low latitudes as will be shown later, so that we are confident that these reduced formats have not affected the rate of detection.
3.4 Projection Effects
All measurements made from coronagraph images are projected into the plane of the sky. The resulting fore-shortening affects the geometric and kinematics properties of CMEs away from that plane when viewed from a single vantage point as it is the case for LASCO. Position angle or latitude are primarily concerned as coronal structures off the plane of the sky and assumed to travel radially will appear at an apparent heliographic latitude \(\varLambda\) larger than the true latitude \(\lambda \) of its source on the Sun. Hundhausen (1993) worked out the geometry and summarized his results in a convenient graph (his Fig. B2) where one can follow the variation of the projected latitude as a function of longitude reckoned from the plane of the sky. As expected, the difference remains small for longitudes up to \(\approx40{^{\circ}}\) but rapidly increases beyond, being the largest at the lowest latitudes.
The kinematics aspects were addressed by Leblanc et al. (2001) who derived corrections for eight CMEs that could be associated with a flare in an active region—thus providing the heliographic coordinates of the source—and based on simplifying geometric assumptions. This method was later slightly improved by Yeh et al. (2005) and applied to 557 LASCO CMEs observed from 1996 through 2003. Apart from correcting the speed and the mean angular width of those CMEs, they reached an interesting conclusions, namely that the weak correlation between the angular width and the speed of CMEs that was present before correction disappears after the correction. Burkepile et al. (2004) selected a set of 111 SMM “limb” CMEs through associations with erupting prominences at the limb, X-ray and limb optical flares thus minimizing projection effects and found that their properties substantially differed from the bulk of the SMM CMEs. Howard and Simnett (2008) considered over 10,000 LASCO CMEs in the CDAW catalog spanning the [1996–2005] interval and could associate 1961 of them with a surface event, either an X-ray or \(\mbox{H}\alpha \) flare or a disappearing filament, and utilized their heliospheric coordinates to estimate the 3-D direction of propagation of the CMEs. De-projected speeds, accelerations, and launch angles were subsequently determined assuming that CMEs propagate radially. A remarkable result of particular relevance to the present article is that statistical trends in CME properties recovered from direct measurements in the plane of the sky are preserved in the corrected CME kinematic properties. However and unsurprisingly, individual values can differ significantly between the projected and corrected parameters requiring a case-by-case analysis.
To summarize, the central position angles, angular widths, and speeds listed in the catalogs, are all projected or apparent; speeds, masses, and kinetic energies are therefore underestimated. Projection also affects the morphology of CMEs (also influenced by the orientation of non-axially symmetric CMEs such as flux ropes), detectability (affecting prominently faint CMEs far from the plane of the sky and narrow CMEs), and in turn occurrence rate (Vourlidas et al. 2013, 2017).
4 Occurrence, Mass, and Intensity
This section is devoted to the temporal evolution of the occurrence rates reported by the four main catalogs, mass rates and mass distributions reported by ARTEMIS, CDAW and CORIMP, and intensity rate and distribution reported by ARTEMIS. We have seen that the occurrence rate tracks solar activity as recorded in sunspot number (Fig. 1). In this section, we make use of the solar decimetric radio flux at 10.7 cm (\(F_{10.7}\)) as we have already done in the past (Lamy et al. 2014). As pointed out by Cremades and St. Cyr (2007), this flux is a more reliable indicator of solar cycle evolution than sunspot number since it is described by a unique number coming from a single station. The radio flux is systematically scaled and vertically shifted to best match the variations of the individual rates during SC 23.
The occurrence and mass rates data were corrected for the LASCO duty cycle as given in Fig. 5. In the case of ARTEMIS, we introduced an additional operation of patching the large data gap of the second half of 1998 so as to remove this discontinuity in our analysis. This was realized by generating semi-random values using the “Kernel Density Estimator” (KDE) which is fed by real data of the ascending phase of SC 23 as a reference; this insures that the statistical distribution of the data is preserved. Among a number of possible realizations of the KDE, we selected the one that best matches the variation of the radio flux (Fig. 6).
4.1 Occurrence Rate
Figure 7 displays the monthly occurrence rates of CMEs reported by the four main catalogs. The CACTus data combine the CMEs and the “flows” as this brings the total occurrence rate to values closer to those reported by the other catalogs.
Monthly occurrence rates of CMEs reported by the four catalogs in comparison with the solar radio flux at 10.7 cm. Note the different scales of the rates for ARTEMIS and SEEDS (0–500), for CACTus (0–350), and for CDAW (0–300). Two solutions of the CDAW rates are displayed in two separate panels. The upper one includes all listed CMEs whereas the lower one omits the “very poor” events (see text for detail). In the case of SEEDS and CACTus, the dashed lines correspond to the monthly rates multiplied by 0.632 from September 2010 to compensate the increase of the image cadence
A first striking point concerns the large difference in numbers of detections by ARTEMIS and SEEDS on the one hand, and by CACTus and CDAW on the other hand. For example, during SC 23, the rates peak at \(\approx400\) CMEs per month for the former two whereas they are of the order of 200 for the latter two. As a side note, the first version of CACTus peaked at \(\approx360\) CMEs per month, more in line with the ARTEMIS and SEEDS peaks. A second striking point concerns the diverging rates during SC 24: whereas ARTEMIS reports rates globally inferior to those of SC 23, the three other catalogs report the opposite situation with SC 24 rates largely exceeding those of SC 23. Failure to account for the increased rate of image cadence starting in September 2010 was suspected in the case of SEEDS and CACTus by Wang and Colaninno (2014) and confirmed in the former case by the exercise performed by Hess and Colaninno (2017) consisting in rerunning the SEEDS detection code on C2 data resampled at the original cadence. They found that the SEEDs occurrence rate must be reduced by a factor of \(0.632\pm 0.047\) to correct for the increased cadence, consistent with the ratio \(67/117 = 0.573\) of the two average values of the cadence given in Sect. 2.2. The so revised SEEDs occurrence rate was then found to better track the sunspot number with a correlation coefficient of 0.92 instead of 0.78 before the correction. Hess and Colaninno (2017) did not perform the same exercise on the CACTus rate but we assume that the same factor of 0.632 may hold as well to correct for the increased image cadence. Consequently and unless otherwise stated, the so revised SEEDS and CACTus rates will be used from now on. The application is straightforward for the variation of parameters with time. In the case of histograms, two are separately calculated using the same minimum, maximum and bin size, one before and the other after the above date, and summing the two.
The atypical behaviour of the CDAW rate has long been a matter of concern and has generally been linked to the visual detection by different operators and the late inclusion of narrow, faint ejections as already mentioned in Sect. 2.3. According to Wang and Colaninno (2014), omitting these “very poor” events—which amounts to 26% of the total population—brings the rate in much better agreement with solar activity. Alternatively, a lower threshold of \(20{^{\circ}}\) (and even \(30{^{\circ}}\)) on the angular width has been imposed in several past studies (e.g., Webb and Howard 2012; Vourlidas et al. 2017) to remove the obvious bias in the temporal evolution of the rate at the expense of reducing the data set by 31% (44% when using the threshold of \(30{^{\circ}}\)). We tested the two alternatives and concluded likewise Wang and Colaninno (2014) that omitting the “very poor” events yields a rate that better tracks solar activity than thresholding the angular width at \(20{^{\circ}}\). It looks also more reasonable than an arbitrary lower limit on the width and more consistent with the other three (automated) catalogs which incorporate narrow CMEs and still display rates satisfactorily tracking solar activity. In other words, a selection on the width does not appear pertinent.
The rates recorded by SEEDS and CACTus and to a lesser extent by CDAW exhibit fluctuations much larger than those present in the ARTEMIS data. This is particularly conspicuous during the declining phase of SC 23 during which these fluctuations were particularly large and often uncorrelated with the radio flux whereas the ARTEMIS rate exquisitely mirrors many of the shorter-term fluctuations of the radio flux.
The correlation coefficients among the occurrence rates for the four catalogs (corrected when appropriate as described above) are presented in Table 4. The catalogs are faily well correlated with one another with ARTEMIS correlating very well with SEEDS (0.90) and CDAW (0.91) but much less so for CACTus for which the correlation coefficients with the other catalogs do not exceed 0.85.
4.2 Mass Rate and Distribution
As justified in Sect. 2.3, we include the CORIMP catalog in addition to ARTEMIS and CDAW in the statistical analysis of mass. We mentioned above that ARTEMIS lists mass for \(\approx60\%\) of the detected CMEs. We checked that this restriction does not introduce a bias by comparing the temporal evolution of the monthly occurrence rate of the whole set of CMEs with that of the CMEs with a calculated mass (Fig. 8). Indeed, they closely track each other and can be matched almost perfectly by multiplicative scaling. To be more precise, two scaling coefficients were applied to the rate of CMEs with mass, a factor of 1.57 for the first 18 years and starting in November 2013, a factor of 2.18. This means that during the latter period, there was a number of CMEs for which our procedure was unable to determine speeds and masses. They are most likely faint events which could not be tracked on the required three synoptic maps. The CDAW catalog also has a restriction on mass determination to 65% of its whole data set since it requires that the CME be seen on more than three images and that its angular width lies between \(20{^{\circ}}\) and \(120{^{\circ}}\) with rare exceptions. Further omitting the “very poor” events decreases the above percentage to 55%. The CORIMP catalog includes only 7945 CMEs with measured mass (compared to 22894 for ARTEMIS and 15840 for CDAW) and covers only 13 years extending over parts of SC 23 (maximum and declining phases) and of SC 24 (ascending phase). Note that no mass is reported during the last three years [2013–2015] of the CORIMP catalog.
Monthly occurrence rates of CMEs derived from the ARTEMIS catalog. The upper panel displays the rate of all detected CMEs (red curve) and the rate of CMEs with known mass (blue curve). In the lower panel, the rate of CMEs with known mass has been scaled to match the rate of all CMEs by a factor 1.57 (solid blue line) and by a factor 2.18 starting from November 2013 (dashed blue line)
Before we proceed with the results, let us address the question of the “true” mass of CMEs as it is often considered that they accumulate extra mass while propagating through the corona and heliosphere via the so-called snow-plow effect. There are however conflicting results on the reality and effectiveness of this process. Combining measurements of eight CMEs observed by C2 and C3 and COR2-A and -B during a period of low solar activity, Colaninno and Vourlidas (2009) found that their mass tends to increase rapidly between 3 and \(8\mbox{--}10~\mbox{R}_{\odot}\) and reaches a plateau beyond. In a subsequent study extending over the full SC 23 and based on LASCO observations and the CDAW catalog, Vourlidas et al. (2010) identified two populations in the mass of the CDAW catalog: the “normal” CMEs which reach a constant mass beyond \(10~\mbox{R}_{\odot}\), and the “pseudo-CMEs” (54% of their total sample) which reach a mass peak below \(7~\mbox{R}_{\odot}\) before they disappear in the C3 field of view. Different conclusions were reached by Bein et al. (2013) based on their study of 25 CMEs observed by both COR2-A and -B: the mass increase was found important at about \(10\mbox{--}15~\mbox{R}_{\odot}\) and to mostly contribute up to \(20~\mbox{R}_{\odot}\), ranging from 2% to 6% per \(\mbox{R}_{\odot}\). As a consequence, these authors estimated the “true” mass values at very low coronal heights (\(<3~\mbox{R}_{\odot}\)) in contradiction with the warning of Vourlidas et al. (2010) “that only CME measurements to at least \(15~\mbox{R}_{\odot}\) can allow the proper measurement of CME properties such as mass and energy”. As a matter of fact, in a recent study of 13 CMEs with well-defined frontal boundaries crossing the LASCO-C2 and C3 field of view, Howard and Vourlidas (2018) concluded that they were in simple radial expansion with no observed pile-up. By relying on mass measurements in the LASCO-C2 field of view, the ARTEMIS catalog is likely to report values close to the “true” mass of CMEs, except for the bias resulting from projection effects.
Figure 9 reveals that altogether the monthly mass rates reported by the three catalogs perform quite well in tracking solar activity. The improvement, compared to the occurrence rates, is particularly spectacular for CDAW as was already shown by Wang and Colaninno (2014) although there appears a deficit of mass in 1999 and 2000. Furthermore, the CDAW rate exhibits very large fluctuations inconsistent with the variations of the radio flux. To the contrary, ARTEMIS and CORIMP (although CORIMP captures only 30% of the CME mass reported by the other two catalogs) perform extremely well in tracking the radio flux with much reduced fluctuations compared with CDAW. Figure 9 displays a direct comparison of the ARTEMIS and CORIMP mass rates where the latter data are scaled by a multiplicative factor of 3.3 leading to a very impressive match between the two. These trends are confirmed by the correlation coefficients among the mass rates for the three (Table 5).
The three-dimensional graph shown in Fig. 10 displays the annual count of CMEs per bin of 0.2 in the logarithm of the mass (expressed in g) from the ARTEMIS catalog. The variation with the solar cycle is quite impressive but is quantitatively misleading as a consequence of the above binning in logarithm. This is circumvented in Fig. 11 which displays the time variation of the mass per CME, arithmetically averaged over each year, at the expense of losing the information on the mass distribution. The three data sets agree on the correlation with the solar activity cycle but there appears significant differences, prominently between the ARTEMIS and CORIMP results on the one hand and that of CDAW on the other hand. The first two follow the same smooth evolution with ARTEMIS displaying slightly larger values than those of CORIMP, for instance in 2002, \(1.4\times 10^{15}\) versus \(1.0\times 10^{15}~\mbox{g}\). The CDAW evolution looks more erratic with large fluctuations (e.g., the high peak of 1998) and systematically exceeds the other two (except for a couple of years), amounting to \(2.6\times 10^{15}~\mbox{g}\) in 2002. The effect is particularly pronounced during SC 23 as the CDAW data imply a much larger average mass per CME than during SC 24 by a factor of \(\approx1.5\); this is not confirmed by the ARTEMIS result which indicates nearly the same average mass during the two cycles.
We now consider the question of the distribution of mass and display in Fig. 12 its histogram on a linear scale of frequency and a logarithmic scale of mass (using a bin of 0.1) over the two solar cycles and separately for SC 23 and 24. Similar histograms are shown in Fig. 13 using now a logarithmic scale for the frequency. The difference of the mass range is quite pronounced with CORIMP reporting masses in the range \(10^{10}\) to \(10^{16}~\mbox{g}\) whereas ARTEMIS and CDAW have a nearly common range of \(10^{12}\) to \(5 \times 10^{16}~\mbox{g}\). This translates naturally in the skewness of the three distributions, CORIMP towards the small masses and ARTEMIS and CDAW towards the large masses, however less pronounced in the latter case. Quite remarkably, the ARTEMIS and CDAW distributions agree quite well at large masses, typically \(\geq 10^{15}~\mbox{g}\), whereas the former largely exceeds the latter at smaller masses. Note that the above results hold independently for the two solar cycles and globally when they are combined.
Same as Fig. 12 except for the log-log scale of frequency
The skewness of the ARTEMIS and CDAW distributions is opposite to that found by Vourlidas et al. (2010) in their analysis based on the CDAW catalog during the [1996–2009] time interval corresponding to SC 23. This is somewhat surprising but may be a consequence of imposing different selection criteria on the CDAW data, namely excluding “very poor events” in the present study and excluding narrow CMES with angular width less than \(20{^{\circ}}\) in that of Vourlidas et al. (2010). In any case, the immediate implication is that they do not follow a log-normal distribution found in some manifestations of solar activity (Abramenko and Longcope 2005). Such a distribution would produce a Gaussian function in the log(mass)–log(frequency) space and this is clearly not the case based on a simple visual inspection of Fig. 13: the departure of the three curves from a Gaussian shape is so pronounced that attempting a fit makes little sense. They could possibly be fitted by a superposition of two or more Gaussian distributions as tested by Vourlidas et al. (2010) but this exercise is of limited interest since the large overlap between the contributing distributions preclude a clear identification of two or more populations of CMEs and moreover the connection to other physical properties (e.g., speed).
We finally focus our attention to a possible power-law tail which can be suspected at large masses in Fig. 13 as the statistics of non-linear processes often ends up in power-law distributions. The three frequency distributions from ARTEMIS, CDAW, and CORIMP are replotted Fig. 14 restricted to masses \(>10^{14}~\mbox{g}\) and with two bin sizes to best sample the distributions. It is readily seen that the three distributions are best fitted by second-order polynomials and that a broken power law with power exponents of \(\approx -1.5\) and \(\approx -2\) would be required to fit the data at masses \(> \sim 10^{15}~\mbox{g}\). In summary, the present data do not really support a power-law tail in the mass distribution of CMEs.
Frequency distributions of the mass of CMEs from the ARTEMIS, CDAW, and CORIMP catalogs using a log-log representation. The vertical dotted line separates the two regions of different mass bins: \(10^{14}~\mbox{g}\) (left side) and \(10^{15}~\mbox{g}\) (right side). The solid lines are second-order polynomial fits to the data
4.3 Intensity Rate and Distribution
The total or integrated intensity as defined in Sect. 2.4 is only reported in the ARTEMIS catalog. Its monthly values displayed in Fig. 15 closely track the radio flux but with different scaling factors for SC 23 and 24, a situation consistent with that of the occurrence rate (Fig. 7). This translates into a relative excess of intensity during SC 24 when the radio flux is used as a baseline and fitted to the intensity during SC 23. A scaling factor of 1.4 brings the intensity in line with the radio flux during SC 24. The distributions of intensity for SC 23 and SC 24 are displayed in Fig. 16. They extend over the same range but differ slightly in their statistical properties with mean/median values of 810/212 for SC 23 and 715/171 for SC 24.
Figure 17 displays a two-dimensional histogram (to avoid the illegible clumping of data points of a scatterplot) between mass and intensity confirming their close relationship as expected. The regression allows deriving the following formula \(\log (\mbox{Mass})=12.17 + 0.92 \times \log (\mbox{Intensity})\). As explained by Floyd et al. (2013), the intensity cannot be strictly converted to mass but the above formula allows estimating the “missing” CME mass (i.e., the mass of CMEs without measured mass) assuming that both groups with and without listed mass have globally the same kinematic properties. We found that this “missing” mass amounts to a modest \(\approx14\%\) of the measured mass.
5 Waiting Time
The waiting-time distribution (WTD), that is the distribution of time intervals \(\Delta t\) between successive events, gives information on the temporal process of their formation, either random or having some form of organization such as memory effect, intermittency, or clusterization. Moreover, the WTDs of two processes may be compared allowing establishing a possible link between them. WTDs are widely used in physics. In the field of solar physics, the WTD of flares received particular attention thanks to the availability of a long sequence of data from the GOES satellites and resulted in conflicting results (e.g., Boffetta et al. 1999; Wheatland 2000; Lepreti et al. 2001; Aschwanden and McTiernan 2010).
The question of the WTD of CME was first addressed by Wagner and Wagner (1984) based on SMM and Skylab data and they found clustering in periods less than 59 hours long and coherence on a grand scale; surprisingly, this early work has been ignored thereafter. Moon et al. (2003) considered the first half of SC 23 [1999–2001] and using the CDAW catalog (fortunately unbiased by very poor events at that time), they found that the WTD of CMEs was well represented by two time-dependent Poisson distributions except at the shortest waiting times. Wheatland (2003) extended the analysis to the first six years of LASCO operation [1996–2001], i.e., including the SC 22/23 minimum, and he concluded that (i) the WTD exhibits a power-law tail with an index \(\gamma \approx -2.36\pm 0.11\) for large waiting times (\(\Delta t> 10~\mbox{hours}\)) and (ii) this index varies with the solar cycle, the power law being steeper at times of high activity.
Let us summarize the theoretical background which is essential for the understanding of the analysis and start with the basic (random) Poisson process where the sequence of events in time is such that there is a constant probability per unit time \(\lambda \) (the rate of the process) of an event occurring. The WTD of the Poisson process is a simple exponential:
Wheatland (2003) noted that the WTD of CMEs did not obey this simple process and he introduced a time-dependent Poisson process where the mean rate \(\lambda = \lambda (t)\) varies slowly with time \(t\) (with respect to the average waiting time) having a distribution:
where \(N\) is the total number of observed events and \(T\) is the total observing time. He limited his analysis to the special case of a piecewise-constant Poisson process, i.e., a Poisson process consisting of a series of constant rates \(\lambda _{i}\) for intervals \(t_{i}\), so that the distribution becomes the sum of individual distributions via:
where \(\lambda _{0}\) is the mean value of \(\lambda (t)\). He then decomposed the occurrence rate of the CMEs in discrete intervals of piecewise-constant rates using the Bayesian Blocks procedure and found that the piecewise-constant model provides a reasonable representation of the observed WTD, including reproducing the extended tail of the distribution whose index \(\gamma \) varied with solar activity. He finally compared his results on CMEs with those of GOES flares and found that they have very comparable indices and time variation. A similar conclusion was reached by Yeh et al. (2005) using a slightly longer time interval [1996–2003]; further considering separately slow and fast CMEs, they found identical indices of their WTDs.
Telloni et al. (2014) noted that the approach of Wheatland (2003) required two untested assumptions: (i) the local Poisson hypothesis and (ii) a power law \(\lambda ^{\alpha }\) of the rate probability density (whose index \(\alpha \) is furthermore constrained to be larger than 3 to ensure that the result holds). Using the CDAW catalog from 1996 to 2012, they found that the first hypothesis does not generally hold and they explained the observed WTD by a certain amount of memory. Such a process can be described by a Weibull distribution of the probability function \(P(\Delta t)\) (Weibull 1951) which was successfully fitted to the CME observations. The problem with this work and its conclusions is that it relies on the early, uncorrected occurrence rate of the CDAW catalog which is distorted by the very poor events during nine years [2004–2012] out of the seventeen years interval [1996–2012] considered by the authors. We therefore re-examined the question of the WTD of CMEs on the basis of the three catalogs extending over 23 years: ARTEMIS, SEEDS (corrected for the change in image cadence), and CDAW (without very poor events).
The left column of Fig. 18 displays the temporal evolutions of the waiting times of CMEs coming from the three data sets. As expected, they are not constant and anti-correlated with the solar cycle with longer waiting times during the minima and larger values for CDAW than for ARTEMIS and SEEDS except during the SC 23/24 minimum. The right column of Fig. 18 displays the histograms of the distribution of WTDs together with different fitted models: Poisson, Weibull, and power law. In addition, in the case of ARTEMIS, we include the non-stationary Poisson model introduced by Li et al. (2014) in their analysis of the WTD of solar energetic particles where the event rate \(f(\lambda )\) follows an exponential law via:
This generalized form reduces to the simpler exponential function of Wheatland (2000) when \(\alpha = 0\) and to Cases (4) and (5) of Aschwanden and McTiernan (2010), when \(\alpha = 0\) and \(\alpha = 1\), respectively. All three distributions of WTDs conspicuously depart from the Poisson model. The CDAW distribution is compatible with the Weibull model and in fact, our fit is superior to that of Telloni et al. (2014) (their Fig. 1) although there persists some deviation at large WTs (\(>60~\mbox{hr}\)). The ARTEMIS and SEEDS distributions significantly depart from the Weibull model and that of ARTEMIS is best fitted by Li’s function; most importantly, both ARTEMIS and SEEDS distributions exhibit long power-law tails over a range of WTs extending from 3 to 100 hr with very close power-law index \(\gamma \approx -2.2\) for ARTEMIS and \(\gamma \approx -2.3\) for SEEDS. The CDAW distribution does exhibit such a tail but on a much restricted range, from 15 to 100 hr with a larger index \(\gamma \approx -2.5\). Our results therefore clearly show that on the long term, namely two solar cycles, the WTD of CMEs does not obey Poisson statistics and that the properties of their observed distribution depends upon the data sets. The agreement between ARTEMIS and SEEDS gives strong support to the prevalence of an extended power-law tail against the Weibull distribution advocated by Telloni et al. (2014). Note that strictly speaking, the Weibull distribution includes the power law in the limit of the “key parameter” \(k \longrightarrow 0\) where \(k\) describes whether the probability of occurrence decreases (\(k<1\)) or increases (\(k>1\)) with time, but then the power law holds over the full interval of WT unlike the observed WTD of CMEs.
The finding of an extended power-law tail in a WTD has no unique interpretation but its slope is indicative of the behaviour of the event rate, e.g., whether it is constant, varies gradually, or is clustered. Non-stationary Poisson processes with continuous occurrence rate functions \(\lambda(t)\) do generate such a behaviour as illustrated by the four cases considered by Aschwanden and McTiernan (2010) where four different analytical expressions for \(\lambda(t)\) were introduced to somehow mimic the solar cycle in a more or less pronounced way. The power-law index is clearly controlled by \(\lambda(t)\) and the values of −2.2 (ARTEMIS) and −2.3 (SEEDS) fall in between the last two (\(\gamma = -2.9\) and −1.9) of the four cases indicating a moderately intermittent CME generation with intervals of high rates (with some form of clustering) alternating with intervals of low rates as precisely observed.
To better characterize this evolution, we split the 23 years coverage of LASCO CMEs into six time intervals of two to four years, isolating characteristic phases of the solar cycles: minimum, ascending phase, maximum, and declining phase. The respective histograms of the distribution of WTDs are displayed in Fig. 19 and indicate considerable changes along the cycles consistently confirmed by the ARTEMIS and SEEDS data sets. There is a systematic trend of the observed WTDs to get close to a Poisson process during the maxima of activity and conspicuously depart from this process during the minima, thus fully contradicting the conclusions of Telloni et al. (2014). Conversely, the WDTs during the minima and ascending/declining phases have more extended power-law tails than during the maxima of solar activity. The time evolution of the nine corresponding power-law indices displayed in Fig. 20 reveals a quasi-periodic variation in anti-phase with the solar cycle and an extremely large range of values from −3.6 (maximum of SC 23) to −1.1 (SC 23/24 anomalous minimum) based on ARTEMIS values; incidentally the WTD of the weaker SC 24 exhibits a shallower slope with an index of −3.3.
Histograms of the distribution of WTDs in nine time intervals spanning solar cycles 23 and 24 constructed from the ARTEMIS (upper nine panels) and SEEDS (lower nine panels) data sets together with two fitted models: Poisson (black curves) and power-laws (blue lines). The power-law index \(\gamma \) is given in each case
The coherent results yielded by the ARTEMIS and SEEDS data sets fully support the early conclusion of Wheatland (2003) based on the first six years of LASCO operation [1996–2001] that the CME waiting time distribution and its variation with the cycle are best explained in terms of CMEs occurring as a time-dependent Poisson process. The time varying occurrence rate of CMEs produces power-law tails despite the intrinsic exponential distribution that is characteristic of stationary Poisson processes (Aschwanden et al. 2016). The power-law index then reflects the temporal variability of the process of CME formation and is found to be anti-correlated with the solar cycle to the point of reproducing the differences between SC 23 and 24. We found that the WTD gets close to a Poisson process during the maxima of activity but departs from this process during the minima, implying high levels of randomness in the former case and a trend of intermittence or clusterization in the latter case.
WTDs of CMEs were traditionally compared to those of flares and Wheatland (2003) found very similar indices and time variation during the first six years of LASCO operation: \(\gamma _{CME} = -1.86 \pm 0.14\) and \(\gamma _{Flare} = -1.75\pm 0.08\) during [1996–1998] and \(\gamma _{CME} = -2.98\pm 0.20\) and \(\gamma _{Flare} = -3.04\pm 0.19\) during [1999–2001]. Aschwanden et al. (2016) compiled the WTDs measured over approximately three decades from solar flares hard and soft X-ray events and tabulated the power-law indices which range from 0.75 to 3.04 (their Table 7). This is quite close to the range we found for CMEs. However, when Aschwanden and McTiernan (2010) considered the specific case of hard X-ray events from the observations of five satellites from 1980 to 2008, they ended up with a single distribution function which has a power-law index of \(\approx -2.0\) at large WTs (\(>1~\mbox{hr}\)). We think that this comes from averaging the WTD over a long time interval very much like what we found for CMEs with \(\gamma = -2.2\) over two solar cycles. As we shall see later in the course of this article, only a small percentage of CMEs may be associated to flares thus the comparison of WTDs should not be over interpreted. Any similarity most likely results from the same driver of the solar eruption processes, namely the magnetic field as controlled by the solar dynamo.
6 Periodicities
Quasi-periodic variations have been found in essentially all physical indicators of solar activity extending from the 27-day synodic rotation period to the \(\approx 11\mbox{-year}\) sunspot cycle. Best examples are: (i) the 154-day periodicity found in the temporal distribution of flares (Rieger et al. 1984) and subsequently in a variety of solar and interplanetary data (Richardson and Cane 2005 and references therein); (ii) the 1.3-year periodicity detected at the base of the solar convection zone (Howe et al. 2000, 2007), in sunspot area (SSA) and sunspot number (SSN) time series (Krivova and Solanki 2002).
These multiple periodicities collectively known as intermediate or mid-term quasi-periodicities together with those in the range of 0.6–4 years are often referred to as quasi-biennial oscillations (QBOs). Barlyaeva et al. (2015) showed that the radiance of the corona exhibits such QBOs sharing the same properties as those resulting from solar activity. These quasi-periodicities carry themselves limited information but commonality among different solar/coronal processes of activity may contribute to establish a relationship. It is conceivable that sunspot area, flares, erupting prominences, and coronal mass ejections which are all some manifestation of the emergence of magnetic flux from the convection zone all exhibit the same periodicities.
The case of CMEs was considered based on LASCO observations since they offer the longest data set to investigate this question. Lou et al. (2003), Lara et al. (2008), Vourlidas et al. (2010, 2011), Choudhary et al. (2014), and Guedes et al. (2015) analyzed the first years of data (at most 13 years for the most recent articles) using either spectral analysis and/or wavelet analysis of either the occurrence or mass rates that led to a variety of periods. Those exceeding two months are: 2.2, 3.1, 3.3, 3.64, 5.06, 6.24, 6.34, 6.44, 8.9, 11.8 months and 1.1 yr (note that for convenience, we use a mean month equals to \(1/12\) of a year). Barlyaeva et al. (2018) presented a comprehensive summary of these past results and a new analysis of 21 years [1996–2016] of LASCO-C2 data supplemented by solar flares, prominences, and several proxies of solar activity, further distinguishing solar hemispheres and SC 23 and 24.
We present below an extension of their work by two additional years thus covering 23 years [1996–2018] and implementing strictly the same procedure which combines frequency (periodogram) and time-frequency (wavelet) analysis; we direct the interested readers to their publication for technical detail of the analysis. Likewise, we include a comparison with: (i) three photospheric indices or proxies of solar activity, sunspot number (SSN), sunspot area (SSA), and total photospheric magnetic flux (TMF) considered globally and by hemispheres; (ii) the GOES flare data and prominence data taken from three different sources: the Nobeyama Radioheliograph (NoRH) and Kislovodsk Observatory databases and the catalog compiled by McCauley et al. (2015) from observations with the Atmospheric Imaging Assembly onboard the Solar Dynamics Observatory restricted to the subset of unconfined events. More information on the data sources are given in Sects. 12.2 and 14. For conciseness, we restrict the periodograms to those obtained with Fourier analysis and we do not present new wavelet spectra because of their similarity with those of Barlyaeva et al. (2018). However, we include the new global wavelet spectra which were constructed from the new wavelet spectra by time-averaging the power in each frequency step limited by the cone of influence. They may be viewed as a bridge between the results of pure frequency analysis and those of time-frequency analysis. In both cases, it is possible to build a statistical test against the white and red noises and deduce the 95% significance level computed from the calculated noise models.
Figure 21 displays the updated periodograms and global wavelet spectra of monthly CME occurrence and mass rates globally and separately for the two hemispheres. We note several improvements brought by the extra two years of data compared with the results of Barlyaeva et al. (2018): (i) several periodicities which barely reached the 95% significance levels now clearly exceed them and (ii) one slight discrepancy between the two methods is solved ending in the same periodicity. Otherwise, the values of periodicity that meet the significance criterion as regrouped in Table 6 in three time domains are similar.
Periodograms and global wavelet spectra of monthly CME occurrence (left column) and mass (right column) rates globally (upper four panels), in the northern (middle four panels) and southern (lower four panels) hemispheres. The most significant peaks are labeled in either month (Mo) or year (Yr) as most appropriate. The 95% significance levels against the red and white noise backgrounds are shown by dashed red curves and dash-dot blue lines, respectively
Figure 22 displays the global wavelet spectra corresponding to the maximum phase of SC 23 and of SC 24 to highlight differences between the two cycles. Most of the periodicities were found by Barlyaeva et al. (2018) but a few changes are noted prominently in the case of the mass rate in the northern hemisphere where the period of 5.9 months which slightly exceeded the significance criterion during SC 24 now barely miss it and vice-versa a period of 4.3 months which barely missed the criterion during SC 23 now meets it.
Global wavelet spectra of monthly CME occurrence (left column) and mass (right column) rates for SC 23 and 24 globally (upper panels), in the northern (middle panels) and southern (lower panels) hemispheres. The spectra are shown by blue curves and the 95% significance levels against the red noise backgrounds by red curves. The continuous and dashed lines correspond to SC 23 and 24, respectively
The periods found in indices/proxies of solar activity and in eruptive processes are listed in Table 6 but to facilitate the comparison with those of CMEs, we offer a graphical presentation in Fig. 23. The few minor changes do not change the main conclusion already reached by Barlyaeva et al. (2018) namely the very limited commonality for periods of less than one year. The few exceptions are the periods of 3.1–3.2 months found in the occurrence rate of the global set of CMEs and in SSA (and marginally, the 3.4-month period seen in TMF) and those of 5.9–6.1 months found in the \(\text{CME}_{\text{N}}\) subgroup and in \(\mbox{SSA}_{north}\). Periods of 1 to 1.2 years are found in the \(\text{CME}_{\text{N}}\) subgroup, in \(\mbox{SSN}_{north}\), in TMF, in \(\mbox{TMF}_{south}\) and in the prominence data sets of both NoRH and Kislovodsk (with however a possible bias inherent to ground-based observations) but are absent in all other cases. Periods clustering around two years are observed in \(\text{CME}_{\text{S}}\), \(\text{CME}_{\text{m,S}}\), SSN, \(\mbox{SSN}_{south}\), SSA, and \(\mbox{SSA}_{south}\) and absent otherwise, suggesting that they may be restricted to southern activity.
The changes noted above between the present results and those of Barlyaeva et al. (2018) raise the question of the stability of the periods, that is how long do the various periodic regimes hold. Barlyaeva et al. (2018) proposed a method of quantifying the duration of these regimes on the wavelet spectra and consisting in integrating the power in slices one month wide bounded by contours defined by the significance level and whose duration exceed a preset integer number \(k\) of the period \(P\) (see their Fig. 14). Figure 24 synthesizes the results for two extreme values \(k=2\) and 4. In the case of the weak constraint \(k=2\), most of the processes exhibit high- and mid-frequency oscillations with periods of \(\approx3\) months and \(\approx1\) year whereas the period of \(\approx6\) months is less frequent. The most striking outcome is the dichotomy between the two hemispheres, with periods of 1–1.5 years prevailing in the northern hemisphere whereas a period of \(\approx2\) years prevails in the southern one. The only notable exception is \(\mbox{TMF}_{south}\) which exhibits in addition a marked one-year period. The more stringent condition \(k=4\) confirms that the \(\approx3\)-month oscillation is present in most—but not all—processes whereas the \(\approx6\)-month period is present in only a few. The one-year period persists in only the TMF and the prominences, and the two-year period has disappeared simply because the condition \(k=4\) translates in a duration of 8 years, largely over what we observe.
Distributions of periods found in CME rates, solar proxies, M- and X-class flares and prominences based on the time-frequency (wavelet) analysis. Two cases of stability are displayed depending upon the number of observed periods: two periods (left panel) and four periods (right panel). The vertical dashed lines at 3, 6, and 12 months are intended to guide the eyes. The results in the two hemispheres are emphasized by different colors: blue (north) and red (south)
7 Angular Width
The angular width \(\mbox{W}\) of a CME estimates its angular extent in the sky plane. It is therefore biased by both projection and geometric effects as discussed in Sect. 3 and in addition, it tends to increase as the CME expands in the corona. In spite of these shortcomings and of the different methods of measurement implemented by the four catalogs which may explain some of the discrepancies, the results are broadly consistent as we now illustrate. An overview of the distribution of angular widths during the 23 years of LASCO observations is presented in two three-dimensional graphs shown in Fig. 25 which display the annual count of CMEs per bin of \(30{^{\circ}}\) from the ARTEMIS catalog in two angular intervals, the whole range [\(0{^{\circ}}\mbox{--}360{^{\circ}}\)] and a zoom on the very wide CMEs with widths exceeding \(180{^{\circ}}\). Two conspicuous features emerge from these graphs, the close similarity between the distributions for SC 23 and 24 for CMEs narrower than \(180{^{\circ}}\) whereas larger CMEs exhibit markedly different distributions. The second aspect is analyzed below in Sect. 13. The first aspect is further investigated in Fig. 26 which displays the annual evolution of the mean and root-mean-squared values of the distributions restricted to widths smaller than \(180{^{\circ}}\) from the four data sets. This restriction eliminates \(\approx1.5\%\) of the total population in the case of ARTEMIS, SEEDS, and CACTus and 4.4% in the case of CDAW. The CDAW results stick out with the largest widths ranging from \(30{^{\circ}}\) to \(60{^{\circ}}\) and the largest dispersions followed by ARTEMIS (\(22{^{\circ}}\leq \mbox{W} \leq 42{^{\circ}}\)), CACTus (\(24{^{\circ}}\leq \mbox{W} \leq 34{^{\circ}}\)), and SEEDS (\(18{^{\circ}}\leq \mbox{W} \leq 28{^{\circ}}\)). The four temporal evolutions track more or less closely the solar cycle with CDAW and ARTEMIS showing the largest range between the SC 23/24 minimum and the two maxima (respectively \(30{^{\circ}}\) and \(20{^{\circ}}\)) and SEEDS and CACTus, the lowest range (\(10{^{\circ}}\)).
Three-dimensional distributions of angular width of CMEs registered in the ARTEMIS catalog. The columns correspond to the annual number of CMEs binned with a step of \(4{^{\circ}}\). The upper panel covers the whole range of widths whereas the lower panel zooms on CME with widths larger than \(180{^{\circ}}\)
We now consider the question of the distribution of angular widths and display in Fig. 27 two histograms on a linear scale of width with a bin size of \(4{^{\circ}}\) and a logarithmic scale of frequency in two different ranges of width, the lower graph zooming on the \(0{^{\circ}}\mbox{--}30{^{\circ}}\) interval. Note that we do not distinguish the two solar cycles as the above results have not shown any marked dissimilarity except for the small populations of very wide CMEs. The agreement between the ARTEMIS and CDAW histograms in the range \(\approx 40{^{\circ}}\mbox{--}270{^{\circ}}\) is quite remarkable. At the lower end, at widths less than \(\approx30{^{\circ}}\), the ARTEMIS and CACTus histograms agree quite well whereas SEEDS reports a larger number of narrow CMES and CDAW a smaller number. At the upper end, at widths larger than \(\approx 300{^{\circ}}\), here again ARTEMIS and CDAW report an increasing number of CMEs with increasing width not seen in the other catalogs except for the peak in the largest bin at \(360{^{\circ}}\) in the CDAW histogram.
Histograms of the apparent angular width of CMEs from the four catalogs over the whole angular range (upper panel) and zoomed over the \(0\mbox{--}30{^{\circ}}\) range (lower panel). The straight lines are the best-fit linear functions to the four distributions. The vertical dotted lines delimit the domain where the fits were performed
All histograms display a linear regime over the mid-range of widths and this is quantified in Fig. 27 where log-lin linear functions are best fitted to the four histograms in the range \(40{^{\circ}}\mbox{--}180{^{\circ}}\) and in Table 7 which gives the slopes. Note that, with the exception of CACTus, the linear regime extends further, to \(\approx 220{^{\circ}}\) for SEEDS and up to \(\approx 300{^{\circ}}\) for both ARTEMIS and CDAW; for ARTEMIS, it even holds down to \(\approx 20{^{\circ}}\). Consistent with the above results, the fits to the ARTEMIS and CDAW data sets are almost indistinguishable. The CACTus fits parallels them whereas SEEDS sticks out with a steeper slope. The linear fits indicate that the distributions of angular width follow an exponential law implying that the angular widths are random and independent. Therefore, we do not support the results of Robbrecht et al. (2009) based on their analysis of CMEs during SC 23 that the CDAW CME widths are log-normally distributed, broadly peaked around \(30{^{\circ}}\), whereas the CACTus CME widths follow a power-law.
8 Apparent Latitude
The angular position of a CME is usually estimated by the position angle of its axis measured counter clockwise from solar north, hence the terminology of “central position angle” abbreviated to CPA. For practical purposes and in particular for comparing with the location of other solar phenomena assuming radial propagation of the CMEs, it is convenient to use instead the heliographic latitude \(\varLambda \). Conversion from CPA to \(\varLambda \) is straightforward for CMEs near the limb but subject to increased projection effects with increasing angles from the plane of the sky. We follow the usual convention and assimilate CPAs to apparent (heliographic) latitudes.
As mentioned in Sect. 2.2, after 29 October 2010 the reference axis of SoHO was fixed to the perpendicular to the ecliptic plane causing the projected direction of the solar rotational axis to oscillate around the vertical direction on the LASCO images. This effect can be seen on Fig. 3 where two images labeled \(c\) and \(d\) are rotated to bring solar north up. It is unclear but very probable that this effect was not taken into account when determining the CPA of CMEs for the SEEDS, CACTus, CDAW, and CORIMP catalogs as their authors are unconnected to the LASCO operations. The maximum error that occurs twice per year amounts to \(7.5{^{\circ}}\). This effect was obviously accounted for when building our synoptic maps so that the CPA are correctly determined in the ARTEMIS catalog.
8.1 Distribution of Apparent Latitude
Figure 28 displays the distribution of apparent latitude obtained from the four catalogs ARTEMIS, SEEDS, CACTus, and CDAW in both absolute and normalized frequencies. The four distributions agree quite well and are nearly symmetric about the solar equator with a profile of continuously decreasing number with increasing latitudes. There are however two noteworthy deviations: (i) a skewness of the CDAW curve which translates into an excess at southern latitudes between −15 and \(-45{^{\circ}}\) and (ii) an excess of CMEs at high latitudes (\(>65{^{\circ}}\)) in both hemispheres present in the CACTus data whereas the three other curves follow a steady decline.
The annual evolution of the distributions is synthesized in two graphs showing the mean values calculated for each calendar year and the corresponding root-mean-squared values (Fig. 29). The mean values from the four catalogs track each other remarkably well with only minor differences and conspicuously reveal a surprising trend when comparing the two solar cycles. Whereas the mean values fluctuate about the solar equator during SC 23 with however two excursions (to the north in 1999 and the south in 2006), they exhibit a rather erratic behaviour during SC 24. They progress to increasing northern latitudes starting during the SC 23/24 minimum to the rising phase of SC 24, then experience a marked decrease to negative latitudes (approximately from \(0{^{\circ}}\) to \(-5{^{\circ}}\)) in 2013, and thereafter move again to positive latitudes (\(\approx+5{^{\circ}}\)). The rms values agree very well during the two solar cycle maxima during which they raise to similar large values of typically \(45{^{\circ}}\), but disagree during the two minima. In the case of the second one (23/24), whereas ARTEMIS and SEEDS roughly agree on rms values of \(\approx 20{^{\circ}}\), those of CACTus reach \(\approx 30{^{\circ}}\) and those of CDAW exceed \(40{^{\circ}}\).
The heliolatitudinal distributions of the CMEs from 1996 to 2018 shown in Fig. 30 allow a deeper insight into the above results. Globally, the four distributions exhibit the same pattern of a confinement to a narrow equatorial band during the minima of solar activity, a rapid poleward spread during the rising phases of the solar cycles which reaches its maximum extension during the maxima of activity followed by a progressive narrowing during the declining phase of activity in agreement with pre-LASCO observations (Hildner 1977; Munro et al. 1979; Howard et al. 1985; Hundhausen 1993). This pattern tracks the excursion of the tilt angle of the heliospheric current sheet (HCS) calculated by the Wilcox Solar ObservatoryFootnote 6 (we used the “classic” potential field model as recommended). Note a marked difference between the two solar cycles as the ARTEMIS, SEEDS, and CDAW data yield asymmetric distributions during SC 23 (rapid poleward spread and slow narrowing) but rather symmetric distributions during SC 24 with little differences between the rising and declining phases. The CACTus distribution is highly distorted by the presence of a large number of high latitude CMEs already detected in Fig. 28 and which are absent in the other three data sets. Incidentally, some high latitude CMEs are present during the minima in the CACTus and CDAW distributions whereas they are totally absent in the ARTEMIS and SEEDS distributions. This explains the different behaviours of the rms values of the latitude seen in their annual variation during the two minima, particularly the 23/24 minimum, during which CACTus and CDAW yield significantly larger values than ARTEMIS and SEEDS. The abrupt change of the mean value of the latitude between 2012 and 2013 is best understood by closely inspecting the ARTEMIS distribution and results from a conspicuous deficit of CMEs in the northern hemisphere which took place in 2013. This opens the questions of north-south asymmetry and of high-latitude CME which are discussed in the next section.
Heliolatitudinal distributions of the CMEs reported by the four catalogs, respectively from top to bottom: ARTEMIS, SEEDS, CACTus and CDAW. The black lines correspond to the tilt angle of the heliospheric current sheet in the northern and southern hemispheres and is plotted separately in the lower panel for legibility
8.2 North-South Asymmetry and High-Latitude CMEs
It is well established that the two solar hemispheres generally exhibit different patterns of activity—often with a phase difference—leading to a more or less pronounced north-south asymmetry (e.g., Bisoi et al. 2014; Gopalswamy et al. 2003b). This results from the general evolution of solar magnetic activity connected to the solar dynamo (Krivodubskij 2005; Brun et al. 2015) and the phase difference appears to belong to a broad secular variation with reversals occurring roughly every eight solar cycles (Zolotova et al. 2010). A global count per hemisphere indicates that a similar asymmetry is observed for CMEs as well. Considering first SC 23 and 24 altogether and on the basis of the ARTEMIS catalog, the northern and southern CMEs amount to respectively 52.7% and 47.3% of the whole population. But separating the two solar cycles reveals a contrasted situation: for SC 23, the above percentages are respectively 49.4% and 50.6% (hence a slight excess of southern CMEs) whereas for SC 24, they respectively amount to 56.2% and 43.8% (hence a marked excess of northern CMEs). The temporal evolution of the two mean latitudes calculated in each hemisphere (Fig. 31) confirms this trend and allows to track the excesses to specific time intervals: [2001–2002] and [2005.5–2006] for the southern excess and a much broader interval [2010–2016] for the northern excess. Note that the asymmetry is totally absent during the two minima of solar activity. Additional information is provided by the heliolatitudinal distributions (Fig. 30) where the excesses may be tracked to prominently high-latitude (HL) CMEs as consistently shown by the four catalogs with an asymmetry especially pronounced during SC 24. These HL CMEs are precisely those which lie outside the envelope defined by the maximum excursion of the tilt angle of the HCS and the question arises as to whether their apparent high latitudes reflect or not their true latitudes. Projection effects are possible and in fact, according to Hundhausen (1993), structures seen at latitudes \(| \varLambda | \) larger than \(\approx 60{^{\circ}}\) could have true latitudes \(| \lambda | \) anywhere in the range \(45{^{\circ}}\) to \(90{^{\circ}}\). But we argue that the bulk of those CMEs have indeed their origin at high altitudes and are associated to polar streamers. Zhukov et al. (2008) convincingly showed that these polar streamers are unrelated to the coronal neutral line and current sheets predicted by potential field models but result from polar coronal current sheets associated with large-scale photospheric magnetic neutral lines around the poles of the Sun, the polar crown neutral lines located at latitudes \(| \lambda | \) of \(70{^{\circ}}\) to \(75{^{\circ}}\) during the maxima of activity. They are “classical” streamers situated above low-lying loops (observed for instance by SoHO/EIT) connecting the regions of opposite magnetic polarity on the two sides of polar crown neutral lines. These authors hypothesized that theses large-scale structures may be involved in the process of CME eruptions and this is precisely what we are seeing in Fig. 31. To ascertain this connection, we compare the temporal occurrence rates of CMEs separately in the two high latitudes regions defined by \(60{^{\circ}}< | \lambda | < 90{^{\circ}}\) with the temporal evolution of the radiance of the K-corona integrated in the two latitude sectors \(30{^{\circ}}\) wide centered on the polar north and south directions, thus extending the work of Barlyaeva et al. (2015) to 2018. The top panel of Fig. 32 shows an impressive agreement between both ARTEMIS and SEEDS occurrence rates with the variation of the integrated radiance; even the CDAW rate follows the same pattern with however lower rates. This agreement is confirmed in higher detail by the graph of the differences between the north and south variations (lower panel of Fig. 32) thus confirming our conjecture of direct connection between HL CMEs and polar steamers.
Temporal variation of the monthly mean values of the apparent latitudes of the ARTEMIS CMEs separately in the northern (solid red line) and southern (solid blue line) hemispheres. These two curves are mirrored with respect to the equator (dashed lines with same color coding) to facilitate the comparison
Upper panel: monthly rate of the high-latitude CMEs from ARTEMIS, SEEDS, and CDAW catalogs to be compared with the integrated radiance of the K-corona in the polar regions (black lines). The north and south variations are simultaneously displayed in the upper and lower halves of the figure. Lower panel: differences (north-south) of the above quantities with the same conventions. The CDAW rate is multiplied by a factor of 2 to better match the other curves. In the two panels, the coronal integrated radiance is arbitrarily scaled to best fit the occurrence rates and their differences
9 Kinematics
9.1 Apparent Speed
The determination of the apparent speed of CMEs is among the most challenging parameters that can be extracted from coronagraphic images for at least three reasons. First, whereas typical CMEs have relatively constant speeds at distances larger than \(\approx2~\mbox{R}_{\odot}\), it is generally admitted that slow CMEs tend to accelerate and to the contrary, fast CMEs tend to decelerate while crossing the C2 and C3 fields of view (Webb and Howard 2012) so differences may be expected between catalogs that use both LASCO-C2 and C3 images (CDAW and CACTus) and those which rely only on C2 images (ARTEMIS and SEEDS). Second, a unique value for the speed of a CME remains a simplistic view as different parts travel at different speeds so that a velocity field would be a much more appropriate description (Boulade et al. 1997; Robbrecht and Berghmans 2004; Colaninno and Vourlidas 2006; Byrne 2015). Generally speaking, the front part has the largest speed with the rear and side parts trailing behind. Third, these catalogs implement different procedures for determining speeds. In the case of ARTEMIS, disregarding the “propagation” velocity which is used as a first estimate, the “global” velocity gives a higher weight to the brightest parts, that is the front and central parts (which are the fastest) whereas the “median” velocity gives an equal weight to every angular section of the CME. The SEEDS speed is taken from the highest peak using the leading-edge segmentation. CACTus measures a linear speed profile as a function of position angle over the CME angular width and lists the median value. The CDAW linear speed is obtained by fitting a straight line to the height-time measurements at the fastest section of CMEs, the so-called measurement position angle (MPA). It is noted that the MPA does not always coincide with the central position angle (CPA), for instance in the case of CMEs which propagate non-radially.
An overview of the distribution of speeds during the 23 years of LASCO observations is presented in the three-dimensional graph shown in Fig. 33 which displays the annual count of CMEs per bin of \(100~\mbox{km}\,\mbox{s}^{-1}\) from the ARTEMIS catalog. Two features emerge from this graph, the low speeds during the solar cycle minima more pronounced during the second one (the anomalous SC 23/24 minimum) and the slight trend to lower speeds in SC 24 compared with SC 23.
The distributions and cumulative distributions of apparent speeds of CMEs from the four catalogs (for ARTEMIS, both “global” and “median” velocities are shown) over the two solar cycles and separately for SC 23 and 24 are displayed in Fig. 34 and Fig. 35, respectively. Two distinct groupings are clearly noticeable, the ARTEMIS “median” and SEEDS speeds on the one hand with distributions peaking at \(\approx 150~\mbox{km}\,\mbox{s}^{-1}\) and the ARTEMIS “global”, CACtus, and CDAW speeds on the other hand with distributions peaking at \(\approx 250\mbox{--}300~\mbox{km}\,\mbox{s}^{-1}\). For the two ARTEMIS speeds, this is consistent with their respective weightings and we had expected the SEEDS distribution to match the “global” one (and the CDAW one as well) whereas it matches the ARTEMIS “median” distribution, a rather surprising result. Likewise, we had expected the CACTus distribution to match the ARTEMIS “median” distribution whereas it is in agreement with the “global” one and that of CDAW. Note that the spread of the cumulative distributions is significantly less during SC 24 than during SC 23. As repeatedly pointed out in past studies, the CACTus distribution exhibits an excess of high speeds \(>1000~\mbox{km}\,\mbox{s}^{-1}\) and up to \(2000~\mbox{km}\,\mbox{s}^{-1}\) which is highly suspicious in view of their very small number in the other data sets.
Figure 36 displays the annual evolution of the mean and standard deviation values of the speed distributions from the four catalogs (specifically the “global” velocity in the case of ARTEMIS) and reveals a striking difference between the two cycles. During most of SC 23, the mean values are spread over a wide range, with maxima of \(\approx250~\mbox{km}\,\mbox{s}^{-1}\) for SEEDS, \(\approx400~\mbox{km}\,\mbox{s}^{-1}\) for ARTEMIS, \(\approx550~\mbox{km}\,\mbox{s}^{-1}\) for CDAW, and \(\approx600~\mbox{km}\,\mbox{s}^{-1}\) for CACTus whereas during SC 24, they all converge to a narrow range of \(\approx300\mbox{--}400~\mbox{km}\,\mbox{s}^{-1}\). Both ARTEMIS and CDAW distributions agree on distinctly lower mean values during solar cycle minima whereas there is only a hint of this behaviour in the SEEDS distribution and a total absence in the CACTus distribution. Curiously, this latter distribution abruptly decreased after 2009 to be more in line with the speeds of the other catalogs, a probable consequence of ceasing recording very large speeds. Finally, note that contrary to the other three data sets, the SEEDs mean values are larger during SC 24 than during SC 23, a very surprising trend indeed since the former is known to be weaker than the latter. Table 1 offers a synthetic comparison with speeds measured by other coronagraphs from which it is however difficult to extract a meaningful trend since they have been obtained during various time intervals and different conditions of solar activity. The Skylab value stands out as well above the others, a rather surprising result since the observations were performed in 1973–1974 very near the SC 20/21 minimum.
9.2 Apparent Acceleration
The determination of the apparent acceleration of CMEs is probably even more challenging than that of the speed and this parameter is reported in only three catalogs, CDAW and CORIMP using LASCO-C2 and C3 images and SEEDS using only C2 images. This obviously should be kept in mind when comparing their results. Likewise the speed, these catalogs implement different procedures for determining the acceleration.
-
CDAW relies on quadratic fits to height-time profiles constructed when manually tracking the CMEs through the \(\mbox{C2}+\mbox{C3}\) field of view.
-
SEEDS accelerations are derived from tracking the highest peak using the leading-edge segmentation.
-
CORIMP isolates the CME structure and automatically tracks its front edge at different position angles. Quadratic fits to the different height-time profiles yield accelerations and three values are reported in the catalog, minimum, maximum, and mean; this last value is generally used in statistical analysis including the present one (their minimum and maximum are mostly the opposite of each other and take excessively large absolute values).
Byrne (2015) compared the accelerations of six CMEs of different types (arcade eruption, gradual, impulsive, faint, fast, and slow) listed in the three catalogs and their Table 1 reveals considerable scatters among the values. This illustrates the considerable difficulty of the exercise.
Early analysis of CDAW accelerations indicated that both positive and negative values were measured ranging from approximately −80 to \(+40~\mbox{m}\,\mbox{s}^{-2}\) resulting from the interplay of the propelling and retarding (drag) forces, with a trend for slow CMEs to accelerate and fast CMEs to decelerate in the LASCO field of view (see for instance Gopalswamy 2004; Vršnak et al. 2004, and Yashiro et al. 2004). The first statistical study of acceleration of 50 CMEs by Zhang and Dere (2006) is superseded by that of Wen et al. (2008) who considered 5594 CMEs and they confirmed that slower CMEs (with speeds between 200 and \(500~\mbox{km}\,\mbox{s}^{-1}\)) tend to have a positive acceleration (\(\approx 1~\mbox{m}\,\mbox{s}^{-2}\)), whereas less than 10% CMEs have an average negative acceleration (\(\approx -2.2~\mbox{m}\,\mbox{s}^{-2}\)) as they propagate from 5 to \(30~\mbox{R}_{\odot}\). They further concluded that “for most individual CMEs, one cannot say if they are accelerated or decelerated, and for only 8% of all observed CMEs can have the sign of the acceleration be extracted”.
Figure 37 displays the distributions of apparent accelerations of CMEs from the three catalogs. The SEEDS data set includes 42449 measurements corresponding to 81% of the listed CMEs, the CDAW data set (excluding the “very poor events”) includes 20766 measurements (98%), and the CORIMP data set includes 5971 measurements (54%). Whereas the SEEDS and CDAW distributions are nearly symmetric extending from −100 to \(+100~\mbox{m}\,\mbox{s}^{-2}\) with mean values of \(-5.4~\mbox{m}\,\mbox{s}^{-2}\) and \(1.2~\mbox{m}\,\mbox{s}^{-2}\), respectively, that of CORIMP is strongly asymmetric and skewed to positive values with accordingly a very small number of negative values in the range −20 to \(0~\mbox{m}\,\mbox{s}^{-2}\).
Figure 38 displays the annual evolution of the mean and standard deviation values of the acceleration distributions from the three catalogs. As a result of its skewed distribution, the CORIMP annual means far exceeds the other two, by a factor which can even exceeds 10 depending upon the years (note that the CORIMP values are divided by a factor of 10 in the figure). The three evolutions are nearly constant except for SEEDS which shows a trend for negative accelerations during SC 24. The slight increase of the CDAW accelerations after 2004 remains much smaller than the standard deviations and is therefore not significant. The mean annual CDAW acceleration displayed by Compagnino et al. (2017) in their Fig. 2 has an anomalous peak of \(\approx17~\mbox{m}\,\mbox{s}^{-2}\) in 2009, far exceeding the other values. We verified that this peak results from the inclusion of the very poor events.
The question of the relationship between speed and acceleration is analyzed by comparing the distributions of accelerations in four interval of speeds: 0–250, 250–450, 450–900, and \(>900~\mbox{km}\,\mbox{s}^{-1}\) (Fig. 39). In the case of CDAW, the trend observed in past studies and notably by Wen et al. (2008) of decreasing acceleration with increasing speed is confirmed but remains modest. The CORIMP accelerations exhibit the exactly opposite behaviour whereas the SEEDS behaviour is quasi neutral. Note that in both cases, the accelerations of the fast CMEs with speeds exceeding \(900~\mbox{km}\,\mbox{s}^{-1}\) are distributed over a very large range but restricted to positive values in the case of CORIMP. This question will be further considered in Sect. 11 which deals with the correlations between CME parameters.
10 Kinetic Energy
The question of the kinetic energy and more generally of the energetics of CMEs has generally not been addressed in the main reviews quoted in the Introduction except that of Webb and Howard (2012) who summarized the results of Vourlidas and coworkers who have been at the forefront of this topics. Vourlidas et al. (2000) considered 11 LASCO CMEs that exhibited flux-rope morphologies and determined the evolution of their potential, kinetic, and magnetic energies with heliocentric distance to conclude that the former two increase at the expense of the latter as the CMEs travel outward. Vourlidas et al. (2002) presented measurements of the kinetic energy for 2449 CDAW CMEs observed during the [1996–2000] interval. They found an average value of \(4.3\times 10^{30}~\mbox{erg}\) (comparable to that of the Solwind CMEs of \(3.5\times 10^{30}~\mbox{erg}\)) and a distribution of kinetic energy that follows a power law with an exponent of about −1. This study was extended to the full SC 23 and to 7668 CMEs by Vourlidas et al. (2010) who found that the distribution of kinetic energy has an average value of \(2.3\times 10^{29}~\mbox{erg}\) and can be fitted by a log-normal function with an excess of low kinetic energy events. Note that this article contains several errors (not affecting the above results) as the authors failed to take into account the \(180{^{\circ}}\) rolls of the SoHO spacecraft; an erratum was published by Vourlidas et al. (2011).
Figure 40 displays the temporal evolutions of the monthly-averaged kinetic energy of CMEs reported by the ARTEMIS, CDAW, and CORIMP catalogs, the latter being included to broaden the comparison as we did for the mass. They all agree quite well in tracking the solar activity with very deep minima during the anomalously weak SC 23/24 minimum. Note the close similarity of the ARTEMIS and CORIMP curves making it difficult to distinguish them whereas the CDAW kinetic energy is generally larger by a factor of \(\approx2\) except during the first two years (1996 and 1997), the declining phase of SC 23, and the second half of SC 24 when it tends to agree with the former two curves. This behaviour is likely associated to larger speeds reported by CDAW (via its square value in the kinetic energy) precisely during the same time intervals as seen in Fig. 36.
We now consider the question of the distribution of kinetic energy of CMEs and display in Fig. 41 its histograms on a log-log scale over eight decades (\(10^{25}\) to \(10^{33}~\mbox{erg}\)) and over the two solar cycles and separately for SC 23 and 24. The statistics of the distributions are summarized in Table 8 which includes two sections depending whether the CORIMP values are included; in this case, all statistics are calculated on the restricted time interval covered by CORIMP. The ARTEMIS distributions are very well fitted by Gaussian curves in the three cases with just slight excesses at both extremities of very low and very large kinetic energies, particularly modest during SC 24. Although not plotted for legibility, it is obvious that the same conclusion holds true for the CDAW distributions although the excesses are more pronounced. To the contrary, the CORIMP distributions strongly depart from Gaussian with a pronounced skewness toward the low kinetic energies. The consistent quasi-Gaussian behaviours of the ARTEMIS and CDAW distributions on a log-log scale implies that the kinetic energy of CMEs follows a log-normal distribution as commonly found in solar physics. This result clearly contradicts conclusion # 3 of Vourlidas et al. (2010), namely that “the energy distribution becomes log-normal only for measurements at around \(10\mbox{--}15~\mbox{R}_{\odot}\)” and that “measurements at lower heights provide an incomplete picture of the event and will bias statistical studies”. This is probably connected to the related question of the mass increase as CMEs propagate that we questioned in Sect. 4.2.
11 Correlations Between Parameters
The question of the correlations between the physical properties of CMEs was considered by Hundhausen et al. (1994) based on their determination from the SMM observations and they found that widths, latitudes, and speeds of mass were only weakly correlated. In particular, speeds varied only slightly with the latitude of the ejection as high-latitude ejections had speeds rather similar to active latitude ejections. The topics was further investigated based on LASCO observations, particularly the speed–width and speed–acceleration relationships. In both cases and based on the CDAW catalog, correlations were established (Gopalswamy 2004; Vršnak et al. 2004; Yashiro et al. 2004; Gopalswamy et al. 2015c). However, Webb and Howard (2012) pointed out several significant discrepancies with results derived from the CACTus catalog. In order to clarify the situation, we performed a systematic study of the correlations between the CME parameters prominently based on the ARTEMIS catalog.
11.1 Speed–Acceleration
This correlation was briefly considered in Sect. 9 and conflicting results were found when considering the accelerations given by the SEEDS, CDAW, and CORIMP catalogs. It is further explored in Fig. 42 where the scatterplots (left panels) display the full range of speeds and accelerations given by the three catalogs highlighting the pronounced differences of the distributions and of the ranges of accelerations. At the scale of these plots, the only common feature that emerges is a common average acceleration of zero independent of speed. To tentatively extract possible subtle information, we switched to two-dimensional histograms to avoid the illegible clumping in the scatterplots and we restricted the ranges of both speed and acceleration (right panels). However, they support the above conclusions that acceleration is independent of speed and has an average value of \(\approx0~\mbox{m}\,\mbox{s}^{-2}\).
11.2 Speed–Width
Past studies indicated a positive correlation between speed and angular width with even distinct behaviours for the two cycles, CMEs of a given width having larger speeds during SC 23 than during SC 24 (Gopalswamy et al. 2015c). After de-projection of the speed of a large number of CDAW CMEs, Howard and Simnett (2008) confirmed the positive correlation and further noted that the linear trend of the speed versus width distribution was stronger with the corrected speeds than with the uncorrected ones. However, the scatterplots illustrating these studies exhibit considerable dispersion implying low Pearson’s linear correlation coefficients. Consequently, the slopes of the linear regressions are essentially determined by the very few events having the largest speeds and widths. Figure 43 displays the two-dimensional histograms of the speed versus width distributions over the two cycles and separately for SC 23 and 24. They do indicate a very weak correlation with speed slightly increasing with width. Rather than using the classical least squares regression (L2-norm) and in order to circumvent the above problem, we opted for the far more robust least absolute deviations (L1-norm) since it is resistant to outliers in the data. The linear regressions yielded the function \(\textit{Width} = 1.12 \times V - 288\) for the two cycles, the same slope of 1.12 for SC 23 and a slightly reduced slope of 1.09 for SC 24. This is in clear disagreement with the results of Gopalswamy et al. (2015c) who found slopes of 0.09 for SC 23 (273 CDAW events) and 0.17 for SC 24 (2014 CDAW events) with very low correlation coefficients (0.56 and 0.71, respectively).
11.3 Speed–Mass
Figure 44 displays the two-dimensional histograms of the speed versus mass distributions which shows a quasi linear trend of increasing speed with increasing mass on a log-log scale fitted by the function \(\log(V) = 0.52 + 0.13 \times \log(M)\) thus yielding a slope of 0.13. As part of his study of the energetics of solar flares and associated CMEs, Aschwanden (2017) considered 334 joint LASCO and AIA events and obtained a scatterplot that exhibits a similar behaviour, however with a larger slope of \(\approx0.25\). His Fig. 8b shows that this slope is consistent with that predicted by the theoretical Rosner-Tucker-Vaiana (RTV) scaling law but that a downward scaling by a multiplicative factor of 1.8 (estimated visually) would better fit the data. The RTV function \(\log(V) = -0.95 + 0.25 \times \log(M)\) is over plotted on our histogram and turns out to clearly deviate from our result. The 334 events considered by Aschwanden (2017) were associated with flares and the slope of 0.25 may perhaps be linked to the this special class of CMEs.
11.4 Speed–Latitude
Figure 45 displays the two-dimensional histogram of the speed versus latitude distribution together with the linear regression \(V = 298 - 0.185 \times \textit{Latitude}\). This corresponds to a very weak trend of decreasing speed with increasing latitude quasi symmetric with respect to the equator. Indeed, the average speed decreases from \(300~\mbox{km}\,\mbox{s}^{-1}\) at the equator to \(280~\mbox{km}\,\mbox{s}^{-1}\) at the poles.
11.5 Mass–Latitude
Figure 46 displays the two-dimensional histograms of the mass versus latitude distribution on a lin-log scale together with the linear regression \(\log(M)=14.5 - 1.5 \times 10^{-4} \times \textit{Latitude}\). Likewise the speed–latitude, the dependence of the mass on latitude is extremely weak with average values of \(3.2\times 10^{14}~\mbox{g}\) at the equator and \(3.1\times 10^{14}~\mbox{g}\) at the poles.
11.6 Mass–Width
Figure 47 displays the two-dimensional histogram of the mass versus width distribution on a log-log scale together with the linear regression \(\log(M)=12.5+1.38 \times \log(\textit{Width})\). As expected, there is a very strong relationship of increasing mass with increasing width.
11.7 Width–Latitude
Figure 48 displays the two-dimensional histogram of the width versus latitude distribution on a lin-lin scale together with two slightly different linear regressions, \(\textit{Width}=26.9-0.05 \times \textit{Latitude}\) for the northern hemisphere and \(\textit{Width}=25.8+0.03 \times \textit{Latitude}\) for the southern one. This leads to an average value of \(26.3{^{\circ}}\) at the equator, to \(22.8{^{\circ}}\) and \(23.5{^{\circ}}\) at the north and south poles, respectively. This correlation is thus extremely weak and quasi independent of the hemisphere.
12 Solar Cycle Activity
Past studies of the occurrence rate of CMEs established a clear correlation with solar activity, usually using the sunspot number index (SSN) as a standard reference. This was already noticed in the Solwind CME data (Howard et al. 1985) and Webb and Howard (1994) found a linear relationship between CME rate and SSN thus concluding that the former tends to track the latter in both amplitude and phase and that “no one class of solar activity was better correlated with CME rate than any other on the long term”. On the basis of the CDAW catalog of LASCO CMEs, Gopalswamy et al. (2004) found that both the CME occurrence rate and the SSN averaged over 13 Carrington rotations exhibited double peaks, but that the CME peaks lagged sunspots by many months during SC 23. Using their CACTus catalog, Robbrecht et al. (2009) agreed on the tracking in amplitude and on a time lag varying from six months to one year. This lag was explained as resulting from high latitude CMEs which arise from polar crown filaments and which experience a “rush to the pole” near the maximum of solar activity and disappear before sunspots reach low latitudes (Gopalswamy 2004; Webb and Howard 2012). The atypical behaviour of the CDAW rate diverging from the SNN temporal evolution starting in 2003 came as a surprise but was later understood as being caused by the inclusion of “very poor” events as discussed in Sect. 4.1. The rate of SEEDS and CACTus CMEs increasing faster than expected during the rising phase of SC 24 raised question, but was tentatively related to the weakness of the polar fields (Luhmann et al. 2011; Petrie 2013). As explained in Sect. 2.2, this was caused by the increased image cadence of the LASCO images in 2010. Once corrected appropriately (Hess and Colaninno 2017), the SEEDS rate was found to be in line with the variation of solar activity. Using masses of the CDAW catalog as more robust against faint events, Wang and Colaninno (2014) found that the mass rate was well correlated with the sunspot number throughout SC 23 and SC 24 until February 2013 and concluded that, in addition to producing fewer CMEs than SC 23, SC 24 was also characterized by slower and less massive ejections. They did consider the correlation of SSN with the CME occurrence rate from the SEEDS and ARTEMIS catalogs and derived correlation coefficients of respectively 0.94 and 0.97. Finally, Gopalswamy et al. (2015c) pointed out that, based on the CDAW catalog restricted to width \(\geq30{^{\circ}}\) (i.e., excluding narrow events), the relationship between SSN and CME rate changed in SC 24, the daily CME rate per SSN being larger during SC 24 than SC 23.
With the end of SC 24 at hand and the appearance of the first signs of SC 25 as weak, short-lived sunspots in HMI images (Hoeksema 2018), we have the unique opportunity to follow and study CMEs over two full contiguous solar cycles homogeneously detected by the same LASCO instrument. Since by all measures SC 24 is the weakest in a century with a particularly strong asymmetry between the north and south hemispheres (Hoeksema 2018), we can look for the implications of these unusual circumstances on CMEs. In this section, we first present the global statistics of CMEs over SC 23 and 24. We then focus on the correlation between CMEs and several indices/proxies of solar activity, paying particular attention to the question of a possible phase shift, and see whether one class of solar activity is better correlated with CMEs than others, thus possibly casting some light on their relationships.
12.1 CMEs in Solar Cycles 23 and 24
Tables 9, 10, 11, and 12 summarize the statistics of the CMEs listed in the ARTEMIS, CDAW, SEEDS, and CACTus catalogs corrected as described in Sect. 4.1. The statistics are considered globally, by hemispheres on the basis of their apparent latitude, and by solar cycle. We further distinguish different cases of width adopting a threshold of \(30{^{\circ}}\) to separate narrow and large CMEs, a threshold of \(300{^{\circ}}\) to isolate the halo CMEs, and a threshold of \(350~\mbox{km}\,\mbox{s}^{-1}\) to separate slow and fast CMEs. SC 24 may not be strictly completed but the contribution of the forthcoming months will be very small as this cycle is heading to its minimum. So this is not going to affect the trends when comparing SC 24 with SC 23 below. We pay particular attention to the variations between these two cycles by giving the ratios “SC 24/SC 23” of the various quantities.
Considering first the counts, SEEDS detected the largest number of CMEs over the two cycles (43559 CMEs), ARTEMIS slightly less by a factor of 0.9, whereas CDAW and CACTus reports nearly the same number drastically less than the other two catalogs, for instance by a factor of 2 with respect to SEEDS. The above ratios hold separately in the two hemispheres, except for CDAW for which it is larger (2.2) in the northern and smaller (1.87) in the southern hemispheres. This trend is further confirmed when considering the ratios “north/south” of the counts in the two hemispheres which lie in the range [1.10–1.14] for ARTEMIS, SEEDS, and CACTus—henceforth a 10–14% excess of northern CMEs—whereas it amounts to only 0.97 for CDAW, henceforth a slight excess (3%) of southern CMEs. The ratio of the numbers of narrow (\(\leq 350~\mbox{km}\,\mbox{s}^{-1}\)) to large (\(>350~\mbox{km}\,\mbox{s}^{-1}\)) CMEs strongly varies between catalogs: 2.84 for SEEDS, 2.23 for CACTus, 1.25 for ARTEMIS, and only 0.49 for CDAW in agreement with the systematic trend of CDAW reporting larger widths than the other three catalogs as pointed out in Sect. 7. The ratio of the numbers of slow (\(\leq 350~\mbox{km}\,\mbox{s}^{-1}\)) to fast (\(>350~\mbox{km}\,\mbox{s}^{-1}\)) CMEs also varies between catalogs: 3.31 for SEEDS, 1.54 for ARTEMIS, 0.92 for CDAW, and 0.91 for CACTus, the very large value for SEEDS resulting from its systematic trend of reporting lower speeds than the other three catalogs as noted Sect. 9. Turning our attention to the variations of the counts between the two cycles and inspecting the “SC 24/SC 23” ratios, SEEDS generally gives more extreme values than the other three catalogs. The general trend from these three catalogs is for a deficit of CMEs of typically 6–20% during SC 24 compared with SC 23. However, this hides a pronounced difference between the two hemispheres with a ratio approaching or even slightly exceeding 1 in the northern hemisphere whereas it does not exceed 0.82 in the southern one. A different picture emerges is the “SC 24/SC 23” ratios are compared to that of the radio flux of 0.86 which provides a normalization to solar activity. Then ARTEMIS and CDAW give a slight excess of CMEs during SC 24 compared with SC 23. The above north/south dichotomy naturally remains, but the relative excess in the northern hemisphere is amplified whereas the deficit in the southern one almost disappears based on ARTEMIS and CDAW. But the strongest solar cycle variation is related to the speed as the proportion of slow to fast CMEs is clearly larger during SC 24 than during SC 23, a situation especially pronounced in the northern hemisphere. Conversely, there is a deficit of fast CMEs during SC 24 with the same north/south asymmetry. Curiously, and as noted in Sect. 9, SEEDS exhibits the opposite behaviour. The solar cycle effect on widths normalized to that of the radio flux remains limited with mainly an excess of wide CMEs (\(>30{^{\circ}}\)) during SC 24 however not supported by SEEDS and CACTus. The case of halo CMEs with width exceeding \(300{^{\circ}}\) is deferred to Sect. 13 below.
The total masses from ARTEMIS and CDAW are in satisfactory agreement and indicate a marked reduction during SC 24 both in absolute and relative (with respect to the variation of the radio flux) values. But here again, the situation in the two hemispheres is contrasted with the reduction being particularly strong in the south and quasi nonexistent (relative to the radio flux) in the north. Inspecting the mean and median values of the distributions of mass during the two cycles, we see that the above north/south dichotomy is much less pronounced than for the global masses to the point of being nearly negligible for the median values. There appears some differences between the ratios of the mean values given by the two catalogs, especially in the northern hemisphere. Quite remarkably, the ratios of the median values are independent of the hemispheres with however different values for ARTEMIS (\(\approx0.85\) similar to the ratio of the radio flux) and for CDAW (\(\approx0.67\)). We therefore do not confirm by far the huge ratios claimed by Gopalswamy et al. (2015c) when comparing SC 23 and SC 24, namely a ratio of 3 between the average masses (\(\mbox{SC 24/SC 23}=0.33\)) and a ratio of 2.2 (\(\mbox{SC 24/SC 23}=0.46\)) between the median masses.
12.2 CMEs and Indices/Proxies of Solar Activity
Solar activity is traditionally represented by the international sunspot number (SSN), but there are many other measures, which may be useful to connect CME variability to solar variability and cast some light on the sources of CMEs. Our comparisons have been based so far on the radio flux at 10.7 cm for reasons stated in Sect. 4. The decimetric radio flux is considered as a coronal index (Tapping 2006) although it is partly chromospheric. It is dominated by free-free emission from plasma concentrations trapped over active regions but also contains a contribution from gyroresonance at low harmonics of the electron gyrofrequency, originating in the corona over sunspots. We introduce another coronal proxy, namely the 1–8 Å soft X-ray background measured by the GOES satellites,Footnote 7 which is probably the “purest” index of coronal activity (Tapping 2006). This radiation is prominently produced in plasmas with electron temperatures of \(10^{6}~\mbox{K}\) or more, henceforth typical of coronal temperatures, by free-free bremsstrahlung. We complete our selection by three photospheric indices/proxies: sunspot number (SSN), sunspot area (SSA), and total photospheric magnetic flux (TMF). The SSN data come from the WDC-SILSO data center,Footnote 8 and the SSA data from the RGO database.Footnote 9 The total photospheric magnetic flux (TMF), calculated from the Wilcox Solar Observatory photospheric field maps, was kindly made available to us by Y.-M. Wang; detail can be found in Wang and Sheeley (2003). All indices are considered globally and, when available, by hemisphere to highlight any north-south asymmetry. Throughout this section, the CME and index/proxy data were sampled into 27.3 day Carrington rotations and the latter data were arbitrarily scaled and shifted in the vertical direction to match the CME data during SC 23. Classically, the comparison with the indices/proxies is performed using the CME occurrence rate and we follow this practice. But based on the arguments given by Wang and Colaninno (2014), we concur that it is physically more meaningful to consider the CME mass rate since this solution is more robust against faint ejections which contribute relatively little to the mass.
As already emphasized in Sect. 4, the ARTEMIS occurrence and mass rates closely track the long- and short-term variations of the radio flux, accurately reproducing its finest fluctuations with very few exceptions (Fig. 49). The only difference between the two CME rates concerns SC 24: whereas the CME mass rate remains close to the radio flux during the two cycles, the occurrence rate presents a systematic excess during SC 24 with respect to the radio flux by a multiplicative factor of \(\approx1.2\). A similar result globally holds for the X-ray background (Fig. 49) although (i) it exhibits much larger fluctuations than the radio flux, (ii) it starts to diverge from the CME occurrence rate during the declining phase of SC 23 and (iii) its match to the CME mass rate during SC 24 is slightly inferior to that of the radio flux.
In a broad stroke, the above tracking is observed for both SSN and SSA, the CME mass rate tracking their evolution throughout the two cycles whereas the occurrence rate presents a systematic excess during SC 24 (Fig. 50 and 51). Having the data available separately for each hemisphere allows having a deeper insight into this difference. This systematic excess comes almost exclusively from the northern hemisphere as seen in both the CME occurrence and mass rates. To the contrary, these rates pretty much track the variations of the indices in the southern hemisphere, the agreement being conspicuously superior for the mass rate than for the occurrence rate. This asymmetry between the two hemispheres is clearly confirmed by the occurrence rates given by the other three catalogs, SEEDS, CACTus, and CDAW with minor differences (Fig. 52). Finally, both occurrence and mass rates track the TMF variations with the restrictions noted above; note in addition, pronounced deviations present in the southern hemisphere during SC 23 which were not present in the case of the SSN and SSA indices (Fig. 53). Finally, we point out that the strong peaks present in both SSA and TMF extending from October 2014 to March 2015 result from the large sunspot complex AR 12192 (Sheeley and Wang 2015) which were extremely CME-poor (Sun et al. 2015).
Table 13 presents the Pearson correlation coefficients between the CME occurrence and mass rates and the selected indices/proxies of solar activity. They offer a quantitative and synthetic view of their relationships over the two solar cycles and separately for SC 23 and 24 on the one hand and globally and separately for each hemisphere on the other hand. They confirm the results of the analysis of the temporal variations and allow to rank the indices/proxies which best track the CME rates according to the values of the correlation coefficient. For the occurrence rate, the order is radio flux (0.87), SSN and TMF (0.86), SSA (0.81), X-ray (0.79) and the coefficients are, with a couple of exceptions, systematically larger in the south hemisphere than in the northern one. For the mass rate, the order is radio flux (0.86), SSA (0.85), SSN and X-ray (0.83), TMF (0.81); however the above south/north dichotomy is much less pronounced. As seen from the above global values, the correlations are all very high. But isolating SC 24 and the northern hemisphere, we note a degradation of the correlation with coefficients dropping to approximately 0.7 and even to 0.55 in one case, a behaviour consistent with the temporal variations.
Figure 54 displays the scatterplots of the occurrence and mass rates against the selected indices and proxies. They all indicate clear linear relationships with however different but consistent slopes for the two solar cycles implying that the CME rates were relatively larger during SC 24 than during SC 23 when compared to any indices/proxies of solar activity. This effect is particularly pronounced for the occurrence rate and less so for the mass rate; it was barely visible in the temporal variations but is revealed by the scatterplots. In other words, the CME activity was stronger during SC 24 than during SC 23 when compared to solar activity as measured by all considered indices or proxies. For instance, using the radio flux as a reference, the occurrence rate was larger by 40% and the mass rate by 9.2%. The dispersion of the data points around the linear regressions reflects the closeness of the tracking and here again, this criterion confirms that the CMEs best track the radio flux.
Scatterplots of the ARTEMIS occurrence (left column) and mass (right column) rates per Carrington rotation against five indices and proxies of solar activity: radio flux, soft X-ray background, SSN, SSA, and TMF. The solid lines are the linear regressions to the data points separately for SC 23 (in black) and for SC 24 (in blue)
The results for the phase lag of the CME occurrence rate with respect to the indices/proxies are presented in Fig. 55. With the exception of the TMF, the maximum correlation corresponds to a phase lag of strictly zero in units of Carrington rotation (27.3 days). The maximum is less pronounced in the case of the TMF and extends in fact over 2 CRs but this does not really affect our conclusion that the ARTEMIS CME occurrence rate rigorously tracks solar activity.
Phase lag of the ARTEMIS CME occurrence rate with respect to the indices/proxies: radio flux, soft X-ray background, SSN, SSA, and TMF. The results are shown for the occurrence (solid lines) and mass (dashed lines) rates, and separately for the northern (red lines) and the southern (blue lines) hemispheres. The lag is expressed in units of Carrington rotation
13 Specific CMEs
13.1 Halo CMEs
From observations with the Solwind coronagraph in 1979, Howard et al. (1982) reported a completely new form of coronal transients as a “halo of excess brightness completely surrounding the occulting disk and propagating radially outward in all directions from the Sun”. This observation had far reaching consequences: (i) it established the three-dimensional structure of CMEs which was a matter of debate at that time, (ii) it recognized its direction toward the Earth thus providing the link with geomagnetic disturbances and (iii) it recognized its association with interplanetary shock wave. In the pre-LASCO era, these events were very rare but the superior performances of the LASCO coronagraphs has greatly facilitated their detection and they became a topic of research on their own (e.g., Sheeley et al. 1999; Webb 2000; Temmer et al. 2008; Yurchyshyn 2008; Zhao 2008; Gopalswamy et al. 2015b; Shanmugaraju et al. 2015). Indeed, halo CMEs are important for several reasons as emphasized by Webb and Howard (2012), notably their source region can be documented in greater detail than other CMEs and the Earth-directed ones can be connected to geomagnetic disturbances.
Gopalswamy et al. (2003a) distinguished three types of halo CMEs. “Full halos” completely surround the occulter and originate close to the center of the Sun seen by the coronagraph (frontside halo) or on the opposite side (backside halo); only the former may be geoeffective. “Partial halos” partially surround the occulter and originate at some distance from the center of the Sun but are wide enough to appear over a sector of variable extent. “Asymmetric halos” are an intermediate type being first observed as partial halos and becoming full halos as they propagate and expand in the field of view of the coronagraph. This is evidently a matter of geometry controlled by the location of the source of the CME and its width and there is a continuum from limb CMEs to full halo CMEs implying that halo CMEs should have physical properties similar to those of the classical limb CMEs. However these geometric conditions bias the detection and characterization of halo CMEs in several ways. First, the line-of-sight integral of the Thomson scattering by electrons is comparably weaker for a CME observed as a halo than observed as a limb event thus reducing their contrast with respect to the background corona; consequently, halo CMEs are under detected. Second, projections effects are maximized for halo CMEs thus biasing the determination of their physical properties such as speed and mass unless these effects are estimated by independent observations (for instance, combining LASCO and SECCHI images). In spite of these restrictions, the CDAW data on halo CMEs revealed that they are faster than average CMEs by a factor of at least two (Yashiro et al. 2004; Gopalswamy et al. 2007, 2010). Later on, Gopalswamy et al. (2015b) compared the numbers of halo CMEs during corresponding time intervals of 73 months in SC 23 (May 1996–June 2002) and in SC 24 (December 2008–December 2014) and found that they are more abundant in SC 24 than in SC 23.
For the purpose of our statistical analysis, a threshold on the width of halo CMEs is required that takes into account the above geometric considerations. Careful inspection of the distributions of width (Fig. 27) indicates that there is a clear turnover at \(\approx 300{^{\circ}}\) with an upward trend beyond best seen in the ARTEMIS and CACTus curves. Note the suspect mere absence of CDAW CMEs in the interval \(300{^{\circ}}\mbox{--}355{^{\circ}}\) and a pronounced peak in the last bin at \(360{^{\circ}}\)—both contrasting with the behaviour of the other data sets—suggesting that the CDAW operators may have classified partial halos as full halos when their widths reached \(\approx300{^{\circ}}\). Gopalswamy et al. (2015b) did indicate that their halo designation is based on the appearance in C3 because some CMEs appear as partial halos in the C2 field of view and become full halos only in that of C3, but that should not affect all of them and that does not explain the deficit of CMEs in the interval \(300{^{\circ}}\mbox{--}355{^{\circ}}\). In addition, CACTus relies on C3 observations as well. Weighting the different arguments, we adopted a threshold of \(300{^{\circ}}\) to declare a halo CME for our statistical analysis.
Figure 56 displays their monthly occurrence rates reported by the four catalogs and Table 14 summarizes their total numbers per solar cycle and globally for the two cycles. A first striking outcome is the exceedingly large number of halos found by CDAW compared with the other three catalogs; this is likely a consequence of CDAW reporting widths systematically larger than those of the other catalogs, see Fig. 26. Both facts probably stem from the capability of the human eye to detect faint extensions that are missed by automatic detection algorithms. A second striking outcome is the larger number of CDAW halos during SC 23 than during SC 24 (a trend also present in the CACTus halos) in contradiction with the report of Gopalswamy et al. (2015b) which was probably biased by their partial census in the two solar cycles. In contrast, SEEDS reports very few halos and even none during SC 23 and thus agrees with ARTEMIS in finding a larger number during SC 24 than during SC 23. Figure 57 which displays the monthly occurrence rate of ARTEMIS CMEs in two intervals of width, \(>180{^{\circ}}\) and \(>300{^{\circ}}\), demonstrates that the trend of larger halos during SC 24 is in fact not limited to halos but affects a very broad range of CMEs.
Figure 58 displays the distributions of speeds of halo-CMEs from the four data sets and Table 14 summarizes the mean and median values. Unlike the other three catalogs, CDAW report speeds in excess of \(2000~\mbox{km}\,\mbox{s}^{-1}\) and its distributions are further strongly skewed toward low speeds. CACTus and CDAW mean and median values are systematically larger than those of ARTEMIS and SEEDS with CACTus reporting the largest values during SC 23; this latter behaviour is consistent with that observed for the whole population of CMEs, see Sect. 9 and Fig. 35. The three data sets ARTEMIS, CACTus, and CDAW which detected halo CMEs during SC 23 and 24 concur in having both mean and median speeds in SC 24 significantly smaller than in SC 23. These distributions and the mean and median values of the projected speeds are markedly larger than those of normal CMEs as illustrated in Fig. 34 and 35. For example, the mean values for the halo CMEs lie in the range \(500\mbox{--}1100~\mbox{km}\,\mbox{s}^{-1}\) to be compared with \(200\mbox{--}400~\mbox{km}\,\mbox{s}^{-1}\) for the global population. Granting that they are underestimated by the projection effect, the real speeds should be even larger which raises the question whether halo CMEs are so special, a question addressed in Sect. 15.
13.2 Stealth CMEs
“Stealth CMEs” refers to CMEs having no distinct solar surface association and have been considered as a special type warranting specific investigations to characterize their properties. This terminology is rather new and was introduced by Ma et al. (2010), but the discovery of “orphan” CMEs dates back to the Skylab and SMM era when Wagner (1984b) found that a considerable number of CMEs had no associated flare, eruptive prominence, X-ray or radio burst. These “spontaneous” CMEs as Wagner (1984b) called them amounted to almost one half of the Skylab CMEs and almost one third of the SMM CMEs. The interest developed with the advent of the STEREO mission, making use of the stereoscopic viewpoints complemented by SoHO and SDO observations to locate CMEs and search for associated events on the Sun. Indeed, several statistical and case-by-case studies showed that a fraction of CMEs do not have any signature on the disk (e.g., Plunkett et al. 2002; Howard and Simnett 2008; Robbrecht et al. 2009; Ma et al. 2010; Vourlidas et al. 2011; Wang et al. 2011; Kilpua et al. 2014; Schanche et al. 2016; Nitta and Mulligan 2017). But even before the STEREO era, \(\approx10\%\) of major geomagnetic storms were known to come from CMEs without clear surface activities (Zhang et al. 2007). They were sometime referred to as “problem storms” and Robbrecht et al. (2009) used by analogy the term “problem CMEs” before the terminology “stealth CMEs” took over usually referring to those CMEs having no obvious on-disk signature. In spite of being often slow and diffuse, although wide, they can cause heliospheric disturbances (e.g., Robbrecht et al. 2009; Kilpua et al. 2014) and a number of them are geoeffective (Nitta and Mulligan 2017). In a recent study, Alzate and Morgan (2017) considered a set of 40 stealth CMEs identified by D’Huys et al. (2014) and applied new image processing techniques that led to an association for all of them with some form of low coronal signatures such as small flares, jets, or filament eruptions. They thus concluded that stealth CMEs arise from observational and processing limitations. However, these features were over the limb so that their techniques did not help in isolating the source region on the disk. Robbrecht et al. (2009) suggested that stealth CMEs have their source high in the corona, thus explaining the lack of on-disk signature whereas Nitta and Mulligan (2017) found a tendency for the source regions to be located near coronal holes or open field regions. This topics of stealth CMEs is extensively covered in the review article of Webb and Howard (2012) and was later put in perspective by Howard and Harrison (2013). In the view of the latter authors, stealth CMEs belong to a large spectrum of coronal responses meaning that their physics is not fundamentally different from CMEs associated with major surface events. We found appropriate to briefly address this aspect of CME study before investigating the question of the sources of CMEs in the next section.
14 Associations and Implications for the Origin of CMEs
The question of the physical relationship between CMEs and other manifestations of transient solar activity received an immediate attention after the discovery of CMEs in an effort to understand their origin and initiation. In the pre-LASCO era, considerable work was already performed and CMEs were observed to occur in conjunction with flares and eruptive prominences or filament disappearances (e.g., Gosling et al. 1974; Munro et al. 1979; Webb and Hundhausen 1987; Harrison 1991; Kahler 1992), and with helmet streamer disruptions or blowouts (e.g., Howard et al. 1985; Illing and Hundhausen 1986; Wolfson et al. 1987; Hundhausen 1993). The LASCO era witnesses an explosion of works that are presented in the following sub-sections organized according to the different associations. They boil down to identify the sources of CMEs and establish whether different sources translate into the existence of different classes of CMEs. Two main procedures were implemented, either a case-by-case analysis (i.e., establishing a direct link) consequently limited number to a small number of events or a statistical approach on a very large number of events associated on the basis of their temporal and spatial proximity. In the framework of this present study, we naturally adopted the second approach and relied on the ARTEMIS CME catalog since it has never been used for this kind of investigation. As a matter of comparison, we performed a parallel analysis using the SEEDS catalog in the case of CME–prominence association.
14.1 CMEs and Flares
The physical connection between solar flares and coronal mass ejections has long been a topic of debate in solar physics and remains the subject of on-going research. Some kind of relationship seems plausible since flares and CMEs are the most energetic processes in the solar corona that are considered as two aspects of large-scale conversion of free coronal magnetic energy into radiative and particle beam (flare) and kinetic (CME) energy. It is generally accepted that the connection is only partial and that there is no one-to-one relationship between CMEs and flares, one being not the cause for the other (Webb and Howard 2012). Numerous articles have been published on the Flare-CME association and most of them are discussed in the review by Webb and Howard (2012). More recent works include Aarnio et al. (2011), Youssef (2012), Nitta et al. (2014), Nindos et al. (2015), Salas-Matamoros and Klein (2015), Mittal et al. (2016), Aschwanden (2017), Compagnino et al. (2017), Murray et al. (2018), and Syed Ibrahim et al. (2018). Note that these past studies rely solely on the CDAW catalog of CMEs with a few exceptions where the CACTus catalog was used, and that the longest time coverage did not extend beyond December 2014. Trends have been observed such as flares with X-ray ejecta being always associated with CMEs (Nitta and Akiyama 1999) and the fastest, most energetic CMEs being associated with the brightest flares (Yashiro et al. 2005). Even the latter association is not without counter-example as large active regions that produced major flares of X-class and M-class types were found to lack associated CMEs, notably AR 5395 in March 1989 (Feynman and Hundhausen 1994) and AR 12192 in October 2014 (Sun et al. 2015).
Very much like many past investigations, we are particularly interested in the following aspects: (i) the fraction of the population of CMEs associated with flares, (ii) the physical properties of CMEs related to different classes of flares, and (iii) their relationship with the properties of flares. Our procedure follows that widely implemented in the past: it makes use of the observations by the GOES satellites which offer a long, homogeneous data set of soft X-ray flares, and applies both temporal and spatial criteria for establishing the flare–CME putative association. With very few exceptions, the past searches have been limited to the highest energy classes, X, M and all or part of C since it is very difficult to associate A and B flares to CMEs (Yashiro et al. 2006). Figure 59 displays the monthly occurrence rates of the X-, M-, and C-class flares together with that of ARTEMIS CMEs for comparison. During SC 23, the rate of C flares is comparable to that of CMEs with listed mass (slightly less during SC 24) giving the impression that all CMEs could be associated with a flare. According to Gopalswamy et al. (2010), this stems from the definition of flares if they are considered “as the enhanced electromagnetic emission from the structures left behind after CME eruptions”. Past studies have generally excluded the low energy C subclasses and retained flare size \(\geq \mbox{C3}\) level (Yashiro et al. 2008) or \(\geq \mbox{C4}\) level (Aschwanden et al. 2016). However, another consideration limits the number of useable flares, the determination of their location on the solar disk since this information is required to implement the spatial criterion. Figure 60 shows the impact of this selection and further reveals two large gaps in the useable data, a two-year gap from June 2007 to June 2009 (due to malfunctioning of the detector) and a one-year gap in 2011 during which the locations of the flares are unavailable. Our search for associations therefore exclude these three years. The first gap fell during the SC 23 minimum during which the number of flares was likely very low so its impact is negligible. This is less so for the second gap which occurred during the ascending phase of SC 24 during which the number of flares was already quite large. Table 15 summarizes separately for the two solar cycles the results of the above selections and constraints. Note that the difference between levels \(\geq\mbox{C3}\) and \(\geq \mbox{C4}\) amounts to 1000 flares during SC 23 and 415 flares during SC 24. The following results are prominently given for flares with levels \(\geq \mbox{C3}\) on the basis that the C3 level is the middle value of C1 and M1 on a logarithmic scale as noted by Yashiro et al. (2005); however, we occasionally include those for the whole C-class and for level \(\geq \mbox{C4}\) to facilitate the comparison with published results.
The temporal criterion is applied first and it requires that both flare and CME occur within a given time interval \(\Delta t = t_{flare} - t_{CME}\). The GOES catalog lists three different times for the flares: start, peak, and end. Aarnio et al. (2011) (see their Fig. 4 based on the CDAW catalog) and Compagnino et al. (2017) (see their Fig. 9 based on the CDAW and CACtus catalogs) concluded that the choice of one of these times has little impact on the association and that a time window of [10–80] min effectively isolates the peak in number of pairs while limiting the contribution of the background events. We performed similar tests and confirm the above conclusions. We finally adopted the flare peak time emphasizing that this choice has little impact on our final results and the above time window thus retaining CMEs which occur 10 to 80 min after the flare peak time. Strictly speaking, the CME launch time is unknown from the LASCO-C2 data unless one extrapolates downward the height-time curves. In practice, the observed “start time” corresponds to the time the CME first appears in the C2 images and more precisely at a height of \(3~\mbox{R}_{\odot}\) in the case of ARTEMIS. To put the upper limit of the time window in perspective, 80 min corresponds to the travel time from the solar surface to \(3~\mbox{R}_{\odot}\) for a limb CME having a constant projected speed of \(290~\mbox{km}\,\mbox{s}^{-1}\).
The application of the spatial criterion assumes nearly radial propagation from the flare site. The heliographic coordinates of the flare given by the GOES catalogFootnote 10 are converted to spherical coordinates and the radial direction from the center of the Sun to the flare location is projected on the sky defining the position angle PA of that flare. The specification of an angular window is complicated by the fact that flares are often spatially offset to one side of the CME being localized at the footpoint, rather than the center of the CME (Simnett and Harrison 1984, 1985). In their thorough analysis of this question, Yashiro et al. (2008) found that, whereas X-class flares tend to lie at the center of the associated CME, C-class flares widely spread to the outside of the CME span. Here again, we rely on the statistical analysis of Aarnio et al. (2011) which shows that the angular separation of flares and CME central position angles exhibits a clear peak at \(0\pm 45~\deg \) (see their Fig. 3) and retain that angular window. An additional spatial criterion bearing on the longitude was introduced by Yashiro et al. (2006). Flares located close to the central meridian are naturally connected to halo or partial halo CMEs whose visibility is reduced in comparison with limb CMEs because of the lower contrast against the background corona. Henceforth, when considering the properties (mass, kinetic energy) of these CMEs, a bias toward high values may be present. Yashiro et al. (2006) set different longitude constraints depending upon the flare class but in a subsequent article (Yashiro et al. 2008), they simplified it to a single constraint excluding the longitude range of \(\pm 45~\deg \) irrespective of the flare class. We incorporated this additional constraint in our analysis to check whether it has any impact on our results.
The search for the associations was independently performed for each class of flares and separately for the two solar cycles and it generally produced a single solution. In the very few cases where two solutions were found (never more), we selected the pair whose time difference was closest to 45 min, that is the closest to the mid-point of the time window.
The statistical results of the association process are presented in Table 16. A noteworthy result is that 5.7% of all ARTEMIS CMEs were associated with \(\mbox{C}+\mbox{M}+\mbox{X}\) class flares during SC 23 in the general case of no constraint on the flare longitude, this percentage dropping to 2.9% during SC 24. The former value may be compared to the 11% found by Aarnio et al. (2011) during the time interval [1996–2006], i.e. very close to SC 23. But two corrections must be introduced accounting for (i) the difference in CME occurrence rates between CDAW (used by Aarnio et al. 2011) and ARTEMIS, that is a factor of \(\approx1.5\) and (ii) the inclusion of the B-class flares by Aarnio et al. (2011) which represent 30% of the total number of flares that they considered. They did not specify the percentage of association per flare class but we can adopt the above 30% to get a rough estimate. Combining the two scaling factors, the original 11% of Aarnio et al. (2011) reduces to 5.6%, well in line with our own result of 5.7%. To put these numbers in perspective, the analysis of the Skylab CME data by Munro et al. (1979) yielded 40% and that of the SMM CME data by Webb and Hundhausen (1987) and St. Cyr and Webb (1991) yielded 26% and 34%, respectively. Note that the above analysis relied on less than a hundred CMEs. From the point of view of the flares with known PA, the percentages of their associations with CMEs are: 12% (SC 23) and 14% (SC 24) for the C-class, 20% (SC 23) and 18% (SC 24) for the M-class, and 31% (SC 23) and 33% (SC 24) for the X-class flares. Interestingly, the results are quasi similar for the two cycles whereas SC 24 was weaker than SC 23. As expected, the percentages increase with the flux of the flares as found for instance by Yashiro et al. (2005) in their analysis which covered the [1996–2004] time interval (that is essentially SC 23), but we strongly disagree with their reported values: 20% for the C-class, 49% for the M-class, and 91% for the X-class flares.
The heliolatitudinal distributions from 1996 to 2017 of the CME-flare associated pairs are displayed in Fig. 61 and offer a visual perception of the angular separations. The butterfly pattern is clearly seen in the distribution of the C-class flares and slightly less so in that of the C3–9 flares (i.e., those with levels \(\geq \mbox{C3}\)) whereas it is far less pronounced for the CMEs. The association process, particularly the spatial criterion, tends to include the very numerous equatorial CMEs to the point of possibly questioning the validity of their association. This possible bias is much weaker to nearly absent for the M- and X-class flares whose associations with CMEs appear on a safer ground.
Figure 62 presents the global view of the physical properties of the CMEs associated with flares depending upon their class. The distributions of mass, speed, and width are systematically compared to those of the overall population of CMEs; note that for the width, this means all CMEs and not the restricted set of CMEs with mass and speeds (a black line is however used in both cases). The two columns correspond to whether or not the restriction on flare longitude is imposed. It is readily seen that this condition has a totally marginal influence on the distributions. Table 17 displays the median values of the three distributions mass, speed, and width in the case of no restriction on flare longitude. The values are given for the whole interval [1996–2018] and separately for each solar cycle. The reference values are for the global set of CMEs in the case of width and for the subset of CMEs with known mass in the case of mass and speed. Our results confirm all past conclusions (Gosling et al. 1976; MacQueen and Fisher 1983; Kahler et al. 1989; Moon et al. 2002; Burkepile et al. 2004; Yashiro et al. 2005; Compagnino et al. 2017) that CMEs associated to the high flux X- and M-class flares have significantly larger mass, speed and width than the overall population of CMEs. The effect is less pronounced for CMEs associated with the lower energy C-class flares and in fact tends to decrease with decreasing flare flux as seen by comparing the results for the whole C-class and for the restricted subclass C3–9. There is no significant systematic trend affecting the distributions of mass, width, and speed between the two solar cycles. Differences are present but they go in both directions being either larger or smaller depending upon the flare class. The case of speed is somehow peculiar: during SC 24, its values are larger for those CMEs associated with \(\mbox{X}+\mbox{M}\) flares whereas the opposite situation prevails for those CMEs associated with the C3–9 flares, and whereas the difference is marginal for those CMEs associated with the whole C-class flares. This behaviour most likely illustrates the fact that there is no one-to-one relationship between CMEs and flares as underlined in the introduction of this section.
Distribution of the physical properties of CMEs associated with different classes of flares: from top to bottom, width, global speed, mass, and kinetic energy. The left column corresponds to the case where there is no condition on the longitude of flares and the right column to the case where the longitude interval \(\pm 45~\deg \) is excluded
Following Aarnio et al. (2011) and Compagnino et al. (2017) who established a relationship between flare flux and CME mass (based on the CDAW catalog), we display in Fig. 63 the scatterplot of the flux of the associated flares integrated from their start to end in the 0.1–0.8 nm range and expressed in \(\mbox{J}\,\mbox{m}^{-2}\) (as listed on the GOES website) versus CME mass from the ARTEMIS catalog. Note that contrary to Compagnino et al. (2017) and us, Aarnio et al. (2011) used the power expressed in \(\mbox{W}\,\mbox{m}^{-2}\). The C-class flares are separated in two sub-classes, C1–2 and C3–9, but both exhibit very large dispersions of values with a very weak trend of increasing CME mass with increasing flare flux. This trend is more pronounced for the M- and X-class flares thanks in part to the large range of flux. We explored whether there is a difference between the two solar cycles but found a very weak effect, the linear regression to the data points being slightly steeper for SC 24 than for SC 23. For better legibility, we regrouped the results for the X, M, and C flares and divide the data range in bins of approximately equal size, with the last one adjusted to missing or excess CME numbers. In practice, the data set of 1063 CMEs associated with \(\mbox{X}+\mbox{M}+\mbox{C}\) flares was divided in 9 bins of 106 CMEs plus one bin of 109 CMEs. For each box, we calculated the mean values of the logarithm of the flare flux and of the CME mass as well as the mass error on the mean (i.e., \({\sigma }/{\sqrt{N}}\)). The results are shown in Fig. 64 where the flux error bars corresponds to the flare flux spanned by each bin. The linear fit to the date yields the following relationship between the logarithm of the flare flux and the CME mass:
that can be directly compared with that of Eq. (1) of Compagnino et al. (2017):
Binned scatterplot of the CME mass as a function of energy flux of the \(\mbox{X}+\mbox{M}+\mbox{C}\) flares. The horizontal error bars give the size of the bins, the vertical error bars represent the error on the mean values of the CME mass (i.e., the standard deviation of the population of the bin divided by the square root of the population size), and the gray bands show the standard deviations
Note the significant difference, a factor of 1.8, between the two slopes. Aarnio et al. (2011) derived a similar relationship but using the power of the flares so that a direct comparison is precluded.
The same exercise is repeated with the kinetic energy of the CMEs since it makes more sense to relate energy to flux than to mass and the results are shown in Fig. 65 and Fig. 66. The linear fit to the date yields the following relationship between the logarithm of the flare flux and the CME kinetic energy:
Binned scatterplot of the CME kinetic energy as a function of energy flux of the \(\mbox{X}+\mbox{M}+\mbox{C}\) flares. See Fig. 64 for explanations
14.2 CMEs and Prominences
Likewise the case of flares, the association of CMEs with prominences, particularly eruptive prominences (EPs), has received considerable attention and in fact has been less disputed since the archetypical three-part of many CME structures with embedded cool prominence material offers a quasi direct proof of the connection. It was first quantitatively assessed by Munro et al. (1979) who investigated the correlation between Skylab CMEs and chromospheric \(\mbox{H}\alpha \) activity and found that 78% were associated with eruptive prominences or filament disappearances. This was later confirmed by Webb and Hundhausen (1987) using the SMM CMEs although at a slightly lower level (66%). Subsequent studies that exploited the first years of LASCO observations (albeit with small sample sizes) led to diverging results on the level of correlation: whereas Gilbert et al. (2000) and Hori and Culhane (2002) confirmed the above large levels, Wang and Goode (1998) and Yang and Wang (2002) reported much poorer associations (36% in the latter case). A more complete analysis was performed by Gopalswamy et al. (2003c) who considered 186 CME–prominence events from August 1996 to 2001 relying on the synthesis imaging in microwaves performed with the Nobeyama Radio-heliograph (NoRH) for detecting and characterizing prominence eruptions. In addition to finding that 73% of their EPs were associated with CMEs, they found that they tend to start roughly at the same time and that there was no solar cycle dependence on the temporal relationship. When comparing statistics from different authors, be aware that they refer to either the fraction of associated CMEs or that of associated prominences. The ups-and-downs of these early works are well illustrated by Subramanian and Dere (2001) who found that 59% of CMEs with signatures on the solar disk were associated with prominence eruptions, whereas Subramanian and Vourlidas (2007) found that only 38% of CMEs with well-defined flux-rope-type structure had a clear association with an eruptive prominence/filament and 44% had none. Some extensions of the study by Gopalswamy et al. (2003c) in the form of a comparison of the heliolatitudinal distributions of CMEs and EPs are found in Gopalswamy et al. (2010) from 1996 to 2007 (see their Fig. 9) and in Webb and Howard (2012) until 2010 (see their Fig. 11). The book entitled “Solar Prominences” published in 2015 includes two chapters that consider several aspects of the CME–prominence association: Gopalswamy (2015) discussed the dynamical properties of EPs in relation to CMEs and Webb (2015) focused on the observational aspects of EPs that are clearly associated with CMEs. While being informative, they mostly synthesize past results and do not present analysis of new data. McCauley et al. (2015) compared observations by the Atmospheric Imaging Assembly (AIA) onboard SDO of 904 prominence and filament eruptions with CMEs listed in the CACTus catalog and found that 72% of the eruptions were associated and 28% were not. These percentages held as well for the different types of eruptions they considered: active region, intermediate, quiescent, and polar crown. The average speed of CMEs associated with the eruptions was \(430~\mbox{km}\,\mbox{s}^{-1}\), nearly the same as for all CMEs detected by CACTus over the SDO mission lifetime.
Similar to the case of flares, a one-to-one correspondence between CMEs and prominences is excluded since only a fraction of the CME population may realistically be associated with EPs. Likewise, not all prominence can produce a CME and it has been conclusively shown by Munro et al. (1979) and confirmed by Gopalswamy et al. (2003c) that only those eruptions reaching a minimum height of \(1.2~\mbox{R}_{\odot}\) are capable of launching a CME (see also Filippov and Zagnetko 2008). As already mentioned above in the survey of past works, there are different types of observation to record prominences, notably \(\mbox{H}\alpha \) and microwave for ground-based observatories and extreme ultraviolet for space-based observatories. In the former case, it is generally considered that eruptive events are under-reported because of visibility and weather restrictions.
Our investigation extends the above past studies to two solar cycles and addresses the same aspects as those of the CME-flare associations. We rely on prominence data from observations at the Nobeyama, Kislovodsk and Meudon observatories and by SDO/AIA. We restricted the lists to eruptive prominences by imposing a minimum height of \(1.2~\mbox{R}_{\odot}\) and a positive velocity when it is listed. Figure 67 displays the monthly occurrence rates of all prominences listed in the four data sets and the yearly occurrence rates of the eruptive prominences resulting from the application of the above restrictions (we switched to yearly values as some monthly values were too low). Our procedure follows that implemented in the case of flares applying both temporal and spatial criteria for establishing the prominence–CME putative association with appropriate tuning of the respective windows. These criteria were selected after considering the distributions of time lag and angular separation between a given prominence and the successive CMEs.
14.2.1 Prominences from the Nobeyama Radioheliograph Database
The Nobeyama Radioheliograph (NoRH) databaseFootnote 11 is based on the detection at 17 GHz of limb prominences thus insuring minimal projection effects. As a ground-based observatory, NoRH operates no more than 8 hr per day with further restrictions during the winters because of snow falls. We use the so-called “complete” listFootnote 12 elaborated to study prominence activity (Shimojo et al. 2006; Shimojo 2013) and updated to 31 August 2013 (Shimojo, personal communication). The upper panel of Fig. 68 displays the heliolatitudinal distributions of the 811 NoRH prominences and of the 28218 ARTEMIS CMEs which occurred during the time interval common to both populations, covering the full SC 23 and the first half of SC 24. The restriction to eruptive prominences limited the above number to 157 events.
The “complete” list gives three times of detection (start, max, and end) and we use the middle one (max) since the differences between the start and end times are usually very small, typically less than one hour. The distributions of time difference and angular separation between prominences and ARTEMIS CMES are displayed in Fig. 69. The former clearly reveals a marked peak in the 0–5 hours time interval and the latter indicates that the range of angular separations can be safely limited to \(\pm25{^{\circ}}\). This yielded 94 associations, nine of them having two solutions; in that case, we retained the couple with the lowest angular separation. In summary, 60% (94 out of 157) of all eruptive prominences were associated with a CME, whereas 0.33% (94 out of 28218) of all CMEs were associated with a prominence. If we consider the ARTEMIS CMEs with a measured mass, the latter percentage raises to 0.49% (89 out of 18010). The lower panel of Fig. 68 displays the heliolatitudinal distributions of the prominence–CME associated pairs which looks far superior to the case of the flare–CME pairs, a consequence of the much reduced restriction on the angular separation in the former case. In spite of the relatively low number of associations, the butterfly pattern of the distribution is clearly perceptible.
Upper panel: distribution of time difference between the CMEs from the ARTEMIS catalog and associated prominences from the NoRH database using a [\(-10;10\)] hours time interval and a [\(-45{^{\circ}};45{^{\circ}}\)] latitude interval. Lower panel: distribution of angular separation between the CMEs and associated prominences using a [\(0;5\)] hours time interval and a [\(-25{^{\circ}};25{^{\circ}}\)] latitude interval
Figure 70 presents the global view of the physical properties of the CMEs associated with EPs and Fig. 71 presents those of the associated prominences. Their distributions are systematically compared to those of the overall population of CMEs (for the width, this means all CMEs and not the restricted set of CMEs with mass and speed), to the overall population of 811 prominences, and to the set of 157 EPs. Table 18 summarizes the mean and median values of these distributions. A systematic trend appears in the distributions of associated CMEs: they have larger mass, larger kinetic energy and slightly larger speed than the overall population. In addition, the distribution of the width of those CMEs is rather flat thus excluding an excess of narrow CMEs contrary to the global population. The distributions of magnitude and speed of EPs and associated EPs are quite similar, a probable consequence of the fact that the latter represent approximately two thirds of the EPs. The comparison is further extended to the overall population of 811 prominences and reveals that the magnitudes of the associated EPs are systematically larger than those of the overall population whereas this is not the case for the speeds. We finally investigated the inter-relationship between associated prominences and CMEs and found little evidence of any trend. Figure 72 illustrates the case of the relationship between EP and CME speeds showing a very weak dependence so that the speed of the associated CMEs can be considered independent of the speed of the associated EPs. Similarly results were obtained for the mass and kinetic energy of CMEs which are independent of the magnitude of the EPs.
We performed a similar study using this time the 38120 CMEs listed in the SEEDS catalog during the time interval common to the NoRH prominences. It led to 100 associations implying that 64% of the EPs were associated with a SEEDS CME to be compared with 94 associations, that is 60%, in the case of ARTEMIS CMEs. This is quite remarkable in view of the very different numbers of CMEs involved in the process, 38120 for SEEDS and 28218 for ARTEMIS, which could have resulted in a significantly larger number of associations. But as a consequence, the percentage of associated SEEDS CMEs reaches a low 0.26%. The properties of associated SEEDS CMEs (limited to speed and angular width) and associated EPs are similar to those found in the study based on ARTEMIS CMEs, in particular slightly larger speed than the overall population of CMEs.
14.2.2 Prominences from the SDO/AIA Database
The catalog of 1038 filament eruptionsFootnote 13 is based on extreme ultraviolet observations by SDO/AIA (McCauley et al. 2015). Although limited to slightly more than four years covering the maximum of SC 24 (April 2010 to September 2014), it has the advantage of being free of biases inherent to ground-based observations. We considered the restricted subset of 598 events that excludes confined and non-radial events to maximize the likelihood of association with a CME and retained the four main types identified by McCauley et al. (2015), Quiescent or Quiet Sun (QS), Polar Crown (PC), Active Region (AR), and Intermediate (IP). The upper panel of Fig. 73 displays the heliolatitudinal distributions of the 598 AIA events and of the 11648 ARTEMIS CMEs which occurred during the time interval common to both populations.
The catalog gives the start and the end detection times of the eruptions and we adopted the mid-point. The distributions of time difference and angular separation between filament eruptions and CMES are displayed in Fig. 74; their profiles led us to select the same criteria as for the NoRH EPs, namely a time interval of 0–5 hours and a range of angular separation of \(\pm25{^{\circ}}\). This yielded 298 associations implying that 50% (298 out of 598) of the filament eruptions were associated with a CME, whereas 2.6% (298 out of 11648) of all CMEs were associated with an eruption. If we consider those CMEs with a measured mass, the latter percentage raises to 3.5% (243 out of 7010). The lower panel of Fig. 73 displays the heliolatitudinal distributions of the eruption-CME associated pairs showing that the quality of the associations is similar to that of the case of the NoRH prominences.
Upper panel: distribution of time difference between the CMEs from the ARTEMIS catalog and associated filament eruptions from the SDO/AIA database using a [\(-10;10\)] hours time interval and a [\(-45{^{\circ}};45{^{\circ}}\)] latitude interval. Lower panel: distribution of angular separation between the CMEs and associated filament eruptions using a [\(0;5\)] hours time interval and a [\(-25{^{\circ}};25{^{\circ}}\)] latitude interval
Figure 75 and Table 19 present the global view of the physical properties of the CMEs associated with filament eruptions. Their distributions and statistical values are systematically compared to those of the overall population of CMEs (for the width, this means all CMEs and not the restricted set of CMEs with mass and speeds). The four distributions are remarkably consistent with those obtained for the CMEs associated with NoRH prominences and the conclusions then reached are now further reinforced since the set of associated filament eruptions (298) is significantly larger than the set of associated NoRH prominences (94). In summary, the associated CMEs have larger mass, larger kinetic energy and slightly larger speed than the overall population and their distribution of width is rather flat.
McCauley et al. (2015) searched for CACTus CMEs matching their events and found that 72% of their eruptions were associated with a CME, to be compared with our value of 50%. However, they do not give any detail on their method of association and it is not clear to which set of eruptions this percentage is referred to. If we accumulate the number of associated events of the four types listed in their Table 2, we end up with 488 associations implying a reference number of eruptions of \(488/0.72 = 678\), a number that does not appear in their table. A comparison of the speeds of the associated CACTus CMEs as listed in the AIA catalog with the global and median speeds of the associated ARTEMIS CMEs is presented in Fig. 76 showing that CACTus gives slightly larger speeds than ARTEMIS with, in addition, a curious peak at \(400~\mbox{km}\,\mbox{s}^{-1}\). Finally, unlike prominences, there is no physical property attached to the filament eruptions thus preventing further analysis.
14.2.3 Prominences from the Kislovodsk Observatory Database
The Kislovodsk Observatory databaseFootnote 14 is based on their detection in \(\mbox{H}\alpha \) (Guseva et al. 2007). The catalog covers the full time interval of LASCO observations listing 33246 prominences from 1996 to 2017, but applying the height limit of \(1.2~\mbox{R}_{\odot}\) yielded only 42 events. However, the NoRH and Kislovodsk databases use different definitions of the height of the prominences, the former considers their center of mass whereas the latter, the highest part of the prominences. This led us to decrease the above limit and we adopted \(1.15~\mbox{R}_{\odot}\) instead, thus increasing the number of events to 187. Applying the same procedure as in the above two cases produced only 28 associations which is much too small to draw any statistically meaningful results.
14.2.4 Prominences from the Meudon Observatory Database
The Heliophysics Feature Catalogue (HFC)Footnote 15 lists the prominences detected by the CAII K3 Spectroheliograph of the Meudon Observatory. It covers 10.5 years from January 2003 to July 2012 corresponding to the declining phase of SC 23, the following minimum, and the rising phase of SC 24 for a total of 27184 prominences to be compared with 10871 ARTEMIS CMEs detected during the same time interval. Applying the height limit of \(1.2~\mbox{R}_{\odot}\) restricted the data set to only 45 events and our standard procedure yielded 14 associations. There is no definition of the height in the HFC catalog so that we do not know whether it would be justified to relax the above limit. Whatever the case and very much like the Kislovodsk data set, the number of associations is much too small to draw any statistically meaningful results.
14.3 CMEs and Active Regions
Unlike the other two previous associations, that of CMEs with active regions (ARs) has received little attention although a connection via the flares points to such an association. In a preliminary investigation of 32 CMEs, Subramanian and Dere (2001) found that 84% were associated with ARs. Yashiro et al. (2005) suggested that almost all CMEs associated with sizable flares (stronger than class C3.0) occur in ARs. Wang and Zhang (2008) presented statistical results on the properties of the solar source regions that produced the 57 fastest (\(>1500~\mbox{km/s}\)) front-side CMEs from June 1996 to January 2007 that revealed a general trend between the scale of an AR and the likelihood of its producing a fast CME. To be more specific, the larger the geometric size, the larger the magnetic flux, the stronger the magnetic field, and the more complex the magnetic configuration, the greater the possibility of producing a fast CME. But the most comprehensive study so far was performed by Michalek and Yashiro (2013) who considered almost 700 CMEs observed near the peak of SC 23 (from 2001 to 2004). Their conclusions confirm and extend those of Wang and Zhang (2008): CMEs are more likely to be associated with mature active regions with complex magnetic fields and the fastest CMEs are associated with active regions that exhibit extreme magnetic complexity and the largest sizes. In contrast, the widest, but slow, CMEs originate from the simplest magnetically source regions. The recent major effort to connect CMEs to their solar active region sources by Murray et al. (2018) looks promising but is presently limited to about 2000 CMEs observed by the STEREO spacecraft. Their initial analysis and scatterplots of AR properties versus CME speed are however not yet very conclusive (their Fig. 7).
In order to search for CME-AR associations, we considered the Heliophysics Feature Catalogue (HFC)Footnote 16 which compiles the partially overlapping observations from SOHO/EIT, SOHO/MDI, and SDO/AIA implementing either the SPoCA software (Verbeeck et al. 2014) or the SMART software (Higgins et al. 2011) for automatic detection of the active regions. We restricted the HFC output to those ARs recorded with an NOAA number to be consistent with past studies. The lower panel of Fig. 77 displays the monthly number of ARs derived from the three sets of observations together with the monthly occurrence rate of ARTEMIS CMEs for comparison and reveals a very poor agreement between these three sets. The SOHO/EIT and SDO/AIA curves exhibits large fluctuations which do not track the pattern of solar activity; note in particular the sharp and suspect drop in the SOHO/EIT curve at the maximum of SC 23. By far, the SOHO/MDI curve stands out by its quality and its peak value of approximately 35 ARs per month at the maximum of SC 23 consistent with the NOAA results as given in Fig. 4 of Wang and Zhang (2008). Unfortunately, the SOHO/MDI data processed with SMART extend only from May 1996 to February 2011, thus missing a large part of SC 24.
A given AR is repeatedly observed by MDI at a typical cadence of 1.5 hour (except in case of missing images) and at different locations as the Sun rotates. This cadence can be viewed as sampling the AR and compared with the maximum occurrence rate of CMEs of approximately 10 per day during the maximum of SC 23. The upper panel of Fig. 77 displays the monthly number of observations obtained by SOHO/MDI to be compared with the monthly number of ARs (lower panel) yielding 190872 observations of 2728 ARs. During the same time interval, ARTEMIS lists 21613 CMEs. The search for time and spatial coincidences between CMEs and ARs was performed with the AR observations as we do not know when an AR may launch a CME. The time sampling of the SOHO/MDI observations and the distribution of angular separation between AR observations and CMEs led us to select a time interval of \(\pm 1~\mbox{hour}\) and a range of angular separation of \(\pm 15{^{\circ}}\) (Fig. 78) to be compared with the criterion of the same quadrant of the solar disk used by Michalek and Yashiro (2013). This led to 6635 associations which involve 1806 ARs. Consequently, 66% of the ARs were associated with a CME and 31% of the CMES were associated with an AR; this latter percentage remains the same if we consider those CMEs with a measured mass. The lower panel of Fig. 79 displays the heliolatitudinal distributions of the AR–CME associated pairs which looks far superior to the previously considered cases of association, a probable consequence of the much reduced domains of time and angular separations.
Figure 80 and Table 20 present a global view of the physical properties of the CMEs associated with active regions. Their distributions and statistical values are systematically compared to those of the overall population of CMEs (for the width, this means all CMEs and not the restricted set of CMEs with mass and speeds). The differences are remarkably small with a minor trend for slightly larger mass, speed, and kinetic energy and the subtle absence of narrow widths in the case of associated CMEs.
The HFC catalog lists several physical parameters of the active regions among which we selected the area, the maximum intensity, and the length of the neutral line which were found relevant to possibly highlight peculiarities of ARs associated with CMEs. The third parameter is uncorrelated with the area so that it may be considered as an unbiased proxy to the complexity of the ARs. Figure 81 displays the distributions of these three parameters distinguishing the set of ARs associated with CMEs and the whole set of ARs. Except for a slightly larger areas of the associated ARs, the distributions are remarkably similar but it should be kept in mind that the fraction of associated ARs is very large (66%).
We finally investigated possible correlations between the physical properties of the associated CMEs and ARs. Scatterplot representations were found impractical for this purpose and we turned to two-dimensional histograms using linear or logarithmic scales as appropriate to the considered parameters. Figure 82 illustrates the case of the speed, mass, and kinetic energy of associated CMEs versus the area of the associated ARs. None of the three histograms indicates any correlation of the three CME parameters with the AR area. Similar negative results were obtained when considering the two-dimensional histograms of the three CME parameters with both the maximum intensity and the length of the neutral line of the ARs which are therefore not presented.
14.4 CMEs and Streamers
The relationship between CMEs and streamers was actively studied in the Skylab/Solwind/SMM era and much less so later on in the SOHO era when the associations of CMEs with flares and prominences received far more attention. On the basis of a comparison of the occurrence rate of CMEs with the time scale of the long-term evolution of the global white-light coronal density distribution over more than 13 years encompassing SC 21, Sime (1989) found a close relationship and concluded that “the key to the physics of CMEs is in the large-scale coronal magnetic field, and not necessarily in the response of the corona to impulsive events in the lower solar atmosphere”. Hundhausen (1993) presented a thorough statistical analysis of 1200 mass ejections observed with SMM in 1980 and 1984–1989 and compared their heliolatitudinal distribution with those of small-scale magnetic structures—sunspots, active regions, and flares—characterized by the butterfly pattern and with those of large-scale magnetic structures—prominences and bright coronal features—that are more broadly distributed in latitude. By far, the pattern of CME latitudes best matched those of the large-scale magnetic structures, notably that of coronal features. Hundhausen (1993) noted that prominences occurred over a wider range of latitudes than did CMEs especially during the SC 21/22 minimum but argued that this could be accounted for by the angular width of the CMEs. He then convincingly concluded in favor of a close connection between CMEs and large-scale, closed magnetic structures in the corona. In fact, many observational evidences supporting this view had accumulated over the previous decade based on detailed examinations of individual CMEs thus providing the first evidences that their formation was a part of a longer-term evolution of closed magnetic structures within a coronal helmet streamer (Fisher et al. 1981; Low et al. 1982; Illing and Hundhausen 1986; Low and Hundhausen 1987; Wolfson et al. 1987).
In the SOHO era, the emphasis switched to the associations of CMEs with flares, active regions, and prominences as witnessed by the large number of articles quoted in the above sections thus largely ignoring the past conclusions from the Skylab/Solwind/SMM studies. Judging from a recent investigation of a possible floor in the CME rate by Webb et al. (2017) and their conclusion supporting the paradigm first demonstrated by Hundhausen (1993) that CMEs arise from large-scale closed-field coronal regions, specifically pre-existing streamers, the pendulum appears to swing back to a more balanced view of the sources of CMEs.
In addition, studies in the SOHO era focused on the interactions between CMEs and streamers, in particular on the disruption, deviation, and restructuring of the streamer belt following an ejection, see Floyd et al. (2013) and references therein. As shown by Liu et al. (2009) based on the 31 December 2007 CME and further extended to January 2008 by Floyd et al. (2013), the interaction may be quite complex, far beyond the simple view of streamer blowout, further involving both a streamer and a pseudostreamer. This opens the question of different classes of CMEs associated with helmet streamers (defined as separating coronal holes of opposite polarity) and those associated with pseudostreamers (streamers that separate coronal holes of the same polarity) addressed by Wang (2015). From their study conducted over the 2007–2011 time interval, they concluded that pseudostreamers give rise to a distinctly different class of CMEs characterized by a fanlike morphology, relatively narrow widths (\(\approx 20\) to \(30{^{\circ}}\)), and constant low velocities (\(\approx 250\) to \(700~\mbox{km}\,\mbox{s}^{-1}\)).
To start with the investigation of the CME–streamer association, we display in Fig. 83 the monthly variation of the global radiance of the K-corona integrated from 2.7 to \(4.5~\mbox{R}_{\odot}\) as constructed from the LASCO-C2 observations together with the occurrence and mass rates of the ARTEMIS CMEs. The CME occurrence rate closely track the coronal radiance during SC 23, but less so during SC 24 when several peaks in the CME rate are not present in the radiance data, notably at the end of 2011 and in late 2013/early 2014. The coincidence between the peaks in late 2014/early 2015 is fortuitous: the radiance peak resulted from an unusual large increase of the solar magnetic field following the emergence of the large sunspot complex AR 12192 (Lamy et al. 2017) that did not produce any CME as already noted. These remarks hold as well for the CME mass rate although it exhibits far larger fluctuations than the radiance, especially during SC 23.
Our procedure to characterize the association follows that of Floyd et al. (2013) developed to study the interaction between CMEs and streamers. It relies on synoptic maps at \(3~\mbox{R}_{\odot}\) where CMEs are detected as described in Sect. 2.4. Streamers are defined as ridges on the same synoptic maps and represent lines of maximum radiance assimilated to boundaries between regions of opposite magnetic polarities. These ridges are detected by applying a watershed filter (Dougherty 1992) which defines different regions at each local minimum, and extends these regions by including the adjacent pixels whose values are under a progressively higher threshold. This defines boundaries that progressively extend until those of two regions come into contact, in which case the regions stop extending transversely to these boundaries. Once every pixel in the image belongs to a given region, the boundaries describe all the ridges in the image. In practice, we applied the filter to sub-images associated with each CME: each sub-image extends longitudinally on both sides of the CME of interest by approximately two days and has the same latitudinal extent as the CME. In addition, the two sides were separately processed so as to decouple the two determinations of the ridge before and after the CME. Once applied, the filter returns the coordinates of the ridges which are then over-plotted on the synoptic maps as white lines for a visual check. Halo CMEs cannot be safely associated with streamer configurations because of their very large latitudinal extent and we excluded those whose width exceeds \(180{^{\circ}}\). The procedure counts the streamers having latitudes comprised in the latitudinal extent (or angular width) of a given CME respectively before (\(N_{\text{b}}\)) and after (\(N_{\text{a}}\)) its occurrence. The outcome is denoted \(\mbox{C}(N_{\text{b}},N_{\text{a}})\) and \(\mbox{C}(0,0)\) obviously corresponds to the case of no association. Finally, the CME–streamer interaction is classified in six categories, two relevant to photometric variations (“brightening” and “dimming”) and three relevant to geometric variations (“emergence”, “disappearance”, and “deviation”). The last category “no-change” contains all cases where none of the above variations is observed. Starting from 38321 CMEs, the procedure successfully returned results for 31763 CMEs, the difference generally corresponding to cases where an unrealistic large number of associated streamers were found. Following Floyd et al. (2013), we systematically performed a parallel analysis of the restricted subset of the 10% brightest CMEs (denoted “top-ten” CMEs thereafter) using the intensity parameter of the ARTEMIS catalog. The results in terms of counts \(\mbox{C}(N_{\text{b}},N_{\text{a}})\) up to the case \(N_{\text{b}}=N_{\text{a}}=3\) are presented in Table 21 for the global statistics and in Fig. 84 for the temporal variations of the five main counts up to \(\mbox{C}(2,2)\).
The number of CME–streamer associations is obviously given by \(\mbox{1-C}(0,0)\). Regarding the global set of CMEs, 51.6% of them are associated with streamers whereas this percentage sharply increases to 94.5% for the “top-ten” subset. When there is an association, the case \(N_{\text{b}}=N_{\text{a}}=1\) (one streamer before and one after the CME) is always the most frequent as the count \(\mbox{C}(1,1)\) significantly exceeds the other counts. The cases involving three streamers either before or after the CME appear quite marginal with counts below 0.9% for the global set and below 4.3% for the “top-ten”. The difference in these two percentages likely stems from the fact that the brightest CMEs are likely to be very wide and therefore connected to several streamers. These results are fully consistent with those obtained by Floyd et al. (2013) with very minor differences in the percentages. The temporal variation of the main counts (Fig. 84) shows that they unsurprisingly track the solar activity but most importantly, that their respective weights are nearly constant; in other words, the relative number of streamers connected to a CME is independent of solar activity. There is one marked exception to this trend as the frequency of the \(\mbox{C}(0,0)\) case for the “top-ten” CMEs appears lower during SC 24 than SC 23 by a factor of \(\approx 2\) indicating a closer association rate during SC 24.
We now turn our attention to the physical properties of CMEs associated with streamers and start with their heliolatitudinal distributions (Fig. 85). Four panels correspond to the four cases of the global population of CMEs, the set of CMEs associated with steamers, the complementary set of non-associated CMEs and the “top-ten” subset. Their color coding was tuned so as to yield the same rendering thus facilitating the visual comparison; therefore, they do not strictly reflect absolute numbers. Strikingly, the four distributions follow the same pattern reproducing similar structures with only minute differences. This is particularly the case of the associated and non-associated CMEs for which a careful examination is required to pinpoint differences. The case of the “top-ten” subset is less conspicuous but still many structures in its distribution may be easily connected to those present in the other distributions. The comparison is further extended to the heliolatitudinal distribution of the electron density which prominently reflect the bright streamers. Two maps are included in Fig. 85, one produced by two-dimensional (2D) inversion of the coronal radiance following the method developed by Quémerais and Lamy (2002) and the other by time-dependent solar rotational tomography (3D inversion) following the method developed by Vibert et al. (2016). Here again, the close similarity of these two distributions with those of the CMEs is striking, particularly with the map produced by the superior 3D inversion. The shortcomings inherent to the 2D inversion result in artifacts most pronounced in the polar regions (for instance the bright feature in the southern hemisphere at the end of 2014) absent in both the distribution based on 3D inversion and in the four CME distributions. In addition to supporting the very close connection between CMEs and streamers, the impressive match between the CME heliolatitudinal distributions and the unbiased distribution of the electron density resulting from 3D inversion demonstrates that the projection effects do not significantly affect the spatial distribution of CMEs, that CMEs do reach high latitudes, and that these HL CMEs are associated with polar streamers as already argued in Sect. 8.2.
Heliolatitudinal distributions of the electron density (upper two panels with the upper one produced by 2D inversion and the lower one, by 3D inversion) and of the CMEs (lower four panels in the following order from top to bottom: global set of CMEs, non-associated CMEs, CMEs associated with streamers, and “top-ten” CMEs associated with streamers)
The physical properties of CMEs associated with streamers is further investigated by considering the distributions of their latitude, speed, angular width, and intensity, distinguishing the different cases of associations as identified by the counts \(\mbox{C}(N_{\text{b}},N _{\text{a}})\). We included the case \(\mbox{C}(0,0)\) of no association as a reference (Fig. 86). The average and median values of the distributions are presented in Table 22. The distributions of latitudes confirm the quasi symmetry with respect to the equatorial plane, well pronounced in the case of the global set of CMEs but less so for the “top-ten” as the counts are affected by small number statistics. The distributions of speeds follow similar homothetic patterns and are thus independent of the number of associated streamers. Quite unexpectedly, the distribution of speeds for the “top-ten” CMEs terminates at approximately \(1000~\mbox{km}\,\mbox{s}^{-1}\), thus excluding fast CMEs, whereas it extends over the full range of speeds for the global set. The other two parameters, angular width and intensity, exhibit distributions that depend upon the number of associated streamers and we therefore included the \(\mbox{C}(0,1)\), \(\mbox{C}(1,0)\), \(\mbox{C}(1,2)\), and \(\mbox{C}(2,1)\) cases. There is a very pronounced trend of the intensity of CMEs increasing with the number of associated streamers. Two features of the distribution of widths of the global set are worth emphasizing: (i) quite naturally, the cases involving the largest number of streamers concern the widest CMEs as they are more likely to be connected to several streamers, and (ii) the non-associated CMEs are prominently the narrowest ones with widths \(<30{^{\circ}}\). This second point warrants further comment as it may underline a bias in the statistics given in Table 21. On the one hand, there exists an unavoidable relationship between the width of a CME and the number of streamers to which it may be associated in agreement with the first remark above. On the other hand, our method of detecting streamers as ridges in the synoptic maps has inherent limitations and certainly tends to favor the brightest ones. Consequently, the large percentage of non-associated CMEs of the global set (48.4%) must be interpreted with caution as it may result from the above biases. In fact, they may well be associated with the streamer belt as supported by their heliolatitudinal distribution well correlated with the distribution of the electron density. The above effect is less pronounced for the “top-ten” CMEs as their intensity range is by definition limited to a narrow domain, approximately from 2000 to 20000.
Distributions of the physical properties of CMEs associated with streamers for the global set of CMEs (upper four panels) and for the “top-ten” subset (lower four panels). The latitude, speed, angular width, and intensity distributions are separately displayed for the \(\mbox{C}(0,0)\), \(\mbox{C}(1,1)\), and \(\mbox{C}(2,2)\) cases. The \(\mbox{C}(0,1)\), \(\mbox{C}(1,0)\), \(\mbox{C}(1,2)\), and \(\mbox{C}(2,1)\) cases are additionally displayed for the angular width and intensity distributions
We finally considered the properties of the streamers associated with CMEs by displaying the temporal variation of the various categories of changes they experience when they interact with a CME: “no-change”, “emergence”, “disappearance”, “brightening”, “dimming”, and “deviation”. The photometric changes and the deviation require that we define thresholds and we used the values selected by Floyd et al. (2013): 1.1 to declare a “brightening”, 0.9 to declare a “dimming”, and a threshold of \(\pm1.6{^{\circ}}\) for a deviation. The monthly ratios displayed in Fig. 87 are calculated using the respective numbers of CMEs which are associated with at least one streamer as references. For the global set of CMEs, emergence and disappearance are the dominant processes affecting the streamers at the level of \(\approx30\%\), almost independent of the solar cycle except during the SC 23/24 minimum where the fraction of emergence decreased whereas that of disappearances increased. The processes of brightening, dimming, and no-change are about equal at a constant level of \(\approx15\%\) except for the number of no-change which experienced a marked increase during the declining phase of SC 24. The case of deviation has a somewhat intermediate behaviour but with fluctuations ranging from 20% to 40%, the largest values being reached during the declining phase of SC 24. The “top-ten” subset exhibits a somewhat different behaviour: the processes of emergence, disappearance, brightening, and dimming all fluctuate in the range \(20\pm 5\%\), that of deviation remains approximately constant at the level of \(\approx 10\%\) except for a few ups and downs, and the no-change case remains at a few percents.
15 Discussion and Summary
Being the first maintained on-line catalog, the CDAW catalog has been of widespread use and the source of numerous publications. Unfortunately, the incorporation of the “very poor” events has spread considerable confusion and has led to erroneous or biased results from authors unaware of this situation. For those aware of it, the alternatives were to exclude possibly “poor” and certainly “very poor” events or exclude CMEs narrower than some threshold (usually \(20{^{\circ}}\) or \(30{^{\circ}}\)) or a combination of both criteria (e.g., Harrison et al. 2018). Our own test of these different alternatives led us to conclude that excluding “very poor” events is the most pertinent solution as already demonstrated by Wang and Colaninno (2014). In view of this confused situation which stems from the intrinsic difficulty of identifying and characterizing CMEs in coronagraphic images, it is surprising and highly puzzling that very few studies made complementary use of the other catalogs which have been available for years to ascertain their results. Whereas the CACTus catalog was sometime used, the SEEDS one has largely been ignored. The evolution to automated cataloguing is irreversible with the advent of massive production of solar/coronal data and is already effective for the automatic detection of many solar features such as active regions. In fact, it is quite revealing that after the CDAW catalog, the manual detection approach was no longer pursued and that all subsequent efforts focused on automatic detection. Apart from the blind reliance on the CDAW catalog, many past publications suffered from being too premature, thus being biased by too few events or too short a time interval leading in the worst cases to incorrect conclusions.
It has been stated that whereas automatic methods are more objective, the results are inconsistent with each other and with the manual catalog (Richardson et al. 2015; Webb et al. 2017). Full consistency is obviously illusory for at least three reasons.
-
CMEs are ill-defined objects on coronagraphic images encompassing an enormous range of brightness and taking very different shapes further evolving with time as they travel outward.
-
In view of this inherent difficulty, the automated catalogs implement different strategies which exploit different aspects of the morphology of CMEs.
-
All automated methods require determining some threshold for which there is no easy objective solution and which further depends upon the method being implemented thus precluding direct comparisons. However, there is a positive aspect as once a threshold is fixed, consistent detection is insured unlike the case of visual detection involving different operators.
The estimation of speeds (and also accelerations) offers a perfect example of these inherent difficulties as different parts of a CME travel at different speeds. By simplifying the problem to the detection of CMEs in the form of vertical streaks on synoptic maps, ARTEMIS is more likely to by-pass many of these difficulties and yield consistent results. In any case, the availability of different catalogs must be viewed as an asset allowing us to perform comparisons and ascertain the results; once again, it is regretful that many past studies have not taken advantage of this asset and have relied on a single catalog. Our analysis reveals that, whereas there does remain inconsistency between catalogs, there are also many points of convergence and we are particularly impressed by the case of SEEDS (once corrected for the image cadence) and ARTEMIS granting that the detections and characterizations of CMEs are achieved by completely different methods. This is partly the case of CACTus although several discrepancies were noted but its authors have warned that their catalog is not really suited to statistical analysis. Even in the case of the manual CDAW catalog and after removing the “very poor” events, several results are consistent with the automated catalogs, notably those concerning the mass rates of CMEs. Let us now discuss and summarize the main results of our investigation.
15.1 Occurrence, Mass, and Intensity
After accounting for the change in image cadence, there is a clear distinction between the four catalogs best illustrated by the peak values of the occurrence rate reached during SC 23. Whereas SEEDS and ARTEMIS monthly rates culminated at \(\approx400\) and \(\approx350\) CMEs, respectively (\(\approx13\) and \(\approx11.5\) CMEs per day, hence a modest difference of 14%), CACTus reached \(\approx200\) and CDAW (excluding “very poor” events) \(\approx150\) CMEs per month (\(\approx6.5\) and \(\approx5\) per day, respectively). The four catalogs agree on lower peak values during SC 24, but with different reduction ratios; however, comparing the integrated numbers of CMEs during a cycle is more significant (see below) because of the large fluctuations during SC 24. Turning to the minimum rates, we concentrate on the extended cycle 23/24 minimum to look for a CME rate floor following the work of Webb et al. (2017). Using the same 1 year time interval from 2008.5 to 2009.5, we obtained mean rates of 0.57 CME per day for ARTEMIS to be compared with 0.69 for SEEDS, 0.65 for CACTus, and 0.74 for CDAW. The mean values during the previous minimum [1996.5–1997.3] can only be estimated from the ARTEMIS and CDAW catalogs and amount to 0.85 and 0.67 CMEs per day, respectively thus in the same range as that given by Webb et al. (2017). The Pearson correlation coefficients given in Table 4 reflect the consistency of the temporal variations of the occurrence rates and are particularly large when comparing ARTEMIS and SEEDS (0.9) and ARTEMIS and CDAW (0.91).
The mass rates of ARTEMIS and CDAW are very consistent agreeing on monthly peak rates of \(\approx 4\times 10^{17}~\mbox{g}\) for SC 23 and \(\approx 3\times 10^{17}~\mbox{g}\) for SC 24. Although it reports lower monthly mass rates (by a factor of 3.3), CORIMP does correlate extremely well with ARTEMIS, the correlation coefficient reaching 0.93 (0.82 with CDAW) confirming the general trend of the temporal evolution of the mass rate. According to ARTEMIS, the annualized average mass of CMEs reached the same peak value of \(\approx 1.5\times 10^{15}~\mbox{g}\) during the maximum of SC 23 and SC 24 and went down to \(\approx2.5\times 10^{14}~\mbox{g}\) during the SC 23/24 minimum. The CDAW average mass followed the same trend with however larger values by roughly a factor of 2 and much larger fluctuations. The ARTEMIS and CDAW distributions of mass agree at large masses (\(\geq 10^{15}~\mbox{g}\)), but diverge below. That of CORIMP is shifted toward low masses and reports a larger frequency of masses \(<10^{13}~\mbox{g}\) than both ARTEMIS and CDAW. Altogether, the mass range of CMEs extend from \(10^{10}\) to \(10^{17}~\mbox{g}\), much larger than the range of \(10^{15\text{--}16}~\mbox{g}\) considered for instance by Zhang and Low (2005). None of the three distributions follow a log-normal law or a clear power-law at large masses, a quite surprising result since these behaviours are quite common to many astrophysical quantities.
The intensity reported in the ARTEMIS catalog exhibits distributions with slightly different statistics during the two solar cycles with intensities recorded during SC 24 lower than during SC 23, consistent with the evolution of the occurrence and mass rates. Intensity and mass are highly correlated allowing an estimation of the “missing” CME mass (i.e., the mass of CMEs without measured mass) which amounts to \(\approx14\%\) of the measured mass.
15.2 Waiting Time
The waiting time distribution of CMEs and its variation with the cycle are best explained in terms of CMEs occurring as a time-dependent Poisson process. The time varying occurrence rate of CMEs produces power-law tails despite the intrinsic exponential distribution that is characteristic of stationary Poisson processes. This has no unique interpretation, but the power-law index is indicative of the behaviour of the event rate. The ARTEMIS and SEEDS datasets agree in producing long power-law tails over a range of waiting times extending from 3 to 100 hr with very close power-law index \(\gamma \approx -2.2\) for ARTEMIS and \(\gamma \approx -2.3\) for SEEDS when calculated over the 23 years of observation. However, the power-law index exhibits significant variations with the solar cycle thus reflecting the temporal variability of the process of CME formation. The CME WTD gets close to a Poisson process during the maxima of activity but departs from this process during the minima, implying high levels of randomness in the former case and a trend of intermittence or clusterization in the latter case.
15.3 Periodicities
The analysis of periodicities in CMEs, proxies of solar activity, flares and prominences reveals an extremely complex situation. On the one hand, these different processes, in addition to following the \(\approx 11\)-year Solar Cycle, exhibit diverse statistically significant oscillations with properties common to all solar, coronal, and heliospheric processes: variable periodicity, intermittence, asymmetric development in the northern and southern solar hemispheres, and largest amplitudes during the maximum phase of solar cycles, being more pronounced during SC 23 than the weaker SC 24. On the other hand, there is very limited commonality among the studied processes, especially for periods of less than one year. The few exceptions are the periods of 3.1–3.2 months found in the occurrence rate of the global set of CMEs and in the sunspot area (and marginally, the 3.4-month period seen in the total magnetic field) and those of 5.9–6.1 months found in the \(\text{CME} _{\text{N}}\) subgroup and in \(\mbox{SSA}_{north}\). We therefore disprove the dozen or so periodicities exceeding two months claimed in past studies which were based on much shorter time intervals (e.g., Lou et al. 2003; Lara et al. 2008; Choudhary et al. 2014), in particular the 154-day (5 months) “Rieger” periodicity detected in flares which has prevailed during past solar cycles (Rieger et al. 1984). We further confirm the lack of commonality of periodicities between CMEs and flares, a result already highlighted by Choudhary et al. (2014). Relaxing the strict localization of periods inherent to spectral analysis, the wavelet spectra yield broad regions where the contours delimiting regions of statistically significant signal for the different CME subgroups, SSN, SSA, and TMF overlap, yielding common mid-range periods with further a striking dichotomy between the two hemispheres: periods of 1–1.5 years in the northern hemisphere and a period of \(\approx2\) years in the southern one. We consider this result as robust, strongly suggesting common underlying processes probably linked to underlying periodicities in the emerging magnetic flux which are themselves thought to be related to the dynamics of the deep layers of the Sun (Rieger et al. 1984; McIntosh et al. 2015) and intrinsic to the solar dynamo mechanism. Prominent periods are then generated by stochastic processes caused by the periodic emergence of magnetic flux as the solar cycle progresses as proposed by Wang and Sheeley (2003), who anticipated that there is no reason for a pattern of stable and reproducible periods on the long term as indeed observed.
15.4 Physical Properties
Considering the annualized average values of angular widths smaller than \(180{^{\circ}}\) (\(>95\%\) of the population), there are significant differences between the different catalogs: CDAW reports the largest widths ranging from \(30{^{\circ}}\) to \(60{^{\circ}}\) and the largest dispersions followed by ARTEMIS (\(22{^{\circ}}\leq \mbox{W} \leq 42{^{\circ}}\)), CACTus (\(24{^{\circ}}\leq \mbox{W} \leq 34{^{\circ}}\)), and SEEDS (\(18{^{\circ}}\leq \mbox{W} \leq 28{^{\circ}}\)); with the exception of CACTus, there are no significant difference in these ranges between SC 23 and SC 24. The temporal evolutions of these annualized average values of angular widths track the solar cycle although this trend is much less pronounced in the case of SEEDS and CACTus. The four distributions of angular width are well-fitted by log-lin linear functions over a broad ranges of width, up to [\(20{^{\circ}}\mbox{--}300{^{\circ}}\)] in the case of ARTEMIS, indicating that they follow an exponential law. We did notice that large CMEs, typically larger than \(180{^{\circ}}\) were more numerous during SC 24 than during SC 23, but this concerns a marginally small number of CMEs and is overwhelmed by the behaviour of the general population.
The distributions of apparent latitudes from the four catalogs agree quite well and are nearly symmetric about the solar equator with a profile of continuously decreasing number with increasing latitudes except for CACTus which exhibits a questionable excess of CMEs at high latitudes (\(>65{^{\circ}}\)) in both hemispheres (CDAW also has an excess at southern latitudes between −15 and \(-45{^{\circ}}\)). A closer inspection on a yearly basis reveals a contrasted situation between SC 23 and SC 24 confirmed by the four catalogs: whereas the mean values fluctuate about the solar equator during SC 23, they exhibit a rather erratic behaviour during SC 24 with however a predominance of CMEs at northern latitudes. This is a direct consequence of a slight excess (7%) of northern CMEs and a substantial deficit (18%) of southern CMEs during SC 24 compared with SC 23 as measured by ARTEMIS.
The heliolatitudinal distributions of CMEs over 23 years raise the question of high latitude (HL) CMEs located well outside the region bounded by the tilt angle of the heliospheric current sheet during the maxima of activity We argue that the bulk of those CMEs have indeed their origin at high altitudes and are associated with polar streamers resulting from polar coronal current sheets formed above the polar crown neutral lines located at latitudes \(| \lambda | \) of \(70{^{\circ}}\) to \(75{^{\circ}}\) during the maxima of activity. This is supported by the impressive correlation between the integrated radiance of the K-corona in the polar regions and the ARTEMIS and SEEDS occurrence rates of CMEs at high latitudes including their asymmetric north/south behaviours. This offers a much more natural explanation consistent with the general CME–streamer association than that proposed by Gopalswamy et al. (2003b) relating the HL CMEs to polarity reversals in the individual hemispheres.
15.5 Kinematic Properties
The temporal variations of the speed of CMEs reported by the four catalog reveal a striking difference between SC 23 where the spread of the mean values ranges from \(\approx 250~\mbox{km}\,\mbox{s}^{-1}\) (SEEDS) to \(\approx 550~\mbox{km}\,\mbox{s}^{-1}\) (CACTus) and SC 24 where it shrinks to \(\approx 300\mbox{--}400~\mbox{km}\,\mbox{s}^{-1}\). The large spread in SC 23 is however imposed by CDAW and CACTus and reduces to \(\approx 250\mbox{--}410~\mbox{km}\,\mbox{s}^{-1}\) when considering only SEEDS and ARTEMIS. CACTus stopped reporting excessively large, probably incorrect, speeds starting in 2010 and bringing its temporal evolution more in line with the other three catalogs. This leaves only CDAW reporting speeds \(>410~\mbox{km}\,\mbox{s}^{-1}\) during most of SC 23. ARTEMIS and CDAW agree on variations that track solar activity—with an amplitude much more pronounced for the latter one—implying lower speeds during SC 24 than during SC 23. Surprisingly, the variation reported by SEEDS goes in the other direction with a mean value during SC 24 (\(310~\mbox{km}\,\mbox{s}^{-1}\)) slightly exceeding the value during SC 23 (\(270~\mbox{km}\,\mbox{s}^{-1}\)). The ARTEMIS mean and median values over the last two solar cycles (360 and \(300~\mbox{km}\,\mbox{s}^{-1}\), respectively) are well in line with those obtained with other coronagraphs (Table 1) except for the Skylab very large mean value of \(470~\mbox{km}\,\mbox{s}^{-1}\) which remains difficult to understand since the Skylab data were obtained near the SC 20/21 minimum.
Acceleration represents one of the two extreme cases (the other being halo CMEs) of discrepancy between the three concerned catalogs. First, the CORIMP annual mean values are approximately ten times larger than those reported by CDAW and SEEDS, and they exhibit a slight trend with solar activity via a modest decrease during the SC 23/24 minimum. The CDAW and SEEDS distributions of acceleration are both approximately symmetric with respect to the zero value until 2010, then diverge to positive values for CDAW and large negative values for SEEDS. This situation reflects the extra difficulty of measuring accelerations compared with velocities which themselves face numerous problems. Reliable accelerations may possibly be obtained only on a case-by-case analysis of the brightest CMEs.
A more positive view is offered by the kinetic energy of CMEs whose temporal evolutions given by the ARTEMIS, CDAW, and CORIMP catalogs are in reasonable agreement between them (within a factor of \(\approx2\)) and in tracking the solar activity in spite of very large fluctuations of the monthly values. Using the values smoothed with a 3-month window to remove the high frequency fluctuations, the kinetic energy extends over approximately four decades; it culminated at \(\approx 10^{33}~\mbox{erg}\) at the maximum of SC 23 but at a slightly reduced value of \(\approx 5\times 10^{32}~\mbox{erg}\) at the maximum of SC 24. During the SC 22/23 minimum, it was down to \(\approx 4 \times 10^{30}~\mbox{erg}\) and further down to \(\approx 3\times 10^{29}~\mbox{erg}\) during the SC 23/24 anomalous minimum. The distributions of kinetic energy extends over eight decades (\(10^{25}\) to \(10^{33}~\mbox{erg}\)) and those of ARTEMIS and CDAW follow a quasi-Gaussian law on a log-log scale implying a log-normal distribution as commonly found in solar physics. This is not the case of the CORIMP distribution which strongly departs from Gaussian with a pronounced skewness toward high kinetic energies.
15.6 Correlation Between Parameters
Generally speaking, we found rather weak correlations between the various CME parameters on the basis of the ARTEMIS data, consistent with the SMM results (Hundhausen et al. 1994) but in disagreement with the CDAW results (Gopalswamy 2004; Vršnak et al. 2004; Yashiro et al. 2004; Gopalswamy et al. 2015c). In summary, we found a lack of correlation between speed and acceleration, a weak correlation between speed and width, and a quasi linear trend of increasing speed with increasing mass on a log-log scale whose slope is inconsistent with the Rosner-Tucker-Vaiana (RTV) scaling law as proposed by Aschwanden (2017). Regarding the latitude, we found extremely weak correlations with both speed and mass. Mass and width are highly correlated with mass increasing with width as expected. Finally, width is very weakly correlated with latitude, the linear regressions being quasi similar in the two hemispheres and indicating slight reductions of a few degrees from equator to poles.
15.7 Solar Cycle Variations
In a broad stroke, the occurrence and mass rates of CMEs closely tracked the solar activity cycle during SC 23 and 24 and we found linear relationships with the selected indices/proxies of activity. The Pearson correlation coefficients with the selected indices/proxies of solar activity are generally very large (\(>0.8\)), with the radio flux ranking first (0.87) and the X-ray background ranking last (0.79), SSN, SSA, and TMF lying in between on the basis of the ARTEMIS data set which further unambiguously demonstrates the total absence of a phase lag. This disproves the early findings of Gopalswamy et al. (2004) based on the CDAW catalog and of Robbrecht et al. (2009) based on the CACTus catalog that the CME rate lagged sunspots by many months up to one year during SC 23. The explanation of this lag as being related to high latitude CMEs arising from polar crown filaments which have a “rush to the poles” near maximum and erupt with a frequency that slightly lags sunspot numbers at low latitudes (Webb and Howard 2012) may be questioned on the basis of the heliolatitudinal distribution of CMEs (Fig. 30) and of our analysis of high-latitude CMEs in Sect. 8.2. Whereas this effect may possibly exist, it would concern only a very small number of CMEs and would consequently be hardly visible in the observations.
A closer examination on the CME rates however revealed several peculiarities.
-
The linear relationships with the selected indices/proxies were different for the two cycles implying that the CME rates were relatively larger during SC 24 than during SC 23 when compared with these indices/proxies. This effect was particularly pronounced for the occurrence rate and less so for the mass rate. However, the average mass of CMEs, while following the pattern of solar activity, remained approximately the same during the maximum phase of SC 23 and SC 24.
-
When considering separately the two hemispheres, SC 24 stood out by the diverging evolution of the CME rates in the northern hemisphere with respect to those of the SSN, SSA, and TMF indices/proxies, most pronounced from mid-2013 to end of 2015. This peculiarity resulting in a relative excess of CMEs was totally absent during SC 23.
Additional detailed peculiarities based on the speed and width of CMEs were discussed in Sect. 12 and are conveniently summarized in the visual presentation of the ratios “SC 24/SC 23” in Fig. 88. Note that the reference value of 0.86 (solid black line) corresponds to the ratio of the radio fluxes separately calculated over the two cycles.
Ratios of the CME counts and masses “SC 24/SC 23” between solar cycles 24 and 23 for the ARTEMIS, SEEDS, CACTus, and CDAW catalogs, globally, by hemisphere, and in different ranges of speed and width. The dotted black line at a value of 1 is intended to guide the eyes. The solid black line at a value of 0.86 corresponds to the ratio of the radio flux
North-South asymmetry of solar activity and the associated phase asynchrony, in particular those of the sunspots, have been known for a long time and recent studies include for example Zolotova and Ponyavin (2006), Carbonell et al. (2007), Donner and Thiel (2007), Li et al. (2009a), McIntosh et al. (2013), Deng et al. (2017). It is beyond the scope of this article to discuss the underlying processes invoked to explain them, but it is considered that the mechanisms which create and transport the magnetic flux from the interior of the Sun to its surface are slowly evolving with time, further loosing coupling across the equator such that those asymmetries can persist for several years. As a consequence, the two hemispheres may be viewed as decoupled and requiring independent treatments. Last but not least, according to Tapping and Morgan (2017), the Sun may be in the process of a significant behavioural change culminating in SC 24, but whose early signs may be traced to SC 21. As far as CMEs are concerned, whereas we did not detect any sign of divergence of their temporal evolution between the two hemispheres during SC 23, SC 24 witnessed a major deviation prominently affecting the northern hemisphere. A tentative explanation invokes the marked weakness of the total magnetic field in the northern hemisphere during most of SC 24 (see Fig. 53) making it easier for the CMEs to erupt and propagate, particularly the small (faint) ones. This explanation would therefore be consistent with the deviation being much more pronounced for the occurrence rate than for the mass rate.
15.8 Halo and Stealth CMEs
Halo CMEs represent a second example (the other being acceleration) of strong divergence between the four catalogs. Adopting a threshold of \(300{^{\circ}}\) to declare a halo CME for statistical analysis as justified in Sect. 13, their numbers during SC 23, SC 24, and altogether during the two cycles differed widely with CDAW reporting a very large number (403) and SEEDS reporting none in SC 23 to give an extreme example (ARTEMIS has 11 and CACTus has 116). Overall, the CDAW count of halos far exceeded the other three, an effect that we attributed to CDAW reporting widths systematically larger than those of the other catalogs. Comparing the production of halo CMEs during SC 23 and SC 24, CDAW and CACTus had counts in SC 23 outnumbering those in SC 24 whereas ARTEMIS and SEEDS report the opposite. In fact, the ARTEMIS data indicate that this latter situation was not limited to halos but that wide CMEs were more numerous during SC 24 than during SC 23. For instance, considering CMEs with width \(>180{^{\circ}}\), their numbers were in a ratio of \(\approx 3\). This may be a consequence of the marked weakness of the total magnetic field during SC 24 (see Fig. 53) allowing a wider expansion of the CMEs. It must be realized that this effect remains largely marginal as it is seen on a very small fraction of the overall population of CMEs (\(\approx1.5\%\) for ARTEMIS, SEEDS, and CACTus and 4.4% for CDAW) and is hardly perceptible on the rest of the population (Fig. 26). Turning to the speed of halo CMEs, the situation is even more confusing with CDAW and CACTus reporting speeds much larger than ARTEMIS and SEEDS. However, there is an agreement on two points: (i) all speeds of halos were substantially larger than the average speed of non-halo CMEs, and (ii) speeds of halos were significantly lower during SC 24 than during SC 23. The first point was debated by Chen (2011) along two lines. Following the work of Andrews (2002) and simulations by Zhang et al. (2010), it has been shown that many narrow and slow CMEs appear fainter when they are observed as halo CMEs to the point of being missed in coronagraphic observations; those which remain observable have speeds larger than average as observed. The second line considers that an observed halo CME is in reality a CME-driven shock wave (Manchester et al. 2008) or a combination of this shock wave with CME material (Lara et al. 2006). This could indeed explain the very large speeds of a small fraction of halo CMEs since the fast-mode wave in the corona is of the order of \(1000~\mbox{km}\,\mbox{s}^{-1}\), but is irrelevant to the large fraction of slower halo CMEs. It is worth keeping in mind that the distribution of CDAW speed peaks at \(\approx 500~\mbox{km}\,\mbox{s}^{-1}\) and that the mean and median speeds of the ARTEMIS distribution are 600 and \(560~\mbox{km}\,\mbox{s}^{-1}\), respectively.
Stealth CMEs could not be directly addressed in the framework of our statistical analysis and we briefly reviewed their status in Sect. 13.2 for the sake of completeness. On the one hand and whereas our analysis of associations summarized in the next subsection indicates that a significant number of CMEs are unrelated to flares, eruptive prominences, filament eruptions, active regions, and streamers, it must be realized that the catalogs of these events are far from being complete and that the procedures of association are certainly not perfect. On the other hand and since stealth CMEs tend to be slow and diffuse, they may escape detection in coronagraph images even though they may be at the origin of major geomagnetic storms. In that respect, it was noted in Sect. 13 that Earth-directed halo CMEs are indeed under detected because of geometric biases. Even if there is some truth in the claim by Howard and Harrison (2013) that their physics is not fundamentally different from CMEs associated with major surface events, it may be premature to consider that the question of the origin of stealth CMEs is settled as we are still lacking the appropriate observations.
15.9 Associations
The results on associations reported in this article were obtained with the ARTEMIS catalog but several tests showed that they are confirmed by the SEEDS data thus emphasizing the general agreement between the two catalogs.
We found that 5.7% of all ARTEMIS CMEs were associated with \(\mbox{C}+\mbox{M}+\mbox{X}\) class flares during SC 23 in the general case of no constraint on the flare longitude, this percentage dropping to 2.9% during SC 24. The former percentage agrees with that found by Aarnio et al. (2011) during SC 23 after proper corrections to account for different conditions. The percentages of flares with known position angle associated with CMEs depend upon the flare class but are independent of the solar cycle; they typically amount to 13% for the C-class, 19% for the M-class, and 32% for the X-class flares. We confirmed past conclusions that CMEs associated with the X- and M-class flares have significantly larger mass, speed, kinetic energy, and width than the overall population of CMEs. This trend tends to decrease with decreasing flare flux and is independent of the solar cycle. Finally, we established linear relationships between the logarithm of both CME mass and kinetic energy with the logarithm of the flare flux.
Using the NoRH database of microwave prominences, we found that 0.33% of all CMEs were associated with an eruptive prominence (EP) and that 60% of all EPs were associated with a CME. The associated CMEs have larger mass and kinetic energy, both independent of the magnitude of the associated EPs. They have slightly larger speed than the overall population weakly correlated with that of the associated EPs. The distribution of their width is rather flat, i.e., without an excess of narrow CMEs contrary to the global population. The distributions of magnitude and speed of EPs and associated EPs are quite similar, but this prominently results from the fact the latter represent approximately two thirds of the EPs. However, when compared with the overall population of prominences, the magnitudes of the associated EPs are systematically larger than those of the overall population whereas this is not the case for the speeds. Using the SDO/AIA database of filament eruptions excluding confined and non-radial events, we found that 2.6% of all CMEs (3.5% of CMEs with a measured mass) were associated with an eruption whereas 50% of the filament eruptions were associated with a CME. The properties of the CMEs associated with filament eruptions differ from the global population of CMEs in a way similar to those of the CMEs associated with NoRH prominences, namely larger mass, kinetic energy, and width. These very low percentages of CMEs associated with prominences may pertinently be questioned on the basis of the unavoidable incompleteness of ground-based observations of prominences as already pointed out in Sect. 14. Interestingly, the case of filaments eruptions observed in space at high spatial resolution leads to a significantly larger number (by a factor of 8) of associated CMEs. A correction factor for the EPs is difficult to estimate, but we very much doubt that they could raise the percentages to the very large values reported in the early studies quoted in Sect. 14. These values obviously resulted from the much lower rates of occurrence found during the first years of CME observations.
Using the SOHO/MDI observations of active regions (ARs) as listed in the Heliophysics Feature Catalogue to study the AR–CME association, we found that 31% of CMES (whether or not they have a measured mass) were associated with an AR and 66% of the ARs were associated with a CME. It should be understood that these percentages are based on time and spatial coincidences between CMEs and ARs without any proof that the ARs actually launched a CME. Therefore, in this framework, they may be considered as upper limits. The physical properties of the associated CMEs are nearly similar to those of the global population with a minor trend for slightly larger mass, speed, and kinetic energy and the subtle absence of narrow widths in the case of the associated CMEs. The distributions of the physical properties (area, maximum intensity, and length of the neutral line) of the associated ARs are remarkably similar to those of the whole set of ARs, except for a slightly larger area but it should be kept in mind that the fraction of associated ARs is very large (66%). Finally, all physical properties of associated CMEs (speed, mass, kinetic energy) are uncorrelated with the above physical properties of the associated ARs.
The association of CMEs with streamers defined as ridges on synoptic maps and representing lines of maximum radiance assimilated to boundaries between regions of opposite magnetic polarities was analyzed in the broader context of the CME–streamer interaction and 52% of all CMEs were found to be associated with streamers. In the case of the brightest “top-ten” CMEs, this percentage sharply increases to 95%. The heliolatitudinal distributions of the associated CMEs, the non-associated CMEs and the overall population of CMEs are quite similar and further in excellent agreement with the unbiased distribution of the electron density resulting from time-dependent solar rotational tomography (3D inversion). This gives further ground to the reality of the association of high latitude CMEs with polar streamers as argued in Sect. 8.2. Whereas the distributions of latitude and speed of the associated CMEs are independent of the number of associated streamers, their intensity and width both increase with the increasing number of associated streamers. However in the case of width, there is an inherent bias as the widest CMEs are more likely to be connected to several streamers. Finally, the dominant processes affecting the associated streamers are emergence and disappearance independent of solar activity, followed by brightening, dimming, and no-change.
All above percentages of association are affected by observational and methodology limitations and biases. Flares, prominences, and active regions are probably underestimated and our method of detecting streamers most probably missed many associations. In addition, the associations are not independent as for instance, streamers are often found above active regions and many streamer blowouts involve a pre-existing prominence which erupts to form the classic “three-part” CME. However, it is highly unlikely that correcting for these limitations (if it was possible) would drastically impact our results and would upset the relative importance and the ranking of the various associations. The lack of commonality of periodicities between CMEs, flares, and prominences provides an indirect evidence that the majority of CMEs are unconnected to these latter recorded eruptive events. The overwhelming domination of the CME–streamer association is further confirmed by (i) the heliolatitudinal distributions (Fig. 85) and by (ii) the conspicuous absence of an equatorial drift at low latitudes (producing the butterfly diagram) and of a poleward drift at high latitudes (the “rush to the pole effect”) limited by the location of the polar crown filaments; this was already noted by Li et al. (2009b) on the basis of the first ten years of observation of LASCO CMEs. These evidences are usually interpreted as proving that CMEs are associated with disruptions of large-scale, close-field magnetic structures rather than to small-scale structures such as sunspots and their active regions. It is not excluded that these latter structures launch a CME but this would remain of minor importance in the overall production of CMEs.
15.10 Is There Two Classes of CMEs?
Many past studies concluded on the possible existence of two classes of CMEs based on different origins, large versus small-scale activity (Dryer 1996), or different properties.
-
A first distinction was based on dynamical arguments, separating slow CMEs, characterized by relatively low speeds and noticeable accelerations, from fast CMEs, characterized by higher speeds and insignificant accelerations. This observational classification was first proposed by MacQueen and Fisher (1983) on the basis of Skylab data and confirmed by Sheeley et al. (1999) relying on the first years of LASCO data. Using height-time maps, Sheeley et al. (1999) distinguished “gradual” and “impulsive” CMEs which they associated with prominences for the first type and to flares and Moreton waves for the second type. This classification was generalized by Andrews and Howard (2001) who added additional, distinct attributes (width, brightness) to the two classes. The question was pursued by Moon et al. (2002) considering two subsets of CMEs, one associated with flares and the other with eruptive filaments. They found some subtle differences between speeds and accelerations that lent support to the concept of two classes. From a statistical analysis of flare-associated and non-flare CMEs, Vršnak et al. (2005) found considerable overlap of accelerations and speeds between the two CME groups thus forming a continuum of events rather than supporting the two-class concept.
-
A second distinction was considered between CMEs associated with helmet streamers (defined as separating coronal holes of opposite polarity) and those associated with pseudostreamers (streamers that separate coronal holes of the same polarity). On the basis of a study conducted over the [2007–2011] time interval, Wang (2015) concluded in favor of two classes, the CMEs associated with pseudostreamers having distinctively a fan-like morphology, narrow widths, and constant low speeds.
Our analysis shows that the first distinction is not justified based on three evidences. First, the correlation speed-acceleration at the heart of this distinction is absent when considering the whole set of CMEs, although it may appear when considering a restricted set of (bright) CMEs. Second, CMEs associated with flares and prominences are altogether characterized by larger mass, speed, and kinetic energy. Third, the distributions of the physical parameters that we constructed do not show any hint of bimodality. This is particularly the case of mass, intensity, speed, acceleration, and furthermore, kinetic energy closely follows a single log-normal law. The only exception is width as three distributions (ARTEMIS, SEEDS, and CACTus) exhibit an excess of narrow CMEs (typically \(<30{^{\circ}}\)) with respect to the exponential laws followed by the larger CMEs (naturally excluding the very large halo CMES resulting from their Earth-directed propagation). Chen (2011) proposed to isolate the narrow CMEs, at least those with widths approximately less than \(10{^{\circ}}\), as a specific group arguing that they show an elongated jet-like shape, whereas the larger “normal” CMEs present a closed (or convex-outward) loop; he did however recognize that many CMEs fall in a fuzzy region of no well-defined shape. The subsequent classification proposed by Vourlidas et al. (2017) where their jet CMEs are narrow and lack a circular front (Sect. 2.2) is incidentally consistent with Chen’s distinction. Several of these white-light narrow structures moving outward from polar coronal holes in the LASCO-C2 field of view were shown by Wang et al. (1998) to be connected to extreme-ultraviolet (EUV) jets originating near flaring EUV bright points seen on EIT images. They presumed that these jets were triggered by reconnection between magnetic bipoles and neighboring unipolar flux. Recent studies indicate that solar coronal jets frequently result from small-scale filaments eruptions (Sterling et al. 2015), the disruption mechanism being similar to that of the largest filaments and in agreement with the breakout model of solar eruptions (Wyper et al. 2018). Since filaments are ubiquitously found above polarity inversion lines throughout the low solar corona, the smaller ones or mini-filaments are a potential source of the numerous narrow jet CMEs present in the ARTEMIS, SEEDS, and CACTus catalogs. The recent discovery of a large number of small-scale magnetic flux ropes in the Ulysses data throughout its whole mission (Chen et al. 2018) leads us to presume that such “mini flux ropes” could be observed as well as narrow CMEs in coronagraphic images, probably with somewhat larger widths of [\(10\mbox{--}30{^{\circ}}\)]. Interestingly, Shen et al. (2012) described a coronal blowout jet event which leads to the eruption of both jetting material (narrow ejection produced by external reconnection) and a flux-rope (bubble-like produced by internal reconnection) CME, both observed faintly by the SECCHI coronagraphs. In summary, whereas we have several evidences that would explain the existence of a large number of narrow CMEs with probable progenitors and mechanisms of eruption basically similar to those of the larger, “normal” CMEs (thus a questionable terminology), we do recognize that the origin of narrow CMEs may still be unsettled, since, for instance, there have been no systematic comparisons of low coronal and coronagraph images for mini-filament eruptions. Whatever the case, we are strongly inclined to think that size does not appear a relevant parameter to distinguish different classes of CMEs.
The second distinction is based on the analysis of \(\approx 100\) CMEs that could be associated with pseudostreamers identified by applying a potential-field source-surface extrapolation (PFSS) to magnetograph measurements during the 2007–2011 time interval (Wang 2015). This interval extending over the SC 23/24 minimum and the rising phase of SC 24 insured a low occurrence rate of CMEs and consequently, their analysis in isolation. These \(\approx 100\) CMEs represent only \(\approx 2.5\%\) of a total of 4000 CMEs listed by the ARTEMIS catalog during the above time interval. The occurrence of pseudostreamers themselves require specific configurations of the photospheric magnetic field that possibly prevail during only parts of a solar cycle. These two facts converge to restricting the number of CMEs associated with pseudostreamers to a very small fraction of the general population. Consequently, their different physical properties as found by Wang (2015) are overwhelmed by those of the general population thus precluding any signature in the statistical distributions.
16 Conclusion
The identification and measurement of CMEs remain difficult due to their complexity and the variety of shapes further complicated by their temporal evolution and the effects of viewing geometry. The development of objective automatic methods represents a real progress and it revealed shortcomings of the inherently subjective visual detection. The complexity of the problem led to the implementation of different techniques with different criteria relying on different characteristic of the CMEs, therefore it is not surprising that they sometime produce inconsistent results. This is prominently seen in the determination of acceleration and in the detection of halo CMEs. Nevertheless, the availability of several automated catalogs must be viewed as an asset and their confrontation, taking into account their specificity and limitations, offers the best approach to ascertain the properties of CMEs and this is the approach we adopted in this article. Let us synthesize the important features that emerge from our analysis. The CME occurrence and mass rates globally track the indices/proxies of solar activity with no time lag, prominently the radio flux F10.7, but the linear relationships were different during the two cycles, implying that the CME rates were relatively larger during SC 24 than during SC 23. Even more important is a marked divergence of the CME rates in the northern hemisphere during SC 24 as these rates were substantially larger than predicted by the temporal variation of the sunspot number. This is tentatively linked to the weakness of the solar magnetic field during SC 24 in general and particularly in this hemisphere. The annualized average mass of CMEs also tracks solar activity but reached the same peak value of \(\approx 1.5\times 10^{15}~\mbox{g}\) during the maximum of SC 23 and SC 24.
Some but not all distributions of physical parameters follow known laws. For instance, the distribution of kinetic energy follows a log-normal law and that of angular width follows an exponential law implying that they are random and independent. The distribution of waiting time (WTD) has a long power-law tail extending from 3 to 100 hr with a power-law index which varies with the solar cycle, thus reflecting the temporal variability of the process of CME formation being close to a random Poisson process during the maxima of activity but exhibiting a trend of intermittence or clusterization during the minima. We found very limited evidence for periodicities in the occurrence and mass rates of CMEs, a striking feature being the dichotomy between the two hemispheres, 1–1.5 years in the northern one and a period of \(\approx 2\) years in the southern one.
Rather weak correlations were found between the various CME parameters consistent with the SMM results (Hundhausen et al. 1994) and particularly a lack of correlation between speed and acceleration. The only counter-example is mass and width which are highly correlated with mass increasing with width as expected.
The association of CMEs with flares and erupting prominences concern only a few percents of the overall population of CMEs; the associated CMEs have distinctly larger mass, speed, kinetic energy and angular width. A more pronounced association is found with active regions but the overwhelming one is with streamers further confirmed by the amazing similarity between the heliolatitudinal distribution of CMEs and that of the electron density reconstructed from time-dependent tomographic inversion.
We found no hint of bimodality in the distributions of physical parameters that would support the existence of two classes, particularly that based on speed and acceleration as they appear uncorrelated. On the contrary, the distributions favor a continuum of properties. Likewise, we questioned the validity of considering the narrow CMEs as a separate class although we found an excess of CMEs with widths less than \(\approx 30{^{\circ}}\) with respect to the exponential laws followed by the larger CMEs. These narrow CMEs may be associated with the ubiquitous mini-filaments eruptions (possibly the jet CMEs) and with mini flux ropes originating from small magnetic bipoles, the disruption mechanisms being similar to those launching larger CMEs. This would support the concept that CMEs at large arise from closed-field coronal regions at both large and small scales.
Notes
References
A.N. Aarnio, K.G. Stassun, W.J. Hughes, S.L. McGregor, Solar flares and coronal mass ejections: a statistically determined flare flux—CME mass correlation. Sol. Phys. 268, 195–212 (2011). https://doi.org/10.1007/s11207-010-9672-7
V.I. Abramenko, D.W. Longcope, Distribution of the magnetic flux in elements of the magnetic field in active regions. Astrophys. J. 619, 1160–1166 (2005). https://doi.org/10.1086/426710
N. Alzate, H. Morgan, Identification of low coronal sources of stealth coronal mass ejections using new image processing techniques. Astrophys. J. 840, 103 (2017). https://doi.org/10.3847/1538-4357/aa6caa
M.D. Andrews, The front-to-back asymmetry of coronal emission. Sol. Phys. 208, 317–324 (2002). https://doi.org/10.1023/A:1020578021120
M.D. Andrews, R.A. Howard, A two-type classification of Lasco coronal mass ejection. Space Sci. Rev. 95, 147–163 (2001)
S.K. Antiochos, C.R. DeVore, J.A. Klimchuk, A model for solar coronal mass ejections. Astrophys. J. 510, 485–493 (1999). https://doi.org/10.1086/306563
M.J. Aschwanden, Global energetics of solar flares. VI. Refined energetics of coronal mass ejections. Astrophys. J. 847, 27 (2017). https://doi.org/10.3847/1538-4357/aa8952
M.J. Aschwanden, J.M. McTiernan, Reconciliation of waiting time statistics of solar flares observed in hard X-rays. Astrophys. J. 717, 683–692 (2010). https://doi.org/10.1088/0004-637X/717/2/683
M.J. Aschwanden, N.B. Crosby, M. Dimitropoulou, M.K. Georgoulis, S. Hergarten, J. McAteer, A.V. Milovanov, S. Mineshige, L. Morales, N. Nishizuka, G. Pruessner, R. Sanchez, A.S. Sharma, A. Strugarek, V. Uritsky, 25 years of self-organized criticality: solar and astrophysics. Space Sci. Rev. 198, 47–166 (2016). https://doi.org/10.1007/s11214-014-0054-6
T. Barlyaeva, P. Lamy, A. Llebaria, Mid-term quasi-periodicities and solar cycle variation of the white-light corona from 18.5 years (1996.0–2014.5) of LASCO observations. Sol. Phys. 290, 2117–2142 (2015). https://doi.org/10.1007/s11207-015-0736-6
T. Barlyaeva, J. Wojak, P. Lamy, B. Boclet, I. Toth, Periodic behaviour of coronal mass ejections, eruptive events, and solar activity proxies during solar cycles 23 and 24. J. Atmos. Sol.-Terr. Phys. 177, 12–28 (2018). https://doi.org/10.1016/j.jastp.2018.05.012
B.M. Bein, M. Temmer, A. Vourlidas, A.M. Veronig, D. Utz, The height evolution of the “true” coronal mass ejection mass derived from STEREO COR1 and COR2 observations. Astrophys. J. 768, 31 (2013). https://doi.org/10.1088/0004-637X/768/1/31
S.K. Bisoi, P. Janardhan, D. Chakrabarty, S. Ananthakrishnan, A. Divekar, Changes in quasi-periodic variations of solar photospheric fields: precursor to the deep solar minimum in cycle 23? Sol. Phys. 289, 41–61 (2014). https://doi.org/10.1007/s11207-013-0335-3
G. Boffetta, V. Carbone, P. Giuliani, P. Veltri, A. Vulpiani, Power laws in solar flares: self-organized criticality or turbulence? Phys. Rev. Lett. 83, 4662–4665 (1999). https://doi.org/10.1103/PhysRevLett.83.4662
S. Boulade, C. Delanné, S. Koutchmy, P. Lamy, A. Llebaria, R. Howard, R. Schwenn, G. Simnett, Analysis of a high latitude slow CME with travelling ejecta, in Fifth SOHO Workshop: The Corona and Solar Wind Near Minimum Activity, vol. 404 (1997), p. 217
Y. Boursier, P. Lamy, A. Llebaria, F. Goudail, S. Robelus, The ARTEMIS catalog of LASCO coronal mass ejections. Automatic recognition of transient events and Marseille inventory from synoptic maps. Sol. Phys. 257, 125–147 (2009). https://doi.org/10.1007/s11207-009-9370-5
G.E. Brueckner, R.A. Howard, M.J. Koomen, C.M. Korendyke, D.J. Michels, J.D. Moses, D.G. Socker, K.P. Dere, P.L. Lamy, A. Llebaria, M.V. Bout, R. Schwenn, G.M. Simnett, D.K. Bedford, C.J. Eyles, The Large Angle Spectroscopic Coronagraph (LASCO). Sol. Phys. 162, 357–402 (1995). https://doi.org/10.1007/BF00733434
A.S. Brun, R.A. García, G. Houdek, D. Nandy, M. Pinsonneault, The solar-stellar connection. Space Sci. Rev. 196, 303–356 (2015). https://doi.org/10.1007/s11214-014-0117-8
J.T. Burkepile, A.J. Hundhausen, A.L. Stanger, O.C. St. Cyr, J.A. Seiden, Role of projection effects on solar coronal mass ejection properties: 1. A study of CMEs associated with limb activity. J. Geophys. Res. Space Phys. 109, 03103 (2004). https://doi.org/10.1029/2003JA010149
J.P. Byrne, Investigating the kinematics of coronal mass ejections with the automated CORIMP catalog. J. Space Weather Space Clim. 5(27), 19 (2015). https://doi.org/10.1051/swsc/2015020
J.P. Byrne, P.T. Gallagher, R.T.J. McAteer, C.A. Young, The kinematics of coronal mass ejections using multiscale methods. Astron. Astrophys. 495(1), 325–334 (2009). https://doi.org/10.1051/0004-6361:200809811
J.P. Byrne, H. Morgan, S.R. Habbal, P.T. Gallagher, Automatic detection and tracking of coronal mass ejections. II. Multiscale filtering of coronagraph images. Astrophys. J. 752, 145 (2012). https://doi.org/10.1088/0004-637X/752/2/145
M. Carbonell, J. Terradas, R. Oliver, J.L. Ballester, The statistical significance of the North-South asymmetry of solar activity revisited. Astron. Astrophys. 476, 951–957 (2007). https://doi.org/10.1051/0004-6361:20078004
P.F. Chen, Coronal mass ejections: models and their observational basis. Living Rev. Sol. Phys. 8, 1 (2011). https://doi.org/10.12942/lrsp-2011-1
Y. Chen, Q. Hu, J. le Roux, J. Zheng, Observational analysis of small-scale magnetic flux ropes from Ulysses in-situ measurements. Abstract SH23D-3349 Presented at 2018 Fall Meeting, AGU, Washington, D.C. (2018)
D.P. Choudhary, J.K. Lawrence, M. Norris, A.C. Cadavid, Different periodicities in the sunspot area and the occurrence of solar flares and coronal mass ejections in solar cycle 23–24. Sol. Phys. 289, 649–656 (2014). https://doi.org/10.1007/s11207-013-0392-7
E.W. Cliver, V. Boriakoff, K.H. Bounar, Geomagnetic activity and the solar wind during the Maunder Minimum. Geophys. Res. Lett. 25, 897–900 (1998). https://doi.org/10.1029/98GL00500
R.C. Colaninno, A. Vourlidas, Analysis of the velocity field of CMEs using optical flow methods. Astrophys. J. 652, 1747–1754 (2006). https://doi.org/10.1086/507943
R.C. Colaninno, A. Vourlidas, First determination of the true mass of coronal mass ejections: a novel approach to using the two STEREO viewpoints. Astrophys. J. 698, 852–858 (2009). https://doi.org/10.1088/0004-637X/698/1/852
A. Compagnino, P. Romano, F. Zuccarello, A statistical study of CME properties and of the correlation between flares and CMEs over solar cycles 23 and 24. Sol. Phys. 292, 5 (2017). https://doi.org/10.1007/s11207-016-1029-4
H. Cremades, O.C. St. Cyr, Coronal mass ejections: solar cycle aspects. Adv. Space Res. 40, 1042–1048 (2007). https://doi.org/10.1016/j.asr.2007.01.088
L. Deng, X. Zhang, J. An, Y. Cai, Statistical properties of solar \(\mbox{H}\alpha\) flare activity. J. Space Weather Space Clim. 7(27), 34 (2017). https://doi.org/10.1051/swsc/2017038
E. D’Huys, D.B. Seaton, S. Poedts, D. Berghmans, Observational characteristics of coronal mass ejections without low-coronal signatures. Astrophys. J. 795, 49 (2014). https://doi.org/10.1088/0004-637X/795/1/49
V. Domingo, B. Fleck, A.I. Poland, SOHO: the Solar and Heliospheric Observatory. Space Sci. Rev. 72, 81–84 (1995). https://doi.org/10.1007/BF00768758
R. Donner, M. Thiel, Scale-resolved phase coherence analysis of hemispheric sunspot activity: a new look at the North-South asymmetry. Astron. Astrophys. 475, 33–36 (2007). https://doi.org/10.1051/0004-6361:20078672
E. Dougherty, Mathematical Morphology in Image Processing (CRC press, Boca Raton, 1992)
M. Dryer, Comments on the origins of coronal mass ejections. Sol. Phys. 169(2), 421–429 (1996). https://doi.org/10.1007/BF00190618
J. Feynman, A.J. Hundhausen, Coronal mass ejections and major solar flares: the great active center of March 1989. J. Geophys. Res. 99, 8451–8464 (1994). https://doi.org/10.1029/94JA00202
B. Filippov, A. Zagnetko, Prominence height shows the proximity of an ejection. J. Atmos. Sol.-Terr. Phys. 70, 614–620 (2008). https://doi.org/10.1016/j.jastp.2007.08.035
R.R. Fisher, R.H. Lee, R.M. MacQueen, A.I. Poland, New Mauna Loa coronagraph systems. Appl. Opt. 20(6), 1094–1101 (1981). https://doi.org/10.1364/AO.20.001094
O. Floyd, P. Lamy, Y. Boursier, A. Llebaria, ARTEMIS II: a second-generation catalog of LASCO coronal mass ejections including mass and kinetic energy. Sol. Phys. 288, 269–289 (2013). https://doi.org/10.1007/s11207-013-0281-0
T.G. Forbes, A review on the genesis of coronal mass ejections. J. Geophys. Res. 105, 23153–23166 (2000). https://doi.org/10.1029/2000JA000005
H.R. Gilbert, T.E. Holzer, J.T. Burkepile, A.J. Hundhausen, Active and eruptive prominences and their relationship to coronal mass ejections. Astrophys. J. 537, 503–515 (2000). https://doi.org/10.1086/309030
N. Gopalswamy, A global picture of CMEs in the inner heliosphere, in The Sun and the Heliosphere as an Integrated System, ed. by G. Poletto, S.T. Suess. Astrophysics and Space Science Library, vol. 317 (2004), p. 201. https://doi.org/10.1007/978-1-4020-2831-9_8
N. Gopalswamy, The dynamics of eruptive prominences, in Solar Prominences, 2015
N. Gopalswamy, A. Lara, S. Yashiro, S. Nunes, R.A. Howard, Coronal mass ejection activity during solar cycle 23, in Solar Variability as an Input to the Earth’s Environment, ed. by A. Wilson. ESA Special Publication, vol. 535 (2003a), pp. 403–414
N. Gopalswamy, A. Lara, S. Yashiro, R.A. Howard, Coronal mass ejections and solar polarity reversal. Astrophys. J. Lett. 598, 63–66 (2003b). https://doi.org/10.1086/380430
N. Gopalswamy, M. Shimojo, W. Lu, S. Yashiro, K. Shibasaki, R.A. Howard, Prominence eruptions and coronal mass ejection: a statistical study using microwave observations. Astrophys. J. 586, 562–578 (2003c). https://doi.org/10.1086/367614
N. Gopalswamy, S. Nunes, S. Yashiro, R.A. Howard, Variability of solar eruptions during cycle 23. Adv. Space Res. 34, 391–396 (2004). https://doi.org/10.1016/j.asr.2003.10.054
N. Gopalswamy, S. Yashiro, S. Akiyama, Geoeffectiveness of halo coronal mass ejections. J. Geophys. Res. Space Phys. 112, 06112 (2007). https://doi.org/10.1029/2006JA012149
N. Gopalswamy, S. Yashiro, G. Michalek, G. Stenborg, A. Vourlidas, S. Freeland, R. Howard, The SOHO/LASCO CME catalog. Earth Moon Planets 104, 295–313 (2009). https://doi.org/10.1007/s11038-008-9282-7
N. Gopalswamy, S. Akiyama, S. Yashiro, P. Mäkelä, Coronal mass ejections from sunspot and non-sunspot regions. Astrophys. Space Sci. Proc. 19, 289–307 (2010). https://doi.org/10.1007/978-3-642-02859-5_24
N. Gopalswamy, P. Makela, S. Akiyama, S. Yashiro, N. Thakur, CMEs during the two activity peaks in Cycle 24 and their space weather consequences. Sun and Geosphere (2015a)
N. Gopalswamy, H. Xie, S. Akiyama, P. Mäkelä, S. Yashiro, G. Michalek, The peculiar behavior of halo coronal mass ejections in solar cycle 24. Astrophys. J. Lett. 804, 23 (2015b). https://doi.org/10.1088/2041-8205/804/1/L23
N. Gopalswamy, B. Tsurutani, Y. Yan, Short-term variability of the Sun-Earth system: an overview of progress made during the CAWSES-II period. Prog. Earth Planet. Sci. 2, 13 (2015c). https://doi.org/10.1186/s40645-015-0043-8
J.T. Gosling, E. Hildner, R.M. MacQueen, R.H. Munro, A.I. Poland, C.L. Ross, Mass ejections from the Sun—a view from SKYLAB. J. Geophys. Res. 79, 4581–4587 (1974). https://doi.org/10.1029/JA079i031p04581
J.T. Gosling, E. Hildner, R.M. MacQueen, R.H. Munro, A.I. Poland, C.L. Ross, Direct observations of a flare related coronal and solar wind disturbance. Sol. Phys. 40, 439–448 (1975). https://doi.org/10.1007/BF00162390
J.T. Gosling, E. Hildner, R.M. MacQueen, R.H. Munro, A.I. Poland, C.L. Ross, The speeds of coronal mass ejection events. Sol. Phys. 48, 389–397 (1976). https://doi.org/10.1007/BF00152004
M.R.G. Guedes, E.S. Pereira, J.R. Cecatto, Wavelet analysis of CME, X-ray flare, and sunspot series. Astron. Astrophys. 573, 64 (2015). https://doi.org/10.1051/0004-6361/201323080
S.A. Guseva, G.D. Kim, A.G. Tlatov, The database of solar prominences by the observations at Kislovodsk Mountain Astronomical Station of the Main (Pulkovo) Observatory during 1957–2006. Proc. SAO RAS “Multiwave studies of the Sun and modern problems of solar activity” (in Russian), 269 (2007)
R.A. Harrison, Coronal transients and their relation to solar flares. Adv. Space Res. 11, 25–36 (1991). https://doi.org/10.1016/0273-1177(91)90085-X
R.A. Harrison, J.A. Davies, D. Barnes, J.P. Byrne, C.H. Perry, V. Bothmer, J.P. Eastwood, P.T. Gallagher, E.K.J. Kilpua, C. Möstl, L. Rodriguez, A.P. Rouillard, D. Odstrčil, CMEs in the heliosphere: I. A statistical analysis of the observational properties of CMEs detected in the heliosphere from 2007 to 2017 by STEREO/HI-1. Sol. Phys. 293, 77 (2018). https://doi.org/10.1007/s11207-018-1297-2
P. Hess, R.C. Colaninno, Comparing automatic CME detections in multiple LASCO and SECCHI catalogs. Astrophys. J. 836, 134 (2017). https://doi.org/10.3847/1538-4357/aa5b85
P.A. Higgins, P.T. Gallagher, R.T.J. McAteer, D.S. Bloomfield, Solar magnetic feature detection and tracking for space weather monitoring. Adv. Space Res. 47, 2105–2117 (2011). https://doi.org/10.1016/j.asr.2010.06.024
E. Hildner, Mass ejections from the solar corona into interplanetary space, in Study of Travelling Interplanetary Phenomena, vol. 71 (1977), pp. 3–20
J.T. Hoeksema, Closing the books on Cycle 24. Abstract SH41C-3661 Presented at 2018 Fall Meeting, AGU, Washington, D.C. (2018)
K. Hori, J.L. Culhane, Trajectories of microwave prominence eruptions. Astron. Astrophys. 382, 666–677 (2002). https://doi.org/10.1051/0004-6361:20011658
T.A. Howard, R.A. Harrison, Stealth coronal mass ejections: a perspective. Sol. Phys. 285, 269–280 (2013). https://doi.org/10.1007/s11207-012-0217-0
T.A. Howard, G.M. Simnett, Interplanetary coronal mass ejections that are undetected by solar coronagraphs. J. Geophys. Res. Space Phys. 113, 08102 (2008). https://doi.org/10.1029/2007JA012920
R.A. Howard, A. Vourlidas, Evolution of CME mass in the corona. Sol. Phys. 293, 55 (2018). https://doi.org/10.1007/s11207-018-1274-9
R.A. Howard, D.J. Michels, N.R. Sheeley Jr., M.J. Koomen, The observation of a coronal transient directed at Earth. Astrophys. J. Lett. 263, 101–104 (1982). https://doi.org/10.1086/183932
R.A. Howard, N.R. Sheeley Jr., D.J. Michels, M.J. Koomen, Coronal mass ejections—1979–1981. J. Geophys. Res. 90, 8173–8191 (1985). https://doi.org/10.1029/JA090iA09p08173
R.A. Howard, J.D. Moses, A. Vourlidas, J.S. Newmark, D.G. Socker, S.P. Plunkett, C.M. Korendyke, J.W. Cook, A. Hurley, J.M. Davila, W.T. Thompson, O.C. St Cyr, E. Mentzell, K. Mehalick, J.R. Lemen, J.P. Wuelser, D.W. Duncan, T.D. Tarbell, C.J. Wolfson, A. Moore, R.A. Harrison, N.R. Waltham, J. Lang, C.J. Davis, C.J. Eyles, H. Mapson-Menard, G.M. Simnett, J.P. Halain, J.M. Defise, E. Mazy, P. Rochus, R. Mercier, M.F. Ravet, F. Delmotte, F. Auchere, J.P. Delaboudiniere, V. Bothmer, W. Deutsch, D. Wang, N. Rich, S. Cooper, V. Stephens, G. Maahs, R. Baugh, D. McMullin, T. Carter, Sun Earth connection coronal and heliospheric investigation (SECCHI). Space Sci. Rev. 136, 67–115 (2008). https://doi.org/10.1007/s11214-008-9341-4
R. Howe, J. Christensen-Dalsgaard, F. Hill, R.W. Komm, R.M. Larsen, J. Schou, M.J. Thompson, J. Toomre, Dynamic variations at the base of the solar convection zone. Science 287, 2456–2460 (2000). https://doi.org/10.1126/science.287.5462.2456
R. Howe, J. Christensen-Dalsgaard, F. Hill, R. Komm, J. Schou, M.J. Thompson, J. Toomre, Temporal variations in solar rotation at the bottom of the convection zone: the current status. Adv. Space Res. 40, 915–918 (2007). https://doi.org/10.1016/j.asr.2006.12.047
A.J. Hundhausen, Sizes and locations of coronal mass ejections—SMM observations from 1980 and 1984–1989. J. Geophys. Res. 98, 13 (1993). https://doi.org/10.1029/93JA00157
A.J. Hundhausen, C.B. Sawyer, L. House, R.M.E. Illing, W.J. Wagner, Coronal mass ejections observed during the solar maximum mission—latitude distribution and rate of occurrence. J. Geophys. Res. 89, 2639–2646 (1984). https://doi.org/10.1029/JA089iA05p02639
A.J. Hundhausen, J.T. Burkepile, O.C. St. Cyr, Speeds of coronal mass ejections: SMM observations from 1980 and 1984–1989. J. Geophys. Res. 99, 6543–6552 (1994). https://doi.org/10.1029/93JA03586
R.M.E. Illing, A.J. Hundhausen, Disruption of a coronal streamer by an eruptive prominence and coronal mass ejection. J. Geophys. Res. 91, 10951–10960 (1986). https://doi.org/10.1029/JA091iA10p10951
B.V. Jackson, Imaging of coronal mass ejections by the HELIOS spacecraft. Sol. Phys. 100, 563–574 (1985). https://doi.org/10.1007/BF00158445
B.V. Jackson, A. Buffington, P.P. Hick, R.C. Altrock, S. Figueroa, P.E. Holladay, J.C. Johnston, S.W. Kahler, J.B. Mozer, S. Price, R.R. Radick, R. Sagalyn, D. Sinclair, G.M. Simnett, C.J. Eyles, M.P. Cooke, S.J. Tappin, T. Kuchar, D. Mizuno, D.F. Webb, P.A. Anderson, S.L. Keil, R.E. Gold, N.R. Waltham, The Solar Mass-Ejection Imager (SMEI) mission. Sol. Phys. 225, 177–207 (2004). https://doi.org/10.1007/s11207-004-2766-3
S. Kahler, Coronal mass ejections. Rev. Geophys. 25, 663–675 (1987). https://doi.org/10.1029/RG025i003p00663
S.W. Kahler, Solar flares and coronal mass ejections. Annu. Rev. Astron. Astrophys. 30, 113–141 (1992). https://doi.org/10.1146/annurev.aa.30.090192.000553
S.W. Kahler, N.R. Sheeley Jr., M. Liggett, Coronal mass ejections and associated X-ray flare durations. Astrophys. J. 344, 1026–1033 (1989). https://doi.org/10.1086/167869
E.K.J. Kilpua, M. Mierla, A.N. Zhukov, L. Rodriguez, A. Vourlidas, B. Wood, Solar sources of interplanetary coronal mass ejections during the solar cycle 23/24 minimum. Sol. Phys. 289, 3773–3797 (2014). https://doi.org/10.1007/s11207-014-0552-4
V.N. Krivodubskij, Turbulent dynamo near tachocline and reconstruction of azimuthal magnetic field in the solar convection zone. Astron. Nachr. 326, 61–74 (2005). https://doi.org/10.1002/asna.200310340
N.A. Krivova, S.K. Solanki, The 1.3-year and 156-day periodicities in sunspot data: wavelet analysis suggests a common origin. Astron. Astrophys. 394, 701–706 (2002). https://doi.org/10.1051/0004-6361:20021063
P. Lamy, A. Llebaria, E. Quemerais, Solar cycle variation of the radiance and the global electron density of the solar corona. Adv. Space Res. 29, 373–378 (2002). https://doi.org/10.1016/S0273-1177(01)00599-3
P. Lamy, T. Barlyaeva, A. Llebaria, O. Floyd, Comparing the solar minima of cycles 22/23 and 23/24: the view from LASCO white light coronal images. J. Geophys. Res. Space Phys. 119, 47–58 (2014). https://doi.org/10.1002/2013JA019468
P. Lamy, O. Floyd, E. Quémerais, B. Boclet, S. Ferron, Coronal mass ejections and solar wind mass fluxes over the heliosphere during solar cycles 23 and 24 (1996–2014). J. Geophys. Res. Space Phys. 122, 50–62 (2017). https://doi.org/10.1002/2016JA022970
A. Lara, N. Gopalswamy, H. Xie, E. Mendoza-Torres, R. PéRez-EríQuez, G. Michalek, Are halo coronal mass ejections special events? J. Geophys. Res. Space Phys. 111, 06107 (2006). https://doi.org/10.1029/2005JA011431
A. Lara, A. Borgazzi, O. Mendes Jr., R.R. Rosa, M.O. Domingues, Short-period fluctuations in coronal mass ejection activity during solar cycle 23. Sol. Phys. 248, 155–166 (2008). https://doi.org/10.1007/s11207-008-9153-4
Y. Leblanc, G.A. Dulk, A. Vourlidas, J.-L. Bougeret, Tracing shock waves from the corona to 1 AU: type II radio emission and relationship with CMEs. J. Geophys. Res. 106, 25301–25312 (2001). https://doi.org/10.1029/2000JA000260
F. Lepreti, V. Carbone, P. Veltri, Solar flare waiting time distribution: varying-rate Poisson or Lévy function? Astrophys. J. Lett. 555, 133–136 (2001). https://doi.org/10.1086/323178
K.J. Li, P.X. Gao, L.S. Zhan, The long-term behavior of the North South asymmetry of sunspot activity. Sol. Phys. 254, 145–154 (2009a). https://doi.org/10.1007/s11207-008-9284-7
K.J. Li, P.X. Gao, Q.X. Li, J. Mu, T.W. Su, Cyclical behavior of coronal mass ejections. Sol. Phys. 257, 149–154 (2009b). https://doi.org/10.1007/s11207-009-9333-x
C. Li, S.J. Zhong, L. Wang, W. Su, C. Fang, Waiting time distribution of solar energetic particle events modeled with a non-stationary Poisson process. Astrophys. J. Lett. 792, 26 (2014). https://doi.org/10.1088/2041-8205/792/2/L26
Y. Liu, J.G. Luhmann, R.P. Lin, S.D. Bale, A. Vourlidas, G.J.D. Petrie, Coronal mass ejections and global coronal magnetic field reconfiguration. Astrophys. J. Lett. 698, 51–55 (2009). https://doi.org/10.1088/0004-637X/698/1/L51
Y.-Q. Lou, Y.-M. Wang, Z. Fan, S. Wang, J.X. Wang, Periodicities in solar coronal mass ejections. Mon. Not. R. Astron. Soc. 345, 809–818 (2003). https://doi.org/10.1046/j.1365-8711.2003.06993.x
B.C. Low, Solar activity and the corona. Sol. Phys. 167, 217–265 (1996). https://doi.org/10.1007/BF00146338
B.C. Low, Coronal mass ejections, magnetic flux ropes, and solar magnetism. J. Geophys. Res. 106, 25141–25164 (2001). https://doi.org/10.1029/2000JA004015
B.C. Low, A.J. Hundhausen, The velocity field of a coronal mass ejection—the event of September 1, 1980. J. Geophys. Res. 92, 2221–2230 (1987). https://doi.org/10.1029/JA092iA03p02221
B.C. Low, R.H. Munro, R.R. Fisher, The initiation of a coronal transient. Astrophys. J. 254, 335–342 (1982). https://doi.org/10.1086/159737
J. Luhmann, Y. Li, Y. Liu, L. Jian, C. Russell, E. Kilpua, G. Petrie, J. Hoeksema, Heliospheric space weather at the start of cycle 24, in AGU Fall Meeting Abstracts (2011)
S. Ma, G.D.R. Attrill, L. Golub, J. Lin, Statistical study of coronal mass ejections with and without distinct low coronal signatures. Astrophys. J. 722, 289–301 (2010). https://doi.org/10.1088/0004-637X/722/1/289
R.M. MacQueen, R.R. Fisher, The kinematics of solar inner coronal transients. Sol. Phys. 89, 89–102 (1983). https://doi.org/10.1007/BF00211955
R.M. MacQueen, J.A. Eddy, J.T. Gosling, E. Hildner, R.H. Munro, G.A. Newkirk Jr., A.I. Poland, C.L. Ross, The outer solar corona as observed from Skylab: preliminary results. Astrophys. J. Lett. 187, 85 (1974). https://doi.org/10.1086/181402
R.M. MacQueen, A. Csoeke-Poeckh, E. Hildner, L. House, R. Reynolds, A. Stanger, H. Tepoel, W. Wagner, The high altitude observatory coronagraph/polarimeter on the solar maximum mission. Sol. Phys. 65, 91–107 (1980). https://doi.org/10.1007/BF00151386
W.B. Manchester IV, A. Vourlidas, G. Tóth, N. Lugaz, I.I. Roussev, I.V. Sokolov, T.I. Gombosi, D.L. De Zeeuw, M. Opher, Three-dimensional MHD simulation of the 2003 October 28 coronal mass ejection: comparison with LASCO coronagraph observations. Astrophys. J. 684, 1448–1460 (2008). https://doi.org/10.1086/590231
P.I. McCauley, Y.N. Su, N. Schanche, K.E. Evans, C. Su, S. McKillop, K.K. Reeves, Prominence and filament eruptions observed by the Solar Dynamics Observatory: statistical properties, kinematics, and online catalog. Sol. Phys. 290, 1703–1740 (2015). https://doi.org/10.1007/s11207-015-0699-7
S.W. McIntosh, R.J. Leamon, J.B. Gurman, J.-P. Olive, J.W. Cirtain, D.H. Hathaway, J. Burkepile, M. Miesch, R.S. Markel, L. Sitongia, Hemispheric asymmetries of solar photospheric magnetism: radiative, particulate, and heliospheric impacts. Astrophys. J. 765, 146 (2013). https://doi.org/10.1088/0004-637X/765/2/146
S.W. McIntosh, R.J. Leamon, L.D. Krista, A.M. Title, H.S. Hudson, P. Riley, J.W. Harder, G. Kopp, M. Snow, T.N. Woods, J.C. Kasper, M.L. Stevens, R.K. Ulrich, The solar magnetic activity band interaction and instabilities that shape quasi-periodic variability. Nat. Commun. 6, 6491 (2015). https://doi.org/10.1038/ncomms7491
G. Michalek, S. Yashiro, CMEs and active regions on the Sun. Adv. Space Res. 52, 521–527 (2013). https://doi.org/10.1016/j.asr.2013.04.001
Z. Mikic, J.A. Linker, Disruption of coronal magnetic field arcades. Astrophys. J. 430, 898–912 (1994). https://doi.org/10.1086/174460
N. Mittal, J. Sharma, V.K. Verma, V. Garg, On the statistical characteristics of radio-loud and radio-quiet halo coronal mass ejections and their associated flares during solar cycles 23 and 24. New Astron. 47, 64–80 (2016). https://doi.org/10.1016/j.newast.2016.02.004
Y.-J. Moon, G.S. Choe, H. Wang, Y.D. Park, N. Gopalswamy, G. Yang, S. Yashiro, A statistical study of two classes of coronal mass ejections. Astrophys. J. 581, 694–702 (2002). https://doi.org/10.1086/344088
Y.-J. Moon, G.S. Choe, H. Wang, Y.D. Park, Sympathetic coronal mass ejections. Astrophys. J. 588, 1176–1182 (2003). https://doi.org/10.1086/374270
R.H. Munro, J.T. Gosling, E. Hildner, R.M. MacQueen, A.I. Poland, C.L. Ross, The association of coronal mass ejection transients with other forms of solar activity. Sol. Phys. 61, 201–215 (1979). https://doi.org/10.1007/BF00155456
S.A. Murray, J.A. Guerra, P. Zucca, S.-H. Park, E.P. Carley, P.T. Gallagher, N. Vilmer, V. Bothmer, Connecting coronal mass ejections to their solar active region sources: combining results from the HELCATS and FLARECAST projects. Sol. Phys. 293, 60 (2018). https://doi.org/10.1007/s11207-018-1287-4
A. Nindos, S. Patsourakos, A. Vourlidas, C. Tagikas, How common are hot magnetic flux ropes in the low solar corona? A statistical study of euv observations. Astrophys. J. 808(2), 117 (2015)
N. Nitta, S. Akiyama, Relation between flare-associated X-ray ejections and coronal mass ejections. Astrophys. J. Lett. 525, 57–60 (1999). https://doi.org/10.1086/312322
N.V. Nitta, T. Mulligan, Earth-affecting coronal mass ejections without obvious low coronal signatures. Sol. Phys. 292, 125 (2017). https://doi.org/10.1007/s11207-017-1147-7
N.V. Nitta, M.J. Aschwanden, S.L. Freeland, J.R. Lemen, J.-P. Wülser, D.M. Zarro, The association of solar flares with coronal mass ejections during the extended solar minimum. Sol. Phys. 289, 1257–1277 (2014). https://doi.org/10.1007/s11207-013-0388-3
O. Olmedo, J. Zhang, H. Wechsler, K. Borne, A. Poland, Solar Eruptive Event Detection System (SEEDS), in American Astronomical Society Meeting Abstracts. Bulletin of the American Astronomical Society, vol. 37 (2005), p. 1342
O. Olmedo, J. Zhang, H. Wechsler, A. Poland, K. Borne, Automatic detection and tracking of coronal mass ejections in coronagraph time series. Sol. Phys. 248, 485–499 (2008). https://doi.org/10.1007/s11207-007-9104-5
G.J.D. Petrie, Solar magnetic activity cycles, coronal potential field models and eruption rates. Astrophys. J. 768, 162 (2013). https://doi.org/10.1088/0004-637X/768/2/162
S.P. Plunkett, G.E. Brueckner, K.P. Dere, R.A. Howard, M.J. Koomen, C.M. Korendyke, D.J. Michels, J.D. Moses, N.E. Moulton, S.E. Paswaters, O.C. St. Cyr, D.G. Socker, D. Wang, G.M. Simnett, D.K. Bedford, D.A. Biesecker, C.J. Eyles, S.J. Tappin, R. Schwenn, P.L. Lamy, A. Llebaria, The relationship of green-line transients to white-light coronal mass ejections. Sol. Phys. 175, 699–718 (1997). https://doi.org/10.1023/A:1004981125702
S.P. Plunkett, R.A. Howard, J.D. Moses, D.G. Socker, SECCHI Consortium, The Sun-Earth Connection Coronal and Heliospheric Investigation (SECCHI), in EGS General Assembly Conference Abstracts, ed. by A. Tzanis. EGS General Assembly Conference Abstracts, vol. 27 (2002)
E.R. Priest, The initiation of solar coronal mass ejections by magnetic nonequilibrium. Astrophys. J. 328, 848–855 (1988). https://doi.org/10.1086/166342
E. Quémerais, P. Lamy, Two-dimensional electron density in the solar corona from inversion of white light images—application to SOHO/LASCO-C2 observations. Astron. Astrophys. 393, 295–304 (2002). https://doi.org/10.1051/0004-6361:20021019
I.G. Richardson, H.V. Cane, The \(\sim150\) day quasi-periodicity in interplanetary and solar phenomena during cycle 23. Geophys. Res. Lett. 32, 02104 (2005). https://doi.org/10.1029/2004GL021691
I.G. Richardson, T.T. von Rosenvinge, H.V. Cane, The properties of solar energetic particle event-associated coronal mass ejections reported in different CME catalogs. Sol. Phys. 290, 1741–1759 (2015). https://doi.org/10.1007/s11207-015-0701-4
E. Rieger, G.H. Share, D.J. Forrest, G. Kanbach, C. Reppin, E.L. Chupp, A 154-day periodicity in the occurrence of hard solar flares? Nature 312, 623–625 (1984). https://doi.org/10.1038/312623a0
E. Robbrecht, D. Berghmans, Automated recognition of coronal mass ejections (CMEs) in near-real-time data. Astron. Astrophys. 425, 1097–1106 (2004). https://doi.org/10.1051/0004-6361:20041302
E. Robbrecht, D. Berghmans, R.A.M. Van der Linden, Automated LASCO CME catalog for solar cycle 23: are CMEs scale invariant? Astrophys. J. 691, 1222–1234 (2009). https://doi.org/10.1088/0004-637X/691/2/1222
C. Salas-Matamoros, K.-L. Klein, On the statistical relationship between CME speed and soft x-ray flux and fluence of the associated flare. Sol. Phys. 290(5), 1337–1353 (2015)
N.E. Schanche, K.K. Reeves, D.F. Webb, The blob connection: searching for low coronal signatures of solar post-CME blobs. Astrophys. J. 831, 47 (2016). https://doi.org/10.3847/0004-637X/831/1/47
R. Schwenn, An essay on terminology, myths and known facts: solar transient-flare-CME-driver gas-piston-BDE-magnetic cloud-shock wave-geomagnetic storm. Astrophys. Space Sci. 243, 187 (1996). https://doi.org/10.1007/BF00644053
R. Schwenn, B. Inhester, S.P. Plunkett, A. Epple, B. Podlipnik, D.K. Bedford, C.J. Eyles, G.M. Simnett, S.J. Tappin, M.V. Bout, P.L. Lamy, A. Llebaria, G.E. Brueckner, K.P. Dere, R.A. Howard, M.J. Koomen, C.M. Korendyke, D.J. Michels, J.D. Moses, N.E. Moulton, S.E. Paswaters, D.G. Socker, O.C. St. Cyr, D. Wang, First view of the extended green-line emission corona at solar activity minimum using the Lasco-C1 coronagraph on SOHO. Sol. Phys. 175, 667–684 (1997). https://doi.org/10.1023/A:1004948913883
A. Shanmugaraju, M. Syed Ibrahim, Y.-J. Moon, A. Mujiber Rahman, S. Umapathy, Empirical relationship between CME parameters and geo-effectiveness of halo CMEs in the rising phase of solar cycle 24 (2011–2013). Sol. Phys. 290, 1417–1427 (2015). https://doi.org/10.1007/s11207-015-0671-6
N.R. Sheeley Jr., Y.-M. Wang, The recent rejuvenation of the Sun’s large-scale magnetic field: a clue for understanding past and future sunspot cycles. Astrophys. J. 809, 113 (2015). https://doi.org/10.1088/0004-637X/809/2/113
N.R. Sheeley, J.H. Walters, Y.-M. Wang, R.A. Howard, Continuous tracking of coronal outflows: two kinds of coronal mass ejections. J. Geophys. Res. 104, 24739–24768 (1999). https://doi.org/10.1029/1999JA900308
Y. Shen, Y. Liu, J. Su, Y. Deng, On a coronal blowout jet: the first observation of a simultaneously produced bubble-like CME and a jet-like CME in a solar event. Astrophys. J. 745, 164 (2012). https://doi.org/10.1088/0004-637X/745/2/164
M. Shimojo, Unusual migration of prominence activities in the southern hemisphere during cycles 23–24. Publ. Astron. Soc. Jpn. 65, 16 (2013). https://doi.org/10.1093/pasj/65.sp1.S16
M. Shimojo, T. Yokoyama, A. Asai, H. Nakajima, K. Shibasaki, One solar-cycle observations of prominence activities using the Nobeyama Radioheliograph 1992–2004. Publ. Astron. Soc. Jpn. 58, 85–92 (2006). https://doi.org/10.1093/pasj/58.1.85
D.G. Sime, Coronal mass ejection rate and the evolution of the large-scale k-coronal density distribution. J. Geophys. Res. 94, 151–158 (1989). https://doi.org/10.1029/JA094iA01p00151
G.M. Simnett, R.A. Harrison, The relationship between coronal mass ejections and solar flares. Adv. Space Res. 4, 279–282 (1984). https://doi.org/10.1016/0273-1177(84)90572-6
G.M. Simnett, R.A. Harrison, The onset of coronal mass ejections. Sol. Phys. 99, 291–311 (1985). https://doi.org/10.1007/BF00157314
O.C. St. Cyr, D.F. Webb, Activity associated with coronal mass ejections at solar minimum—SMM observations from 1984–1986. Sol. Phys. 136, 379–394 (1991). https://doi.org/10.1007/BF00146543
O.C. St. Cyr, J.T. Burkepile, A.J. Hundhausen, A.R. Lecinski, A comparison of ground-based and spacecraft observations of coronal mass ejections from 1980–1989. J. Geophys. Res. 104, 12493–12506 (1999). https://doi.org/10.1029/1999JA900045
O.C. St. Cyr, S.P. Plunkett, D.J. Michels, S.E. Paswaters, M.J. Koomen, G.M. Simnett, B.J. Thompson, J.B. Gurman, R. Schwenn, D.F. Webb, E. Hildner, P.L. Lamy, Properties of coronal mass ejections: SOHO LASCO observations from January 1996 to June 1998. J. Geophys. Res. 105, 18169–18186 (2000). https://doi.org/10.1029/1999JA000381
O.C. St. Cyr, Q.A. Flint, H. Xie, D.F. Webb, J.T. Burkepile, A.R. Lecinski, C. Quirk, A.L. Stanger, MLSO mark III K-coronameter observations of the CME rate from 1989–1996. Sol. Phys. 290, 2951–2962 (2015). https://doi.org/10.1007/s11207-015-0780-2
A.C. Sterling, R.L. Moore, D.A. Falconer, M. Adams, Small-scale filament eruptions as the driver of X-ray jets in solar coronal holes. Nature 523, 437–440 (2015). https://doi.org/10.1038/nature14556
P. Subramanian, K.P. Dere, Source regions of coronal mass ejections. Astrophys. J. 561, 372–395 (2001). https://doi.org/10.1086/323213
P. Subramanian, A. Vourlidas, Energetics of solar coronal mass ejections. Astron. Astrophys. 467, 685–693 (2007). https://doi.org/10.1051/0004-6361:20066770
X. Sun, M.G. Bobra, J.T. Hoeksema, Y. Liu, Y. Li, C. Shen, S. Couvidat, A.A. Norton, G.H. Fisher, Why is the great solar active region 12192 flare-rich but CME-poor? Astrophys. J. Lett. 804, 28 (2015). https://doi.org/10.1088/2041-8205/804/2/L28
M. Syed Ibrahim, A. Shanmugaraju, Y.-J. Moon, B. Vrsnak, S. Umapathy, Properties and relationship between solar eruptive flares and coronal mass ejections during rising phase of solar cycles 23 and 24. Adv. Space Res. 61, 540–551 (2018). https://doi.org/10.1016/j.asr.2017.09.015
K. Tapping, Solar Activity Indices, ed. by P. Murdin 2006, p. 1. https://doi.org/10.1888/0333750888/2047
K. Tapping, C. Morgan, Changing relationships between sunspot number, total sunspot area and \(F_{\{}10.7\}\) in cycles 23 and 24. Sol. Phys. 292, 73 (2017). https://doi.org/10.1007/s11207-017-1111-6
D. Telloni, V. Carbone, F. Lepreti, E. Antonucci, Stochasticity and persistence of solar coronal mass ejections. Astrophys. J. Lett. 781, 1 (2014). https://doi.org/10.1088/2041-8205/781/1/L1
M. Temmer, A.M. Veronig, B. Vršnak, J. Rybák, P. Gömöry, S. Stoiser, D. Maričić, Acceleration in fast halo CMEs and synchronized flare HXR bursts. Astrophys. J. Lett. 673, 95 (2008). https://doi.org/10.1086/527414
R. Tousey, J.D.F. Bartoe, J.D. Bohlin, G.E. Brueckner, J.D. Purcell, V.E. Scherrer, N.R. Sheeley Jr., R.J. Schumacher, M.E. Vanhoosier, A preliminary study of the extreme ultraviolet spectroheliograms from Skylab. Sol. Phys. 33, 265–280 (1973). https://doi.org/10.1007/BF00152418
D. Tripathi, V. Bothmer, H. Cremades, The basic characteristics of EUV post-eruptive arcades and their role as tracers of coronal mass ejection source regions. Astron. Astrophys. 422, 337–349 (2004). https://doi.org/10.1051/0004-6361:20035815
C. Verbeeck, V. Delouille, B. Mampaey, R. De Visscher, The SPoCA-suite: software for extraction, characterization, and tracking of active regions and coronal holes on EUV images. Astron. Astrophys. 561, 29 (2014). https://doi.org/10.1051/0004-6361/201321243
D. Vibert, C. Peillon, P. Lamy, R.A. Frazin, J. Wojak, Time-dependent tomographic reconstruction of the solar corona. Astron. Comput. 17, 144–162 (2016). https://doi.org/10.1016/j.ascom.2016.09.001
A. Vourlidas, P. Subramanian, K.P. Dere, R.A. Howard, Large-angle spectrometric coronagraph measurements of the energetics of coronal mass ejections. Astrophys. J. 534, 456–467 (2000). https://doi.org/10.1086/308747
A. Vourlidas, D. Buzasi, R. Howard, E. Esfandiari, Mass and energy properties of LASCO CMEs, in Solar Variability: From Core to Outer Frontiers, vol. 506 (2002), pp. 91–94
A. Vourlidas, R.A. Howard, E. Esfandiari, S. Patsourakos, S. Yashiro, G. Michalek, Comprehensive analysis of coronal mass ejection mass and energy properties over a full solar cycle. Astrophys. J. 722, 1522–1538 (2010). https://doi.org/10.1088/0004-637X/722/2/1522
A. Vourlidas, R.A. Howard, E. Esfandiari, S. Patsourakos, S. Yashiro, G. Michalek, Erratum: Comprehensive analysis of coronal mass ejection mass and energy properties over a full solar cycle. Astrophys. J. 730, 59 (2011). https://doi.org/10.1088/0004-637X/730/1/59
A. Vourlidas, B.J. Lynch, R.A. Howard, Y. Li, How many CMEs have flux ropes? Deciphering the signatures of shocks, flux ropes, and prominences in coronagraph observations of CMEs. Sol. Phys. 284, 179–201 (2013). https://doi.org/10.1007/s11207-012-0084-8
A. Vourlidas, L.A. Balmaceda, G. Stenborg, A. Dal Lago, Multi-viewpoint coronal mass ejection catalog based on STEREO COR2 observations. Astrophys. J. 838, 141 (2017). https://doi.org/10.3847/1538-4357/aa67f0
B. Vršnak, D. Ruždjak, D. Sudar, N. Gopalswamy, Kinematics of coronal mass ejections between 2 and 30 solar radii. What can be learned about forces governing the eruption? Astron. Astrophys. 423, 717–728 (2004). https://doi.org/10.1051/0004-6361:20047169
B. Vršnak, D. Sudar, D. Ruždjak, The CME-flare relationship: are there really two types of CMEs? Astron. Astrophys. 435, 1149–1157 (2005). https://doi.org/10.1051/0004-6361:20042166
W.J. Wagner, Coronal mass ejections. Annu. Rev. Astron. Astrophys. 22, 267–289 (1984a). https://doi.org/10.1146/annurev.aa.22.090184.001411
W.J. Wagner, Spontaneous coronal mass ejections, in Bulletin of the American Astronomical Society. Bull. Am. Astron. Soc., vol. 16 (1984b), p. 536
W.J. Wagner, J.J. Wagner, Coronal mass ejection recurrence studies indicating global activity and local suppression. Astron. Astrophys. 133, 288–292 (1984)
Y.-M. Wang, Pseudostreamers as the source of a separate class of solar coronal mass ejections. Astrophys. J. Lett. 803, 12 (2015). https://doi.org/10.1088/2041-8205/803/1/L12
Y.-M. Wang, R. Colaninno, Is solar cycle 24 producing more coronal mass ejections than cycle 23? Astrophys. J. Lett. 784, 27 (2014). https://doi.org/10.1088/2041-8205/784/2/L27
H. Wang, P.R. Goode, Synoptic observing programs at Big Bear Solar Observatory, in Synoptic Solar Physics, ed. by K.S. Balasubramaniam, J. Harvey, D. Rabin. Astronomical Society of the Pacific Conference Series, vol. 140 (1998), p. 497
Y.-M. Wang, N.R. Sheeley Jr., On the topological evolution of the coronal magnetic field during the solar cycle. Astrophys. J. 599, 1404–1417 (2003). https://doi.org/10.1086/379348
Y. Wang, J. Zhang, A statistical study of solar active regions that produce extremely fast coronal mass ejections. Astrophys. J. 680, 1516–1522 (2008). https://doi.org/10.1086/587619
Y.-M. Wang, N.R. Sheeley Jr., D.G. Socker, R.A. Howard, G.E. Brueckner, D.J. Michels, D. Moses, O.C. St. Cyr, A. Llebaria, J.-P. Delaboudinière, Observations of correlated white-light and extreme-ultraviolet jets from polar coronal holes. Astrophys. J. 508, 899–907 (1998). https://doi.org/10.1086/306450
Y. Wang, C. Chen, B. Gui, C. Shen, P. Ye, S. Wang, Statistical study of coronal mass ejection source locations: understanding CMEs viewed in coronagraphs. J. Geophys. Res. Space Phys. 116, 04104 (2011). https://doi.org/10.1029/2010JA016101
D.F. Webb, Understanding CMEs and their source regions. J. Atmos. Sol.-Terr. Phys. 62, 1415–1426 (2000). https://doi.org/10.1016/S1364-6826(00)00075-4
D.F. Webb, Eruptive prominences and their association with coronal mass ejections, in Solar Prominences, ed. by J.-C. Vial, O. Engvold Astrophysics and Space Science Library, vol. 415 (2015), p. 411. https://doi.org/10.1007/978-3-319-10416-4_16
D.F. Webb, R.A. Howard, The solar cycle variation of coronal mass ejections and the solar wind mass flux. J. Geophys. Res. 99, 4201–4220 (1994). https://doi.org/10.1029/93JA02742
D.F. Webb, T.A. Howard, Coronal mass ejections: observations. Living Rev. Sol. Phys. 9, 3 (2012). https://doi.org/10.12942/lrsp-2012-3
D.F. Webb, A.J. Hundhausen, Activity associated with the solar origin of coronal mass ejections. Sol. Phys. 108, 383–401 (1987). https://doi.org/10.1007/BF00214170
D.F. Webb, R.A. Howard, O.C. St. Cyr, A. Vourlidas, Is there a CME rate floor? CME and magnetic flux values for the last four solar cycle minima. Astrophys. J. 851, 142 (2017). https://doi.org/10.3847/1538-4357/aa9b81
W. Weibull, Wide applicability. J. Appl. Mech. 103(730), 293–297 (1951)
Y. Wen, J. Wang, H. Zhao, D.J. Filipe Maia, Coronal mass ejections acceleration problem. Adv. Space Res. 42, 852–857 (2008). https://doi.org/10.1016/j.asr.2007.05.036
M.S. Wheatland, The origin of the solar flare waiting-time distribution. Astrophys. J. Lett. 536, 109–112 (2000). https://doi.org/10.1086/312739
M.S. Wheatland, The coronal mass ejection waiting-time distribution. Sol. Phys. 214, 361–373 (2003). https://doi.org/10.1023/A:1024222511574
R. Wolfson, C. Conover, R.M.E. Illing, The evolution of a coronal streamer prior to mass ejection. J. Geophys. Res. 92, 13641–13646 (1987). https://doi.org/10.1029/JA092iA12p13641
P.F. Wyper, C.R. DeVore, S.K. Antiochos, A breakout model for solar coronal jets with filaments. Astrophys. J. 852, 98 (2018). https://doi.org/10.3847/1538-4357/aa9ffc
G. Yang, H. Wang, Statistical studies of filament disappearances and CMEs, in Solar-Terrestrial Magnetic Activity and Space Environment, ed. by H. Wang, R. Xu (2002), p. 113
S. Yashiro, N. Gopalswamy, G. Michalek, O.C. St. Cyr, S.P. Plunkett, N.B. Rich, R.A. Howard, A catalog of white light coronal mass ejections observed by the SOHO spacecraft. J. Geophys. Res. Space Phys. 109, 07105 (2004). https://doi.org/10.1029/2003JA010282
S. Yashiro, N. Gopalswamy, S. Akiyama, G. Michalek, R.A. Howard, Visibility of coronal mass ejections as a function of flare location and intensity. J. Geophys. Res. Space Phys. 110, A12S05 (2005). https://doi.org/10.1029/2005JA011151
S. Yashiro, S. Akiyama, N. Gopalswamy, R.A. Howard, Different power-law indices in the frequency distributions of flares with and without coronal mass ejections. Astrophys. J. Lett. 650, 143–146 (2006). https://doi.org/10.1086/508876
S. Yashiro, G. Michalek, S. Akiyama, N. Gopalswamy, R.A. Howard, Spatial relationship between solar flares and coronal mass ejections. Astrophys. J. 673, 1174–1180 (2008). https://doi.org/10.1086/524927
C.-T. Yeh, M.D. Ding, P.F. Chen, Kinetic properties of CMEs corrected for the projection effect. Sol. Phys. 229, 313–322 (2005). https://doi.org/10.1007/s11207-005-6883-4
M. Youssef, On the relation between the CMEs and the solar flares. NRIAG J. Astron. Geophys. 1, 172–178 (2012). https://doi.org/10.1016/j.nrjag.2012.12.014
V. Yurchyshyn, Relationship between EIT posteruption arcades, coronal mass ejections, the coronal neutral line, and magnetic clouds. Astrophys. J. Lett. 675, 49 (2008). https://doi.org/10.1086/533413
J. Zhang, K.P. Dere, A statistical study of main and residual accelerations of coronal mass ejections. Astrophys. J. 649, 1100–1109 (2006). https://doi.org/10.1086/506903
M. Zhang, B.C. Low, The hydromagnetic nature of solar coronal mass ejections. Annu. Rev. Astron. Astrophys. 43, 103–137 (2005). https://doi.org/10.1146/annurev.astro.43.072103.150602
J. Zhang, I.G. Richardson, D.F. Webb, N. Gopalswamy, E. Huttunen, J.C. Kasper, N.V. Nitta, W. Poomvises, B.J. Thompson, C.-C. Wu, S. Yashiro, A.N. Zhukov, Solar and interplanetary sources of major geomagnetic storms (\(\mathit{Dst} \leq -100~\mbox{nT}\)) during 1996–2005. J. Geophys. Res. Space Phys. 112(A10), 10102 (2007). https://doi.org/10.1029/2007JA012321
Q.-M. Zhang, Y. Guo, P.-F. Chen, M.-D. Ding, C. Fang, Why are halo coronal mass ejections faster? Res. Astron. Astrophys. 10, 461–472 (2010). https://doi.org/10.1088/1674-4527/10/5/006
X.P. Zhao, Inversion solutions of the elliptic cone model for disk frontside full halo coronal mass ejections. J. Geophys. Res. Space Phys. 113, 02101 (2008). https://doi.org/10.1029/2007JA012582
A.N. Zhukov, F. Saez, P. Lamy, A. Llebaria, G. Stenborg, The origin of polar streamers in the solar corona. Astrophys. J. 680, 1532–1541 (2008). https://doi.org/10.1086/587924
N.V. Zolotova, D.I. Ponyavin, Phase asynchrony of the North-South sunspot activity. Astron. Astrophys. 449, 1–4 (2006). https://doi.org/10.1051/0004-6361:200600013
N.V. Zolotova, D.I. Ponyavin, R. Arlt, I. Tuominen, Secular variation of hemispheric phase differences in the solar cycle. Astron. Nachr. 331, 765 (2010). https://doi.org/10.1002/asna.201011410
Acknowledgements
We thank Y. Boursier, A. Llebaria, J. Loirat, and T. Podladchikova for their contributions to an early phase of this study. We are grateful to H.-M. Wang for providing the total magnetic field data and to M. Shimojo for providing an updated list of NoRH prominences. We acknowledge fruitful discussions with A. Zhukov as well as several valuable comments. We thank the anonymous Reviewer for enlightening information on stealth CMEs. This work makes use of the following facilities and catalogs. The LASCO coronagraph was built by a consortium of the Naval Research Laboratory, USA, the Laboratoire d’Astrophysique de Marseille (formerly Laboratoire d’Astronomie Spatiale), France, the Max-Planck-Institut für Sonnensystemforschung (formerly Max Planck Institute für Aeronomie), Germany, and the School of Physics and Astronomy, University of Birmingham, UK. The CACTus CME catalog is generated and maintained by the SIDC at the Royal Observatory of Belgium. The SEEDS CME catalog is generated and maintained by the Space Weather Laboratory at the George Mason University. The CDAW Data Center CME catalog is generated and maintained by NASA and The Catholic University of America in cooperation with the Naval Research Laboratory. The CORIMP catalog was generated by the Institute of Astronomy, Hawaii, the Aberystwyth University, Wales, and the Trinity College Dublin, Ireland. The ARTEMIS catalog is part of the LASCO-C2 project at the Laboratoire d’Astrophysique de Marseille and at Laboratoire Atmosphères, Milieux et Observations Spatiales and is funded by the Centre National d’Etudes Spatiales (CNES). SOHO is a project of international cooperation between ESA and NASA.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Lamy, P.L., Floyd, O., Boclet, B. et al. Coronal Mass Ejections over Solar Cycles 23 and 24. Space Sci Rev 215, 39 (2019). https://doi.org/10.1007/s11214-019-0605-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11214-019-0605-y