A model of a three-layered relativistic star

Abstract

We generate new exact solutions to the Einstein-Maxwell field equations for charged anisotropic stellar objects comprising three interior layers. We develop charged stellar models comprising three interior layers with a specified equation of state: the linear quark equation of state at the core layer, the quadratic equation of state at the intermediate layer, and the Chaplygin equation of state at the envelope layer. Earlier uncharged solutions, with different equations of state, are regained as special cases. We plot graphs for the geometrical and matter variables indicating that the matter, gravitational potentials, and other physical conditions are well behaved and consistent with astrophysical studies. A notable feature is that the outer layer satisfies the Chaplygin equation of state.

1 Introduction

The study of the interior in stellar objects is an influential subject to many researchers in astronomy, astrophysics, and other related disciplines. A number of mathematical models have been established which provide a satisfactory explanation for the matter distribution within stellar bodies. Various configurations of the matter content in superdense stellar objects account for an extensive variation of physical features such as radii, charge densities, electric fields, radial and tangential pressures, gravitational potentials, and many other features in astrophysical studies. Relevant superdense stellar bodies with the required physical characteristics include neutron stars, white dwarfs, strange stars, and pulsars. These are massive compact objects having special interior structures which require additional gravitational descriptions for stellar spheres (Itoh (1970), Durgapal and Bannerji (1982)). Most stellar models have a single energy momentum tensor describing the interior. Some known models have two matter tensors for the core and the envelope. It is necessary to consider the dynamical effect of three layers for a deeper understanding of the behaviour within stellar bodies. However, the existence of more than two interior layers in physics is still a challenging question to be answered by researchers in relativistic astrophysics. A detailed analysis of the physical properties of neutron stars and other relativistic stellar bodies with several layers needs to be performed.

For some years, researchers formulated simple models consisting of two interior layers describing the interior physical matter of stellar spheres. This has been shown in the treatment of Gedela et al. (2019) who generated an uncharged model in two regions containing a new choice for one of the metric potentials. Models developed by Mafa Takisa and Maharaj (2016) and Mafa Takisa et al. (2019) show that the core layer is compact and is enclosed by a crust of baryonic matter. The core-envelope study performed by Metcalfe et al. (2003) highlighted the properties of white dwarfs in comparison to those of single-layered models performed in the past. The model generated by Montgomery et al. (2003) showed that for average to high frequency pulsars, there exist invariants in the physical features in the core and the corresponding envelope. Other models developed with two regions include the works of Pant et al. (2019), Paul and Tikekar (2005), Sharma and Mukherjee (2002), Thomas et al. (2005) and Tikekar and Jotania (2009). We seek to extend these results with an extra internal layer by solving the Einstein-Maxwell field equations with various equations of state.

Recently, a study performed by Pant et al. (2020) has shown that the interior structure of stellar bodies includes a sublayer in the core-envelope colligation. The model describes three interior layers of an uncharged neutron star among superdense objects. The core layer is equipped with the linear equation of state (EoS), with intermediate and envelope layers satisfying a quadratic EoS. However in our study, we consider a charged model containing three layers: with linear EoS for the core layer, the quadratic EoS for the intermediate layer, and Chaplygin EoS in the envelope layer.

In order to develop the stellar model, we incorporate equations of state which depict the relation between radial pressure and energy density. A number of studies conducted in the past use an EoS satisfying the required general physical conditions within the stellar interior. The models developed using a linear EoS include the works of Chaisi and Maharaj (2006a,b), Sharma and Maharaj (2007), Maharaj et al. (2014), Murad (2016), Sunzu et al. (2014a,b), Thirukkanesh and Maharaj (2008, 2009), Sunzu and Danford (2017), Varela et al. (2010) and Sunzu et al. (2019). Models with a quadratic EoS include the papers of Bhar et al. (2016, 2017), Maharaj and Mafa Takisa (2012), Malaver (2014a,b, 2017a,b), Sen and Ayun (2017), and Sunzu and Mashiku (2018). Some models have been formulated using the Chaplygin EoS relevant to the gaseous state. These include the treatments of Baruah (2016), Bhar et al. (2017), Bhar (2015), Gorini and Moschella (2008), Rahaman et al. (2010), Singh and Baruah (2016), and Bhar et al. (2018).

On physical grounds it is crucial to include the electric field in describing the physical behaviour of the matter content in the interior as shown by Varela et al. (2010). In existing research works, it has been shown that the electric field does affect causal signals for a specific range of parameters, redshift, luminosity and masses of dense stellar objects. It also improves stability due to its presence in the stellar object. A thorough analysis done by Rahaman et al. (2010) revealed that the existence of the charge surrounding the object increases stability which helps to prevent gravitational collapse. This has also been highlighted in the studies performed by Sharma and Maharaj (2007), Sharma and Mukherjee (2002), Sunzu and Danford (2017), Sunzu et al. (2014a,b, 2019), and Thirukkanesh and Maharaj (2008, 2009). Importantly, in this work we have omitted the singularity at the centre (as discussed in Mafa Takisa and Maharaj (2016)) to properly analyse the physical features of charged stellar objects. We should also point out that in the recent past several papers have been published with anisotropic fluids, equations of state, multi-layered fluids and their connection to the Einstein equations or the Einstein-Maxwell equations. These include the treatments of Gedela et al. (2018), Gedela et al. (2021), Pant et al. (2016), Pant et al. (2021) and Singh et al. (2021)

The principal objective of this paper is to investigate and analyse the interior physical features of relativistic stellar objects containing three distinctive layers, namely the core, the intermediate layer, and the envelope. Realistically, a single equation of state cannot describe the whole interior of the stellar object having non-uniform density matter in distinctive layers. We generate charged stellar models comprising three interior layers to extend the work performed by Pant et al. (2020) where in each layer a specified equation of state is applied. The results of Pant et al. (2020) are contained in our new class of solutions as a special case. The linear equation of state is assumed for the quark core, the intermediate layer obeys the quadratic equation of state, and the envelope layer satisfies the Chaplygin equation of state. We specify one of the gravitational potentials, and match the three layers to the Reissner-Nordstrom exterior spacetime. The physical features of the model are then investigated.

2 Fundamental equations

We describe the interior spacetime of the stellar object by considering the static and spherically symmetric line element given in Schwarzschild coordinates ($x^{i}= t, r, \theta , \phi$) so that

$$ ds^{2}=-e^{2\nu (r)}dt^{2}+e^{2\lambda (r)}dr^{2}+r^{2}(d\theta ^{2}+ \sin ^{2}\theta d\phi ^{2}). $$

(1)

The exterior spacetime is given by the line element

$$\begin{array}{rl}d{s}^2=& -\left(\begin{array}{c}1-\frac{2M}{r}+\frac{Q^2}{r^2}\end{array}\right)d{t}^2+(\begin{array}{c}1-\frac{2M}{r}\end{array}\\ & +{\begin{array}{c}\frac{Q^2}{r^2}\end{array})}^{-1}d{r}^2+r^2(d{\theta }^2+{sin}^2\theta d{\varphi }^2).\end{array}$$

(2)

Here $\nu (r)$ and $\lambda (r)$ are the metric potentials, $Q$ is the total charge, and $M$ is the total mass of the charged superdense stellar object. The energy momentum tensor for charged stellar objects is described by

$$\begin{array}{rl}{\tau }_{ij}=& \text{ diag}(\begin{array}{c}-\rho -\frac{1}{2}{E}^2,p_r-\frac{1}{2}{E}^2,\end{array}\\ & \begin{array}{c}{p}_t+\frac{1}{2}{E}^2,p_t+\frac{1}{2}{E}^2\end{array}),\end{array}$$

(3)

where $\rho$ is energy density, $E$ is electric field, $p_{r}$ and $p_{t}$ are radial and tangential pressures respectively.

The nonlinear system of the Einstein-Maxwell field equations for the interior of charged stellar objects are then obtainable in units $8\pi G=c=1$. The field equations can be written as

$$\begin{aligned} \rho +\dfrac{1}{2}E^{2} =&\dfrac{1}{r^{2}}(1-e^{-2\lambda })+ \dfrac{2\lambda ^{\prime }}{r}e^{-2\lambda }, \end{aligned}$$

(4a)

$$\begin{aligned} p_{r}-\dfrac{1}{2}E^{2} =&-\dfrac{1}{r^{2}}(1-e^{-2\lambda })+ \dfrac{2\nu ^{\prime }}{r}e^{-2\lambda }, \end{aligned}$$

(4b)

$$\begin{array}{rcl}{p}_t+\frac{1}{2}{E}^2& =& e^{-2\lambda }\left(\begin{array}{c}{\nu }^{″}+{\nu }^{{\prime }^2}-{\nu }^{\prime }{\lambda }^{\prime }+\frac{{\nu }^{\prime }}{r}-\frac{{\lambda }^{\prime }}{r}\end{array}\right)\\ & & +\frac{2{\lambda }^{\prime }}{r}{e}^{-2\lambda },\end{array}$$

(4c)

$$\begin{aligned} \sigma =&\dfrac{1}{r^{2}}e^{-\lambda }(r^{2}E)^{\prime }, \end{aligned}$$

(4d)

where primes $(\prime )$ represent differentiation with respect to the radial coordinate $r$. We use the transformation introduced by Durgapal and Bannerji (1983) in the form

$$ x=r^{2},Z(x)=e^{-2\lambda },e^{2\nu }=A^{2}y^{2}(x). $$

(5)

When the system (4a)–(4d) is transformed using equations (5), the simplified Einstein-Maxwell field equations become

$$\begin{aligned} \rho =&\dfrac{1-Z}{x}-2\dfrac{dZ}{dx}-\dfrac{1}{2}E^{2}, \end{aligned}$$

(6a)

$$\begin{aligned} p_{r} =&-\dfrac{1}{x}(1-Z)+4Z\dfrac{1}{y}\dfrac{dy}{dx}+\dfrac{1}{2}E^{2}, \end{aligned}$$

(6b)

$$\begin{array}{rcl}{p}_t& =& 4xZ\frac{1}{y}\frac{d^{2}y}{d{x}^2}+\left(\begin{array}{c}4Z+2x\frac{dZ}{dx}\end{array}\right)\frac{1}{y}\frac{dy}{dx}\\ & & +\frac{dZ}{dx}-\frac{1}{2}{E}^2,\end{array}$$

(6c)

$$\begin{array}{rcl}\mathrm{\Delta }& =& p_t-p_r,\\ & =& 4xZ\frac{1}{y}\frac{d^{2}y}{d{x}^2}+\left(\begin{array}{c}4xZ+2x\frac{dZ}{dx}-2Z\end{array}\right)\frac{1}{y}\frac{dy}{dx}\\ & & +\frac{dZ}{dx}+\frac{1}{x}(1-Z)-E^2,\end{array}$$

(6d)

$$\sigma =2\left(\begin{array}{c}x\frac{dE}{dx}+E\end{array}\right)\sqrt{\frac{Z}{x}},$$

(6e)

where $\Delta$ stands for the measure of anisotropy.

The system (6a)–(6e) above has five equations and eight variables $(\rho , p_{t} , p_{r},\Delta , Z, y ,\sigma , E)$. To solve these equations, two variables among the eight can be specified in order to find the others. We specify the metric potential $Z$ and electric field $E^{2}$ in the form

$$\begin{aligned} Z(x)=&\quad 1-\gamma x+mx^{n},\qquad n\geq 3 \end{aligned}$$

(7)

$$\begin{aligned} E^{2}=&\quad \dfrac{fx}{1+bx^{2}}, \end{aligned}$$

(8)

where $m$, $n$, $f$, $b$, and $\gamma$ are arbitrary real constants. When $n=2$, and $f=0$ in our choice, we regain the potential $Z$ given by Pant et al. (2020).

3 The model

In order to achieve our objective, the three interior regions of the stellar sphere, namely the core ($\xi$), the intermediate ($\delta$) and the envelope ($\psi$) are specified with the following regions:

• The core layer (Region I): $0\leq r\leq R_{\xi }$,

• The intermediate layer (Region II): $R_{\xi }\leq r \leq R_{\delta }$, and

• The envelope layer (Region III): $R_{\delta } \leq r \leq R_{\psi }$.

With consideration of equation (1), the interior line elements of the three layers are

$$\begin{aligned} ds^{2}|_{I} =&-e^{2\nu _{\xi }}dt^{2}+e^{2\lambda _{\xi }}dr^{2} \\ &+r^{2}(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}), \end{aligned}$$

(9a)

$$\begin{aligned} ds^{2}|_{II} =&-e^{2\nu _{\delta }}dt^{2}+e^{2\lambda _{\delta }}dr^{2} \\ &+r^{2}(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}), \end{aligned}$$

(9b)

$$\begin{aligned} ds^{2}|_{III} =&-e^{2\nu _{\psi }}dt^{2}+e^{2\lambda _{\psi }}dr^{2} \\ &+r^{2}(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}). \end{aligned}$$

(9c)

For the three regions given above, we generate new exact solutions in three different layers. Each layer is equipped with a separate equation of state.

3.1 Region I (core layer)

Here we assume the innermost layer is quark matter satisfying the linear equation of state in the form

$$ p_{r_{\xi }}=\alpha \rho _{\xi }-\beta , $$

(10)

where $\alpha$ and $\beta$ are real arbitrary constants. We choose to use the linear equation of state as it is convenient in describing heavy quark matter. When equations (6a) and (10) are combined we obtain

$$p_{r_{\xi }}=\alpha \left(\begin{array}{c}\frac{1-Z}{x}-2\frac{dZ}{dx}-\frac{1}{2}{E}^2\end{array}\right)-\beta .$$

(11)

Equating equations (6b) and (11) we have

$$ \dfrac{1}{y}\dfrac{dy}{dx} = (\alpha +1)\dfrac{1-Z}{2xZ}+ \dfrac{\alpha }{2Z}\dfrac{dZ}{dx}+\dfrac{E^{2}(\alpha -1)}{4Z}- \dfrac{\beta }{4Z}. $$

(12)

We can eliminate $Z$ and $E$ in (12). Then the differential equation (12) becomes

$$\begin{aligned} \dfrac{1}{y}\dfrac{dy}{dx}= &[-fx^{2}(\alpha -1)+2(1+bx^{2})(-m(2n-1)x^{n} \alpha \\ &+x(\beta +\alpha \gamma )][4x(1+bx^{2})(x\gamma \\ &-mx^{n}-1)]^{-1}. \end{aligned}$$

(13)

Substituting equations (7), (8) and (13) into the system (6a)–(6e), the matter variables of the core region become

$$\begin{aligned} e^{2\lambda _{\xi }} =&\left [1-\gamma x+mx^{n}\right ]^{-1}, \end{aligned}$$

(14a)

$$\begin{aligned} e^{2\nu _{\xi }} =& A^{2} [\exp (S_{0}(x))]^{2}, \end{aligned}$$

(14b)

$$\begin{aligned} \rho _{\xi } =&[6\gamma (1+bx^{2})-2m(1+bx^{2})(1+2n)x^{n-1} \\ &+fx][2+2bx^{2}]^{-1}, \end{aligned}$$

(14c)

$$\begin{aligned} p_{r_{\xi }} =&mx^{n-1}(1+(2n-1)\alpha )+[fx\alpha \\ &-2(1+bx^{2})(\beta +\gamma +\alpha \gamma )][2+2bx^{2}]^{-1}, \end{aligned}$$

(14d)

$$\begin{aligned} p_{t_{\xi }} =&S_{1}(x)+S_{2}(x)-S_{3}(x)+S_{4}(x), \end{aligned}$$

(14e)

$$\begin{aligned} \Delta _{\xi } =&p_{t_{\xi }}-p_{r_{\xi }}, \end{aligned}$$

(14f)

$$\begin{aligned} \sigma _{\xi } =&\left [x^{-1}(3+bx^{2})\left (\dfrac{fx}{1+bx^{2}} \right )^{3/2}\right . \\ &\times \left .\sqrt{\dfrac{1+mx^{n}-x\gamma }{x}}\right ]f^{-1}, \quad f\neq 0 \end{aligned}$$

(14g)

$$\begin{aligned} E^{2}_{\xi } =&fx\left [1+bx^{2}\right ]^{-1}. \end{aligned}$$

(14h)

In the above, we have set for convenience

$$\begin{aligned} S_{0}(x) =& \int {[-fx(\alpha -1)+2(1+bx^{2})(-m(2n} \\ &{-1)x^{n-1}\alpha +(\beta +\alpha \gamma )][4(1+bx^{2})} \\ &\times {(x\gamma -mx^{n}-1)]^{-1}} dx, \\ S_{1}(x) =& [2f(4\alpha -5+mx^{n}(n(1+bx^{2}) \\ &\times (\alpha -1)(4\alpha -1)+ bx^{2}(-1 \\ &-2(\alpha -1)\alpha )))+2fx(4\alpha -5 \\ &+mx^{n}(-5-2(\alpha -3)\alpha )-f^{2}x^{3} \\ &\times (\alpha -1)^{2}][4(1+bx^{2})^{2}(x\gamma \\ &-mx^{n}-1)]^{-1}, \\ S_{2}(x) =&\left [2fx^{2}(2(\alpha -1)\beta +x^{-1}(\alpha -4+2 \alpha ^{2})\right . \\ &\times \gamma +b(1+2x(\alpha -1)\beta +\left .\alpha (2\alpha -3) \gamma ))\right ] \\ &\times [4(1+bx^{2})^{2}(x\gamma -mx^{n}-1)]^{-1}-\gamma , \\ S_{3}(x) =&\left [-4(1+bx^{2})^{2}(m^{2}x^{2n}(n+n(2n-1)\alpha \right . \\ &+(1-2n)^{2}\alpha ^{2}+x(\beta +\alpha \gamma )(-2+x(\beta \\ &+\left .\alpha \gamma ))))][4(1+bx^{2})^{2}(x\gamma -mx^{n}-1) \right ]^{-1}, \\ S_{4}(x) =&[4mx^{n-1}(1+bx^{2})^{2}(2x\beta +4n^{2}\alpha (x\gamma -1) \\ &+x\alpha (-2\beta +(3-2\alpha )\gamma )) +4mx^{n-1} \\ &\times (1+bx^{2})^{2}(2\alpha -1-x\beta +x(\alpha -1) \\ &\times (4\alpha -1)\alpha )] [4(1+bx^{2})^{2}(x\gamma \\ &-mx^{n}-1)]^{-1}. \end{aligned}$$

The total mass of the sphere is given by

$$\begin{aligned} M(r) =\quad &4\pi \int {r^{2}\rho _{\xi }dr}, \qquad r^{2}=x \\ = \quad &2\pi \left (x\left (fb^{-1}-(2m(1+2n)x^{n})(n+1)^{-1}\right . \right . \\ &+\left .\left .3x\gamma \right )-fxb^{-3/2} \arctan \sqrt{b}\right )+k_{0}, \end{aligned}$$

(16)

where $k_{0}$ is a constant of integration.

3.2 Region II (intermediate layer)

The density profiles of interior layers in stellar objects are decreasing, consequently the middle layer should be less dense than the core. The quadratic equation of state is relevant in describing the physical features of the intermediate region. The equation is given by

$$ p_{r_{\delta }}=\alpha \rho ^{2}_{\delta }+\beta \rho _{\delta }-\mu , $$

(17)

where $\alpha$, $\beta$ and $\mu$ are arbitrary real constants. In the intermediate layer the energy density and the radial pressure are given by

$$ \rho _{\delta }=\dfrac{1-Z}{x}-2\dfrac{dZ}{dx}+\dfrac{1}{2}E^{2}, $$

(18)

and

$$ p_{r_{\delta }} = -\dfrac{1-Z}{x}+4Z\dfrac{1}{y}\dfrac{dy}{dx}+ \dfrac{E^{2}}{2}. $$

(19)

Substituting equation (18) into equation (17) we obtain

$$\begin{array}{rl}{p}_{r_{\delta }}=& \alpha {\left(\begin{array}{c}\frac{1-Z}{x}-2\frac{dZ}{dx}+\frac{1}{2}{E}^2\end{array}\right)}^2\\ & +\beta \left(\begin{array}{c}\frac{1-Z}{x}-2\frac{dZ}{dx}+\frac{1}{2}{E}^2\end{array}\right)-\mu .\end{array}$$

(20)

Equating equation (19) and (20) we have

$$\begin{array}{rl}\frac{1}{y}\frac{dy}{dx}=& \frac{\alpha }{2Z}{\left(\begin{array}{c}\frac{1-Z}{x}-2\frac{dZ}{dx}+\frac{1}{2}{E}^2\end{array}\right)}^2\\ & +\frac{\beta }{2Z}\left(\begin{array}{c}\frac{1-Z}{x}-2\frac{dZ}{dx}+\frac{1}{2}{E}^2\end{array}\right)\\ & +\frac{1}{2Z}\left(\begin{array}{c}\frac{1-Z}{x}-\frac{1}{2}{E}^2\end{array}\right)-\frac{\mu }{2Z}.\end{array}$$

(21)

Eliminating the metric function $Z$ and electric charge $E^{2}$ in (21) gives

$$\begin{aligned} \dfrac{1}{y}\dfrac{dy}{dx} =\quad &[\left (-2mx^{n-1}-fx(1+bx^{2})^{-1}+2 \gamma \right . \\ &+2\beta (-m(1+2n)x^{n-1}+fx(2+2bx^{2})^{-1} \\ &\left .+3\gamma \right ) +2\alpha \left (-m(1+2n)x^{n-1}\right . \\ &\left .+fx(2+2bx^{2})^{-1}+3\gamma \right )^{2}-2\mu )] \\ &\times [4(1+mx^{n}-x\gamma )]^{-1}. \end{aligned}$$

(22)

Substituting equations (7), (8) and (22) into the system (6a)–(6e), the intermediate matter variables become

$$\begin{aligned} e^{2\lambda _{\delta }} =&\left [1-\gamma x+mx^{n}\right ]^{-1}, \end{aligned}$$

(23a)

$$\begin{aligned} e^{2\nu _{\delta }} =&A^{2}y^{2}(x)= A^{2} [\exp (\tau _{0}(x))]^{2}, \end{aligned}$$

(23b)

$$\begin{aligned} \rho _{\delta } =&[6\gamma (1+bx^{2})-2m(1+bx^{2})(1 \\ &+2n)x^{n-1}+fx][2+2bx^{2}]^{-1}, \end{aligned}$$

(23c)

$$\begin{aligned} p_{r_{\delta }} =&\beta \left (-m(1+2n)x^{n-1}+fx[2\right . \\ &\left .+2bx^{2}]^{-1}\right .\left .+3\gamma \right ) +\alpha \left (-m(1+2n)\right . \\ &\times \left .x^{n-1}+fx[2+2bx^{2}]^{-1}+3\gamma \right )^{2}-\mu , \end{aligned}$$

(23d)

$$\begin{aligned} p_{t_{\delta }} =&\tau _{1}(x)-\tau _{2}(x)+\tau _{3}(x)+\tau _{4}(x) \\ &+\tau _{5}(x)+\tau _{6}(x)+\tau _{7}(x) \\ &+\tau _{8}(x)+\tau _{9}(x), \end{aligned}$$

(23e)

$$\begin{aligned} \Delta _{\delta } =&p_{t_{\delta }}-p_{r_{\delta }}, \end{aligned}$$

(23f)

$$\begin{aligned} \sigma _{\delta } =&\left [x^{-1}(3+bx^{2})\left (\dfrac{fx}{1+bx^{2}} \right )^{3/2}\right . \\ &\left .\times \sqrt{(1+mx^{n}-x\gamma )x^{-1}}\right ]f^{-1}, \quad f\neq 0 \end{aligned}$$

(23g)

$$\begin{aligned} E^{2}_{\delta } =&fx\left [1+bx^{2}\right ]^{-1}. \end{aligned}$$

(23h)

For simplicity we have set

$$\begin{aligned} \tau _{0}(x) =& \int {(-2mx^{n-1}-fx(1+bx^{2})^{-1}+2\gamma } \\ &+{2\beta (-m(1+2n)x^{n-1}) +fx(2} \\ &+{2bx^{2})^{-1} +3\gamma +2\alpha (-m(1+2n)x^{n-1}} \\ &+{fx(2 +2bx^{2})^{-1}+3\gamma )^{2}-2\mu )(4(1} \\ &+{mx^{n}-x\gamma ))^{-1}}dx, \\ \tau _{1}(x) =& mnx^{n-1}-\gamma -fx(1+bx^{2})^{-1} \\ &+\dfrac{1}{2}\left (4+2m(2+n)x^{n}-6x\gamma \right )J_{0}(x), \\ \tau _{2}(x) =&\dfrac{1}{2}\left (4+2m(2+n)x^{n}-6x\gamma \right ) \left ([\beta \left (-m(1\right .\right . \\ &+2n)x^{n-1}+\left .\left .fx[2+2bx^{2}]^{-1}+3\gamma \right )] \right . \\ &\left .\times [1+mx^{n}-x\gamma ]^{-1}\right ), \\ \tau _{3}(x) =&\dfrac{1}{2}\left (4+2m(2+n)x^{n}-6x\gamma \right ) \left (\alpha \left (-m(1\right .\right . \\ &+\left .\left .2n)x^{n-1}\right .\right . +\left .\left .fx[2+2bx^{2}]^{-1}+3 \gamma \right )^{2}\right . \\ &\left .-\mu \right )(1+mx^{n}-x\gamma )^{-1}, \\ \tau _{4}(x) =& x(1+mx^{n}-x\gamma )\left (-4m(n-1)x^{n-2}\right . \\ &+\left .4bfx^{2}[(1+bx^{2})^{2}]^{-1}-fx[1+bx^{2}]^{-1}\right ), \\ \tau _{5}(x) =& x(1+mx^{n}-x\gamma )\left (2\beta (mnx^{n-1}-\gamma ) \right . \\ &\times (\left (-m(1+2n)x^{n-1} +fx(2+2bx^{2})^{-1}\right . \\ &+\left .\left .3\gamma \right ))((1+mx^{n}-x\gamma )^{2})^{-1} \right ), \\ \tau _{6}(x) =& x(1+mx^{n}-x\gamma )\left (2\beta (mnx^{n-1}-\gamma ) \right . \\ &\times \left (-m(1+2n)x^{n-1}\right . +\left .\left .fx(2+2bx^{2})^{-1} \right .\right . \\ &\left .\left .+3\gamma \right )(1+mx^{n}-x\gamma )^{2})^{-1}\right ), \\ \tau _{7}(x) =&(2x(1+mx^{n}-x\gamma )\left (m(1+n-2n^{2})x^{n-2} \right . \\ &+\left .(f-bfx^{2})(2(1+bx^{2})^{2})^{-1}\right )\beta ) \\ &\times (1+mx^{n}-x\gamma )^{-1}+(2x(1+mx^{n}-x\gamma ) \\ &\times (mnx^{n-1}-\gamma )\mu )(\left (-m(1+2n)x^{n-1}\right .+fx \\ &\times (2\left .+2bx^{2})^{-1}+3\gamma \right )^{2})(1+mx^{n}-x \gamma )^{2})^{-1}, \\ \tau _{8}(x) =& 4x(1+mx^{n}-x\gamma )\left (m(1+n-2n^{2})x^{n-2} \right . \\ &+\left .(f-bfx^{2})(2(1+bx^{2})^{2})^{-1}\right )J_{1}(x)) \\ &\times (1+mx^{n}-x\gamma )^{-1}, \\ \tau _{9}(x) =& x(1+mx^{n}-x\gamma )\left (J_{2}(x)-\beta \left (-m(1\right .\right . \\ &+2n)x^{n-1}+\left .\left .fx(2+2bx^{2})^{-1}+3\gamma \right )) \right . \\ &\left .\times (1+mx^{n}-x\gamma )^{-1}\right )^{2}, \\ J_{0}(x) =&\left (-2mx^{n-1}-fx(1+bx^{2})^{-1}+2\gamma \right ), \\ J_{1}(x) =&\alpha \left (-m(1+2n)x^{n-1}+fx(2+2bx^{2})^{-1}+3\gamma \right ), \\ J_{2}(x) =& 2mx^{n-1}+fx(1+bx^{2})^{-1}-2\gamma -\alpha \left (-m(1 \right . \\ &\left .+2n)x^{n-1}\right .+\left .fx(2+2bx^{2})^{-1}+3\gamma \right )^{2}+\mu ) \\ &\times (1+mx^{n}-x\gamma )^{-1}. \end{aligned}$$

3.3 Region III (envelope layer)

The envelope region may be modelled to be a pressure-less fluid (gaseous state) which implies that it has smallest density of all three interior regions. We take the Chaplygin equation of state, which is adequately gaseous to describe the outermost layer, in the form

$$ p_{r_{\psi }}=\alpha \rho _{\psi }-\dfrac{\beta }{\rho _{\psi }}, $$

(25)

where $\alpha$ and $\beta$ are the arbitrary real constants. Then the energy density and radial pressure are respectively

$$ \rho _{\psi }=\dfrac{1-Z}{x}-2\dfrac{dZ}{dx}+\dfrac{1}{2}E^{2}, $$

(26)

and

$$ p_{r_{\psi }}=-\dfrac{1-Z}{x}+4Z\dfrac{1}{y}\dfrac{dy}{dx}+ \dfrac{E^{2}}{2}. $$

(27)

Substituting equation (26) into (25) we obtain

$$\begin{array}{rl}{p}_{r_{\psi }}=& \alpha \left(\begin{array}{c}\frac{1-Z}{x}-2\frac{dZ}{dx}+\frac{E^2}{2}\end{array}\right)\\ & -\beta {\left(\begin{array}{c}\frac{1-Z}{x}-2\frac{dZ}{dx}+\frac{E^2}{2}\end{array}\right)}^{-1}.\end{array}$$

(28)

Equations (27) and (28) yield

$$\begin{array}{rl}\frac{1}{y}\frac{dy}{dx}& =\frac{1}{2Z}\left(\begin{array}{c}\frac{1-Z}{x}+\frac{E^2}{2}\end{array}\right)\\ & +\frac{\alpha }{2Z}\left(\begin{array}{c}\frac{1-Z}{x}-2\frac{dZ}{dx}+\frac{E^2}{2}\end{array}\right)\\ & -\frac{\beta }{2Z}{\left(\begin{array}{c}\frac{1-Z}{x}-2\frac{dZ}{dx}+\frac{E^2}{2}\end{array}\right)}^{-1}.\end{array}$$

(29)

Using the specified forms of the metric potential $Z$ and the charge $E^{2}$ we get

$$\begin{aligned} \dfrac{1}{y}\dfrac{dy}{dx} =& \left (6\alpha \gamma -2mx^{n-1}(1+ \alpha +2n\alpha )+2\gamma \right . \\ &\left .+fx(\alpha -1)(1+bx^{2})^{-1}-2\beta (3\gamma \right . \\ &-\left .m(1+2n)x^{n-1})^{-1}\right . \left .+fx(2\right . \\ &\left .+2bx^{2})^{-1}\right )(4(1+mx^{n}-x\gamma ))^{-1}. \end{aligned}$$

(30)

Therefore the matter variables in the envelope layer become

$$\begin{aligned} e^{2\lambda _{\psi }} =&\left [1-\gamma x+mx^{n}\right ]^{-1}, \end{aligned}$$

(31a)

$$\begin{aligned} e^{2\nu _{\psi }} =&A^{2}y^{2}(x)=A^{2} [\exp (G_{0}(x))]^{2}, \end{aligned}$$

(31b)

$$\begin{aligned} \rho _{\psi } =&\left [6\gamma (1+bx^{2})-2m(1+bx^{2})(1\right . \\ &\left .+2n)x^{n-1}\right .+\left .fx\right ][2+2bx^{2}]^{-1}, \end{aligned}$$

(31c)

$$\begin{aligned} p_{r_{\psi }} =&3\alpha \gamma -m(1+2n)x^{n-1}\alpha +\left [\alpha fx \right ] \\ &\times [2+2bx^{2}]^{-1}-\beta \left [3\gamma -m(1\right . \\ &+\left .2n)x^{n-1}\right ]^{-1}+fx\left [2+2bx^{2}\right ]^{-1}, \end{aligned}$$

(31d)

$$\begin{aligned} p_{t_{\psi }} =&G_{1}(x)-G_{2}(x)+G_{3}(x)+G_{4}(x) \\ &-G_{5}(x)+G_{6}(x)+G_{7}(x), \end{aligned}$$

(31e)

$$\begin{aligned} \Delta _{\psi } =&p_{t_{\psi }}-p_{r_{\psi }}, \end{aligned}$$

(31f)

$$\begin{aligned} \sigma _{\psi } =&\left [x^{-1}(3+bx^{2})\left (\dfrac{fx}{1+bx^{2}} \right )^{3/2}\right . \\ &\times \left .\sqrt{(1+mx^{n}-x\gamma )x^{-1}}\right ]f^{-1}, f \neq 0 \end{aligned}$$

(31g)

$$\begin{aligned} E^{2}_{\psi } =&fx\left [1+bx^{2}\right ]^{-1}. \end{aligned}$$

(31h)

For simplicity we have defined

$$\begin{aligned} G_{0}(x) =& \int {6\alpha \gamma -2mx^{n-1}(1+\alpha +2n\alpha )} \\ &+{2\gamma +fx(\alpha -1)(1+bx^{2})^{-1} (4(1} \\ &+{mx^{n}-x\gamma ))-(2\beta (3\gamma -m(1} \\ &+{2n)x^{n-1})^{-1}+4fx(1} \\ &+{mx^{n})-x\gamma ))(2+2bx^{2})^{-1}} \\ &\times {(4(1+mx^{n}-x\gamma ))^{-1}}dx, \\ G_{1}(x) =& mnx^{n-1}+\gamma +fx(2(1+bx^{2}))^{-1} \\ &+\left ((4+2m(2+n)x^{n}\right .-6x\gamma )(fx \\ &\times \left .(\alpha -1))\right . \\ &\times \left .(1+bx^{2})^{-1}\right )(4(1+mx^{n}-x\gamma ))^{-1}, \\ G_{2}(x) =&\left (2\left (mx^{n-1}(1+\alpha +2n\alpha )-\alpha -3 \alpha \gamma \right .\right . \\ &+\left .\left .\beta (-m(1+2n)x^{n-1})^{-1}\right )\right . +fx(2 \\ &+2bx^{2})^{-1}+3\gamma )(4(1+mx^{n}-x\gamma ))^{-1}, \\ G_{3}(x) =& x(-mnx^{n-1}+\gamma )fx(\alpha -1)(1+bx^{2})^{-1} \\ &-2mx^{n-1}(1+\alpha )+2n\alpha )(1+mx^{n}-x\gamma )^{-1}, \\ G_{4}(x) =& x(-mnx^{n-1}+\gamma )\left (2\alpha +6\alpha \gamma +3 \gamma \right . \\ &+2\beta (-m(1+2n)x^{n-1})^{-1} \\ &\left .+fx(2+2bx^{2})^{-1}\right )(4(1+mx^{n}-x\gamma ))^{-1}, \\ G_{5}(x) =&\dfrac{1}{4}\left (fx(\alpha -1)(1+bx^{2})^{-1}-2mx^{n-1} \right . \\ &\left .\times (1+\alpha +2n\alpha )\right . \left .+2\gamma +6 \alpha \gamma -J_{3}(x)\right )^{2}, \\ G_{6}(x) =& (1+mx^{n}-x\gamma )(2bfx^{2}(\alpha -1)((1+bx^{2})^{2})^{-1} \\ &+ f(\alpha -1)(1+bx^{2})^{-1}-2m(n-1)x^{n-2} \\ &\times (1+\alpha +2n\alpha )), \\ G_{7}(x) =&\dfrac{1}{4}(1+mx^{n}-x\gamma )\left [4(fx^{2}(bx^{2}-1) \right . \\ &+\left .2m(n-1)(1+2n)x^{n}\right .(1+bx^{2})^{2}\beta )] \\ &\times \left [(fx^{2}-2(1+bx^{2})(m(1+2n)x^{n}\right . \\ &\left .-3x\gamma ))^{2}\right ]^{-1}, \\ J_{3}(x) =& 2\gamma (3\gamma -m(1+2n)x^{n-1}+fx(2+2bx^{2})^{-1}. \end{aligned}$$

4 Matching conditions

We consider the matching criteria for the radial pressures and gravitational potentials to be continuous at the interfaces between the layers and at the stellar boundary. The matching conditions are given below. The junction conditions at the core-intermediate interface become

$$\begin{aligned} e^{2\lambda _{\xi }}(R_{\xi }) =&e^{2\lambda _{\delta }}(R_{\xi }), \end{aligned}$$

(33a)

$$\begin{aligned} e^{2\nu _{\xi }}(R_{\xi }) =&e^{2\nu _{\delta }}(R_{\xi }), \end{aligned}$$

(33b)

$$\begin{aligned} p_{r_{\xi }}(R_{\xi }) =&p_{r_{\delta }}(R_{\xi }). \end{aligned}$$

(33c)

The junction conditions at the intermediate-envelope interface become

$$\begin{aligned} e^{2\lambda _{\delta }}(R_{\delta }) =&e^{2\lambda _{\psi }}(R_{\delta }), \end{aligned}$$

(34a)

$$\begin{aligned} e^{2\nu _{\delta }}(R_{\delta }) =&e^{2\nu _{\psi }}(R_{\delta }), \end{aligned}$$

(34b)

$$\begin{aligned} p_{r_{\delta }}(R_{\delta }) =&p_{r_{\psi }}(R_{\delta }). \end{aligned}$$

(34c)

The junction conditions at the envelope-surface interface require that the interior and exterior line elements (1) and (2) should match smoothly at the surface $r=R_{\psi }$. We have

$$e^{2{\lambda }_{\psi }}(R_{\psi })={\left(\begin{array}{c}1-\frac{2M}{R_{\psi }}+\frac{Q^2}{R_{\psi }^2}\end{array}\right)}^{-1},$$

(35a)

$$e^{2{\nu }_{\psi }}(R_{\psi })=\left(\begin{array}{c}1-\frac{2M}{R_{\psi }}+\frac{Q^2}{R_{\psi }^2}\end{array}\right),$$

(35b)

$$\begin{aligned} p_{r_{\psi }}(R_{\psi }) =&0. \end{aligned}$$

(35c)

These conditions give the equations

$$\begin{aligned} \left (1+\gamma R_{\psi }^{2}+mR_{\psi }^{2n}\right ) =& H_{1}(x), \end{aligned}$$

(36a)

$$\begin{aligned} A^{2}[\exp (G_{0}(x))]^{2} =& H_{2}(x), \end{aligned}$$

(36b)

$$\begin{aligned} 3\alpha \gamma -m(1+2n)R_{\psi }^{n-1}\alpha =& \dfrac{\alpha fR_{\psi }}{(2+2b)R_{\psi }^{2}} \\ &+H_{3}(x), \end{aligned}$$

(36c)

where for simplicity we have set

$$\begin{aligned} H_{0}(x) =&2\pi \left (R_{\psi }^{2}\left (fb^{-1}-(2m(1\right . \right . \\ &+2n)R_{\psi }^{2n})(n+1)^{-1} \\ &+\left .\left .3R_{\psi }^{2}\gamma \right )- \dfrac{R_{\psi }^{2}f \arctan \sqrt{b}}{b^{3/2}}\right )+k_{0}, \\ H_{1}(x) =&\left (1-\dfrac{2H_{0}(x)}{R_{\psi }}\right .+\left . \dfrac{fR_{\psi }^{2}}{1+bR_{\psi }^{4}}\right )^{-1}, \\ H_{2}(x) =&1-\dfrac{2H_{0}(x)}{R_{\psi }}+ \dfrac{fR_{\psi }^{2}}{1+bR_{\psi }^{4}}, \\ H_{3}(x) =&\dfrac{\beta }{3\gamma -m(1+2n))R_{\psi }^{n-1}}+ \dfrac{fR_{\psi }}{(2+2b)R_{\psi }^{2}}. \end{aligned}$$

The existence of sufficient number of free parameters in the three equations in (36a)–(36c) indicates that the matching conditions are satisfied in our study.

5 Physical conditions

The regularity conditions for the potentials and the matter variables, and other physical properties in the interior of the stellar object have to obey particular criteria. These are given by

• (i) The radial pressure $(p_{r})$, the tangential pressure $(p_{t})$ and the energy density $(\rho )$ need to be finite and greater or equal to zero, i.e. $\rho \geq 0, p_{r}\geq 0, p_{t}\geq 0$, and decreasing away from the centre towards the boundary.

• (ii) The gravitational potentials $e^{2\lambda }$ and $e^{2\nu }$ must be positive at the centre and continuous.

• (iii) The radial sound speed must be less than the speed of light so as to obey the causality condition, i.e. $\dfrac{dp_{r}}{d\rho }< 1$. For each layer we obtain the following in our model

  $$\begin{aligned} \nu _{\xi } =&[-f(bx^{2}-1)\alpha +m(n-1)x^{n-2}(1+(2n \\ &-1)\alpha )][m(1+n+2n^{2})x^{n-2}+(f \\ &-bfx^{2})(2(1+bx^{2})^{2})^{-1}]^{-1}, \end{aligned}$$

  (38a)
  $$\begin{aligned} \nu _{\delta } =&[fx\alpha +(1+bx^{2}(-2m(1+2n)x^{n-1}\alpha \\ &+x(\beta +6\alpha \gamma )))][1+bx^{2}]^{-1}, \end{aligned}$$

  (38b)
  $$\begin{aligned} \nu _{\psi } =&\alpha +4(x+bx^{3})^{2}\beta [(fx^{2}-2(1+bx^{2}) \\ &\times (m(1+2n)x^{n}-3x\gamma )^{2})]^{-1}, \end{aligned}$$

  (38c)

  where $\nu _{\xi }, \nu _{\delta }$ and $\nu _{\psi }$ are the speeds of sound in the core layer, the intermediate layer and the envelope layer respectively.

• (iv) The energy distributions in the interior must be continuous functions complying with the strong energy condition (SEC), weak energy condition (WEC) and the null energy condition (NEC), i.e. SEC: $\rho -p_{r}-2p_{t}\geq 0$, WEC: $\rho -3p_{t}\geq 0$, $\rho -3p_{r}\geq 0$, NEC: $\rho -p_{r}\geq 0$, $\rho -p_{t}\geq 0$. For the null, weak and strong energy conditions we obtain the following:

  (a) Null energy condition

  $$\begin{aligned} \mbox{NEC}_{\xi } =&-fx(\alpha -1)(2+2bx^{2})^{-1} \\ &+mn^{n-1}(\alpha -2-2n(\alpha +1) \\ &+\beta +\gamma (\alpha +4)), \end{aligned}$$

  (39a)
  $$\begin{aligned} \mbox{NEC}_{\delta } =&-m(1+2n)x^{n-1}+fx(2 \\ &+2bx^{2})^{-1}+m(1+2n)x^{n-1}\beta \\ &-fx\beta (2+2bx^{2})^{-1} \\ &+3\gamma -3\beta \gamma +\mu -\alpha \left (-m(1\right . \\ &+2n)x^{n-1}+fx(2+2bx^{2})^{-1} \\ &\left .+3\gamma \right )^{2}, \end{aligned}$$

  (39b)
  $$\begin{aligned} \mbox{NEC}_{\psi } =& m(1+2n)x^{n-1}(\alpha -1)+3\gamma \\ &-3\alpha \gamma -fx(\alpha -1)(2+2bx^{2})^{-1} \\ &+\beta (-m(1+2n)x^{n-1}+fx(2 \\ &+2bx^{2})+3\gamma )^{-1}. \end{aligned}$$

  (39c)

  (b) Weak energy condition

  $$\begin{aligned} \mbox{WEC}_{\xi } =& fx(1-3\alpha )(2+2bx^{2})^{-1}-mx^{n-1} \\ &\times (4-3\alpha +n(2+6\alpha )) \\ &+3(\beta +(2+\alpha )\gamma , \end{aligned}$$

  (40a)
  $$\begin{aligned} \mbox{WEC}_{\delta } =&-m(1+2n)x^{n-1}+fx[2+2bx^{2}]^{-1} \\ &+3\gamma - 3\beta \left (-m(1+2n)x^{n-1}+fx[2\right . \\ &+\left .2bx^{2}]^{-1}+3\gamma \right )+\quad 3\mu -3\alpha \left (-m(1 \right . \\ &+\left .2n)x^{n-1}+fx[2+2bx^{2}]^{-1}\right . \\ &+\left .3\gamma \right )^{2}, \end{aligned}$$

  (40b)
  $$\begin{aligned} \mbox{WEC}_{\psi } =& fx(1-3\alpha )[2+2bx^{2}]^{-1}+m(1 \\ &+2n)x^{n-1}(3\alpha -1)+3\gamma -9\alpha \gamma ^{2} \\ &+ 3\beta [\left (-m(1+2n)x^{n-1}+fx[2\right . \\ &+\left .2bx^{2}]^{-1}+3\gamma \right )]^{-1}. \end{aligned}$$

  (40c)

  (c) Strong energy condition

  $$\begin{aligned} \mbox{SEC}_{\xi } =&(f x^{2} \left (9 \alpha +m x^{n} \left (\alpha (13-4 \alpha )\right .\right . \\ &+\left .2 (\alpha -1) (4 \alpha -1) n \left (b x^{2}+1\right ) \right . \\ &\left .\left .+((5-4 \alpha ) \alpha -3) b x^{2}-11\right )\right ))(2 x \\ &\times \left (b x^{2}+1\right )^{2} \left (-m x^{n}+\gamma x-1 \right ))^{-1} \\ &+ (x \left (-4 (\alpha -1) \beta +(9-\alpha (4 \alpha +3)) \right . \\ &\times \gamma +b x \left (\alpha -4 \alpha ^{2} \gamma x-4 \alpha \beta x+5 \alpha \gamma x\right . \\ &\left .\left .+4 \beta x+\gamma x-3\right )\right ))(2 x \left (b x^{2}+1 \right )^{2} \\ &\times \left (-m x^{n}+\gamma x-1\right ))^{-1} \\ &+(2 \left (b x^{2}+1\right )^{2} \left (m^{2} \left (\alpha \left (4 n^{2}-1\right )\right .\right . \\ &+\left .\left .2 \alpha ^{2} (1-2 n)^{2}+4 n+2\right ) x^{2 n}-11 \right )) \\ &\times (2 x \left (b x^{2}+1\right )^{2} \left (-m x^{n}+\gamma x-1 \right ))^{-1} \\ &-(m x^{n} \left (\alpha -8 \alpha n^{2}+\gamma x \left (6 \alpha +4 \alpha ^{2} (2 n\right .\right . \\ &\left .\left .-1)+8 \alpha (n-1) n+4 n+3\right )\right )) \\ &\times (2 x \left (b x^{2}+1\right )^{2} \left (-m x^{n}+\gamma x-1 \right ))^{-1} \\ &+(2 n\left (\alpha +(4 \alpha -1) \beta x-2-4 \alpha \beta x\right . \\ &\left .+5 \beta x-2\right )+x \left (\beta ((4 \alpha +3) \gamma x-5 \right ) \\ &\times (2 x \left (b x^{2}+1\right )^{2} \left (-m x^{n}+\gamma x-1 \right ))^{-1} \\ &+(\gamma \left (-5 \alpha +(\alpha +1) (2 \alpha +1) \gamma x-1) \right . \\ &+\left .2 \beta ^{2} x\right )+(\alpha -1)^{2} f^{2} x^{4})(2 x \left (b x^{2}+1\right )^{2} \\ &\left (-m x^{n}+\gamma x-1\right ))^{-1}+5 \gamma , \end{aligned}$$

  (41a)
  $$\begin{aligned} \mbox{SEC}_{\delta } =& ( 2mnx^{n-1}-m(1+2n)x^{n-1}+(3fx))((2 \\ &+2bx^{2}))^{-1}+m(1+ 2n)x^{n-1}\beta -fx\beta (2 \\ &+2bx^{2})^{-1}+5\gamma\! -\!3\beta \gamma -\alpha (-m(1+2n)x^{n-1} \\ &+(fx(2+2bx^{2})^{-1}+3\gamma )^{2}+\mu -(4+2m(2 \\ &+n)x^{n}-6x\gamma )-2mx^{n-1}-fx(1+bx^{2})^{-1} \\ &+2\gamma +\beta ((-m(1+2n)x^{n-1}+fx(2 \\ &+2bx^{2})^{-1}+3\gamma ((1+mx^{n}-x\gamma ) +(\alpha (-m \\ &\times (1+2n)x^{n-1})))^{-1}+fx(2+2bx^{2})^{-1} \\ &+3\gamma ^{2}(1+mx^{n}-x\gamma )^{-1}+4bfx^{2}((1 \\ &+bx^{2})^{2})^{-1}-2f(1+bx^{2})^{-1}-\mu ((1+mx^{n} \\ &-x\gamma )-2x(1+mx^{n}-x\gamma )-4m(n \\ &-1)x^{n-2})^{-1}-(2\beta (mnx^{n-1}-\gamma )(-m(1 \\ &+2n)x^{n-1}+fx(2+2bx^{2})+3\gamma )^{-1}(1 \\ &+mx^{n} -x\gamma )^{2}-(2\alpha (mnx{n-1}-\gamma )(-m(1 \\ &+2n)x^{n-1}))+fx(2+2bx^{2})^{-1} \\ &+6\gamma ^{2}((1+mx^{n}-x\gamma )^{2}+(2(m(1+n \\ &-2n^{2})x^{n-2})))^{-1}+(f-bfx^{2})((2(1 \\ & +bx^{2})^{2}) \beta )^{-1}(1+mx^{n}-x\gamma )+(4(m(1+n \\ &-2n^{2})x^{n-2}+(f-bfx^{2})((2(1+bx^{2})^{2}) \\ &\times \alpha (-m(1+2n)x^{n-1}))^{-1}+fx(2 \\ &+2bx^{2})^{-1} +3\gamma ((1+mx^{n}-x\gamma ) \\ &+2(mnx^{n-1}-\mu ))^{-1} \\ &\times (1+mx^{n}-x\gamma )^{2}+(2mx^{n-1})+fx(1 \\ &+bx^{2})^{-1}-2\gamma -\beta (-m(1+2n)x^{n-1}) \\ &+fx(2 +2bx^{2})^{-1}+3\gamma ((1+mx^{n}-x\gamma ) \\ & -(\alpha -m(1 +2n))x^{n-1})^{-1}+fx(2 \\ &+2bx^{2})^{-1}+3\gamma ^{2}((1 +mx^{n}-x\gamma ) \\ &+\mu ((1+mx^{n} -x\gamma )^{2})^{-1})^{-1}, \end{aligned}$$

  (41b)
  $$\begin{aligned} \mbox{SEC}_{\psi } =& 2mnx^{n-1}-m(1+2n)x^{n-1}+fx(1 \\ &+bx^{2})^{-1} +fx(2+2bx^{2})^{-1}+ m(1 \\ &+2n)x^{n-1}\alpha -fx\alpha (2+2bx^{2})^{-1} \\ &+5\gamma -3\alpha \gamma +\beta (-m \\ &\times (1+2n)x^{n-1}+ fx(2+2bx^{2})^{-1}+3\gamma )^{-1} \\ &-((4+2m(2+n)x^{n}-6x\gamma ) fx(\alpha -1)((1 \\ &+bx^{2})-2mx^{n-1}(1+\alpha +2n\alpha )+2\gamma \\ &+6\alpha \gamma -(2\beta ))^{-1}+(-m(1+2n)x^{n-1} \\ &+fx)((2+2bx^{2})+3\gamma )))(2(1+mx^{n} \\ &-x\gamma ))^{-1}-(2(1+mx^{n}-x\gamma )))+x(4( \\ &-mnx^{n-1}+\gamma )((fx(\alpha -1))^{-1} \\ &\times [(1+bx^{2})-2mx^{n-1}(1+\alpha +2n\alpha ) \\ &+2\gamma +6\alpha \gamma -(2\beta )(-m(1+2n)x^{n-1} \\ &+fx(2+2bx^{2})+3\gamma ))+((fx(\alpha -1)) \\ &+2m(n-1(1+2n)x^{n}(1+bx^{2})^{2})\beta )(1 \\ &+bx^{2})-2mx^{n-1}(1+\alpha +2n\alpha )+2\gamma \\ &+6\alpha \gamma -2\beta (-m(1+2n)x^{n-1} \\ &+fx(2+2bx^{2})+3\gamma ))^{2}+4(1+mx^{n} \\ &-x\gamma )(-((2bfx^{2}(\alpha -1))(1+bx^{2})^{2} \\ &\times (1+bx^{2})-2m(n-1)x^{(-2+n)}(1+\alpha \\ &+2n\alpha )-(4(fx^{2}(bx^{2}-1)(fx^{2}-2(1 \\ &+bx^{2})(m(1+2n)x^{n}-3x\gamma ))^{2} \\ &+(f(\alpha -1)))]. \end{aligned}$$

  (41c)

• (v) The stability of the stellar sphere, either in Newtonian theory or in general relativity, with perfect or imperfect fluids is determined by the adiabatic index $\Gamma$. For the stellar object to be stable, the adiabatic index condition must hold throughout the interior. In Newtonian perfect fluids the collapse limit of the sphere is known to be $\Gamma \leq \dfrac{4}{3}$, while for imperfect fluids in general relativity the sphere is stable if $\Gamma =\dfrac{\rho +p_{r}}{p_{r}}\dfrac{dp_{r}}{d\rho } \geq \dfrac{4}{3}$. For our model in general relativity the adiabatic index for each region becomes

  $$\begin{aligned} \Gamma _{\xi } =& B_{1}(x)\left ((\alpha +1) f x^{2}-2 \left (b x^{2}+1 \right )\right . \\ &\times \left (-2 (\alpha -1) m n x^{n}+\alpha m x^{n}+(\alpha -2) \right . \\ &\times \left .\left .\gamma x+\beta x\right )\right ))(B_{2}(x) \left (x \left (\alpha f x-2 \left (b x^{2}\right .\right .\right . \\ &\left .+1\right ) \left .(\alpha \gamma +\beta +\gamma )\right )+ \left .2 m \left (b x^{2}+1\right )\right . \\ &\times \left .(\alpha (2 n-1)+1) x^{n}\right ))^{-1}, \end{aligned}$$

  (42a)
  $$\begin{aligned} \Gamma _{\delta } =&(-B_{3}(x) -\beta \left (f x(2 b x^{2}+2)^{-1}+3 \gamma \right . \\ &-m (2 n+\left .1) x^{n-1}\right )-f x(2 b x^{2}+2)^{-1} \\ &-3 \gamma -\mu +m (2 n+1) x^{n-1})(2 \left (b x^{3}+x\right )^{3} \\ &\times \left (f-b f x^{2})(2 \left (b x^{2}\right .\right .+\left . \left .1\right )^{2})^{-1}\right . \\ &+\left .m \left (-2 n^{2}+n+1\right ) x^{n-2}\right ))^{-1}, \end{aligned}$$

  (42b)
  $$\begin{aligned} \Gamma _{\psi } =&[B_{4}(x) \left (\alpha +4 \beta \left (b x^{3}+x \right )^{2}(\left (f x^{2}\right .\right . \\ &-2 \left (b x^{2}+1\right )\left (m (2 n+1) x^{n}\right . \\ &\left .\left .\left .-3 \gamma x\right )\right )^{2})^{-1}\right )] [3 \alpha \gamma -\beta (f x \\ &\times (2 b x^{2}+2)^{-1}+3 \gamma -m (2 n \\ &+1) x^{n-1})^{-1}+\alpha f x(2 b x^{2}+2)^{-1} \\ &+\alpha (-m)(2 n+1) x^{n-1}]^{-1}, \end{aligned}$$

  (42c)

where for simplicity we have set

$$\begin{aligned} B_{1}(x) =&\left (m (n-1) (\alpha (2 n-1)+1) x^{n-2}\right . \\ &-\left .\alpha f \left (b x^{2}-1\right )(2 \left (b x^{2}+1\right )^{2})^{-1} \right ), \\ B_{2}(x) =& (f-b f x^{2})(2 \left (b x^{2}+1\right )^{2})^{-1} \\ &+m \left (-2 n^{2}+n+1\right ) x^{n-2}, \\ B_{3}(x) =&\left ( f x^{2} (b x^{2}-1)+2 m (n-1) (2 n+1)\right . \\ &\times \left . (b x^{2}+1)^{2} x^{n}\right ) \left (\left (b x^{2}+1 \right )\right . \\ &\times \left .\left (x (6 \alpha \gamma +\beta )-2 \alpha m (2 n+1) x^{n} \right )\right . \\ &+\left .\alpha f x^{2}\right )\alpha \left (f x(2 b x^{2}+2)^{-1}+3 \right . \gamma \\ &-\left .m (2 n+1) x^{n-1}\right )^{2}, \\ B_{4}(x) =&\left (3 (\alpha +1) \gamma -\beta (f x(2 b x^{2}+2)^{-1} \right . \\ &+\left .3 \gamma -m (2 n+1) x^{n-1})^{-1}(\alpha +1)\right . \\ &\times \left . f x)(2 b x^{2}+2)^{-1}\right ) +\left (\alpha +1) (-m) \right . \\ &\times \left . (2 n+1) x^{n-1}.\right . \end{aligned}$$

6 Physical analysis

In this work, we described the interior of stellar objects containing three distinct layers in the presence of an electric field. We now discuss the physical features of the matter variables and other physical conditions that are generated by using the Python programming language. Plots generated include the gravitational potentials, energy density, radial pressure, tangential pressure, the measure of anisotropy, mass, adiabatic index, electric field, charge density, radial sound speed, and energy conditions. The plots are generated in the interval $(0-2.5)$ km, $(2.5-4.0)$ km and $(4.0-10)$ km for the core layer, intermediate layer, and the envelope layer respectively. All graphs are plotted against the radial distance in the specified domain of radius as contained in Pant et al. (2020). This assists in comparing our results with those found in Pant et al. (2020). We obtain the graphs by using the following values of the constants: $b=\pm 0.0003, f=\pm 0.0002, m=\pm 0.0001, n=3.00, \alpha =0.00001, \beta =\pm 0.0000847, \gamma =\pm 2.39, k_{o}=0.5, A=0.01$ and $\mu =\pm 6.88$.

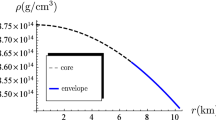
Figures 1 and 2 show that the energy density and the radial pressure are consistently decreasing functions from the centre towards the surface, where both vanish at the boundary. The same profiles are also found in the treatments of Pant et al. (2019, 2020), Gedela et al. (2019), Maharaj and Mafa Takisa (2013), and Sunzu and Danford (2017). We also observe that the tangential pressure in Fig. 3 is monotonically increasing function with radial distance. This profile is also obtained in the studies performed by Mafa Takisa and Maharaj (2016) and Ngubelanga and Maharaj (2015). The measure of anisotropy in Fig. 4 is generally an increasing function. It is zero at the centre and slowly increases away from the centre. It is a physical requirement that the measure of anisotropy should vanish at the centre when we set $x=0$. The positivity of the measure of anisotropy implies that the tangential pressure is greater than the radial pressure. These results also arise in the papers by Pant et al. (2020) and Ngubelanga et al. (2015). The gravitational potentials are regular and finite: $e^{2\nu }$ and $e^{-2\lambda }$ have been plotted in Fig. 5, and we show that they have equal values at the boundary. The energy conditions in Figs. 6, 7, 8, 9, and 10 are continuously increasing functions satisfying the condition of being greater or equal to zero. We observe in Fig. 11 that the model is stable and satisfies the stability condition $\left (\Gamma \geq \frac{4}{3}\right )$. In our model, we obtain the minimum value for the adiabatic index at $x=0$ to be $\Gamma _{0}=1.39446$ which is physically acceptable. Similar trends are also found in the works of Pant et al. (2019, 2020) and Gedela et al. (2019). Figure 12 indicates that the radial sound speed is in the acceptable range of $0.196653 \leq \nu \leq 0.820084$ which is less than the speed of light. Figure 13 depicts the charge density as a decreasing function. Figure 14 indicates that the electric field is an increasing function. This feature for the electric field is also found in models by Maharaj et al. (2014), and Sunzu and Danford (2017). Figure 15 shows that the mass is an increasing function with radial coordinate. Hence the model has acceptable behaviour in all the three layers, and matches to the exterior spacetime.

Fig. 1

Energy density against radial distance

Fig. 2

Radial pressure against radial distance

Fig. 3

Tangential pressure against radial distance

Fig. 4

Measure of anisotropy against radial distance

Fig. 5

Gravitational potential against radial distance

Fig. 6

Energy condition against radial distance

Fig. 7

Energy condition against radial distance

Fig. 8

Energy condition against radial distance

Fig. 9

Energy condition against radial distance

Fig. 10

Energy condition against radial distance

Fig. 11

Adiabatic index against radial distance

Fig. 12

Radial speed against radial distance

Fig. 13

Charge density against radial distance

Fig. 14

Electric field against radial distance

Fig. 15

Mass against radial distance

7 Stability

7.1 The TOV equation

With consideration of the Tolman-Oppenheimer-Volkoff (TOV) equation, we can determine the variation of the equilibrium forces for the relativistic stellar models (Maurya and Ortiz (2019)). These are the forces which counterbalance the system. For our charged model, the four different interior forces are gravitational ($F_{g}$), hydrostatic ($F_{h}$), anisotropic ($F_{a}$), and electric ($F_{e}$). The forces sum up to zero: $F_{g}+F_{h}+F_{a} + F_{e} =0$. The TOV equation is given in the form

$$\begin{aligned} -\dfrac{\nu ^{\prime }}{2}(\rho +p_{r})-\dfrac{dp_{r}}{dr}+ \dfrac{2}{r}(p_{t}-p_{r})+\sigma E e^{-2\lambda }=0, \end{aligned}$$

(44)

where in our model, we obtain

$$\begin{aligned} F_{g} =&-\dfrac{\nu ^{\prime }}{2}(\rho +p_{r}), \end{aligned}$$

(45)

$$\begin{aligned} F_{h} =&-\dfrac{dp_{r}}{dr} \\ =&-(f x^{2} (1 - b x^{2}) \alpha +m x^{n} ( n-1 + b ( n \\ &-3) x^{2})(1 + ( 2 n-1) \alpha ))(2 (x + b x^{3})^{2})^{-1}, \end{aligned}$$

(46)

$$\begin{aligned} F_{a} =&\dfrac{2}{r}(p_{t}-p_{r})=\dfrac{2}{r}\Delta , \end{aligned}$$

(47)

$$\begin{aligned} F_{e} =&\sigma E e^{-2\lambda } \\ =&((3 + bx^{2})^{3} fx^{3} \left (\dfrac{1 + mx^{n} -x \gamma }{x} \right )^{1/2} \\ &\times (2 (1+ bx^{2})^{3} x^{2} (1+bx^{2}) \\ &\times (1 + m x^{n} -x \gamma ))^{-1}. \end{aligned}$$

(48)

Figure 16 indicates the behaviour of the equilibrium forces which are physically acceptable. We observe in Fig. 16 that the anisotropic repulsive force ($F_{a}$), gravitational force ($F_{g}$), hydrostatic force ($F_{h}$) and electric force ($F_{e}$) are well behaved and in equilibrium. Similar profiles are also found in the paper by Jasim et al. (2020), Das et al. (2016), Maurya and Ortiz (2019), Fulara and Sah (2018) and Jasim et al. (2018).

Fig. 16

Variation of forces against radial distance

7.2 Harrison-Zeldovich stability

A detailed analysis of the stability (adiabatic index) for a pulsar are discussed in Harrison et al. (1965) and Zeldovich and Novikov (1971). In their works, they assumed that the adiabatic index of the pulsar is identical which provides a stable model only if the mass of the stellar sphere is monotonically increasing with respect to the central density. Thus $\frac{\partial m}{\partial \rho }>0$ for a stable model, and $\frac{\partial m}{\partial \rho }<0$ and $\frac{\partial m}{\partial \rho }=0$ for an unstable model (Jasim et al. (2020)). This condition in our model becomes

$$\begin{aligned} \dfrac{\partial m}{\partial \rho } =&(f x^{2} ( b x^{2}-1) \alpha - 2 m ( n-1) x^{n} (1 + b x^{2})^{2} \\ & \times (1 + ( 2 n-1) \alpha ))( f x^{2} ( b x^{2}-1) + 2 m ( n-1) \\ & \times (1 + 2 n) x^{n} (1 + b x^{2})^{2})^{-1}. \end{aligned}$$

(49)

We observe in Fig. 18 that the mass-density ratio is greater than zero, which obey the Harrison-Zeldovich condition for the model to be stable. Similar results are also found in the work of Maurya and Ortiz (2019), Jasim et al. (2020) and Fulara and Sah (2018).

7.3 Bondi stability

Here we consider the stability for both Newtonian and relativistic models. It has been noted that when the adiabatic index in both Newtonian and relativistic objects is exactly $\Gamma =\frac{4}{3}$, the model is in neutral equilibrium (Jasim et al. (2020)). This condition was observed in the work by Bondi (1964), who discussed the stability of the stellar sphere in both Newtonian and relativistic approaches. From Fig. 11 we see that adiabatic index in our study is greater than $\frac{4}{3}$, which increases the stability range of $\Gamma$.

7.4 Herrera cracking condition

Another condition was established by Herrera (1992) to study the stability of the stellar object under radial perturbations through the cracking approach. The concept of Herrera has been extended by Abreu et al. (2007) coming up with the stability factor [$v_{t}^{2}(r)-v_{r}^{2}(r)$] to examine the stability for anisotropic relativistic stellar objects. According to Abreu et al. (2007) the cracking condition has two inequality equations

• (i) $0< v_{t}^{2}(r)-v_{r}^{2}(r)<1$ for unstable region,

• (ii) $-1< v_{t}^{2}(r)-v_{r}^{2}(r)<0$ for stable region.

In our study we obtain the following expressions

$$\begin{aligned} v_{t}^{2}(r) =&\dfrac{dp_{t}}{d\rho } \\ =&(8 f \alpha + m n x^{ n-1} (-5 - 2 (-3 + \alpha ) \alpha ) \\ &+ 2 f m x^{n-1} (n^{2} (1 + b x^{2}) (-1 + \alpha ) (-1 \\ &+ 4 \alpha )-2bx^{2}(1+2(-1+\alpha )\alpha )+bnx^{2}(1 \\ &-8\alpha +6\alpha ^{2}))+(-mx^{n-1}+\gamma )(4(1+bx^{2})^{2} \\ &\times (1+mx^{n}-x\gamma )^{2})^{-1}+bx((1+bx^{2})^{3}(-1 \\ &-mx^{n}+x\gamma ))^{-1})(m(1+n-2n^{2})x^{ n-2} \\ &+ (f- b f x^{2})(2 (1 +bx^{2})^{2})^{-1})^{-1}, \end{aligned}$$

(50)

$$\begin{aligned} v_{r}^{2}(r) =&\dfrac{dp_{r}}{d\rho } \\ =&(f x^{2} (1 - b x^{2}) \alpha + m x^{n} (-1 + n + b (n \\ &-3) x^{2})(1 + (2 n-1) \alpha ))(2 (x +b x^{3})^{2} (m (1 \\ &+ n - 2 n^{2}) x^{n-1} + (f - b f x^{2})(2 (1 \\ &+ b x^{2})^{2})^{-1}))^{-1}. \end{aligned}$$

(51)

From Fig. 17 we observe the region as suggested in the Herrera cracking condition for a model to be stable. The behaviour shown in Fig. 17 ensures that our model satisfies, and meets the physical requirements for the stability condition. Similar trends are also observed in the work by Jasim et al. (2020), Das et al. (2016), Maurya and Ortiz (2019), Fulara and Sah (2018) and Jasim et al. (2018).

Fig. 17

Herrera cracking condition against radial distance

Fig. 18

Mass-density ratio against radial distance

8 Conclusion

In this paper we have developed a new model for a dense relativistic star with three interior layers, each layer satisfies a distinct equation of state. The core and intermediate layers satisfy the quark and quadratic equation of state respectively. Notably the envelope satisfies the gaseous Chaplygin equation of state which ensures that the outer layer of the star is less dense than the interior. The Einstein-Maxwell field equations are satisfied in each layer, and there is smooth matching between each layer and the exterior Reissner-Nordstrom spacetime. A detailed physical analysis shows that the model is well behaved; in particular there is smooth matching of the physical quantities between the three layers. It is for some interest to note that our model satisfies all stability conditions. This is graphically illustrated in various figures. Our result is a generalization of earlier works and shows that the approach of three interior layers is viable and contains interesting physical features. In particular we regain the work of Pant et al. (2020) for a suitable choice of parameters. In addition our model contains an electromagnetic field which is absent in the treatment of Pant et al. (2020). Our generalized charged model contains the results o f Pant et al. (2020) in the uncharged limit and therefore is applicable in the description of strange stars such as SAX J1808.4-3658 and binary stars such as Vela X-1. Our results emphasize the importance of considering three layers in the modelling process. In future work we will develop models with different forms of the gravitational potentials, electric field and equations of state.