Abstract
This paper investigates the optimal observational array for improving the initialization of El Niño-Southern Oscillation predictions by exploring the sensitive areas for target observations of two types of El Niño predictions. The sensitive areas are identified by calculating the optimally growing errors (OGEs) of the Zebiak–Cane model, as corrected by the optimal forcing vector that is determined by assimilating the observed sea surface temperature anomalies (SSTAs). It is found that although the OGEs have similar structures for different start months of predictions, the regions covered by much large errors for the SSTA component tend to locate at different zonal positions and depends on the start months. Furthermore, these regions are also in difference between two types of El Niño events. The regions covered by large errors of OGEs represent the sensitive areas for target observations. Considering the dependence of the sensitive areas on related El Niño types and the start months of predictions, the present study propose a quantitative frequency method to determine the sensitive areas for target observations associated with two types of El Niño predictions, which is expected to be applicable for both types of El Niño predictions with different start months. As a result, the sensitive areas that describe the array of target observations are presented with a reversal triangle-like shape locating in the eastern Pacific, specifically the area of 120°W–85°W, 0°S–11°S, and an extension to the west along the equator and then gathering at the 180° longitude and the western boundary. “Hindcast” experiments demonstrated that such observational array is very useful in distinguishing two types of El Niño and superior to the TAO/TRITON array. It is therefore suggested that the observational array provided in the present study is towards the optimal one and the original TAO/TRITON array should be further optimized when applied to predictions of the diversities of El Niño events.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
El Niño-Southern Oscillation (ENSO) is the most dominant climate mode in the tropical Pacific. It was manifested that a new type of El Niño events (denoted as CP-El Niño) had become more and more common since 1990s. The CP-El Niño is characterized by the most warming SSTA in the central equatorial Pacific Ocean during peak time, in contrasting to the canonical El Niño (denoted as EP-El Niño) characterized by the most warming SSTA in the eastern equatorial Pacific Ocean (Ashok et al. 2007; Kao and Yu 2009; Kug et al. 2009; Weng et al. 2007). It was suggested that the evolution of CP-El Niño events and its influence on the global weather and climate are considerably different from those of EP-El Niño events (Ashok et al. 2007; Weng et al. 2007; Yeh et al. 2009; Chen and Tam 2010; Marathe et al. 2015). Considering the differences between the two types of El Niño events, it is of great values to distinguish the types of El Niño events when making ENSO predictions. Many studies claimed that the prediction skill of ENSO varies from several seasons to 2 years in hindcast experiments. However, the real forecasts for ENSO are skillful only within several months. Especially, most of them cannot distinguish the types of El Niño events in forecasts (Barnston et al. 2012; Chen et al. 2004; Jin et al. 2008). Hendon et al. (2009) reported that they had limited success in predicting differences between the two El Niño types using the Australian Bureau of Meteorology’s Predictive Ocean Atmosphere Model for Australia (POAMA) coupled seasonal forecast model and the effective prediction skill could hold only 1 month ahead. Jeong et al. (2012) demonstrated that the useful prediction skill for predicting two types of El Niño events, even though an ensemble forecast technique was used, was only possible within a 4-month lead time.
In order to get the skillful predictions of two types of El Niño events, it is necessary to understand their predictability dynamics. The studies of predictability dynamics problems can be separated into two categories: the first kind problem of predictability associated with initial errors and the second kind problem of predictability related to model errors (Lorenz 1975). Quite a few studies have explored the important role of the initial errors in ENSO prediction uncertainties (Chen et al. 1995, 2004; Moore and Kleeman 1996; Mu et al. 2007; Thompson 1998; Xue et al. 1997a, b) or emphasized the importance of the accuracy of initial analysis fields in improving ENSO forecast skill (Keenlyside et al. 2005; Zheng et al. 2006, 2007; Zhu et al. 2017). Moreover, recent studies showed that the initial errors with particular spatial structures cause much larger prediction uncertainty for ENSO (Mu et al. 2007; Yu et al. 2009; Duan et al. 2009; Duan and Hu 2016). Specifically, Duan et al. (2009) pointed out that the initial errors with a dipole structure of sea surface temperature anomalies (SSTAs) along the tropical Pacific are most likely to cause a significant spring predictability barrier (SPB) phenomenon for El Niño events. Duan and Wei (2012) further showed the existence of these initial errors in realistic predictions for El Niño. These studies therefore provided a possible way to improve ENSO forecast skill by filtering out the initial errors of particular structures. Correspondingly, Mu et al. (2014) proposed an idea that the ENSO forecast skill can be greatly improved by assimilating observations in some key areas that locate in the above-mentioned initial errors of special structure and are covered by large errors. Such idea is related to target observations (Mu et al. 2014; Duan and Hu 2016; Hu and Duan 2016).
The so-called target observation is an economic and practical observation strategy to improving the initial state for weather and climate prediction, in which a limited number of observations are placed in some key areas and expected to have a considerable impact on prediction skills [see Sect. 2; also see the review of Mu (2013) and Mu et al. (2015)]. The key of the target observations is to determine the key areas (i.e. the optimal observation location for targeting or sensitive areas). In fact, Morss and Battisti (2004a, b), based on observation system simulation experiment (OSSE), suggested that for ENSO forecasting longer than a few months, the most important area for observations is the eastern equatorial Pacific, south of the equator; a secondary region of importance is the western equatorial Pacific. Yu et al. (2012) used the Zebiak–Cane model (Zebiak and Cane 1987) and explored the target observations for El Niño events. They argued that the eastern equatorial Pacific is the sensitive areas for targeting observations associated with EP-El Niño forecasting. Considering that the Zebiak–Cane model is an intermediate ENSO model and does not have enough description of the subsurface layers, Duan and Hu (2016) and Hu and Duan (2016) further adopted a complex GCM and showed that the subsurface layer of western equatorial Pacific represent another sensitive area for El Niño forecasting. However, most of these above studies only focus on EP-El Niño events because most models do not have the ability to simulate two types of El Niño events well (Ham and Kug 2012; Kim and Yu 2012; Kug et al. 2012). Although the models participating in phases 5 of the Coupled Model Intercomparison Project (CMIP5) were improved compared with the models in CMIP3, most of them still exist significant uncertainties in simulating both types of El Niño events (Kim and Yu 2012; Kug et al. 2012). It was shown that the model bias occurring in the annual-mean SST, convective precipitation, nonlinear temperature advection, etc. may induce the systematic errors for the simulation of the two types of El Niño (Duan et al. 2014; Hendon et al. 2009; Jeong et al. 2012; Kim et al. 2012; Kug et al. 2012). In other words, it is the model errors that weaken the models’ abilities in differentiating two types of El Niño events.
Considering that the model errors are from different sources and the interaction mechanism among them is relatively complicate, it is necessarily to consider the combined effect of all types of model errors on ENSO forecasting. Tsyrulnikov (2005) utilized this idea to characterize the combined effect of the sub-grid parameterization, the unrecognized physical processes, and the atmospheric noise by adopting the Markov chain models; Jin et al. (2007) used state-dependent stochastic noise to represent combined model errors and study the predictability and dynamics of the ENSO recharge oscillator. Zheng and Zhu (2016) added random terms to the tendency of an ENSO model and explicitly defined them as model errors. In fact, Duan et al. (2014) also proposed an approach of optimal forcing vector (OFV) to depict the combined effect of kinds of model errors and used it to correct the Zebiak–Cane model, finally reproducing successfully the observed two types of El Niño events. Based on the reproduced two types of El Niño events, Tian and Duan (2016) demonstrated that the initial SSTA errors that mainly concentrate in the central-eastern equatorial Pacific are mostly likely to induce SPB for both types of El Niño events. This implied that the predictions for two types of El Niño events are most sensitive to the initial SSTA errors in the central-eastern equatorial Pacific and, if increasing the observations over this region and assimilating them to the initial fields, the ENSO forecast skill can be greatly improved, as compared with doing it in other regions. That is to say, Tian and Duan (2016) showed that the sensitive areas for targeting observations (or the optimal observational locations) for two types of El Niño events locate the central-eastern equatorial Pacific. However, it should be pointed out that in this previous study, they did not care the effect of start months of ENSO predictions on the sensitive areas for targeting observations.
In the present study, we would explore the difference of the sensitive areas for target observation associated with two types of El Niño with different start months. The remainder of this paper is organized as follows. In Sect. 2, we introduce the data, model and methods used in this paper. In Sect. 3, we reproduce 8 El Niño events occurring during 1981–2010 and investigate the characteristics of optimally growing initial errors (OGEs; see Sect. 3) calculated at different start months. Section 4 is the core of the paper, we investigate the possible change of the sensitive area when the start month varies and then propose a quantitative method to determine the location of the sensitive area for target observation. In Sect. 5, we design a series of “hindcast” experiments to explore the role of target observation in the forecasting of two types of El Niño and suggest a more applicable observational array for two types of El Niño predictions. Finally, Sect. 6 is the summary and discussion.
2 Data, model, methods and target observation
2.1 Data
There are 9 El Niño events during 1981–2010. Previous studies used three different approaches to identify CP- and EP-El Niño events (Ashok et al. 2007; Ren and Jin 2011; Yu and Kim 2013; Zheng and Yu 2017), which made the identified EP- and CP- El Niño cases somewhat different in these studies. Therefore, a consensus of the El Niño cases identified by the previous studies is often adopted (Yu and Kim 2013; Zheng and Yu 2017). Referring to this, three of the nine El Niño events (i.e. 1982/1983, 1986/1987, 1997/1998) can be categorized as EP-El Niño events and five of them (i.e. 1991/1992, 1993/1994, 2002/2003, 2004/2005, 2009/2010) can be as CP-El Niño events. The exceptional 2006/2007 event has a strong hybrid character and is excluded in the present study. For these observed eight El Niño events, the SST data from the Hadley Center Global Sea Ice and Sea Surface Temperature (HadISST) analyses data sets (Rayner et al. 2003) are adopted. And the monthly wind stress anomalies derived from Florida State University analyses (Bourassa et al. 2001) are used to initialize the Zebiak–Cane model and then to make hindcast experiments for these El Niño events.
2.2 The Zebiak–Cane model
The Zebiak–Cane model was the first coupled ocean–atmosphere model to simulate the observed ENSO inter-annual variability. The model is composed of a Gill-type steady-state linear atmospheric model and a reduced-gravity oceanic model, which depict the thermo-dynamics and atmospheric dynamics of the tropical Pacific with oceanic and atmospheric anomalies near the mean climatological state specified from observations (see Zebiak and Cane 1987). It wins its fame for predicting the 1986–1987 El Niño events and thus has been widely used to study ENSO dynamics and predictability (Zebiak and Cane 1987; Blumenthal 1991; Xue et al. 1994; Chen et al. 2004; Tang et al. 2008). However, the Zebiak–Cane model can only depict EP-El Niño events (Chen and Cane 2008; Chen et al. 2004) but not simulate CP El Niño events well, which have been shown to be caused by the effect of model errors (Duan et al. 2014). As mentioned above, Duan et al. (2014), considering that the model errors are from different sources and cannot be exactly separated, proposed the OFV approach to reduce the model errors and finally reproduced successfully the observed two types of El Niño events. In the present study, we also use the El Niño events reproduced by the OFV to explore the target observations for two types of El Niño events. For convenience, we give the details of the OFV in Sect. 2.3.
2.3 The optimal forcing vector approach
Suppose the following nonlinear partial differential equation is a state equations associated with atmospheric or oceanic motions:
where \({\varvec{u}}({\varvec{x}},t)=[~{u_1}({\varvec{x}},t),~{u_2}({\varvec{x}},t), \ldots ,~{u_n}({\varvec{x}},t)]\) is the state vector, \(F\) is a nonlinear operator, \({{\varvec{u}}_0}\) is the initial state, \(\left( {{\varvec{x}},t} \right) \in {\mathbf{\Omega }} \times \left[ {0,T} \right]\), \({\mathbf{\Omega }}\) is a domain in \({{\varvec{R}}^n}\), \(T<+\infty\), \(~{\varvec{x}}=({x_1},{x_2}, \ldots ,{x_n})\), and \(t\) is the time. For the given initial field \({{\varvec{u}}_0}\), the solution to Eq. (1) for the state vector \({\varvec{u}}\) at time \(\tau\) is given by
where \({{\varvec{M}}_{{t_0},\tau }}\) denotes the propagator of Eq. (1) from time \({t_0}\) to \(\tau\).
Suppose the model described by Eq. (1) is imperfect and the model errors can yield prediction uncertainties when the model is used to predict the motion of the atmosphere or oceans. In order to offset the model error effects, one could superimpose a time-variant external forcing \({\varvec{f}}({\varvec{x}},t)\) for Eq. (3) to force the model to agree with the observation:
Thus, this problem can be transferred into a type of nonlinear optimization problem. The optimization problem can consider that certain f(x, t) are chosen such that the differences between the model simulation and the observations are minimized. That is, an external forcing should be chosen to satisfy the following optimization problem:
where \({t_i},{t_{i+1}} \in [{t_0},{t_k}]\), \({{\varvec{M}}_{{t_i},{t_{i+1}}}}({{\varvec{f}}_{~{t_i}}})\) is the propagator of Eq. (3) from time \({t_i}\) to \({t_{i+1}}\), and \({\varvec{u}}={{\varvec{M}}_{{t_i},{t_{i+1}}}}({{\varvec{f}}_{~{\text{min}},{t_{i - 1}}}})({{\varvec{u}}_{{t_{i - 1}}}})\). Note that the time intervals \([{t_i},{t_{i+1}}]\). can be several days, a month, a season or others, not necessary to be a time step of numerical integration, and depends on which is responsible for the smallest value of the Eq. (4). An external forcing vector \({{\mathbf{f}}_{{\text{min}},~{t_k} - {t_0}}}=({f_{~{\text{min}},{t_0}}},{f_{~{\text{min}},{t_1}}}, \ldots ,{f_{~{\text{min}},{t_{k - 1}}}})\) can be obtained by solving Eq. (4.) This forcing vector \({{\mathbf{f}}_{{\text{min}},~{t_k} - {t_0}}}\) is the OFV, which makes the model simulation closest to the observation during the time window \([{t_0},{t_k}]\).
It is easy to understand that for a given norm, the Eq. (4) defines an unconstrained optimization problem, with the OFV (\({{\mathbf{f}}_{{\text{min}},~{t_k} - {t_0}}}\)) being the minimum point of the objective function in the phase space. It’s worth noting that the OFV is still time-independent during the time interval \([{t_i},{t_{i+1}}]\). This means that we can compute the OFV as the constant FSV, proposed by Barkmeijer et al. (2003), using the limited memory Broyden–Fletcher–Goldfarb–Shanno (L-BFGS; Liu and Nocedal 1989) algorithm. This algorithm is based on the gradient-steepest descent method and finds the minimum value of an objective function, in which the gradient of the objective function with respect to the external forcing is needed. In this paper, we adopt the approach proposed by Feng and Duan (2013) to calculate the gradient of the objective function with respect to the external forcing [see Feng and Duan (2013) for more details]. Using this gradient information, the OFV of the Zebiak–Cane model is computed by using the L-BFGS solver in this paper.
2.4 The conditional nonlinear optimal perturbation
Similar to Tian and Duan (2016), we use the conditional nonlinear optimal perturbation (CNOP) to identify the sensitive area for target observations. The CNOP is the initial perturbation which satisfies a given constraint and has the largest nonlinear evolution at prediction time (Mu et al. 2003). For the corrected model Eq. (3), an initial perturbation \({{\varvec{u}}_{0\delta ~}}\) is the CNOP if and only if it satisfies the equation:
where \(\| {{\varvec{u}}_{0}} \| < \delta\) is the initial constraint defined by the chosen norm. The constraint condition could reflect physical laws that the initial perturbation should satisfy.
The CNOP can be computed by solving the maximization problem in Eq. (5). To do this, we firstly transform Eq. (5) into a minimization problem by considering the reciprocal of the cost function. Then we can solve this minimization problem by some minimization solvers such as the spectral projected gradient 2 (SPG2; Birgin et al. 2000), sequential quadratic programming (SQP; Powell 1983), or the limited memory Broyden–Fletcher–Goldfarb–Shanno method (L-BFGS; Liu and Nocedal 1989).
In this paper, we apply the CNOP approach to the Zebiak–Cane model which is corrected by OFV. The CNOP, when applied to the corrected Zebiak–Cane model, can be obtained by solving the following nonlinear optimization problem:
where \({{\varvec{u}}_{0~}}=({w_1}{{\varvec{T}}_0},~{w_2}{{\varvec{H}}_0})\), and \({{\varvec{T}}_0}\). and \({{\varvec{H}}_0}\) are the SSTA and thermocline depth component of the initial error respectively; \({w_1}={(2\;^\circ {\text{C}})^{ - 1}}\) and \({w_2}={(50\;{\text{m}})^{ - 1}}\) are the characteristic scales of SST and thermocline depth; \({{\varvec{U}}_0}\) is the initial value of the reference state; \(\left\| \cdot \right\|\) represents the L-2 norm; \(\| {{\varvec{u}}_{0}} \| < \delta\) is the constraint condition and δ is set at 1 experimentally; \({\varvec{T}}{'_t}\) is the prediction error of SSTA.
2.5 The target observation
The target observation, as the introduction mentioned, is an economic and practical observation strategy to improving the initial state for weather and climate prediction. This observation strategy is a new one developed since 1990s. Its general idea is as follows. To better predict a climate or weather event at a future time\(~{t_1}\) (verification time) in a focused area (verification area), additional observations are deployed at a future time\(~{t_2}\) (target time, \(~{t_2}<~{t_1}\)) in some special areas (sensitive areas) where the additional observations are expected to improve the forecast skills in the verification area (Synder 1996). Generally speaking, these additional observations would be assimilated by a data assimilation system to provide the numerical model a more reliable initial state. The idea of the target observation has been applied to some weather and climate events forecasting, such as Fronts and Atlantic Storm-Track Experiment (FASTEX; Synder 1996), North Pacific Experiment (NORPEX; Langland et al. 1999), tropical cyclone (TC; Qin et al. 2013; Qin and Mu 2012; Zhou and Mu 2011), Kuroshio large meander (KLM; Wang et al. 2013), India Ocean Dipole (IOD; Feng et al. 2014), ENSO (Yu et al. 2012; Hu and Duan 2016), etc.
The key of target observations is to determine the sensitive areas. Traditionally, there are two types of mathematical techniques: the one is based on sensitivity analysis, such as adjoint sensitivity (Bergot 1999), singular vectors (SVs; Palmer et al. 1998), and the adjoint-derived sensitivity steering vector (ADSSV; Wu et al. 2007), etc.; and the other is related with data assimilation methods, such as the ensemble transform technique (Bishop and Toth 1999); the ensemble transform Kalman filter (ETKF; Bishop et al. 2001), the ensemble Kalman filter (EnKF; Liu and Kalnay 2008); the piece-by-piece data assimilation targeting method (PBPDA; Huang and Meng 2014), etc. However, most of these methods are limited by the use of linear approximation. For some high-impact ocean-atmospheric environmental events, such as TC, ENSO, the impact of nonlinearity plays an important role (Fiorino and Elsberry 1989; Mu et al. 2009; An and Jin 2004; Duan et al. 2008, 2017). Thus, it may induce extra errors to apply these linear methods to such events.
Recently, the nonlinear approach of CNOP has been successfully used to determine the sensitive areas for targeting in TC, IOD, KLM forecasting (Qin et al. 2013; Qin and Mu 2012; Zhou and Mu 2011; Feng et al. 2014; Wang et al. 2013). For the TC forecasting, the CNOP is computed case by case and the sensitive areas for targeting observation are case dependent (Qin et al. 2013; Qin and Mu 2012; Zhou and Mu 2011). However, the observations for ENSO is such a complex project with large investment and time consuming that we expect it can provide information for more than just one specific El Niño prediction. That is to say, the sensitive areas should be applicable for most of El Niño events predictions. Although Yu et al. (2012) identified the sensitive area according to the composite of CNOPs calculated based on all the El Niño events involved in the study, they, as mentioned in the introduction, did not consider the effect of start months of predictions on target observations and only gave the approximate range of the sensitive area for targeting. In this paper, in order to identify the optimal layout of observation locations for targeting, we proposed a quantitative method which considers the differences among the CNOP-type initial errors calculated at different start months of predictions (see Sect. 4).
3 The optimally growing initial error of the reproduced EP- and CP-El Niño events
As mentioned in Sect. 2.2, the Zebiak–Cane model cannot depict CP–El Niño events well, mostly due to the effect of model errors (Duan et al. 2014). Duan et al. (2014) proposed an OFV approach to consider and reduce the combined effects of different model errors for the Zebiak–Cane model, finally reproducing the two types of observed El Niño events. Tian and Duan (2016) has further applied this method to the Zebiak–Cane model to study the SPB phenomenon of two types of El Niño events. Recently, Duan et al. (2017) has also adopted such method and revealed the modulation effect of nonlinearity on two types of El Niño events by using the Zebiak–Cane model. In the present study, we follow Duan et al. (2014, 2017) and use the corrected Zebiak–Cane model to reproduce the 8 El Niño events (including 3 EP- and 5 CP–El Niño events) mentioned in Sect. 2.1. Specifically, the OFV forcings are added to the SSTA governing equation of the Zebiak–Cane model and correct the model errors by assimilating a series of HadISST analytical data, finally making the simulated SSTA closest to the observations. For each of the 8 El Niño events, we reproduce its SSTA for 3-year period from the year before the El Niño event to the year the event demises [denoted as year (− 1), year (0) and year (1), respectively]. To avoid getting unreasonably large OFVs which may make the relevant state variables fail to satisfy dynamics and/or physics, we adopt the initialization scheme developed by Chen et al. (1995) to obtain the initial conditions of the corrected Zebiak–Cane model starting on January (− 1) of every El Niño events and obtain high consistence between the observed and simulated SSTA of two types of El Niño events (Fig. 1). For convenience, we still refer to the corrected Zebiak–Cane model as the “Zebiak–Cane model” hereafter.
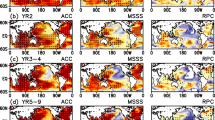
The mean of the SSTAs during the mature phase for three EP-El Niño events (1982/1983, 1986/1987 and 1997/1998) and five CP-El Niño events (1991/1992, 1994/1995, 2002/2003, 2004/2005 and 2009/2010): a observed EP-El Niño; b EP-El Niño reproduced by the Zebiak–Cane model with an OFV; c observed CP-El Niño; d CP-El Niño reproduced by the Zebiak–Cane model with an OFV. The mature phases here are the period of July–August–September (denoted by JAS) for the 1986/1987 EP-El Niño and the period of October–November–December (denoted by OND) for other EP- and CP-El Niño events
The CNOP approach is applied to the Zebiak–Cane model to compute the optimally growing initial errors (OGEs) of two types of El Niño events. Because the CNOP, by definition, represents the initial error whose nonlinear evolution attains the maximum at the prediction time under some certain constraint conditions, the CNOP-type initial error represents the OGE of ENSO events. For the seven reproduced El Niño events excluding 1986/1987, we calculate the CNOP-type initial errors superimposed on the tropical SSTA and thermocline depth anomaly fields with the lead time 1 year of predictions and start months January (0), April (0), July (0), and October (0), respectively. As most of the El Niño events usually have a strong phase-locking character in which the El Niño attains its peak at the end of the calendar year, the 4 start months here actually mean that the initial times of predictions correspond to 1–4 seasons ahead the mature phase of the El Niño events, respectively. For the 1986/1987 EP-El Niño, since it attained the mature phase in boreal autumn instead of winter, the OGEs are calculated with start months October (− 1), January (0), April (0) and July (0), also corresponding to 1–4 seasons ahead the mature phase of the event. For convenience, when mentioned to the start months in the Figures, the labels of the x-axis only show January (0), April (0), July (0), and October (0), which also in order correspond to October (− 1), January (0), April (0) and July (0) for the 1986/1987 El Niño event.
For each of the three EP-El Niño events (1982/1983, 1986/1987, 1997/1998), we predict it with the four start months and get 4 OGEs. And a total of 12 OGEs can be obtained for three El Niño events. Similarly, for the five CP-El Niño events (1991/1992, 1994/1995, 2002/2003, 2004/2005, 2009/2010), we get 20 OGEs totally. All the OGEs have similar large-scale structure with the SSTA component exhibiting a zonal dipolar pattern and the thermocline depth component exhibiting a consistently deepened or shoaling pattern across the equatorial Pacific. However, as the start month changes from January (0), April (0), July (0) to October (0), the OGEs present the regions with large values of SSTA components to be gradually much westward. Figure 2 shows two examples with the SSTA components of OGEs for the 1982/83 EP-El Niño event and 2009/2010 CP-El Niño event. It can be seen that the region with large errors, especially the western polar of the dipolar structure, moves towards west, as the start month changes from January (0) through April (0) and July (0) to October (0). In order to quantify this character, we calculated the zonal center of the OGEs’ SSTA components for each of EP-and CP-El Niño events (Fig. 3). The formula of zonal center is derived from Ham and Kug (2015) and can be represented as:
The SSTA components of OGEs for 1982/1983 EP-El Niño (left column) and 2009/2010 CP-El Niño (right column) with different start months. a–d SSTA components of OGEs for 1982/83 EP-El Niño event predictions with the start months January (0), April (0), July (0) and October (0), respectively; e–h are as in a–d, but for the 2009/2010 CP-El Niño event; the rectangles shown in the figures represent the areas that are covered by much large errors
The Box–Whisker plot of the zonal centers for the SSTA components of the OGEs associated with the predetermined eight El Niño events predictions with the start months October (− 1), January (0), April (0) and July (0) for the 1986/1987 EP-El Niño event and January (0); April (0), July (0) and October (0) for other EP- and CP-El Niño events; the bold black lines represent the medians and the red dots represent the means
where \(x\) represents the longitude; \({e^2}(x)\) represents the meridional average (19°N–19°S) square error of the OGEs’ SSTA components at \(x\); the integral range is from 129.375°E to 84.375°W. It is shown from Fig. 3 that the zonal centers of OGEs for each of the EP- and CP-El Niño events with the start month October (0) are farther to the west than that of OGEs with the start months from July (0) to April (0) and then January (0), which indicates that the westward trend of the OGEs is a general feature of all the El Niño events and is possibly associated with the westward propagation of the climatological Rossby wave.
The equal-sized regional division of the tropical Pacific suggested by Yu et al. (2012); the number 1–6 represent the six equal-sized rectangular areas (i.e. domains 1–6)
4 The determination of sensitive area for target observation
Section 3 reveals that the OGEs for two types of El Niño events concentrate few regions but possess westward trend with the start months changing from January (0) to October (0). Previous studies showed that the region with large values of the OGEs represent the sensitive area for target observation associated with El Niño predictions (Duan and Hu 2016; Hu and Duan 2016; Tian and Duan 2016; Mu et al. 2014; Yu et al. 2012); and the initial errors in these sensitive areas make greatest contribution to the prediction error and the prediction skills can be improved when these initial errors are reduced. Especially, Yu et al. (2012) divided the tropical Pacific into six equal-sized rectangular domains denoted as domain i (i = 1, …, 6) (Fig. 4) and concludes that the eastern-central equatorial Pacific (domain 5, 157.5°W–90°W, 5°S–5°N) is the sensitive area for target observation of EP-El Niño events. Tian and Duan (2016) investigated the initial errors which can cause SPB phenomenon of two types of El Niño and argued that the eastern-central equatorial Pacific may be the sensitive area for target observation of both types of El Niño. However, these works did not care the westward trend of OGEs for El Niño events with the changing start months, as shown in the present study. Actually, if the regions with large values of the OGE represent the sensitive areas for target observations, the OGEs showed by the present study may suggest that the sensitive areas for two types of El Niño events move westward gradually as the start month changes from January (0), April (0), July (0) to October (0). Correspondingly, if the target observations in the sensitive areas presented by Tian and Duan (2016) are used to decrease the initial errors, the forecast skill of the two types of El Niño would decrease with the start months changing from January (0) to October (0). Next, we show the correctness of this inference by using the regional division suggested by Yu et al. (2012) (Fig. 4).
The control forecasts are made to the reproduced 1986/1987 El Niño event for 1-year lead time with the start months October (− 1), January (0), April (0) and July (0) but to the rest of the reproduced El Niño events with the start months January (0), April (0), July (0), and October (0), where the initial SSTA and thermocline depth anomaly fields of the reproduced El Niño events are superimposed with their respective OGEs. Based on the control forecasts, we deduct the initial errors in Domain 1–6 in Fig. 4 respectively and keep the initial conditions in other domains unchanged, forming updated initial conditions of El Niño forecast. With these updated initial conditions, we make 1-year integrations of the Zebiak–Cane model and obtain updated forecasts for the corresponding El Niño events, finally comparing them with the control forecast and investigating the benefit of the forecast skill.
To measure the prediction skills, we define the prediction error (denoted by E) as follows:
where \({{\varvec{T}}^\prime }\) represents the difference between the predicted SSTA and the true state, and (i, j) represents the grid point in the tropical Pacific referred by the Zebiak–Cane model (129.375°E to 84.375°W by 5.625° and from 19°S to 19°N by 2°). To measure the improvement of prediction skills of the updated forecasts, we define the rate R as in Eq. (11.)
where \({E_c}\) represents the prediction error of the control forecasts and \({E_u}\) represents the prediction error of the updated forecasts.
Figure 5 shows the R indices of the predictions for the eight reproduced El Niño events. It is shown that the R indices, when deducting the initial errors in the eastern-central equatorial Pacific [i.e. the domain 5, the sensitive area suggested by Tian and Duan (2016)], decrease as the start month changes from January (0) through April (0) and July (0) to October (0) (Fig. 5b); meanwhile the R indices increase when deducting the initial errors in the western-central equatorial Pacific (domain 2) (Fig. 5b). This result verifies the inference in the last paragraph. Furthermore, it also shows the role of domain 2 and further indicates that the sensitive areas for targeting observation of two types of El Niño events could be varying with the start months, i.e. the westward trend of the sensitive areas with the start months changing from January (0) to October (0), as suggested by the CNOP-type errors in Fig. 3.
a The Box–Whisker plot of the R indices of the updated forecasts when deducting the initial errors in domian i (Di; i = 1,…,6) respectively and keeping the initial conditions in other domains to be the same as the control forecasts, where each box is calculated based on the updated forecasts for EP- and CP-El Niño events with Jan (0), April (0), July (0) and October (0) but October (− 1), January (0), April (0) and July (0) for the 1986/1987 El Niño event. The bold black lines and the red dots represent the medians and means, respectively. b The R indices (averaged for the reproduced eight El Niño events) of the updated forecasts when deducting the initial errors in domain 2 (red color) and domain 5 (orange color) and keeping the initial conditions in other domains be the same as the control forecasts, where the start months of the predictions are respectively January (0), April (0), July (0) and October (0) but October (− 1), January (0), April (0) and July (0) for the 1986/1987 El Niño event
The sensitive areas for target observation associated with two types of El Niño predictions are dependent on the start months of predictions. Then in this specific situation how do the observations display in operational forecast for ENSO? One of the ideas to solve this problem is to determine the sensitive area case by case, just like the general operations adopted in the target observation for Tropical cyclone (Qin et al. 2013; Qin and Mu 2012; Zhou and Mu 2011). However, the observations for ENSO are such a complex project with large investment and time consuming that we expect it can provide information for as many El Niño events as possible and is applicable for different start months of predictions. According to this requirement, we propose a quantitative frequency method to identify the sensitive area for target observation. By this method, the identified sensitive areas for target observations comprise the space grids that correspond to much larger error in most of the OGEs for the predetermined eight El Niño events predictions. The method can be described as follow.
For each of the OGEs, we sort its spatial grid points with a descending order according to their corresponding error amplitudes and chose the top 50 ones. Then we can get 32 series and each contains the 50 grid points. For each grid point of the model domain (129.375°E to 84.375°W by 5.625° and from 19°S to 19°N by 2°), we compute its frequency of arising in the 32 series and denoted by F index as in Eq. (12).
where \({c_{i,j}}\) is the count of the grid point (i, j) arising in the 32 series; N is the “32” series. Then we select the lead 50 grid points with the large F indices and use the region covered by these lead 50 grid points as the sensitive area for two types of El Niño events predictions.
We note that the F index is estimated based on the SSTA and thermocline depth anomaly components of the OGEs, respectively (Fig. 6a, b). Accordingly, the sensitive areas are identified for the SSTA and thermocline depth anomaly and denoted as SASST and SATHD (Fig. 6c, d), respectively. The shape of the SASST looks like a reversal triangle locating in the eastern Pacific, specifically the area of 120°W–85°W, 0°–11°S; and it extends to the west along the equator and gathers at the western boundary and the 180° longitude (Fig. 6c). The SATHD shows a quite scattered distribution along the equator, with its bulk locating in the eastern-central equatorial Pacific (Fig. 6d).
We compare SASST with SATHD and explore which one is more important for target observation of two types of El Niño. Based on the predetermined control forecasts, we designed another two groups of updated forecasts where we deduct the initial errors in SATHD and SATHD respectively and keep the initial conditions in other domains unchanged. Figure 7a shows the R indices of these two groups of updated forecasts and the updated forecasts shown in Fig. 5 where the initial errors in domains 2 and 5 are deducted. It is shown that the R indices for deducting the initial errors in SASST are almost the largest. Figure 7b shows the R indices when predicting at different stating months. It can be seen that the R indices of deducting the initial errors in SASST tend to be the largest and have the least fluctuation with the changing start months, while others are significantly dependent on start months and especially show to be much small. This result indicates that if target observations are preferentially deployed in SASST, the El Niño prediction errors will be much greatly reduced compared to doing it in other regions. In addition, we consider here the two types of El Niño events predictions. Then whether or not the differences between them can be distinguished by the sensitive area-related target observations? To address it, we examine the role of the associated target observations in predicting two types of El Niño events. Figure 8 show the SSTA patterns during El Niño mature phase [i.e. the period of July–August–September (denoted by JAS) for the 1986/1987 EP-El Niño and the period of October–November–December (denoted by OND) for other predetermined EP- and CP-El Niño events] of the control and updated forecasts with the start month April (0) [January (0) for the 1986/1987 EP-El Niño]. It is shown that the SSTA patterns of the updated forecasts are improved obviously when deducting the initial errors in SASST for both types of El Niño. Especially for the CP-El Niño events, the warmest SSTA locates in the eastern equatorial Pacific for the control forecast but the central equatorial Pacific for the updated forecasts and much closer to the true state CP-El Niño events. It is therefore suggested that the SASST can be the sensitive area for target observations of two types of El Niño and applicable for predictions with different start months.
a The Box–Whisker plot of the R indices of the updated forecasts when deducting respectively the initial errors in SASST, SATHD, domain 2 (D2) and domain 5 (D5) and keeping the initial conditions outside the area to be the same as the control forecasts, where each box is computed based on the updated forecasts for the reproduced EP- and CP-El Niño events predictions with the start months January (0), April (0), July (0) and October (0) [but October (− 1), January (0), April (0) and July (0) for the 1986/1987 El Niño event]. The bold black lines and the red dots represent the medians and means, respectively. b The R indices (averaged for the eight El Niño events) of the updated forecasts when deducting the initial errors in SASST (red color), SATHD (orange color), domain 2 (blue color) and Domain 5 (green color) and keeping the initial conditions outside the area to be the same as the control forecasts, with the start months January (0), April (0), July (0) and October (0) [but October (− 1), January (0), April (0) and July (0) for the 1986/1987 El Niño event]
The mean of the SSTA patterns during the mature phase for El Niño (i.e. JAS for the 1986/1987 EP-El Niño event but OND for other predetermined EP- and CP-El Niño events). a–c Reproduced EP-El Niño events (simulated by the Zebiak–Cane model with OFV correction), and their control forecasts (with the OGEs superimposed on the initial fields of the reproduced events) and updated forecasts (with the initial errors of the OGEs in the SASST being deducted and the initial conditions outside the SASST being kept to be the same as the control forecasts), respectively; d–f are as in a–c, but for the CP-El Niño events. The start month is April (0) [but January (0) for the 1986/1987 EP-El Niño event]
5 The role of target observations in the “hindcast” experiments of two types of El Niño events
The sensitive area SASST is suggested based on the OGEs and their related control and updated forecasts (see Sect. 4), where the initial errors of the control forecasts are the OGEs but those of the updated forecasts eliminate the initial errors in the SASST. Since it is the OGEs that possess regions that are covered by the initial errors of large values and provide the location of sensitive area, it is certainly reasonable that the sensitivity of the SASST can be confirmed by the OGEs-related control and updated forecasts. More generally, the updated forecasts should be made on the control forecasts whose initial conditions are much like in realistic predictions and yielded by an initialization procedure. In this situation, the confirmation of the sensitivity of the sensitive area is much convinced. To do it, we adopt the initialization scheme developed by Chen et al. (1995), where the model was initialized in a coupling manner with the coupled model wind stress anomalies being nudged toward observations. More details can be found in Chen et al. (1995). We note that this initialization scheme can lead to a high prediction skill which can partly eliminate the SPB phenomenon (Chen et al. 1995); and as a result, it is a good benchmark to measure the effectiveness of target observation. In the present study, we would use this initialization scheme to make “hindcast” experiments for the predetermined El Niño events with the lead time one year starting from January (0), April (0), July (0) and October (0) [but October (− 1), January (0), April (0) and July (0) for 1986/1987 El Niño event] respectively. But we note that the “hindcast” experiments here are based on the corrected Zebiak–Cane model, which used the SSTA observations during the El Niño events and determined the OFV to correct the model (see Sect. 3). So the “hindcast” here is not a real one. However, the corrected Zebiak–Cane model can be assumed as perfect model and the prediction uncertainties can be considered as only caused by initial errors. Therefore, the “hindcast” generated by the Corrected Zebiak–Cane model is feasible for examining the role of initial errors in causing predictions uncertainties.
We use these “hindcasts” as control forecasts and base on them to make updated forecasts. To confirm the sensitivity of sensitive area SASST (see Fig. 9a), we choose another two sets of representative regions: the eastern equatorial Pacific area (AE, similar to the domain 5; Fig. 9b) and random areas. Here the random area is composed of the randomly-choosing grid points in the model domain. Then for the initial fields of the control forecasts we assimilate the initial SSTAs and thermocline depth anomalies of the predetermined 8 El Niño events in the SASST and these two areas and obtain initial conditions of updated forecasts, finally making 1-year lead time forecasts. To be fair, each of the above areas include 50 grid points, which means that the numbers of the assimilated observations in the three areas are the same as 50. Especially, to make the results more convincing, we realize the random areas for ten times and get ten realizations of random areas (for simplicity, we denote these random areas “AR”), which are finally compared with the SASST. As an example, we plot in Fig. 9c one realization of random areas. Since the “hindcast” experiments are ideal ones, the so-called “observation” information to be assimilated here are actually from the initial conditions of the 8 reproduced El Niño events, instead of the real observations. The general idea of the assimilation is to find a proper initial state of forecasts. In the present study, the assimilation just is to solve the Eq. (13).
The locations of the sensitive area SASST (a), the tropical eastern Pacific area AE (b) and one of the random areas AR (c). The Box–Whisker plot of the prediction errors (d) and the similarity coefficients (e) of the control forecasts [based on the initialization scheme developed by Chen et al. (1995)] for the eight El Niño events (denoted as Con), the related updated forecasts with data assimilations made in the SASST (denoted as SASST) and AE (denoted as AE) respectively, and the multi-ensemble results of assimilations made in the ten random areas (denoted as AR). The start months are as in Fig. 3. The bold black lines and the red dots in d, e represent the medians and means, respectively
where \({{\varvec{U}}_{{t_0} - \tau }}\) is a vector including SST and thermocline depth anomalies components at time \({t_0} - \tau\), where \({t_0}\) is the start time of the updated forecasts and \(\tau\) is a positive number and represents the time period of the assimilation window; \(\tau\) is experimentally set to be 6 months in the present study; S is the assimilation area, which corresponds to the above areas SASST, AE, and the ten random areas; \(T_{{i,~j}}^{m}({t_0})\) and \(H_{{i,~j}}^{m}({t_0})\) represent the SSTA and thermocline depth anomaly obtained by integrating the model from \({t_0} - \tau\) to \({t_0}\) with \({{\varvec{U}}_{{t_0} - \tau }}\) being initial values; \(T_{{i,~j}}^{t}({t_0})\) and \(H_{{i,~j}}^{t}({t_0})\) represent the “observed” SSTA and thermocline depth anomaly of the predetermined El Niño events. By the Eq. (13), one can get the state \({\varvec{U}}_{{{t_0} - \tau }}^{*}\) at \({t_0} - \tau\). With \({\varvec{U}}_{{{t_0} - \tau }}^{*}\) as initial values, we integrate the Zebiak–Cane model from \({t_0} - \tau\) to \({t_0}\) and obtain a state at \({t_0}\), whose SST and thermocline depth anomalies are closest to the “observations” of the predetermined El Niño events at \({t_0}\). With the state at \({t_0}\) as initial value, we integrate the Zebiak–Cane model for one year and obtain the updated forecast for the predetermined El Niño events.
In order to compare the forecast skills of updated forecasts and control forecasts, we adopt the prediction error to measure the prediction uncertainties and the similarity coefficient (S index; Buizza 1994; Dai et al. 2016) to evaluate the similarity between the spatial patterns of relevant state variables for two types of El Niño events.
where \({{\varvec{X}}_t}\) is the physical variable field of the “observations”; \({{\varvec{X}}_f}\) is that of the forecast; \(\left\| \cdot \right\|\) is the L-2 norm.
The results of prediction errors and similarity coefficients are shown in Fig. 9d, e. It is shown that the updated forecast with the assimilation in the SASST presents the smallest prediction error and the highest similarity coefficient. Furthermore, we find that the spread of prediction errors and similarity coefficients with respect to El Niño events cases is the smallest in the updated forecasts with assimilation in the SASST, which indicates that the improvement of prediction skills of the updated forecasts with assimilation in the SASST is more robust for different El Niño events. Furthermore, when the comparison comes to the specific SSTA patterns during El Niño mature phase (OND, but JAS for the 1986/1987 El Niño), it is shown that the updated forecast with assimilation in the SASST can make the predicted SSTA patterns for El Niño events closer to the “observations”, especially for the CP-El Niño events (e.g. the predictions for the 1991/1992 and 2009/2010 events) (Fig. 10). Obviously, for more general initializations, the SASST can also be verified as the sensitive area for target observation associated with two types of El Niño predictions.
The mean of the SSTA during the mature phase for El Niño (i.e. JAS for the 1986/1987 EP-El Niño event but OND for other predetermined EP- and CP-El Niño events). a–c, e Reproduced EP- and CP-El Niño events (simulated by the Zebiak–Cane model with OFV correction), and their control forecasts [with the initialization scheme developed by Chen et al. (1995)] and updated forecasts (with data assimilations made in the SASST, AE and AR, respectively). The start month is April (0) [but January (1) for the 1986/1987 EP-El Niño event]
In addition, when mentioned to the ENSO observation system, the 10-year (1985–1994) international Tropical Ocean Global Atmosphere (TOGA; World Climate Research Program 1985) program may be the most fundamental. This observation system mainly includes the Tropical Atmosphere Ocean (TAO) array of moored buoys, an array of drifting buoys, volunteer observing ship (VOS) measurements, a network of island and coastal sea level measurement stations, and a constellation of complementary satellites (McPhaden et al. 1998, 2001). The TAO array was renamed to TAO/TRITON array on 1 January 2000, with the Triangle Trans-Ocean Buoy Network (TRITON) joining in, which focuses on the observation over the western tropical Pacific. This observation system has made great contributions to the understanding and forecasting of ENSO. Figure 11 shows the locations of the TAO/TRITON array and SASST. It can be seen that there are many overlaps between the two observation layouts. But the TAO/TRITON array has 68 observation points, which are of 18 ones more than that of SASST. Then we naturally ask: is the SASST of stronger sensitivity than the TAO/TRITON array for target observation?
The locations of SASST (the blue rectangles) and the TAO/TRITON array (the red dots) (the TAO/TRITON array is from http://www.pmel.noaa.gov/tao/drupal/disdel/)
To address this question, we compared the prediction skills between the updated forecast with assimilation in the SASST and the area covered by the TAO/TRITON array. Because the TAO/TRITON array does not match the grid points in the Zebiak–Cane model, the bilinear interpolation [Press et al. 1992, Eq. (3.6.5)] is used in the assimilation of the initial SSTAs and thermocline depth anomalies of the predetermined eight El Niño events. The interpolation would bring about additional initial analysis errors. However, for the updated forecasts with the assimilation in the SASST, because the SASST is directly derived from the Zebiak–Cane model and the related grid points certainly match the Zebiak–Cane model, no additional initial errors are caused by interpolation. As such, the comparison is not fair. To avoid this unfairness, we choose the observed SSTA from the Hadley Center Global Sea Ice and Sea Surface Temperature (HadISST) analyses data sets (Rayner et al. 2003) and the re-analysis thermocline depth from the NOAA NCEP EMC CMB Pacific (Behringer et al. 1998), whose grid points possess much higher resolutions and do not match those in the Zebiak–Cane model. We assimilate them in the SASST and TAO/TRITON arrays and compare the updated forecasts with the observed El Niño events described by the HadISST and re-analysis thermocline depth. Here, because of the disunion grid points between assimilated observations and the TAO/TRITON and the output of the Zebiak–Cane model, the bilinear interpolation has to be adopted and certainly brings about additional initial errors when assimilations occurring in both SASST and TAO/TRITON arrays. Thus the comparison between the updated forecasts with assimilation in SASST and TAO/TRITON arrays becomes much fair. The comparison demonstrates that the mean of the prediction errors is smaller and the mean of the similarity coefficients is slightly higher for the updated forecast with assimilation in the SASST than for those with assimilation in the area covered by TAO/TRITON array (Fig. 12a, b). Meanwhile, considering that the observations of the SASST are 18 ones less than those of TAO/TRITON array, we conclude that the target observations in the SASST is more important than those in the TAO/TRITON array for improving two types of El Niño prediction skills. And the SASST could represent the optimal observational array for tropical SST associated with the improvement of two types of El Niño events predictions skill. This indicates that the TAO/TRITON array should be optimized, practically for the requirement of two types of El Niño events predictions.
The Box–Whisker plot of the skills of the updated forecast when data assimilations made in the SASST and the area covered by the TAO/TRITON arrays. a The prediction errors; b the similarity coefficients. The bold black lines represent the medians of the prediction errors for seven El Niño events predictions with different start months and the red dots represent the means
6 Summary and discussion
In this study, we correct the model errors of the Zebiak–Cane model by applying the OFV approach, and successfully reproduce three EP- and five CP-El Niño events. Based on these eight reproduced El Niño events, we investigate the OGEs of EP- and CP-El Niño events by using the CNOP approach and explore the sensitive areas for target observations for two types of El Niño events. It is found that the OGEs present similar dipolar structures for different start months of predictions while the regions with large errors for their SSTA components exhibit different zonal positions. Specifically, with the start months changing from January through April and July to October, the regions of large errors tend to move westward. The regions of large errors for OGEs are shown to be the sensitive area for target observations, i.e., the area that the additional observations should be preferentially deployed (Duan and Hu 2016; Hu and Duan 2016; Tian and Duan 2016; Mu et al. 2014; Yu et al. 2012). Therefore, the result indicates that the sensitive areas for targeting observations associated with two types of El Niño events are dependent of the start months. Keep these in mind, we propose a quantitative frequency method to determine the sensitive areas for target observation. For such sensitive areas, we expect related target observations to be useful in improving the skills of the predictions with different start months and also applicable to both types of El Niño events predictions. It is found that the identified sensitive areas look like a reversal triangle locating in the eastern Pacific, specifically the area of 120°W–85°W, 0°–11°S; and then extend to the west along the equator and gather at the western boundary and the 180° longitude.
Several groups of “hindcast” experiments are used to examine the validity of the sensitive areas-related target “observations” in improving the prediction skill for two types of El Niño events. It is shown that the sensitive areas identified by the quantitative frequency method, compared with other areas, can present the additional observations that help to improve much significantly the skill of two types of El Niño events predictions with different start months. Furthermore, such additional observations, when compared with the TAO/TRITON array, show to be more potential for selecting the El Niño type in predictions. It is indicated that the observational array described by the sensitive areas in the present study is superior to the TAO/TRITON array and represents the optimal observational array for improving the forecast skill of two types of El Niño events. This suggests that the TAO/TRITON array should be optimized to be applicable for distinguishing the types of El Niño in predictions.
The sensitive area for target observations identified in the present study emphasizes the importance of both the eastern and western equatorial Pacific SSTA. Morss and Battisti (2004a, b) also suggested that for ENSO forecasting the most important and secondary important area for observations are the eastern and western equatorial Pacific respectively. However, they only focused on the EP-El Niño predictions while the present study showed that both the eastern and western equatorial Pacific SSTA are also important for the CP-El Niño predictions. Especially, in the present study, we show that when the 1-year lead time forecasts are made to the EP- and CP-El Niño events and initialized in January and April (July and October), they mainly experience the growth phase (decay phase) of El Niño events and exhibit the stronger sensitivity of two types of El Niño predictions on tropical eastern (western) Pacific initial SSTA field. This reveals that the tropical eastern Pacific SSTA observations are much important for predictions bestriding the growth phase for two types of El Niño while the tropical western Pacific SSTA is much useful for predictions through the decay phase for El Niño.
With the assumption of perfect model, Tian and Duan (2016) argued that the EP-El Niño events are more likely to occur a spring predictability barrier than the CP-El Niño events. In the present study, it can be seen from Figs. 8 and 10 that the benefit of prediction skills for the CP-El Niño events is more obvious than that of the EP-El Niño events when improving the initial state in the sensitive areas. All these may suggest that the EP-El Niño events are less predictable than the CP-El Niño events when only considering the effect of initial errors. Luo et al. (2008) also reported that the CP-El Niño event during 2004/2005 is more predictable than the strong EP-El Niño event during 1997/1998. Recently, Duan et al. (2017) showed that the nonlinearity presents more influences in EP-El Niño than in CP-El Niño, which may cause more irregularities in EP-El Niño and then limit the predictability of EP-El Niño much more. There also exist a few studies that performed seasonal prediction experiments and argued that the CP-El Niño present much lower forecast skill than the EP-El Niño (Jeong et al. 2012; Imada et al. 2015; Luo et al. 2016; Zheng and Yu 2017). In fact, these studies did not separate the impact of initial errors and model errors and are hardly regarded as evidence that CP-El Niño is less predictable than EP-El Niño. Of course, it should be further explored whether or not CP-El Niño is indeed more predictable than EP-El Niño. It is expected that the results can provide useful information on improving the prediction skill for two types of El Niño events.
This paper did not consider La Niña and neutral years. In fact, La Nina is almost mirrored with EP-El Niño and they are controlled by the same feedback mechanisms such as the delayed oscillator (Suarez and Schopf 1988) or recharge oscillator (Jin 1997). It is therefore inferred that the sensitive areas for target observations for EP-El Niño and La Niña are similar and the observational array SASST revealed in the present study is also useful for La Nina predictions. When mentioning to the neutral years, previous studies showed the similarity between the optimal precursors (OPRs) and the OGEs of El Niño (Mu et al. 2014; Duan and Hu 2016). Here, the so-called OPR is the initial perturbations that are superimposed to neutral states and can trigger an El Niño event. And the similarity between OPRs and OGEs indicates that the sensitive areas for target observations associated with the predictions of neutral years are similar to those of El Niño.
The present study suggests that the existing TAO/TRITON array should be further optimized to satisfy the requirement of two types of El Niño events predictions. In fact, after working persistently for over 20 years, the TAO/TRITON array has partially collapsed (Cravatte et al. 2015). Meanwhile, the appearance of CP-El Niño poses new challenges for the tropical Pacific Observing System (TPOS). Under this background, a new international program called TPOS-2020 has been established to redesign and optimize the tropical Pacific observation network, aiming to meet both the needs of climate change and operational forecasting systems (Cravatte et al. 2015). We expect that the present study is useful for the establishment of TPOS-2020.
References
An S-I, Jin F-F (2004) Nonlinearity and asymmetry of ENSO. J Clim 17:2399–2412
Ashok K, Behera SK, Rao SA, Weng H, Yamagata T (2007) El Niño Modoki and its possible teleconnection. J Geophys Res Oceans 112:C11007
Barkmeijer J, Iversen T, Palmer T (2003) Forcing singular vectors and other sensitive model structures. Q J R Meteorol Soc 129:2401–2423
Barnston AG, Tippett MK, L’Heureux ML, Li S, DeWitt DG (2012) Skill of real-time seasonal ENSO model predictions during 2002–11: is our capability increasing? Bull Am Meteorol Soc 93:631–651
Behringer DW, Ji M, Leetmaa A (1998) An improved coupled model for ENSO prediction and implications for ocean initialization. Part I: the ocean data assimilation system. Mon Weather Rev 126(4):1013–1021
Bergot T (1999) Adaptive observations during FASTEX: A systematic survey of upstream flights. Q J R Meteorol Soc 125:3271–3298
Birgin EG, Martínez JM, Raydan M (2000) Nonmonotone spectral projected gradient methods on convex sets. SIAM J Optim 10:1196–1211. https://doi.org/10.1137/s1052623497330963
Bishop CH, Toth Z (1999) Ensemble transformation and adaptive observations. J Atmos Sci 56:1748–1765
Bishop CH, Etherton BJ, Majumdar SJ (2001) Adaptive sampling with the ensemble transform Kalman filter. Part I: theoretical aspects. Mon Weather Rev 129:420–436
Blumenthal MB (1991) Predictability of a coupled ocean–atmosphere model. J Clim 4:766–784
Bourassa MA, Smith SR, O Brien JJ (2001) A new FSU winds and flux climatology. World Meteorological Organization-Publications-WMO TD, Geneva, pp 41–44
Buizza R (1994) Sensitivity of optimal unstable structures. Q J R Meteorol Soc 120:429–451
Chen D, Cane MA (2008) El Niño prediction and predictability. J Comput Phys 227:3625–3640
Chen G, Tam CY (2010) Different impacts of two kinds of Pacific Ocean warming on tropical cyclone frequency over the western North Pacific. Geophys Res Lett 37:L01803
Chen D, Zebiak SE, Busalacchi AJ, Cane MA (1995) An improved procedure for El Niño forecasting: implications. for predictability. Science 269:1699
Chen D, Cane MA, Kaplan A, Zebiak SE, Huang D (2004) Predictability of El Niño over the past 148 years. Nature 428:733–736
Cravatte S, Ganachaud A, Dewitte B, Hernandez F (2015) TPOS2020: tropical pacific observing system for 2020 editorial—May 2015—special issue jointly coordinated by Mercator Ocean and Coriolis focusing on Ocean Observations
Dai G, Mu M, Jiang Z (2016) Relationships between optimal precursors triggering NAO onset and optimally growing initial errors during NAO prediction. J Atmos Sci 73:293–317
Duan W, Hu J (2016) The initial errors that induce a significant “spring predictability barrier” for El Niño events and their implications for target observation: results from an earth system model. Clim Dyn 46:3599–3615
Duan W, Wei C (2012) The ‘spring predictability barrier’ for ENSO predictions and its possible mechanism: results from a fully coupled model. Int J Climatol 10:1002
Duan W, Xu H, Mu M (2008) Decisive role of nonlinear temperature advection in El Niño and La Niña amplitude asymmetry. J Geophys Res Oceans 113:C01014
Duan W, Liu X, Zhu K, Mu M (2009) Exploring the initial errors that cause a significant “spring predictability barrier” for El Niño events. J Geophys Res Oceans 114:C06018
Duan W, Tian B, Xu H (2014) Simulations of two types of El Niño events by an optimal forcing vector approach. Clim Dyn 43:1677–1692
Duan W, Huang C, Xu H (2017) Nonlinearity modulating intensities and spatial structures of central Pacific and eastern Pacific El Niño events. Adv Atmos Sci 34:737–756. https://doi.org/10.1007/s00376-017-6148-9
Feng F, Duan WS (2013) The role of constant optimal forcing in correcting forecast models. Sci China Earth Sci 56(3):434–443
Feng R, Duan W, Mu M (2014) The “winter predictability barrier” for IOD events and its error growth dynamics: results from a fully coupled GCM. J Geophys Res Oceans 119:8688–8708
Fiorino M, Elsberry RL (1989) Some aspects of vortex structure related to tropical cyclone motion. J Atmos Sci 46:975–990. https://doi.org/10.1175/1520-0469(1989)046<0975:saovsr>2.0.co;2
Ham Y-G, Kug J-S (2012) How well do current climate models simulate two types of El Niño? Clim Dyn 39:383–398
Ham Y-G, Kug J-S (2015) Improvement of ENSO simulation based on intermodel diversity. J Clim 28:998–1015
Hendon HH, Lim E, Wang G, Alves O, Hudson D (2009) Prospects for predicting two flavors of El Niño. Geophys Res Lett 36:L19713
Hu J, Duan W (2016) Relationship between optimal precursory disturbances and optimally growing initial errors associated with ENSO events: Implications to target observations for ENSO prediction. J Geophys Res Oceans 121:2901–2917
Huang L, Meng Z (2014) Quality of the target area for metrics with different nonlinearities in a mesoscale convective system. Mon Weather Rev 142:2379–2397. https://doi.org/10.1175/mwr-d-13-00244.1
Imada Y, Tatebe H, Ishii M et al (2015) Predictability of two types of El Niño assessed using an extended seasonal prediction system by MIROC. Mon Weather Rev 143:4597–4617. https://doi.org/10.1175/MWR-D-15-0007.1
Jeong H-I et al (2012) Assessment of the APCC coupled MME suite in predicting the distinctive climate impacts of two flavors of ENSO during boreal winter. Clim Dyn 39:475–493. https://doi.org/10.1007/s00382-012-1359-3
Jin FF (1997) An equatorial ocean recharge paradigm for ENSO. Part I: conceptual model. J Atmos Sci 54(7):811–829
Jin FF, Lin L, Timmermann A, Zhao J (2007) Ensemble-mean dynamics of the ENSO recharge oscillator under state-dependent stochastic forcing. Geophys Res Lett 34:L03807. https://doi.org/10.1029/2006GL027372
Jin EK et al (2008) Current status of ENSO prediction skill in coupled ocean–atmosphere models. Clim Dyn 31:647–664
Kao H-Y, Yu J-Y (2009) Contrasting eastern-Pacific and central-Pacific types of ENSO. J Clim 22:615–632
Keenlyside NS, Latif M, Botzet M, Jungclaus J, Schulzweida U (2005) A coupled method for initializing El Niño-Southern Oscillation forecasts using sea surface temperature. Tellus 57A:340–356
Kim ST, Yu JY (2012) The two types of ENSO in CMIP5 models. Geophys Res Lett 39:L11704
Kim ST, Yu J-Y, Kumar A, Wang H (2012) Examination of the two types of ENSO in the NCEP CFS model and its extratropical associations. Mon Weather Rev 140:1908–1923
Kug J-S, Jin F-F, An S-I (2009) Two types of El Niño events: cold tongue El Niño and warm pool El Niño. J Clim 22:1499–1515
Kug J-S, Ham Y-G, Lee J-Y, Jin F-F (2012) Improved simulation of two types of El Niño in CMIP5 models. Environ Res Lett 7:034002
Langland RH et al (1999) The North Pacific Experiment (NORPEX-98): targeted observations for improved North American weather forecasts. Bull Am Meteorol Soc 80:1363–1384
Liu J, Kalnay E (2008) Estimating observation impact without adjoint model in an ensemble Kalman filter. Q J R Meteorol Soc 134:1327–1335
Liu DC, Nocedal J (1989) On the limited memory BFGS method for large scale optimization. Math Program 45:503–528
Lorenz EN (1975) Climate predictability vol Appendix 2.1. Global Atmospheric Research Programme Publication Series. World Meteorology Organization, Geneva
Luo J-J, Masson S, Behera SK, Yamagata T (2008) Extended ENSO predictions using a fully coupled ocean–atmosphere model. J Clim 21:84–93. https://doi.org/10.1175/2007jcli1412.1
Luo J-J, Yuan C-X, Sasaki W et al (2016) Current status of intraseasonal-seasonal-to-interannual prediction of the Indo-Pacific climate. In: Yamagata T, Behera S (eds) The indo-Pacific climate variability and predictability. The World Scientific Publisher, Singapore. https://doi.org/10.1142/9789814696623_0003
Marathe S, Ashok K, Swapna P, Sabin T (2015) Revisiting El Niño Modokis. Clim Dyn 45:3527
McPhaden MJ et al (1998) The tropical ocean-global atmosphere observing system: a decade of progress. J Geophys Res Oceans 103:14169–14240
McPhaden M, DelcR indicesx T, Hanawa K, Kuroda Y, Meyers G et al (2001) The El Niño/Southern Oscillation (ENSO) observing system, observing the ocean in the 21st century, Australian Bureau of Meteorology, Melbourne
Moore AM, Kleeman R (1996) The dynamics of error growth and predictability in a coupled model of. ENSO Q J R Meteorol Soc 122:1405–1446
Morss RE, Battisti DS (2004a) Designing efficient observing networks for ENSO prediction. J Clim 17:3074–3089. 10.1175/1520-0442(2004)017<3074:deonfe>2.0.co;2
Morss RE, Battisti DS (2004b) Evaluating observing requirements for ENSO prediction: experiments with an intermediate coupled model. J Clim 17:3057–3073. 10.1175/1520-0442(2004)017<3057:eorfep>2.0.co;2
Mu M (2013) Methods, current status, and prospect of targeted observation. Sci China Earth Sci 56:1997–2005
Mu M, Duan W, Wang B (2003) Conditional nonlinear optimal perturbation and its applications Nonlinear. Processes in Geophysics 10:493–501
Mu M, Xu H, Duan W (2007) A kind of initial errors related to “spring predictability barrier” for El Niño events in Zebiak–Cane model Geophys Res Lett 34:L03709
Mu M, Zhou F, Wang H (2009) A method for identifying the sensitive areas in targeted observations for tropical cyclone prediction: conditional nonlinear optimal perturbation. Mon Weather Rev 137:1623–1639. https://doi.org/10.1175/2008mwr2640.1
Mu M, Yu Y, Xu H, Gong T (2014) Similarities between optimal precursors for ENSO events and optimally growing initial errors in El Niño predictions. Theor Appl Climatol 115:461–469. https://doi.org/10.1007/s00704-013-0909-x
Mu M, Duan W, Chen D, Yu W (2015) Target observations for improving initialization of high-impact ocean-atmospheric environmental events forecasting. Natl Sci Rev 2:226–236
Palmer T, Gelaro R, Barkmeijer J, Buizza R (1998) Singular vectors, metrics, and adaptive observations. J Atmos Sci 55:633–653
Powell MJD (1983) VMCWD: a Fortran subroutine for constrained optimization. SIGMAP Bull 4:16. https://doi.org/10.1145/1111272.1111273
Press WH, Teukolsky SA, Vetterling WT, Flannery BP (1992) Numerical recipes in FORTRAN: the art of scientific computing, 2nd edn. Cambridge University Press, Cambridge, p 963
Qin X, Mu M (2012) Influence of conditional nonlinear optimal perturbations sensitivity on typhoon track forecasts. Q J R Meteorol Soc 138:185–197
Qin X, Duan W, Mu M (2013) Conditions under which CNOP sensitivity is valid for tropical cyclone adaptive observations. Q J R Meteorol Soc 139:1544–1554
Rayner N et al (2003) Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J Geophys Res Atmos 108:4407
Ren HL, Jin FF (2011) Niño indices for two types of ENSO. Geophys Res Lett 38:L04704. https://doi.org/10.1029/2010GL046031
Suarez MJ, Schopf PS (1988) A delayed action oscillator for ENSO. J Atmos Sci 45(21):3283–3287
Synder C (1996) Summary of an informal workshop on adaptive observations and. FASTEX Bull Am Meteorol Soc 77:953–961
Tang Y, Deng Z, Zhou X, Cheng Y, Chen D (2008) Interdecadal variation of ENSO predictability in multiple models. J Clim 21:4811–4833
Thompson C (1998) Initial conditions for optimal growth in a coupled ocean–atmosphere model of ENSO. J Atmos Sci 55:537–557
Tian B, Duan W (2016) Comparison of the initial errors most likely to cause a spring predictability barrier for two types of El Niño events. Clim Dyn 47:779–792
Tsyrulnikov MD (2005) Stochastic modelling of model errors: a simulation study. Q J R Meteorol Soc 131:3345–3371. https://doi.org/10.1256/qj.05.19
Wang Q, Mu M, Dijkstra HA (2013) The similarity between optimal precursor and optimally growing initial error in prediction of Kuroshio large meander and its application to targeted observation. J Geophys Res Oceans 118:869–884
Weng H, Ashok K, Behera SK, Rao SA, Yamagata T (2007) Impacts of recent El Niño Modoki on dry/wet conditions in the Pacific rim during boreal summer. Clim Dyn 29:113–129
World Climate Research Program (1985) Scientific plan for the Tropical Ocean and Global Atmosphere Program, technical document WMOfTD-6J. World Meteorological Organization, Geneva
Wu C-C, Chen J-H, Lin P-H, Chou K-H (2007) Targeted observations of tropical cyclone movement based on the adjoint-derived sensitivity steering vector. J Atmos Sci 64:2611–2626
Xue Y, Cane M, Zebiak S, Blumenthal M, Earth L-D (1994) On the prediction of ENSO: a study with a. low-order. Tellus 46:512–528
Xue Y, Cane M, Zebiak S (1997a) Predictability of a coupled model of ENSO using singular vector analysis. Part I: optimal growth in seasonal background and ENSO cycles. Mon Weather Rev 125:2043–2056
Xue Y, Cane M, Zebiak S, Palmer T (1997b) Predictability of a coupled model of ENSO using singular vector analysis. Part II: optimal growth and forecast skill. Mon Weather Rev 125:2057–2073
Yeh S-W, Kug J-S, Dewitte B, Kwon M-H, Kirtman BP, Jin F-F (2009) El Niño in a changing climate. Nature 461:511–514
Yu J-Y, Kim S-T (2013) Identifying the types of major El Niño events since 1870. Int J Climatol 33:2105–2112. https://doi.org/10.1002/joc.3575
Yu Y, Duan W, Xu H, Mu M (2009) Dynamics of nonlinear error growth and season-dependent predictability of El Niño events in the Zebiak–Cane model. Q J R Meteorol Soc 135:2146
Yu Y, Mu M, Duan W, Gong T (2012) Contribution of the location and spatial pattern of initial error to uncertainties in El Niño predictions. J Geophys Res Oceans 117:L03709
Zebiak SE, Cane MA (1987) A model El Niñ-Southern Oscillation. Mon Weather Rev 115:2262–2278
Zheng F, Yu J-Y (2017) Contrasting the skills and biases of deterministic predictions for the two types of El Niño. Adv Atmos Sci. https://doi.org/10.1007/s00376-017-6324-y
Zheng F, Zhu J (2016) Improved ensemble-mean forecasting of ENSO events by a zero-mean stochastic error model of an intermediate coupled model. Clim Dyn 47:3901–3915. https://doi.org/10.1007/s00382-016-3048-0
Zheng F, Zhu J, Zhang R-H, Zhou G-Q (2006) Ensemble hindcasts of SST anomalies in the tropical Pacific using an intermediate coupled model. Geophys Res Lett 33:L19604. https://doi.org/10.1029/2006GL026994
Zheng F, Zhu J, Zhang R-H (2007) The impact of altimetry data on ENSO ensemble initializations and predictions. Geophys Res Lett 34:L13611. https://doi.org/10.1029/2007GL030451
Zhou F, Mu M (2011) The impact of verification area design on tropical cyclone targeted observations based on the CNOP method. Adv Atmos Sci 28:997–1010
Zhu J, Kumar A, Lee H-C, Wang H (2017) Seasonal predictions using a simple ocean initialization scheme. Clim Dyn. https://doi.org/10.1007/s00382-017-3556-6 (published online)
Acknowledgements
The authors are very grateful for the useful comments provided by the two anonymous reviewers. This work was jointly sponsored by the National Natural Science Foundation of China (Grant nos. 41525017, 41230420, 41690124 and 41606019), and National Programme on Global Change and Air-Sea Interaction (GASI-IPOVAI-06).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Duan, W., Li, X. & Tian, B. Towards optimal observational array for dealing with challenges of El Niño-Southern Oscillation predictions due to diversities of El Niño. Clim Dyn 51, 3351–3368 (2018). https://doi.org/10.1007/s00382-018-4082-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-018-4082-x