Data envelopment analysis for scale elasticity measurement in the stochastic case: with an application to Indian banking

Abstract

In the nonparametric data envelopment analysis literature, scale elasticity is evaluated in two alternative ways: using either the technical efficiency model or the cost efficiency model. This evaluation becomes problematic in several situations, for example (a) when input proportions change in the long run, (b) when inputs are heterogeneous, and (c) when firms face ex-ante price uncertainty in making their production decisions. To address these situations, a scale elasticity evaluation was performed using a value-based cost efficiency model. However, this alternative value-based scale elasticity evaluation is sensitive to the uncertainty and variability underlying input and output data. Therefore, in this study, we introduce a stochastic cost-efficiency model based on chance-constrained programming to develop a value-based measure of the scale elasticity of firms facing data uncertainty. An illustrative empirical application to the Indian banking industry comprising 71 banks for eight years (1998–2005) was made to compare inferences about their efficiency and scale properties. The key findings are as follows: First, both the deterministic model and our proposed stochastic model yield distinctly different results concerning the efficiency and scale elasticity scores at various tolerance levels of chance constraints. However, both models yield the same results at a tolerance level of 0.5, implying that the deterministic model is a special case of the stochastic model in that it reveals the same efficiency and returns to scale characterizations of banks. Second, the stochastic model generates higher efficiency scores for inefficient banks than its deterministic counterpart. Third, public banks exhibit higher efficiency than private and foreign banks. Finally, public and old private banks mostly exhibit either decreasing or constant returns to scale, whereas foreign and new private banks experience either increasing or decreasing returns to scale. Although the application of our proposed stochastic model is illustrative, it can be potentially applied to all firms in the information and distribution-intensive industry with high fixed costs, which have ample potential for reaping scale and scope benefits.

Introduction

Performance analysis of multi-product firms has been conducted using several economic concepts, such as economies of scale (returns to scale), economies of scope, and marginal rates of technical substitutions. However, this study concentrates on the determination and measurement of returns to scale, as it has important implications for policy design and industry regulation. Scale elasticity is a quantitative measure of the returns-to-scale characterization of a firm¹ operating on the production frontier, and is used to determine improvement or deterioration in productivity by resizing their scales of operation.

In the literature, there are two analytical approaches to the empirical estimation of scale elasticity: the neoclassical and axiomatic approaches (Färe et al. 1988). While the former is usually estimated using parametric techniques such as stochastic frontier analysis (SFA), the latter is estimated nonparametric via data envelopment analysis (DEA). However, DEA² has distinct advantages over stochastic frontier estimation (Sahoo and Tone 2022). First, DEA avoids the choice of specific functional forms and the choice of the stochastic structure, which the stochastic frontier approach suffers from due to which it can confound the effects of misspecification of functional form with scale economies (Fusco et al. 2018; Sahoo and Acharya 2010; Sahoo et al. 2017; Sahoo and Gstach 2011). Second, contrary to the general belief, DEA is a full-fledged statistical methodology based on the characterization of firm efficiency as a stochastic variable. DEA estimators have desirable properties and provide a basis for constructing a wide range of formal statistical tests (Banker 1993; Banker and Natarajan 2004; Banker et al. 2022). Third, DEA reflects individual firm efficiency or inefficiency, which is particularly convenient for managerial decision making.

In the DEA literature, both qualitative and quantitative approaches are used to evaluate the returns-to-scale characterization of firms. While the former deals with the identification of the types of returns to scale (i.e., increasing, decreasing, or constant), the latter deals with the computation of scale elasticity (Førsund 1996; Sahoo et al. 1999, 2012; Tone and Sahoo 2003, 2004; Podinovski et al. 2009; Sahoo and Sengupta 2014; Sahoo and Tone 2015). Most studies that apply bespoke computational methods to evaluate scale economies are confined to specific DEA technologies under the constant returns to scale (CRS) specification of Charnes et al. (1978) and the variable returns to scale (VRS) specification of Banker et al. (1984). However, there is a large class of polyhedral technologies that include CRS and VRS technologies with production trade-offs and weight restrictions (Tone 2001; Atici et al. 2015; Podinovski 2004a; 2007, 2015, 2016), and weak and managerially disposable technologies (Kuosmanen 2005; Kuosmanen and Podinovski. 2009), hybrid returns to scale (Podinovski 2004b), technology with multiple component processes (Cook and Zhu 2011; Cherchye et al. 2013, 2015, 2016), and network technologies (Sahoo et al. 2014a, b), etc. See Podinovski et al. (2016) for a discussion of scale elasticity evaluation using a more general methodology.

Scale elasticity evaluation was also performed using the cost efficiency model of Färe et al. (1985) (Sueyoshi 1997; Tone and Sahoo 2005, 2006). The use of this model requires that input prices are exogenously given and measured with full certainty. However, in real-life situations, input prices are not exogenous but vary according to the actions of firms (Sahoo and Tone 2013). In addition, firms often face ex-ante price uncertainty³ when making production decisions (Camanho and Dyson 2005). Furthermore, input prices are synthetically constructed and hence represent average prices. Since decisions are made at the margin, the measure of allocative efficiency based on average prices can be distorted (Fukuyama and Weber 2008). Finally, the cost efficiency measure of Färe et al. (1985) reflects only input inefficiencies, but not market (price) inefficiencies (Camanho and Dyson 2008).⁴ Therefore, to account for both input and market inefficiencies, Tone’s (2002) alternative cost-efficiency model can be used. Furthermore, the use of this value-based technology is more appropriate for computing the scale elasticity scores of real-life firms in several situations, for example (a) when input proportions change in the long run, (b) when inputs are heterogeneous, and (c) as the cost can be more easily related to economies of scale and size-specific costs due to indivisibility.

Scale elasticity evaluation in DEA has thus far been made using only deterministic technologies. These technologies were developed based on the premise that the inputs and outputs are precisely measured. However, in real-life situations, general production processes are often stochastic,⁵ and the concepts of efficiency and scale elasticity are inextricably related to how firms deal with uncertainty underlying stochastic inputs and outputs. Therefore, when there are variations in inputs and outputs owing to uncertainty, the evaluation of efficiency and scale elasticity in a deterministic DEA setting becomes sensitive to such variations. Consequently, one expects to observe whether the efficiency and returns-to-scale characteristics of firms are subject to change in this stochastic environment.

To account for random variations in inputs and outputs underlying any production process, several authors (Banker and Morey 1986; Cooper et al. 2004, 2011, 1996, 1998; Jess et al. 2001; Lamb and Tee 2012; Olesen 2006; Sengupta 1990) have considered various approaches in DEA setting to compute efficiency. Sengupta (1982) and Cooper et al. (1996) were the first to introduce the theory of chance constraints in DEA to formulate an efficiency evaluation for firms. This formulation was later extended by several scholars (Sengupta and Sfeir 1988; Land et al. 1993, 1994; Li 1995a, b, 1998; Olesen and Petersen 1995, 2000; Grosskopf 1996; Morita and Seiford 1999; Huang and Li 2001; Kao and Liu 2014; Wei et al. 2014). Cooper et al. (2011), Simar and Wilson (2015), and Olesen and Petersen (2016) provided extensive reviews of the development of various stochastic DEA models.

To the best of our knowledge, no studies in the DEA literature has dealt with the estimation of scale elasticity using a technology setup that allows such stochastic variations in the data. Therefore, in this study, we focus on the estimation of scale elasticity when inputs and outputs are uncertain in stochastic form. The existence of random changes in the data permits the prediction of changes in the inputs and outputs. Because deterministic programs are sensitive to such variations, we need the technique of chance-constrained (CC) programming⁶ (see Charnes and Cooper (1959, 1962, 1963) for its early developments) because this method can potentially deal with the cases in which the constraints–the minimal (maximal) inputs (outputs)–are required to be no more (less) than the actual inputs (outputs) may be violated, but not too frequently. Although stochastic variation around the production function is allowed, most observations must fall below it.

To set up value-based measures of efficiency and scale elasticity, first, we formulate, using the CC-programming method, the stochastic version of the alternative cost efficiency model of Tone (2002), which is essentially a quadratic model. Second, we set up a deterministic equivalent of the stochastic quadratic model. Third, with the help of a one-factor assumption, we converted this deterministic quadratic model into a linear model using the goal programming theory of Charnes and Cooper (1977). Fourth, we solved this linear model to compute the value-based efficiency scores of firms at pre-determined tolerance levels of chance constraints. Finally, we set up the dual of this linear model to compute the value-based scale elasticity scores of firms at these tolerance levels.

The method employed to convert the quadratic model into a linear model is based on a simplified single-factor assumption, which has long been used in economics. This single-factor assumption is extremely convenient for finding solutions but requires some additional assumptions that the correlation coefficient between any two stochastic inputs/outputs and between input and output for any firm is always 1 (Kao and Liu 2019). Thus, there is a tradeoff between a quadratic (nonlinear) model, which is inconvenient to solve, and a linear model, which is easy to solve but requires some additional assumptions. However, we believe that this perfect correlation assumption between inputs/outputs is certainly important as it helps convert a quadratic model into a linear one, which not only removes the inconveniences associated with solving a quadratic model, but also helps compute the scale elasticity scores of firms using its dual.

To demonstrate the ready applicability of our proposed model, we exhibited an illustrative empirical application wherein we employ Indian banking data, which was used earlier by Sahoo and Tone (2009a, b). It is important to investigate the extent of economies of scale in the banking industry in general, and the banking industry of a fast-growing economy like India, in particular. The banking industry is technology-driven, and technical progress is scale augmenting (Berger 2003). The evaluation of scale economies in India’s banking industry during the post-reform period from 1998 to 2005 is considered important because this exercise has important implications for policy design and regulation due to changing regulatory environments and different ownership types (public, private, and foreign). The Indian financial sector had initially been operating in a closed and regulated environment until 1992 and then underwent a radical change during the nineties. To promote the efficiency and profitability of banks, in 1991–92 the Reserve Bank of India (RBI) initiated a process of liberalization through various reforms such as entry deregulation, branch de-licensing, deregulation of interest rates, allowing public banks to raise their equity in the capital markets, gradual reduction in cash reserve ratio, statutory liquidity ratio, and relaxation of several restrictions on the composition of their portfolios. All of these have given rise to heightened competitive pressure in the banking industry. In this scenario, we believe that banks were in the pursuit of enlarging their size using available scale economies to enhance their asset base and profit to create systemic financial efficiency and shareholder value. Furthermore, the introduction of several reform measures and technological advances has put the banking industry in a more challenging and volatile position, making the underlying bank production processes stochastic. In this environment, following Shiraz et al. (2018), stochasticity in the inputs and outputs is first introduced, and our proposed stochastic efficiency model is then applied to these stochastic input–output data to produce valid efficiency and scale elasticity estimates.

In our empirical illustration, we examine the efficiency and returns-to-scale characteristics of banking in India across three ownership types: public, private, and foreign. This enables us to investigate the economic linkage between ownership and efficiency performance by considering the property rights hypothesis (De Alessi 1980) and public choice theory (Levy 1987; Niskanen 1975). According to the property rights hypothesis, private enterprises should perform more efficiently than public enterprises because of the strong link between the markets for corporate control and the efficiency of private enterprises. While this argument may apply more to developed countries, testing for efficiency differentials across ownership types in the banking industry of a developing country such as India can yield insights into the success of the reform process.

Although our current empirical application to Indian banking is illustrative, our proposed chance-constraint efficiency model can potentially be applied to analyze the efficiency and scale properties of many real-life firms whose underlying production processes are stochastic. Examples of these firms can be found in many industries, for example agriculture, where unpredictability in weather makes the input–output relationship stochastic; manufacturing industries, where firms face considerable variation in the quality of their inputs and outputs produced; product development industries, where firms face uncertainty regarding their new designs; and high-technology industries, where firms face hyper (dynamic) completion in the new (Internet) economy.

Finally, Fig. 1 depicts the conceptual framework of our investigation, highlighting both the methodological and applied approaches.

Fig. 1

Conceptual framework

The remainder of the paper is organized as follows: “A value-based measure of efficiency and scale elasticity in the deterministic case” section discusses the evaluation of value-based scale elasticity measures in a deterministic DEA technology defined in the cost-output space. In “A value-based measure of TE and SE in the stochastic case” section, we first set up the stochastic version of Tone’s (2002) value-based cost efficiency model and then propose its transformation in a deterministic setting for the computations of value-based measures of efficiency and scale elasticity scores. “The illustrative empirical application” section demonstrates an illustrative empirical application of our proposed stochastic efficiency model to data on 71 banks in India. “Discussions” section presents a discussion of the results. Finally, we conclude with remarks in “Concluding remarks” section, followed by the limitations of our study and future recommendations.

A value-based measure of efficiency and scale elasticity in the deterministic case

We suppose there are $n$ firms to be evaluated and each firm uses $m$ inputs to produce $s$ outputs. Let ${x}_{j} = {\left({x}_{1j} , . . . , {x}_{mj} \right)}^{T}\in {\mathbb{R}}_{\ge 0}^{m}$ and ${y}_{j}={\left({y}_{1j}, . . . , {y}_{sj} \right)}^{T}\in {\mathbb{R}}_{\ge 0}^{s}$ be the input and output vectors of firm$j$, respectively, ${w}_{j}=\left({w}_{1j}, . . . , {w}_{mj}\right)\in {\mathbb{R}}_{\ge 0}^{m}$ be its unit price vector, and $J$ be the index set of all firms, that is, $J = \{1, . . . , n\}$. We set up a value-based technology ${(T}^{V})$ set as

$${T}^{V}=\left\{{\left(c,y\right)}^{T} | \sum_{j=1}^{n}{\lambda }_{j}{c}_{j}\le c, \sum_{j=1}^{n}{\lambda }_{j}{y}_{rj}\ge {y}_{r} (\forall r), \sum_{j=1}^{n}{\lambda }_{j}=1, \lambda \ge 0\right\},$$

(1)

where ${c}_{j}=\sum_{i=1}^{m}{w}_{ij}{x}_{ij}.$ The ${\lambda =(\lambda }_{1}, {\lambda }_{2}, \dots , {\lambda }_{n})$ is an intensity vector of dimension n.

To produce the output vector $\beta {y}_{o}$ by firm $o$, its value-based measure of technical efficiency $(TE)$, $\overline{\alpha }\left(\beta \right)$ is defined as

$$\overline{\alpha }\left(\beta \right)=\mathrm{min} \left\{\alpha \right|\left(\alpha {c}_{o}, \beta {y}_{o}\right)\in {T}^{V}\}.$$

(2)

$\beta$ is a user-defined value that reflects the proportional output change, and $\overline{\alpha }(\beta )$ is defined for all $\beta \in [0,\widehat{\beta }]$, where $\widehat{\beta }$ is the largest proportion of the output vector ${y}_{o}$ found in units of technology ${T}^{V}$.

Based on the definition in (2), $\overline{\alpha }\left(\beta \right)$ can be determined using the following linear program (LP):

$$\overline{\alpha }\left(\beta \right)=\mathrm{min}\alpha$$

(3)

$s.t.$ $\sum_{j=1}^{n}{\lambda }_{j}{c}_{j}\le \alpha {c}_{o},$ $\sum_{j=1}^{n}{\lambda }_{j}{y}_{rj}\ge \beta {y}_{ro} \left(\forall r\right),$ $\sum_{j=1}^{n}{\lambda }_{j}=1,$ ${\lambda }_{j}\ge 0 \left(\forall j\right),\mathrm{ and }\alpha :\mathrm{free}.$

Program (3) was used to identify explicit real peer units for each unit under evaluation. As previously stated, ${\lambda =(\lambda }_{1}, {\lambda }_{2}, \dots , {\lambda }_{n})$ is an intensity vector in which each ${\lambda }_{j}$ shows the effect of ${DMU}_{j}$ on constructing the peer unit for ${DMU}_{o}$ under evaluation.

The dual formulation of the program (3) can be set up as

$$\overline{\alpha }\left(\beta \right)=\mathrm{max} \beta \sum_{r=1}^{s}{u}_{r}{y}_{ro}+{\omega }_{0}$$

(4)

$s. t.$ $\sum_{r=1}^{s}{u}_{r} {y}_{rj}-v{c}_{j}+{\omega }_{0}\le 0,$ $v{c}_{o}=1,$ $v,u\ge 0.$

Based on program (4) for firm $o$, we derive its transformation function as

$$\psi \left(\overline{\alpha }(\beta ){c}_{o}, \beta {y}_{o}\right)=\beta \sum_{r=1}^{s}{u}_{r} {y}_{ro}-v\left(\overline{\alpha }\left(\beta \right){c}_{o}\right)+{\omega }_{0}=0,$$

(5)

We assume that the transformation function (5) is differentiable. Differentiating (5) with respect to $\beta$ yields.

$$\frac{\partial \psi \left(\overline{\alpha }(\beta ){c}_{o}, \beta {y}_{o}\right)}{\partial \beta }=\sum_{r=1}^{s}\frac{\partial \psi \left(\overline{\alpha }(\beta ){c}_{o}, \beta {y}_{o}\right)}{\partial \left(\beta {y}_{ro}\right)}{y}_{ro}+\frac{\partial \psi \left(\overline{\alpha }(\beta ){c}_{o}, \beta {y}_{o}\right)}{\partial \left(\overline{\alpha }(\beta ){c}_{o}\right)}{c}_{o}\frac{\partial \alpha }{\partial \beta }=0,$$

$$\Rightarrow \frac{\partial \overline{\alpha }(\beta )}{\partial \beta }=-\frac{\sum_{r=1}^{s}\frac{\partial \psi \left(\overline{\alpha }(\beta ){c}_{o}, \beta {y}_{o}\right)}{\partial \left(\beta {y}_{ro}\right)}{y}_{ro}}{\frac{\partial \psi \left(\overline{\alpha }(\beta ){c}_{o}, \beta {y}_{o}\right)}{\partial \left(\overline{\alpha }(\beta ){c}_{o}\right)}{c}_{o}}=-\frac{\sum_{r=1}^{s}{u}_{r}{y}_{ro}}{-v{c}_{o}}=\frac{\frac{\overline{\alpha }\left(\beta \right)-{\omega }_{o}}{\beta }}{v{c}_{o}}=\frac{\frac{\overline{\alpha }\left(\beta \right)-{\omega }_{o}}{\beta }}{1}=\frac{\overline{\alpha }\left(\beta \right)-{\omega }_{o}}{\beta }$$

In the spirit of Panzar and Willig (1977), Baumol et al. (1982), and Banker et al. (2004), we define the value-based scale elasticity $(SE)$ measure of firm $o$, $\varepsilon \left(\overline{\alpha }(\beta ){c}_{o}, \beta {y}_{o}\right)$ as the ratio of its marginal utilization of input $\frac{\partial \overline{\alpha }(\beta )}{\partial \beta }$ to its average utilization of input $\frac{\overline{\alpha }(\beta )}{\beta }$. In other words,

$$\varepsilon \left(\overline{\alpha }(\beta ){c}_{o}, \beta {y}_{o}\right)=\frac{\partial \overline{\alpha }(\beta )}{\partial \beta }\bullet \frac{\beta }{\overline{\alpha }\left(\beta \right)}=\frac{\overline{\alpha }\left(\beta \right)-{\omega }_{o}}{\beta }\bullet \frac{\beta }{\overline{\alpha }\left(\beta \right)}=1-\frac{{\omega }_{o}}{\overline{\alpha }\left(\beta \right)}$$

(6)

If the firm $o$ is technically efficient, we have $\beta =\overline{\alpha }\left(\beta \right)=1$ and $\varepsilon \left({c}_{o}, {y}_{o}\right)=1-{\omega }_{o}$.

In the immediately following section, we extend these results to the stochastic case.

A value-based measure of ${\varvec{T}}{\varvec{E}}$ and ${\varvec{S}}{\varvec{E}}$ in the stochastic case

Stochastic value-based ${\varvec{T}}{\varvec{E}}$ measure

Let ${\widetilde{x}}_{j}={\left({\widetilde{x}}_{1j}, {\widetilde{x}}_{2j},\dots ,{\widetilde{x}}_{Mj}\right)}^{T}\in {\mathbb{R}}_{\ge 0}^{m}$ and ${\widetilde{y}}_{j}={\left({\widetilde{y}}_{1j}, {\widetilde{y}}_{2j},\dots ,{\widetilde{y}}_{Sj}\right)}^{T}\in {\mathbb{R}}_{\ge 0}^{s}$ be the random input and output vectors of firm $j$, respectively. Furthermore, let $\left({\widetilde{x}}_{j}\right)=$ ${x}_{j}$, $E\left({\widetilde{y}}_{j}\right)={y}_{j}$, and all random inputs and outputs are jointly and normally distributed. The structure of our stochastic value-based technology set ${(T}^{V(S)})$ in the CC programming setup is related to the technology set employed in the BCC program. ${T}^{V(S)}$ is the union of confidence regions ${D}_{j}\left({1-\gamma }_{j}\right)$ with a probability level $(1-{\gamma }_{j})$ $(j=1,\dots ,n)$. In other words, ${T}^{V(S)}$ is the union of the input and output values that are probably observed for ${DMU}_{j} (j=1,\dots ,n)$ with probability ${1-\gamma }_{j}$. Using the axioms of free disposability, unbounded rays, convexity, minimal extrapolation, and inclusion of observations within confidence regions, ${T}^{V(S)}$ can be set up as follows:

$$\begin{aligned} T^{V\left( S \right)} = & \left\{ {\left( {c,y^{T} } \right)^{T} \in {\mathbb{R}}_{ + }^{1 + S} | \exists \left( {\hat{x}_{j}^{T} , \hat{y}_{j}^{T} } \right)^{T} \in D_{j} \left( {1 - \gamma_{j} } \right) {\text{and }} \lambda_{j} \ge 0, j \in \left\{ {1, \ldots ,n} \right\} {\text{such that}}} \right. \\ & \left. { \mathop \sum \limits_{j = 1}^{n} \lambda_{j} \hat{c}_{j} \le c\, {\text{and}}\; \mathop \sum \limits_{j = 1}^{n} \lambda_{j} \hat{y}_{rj} \ge y_{r} \left( {\forall r} \right), \mathop \sum \limits_{j = 1}^{n} \lambda_{j} = 1} \right\} \\ \end{aligned}$$

(7)

where ${\widehat{c}}_{j}=\sum_{i=1}^{m}{w}_{ij}{\widehat{x}}_{ij}$ and ${D}_{j}\left({1-\gamma }_{j}\right)$ is defined as follows:

$${D}_{j}\left({1-\gamma }_{j}\right)=\left\{{\left({\widehat{x}}^{T},{\widehat{y}}^{T}\right)}^{T}\in {\mathbb{R}}_{+}^{M+S}| \left[{\left(\widehat{x}-{x}_{j}\right)}^{T}, {\left(\widehat{y}-{y}_{j}\right)}^{T}\right]{\Lambda }_{\mathrm{j}}^{-1} {\left[{\left(\widehat{x}-{x}_{j}\right)}^{T}, {\left(\widehat{y}-{y}_{j}\right)}^{T}\right]}^{T}\le {c}_{j}^{2}\right\},$$

(8)

where ${\Lambda }_{j}^{-1}$ represents the inverse of the variance–covariance matrix of $({\widetilde{x}}_{j}, {\widetilde{y}}_{j})$. Moreover, ${c}_{j}$ is determined by ${\mathbb{P}}\left({\chi }_{M+S}^{2}\le {c}_{j}^{2}\right)=1-{\gamma }_{j}$, and ${\chi }_{M+S}^{2}$ is the Chi-square random variable with $M+S$ degrees of freedom.

Inspired by the deterministic value-based $TE$ measure $\overline{\alpha }\left(\beta \right)$ in program (3), we define its stochastic counterpart as the greatest possible radial contraction of ${\widetilde{c}}_{o}$ possible in ${T}^{V(S)}$ to produce $\beta {\widetilde{y}}_{o}$. Mathematically, the stochastic value-based $TE$ measure of firm $o$ can be computed by solving Eq. (9), where $\beta$ is a predefined parameter.

$$\overline{\alpha }\left(\beta \right)=\mathrm{min}\alpha$$

(9)

$$s.t.\;{\mathbb{P}}\left( {\mathop \sum \limits_{j = 1}^{n} \lambda_{j} \tilde{c}_{j} \le \alpha \tilde{c}_{o} } \right) \ge 1 - \gamma ,$$

(9.1)

$${\mathbb{P}}\left(\sum_{j=1}^{n}{\lambda }_{j}{\widetilde{y}}_{rj}\ge \beta {\widetilde{y}}_{ro}\right)\ge 1-\gamma (\forall r),$$

(9.2)

$$\sum_{j=1}^{n}{\lambda }_{j}=1,$$

(9.3)

${\lambda }_{j}\ge 0 \left(\forall j\right),$ and $\alpha :\mathrm{free}.$

In program (9), we used the “E-model” form of the marginal chance-constrained DEA program, which was introduced by Cooper et al. (2002) with the help of the BCC model of Banker et al. (1984). Therefore, we used two separate probability constraints: one for the input cost and the other for the set of outputs.

The objective of program (9) is to measure the stochastic value-based TE of any firm $o$ $(o=\mathrm{1,2},\dots ,n)$ because its input and outputs are all assumed to be stochastic. This is achieved by minimizing the contraction factor $\alpha$ under certain input and output constraints. On the input side, there is a chance constraint, that is, the best-practice (minimum) cost must not exceed the observed cost more than $\gamma \%$ of the time. With regard to the output side, there are chance constraints that each observed output must not exceed its maximum by more than $\gamma \%$ of the time. Finally, there is a convexity constraint, that is, the sum of the intensity coefficients equals 1. $\gamma$ is interpreted as the tolerance level for the chance constraint.

In stochastic efficiency program (9), the random inputs and outputs of firm $j$ are expressed as follows:

$${\widetilde{x}}_{ij}={x}_{ij}+{a}_{ij}{\varepsilon }_{ij} \left(\forall i\right), \mathrm{and} {\widetilde{y}}_{rj}={y}_{rj}+{b}_{rj}{\eta }_{rj} \left(\forall r\right),$$

(10)

where the error terms ${a}_{ij}{\varepsilon }_{ij} \mathrm{and} {b}_{rj}{\eta }_{rj}$ represent the symmetric disturbances of inputs and outputs, respectively, which arise because of factors that are entirely outside the firm’s control. Furthermore, ${\varepsilon }_{ij}$ $\left(\forall i\right)$ and ${\eta }_{rj}$ $\left(\forall r\right)$ are all assumed to follow a multivariate normal distribution, with zero means, that is, $E({\varepsilon }_{ij})=E({\eta }_{rj})=0 \left(\forall i,r\right)$, and unity variances, that is, $Var({\varepsilon }_{ij})=Var({\eta }_{rj})=1 \left(\forall i,r\right)$. Then, for each firm $j (j=1,\dots ,n)$, ${\widetilde{x}}_{ij}\sim N\left({x}_{ij},{a}_{ij}^{2}\right)$ and ${\widetilde{y}}_{rj}\sim N\left({y}_{rj},{b}_{rj}^{2}\right)$, where ${E({\widetilde{x}}_{ij})=x}_{ij}$ $\left(\forall i\right)$, ${E({\widetilde{y}}_{rj})=y}_{ij}$ $\left(\forall r\right)$, $Var({\widetilde{x}}_{ij})={a}_{ij}^{2}$ $\left(\forall i\right)$, and $Var\left({\widetilde{y}}_{rj}\right)={b}_{rj}^{2}$ $\left(\forall r\right)$.

The firm-specific symmetric disturbance terms—${\varepsilon }_{ij}$ $\left(\forall i\right)$ and ${\eta }_{rj}$ $\left(\forall r\right)$ allow the technology set and its resulting efficiency frontier to vary arbitrarily across firms and capture the presence of measurement and specification errors, if any, in the data. It is also important to note that these errors vary with the confidence level specified by the user.

Using the CC-programming theory, Land et al. (1993, 1994) proposed a method to transform the stochastic efficiency program (9) into a nonlinear programming (NLP) problem. However, solving this NLP problem requires information on a substantial number of parameters in the covariance matrix between the input and output components. Therefore, to reduce the computational time involved in the estimation of such parameters, Cooper et al. (1996) suggested a linearization method using a simplified assumption that the components of the inputs and outputs are related only through a common relationship with a single factor, which has long been used in economics (Sharpe 1963; Kahane 1977; Huang and Li 1996, 2001; Li 1995a, b, 1998; Li and Huang 1996. Following Cooper et al. (1996), we use this single-factor assumption in our proposed stochastic approach. In other words, ${\widetilde{x}}_{ij}={x}_{ij}+{a}_{ij}\varepsilon \left(\forall i\right)$ and ${\widetilde{y}}_{rj}={y}_{rj}+{b}_{rj}\varepsilon \left(\forall r\right)$ where $\varepsilon$ is a standard normal random variable with mean $E\left(\varepsilon \right)=0$ and a constant (finite) standard deviation $\sigma (\varepsilon )$.

The use of the single-factor assumption for linearization is not free. This simplifying assumption, as Cooper et al. (1996) rightly pointed out, requires further assumptions in the resulting linear program that the correlation coefficient between any two stochastic inputs/outputs, and between input and output, for any firm $j$ is always 1, that is, $\rho \left({\widetilde{{\varvec{x}}}}_{pj}, {\widetilde{{\varvec{x}}}}_{qj}\right)=1$ ($p\ne q)$, $\rho \left({\widetilde{{\varvec{y}}}}_{rj}, {\widetilde{{\varvec{y}}}}_{sj}\right)=1$ ($r\ne s)$, and $\rho \left({\widetilde{{\varvec{x}}}}_{pj}, {\widetilde{{\varvec{y}}}}_{sj}\right)=1$, which may not be easy to meet in practical applications. However, we believe that this convenient unit correlation coefficient assumption is important as it helps convert an NLP problem into an LP problem, which not only removes the inconveniences associated with solving an NLP problem but also helps one, as we will show later, compute the $SE$ behavior of firms using its dual.

Using the single factor assumption, we express, for each firm j ($j=1,\dots ,n)$, the constraint (9.1) as follows:

$$\begin{aligned} \tilde{h} = & \mathop \sum \limits_{j = 1}^{n} \lambda_{j} \left( {\mathop \sum \limits_{i = 1}^{m} w_{io} \tilde{x}_{ij} } \right) - \alpha \mathop \sum \limits_{i = 1}^{m} w_{io} \tilde{x}_{io} \\ = & \mathop \sum \limits_{j = 1}^{n} \lambda_{j} \left( {\mathop \sum \limits_{i = 1}^{m} w_{io} \left( {x_{ij} + a_{ij} {\tilde{\varepsilon }}} \right) } \right) - \alpha \mathop \sum \limits_{i = 1}^{m} w_{io} \left( {x_{io} + a_{io} {\tilde{\varepsilon }}} \right) \\ = & \mathop \sum \limits_{j = 1}^{n} \lambda_{j} \left( {\mathop \sum \limits_{i = 1}^{m} w_{io} x_{ij} } \right) + \mathop \sum \limits_{j = 1}^{n} \lambda_{j} \left( {\mathop \sum \limits_{i = 1}^{m} w_{io} a_{ij} {\tilde{\varepsilon }}} \right) - \alpha \mathop \sum \limits_{i = 1}^{m} w_{io} x_{io} - \alpha \mathop \sum \limits_{i = 1}^{m} w_{io} a_{io} {\tilde{\varepsilon }} \\ \end{aligned}$$

Hence, we can see that $\widetilde{h}\sim N\left(\sum_{j=1}^{n}{\lambda }_{j}\left(\sum_{i=1}^{m}{w}_{io}{x}_{ij}\right)-\alpha \sum_{i=1}^{m}{w}_{io}{x}_{io}, {\left(\sum_{j=1}^{n}{\lambda }_{j}\left(\sum_{i=1}^{m}{w}_{io}{a}_{ij}\right)-\alpha \sum_{i=1}^{m}{w}_{io}{a}_{io}\right)}^{2}\right) .$

Now, consider a new variable $\widetilde{z}=\frac{\widetilde{h}-E(\widetilde{h})}{{\sigma }_{\widetilde{h}}}$ that follows a standard normal distribution. As per the Central Limit Theorem, we have ${\mathbb{P}}\left(\widetilde{z}\le \frac{-\left(\sum_{j=1}^{n}{\lambda }_{j}\left(\sum_{i=1}^{m}{w}_{io}{x}_{ij}\right)-\alpha \sum_{i=1}^{m}{w}_{io}{x}_{io}\right)}{\tilde{\sigma }\left|\sum_{j=1}^{n}{\lambda }_{j}\left(\sum_{i=1}^{m}{w}_{io}{a}_{ij}\right)-\alpha \sum_{i=1}^{m}{w}_{io}{a}_{io}\right|}\right)\ge 1-\gamma .$ Then, $\Phi \left(\frac{-\left(\sum_{j=1}^{n}{\lambda }_{j}\left(\sum_{i=1}^{m}{w}_{io}{x}_{ij}\right)-\alpha \sum_{i=1}^{m}{w}_{io}{x}_{io}\right)}{\tilde{\sigma }\left|\sum_{j=1}^{n}{\lambda }_{j}\left(\sum_{i=1}^{m}{w}_{io}{a}_{ij}\right)-\alpha \sum_{i=1}^{m}{w}_{io}{a}_{io}\right|}\right)\ge 1-\gamma .$ Therefore, using the property of invertibility of $\Phi (\bullet )$, we have $\frac{-\left(\sum_{j=1}^{n}{\lambda }_{j}\left(\sum_{i=1}^{m}{w}_{io}{x}_{ij}\right)-\alpha \sum_{i=1}^{m}{w}_{io}{x}_{io}\right)}{\tilde{\sigma }\left|\sum_{j=1}^{n}{\lambda }_{j}\left(\sum_{i=1}^{m}{w}_{io}{a}_{ij}\right)-\alpha \sum_{i=1}^{m}{w}_{io}{a}_{io}\right|}\ge {\Phi }^{-1}\left(1-\gamma \right).$

Consequently, the deterministic form of Constraint (9.1) is expressed as $\sum_{j=1}^{n}{\lambda }_{j}\left(\sum_{i=1}^{m}{w}_{io}{x}_{ij}\right)-{\Phi }^{-1}(\gamma )\left|\sum_{j=1}^{n}{\lambda }_{j}\left(\sum_{i=1}^{m}{w}_{io}{a}_{ij}\right)-\alpha \sum_{i=1}^{m}{w}_{io}{a}_{io}\right|\le \alpha \sum_{i=1}^{m}{w}_{io}{x}_{io}.$ Similarly, Constraint (9.2) can be expressed as $\sum_{j=1}^{n}{\lambda }_{j} {y}_{rj}+{\Phi }^{-1}\left(\gamma \right)\tilde{\sigma } \left|\sum_{j=1}^{n}{\lambda }_{j} {b}_{rj}-\beta {b}_{ro}\right|\ge \beta {y}_{ro} (\forall r).$

Thus, we set up the deterministic version of program (9) as

$$\overline{\alpha }\left(\beta \right)=\mathrm{min}\alpha$$

(11)

$$s.t.\sum_{j=1}^{n}{\lambda }_{j}\left(\sum_{i=1}^{m}{w}_{io}{x}_{ij}\right)-{\Phi }^{-1}\left(\gamma \right)\left|\sum_{j=1}^{n}{\lambda }_{j}\left(\sum_{i=1}^{m}{w}_{io}{a}_{ij}\right)-\alpha \sum_{i=1}^{m}{w}_{io}{a}_{io}\right|\le \alpha \sum_{i=1}^{m}{w}_{io}{x}_{io},$$

$$\sum_{j=1}^{n}{\lambda }_{j} {y}_{rj}+{\Phi }^{-1}\left(\gamma \right)\overline{\sigma }\left|\sum_{j=1}^{n}{\lambda }_{j} {b}_{rj}-\beta {b}_{ro}\right|\ge \beta {y}_{ro} (\forall r),$$

$$\sum_{j=1}^{n}{\lambda }_{j}=1,$$

${\lambda }_{j}\ge 0 \left(\forall j\right),$ and $\alpha :\mathrm{free}.$

Program (11) is nonlinear owing to the existence of an absolute function. Using the goal programming theory of Charnes and Cooper (1977), we transformed it into a quadratic programming problem.⁷ To proceed, we use the following transformations:

$$\left|\sum_{j=1}^{n}{\lambda }_{j}\left(\sum_{i=1}^{m}{w}_{io}{a}_{ij}\right)-\alpha \sum_{i=1}^{m}{w}_{io}{a}_{io}\right|={p}^{+}+{p}^{-},$$

$$\sum_{j=1}^{n}{\lambda }_{j}\left(\sum_{i=1}^{m}{w}_{io}{a}_{ij}\right)-\alpha \sum_{i=1}^{m}{w}_{io}{a}_{io}={p}^{+}-{p}^{-},$$

$${p}^{+}{p}^{-}=0,$$

$$\left|\sum_{j=1}^{n}{\lambda }_{j} {b}_{rj}-\beta {b}_{ro}\right|={q}_{r}^{+}+{q}_{r}^{-} (\forall r),$$

$$\sum_{j=1}^{n}{\lambda }_{j} {b}_{rj}-\beta {b}_{ro}={q}_{r}^{+}-{q}_{r}^{-} (\forall r),$$

$${q}_{r}^{+}{q}_{r}^{-}=0 \left(\forall r\right).$$

The existence of two constraints, − ${p}^{+}{p}^{-}=0 \mathrm{and } {q}_{r}^{+}{q}_{r}^{-}=0$, in our suggested transformations makes program (11) non-linear. However, if an LP problem exhibits an optimal solution vector, it also has an extreme optimal solution vector in which at least one of the variables from (${p}^{+}, {p}^{-})$ and $({q}_{r}^{+}, {q}_{r}^{-})$ is zero. Hence, the nonlinear constraints ${p}^{+}{p}^{-}=0$ and ${q}_{r}^{+}{q}_{r}^{-}=0$ can be safely ignored. Consequently, using the simplex algorithm, program (11) can be solved to find extreme optimal solutions.

Using the above transformations and notations, program (11) is converted into the following:

$$\overline{\alpha }\left(\beta \right)=\mathrm{min}\alpha$$

(12)

$s.t$.$\sum_{j=1}^{n}{\lambda }_{j}\left(\sum_{i=1}^{m}{w}_{io}{x}_{ij}\right)-{\Phi }^{-1}\left(\gamma \right)\tilde{\sigma }\left({p}^{+}+{p}^{-}\right)\le \alpha \sum_{i=1}^{m}{w}_{io}{x}_{io},$

$$\sum_{j=1}^{n}{\lambda }_{j}\left(\sum_{i=1}^{m}{w}_{io}{a}_{ij}\right)-\alpha \sum_{i=1}^{m}{w}_{io}{a}_{io}={p}^{+}-{p}^{-},$$

$$\sum_{j=1}^{n}{\lambda }_{j} {y}_{rj}+{\Phi }^{-1}\left(\gamma \right)\left({q}_{r}^{+}+{q}_{r}^{-}\right)\ge \beta {y}_{ro} (\forall r),$$

$$\sum_{j=1}^{n}{\lambda }_{j} {b}_{rj}-\beta {b}_{ro}={q}_{r}^{+}-{q}_{r}^{-} (\forall r),$$

$$\sum_{j=1}^{n}{\lambda }_{j}=1,$$

$\lambda ,{p}^{+},{p}^{-},{q}^{+},{q}^{-}\ge 0,$ and $\alpha :\mathrm{free}.$

Stochastic value-based ${\varvec{S}}{\varvec{E}}$ measure

To compute the value-based measure of $SE$ of firm $o$, we set up the dual program (12) as

$$\overline{\alpha }\left(\beta \right)=\mathrm{max }\beta \left(\sum_{r=1}^{S}({u}_{r}{y}_{ro}+{\mu }_{r}{b}_{ro})\right)+{\omega }_{0}$$

(13)

$$s.t. \sum_{r=1}^{S}\left({u}_{r}{y}_{rj}+{\mu }_{r}{b}_{rj}\right)-\sum_{i=1}^{m}{w}_{io}\left(v{x}_{ij}-\vartheta {a}_{ij}\right)+{\omega }_{0}\le 0 \left(\forall j\right),$$

$$\sum_{i=1}^{m}{w}_{io}\left(v{x}_{io}-\vartheta {a}_{io}\right)=1,$$

$${\Phi }^{-1}\left(\gamma \right)v-\vartheta \le 0,$$

$${\Phi }^{-1}\left(\gamma \right)v+\vartheta \le 0,$$

$${\Phi }^{-1}\left(\gamma \right)\sum_{r=1}^{S}{u}_{r}-\sum_{r=1}^{S}{\mu }_{r}\le 0,$$

$${\Phi }^{-1}\left(\gamma \right)\sum_{r=1}^{S}{u}_{r}+\sum_{r=1}^{S}{\mu }_{r}\le 0,$$

$$v,u\ge 0, \vartheta ,\mu ,{\omega }_{0}: \mathrm{free}.$$

For each firm $o\in \left\{1,\dots ,n\right\}$, its transformation function is considered as follows:

$$\psi \left(\overline{\alpha }\left(\beta \right){x}_{o},\overline{\alpha }\left(\beta \right){a}_{o},\beta {y}_{o},\beta {b}_{o}\right)\equiv \beta \sum_{r=1}^{S}\left({u}_{r}{y}_{ro}+{\mu }_{r}{b}_{ro}\right)-\overline{\alpha }\left(\beta \right)\sum_{i=1}^{m}{w}_{io}\left(v{x}_{io}-\vartheta {a}_{io}\right)+{\omega }_{0}=0$$

(14)

On differentiation of (14) with respect to $\beta$ yields

$$\begin{aligned} \frac{\partial \psi \left( \cdot \right)}{{\partial \beta }} & = \mathop \sum \limits_{r = 1}^{s} \frac{\partial \psi \left( . \right)}{{\partial \left( {\beta y_{ro} } \right)}}y_{ro} + \mathop \sum \limits_{r = 1}^{s} \frac{\partial \psi \left( \cdot \right)}{{\partial \left( {\beta b_{ro} } \right)}}b_{ro} + \mathop \sum \limits_{i = 1}^{m} \frac{\partial \psi \left( . \right)}{{\partial \left( {\alpha x_{io} } \right)}}x_{io} \frac{\partial \alpha }{{\partial \beta }} + \mathop \sum \limits_{i = 1}^{m} \frac{\partial \psi \left( . \right)}{{\partial \left( {\alpha a_{io} } \right)}}a_{io} \frac{\partial \alpha }{{\partial \beta }} = 0, \\ \Rightarrow \frac{\partial \alpha }{{\partial \beta }} & = - \frac{{\mathop \sum \nolimits_{r = 1}^{s} \frac{\partial \psi \left( \cdot \right)}{{\partial \left( {\beta y_{ro} } \right)}}y_{ro} + \mathop \sum \nolimits_{r = 1}^{s} \frac{\partial \psi \left( \cdot \right)}{{\partial \left( {\beta b_{ro} } \right)}}b_{ro} }}{{\mathop \sum \nolimits_{i = 1}^{m} \frac{\partial \psi \left( \cdot \right)}{{\partial \left( {\alpha x_{io} } \right)}}x_{io} + \mathop \sum \nolimits_{i = 1}^{m} \frac{\partial \psi \left( \cdot \right)}{{\partial \left( {\alpha a_{io} } \right)}}a_{io} }} \\ & = - \frac{{\mathop \sum \nolimits_{r = 1}^{s} u_{r} y_{ro} + \mathop \sum \nolimits_{r = 1}^{s} \mu_{r} b_{ro} }}{{ - \mathop \sum \nolimits_{i = 1}^{m} vw_{io} x_{io} + \mathop \sum \nolimits_{i = 1}^{m} \vartheta w_{io} a_{io} }} \\ & = \frac{{\overline{\alpha }\left( \beta \right)\mathop \sum \nolimits_{i = 1}^{m} w_{io} \left( {vx_{io} - \vartheta a_{io} } \right) - \omega_{0} }}{\beta } = \frac{{\overline{\alpha }\left( \beta \right) - \omega_{0} }}{\beta } \\ \end{aligned}$$

(15)

The (input-oriented) value-based measure of $SE$ of firm $o$ can then be obtained as follows:

$$\varepsilon \left(\gamma \right)=\frac{\partial \overline{\alpha }(\beta )}{\partial \beta } \frac{\beta }{\overline{\alpha }(\beta )}=\frac{\overline{\alpha }\left(\beta \right)-{\omega }_{0}}{\beta }\frac{\beta }{\overline{\alpha }(\beta )}=\frac{\overline{\alpha }\left(\beta \right)-{\omega }_{0}}{\overline{\alpha }(\beta )}$$

(16)

Because DEA technologies are not smooth at vertices, we face multiple optimal values for ${\omega }_{0}$. Therefore, to compute the maximum (minimum) value of ${\omega }_{0}$ for firm $o$, we set the following program.

$${\omega }_{0}^{+}\left({\omega }_{0}^{-}\right)=\mathrm{max} (\mathrm{min}) {\omega }_{0}$$

(17)

$$s.t.\beta \left(\sum_{r=1}^{S}({u}_{r}{y}_{ro}+{\mu }_{r}{b}_{ro})\right)+{\omega }_{0}=\overline{\alpha }\left(\beta \right),$$

$$\sum_{r=1}^{S}\left({u}_{r}{y}_{rj}+{\mu }_{r}{b}_{rj}\right)-\sum_{i=1}^{m}{w}_{io}\left(v{x}_{ij}-\vartheta {a}_{ij}\right)+{\omega }_{0}\le 0, (\forall j\ne o)$$

$$\sum_{i=1}^{m}{w}_{io}\left(v{x}_{io}-\vartheta {a}_{io}\right)=1,$$

$${\Phi }^{-1}\left(\gamma \right)v-\vartheta \le 0,$$

$${\Phi }^{-1}\left(\gamma \right)v+\vartheta \le 0,$$

$${\Phi }^{-1}\left(\gamma \right)\sum_{r=1}^{S}{u}_{r}-\sum_{r=1}^{S}{\mu }_{r}\le 0,$$

$${\Phi }^{-1}\left(\gamma \right)\sum_{r=1}^{S}{u}_{r}+\sum_{r=1}^{S}{\mu }_{r}\le 0,$$

$$v,u\ge 0,\, \vartheta ,\mu ,{\omega }_{0}: \mathrm{free}.$$

Using the optimal values of program (17), the (input-oriented) right- and left-hand value-based $SE$ scores of firm $o$ can be calculated as follows:

$${\varepsilon }^{+}\left(\gamma \right)=\frac{\overline{\alpha }\left(\beta \right)-{\omega }_{0}^{-}}{\overline{\alpha }\left(\beta \right)},\mathrm{ and}\, {\varepsilon }^{-}\left(\gamma \right)=\frac{\overline{\alpha }\left(\beta \right)-{\omega }_{0}^{+}}{\overline{\alpha }\left(\beta \right)}.$$

(18)

We present Theorem 1 to determine, using the formulae in (18), the returns-to-scale types at each confidence level given the values of ${\omega }_{0}^{-}$ and ${\omega }_{0}^{+}$.

Theorem 1

For every confidence level $\gamma$, the (input-oriented) returns to scale of firm $o$ are (a) decreasing (DRS) (i.e., ${\varepsilon }_{I}^{-}\left(\gamma \right)>1$) if ${\omega }_{0}^{+}<0,$ (b) constant (CRS) (i.e., ${\varepsilon }_{I}^{-}\left(\gamma \right)\le 1\le {\varepsilon }_{I}^{+}\left(\gamma \right))$ if ${\omega }_{0}^{-}\le 0\le {\omega }_{0}^{+},$ and (c) increasing (IRS) (i.e., ${\varepsilon }_{I}^{+}\left(\gamma \right)<1$) if ${\omega }_{0}^{-}>0.$

Proof

Let ${v}^{*},{u}^{*}, {\vartheta }^{*},{\mu }^{*}$, and ${\omega }_{0}^{*}$ be optimal solutions of the LP program (13) for the radial efficient firm $({\widetilde{x}}_{o}, {\widetilde{y}}_{o})$, which is defined according to (10) as ${\widetilde{x}}_{io}={x}_{io}+{a}_{io}{\varepsilon }_{io} (\forall i)$ and ${\widetilde{y}}_{ro}={y}_{ro}+{b}_{ro}{\eta }_{ro} \left(\forall r\right).$ So, $\sum_{r=1}^{S}\left({u}_{r}^{*}{y}_{ro}+{\mu }_{r}^{*}{b}_{ro}\right)+{\omega }_{0}^{*}=\sum_{i=1}^{m}{w}_{io}\left({v}^{*}{x}_{io}-{\vartheta }^{*}{a}_{io}\right)=1$. Furthermore, $\sum_{r=1}^{S}\left({u}_{r}^{*}{y}_{rj}+{\mu }_{r}^{*}{b}_{rj}\right)-\sum_{i=1}^{m}{w}_{io}\left({v}^{*}{x}_{ij}-{\vartheta }^{*}{a}_{ij}\right)+{\omega }_{0}^{*}=0$ is a supporting hyperplane to ${T}^{V(S)}$ in (7), and the corresponding value at $\left(\overline{\alpha }\left(\beta \right), \beta \right)$ is presented in (14). Differentiating (14) for $\beta$, the following measure of SE was used: $\varepsilon \left(\gamma \right)=\frac{\overline{\alpha }\left(\beta \right)-{\omega }_{o}^{*}}{\overline{\alpha }\left(\beta \right)}$. The right- and left-hand SEs can then be easily computed as ${\varepsilon }^{+}\left(\gamma \right)=\frac{\overline{\alpha }\left(\beta \right)-{\omega }_{o}^{*-}}{\overline{\alpha }\left(\beta \right)} \mathrm{and} {\varepsilon }^{-}\left(\gamma \right)=\frac{\overline{\alpha }\left(\beta \right)-{\omega }_{o}^{*+}}{\overline{\alpha }\left(\beta \right)}$, respectively. It then immediately follows that

• (a) ${\varepsilon }^{-}\left(\gamma \right)>1$if ${\omega }_{o}^{*+}<0$ and since ${\omega }_{o}^{*-}<{\omega }_{o}^{*+}$, then ${\varepsilon }^{+}\left(\gamma \right)>1$. Thus, returns to scale decrease (DRS).

• (b) If ${\omega }_{o}^{*-}<0$ then ${\varepsilon }^{+}\left(\gamma \right)>1$ and if ${\omega }_{o}^{*+}>0$ then ${\varepsilon }^{-}\left(\gamma \right)<1$. Therefore, ${\varepsilon }^{-}\left(\gamma \right)\le 1\le {\varepsilon }^{+}\left(\gamma \right)$ and returns to scale are constant (CRS).

• (c) If ${\omega }_{o}^{*-}>0$ then ${\varepsilon }^{+}\left(\gamma \right)<1$ and since ${\omega }_{o}^{*+}>{\omega }_{o}^{*-}$ then ${\varepsilon }^{-}\left(\gamma \right)<1$. Thus, returns to scale (IRS) are increasing.

  $$\square$$

Regarding the returns-to-scale types between deterministic and stochastic cases, we present Theorem 2.

Theorem 2

For a predetermined significance level of $\gamma =0.5$, the returns-to-scale types obtained from deterministic and stochastic programs were the same.

Proof

To prove this, it suffices to show that for $\gamma =0.5$, programs (12) and (3) are equivalent. To this end, since programs (12) and (11) are equivalent and ${\Phi }^{-1}\left(0.5\right)=0$, replacing it in the constraints of program (11) yields program (3).

$$\square$$

For the visual presentation of technology, we consider in Table 1 a hypothetical dataset of six firms, each producing one output using one input.

Table 1 Hypothetical data set

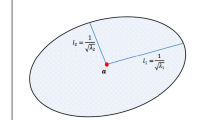
Based on the data in Table 1, we constructed the stochastic production frontiers in Fig. 2 by considering three different levels of tolerance ($\gamma =0.1, 0.3,\mathrm{ and }0.5$).⁸

The piecewise linear line (L3) passing through the mean points of the centers of circles represents the production frontier at the tolerance level of 0.5 and according to Theorem 2, this stochastic frontier is the same as the deterministic frontier. Similarly, lines L2 and L1 represent the production frontiers at tolerance levels $\mathrm{of} 0.3$ and 0.1, respectively. The TE scores at these tolerance levels are presented in Table 2. At each of these three tolerance levels, four firms, A, B, C, and D, are consistently found to be technically efficient. Of the remaining two firms, F becomes efficient at a tolerance level of 0.1, but inefficient at tolerance levels of $0.3$ and 0.5. However, E was inefficient at all three tolerance levels. This finding suggests that a firm’s efficiency status in a deterministic environment can be subject to change in the stochastic case.

Fig. 2

DEA stochastic production frontiers under chance constraints at $\gamma =0.5, 0.3$ and $0.1$

Table 2 Stochastic TE and SE scores of six firms

Input-oriented right- and left-hand SE scores were computed using value-based technology (7) in a stochastic environment $({T}^{V(S)})$, the input-oriented right- and left-hand $SE$ scores are computed. Table 2 presents the results.

At each of these three tolerance levels considered, out of the four stochastically technically efficient firms (A, B, C, and D), B is CCR-efficient and hence exhibits CRS because its left-hand SE scores are all less than 1, and the right-hand SE scores are all greater than 1. D is CCR-efficient only at tolerance levels of $0.1$ and 0.3 and hence exhibits CRS at those tolerance levels, but IRS at the tolerance level of 0.5 (as its right-hand SE score is less than 1). Of the remaining two stochastically technically efficient firms, A exhibits IRS (as its right-hand SE score is less than 1) and C exhibits DRS (as its left-hand SE score is greater than 1) at each of the three tolerance levels. Finally, regarding the returns-to-scale types of inefficient firms, since E’s projection onto the frontier is located on the interior point of the facet DB (see Fig. 2), its right- and left-hand SE values are all equal, but all less than one, implying IRS. As is evident from Table 2, the efficiency status of F is the mix, that is, it is efficient at a tolerance level of 0.1, but inefficient at other tolerance levels. However, at all these tolerance levels, DRS is exhibited because its left-hand SE values are all greater than one. The finding that D exhibits IRS at the tolerance level of 0.5, but CRS at the other tolerance levels, indicates that the returns-to-scale characterizations of firms in a deterministic technology is subject to change in the stochastic case.

The illustrative empirical application

We now demonstrate an illustrative empirical application of our proposed stochastic efficiency program using a dataset used earlier by Sahoo and Tone (2009a, b) for analyzing capacity utilization and profit change behaviors of Indian banks for eight years (1998–2005).

The data

The dataset consists of 71 banks (26 public banks, 27 private banks, and 18 foreign banks), each using three inputs, borrowed funds $\left({x}_{1}\right)$, fixed assets $\left({x}_{2}\right)$, and labor $\left({x}_{3}\right)$, to produce three outputs, investments $\left({y}_{1}\right)$, performing loan assets $\left({y}_{2}\right)$, and non-interest income $\left({y}_{3}\right)$. All monetary values of the input and output quantities are deflated by the wholesale price index with a base of 1993–94 to obtain their present (implicit) quantities. All monetary values are measured for Indian rupees (Rs.) for crores (Rs. 1 crore = Rs. 10 million). Concerning the prices of inputs, the unit prices of ${x}_{1}$, ${x}_{2}$, and ${x}_{3}$ are measured as the average interest paid per rupee of ${x}_{1}\left({w}_{1}\right)$, non-labor operational cost per rupee amount of ${x}_{2}$ $\left({w}_{2}\right)$, and average staff cost $\left({w}_{3}\right)$, respectively. The input and output quantities are all assumed to be random, with each following a normal distribution with a known mean (presented in Table 3) and known standard deviation (shown in Table 4).

Table 3 The means of the inputs and outputs along with unit input prices of 71 banks

Table 4 The standard deviations of the inputs and outputs of 71 banks

In DEA, if the number of DMUs ($n$) is less than the combined number of inputs (m) and outputs (s), many DMUs are efficient. Therefore, $n$ must exceed ($m$ + $s$). The rule of thumb in the DEA literature suggests that $n$ ≥ max {$m$ × $s$, 3 × ($m$ +$s$)}. In our dataset, $n$ = 71, and $m$ = $s$  = 3. Therefore, the thumb rule was satisfied at 71 ≥ max {9, 18}.

We used the GAMS software on a machine with the following specifications to compute the efficiency and scale elasticity scores of banks: CPU, Intel Pentium 4 at 2 GHz and RAM, 1024 MB.

Results

Stochastic value-based $TE$ scores

Table 5 presents the value-based TE scores of 71 banks in the stochastic environment at the three different confidence levels considered. As observed, only 38 banks were efficient at all three confidence levels. It is also interesting to observe that inefficient banks tend to experience a decline in their efficiency performance with an increase in $\gamma .$

Table 5 Stochastic value-based $TE$ scores of 71 banks

Stochastic value-based $SE$ scores

The results for both the lower and upper bounds of the stochastic value-based $SE$ scores for all 71 banks are presented in Tables 6 and 7 for $\beta =0.99$ and $\beta =1.01$, respectively.

Table 6 The stochastic value-based scale elasticity scores of 71 banks $\left(\beta =0.99\right)$

Table 7 The stochastic value-based scale elasticity scores of 71 banks $\left(\beta =1.01\right)$

It is well known that scale elasticity is defined only for efficient units, and for inefficient units, this computation can be performed only at their input- or output-oriented projections. However, in our case, we considered input-oriented projections. To interpret our results for $\beta =0.99$ in Table 6, for example, for bank 20, which is efficient at all three tolerance levels, the lower-bound $SE$ score is less than 1 and its upper-bound value is more than 1, that is, ${\varepsilon }^{-}<1<{\varepsilon }^{+}$, implying that its returns to scale are constant [as per Theorem 1 (b)]. For efficient bank 54, the upper bound $SE$ scores are all less than 1 (i.e., ${\varepsilon }^{+}<1)$ at all three tolerance levels, implying that its returns to scale are increasing [as per Theorem 1 (c)]; for the remaining efficient banks such as 1, 2, and 3, since the lower bound of $SE$ is greater than 1 at all three tolerance levels (i.e., ${\varepsilon }^{+}>1),$ it exhibits a decreasing return to scale [as per Theorem 1 (a)].

Note that for some stochastically inefficient banks, such as 4, 12, 14, and 23, both lower- and upper-bound $SE$ scores are equal at all three tolerance levels, implying that their projections onto the boundary are all located on interior points of the facet. Of the 71 banks, we find 30 banks exhibiting DRS, 10 banks exhibiting CRS, and 11 banks exhibiting IRS, at all three tolerance levels. Two more interesting observations were made in this study. First, some banks exhibit returns to scales of different types at different tolerance levels. For example, for $\beta =0.99$ in Table 6, inefficient bank 37 (at $\gamma =0.1\mathrm{ and }0.3$) exhibits DRS. This means that its projections onto the efficient frontier are all located on points of the facet exhibiting DRS. However, the projection of this inefficient bank at $\gamma =0.5$ onto the efficient frontier exhibits IRS. Furthermore, bank 51 at $\gamma =0.1\mathrm{ and }0.3$ is both VRS- and CRS-efficient and hence exhibits CRS. However, this bank was inefficient at $\gamma =0.5$. Hence, its projection onto the efficient frontier exhibits IRS. In addition, the SE results for $\beta =1.01$ in Table 7, can be interpreted analogously.

Furthermore, for $\beta =0.99$ (Table 6), the upper-bound $SE$ scores of some banks, such as 1, 6, and 10, are unbounded. This implies that any proportional increase in output lies outside the technology set. However, in Tables 6 and 7, both lower- and upper-bounds of $SE$ s of some banks, such as 45 in Table 6 and 48 in Table 7, are indicated by a dashed line, implying that model (12) is infeasible because changing $\beta$ from 1 to 0.99 or 1.01, these units appear outside the feasible region. Therefore, program (12) becomes infeasible when there is no data available outside the feasible region to determine returns to scale (Grosskopf 1996).

Deterministic value-based $SE$ scores of the banks

In addition to program (17), we ran the valued-based LP (4) to compute the lower and upper bounds of the $SE$ scores of 71 banks in a deterministic environment for $\beta =0.99$ and $\beta =1.01$, which are presented in Table 8. The results show that the 38 efficient banks that are found to be fully technically efficient in a stochastic environment are also efficient, and the remaining 33 banks are inefficient. Regarding their returns-to-scale characterizations, for the case of $\beta =1.01$, we find six efficient banks (i.e., 5, 20, 31, 35, 49, and 69) exhibiting CRS. For the five efficient banks (i.e., 44, 45, 54, 64, and 68), returns to scale increase because their upper bounds of $SE$ scores are all less than unity. Finally, for some efficient banks, such as 1, 6, 9, 10, 11, 13, 19, 21, 22, 30, 34, 48, 52, and 61, both lower- and upper-bound $SE$ scores are indicated by dashed lines. Hence, as discussed in Sect. 4.3, no data are available to determine the returns-to-scale type. This is because, as we consider $\beta$ from 1 to 0.99 or 1.01, these banks appear outside the feasible region. Therefore, program (3) becomes infeasible when there is no data available outside the feasible region to determine their returns-to-scale possibilities. The remaining 13 efficient banks operate under the DRS.

Table 8 Deterministic value-based TE and SE scores of the banks

For $\beta =0.99$, some efficient banks (1, 6, 9, and 13) exhibit DRS and some efficient banks (10, 19, 21, 34, and 61) exhibit CRS. However, as pointed out earlier, the returns-to-scale types of these banks for the case of $\beta =1.01$ were not determined. Moreover, for bank 8, while returns to scale are constant for $\beta =0.99$, they decrease for $\beta =1.01$.

A comparison between the deterministic and stochastic methods

Regarding the comparison between deterministic and stochastic $TE$ estimates, a few observations are noteworthy. First, both deterministic and stochastic methods are in complete agreement in declaring the same 38 banks to be fully technically efficient. Second, both methods yield the same value-based $TE$ scores for banks $\gamma =0.5$. This finding is consistent with our expectation (see Theorem 2), which leads us to conclude that deterministic technology is a special case of stochastic technology for $\gamma =0.5$ in exhibiting the same $TE$ scores. Third, the stochastic $TE$ scores of inefficient states are higher than their deterministic counterparts. This finding is also expected, because the main purpose of our chance-constrained formulation is to allow the observed inputs and outputs of banks to cross the efficiency frontier, but not too often. For any given observed input–output vector, the efficiency frontier in the stochastic case is now located closer than before. Finally, the efficiency scores of banks increase with sharpening (decreasing) the tolerance level of chance constraints.

Regarding the comparison between deterministic and stochastic $SE$ estimates, we find apparent differences in their returns-to-scale characterizations. First, while the stochastic method finds efficient bank 13 exhibiting DRS at all three tolerance levels considered, the deterministic method is unable to find its returns-to-scale status for $\beta =1.01$ but finds the same DRS type for $\beta =0.99$. Second, although the returns-to-scale types of the remaining banks are the same in both deterministic and stochastic methods, the degree of returns to scale (i.e., lower and upper bounds of the SE) vary to some degree. For example, consider bank 65. For the case of $\beta =0.99,$ and $\gamma$= 0.1, the stochastic lower and upper bounds of the SE estimates suggest that a 1% increase in cost raises the output by 4.78% and 8.81%, respectively. However, for $\beta =0.99$ in the deterministic case, the lower and upper $SE$ bounds suggest that a 1% increase in cost yields the same 7.03% increase in output. Third, for $\gamma =0.5,$ the value-based $SE$ scores of banks were the same between the two methods. According to Theorem 2, this finding is not contrary to our expectations. Therefore, one can conclude that deterministic technology is again a special case of stochastic technology for $\gamma =0.5$ in exhibiting the same returns-to-scale characterization of banks.

$TE$ vis-à-vis ownership

We examine banks’ $TE$ performance across ownership types. The results are presented in Table 9. As shown in Table 9, public banks exhibit higher $TE$ scores than private and foreign banks at all three tolerance levels. The finding of higher efficiency accrual of public banks over private and foreign banks may be due to their long-held formal status, wherein these banks have constantly been facilitating their access to scarce resources such as credit, foreign exchange, licenses, and skilled labor, which are necessary for efficient production.

Table 9 A comparison of stochastic $TE$ scores of banks across ownership types

Returns to scale across ownership

Finally, we examined the distribution of returns-to-scale types across ownership types. For β = 0.99, out of 44 public and private banks, 28 (68%) operate under DRS at a confidence level γ of 0.1. As shown in Table 10, while public sector banks mostly exhibit DRS, foreign banks exhibit IRS. Returns-to-scale types of private banks are a mix that supports all types of returns-to-scale, that is, IRS, CRS, and DRS. This may be because private banks are of two types: old and new, with the former type following the tradition of public sector banks and the latter type following that of foreign banks.

Table 10 A comparison of stochastic returns-to-scale types of banks across ownership types

In the next section, we discuss the results of our illustrative empirical application of Indian banks from 1998 to 2005.

Discussions

As observed from our empirical results, different values of $\beta$ and $\gamma$ lead to varying results.

for returns-to-scale bank types. In such cases, the relevant question arises as to how bank management makes an appropriate judgment for its scale decisions. As noted earlier, the possible values of $\beta$ are user-defined values that reflect the proportional output change, and the value-based $TE$ function $\overline{\alpha }(\beta )$ for any bank $o$ is defined for all $\beta \in [0,\widehat{\beta }]$, where $\widehat{\beta }$ is the largest proportion of its output vector ${y}_{o}$ found on ${T}^{V}$. However, the scale elasticity of any radial technically efficient bank $\left({x}_{o}, {y}_{o}\right)$ is well defined at $\beta =\alpha \left(\beta \right)=1$ as we determine its returns-to-scale status locally at the neighborhood of point $\left({x}_{o}, {y}_{o}\right)$, where a derivative is to be evaluated. Since scale elasticity is a one-sided concept, one can therefore determine a bank’s (local) returns-to-scale type at its right or left by measuring the response to outputs by considering only a one percent increase or decrease in inputs, that is, $\beta =1.01$ (right) and $\beta =0.99$ (left) at a specific confidence level.⁹

Regarding the values of tolerance level $\gamma$, a pre-determined parameter ($0<\gamma \le 0.5$) makes the confidence level of each firm large or small, that is, the confidence level that forms an ellipse around the mean value of the inputs and outputs of each firm, increase or decrease. Consequently, a bank may experience a change in the returns-to-scale status for a change in $\gamma$. Therefore, the relevant question for any bank facing uncertainty is at what level of $\gamma$ should it consider making an appropriate judgment about its scale decision. Because our proposed stochastic approach generates only expected $SE$ scores rather than distributions of random $SE$ scores, we are at odds to answer this question. Our focus in this study is, however, on ex-post-facto analysis of already affected decisions, which can have certain uses in the control aspects of bank management where evaluations of returns-to-scale performance are required. We need to address the ex-ante (planning) problem of how to use this knowledge to arrive at the possible value of $\gamma$, which can be used while affecting future-oriented decisions regarding whether to scale up or scale down operations.

Regarding the results concerning bank efficiency performance across ownership types, we find that public banks exhibit higher efficiency than private and foreign banks. This finding fails to provide empirical support for the property rights hypothesis that private enterprises should perform better than public enterprises, which precisely holds in a developed country where there is a strong link between the market for takeover and the efficiency of private enterprises. In India, public banks are known for their better organizational structure and greater penetration into the customer base. During the post-reform period of our study (1998–2005), government policies favored public banks in managing their expansionary activities well because of their age-old learning experience. In the absence of an active market for corporate control, substantial government ownership, and a relatively low level of technological advancement, conventional wisdom that private banks should perform better needs to be challenged.

The returns-to-scale results during our study period reveal that, while large public and old private banks mostly exhibit either DRS¹⁰ or CRS, small foreign and new private banks experience returns-to-scale possibilities of all types. Therefore, the finding of large public and old private banks exhibiting DRS does not bode well with the perception that regulators consider very large-size banks “too-big-to-fall,” which would encourage large or excessive risk-taking to drive bank growth. On the contrary, the finding of new small- and medium-sized private and foreign banks exhibiting IRS suggests that these banks have enough opportunity to increase output by either increasing the scale or merging with other banks to improve their performance.

Concluding remarks

Using the CC programming method, value-based measures of efficiency and scale economies’ behavior of firms are investigated from the viewpoint of the economic theory of production in the possible presence of stochastic variability in the underlying input and output data. There is considerable variation in the results concerning both the efficiency and returns-to-scale characterizations of banks between the deterministic and stochastic models. These differences are precisely due to the existence of confidence regions for various tolerance levels of the chance constraints. However, deterministic technology is a special case of stochastic technology at a tolerance level of 0.5, exhibiting both the efficiency and returns-to-scale characterizations of firms. Regarding the key empirical findings of our illustrative application to the Indian banking industry during the post-reform period (1998–2005), we have a few key findings. First, as expected, the stochastic model generates higher efficiency scores for inefficient banks as compared to the deterministic model. Second, public banks are more efficient than private and foreign banks, which challenges the property rights hypothesis. However, this finding is not unusual because the Indian banking industry is characterized by the absence of an active market for corporate control and substantial government ownership. Third, large public and old private banks mostly exhibit either decreasing or constant returns to scale, whereas small foreign and new private banks experience either increasing or decreasing returns to scale. Finally, based on bank-specific scale properties, the management can decide on the expansion or contraction of their operations in the subsequent operation period, which provides a vision of how to change outputs for changing inputs to preserve efficiency status in the subsequent period of activities.

Limitations and future recommendations

The proposed stochastic model requires information on the joint probability distributions of random inputs and outputs, which are generally inferred from their respective frequency distributions. Because this information is often not available in practice, we are at a loss to estimate them empirically. Given the nature of the input and output data that we deal with in this study, they are all subject to uncertainties; therefore, the requirement of availability of data on their joint probability distributions should not constrain the use of our empirically appealing stochastic model.

However, our stochastic model cannot be used freely. First, the inputs and outputs are assumed to be well approximated by a normal distribution, although they are all subject to empirical testing. Second, the use of a single-factor assumption for linear transformation requires further assumptions in the resulting LP problem that there are perfect correlations between any two inputs/outputs, or between input and output. We strongly believe that in any real-life decision-making situation characterized by the presence of uncertainty, the benefit of using the stochastic model outweighs its cost. For example, if the underlying objective is to analyze the efficiency, returns to scale, and returns to growth behavior of technology-intensive firms in the new economy, one must resort to the use of a stochastic model because these firms are all characterized by the presence of uncertainty concerning inventory holdings, excess capacity, and organizational slack as contingencies against uncertain future developments.

Finally, we point to some avenues for future potential research subjects.

• From our proposed stochastic model, the possible presence of input and output slack for individual banks can be explored. Unlike in the case of a deterministic model, the slacks here can presumably be interpreted as inventory (i.e., excess reserves), desired excess capacity, and organizational slack, which firms must hold as contingencies against uncertain future developments. This analysis will aid management in deciding the accumulation of optimal slack to sustain market competition and price uncertainty.

• One could also extend our stochastic model to network production technologies to analyze the efficiency and returns-to-scale characterizations of firms.

• Both the chance-constrained program and stochastic frontier analysis can be compared to analyze and contrast the efficiency and returns-to-scale classification of firms.

• Because the linear transformation method used in our proposed stochastic model requires the assumption of perfect correlations between inputs/outputs, the desired future research involves the development of an alternative linear transformation method, which could assume such assumptions.

• Our proposed stochastic approach yields the expected efficiencies rather than the distribution of random efficiencies. Therefore, one can use the probabilistic approach by Kao and Liu (2009, 2019) to generate distributions of efficiency and scale elasticity scores for each firm, which could be more informative for better decision-making.

• Our focus in this study is on the ex-post-facto analysis of already affected decisions, which can be used in the control aspects of management. However, future research requires an ex-ante (planning) analysis of how to use the returns to scale results based on various possible pre-defined tolerance levels to arrive at the precise tolerance level using which future-oriented decisions regarding whether to scale up or scale down operations can be affected.

• Our empirical application of 71 banks over eight years (1998–2005) is primarily for illustrative purposes. However, an extension of the data set to the year 2021 is required to conduct a detailed empirical investigation concerning whether the effects of global extreme events such as COVID-19 and internal events such as the adoption of the Insolvency and Bankruptcy Code (IBC) Bill influence banks’ efficiency and scale performance differentials. Further, since our findings are not clear as to whether scale economies still provide an impetus for banks to become larger, we expect future researchers to examine returns to scale from either revenue or profit perspectives, which can provide a more complete picture of scale economies in the Indian banking industry.

• Although the application of our proposed chance-constraint efficiency model is in banking to analyze efficiency and scale properties, it can potentially be applied to a wide selection of areas studied earlier, such as deriving innovative carbon-reducing emission strategies to increase the performance of solar energy investment projects in the transportation sector (Kou et al. 2022), evaluating the credit risks of small and medium-sized enterprises (SMEs) using payment and transactional data (Kou et al. 2021), evaluating credit ratings of online peer-to-peer (P2P) loans to control default risk and improve profit for lenders and platforms (Wang et al. 2021), evaluating the performance of various clustering algorithms that are used to assess financial risk (Kou et al. 2014), and detecting clusters in financial data to infer users’ behaviors and identify potential risks (Li et al. 2021).

• Although our current empirical application to Indian banking is illustrative, our proposed chance-constraint efficiency model can potentially be applied to analyze the efficiency and scale properties of real-life firms with stochastic underlying production processes. Examples of these firms can be found in industries such as agriculture, where unpredictability in weather makes the input–output relationship stochastic; manufacturing industry, where firms face considerable variation in the quality of their inputs and outputs produced; product development industry, where firms face uncertainty regarding their new designs; and high-technology industries, where firms face hyper (dynamic)completion in the new (Internet) economy.