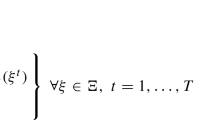Comparing and Combining Two Approaches for Chance Constrained DEA

Abstract

This paper presents a comparison of two different models (Land et al (1993) and Olesen and Petersen (1995)), both designed to extend DEA to the case of stochastic inputs and outputs. The two models constitute two approaches within this area, that share certain characteristics. However, the two models behave very differently, and the choice between these two models can be confusing. This paper presents a systematic attempt to point out differences as well as similarities. It is demonstrated that the two models under some assumptions do have Lagrangian duals expressed in closed form. Similarities and differences are discussed based on a comparison of these dual structures. Weaknesses of the each of the two models are discussed and a merged model that combines attractive features of each of the two models is proposed.

Appendices

Appendix: Proofs of the Lagrangian duals assuming that all variance-covariances matrices are identity matrices.

Two Lemmas.

In this appendix we will use the following notation:

$$ \begin{aligned} e_{p}\in \mathbb{R}^{p}\hbox{ is a }p-\hbox{vector of ones} \\ neg\left[ \alpha _{1},\ldots ,\alpha _{p}\right] ^{t}\equiv \left[ \beta_{1},\ldots ,\beta _{p}\right] ^{t},\beta _{j}=\left\{ \begin{array}{ll} \alpha _{j} & \hbox{ if }\alpha _{j}\leq 0 \\ 0 & \hbox{otherwise}\\ \end{array} \right. \\ \left\| x\right\| _{1}\equiv \sum\limits_{j=1}^{n}|x_{j}|,\left\| x\right\|_{2}\equiv \sqrt{\sum\limits_{j=1}^{n}x_{j}^{2}}\\ \end{aligned} $$

The following lemmas will be useful later:

Lemma 7

Let $\alpha \in \mathbb{R}^{p}. max_{\left\| \lambda \right\| _{2}\leq 1}\alpha^{t}\lambda =\left\| \alpha \right\| _{2} (or\, min_{\left\| \lambda \right\| _{2}\leq 1}\alpha^{t}\lambda =\left\| \alpha \right\| _{2})$ for the optimal vector $\lambda ^{\ast }=\left( \left\| \alpha \right\| _{2}\right) ^{-1}\alpha (or\,\lambda^{\ast }=-\left( \left\| \alpha \right\| _{2}\right) ^{-1}\alpha$).

Lemma 8

Consider the following minimization problem for $\gamma \in \mathbb{R}_{-}^{p}$ and $k\in \mathbb{R}_{+}.$

$$\min_{\lambda \geq 0}\gamma ^{t}\lambda +k\left\| \lambda \right\| _{2} $$

The set of (γ ,k) for which this minimization is not unbounded is

$$ A\equiv \left\{ \left( \gamma ,k\right) \in \mathbb{R}_{-}^{p}\times \mathbb{ R}_{+}:\left\| \gamma \right\|_{2}\leq K\right\} $$

For (γ, k) ∈A the minimum is attained for λ ^* =  − γ. For (γ ,k) ∈ ∂ A and λ ^* =  − γ we have $\gamma ^{t}\lambda ^{\ast }+k\left\| \lambda ^{\ast }\right\| _{2}=0$.

Proof

Notice, $\gamma \in \mathbb{R}_{-}^{p}$. Since $k\left\|\lambda \right\|_{2}\geq 0,\forall\lambda\geq 0$ we have a bounded solution for (γ ,k) in

$$ \begin{aligned} &\left\{\left(\gamma, k\right)\in \mathbb{R}_{-}^{p} \times \mathbb{R}_{+}:\gamma^{t}\lambda +k\left\|\lambda\right\| _{2}\geq 0,\forall \lambda \geq 0\right\}\\ =&\left\{ \left( \gamma ,k\right) \in \mathbb{R}_{-}^{p}\times \mathbb{R} _{+}:-\gamma ^{t}\left( \left\| \lambda \right\|_{2}\right)^{-1}\lambda \leq k,\forall \lambda \geq 0\right\} \end{aligned} $$

((13))

From lemma 7 (with α ≡  − γ), we have that $-\gamma^{t}\left(\left\|\lambda\right\|_{2}\right)^{-1}\lambda$ attains its maximum value over all λ  ≥  0 for λ ^* =  − γ, since

$$ \max_{\lambda\geq 0}\left(-\gamma^{t}{\frac{\lambda}{\left\|\lambda \right\|_{2}}}\right) =\max_{\lambda\geq 0,\left\| \lambda \right\|_{2}\leq 1}\left( -\gamma^{t}\lambda\right) =-\gamma ^{t}\left[ {\frac{ \left( -\gamma \right)}{\left\| -\gamma \right\|_{2}}}\right] =\left\| \gamma \right\|_{2} $$

Hence, inserting this λ^* in (13) gives A as the set of (γ ,k) for which the minimization is not unbounded. ■

Dual formulations to the LLT- and the OP-models (no correlation between DMUs in the LLT-model and between inputs, outputs and inputs and outputs in the OP -model).

Let us consider a radial efficiency evaluation of a mean vector from DMU _j0 (X _j0,Y _j0) regarded as a realization, i.e. a random vector with zero variance. Let us first consider the Land etal. (1993) chance constraint formulation with no correlation between DMUs (here also homoscedacity):

$$ \begin{array}{lllll} \min & \theta & & & \\ s.t. & \sum\limits_{j=1}^{n}\lambda _{j}\overline{Y}_{kj}-{\frac{1}{\eta }}\left\| \lambda \right\| _{2} & \geq & Y_{kj_{0}} & k=1,\ldots ,s \\ & -\sum\limits_{j=1}^{n}\lambda _{j}\overline{X}_{ij}-{\frac{1}{\eta }}\left\| \lambda \right\| _{2}+\theta X_{ij_{0}} & \geq & 0 & i=1,\ldots ,m \\ & \theta \in \mathbb{R},\lambda \in \mathbb{R}_{+}^{n} & & & \\ \end{array} $$

(14)

where η⁻¹ is the fractile corresponding to the chosen probability level α. Assuming ${\frac{1}{\eta }}\geq 0$ implies that (14) a convex programming problem and it is well known that the Lagrangian dual (sometimes called the minimax dual) exists and that there is no duality gap if Slater’s condition is satisfied, see e.g. Theorem 1 (Lasdon 1970, p. 435). Slater’s condition states:

Condition 9

$Let g\left( \theta ,\lambda \right) =\left[ -\sum\limits_{j=1}^{n}\lambda _{j}\overline{Y}_{kj}+{\frac{1}{\eta }}\left\|\lambda \right\|_{2}+Y_{kj_{0}},\forall k,\sum\limits_{j=1}^{n}\lambda _{j}\overline{X}_{ij}+{\frac{1}{\eta }}\left\|\lambda\right\|_{2}-\theta X_{ij_{0}},\forall i\right]$. Assume that there exists a point $\left( \theta ,\lambda \right)\in S\equiv \mathbb{R}\times \mathbb{R}_{+}^{n}$ such that g(θ ,λ ) < 0.

Slater’s condition is satisfied under the following mild regularity condition:

Lemma 10

(Regularity condition): Assume that $\overline{Y}_{kj} > 0,Y_{kj_{0}} > 0,\forall k,j, \overline{X}_{ij} > 0,X_{ij_{0}} > 0,\forall i,j$. Then there exists a $\left(\theta,\lambda \right) \in \mathbb{R}\times \mathbb{R}_{+}^{n}$ such that g(θ,λ )  < 0.

Proof

We first look for $\lambda^{\ast}\in \mathbb{R}_{+}^{n}$ such that the s output inequalities are satisfied with strict inequalities. Let us assume that λ _j  = λ₁,j = 2,...,n then we get:

$$ \begin{aligned} \lambda_{1}\sum\limits_{j=1}^{n}\overline{Y}_{kj}-\lambda_{1}{\frac{1}{\eta }}\left\| e_{n}\right\|_{2} > &Y_{kj_{0}},k=1,\ldots s {or} \\ \lambda_{1}^{\ast} =&\max_{k=1,\ldots s}\left\{Y_{kj_{0}}\left( \sum\limits_{j=1}^{n}\overline{Y}_{kj}-{\frac{\sqrt{n}}{\eta}}\right)^{-1}\right\} > 0 \end{aligned} $$

Next from the input inequalities we get

$$ \begin{aligned} \theta X_{ij_{0}} > &\lambda_{1}^{\ast}\left(\sum\limits_{j=1}^{n} \overline{X}_{ij}+{\frac{\sqrt{n}}{\eta}}\right),i=1,\ldots m\ \hbox{or}\\ \theta^{\ast}=&\max_{i=1,\ldots m}\lambda _{1}^{\ast}\left(\sum\limits_{j=1}^{n}\overline{X}_{ij}+{\frac{\sqrt{n}} {\eta}}\right)X_{ij_{0}}^{-1} \end{aligned} $$

λ^* = λ ^*₁ (e _n )^t implies that all s output inequalities are satisfied strictly and g(θ^*,λ^*) < 0 as required.■

Let us formulate the Lagrangian dual:

$$\min_{\theta,\lambda \geq 0}\max_{u\geq 0,v\geq 0}h\left(\theta , \lambda ;u,v\right) $$

(15)

where

$$ \begin{aligned} &h\left(\theta,\lambda;u,v\right)\\ \equiv &\theta +u^{t}\left( -\overline{Y}\lambda +Y_{j_{0}}+{\frac{1}{\eta}} \left\| \lambda \right\| _{2}e_{s}\right) +v^{t}\left( \overline{X}\lambda -\theta X_{j_{0}}+{\frac{1}{\eta}}\left\| \lambda \right\| _{2}e_{m}\right) \notag &\\ =&u^{t}Y_{j_{0}}+\left( -u^{t}\overline{Y}+v^{t}\overline{X}\right) \lambda +\left( {\frac{1}{\eta }}\left\| \lambda \right\| _{2}\right)\times \left( u^{t}e_{s}+v^{t}e_{m}\right) +\left( 1-v^{t}X_{j_{0}}\right) \theta \notag &\\ \end{aligned} $$

(16)

Rearranging we get

$$ \max_{u\geq 0,v\geq 0}\left\{u^{t}Y_{j_{0}}+ \min_{\theta}g\left(\theta,\lambda ;u,v\right)\right\} $$

(17)

where

$$ g\left(\theta,\lambda;u,v\right)\equiv \left(1-v^{t}X_{j_{0}}\right) \theta +\min_{\lambda\geq 0}\left\{\left(-u^{t}\overline{Y}+v^{t} \overline{X}\right)\lambda +\left({\frac{1}{\eta}}\left\|\lambda \right\|_{2}\right)\left(u^{t}e_{s}+v^{t}e_{m}\right)\right\} $$

The minimization over λ  ≥  0 involved in g(θ ,λ ;u,v) is bounded if $\left( -u^{t}\overline{Y}+v^{t}\overline{X}\right)\geq 0$. Allowing some components in this vector to be negative, i.e. $J_{0}\subseteq \left\{ 1,\ldots ,n\right\},$such that $-u^{t}\overline{Y}_{j}+v^{t}\overline{X}_{j} < 0$ for j∈J ₀ we have from lemma 8 ¹³ that this minimization is bounded if

$$ \sqrt{\sum_{j\in J_{0}}\left(-u^{t}\overline{Y}_{j}+v^{t} \overline{X}_{j}\right)^{2}}\leq{\frac{1}{\eta}}\left(u^{t} e_{s}+v^{t}e_{m}\right) $$

(18)

or

$$ \left\|neg\left(-u^{t}\overline{Y}_{j}+v^{t}\overline{X}_{j}\right) \right\|_{2}\leq {\frac{1}{\eta}}\left(u^{t}e_{s}+v^{t}e_{m}\right) $$

(19)

Hence the Lagrangian dual to (14) corresponds to

$$ \begin{array}{llll} \hbox{max}&u^{t}Y_{j_{0}}&&\\ s.t.&\left\|neg\left(-u^{t}\overline{Y}+v^{t}\overline{X}\right)\right\| _{2}-\eta ^{-1}\left( u^{t}e_{s}+v^{t}e_{m}\right)&\leq&0\\ &1-v^{t}X_{j_{0}}&=&0\\ &u\in\mathbb{R}_{+}^{s},v\in \mathbb{R}_{+}^{m}&&\\ \end{array} $$

(20)

or

$$ \begin{array}{lllll} \max&u^{t}Y_{j_{0}}&&&\\ s.t.&\left\| s^{+}\right\|_{2}-\eta ^{-1}\left\| u,v\right\| _{1}&\leq&0&\\ &1-v^{t}X_{j_{0}}&=&0&\\ &\left(-u^{t}\overline{Y}_{j}+v^{t}\overline{X}_{j}\right) +s_{j}^{+}&\geq&0&j=1,\ldots,n\\ &u\in\mathbb{R}_{+}^{s},v\in\mathbb{R}_{+}^{m},s^{+}\in \mathbb{R}_{+}^{n}&&&\\ \end{array} $$

(21)

(21) follows from (20) based on the following argument: Consider the j ₀′th component in the vector $-u^{t}\overline{Y}+v^{t}\overline{X}$ and consider the following two cases:

• If $-u^{t}\overline{Y}_{j_{0}}+v^{t}\overline{X}_{j_{0}} < 0$ then by the third set of constraints in (A8) we have $-u^{t}\overline{Y}_{j_{0}}+v^{t}\overline{X}_{j_{0}}\geq -s_{j_{0}}^{+}$ and  − s ⁺ _j0  ≤ 0. Hence, s ⁺ _j0  > 0. To allow as large a set of feasible u,v determined from the first constraint $\eta ^{-1}\left\| u,v\right\| _{1}\geq \left\|s^{+}\right\|_{2}$ we choose s ⁺ _j0 as small as possible, i.e. $-u^{t}\overline{Y}_{j_{0}}+v^{t}\overline{X}_{j_{0}}=-s_{j_{0}}^{+}$.

• If $-u^{t}\overline{Y}_{j_{0}}+v^{t}\overline{X}_{j_{0}} > 0$ then by the third set of constraints in (21) we have $-u^{t}\overline{Y}_{j_{0}}+v^{t}\overline{X}_{j_{0}}\geq -s_{j_{0}}^{+}$ and  − s ⁺ _j0  ≤ 0. Hence, s ⁺ _j0  ≥ 0. To allow as large a set of feasible u,v determined from the first constraint $\eta ^{-1}\left\| u,v\right\| _{1}\geq \left\| s^{+}\right\| _{2}$ we choose s ⁺ _j0  = 0, i.e. as small as possible.

Next, let us consider a radial efficiency evaluation of this mean vector from $\hbox{DMU}_{j_0}\;\left( X_{j_0},Y_{j_0}\right)$ regarded as a realization, in the Olesen and Peterson (1995) chance constraint formulation. We focus on the situation with no correlation between inputs, outputs and inputs and outputs (here also homoscedacity). The model for this case is:

$$ \begin{array}{lllll} \max&u^{t}Y_{j_{0}}&&&\\ s.t.&-u^{t}\overline{Y}_{j}+v^{t}\overline{X}_{j}-\kappa ^{-1}\left\| u,v\right\|_{2}&\geq&0&j=1,\ldots,n\\ &1-v^{t}X_{j_{0}}&=&0&\\ &u\in\mathbb{R}_{+}^{s},v\in \mathbb{R}_{+}^{m}&&&\\ \end{array} $$

(22)

where κ⁻¹ is the fractile corresponding to the chosen probability level α. Notice, that the constraint v ^t X _j0 = 1 can be replaced by v ^t X _j0 ≤ 1 since this inequality always will hold as an equality in optimum ¹⁴. In this context Slater’s condition states:

Condition 11

Let $g\left(u,v\right) =\left[ u^{t}\overline{Y}_{j}-v^{t}\overline{X}_{j}+\kappa^{-1}\left\| u,v\right\|_{2},\forall j,v^{t}X_{j_{0}}-1\right]$. Assume that there exists a point $\left( u,v\right)\in S\equiv \mathbb{R}_{+}^{s+m}$ such that g(u,v) < 0.

Slater’s condition is satisfied under the following mild regularity condition:

Lemma 12

(Regularity condition): Assume Y _{kj_0} > 0, k, X _{ij_0} > 0, i and that for all (δ⁺,δ⁻) where $\left\|\left(\delta ^{+},\delta ^{-}\right) \right\| _{2}\leq \kappa$ we have $\left(\overline{Y}_{kj}+\delta _{k}^{+}\right) > 0,\left( \overline{X}_{ij}+\delta _{i}^{-}\right) > 0,\forall i,j$. Then there exists a $\left( u,v\right) \in \mathbb{R}_{+}^{s+m}$ such that g(u,v) < 0.

Proof.

The regularity condition states that all confidence regions (balls of radius κ with centers at the mean input output vectors) are strictly contained in the non-negative orthant. Hence there exists a hyperplane with a normal vector $\left( u^{\ast},v^{\ast }\right)\in \mathbb{R}_{+}^{s+m}$ such that all confidence regions are located in the open halfspace bounded by this hyperplane. More formally, for j = 1,...,n

$$ \begin{aligned} u^{\ast t}\left(\overline{Y}_{j}+\delta ^{+}\right) -v^{\ast t}\left(\overline{X}_{j}+\delta ^{-}\right) =&u^{\ast t}\overline{Y}_{j}-v^{\ast t} \overline{X}_{j}+\left( u^{\ast t}\delta ^{+}-v^{\ast t}\delta ^{-}\right) < 0,\\ \hbox{for all}\left(\delta ^{+},\delta ^{-}\right) \hbox{where}\left\|\left( \delta ^{+},\delta ^{-}\right) \right\| _{2} \leq &\kappa\\ \end{aligned} $$

From Lemma 7 we have that

$$ \max_{\left\| \left( \delta ^{+},\delta ^{-}\right) \right\|_{2}\leq 1}u^{\ast t}\delta ^{+}-v^{\ast t}\delta ^{-}=\left\| u^{\ast },v^{\ast }\right\|_{2} $$

from which follows that in particular we have for j = 1,... ,n

$$ u^{\ast t}\overline{Y}_{j}-v^{\ast t}\overline{X}_{j}+\kappa^{-1}\left\| u^{\ast },v^{\ast }\right\| _{2} < 0 $$

Finally, notice that feasibility of (u ^*,v ^*) in the first n constraints implies feasibility of k(u ^*,v ^*) , for $k\in \mathbb{R}_{+}$. Hence to assure that v ^t X _j0 − 1 < 0 we simply downscale (u ^*,v ^*) until g(u ^*,v ^*)  < 0 as required.■

Let us formulate the Lagrangian ¹⁵ dual:

$$ \min_{\theta ,\lambda \geq 0}\max_{u\geq 0,v\geq 0}g\left( \theta,\lambda ;u,v\right) $$

(23)

where

$$ \begin{aligned} g\left( \theta ,\lambda ;u,v\right) \equiv u^{t}Y_{j_{0}}+\left( -u^{t} \overline{Y}+v^{t}\overline{X}-\kappa ^{-1}\left\| u,v\right\| _{2}e_{n}^{t}\right) \lambda +\left( 1-v^{t}X_{j_{0}}\right) \theta\\ =\theta +\left( u^{t},v^{t}\right) \left[ \left( -\overline{Y}\lambda +Y_{j_{0}}\right) ,\left( \overline{X}\lambda -\theta X_{j_{0}}\right) \right] -\left( \kappa ^{-1}\left\| u,v\right\| _{2}\right) e_{n}^{t}\lambda \notag \end{aligned} $$

(24)

Hence,

$$ \max_{u\geq 0,v\geq 0}g\left( \theta ,\lambda ;u,v\right) =\theta +\max_{u\geq 0,v\geq 0}\left( u^{t},v^{t}\right) \left[ \left( -\overline{Y} \lambda +Y_{j_{0}}\right) ,\left( \overline{X}\lambda -\theta X_{j_{0}}\right) \right] -\left( \kappa ^{-1}e_{n}^{t}\lambda \right) \left\| u,v\right\| _{2} $$

(25)

A sufficient condition for this maximization to be bounded is $\left[ \left( -\overline{Y}\lambda +\overline{Y}_{j_{0}}\right) ,\left( \overline{X}\lambda -\theta \overline{X}_{j_{0}}\right) \right] \leq 0$. However, we can allow components in this vector to be positive. A necessary and sufficient condition ¹⁶ (see again (lemma 8)) is

$$ \left\| neg\left[ \left( \overline{Y}\lambda -Y_{j_{0}}\right) ,\left( - \overline{X}\lambda +\theta X_{j_{0}}\right) \right] \right\| _{2}\leq \kappa ^{-1}e_{n}^{t}\lambda $$

(27)

Hence the Lagrangian dual corresponds to

$$ \begin{array}{llll} \min & \theta & & \\ s.t. & \left\| neg\left[ \left( \overline{Y}\lambda -Y_{j_{0}}\right) ,\left( -\overline{X}\lambda +\theta X_{j_{0}}\right) \right] \right\| _{2}-\kappa ^{-1}e_{n}^{t}\lambda & \leq & 0 \\ & \lambda \in \mathbb{R}_{+}^{n},\theta \in \mathbb{R} & & \\ \end{array} $$

(28)

or

$$ \begin{array}{llll} \min & \theta & & \\ s.t. & \left\| \xi ^{+},\xi ^{-}\right\| _{2}-\kappa ^{-1}\left\| \lambda \right\| _{1} & \leq & 0 \\ & \left( \overline{Y}\lambda -Y_{j_{0}}\right) +\xi ^{+} & \geq & 0 \\ & \left( -\overline{X}\lambda +\theta X_{j_{0}}\right) +\xi ^{-} & \geq & 0 \\ & \lambda \in \mathbb{R}_{+}^{n},\theta \in \mathbb{R},\xi ^{-}\in \mathbb{R}_{+}^{m},\xi ^{+}\in \mathbb{R}_{+}^{s} & & \\ \end{array} $$

(29)

As above (28) follows from (27) based on the following argument: Consider the k th component in the vector $\left[ \left( \overline{Y}\lambda -Y_{j_{0}}\right) ,\left( -\overline{X}\lambda +\theta X_{j_{0}}\right) \right]$, say $\overline{Y}^{k}\lambda -Y_{kj_{0}}$, and consider the following two cases ¹⁷

• If $\overline{Y}^{k}\lambda -Y_{kj_{0}} < 0$ then by the second set of s constraints in (28) we have $\overline{Y}^{k}\lambda -Y_{kj_{0}}\geq -\xi _{k}^{+}$ and  − ξ ⁺ _k  ≤ 0. Hence, ξ ⁺ _k  > 0. To allow as large a set of feasible λ determined from the first constraint $\kappa ^{-1}\left\| \lambda \right\| _{1}\geq \left\| \xi ^{+},\xi ^{-}\right\| _{2}$ we choose ξ ⁺ _k as small as possible, i.e. $\overline{Y}^{k}\lambda -Y_{kj_{0}}=-\xi _{k}^{+}$.

• If $\overline{Y}^{k}\lambda -Y_{kj_{0}} > 0$ then by the second set of s constraints in (28) we have $\overline{Y}^{k}\lambda -Y_{kj_{0}}\geq -\xi _{k}^{+}$ and  − ξ ⁺ _k  ≤ 0. Hence, ξ ⁺ _k  ≥ 0. To allow as large a set of feasible λ determined from the first constraint $\kappa ^{-1}\left\| \lambda \right\| _{1}\geq \left\| \xi ^{+},\xi ^{-}\right\| _{2}$ we choose ξ ⁺ _k  = 0, i.e. as small as possible.