1 Introduction

Fractional calculus and the existing notions in it are of high interest in different aspects of applied sciences, and one can find some instances of applications like signal and image processing, control theory, economics, optical systems, thermal materials, aerodynamics, mechanical systems, biology, and bio-mathematics [1–10]. The starting point for such a topic can be seen in many published papers in which mathematicians deal with some properties such as the existence of solution, uniqueness property, the property of stability, positivity, etc., and establish these properties to various abstract boundary value problems. Such a diversity and importance led to the publication of many research papers in this field, which revealed the flexibility of fractional calculus theory in designing various mathematical models. The main methods conducted in these articles are by terms of fixed point techniques [11–33].

Along with the investigation of existence theory, the approximation of solution and numerical methods are also of interest. Al-Smadi et al. [34] utilized a method based on the homotopy analysis for finding approximate solutions of a SEIR epidemic model in the fractional settings. Dhage, Dhage, and Ntouyas in [35] applied two notions of partial compactness and continuity to develop the method of Kranoselskii theorem and found the approximation of solutions regarding a hybrid ODE. Chadha et al. published a paper on the Faedo–Galerkin approximation for solutions of a neutral nonlocal FDE in a separable Hilbert space [36]. Other applications of approximate techniques can be found in [37–40]. The Bernstein polynomials are one of the strongest numerical techniques which possess some important properties such as the unity partition and continuity on \([0,1]\) [41]. In recent years, due to the importance and accuracy of this technique, the numerical solutions of a wide range of linear∖nonlinear BVPs have been obtained for Riccati type FDEs, Bessel FDE, Lane–Emden equations, etc., [11–13, 42–44]. We here use these polynomials to find approximate solution of our given multi-point FBVP introduced in the sequel.

In 2006, two mathematicians, Infante and Webb, simulated a mathematical model of a mechanical instrument named thermostat in the form of a second-order boundary problem on the interval \([0,1]\) which is insulated at \(s=0\) via the controller for \(s=1\) [45]. This model has the following mathematical structure:

$$ \textstyle\begin{cases} u''(s) = \mathfrak{g} (s , u(s)),\quad (s \in J := [0,1]), \\ u'(0)=0, \quad \mu u'(1)+ u(\zeta ) = 0, \end{cases} $$
(1)

where \(\zeta \in J\) and the parameter \(\mu > 0\). Further, two other mathematicians, Nieto and Pimentel, converted the above problem to a similar version of arbitrary order [46] which takes the following structure:

$$ \textstyle\begin{cases} {}^{c} \mathfrak{D}^{p} u(s) = \mathfrak{g} (s , u(s)) ,\quad (s \in J := [0,1]), \\ u'(0)=0, \qquad \mu {}^{c}\mathfrak{D}^{ p -1}u(1)+ u(\zeta ) = 0, \quad \mu > 0, p\in (1,2], p-1\in (0,1], \end{cases} $$
(2)

where \(^{c}\mathfrak{D}^{p} \) is the Caputo derivative and \(\zeta \in J\). In fact, at the time \(s= \zeta \) and based on the existing temperature, the sensor detects that the thermostat discharges or adds heat.

In this manuscript, we concentrate on this aim in which some existence and uniqueness aspects and numerical analysis of solutions for a generalized fractional boundary value problem (GFBVP) based on thermostat model are investigated. Indeed, we formulate the following structure of a generalized multi-point thermostat control model motivated by the standard model (1):

$$ \textstyle\begin{cases} {}^{c}\mathfrak{D}^{p} u(s) = \mathfrak{g} (s, \beta u(s), {}^{c} \mathfrak{D}^{\sigma }u(s), \mathcal{I}^{\rho }u(s) ),\quad (s \in J := [0,1]),\\ {}^{c}\mathfrak{D}^{1} u(0)= \varepsilon _{1} \int _{0}^{1} u(r)\,\mathrm{d}r,\qquad \sum_{j=1}^{m} u( \zeta _{j} ) + k {}^{c} \mathfrak{D}^{ p -1}u(1) = \varepsilon _{2} \int _{0}^{1} u(r)\,\mathrm{d}r, \end{cases} $$
(3)

in which \(p \in (1,2]\), \(\sigma \in (0,1)\), \(p -1 \in (0,1]\), \(k, \beta , \rho >0\), \(0< \zeta _{1} < \zeta _{2} < \cdots < \zeta _{m} < 1\), \(m\in \mathbb{N}\), \(\varepsilon _{1} , \varepsilon _{2} \in \mathbb{R}\), and \({}^{c}\mathfrak{D}^{1} = \frac{\mathrm{d}}{\mathrm{d}\mathfrak{s}}\). Along with these, the mapping \(\mathfrak{g}: J \times (\mathbb{R}^{\geq 0})^{3} \to \mathbb{R}^{ \geq 0}\) is continuous and \({}^{c}\mathfrak{D}^{\ell }\) and \(\mathcal{I}^{\ell }\) display the derivation and integration operators of order \(\ell \in \{1, p , p-1 , \sigma , \rho \}\) in the sense of Caputo and Riemann–Liouville.

The novelty, motivation, and objective of this research are:

  • The multi-point nonlinear system (3) is a generalized form of the mathematical model of thermostat that by assuming \(p=2\), \(\mu =k>0\), \(m=1\), \(\zeta _{1}=\cdots = \zeta _{m} = \zeta \in (0,1)\), \(\varepsilon _{1} =0\), \(\varepsilon _{2}=0\), and \(\beta =1\), we obtain the second-order integro-differential FBVP (1);

  • The existence property of solutions to the generalized nonlinear GFBVP (3) is derived by terms of a special case of contractions entitled \(\mu -\varphi \)-contraction and μ-admissible maps;

  • The approximate solution of this generalized nonlinear GFBVP of thermostat is obtained via Bernstein polynomials;

  • The accuracy and absolute errors of the mentioned numerical technique are examined in different examples of thermostat model.

The rest of the manuscript is provided as follows: The primitive notions are indicated and recalled in Sect. 2. The existence property along with the uniqueness property are investigated in Sect. 3. Bernstein polynomials and numerical solutions obtained by them are presented in Sect. 4. In Sect. 5, three different structures of nonlinear thermostat GFBVP are designed, and the results are examined. We end the manuscript by giving conclusions in Sect. 6.

2 Basic notions

In this section, we provide some general basic tools and results of fractional calculus that allow us to achieve our desired results. For more details on this subject, we advise the authors to consult, for example, [47, 48].

Definition 2.1

The Riemann–Liouville fractional integral (FRL-integral) of order \(\nu >0\) for a continuous function \(f:\mathbb{R}^{\geq 0}\to \mathbb{R}\) is defined by

$$\begin{aligned} \mathcal{I}^{\nu }f(t)=\frac{1}{\Gamma (\nu )} \int _{0}^{t}(t-\tau )^{ \nu -1}f(\tau ) \,d\tau , \end{aligned}$$
(4)

such that integral (4) converges.

Definition 2.2

The Caputo derivative of order \(\nu >0\) for a continuous function \(f:\mathbb{R^{\star }_{+}}\to \mathbb{R}\) is defined by

$$\begin{aligned} {}^{c}\mathfrak{D}^{\nu }f(t)= \frac{1}{\Gamma (n-\nu )} \int _{0}^{t}(t- \tau )^{n-\nu -1}f^{(n)}( \tau )\,d\tau , \end{aligned}$$
(5)

such that integral (5) exists, where \(n=[\nu ]+1\).

Lemma 2.3

([49])

For \(p>0\) and \(\alpha >0\),

• \({}^{c}\mathfrak{D}_{0^{+}}^{p}z^{\alpha }= \frac{\Gamma (\alpha +1)}{\Gamma (\alpha +1-p)}z^{\alpha -p}\) if \(\alpha \in \{0\}\cup \mathbb{N}\) and \(\alpha \geq \lceil p\rceil \) or \(\alpha \notin \mathbb{N}\) and \(\alpha >\lfloor p\rfloor \),

• \({}^{c}\mathfrak{D}_{0^{+}}^{p}z^{\alpha -1}=0\) if \(\alpha \in \{0\}\cup \mathbb{N}\) and \(\alpha < \lceil p\rceil \),

• \(\mathcal{I}_{0^{+}}^{p}z^{\alpha }= \frac{\Gamma (\alpha +1)}{\Gamma (\alpha +p+1)}z^{\alpha +p}\).

• \({}^{c}\mathfrak{D}_{0^{+}}^{p}C =0\) for all constant C.

Now, consider the family Φ of all nondecreasing functions \(\varphi :\mathbb{R^{+}}\to \mathbb{R^{+}}\) which satisfy \(\sum_{n=1}^{+\infty }\varphi ^{n}(t)<+\infty \), \(\forall t>0\). Consider \((H,\mathbf{d})\) as a metric space, F as a self-map on H, and \(\mu :H\times H\to \mathbb{R^{+}}\).

Definition 2.4

([50])

F is said to be a \(\mu -\varphi \)-contraction if

$$ \mu (x,y)\mathbf{d}(Fx,Fy)\leq \varphi \bigl(\mathbf{d}(x,y)\bigr),\quad \forall x,y \in H. $$

Definition 2.5

([50])

F is said to be μ-admissible if

$$ \mu (x,y)\geq 1\quad \Rightarrow\quad \mu (Fx,Fy)\geq 1,\quad \forall x,y \in H. $$

Theorem 2.6

([50])

Let \((H, \mathbf{d})\) be a complete metric space and \(F:H\to H\) be a \(\mu -\varphi \)-contraction. Assume:

  1. (i)

    F is μ-admissible,

  2. (ii)

    There exists \(x^{\star }\in H\) such that \(\mu (x^{\star },Fx^{\star })\geq 1\),

  3. (iii)

    For each sequence \(x_{n}\) in H which converges to \(x\in H\) such that \(\mu (x_{n},x_{n+1})\geq 1\) for all n, we have \(\mu (x_{n},x)\geq 1\) for all n.

Then there exists \(z\in H\) satisfying the operator equation \(Fz=z\).

3 The existence property

It is known that \(X = \{ u : u, {}^{c}\mathfrak{D}^{\sigma }u \in C_{\mathbb{R}}(J) \} \) is a Banach space with the sup norm \(\Vert u \Vert _{X} := \sup_{s \in J} \vert u ( s) \vert + \sup_{s \in J} \vert {}^{c}\mathfrak{D}^{\sigma }u ( s) \vert \), where \(C_{\mathbb{R}}(J)\) denotes the collection of all continuous real-valued functions on J. In the following, we characterize the structure of the solutions for given GFBVP caused by thermostat model (3) which plays a key role in our required method. Before it, we introduce some notations for simplicity:

$$\begin{aligned} V_{1} &:= \varepsilon _{1}, \qquad V_{2} := 1 - \frac{\varepsilon _{1}}{2}, \qquad V_{3} := m- \varepsilon _{2}, \\ V_{4} &:= \Biggl( \frac{k}{\Gamma (3-p)} - \frac{\varepsilon _{2}}{2} + \sum_{j=1}^{m} \zeta _{j} \Biggr),\qquad V:= V_{2}V_{3} + V_{1}V_{4}. \end{aligned}$$
(6)

Proposition 3.1

Let \(p \in (1,2]\), \(p -1 \in (0,1]\), \(k >0\), \(0< \zeta _{1} < \zeta _{2} < \cdots < \zeta _{m} < 1\), \(m\in \mathbb{N}\), \(\varepsilon _{1} , \varepsilon _{2} \in \mathbb{R}\), and \(h \in C_{\mathbb{R}}(J)\). Then the solution of the linear thermostat GFBVP

$$ \textstyle\begin{cases} {}^{c}\mathfrak{D}^{p} u(s) = h(s),\quad (s \in J := [0,1]), \\ {}^{c}\mathfrak{D}^{1} u(0)= \varepsilon _{1} \int _{0}^{1} u(r)\,\mathrm{d}r,\qquad \sum_{j=1}^{m} u( \zeta _{j} ) + k {}^{c} \mathfrak{D}^{ p -1}u(1) = \varepsilon _{2} \int _{0}^{1} u(r)\,\mathrm{d}r, \end{cases} $$
(7)

is given by

$$\begin{aligned} u(s) ={}& \int _{0}^{s} \frac{(s- r )^{p -1}}{\Gamma (p)} h(r )\, \mathrm{d}r - \frac{kA(s)}{V} \int _{0}^{1} h(r) \, \mathrm{d}r \\ &{}- \frac{A(s)}{V} \sum_{j=1}^{m} \int _{0}^{\zeta _{j}} \frac{(\zeta _{j} -r )^{p -1}}{\Gamma (p)} h(r)\, \mathrm{d}r + \frac{G(s)}{V} \int _{0}^{1} \int _{0}^{r} \frac{(r-q)^{p-1}}{\Gamma (p)} h(q)\, \mathrm{d}q \,\mathrm{d}r , \end{aligned}$$
(8)

where \(A,G\in C_{\mathbb{R}}(J)\) are introduced as

$$ A(s) := V_{2} + V_{1} s, \qquad G(s):= (\varepsilon _{2} V_{2} - \varepsilon _{1} V_{4}) + (\varepsilon _{1} V_{3} + \varepsilon _{2} V_{1})s. $$
(9)

Proof

We assume that \(u_{*}\) satisfies the linear thermostat GFBVP (7). Then \({}^{c}\mathfrak{D}^{p} u_{*}(s) = h(s)\). By integrating of order \(1 < p \leq 2\) on both sides of it, we get

$$ u_{*}(s) = \frac{1}{\Gamma (p)} \int _{0}^{s} (s- r )^{p -1} h(r )\, \mathrm{d}r + c_{0} + c_{1} s, $$
(10)

where we try to obtain the constant values of the coefficients \(c_{0}, c_{1}\in \mathbb{R}\). On the other hand, we have

$$ {}^{c}\mathfrak{D}^{1} u_{*}(s) = \frac{1}{\Gamma (p - 1)} \int _{0}^{s} (s- r )^{p - 2} h(r )\, \mathrm{d}r + c_{1} $$
(11)

and

$$ {}^{c}\mathfrak{D}^{p - 1} u_{*}(s) = \int _{0}^{s} h(r )\, \mathrm{d}r + c_{1} \frac{ s^{2-p }}{\Gamma (3- p) }, $$
(12)

and

$$ \int _{0}^{1} u_{*}(r) \, \mathrm{d}r = \frac{1}{\Gamma (p)} \int _{0}^{1} \int _{0}^{r} (r-q)^{p-1} h(q)\, \mathrm{d}q \,\mathrm{d}r + c_{0} + \frac{1}{2} c_{1}. $$
(13)

Now, in view of notations (6) and by using boundary conditions (7) and by invoking relations (11), (12), and (13), we reach

$$\begin{aligned} c_{0} ={}& {-} \frac{kV_{2}}{V} \int _{0}^{1} h(r)\, \mathrm{d}r - \frac{V_{2}}{V} \sum_{j=1}^{m} \int _{0}^{\zeta _{j}} \frac{(\zeta _{j} - r)^{p-1}}{\Gamma (p)} h(r)\, \mathrm{d}r \\ &{}+\frac{(\varepsilon _{2}V_{2} - \varepsilon _{1}V_{4})}{V} \int _{0}^{1} \int _{0}^{r} \frac{(r-q)^{p-1}}{\Gamma (p)}h(q)\, \mathrm{d}q \,\mathrm{d}r \end{aligned}$$
(14)

and

$$\begin{aligned} c_{1} ={}& {-} \frac{kV_{1}}{V} \int _{0}^{1} h(r)\, \mathrm{d}r - \frac{V_{1}}{V} \sum_{j=1}^{m} \int _{0}^{\zeta _{j}} \frac{(\zeta _{j} - r)^{p-1}}{\Gamma (p)} h(r)\, \mathrm{d}r \\ &{}+\frac{(\varepsilon _{1}V_{3} + \varepsilon _{2}V_{1})}{V} \int _{0}^{1} \int _{0}^{r} \frac{(r-q)^{p-1}}{\Gamma (p)}h(q)\, \mathrm{d}q\, \mathrm{d}r. \end{aligned}$$
(15)

Eventually, by (14) and (15), we substitute the obtained values for the coefficients \(c_{0}\) and \(c_{1}\) in (10) and it becomes

$$\begin{aligned} u_{*}(s) ={}& \int _{0}^{s} \frac{(s- r )^{p -1}}{\Gamma (p)} h(r )\, \mathrm{d}r - \frac{kA(s)}{V} \int _{0}^{1} h(r) \, \mathrm{d}r \\ &{}- \frac{A(s)}{V} \sum_{j=1}^{m} \int _{0}^{\zeta _{j}} \frac{(\zeta _{j} -r )^{p -1}}{\Gamma (p)} h(r)\, \mathrm{d}r + \frac{G(s)}{V} \int _{0}^{1} \int _{0}^{r} \frac{(r-q)^{p-1}}{\Gamma (p)} h(q)\, \mathrm{d}q \,\mathrm{d}r , \end{aligned}$$

which confirms that \(u_{*}\) satisfies (8), and accordingly, the proof is finished. □

To follow the procedure of the paper, we introduce the operator \(\mathbb{K}: X \to X\) associated with the nonlinear thermostat GFBVP which takes the form

$$\begin{aligned} (\mathbb{K}u) (s) ={}& \int _{0}^{s} \frac{(s- r )^{p -1}}{\Gamma (p)} \mathfrak{g} \bigl(r, \beta u(r), {}^{c}\mathfrak{D}^{\sigma }u(r), \mathcal{I}^{\rho }u(r) \bigr)\, \mathrm{d}r \\ &{}- \frac{kA(s)}{V} \int _{0}^{1} \mathfrak{g} \bigl(r, \beta u(r), {}^{c} \mathfrak{D}^{\sigma }u(r), \mathcal{I}^{\rho }u(r) \bigr)\, \mathrm{d}r \\ &{}- \frac{A(s)}{V} \sum_{j=1}^{m} \int _{0}^{\zeta _{j}} \frac{(\zeta _{j} -r )^{p -1}}{\Gamma (p)} \mathfrak{g} \bigl(r, \beta u(r), {}^{c}\mathfrak{D}^{\sigma }u(r), \mathcal{I}^{\rho }u(r) \bigr)\, \mathrm{d}r \\ &{}+ \frac{G(s)}{V} \int _{0}^{1} \int _{0}^{r} \frac{(r-q)^{p-1}}{\Gamma (p)} \mathfrak{g} \bigl(q, \beta u(q), {}^{c} \mathfrak{D}^{\sigma }u(q), \mathcal{I}^{\rho }u(q) \bigr)\, \mathrm{d}q \mathrm{d}r , \end{aligned}$$
(16)

where the functions \(A,G\in C_{\mathbb{R}}(J)\) are introduced by (9).

Before presenting our main theorems, we equip the space X with the metric d formulated as \(\mathbf{d}(x,y)=\|x-y\|_{X} \).

It is well known that \((X,\mathbf{d})\) is a complete metric space (see [51]).

Theorem 3.2

Consider a continuous function \(\mathfrak{g}:J\times \mathbb{R}^{3}\to \mathbb{R}\) and assume that the following assumptions hold:

\((ASS1)\) There are a map \(\varphi \in \Phi \) (Φ is the family defined in Section 2) and a function \(w: \mathbb{R}^{2}\to \mathbb{R}\) such that for all \(x,\widehat{x},y,\widehat{y},z,\widehat{z}\in \mathbb{R}\) we have \(w(x,y)\geq 0\) and

$$ \bigl\vert \mathfrak{g}(s,x,y,z)-\mathfrak{g}(s,\widehat{x},\widehat{y}, \widehat{z}) \bigr\vert \leq \frac{1}{\vartheta _{1}+\vartheta _{2}} \varphi \bigl( \vert x- \widehat{x} \vert + \vert y-\widehat{y} \vert + \vert z-\widehat{z} \vert \bigr), $$

where \(\vartheta _{1}\) and \(\vartheta _{2}\) are two positive real constants which satisfy the following inequalities:

$$ \vartheta _{1}>\frac{1}{\Gamma (p+1)}+\frac{k( \vert V_{2} \vert + \vert V_{1} \vert )}{ \vert V \vert }+ \frac{ \vert V_{2} \vert + \vert V_{1} \vert }{ \vert V \vert \Gamma (p+1)}\sum_{j=1}^{m} \zeta _{j} ^{p} + \frac{ \vert \varepsilon _{2} V_{2}-\varepsilon _{1} V_{4} \vert + \vert \varepsilon _{1} V_{3}+\varepsilon _{2} V_{1} \vert }{ \vert V \vert \Gamma (p+2)} $$

and

$$\begin{aligned} \vartheta _{2} >&\frac{1}{\Gamma (p-\sigma +1)}+ \frac{k( \vert V_{2} \vert + \vert V_{1} \vert )}{ \vert V \vert \Gamma (2-\sigma )}+ \frac{ \vert V_{2} \vert + \vert V_{1} \vert }{ \vert V \vert \Gamma (p-\sigma +1)}\sum_{j=1}^{m} \zeta _{j} ^{p-\sigma } \\ &{}+ \frac{ \vert \varepsilon _{2} V_{2}-\varepsilon _{1} V_{4} \vert + \vert \varepsilon _{1} V_{3}+\varepsilon _{2} V_{1} \vert }{ \vert V \vert \Gamma (p-\sigma +2)}. \end{aligned}$$

\((ASS2)\) \(\exists \, x^{\star }\in X\quad s.t. \quad w(x^{\star }(s),\mathbb{K}x^{ \star }(s))\geq 0\), \(\forall s\in J\).

\((ASS3)\) \(\forall x,y\in X\), we have

$$ w\bigl(x(s),y(s)\bigr)\geq 0\quad \Rightarrow\quad w\bigl(\mathbb{K}x(s),\mathbb{K}y(s) \bigr)\geq 0 \quad \textit{for all } s\in J. $$

\((ASS4)\) For each sequence \(x_{n}\in X\) which converges to x in X and \(w(x_{n}(s),x_{n+1}(s))\geq 0\), \(\forall s\in J\) and \(\forall n\in \mathbb{N}\), we have \(w(x_{n}(s),x(s))\geq 0\).

\((ASS5)\) the constants β and ρ are linked by the relation \(\beta +\frac{1}{\Gamma (\rho +1)}<1\).

Then problem (3) has a solution.

Proof

Let us define a map \(\mu :X\times X\to \mathbb{R}^{+}\) as

$$ \mu (x,y)= \textstyle\begin{cases} 1,& \text{if } w(x(s),y(s ))\geq 0, \\ 0,& \text{otherwise}. \end{cases} $$

\(\text{For all } x,y\in X\) and \(w(x(s),y(s))\geq 0\) for each \(s\in J\), we have

$$\begin{aligned} & \bigl\vert \mathbb{K}x(s)-\mathbb{K}y(s) \bigr\vert \\ &\quad = \frac{1}{\Gamma (p)} \int _{0}^{s} \vert s-r \vert ^{p-1} \bigl\vert \mathfrak{g} \bigl(r, \beta x(r), {}^{c}\mathfrak{D}^{\sigma }x(r), \mathcal{I}^{\rho }x(r) \bigr)-\mathfrak{g} \bigl(r, \beta y(r), {}^{c}\mathfrak{D}^{\sigma }y(r), \mathcal{I}^{\rho }y(r) \bigr) \bigr\vert \, \mathrm{d}r \\ &\qquad {}+\frac{k \vert A(s) \vert }{ \vert V \vert } \\ &\qquad {}\times \int _{0}^{s} \bigl\vert \mathfrak{g} \bigl(r, \beta x(r), {}^{c} \mathfrak{D}^{\sigma }x(r), \mathcal{I}^{\rho }x(r) \bigr)-\mathfrak{g} \bigl(r, \beta y(r), {}^{c}\mathfrak{D}^{\sigma }y(r), \mathcal{I}^{\rho }y(r) \bigr) \bigr\vert \, \mathrm{d}r \\ &\qquad {}+\frac{ \vert A(s) \vert }{ \vert V \vert \Gamma (p)} \\ &\qquad {}\times \sum_{j=1}^{m} \int _{0}^{\zeta _{j}} \vert \zeta _{j} -r \vert ^{p -1} \bigl\vert \mathfrak{g} \bigl(r, \beta x(r), {}^{c}\mathfrak{D}^{\sigma }x(r), \mathcal{I}^{\rho }x(r) \bigr) \\ &\qquad {}-\mathfrak{g} \bigl(r, \beta y(r), {}^{c} \mathfrak{D}^{\sigma }y(r), \mathcal{I}^{\rho }y(r) \bigr) \bigr\vert \, \mathrm{d}r \\ &\qquad {}+\frac{ \vert G(s) \vert }{ \vert V \vert \Gamma (p)} \\ &\qquad {}\times \int _{0}^{1} \int _{0}^{r} \vert r-q \vert ^{p-1} \bigl\vert \mathfrak{g} \bigl(r, \beta x(r), {}^{c}\mathfrak{D}^{\sigma }x(r), \mathcal{I}^{\rho }x(r) \bigr) \\ &\qquad {}-\mathfrak{g} \bigl(r, \beta y(r), {}^{c}\mathfrak{D}^{\sigma }y(r), \mathcal{I}^{\rho }y(r) \bigr) \bigr\vert \,\mathrm{d}q \mathrm{d}r \\ &\quad \leq \Biggl[\frac{1}{\Gamma (p+1)}+\frac{k( \vert V_{2} \vert + \vert V_{1} \vert )}{ \vert V \vert }+ \frac{ \vert V_{2} \vert + \vert V_{1} \vert }{ \vert V \vert \Gamma (p+1)} \sum_{j=1}^{m} \zeta _{j} ^{p} \\ &\qquad {}+ \frac{ \vert \varepsilon _{2} V_{2}-\varepsilon _{1} V_{4} \vert + \vert \varepsilon _{1} V_{3}+\varepsilon _{2} V_{1} \vert }{ \vert V \vert \Gamma (p+2)} \Biggr] \\ &\qquad {}\times \sup_{s\in J} \bigl\vert \mathfrak{g} \bigl(s, \beta x(s), {}^{c} \mathfrak{D}^{\sigma }x(s), \mathcal{I}^{\rho }x(s) \bigr)-\mathfrak{g} \bigl(s, \beta y(s), {}^{c}\mathfrak{D}^{\sigma }y(s), \mathcal{I}^{\rho }y(s) \bigr) \bigr\vert \\ &\quad \leq \vartheta _{1}\sup_{s\in J} \bigl\vert \mathfrak{g} \bigl(s, \beta x(s), {}^{c}\mathfrak{D}^{\sigma }x(s), \mathcal{I}^{\rho }x(s) \bigr)- \mathfrak{g} \bigl(s, \beta y(s), {}^{c}\mathfrak{D}^{\sigma }y(s), \mathcal{I}^{\rho }y(s) \bigr) \bigr\vert , \end{aligned}$$
(17)

and

$$\begin{aligned} & \bigl\vert {}^{c} \mathfrak{D}^{\sigma } \mathbb{K}x(s)-{}^{c} \mathfrak{D}^{\sigma }\mathbb{K}y(s) \bigr\vert \\ &\quad = \frac{1}{\Gamma (p-\sigma )} \\ &\qquad {}\times \int _{0}^{s} \vert s-r \vert ^{p-\sigma -1} \bigl\vert \mathfrak{g} \bigl(r, \beta x(r), {}^{c}\mathfrak{D}^{\sigma }x(r), \mathcal{I}^{\rho }x(r) \bigr)-\mathfrak{g} \bigl(r, \beta y(r), {}^{c}\mathfrak{D}^{\sigma }y(r), \mathcal{I}^{\rho }y(r) \bigr) \bigr\vert \, \mathrm{d}r \\ &\qquad {}+\frac{k \vert A(s) \vert }{ \vert V \vert \Gamma (1-\sigma )} \\ &\qquad {}\times \int _{0}^{s} \vert 1-\sigma \vert ^{-\sigma } \bigl\vert \mathfrak{g} \bigl(r, \beta x(r), {}^{c}\mathfrak{D}^{\sigma }x(r), \mathcal{I}^{\rho }x(r) \bigr)-\mathfrak{g} \bigl(r, \beta y(r), {}^{c}\mathfrak{D}^{\sigma }y(r), \mathcal{I}^{\rho }y(r) \bigr) \bigr\vert \, \mathrm{d}r \\ &\qquad {}+\frac{ \vert A(s) \vert }{ \vert V \vert \Gamma (p-\sigma )} \\ &\qquad {}\times \sum_{j=1}^{m} \int _{0}^{\zeta _{j}} \vert \zeta _{j} -r \vert ^{p- \sigma -1} \bigl\vert \mathfrak{g} \bigl(r, \beta x(r), {}^{c}\mathfrak{D}^{\sigma }x(r), \mathcal{I}^{\rho }x(r) \bigr) \\ &\qquad {}-\mathfrak{g} \bigl(r, \beta y(r), {}^{c}\mathfrak{D}^{\sigma }y(r), \mathcal{I}^{\rho }y(r) \bigr) \bigr\vert \, \mathrm{d}r \\ &\qquad {}+\frac{ \vert G(s) \vert }{ \vert V \vert \Gamma (p-\sigma )} \\ &\qquad {}\times \int _{0}^{1} \int _{0}^{r} \vert r-q \vert ^{p-\sigma -1} \bigl\vert \mathfrak{g} \bigl(r, \beta x(r), {}^{c}\mathfrak{D}^{\sigma }x(r), \mathcal{I}^{\rho }x(r) \bigr) \\ &\qquad {}-\mathfrak{g} \bigl(r, \beta y(r), {}^{c} \mathfrak{D}^{\sigma }y(r), \mathcal{I}^{\rho }y(r) \bigr) \bigr\vert \, \mathrm{d}q \mathrm{d}r \\ &\quad \leq \Biggl[\frac{1}{\Gamma (p-\sigma +1)}+ \frac{k( \vert V_{2} \vert + \vert V_{1} \vert )}{ \vert V \vert \Gamma (2-\sigma )} \\ &\qquad {}+\frac{ \vert V_{2} \vert + \vert V_{1} \vert }{ \vert V \vert \Gamma (p-\sigma +1)}\sum_{j=1}^{m} \zeta _{j} ^{p-\sigma } + \frac{ \vert \varepsilon _{2} V_{2}-\varepsilon _{1} V_{4} \vert + \vert \varepsilon _{1} V_{3}+\varepsilon _{2} V_{1} \vert }{ \vert V \vert \Gamma (p-\sigma +2)} \Biggr] \\ &\qquad {}\times \sup_{s\in J} \bigl\vert \mathfrak{g} \bigl(s, \beta x(s), {}^{c} \mathfrak{D}^{\sigma }x(s), \mathcal{I}^{\rho }x(s) \bigr)-\mathfrak{g} \bigl(s, \beta y(s), {}^{c}\mathfrak{D}^{\sigma }y(s), \mathcal{I}^{\rho }y(s) \bigr) \bigr\vert \\ &\quad \leq \vartheta _{2}\sup_{s\in J} \bigl\vert \mathfrak{g} \bigl(s, \beta x(s), {}^{c}\mathfrak{D}^{\sigma }x(s), \mathcal{I}^{\rho }x(s) \bigr)- \mathfrak{g} \bigl(s, \beta y(s), {}^{c}\mathfrak{D}^{\sigma }y(s), \mathcal{I}^{\rho }y(s) \bigr) \bigr\vert . \end{aligned}$$
(18)

Therefore, from (17) and (18) it follows that

$$\begin{aligned} \mathbf{d}(\mathbb{K}x,\mathbb{K}y)={}&\sup_{s\in J} \bigl\vert \mathbb{K}x(s)- \mathbb{K}y(s) \bigr\vert +\sup _{s\in J} \bigl\vert {}^{c} \mathfrak{D}^{\sigma } \mathbb{K}x(s)-{}^{c} \mathfrak{D}^{\sigma }\mathbb{K}y(s) \bigr\vert \\ \leq {}&(\vartheta _{1}+\vartheta _{2})\sup _{s\in J} \bigl\vert \mathfrak{g} \bigl(s, \beta x(s), {}^{c}\mathfrak{D}^{\sigma }x(s), \mathcal{I}^{\rho }x(s) \bigr)-\mathfrak{g} \bigl(s, \beta y(s), {}^{c}\mathfrak{D}^{\sigma }y(s), \mathcal{I}^{\rho }y(s) \bigr) \bigr\vert \\ \leq {}&(\vartheta _{1}+\vartheta _{2})\sup _{s\in J} \biggl[ \frac{1}{\vartheta _{1}+\vartheta _{2}}\varphi \bigl(\beta \bigl\vert x(s)-y(s) \bigr\vert + \bigl\vert {}^{c} \mathfrak{D}^{\sigma }x(s)-{}^{c} \mathfrak{D}^{\sigma }y(s) \bigr\vert \\ & {}+ \bigl\vert \mathcal{I}^{\rho }x(s)-\mathcal{I}^{\rho }y(s) \bigr\vert \bigr) \biggr] \\ \leq {}&\varphi \Bigl(\beta \sup_{s\in J} \bigl\vert x(s)-y(s) \bigr\vert + \sup_{s\in J} \bigl\vert {}^{c} \mathfrak{D}^{\sigma }x(s)-{}^{c} \mathfrak{D}^{\sigma }y(s) \bigr\vert +\sup_{s\in J} \bigl\vert \mathcal{I}^{\rho }x(s)- \mathcal{I}^{\rho }y(s) \bigr\vert \Bigr) \\ \leq {}&\varphi \biggl(\beta \sup_{s\in J} \bigl\vert x(s)-y(s) \bigr\vert + \sup_{s\in J} \bigl\vert {}^{c} \mathfrak{D}^{\sigma }x(s)-{}^{c} \mathfrak{D}^{\sigma }y(s) \bigr\vert \\ &{}+\frac{1}{\Gamma (\rho )}\sup_{s\in J} \bigl\vert x(s)- y(s) \bigr\vert \int _{0}^{s} \vert s-r \vert ^{ \rho -1}\, \mathrm{d}r \biggr) \\ \leq {}&\varphi \biggl( \biggl(\beta +\frac{1}{\Gamma (\rho +1)} \biggr) \sup _{s \in J} \bigl\vert x(s)-y(s) \bigr\vert + \sup _{s\in J} \bigl\vert {}^{c} \mathfrak{D}^{\sigma }x(s)-{}^{c} \mathfrak{D}^{\sigma }y(s) \bigr\vert \biggr) \\ \leq {}&\varphi \Bigl( \sup_{s\in J} \bigl\vert x(s)-y(s) \bigr\vert + \sup_{s\in J} \bigl\vert {}^{c} \mathfrak{D}^{\sigma }x(s)-{}^{c} \mathfrak{D}^{\sigma }y(s) \bigr\vert \Bigr). \end{aligned}$$

This means that \(\mathbf{d}(\mathbb{K}x,\mathbb{K}y)\leq \varphi (\mathbf{d}(x,y) )\). Consequently, from the definition of the map μ it follows that

$$ \mu (x,y)\mathbf{d}(\mathbb{K}x,\mathbb{K}y)\leq \varphi \bigl( \mathbf{d}(x,y) \bigr),\quad \forall x,y\in X, $$

which means that \(\mathbb{K}\) is a \(\mu -\varphi -\) contraction. Furthermore, in view of the definition of the map μ and assumption \((ASS3)\), we can easily verify that \(\mathbb{K}\) is μ-admissible.

Let now \(x_{n}\) be a sequence in X which approaches to x in X and satisfies \(\mu (x_{n},x_{n+1})\geq 1\), \(\forall n\in \mathbb{N}\) and \(\omega (x_{n}(s),x_{n+1}(s))\geq 0\). Then from the definition of the map μ together with assumption \((ASS5)\), we can directly verify that \(\mu (x_{n},x)\geq 1\). At this time, all the assumptions of Theorem 2.6 are fulfilled. Consequently, the operator \(\mathbb{K}\) admits a fixed point which is solution of our nonlinear thermostat GFBVP (3). □

Theorem 3.3

Let \(\mathfrak{g}:J\times \mathbb{R}^{3}\to \mathbb{R}\) be continuous and the following assumptions hold:

\((ASS6)\) \(\exists \, R>0\), \(s.t.~\forall s\in J\), \(\mathrm{and}\, \forall x, \widehat{x},y,\widehat{y},z,\widehat{z}\in \mathbb{R}\),

$$ \bigl\vert \mathfrak{g}(s,x,y,z)-\mathfrak{g}(s,\widehat{x},\widehat{y}, \widehat{z}) \bigr\vert \leq R \bigl( \vert x-\widehat{x} \vert + \vert y- \widehat{y} \vert + \vert z- \widehat{z} \vert \bigr), $$

\((ASS7)\) The constants β and ρ are linked by the relation \(\beta +\frac{1}{\Gamma (\rho +1)}<1\) and

$$\begin{aligned} \gamma ={}& R \Biggl(\frac{1}{\Gamma (p+1)}+ \frac{k( \vert V_{2} \vert + \vert V_{1} \vert )}{ \vert V \vert }+ \frac{ \vert V_{2} \vert + \vert V_{1} \vert }{ \vert V \vert \Gamma (p+1)}\sum_{j=1}^{m} \zeta _{j} ^{p} \\ &{}+ \frac{ \vert \varepsilon _{2} V_{2}-\varepsilon _{1} V_{4} \vert + \vert \varepsilon _{1} V_{3}+\varepsilon _{2} V_{1} \vert }{ \vert V \vert \Gamma (p+2)} +\frac{1}{\Gamma (p-\sigma +1)}+ \frac{k( \vert V_{2} \vert + \vert V_{1} \vert )}{ \vert V \vert \Gamma (2-\sigma )} \\ &{}+\frac{ \vert V_{2} \vert + \vert V_{1} \vert }{ \vert V \vert \Gamma (p-\sigma +1)}\sum_{j=1}^{m} \zeta _{j} ^{p-\sigma } + \frac{ \vert \varepsilon _{2} V_{2}-\varepsilon _{1} V_{4} \vert + \vert \varepsilon _{1} V_{3}+\varepsilon _{2} V_{1} \vert }{ \vert V \vert \Gamma (p-\sigma +2)} \Biggr) < 1. \end{aligned}$$
(19)

Then the nonlinear thermostat GFBVP (3) has exactly one solution.

Proof

By following the same arguments of the calculations used in Theorem 3.2 together with the hypotheses of Theorem 3.3, we write

$$\begin{aligned} & \bigl\vert \mathbb{K}x(s)-\mathbb{K}y(s) \bigr\vert \\ &\quad \leq \Biggl[\frac{1}{\Gamma (p+1)}+\frac{k( \vert V_{2} \vert + \vert V_{1} \vert )}{ \vert V \vert }+ \frac{ \vert V_{2} \vert + \vert V_{1} \vert }{ \vert V \vert \Gamma (p+1)} \sum_{j=1}^{m} \zeta _{j} ^{p} \\ &\qquad {}+ \frac{ \vert \varepsilon _{2} V_{2}-\varepsilon _{1} V_{4} \vert + \vert \varepsilon _{1} V_{3}+\varepsilon _{2} V_{1} \vert }{ \vert V \vert \Gamma (p+2)} \Biggr] \\ &\qquad {}\times \sup_{s\in J} \bigl\vert \mathfrak{g} \bigl(s, \beta x(s), {}^{c} \mathfrak{D}^{\sigma }x(s), \mathcal{I}^{\rho }x(s) \bigr)-\mathfrak{g} \bigl(s, \beta y(s), {}^{c}\mathfrak{D}^{\sigma }y(s), \mathcal{I}^{\rho }y(s) \bigr) \bigr\vert \\ &\quad \leq R \Biggl[\frac{1}{\Gamma (p+1)}+\frac{k( \vert V_{2} \vert + \vert V_{1} \vert )}{ \vert V \vert }+ \frac{ \vert V_{2} \vert + \vert V_{1} \vert }{ \vert V \vert \Gamma (p+1)}\sum_{j=1}^{m} \zeta _{j} ^{p} \\ &\qquad {}+ \frac{ \vert \varepsilon _{2} V_{2}-\varepsilon _{1} V_{4} \vert + \vert \varepsilon _{1} V_{3}+\varepsilon _{2} V_{1} \vert }{ \vert V \vert \Gamma (p+2)} \Biggr] \\ &\qquad {}\times \sup_{s\in J} \bigl[\beta \bigl\vert x(s)-y(s) \bigr\vert + \bigl\vert {}^{c} \mathfrak{D}^{\sigma }x(s)-{}^{c} \mathfrak{D}^{\sigma }y(s) \bigr\vert + \bigl\vert \mathcal{I}^{\rho }x(s)-\mathcal{I}^{\rho }y(s) \bigr\vert \bigr] \\ &\quad \leq R \Biggl[\frac{1}{\Gamma (p+1)}+\frac{k( \vert V_{2} \vert + \vert V_{1} \vert )}{ \vert V \vert }+ \frac{ \vert V_{2} \vert + \vert V_{1} \vert }{ \vert V \vert \Gamma (p+1)}\sum_{j=1}^{m} \zeta _{j} ^{p} \\ &\qquad {}+ \frac{ \vert \varepsilon _{2} V_{2}-\varepsilon _{1} V_{4} \vert + \vert \varepsilon _{1} V_{3}+\varepsilon _{2} V_{1} \vert }{ \vert V \vert \Gamma (p+2)} \Biggr] \\ &\qquad {}\times \biggl( \biggl(\beta +\frac{1}{\Gamma (\rho +1)} \biggr) \sup _{s \in J} \bigl\vert x(s)-y(s) \bigr\vert + \sup _{s\in J} \bigl\vert {}^{c} \mathfrak{D}^{\sigma }x(s)-{}^{c} \mathfrak{D}^{\sigma }y(s) \bigr\vert \biggr) \\ &\quad \leq R \Biggl[\frac{1}{\Gamma (p+1)}+\frac{k( \vert V_{2} \vert + \vert V_{1} \vert )}{ \vert V \vert }+ \frac{ \vert V_{2} \vert + \vert V_{1} \vert }{ \vert V \vert \Gamma (p+1)}\sum_{j=1}^{m} \zeta _{j} ^{p} \\ &\qquad {}+ \frac{ \vert \varepsilon _{2} V_{2}-\varepsilon _{1} V_{4} \vert + \vert \varepsilon _{1} V_{3}+\varepsilon _{2} V_{1} \vert }{ \vert V \vert \Gamma (p+2)} \Biggr] \\ &\qquad {}\times \Bigl( \sup_{s\in J} \bigl\vert x(s)-y(s) \bigr\vert + \sup_{s\in J} \bigl\vert {}^{c} \mathfrak{D}^{\sigma }x(s)-{}^{c} \mathfrak{D}^{\sigma }y(s) \bigr\vert \Bigr). \end{aligned}$$

Similarly, we obtain

$$\begin{aligned} & \bigl\vert {}^{c} \mathfrak{D}^{\sigma } \mathbb{K}x(s)-{}^{c} \mathfrak{D}^{\sigma }\mathbb{K}y(s) \bigr\vert \\ &\quad \leq R \Biggl[\frac{1}{\Gamma (p-\sigma +1)}+ \frac{k( \vert V_{2} \vert + \vert V_{1} \vert )}{ \vert V \vert \Gamma (2-\sigma )} \\ &\qquad {} +\frac{ \vert V_{2} \vert + \vert V_{1} \vert }{ \vert V \vert \Gamma (p-\sigma +1)}\sum_{j=1}^{m} \zeta _{j} ^{p-\sigma } \\ &\qquad {}+ \frac{ \vert \varepsilon _{2} V_{2}-\varepsilon _{1} V_{4} \vert + \vert \varepsilon _{1} V_{3}+\varepsilon _{2} V_{1} \vert }{ \vert V \vert \Gamma (p-\sigma +2)} \Biggr] \\ &\qquad {}\times \Bigl( \sup_{s\in J} \bigl\vert x(s)-y(s) \bigr\vert + \sup_{s\in J} \bigl\vert {}^{c} \mathfrak{D}^{\sigma }x(s)-{}^{c} \mathfrak{D}^{\sigma }y(s) \bigr\vert \Bigr). \end{aligned}$$

Thus,

$$\begin{aligned} \Vert \mathbb{K}x-\mathbb{K}y \Vert _{X}\leq{} & R \Biggl( \frac{1}{\Gamma (p+1)}+\frac{k( \vert V_{2} \vert + \vert V_{1} \vert )}{ \vert V \vert } \\ &{}+\frac{ \vert V_{2} \vert + \vert V_{1} \vert }{ \vert V \vert \Gamma (p+1)}\sum_{j=1}^{m} \zeta _{j} ^{p} \\ &{}+ \frac{ \vert \varepsilon _{2} V_{2}-\varepsilon _{1} V_{4} \vert + \vert \varepsilon _{1} V_{3}+\varepsilon _{2} V_{1} \vert }{ \vert V \vert \Gamma (p+2)} \\ &{}+\frac{1}{\Gamma (p-\sigma +1)}+ \frac{k( \vert V_{2} \vert + \vert V_{1} \vert )}{ \vert V \vert \Gamma (2-\sigma )}+ \frac{ \vert V_{2} \vert + \vert V_{1} \vert }{ \vert V \vert \Gamma (p-\sigma +1)}\sum _{j=1}^{m} \zeta _{j} ^{p-\sigma } \\ &{}+ \frac{ \vert \varepsilon _{2} V_{2}-\varepsilon _{1} V_{4} \vert + \vert \varepsilon _{1} V_{3}+\varepsilon _{2} V_{1} \vert }{ \vert V \vert \Gamma (p-\sigma +2)} \Biggr) \Vert x-y \Vert _{X}. \end{aligned}$$

It yields \(\|\mathbb{K}x-\mathbb{K}y \|_{X}\leq \gamma \|x-y \|_{X}\), \(\forall x,y\in X\). Now, from the assumption \(\gamma <1\) and the Banach contraction principle, we conclude that \(\mathbb{K}\) admits a unique fixed point which represents the unique solution of our nonlinear thermostat GFBVP (3). □

4 Numerical solutions via Bernstein polynomials

In the first place, we describe the basic formulation of Bernstein polynomials which are necessary to derive our developed results.

Definition 4.1

[41] The \(m+1\) Bernstein basis polynomials of degree m are defined on \([0,1]\) by

$$ b_{j,m}(z)=\binom{m}{j}z^{j}(1-z)^{m-j}, \quad 0\leq j\leq m, $$

where \(\binom{m}{j}=\frac{m!}{j!(m-j)!} \).

A recursive expression also can be used to formulate the Bernstein basis polynomials on the interval \([0,1]\) such that the Bernstein polynomials of \((j,m)\)th degree can be rewritten as

$$ b_{j,m}(z)=(1-z)b_{j,m-1}(z)+zb_{j-1,m-1}(z). $$

We can easily show that each of Bernstein basis polynomials is positive and also the sum of all Bernstein basis polynomials is equal to unity for any real z belonging to the interval \([0,1]\); in other words, \(\sum_{j=0}^{m}b_{j,m}(z)=1\).

It is easy to show that any given polynomial of degree m can be developed as a linear combination of basic functions

$$ \phi (z)=\sum_{j=0}^{m}c_{j}b_{j,m}(z)=C^{T}B(z), \quad m\geq 1, $$

in which the Bernstein vector \(B(z)\) and the Bernstein coefficient vector C are defined as

$$ B(z)= \bigl[b_{0,m}(z),b_{1,m}(z),\dots ,b_{m,m}(z) \bigr], $$

and \(C^{T}= [c_{0},c_{1},\dots ,c_{m} ]\) with

$$ c_{j}= \int _{0}^{1}\phi (z)d_{j,m}(z) \,\mathrm{d}z,\quad 0\leq j\leq m. $$
(20)

In [52], Juttler has explicitly represented \(d_{j,m}(z)\) by the following formula:

$$ d_{j,m}(z)=\sum_{k=0}^{m} \lambda _{j,k}b_{k,m}(z),\quad 0\leq j \leq m, $$
(21)

where for \(0\leq j\), \(k \leq m\),

$$ \lambda _{j,k}=\frac{(-1)^{j+k}}{\binom{m}{j}\binom{m}{k}}\sum _{i=0}^{ \min (j,k)}(2i+1)\binom{m+i+1}{m-j} \binom{m-i}{m-j} \binom{m+i+1}{m-k}\binom{m-i}{m-k}. $$
(22)

Furthermore,

$$ \mathcal{I}^{\nu }B(z) \simeq \mathbf{I}^{(\nu )}B(z), \quad \nu >0, $$
(23)

where \(\mathcal{I}^{\nu }\) denotes the \(\nu ^{th}\)-FRL-integral and \(\mathbf{I}^{(\nu )}\) represents the \((m+1)\times (m+1)\) operational matrix of the \(\nu ^{th}\)-FRL-integral.

Also, by using the binomial expansion of \((1-z)^{m-j}\), we can write

$$\begin{aligned} b_{j,m}(z)=&\binom{m}{j}z^{j}(1-z)^{m-j} \\ =&\binom{m}{j}z^{j} \Biggl(\sum _{k=0}^{m-j}(-1)^{k} \binom{m-j}{k}z^{k} \Biggr) \\ =&\sum_{k=0}^{m-j}(-1)^{k} \binom{m}{j}\binom{m-j}{k}z^{j+k} \\ =&\sum_{i=j}^{m}(-1)^{i-j} \binom{m}{j}\binom{m-j}{i-j}z^{i},\quad 0 \leq j\leq m. \end{aligned}$$
(24)

As we can find in [52], an approach for the direct least squares approximation with the help of Bernstein polynomials is based on the construction of the basis \(\{d_{0, m} (z), d_{1, m} (z),\dots , d_{m, m} (z)\}\) which represents the dual in Bernstein basis of mth-degree on \([0, 1]\). It is specified as

$$\begin{aligned} \int _{0}^{1}b_{j,m}(z)d_{k,m}(z) \mathrm{d}z =\delta _{jk},\quad 0 \leq j,k \leq m, \end{aligned}$$
(25)

where \(\delta _{jk}\) denotes the Kronecker symbol.

4.1 Fractional matrix of integration

The conclusion of the next theorem is useful for us.

Theorem 4.2

Let \(B(z)\) be the Bernstein vector introduced in (23) and \(\mathbf{I}^{(\nu )}\) be the \((m+1)\times (m+1)\) operational matrix of the \(\nu ^{th}\)-FRL-integral which is formulated by

$$ \mathbf{I}^{(\nu )} = \begin{pmatrix} w_{0, 0} & w_{0, 1} & \cdots & w_{0, j}&\cdots & w_{0, m} \\ w_{1, 0} & w_{1, 1} & \cdots & w_{1, j}&\cdots & w_{1, m} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ w_{i, 0} & w_{i, 1} & \cdots & w_{i, j}&\cdots & w_{i, m} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ w_{m, 0} & w_{m, 1} & \cdots & w_{m, j}&\cdots & w_{m, m} \end{pmatrix} . $$
(26)

Then we have

$$ w_{i, j} =\sum_{q=i}^{m} \sum_{k=0}^{m}(-1)^{q-i} \binom{m}{i} \binom{m-i}{q-i}\lambda _{jk}\mu _{qk} \frac{\Gamma (q+1)}{\Gamma (q+\nu +1)}, $$
(27)

where

$$ \mu _{qk}=\sum_{p=k}^{m} \frac{(-1)^{p-k}}{q+p+\nu +1}\binom{m}{k} \binom{m-k}{p-k}, $$

and \(\lambda _{jk}\) are the coefficients expressed by (22).

Proof

From expression (23) and by exploiting relationship (25) which connects Bernstein polynomials with their dual, we can write

$$ \mathbf{I}^{(\nu )}=\bigl\langle \mathcal{I}^{\nu }B(z),D^{T} \bigr\rangle , $$

where D denotes the vector of dual polynomials of Bernstein polynomials and \(\langle \mathcal{I}^{\nu }B(z),D^{T} \rangle \) stands for the \((m+1)\times (m+1)\)-matrix formulated as

$$ \bigl\langle \mathcal{I}^{\nu }B(z),D^{T} \bigr\rangle = \bigl\langle \mathcal{I}^{\nu }b_{i,m}(z),d_{j,m}(z) \bigr\rangle ,\quad 0\leq i, j\leq m. $$

Here, we have

$$ w_{ij}=\bigl\langle \mathcal{I}^{\nu }b_{i,m}(z),d_{j,m}(z) \bigr\rangle = \int _{0}^{1} \mathcal{I}^{\nu }b_{i,m}(z)d_{j,m}(z) \,\mathrm{d}z. $$

By applying (24), we get

$$ \mathcal{I}^{\nu }b_{i,m}(z)=\sum _{q=i}^{m}(-1)^{q-i} \binom{m}{i} \binom{m-i}{q-i}\frac{\Gamma (q+1)}{\Gamma (q+\nu +1)}. $$

Afterwards, in view of (21) we conclude that

$$\begin{aligned} w_{ij}=\sum_{q=i}^{m} \sum_{k=0}^{m}(-1)^{q-i} \binom{m}{i} \binom{m-i}{q-i}\lambda _{jk} \frac{\Gamma (q+1)}{\Gamma (q+\nu +1)} \int _{0}^{1} z^{q+\nu }b_{k,m}(z) \,\mathrm{d}z, \end{aligned}$$
(28)

but we have

$$\begin{aligned} \int _{0}^{1} z^{q+\nu }b_{k,m}(z) \mathrm{d}z=\sum_{p=k}^{m} \frac{(-1)^{p-k}}{q+p+\nu +1}\binom{m}{k}\binom{m-k}{p-k}=\mu _{qk}. \end{aligned}$$
(29)

Therefore, a combination of (28) and (29) ends the proof of our Theorem 4.2. □

4.2 Fractional matrix of derivative

We can write the derivative of \(B(z)\) as

$$ \frac{d B(z)}{dz}=\mathbf{D}^{(1)}B(z), $$
(30)

where \(\mathbf{D}^{(1)}\) stands for the \((m+1)\times (m+1)\)-operational matrix of derivative given in the following format:

$$ \mathbf{D}^{(1)}=AWB^{\star }. $$
(31)

For more details, we refer to [43, 53–55].

By applying (30), it is obvious that for each \(n\in \mathbb{N}\) we have

$$ \frac{d^{n} B(z)}{dz^{n}}= \bigl(\mathbf{D}^{(1)} \bigr)^{n}B(z). $$

Consequently,

$$ \mathbf{D}^{(n)}= \bigl(\mathbf{D}^{(1)} \bigr)^{n},\quad n=1,2,\dots $$

Now, in order to generalize the operational matrix of derivative, we indicate the following formulations.

For \(\nu > 0\), the \(\nu ^{th}\)-Caputo derivative of \(B(z)\) is given as

$$ {}^{c}\mathfrak{D}^{\nu }B(z)\simeq {}^{c}\mathbf{D}^{(\nu )}B(z), $$
(32)

in which \({}^{c}\mathbf{D}^{(\nu )}\) stands for the \((m+1)\times (m+1)\)-operational matrix of the \(\nu ^{th}\)-Caputo derivative which is given by

$$\begin{aligned} {}^{c}\mathbf{D}^{(\nu )} = \begin{pmatrix} \sum_{j=\lceil \nu \rceil }^{m}\omega _{0,j,0} & \sum_{j=\lceil \nu \rceil }^{m}\omega _{0,j,1} & \cdots & \sum_{j=\lceil \nu \rceil }^{m}\omega _{0,j,2}&\cdots & \sum_{j=\lceil \nu \rceil }^{m}\omega _{0,j,m} \\ \sum_{j=\lceil \nu \rceil }^{m}\omega _{1,j,0} & \sum_{j=\lceil \nu \rceil }^{m}\omega _{1,j,1} & \cdots & \sum_{j=\lceil \nu \rceil }^{m}\omega _{1,j,2}&\cdots & \sum_{j=\lceil \nu \rceil }^{m}\omega _{1,j,m} \\ \vdots & \vdots & \vdots & \vdots & \vdots &\vdots \\ \sum_{j=\lceil \nu \rceil }^{m}\omega _{i,j,0} & \sum_{j=\lceil \nu \rceil }^{m}\omega _{i,j,1} & \cdots & \sum_{j=\lceil \nu \rceil }^{m}\omega _{i,j,2}&\cdots & \sum_{j=\lceil \nu \rceil }^{m}\omega _{i,j,m} \\ \vdots & \vdots & \vdots & \vdots & \vdots &\vdots \\ \sum_{j=\lceil \nu \rceil }^{m}\omega _{m,j,0} & \sum_{j=\lceil \nu \rceil }^{m}\omega _{m,j,1} & \cdots & \sum_{j=\lceil \nu \rceil }^{m}\omega _{m,j,2}&\cdots & \sum_{j=\lceil \nu \rceil }^{m}\omega _{m,j,m} \end{pmatrix}, \end{aligned}$$
(33)

where

$$ \omega _{i,j,p}=(-1)^{j-i}\binom{m}{i} \binom{m-i}{j-i} \frac{\Gamma (j+1)}{\Gamma (j+1-\nu )}\sum_{k=0}^{m} \lambda _{pk} \mu _{kj}, $$

\(\lambda _{pk}\) is defined as (22) and

$$ \mu _{kj}=\sum_{s=k}^{m} \frac{(-1)^{s-k}}{j-\nu +s+1} \binom{m-k}{s-k}. $$

5 Some simulative examples

Before illustrating our theoretical results by some numerical examples, we present, in general, the principle of the Bernstein collocation method applied to our problem (3) to obtain an accurate numerical solution. For this fact, let us consider for all \(s \in J \)

$$\begin{aligned} {}^{c}\mathfrak{D}^{p} u(s) = \mathfrak{g} \bigl(s, \beta u(s), {}^{c} \mathfrak{D}^{\sigma }u(s), \mathcal{I}^{\rho }u(s) \bigr), \end{aligned}$$
(34)

with the following conditions:

$$\begin{aligned} {}^{c}\mathfrak{D}^{1} u(0)= \varepsilon _{1} \int _{0}^{1} u(r)\,\mathrm{d}r,\qquad \sum _{j=1}^{m} u( \zeta _{j} ) + k {}^{c} \mathfrak{D}^{ p -1}u(1) = \varepsilon _{2} \int _{0}^{1} u(r)\,\mathrm{d}r. \end{aligned}$$
(35)

Now, to determine an approximation of the exact solution \(u(s)\) by Bernstein polynomials, we utilize the FRL-integral of Bernstein polynomials with the operational matrix of the Caputo derivative used in [53].

We know that the approximate solution of \(u(s)\) by Bernstein polynomials is defined by

$$\begin{aligned} u(s)\approx \phi (s)=\sum_{j=0}^{m}c_{j}b_{j,m}(s)=C^{T}B(s), \end{aligned}$$
(36)

such that C is an indeterminate vector. By replacing the approximate solution given by (36) in (34) and (35), we can write respectively

$$\begin{aligned} C^{T}{}^{c}\mathbf{D}^{(p)}B(s)= \mathfrak{g} \bigl(s, \beta C^{T} B(s),C^{T} {}^{c}\mathbf{D}^{(\sigma )} B(s),C^{T} \mathbf{I}^{(\rho )} B(s) \bigr) \end{aligned}$$
(37)

and

$$\begin{aligned} &-c_{0}m+c_{1}m=\frac{\varepsilon _{1}}{m+1}C^{T} \mathbf{1} , \end{aligned}$$
(38)
$$\begin{aligned} &C^{T}\sum_{j=1}^{3}B( \zeta _{j})+k C^{T}{}^{c} \mathbf{D}^{ (p -1)}B(1)= \frac{\varepsilon _{2}}{m+1}C^{T}\mathbf{1} , \end{aligned}$$
(39)

where \(\mathbf{1}=[\underbrace{1,1,\dots ,1}_{\text{m+1 }}]^{T}\).

For convenience of computations, we consider equidistant points and the roots of the Legendre polynomial of degree (m-1) in \([0,1]\). So, to obtain the solution \(u(s)\), we collocate equation (37) at \((m-1)\) points together with equations (38) and (39). Therefore, we get \((m+1)\) equations with \((m+1)\) indeterminate coefficients. Consequently, the approximate solution can be determined.

At the moment, we are ready to illustrate the Bernstein collocation method with some simulative examples.

Example 5.1

According to the nonlinear thermostat GFBVP (3), consider

$$ \textstyle\begin{cases} {}^{c} \mathfrak{D}^{\frac{5}{4}} u(s) = \phi (s)+ \frac{s}{10}u(s)-\frac{\sin (s)}{20} {}^{c} \mathfrak{D}^{ \frac{1}{4}}u(s) -\frac{1}{11}\mathcal{I}^{\frac{7}{3}} u(s), \\ {}^{c} \mathfrak{D}^{1}u(0)=0, \qquad \sum_{j=1}^{3}u (\frac{j}{j+1} )+\frac{11\Gamma (\frac{11}{4} )}{118} {}^{c} \mathfrak{D}^{\frac{1}{4}}u(1) =\frac{3407}{720}\int _{0}^{1}u(r)\, \mathrm{d}r. \end{cases} $$
(40)

In this example, we have \(p=\frac{5}{4}\), \(\sigma =\frac{1}{4}\), \(\rho =\frac{7}{3}\), \(\varepsilon _{1}=0\), \(\varepsilon _{2}= \frac{3407}{720}\), \(\beta = \frac{1}{10}\), \(k=\frac{11\Gamma (\frac{11}{4} )}{118}\), and \(\zeta _{j}=\frac{j}{j+1}\) for \(j\in \{1,2,3\} \), and

$$\begin{aligned} \phi (s)={}&\frac{3}{\Gamma (\frac{7}{4} )}s^{\frac{3}{4}}+ \frac{24}{\Gamma (\frac{11}{4} )}s^{\frac{7}{4}}- \frac{1}{10} \bigl(s^{3}+2s^{4} \bigr)+\sin (s) \biggl( \frac{1}{10\Gamma (\frac{11}{4} )}s^{\frac{7}{4}} + \frac{6}{5\Gamma (\frac{15}{4} )}s^{\frac{11}{4}} \biggr) \\ &{}+ \frac{2}{11\Gamma (\frac{16}{3} )}s^{\frac{13}{3}}+ \frac{48}{11\Gamma (\frac{19}{3} )}s^{\frac{16}{3}}. \end{aligned}$$

We take \(w(x,y)=1\), \(\forall x,y\in X\) and \(\varphi (s)=\frac{1}{2}s\) for any \(s\in J\). Therefore, it is easy to verify that our nonlinear thermostat GFBVP (40) satisfies all assumptions of Theorem 3.2, and its exact solution is \(u(s)=s^{2}+2s^{3}\).

Now, we substitute \(u(s)\) by \(C^{T}B(s)\) in the nonlinear thermostat GFBVP (40), from which we get the following system:

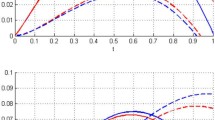
$$ \textstyle\begin{cases} C^{T} {}^{c}\mathbf{D}^{ (\frac{5}{4} )} B(s) = \phi (s)+C^{T}\frac{s}{10}B(s)-C^{T}\frac{\sin (s)}{20}{}^{c} \mathbf{D}^{ (\frac{1}{4} )}B(s) -C^{T}\frac{1}{11}\mathbf{I}^{ (\frac{7}{3} )} B(s), \\ -c_{0}+c_{1}=0, \qquad C^{T}\sum_{j=1}^{3}B ( \frac{j}{j+1} )+\frac{11\Gamma (\frac{11}{4} )}{118}C^{T} {}^{c} \mathbf{D}^{ (\frac{1}{4} )}B(1) =\frac{3407}{720(m+1)}C^{T} \mathbf{1}. \end{cases} $$

In Table 1 we list the absolute errors \(|u_{m}(s)-u(s)|\) of approximate solution \(u_{m}(s)\) computed via the roots of shifted Legendre polynomials at \(m=4\). Also, the graphs are plotted in Fig. 1.

Figure 1
figure 1

The graphs of the exact solution and the approximate solution truncated at level \(m=4\)

Full size image
Table 1 Legendre polynomials and exact solution at different values of variable with absolute error
Full size table

Now, we investigate the next example.

Example 5.2

According to the nonlinear thermostat GFBVP (3), consider

$$ \textstyle\begin{cases} {}^{c} \mathfrak{D}^{\frac{5}{3}} u(s) = \phi (s)+ \frac{s}{10}u(s)+\frac{\sin (s)}{2} {}^{c} \mathfrak{D}^{\frac{1}{5}}u(s) -\frac{7s}{100}\mathcal{I}^{\frac{7}{3}} u(s), \\ {}^{c} \mathfrak{D}^{1} u(0)=0, \qquad \sum_{j=1}^{3}u (\sqrt[3]{\frac{1}{(4-j)(5-j)}} )+ \frac{\Gamma (\frac{10}{3} )}{6} {}^{c} \mathfrak{D}^{ \frac{2}{3}}u(1) =7\int _{0}^{1}u(r)\,\mathrm{d}r, \end{cases} $$
(41)

where

$$\begin{aligned} \phi (s)=&\frac{6}{\Gamma (\frac{7}{3} )}s^{\frac{4}{3}}- \frac{s^{4}}{10}- \frac{3\sin (s)}{\Gamma (\frac{19}{5} )}s^{ \frac{14}{5}}+\frac{21s}{50\Gamma (\frac{19}{3} )}s^{ \frac{16}{3}} . \end{aligned}$$

In the present example, we have \(p=\frac{5}{3}\), \(\sigma =\frac{1}{5}\), \(\rho =\frac{7}{3}\), \(\varepsilon _{1}=0\), \(\varepsilon _{2}= 7\), \(\beta =\frac{1}{10}\), \(k=\frac{\Gamma (\frac{10}{3} )}{6}\), and \(\zeta _{j}=\sqrt[3]{\frac{1}{(4-j)(5-j)}}\) for \(j\in \{1,2,3\}\).

We take \(w(x,y)=x\), \(\forall x,y\in X\) and \(\varphi (s)=\frac{1}{2}s\), \(\forall s\in J\). Hence, all assumptions of Theorem 3.2 are satisfied and the exact solution of the nonlinear thermostat GFBVP (41) is given by \(u(s)=s^{3}\). By the same arguments used in problem (40), we get the following system:

$$ \textstyle\begin{cases} C^{T} {}^{c}\mathbf{D}^{ (\frac{5}{3} )} B(s) = \phi (s)+C^{T}\frac{s}{10}B(s)+C^{T}\frac{\sin (s)}{2}{}^{c} \mathbf{D}^{ (\frac{1}{5} )}B(s) -C^{T}\frac{7s}{100} \mathbf{I}^{ (\frac{7}{3} )} B(s), \\ -c_{0}+c_{1}=0, \qquad C^{T}\sum_{j=1}^{3}B ( \sqrt[3]{\frac{1}{(4-j)(5-j)}} )+ \frac{\Gamma (\frac{10}{3} )}{6}C^{T} {}^{c} \mathbf{D}^{ ( \frac{2}{3} )}B(1) =\frac{7}{m+1}C^{T}\mathbf{1}. \end{cases} $$

Now, we list the absolute errors \(|u_{m}(s)-u(s)|\) of approximate solution \(u_{m}(s)\) by utilizing the roots of shifted Legendre polynomials at \(m=7\) in Table 2, and the graphs are plotted in Fig. 2.

Figure 2
figure 2

The graphs of the exact solution and the approximate solution truncated at \(m=7\)

Full size image
Table 2 Legendre polynomials and exact solution at different values of variable with absolute error
Full size table

Example 5.3

According to the nonlinear thermostat GFBVP (3), consider

$$ \textstyle\begin{cases} {}^{c} \mathfrak{D}^{\frac{7}{5}} u(s) = \phi (s)+ \frac{0.3 u(s)}{15+2 u^{2}(s)}+\frac{s\sin (s)}{10} {}^{c} \mathfrak{D}^{\frac{1}{3}}u(s) +\frac{1}{14 (1+e^{-s} )} \mathcal{I}^{\frac{7}{4}} u(s), \\ {}^{c}\mathfrak{D}^{1} u(0)= 3 \int _{0}^{1} u(r)\, \mathrm{d}r, \\ \sum_{j=1}^{2}u (\frac{j}{j+1} )+ \frac{13\Gamma (\frac{13}{5} )\Gamma (\frac{8}{5} )}{72 (\Gamma (\frac{13}{5} )-\Gamma (\frac{8}{5} ) )} {}^{c} \mathfrak{D}^{\frac{2}{5}}u(1) =3\int _{0}^{1}u(r)\, \mathrm{d}r, \end{cases} $$
(42)

where

$$\begin{aligned} \phi (s)={}&\frac{2}{\Gamma (\frac{8}{5} )}s^{\frac{3}{5}}- \frac{0.3 (s^{2}-2s )}{15+2 (s^{2}-2s )}- \frac{1}{5\Gamma (\frac{8}{3} )}s^{\frac{8}{3}} + \frac{1}{5\Gamma (\frac{8}{3} )}s^{\frac{5}{3}} - \frac{1}{7\Gamma (\frac{19}{4} )}\times \frac{s^{\frac{15}{4}}}{1+e^{-s}} \\ &{}+\frac{1}{7\Gamma (\frac{15}{4} )}\times \frac{s^{\frac{11}{4}}}{1+e^{-s}}. \end{aligned}$$

In this example, we have \(p=\frac{7}{54}\), \(\sigma =\frac{1}{3}\), \(\rho =\frac{7}{4}\), \(\varepsilon _{1}=3\), \(\varepsilon _{2}=3\), \(\beta =0.3\), \(k= \frac{13\Gamma (\frac{13}{5} ) \Gamma (\frac{8}{5} )}{72 (\Gamma (\frac{13}{5} )-\Gamma (\frac{8}{5} ) )}\), and \(\zeta _{j}=\frac{j}{j+1}\) for \(j\in \{1,2\}\). Take \(R=0.03\). Then, by direct calculation, we find

$$ \beta +\frac{1}{\Gamma (\rho +1)}\approx 0.9218\ldots< 1, $$

and \(\gamma \approx 0.8922\ldots<1\). Consequently, Theorem 3.3 ensures the existence of a unique solution of the nonlinear thermostat GFBVP (42).

6 Conclusions

In this work, we introduced a new generalized version of the mathematical model of the thermostat in the form of the nonlinear GFBVP given as (3). The existence property for its solutions was established via a special form of contractions and μ-admissible maps. The uniqueness property was verified by the Banach principle. Further, we used the Bernstein operational matrix of the Caputo fractional derivative and the Bernstein operational matrix of FRL-integral which are necessary to obtain accurate numerical solutions to the nonlinear thermostat GFBVP (3) via Bernstein polynomials. We have designed two examples to illustrate the accuracy of the numerical method in finding the exact and approximate solutions. Then we checked the uniqueness property in the third example. For the next works, we will apply these methods on different mathematical models designed by nonsingular operators.