1 Introduction

During the past decades, several mathematical models have been investigated to model prey–predator systems [1–16]. The understanding of the relationship between herbivores and plants is extremely important in the behavior of the ecosystems. Those studies have been implemented in dynamical systems of organic models incorporating integer-order differential equations. However, in these models, the effects of long-range memories are neglected. Recently, mathematical systems with fractional order (FO) have become more worthy than classical systems as FO models provide the description of the memory effects [17–29]. Owolabi et al. in [30] studied local and global stability of the fractional dynamical system of prey–predator with Holling type-II involving a time delay. Javidi and Nyamoradi provided a detailed study of the local stability of the FO predator–prey model [31]. Alkahtani in [32] investigated the FO triadic predator–prey model. This system was produced utilizing the latest FO differentiation related to the function of generalized Mittag-Leffler (GML). In [33], the authors proposed harvesting terms of a FO delayed predator–prey system. The stability of the model was studied and numerical results were presented to verify the theoretical outcomes. In [34], a FO singular predator–prey model with Holling type-II functional response was studied. The authors investigated the local stability and the solvability condition of this model. Numerical simulations were obtained for different values of the order of the FO derivative. Owolabi in [35] analyzed a FO predator–prey model. The Riemann–Liouville operator based on the pseudo-spectral technique was considered.

In this work, we develop a FO predator–prey system with constant and variable-order Atangana–Baleanu FO operator in the Liouville–Caputo sense. We assume the deterministic integer-order predator–prey model analyzed and studied by Li in [36]. Our system assumes a more realistic prey–predator model with two properties with and without time delay. The mathematical model is built using this FO derivative with the generalized Mittag-Leffler law as a kernel caused by nonlocality of the model and broad usability of the GML function. The Mittag-Leffler kernel applied in Atangana–Baleanu FO differentiation ordinarily exists in various physical models as a generalized exponential decay and as power-law asymptotic for a very large time.

The paper is organized as follows: In Sect. 2, the FO model involving Atangana–Baleanu–Caputo (ABC) operators is disputed. Results are displayed in Sect. 3 numerically, and conclusion is given in Sect. 4.

2 Predator–prey model

In this paper, we study the mathematical system proposed by Li in [36] and assume Atangana–Baleanu FO operator with constant and variable order. We aim to manufacture a superior estimate model to the real dynamics of a predator–prey system involving a prey refuge among heterogeneous populations. In this investigation, two FO models are treated. The first one depends on the Atangana–Baleanu–Caputo FO differential equations with constant order. We present the existence of positive solutions for the unique proposed design. We study the uniqueness and existence of the solutions. Furthermore, we consider this model involving FO differential equations of Atangana–Baleanu–Caputo type with variable order. Variable order is fixed as a smooth function to specify time differentiation bounded in (0;1]. To get simulation solutions for the suggested system, we employ the Adams process. Finally, the second one assumes a FO model with time delay; in this scenario, we portray the computative technique focused on the Adams–Bashforth–Moulton method to clarify FO delay differential equations relative to variable order through the Atangana–Baleanu–Caputo FO derivative.

In the first case, the system considered is defined as [36]

$$\begin{aligned}& {}^{ABC}_{0}{\mathcal{D}}_{\tau }^{\epsilon } \mathbf{x}(\tau )=h \mathbf{x}(\tau ) \biggl(1-\frac{\mathbf{x}(\tau )}{k} \biggr)-\lambda (1- \mathfrak{M})\mathbf{x}(\tau )\mathbf{y}(\tau ),\quad \mathbf{x}( \tau _{0})=\mathbf{x}_{\tau {(0)}}, \\& {}^{ABC}_{0}{\mathcal{D}}_{\tau }^{\varsigma } \mathbf{y}(\tau )=e \lambda (1-\mathfrak{M})\mathbf{x}(\tau )\mathbf{y}(\tau )-d \mathbf{y}( \tau ),\quad \xi (\tau _{0})=\mathbf{y}_{\tau {(0)}}, \end{aligned}$$
(2.1)

with the initial conditions \(\mathbf{x}(\tau _{0})=\mathbf{x}_{\tau {(0)}}\) and \(\mathbf{y}(\tau _{0})=\mathbf{y}_{\tau {(0)}}\). Fractional-order operator used in the proposed model (2.1) is in the ABC sense, \({}^{ABC}_{0}{\mathcal{D}}_{\tau }^{\epsilon }\). FO derivative with constant order is defined as [37]

$$ {}^{ABC}_{0}{\mathcal{D}}_{\tau }^{\epsilon } \bigl\{ f(\tau ) \bigr\} = \frac{\varrho (\epsilon )}{\mathbf{r}_{1}-\epsilon } \int _{0}^{\tau }\frac{d^{\mathbf{r}_{1}}}{d\tau ^{\mathbf{r}_{1}}}{f}(\wp )E_{ \epsilon } \biggl[-\epsilon \frac{(\tau -\wp )^{\epsilon }}{\mathbf{r}_{1} -\epsilon } \biggr]\,d\wp , $$
(2.2)

where the function \(\varrho (\epsilon )\) represents normalization, \(1=\varrho (0)=\varrho (1)\). FO operator is using the Mittag-Leffler rule as a nonsingular and nonlocal kernel, where \(E_{\epsilon }\) is a Mittag-Leffler function of one parameter

$$ E_{\epsilon }(v)=\sum_{r=0}^{\infty } \frac{v^{r}}{\Gamma (\epsilon r+1)} \quad r\in \mathbb{C}; \mathbb{R}(\epsilon )>0. $$
(2.3)

The Atangana–Baleanu FO integral of function \(f(\tau )\) with order ϵ is characterized as [37]

$$ {}^{AB}_{0}{\mathcal{I}}_{\tau }^{\epsilon } \bigl\{ f(\tau ) \bigr\} =f(\tau )-f(0)= \frac{1-\epsilon }{\varrho (\epsilon )}f(\tau )+ \frac{\epsilon }{\varrho (\epsilon )\Gamma (\epsilon )} \int _{0}^{\tau }f( \wp ) (\tau -\wp )^{\epsilon -1} \,d \wp . $$
(2.4)

System (2.1) can be made more realistic as the prey and the predators should not follow the same FO dynamics. For this reason, we provide two various orders of the fractional-differential derivatives \(\epsilon \in (0,1]\) and \(\varsigma \in (0,1]\).

In our model, \(\mathbf{x}(\tau )\) and \(\mathbf{y}(\tau )\) represent prey and predator populations at time τ, respectively. The environmental carrying capacity of prey and intrinsic growth rate and population are denoted by k and r, respectively; c represents predators attack rate on prey population; e denotes recently conceived predators for each prey catch; d represents the predator mortality rate. This system involves a constant shelter covering \(\mathfrak{M}\mathbf{x}(\tau )\) of the prey such that \(m\in [0,1)\), allowing \((1-\mathfrak{M})\mathbf{x}(\tau )\) of the prey be accessible to the predator [36]. These constants are all positive.

On the other hand, compared with constant FO systems, the research on variable FO differential equations is relatively new, and a numerical approximation of these equations is still at an early stage of development [37–49]. The variable FO operator of Atangana–Baleanu type in the sense of Liouville–Caputo is given as follows:

$$ \begin{aligned}[b] & {}^{ABC}_{0} { \mathcal{D}}_{\tau }^{\epsilon (\tau )} \bigl\{ f(\tau ) \bigr\} \\ &\quad = \frac{\varrho (\epsilon (\tau ))}{1-\epsilon (\tau )} \int _{0}^{\tau } \frac{d}{d\tau }f(\wp ) E_{\epsilon (\tau )} \biggl[ - \epsilon (\tau ) \frac{(\tau -\wp )^{\epsilon (\tau )}}{1-\epsilon (\tau )} \biggr] \,d \wp , \quad 0< \epsilon (\tau ) \leq 1,\end{aligned} $$
(2.5)

where the normalized function \(\varrho (\epsilon (\tau ))=1- \epsilon (\tau ) + \frac{\epsilon (\tau )}{\Gamma (\epsilon (\tau ))}\).

A variable FO integral in the sense of Atangana–Baleanu is listed as follows:

$$ \begin{aligned}[b] {}^{AB}_{0} { \mathcal{I}}_{\tau }^{\epsilon (\tau )} \bigl\{ f(\tau ) \bigr\} &= \frac{1-\epsilon (\tau )}{\varrho (\epsilon (\tau ))} f(\tau ) \\ &\quad{} + \frac{\epsilon (\tau )}{\varrho (\epsilon (\tau ))\Gamma (\epsilon (\tau ))} \int _{0}^{\tau } f(\wp ) (\tau -\wp )^{\epsilon (\tau )-1} \,d \wp , \quad \mathbf{r}_{1}-1< \epsilon (\tau )\leq \mathbf{r}_{1}.\end{aligned} $$
(2.6)

System (2.1) with the support of variable FO Atangana–Baleanu–Caputo derivatives produces

$$\begin{aligned}& {}^{ABC}_{0}{\mathcal{D}}_{\tau }^{\epsilon (\tau )} \mathbf{x}(\tau )=h \mathbf{x}(\tau ) \biggl(1-\frac{\mathbf{x}(\tau )}{k} \biggr)-\lambda (1- \mathfrak{M})\mathbf{x}(\tau )\mathbf{y}(\tau ), \\& {}^{ABC}_{0}{\mathcal{D}}_{\tau }^{\varsigma (\tau )} \mathbf{y}(\tau )=e \lambda (1-\mathfrak{M})\mathbf{x}(\tau )\mathbf{y}(\tau )-d \mathbf{y}( \tau ). \end{aligned}$$
(2.7)

In the second case, we consider that the predatory-prey species is not an instantaneous operation; for this case, the model given by Eq. (2.1) is defined as

$$\begin{aligned}& {}^{ABC}_{0}{\mathcal{D}}_{\tau }^{\epsilon (\tau )} \mathbf{x}(\tau )=h \mathbf{x}(\tau -\kappa ) \biggl(1-\frac{\mathbf{x}(\tau -\kappa )}{k} \biggr)- \lambda (1-\mathfrak{M})\mathbf{x}(\tau -\kappa )\mathbf{y}( \tau ), \\& {}^{ABC}_{0}{\mathcal{D}}_{\tau }^{\varsigma (\tau )} \mathbf{y}(\tau )=e \lambda (1-\mathfrak{M})\mathbf{x}(\tau -\kappa )\mathbf{y}( \tau )-d \mathbf{y}(\tau ), \end{aligned}$$
(2.8)

where the variable FO operator \({}^{ABC}_{0}{\mathcal{D}}\tau ^{\epsilon (\tau )}\) denotes Atangana–Baleanu–Caputo for each operator, and time delay κ represents the gestation delay.

3 Predator–prey model involving constant-order fractional derivative

First case

This portion is to investigate the existence and uniqueness of the solutions under constant order assuming the Atangana–Baleanu–Caputo FO operator.

Existence and uniqueness of the solution

For every real-valued continuous function, let \(\mathbf{y}=\lambda [a^{\circ },a^{\circ }_{1}]\) be the Banach space in \([a^{\circ },a^{\circ }_{1}]\), containing the subnorm and shaft Φ ={\(\mathbf{x},\mathbf{y} \in \mathbf{y}\), \(\mathbf{x}(\tau )>0\) and \(\mathbf{y}(\tau )\geq 0\), \(a^{\circ }\leq \tau \leq a^{\circ }_{1}\)}. Let Ψ be a real Banach space with a cone H. H initiates a restricted order in the succeeding approach [45]

$$ u\leq v \quad \rightarrow \quad v-u \in H. $$
(3.1)

The order interval for each \(u, v \in \Phi \) is specified as \(\langle a^{\circ }, a^{\circ }_{1}\rangle =\{f\in \Psi : a^{\circ }\leq f\leq a^{\circ }_{1} \}\). A cone Π speaks to typical if one can locate a positive constant α with the end goal that \(\mathbf{r}, l, \in \Pi \), \(\Upsilon <\mathbf{r}<l \rightarrow \Vert \mathbf{r} \Vert \leq \alpha \Vert l \Vert \), where ϒ is the zero component of Π.

Theorem 1

Let a Banach space Z have a closed set subspace H and \(T:H\rightarrow H\) with Lipschitz constant \(\upsilon <1\) be a contraction mapping so that T carries a fixed point \(\tau ^{*}\in H\). Furthermore, a sequence \(\{\tau _{\mathfrak{M}}\}\) is interpreted as \(\tau _{\mathfrak{M}+1}=T\tau _{\mathfrak{M}}\) (\(\mathfrak{M}=0,1,2,\ldots \)) for a random point \(\tau _{0}\in H\), then \(\tau _{\mathfrak{M}}\rightarrow \tau ^{*}\) in H for a large number \(\mathfrak{M}\) and \(l(\tau _{\mathfrak{M}},\tau ^{*})\leq (\upsilon ^{\mathfrak{M}}/(1- \upsilon ))l(\tau _{1},\tau _{0})\) [45]. To study the existence of solutions, let us assume the system given by Eq. (2.1).

Model (2.1) is identical to that of Volterra when it is integral in the Atangana–Baleanu sense. We apply the AB fractional integral in Eq. (2.1) to get the system

$$\begin{aligned}& \begin{aligned} \mathbf{x}(\tau )-\mathbf{x}(0)={}& \frac{1-\epsilon }{\varrho (\epsilon )} \biggl\{ h \mathbf{x}(\tau ) \biggl(1- \frac{\mathbf{x}(\tau )}{k} \biggr)-\lambda (1-\mathfrak{M}) \mathbf{x}( \tau )\mathbf{y}(\tau ) \biggr\} \\ &{} +\frac{\epsilon }{\varrho (\epsilon )\Gamma (\epsilon )} \int _{0}^{ \tau }(\tau -\wp )^{\epsilon -1} \biggl\{ h \mathbf{x}(\wp ) \biggl(1- \frac{\mathbf{x}(\wp )}{k} \biggr)-\lambda (1-\mathfrak{M}) \mathbf{x}( \wp )\mathbf{y}(\wp ) \biggr\} \,d\wp , \end{aligned} \\& \begin{aligned}[b] \mathbf{y}(\tau )-\mathbf{y}(0)={}& \frac{1-\varsigma }{\varrho (\varsigma )} \bigl\{ e\lambda (1-\mathfrak{M}) \mathbf{x}(\tau )\mathbf{y}(\tau )-d\mathbf{y}(\tau ) \bigr\} \\ &{} +\frac{\varsigma }{\varrho (\varsigma )\Gamma (\varsigma )} \int _{0}^{ \tau }(\tau -\wp )^{\varsigma -1} \bigl\{ e \lambda (1-\mathfrak{M}) \mathbf{x}(\wp )\mathbf{y}(\wp )-d\mathbf{y}(\wp ) \bigr\} \,d\wp . \end{aligned} \end{aligned}$$
(3.2)

Now we assume the following lemmas.

Lemma 1

Suppose that \(T:H\rightarrow H\) is a mapping and gives

$$\begin{aligned}& T \bigl[\mathbf{x}(\tau ) \bigr]=\frac{1-\epsilon }{\varrho (\epsilon )}S \bigl(\tau , \mathbf{x}(\tau ) \bigr)+ \frac{\epsilon }{\varrho (\epsilon )\Gamma (\epsilon )} \int _{0}^{\tau }( \tau -\wp )^{\epsilon -1}S \bigl( \theta ,\mathbf{x}(\wp ) \bigr)\,d\wp , \\& T \bigl[\mathbf{y}(\tau ) \bigr]=\frac{1-\varsigma }{\varrho (\varsigma )}S \bigl(\tau , \mathbf{y}( \tau ) \bigr)+ \frac{\varsigma }{\varrho (\varsigma )\Gamma (\varsigma )} \int _{0}^{ \tau }(\tau -\wp )^{\varsigma -1}S \bigl(\wp ,\mathbf{y}(\wp ) \bigr)\,d\wp . \end{aligned}$$
(3.3)

To handle this more easily, let us assume the following:

$$\begin{aligned}& S \bigl(\tau ,\mathbf{x}(\tau ) \bigr)= \biggl\{ h\mathbf{x}(\tau ) \biggl(1- \frac{\mathbf{x}(\tau )}{k} \biggr)-\lambda (1-\mathfrak{M})\mathbf{x}( \tau )\mathbf{y}( \tau ) \biggr\} , \\& S \bigl(\tau ,\mathbf{y}(\tau ) \bigr)= \bigl\{ e\lambda (1-\mathfrak{M}) \mathbf{x}( \tau )\mathbf{y}(\tau )-d\mathbf{y}(\tau ) \bigr\} . \end{aligned}$$
(3.4)

Lemma 2

Let \(M \subset H\) be bounded and constants \(\beta , \delta >0\)

$$\begin{aligned}& \bigl\Vert \mathbf{x}(\tau _{2})-\mathbf{x}(\tau _{1}) \bigr\Vert \leq \beta \Vert \tau _{2}- \tau _{1} \Vert , \\& \bigl\Vert \mathbf{y}(\tau _{2})-\mathbf{y}(\tau _{1}) \bigr\Vert \leq \delta \Vert \tau _{2}- \tau _{1} \Vert ,\quad \forall \mathbf{x},\mathbf{y} \in M. \end{aligned}$$
(3.5)

Thus, \(\bar{T(M)}\) is compact.

Proof

Let us consider \(\Theta =\max\{((1-\epsilon )/(\varrho (\epsilon )))+S(\tau , \mathbf{x}(\tau ))\}\), \(0\leq \mathbf{x}(\tau )\leq P\). Therefore, for \(\mathbf{x}(\tau ) \in M\), we have

$$\begin{aligned} \bigl\Vert T \bigl[\mathbf{x}(\tau ) \bigr] \bigr\Vert ={}&\frac{1-\epsilon }{\varrho (\epsilon )} \bigl\Vert S \bigl( \tau ,\mathbf{x}(\tau ) \bigr) \bigr\Vert + \frac{\epsilon }{\varrho (\epsilon )\Gamma (\epsilon )} \int _{0}^{\tau }( \tau -\wp )^{\epsilon -1} \bigl\Vert S \bigl(\wp ,\mathbf{x}(\wp ) \bigr) \bigr\Vert \,d\wp \\ \leq {}&\frac{1-\epsilon }{\varrho (\epsilon )}\Theta + \frac{\epsilon }{\varrho (\epsilon )\Gamma (\epsilon )}\Theta \biggl( \frac{\tau ^{\epsilon }}{\epsilon } \biggr) \\ \leq {}&\frac{1-\epsilon }{\varrho (\epsilon )}\Theta + \frac{\epsilon \tau ^{\epsilon }}{\varrho (\epsilon )\Gamma (\epsilon +1)} \Theta . \end{aligned}$$
(3.6)

If \(\eta =\max\{((1-\varsigma )/(\varrho (\varsigma )))+S(\tau , \mathbf{x}(\tau ))\}\), \(0\leq \mathbf{y}(\tau )\leq Q\) for \(\mathbf{y}(\tau ) \in M\), then we have

$$\begin{aligned} \bigl\Vert T \bigl[\mathbf{y}(\tau ) \bigr] \bigr\Vert ={}& \frac{1-\varsigma }{\varrho (\varsigma )} \bigl\Vert S \bigl( \tau ,\mathbf{y}(\tau ) \bigr) \bigr\Vert + \frac{\varsigma }{\varrho (\varsigma )\Gamma (\varsigma )} \int _{0}^{ \tau }(\tau -\wp )^{\varsigma -1} \bigl\Vert S \bigl(\wp ,\mathbf{y}(\wp ) \bigr) \bigr\Vert \,d\wp \\ \leq {}&\frac{1-\varsigma }{\varrho (\varsigma )}\eta + \frac{\varsigma }{\varrho (\varsigma )\Gamma (\varsigma )}\eta \biggl( \frac{\tau ^{\varsigma }}{\varsigma } \biggr) \\ \leq{}& \frac{1-\varsigma }{\varrho (\varsigma )}\eta + \frac{\varsigma \tau ^{\varsigma }}{\varrho (\varsigma )\Gamma (\varsigma +1)} \eta . \end{aligned}$$
(3.7)

Due to Eqs. (3.6) and (3.7), we assume that T is bounded. Now observe \(\mathbf{x}(\tau ) \in M\), \(\tau _{1}\), \(\tau _{2}\); \(\tau _{1}<\tau _{2}\) and if \(\vert \tau _{2}-\tau _{1} \vert <\mu \) for given \(\phi >0\), hence

$$\begin{aligned} \bigl\Vert T \bigl[\mathbf{x}(\tau _{2}) \bigr]-T \bigl[\mathbf{x}( \tau _{1}) \bigr] \bigr\Vert &\leq \frac{1-\epsilon }{\varrho (\epsilon )} \bigl\Vert S \bigl(\tau _{2},\mathbf{x}(\tau _{2}) \bigr)-S \bigl( \tau _{1},\mathbf{x}(\tau _{1}) \bigr) \bigr\Vert \\ &\quad{} + \biggl\Vert \frac{\epsilon }{\varrho (\epsilon )\Gamma (\epsilon )} \int _{0}^{\tau _{2}}(\tau _{2}-\theta )^{\epsilon -1} \bigl\Vert S \bigl(\theta , \mathbf{x}(\theta ) \bigr) \bigr\Vert \,d\theta \\ &\quad{} - \frac{\epsilon }{\varrho (\epsilon )\Gamma (\epsilon )} \int _{0}^{ \tau _{1}}(\tau _{1}-\wp )^{\epsilon -1} \bigl\Vert S \bigl(\wp ,\mathbf{x}(\wp ) \bigr) \bigr\Vert \,d \wp \biggr\Vert \\ &\leq \frac{1-\epsilon }{\varrho (\epsilon )} \bigl\Vert S \bigl(\tau _{2},\mathbf{x}( \tau _{2}) \bigr)-S \bigl(\tau _{1},\mathbf{x}(\tau _{1}) \bigr) \bigr\Vert \\ &\quad{} + \frac{\epsilon P}{\varrho (\epsilon )\Gamma (\epsilon )} \biggl\{ \int _{0}^{ \tau _{2}}(\tau _{2}-\chi )^{\epsilon -1}\,d\chi - \int _{0}^{\tau _{1}}( \tau _{1}-\chi )^{\epsilon -1}\,d\chi \biggr\} . \end{aligned}$$
(3.8)

Now we assume an integral part

$$\begin{aligned}& \int _{0}^{\tau _{2}}(\tau _{2}-\chi )^{\epsilon -1}\,d\chi - \int _{0}^{ \tau _{1}}(\tau _{1}-\chi )^{\epsilon -1}\,d\chi \\& \quad = \int _{0}^{\tau _{1}} \bigl\{ (\tau _{1}-\chi )^{\epsilon -1}-(\tau _{2}- \chi )^{\epsilon -1} \bigr\} \,d\chi + \int _{\tau _{1}}^{\tau _{2}} \bigl\{ (\tau _{2}- \chi )^{\epsilon -1} \bigr\} \,d\chi =2 \frac{(\tau _{2}-\tau _{1})^{\epsilon }}{\epsilon }. \end{aligned}$$
(3.9)

Now we will study the following:

$$\begin{aligned} S \bigl(\tau _{2},\mathbf{x}(\tau _{2}) \bigr)-S \bigl( \tau _{1},\mathbf{x}(\tau _{1}) \bigr)\Vert ={}& \biggl\Vert h \bigl(\mathbf{x}(\tau -2) \bigr)-\mathbf{x}(\tau _{1})) \biggl[1- \frac{(\mathbf{x}(\tau _{2})-\mathbf{x}(\tau _{1}))}{\mathbf{r}} \biggr] \\ &{} -\lambda (1-\mathfrak{M}) \bigl[ \bigl(\mathbf{x}(\tau _{2})- \mathbf{x}(\tau _{1}) \bigr) \bigl( \mathbf{y}(\tau _{2})- \mathbf{y}(\tau _{1}) \bigr) \bigr] \biggr\Vert . \end{aligned}$$
(3.10)

Equation (3.10) by taking the Lipschitz condition of the operator becomes

$$\begin{aligned} \bigl\Vert S \bigl(\tau _{2},\mathbf{x}(\tau _{2}) \bigr)-S \bigl(\tau _{1},\mathbf{x}(\tau _{1}) \bigr) \bigr\Vert &\leq \Vert hA \Vert \biggl[ \biggl\Vert 1-\frac{A}{\mathbf{r}} \biggr\Vert \biggr]- \bigl\Vert \lambda (1- \mathfrak{M}) (AB) \bigr\Vert \\ &\leq \biggl\{ h \biggl(1-\frac{A}{\mathbf{r}} \biggr)-\lambda (1-\mathfrak{M}) (B) \biggr\} \bigl\Vert \bigl( \mathbf{x}(\tau _{2})-\mathbf{x}(\tau _{1}) \bigr) \bigr\Vert \\ &\leq \{\varphi \mathfrak{M}\} \bigl\Vert (\tau _{2}-\tau _{1} \bigr\Vert \\ &\leq \mathbf{x} \bigl\Vert (\tau _{2}-\tau _{1} \bigr\Vert , \end{aligned}$$
(3.11)

where \(\varphi =h (1-\frac{A}{k} )-\lambda (1-\mathfrak{M})(B)\).

Now putting Eqs. (3.9)–(3.11) in Eq. (3.8), we get

$$\begin{aligned}& \begin{aligned} \bigl\Vert T \bigl[\mathbf{x}(\tau _{2}) \bigr]-T \bigl[\mathbf{x}(\tau _{1}) \bigr] \bigr\Vert &\leq \frac{1-\epsilon }{\varrho (\epsilon )} \mathbf{x} \Vert \tau _{2}-\tau _{1} \Vert + \frac{\epsilon P}{\varrho (\epsilon )\Gamma (\epsilon )}2 \frac{ \Vert \tau _{2}-\tau _{1} \Vert ^{\epsilon }}{\epsilon } \\ &\leq \frac{1-\epsilon }{\varrho (\epsilon )}\mathbf{x} \Vert \tau _{2}- \tau _{1} \Vert + \frac{2\epsilon P}{\varrho (\epsilon )\Gamma (\epsilon +1)} \bigl( \Vert \tau _{2}- \tau _{1} \Vert ^{\epsilon } \bigr), \end{aligned} \\& \Delta _{1}= \frac{\rho }{\frac{1-\epsilon }{\varrho (\epsilon )}\mathbf{x} \Vert \tau _{2}-\tau _{1} \Vert +\frac{2\epsilon P}{ \varrho (\epsilon )\Gamma (\epsilon +1)}} \end{aligned}$$
(3.12)

such that \(\Vert T[\mathbf{x}(\tau _{2})]-T[\mathbf{x}(\tau _{1})] \Vert <\rho \) is satisfied.

Now, for \(\mathbf{y}(\tau )\), we have

$$ \begin{aligned}[b] & \bigl\Vert S \bigl[\mathbf{y}(\tau _{2}) \bigr]-S \bigl[\mathbf{y}( \tau _{1}) \bigr] \bigr\Vert \\ &\quad = \bigl\Vert e \lambda (1- \mathfrak{M}) \bigl[ \bigl(\mathbf{x}(\tau _{2})-\mathbf{x}(\tau _{1}) \bigr) \bigl( \mathbf{y}(\tau _{2})-\mathbf{y}(\tau _{1}) \bigr) \bigr]-d \bigl[ \bigl( \mathbf{y}( \tau _{2})- \mathbf{y}(\tau _{1}) \bigr) \bigr] \bigr\Vert . \end{aligned} $$
(3.13)

Taking the Lipschitz condition of the operator and Eq. (3.13), we consider the following:

$$\begin{aligned} \bigl\Vert S \bigl(\tau _{2},\mathbf{x}(\tau _{2}) \bigr)-S \bigl(\tau _{1},\mathbf{x}(\tau _{1}) \bigr) \bigr\Vert &\leq \bigl\Vert e\lambda (1-\mathfrak{M}) (AB) \bigr\Vert - \bigl\Vert d(B) \bigr\Vert \\ &\leq \bigl\{ e\lambda (1-\mathfrak{M}) (A)-d \bigr\} \bigl\Vert \mathbf{y}( \tau _{2})- \mathbf{y}(\tau _{1}) \bigr\Vert \\ &\leq \{\mathbf{x} \mathfrak{M}\} \bigl\Vert (\tau _{2}-\tau _{1} \bigr\Vert \\ &\leq \epsilon _{1} \bigl\Vert (\tau _{2}-\tau _{1} \bigr\Vert , \end{aligned}$$
(3.14)

where \(\mathbf{x}=e\lambda (1-\mathfrak{M})(A)-d\).

Now we get

$$\begin{aligned}& \begin{aligned} \bigl\Vert T \bigl[\mathbf{y}(\tau _{2}) \bigr]-T \bigl[\mathbf{y}(\tau _{1}) \bigr] \bigr\Vert &\leq \frac{1-\varsigma }{\varrho (\varsigma )} \epsilon \Vert \tau _{2}-\tau _{1} \Vert + \frac{\varsigma Q}{B(\varsigma )\Gamma (\varsigma )}2 \frac{ \Vert \tau _{2}-\tau _{1} \Vert ^{\varsigma }}{\varsigma } \\ &\leq \frac{1-\varsigma }{\varrho (\varsigma )}\epsilon \Vert \tau _{2}- \tau _{1} \Vert + \frac{2\varsigma Q}{\varrho (\varsigma )\Gamma (\varsigma +1)} \bigl( \Vert \tau _{2}- \tau _{1} \Vert ^{\varsigma } \bigr), \end{aligned} \\& \Delta _{2}= \frac{\rho }{\frac{1-\varsigma }{\varrho (\varsigma )}\mathbf{x} \Vert \tau _{2}-\tau _{1} \Vert + \frac{2\varsigma Q}{\varrho (\varsigma ) \Gamma (\varsigma +1)}}. \end{aligned}$$
(3.15)

Such that \(\Vert T[\mathbf{x}(\tau _{2})]-T[\mathbf{x}(\tau _{1})] \Vert <\epsilon \) and \(\Vert T[\mathbf{y}(\tau _{2})]-T[\mathbf{y}(\tau _{1})] \Vert <\epsilon \) hold. So \(\bar{T(M)}\) is equicontinuous and compact [45] due to the Arzela–Ascoli principle. This completes the proof. □

Theorem 2

Assume that the function \(S:[x_{1},x_{2}]\times [0,\infty )\rightarrow [0,\infty )\) is continuous and \(S(\tau ,\cdot )\) is increasing for each \(\tau \in [x_{1},x_{2}]\). Consider a constant \(\bar{\psi }^{\star }_{1}\) satisfying \(x(s)\bar{\psi }^{\star }_{1} \leq S(\tau ,\bar{\psi }^{\star }_{1})\), \(x(s)\bar{\psi }^{\star }_{2}\geq S(\tau ,\bar{\psi }^{\star }_{2})\), \(0\leq \bar{\psi }^{\star }_{1}(\tau )\leq \bar{\psi }^{\star }_{2}(\tau )\), \(x_{1}\leq \tau \leq x_{2}\). Then the concluding equation has a positive solution.

Proof

We require a fixed point operator of T to research the existence of a positive solution. With Lemma 1 structure, assume that the operator \(T: H\rightarrow H\) is entirely continuous. Consider two arbitrary predator population densities of \(x_{1} \) and \(x_{2} \) in H which meet \(x_{1}\leq x_{2} \) as well as the densities of prey population \(S_{1} \)and \(S_{2} \) in H which satisfy \(S_{1}\leq S_{2}\), then S is a positive function and

$$\begin{aligned}& \begin{aligned}& \bigl\Vert T \bigl[x_{1}(\tau ) \bigr] \bigr\Vert \\ &\quad \leq \frac{1-\epsilon }{\varrho (\epsilon )} \bigl\Vert S \bigl( \tau ,x_{1}(\tau ) \bigr) \bigr\Vert + \frac{\epsilon }{\varrho (\epsilon )\Gamma (\epsilon )} \int _{0}^{\tau }( \tau -\wp )^{\epsilon -1} \bigl\Vert S \bigl(\wp ,x_{1}(\wp ) \bigr) \bigr\Vert \,d\wp ,\quad \leq Tx_{2}( \tau ), \end{aligned} \\& \begin{aligned} & \bigl\Vert T \bigl[S_{1}(\tau ) \bigr] \bigr\Vert \\ &\quad \leq \frac{1-\varsigma }{\varrho (\varsigma )} \bigl\Vert S \bigl( \tau ,S_{1}(\tau ) \bigr) \bigr\Vert + \frac{\varsigma }{\varrho (\varsigma )\Gamma (\varsigma )} \int _{0}^{ \tau }(\tau -\wp )^{\varsigma -1} \bigl\Vert S \bigl(\wp ,S_{1}(\wp ) \bigr) \bigr\Vert \,d\wp ,\quad \leq TS_{2}(\tau ), \end{aligned} \end{aligned}$$

are satisfied, thus the mapping T is increasing, we have \(T\bar{\psi }^{\star }_{2}\geq \bar{\psi }^{\star }_{2}\) and \(T\bar{\psi }^{\star }_{2}\leq \bar{\psi }^{\star }_{2}\). So \(T:\langle \bar{\psi }^{\star }_{1},\bar{\psi }^{\star }_{2}\rangle \rightarrow \langle \bar{\psi }^{\star }_{1},\bar{\psi }^{\star }_{2}\rangle \) is a compact operator by the guideline of Lemma 2 and continuous by the perspective of Lemma 1. As H is a normal cone of T [45], this completes the proof. □

Uniqueness of the special solution

Consider

$$\begin{aligned} & \bigl\Vert T \bigl[x_{1}(\tau ) \bigr]-T \bigl[x_{2}( \tau ) \bigr] \bigr\Vert \\ &\quad \leq \biggl\Vert \frac{1-\epsilon }{\varrho (\epsilon )}(S \bigl(\tau ,x_{1}(\tau ) \bigr)-S \bigl(\tau ,x_{2}( \tau ) \bigr) \\ &\quad \quad{} +\frac{\epsilon }{\varrho (\epsilon )\Gamma (\epsilon )} \int _{0}^{ \tau }(\tau -\wp )^{\epsilon -1} \bigl(S \bigl(\wp ,x_{1}(\wp ) \bigr)-S \bigl(\wp ,x_{2}( \theta ) \bigr) \bigr)\,d\wp \biggr\Vert \\ &\quad \leq \frac{1-\epsilon }{\varrho (\epsilon )} \bigl\Vert (S \bigl(\tau ,x_{1}(\tau ) \bigr)-S \bigl( \tau ,x_{2}(\tau ) \bigr) \bigr\Vert \\ &\quad\quad{} + \frac{\epsilon }{\varrho (\epsilon )\Gamma (\epsilon )} \int _{0}^{\tau }( \tau -\wp )^{\epsilon -1} \bigl\Vert \bigl(S \bigl(\wp ,x_{1}(\wp ) \bigr)-S \bigl(\wp ,x_{2}(\wp ) \bigr) \bigr) \bigr\Vert \,d \wp \\ &\quad \leq \frac{1-\epsilon }{\varrho (\epsilon )}K_{1} \bigl\Vert x_{1}(\tau )-x_{2}( \tau ) \bigr\Vert +\frac{\epsilon }{\varrho (\epsilon )\Gamma (\epsilon )}K_{1} \int _{0}^{\tau }(\tau -\wp )^{\epsilon -1} \bigl\Vert x_{1}(\wp )-x_{2}(\wp ) \bigr\Vert \,d \wp . \end{aligned}$$
(3.16)

Thus

$$ \bigl\Vert T \bigl[x_{1}(\tau ) \bigr]-T \bigl[x_{2}( \tau ) \bigr] \bigr\Vert \leq \biggl\{ \frac{1-\epsilon }{\varrho (\epsilon )}K_{1}+ \frac{\epsilon K_{1} \epsilon ^{\epsilon }}{\varrho (\epsilon )\Gamma (\epsilon +1)} \biggr\} \bigl\Vert x_{1}(\tau )-x_{2}( \tau ) \bigr\Vert , $$
(3.17)

and

$$ \bigl\Vert T \bigl[S_{1}(\tau ) \bigr]-T \bigl[S_{2}( \tau ) \bigr] \bigr\Vert \leq \biggl\{ \frac{1-\varsigma }{\varrho (\varsigma )}K_{2}+ \frac{\varsigma K_{2} \epsilon ^{\varsigma }}{\varrho (\varsigma )\Gamma (\varsigma +1)} \biggr\} \bigl\Vert S_{1}(\tau )-S_{2}( \tau ) \bigr\Vert . $$
(3.18)

Therefore, if the following conditions hold:

$$ \biggl\{ \frac{1-\epsilon }{\varrho (\epsilon )}K_{1}+ \frac{\epsilon K_{1} \epsilon ^{\epsilon }}{\varrho (\epsilon )\Gamma (\epsilon +1)} \biggr\} < 1 $$
(3.19)

and

$$ \biggl\{ \frac{1-\varsigma }{\varrho (\varsigma )}K_{2}+ \frac{\varsigma K_{2} \epsilon ^{\varsigma }}{\varrho (\varsigma )\Gamma (\varsigma +1)} \biggr\} < 1, $$
(3.20)

then the system produces a unique positive solution because mapping T is a contraction with fixed point.

Numerical approximation

The Atangana–Baleanu FO integral numerical approximation by imposing the Adams–Moulton rule is granted by [24]

$$ {}^{AB}_{0}{\mathcal{I}}_{\tau }^{\epsilon } \bigl[f(\tau _{\mathbf{r}_{1}+1}) \bigr] = \frac{1-\epsilon }{\varrho (\epsilon )} \biggl[ \frac{f(\tau _{\mathbf{r}_{1}+1})-f(\tau _{\mathbf{r}_{1}})}{2} \biggr]+ \frac{\epsilon }{\Gamma (\epsilon )}\sum_{\mathbf{r}=0}^{\infty } \biggl[ \frac{f(\tau _{\mathbf{r}+1})-f(\tau _{\mathbf{r}})}{2} \biggr]b_{ \mathbf{r}}^{\epsilon }, $$
(3.21)

where \(b_{\mathbf{r}}^{\epsilon }=(\mathbf{r}+1)^{1-\epsilon }-(\mathbf{r})^{1- \epsilon }\).

With a similar previous numerical method, we have

$$\begin{aligned}& \begin{aligned} &x_{{(\mathbf{r}_{1}+1)}}(\tau )-x_{{(\mathbf{r}_{1})}}(\tau ) \\ &\quad =x_{0}^{ \mathbf{r}_{1}}(\tau )+ \biggl\{ \frac{1-\epsilon }{\varrho (\epsilon )} \biggl[r \biggl( \frac{x_{{(\mathbf{r}_{1}+1)}}(\tau )-x_{{(\mathbf{r}_{1})}}(\tau )}{2} \biggr) \biggl(1-\mathbf{r}^{-1} \biggl( \frac{x_{{(\mathbf{r}_{1}+1)}}(\tau )-x_{{(\mathbf{r}_{1})}}(\tau )}{2} \biggr) \biggr) \\ &\quad\quad {} -\lambda (1-\mathfrak{M}) \biggl( \frac{x_{{(\mathbf{r}_{1}+1)}}(\tau )-x_{{(\mathbf{r}_{1})}}(\tau )}{2} \biggr) \biggl( \frac{y_{{(\mathbf{r}_{1}+1)}}(\tau )-y_{{(\mathbf{r}_{1})}}(\tau )}{2} \biggr) \biggr] \biggr\} \\ &\quad\quad {} +\frac{\epsilon }{\varrho (\epsilon )}\sum_{\mathbf{r}=0}^{\infty }b_{ \mathbf{r}}^{\epsilon } \biggl[r \biggl( \frac{x_{{(\mathbf{r}+1)}}(\tau )-x_{{(\mathbf{r})}}(\tau )}{2} \biggr) \biggl(1-\mathbf{r}^{-1} \biggl( \frac{x_{{(\mathbf{r}+1)}}(\tau )-x_{{(\mathbf{r})}}(\tau )}{2} \biggr) \biggr) \\ &\quad\quad {} -\lambda (1-\mathfrak{M}) \biggl( \frac{x_{{(\mathbf{r}+1)}}(\tau )-x_{{(\mathbf{r})}}(t)}{2} \biggr) \biggl( \frac{y_{{(\mathbf{r}+1)}}(\tau )-y_{{(\mathbf{r})}}(\tau )}{2} \biggr) \biggr], \end{aligned} \\& \begin{aligned}[b] &y_{{(\mathbf{r}_{1}+1)}}(\tau )-y_{{(\mathbf{r}_{1})}}(\tau ) \\ &\quad =y_{0}^{ \mathbf{r}_{1}}(\tau )+ \biggl\{ \frac{1-\epsilon }{\varrho (\epsilon )} \biggl[e \lambda (1-\mathfrak{M}) \biggl( \frac{x_{{(\mathbf{r}_{1}+1)}}(\tau )-x_{{(\mathbf{r}_{1})}}(\tau )}{2} \biggr) \biggl( \frac{y_{{(\mathbf{r}_{1}+1)}}(\tau )-y_{{(\mathbf{r}_{1})}}(\tau )}{2} \biggr) \\ &\quad\quad {}-d \biggl( \frac{y_{{(\mathbf{r}_{1}+1)}}(\tau )-y_{{(\mathbf{r}_{1})}}(\tau )}{2} \biggr) \biggr] \biggr\} + \frac{\epsilon }{\varrho (\epsilon )}\sum_{ \mathbf{r}=0}^{\infty }b_{\mathbf{r}}^{\epsilon } \biggl[e\lambda (1- \mathfrak{M}) \biggl( \frac{x_{{(\mathbf{r}+1)}}(\tau )-x_{{(\mathbf{r})}}(\tau )}{2} \biggr) \hspace{-20pt} \\ &\quad\quad {} \times \biggl( \frac{y_{{(\mathbf{r}+1)}}(\tau )-y_{{(\mathbf{r})}}(\tau )}{2} \biggr)-d \biggl( \frac{y_{{(\mathbf{r}+1)}}(\tau )-y_{{(\mathbf{r})}}(\tau )}{2} \biggr) \biggr]. \end{aligned} \end{aligned}$$
(3.22)

Now consider FO differential equations with variable-order ABC of model Eq. (2.7), in which, to justify temporal changes, a FO derivative as a variable is used instead of integer-order derivatives.

3.1 Predator–prey model involving variable-order fractional derivative

Adams–Moulton method with variable order

Now, we show an alteration of variable order \(\epsilon (\tau )\) of the Adams–Moulton approach. Along these lines, the algorithm computes numerical results of a FO differential equation of the kind

$$ {}^{ABC}_{0}{\mathcal{D}}_{\tau }^{\epsilon (\tau )}f(\tau )=g \bigl(\tau ,f( \tau ) \bigr), \quad f^{\mathbf{r}}(0)=f^{\mathbf{r}}_{0}, \mathbf{r}=0,1,\ldots,\mathbf{r}_{1}-1, $$
(3.23)

where \(\epsilon (\tau )>0\) and \({}^{ABC}_{0}D_{\tau }^{\epsilon (\tau )}\) is the variable-order Atangana–Baleanu–Caputo FO derivative.

Equation (3.23) has one solution categorized in \(\tau \in [0,T]\), which can be reformulated by applying the FO Atangana–Baleanu integral as follows:

$$ f(\tau )=f_{0}+\frac{1-\epsilon (\tau )}{\varrho (\epsilon (\tau ))}g \bigl( \tau ,f(\tau ) \bigr)+ \frac{\epsilon (\tau )}{\varrho (\epsilon (\tau ))\Gamma (\epsilon (\tau ))} \int _{0}^{\tau }g \bigl(\wp ,f(\wp ) \bigr) (\tau -\wp )^{\epsilon (\tau )-1}\,d\wp , $$
(3.24)

where \(\varrho (\epsilon (\tau ))=1- \epsilon (\tau ) + \frac{\epsilon (\tau )}{\Gamma (\epsilon (\tau ))}\) represents a normalization function.

The solution plot by applying the trapezoidal quadrature formulation appears as described:

$$\begin{aligned}& f^{P}_{i+1}=f_{0}+ \frac{1-\epsilon (\tau _{i+1})}{\varrho (\epsilon (\tau _{i+1}))}g( \tau _{i+1},f_{i+1})+ \frac{\epsilon (\tau _{i+1})}{\Gamma (\epsilon (\tau _{i+1}))\varrho (\epsilon (\tau _{i+1}))} \sum _{j=0}^{i}b_{j,i+1}g(\tau _{j},f_{j}), \end{aligned}$$
(3.25)
$$\begin{aligned}& \begin{aligned}[b] f_{i+1}={}&f_{0}+ \frac{1-\epsilon (\tau _{i+1})}{\varrho (\epsilon (\tau _{i+1}))}g \bigl( \tau _{i+1},f^{P}_{i+1} \bigr)+ \frac{\epsilon (\tau _{i+1})}{\varrho (\epsilon (\tau _{i+1}))} \\ &{}\times \Biggl[ \frac{h^{\epsilon (\tau _{i+1})}}{\Gamma (\epsilon (\tau _{i+1})+2)}g \bigl( \tau _{i+1},f^{P}_{i+1} \bigr)+ \frac{h^{\epsilon (\tau _{i+1})}}{\Gamma (\epsilon (\tau _{i+1})+2)} \sum_{j=0}^{i}a_{j,i+1}g( \tau _{j},f_{j}) \Biggr], \end{aligned} \end{aligned}$$
(3.26)

where

$$\begin{aligned}& a_{j,i+1}= \textstyle\begin{cases} i^{\epsilon (\tau _{i+1})+1}-(i-\epsilon (\tau _{i+1}))(i+1)^{ \epsilon (\tau _{i+1})}, &j=0, \\ (i-j+2)^{\epsilon (\tau _{i+1})+1}+(i-j)^{\epsilon (\tau _{i+1})+1}-2(i-j+1)^{ \epsilon (\tau _{i+1})+1}, &1\leq j \leq i, \end{cases}\displaystyle \end{aligned}$$

and

$$\begin{aligned}& b_{j,i+1}=\frac{h^{\epsilon (\tau _{i+1})}}{\epsilon (\tau _{i+1})} \bigl((i+1-j)^{ \epsilon (\tau _{i+1})}-(i-j)^{\epsilon (\tau _{i+1})} \bigr), \quad j=0,1,2,\ldots,i. \end{aligned}$$

  • Existence and uniqueness of the solution

Theorem 3

We show the existence and uniqueness of the solution.

Proof

Assuming that the space

$$ M_{(T_{\max }},{y_{\max }}_{)}=A_{T_{\max }}(\tau _{0})\times D_{y_{\max }}( \tau _{0}), $$
(3.27)

we define

$$ \bar{A}_{T_{\max }}=[\tau _{0}-\tau _{\max },\tau _{0}+\tau _{\max }] $$
(3.28)

and

$$ \bar{D}_{y_{\max }}=[y_{0}-y_{\max },y_{0}+y_{\max }], $$
(3.29)

a compact cylinder of function f in Eq. (3.23) and Eq. (3.24) is \(M_{(T_{\max }},{y_{\max }}_{)}\) and the maximum gradient \(M_{(T_{\max }},{y_{\max }}_{)}\) of a module function is \(K=\sup \Vert f \Vert \). Additionally, \(\mathfrak{F}\) is the time constant for a Lipschitz function f. The Banach fixed point theorem will be used by the metric on its own built-in space \(M {(T {\max }},{y {\max }} )\), which will influence the uniform m norm

$$ \Vert \Phi \Vert _{\infty }=\sup_{\tau \in \bar{A}_{\max }} \bigl\vert \Phi (\tau ) \bigr\vert . $$
(3.30)

Create Picard’s operator

$$ \Phi :M_{(T_{\max }},{y_{\max }}_{)}\rightarrow M_{(T_{\max }},{y_{\max }}_{)}, $$
(3.31)

defined by

$$ \begin{aligned}[b] \Phi f(\tau )={}&y_{0}+ \frac{1-\epsilon (\tau )}{\varrho (\epsilon (\tau ))}g \bigl(\tau ,f(\tau ) \bigr) \\ &{}+ \frac{\epsilon (\tau )}{\varrho (\epsilon (\tau ))\Gamma (\epsilon (\tau ))} \int _{0}^{\tau }g \bigl(\wp ,f(\wp ) \bigr) (\tau -\wp )^{\epsilon (\tau )-1}\,d\wp . \end{aligned} $$
(3.32)

Find \(\Vert g\Phi f(\tau )-y_{0} \Vert < y_{\max }\) to establish the condition of well-posedness for which

$$ \begin{aligned}[b] & \bigl\Vert \Phi f(\tau )-y_{0} \bigr\Vert \\ &\quad = \biggl\Vert \frac{1-\epsilon (\tau )}{\varrho (\epsilon (\tau ))}g \bigl(\tau ,f(\tau ) \bigr)+ \frac{\epsilon (\tau )}{\varrho (\epsilon (\tau ))\Gamma (\epsilon (\tau ))} \int _{0}^{\tau }g \bigl(\wp ,f(\wp ) \bigr) (\tau -\wp )^{\epsilon (\tau )-1}\,d\wp \biggr\Vert . \end{aligned} $$
(3.33)

Taking the triangular inequality, we obtain

$$\begin{aligned} \bigl\Vert \Phi f(\tau )-y_{0} \bigr\Vert _{\infty }&\leq \biggl\vert \frac{1-\epsilon (\tau )}{\varrho (\epsilon (\tau ))} \vert \vert \bigl\vert g \bigl( \tau ,f( \tau ) \bigr) \bigr\vert \biggr\vert _{\infty } \\ &\quad{} + \biggl\vert \frac{\epsilon (\tau )}{\varrho (\epsilon (\tau ))\Gamma (\epsilon (\tau ))} \biggl\vert \int _{0}^{\tau }(\tau -\theta )^{\epsilon (\tau )} \biggr\vert \bigl\vert g \bigl( \tau ,\mathbf{x}(\tau ) \bigr) \bigr\vert \biggr\vert _{\infty }\,d\theta \\ &\leq \biggl\vert \frac{1-\epsilon (\tau )}{\varrho (\epsilon (\tau ))} \biggr\vert K+ \biggl\vert \frac{\epsilon (\tau )}{\varrho (\epsilon (\tau ))\Gamma (\epsilon (\tau ))} \biggr\vert K \vert \tau \vert \\ &\leq \frac{1-\epsilon (\tau )}{\varrho (\epsilon (\tau ))}K+ \frac{\epsilon (\tau )}{\varrho (\epsilon (\tau ))\Gamma (\epsilon (\tau )+1)}K T_{\max }^{ \epsilon (\tau )} \leq y_{\max }. \end{aligned}$$
(3.34)

For the above, we need to have

$$ K< \frac{y_{\max }}{\frac{1-\epsilon (\tau )}{\varrho (\epsilon (\tau ))}+\frac{\epsilon ( \tau )T_{\max }^{\epsilon (\tau )}}{\varrho (\epsilon (\tau ))\Gamma (\epsilon (\tau )+1)}}. $$
(3.35)

Presently, use an operator of Picard to contract on \(T_{\max }\) under some condition.

Let \(f_{1}\) and \(f_{2}\) be two functions in \(\mathbb{C}[A_{T_{\max }}(\tau _{0}),D_{y_{\max }}(y_{0})]\), then let us calculate the following:

$$\begin{aligned} & \bigl\Vert \Phi (f_{1})-\Phi (f_{2}) \bigr\Vert _{\infty } \\ &\quad = \biggl\Vert \frac{1-\epsilon (\tau )}{\varrho (\epsilon (\tau ))}g \bigl(\tau ,f_{1}( \tau ) \bigr)+ \frac{\epsilon (\tau )}{\varrho (\epsilon (\tau ))\Gamma (\epsilon (\tau ))} \int _{0}^{\tau }g \bigl(\wp ,f_{1}(\wp ) \bigr) (\tau -\wp )^{\epsilon (\tau )-1}\,d \wp \\ &\quad\quad {} -\frac{1-\epsilon (\tau )}{\varrho (\epsilon (\tau ))}g \bigl(\tau ,f_{2}( \tau ) \bigr)- \frac{\epsilon (\tau )}{\varrho (\epsilon (t))\Gamma (\epsilon (\tau ))} \int _{0}^{\tau }g \bigl(\wp ,f_{2}(\wp ) \bigr) (\tau -\wp )^{\epsilon (\tau )-1}\,d \wp \biggr\Vert \\ &\quad \leq \frac{1-\epsilon (\tau )}{\varrho (\epsilon (t))} \biggl\vert \bigl\vert g \bigl( \tau ,f_{1}(\tau ) \bigr)-g \bigl(\tau ,f_{2}(\tau ) \bigr) \bigr\vert \biggl\vert _{\infty } \\ &\quad\quad {} + \frac{\epsilon (\tau )}{\varrho (\epsilon (t))\Gamma (\epsilon (\tau ))} \int _{0}^{\tau } \biggr\vert \bigl\vert g \bigl( \wp ,f_{1}(\wp ) \bigr)-g \bigl(\wp ,f_{2}(\wp ) \bigr) \bigr\vert \biggr\vert (\tau -\wp )^{\epsilon (\tau )-1}\,d\wp \\ &\quad \leq \biggl(\frac{1-\epsilon (\tau )}{\varrho (\epsilon (\tau ))} \biggr)L \biggl\vert \bigl\vert f_{1}(\tau )-f_{2}(\tau ) \bigr\vert \biggl\vert _{\infty }+ \frac{\epsilon (\tau )}{\varrho (\epsilon (\tau ))\Gamma (\epsilon (\tau )+1)}L T_{\max }^{ \epsilon (\tau )} \biggr\vert \bigl\vert f_{1}(\tau )-f_{2}(\tau ) \bigr\vert \biggr\vert _{ \infty } \\ &\quad \leq \biggl(\frac{1-\epsilon (\tau )}{\varrho (\epsilon (\tau ))}L+ \frac{\epsilon (\tau )}{B(\epsilon (\tau ))\Gamma (\epsilon (\tau )+1)}L T_{\max }^{ \epsilon (\tau )} \biggr) \bigl\Vert f_{1}(\tau )-f_{2}(\tau ) \bigr\Vert _{ \infty }. \end{aligned}$$
(3.36)

The condition for contraction is

$$ \frac{1-\epsilon (\tau )}{\varrho (\epsilon (\tau ))}+ \frac{\epsilon (\tau )}{\varrho (\epsilon (\tau ))\Gamma (\epsilon (\tau )+1)}T_{\max }^{ \epsilon (\tau )}< \frac{1}{L}. $$
(3.37)

Under the prior setting, the derived Picard’s operation on a Banach space with the measurement included by norm uniformly is a contraction, hence Φ has the feature that an exceptional function x exists means \(\Phi \mathbf{x}=\mathbf{x}\), which is the special solution of Eq. (3.24). □

4 Predator–prey model with time delay variable-order fractional derivative

Second case

Now we assume the system given by Eq. (2.8). The underneath calculation ascertains a numerical solution of a time delayed FO system:

$$\begin{aligned}& {}^{ABC}_{0}D_{\tau }^{\epsilon (\tau )}\mathbf{y}(\tau )=f \bigl(\tau , \mathbf{y}(\tau ),\mathbf{y}(\tau - \delta ) \bigr), \quad 0 \leq \tau \leq T, 0< \epsilon (\tau )\leq 1, \\& \mathbf{y}(\tau )=g(\tau ), \quad -\delta \leq \tau \leq 0, \end{aligned}$$
(4.1)

where \(T\in \mathbb{R}^{+}\), \(g(\tau )\), \(\mathbf{y}(\tau )\) and \(\mathbf{y}(\tau -\delta )\) denote smooth functions and delay by \(\delta \in \mathbb{R}^{+}\).

If f is a continuous function, the solution of Eq. (4.1) with FO Atangana–Baleanu integral may be restated as follows:

$$\begin{aligned} \mathbf{y}(\tau )={}&\mathbf{y}_{0}+ \frac{1-\epsilon (\tau )}{\varrho (\epsilon (\tau ))}f \bigl(\tau , \mathbf{y}(\tau ),\mathbf{y}(\tau -\delta ) \bigr) \\ &{}+ \frac{\epsilon (\tau )}{\varrho (\epsilon (\tau ))\Gamma (\epsilon (\tau ))} \int _{0}^{\tau }f \bigl(\wp ,\mathbf{y}(\wp ), \mathbf{y}(u-\delta ) \bigr) (\tau - \wp )^{\epsilon (\tau )-1}\,d\wp . \end{aligned}$$
(4.2)

While implementing the predictor-corrector algorithm, Eq. (4.2) solution can be discrete where \(\mathbf{y}(\tau )\) should be consistent in \([0,T]\) and differential consistent in \((0,T)\).

Assume a uniform grid \(\{\tau _{\mathbf{r}_{1}}=\mathbf{r}_{1}h:\mathbf{r}_{1}=-\mathfrak{M},- \mathfrak{M}+1,\ldots,-1,0,1,\ldots,N\}\), \(\mathfrak{M}\) and N are integers such that \(\mathfrak{M}=\frac{\delta }{h}\) and \(N=\frac{T}{h}\). Let

$$ \mathbf{y}(\tau _{\mathbf{r}_{1}})=g(\tau _{\mathbf{r}_{1}}), \quad \mathbf{r}_{1}=-\mathfrak{M},-\mathfrak{M}+1,\ldots,-1,0, $$
(4.3)

notice

$$ \mathbf{y}(\tau _{n}-\delta )=\mathbf{y}(\mathbf{r}_{1}h- \mathfrak{M}h)= \mathbf{y}(\tau _{\mathbf{r}_{1}-\mathfrak{M}}), \quad \mathbf{r}_{1}=0,1,2, \ldots, N. $$
(4.4)

Now (4.2) is measured by assigning a trapezoidal quadrature scheme and

$$\begin{aligned} \mathbf{y}(\tau _{\mathbf{r}_{1}+1})={}&y_{0}+ \frac{1-\epsilon (\tau _{\mathbf{r}_{1}+1})}{\varrho (\epsilon (\tau _{\mathbf{r}_{1}+1}))}f \bigl( \tau _{\mathbf{r}_{1}+1},y^{P}_{n+1},y_{\mathbf{r}_{1}+1-\mathfrak{M}} \bigr)+ \frac{\epsilon (\tau _{\mathbf{r}_{1}+1})}{\varrho (\epsilon (\tau _{\mathbf{r}_{1}+1}))} \\ &{} \times \Biggl[ \frac{h^{\epsilon (\tau _{\mathbf{r}_{1}+1})}}{\Gamma (\epsilon (\tau _{\mathbf{r}_{1}+1})+2)}f \bigl( \tau _{\mathbf{r}_{1}+1},y^{P}_{\mathbf{r}_{1}+1},y_{n+1-\mathfrak{M}} \bigr) \\ &{} + \frac{h^{\epsilon (\tau _{\mathbf{r}_{1}+1})}}{\Gamma (\epsilon (\tau _{\mathbf{r}_{1}+1})+2)} \sum_{j=0}^{\mathbf{r}_{1}}a_{j,\mathbf{r}_{1}+1}f( \tau _{j},y_{j},y_{j- \mathfrak{M}}) \Biggr], \end{aligned}$$
(4.5)

where

$$\begin{aligned}& a_{j,\mathbf{r}_{1}+1}= \textstyle\begin{cases} n^{\epsilon (\tau _{\mathbf{r}_{1}+1})+1}-(\mathbf{r}_{1}-\epsilon ( \tau _{n+1}))(n+1)^{\epsilon (\tau _{\mathbf{r}_{1}+1})} &j=0, \\ (\mathbf{r}_{1}-j+2)^{\epsilon (\tau _{\mathbf{r}_{1}+1})+1}+( \mathbf{r}_{1}-j)^{\epsilon (\tau _{\mathbf{r}_{1}+1})+1}-2( \mathbf{r}_{1}-j+1)^{\epsilon (\tau _{\mathbf{r}_{1}+1})+1} &1\leq j \leq \mathbf{r}_{1}, \end{cases}\displaystyle \end{aligned}$$

the predicted value \(y^{P}(\tau _{\mathbf{r}_{1}+1})\) is given by

$$\begin{aligned} y^{P}(\tau _{\mathbf{r}_{1}+1})={}&y_{0}+ \frac{1-\epsilon (\tau _{\mathbf{r}_{1}+1})}{\varrho (\epsilon (\tau _{\mathbf{r}_{1}+1}))}f( \tau _{\mathbf{r}_{1}+1},y_{\mathbf{r}_{1}+1},y_{\mathbf{r}_{1}+1- \mathfrak{M}}) \\ &{} + \frac{\epsilon (\tau _{\mathbf{r}_{1}+1})}{\Gamma (\epsilon (\tau _{\mathbf{r}_{1}+1}))\varrho (\epsilon (\tau _{\mathbf{r}_{1}+1}))} \sum_{j=0}^{\mathbf{r}_{1}}b_{j,\mathbf{r}_{1}+1}f( \tau _{j},y_{j-\mathfrak{M}}), \end{aligned}$$

where \(b_{j,\mathbf{r}_{1}+1}= \frac{h^{\epsilon (\tau _{\mathbf{r}_{1}+1})}}{\epsilon (\tau _{\mathbf{r}_{1}+1})}(( \mathbf{r}_{1}+1-j)^{\epsilon (\tau _{\mathbf{r}_{1}+1})}-(\mathbf{r}_{1}-j)^{ \epsilon (\tau _{\mathbf{r}_{1}+1})})\), \(j=0,1,2,\ldots,\mathbf{r}_{1}\).

The proof of existence and uniqueness given by Eq. (4.5) is acquired according to the past case.

5 Numerical simulations

In this section, we show the dynamics of the fractional-order operator on the proposed model in the sense of constant fractional-order ϵ and variable fractional-order operator \(\epsilon (\tau )\). By assuming the parameter values and choosing a numerical method, we illustrate the mathematical results of the system by Eqs. (2.1), (2.7), and (2.8) with the numerical simulations (3.22), (3.26), and (4.5). We observed in the Figs. 2a–2f and 3a–3f that convergency of fractional-order derivative is faster than that of noninteger operator. We analyze the system’s dynamic characteristics to variate fractional-order derivative ϵ and \(\epsilon (\tau )\), individually. Simulated values are \(h=1.2\), \(\mathbf{r}=40\), \(\lambda =1\), \(d=0.4\), \(e=0.2\), \(\mathfrak{M}=0.1\) and the initial conditions are \(\mathbf{x}(0)=3\) and \(\mathbf{y}(0)=1\). In calculating the estimated solution, the step size used was \(Z=0.0001\). The solutions noted in Figs. 1a–1f, 2a–2f, and 3a–3f show numerical analysis of the suggested model’s special solution as a function of time for various estimations of \((\epsilon - \varsigma )\), \((\epsilon (\tau ) - \varsigma (\tau ))\) or delay \((\kappa )\), arbitrary selected. It is significant that expectation relies upon the estimation of alpha not just close to the hypothetical boundaries.

Figure 1
figure 1

Numerical simulation for the prey–predator model via Atangana–Baleanu–Caputo fractional derivative with constant order (2.1) via the numerical scheme given by Eq. (3.22). In (a)–(b) phase portrait and time series \(\mathbf{x}(\tau )\) and \(\mathbf{y}(\tau )\) for \(\epsilon =1\) and \(\varsigma =1\). In (c)–(d) phase portrait and time series \(\mathbf{x}(\tau )\) and \(\mathbf{y}(\tau )\) for \(\epsilon =0.95\) \(\varsigma =0.9\). In (e)–(f) phase portrait and time series \(\mathbf{x}(\tau )\) and \(\mathbf{y}(\tau )\) for \(\epsilon =0.9\) and \(\varsigma =0.95\)

Full size image
Figure 2
figure 2

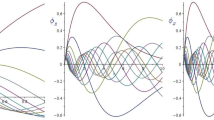
Mathematical reproduction for the prey–predator design by means of the Atangana–Baleanu–Caputo fractional derivative with variable order (2.7) through the numerical plan indicated by Eq. (3.26). In (a)–(b) phase portrait and time series \(\mathbf{x}(\tau )\) and \(\mathbf{y}(\tau )\) for \(\epsilon = \vert \sin (\epsilon \tau ) \vert \) and \(\varsigma =\tanh (3-\tau )\). In (c)–(d) phase portrait and time series \(\mathbf{x}(\tau )\) and \(\mathbf{y}(\tau )\) for for \(\epsilon =1-\frac{1}{10}\exp (-\frac{1}{2} \tau )\) and \(\varsigma =\frac{\sqrt{\tau }}{2}\). In (e)–(f) phase portrait and time series \(\mathbf{x}(\tau )\) and \(\mathbf{y}(\tau )\) for \(\epsilon = \vert \sin (\epsilon \tau ) \vert \) and \(\varsigma =1-\frac{1}{10}\exp (-\frac{1}{2} \tau )\)

Full size image
Figure 3
figure 3

Simulation for the delay prey–predator model of variable order (2.8) of the Atangana–Baleanu–Caputo fractional derivative numerically mentioned as Eq. (4.5). In (a)–(b) phase portrait and time series \(\mathbf{x}(\tau )\) and \(\mathbf{y}(\tau )\) for \(\epsilon = \vert \sin (\epsilon \tau ) \vert \), \(\varsigma =\tanh (3-\tau )\), and \(\kappa =0.01\) seconds. In (c)–(d) phase portrait and time series \(\mathbf{x}(\tau )\) and \(\mathbf{y}(\tau )\) for \(\epsilon =1-\frac{1}{10}\exp (-\frac{1}{2} \tau )\), \(\varsigma =\frac{\sqrt{t}}{2}\), and \(\kappa =0.03\) seconds. In (e)–(f) phase portrait and time series \(\mathbf{x}(\tau )\) and \(\mathbf{y}(\tau )\) for \(\epsilon = \vert \sin (\epsilon \tau ) \vert \), \(\varsigma =1-\frac{1}{10}\exp (-\frac{1}{2} \tau )\), and \(\kappa =0.5\) seconds

Full size image

6 Conclusions

A model of predator–prey consisting of constant and variable-order time FO with and without delay (gestation delay) involving operators related to a Mittag-Leffler kernel of type Liouville–Caputo is investigated in this paper. Because of this system’s nonlocality, the predator–prey model was manufactured utilizing another FO differentiation developed along with the generalized Mittag-Leffler function as a kernel. With finality to make our model more realistic, preys and predators did not follow the same fractional dynamics and the orders of FO derivatives of prey and predator population concerning time \(\epsilon \in (0,1]\) and \(\varsigma \in (0,1]\) were not equal. The fixed point theorem is beneficial to explain the existence of a novel model having a special set of solutions. We offered a numerical pattern dependent on the Adams–Bashforth–Moulton method for variable order. The existence and uniqueness of this numerical framework and complex dynamics of the structure were studied with modification of fractional orders \((\epsilon - \varsigma )\), \((\epsilon (\tau ) - \varsigma (\tau ))\) or delay \((\kappa )\).

The presented findings emphasize that the variable-order fractional methodology was more appropriate to explain complex dynamics configurations under investigation. Eventually, the predator–prey model may show rich dynamical conduct. An Intel Core i7, 2.6 GHz CPU, 16.0-GB RAM (Matlab R.2013a) computer program was used to get the results in this article.