On high-order compact schemes for the multidimensional time-fractional Schrödinger equation

Abstract

In this article, some high-order compact finite difference schemes are presented and analyzed to numerically solve one- and two-dimensional time fractional Schrödinger equations. The time Caputo fractional derivative is evaluated by the L1 and L1-2 approximation. The space discretization is based on the fourth-order compact finite difference method. For the one-dimensional problem, the rates of the presented schemes are of order $O(\tau ^{2-\alpha }+h^{4})$ and $O(\tau ^{3-\alpha }+h^{4})$, respectively, with the temporal step size τ and the spatial step size h, and $\alpha \in (0,1)$. For the two-dimensional problem, the high-order compact alternating direction implicit method is used. Moreover, unconditional stability of the proposed schemes is discussed by using the Fourier analysis method. Numerical tests are performed to support the theoretical results, and these show the accuracy and efficiency of the proposed schemes.

1 Introduction

Nowadays fractional differential equations have been widely studied in many fields, owing to their diverse applications in physics, biology, chemistry, mechanics, and finance theory [1–9]. These applications have contributed to the emergence of various fractional differential equations in the mathematical and physical world. In [10–14], the authors have published some new results of fractional operators and their applications. In fact, it is difficult to gain analytic solutions of fractional differential equations. Therefore, it is important to obtain highly accurate numerical methods for solving these fractional differential equations.

For time-fractional partial differential equations, many different numerical methods have been introduced, including theoretical analysis and numerical computing. Authors in [15, 16] have proposed various spatial second-order finite difference methods for a one-dimensional problem. For two-dimensional time-fractional partial differential equations, several numerical methods have been proposed [17, 18]. To improve the numerical accuracy, some fourth-order compact finite difference methods have been proposed for one- and two-dimensional time-fractional partial differential equations. Cui [19] constructed high-order compact alternating direction implicit schemes for two-dimensional time-fractional diffusion equations. Gao and Sun [20] focused on the study of spatial sixth-order accurate combined compact alternating direction implicit difference schemes for solving two-dimensional time-fractional advection-diffusion equations. Zhai and Feng [21] investigated several compact alternating direction implicit methods for a two-dimensional time-fractional diffusion equation.

In this paper, we consider the following multidimensional time-fractional Schrödinger equation (TFSE):

$$\begin{aligned} &i\frac{\partial ^{\alpha }u(\mathbf{x},t)}{\partial t^{\alpha }}= \nabla ^{2}u(\mathbf{x},t)+f(\mathbf{x},t), \quad \mathbf{x}\in \Omega , t\in (0,T] , \end{aligned}$$

(1.1)

with the initial and boundary conditions

$$\begin{aligned} &u(\mathbf{x},0)=u_{0}(\mathbf{x}), \quad \mathbf{x}\in \Omega , \end{aligned}$$

(1.2)

$$\begin{aligned} &u(\mathbf{x},t)=\varphi (\mathbf{x},t), \quad \mathbf{x}\in \partial \Omega , t \in (0,T], \end{aligned}$$

(1.3)

where Ω is a rectangular domain in $\mathbf{R}^{d}$ ($d=1,2$), ∂Ω is the boundary of Ω, $i=\sqrt{-1}$, and $u_{0}$ and f are known smooth functions. The fractional derivative $\partial ^{\alpha }u(\mathbf{x},t)/\partial t^{\alpha }$ is the αth order Caputo time fractional derivative defined by

$$\begin{aligned} &\frac{\partial ^{\alpha }u(\mathbf{x},t)}{\partial t^{\alpha }}= \frac{1}{\Gamma (1-\alpha )} \int _{0}^{t}(t-s)^{-\alpha }\partial _{s} u( \mathbf{x},s)\,ds \end{aligned}$$

(1.4)

with $\alpha \in (0,1)$.

In recent years, some researchers have presented numerical solutions for the time-fractional Schrödinger equation. Mohebbi et al. [22] investigated meshless method based on collocation method for the numerical solutions of time fractional nonlinear Schrödinger equation. Wei et al. [23] proposed an implicit fully discrete local discontinuous Galerkin method for the TFSE. Li et al. [24] proposed L1-Galerkin finite element method for the numerical and stability analysis of multidimensional TFSEs. In [25], the space–time Jacobi spectral collocation method is used to solve the time-fractional nonlinear Schrödinger equations subject to the appropriate initial and boundary conditions. Chen et al. [26] also proposed linearized compact alternating direction implicit schemes for nonlinear TFSEs.

The main purpose of this paper is to construct some efficient high-order compact difference schemes for solving TFSE (1.1) with (1.2) and (1.3). We apply the L1 and L1-2 formulas to approximate the time-fractional derivative and use compact operators to approximate spatial second-order derivatives. We treat the two-dimensional problem using the compact alternating direction implicit (ADI) scheme. The computational complexity is reduced to some extent. The L1 formula is the main approximation formula for approximating the time-fractional derivative, in which the truncation error is $O(\tau ^{2-\alpha })$ [27, 28]. In [29], Gao et al. proposed a new difference analog of the Caputo fractional derivative with convergence order $O(\tau ^{3-\alpha })$, called the L1-2 formula.

The remainder of our paper is organized as follows. In Sect. 2, we introduce some notations and useful results, and then two high-order compact finite difference schemes are constructed for the one-dimensional TFSE. We use the Fourier analysis method to investigate the stability of the two schemes. In Sect. 3, we extend our methods to the two-dimensional case and propose two compact ADI difference schemes by adding the perturbation term. Furthermore, a stability analysis is presented. In Sect. 4, we present numerical examples and detailed numerical results to confirm our theoretical analysis. Finally, a brief conclusion is provided in Sect. 5.

2 High-order compact difference schemes for the one-dimensional TFSE

In this section, we consider the following one-dimensional (1D) TFSE:

$$\begin{aligned} &i\frac{\partial ^{\alpha }u(x,t)}{\partial t^{\alpha }}= \frac{\partial ^{2} u(x,t)}{\partial x^{2}}+f(x,t), \quad x\in \Omega =(0,L), t\in [0,T] , \end{aligned}$$

(2.1)

$$\begin{aligned} &u(x,0)=u_{0}(x), \quad x\in \Omega , \end{aligned}$$

(2.2)

$$\begin{aligned} &u(x,t)\vert _{\partial \Omega }=\varphi (x,t), \quad (x,t)\in \partial \Omega \times (0,T], \end{aligned}$$

(2.3)

where L and T are positive constants. $u_{0}(x)$, $\varphi (x,t)$, and $f(x,t)$ are given smooth functions.

We first present some notations and useful results, which provide the basis for the theoretical analysis of our numerical methods. Let $N_{x}$ and N be two positive integers, $h=\frac{L}{N_{x}}$ be the spatial step size, and $\tau =\frac{T}{N}$ be the time step size. Define $\Omega _{h}=\{x_{j}\vert 0\leqslant j\leqslant N_{x}\}$ with $x_{j}=jh$, and $\Omega _{\tau }=\{t_{n}\vert 0\leqslant n\leqslant N\}$ with $t_{n}=n\tau$. Then the domain $[0,L]\times [0,T]$ is covered by $\Omega _{h}\times \Omega _{\tau }$. Let $\hat{u}=\{u_{j}^{n}\vert 0\leqslant j\leqslant N_{x}, 0\leqslant n \leqslant N\}$ be a grid function on $\Omega _{h}\times \Omega _{\tau }$, and define

$$ \textstyle\begin{cases} \delta _{x}^{2}u_{j}^{n}=\frac{1}{h^{2}} (u_{j-1}^{n}-2u_{j}^{n}+u_{j+1}^{n} ), \\ L_{x}u_{j}^{n}= (I+\frac{h^{2}}{12}\delta _{x}^{2} )u_{j}^{n}. \end{cases} $$

(2.4)

Next we introduce some useful results and design several compact finite difference schemes.

Lemma 2.1

(The L1 formula, see [30, 31])

Suppose that $\alpha \in (0,1)$and $u(t)\in C^{2}[0,T]$. Then we have

$$\begin{aligned} &{}^{C}_{0}\mathcal{D}_{t}^{\alpha }u(t_{n})= \frac{1}{\tau ^{\alpha }\Gamma (2-\alpha )} \Biggl[a_{0}u^{n}-\sum _{l=1}^{n-1}(a_{n-l-1}-a_{n-l})u^{l}-a_{n-1}u^{0} \Biggr]+O\bigl(\tau ^{2-\alpha }\bigr), \end{aligned}$$

(2.5)

where $a_{l}=(l+1)^{1-\alpha }-l^{1-\alpha }$, $l\geqslant 0$, and the coefficients $a_{l}$satisfy

$$\begin{aligned} & 1=a_{0}>a_{1}>a_{2}>\cdots>a_{l}> \cdots\rightarrow 0, \\ &(1-\alpha ) (l+1)^{-\alpha }< a_{l}< (1-\alpha )l^{-\alpha }. \end{aligned}$$

Lemma 2.2

(The L1-2 formula, see [29])

Suppose that $\alpha \in (0,1)$and $u(t)\in C^{3}[0,T]$. Then we have

$$\begin{aligned} {}^{C}_{0}\mathcal{D}_{t}^{\alpha }u(t_{n})= \frac{1}{\tau ^{\alpha }\Gamma (2-\alpha )} \Biggl[c_{0}u^{n}-\sum _{l=1}^{n-1}(c_{n-l-1}-c_{n-l})u^{l}-c_{n-1}u^{0} \Biggr]+O\bigl(\tau ^{3-\alpha }\bigr), \end{aligned}$$

(2.6)

where $c_{0}=a_{0}=1$for $n=1$; and for $n\geqslant 2$,

$$ c_{l}= \textstyle\begin{cases} a_{0}+b_{0}, &l=0, \\ a_{l}+b_{l}-b_{l-1}, &1\leqslant l\leqslant n-2, \\ a_{l}-b_{l-1}, &l=n-1, \end{cases} $$

with

$$\begin{aligned} &a_{l}=(l+1)^{1-\alpha }-l^{1-\alpha }, \\ &b_{l}=\frac{1}{2-\alpha } \bigl[(l+1)^{2-\alpha }-l^{2-\alpha } \bigr]- \frac{1}{2} \bigl[(l+1)^{1-\alpha }-l^{1-\alpha } \bigr]. \end{aligned}$$

Now, we consider the derivation of the high-order compact finite difference schemes. Applying the fourth-order Padé scheme for the second-order derivative, we have

$$\begin{aligned} &\frac{\partial ^{2}u}{\partial x^{2}}(x_{j},t_{n})=L^{-1}_{x} \delta _{x}^{2}u_{j}^{n}+O \bigl(h^{4}\bigr). \end{aligned}$$

(2.7)

Using (2.7), we obtain the following semi-discrete fourth-order approximation for the 1D problem (2.1):

$$\begin{aligned} i \bigl[ {}^{C}_{0}\mathcal{D}_{t}^{\alpha }u \bigr]_{j}^{n} ={}&L^{-1}_{x} \delta _{x}^{2}u_{j}^{n}+f_{j}^{n}+O \bigl(h^{4}\bigr). \end{aligned}$$

(2.8)

Then, plugging (2.4)–(2.5) into (2.8) and neglecting the small truncation errors, we obtain the high-order compact scheme (CS1DI) for (2.1)–(2.3) as follows:

$$\begin{aligned} \textit{CS1DI}: \quad \textstyle\begin{cases} [ia_{0}-\frac{12}{h^{2}}\tau ^{\alpha }\Gamma (2-\alpha ) ]u_{j-1}^{1}+ [10ia_{0}+\frac{24}{h^{2}}\tau ^{\alpha }\Gamma (2-\alpha ) ]u_{j}^{1} \\ \quad\quad {} + [ia_{0}-\frac{12}{h^{2}}\tau ^{\alpha }\Gamma (2-\alpha ) ]u_{j+1}^{1} \\ \quad =ia_{0}u_{j-1}^{0}+10ia_{0}u_{j}^{0}+ia_{0}u_{j+1}^{0} \\ \quad\quad {} +\tau ^{\alpha }\Gamma (2-\alpha ) [f_{j-1}^{1}+10f_{j}^{1}+f_{j+1}^{1} ],\quad n=1; \\ [ia_{0}-\frac{12}{h^{2}}\tau ^{\alpha }\Gamma (2-\alpha ) ]u_{j-1}^{n}+ [10ia_{0}+\frac{24}{h^{2}}\tau ^{\alpha }\Gamma (2-\alpha ) ]u_{j}^{n} \\ \quad\quad {} + [ia_{0}-\frac{12}{h^{2}}\tau ^{\alpha }\Gamma (2-\alpha ) ]u_{j+1}^{n} \\ \quad =i [\sum_{l=1}^{n-1}(a_{n-l-1}-a_{n-l})u_{j-1}^{l}+a_{n-1}u_{j-1}^{0} ] \\ \quad\quad {} +10i [\sum_{l=1}^{n-1}(a_{n-l-1}-a_{n-l})u_{j}^{l}+a_{n-1}u_{j}^{0} ] +i [\sum_{l=1}^{n-1}(a_{n-l-1}-a_{n-l})u_{j+1}^{l} \\ \quad\quad {} +a_{n-1}u_{j+1}^{0} ] +\tau ^{\alpha }\Gamma (2-\alpha ) [f_{j-1}^{n}+10f_{j}^{n}+f_{j+1}^{n} ], \quad 2\leqslant n \leqslant N; \\ u_{j}^{0}=u_{0}(x_{j}),\quad 0\leqslant j\leqslant N_{x}, \\ u_{j}^{n}=\varphi (x_{j},t_{n}), \quad j\in \partial \Omega _{h}, 1\leqslant n\leqslant N. \end{cases}\displaystyle \end{aligned}$$

(2.9)

We now present the second difference scheme for (2.1)–(2.3). Substituting (2.4) and (2.6) into (2.8) and omitting the small terms, we obtain the second high-order compact scheme (CS1DII) in the form of

$$\begin{aligned} \textit{CS1DII}: \quad \textstyle\begin{cases} [ic_{0}-\frac{12}{h^{2}}\tau ^{\alpha }\Gamma (2-\alpha ) ]u_{j-1}^{1}+ [10ic_{0}+\frac{24}{h^{2}}\tau ^{\alpha }\Gamma (2-\alpha ) ]u_{j}^{1} \\ \quad\quad {} + [ic_{0}-\frac{12}{h^{2}}\tau ^{\alpha }\Gamma (2-\alpha ) ]u_{j+1}^{1} \\ \quad =ic_{0}u_{j-1}^{0}+10ic_{0}u_{j}^{0}+ic_{0}u_{j+1}^{0} \\ \quad\quad {} +\tau ^{\alpha }\Gamma (2-\alpha ) [f_{j-1}^{1}+10f_{j}^{1}+f_{j+1}^{1} ],\quad n=1; \\ [ic_{0}-\frac{12}{h^{2}}\tau ^{\alpha }\Gamma (2-\alpha ) ]u_{j-1}^{n}+ [10ic_{0}+\frac{24}{h^{2}}\tau ^{\alpha }\Gamma (2-\alpha ) ]u_{j}^{n} \\ \quad \quad{} + [ic_{0}-\frac{12}{h^{2}}\tau ^{\alpha }\Gamma (2-\alpha ) ]u_{j+1}^{n} \\ \quad =i [\sum_{l=1}^{n-1}(c_{n-l-1}-c_{n-l})u_{j-1}^{l}+c_{n-1}u_{j-1}^{0} ] \\ \quad\quad {} +10i [\sum_{l=1}^{n-1}(c_{n-l-1}-c_{n-l})u_{j}^{l}+c_{n-1}u_{j}^{0} ] +i [\sum_{l=1}^{n-1}(c_{n-l-1}-c_{n-l})u_{j+1}^{l} \\ \quad\quad {} +c_{n-1}u_{j+1}^{0} ]+\tau ^{\alpha }\Gamma (2-\alpha ) [f_{j-1}^{n}+10f_{j}^{n}+f_{j+1}^{n} ], \quad 2\leqslant n \leqslant N; \\ u_{j}^{0}=u_{0}(x_{j}),\quad 0\leqslant j\leqslant N_{x}, \\ u_{j}^{n}=\varphi (x_{j},t_{n}), \quad j\in \partial \Omega _{h}, 1\leqslant n\leqslant N. \end{cases}\displaystyle \end{aligned}$$

(2.10)

From Lemma 2.1, Lemma 2.2, and (2.7), it is obvious that schemes CS1DI and CS1DII have truncation errors of order $O(\tau ^{2-\alpha }+h^{4})$ and $O(\tau ^{3-\alpha }+h^{4})$, respectively.

We now investigate the stability of the above schemes by using the Fourier analysis method. For the simplicity of illustration, we consider the case that $f(x,t)=0$.

Let the numerical solution be represented by

$$\begin{aligned} u_{j}^{n}={}&v^{n}e^{i\theta jh}, \end{aligned}$$

(2.11)

where $i=\sqrt{(-1)}$, $v^{n}$ is the amplitude at time $t_{n}$, and θ is the wave number in the x direction. We define the discrete $L^{2}$ norm by $\Vert u^{n}\Vert _{L^{2}}^{2}=h\sum _{j=1}^{N_{x}}\vert u^{n}_{j}\vert ^{2}$. For the fully discrete schemes CS1DI and CS1DII, we have the following stability results.

Theorem 1

Schemes CS1DI and CS1DII, defined by (2.9) and (2.10) respectively, are unconditionally stable for $\alpha \in (0,1)$.

Proof

We will complete the proof using mathematical induction. For convenience, we only give the proof for scheme CS1DI, and the case for scheme CS1DII can be completed using a similar idea.

We rewrite (2.9) as follows:

$$\begin{aligned} \bigl[12ia_{0}+\bigl(ia_{0}h^{2}-12\tau ^{\alpha }\Gamma (2-\alpha )\bigr) \delta _{x}^{2} \bigr]u_{j}^{1} ={}&\bigl[12ia_{0}+ia_{0}h^{2} \delta _{x}^{2}\bigr]u_{j}^{0} \end{aligned}$$

(2.12)

for $n=1$, and for $n\geqslant 2$ we rewrite it as

$$\begin{aligned} & \bigl[12ia_{0}+\bigl(ia_{0}h^{2}-12\tau ^{\alpha }\Gamma (2-\alpha )\bigr) \delta _{x}^{2} \bigr]u_{j}^{n} \\ &\quad = \bigl[12i+ih^{2}\delta _{x}^{2} \bigr] \Biggl[\sum_{l=1}^{n-1}(a_{n-l-1}-a_{n-l})u_{j}^{l}+ a_{n-1}u_{j}^{0} \Biggr]. \end{aligned}$$

(2.13)

Substituting (2.11) into (2.12) and (2.13), we obtain

$$\begin{aligned} & \biggl[12ia_{0}-4ia_{0}\sin ^{2} \frac{\theta h}{2}+\frac{48}{h^{2}} \tau ^{\alpha }\Gamma (2-\alpha )\sin ^{2}\frac{\theta h}{2} \biggr]v^{1} \\ &\quad = \biggl[12ia_{0}-4ia_{0}\sin ^{2} \frac{\theta h}{2} \biggr]v^{0} \end{aligned}$$

(2.14)

and

$$\begin{aligned} & \biggl[12ia_{0}-4ia_{0}\sin ^{2} \frac{\theta h}{2}+\frac{48}{h^{2}} \tau ^{\alpha }\Gamma (2-\alpha )\sin ^{2}\frac{\theta h}{2} \biggr]v^{n} \\ &\quad = \biggl[12i-4i\sin ^{2}\frac{\theta h}{2} \biggr] \Biggl[\sum _{l=1}^{n-1}(a_{n-l-1}-a_{n-l})v^{l}+ a_{n-1}v^{0} \Biggr]. \end{aligned}$$

(2.15)

Then

$$\begin{aligned} v^{1} ={}& \frac{ [12ia_{0}-4ia_{0}\sin ^{2}\frac{\theta h}{2} ]}{ [12ia_{0}-4ia_{0}\sin ^{2}\frac{\theta h}{2}+\frac{48}{h^{2}}\tau ^{\alpha }\Gamma (2-\alpha )\sin ^{2}\frac{\theta h}{2} ]} v^{0}. \end{aligned}$$

Since $a_{0}=1$, we can easily obtain

$$\begin{aligned} \bigl\vert v^{1} \bigr\vert \leqslant \bigl\vert v^{0} \bigr\vert . \end{aligned}$$

Suppose that $\vert v^{m}\vert \leqslant \vert v^{0}\vert$ holds for $m=1,2,\ldots,n-1$. Then, using (2.15) and Lemma 2.1, we have

$$\begin{aligned} \bigl\vert v^{n} \bigr\vert \leqslant {}&\sum _{l=1}^{n-1}(a_{n-l-1}-a_{n-l}) \bigl\vert v^{l} \bigr\vert + a_{n-1} \bigl\vert v^{0} \bigr\vert \\ \leqslant {}& \Biggl[\sum_{l=1}^{n-1}(a_{n-l-1}-a_{n-l})+ a_{n-1} \Biggr] \bigl\vert v^{0} \bigr\vert = \bigl\vert v^{0} \bigr\vert . \end{aligned}$$

That is,

$$\begin{aligned} \bigl\vert v^{n} \bigr\vert \leqslant \bigl\vert v^{0} \bigr\vert \end{aligned}$$

(2.16)

holds true for all $m=n$. Moreover, applying (2.16) and Parseval’s equality, we obtain

$$\begin{aligned} \bigl\Vert u^{n} \bigr\Vert _{L^{2}}^{2}={}&h\sum _{j=1}^{N_{x}} \bigl\vert u^{n}_{j} \bigr\vert ^{2}=h \sum_{j=1}^{N_{x}} \bigl\vert v^{n}e^{i\theta jh} \bigr\vert ^{2}=h\sum _{j=1}^{N_{x}} \bigl\vert v^{n} \bigr\vert ^{2} \\ \leqslant {}& h\sum_{j=1}^{N_{x}} \bigl\vert v^{0} \bigr\vert ^{2}= h\sum_{j=1}^{N_{x}} \bigl\vert v^{0}e^{i \theta jh} \bigr\vert ^{2} =h\sum _{j=1}^{N_{x}} \bigl\vert u^{0}_{j} \bigr\vert ^{2}= \bigl\Vert u^{0} \bigr\Vert _{L^{2}}^{2}, \quad n=1,\ldots,N, \end{aligned}$$

which proves that scheme CS1DI is unconditionally stable. Thus, the proof is completed. □

3 High-order compact ADI schemes for the two-dimensional TFSE

In this section, we develop two high-order compact ADI schemes for two-dimensional (2D) TFSE with the following initial and boundary conditions:

$$\begin{aligned} &i\frac{\partial ^{\alpha }u(x,y,t)}{\partial t^{\alpha }}= \biggl( \frac{\partial ^{2}}{\partial x^{2}}+ \frac{\partial ^{2}}{\partial y^{2}} \biggr)u(x,y,t)+f(x,y,t), \quad (x,y) \in \Omega , t\in (0,T] , \end{aligned}$$

(3.1)

$$\begin{aligned} &u(x,y,0)=u_{0}(x,y), \quad (x,y)\in \Omega , \end{aligned}$$

(3.2)

$$\begin{aligned} &u(x,y,t)\vert _{\partial \Omega }=\varphi (x,y,t), \quad (x,y,t)\in \partial \Omega \times (0,T], \end{aligned}$$

(3.3)

where L and T are positive constants, $\Omega =(0,L)\times (0,L)$. $u_{0}(x,y)$, $\varphi (x,y,t)$, and $f(x,y,t)$ are given smooth functions.

Let M, N be positive integers, $h=\frac{L}{M}$ be the spatial step size, and $\tau =\frac{T}{N}$ be the time step size. Define $\Omega _{h}=\{(x_{j}, y_{k})\vert 0\leqslant j,k\leqslant M\}$ with $x_{j}=jh$ and $y_{k}=kh$; and $\Omega _{\tau }=\{t_{n}\vert 0\leqslant n\leqslant N\}$ with $t_{n}=n\tau$. Then the domain $[0,L]^{2}\times [0,T]$ is covered by $\Omega _{h}\times \Omega _{\tau }$. Let $\hat{u}=\{u_{jk}^{n}\vert 0\leqslant j,k\leqslant M, 0\leqslant n \leqslant N\}$ be a grid function on $\Omega _{h}\times \Omega _{\tau }$, and define

$$ \textstyle\begin{cases} \delta _{x}^{2}u_{jk}^{n}=\frac{1}{h^{2}} (u_{j-1,k}^{n}-2u_{jk}^{n}+u_{j+1,k}^{n} ), \\ L_{x}u_{jk}^{n}= (I+\frac{h^{2}}{12}\delta _{x}^{2} )u_{jk}^{n}. \end{cases} $$

(3.4)

The notations $\delta _{y}^{2}u_{jk}^{n}$ and $L_{y}u_{jk}^{n}$ can be defined similarly.

Applying the fourth-order Padé scheme for the second-order derivatives, we have

$$\begin{aligned} &\frac{\partial ^{2}u}{\partial x^{2}}(x_{j},y_{k},t_{n})=L^{-1}_{x} \delta _{x}^{2}u_{jk}^{n}+O \bigl(h^{4}\bigr), \end{aligned}$$

(3.5)

$$\begin{aligned} &\frac{\partial ^{2}u}{\partial y^{2}}(x_{j},y_{k},t_{n})=L^{-1}_{y} \delta _{y}^{2}u_{jk}^{n}+O \bigl(h^{4}\bigr). \end{aligned}$$

(3.6)

Using (3.5) and (3.6), we can obtain the following semi-discrete fourth-order approximation for the 2D problem (3.1):

$$\begin{aligned} &i \bigl[ {}^{C}_{0}\mathcal{D}_{t}^{\alpha }u \bigr]_{jk}^{n} =L^{-1}_{x} \delta _{x}^{2}u_{jk}^{n}+L^{-1}_{y} \delta _{y}^{2}u_{jk}^{n}+f_{jk}^{n}+O \bigl(h^{4}\bigr). \end{aligned}$$

(3.7)

Thus, by using Lemma 2.1 for (3.7) and neglecting the small truncation errors, we obtain the following scheme:

$$\begin{aligned} &\frac{i}{\tau ^{\alpha }\Gamma (2-\alpha )} \Biggl[a_{0}u_{jk}^{n}- \sum _{l=1}^{n-1}(a_{n-l-1}-a_{n-l})u_{jk}^{l}-a_{n-1}u_{jk}^{0} \Biggr] \\ &\quad =L^{-1}_{x}\delta _{x}^{2}u_{jk}^{n}+L^{-1}_{y} \delta _{y}^{2}u_{jk}^{n}+f_{jk}^{n}. \end{aligned}$$

(3.8)

Act with the operator $(-i\tau ^{\alpha }\Gamma (2-\alpha ))L_{x}L_{y}$ on both sides of (3.8). By noting that $a_{0}=1$, after rearranging the terms we have the equivalent forms

$$\begin{aligned} & \bigl[L_{x}L_{y}+i\tau ^{\alpha }\Gamma (2-\alpha ) \bigl(\delta _{x}^{2}L_{y}+ \delta _{y}^{2}L_{x}\bigr) \bigr]u_{jk}^{n} \\ &\quad =L_{x}L_{y} \Biggl[\sum _{l=1}^{n-1}(a_{n-l-1}-a_{n-l})u_{jk}^{l}+a_{n-1}u_{jk}^{0} \Biggr] -i\tau ^{\alpha }\Gamma (2-\alpha )L_{x}L_{y}f_{jk}^{n}. \end{aligned}$$

(3.9)

Next we consider the derivation of the ADI difference scheme so that some small splitting terms should be added onto the left-hand side of (3.9) in order to achieve the operator splitting scheme. By adding the splitting term

$$\begin{aligned} \bigl[i\tau ^{\alpha }\Gamma (2-\alpha ) \bigr]^{2}\delta _{x}^{2} \delta _{y}^{2} \bigl(u_{jk}^{n}- u_{jk}^{n-1} \bigr) \end{aligned}$$

to the left-hand side of (3.9) and rearranging the terms of the resulting scheme, we obtain an approximate scheme for $n > 1$ as follows:

$$\begin{aligned} & \bigl(L_{x}+i\tau ^{\alpha }\Gamma (2-\alpha )\delta _{x}^{2} \bigr) \bigl(L_{y}+i\tau ^{\alpha } \Gamma (2-\alpha )\delta _{y}^{2} \bigr)u_{jk}^{n} \\ &\quad =L_{x}L_{y} \Biggl[\sum _{l=1}^{n-1}(a_{n-l-1}-a_{n-l})u_{jk}^{l}+a_{n-1}u_{jk}^{0} \Biggr] \\ &\quad \quad{} + \bigl[i\tau ^{\alpha }\Gamma (2-\alpha ) \bigr]^{2} \delta _{x}^{2} \delta _{y}^{2}u_{jk}^{n-1} -i\tau ^{\alpha }\Gamma (2-\alpha )L_{x}L_{y}f_{jk}^{n}. \end{aligned}$$

(3.10)

Introducing the intermediate variables $u^{1(*)}$ and $u^{n(*)}$, we can obtain the following high-order compact ADI scheme (CS2DI) for (3.1)–(3.3):

$$\begin{aligned} \textit{CS2DI}: \quad \textstyle\begin{cases} (L_{x}+i\tau ^{\alpha }\Gamma (2-\alpha )\delta _{x}^{2} )u_{jk}^{1(*)}= L_{x}L_{y}u_{jk}^{0}+ [i\tau ^{\alpha }\Gamma (2-\alpha ) ]^{2} \delta _{x}^{2}\delta _{y}^{2} u_{jk}^{0} \\ \hphantom{(L_{x}+i\tau ^{\alpha }\Gamma (2-\alpha )\delta _{x}^{2} )u_{jk}^{1(*)}=}{} -i\tau ^{\alpha }\Gamma (2-\alpha )L_{x}L_{y}f_{jk}^{1}, \\ (L_{y}+i\tau ^{\alpha }\Gamma (2-\alpha )\delta _{y}^{2} )u_{jk}^{1}=u_{jk}^{1(*)}, \quad n=1; \\ (L_{x}+i\tau ^{\alpha }\Gamma (2-\alpha )\delta _{x}^{2} )u_{jk}^{n(*)} \\ \quad = L_{x}L_{y} [\sum_{l=1}^{n-1}(a_{n-l-1}-a_{n-l})u_{jk}^{l}+a_{n-1}u_{jk}^{0} ] \\ \quad\quad {} + [i\tau ^{\alpha }\Gamma (2-\alpha ) ]^{2}\delta _{x}^{2} \delta _{y}^{2} u_{jk}^{n-1}-i\tau ^{\alpha }\Gamma (2-\alpha )L_{x}L_{y}f_{jk}^{n}, \\ (L_{y}+i\tau ^{\alpha }\Gamma (2-\alpha )\delta _{y}^{2} )u_{jk}^{n}=u_{jk}^{n(*)}, \quad 2\leqslant n\leqslant N; \\ u_{jk}^{0}=u_{0}(x_{j},y_{k}),\quad 0\leqslant j,k\leqslant M, \\ u_{jk}^{n}=\varphi (x_{j},y_{k},t_{n}), \quad (j,k)\in \partial \Omega _{h},1\leqslant n\leqslant N. \end{cases}\displaystyle \end{aligned}$$

(3.11)

To solve (3.11), we need to give the values of $u^{1(*)}$ and $u^{n(*)}$ on the boundary, and these are obtained from the second and fourth equation in (3.11), respectively.

Now, we present the second difference scheme for (3.1)–(3.3). Using Lemma 2.2 for (3.7) and omitting the small terms, the second difference scheme can be given in the form of

$$\begin{aligned} &\frac{i}{\tau ^{\alpha }\Gamma (2-\alpha )} \Biggl[c_{0}u_{jk}^{n}- \sum _{l=1}^{n-1}(c_{n-l-1}-c_{n-l})u_{jk}^{l}-c_{n-1}u_{jk}^{0} \Biggr] \\ &\quad =L^{-1}_{x}\delta _{x}^{2}u_{jk}^{n}+L^{-1}_{y} \delta _{y}^{2}u_{jk}^{n}+f_{jk}^{n}. \end{aligned}$$

(3.12)

By acting on both sides of (3.12) with the operator $(\frac{-i\tau ^{\alpha }\Gamma (2-\alpha )}{c_{0}} )L_{x}L_{y}$ and rearranging the terms, we obtain

$$\begin{aligned} & \biggl[L_{x}L_{y}+\frac{i\tau ^{\alpha }\Gamma (2-\alpha )}{c_{0}}\bigl( \delta _{x}^{2}L_{y}+\delta _{y}^{2}L_{x} \bigr) \biggr]u_{jk}^{n} \\ &\quad =L_{x}L_{y} \Biggl[\sum _{l=1}^{n-1} \frac{c_{n-l-1}-c_{n-l}}{c_{0}}u_{jk}^{l}+ \frac{c_{n-1}}{c_{0}}u_{jk}^{0} \Biggr] \\ &\quad \quad{} -\frac{i\tau ^{\alpha }\Gamma (2-\alpha )}{c_{0}}L_{x}L_{y}f_{jk}^{n}. \end{aligned}$$

(3.13)

By adding the splitting term $(\frac{i\tau ^{\alpha }\Gamma (2-\alpha )}{c_{0}} )^{2} \delta _{x}^{2}\delta _{y}^{2} (u_{jk}^{n}- u_{jk}^{n-1} )$ to the left-hand side of (3.13) and rearranging the terms of the resulting scheme, we obtain the following scheme for $n > 1$:

$$\begin{aligned} & \biggl(L_{x}+\frac{i\tau ^{\alpha }\Gamma (2-\alpha )}{c_{0}}\delta _{x}^{2} \biggr) \biggl(L_{y}+\frac{i\tau ^{\alpha }\Gamma (2-\alpha )}{c_{0}} \delta _{y}^{2} \biggr)u_{jk}^{n} \\ &\quad =L_{x}L_{y} \Biggl[\sum _{l=1}^{n-1} \frac{c_{n-l-1}-c_{n-l}}{c_{0}}u_{jk}^{l}+ \frac{c_{n-1}}{c_{0}}u_{jk}^{0} \Biggr] \\ &\quad\quad{} + \biggl[\frac{i\tau ^{\alpha }\Gamma (2-\alpha )}{c_{0}} \biggr]^{2} \delta _{x}^{2}\delta _{y}^{2}u_{jk}^{n-1} - \frac{i\tau ^{\alpha }\Gamma (2-\alpha )}{c_{0}}L_{x}L_{y}f_{jk}^{n}. \end{aligned}$$

(3.14)

Upon introducing the intermediate variables $u^{1(*)}$ and $u^{n(*)}$ and noticing that $c_{0}=1$ for $n=1$, we obtain the following additional high-order compact ADI scheme (CS2DII) for (3.1)–(3.3):

$$\begin{aligned} \textit{CS2DII}: \quad \textstyle\begin{cases} (L_{x}+i\tau ^{\alpha }\Gamma (2-\alpha )\delta _{x}^{2} )u_{jk}^{1(*)} \\ \quad= L_{x}L_{y}u_{jk}^{0} + [i\tau ^{\alpha }\Gamma (2-\alpha ) ]^{2}\delta _{x}^{2} \delta _{y}^{2} u_{jk}^{0}-i\tau ^{\alpha }\Gamma (2-\alpha )L_{x}L_{y}f_{jk}^{1}, \\ (L_{y}+i\tau ^{\alpha }\Gamma (2-\alpha )\delta _{y}^{2} )u_{jk}^{1}=u_{jk}^{1(*)}, \quad n=1; \\ (L_{x}+\frac{i\tau ^{\alpha }\Gamma (2-\alpha )}{c_{0}}\delta _{x}^{2} )u_{jk}^{n(*)} \\ \quad = L_{x}L_{y} [\sum_{l=1}^{n-1} \frac{c_{n-l-1}-c_{n-l}}{c_{0}}u_{jk}^{l}+\frac{c_{n-1}}{c_{0}}u_{jk}^{0} ] \\ \quad\quad {} + [\frac{i\tau ^{\alpha }\Gamma (2-\alpha )}{c_{0}} ]^{2} \delta _{x}^{2}\delta _{y}^{2} u_{jk}^{n-1}- \frac{i\tau ^{\alpha }\Gamma (2-\alpha )}{c_{0}}L_{x}L_{y}f_{jk}^{n}, \\ (L_{y}+\frac{i\tau ^{\alpha }\Gamma (2-\alpha )}{c_{0}}\delta _{y}^{2} )u_{jk}^{n}=u_{jk}^{n(*)}, \quad 2\leqslant n \leqslant N; \\ u_{jk}^{0}=u_{0}(x_{j},y_{k}),\quad 0\leqslant j,k\leqslant M, \\ u_{jk}^{n}=\varphi (x_{j},y_{k},t_{n}), \quad (j,k)\in \partial \Omega _{h},1\leqslant n\leqslant N. \end{cases}\displaystyle \end{aligned}$$

(3.15)

To solve (3.15), we need to give the values of $u^{1(*)}$ and $u^{n(*)}$ on the boundary, and these are obtained from the second and fourth equations in (3.15), respectively.

From (3.7), it is obvious that schemes CS2DI and CS2DII can maintain fourth-order accuracy in space, and from Lemmas 2.1 and 2.2 we know that schemes (3.9) and (3.13) have temporal convergence rates of $O(\tau ^{2-\alpha })$ and $O(\tau ^{3-\alpha })$, respectively. We note the fact that if the splitting errors are much larger than the truncation error, as pointed out by Douglas and Kim [32], a splitting term will play an important role in the accuracy of the solution. This phenomenon has also been pointed out by Zhai et al. [33]. From the splitting term $[i\tau ^{\alpha }\Gamma (2-\alpha ) ]^{2}\delta _{x}^{2} \delta _{y}^{2} (u_{jk}^{n}- u_{jk}^{n-1} )$, we find that the splitting errors are $O(\tau ^{2\alpha +1})$ in schemes CS2DI and CS2DII, respectively. This means that the temporal convergence rates for these schemes will tend to $\alpha +1$. The numerical results in Sect. 4 further confirm this judgment.

In the following, we investigate the stability of the high-order compact ADI schemes (CS2DI and CS2DII) using the Fourier analysis method. Here, in order to simplify the notations and without loss of generality, we consider the case that $f(x,y,t)=0$.

Suppose that the numerical solution is represented by

$$\begin{aligned} u_{jk}^{n}={}&v^{n}e^{i(\theta _{x} jh+\theta _{y} kh)}, \end{aligned}$$

(3.16)

where $i=\sqrt{(-1)}$, $v^{n}$ is the amplitude at time $t_{n}$, and $\theta _{x}$, $\theta _{y}$ are the wave numbers in the x and y directions, respectively. We define the discrete $L^{2}$ norm by $\Vert u^{n}\Vert _{L^{2}}^{2}=h^{2}\sum _{j=1}^{M}\sum _{k=1}^{M}\vert u^{n}_{jk}\vert ^{2}$. For the fully discrete schemes CS2DI and CS2DII, we have the following stability results.

Theorem 2

Schemes CS2DI and CS2DII, defined by (3.11) and (3.15) respectively, are unconditionally stable for $\alpha \in (0,1)$.

Proof

We apply mathematical induction to complete the proof. For convenience, we only give the proof for scheme CS2DI, and the case for scheme CS2DII can be completed using a similar idea.

First, we rewrite (3.11) as

$$\begin{aligned} & \bigl(L_{x}+i\tau ^{\alpha }\Gamma (2-\alpha )\delta _{x}^{2} \bigr) \bigl(L_{y}+i\tau ^{\alpha } \Gamma (2-\alpha )\delta _{y}^{2} \bigr)u_{jk}^{1} \\ &\quad =L_{x}L_{y}u_{jk}^{0} + \bigl[i\tau ^{\alpha }\Gamma (2-\alpha ) \bigr]^{2}\delta _{x}^{2}\delta _{y}^{2} u_{jk}^{0} \end{aligned}$$

(3.17)

for $n=1$, and for $2\leqslant n\leqslant N$, we write this as follows:

$$\begin{aligned} & \bigl(L_{x}+i\tau ^{\alpha }\Gamma (2-\alpha )\delta _{x}^{2} \bigr) \bigl(L_{y}+i\tau ^{\alpha } \Gamma (2-\alpha )\delta _{y}^{2} \bigr)u_{jk}^{n} \\ &\quad =L_{x}L_{y} \Biggl[\sum _{l=1}^{n-1}(a_{n-l-1}-a_{n-l})u_{jk}^{l}+ a_{n-1}u_{jk}^{0} \Biggr] \\ &\quad \quad{} + \bigl[i\tau ^{\alpha }\Gamma (2-\alpha ) \bigr]^{2} \delta _{x}^{2} \delta _{y}^{2} u_{jk}^{n-1}. \end{aligned}$$

(3.18)

Substituting (3.16) into (3.17) and (3.18) and denoting $r=\tau ^{\alpha }\Gamma (2-\alpha )/h^{2}$, $s_{1}=\sin ^{2}\frac{\theta _{x}h}{2}$, and $s_{2}=\sin ^{2}\frac{\theta _{y}h}{2}$ for simplicity, where $0\leqslant s_{1}, s_{2} \leqslant 1$, for $n=1$ we obtain

$$\begin{aligned} & \biggl[ \biggl(1-\frac{1}{3}s_{1} \biggr)-4irs_{1} \biggr] \biggl[ \biggl(1- \frac{1}{3}s_{2} \biggr)-4irs_{2} \biggr]v^{1} \\ &\quad = \biggl[ \biggl(1-\frac{1}{3}s_{1} \biggr) \biggl(1- \frac{1}{3}s_{2} \biggr) -16r^{2}s_{1}s_{2} \biggr]v^{0}, \end{aligned}$$

and for $2\leqslant n\leqslant N$ we obtain

$$\begin{aligned} & \biggl[ \biggl(1-\frac{1}{3}s_{1} \biggr)-4irs_{1} \biggr] \biggl[ \biggl(1- \frac{1}{3}s_{2} \biggr)-4irs_{2} \biggr]v^{n} \\ &\quad = \biggl(1-\frac{1}{3}s_{1} \biggr) \biggl(1- \frac{1}{3}s_{2} \biggr) \Biggl[\sum _{l=1}^{n-1}(a_{n-l-1}-a_{n-l})v^{l}+ a_{n-1}v^{0} \Biggr]-16r^{2}s_{1}s_{2}v^{n-1} \\ &\quad = \biggl[ \biggl(1-\frac{1}{3}s_{1} \biggr) \biggl(1- \frac{1}{3}s_{2} \biggr) (1-a_{1})-16r^{2}s_{1}s_{2} \biggr]v^{n-1} \\ &\quad \quad{} + \biggl(1-\frac{1}{3}s_{1} \biggr) \biggl(1- \frac{1}{3}s_{2} \biggr) \Biggl[\sum _{l=1}^{n-2}(a_{n-l-1}-a_{n-l})v^{l}+ a_{n-1}v^{0} \Biggr]. \end{aligned}$$

Consequently, we have

$$ \textstyle\begin{cases} v^{1}= \frac{ (1-\frac{1}{3}s_{1} ) (1-\frac{1}{3}s_{2} ) -16r^{2}s_{1}s_{2}}{ (1-\frac{1}{3}s_{1} ) (1-\frac{1}{3}s_{2} ) -16r^{2}s_{1}s_{2}-i [4rs_{2} (1-\frac{1}{3}s_{1} )+ 4rs_{1} (1-\frac{1}{3}s_{2} ) ]}v^{0}\equiv \mu _{0}v^{0}, \\ v^{n}= \frac{ (1-\frac{1}{3}s_{1} ) (1-\frac{1}{3}s_{2} ) (1-a_{1})-16r^{2}s_{1}s_{2}}{ (1-\frac{1}{3}s_{1} ) (1-\frac{1}{3}s_{2} ) -16r^{2}s_{1}s_{2}-i [4rs_{2} (1-\frac{1}{3}s_{1} )+ 4rs_{1} (1-\frac{1}{3}s_{2} ) ]}v^{n-1} \\ \hphantom{v^{n}=}{} + \frac{ (1-\frac{1}{3}s_{1} ) (1-\frac{1}{3}s_{2} )}{ [ (1-\frac{1}{3}s_{1} )-4irs_{1} ] [ (1-\frac{1}{3}s_{2} )-4irs_{2} ]} [ \sum_{l=1}^{n-2}(a_{n-l-1}-a_{n-l})v^{l}+ a_{n-1}v^{0} ], \\ \quad 2\leqslant n\leqslant N. \end{cases} $$

(3.19)

We note that $0\leqslant s_{1}, s_{2} \leqslant 1$, and from the first equation of (3.19) we can easily see that $0\leqslant \vert \mu _{0}\vert \leqslant 1$. Therefore,

$$\begin{aligned} \vert v_{1} \vert = \vert \mu _{0} \vert \vert v_{0} \vert \leqslant \vert v_{0} \vert . \end{aligned}$$

Assume that we have proved that

$$\begin{aligned} \bigl\vert v^{m} \bigr\vert \leqslant \bigl\vert v^{0} \bigr\vert , \quad m=1,2,\ldots,n-1. \end{aligned}$$

Then, applying Lemma 2.1 and (3.19), we obtain

$$\begin{aligned} \bigl\vert v^{n} \bigr\vert \leqslant {}&\frac{ \vert (1-\frac{1}{3}s_{1} ) (1-\frac{1}{3}s_{2} ) (1-a_{1})-16r^{2}s_{1}s_{2} \vert }{ \vert (1-\frac{1}{3}s_{1} ) (1-\frac{1}{3}s_{2} ) -16r^{2}s_{1}s_{2}-i [4rs_{2} (1-\frac{1}{3}s_{1} )+ 4rs_{1} (1-\frac{1}{3}s_{2} ) ] \vert } \bigl\vert v^{n-1} \bigr\vert \\ & {} + \frac{ \vert (1-\frac{1}{3}s_{1} ) (1-\frac{1}{3}s_{2} ) \vert }{ \vert [ (1-\frac{1}{3}s_{1} )-4irs_{1} ] [ (1-\frac{1}{3}s_{2} )-4irs_{2} ] \vert } \Biggl[\sum_{l=1}^{n-2} (a_{n-l-1}-a_{n-l}) \bigl\vert v^{l} \bigr\vert +a_{n-1} \bigl\vert v^{0} \bigr\vert \Biggr] \\ \leqslant {}&\frac{ \vert (1-\frac{1}{3}s_{1} ) (1-\frac{1}{3}s_{2} ) (1-a_{1})-16r^{2}s_{1}s_{2} \vert }{ \vert (1-\frac{1}{3}s_{1} ) (1-\frac{1}{3}s_{2} ) -16r^{2}s_{1}s_{2}-i [4rs_{2} (1-\frac{1}{3}s_{1} )+ 4rs_{1} (1-\frac{1}{3}s_{2} ) ] \vert } \bigl\vert v^{0} \bigr\vert \\ & {} + \frac{ \vert (1-\frac{1}{3}s_{1} ) (1-\frac{1}{3}s_{2} )a_{1} \vert }{ \vert (1-\frac{1}{3}s_{1} )-4irs_{1} \vert \vert (1-\frac{1}{3}s_{2} )-4irs_{2} \vert } \bigl\vert v^{0} \bigr\vert , \end{aligned}$$

and it is not difficult to prove that the following inequalities hold:

$$\begin{aligned} &\biggl\vert \biggl(1-\frac{1}{3}s_{1} \biggr) \biggl(1- \frac{1}{3}s_{2} \biggr) -16r^{2}s_{1}s_{2}-i \biggl[4rs_{2} \biggl(1-\frac{1}{3}s_{1} \biggr)+ 4rs_{1} \biggl(1- \frac{1}{3}s_{2} \biggr) \biggr] \biggr\vert \\ &\quad \geqslant \biggl\vert \biggl(1-\frac{1}{3}s_{1} \biggr) \biggl(1- \frac{1}{3}s_{2} \biggr) (1-a_{1})-16r^{2}s_{1}s_{2} \biggr\vert \end{aligned}$$

and

$$\begin{aligned} \biggl\vert \biggl(1-\frac{1}{3}s_{1} \biggr)-4irs_{1} \biggr\vert \biggl\vert \biggl(1-\frac{1}{3}s_{2} \biggr)-4irs_{2} \biggr\vert \geqslant \biggl\vert \biggl(1- \frac{1}{3}s_{1} \biggr) \biggl(1-\frac{1}{3}s_{2} \biggr)a_{1} \biggr\vert . \end{aligned}$$

That is,

$$\begin{aligned} \bigl\vert v^{n} \bigr\vert \leqslant \bigl\vert v^{0} \bigr\vert \end{aligned}$$

(3.20)

holds for all $m=n$. Furthermore, using (3.20) and Parseval’s equality, we obtain

$$\begin{aligned} \bigl\Vert u^{n} \bigr\Vert _{L^{2}}^{2}={}&h^{2} \sum_{j=1}^{M}\sum _{k=1}^{M} \bigl\vert u^{n}_{jk} \bigr\vert ^{2}= h^{2}\sum_{j=1}^{M} \sum_{k=1}^{M} \bigl\vert v^{n}e^{i(\theta _{x} jh+\theta _{y}kh)} \bigr\vert ^{2}=h^{2}\sum _{j=1}^{M}\sum_{k=1}^{M} \bigl\vert v^{n} \bigr\vert ^{2} \\ \leqslant {}& h^{2}\sum_{j=1}^{M} \sum_{k=1}^{M} \bigl\vert v^{0} \bigr\vert ^{2}= h^{2}\sum_{j=1}^{M} \sum_{k=1}^{M} \bigl\vert v^{0}e^{i(\theta _{x} jh+\theta _{y}kh)} \bigr\vert ^{2} =h^{2}\sum _{j=1}^{M}\sum_{k=1}^{M} \bigl\vert u^{0}_{jk} \bigr\vert ^{2} \\ ={}& \bigl\Vert u^{0} \bigr\Vert _{L^{2}}^{2}, \quad n=1,\ldots,N, \end{aligned}$$

and the proof is completed. □

4 Numerical results

In this section, three numerical examples, which verify the efficiency and accuracy of the proposed schemes, are presented.

Example 1

Let us consider the following 1D time-fractional Schrödinger equation:

$$ \textstyle\begin{cases} i\frac{\partial ^{\alpha }u(x,t)}{\partial t^{\alpha }}= \frac{\partial ^{2} u(x,t)}{\partial x^{2}}+f(x,t), \\ f(x,t)=(1+i)t^{2}\pi ^{2}\sin \pi x+ \frac{2t^{2-\alpha }}{\Gamma (3-\alpha )}(i-1)\sin \pi x, \\ \quad x\in \Omega =[0,2], t\in (0,1), \end{cases} $$

with the exact solution $u(x,t)=(1+i)t^{2}\sin \pi x$. The initial and boundary conditions can be obtained from the exact solution.

Now, we investigate the spatial convergence rates for schemes CS1DI and CS1DII. We choose $N=1000$ to avoid the influence of the temporal approximation. Table 1 gives the $L^{\infty }$-norm errors (denoted by $L^{\infty }$-error) and convergence orders at time $T=1$ for $\alpha =0.25$ (or $\alpha =0.5$) and various values of $N_{x}$. From Table 1, we conclude that schemes CS1DI and CS1DII are verified to have fourth-order accuracy in space. Regarding the time accuracy, by fixing $N_{x}$ to eliminate the contamination of the spatial error, the numerical results at $T=1$ for different α and N values are presented in Table 2. In Fig. 1, we also present the errors in the $L^{\infty }$-norm and $L^{2}$-norm as a function of the time step sizes for $\alpha =0.25$, where $N_{x}=50$ in scheme CS1DI and $N_{x}=250$ in scheme CS1DII. From these results, we find that the convergence order in time for schemes CS1DI and CS1DII is close to $2-\alpha$ and $3-\alpha$, respectively.

Figure 1

Time errors as a function of the time step sizes with $\alpha =0.25$ for Example 1. (a) Scheme CS1DI, (b) scheme CS1DII

Table 1 Numerical comparison results of schemes CS1DI and CS1DII for Example 1, at $T=1$ with $N=1000$ and different $N_{x}$ and α

Table 2 Numerical comparison results of schemes CS1DI and CS1DII for Example 1, at $T=1$ with $N_{x}=2000$ and different N and α

Example 2

Here, we consider the alternative 1D time-fractional Schrödinger equation

$$ \textstyle\begin{cases} i\frac{\partial ^{\alpha }u(x,t)}{\partial t^{\alpha }}= \frac{\partial ^{2} u(x,t)}{\partial x^{2}}+f(x,t), \\ f(x,t)=i (\frac{2t^{2-\alpha } \cos x}{\Gamma (3-\alpha )}+t^{2} \sin x ) -\frac{2t^{2-\alpha }\sin x}{\Gamma (3-\alpha )}+t^{2} \cos x, \\ \quad x\in \Omega =[0,2\pi ], t\in (0,1). \end{cases} $$

The exact solution to the problem is $u(x,t)=t^{2}(\cos x+i\sin x)$. The initial and boundary conditions can be obtained from the exact solution.

In this example, we first use schemes CS1DI and CS1DII to verify the spatial convergence rates. Table 3 presents the $L^{\infty }$-errors and convergence orders with $N=1000$ and various values of $N_{x}$ and α at time $T=1$, from which we find that schemes CS1DI and CS1DII both achieve fourth-order accuracy regardless of the value of α. Next, we test the temporal convergence rate for the case that $T=1$ and $N_{x}=2000$. The results for different N and α values are listed in Table 4. In Fig. 2, we plot the errors in the $L^{\infty }$-norm and $L^{2}$-norm as a function of the time step sizes for $N_{x}=50$ in scheme CS1DI and $N_{x}=250$ in scheme CS1DII, where $\alpha =0.75$. It shows that the slopes of the error curves obtained for scheme CS1DI is 1.25, which accords with the theoretical estimates 2-α. However, scheme CS1DII yields a temporal approximation order 3-α, i.e., the slopes of the error curves is 2.25. Again, as expected it is clearly shown that scheme CS1DII has higher accuracy than scheme CS1DI.

Figure 2

Time errors as a function of the time step sizes with $\alpha =0.75$ for Example 2. (a) Scheme CS1DI, (b) scheme CS1DII

Table 3 Numerical comparison results of schemes CS1DI and CS1DII for Example 2, at $T=1$ with $N=1000$ and different $N_{x}$ and α

Table 4 Numerical comparison results of schemes CS1DI and CS1DII for Example 2, at $T=1$ with $N_{x}=2000$ and different N and α

Example 3

We consider the following 2D time-fractional Schrödinger equation:

$$ \textstyle\begin{cases} i\frac{\partial ^{\alpha }u}{\partial t^{\alpha }}= \frac{\partial ^{2}u}{\partial x^{2}}+ \frac{\partial ^{2}u}{\partial y^{2}}+f(x,y,t), \\ f(x,y,t)=(1+i) (2t^{2}((1-y)y+(1-x)x)+i(1-x)(1-y)xy \frac{2t^{2-\alpha }}{\Gamma (3-\alpha )} ), \\ \quad (x,y)\in \Omega =[0,1]\times [0,1], t\in [0,1]. \end{cases} $$

Its exact solution is $u(x,y,t)=(1+i)(1-x)(1-y)xyt^{2}$. The initial and boundary conditions of this problem can be extracted from the exact solution.

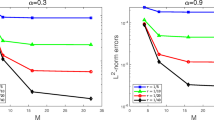
First, the spatial accuracy is numerically examined. We decrease the mesh size of h to $h/2$ and τ to $\tau /2^{4/1+\alpha }$, and the errors and orders for schemes CS2DI and CS2DII are shown in Table 5 for different α values. We can see that the experimental convergence order is approximately four. Second, the numerical accuracy in time is verified. The numerical results at $T=1$ for $\alpha =0.1, 0.5$, and 0.9 are listed in Table 6. Meanwhile, the numerical results are plotted in Fig. 3. From these results, we find that schemes CS2DI and CS2DII yield a temporal approximation order close to $1+\alpha$, i.e., the slopes of the error curves are 1.25 and 1.75, respectively, for $\alpha =0.25$ and $\alpha =0.75$. We also plot the contour graphs of the numerical errors using schemes CS2DI and CS2DII with $N=M=100$ for $\alpha =0.1, 0.5, 0.9$ in Fig. 4. From these results, we find that two methods have the same temporal convergence rates, and the convergence rate of scheme CS2DII is lower than $3-\alpha$ because of the splitting term.

Figure 3

Time errors as a function of the time step sizes for Example 3. (a) Scheme CS2DI with $\alpha =0.25$, (b) scheme CS2DII with $\alpha =0.75$

Figure 4

The contour plot of the $L^{\infty }$-error using two schemes at $T=1$, with $N=M=100$, and different α for Example 3. Left panel for scheme CS2DI and right panel for scheme CS2DII, respectively

Table 5 Errors and convergence orders of schemes CS2DI and CS2DII for Example 3, at $T=1$ with different α, M, and N

Table 6 Numerical comparison results of schemes CS2DI and CS2DII for Example 3, at $T=1$ with $M=100$ and different N and α

5 Conclusions

In this paper, we have proposed two kinds of high-order compact finite difference schemes with order $O(\tau ^{2-\alpha }+h^{4})$ and $O(\tau ^{3-\alpha }+h^{4})$, respectively, for solving the one-dimensional time-fractional Schrödinger equation. Here, the time discretization is replaced by the L1 and L1-2 formulas, and the space discretization is derived using the high-order compact finite difference method. Then, the extension to the two-dimensional problem is considered. We have designed two high-order compact ADI difference schemes with accuracy $O(\tau ^{1+\alpha }+h^{4})$. In the two-dimensional case, it is worth noting that the splitting term can affect the local truncation error for the time accuracy. Moreover, both theoretical analysis and numerical examples show that all schemes are unconditionally stable for $\alpha \in (0,1)$ and have the high accuracy. Evidently, the proposed schemes are easy to be implemented and extended to solve other fractional PDEs.