1 Introduction

Mutualism is one of the most important relationships in the real world. For example, ants deter herbivores from feeding on plants [1] and deter predators from feeding on aphids [2, 3]. Some the predator-prey-mutualist models have been studied by several scholars [4–9]. For instance, Xiang et al. [5] consider a mutualistic model with saturating terms and effects of toxic substances, investigate the permanence of the system, and study the local or global stability of the positive equilibrium. Wu [6] studies the positive periodic solutions for a mutualistic model with saturating term and the effects of toxic substance by using Mawhin’s continuation theorem of coincidence degree theory [10]. Huo et al. [8] propose a nonautonomous mutualistic system with stage structure and prove the global asymptotical stability of a periodic solution. Rai and Krawcewicz [9] describe the symmetric predator-prey-mutualist model

$$ \left \{ \textstyle\begin{array}{l} x'(t)=rx(t)(1-\frac{x(t)}{L_{0}+ly(t)}), \\ y'(t)=\alpha y(t)(1-\frac{y(t)}{k})-\frac{\beta y(t)z(t)}{1+mx(t)}, \\ z'(t)=-sz(t)+\frac{c\beta y(t)z(t)}{1+mx(t)}, \end{array}\displaystyle \right . $$
(1.1)

where \(x(t)\), \(y(t)\), and \(z(t)\) denote the populations of mutualist, prey, and predator at any time t, respectively. They apply the equivariant degree method to study the Hopf bifurcation of the system.

However, it is generally believed that the delay in the interaction between populations is inevitable, and sometimes the delay can break the stability of the positive equilibrium; therefore, it is more reasonable to add a time delay in a mutualist system. In this paper, we study the following delayed predator-prey-mutualist model:

$$ \left \{ \textstyle\begin{array}{l} x'(t)=rx(t)(1-\frac{x(t)}{L_{0}+ly(t)}), \\ y'(t)=\alpha y(t)(1-\frac{y(t)}{k})-\frac{\beta y(t)z(t)}{1+mx(t)}, \\ z'(t)=-sz(t)+\frac{c\beta y(t-\tau)z(t-\tau)}{1+mx(t-\tau)}, \end{array}\displaystyle \right . $$
(1.2)

where γ and α are the specific growth rates of the mutualist population \(x(t)\) and the prey population \(y(t)\), and \(L_{0}\) stands for the carrying capacity of the mutualist population. The constant k is the carrying capacity of the environment for \(y(t)\), and the predator \(z(t)\) has been taken to be of Lotka-Volterra type. The effect of mutualist is to decrease the predation on prey, the feature which is obtained by taking the parameter m to be positive. The parameter c is called the conversion ratio, and l and m are the mutualism parameters. All the parameters appearing in (1.2) are positive.

The paper is organized as follows: In the next section, we obtain the threshold value \(\tau_{0}\) and verify that when \(0\leq\tau<\tau_{0}\), the positive equilibrium is locally asymptotically stable, whereas if \(\tau=\tau_{0}\), then the system undergoes a Hopf bifurcation at the positive equilibrium. In Section 3, we discuss the direction and stability of the Hopf bifurcation by using the normal form theory and center manifold theorem. In Section 4, we give an interesting numerical analysis to illustrate the main results. In the last section, we make a brief summary.

2 Local stability of positive equilibrium and existence of Hopf bifurcation

In this section, we analyze the local asymptotic stability of the positive equilibrium and the existence of the Hopf bifurcation occurring at the positive equilibrium. It is easy to verify that system (1.2) has a unique positive equilibrium \(E^{*}(x^{*},y^{*},z^{*})\) when the condition

  1. (H1)

    \(c\beta k>s[1+m(L_{0}+lk)] \)

is satisfied, where

$$x^{*}=\frac{c\beta L_{0}+ls}{c\beta-sml}, \qquad y^{*}=\frac {s(1+mL_{0})}{c\beta-sml}, \qquad z^{*}=\frac{\alpha c[c\beta k-s(1+m(L_{0}+lk))](1+mL_{0})}{k(c\beta-sml)^{2}}. $$

Let \(\overline{x}(t)=x(t)-x^{*}\), \(\overline{y}(t)=y(t)-y^{*}\), \(\overline {z}(t)=z(t)-z^{*}\). Dropping the bars for convenience and expanding the nonlinear part by Taylor expansion, we rewrite system (1.2) in the following form:

$$ \left \{ \textstyle\begin{array}{l} x'(t)=a_{11}x(t)+a_{12}y(t)+f_{1}, \\ y'(t)=a_{21}x(t)+a_{22}y(t)+a_{23}z(t)+f_{2}, \\ z'(t)=a_{33}z(t)+b_{31}x(t-\tau)+b_{32} y(t-\tau)+b_{33}z(t-\tau)+f_{3}, \end{array}\displaystyle \right . $$
(2.1)

where

$$\begin{aligned}& a_{11}=-r, \qquad a_{12}=rl, \qquad a_{21}= \frac{\alpha mas}{c\beta bk}, \\& a_{22}=-\frac{\alpha s(1+mL_{0})}{bk}, \qquad a_{23}=-\frac{s}{c}, \qquad a_{33}=-s, \\& b_{31}=-\frac{\alpha mas}{\beta bk}, \qquad b_{32}=\frac{\alpha ca}{bk}, \qquad b_{33}=s, \end{aligned}$$

and

$$\begin{aligned}& f_{1}=a_{14}x^{2}(t)+a_{15}y^{2}(t)+a_{16}x(t)y(t)+a_{17}x^{2}(t)y(t)+a_{18}x(t)y^{2}(t) +a_{19}y^{3}(t)+\cdots, \\& f_{2}=a_{24}x^{2}(t)+a_{25}y^{2}(t)+a_{26}x(t)y(t)+a_{27}x(t)z(t)+a_{28}y(t)z(t)+a_{29}x^{3}(t) \\& \hphantom{f_{2}={}}{}+a_{210}x^{2}(t)y(t)+a_{211}x^{2}(t)z(t)+a_{212}x(t)y(t)z(t)+ \cdots, \\& f_{3}=a_{34}x^{2}(t-\tau)+a_{35}x(t- \tau)y(t-\tau)+a_{36}x(t-\tau )z(t-\tau) +a_{37}y(t-\tau)z(t- \tau) \\& \hphantom{f_{3}={}}{}+a_{38}x^{3}(t-\tau)+a_{39}x^{2}(t- \tau)y(t-\tau)+a_{310}x^{2}(t-\tau )z(t-\tau) \\& \hphantom{f_{3}={}}{}+a_{311}x(t-\tau)y(t-\tau)z(t-\tau)+\cdots, \end{aligned}$$

with

$$\begin{aligned}& a_{14}=-\frac{rb}{c\beta L_{0}+ls},\qquad a_{15}=-\frac{rl^{2}b}{c\beta L_{0}+ls}, \qquad a_{16}=\frac{rlb}{c\beta L_{0}+ls}, \\& a_{17}=\frac{rlb^{2}}{(c\beta L_{0}+ls)^{2}},\qquad a_{18}=-\frac {2rl^{2}b}{c\beta L_{0}+ls}, \qquad a_{19}=\frac{rl^{3}b^{2}}{(c\beta L_{0}+ls)^{2}}, \\& a_{24}=-\frac{\alpha m^{2}as}{c^{2}\beta^{2}k(1+mL_{0})},\qquad a_{25}=- \frac {\alpha}{k},\qquad a_{26}=\frac{\alpha ma}{c\beta k(1+mL_{0})}, \\& a_{27}=\frac{msb}{c^{2}\beta(1+mL_{0})},\qquad a_{28}=-\frac {b}{c(1+mL_{0})}, \qquad a_{29}=\frac{\alpha m^{3}asb}{c^{3}\beta ^{3}k(1+mL_{0})}, \\& a_{210}=-\frac{\alpha m^{2}ab}{c^{2}\beta ^{2}k(1+mL_{0})^{2}},\qquad a_{211}=- \frac{m^{2}sb^{2}}{c^{3}\beta^{2}(1+mL_{0})},\qquad a_{212}=\frac{2mb^{2}}{c^{2}\beta(1+mL_{0})^{2}}, \\& a_{34}=\frac{\alpha m^{2}as}{c\beta^{2}k(1+mL_{0})},\qquad a_{35}=-\frac {\alpha ma}{\beta k(1+mL_{0})}, \qquad a_{36}=-\frac{msb}{c^{2}\beta(1+mL_{0})}, \\& a_{37}=\frac{b}{1+mL_{0}},\qquad a_{38}=-\frac{\alpha m^{3}asb}{c^{2}\beta ^{3}k(1+mL_{0})}, \qquad a_{39}=\frac{\alpha m^{2}ab}{c\beta^{2}k(1+mL_{0})^{2}}, \\& a_{310}=\frac{m^{2}sb^{2}}{c^{2}\beta^{2}(1+mL_{0})}, \qquad a_{311}=- \frac {2mb^{2}}{c\beta(1+mL_{0})^{2}}. \\& a=c\beta k-s\bigl[1+m(L_{0}+lk)\bigr],\qquad b=c\beta-sml= \frac{a+s(1+mL_{0})}{k}. \end{aligned}$$

The linearized system of (2.1) is

$$ \left \{ \textstyle\begin{array}{l} x'(t)=a_{11}x(t)+a_{12}y(t), \\ y'(t)=a_{21}x(t)+a_{22}y(t)+a_{23}z(t), \\ z'(t)=a_{33}z(t)+b_{31}x(t-\tau)+b_{32}y(t-\tau)+b_{33}z(t-\tau). \end{array}\displaystyle \right . $$
(2.2)

The characteristic equation of (2.2) at \(E^{*}\) is of the form

$$ \lambda^{3}+A_{2}\lambda^{2}+A_{1} \lambda+A_{0}+\bigl[B_{2}\lambda ^{2}+B_{1} \lambda+B_{0}\bigr]e^{-\lambda\tau}=0. $$
(2.3)

It is easy to check that

$$\begin{aligned}& A_{0}=a_{12}a_{21}a_{33}-a_{11}a_{22}a_{33}, \qquad A_{1}=a_{11}a_{22}+a_{11}a_{33}+a_{22}a_{33}-a_{12}a_{21}, \\& A_{2}=-(a_{11}+a_{22}+a_{33}),\qquad B_{0}=a_{12}a_{21}b_{33}+a_{11}a_{23}b_{32}-a_{11}a_{22}b_{33}-a_{12}a_{23}b_{31}, \\& B_{1}=a_{11}b_{33}+a_{22}b_{33}-a_{23}b_{32}, \qquad B_{2}=-b_{33}. \end{aligned}$$

When \(\tau=0\), we have the following theory according to the Routh-Hurwitz criterion.

Theorem 2.1

When \(\tau=0\), if (H1) holds and \(s>r\), then the positive equilibrium \(E^{*}\) is locally asymptotically stable.

Proof

When \(\tau=0\), Eq. (2.3) becomes

$$ \lambda^{3}+m_{2}\lambda^{2}+m_{1} \lambda+m_{0}=0, $$
(2.4)

where

$$\begin{aligned}& m_{0}=A_{0}+B_{0}=\frac{\alpha rsa(c\beta-sml)}{c\beta bk}, \\& m_{1}=A_{1}+B_{1}=\frac{\alpha s[c\beta a+c\beta r(1+mL_{0})]}{c\beta bk}, \\& m_{2}=A_{2}+B_{2}=r+\frac{\alpha s(1+mL_{0})}{bk}. \end{aligned}$$

From (H1) we get that \(m_{i}>0\) (\(i=0,1,2\)). Denote

$$\Delta_{1}=m_{2},\qquad \Delta_{2}=m_{2}m_{0}-m_{1}, \qquad \Delta _{3}=(m_{2}m_{0}-m_{1})m_{0}. $$

Then we obtain \(\Delta_{i}>0\) (\(i=1,2,3\)) by directly computing. By the well-known Routh-Hurwitz criterion we get that positive equilibrium \(E^{*}\) is locally asymptotically stable for \(\tau=0\). □

We further investigate the existence of purely imaginary roots to (2.3) with \(\tau>0\).

Suppose that iω (\(\omega>0\)) is the solution of (2.3). Then we have

$$ -i\omega^{3}-A_{2}\omega^{2}+iA_{1} \omega+A_{0}+\bigl[-B_{2}\omega ^{2}+iB_{1} \omega+B_{0}\bigr](\cos\omega\tau-i\sin\omega\tau)=0. $$
(2.5)

Separating the real and imaginary parts, we derive that

$$ \left \{ \textstyle\begin{array}{l} \omega^{3}-A_{1}\omega=B_{1}\omega\cos\omega\tau+(B_{2}\omega ^{2}-B_{0})\sin\omega\tau, \\ A_{2}\omega^{2}-A_{0}=B_{1}\omega\sin\omega\tau+(B_{2}\omega ^{2}-B_{0})\cos\omega\tau. \end{array}\displaystyle \right . $$
(2.6)

Squaring and adding the two equations of (2.6), we have that

$$ \omega^{6}+e_{32}\omega^{4}+e_{31} \omega^{2}+e_{30}=0 , $$
(2.7)

where

$$e_{30}=A_{0}^{2}-B_{0}^{2}, \qquad e_{31}=A_{1}^{2}-2A_{2}A_{0}+2B_{2}B_{0}-B_{1}^{2}, \qquad e_{32}=A_{2}^{2}-2A_{1}-B_{2}^{2}. $$

Let \(\nu=\omega^{2}\). Then (2.7) becomes

$$ \nu^{3}+e_{32}\nu^{2}+e_{31} \nu+e_{30}=0. $$
(2.8)

Hence, by calculating we see that if

  1. (H2)

    \(a>2s(1+mL_{0})\),

then \(e_{32}>0\) and \(e_{30}<0\), that is, (2.8) has a unique positive solution \(\omega_{0}\). The corresponding critical value of time delay is

$$ \tau_{j}=\frac{1}{\omega_{0}}\arccos\frac{(B_{1}-B_{2}A_{2})\omega _{0}^{4}+(B_{2}A_{0}+B_{0}A_{2} -B_{1}A_{1})\omega_{0}^{2}-B_{0}A_{0}}{B_{2}\omega _{0}^{4}+(B_{1}^{2}-2B_{2}B_{0})\omega_{0}^{2}+B_{0}^{2}} + \frac{2j\pi}{\omega_{0}}, $$
(2.9)

where \(j=0,1,2,\ldots\) .

Now, we discuss the sign of \(\operatorname{Re}\{\frac{{\mathrm{d}}\lambda }{{\mathrm{d}}\tau}\}|_{\tau=\tau_{0}}\).

Differentiating the two sides of (2.3) with respect to τ, it follows that

$$\biggl(\frac{{\mathrm{d}}\lambda}{{\mathrm{d}}\tau}\biggr)^{-1}=\frac{(3\lambda ^{2}+2A_{2}\lambda+A_{1})e^{\lambda\tau}+(2B_{2}\lambda+B_{1})}{ B_{2}\lambda^{3}+B_{1}\lambda^{2}+B_{0}\lambda} - \frac{\tau}{\lambda}. $$

If \(\tau=\tau_{0}\), that is, \(\lambda=i\omega_{0}\), we obtain

$$\biggl[\frac{{\mathrm{d}}\lambda}{{\mathrm{d}}\tau}\biggr]^{-1}\bigg|_{\lambda=i\omega_{0}}= \frac{(-3\omega_{0}^{2}+2iA_{2}\omega_{0}+A_{1})e^{i\omega_{0}\tau _{0}}+(2iB_{2}\omega_{0}+B_{1})}{ -iB_{2}\omega_{0}^{3}-B_{1}\omega_{0}^{2}+iB_{0}\omega_{0}} -\frac {\tau_{0}}{i\omega_{0}}. $$

Therefore,

$${\operatorname{Re}}\biggl\{ \frac{{\mathrm{d}}\lambda}{{\mathrm{d}}\tau}\biggr\} ^{-1}\bigg|_{\lambda=i\omega_{0}} =\frac{P_{1}O_{1}+P_{2}Q_{2}}{Q_{1}^{2}+Q_{2}^{2}}, $$

where

$$\begin{aligned}& P_{1}=\bigl(3\omega_{0}^{2}-A_{1} \bigr)\cos\omega_{0}\tau_{0}+2A_{2}\omega _{0}\sin\omega_{0}\tau_{0}-B_{2} \omega_{0}^{2}\tau_{0} +B_{0} \tau_{0}-B_{1}, \\& P_{2}=2A_{2}\omega_{0}\cos\omega_{0} \tau_{0}+\bigl(A_{1}-3\omega _{0}^{2} \bigr)\sin\omega_{0}\tau_{0}+2B_{2} \omega_{0}-B_{0}\omega_{0}\tau _{0}, \\& Q_{1}=B_{0}\omega_{0}^{2},\qquad Q_{2}=-B_{2}\omega_{0}^{3}+B_{0} \omega_{0}, \end{aligned}$$

and thus

$${\operatorname{sign}}\biggl[{\operatorname{Re}}\biggl\{ \frac{{\mathrm{d}}\lambda}{{\mathrm{d}}\tau}\biggr\} ^{-1}\bigg|_{\tau =\tau_{0}}\biggr] ={\operatorname{sign}}(P_{1}O_{1}+P_{2}Q_{2}). $$

Obviously, if \(P_{1}O_{1}+P_{2}Q_{2}\neq0\), then \([{\operatorname{Re}}\{\frac{{\mathrm{d}}\lambda}{{\mathrm{d}}\tau}\}^{-1}|_{\tau=\tau_{0}}]\neq0\). Thus, by the Hopf bifurcation theorem for functional differential equation [11], we get the following result.

Theorem 2.2

If \(\tau>0\) and \(P_{1}O_{1}+P_{2}Q_{2}\neq0\), then the positive equilibrium \(E^{*}\) is asymptotically stable for \(0<\tau<\tau_{0}\), and it becomes unstable for τ staying in some right neighborhood of \(\tau_{0}\), with a Hopf bifurcation occurring when \(\tau=\tau_{0}\).

3 The stability and direction of the Hopf bifurcation

In this section, we present formulae for determining the direction of the Hopf bifurcation and stability of bifurcation periodic solutions of system (2.1) when \(\tau=\tau_{0}\) by employing the normal form method and center manifold theorem introduced by Hassard et al. [12].

Let \(u_{1}(t)=x(\tau t)\), \(u_{2}(t)=y(\tau t)\), \(u_{3}(t)=z(\tau t)\), \(\tau =\tau_{0}+\mu\), \(\mu\in R\). Then system (2.1) is transformed into the system

$$ \left \{ \textstyle\begin{array}{l} {u}_{1}'(t)= (\tau_{0}+\mu )[a_{11}u_{1}(t)+a_{12}u_{2}(t)+a_{13}u_{3}(t)+f_{11}(t)], \\ {u}_{2}'(t)= (\tau_{0}+\mu )[a_{21}u_{1}(t)+a_{22}u_{2}(t)+a_{23}u_{3}(t)+f_{22}(t)], \\ {u}_{3}'(t)= (\tau_{0}+\mu)[a_{33}u_{3}(t)+b_{31}u_{1}(t-1) \\ \hphantom{{u}_{3}'(t)={}}{}+b_{32}u_{2}(t-1)+b_{33}u_{3}(t-1)+f_{33}(t)], \end{array}\displaystyle \right . $$
(3.1)

where

$$\begin{aligned}& f_{11}=a_{14}u_{1}^{2}(t)+a_{15}u_{2}^{2}(t)+a_{16}u_{1}(t)u_{2}(t)+a_{17}u_{1}^{2}(t)u_{2}(t) +a_{18}u_{1}(t)u_{2}^{2}(t) \\& \hphantom{f_{11}={}}{}+a_{19}u_{2}^{3}(t)+\cdots, \\& f_{22}=a_{24}u_{1}^{2}(t)+a_{25}u_{2}^{2}(t)+a_{26}u_{1}(t)u_{2}(t)+a_{27}u_{1}(t)u_{3}(t)+a_{28}u_{2}(t)u_{3}(t) \\& \hphantom{f_{22}={}}{}+a_{29}u_{1}^{3}(t)+a_{210}u_{1}^{2}(t)u_{2}(t)+a_{211}u_{1}^{2}(t)u_{3}(t)+a_{212}u_{1}(t)u_{2}(t)u_{3}(t)+ \cdots, \\& f_{33}=a_{34}u_{1}^{2}(t- \tau)+a_{35}u_{1}(t-\tau)u_{2}(t-\tau )+a_{36}u_{1}(t-\tau)u_{3}(t-\tau) \\& \hphantom{f_{33}={}}{}+a_{37}u_{2}(t-\tau)u_{3}(t- \tau)+a_{38}u_{1}^{3}(t-\tau )+a_{39}u_{1}^{2}(t- \tau)u_{2}(t-\tau) \\& \hphantom{f_{33}={}}{}+a_{310}u_{1}^{2}(t- \tau)u_{3}(t-\tau)+a_{311}u_{1}(t- \tau)u_{2}(t-\tau )u_{3}(t-\tau)+\cdots. \end{aligned}$$

Denote

$$\begin{aligned} C^{k}[-1,0] =&\bigl\{ \varphi\mid\varphi:[-1,0]\rightarrow{R^{3}}, \\ &{}\mbox{each component of }\varphi\mbox{ has a }k\mbox{th-order continuous derivative}\bigr\} . \end{aligned}$$

Let \(\phi(\theta)=(\phi_{1}(\theta),\phi_{2}(\theta),\phi_{3}(\theta ))^{T}\in C[-1,0]\) be the initial data of system (2.1). Define the operators

$$\begin{aligned}& L_{\mu}\phi=(\tau_{0}+\mu)\bigl[A' \phi(0)+B'\phi(-1)\bigr], \\& f(\mu,\phi)=(\tau_{0}+\mu) (f_{11}, f_{22},f_{33}), \end{aligned}$$

with

$$\begin{aligned}& \phi(\theta)=\bigl(\phi_{1}(\theta),\phi_{2}(\theta), \phi_{3}(\theta)\bigr)\in C\bigl([-1,0],R^{3} \bigr], \\& A'= \left( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} a_{11} & a_{12} & 0 \\ a_{21} & a_{22} & a_{23} \\ 0 & 0 & a_{33} \end{array}\displaystyle \right),\qquad B'= \left( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 0 & 0 & 0 \\ 0 & 0 & 0 \\ b_{31} & b_{32} & b_{33} \end{array}\displaystyle \right), \end{aligned}$$

and \(L_{\mu}:C[-1,0]\rightarrow{R^{3}}\), \(f:R\times{C[-1,0]}\rightarrow {R^{3}}\). Then (3.1) can be rewritten as

$$u'_{t}=L_{\mu}u_{t}+f( \mu,u_{t}). $$

By the Riesz representation theorem there exists a function \(\eta(\theta ,\mu)\) of bounded variation for \(\theta\in[-1,0]\) such that

$$L_{\mu}{\phi}= \int_{-1}^{0}{\mathrm{d}}\eta(\theta,\mu)\phi(\theta) \quad \mbox{for } {\phi}\in{C[-1,0]}. $$

In fact, we can choose

$$\eta(\theta,\mu)=(\tau_{0}+\mu) \left( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} a_{11} & a_{12} & 0 \\ a_{21} & a_{22} & a_{23} \\ 0 & 0 & a_{33} \end{array}\displaystyle \right)\delta(\theta)-(\tau_{0}+\mu) \left( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 0 & 0 & 0 \\ 0 & 0 & 0 \\ b_{31} & b_{32} & b_{33} \end{array}\displaystyle \right) \delta(\theta+1), $$

where \(\delta(\theta)\) is the Dirac function.

For \(\phi\in C^{1}[-1,0]\), define

$$ (A_{\mu}\phi) (\theta)=\left \{ \textstyle\begin{array}{l@{\quad}l} \frac{{\mathrm{d}}\phi(\theta)}{{\mathrm{d}}\theta}, & \theta\in[-1, 0), \\ \int_{-1}^{0}{\mathrm{d}}\eta(\theta, \mu)\phi(\theta), & \theta=0, \end{array}\displaystyle \right . $$
(3.2)

and

$$ (R_{\mu}\phi) (\theta)=\left \{ \textstyle\begin{array}{l@{\quad}l} 0, & \theta\in[-1, 0), \\ f(\mu,\theta), & \theta=0. \end{array}\displaystyle \right . $$
(3.3)

Then system (3.1) is equivalent to

$$ u'_{t}=A_{\mu}u_{t}+R_{\mu}u_{t}, $$
(3.4)

where \(u_{t}=u(t+\theta)\), \(\theta\in[-1,0]\).

For \(\varphi\in C^{1}[0,1]\), define

$$ \bigl(A^{*}\psi\bigr) (s)=\left \{ \textstyle\begin{array}{l@{\quad}l} -\frac{{\mathrm{d}}\psi(s)}{{\mathrm{d}}s}, & s\in(0, 1], \\ \int_{-1}^{0}{\mathrm{d}}\eta^{T}(s,0)\psi(-s), & s=0, \end{array}\displaystyle \right . $$
(3.5)

and the bilinear inner product

$$ \bigl\langle \psi(s),\phi(\theta)\bigr\rangle =\overline{\psi}(0)\phi(0)- \int_{-1}^{0} \int_{\xi =0}^{\theta} \overline{\psi}(\xi-\theta)\, { \mathrm{d}}\eta(\theta)\phi(\xi)\, {\mathrm{d}}\xi, $$
(3.6)

where \(\psi(\theta)\in C^{1}[-1,0]\), \(\eta(\theta)=\eta(\theta,0)\), and \(A_{0}\) and \(A^{*}\) are adjoint operators. By discussion in Section 2 and the transformation \(t=t\tau\) we know that \(\pm i\omega _{0}\tau_{0}\) are the eigenvalues of \(A_{0}\). Hence, \(\mp i\omega_{0}\tau_{0}\) are the eigenvalues of \(A^{*}\). Next, we compute the eigenvector q of \(A_{0}\) belonging to the eigenvalue \(i\omega_{0}\tau_{0}\) and the eigenvector \(q^{*}\) of \(A^{*}\) belonging to the eigenvalue \(-i\omega_{0}\tau_{0}\).

Suppose \(q(\theta)=(1,q_{1},q_{2})^{T}e^{i\omega_{0}\tau_{0}\theta}\). Then \(q(0)=(1,q_{1},q_{2})^{T}\) and \(q(-1)=q(0)e^{-i\omega_{0}\tau_{0}}\). From (3.2) we have

$$\tau_{0}\left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} a_{11} & a_{12} & 0 \\ a_{21} & a_{22} & a_{23} \\ b_{31}e^{-i\omega_{0}\tau_{0}} & b_{32}e^{-i\omega_{0}\tau_{0}} & a_{33}+b_{33}e^{-i\omega_{0}\tau_{0}} \end{array}\displaystyle \right )q(0)=i \omega_{0}\tau_{0} \left ( \textstyle\begin{array}{@{}c@{}} 1 \\ q_{1} \\ q_{2} \end{array}\displaystyle \right ). $$

Thus,

$$q_{1} = \frac{i\omega_{0}-a_{11}}{a_{12}},\qquad q_{2} = \frac{(i\omega_{0}-a_{11})(i\omega _{0}-a_{22})-a_{12}a_{21}}{a_{12}a_{23}}. $$

Similarly, we can calculate the eigenvector \(q^{*}(s)=D(1,q^{*}_{1},q^{*}_{2})e^{i\omega_{0}\tau_{0}s}\) of \(A^{*}\) belonging to the eigenvalue \(-i\omega_{0}\tau_{0}\), where

$$\begin{aligned}& q_{1}^{*} = \frac{-a_{12}(a_{33}+b_{33}e^{i\omega_{0}\tau_{0}}+i\omega _{0})}{(i\omega_{0}+a_{22})(a_{33} +b_{33}e^{i\omega_{0}\tau_{0}}+i\omega_{0})-a_{23}b_{32}e^{i\omega _{0}\tau_{0}}}, \\& q_{2}^{*} = \frac{a_{12}a_{23}}{(i\omega _{0}+a_{22})(a_{33}+b_{33}e^{i\omega_{0}\tau_{0}}+i\omega_{0}) -a_{23}b_{32}e^{i\omega_{0}\tau_{0}}}. \end{aligned}$$

In order to determine the value of D, we normalize q and \(q^{*}\) by the condition \(\langle q^{*}(s),q(\theta)\rangle=1\). From (3.5) we have

$$\begin{aligned} \bigl\langle q^{\ast}(s),q(\theta)\bigr\rangle =&\overline{D}\bigl(1, \overline{q}^{\ast}_{1},\overline{q}^{\ast }_{2} \bigr) (1,q_{1},q_{2})^{T} \\ &{} - \int_{-1}^{0} \int_{\xi=0}^{\theta}\overline{D} \bigl(1, \overline{q}^{\ast}_{1},\overline{q}^{\ast}_{2} \bigr)e^{-{i\omega_{0}\tau _{0}(\xi-\theta)}} \, {\mathrm{d}}\eta(\theta) (1,q_{1},q_{2})^{T} e^{i\omega_{0}\tau_{0}{\xi }}\, {\mathrm{d}}\xi \\ =&\overline{D}\biggl[1+q_{1}\overline{q}^{\ast}_{1}+q_{2} \overline{q}^{\ast}_{2}- \int_{-1}^{0} \bigl(1,\overline{q}^{\ast}_{1}, \overline{q}^{\ast}_{2}\bigr)\theta e^{i\omega _{0}\tau_{0}\theta}\, {\mathrm{d}} \eta(\theta) (1,q_{1},q_{2})^{T}\biggr] \\ =&\overline{D}\bigl[1+q_{1}\overline{q}^{\ast}_{1}+q_{2} \overline{q}^{\ast}_{2} +\tau_{0} \overline{q}^{\ast }_{2}(b_{31}+b_{32}q_{1}+b_{22}q_{2})e^{-i\omega_{0}\tau_{0}} \bigr]. \end{aligned}$$

Therefore, let

$$\overline{D}=\frac{1}{1+q_{1}\overline{q}^{\ast}_{1}+q_{2}\overline {q}^{\ast}_{2} +\tau_{0}\overline{q}^{\ast }_{2}(b_{31}+b_{32}q_{1}+b_{22}q_{2})e^{-i\omega_{0}\tau_{0}}}. $$

In the remainder of this section, following the algorithms given in [12] and using a similar computation process as in [13], we get the coefficients that will be used to determine several important qualities:

$$ \left \{ \textstyle\begin{array}{l} g_{20}=2\tau_{0}\overline{D}(k_{11}+k_{21}\overline {q}^{*}_{1}+k_{31}\overline{q}^{*}_{2}), \qquad g_{11}=2\tau_{0}\overline{D}(k_{12}+k_{22}\overline {q}^{*}_{1}+k_{32}\overline{q}^{*}_{2}), \\ g_{02}=2\tau_{0}\overline{D}(k_{13}+k_{23}\overline {q}^{*}_{1}+k_{33}\overline{q}^{*}_{2}), \qquad g_{21}= \tau_{0}\overline{D}(k_{14}+k_{24}\overline {q}^{*}_{1}+k_{34}\overline{q}^{*}_{2}), \end{array}\displaystyle \right . $$
(3.7)

where

$$\begin{aligned}& k_{11}=a_{14}+a_{15}q_{1}^{2}+a_{16}q_{1}, \qquad k_{21}=a_{24}+a_{25}q_{1}^{2}+a_{26}q_{1}+a_{27}q_{2}+a_{28}q_{1}q_{2}, \\& k_{31}=(a_{34}+a_{35}q_{1}+a_{36}q_{2}+a_{37}q_{1}q_{2})e^{-2i\omega _{0}\tau_{0}}, \qquad k_{12}=a_{14}+a_{15}q_{1} \overline{q}_{1}+a_{16}{\operatorname{Re}}\{q_{1} \}, \\& k_{22}=a_{24}+a_{25}q_{1} \overline{q}_{1}+a_{26}{\operatorname{Re}}\{q_{1} \} +a_{27}{\operatorname{Re}}\{q_{2}\} +a_{28}{ \operatorname{Re}}\{q_{1}\overline{q}_{2}\}, \\& k_{32}=a_{34}+a_{35}{\operatorname{Re}} \{q_{1}\}+a_{36}{\operatorname{Re}}\{q_{2}\} +a_{37}{\operatorname{Re}}\{q_{1}\overline{q}_{2} \},\qquad k_{13}=a_{14}+a_{15}\overline{q}_{1}^{2}+a_{16} \overline{q}_{1}, \\& k_{23}=a_{24}+a_{25}\overline{q}_{1}^{2}+a_{26} \overline {q}_{1}+a_{27}\overline{q}_{2}+a_{28} \overline{q}_{1}\overline{q}_{2}, \\& k_{33}=(a_{34}+a_{35}\overline{q}_{1}+a_{36} \overline {q}_{2}+a_{37}\overline{q}_{1} \overline{q}_{2})e^{2i\omega_{0}\tau _{0}}, \\& k_{14}=2a_{14}\bigl[W_{20}(0)+2W_{11}(0) \bigr]+2a_{15}\bigl[2q_{1}W_{11}(0)+\overline {q}_{1}W_{20}(0)\bigr]+a_{16}\bigl[(1+ \overline{q}_{1})W_{20}(0) \\& \hphantom{k_{14}={}}{}+2(1+q_{1})W_{11}(0)\bigr]+2a_{17}(2q_{1}+ \overline {q}_{1})+2a_{18}\bigl(q_{1}^{2}+2q_{1} \overline{q}_{1}\bigr) +6a_{19}q_{1}^{2} \overline{q}_{1}, \\& k_{24}=2a_{24}\bigl[W_{20}(0)+2W_{11}(0) \bigr]+2a_{25}\bigl[2q_{1}W_{11}(0)+\overline {q}_{1}W_{20}(0)\bigr]+a_{26}\bigl[2W_{11}(0) \\& \hphantom{k_{24}={}}{}+W_{20}(0)+2q_{1}W_{11}(0)+ \overline {q}_{1}W_{20}(0)\bigr]+a_{27} \bigl[2W_{11}(0)+W_{20}(0)+2q_{1}W_{11}(0) \\& \hphantom{k_{24}={}}{}+\overline {q}_{1}W_{20}(0) \bigr]+a_{28}\bigl[2q_{1}W_{11}(0)+q_{2}W_{11}(0)+ \overline {q}_{1}W_{20}(0)+\overline{q}_{2}W_{20}(0) \bigr]+3a_{29} \\& \hphantom{k_{24}={}}{}+a_{210}(2q_{1}+\overline{q}_{1})+2a_{211}(2q_{2}+ \overline {q}_{2})+2a_{212}(q_{1}q_{2}+q_{1} \overline{q}_{2}+\overline {q}_{1}q_{2}), \\& k_{34}=2a_{34}\bigl[W_{20}(-1)e^{i\omega_{0}\tau_{0}}+2W_{11}(-1)e^{-i\omega _{0}\tau_{0}} \bigr]+a_{35}\bigl[2(1+q_{1})W_{11}(-1)e^{-i\omega_{0}\tau_{0}} \\& \hphantom{k_{34}={}}{}+(1+\overline{q}_{1})W_{20}(-1)e^{i\omega_{0}\tau _{0}} \bigr]+a_{36}\bigl[2(1+q_{2})W_{11}(-1)e^{-i\omega_{0}\tau_{0}} \\& \hphantom{k_{34}={}}{}+(1+\overline{q}_{2})W_{20}(-1)e^{i\omega_{0}\tau _{0}} \bigr]+a_{37}\bigl[2(q_{1}+q_{2})W_{11}(-1)e^{-i\omega_{0}\tau_{0}} \\& \hphantom{k_{34}={}}{}+(\overline{q}_{1}+\overline{q}_{2})W_{20}(-1)e^{i\omega_{0}\tau _{0}} \bigr]+6a_{38}e^{-i\omega_{0}\tau_{0}} +2a_{39}(2q_{1}+ \overline{q}_{1})e^{-i\omega_{0}\tau_{0}} \\& \hphantom{k_{34}={}}{}+2a_{310}(2q_{2}+\overline{q}_{2})e^{-i\omega_{0}\tau _{0}}+2a_{311}(q_{1}q_{2}+q_{1} \overline{q}_{2}+\overline {q}_{1}q_{2})e^{-i\omega_{0}\tau_{0}}, \end{aligned}$$

and

$$\begin{aligned}& W_{20}(\theta) = \frac{ig_{20}}{\omega_{0}\tau_{0}}q(\theta)+\frac {i\overline{g}_{02}}{3\omega_{0}\tau_{0}} \overline{q}(\theta) +E_{1}e^{2i\omega_{0}\tau_{0}\theta}, \end{aligned}$$
(3.8)
$$\begin{aligned}& W_{11}(\theta) = -\frac{ig_{11}}{\omega_{0}\tau_{0}}q(\theta)+\frac {i\overline{g}_{11}}{ \omega_{0}\tau_{0}} \overline{q}(\theta)+E_{2}. \end{aligned}$$
(3.9)

Moreover \(E_{1}\) and \(E_{2}\) satisfy the following equations, respectively:

$$\begin{aligned}& \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 2i\omega_{0}\tau_{0}-a_{11} & -a_{12} & 0 \\ -a_{21} & 2i\omega_{0}\tau_{0}-a_{22} & -a_{23} \\ -b_{31}e^{-2i\omega_{0}\tau_{0}} & -b_{31}e^{-2i\omega_{0}\tau_{0}} & 2i\omega_{0}\tau_{0}-(a_{33}+b_{33}e^{-2i\omega_{0}\tau_{0}}) \end{array}\displaystyle \right )E_{1} \\& \quad = 2\left ( \textstyle\begin{array}{@{}c@{}} a_{14}+a_{15}q_{1}^{2}+a_{16}q_{1}\\ a_{24}+a_{25}q_{1}^{2}+a_{26}q_{1}+a_{27}q_{2}+a_{28}q_{1}q_{2}\\ (a_{34}+a_{35}q_{1}+a_{36}q_{2}+a_{37}q_{1}q_{2})e^{-2i\omega_{0}\tau_{0}} \end{array}\displaystyle \right ) \\& \qquad {} -\left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} a_{11} & a_{12} & 0 \\ a_{21} & a_{22} & a_{23} \\ b_{31} & b_{32} & a_{33}+b_{33} \end{array}\displaystyle \right )E_{2} \\& \quad =2\left ( \textstyle\begin{array}{@{}c@{}} a_{14}+a_{15}q_{1}\overline{q}_{1}+a_{16}{\operatorname{Re}}{\{q_{1}\}}\\ a_{24}+a_{25}q_{1}\overline{q}_{1}+a_{26}{\operatorname{Re}}{\{q_{1}\} }+a_{27}{\operatorname{Re}}{\{q_{2}\}} +a_{28}{\operatorname{Re}}{\{q_{1}\overline{q}_{2}\}}\\ a_{34}+a_{35}{\operatorname{Re}}{\{q_{1}\}}+a_{36}{\operatorname{Re}}{\{q_{2}\}}+a_{37}{\operatorname{Re}}{\{q_{1}\overline{q}_{2}\}} \end{array}\displaystyle \right ). \end{aligned}$$

\(E_{1}\) and \(E_{2}\) can be calculated by solving the above systems. Thus, \(W_{20}(\theta) \) and \(W_{11}(\theta) \) are obtained from (3.8) and (3.9). Finally, we get \(g_{21}\). The following parameters can be computed:

$$ \begin{aligned} &c_{1}(0) =\frac{i}{2\omega_{0}\tau _{0}} \biggl(g_{20}g_{11}-2{|g_{11}|^{2}}- \frac{|g_{02}|^{2}}{3}\biggr)+\frac {g_{21}}{2}, \\ &\mu_{2} =-\frac{{\operatorname{Re}}\{c_{1}(0)\}}{{\operatorname{Re}}\{\lambda^{'}(\tau_{0})\} }, \\ &\beta_{2} =2{\operatorname{Re}}\bigl\{ c_{1}(0)\bigr\} , \\ &T_{2} =-\frac{{{\operatorname{Im}}\{c_{1}(0)\}+\mu_{2}}{\operatorname{Im}}\{\lambda^{'}(\tau _{0})\}}{\omega_{0}\tau_{0}}. \end{aligned} $$
(3.10)

Theorem 3.1

The values of (3.10) determine the qualities of bifurcating periodic solutions in the center manifold at the critical value \(\tau=\tau_{0}\); we have the following conclusions:

  1. (i)

    the sign of \(\mu_{2}\) determines the directions of the Hopf bifurcation: if \(\mu_{2}>0\) (\(\mu_{2}<0\)), then the Hopf bifurcation is supercritical (subcritical), and the bifurcation periodic solutions exist for \(\tau>\tau_{0}\) (\(\tau<\tau_{0}\));

  2. (ii)

    the sign of \(\beta_{2}\) determines the stability of the bifurcation periodic solutions: the bifurcation periodic solutions are stable (unstable) if \(\beta _{2}<0\) (\(\beta_{2}>0\)) ;

  3. (iii)

    the sign of \(T_{2}\) determines the period of the bifurcation periodic solutions: the period increases (decreases) if \(T_{2}>0\) (\(T_{2}<0\)).

4 Numerical simulations

We give some numerical simulations in this section in order to demonstrate the theoretical results obtained in this paper. Let the initial value be \((700, 10, 10)\), and parameter values be: \(r=0.7\), \(L_{0}=0.5\), \(l=0.3\), \(k=8\), \(\alpha=0.8\), \(\beta=0.75\), \(m=0.3\), \(s=0.75\), \(c=0.8\).

(1) When \(\tau=0\), it is easy to show that system (1.2) has a unique positive equilibrium \(E^{*}(0.97, 1.62, 1.10)\). By calculation, the condition of Theorem 2.1 is satisfied, so that \(E^{*}\) is locally asymptotically stable (see Figure 1).

Figure 1
figure 1

The positive equilibrium \(\pmb{E^{\ast}}\) of system ( 1.2 ) is asymptotically stable when \(\pmb{\tau=0}\) .

Full size image

(2) When \(\tau>0\), according to Theorem 2.2, system (1.2) undergoes a Hopf bifurcation at the equilibrium \(E^{*}\) when \(\tau=\tau_{0}\). By directly computing we can obtain \(\tau_{0}\approx0.5521\), and the positive equilibrium is \(E^{*}(0.97, 1.62, 1.10)\). We choose \(\tau=0.5<\tau_{0}\), and then \(E^{*}\) is locally asymptotically stable (see Figure 2); On the contrary, we choose \(\tau=0.6>\tau_{0}\), and then \(E^{*}\) is unstable (see Figure 3).

Figure 2
figure 2

The positive equilibrium \(\pmb{E^{\ast}}\) of system ( 1.2 ) is locally asymptotically stable when \(\pmb{\tau=0.5<\tau_{0}}\) .

Full size image
Figure 3
figure 3

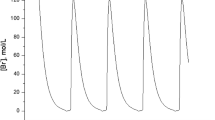
The positive equilibrium \(\pmb{E^{\ast}}\) of system ( 1.2 ) is unstable, and there exists a bifurcating periodic solutions when \(\pmb{\tau=0.6>\tau_{0}}\) .

Full size image

By Theorem 3.1 we know that, under the set of parameters, when \(\tau =\tau_{0}\), a Hopf bifurcation occurs. Furthermore, we can obtain that \(\mu_{2}>0\), \(\beta_{2}<0\), the bifurcating periodic solutions exist, and the corresponding periodic orbits are orbitally asymptotically stable (see Figure 3).

5 Conclusion

A predator-prey-mutualist model is studied in this paper. To be more realistic, it is very necessary to introduce the digestion delay. We consider the asymptotic stability of the positive equilibrium when \(\tau=0\); In addition, when \(\tau>0\), the stability of the positive equilibrium and the existence of Hopf bifurcation are studied; we also discuss the direction and stability of Hopf bifurcation. Some numerical analysis is finally given.