1 Introduction

The rotational motion of a charged RB containing a high-viscosity liquid is examined. It will depend on several complex factors related to its geometry, material properties, and external environment. Accurate modeling and analysis of these systems can be challenging but is important for understanding their behaviors in various applications. It is really a complex phenomenon. It has been examined according to several different cases by distinguished researchers [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21], due to its applications in the industrial field for wagons, spaceships, and airplanes. The difficulty of such a problem is due to its governing system of motion (GSM), which is controlled by nonlinear differential equations (NDEs).

Zhukovskii [2] was the first notable scientist to tackle this issue in 1885, and he studied the motion of a RB with an ideal incompressible fluid and a completely filled hollow. It is presumed that the fluid's impact on the RB can be explained by its relationship to some other bodies, where the centers of mass of the fluid together with those other bodies meet. Many scientific papers have examined such motions' stability, including [15,16,17,18,19,20,21]. In [3], the coupled system made up of a RB with a hollow wholly filled with a viscous liquid is investigated. It is demonstrated that for arbitrary initial data and finite kinetic energy, every associated weak solution converges to a uniform rotation as time increases infinitely. An asymptotic approach was applied in [4] to examine the inertial movement of a rotating top having a spherical hollow filled with a viscous liquid. The evolution of the system's motion in Andoyer's canonical coordinates was described by a first approximation of this technique. The short-term oscillations of a spinning top with a cavity fully filled with an incompressible viscous liquid are investigated in [5]. There are no limitations on how the body's bulk is distributed or how the cavity is shaped. Aspects of the evolution operator that correspond to the linear equations' spectral features are also examined as the system approaches its stability criteria. The influence of a solid cylindrical body on the surface of a cylindrical cavity is discussed in [6] for gaps between the cavity surface and the body surface that are zero and nonzero. Hydrodynamic and kinematic properties are obtained. Several analytical and numerical discoveries about the movement of a system made up of a RB with a hollow cavity filled entirely with a Navier–Stokes liquid that flows devoid of external influences are presented in [7]. In [8], the authors studied the fast rotation of a non-symmetric satellite that is a viscous liquid in a bore filled with respect to its center of mass if a gravitational torque is applied to the body. The GSM has been averaged and analyzed to establish the direction of the kinetic moment's vector in the orbital coordinate system. Generalization of this issue has been found in [9] when the force of light pressure is taken into account. The system’s inertial motion consists of a RB with a stationary point and a viscous incompressible fluid occupying an ellipsoidal bore inside it was examined in [10]. The averaging method was utilized to get the desired results, demonstrating that the system's motion tends to be a continuous rotation around the greatest inertia moment axis, where it is directed along the system's constant angular momentum vector. In [12], the author derived a full solution for a dynamically asymmetric satellite with a spherical hollow filled with viscous liquid, in addition to its stabilization and orientation. In [13], the authors approached a complete study of the rotational motion of a RB under the influence of body-constant torque and the action of the torque of a resistant force, due to the shape of the liquid, in the absence of the GM and the electromagnetic field during its movement. An approach was done to develop some technical details for the model of Chernousko [14], exploring the situation of limited dynamics while providing a coordinate-free representation for some fundamental formulas. They use fractal geometry to describe the patterns and behavior of fluids at different scales, from the large-scale flow of ocean currents to the small-scale behavior of individual molecules. The stabilization of such a system was examined in [15]. In [16], the author used a stabilizing feedback control with system-active program control to get close to an accurate analytical solution regarding the category of continuous functions. The potential for stabilizing the monoaxial attitude of an artificial earth satellite in the orbital coordinate frame is examined in [17] using an electrodynamic control of attitude system. The authors demonstrated a theorem regarding the asymptotic stability of body-controlled attitude motion. The numerical modeling supports the effectiveness of the built-in controls for attitude with a distributed delay. In [18], a symmetric RB with a spherical base, a rotor, and a cavity in the shape of an ellipsoid of rotation is investigated. This cavity is entirely filled with an ideal incompressible fluid in uniform vortex movement. A geometrical integral, an energy integral, Jellett’s integral, and the integral of constant vorticity are all proven to be valid for this system. In [19], the issue of stabilization over areas with the planned orientation motion of gyrostat is studied using the approach of Lyapunov functions and the method of limit equations and systems. In [20], the issue of global stabilization around a gyrostat's center of mass is explored. The author used a combination of Lyapunov functions, limit systems, and limit equations to solve the problem of the universal balancing program motions of a containing gyrostat with fluid. The motion of a body point close to an attracting center is examined in [21]. It is demonstrated that the area of space where the body point's trajectory is situated may be understood as the orbital of an electron in a hydrogen atom. All theoretical findings identified in this study are new since the problem of body-point motion near an attractive center is being explored for the first time. In [22], the technique of a large parameter is applied to demonstrate the asymptotic solutions of the GSM for a constrained gyrostatic system. Certain uses for the RB movement in space have been investigated in [23] when the body rotates under the effects of gravity force, the Newtonian field of force (NFF), and GM, while the stability of a single-rotor gyrostat rotating freely with an internal moment exists is explored in [24]. In [25], the author found that the presence of the GM may have a considerable influence on the control of the rotatory motion of the RB. The small parameter method of Poincaré is used to get the solutions of the GSM, which allows him to gain the required analytical expressions for time-varying control torques. It is found in [26] that as the RB moved through the electromagnetic field, it gained a net positive charge which led to an increase in its motion. The reason is due to the interaction between the RB's charge and magnetic field. Moreover, it is noted that the body’s motion is dependent on the strength and direction of the magnetic field, as well as the initial charge of the body. In [27], the impact of the different body parameter values on the motion’s behavior is theoretically explained for a charged RB containing a viscous incompressible liquid. The rotating RB enclosing a viscous fluid is a conundrum, in which it illustrates how the body characteristics impact the fluid's dynamic behavior. In [28], the gyrostatic effect on the dynamical motion of a symmetric RB around a principal axis is discussed. It is considered that the body has a movable mass associated double elastically with a located point on the dynamical symmetry axis and a completely spherical hollow cavity with a viscous liquid.

In this paper, the 3D motion of a charged RB containing a spherical cavity is examined, in which it contains a viscous incompressible liquid. It is assumed that the RB spins in the presence of constant torques at the axes related to the body, a GM, an electromagnetic field that is due to a point charge, and a resisting force torque brought on by the shape of the cavity. Take into consideration that the liquid is considered to move sufficiently fast, so the Reynolds number undoubtedly has a very tiny value. The GSM that regulates the motion is derived through Euler's dynamic equations, and the averaging of the generated system is also approached to simplify the procedure of the required solutions. In the process of applying Taylor's method to roughly solve the issue, some initial conditions are obtained. The influence of external forces and torques on the body’s motion is graphed at several values of the GM, the resistance force torque, the body constant torques, and the charge. The obtained outcomes in certain graphs are visualized along with the related phase plane curves to highlight the beneficial effects of several values of the body's parameters on the stability behavior of the motion. These findings are thought of as a generalization of those that had previously been reported for the case of an uncharged body or without the GM, as they show the various trajectories and paths that the RB takes while dealing with several forces affecting its motion. The obtained outcomes are considered significant because they have numerous practical uses, such as for liquid fuel wagons and spacecraft.

2 Problem’s description

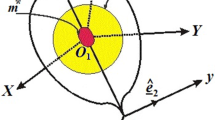
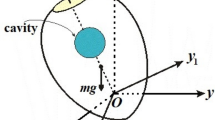
In this section, the rotational motion of a charged RB containing a spherical cavity of radius \(h\) filled with a high-viscosity liquid with density \(\rho\), relative to its inertia's center is examined. Therefore, considering two Cartesian frames with the same origin \(O\); the first \(Oxyz\) is a fixed one and the second \(Ox_{1} y_{1} z_{1}\) is a moving frame that coincides with the system’s inertia center and rotates with the body, see Fig. 1. Let \(\underline{\Omega } = (p,q,r)\) be the body’s angular velocity vector in which its components are directed along the body's principal axes and \(D = (D_{1} ,D_{2} ,D_{3} )\) represents the inertia tensor of the body. Take into account that the body is acted by a GM \(\underline{\lambda } = (0,0,\lambda_{3} )\) along the same inertia axes, in which its third component \(\lambda_{3}\) has a nonzero value while the other two components \(\lambda_{1}\) and \(\lambda_{2}\) do, the viscosity force, and the electromagnetic field which is owing to the charged body. Moreover, the cavity configuration has an impact on the constant tensor \(P = P_{0} \delta_{lm} ;\,\,\,P_{0} > 0,\,\,(l,m = 1,2,3)\), where \(\delta_{lm}\) points to a Kronecker delta symbol and \(P_{0} = {{8\,\pi \,h^{7} } \mathord{\left/ {\vphantom {{8\,\pi \,h^{7} } {525}}} \right. \kern-0pt} {525}}\) [11, 13].

Fig. 1
figure 1

Portrays the RB's motion

Full size image

The torques that are related to the body-connected axes are given as

$$M_{l}^{c} = \varepsilon^{2} M_{l} = {\text{const}},\,\,\,\,\,(l = 1,2,3),$$
(1)

where \(\varepsilon\) is a small parameter, as \(0 < \varepsilon < < 1\).

In this case for a cavity holding a "frozen" fluid, the resistive forces' torque is supposed to be proportional to the body's angular momentum [1, 10, 15].

$$\underline {M}^{r} = - \varepsilon^{2} \zeta D\underline {\Omega } .$$
(2)

where \(\zeta\) is a proportionality positive factor that is influenced by the medium’s characteristics and the body's shape.

Therefore, the GSM of the RB can be written as follows [1, 13, 27]

$$\begin{aligned} D_{1} \frac{{{\text{d}}p}}{{{\text{d}}t}} + [(\,D_{3} - D_{2} {\kern 1pt} )r + (\lambda_{3} {\kern 1pt} - eHl^{^{\prime}2} \cos \theta )]q & = \frac{{\rho \,P_{0} p}}{{\nu D_{1} D_{2} D_{3} }}[D_{3} (D_{1} - D_{3} )(D_{1} + D_{3} - D_{2} )r^{2} \\ & \;\;\;\; + D_{2} {\kern 1pt} (D_{1} - D_{2} {\kern 1pt} )(D_{1} + D_{2} - D_{3} )q^{2} ] - \varepsilon^{2} \zeta D_{1} p + \varepsilon^{2} M_{1} , \\ D_{2} \frac{{{\text{d}}q}}{{{\text{d}}t}} + [(D_{1} - D_{3} )r - (\lambda_{3} - eHl^{^{\prime}2} \cos \theta )]p & = \frac{{\rho P_{0} q}}{{\nu D_{1} D_{2} D_{3} }}[D_{1} (D_{2} {\kern 1pt} - D_{1} )(D_{2} {\kern 1pt} + D_{1} - D_{3} )p^{2} \\ & \;\;\;\; + D_{3} (D_{2} - D_{3} )(D_{2} {\kern 1pt} + D_{3} - D_{1} )r^{2} ] - \varepsilon^{2} \zeta D_{2} q + \varepsilon^{2} M_{2} , \\ D_{3} {\kern 1pt} \frac{{{\text{d}}r}}{{{\text{d}}t}} + (D_{2} - D_{1} ){\kern 1pt} {\kern 1pt} pq & = \frac{{\rho \,P_{0} r}}{{\nu D_{1} D_{2} D_{3} }}[D_{2} {\kern 1pt} (D_{3} - D_{2} {\kern 1pt} )(D_{3} + D_{2} - D_{1} )q^{2} + D_{1} (D_{3} - D_{1} ) \\ & \;\;\;\; \times \,(D_{3} + D_{1} - D_{2} )p^{2} ] - \varepsilon^{2} \zeta D_{3} r + \varepsilon^{2} M_{3} . \\ \end{aligned}$$
(3)

where \(\nu\) denotes the coefficient of kinematic viscosity, \(D_{j} \,(j = 1,2,3)\) are the RB’s principal moments of inertia and \(t\) represent the time.

Let us consider the scenario of a virtually dynamically spherical RB in which the main core moments of inertia of a frozen body are close to each other. Hence, one can write

$$D_{1} = J_{0} + \varepsilon \,D_{1}^{\prime} ,\,\,\,\,\,\,\,\,\,D_{2} = J_{0} + \varepsilon \;D_{2}^{\prime} ,\,\,\,\,\,\,\,\,D_{3} = J_{0} ,$$
(4)

where \(J_{0}\) is the characteristic value of the principal moments of inertia, \(D_{1}^{\prime}\) and \(D_{2}^{\prime}\) are the small deviations values from the corresponding parameters \(D_{1}\) and \(D_{2}\).

It must be noted that when \(\varepsilon = 0\), the motion is restricted to be for a symmetric RB. Additionally, consider the following

$$\left| {D_{1}^{\prime} - D_{2}^{\prime} } \right| = O(\varepsilon J^{\prime} ),\,\,\,\,\left| {D_{1} - D_{2} } \right| = O(\varepsilon^{2} J^{\prime} ),\,\,\,\,\,J^{\prime} \approx J_{0} ,\,\,\,\,\,\lambda_{3} = \varepsilon \lambda_{3}^{\prime} ,\,\,\,\,\,l^{\prime} = \sqrt \varepsilon l_{1}^{\prime} .$$
(5)

Based on (4) and (5), one can obtain

$$D_{2} - D_{1} = \varepsilon (D_{2}^{\prime} - D_{1}^{\prime} ) = \varepsilon^{2} J^{*} ,\,\,\,\,\,\,\,D_{1} - D_{3} = \varepsilon \,D_{1}^{\prime} ,\,\,\,\,\,D_{3} - D_{2} = - \varepsilon D_{2}^{\prime} .$$
(6)

The substitution from (4)-(6) into Eqs. (3), yields the below GSM related to the slow time parameter \(\tau = \varepsilon t\)

$$\begin{aligned} \frac{{{\text{d}}p}}{{{\text{d}}\tau }} & = \frac{{[D_{2}^{\prime} \,r - \,(\lambda_{3}^{\prime} - eHl_{1}^{^{\prime}2} \cos \theta )]}}{{J_{0} }}\left( {1 - \varepsilon \frac{{D_{1}^{\prime} }}{{J_{0} }}} \right)q + \varepsilon f_{p} ,{\kern 1pt} {\kern 1pt} \\ \frac{{{\text{d}}q}}{{{\text{d}}\tau }} & = - \frac{{[D_{3}^{\prime} \,r - \,(\lambda_{3}^{\prime} - eHl_{1}^{^{\prime}2} \cos \theta )]}}{{J_{0} }}\left( {1 - \varepsilon \frac{{D_{2}^{\prime} }}{{J_{0} }}} \right)p + \varepsilon f_{q} , \\ \frac{{{\text{d}}r}}{{{\text{d}}\tau }} & = \frac{{D_{1}^{\prime} - D_{2}^{\prime} }}{{J_{0} }}pq + \varepsilon f_{r} . \\ \end{aligned}$$
(7)

with the following initial conditions

$$p(0) = p_{0} ,\,\,\,q(0) = q_{0} ,\,\,\,r(0) = r_{0} .$$
(8)

It is important to emphasize that the system (7) consists of three first-order NDEs on which its frequency depends on \(r\). A close look at the third equation in this system reveals that it is explicitly given in terms of \(\varepsilon\), and then the third equation of this system is therefore regarded as a slow variable. The perturbation terms \(\varepsilon \,f_{p}\), \(\varepsilon \,f_{q}\), and \(\varepsilon \,f_{r}\) are expressed [13] as

$$\begin{aligned} \varepsilon \,f_{p} & = \frac{{\rho P_{0} }}{{\nu \,J_{0}^{3} }}p\left\{ {D^{\prime}_{1} \,[J_{0} + \varepsilon (D^{\prime}_{1} \, - D^{\prime}_{2} \,)]r^{2} + (D^{\prime}_{1} \, - D^{\prime}_{2} \,)[J_{0} + \varepsilon (D^{\prime}_{1} \, + 2D^{\prime}_{2} \,)]q^{2} } \right\} - \varepsilon \left( {\zeta p - \frac{{M_{1} }}{{J_{0} }}} \right), \\ \varepsilon \,f_{q} & = \frac{{\rho P_{0} }}{{\nu \,J_{0}^{3} }}q\left\{ {(D^{\prime}_{2} \, - D^{\prime}_{1} \,)[J_{0} + \varepsilon (2D^{\prime}_{1} \, + D^{\prime}_{2} \,)]p^{2} + D^{\prime}_{2} \,[J_{0} + \varepsilon (D^{\prime}_{2} \, - D^{\prime}_{1} \,)]r^{2} } \right\} - \varepsilon \left( {\zeta q - \frac{{M_{2} }}{{J_{0} }}} \right), \\ \varepsilon \,f_{r} & = - \frac{{\rho P_{0} }}{{\nu \,J_{0}^{3} }}r\left\{ {D^{\prime}_{2} \,[J_{0} + \varepsilon (2D^{\prime}_{2} \, - D^{\prime}_{1} \,)]q^{2} + D^{\prime}_{1} \,[J_{0} + \varepsilon (2D^{\prime}_{1} \, - D^{\prime}_{2} \,)]p^{2} } \right\} - \varepsilon \left( {\zeta r - \frac{{M_{3} }}{{J_{0} }}} \right). \\ \end{aligned}$$
(9)

It is obvious that the friction force's moment is relatively modest.

3 The proposed method

The unperturbed form of system (7) at \(\varepsilon = 0\) when \(\,\nu^{ - 1} = 0\), can be written as [13, 27]

$$\begin{aligned} \frac{{{\text{d}}p}}{{{\text{d}}\tau }} & = \,{{[D^{\prime}_{2} \,\,r - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]q} \mathord{\left/ {\vphantom {{[D^{\prime}_{2} \,\,r - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]q} {J_{0} }}} \right. \kern-0pt} {J_{0} }},{\kern 1pt} \\ \frac{{{\text{d}}q}}{{{\text{d}}\tau }} & = - \,{{[D^{\prime}_{1} \,\,r - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]p} \mathord{\left/ {\vphantom {{[D^{\prime}_{1} \,\,r - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]p} {J_{0} }}} \right. \kern-0pt} {J_{0} }},{\kern 1pt} \\ \frac{{{\text{d}}r}}{{{\text{d}}\tau }} & = 0. \\ \end{aligned}$$
(10)

The integration of the last equation of the above system (10) yields \(r = r_{0}\).

Now, some mathematical manipulations are being performed on the first two equations of (10), i.e., differentiating the first one with respect to \(\tau\) and then using the second one, yields

$$\frac{{d^{2} p}}{{d\tau^{2} }} + \omega^{2} p = 0,$$
(11)

where

$$\omega^{2} = {{\left[ {D^{\prime}_{2} \,\,r_{0} - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )} \right]\left[ {D^{\prime}_{1} \,r_{0} - \,\,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )} \right]} \mathord{\left/ {\vphantom {{\left[ {D^{\prime}_{2} \,\,r_{0} - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )} \right]\left[ {D^{\prime}_{1} \,r_{0} - \,\,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )} \right]} {J_{0}^{2} }}} \right. \kern-0pt} {J_{0}^{2} }} > 0.$$

The solution of the aforementioned Eq. (11) can be determined via Laplace transformation and the initial conditions (8), as

$$p(\tau ) = p_{0} \cos \omega \tau + ({{\dot{p}_{0} } \mathord{\left/ {\vphantom {{\dot{p}_{0} } \omega }} \right. \kern-0pt} \omega })\sin \omega \tau ;\;\;\;\;( \cdot = {d \mathord{\left/ {\vphantom {d {d\tau }}} \right. \kern-0pt} {d\tau }})$$
(12)

which might be expressed as

$$p = a\cos \varphi ,\,\,\,\,\,\,q = - {{J_{0} a\omega \sin \varphi } \mathord{\left/ {\vphantom {{J_{0} a\omega \sin \varphi } {[D^{\prime}_{2} \,\,r_{0} - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]}}} \right. \kern-0pt} {[D^{\prime}_{2} \,\,r_{0} - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]}},\,\,\,\,r = r_{0} .$$
(13)

where \(a = \sqrt {p_{0}^{2} + ({{\dot{p}_{0} } \mathord{\left/ {\vphantom {{\dot{p}_{0} } \omega }} \right. \kern-0pt} \omega })^{2} }\) and \(\varphi = \omega \tau + \varphi_{0}\) are, respectively, the amplitude and phase of Eq. (11). Here \(\varphi_{0}\) is the initial phase, \(\omega\) is the frequency, \(\cos \varphi_{0} = {{p_{0} } \mathord{\left/ {\vphantom {{p_{0} } a}} \right. \kern-0pt} a}\), and \(\sin \varphi_{0} = \frac{{q_{0} }}{a}\sqrt {\frac{{D^{\prime}_{2} \,\,r_{0} - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )}}{{D^{\prime}_{1} \,\,r_{0} - \,\,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )}}}\).

Now, a transformation from the slow variables to new ones is executed, i.e., from variables \(p\), \(q\), and \(r\) to the variables \(a\), \(r\), and \(\varphi\).

$$p = a\cos \varphi ,\;\;\;q = - {{J_{0} a\omega \sin \varphi } \mathord{\left/ {\vphantom {{J_{0} a\omega \sin \varphi } {[D_{2}^{\prime} \;r - (\lambda_{3}^{\prime} - eHl_{1}^{^{\prime}2} \cos \theta )]}}} \right. \kern-0pt} {[D_{2}^{\prime} \;r - (\lambda_{3}^{\prime} - eHl_{1}^{^{\prime}2} \cos \theta )]}},\;\;\;r = r.$$
(14)

As consequence of the above system (14), it may be differentiated regarding \(\tau\). Therefore, the substitution in (7) about \({{{\text{d}}p} \mathord{\left/ {\vphantom {{{\text{d}}p} {{\text{d}}\tau }}} \right. \kern-0pt} {{\text{d}}\tau }}\), \({{{\text{d}}q} \mathord{\left/ {\vphantom {{{\text{d}}q} {{\text{d}}\tau }}} \right. \kern-0pt} {{\text{d}}\tau }}\), and \({{{\text{d}}r} \mathord{\left/ {\vphantom {{{\text{d}}r} {{\text{d}}\tau }}} \right. \kern-0pt} {{\text{d}}\tau }}\) yields

$$\begin{aligned} \dot{a}\cos \varphi - a\,\dot{\varphi }\sin \varphi & = - \left( {1 - \varepsilon \frac{{D^{\prime}_{1} }}{{J_{0} }}} \right)a\omega \sin \varphi - \varepsilon \left( {\zeta a\cos \varphi - \frac{{M_{1} }}{{J_{0} }}} \right) + \frac{{\rho p_{0} a\cos \varphi }}{{\nu J_{0}^{3} }} \\ & \;\;\;\; \times \Bigg\{ D^{\prime}_{1} \,\,[J_{0} + \varepsilon (D^{\prime}_{1} \,\, - D^{\prime}_{2} \,\,)]r^{2} \, + (D^{\prime}_{1} \,\, - D^{\prime}_{2} \,\,)\,[J_{0} + \varepsilon (D^{\prime}_{1} \, + 2D^{\prime}_{2} \,)] \\ & \;\;\;\; \times {\frac{{[D^{\prime}_{1} \,r - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]}}{{[D^{\prime}_{2} \,r - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]}}a^{2} \sin^{2} \varphi } \Bigg\}, \\ \end{aligned}$$
(15)
$$\begin{aligned} \dot{a}\sin \varphi + a\,\dot{\varphi }\cos \varphi & = \left( {1 - \varepsilon \frac{{D^{\prime}_{2} \,}}{{J_{0} }}} \right)a\omega \cos \varphi - \varepsilon \left( {\zeta a\sin \varphi + \sqrt {\frac{{[D^{\prime}_{2} \,r - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]}}{{[D^{\prime}_{1} \,r - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]}}} \frac{{M_{2} }}{{J_{0} }}} \right) \\ & \;\;\;\; + \frac{{\rho p_{0} a\sin \varphi }}{{\nu J_{0}^{3} }}\left\{ {(D^{\prime}_{2} \,\, - D^{\prime}_{1} )\left[ {J_{0} + \varepsilon (2D^{\prime}_{1} \, + D^{\prime}_{2} )} \right]a^{2} \cos^{2} \varphi } \right. \\ & \;\;\;\; + \left. {D^{\prime}_{2} \,\,[J_{0} + \varepsilon (D^{\prime}_{2} \, - D^{\prime}_{1} )]r^{2} } \right\}, \\ \end{aligned}$$
(16)
$$\begin{aligned} \dot{r} & = \frac{{D^{\prime}_{2} \, - D^{\prime}_{1} \,}}{{J_{0} }}\sqrt {\frac{{[D^{\prime}_{1} \,r - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]}}{{[D^{\prime}_{2} \,r - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]}}} a^{2} \sin \varphi \cos \varphi - \varepsilon \left( {\zeta r - \frac{{M_{3} }}{{J_{0} }}} \right) \\ & \;\;\;\; - \frac{{\rho p_{0} r}}{{\nu J_{0}^{3} }}\left\{ {D^{\prime}_{2} \,\,\,[J_{0} + \varepsilon (2D^{\prime}_{2} \, - D^{\prime}_{1} \,\,)]\,\frac{{[D^{\prime}_{1} \,r - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]}}{{[D^{\prime}_{2} \,r - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]}}a^{2} \sin^{2} \varphi \,} \right. \\ & \;\;\;\; + \left. {D^{\prime}_{1} \,\,[J_{0} + \varepsilon (2D^{\prime}_{1} \, - D^{\prime}_{2} \,)]a^{2} \cos^{2} \varphi } \right\}. \\ \end{aligned}$$
(17)

Solving Eqs. (15) and (16) to obtain \(\dot{a}\) and \(\dot{\varphi }\) as

$$\begin{aligned} \dot{a} & = \varepsilon \frac{{D^{\prime}_{1} \, - D^{\prime}_{2} \,}}{{J_{0} }}a\omega \sin \varphi \cos \varphi - \varepsilon \left\{ {\zeta a - \frac{{M_{1} }}{{J_{0} }}\cos \varphi + \frac{{M_{2} }}{{J_{0} }}\sqrt {\frac{{[D^{\prime}_{2} \,r - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]}}{{[D^{\prime}_{1} \,r - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]}}} \sin \varphi } \right\} \\ & \;\;\;\; + \frac{{\rho p_{0} a}}{{\nu J_{0}^{3} }}\left\{ {r^{2} \left[ {D^{\prime}_{1} \,\cos^{2} \varphi (J_{0} + \varepsilon D^{\prime}_{1} ) + D^{\prime}_{2} \,\sin^{2} \varphi (J_{0} + \varepsilon D^{\prime}_{2} ) - \varepsilon D^{\prime}_{1} \,D^{\prime}_{2} } \right] + a^{2} \sin^{2} \varphi \cos^{2} \varphi } \right. \\ & \;\;\;\; \times \,\left. {(D^{\prime}_{1} \, - D^{\prime}_{2} )\left( {[J_{0} + \varepsilon (D^{\prime}_{1} \, + 2D^{\prime}_{2} )]\frac{{[D^{\prime}_{1} \,r - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]}}{{[D^{\prime}_{2} \,r - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]}} - [J_{0} + \varepsilon (2D^{\prime}_{1} \, + D^{\prime}_{2} )]} \right)} \right\}. \\ \end{aligned}$$
(18)
$$\begin{aligned} \dot{\varphi } & = \omega (r) - \varepsilon \frac{\omega (r)}{{J_{0} }}(D^{\prime}_{1} \,\sin^{2} \varphi + D^{\prime}_{2} \,\cos^{2} \varphi ) - \frac{\varepsilon }{a}\left\{ {\frac{{M_{2} }}{{J_{0} }}\sqrt {\frac{{[D^{\prime}_{2} \,r - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]}}{{[A^{\prime}r - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]}}} \cos \varphi } \right. \\ & \;\;\;\; + \left. {\frac{{M_{1} }}{{J_{0} }}\sin \varphi } \right\} + \frac{{\rho p_{0} \sin \varphi \cos \varphi }}{{\nu J_{0}^{3} }}(D^{\prime}_{2} \,\, - D^{\prime}_{1} \,)\left\{ {[J_{0} + \varepsilon (D^{\prime}_{1} \, + D^{\prime}_{2} \,\,)]r^{2} \, + a^{2} \,([J_{0} + \varepsilon (2D^{\prime}_{1} + D^{\prime}_{2} \,)]} \right. \\ & \;\;\;\; \times \left. {\cos^{2} \varphi + \left[ {J_{0} + \varepsilon (D^{\prime}_{1} + 2D^{\prime}_{2} \,)} \right]\frac{{[D^{\prime}_{1} \,r - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]}}{{[D^{\prime}_{2} \,r - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]}}\sin^{2} \varphi )} \right\}. \\ \end{aligned}$$
(19)

Here, the quantity \(\omega (r)\) preserves the definition of the system’s perturbed frequency. In light of averaging Eqs. (17)–(19) over the phase \(\varphi\) [11, 13], it is easy to get

$$\begin{aligned} \dot{a} & = \Lambda a\left\{ {\frac{{r^{2} }}{2}\,[J_{0} (D^{\prime}_{1} + D^{\prime}_{2} ) + \varepsilon (D^{\prime}_{1} - D^{\prime}_{2} )^{2} ] + \frac{{D^{\prime}_{1} - D^{\prime}_{2} \,}}{4}([J_{0} + \varepsilon (D^{\prime}_{1} + 2D^{\prime}_{2} )]} \right. \\ & \;\;\;\; \times \,\left. {\frac{{[D^{\prime}_{1} \,r - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]}}{{[D^{\prime}_{2} \,r - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]}} - [J_{0} + \varepsilon (2D^{\prime}_{1} + D^{\prime}_{2} )])} \right\} - \varepsilon \zeta a. \\ \end{aligned}$$
(20)
$$\,\dot{\varphi } = \omega \left[ {1 - \frac{{\varepsilon (\,D^{\prime}_{1} + D^{\prime}_{2} \,)}}{{2J_{0} }}} \right],$$
(21)
$$\begin{aligned} \dot{r} & = - \frac{{\Lambda ra^{2} }}{2}\left\{ {D^{\prime}_{2} \,\,\,[J_{0} + \varepsilon (2D^{\prime}_{2} \, - D^{\prime}_{1} \,)]\frac{{[D^{\prime}_{1} \,r - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]}}{{[D^{\prime}_{2} \,r - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]}}\,} \right. \\ & \;\;\;\; + \left. {D^{\prime}_{1} \,\,[J_{0} + \varepsilon (2D^{\prime}_{1} \, - D^{\prime}_{2} \,)]} \right\} - \varepsilon \left( {\zeta r - \frac{{M_{3} }}{{J_{0} }}} \right). \\ \end{aligned}$$
(22)

where

$$\Lambda = {{\rho p_{0} } \mathord{\left/ {\vphantom {{\rho p_{0} } {\nu J_{0}^{3} }}} \right. \kern-0pt} {\nu J_{0}^{3} }}.$$
(23)

As a result, the numerical solutions of Eqs. (20)–(22) can be determined using Taylor’s method [13] in the presence of the initial conditions \(\tau = \tau_{0}\), \(a(\tau_{0} ) = a_{0}\), \(r(\tau_{0} ) = r_{0}\), and \(\varphi (\tau_{0} ) = \varphi_{0}\) as follows

$$\begin{aligned} a(\tau ) & = a(\tau_{0} ) + (\tau - \tau_{0} )\left\{ {\Lambda a(\tau_{0} )\frac{{r^{2} (\tau_{0} )}}{2}\,[J_{0} (D^{\prime}_{1} \, + D^{\prime}_{2} \,) + \varepsilon (D^{\prime}_{1} \, - D^{\prime}_{2} \,)^{2} ] + \Lambda a(\tau_{0} )\,\,\frac{{D^{\prime}_{1} \, - D^{\prime}_{2} \,}}{4}} \right. \\ & \;\;\;\; \times \left(\,[J_{0} + \varepsilon (D^{\prime}_{1} \, + 2D^{\prime}_{2} \,)]\,\frac{{[D^{\prime}_{1} \,r(\tau_{0} ) - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]}}{{[D^{\prime}_{2} \,r(\tau_{0} ) - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]}}\, - [J_{0} + \varepsilon (2D^{\prime}_{1} \, + D^{\prime}_{2} \,)]\right) \\ & \;\;\;\; - \left. {\varepsilon \lambda a(\tau_{0} )} \right\} + \frac{{(\tau - \tau_{0} )^{2} }}{2!}\left\{ {\left[ {\frac{{\Lambda f_{1} (\tau_{0} )r^{2} (\tau_{0} )}}{2} + \Lambda a(\tau_{0} )r(\tau_{0} )f_{2} (\tau_{0} )} \right]\,[J_{0} (D^{\prime}_{1} \, + D^{\prime}_{2} \,)} \right. \\ & \;\;\;\; + \varepsilon (D^{\prime}_{1} \, - D^{\prime}_{2} \,)^{2} ]\, + [J_{0} + \varepsilon (D^{\prime}_{1} \, + 2D^{\prime}_{2} \,)]\left\{ {f_{1} (\tau_{0} )\frac{{[D^{\prime}_{1} \,r(\tau_{0} ) - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]}}{{[D^{\prime}_{2} \,r(\tau_{0} ) - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]}}} \right. \\ & \;\;\;\; + \left. {a(\tau_{0} )\frac{{[(D^{\prime}_{2} \, - D^{\prime}_{1} \,)\,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]f_{2} (\tau_{0} )}}{{[D^{\prime}_{2} \,r(\tau_{0} ) - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]^{2} }}} \right\}\frac{{\Lambda (D^{\prime}_{1} \, - D^{\prime}_{2} \,)}}{4} - \frac{{\Lambda f_{1} (\tau_{0} )(D^{\prime}_{1} \, - D^{\prime}_{2} \,)}}{4} \\ & \;\;\;\; \times [J_{0} + \varepsilon (2D^{\prime}_{1} \, + D^{\prime}_{2} \,)] - \varepsilon \zeta f_{1} (\tau_{0} )\} + O(\tau^{3} ), \\ \end{aligned}$$
(24)
$$\begin{aligned} \varphi (\tau ) & = \varphi (\tau_{0} ) + (\tau - \tau_{0} )\left\{ {\frac{{\sqrt {[D^{\prime}_{2} \,\,r(\tau_{0} ) - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )][D^{\prime}_{1} \,\,r(\tau_{0} ) - \,\,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]} }}{{J_{0} }}} \right. \\ & \;\;\;\; \times \left. {\left( {1 - \frac{{\varepsilon (D^{\prime}_{1} \, + D^{\prime}_{2} \,)}}{{2J_{0} }}} \right)} \right\}\, + \frac{{(\tau - \tau_{0} )^{2} }}{2!}\left\{ {\frac{1}{{2J_{0} }}\left( {1 - \frac{{\varepsilon (D^{\prime}_{1} \, + D^{\prime}_{2} \,)}}{{2J_{0} }}} \right)} \right. \\ & \;\;\;\; \times \left. {\frac{{[2D^{\prime}_{1} \,D^{\prime}_{2} \,r(\tau_{0} )\, - (D^{\prime}_{1} \, + D^{\prime}_{2} \,)\,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]f_{2} (\tau_{0} )}}{{\sqrt {[B^{\prime}\,r(\tau_{0} ) - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )][D^{\prime}_{1} \,\,r(\tau_{0} ) - \,\,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]} }}} \right\} + O(\tau^{3} ), \\ \end{aligned}$$
(25)
$$\begin{aligned} r(\tau ) & = r(\tau_{0} ) - (\tau - \tau_{0} )\left\{ {\frac{{\Lambda r(\tau_{0} )a^{2} (\tau_{0} )}}{2}\{ D^{\prime}_{2} \,\,\,[J_{0} + \varepsilon (2D^{\prime}_{2} \, - D^{\prime}_{1} \,\,)]\,\frac{{[D^{\prime}_{1} \,r(\tau_{0} ) - \,(\lambda^{\prime}_{3} - eH_{1}^{^{\prime}2} \cos \theta )]}}{{[D^{\prime}_{2} \,r(\tau_{0} ) - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]}}} \right. \\ & \;\;\;\; + \left. {D^{\prime}_{1} \,[J_{0} + \varepsilon (2D^{\prime}_{1} \, - D^{\prime}_{2} \,)]} \right\} + \varepsilon \left( {\zeta r(\tau_{0} ) - \frac{{M_{3} }}{{J_{0} }}} \right)\} + \frac{{(\tau - \tau_{0} )^{2} }}{2!}\left\{ { - \frac{{\Lambda a(\tau_{0} )}}{2}} \right. \\ & \;\;\;\; \times \,D^{\prime}_{2} \,[J_{0} + \varepsilon (2D^{\prime}_{2} \, - D^{\prime}_{1} \,\,)]\,\left\{ {[2r(\tau_{0} )f_{1} (\tau_{0} ) + f_{2} (\tau_{0} )a(\tau_{0} )]\frac{{[D^{\prime}_{1} \,r(\tau_{0} ) - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]}}{{[D^{\prime}_{2} \,r(\tau_{0} ) - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]}}} \right. \\ & \;\;\;\; + \left. {r(\tau_{0} )a(\tau_{0} )\,\frac{{[(D^{\prime}_{2} \, - D^{\prime}_{1} \,)\,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]f_{2} (\tau_{0} )}}{{[D^{\prime}_{2} \,r(\tau_{0} ) - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]^{2} }}} \right\} - \frac{{\Lambda a(\tau_{0} )}}{2}D^{\prime}_{1} \,[2r(\tau_{0} )f_{1} (\tau_{0} ) \\ & \;\;\;\; + f_{2} (\tau_{0} )a(\tau_{0} )][J_{0} + \varepsilon (2D^{\prime}_{1} \, - D^{\prime}_{2} \,\,)] - \varepsilon \zeta f_{2} (\tau_{0} )\} + O(\tau^{3} ), \\ \end{aligned}$$
(26)

where

$$\begin{aligned} f_{1} (\tau_{0} ) & = \Lambda a(\tau_{0} )\left\{ {\frac{{r^{2} (\tau_{0} )}}{2}\,[J_{0} (D^{\prime}_{1} \, + D^{\prime}_{2} \,) + \varepsilon (D^{\prime}_{1} \, - D^{\prime}_{2} )^{2} ] + \frac{{D^{\prime}_{1} \, - D^{\prime}_{2} }}{4}(\,[J_{0} + \varepsilon (D^{\prime}_{1} \, + 2D^{\prime}_{2} )]} \right. \\ & \;\;\;\; \times \left. {\frac{{[D^{\prime}_{1} \,r(\tau_{0} ) - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]}}{{[D^{\prime}_{2} r(\tau_{0} ) - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]}} - [J_{0} + \varepsilon (2D^{\prime}_{1} \, + D^{\prime}_{2} )])} \right\} - \varepsilon \zeta a(\tau_{0} ), \\ \end{aligned}$$
(27)
$$\begin{aligned} f_{2} (\tau_{0} ) & = - \frac{{\Lambda r(\tau_{0} )a^{2} (\tau_{0} )}}{2}\left\{ {D^{\prime}_{2} \,\,[J_{0} + \varepsilon (2D^{\prime}_{2} - D^{\prime}_{1} \,)]\frac{{[D^{\prime}_{1} r(\tau_{0} ) - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]}}{{[D^{\prime}_{2} r(\tau_{0} ) - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]}}} \right. \\ & \;\;\;\; + \left. {D^{\prime}_{1} \,[J_{0} + \varepsilon (2D^{\prime}_{1} - D^{\prime}_{2} )]} \right\} - \varepsilon \left[ {\zeta r(\tau_{0} ) - \frac{{M_{3} }}{{J_{0} }}} \right], \\ \end{aligned}$$
(28)
$$\begin{aligned} f_{3} (\tau_{0} ) & = \frac{1}{{J_{0} }}\sqrt {[D^{\prime}_{2} \,r(\tau_{0} ) - \,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )][D^{\prime}_{1} \,r(\tau_{0} ) - \,\,(\lambda^{\prime}_{3} - eHl_{1}^{^{\prime}2} \cos \theta )]} \\ & \;\;\;\; \times \,\,[1 - \frac{{\varepsilon (D^{\prime}_{1} + D^{\prime}_{2} )}}{{2J_{0} }}]. \\ \end{aligned}$$
(29)

4 Discussion of outcomes

The major goal of this section is to present a graphical simulation of the required solutions \(p,q,\) and \(r\) in Eq. (14) as well as the solutions \(a\) and \(\phi\) in Eqs. (24) and (25). Additionally, it gives a description of the stable and unstable behavior of the body's motion. Therefore, let us consider the following data:

$$\begin{aligned} D & = (9.51,9.3,9)\,{\text{kg}} \cdot {\text{m}}^{2} ,\,\,\,\,e = (10^{ - 2} ,10^{3} ,10^{4} )C,\,\,\,\,\zeta = (1.5,2,2.5)\,{\text{rad}} \cdot {\text{s}}^{ - 1} , \\ P_{0} & = 1.9\,m^{7} ,\,\,\,\,\nu = 1000\,{\text{m}}^{2} \cdot {\text{s}}^{ - 1} ,\,\,\,\,H = 100\,{\text{T}},\,\,\,\,M_{3} = ( - 3\,, - 6, - 9){\text{kg}} \cdot {\text{m}} \cdot {\text{s}}^{ - 2} . \\ l^{\prime} & = 0.01\,{\text{m}},\,\,\,\,\theta = 0.3\,{\text{rad}},\,\,\,\,\,\rho = 1250\,{\text{kg}} \cdot {\text{m}}^{ - 3} ,\,\,\,\,\,\varepsilon = 0.1. \\ \end{aligned}$$

It is worthy that all numerical results for Eqs. (24)-(26) are calculated with the initial conditions \(\tau_{0} = 0\), \(a(0) = 1\), \(r(0) = 1\), and \(\varphi (0) = 0\).

The investigation through this section goes on with four different cases presented as follows:

4.1 The GM

In this case, the impact of the third component \(\lambda_{3}\) of the GM on the RB's motion relative to the trajectories of its angular velocities is investigated. Curves in Figs. 2 and 3 reveal, respectively, the variation of \(a\), \(r\), \(\varphi\), \(p\), and \(q\) in which they are calculated, when \(\lambda_{3} ( = 0.1,0.15,0.2)\,{\text{kg}} \cdot {\text{m}}^{2} \cdot {\text{s}}^{ - 1}\), and \(\lambda_{3} ( = 15,20,25)\,{\text{kg}} \cdot {\text{m}}^{2} \cdot {\text{s}}^{ - 1}\). An examination of the drawn curves in parts of Fig. 2 shows that the curvatures of these curves increase as time goes on, which are consistent with the formulas (24) and (25). The mentioned various values of \(\lambda_{3}\) are considered to reveal the change on the curves according to these values. In other words, if the same values are considered, no variation can be observed in the waves of the solutions \(p\) and \(q\). The variation of the solutions \(p\) and \(q\) with time \(t\) has the simulation of the decay waves during the investigated period of time as \(\lambda_{3}\) has the aforementioned values, which indicates that these waves have a stable behavior. The oscillations’ number increases with the increase of the GM values, in which the corresponding wavelengths decrease. This conclusion approves the mathematical forms of Eq. (14). Curves of Fig. 4, when examined in further detail, show the phase plane of the solutions \(p\) and \(q\) at the same values of the third component of the GM in the direction of \(Oz_{1}\). Closed curves have been graphed in portions (a) and (b) of this figure, which demonstrate that these solutions have stationary behaviors and a stable manner.

Fig. 2
figure 2

Portrays the temporal behaviors for the waves of: a \(a\), b \(r\), and c \(\varphi\) when \(\lambda_{3} ( = 0.1,0.15,0.2)\,{\text{kg}} \cdot {\text{m}}^{2} \cdot {\text{s}}^{ - 1}\)

Full size image
Fig. 3
figure 3

Shows the variations of the functions: a \(p(t)\) and b \(q(t)\) when \(\lambda_{3} ( = 15,20,25)\,{\text{kg}} \cdot {\text{m}}^{2} \cdot {\text{s}}^{ - 1}\)

Full size image
Fig. 4
figure 4

Describes the phase plane curves at the same values of Fig. 3 for: a \(p\) and b \(q\)

Full size image

Therefore, the main outcome result of this case is that the increase of the GM value for the RB's motion yields a decrease of the amplitude in the angular velocity trajectories, increasing the frequency, decreasing the wavelength, and maintaining the stability of the motion as time goes on.

4.2 The resistive force torque

In this case, the effect of the resistance force torque on the body's motion is investigated according to the values of the positive factor \(\zeta\) which have determined by the medium’s characteristics and the body's shape. The time histories of the functions \(a\), \(r\), \(\varphi\), \(p\), and \(q\) at different values of \(\zeta ( = 1.5,2,2.5)\,{\text{rad}} \cdot {\text{s}}^{ - 1}\) besides the aforementioned data above are graphed in Figs. 5, 6, 7. The graphed curves in potions (a) and (b) of Fig. 5 decrease gradually with the increase of \(\zeta\) for the functions \(a\) and \(r\). On the other hand, the behavior of the function \(\varphi\) increases tile a certain value of time and then decreases during the examined time interval. Standing waves with some nodes have been drawn in parts (a) and (b) of Fig. 6 to reveal the influence of the parameter \(\zeta\) on the solutions \(p\) and \(q\). The plotted waves have a decay behavior through the investigated period of time, where their amplitudes decrease with the increase of values \(\zeta\). Moreover, the wavelengths remain steady and consequently their frequencies are still unchanged. The phase plane curves of the presented solutions in Fig. 6 have been graphed in parts of Fig. 7. These curves have spiral forms and are directed toward one point, which indicates that the waves of the solutions have a stable behavior.

Fig. 5
figure 5

Illustrates the influence of \(\zeta ( = 1.5,2,2.5)\,{\text{rad}} \cdot {\text{s}}^{ - 1}\) on the behavior of: a \(a\), b \(r\), and c \(\varphi\)

Full size image
Fig. 6
figure 6

Describes the impact of the values of \(\zeta ( = 1.5,2,2.5)\,{\text{rad}} \cdot {\text{s}}^{ - 1}\) on the functions: a \(p(t)\) and b \(q(t)\)

Full size image
Fig. 7
figure 7

Sketches the good action of \(\zeta ( = 1.5,2,2.5)\,{\text{rad}} \cdot {\text{s}}^{ - 1}\) on the curves in the planes: a Phase plane plots for \(p\dot{p}\) and b \(q\dot{q}\)

Full size image

The main result of this case is that decreasing the resistive force torque values on the RB's motion will decrease the amplitude of the angular velocity wave trajectories, keeping the stability of the motion as time goes on while the frequency and wavelength remain the same.

4.3 The body-constant torque

The influence of the body-constant torque on the RB's motion has been presented in this case. Curves in Figs. 8, 9, 10 show the impact of various values of the third constant torque component \(M_{3} = ( - 3, - 6, - 9)\,{\text{kg}} \cdot {\text{m}} \cdot {\text{s}}^{ - 2}\) on the manner of the describing waves of the solutions functions \(a\), \(r\), \(\varphi\), \(p\), and \(q\). Therefore, previous data have been considered to output the curves of these figures. As mentioned above, portions of Fig. 8 show the plotted curves of the functions \(a\), \(r\), and \(\varphi\) during the interval \(t \in [0,20]{\text{s}}[0,20]\)\({\text{s}}\). These curves decrease when time goes on for the waves describing \(a\) and \(r\), while the behavior of the function \(\varphi\) increases until it reaches a specified value and then decreases. Accordingly, the impression that is taken from these curves is that they are stable. The inspection of the portions in Fig. 9, shows that the behavior of the waves that describe the change of solutions \(p\) and \(q\) with time has decayed during the same studied period of time, which confirms the stability of these solutions. This decay increases with the decrease of \(M_{3}\) values over time. The corresponding diagrams of these solutions in the planes \(p\dot{p}\) and \(q\dot{q}\) have been drawn, respectively, in parts (a) and (b) of Fig. 10. The behaviors of the plotted curves in these planes have spiral forms that are directed toward the center of these curves, which assert the stable behavior of these solutions.

Fig. 8
figure 8

The impact of \(M_{3}\) values on the behavior of: a \(a\), b \(r\), and c \(\varphi\)

Full size image
Fig. 9
figure 9

Reveals the decay behavior of: a \(p(t)\) and b \(q(t)\) at various values of \(M_{3}\)

Full size image
Fig. 10
figure 10

Presents the spiral curves in the planes: a \(p\dot{p}\) and b \(q\dot{q}\)

Full size image

Therefore, one can conclude for this scenario that the decrease of the body constant torque values for the RB's motion as time goes on produces a decrease in the angular velocity amplitudes, increases the oscillation number, decreases the wavelength, and maintains the stability of the motion.

4.4 The charge

In the present scenario, the impact of various values of the charge \(e\) on the trajectories of the RB angular velocities is investigated. In Figs. 11 and 12, the curves describe the time histories of \((a,r,\varphi )\) and \((p,q)\), respectively, when the charge \(e\) has the values \((10^{ - 2} ,10^{3} ,10^{4} )\,C\). The impact of these values yields a decrease of the behavior of the functions \(a\) and \(r\), as seen in Figs. 11a and b. The wave describes \(\varphi\) behavior increases during the studied time period and then decreases at the end of this period. On the other side, decaying waves are plotted in Fig. 12 to describe the behavior of the solutions \(p\) and \(q\). The action of \(e\) values seems slightly, to some extent, on these solutions. Figure 13 depicts the projections of these waves in the planes \(p\dot{p}\) and \(q\dot{q}\), which shows that they have spiral patterns, which point to their stability.

Fig. 11
figure 11

Presents the action of \(e = (10^{ - 2} ,10^{3} ,10^{4} )\,{\text{C}}\) on the behavior of: a \(a\), b \(r\), and c \(\varphi\)

Full size image
Fig. 12
figure 12

Shows the impact of \(e\) values on: a \(p(t)\) and b \(q(t)\)

Full size image
Fig. 13
figure 13

Presents the projections of \(p\) and \(q\) in the planes: a \(p\dot{p}\) and b \(q\dot{q}\)

Full size image

It must be mentioned that the increase of the charge’s value as time goes on yields a slight deviation of the body’s angular velocity, as it impacts a decrease in the amplitude and keeps the stability of the body’s motion while the frequency and wavelength remain the same.

References [13] and [27] are the closest works to our subject and provide an identical result with 0% error between both techniques. For comparison purposes with these works, the zero values of the GM and the point charge are considered to ensure the accuracy of the above-presented methodology. Therefore, the obtained results are considered generalizations of those obtained previously in [13, 27], which is because the viewpoint considered in studying the influence of the GM and the charge is not related before.

5 Conclusion

The 3D motion of a charged RB with a spherical cavity filled with an incompressible viscid liquid has been studied. The charged RB in such a case revolves under the influence taken by the body-constant torques, the GM, and a torque of resistive forces that resulted from the cavity's geometry. The liquid is considered to move sufficiently fast, and therefore the Reynolds number has a very small value. The GSM is derived in light of the dynamic equations of Euler. The averaging technique has been applied to the derived GSM to transform this system into a suitable one to easily achieve the required solutions, in which Taylor's method has also been applied. In view of the selected values of the GM, resistive force torque, body-constant torques, and charge, those derived solutions and their projections in the diagrams of phase planes have been graphed to reveal the impact of these parameters on the behavior of these outcomes. The results of this investigation are presented in four cases: (1) the increase of the GM values on the RB's motion will decrease the amplitude of the angular velocity trajectories, increasing the frequency, and decreasing the wavelength, (2) the decrease of the resistive force torque on the RB’s motion will decrease the amplitude of the angular velocity wave trajectories, while the frequency and wavelength are still stationary, (3) the decrease in the body constant torque values decreases the amplitude and wavelength of the angular velocity trajectories and increases the frequency, which is similar to the impact of increasing the GM, (4) the increase of the charge yields decrease the amplitude of the angular velocity wave trajectories, while the frequency and wavelength will remain stationary. The body's stability is still stationary in all four scenarios. Those outcomes make it possible for the analysis of astronomical body motions influenced by minimal internal and external torques. The momentousness of this study is due to its numerous practical applications, including those for spacecraft and wagons that transport liquid fuel and are influenced by external forces.