Introduction

The rigid body problem is looked at, as one of the most attractive problems in mechanics, which is attributable to its practical significance for engineering applications especially for the rotational motion of a spacecraft, as well as for the theory of the gyro motion. Such problems are considered very complex to deal with because they involve both the difficulties of both rigid body and hydrodynamics problems. The outgrowth and generalization of the present problem are the problems of rigid bodies that contain a fluid in a cavity. Zhukovskii [1] in 1885, was the first scientist to deal with such a topic. In the general context, he investigated the body's motion when the cavity is entirely filled with an ideal incompressible fluid. He supposed that the impact of the fluid on the rigid body can be considered as a connection with another body, in which the centers of masses of the fluid and body coincide with each other. The stability of a steady body with a uniform vortices flow in a cavity was investigated firstly in [2] and [3]. Numerous works have investigated the stability of the rigid body motion in which it contains cavities filled with a fluid such as [4,5,6,7].

The problems relating to the rigid bodies dynamics contain cavities filled with a viscous fluid are considered that have difficulties than those of an ideal fluid. Chernous’ko F. L. in [8, 9] has made a major contribution to deal with such problems. The impact of the fluid on the parametric motion is reduced to the existence of specific moments of disturbance for a fictitious body in the Euler’s dynamic equations. Several works were dedicated to investigate the passive motion of bodies with cavities fully filled with a viscous fluid, e.g., [10,11,12]. In [10], the author studied the stabilizing influence of the liquid on the motion of an anti-symmetric top with cavities entirely filled with incompressible liquid. In [11], the governing equations describing the evolution of the rotational motion of asymmetric rigid body containing cavities completely filled with a viscous fluid are derived; while in [12], the case of inertia's ellipsoid that is close to the rotation's ellipsoid is considered. In [13, 14], the stabilization of the rotary motion of a symmetrical gyrostat, having a spherical cavity contains a viscous fluid, about the dynamic symmetry axis is studied. The approach presented in [9] has been revisited in [15] to simulate the dynamics of a rigid body that has a cavity fully filled with high-viscosity viscous fluid.

The motion of satellite under the action only of gravitational torques was investigated in [16], while the formulas for the light pressure torque, acting on a body (without cavity with fluid) bounded by a surface of revolution were obtained in [17]. The rotatory relative motion of a satellite contains a viscous fluid in a cavity to the center of mass is studied in [18,19,20,21,22]. This motion is examined under the effectiveness of various forces and moments such that; gravitational moment due to the gravity force [18], or in the presence of light pressure force only [19], or both of them [20]. The asymptotic study of the controlling system is carried out applying the modified averaging method [16, 23, 24] and the numerical results are analyzed. Moreover, some special cases of the motion of a symmetric satellite are investigated in [20].

Recently, the averaging technique [25] is used in [26] and [27] to obtain the analytic solutions of a charged rigid body under the action of a full vector of a gyro moment and electromagnetic field, respectively. Some interesting applications related with the restoring moment, perturbing moments and others are presented. The motion of an electromagnetic gyrostat is examined in [28], in which the Euler’s angles are estimated analytically and numerically to determine the orientation of the gyro at any instant. On the other hand, the case of irrational frequencies for the rigid body motion is investigated in [29] using the small parameter method of Poincaré [25], while the method of Krylov–Bogoliubov–Mitropolski [25] is used in [30,31,32] to get the asymptotic solutions of the system of motion for the rigid body motion when the ellipsoids of inertia and rotation are closed with each other, in which its generalization is found in [33]. The method of immersed boundary projection is used in [34] to deal with the interaction between the fluid and the rigid bodies. This technique is subedited in affixed reference system on the body under the influence of flow structure. Therefore, the controlling system of motion can be solved without duplicates, efficiently and accurately. In [35], the author examined the free rotational motion of a whole body which contains a spherical cavity completely filled with an incompressible fluid flow. The existence of the solutions whether global weak or local strong is demonstrated. Moreover, the fluid's velocity as well as the angular velocity, with respect to the outer solid material, converges to zero when time tends to infinity.

In [36], the authors provided a well-developed method for the motion of rigid bodies under the influence of perturbation moments according to the physical nature of these bodies. They covered the fundamentals of rigid body dynamics as well as the averaging method, in which a thorough approach based on the averaging procedure that can be used to bodies with any inertia ellipsoids can be used. In a weakly resistant medium, a heavy asymmetric rigid body contains a spherical cavity filled with a high-viscosity liquid rapidly rotating around a fixed point is studied in [37]. Two problems of the dynamical motion of a symmetric rigid body having a cavity fully filled with a viscous liquid in the presence of a movable mass were investigated in [38]. The combined action of this fluid and the mass on the body’s motion is examined.

The fast dynamical motion of asymmetric satellite in relation to its center of mass is investigated in [39]. It is considered that the satellite having a hollow filled with viscous fluid with low Reynolds numbers and the motion under the action of gravitational and external resistance torques. Low Reynolds numbers are used to investigate rotatory motion of a dynamically asymmetric satellite around its center of mass is investigated in [40], in which the author considered a spherical cavity filled with viscous liquid in the satellite. A numerical investigation of a solid body's vector change in kinetic momentum was carried out. The inertial movements of a coupled system made up of a rigid body with a hollow completely filled with a viscous liquid are studied in [41]. The authors focus on the asymptotic behavior of these movements over time.

The steady rotational motion of a spherical solid particle in a spherical cavity filled with nanofluid is investigated in [42]. It is considered that, the rotation of both the particle and the cavity around an axis that connecting their centers with two distinct angular velocities. The behavior of a vibrating solid cylinder in an incompressible fluid inside a rectangular cavity is studied experimentally in [43], while the mechanical motion of a solid body having an inner chamber filled with an incompressible viscous fluid is considered in [44]. The authors identified the system's equilibria, and investigated the various stability characteristics. Recently, the influence of the gyro torques on the motion of a symmetric body containing a viscous fluid inside a spherical cavity is examined in [45] analytically and numerically, in which the obtained analytical solutions generalized one of the examined problems in [38].

In this paper, we will examine the motion of a rigid body around its center of mass in which it has a cavity, close to a spherical case, filled with a viscous incompressible fluid. The Reynolds number is supposed to be small owing to the velocity of the fluid is sufficiently high. The body rotates under a force that acting from the side of viscous fluid and in the presence of a gyrostatic torque to achieve new results of the field of interest. The governing system of regulating motion is derived and the averaging of the Cauchy problem of this system is analyzed. The asymptotic and numerical results are obtained and plotted graphically to evaluate the considered motion of the body completely at any instant. The achieved results are considered a new contribution of the gyrostatic motion field and a generalization of some previous works.

Mathematical Construction of the Problem

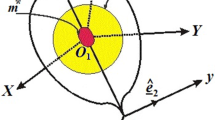
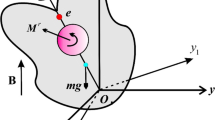
In this part, we consider the motion of a rigid body, contains a spherical cavity of radius \(a\) filled with a viscous incompressible fluid with density \(\rho\), relative to the center of principal inertia's axes. Let \(Oxyz\) is a fixed coordinate system with an origin \(O\), \(Ox_{1} y_{1} z_{1}\) is a mobile coordinate one (connected rigidly with the body) coincides with the inertia's center of the system, \(\underline{\omega }\) is the angular velocity vector in which \(p,q,r\) denote their projections on the principal axes of the body,\(I \equiv (I_{1} ,I_{2} ,I_{3} )\) is the inertia's principal moments tensor and \(P\) refers to a constant tensor for the case of the spherical cavity, see Fig. 1.

Fig. 1
figure 1

The dynamical model

Full size image

The components of \(P\) are reefed with \(P_{ij} = P_{0} \delta_{ij} ;\,\,\,P_{0} > 0\), in which \(\delta_{ij}\) is a Kronecker delta symbol and \(P_{0} = {{8\,\pi \,a^{7} } \mathord{\left/ {\vphantom {{8\,\pi \,a^{7} } {525}}} \right. \kern-\nulldelimiterspace} {525}}\) for the case of a spherical cavity. It is considered that the body rotates in the presence of a gyrostatic moment vector \(\underline{\ell } \equiv (\ell_{1} ,\ell_{2} ,\ell_{3} )\) in which the first two projections equal null while the third one \(\ell_{3}\) goes away from zero. Therefore, Euler's dynamic equations take the form [46, 47]

$$I\underline{{\dot{\omega }}} + \underline{\omega } \times (I\underline{\omega } + \underline{\ell } ) = \underline{M} ,$$
(1)

where dot denotes the derivative with respect to time \(t\), \(M\) represents the moment of all external forces affecting on the body due to the viscosity of the fluid in the cavity and it is defined as [48]

$$\underline{M} = \frac{\rho }{\nu }(P\underline{b} + \underline{\omega } \times P\underline{d} ).$$
(2)

Here,

$$\underline{d} = - \frac{{\underline{\omega } \times I\underline{\omega } }}{I},\,\,\,\,\,\,\,\underline{b} = \frac{1}{I}(J\underline{\omega } \times \underline{d} + I\underline{d} \times \underline{\omega } ),$$
(3)

and \(\nu\) is the kinematic viscosity.

Substituting (2) and (3) into (1) to get the equations of motion (EOM) in the form

$$\begin{gathered} I_{1} \dot{p} + [(\,I_{3} - I_{2} {\kern 1pt} )r + \ell_{3} {\kern 1pt} {\kern 1pt} ]q{\kern 1pt} = \frac{{\rho \,P_{0} }}{{\nu \,I_{1} I_{2} {\kern 1pt} I_{3} }}p[I_{3} (I_{1} - I_{3} )(I_{1} + I_{3} - I_{2} {\kern 1pt} )r^{2} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + I_{2} {\kern 1pt} (I_{1} - I_{2} {\kern 1pt} )(I_{1} + I_{2} {\kern 1pt} - I_{3} )q^{2} ], \hfill \\ I_{2} {\kern 1pt} \dot{q} + [(I_{1} {\kern 1pt} - I_{3} \,){\kern 1pt} {\kern 1pt} r - \ell_{3} ]p{\kern 1pt} \, = \frac{{\rho \,P_{0} }}{{\nu \,I_{1} I_{2} {\kern 1pt} I_{3} }}q[I_{1} (I_{2} {\kern 1pt} - I_{1} )(I_{2} {\kern 1pt} + I_{1} - I_{3} )P^{2} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + I_{3} (I_{2} {\kern 1pt} - I_{3} )(I_{2} {\kern 1pt} + I_{3} - I_{1} )r^{2} ], \hfill \\ I_{3} {\kern 1pt} {\kern 1pt} \dot{r} + (\,I_{2} {\kern 1pt} - I_{1} {\kern 1pt} \,){\kern 1pt} {\kern 1pt} p{\kern 1pt} q = \frac{{\rho \,P_{0} }}{{\nu I_{1} I_{2} {\kern 1pt} I_{3} }}r[I_{2} {\kern 1pt} (I_{3} - I_{2} {\kern 1pt} )(I_{3} + I_{2} {\kern 1pt} - I_{1} )q^{2} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + I_{1} (I_{3} - I_{1} )(I_{3} + I_{1} - I_{2} {\kern 1pt} )p^{2} ]. \hfill \\ \end{gathered}$$
(4)

Now, we investigate the case when the values of the principal moments of inertia that are close to each other i.e.,

$$I_{1} = J_{0} + \varepsilon \,I^{\prime}_{1} ,\,\,\,\,\,\,\,\,\,I_{2} = J_{0} + \varepsilon \;I^{\prime}_{2} ,\,\,\,\,\,\,\,\,\,I_{3} = J_{0} ,$$
(5)

where \(0 < \varepsilon < < 1\) represents a small parameter.

In addition, we assume that

$$J_{ * } \approx J_{0} ,\,\,\,\,\,\,\,\,\,\,\,\,\ell_{3} = \varepsilon \,\ell_{3}^{ * } ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| {I_{1} - I_{2} } \right| = O(\varepsilon^{2} J_{ * } ),\,\,\,\,\,\,\,\,\,\,\,\left| {I^{\prime}_{1} - I^{\prime}_{2} } \right| = O(\varepsilon J_{ * } ).$$
(6)

According to (5) and (6), we can write

$$I_{1} - I_{2} = \varepsilon (I^{\prime}_{1} - I^{\prime}_{2} ) = \varepsilon^{2} J_{ * } ,\,\,\,\,\,\,\,\,\,\,I_{1} - I_{3} = \varepsilon \,I^{\prime}_{1} ,\,\,\,\,\,\,\,\,\,I_{2} - I_{3} = \varepsilon \,I^{\prime}_{2} .$$
(7)

Taking into account (5)–(7), the EOM according to the slow time parameter \(\tau = \varepsilon \;t\) can be rewritten in the form

$$\begin{gathered} \frac{dp}{{d\tau }} = \frac{{(I^{\prime}_{2} \,r - \ell_{3}^{ * } )}}{{J_{0} }}\left( {1 - \varepsilon \frac{{I^{\prime}_{1} }}{{J_{0} }}} \right)q + \varepsilon f_{p} ,{\kern 1pt} {\kern 1pt} \hfill \\ \frac{dq}{{d\tau }} = \frac{{(I^{\prime}_{1} \,r - \ell_{3}^{ * } )}}{{J_{0} }}\left( {\varepsilon \frac{{I^{\prime}_{2} }}{{J_{0} }} - 1} \right)p + \varepsilon f_{q} , \hfill \\ \frac{dr}{{d\tau }} = \varepsilon \frac{{J_{*} }}{{J_{0} }}pq + \varepsilon f_{r} , \hfill \\ \end{gathered}$$
(8)

besides the initial conditions

$$p(0) = p_{0} ,\,\,\,\,q(0) = q_{0} ,\,\,\,\,r(0) = r_{0} .$$
(9)

It clear that the previous system (8) consisting of three first-order nonlinear differential equations with respect to the slow time parameter \(\tau\). An inspection of the third one reveals that \(r\) is a slow variable due to the small parameter \(\varepsilon\) and the frequency of that system depending on \(r\). Therefore, the perturbations \(\varepsilon \,f_{p} ,\varepsilon \,f_{q}\) and \(\varepsilon \,f_{r}\) take the form

$$\begin{gathered} \varepsilon \,f_{p} = \frac{{\rho P_{0} }}{{\nu J_{0}^{3} }}p\{ q^{2} (I^{\prime}_{1} - I^{\prime}_{2} )[J_{0} + \varepsilon (I^{\prime}_{1} + 2I^{\prime}_{2} )] + r^{2} A^{\prime}[J_{0} + \varepsilon (I^{\prime}_{1} - I^{\prime}_{2} )]\} , \hfill \\ \varepsilon \,f_{q} = \frac{{\rho P_{0} }}{{\nu J_{0}^{3} }}q\{ r^{2} I^{\prime}_{2} [J_{0} + \varepsilon (I^{\prime}_{2} - I^{\prime}_{1} )] + p^{2} (I^{\prime}_{2} - I^{\prime}_{1} )[J_{0} + \varepsilon (2I^{\prime}_{1} + I^{\prime}_{2} )]\} , \hfill \\ \varepsilon \,f_{r} = \frac{{\rho P_{0} }}{{\nu J_{0}^{3} }}r\{ p^{2} I^{\prime}_{1} \,[ - J_{0} + \varepsilon (I^{\prime}_{2} - 2I^{\prime}_{1} )] + q^{2} I^{\prime}_{2} [ - J_{0} + \varepsilon (I^{\prime}_{1} - 2I^{\prime}_{2} )]\} . \hfill \\ \end{gathered}$$
(10)

It is worthwhile to mention that, the moment of friction forces due to the existence of the viscous fluid inside the cavity is very minimal.

Methodology of the Research

Now, we are going to obtain the solution of system (8) for \(\varepsilon = 0\) when \(\,{1 \mathord{\left/ {\vphantom {1 \nu }} \right. \kern-\nulldelimiterspace} \nu } = 0\) in accordance with the used approach in [22]. Therefore, system (8) becomes

$$\begin{gathered} \frac{dp}{{d\tau }} = \frac{{(I^{\prime}_{2} \,r - \ell_{3}^{ * } )}}{{J_{0} }}q,{\kern 1pt} \hfill \\ \frac{dq}{{d\tau }} = - \frac{{(I^{\prime}_{1} \,r - \ell_{3}^{ * } )}}{{J_{0} }}p,{\kern 1pt} \hfill \\ \frac{dr}{{d\tau }} = 0. \hfill \\ \end{gathered}$$
(11)

Integration of the third equation in (11) yields \(r = r_{0}\), then substituting into the first two equations, differentiating the first equation with respect to \(\tau\) and using the second one to obtain

$$\frac{{d^{2} p}}{{d\tau^{2} }} + \varpi^{2} p = 0;{\kern 1pt} \,\,\,\,\,\,\,\,\varpi^{2} = {\kern 1pt} \frac{1}{{J_{0}^{2} }}(I^{\prime}_{2} \,r_{0} - \ell_{3}^{ * } )(I^{\prime}_{1} \,r_{0} - \ell_{3}^{ * } ),$$
(12)

where

$$(I^{\prime}_{2} \,r_{0} - \ell_{3}^{ * } )(I^{\prime}_{1} \,r_{0} - \ell_{3}^{ * } ) > 0.$$

The previous equation represents a simple harmonic equation that can be solved using Laplace transformation with the above initial conditions (9) to obtain

$$p(\tau ) = p{}_{0}\cos (\varpi \tau ) + \frac{{\dot{p}_{0} }}{\varpi }\sin (\varpi \tau );\,\,\,\,\,\,\,\,\,\,\,\left( { \cdot = \frac{d}{d\tau }} \right)$$
(13)

which can be replicated in the equivalent form below

$$p = h\sin \phi ,\,\,\,\,\,\,\,\,\,\,\,q = h\sqrt {\frac{{(I^{\prime}_{1} \,r - \ell_{3}^{ * } )}}{{(I^{\prime}_{2} \,r - \ell_{3}^{ * } )}}} \cos \phi ,\,\,\,\,\,\,\,\,\,\,\,r = r_{0} ,$$
(14)

where \(h = \sqrt {p_{0}^{2} + ({{\dot{p}_{0} } \mathord{\left/ {\vphantom {{\dot{p}_{0} } \varpi }} \right. \kern-\nulldelimiterspace} \varpi })^{2} }\) and \(\phi\) are the amplitude and the phase of (12).

Differentiating the first equation of (14) with respect to \(\tau\) and then using the first equation of system (8) to get

$$\begin{gathered} \dot{h}\sin \phi + h\left[ {\dot{\phi } - \frac{{\sqrt {(I^{\prime}_{1} \,r - \ell_{3}^{ * } )(I^{\prime}_{2} \,r - \ell_{3}^{ * } )} }}{{J_{0} }}} \right]\cos \phi = \frac{{\rho p_{0} h\sin \phi }}{{\nu J_{0}^{3} }}\{ I^{\prime}_{1} \,[J_{0} + \varepsilon (I^{\prime}_{1} - I^{\prime}_{2} )]r^{2} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{{h^{2} (I^{\prime}_{1} - I^{\prime}_{2} )(I^{\prime}_{1} r - \ell_{3}^{ * } )}}{{(I^{\prime}_{2} \,r - \ell_{3}^{ * } )}}[J_{0} + \varepsilon (I^{\prime}_{1} + 2I^{\prime}_{2} )]\cos^{2} \phi \} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \varepsilon \frac{{I^{\prime}_{1} \,h\,}}{{J_{0}^{2} }}\sqrt {(I^{\prime}_{1} \,r - \ell_{3}^{ * } )(I^{\prime}_{2} \,r - \ell_{3}^{ * } )} \cos \phi . \hfill \\ \end{gathered}$$
(15)

Making use of the third equation in (8) and (14) to obtain

$$\begin{gathered} \dot{r} = \frac{{(I^{\prime}_{1} - I^{\prime}_{2} )}}{{J_{0} }}h^{2} \sqrt {\frac{{(I^{\prime}_{1} \,r - \ell_{3}^{ * } )}}{{(I^{\prime}_{2} \,r - \ell_{3}^{ * } )}}} \sin \phi \cos \phi \hfill \\ \,\,\, - \frac{{h^{2} r\rho p_{0} }}{{\nu J_{0}^{3} }}\{ {\kern 1pt} I^{\prime}_{2} \,[J_{0} + \varepsilon (2I^{\prime}_{2} - I^{\prime}_{1} )]\frac{{(I^{\prime}_{1} \,r - \ell_{3}^{ * } )}}{{(I^{\prime}_{2} \,r - \ell_{3}^{ * } )}}\cos^{2} \phi \hfill \\ \,\,\, + I^{\prime}_{1} \,[J_{0} + \varepsilon (2I^{\prime}_{1} - I^{\prime}_{2} )]\sin^{2} \phi \} . \hfill \\ \end{gathered}$$
(16)

Now, we are going to solve Eqs. (15) and (16) with respect to \(\dot{h}\) and \(\dot{\phi }\). Therefore, equating the coefficients of \(\sin \phi\) and \(\cos \phi\) in both sides of (15), and then averaging the resulted equation to obtain [49]

$$\begin{gathered} \dot{h} = \eta h(\beta r^{2} + \alpha h^{2} ), \hfill \\ \dot{\phi } = {\kern 1pt} {\kern 1pt} \varpi (1 - \varepsilon \frac{{{\kern 1pt} I^{\prime}_{1} }}{{J_{0} }}), \hfill \\ \end{gathered}$$
(17)

where

$$\begin{gathered} \eta = \frac{{\rho p_{0} }}{{\nu J_{0}^{3} }},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\alpha = \frac{{(I^{\prime}_{1} - I^{\prime}_{2} )(I^{\prime}_{1} \,r - \ell_{3}^{ * } )}}{{2(I^{\prime}_{2} \,r - \ell_{3}^{ * } )}}[J_{0} + \varepsilon (I^{\prime}_{1} + 2I^{\prime}_{2} )], \hfill \\ \beta = I^{\prime}_{1} \,[J_{0} + \varepsilon (I^{\prime}_{1} - I^{\prime}_{2} )]. \hfill \\ \end{gathered}$$
(18)

Averaging of Eq. (16) gives

$$\dot{r} = \eta h^{2} r\gamma ,$$
(19)

where

$$\gamma = - \frac{1}{2}\left\{ {\frac{{I^{\prime}_{2} (I^{\prime}_{1} \,r - \ell_{3}^{ * } )}}{{(I^{\prime}_{2} \,r - \ell_{3}^{ * } )}}\left[ {J_{0} + \varepsilon \left( {2I^{\prime}_{2} - I^{\prime}_{1} )] + I^{\prime}_{1} \,\,[J_{0} + \varepsilon (2I^{\prime}_{1} - I^{\prime}_{2} } \right)} \right]} \right\}.$$
(20)

Now, we are going to transform the variables \(h\) and \(r\) to other ones \(x\) and \(y\) according to the following substitutions

$$x = h^{2} ,\,\,\,\,\,\,y = r^{2} .$$
(21)

Here, \(x\) and \(y\) are considered slow variables. According to (17), (19), and (21) besides its first derivative, we obtain

$$\begin{gathered} \dot{x} = 2\,\eta \,x\,(\beta \,y + \alpha \,x), \hfill \\ \dot{y} = 2\,\eta \,\gamma \,x\,y. \hfill \\ \end{gathered}$$
(22)

It is worthy to mention that, the procedure for solving system (22) is close to that described in the previous article [22]. Based on the previous two equations in (22), one writes

$$\frac{dx}{{dy}} = \frac{\alpha }{\gamma }\left( \frac{x}{y} \right) + \frac{\beta \,}{{\gamma \,}}.$$
(23)

Inserting new parameters \(z,\tilde{\alpha }\) and \(\tilde{\beta }\) according to the following forms

$$z = \frac{x}{y},\,\,\,\,\,\,\,\,\,\,\,\,\tilde{\alpha } = \frac{\alpha }{\gamma },\,\,\,\,\,\,\,\,\,\,\,\,\tilde{\beta } = \frac{\beta }{\gamma },$$
(24)

into (23) to obtain

$$y\frac{dz}{{dy}} = (\tilde{\alpha } - 1)z + \tilde{\beta }.$$
(25)

Let us consider the transformation \(\theta = \ln \,y\), therefore \(\frac{dz}{{d\theta }} = y\frac{dz}{{dy}}\) and according to (25), one obtains the following nonhomogeneous linear equation

$$\frac{dz}{{d\theta }} = (\tilde{\alpha } - 1)z + \tilde{\beta }.$$
(26)

The general solution of the previous equation has the form

$$z = \frac{{\tilde{\beta }}}{{(1 - \tilde{\alpha })}} + C_{1} \,e^{{(\tilde{\alpha } - 1)\theta }} ,$$
(27)

where \(C_{1}\) is the integration constant.

According to the above transformations, we can rewrite Eq. (27) in terms of the slow variables \(x\) and \(y\) as

$$x = \frac{{\tilde{\beta }}}{{(1 - \tilde{\alpha })}}y + C_{1} \,y^{{\tilde{\alpha }}} .$$
(28)

Substituting (28) into the second equation of (22), we get

$$\dot{y} = \eta \,\gamma \,y^{2} \left[ {\frac{{\tilde{\beta }}}{{(1 - \tilde{\alpha })}} + C_{1} \,y^{{(\tilde{\alpha } - 1)}} } \right],$$
(29)

which can be integrated using separation of variables [22].

Discussion of the Results

This section outlines on the graphical representations of the system of Eqs. (14) for the solutions \(p\) and \(q\), for the integration of the second equation in (17), and the equations of system (22).

Figures 2 and 3 describe the time history of the first two components of the angular velocity in which they are calculated when \(I_{1} = 15\,kg.m^{2} ,\,\,I_{2} = 12\,kg.m^{2} ,\,\,J_{0} = 10\,kg.m^{2} ,\,\,\varepsilon = 0.01,\,\,r_{0} = 0.01\,rad.s^{ - 1}\) and \(p_{0} = 0.01\,rad.s^{ - 1}\). An inspection of these figures shows that we have obtained progressive waves when \(\ell_{3}\) has the values \((0.3,\,0.4,\,0.5)\,kg.m^{2} .s^{ - 1}\). The amplitudes of the waves plotted in these figures decrease with the increasing of \(\ell_{3}\), as predicted from Eq. (14). Moreover, the wavelength of the waves increases when \(\ell_{3}\) growing up and the motion is stable. The phase plane plots of the angular velocity components \(p\) and \(q\) are presented in the parts of Fig. 3 to reveal the stability of the behavior of these components at \(\ell_{3} = 0.3 \, kg.m^{2} .s^{ - 1}\) (Fig. 4).

Fig. 2
figure 2

The time history of the angular velocity component \(p\) when \(\ell_{3} = { (0}{\text{.3, 0}}{.4, 0}{\text{.5)}}\)

Full size image
Fig. 3
figure 3

The time history of the angular velocity component \(q\) when \(\ell_{3} = { (0}{\text{.3, 0}}{.4, 0}{\text{.5)}}\)

Full size image
Fig. 4
figure 4

The phase plane of the components \(p\) and \(q\) at \(\ell_{3} = 0.3\)

Full size image

The presented curves in Figs. 5 and 6 describe the behavior of \(\phi\) when \(\ell_{3}\) and \(r_{0}\) have different values, respectively. These figures are calculated according to the general data \(I_{1} = 15\, \, kg.m^{2} ,I_{2} = 12 \, \,kg.m^{2} ,J_{0} = 10\, \, kg.m^{2} ,\varepsilon = 0.01\) and \(p_{0} = 0.01\, \, rad.s^{ - 1}\) in which they are plotted when \(r_{0} = 0.01 \, \,rad.s^{ - 1} ,\, \, \ell_{3} = (0.3,\,\,0.4,\,\,0.5) \, kg.m^{2} .s^{ - 1}\) and \(\ell_{3} = 0.5 \, kg.m^{2} .s^{ - 1} ,\) \(r_{0} = (0.01, \, 0.02, \, 0.03) \, rad.s^{ - 1}\), respectively.

Fig. 5
figure 5

The variation of \(\phi\) via time \(t\) when \(\ell_{3} = (0.3,\,\,0.4,\,\,0.5)\) and \(r_{0} = 0.01\)

Full size image
Fig. 6
figure 6

The time variation of \(\phi\) at \(r_{0} = (0.01,\,\,0.02,\,\,0.03)\) and \(\ell_{3} = 0.5\)

Full size image

It is worthwhile to mention that \(\phi\) increases gradually when time goes on and we have different straight lines corresponding to the different data of \(\ell_{3}\) and \(r_{0}\) as expected from the second equation in (17).

Figures 7, 8, and 9, 10 reveal the variation of \(x\) and \(y\) via time \(t\). These figures are generally calculated at the values \(I_{1} = 1 \, kg.m^{2} ,I_{2} = 0.2 \, kg.m^{2} ,\)\(J_{0} = 0.1 \, kg.m^{2} ,\nu = 0.001 \, m^{2} .s^{ - 1} ,\)\(\varepsilon = 0.01,\)\(r_{0} = 0.01 \, rad.s^{ - 1} ,\)\(\ell_{3} = 0.5 \, kg.m^{2} .s^{ - 1} ,\beta = 81 \, kg.m^{2} ,\) and especially when \(\alpha = { 47}{\text{.2305}}\,,\) \(\eta = (2600, \, 2800, \, 3000)\) and \(\alpha = 47.2305,\)\(\eta = (28.88, \, 31.11, \, 33.33)\) for Figs. 7, 8, and 9, 10, respectively. In additions Figs. 9 and 10 are calculated also at \(\rho = (0.2,0.3,0.4) \, kg.m^{ - 3}\).

Fig. 7
figure 7

The time history of \(x\) at \(p_{0} = (0.013,0.014,0.015)\)

Full size image
Fig. 8
figure 8

The time history of \(y\) when \(p_{0} = (0.013,0.014,0.015)\)

Full size image
Fig. 9
figure 9

The change of \(x\) with time \(t\) at \(\rho = (0.2,0.3,0.4)\)

Full size image
Fig. 10
figure 10

The variation of \(y\) against time \(t\) at \(\rho = (0.2,0.3,0.4)\)

Full size image

To visualize the motion according to the initial value \(p_{0}\) and the density \(\rho\) of the fluid, Figs. 7, 8, and 9, 10 are represented graphically. A closer look at these graphs reveals that the different values of \(p_{0}\) and \(\rho\) have a good impact on the motion of the body. The curves included in these figures obey carefully to the equations of (22) when \(\ell_{3}\) has a constant value. It should be noted that Figs. 7, 8, 9, 10 can be considered as a generalization of those which were obtained in [22], since when the value of the third compound is absent, and taking into account the same values for the different parameters of the body in [22], one can get the same results directly. Therefore, parts of Fig. 11 have been drawn as special case when \(\ell_{3} = 0\) and \(p_{0} = 0.013\) besides the other data mentioned above to represent the time histories of \(x\) and \(y\).

Fig. 11
figure 11

The variation of \(x(t)\) and \(y(t)\) at \(\ell_{3} = 0\) and \(p_{0} = 0.013\)

Full size image

Conclusion

The motion of a rigid body contains a viscous incompressible fluid in a cavity; with a very minimal Reynolds number about its center of mass has been examined. The motion of the body is considered under the influence of a gyrostatic moment vector and a viscous fluid force. The governing system of motion is derived and the averaging of the Cauchy problem of this system is analyzed. Some transformations are used to reduce the required parameters to their suitable form. Therefore, the analytic solutions have been achieved and drawn in some plots to show the time behavior of the solution at any instant. Moreover, the phase plane diagrams have been plotted to reveal the stability of these solutions. The acquired new results are regarded as a generalization of those obtained in [21] and [22] for the case of absence gyrostatic moment, in which the attained results and the presented figures support this this statement. The significant impact of the various parameters of the body like the axial angular velocity, density of the fluid, inertia's principal moments, and gyrostatic moment is evident from the presented graphs. The importance of the gained results is due to its applications in life such as in submarines, ships, and for different applications that used the gyroscopic theory.