1 Introduction

In the past twenty years many candidates of exotic hadrons were observed in particle experiments, which can not be well explained in the traditional quark model [1]. Most of them still have the “traditional” quantum numbers that the traditional \(\bar{q} q\) mesons and qqq baryons can also reach, making them not so easy to be clearly identified as exotic hadrons. However, there are some “exotic” quantum numbers that the traditional hadrons can not reach, such as the spin-parity quantum numbers \(J^{PC} = 0^{--}/0^{+-}/1^{-+}/2^{+-}/3^{-+}/4^{+-}/\cdots \). The hadrons with such exotic quantum numbers are of particular interests, since they can not be explained as traditional hadrons any more. Their possible interpretations are compact multiquark states [2,3,4,5], hadronic molecules [6,7,8], glueballs [9,10,11,12,13,14,15,16], and hybrid states [17,18,19,20,21,22,23,24,25,26], etc.

Among these exotic quantum numbers, the states of \(J^{PC} = 1^{-+}\) have been extensively studied in the literature [2, 3, 5,6,7, 17,18,19,20,21,22,23,24,25,26], since they are predicted to be the lightest hybrid states [27]. Up to now there have been four structures observed in experiments with \(J^{PC} = 1^{-+}\), including three isovector states \(\pi _1(1400)\) [28], \(\pi _1(1600)\) [29], and \(\pi _1(2015)\) [30] as well as one isoscalar state \(\eta _1(1855)\) [31]. Besides, the states of \(J^{PC} = 0^{--}/0^{+-}/2^{+-}/3^{-+}\) have also been studied to some extent [4, 8,9,10,11,12,13,14,15,16]. These theoretical and experimental studies have significantly improved our understanding on the non-perturbative behaviors of the strong interaction in the low energy region. However, there has not been any investigation on the exotic quantum number \(J^{PC} = 4^{+-}\) yet.

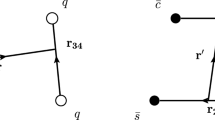
In this paper we shall investigate for the first time the exotic quantum number \(J^{PC}=4^{+-}\), and study the fully-strange tetraquark states with such an exotic quantum number. We shall work within the diquark–antidiquark picture, and systematically construct all the diquark–antidiquark currents of \(J^{PC} = 4^{+-}\), as depicted in Fig. 1a. We shall apply the method of QCD sum rules to study these currents as a whole, and extract the mass of the lowest-lying state to be \(2.85^{+0.19}_{-0.22}\) GeV.

Fig. 1
figure 1

Two configurations for the fully-strange tetraquark states: a the diquark–antidiquark system with the internal orbital angular momenta \(l_\lambda /l_\rho /l_{\rho ^\prime }\) and b the meson–meson system with \(l_\lambda ^\prime /l_\rho ^\prime /l_{\rho ^\prime }^\prime \)

Full size image

Besides, we shall also systematically construct all the meson–meson currents of \(J^{PC}=4^{+-}\), as depicted in Fig. 1b. We shall relate these currents and the diquark–antidiquark currents through the Fierz rearrangement. The obtained Fierz identity suggests that the lowest-lying state dominantly decays into the P-wave \(\phi (1020) f_2^\prime (1525)\) channel. Accordingly, we propose to search for it in the \(X \rightarrow \phi (1020) f_2^\prime (1525) \rightarrow \phi K \bar{K}\) decay process. With a large amount of \(J/\psi \) sample, the BESIII collaboration are intensively studying the physics happening around here. Such experiments can also be performed by Belle-II, COMPASS, GlueX, and PANDA, etc. Accordingly, this fully-strange tetraquark state of \(J^{PC}=4^{+-}\) is a purely exotic hadron to be potentially observed in future particle experiments.

This paper is organized as follows. In Sect. 2 we systematically construct the local fully-strange tetraquark currents with the exotic quantum number \(J^{PC} = 4^{+-}\). We use them to perform QCD sum rule analyses in Sect. 3, where we calculate both their diagonal and off-diagonal two-point correlation functions. Based on the obtained results, we use the three single currents to perform numerical analyses in Sect. 4, while their mixing currents are investigated in Sect. 5. Section 6 is a summary.

2 Fully-strange tetraquark currents

As the first step, we construct the local fully-strange tetraquark currents with the exotic quantum number \(J^{PC} = 4^{+-}\). This quantum number can not be reached by simply using one quark and one antiquark, and moreover, we need two quarks and two antiquarks together with at least two derivatives to reach such a quantum number.

As depicted in Fig. 1, there are two possible configurations, the diquark–antidiquark configuration and the meson–meson configuration. When investigating the former configuration, the two covalent derivative operators \(D_\alpha (\equiv \partial _\alpha + i g_s A_\alpha )\) and \(D_\beta \) can be either inside the diquark/antidiquark field or between them:

$$\begin{aligned} \eta= & {} \big [s_a^T C \varGamma _1 {\overset{\leftrightarrow }{D}}_\alpha {\overset{\leftrightarrow }{D}}_\beta s_b \big ] (\bar{s}_c \varGamma _2 C \bar{s}_d^T) \pm h.c. \, , \nonumber \\ \eta ^{\prime }= & {} \big [s_a^T C \varGamma _3 {\overset{\leftrightarrow }{D}}_\alpha s_b \big ] \big [\bar{s}_c \varGamma _4 C {\overset{\leftrightarrow }{D}}_\beta \bar{s}_d^T \big ] \pm h.c. \, , \nonumber \\ \eta ^{\prime \prime }= & {} \big [\big [s_a^T C \varGamma _5 {\overset{\leftrightarrow }{D}}_\alpha s_b \big ] {\overset{\leftrightarrow }{D}}_\beta (\bar{s}_c \varGamma _6 C \bar{s}_d^T)\big ] \pm h.c. \, , \nonumber \\ \eta ^{\prime \prime \prime }= & {} \big [(s_a^T C \varGamma _7 s_b) {\overset{\leftrightarrow }{D}}_\alpha {\overset{\leftrightarrow }{D}}_\beta (\bar{s}_c \varGamma _8 C \bar{s}_d^T)\big ] \pm h.c. \, , \end{aligned}$$
(1)

where \(\big [ A {\overset{\leftrightarrow }{D}}_\alpha B \big ] \equiv A [D_\alpha B] - [D_\alpha A] B\), \(a \cdots d\) are color indices, and \(\varGamma _{1\cdots 8}\) are Dirac matrices. The internal orbital angular momenta contained in these currents are

$$\begin{aligned} \eta&:&l_\lambda = 0 , \, l_\rho = 2/0 , \, l_{\rho ^\prime } = 0/2 , \nonumber \\ \eta ^{\prime }&:&l_\lambda = 0 , \, l_\rho = 1 , \, l_{\rho ^\prime } = 1 , \nonumber \\ \eta ^{\prime \prime }&:&l_\lambda = 1 , \, l_\rho = 1/0 , \, l_{\rho ^\prime } = 0/1 , \nonumber \\ \eta ^{\prime \prime \prime }&:&l_\lambda = 2 , \, l_\rho = 0 , \, l_{\rho ^\prime } = 0 . \end{aligned}$$
(2)

After carefully examining all the possible combinations, we find that only the \(\eta \) currents can reach \(J^{PC} = 4^{+-}\), as depicted in Fig. 2, while the \(\eta ^{\prime }/\eta ^{\prime \prime }/\eta ^{\prime \prime \prime }\) currents can not. Altogether, we can construct three independent diquark–antidiquark currents of \(J^{PC} = 4^{+-}\):

$$\begin{aligned} \eta ^{1}_{\alpha _1\alpha _2\alpha _3\alpha _4}= & {} \epsilon ^{abe} \epsilon ^{cde} \nonumber \\&\times \mathcal {S} \Big \{ \big [s_a^T C \gamma _{\alpha _1} {\overset{\leftrightarrow }{D}}_{\alpha _3}{\overset{\leftrightarrow }{D}}_{\alpha _4} s_b \big ] (\bar{s}_c \gamma _{\alpha _2} C \bar{s}_d^T) \nonumber \\&~ - (s_a^T C \gamma _{\alpha _1} s_b ) \big [\bar{s}_c \gamma _{\alpha _2} C {\overset{\leftrightarrow }{D}}_{\alpha _3} {\overset{\leftrightarrow }{D}}_{\alpha _4} \bar{s}_d^T\big ] \Big \}, \nonumber \\ \eta ^{2}_{\alpha _1\alpha _2\alpha _3\alpha _4}= & {} (\delta ^{ac} \delta ^{bd} + \delta ^{ad} \delta ^{bc} ) \nonumber \\&\times \mathcal {S} \Big \{ \big [s_a^T C \gamma _{\alpha _1} \gamma _5 {\overset{\leftrightarrow }{D}}_{\alpha _3}{\overset{\leftrightarrow }{D}}_{\alpha _4} s_b \big ] (\bar{s}_c \gamma _{\alpha _2} \gamma _5 C \bar{s}_d^T) \nonumber \\&~ - (s_a^T C \gamma _{\alpha _1} \gamma _5 s_b ) \big [\bar{s}_c \gamma _{\alpha _2} \gamma _5 C {\overset{\leftrightarrow }{D}}_{\alpha _3} {\overset{\leftrightarrow }{D}}_{\alpha _4} \bar{s}_d^T\big ] \Big \}, \nonumber \\ \eta ^{3}_{\alpha _1\alpha _2\alpha _3\alpha _4}= & {} \epsilon ^{abe} \epsilon ^{cde} g^{\mu \nu } \nonumber \\&\times \mathcal {S} \Big \{ \big [s_a^T C \sigma _{\alpha _1\mu } {\overset{\leftrightarrow }{D}}_{\alpha _3}{\overset{\leftrightarrow }{D}}_{\alpha _4} s_b \big ] (\bar{s}_c \sigma _{\alpha _2\nu } C \bar{s}_d^T) \nonumber \\&~ - (s_a^T C \sigma _{\alpha _1\mu } s_b ) \big [\bar{s}_c \sigma _{\alpha _2\nu } C {\overset{\leftrightarrow }{D}}_{\alpha _3} {\overset{\leftrightarrow }{D}}_{\alpha _4} \bar{s}_d^T\big ] \Big \}. \end{aligned}$$
(3)

The symbol \(\mathcal {S}\) denotes symmetrization and subtracting the trace terms in the set \(\{\alpha _1 \cdots \alpha _J\}\). Among these currents, \(\eta ^{1}_{\cdots }\) and \(\eta ^{3}_{\cdots }\) have the antisymmetric color structure \([ss]_{{\bar{3}}_C} [\bar{s} \bar{s}]_{{3}_C}\), and \(\eta ^{2}_{\cdots }\) has the symmetric color structure \([ss]_{{6}_C}[\bar{s} \bar{s}]_{ {\bar{6}}_C}\).

After similarly investigating the meson–meson configuration, we can also construct three independent meson–meson currents of \(J^{PC} = 4^{+-}\):

$$\begin{aligned} \xi ^{1}_{\alpha _1\alpha _2\alpha _3\alpha _4}= & {} \mathcal {S} \Big \{ \big [\bar{s}_a \gamma _{\alpha _1} {\overset{\leftrightarrow }{D}}_{\alpha _3} s_a \big ] {\overset{\leftrightarrow }{D}}_{\alpha _4} (\bar{s}_b \gamma _{\alpha _2} s_b) \Big \} , \nonumber \\ \xi ^{2}_{\alpha _1\alpha _2\alpha _3\alpha _4}= & {} \mathcal {S} \Big \{ \big [\bar{s}_a \gamma _{\alpha _1} \gamma _5 {\overset{\leftrightarrow }{D}}_{\alpha _3} s_a \big ] {\overset{\leftrightarrow }{D}}_{\alpha _4} (\bar{s}_b \gamma _{\alpha _2} \gamma _5 s_b) \Big \} , \nonumber \\ \xi ^{3}_{\alpha _1\alpha _2\alpha _3\alpha _4}= & {} g^{\mu \nu } \mathcal {S} \Big \{ \big [\bar{s}_a \sigma _{\alpha _1\mu } {\overset{\leftrightarrow }{D}}_{\alpha _3} s_a \big ] {\overset{\leftrightarrow }{D}}_{\alpha _4} (\bar{s}_b \sigma _{\alpha _2\nu } s_b) \Big \} . \end{aligned}$$
(4)

As depicted in Fig. 2, the internal orbital angular momenta contained in these currents are

$$\begin{aligned} \xi&:&l_\lambda ^\prime = 1 , \, l_\rho ^\prime = 1 , \, l_{\rho ^\prime }^\prime = 0 . \end{aligned}$$
(5)
Fig. 2
figure 2

Possible internal orbital angular momenta contained in the fully-strange tetraquark currents of \(J^{PC} = 4^{+-}\). The Fierz identity given in Eq. (6) indicates that the internal orbital angular momenta contained in the diquark–antidiquark system \(\{l_\lambda = 0\), \(l_\rho = 2/0\), \(l_{\rho ^\prime } = 0/2\}\) correspond to those contained in the meson–meson system \(\{l_\lambda ^\prime = 1\), \(l_\rho ^\prime = 1\), \(l_{\rho ^\prime }^\prime = 0\}\)

Full size image

After applying the Fierz rearrangement, we obtain

$$\begin{aligned} \left( \begin{array}{c} \eta ^{1}_{\cdots } \\ \eta ^{2}_{\cdots } \\ \eta ^{3}_{\cdots } \end{array}\right) = \left( \begin{array}{ccc} 2 &{} -2 &{} -2 \\ -2 &{} 2 &{} -2 \\ -4 &{} -4 &{} 0 \end{array}\right) \left( \begin{array}{c} \xi ^{1}_{\cdots } \\ \xi ^{2}_{\cdots } \\ \xi ^{3}_{\cdots } \end{array}\right) \, . \end{aligned}$$
(6)

This Fierz identity will be used to study the decay behaviors later.

3 QCD sum rule analysis

We apply the QCD sum rule method [32, 33] to study the fully-strange tetraquark currents \(\eta ^{1,2,3}_{\alpha _1\alpha _2\alpha _3\alpha _4}\) with the exotic quantum number \(J^{PC} = 4^{+-}\). This non-perturbative method has been successfully applied to study various conventional and exotic hadrons in the past 50 years [34].

We generally assume that the current \(\eta ^{i}_{\alpha _1\alpha _2\alpha _3\alpha _4}\) (\(i=1\cdots 3\)) couples to the fully-strange tetraquark states \(X_n\) (\(n=1 \cdots N\)) through

$$\begin{aligned} \langle 0| \eta ^i_{\alpha _1\alpha _2\alpha _3\alpha _4} | X_n \rangle = f_{in} \epsilon _{\alpha _1\alpha _2\alpha _3\alpha _4} \, , \end{aligned}$$
(7)

where \(f_{in}\) is the \(3 \times N\) matrix for the decay constants, and \(\epsilon _{\alpha _1\alpha _2\alpha _3\alpha _4}\) is the traceless and symmetric polarization tensor satisfying

$$\begin{aligned} \epsilon _{\alpha _1\alpha _2\alpha _3\alpha _4} \epsilon ^*_{\beta _1\beta _2\beta _3\beta _4} = \mathcal {S}^\prime [\tilde{g}_{\alpha _1 \beta _1} \tilde{g}_{\alpha _2 \beta _2} \tilde{g}_{\alpha _3 \beta _3} \tilde{g}_{\alpha _4 \beta _4}] \, , \end{aligned}$$
(8)

with \(\tilde{g}_{\mu \nu } = g_{\mu \nu } - q_\mu q_\nu / q^2\). The symbol \(\mathcal {S}^\prime \) denotes symmetrization and subtracting the trace terms in the sets \(\{\alpha _1\alpha _2\alpha _3\alpha _4\}\) and \(\{\beta _1\beta _2\beta _3\beta _4\}\).

Based on Eq. (7), we can investigate both the diagonal and off-diagonal correlation functions:

$$\begin{aligned}&\varPi ^{ij}_{\alpha _1\alpha _2\alpha _3\alpha _4;\beta _1\beta _2\beta _3\beta _4}(q^2) \nonumber \\&\quad \equiv i \int d^4x e^{iqx} \langle 0 | \mathbf{T}[ \eta ^i_{\alpha _1\alpha _2\alpha _3\alpha _4}(x) { \eta _{\beta _1\beta _2\beta _3\beta _4}^{j,\dagger } } (0)] | 0 \rangle \nonumber \\&\quad =\varPi _{ij}(q^2) \times \mathcal {S}^\prime [\tilde{g}_{\alpha _1 \beta _1} \tilde{g}_{\alpha _2 \beta _2} \tilde{g}_{\alpha _3 \beta _3} \tilde{g}_{\alpha _4 \beta _4}] \, . \end{aligned}$$
(9)

At the hadron level we express \(\varPi _{ij}(q^2)\) using the dispersion relation as

$$\begin{aligned} \varPi _{ij}(q^2) = \int ^\infty _{s_<}\frac{\rho ^\mathrm{phen}_{ij}(s)}{s-q^2-i\varepsilon }ds \, , \end{aligned}$$
(10)

with \(s_< = 16 m_s^2\) the physical threshold. We parameterize the spectral density \(\rho ^\mathrm{phen}_{ij}(s)\) for the states \(X_n\) together with a continuum contribution as

$$\begin{aligned}&\rho ^\mathrm{phen}_{ij}(s) \times \mathcal {S}^\prime [\cdots ] \nonumber \\\equiv & {} \sum _n \delta (s-M^2_n) \langle 0| \eta ^i_{\cdots } | n \rangle \langle n | {\eta ^{j\dagger }_{\cdots }} |0 \rangle + \cdots \nonumber \\= & {} \sum _n f_{in}f_{jn} \delta (s-M^2_n) \times \mathcal {S}^\prime [\cdots ] + \cdots \, , \end{aligned}$$
(11)

with \(M_n\) the mass of \(X_n\).

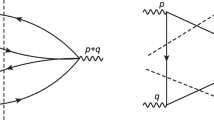
At the quark–gluon level we calculate \(\varPi _{ij}(q^2)\) using the method of operator product expansion (OPE), and extract the OPE spectral density \(\rho _{ij}(s) \equiv \rho ^\mathrm{OPE}_{ij}(s)\) [35]. In the calculations we take into account the Feynman diagrams depicted in Fig. 3. We consider the perturbative term, the strange quark mass \(m_s\), the quark condensate \(\langle \bar{s} s \rangle \), the quark–gluon mixed condensate \(\langle g_s \bar{s} \sigma G s \rangle \), the gluon condensate \(\langle g_s^2 GG \rangle \), and their combinations. We calculate all the diagrams proportional to \(g_s^{N=0}\) and \(g_s^{N=1}\), where we find the \(D=6\) term \(\langle \bar{s} s \rangle ^2\) and the \(D=8\) term \(\langle \bar{s} s \rangle \langle g_s \bar{s} \sigma G s \rangle \) to be important. We partly calculate the diagrams proportional to \(g_s^{N\ge 2}\), whose contributions are found to be small. Especially, we have not taken into account the radiative corrections in our QCD sum rule calculations.

Fig. 3
figure 3

Feynman diagrams for the fully-strange tetraquark currents of \(J^{PC} = 4^{+-}\). The covariant derivative operator \(D_\alpha = \partial _\alpha + i g_s A_\alpha \) contains two terms, and we depict the latter term using a green vertex

Full size image

Then we perform the Borel transformation at both the hadron and quark–gluon levels. After approximating the continuum using \(\rho _{ij}(s)\) above the threshold value \(s_0\), we obtain the sum rule equation

$$\begin{aligned} \varPi _{ij}(s_0, M_B^2)\equiv & {} \sum _n f_{in}f_{jn} e^{-M_n^2/M_B^2} \nonumber \\= & {} \int ^{s_0}_{s_<} e^{-s/M_B^2} \rho _{ij}(s) ds \, . \end{aligned}$$
(12)

We shall investigate it through two steps, the single-channel analysis and the multi-channel analysis, as follows.

4 Single-channel analysis

To perform the single-channel analysis, we neglect the off-diagonal correlation functions by setting \(\rho _{ij}(s)|_{i \ne j} = 0\) so that only \(\rho _{ii}(s) \ne 0\). This assumption means that the three currents \(\eta ^{1,2,3}_{\alpha _1\alpha _2\alpha _3\alpha _4}\) are “non-correlated”, and any two of them can not mainly couple to the same state X, otherwise,

$$\begin{aligned}&\rho _{ij}(s) \times \mathcal {S}^\prime [\cdots ] \nonumber \\\equiv & {} \sum _n \delta (s-M^2_n) \langle 0| \eta ^i_{\cdots } | n \rangle \langle n | {\eta ^{j\dagger }_{\cdots }} |0 \rangle + \cdots \nonumber \\\approx & {} \delta (s-M^2_X) \langle 0| \eta ^i_{\cdots } | X \rangle \langle X | {\eta ^{j\dagger }_{\cdots }} |0 \rangle + \cdots \nonumber \\\ne & {} 0 \, . \end{aligned}$$
(13)

Accordingly, we assume that there are three states \(X_{1,2,3}\) corresponding to the three currents \(\eta ^{1,2,3}_{\alpha _1\alpha _2\alpha _3\alpha _4}\) through

$$\begin{aligned} \langle 0| \eta ^i_{\alpha _1\alpha _2\alpha _3\alpha _4} | X_i \rangle = f_{ii} \epsilon _{\alpha _1\alpha _2\alpha _3\alpha _4} \, . \end{aligned}$$
(14)

After parameterizing the spectral density \(\rho _{ii}(s)\) as one pole dominance for the state \(X_i\) together with a continuum contribution, Eq. (12) is simplified to be

$$\begin{aligned} \varPi _{ii}(s_0, M_B^2) \equiv f_{ii}^2 e^{-M_i^2/M_B^2} = \int ^{s_0}_{s_<} e^{-s/M_B^2} \rho _{ii}(s) ds \, , \end{aligned}$$
(15)

which can be used to calculate \(M_i\) through

$$\begin{aligned} M^2_i(s_0, M_B) = \frac{\int ^{s_0}_{s_<} e^{-s/M_B^2} s \rho _{ii}(s) ds}{\int ^{s_0}_{s_<} e^{-s/M_B^2} \rho _{ii}(s) ds} \, . \end{aligned}$$
(16)

We use the spectral density \(\rho _{11}(s)\) extracted from the current \(\eta ^1_{\alpha _1\alpha _2\alpha _3\alpha _4}\) as an example to perform the numerical analysis. We take the following values for various QCD parameters [1, 36,37,38,39,40,41,42]:

$$\begin{aligned} m_{s}(2~\mathrm{GeV})= & {} 93_{-~5}^{+11} \mathrm{~MeV} \, , \nonumber \\ \left\langle g_{s}^{2} G G\right\rangle= & {} (0.48 \pm 0.14) \mathrm{~GeV}^{4} \, , \nonumber \\ \langle \bar{s}s\rangle= & {} -(0.8\pm 0.1)\times (0.240 \text{ GeV})^3\, , \nonumber \\ \left\langle g_{s} \bar{s} \sigma G s\right\rangle= & {} -M_{0}^{2} \times \langle \bar{s} s\rangle \, , \nonumber \\ M_{0}^{2}= & {} (0.8 \pm 0.2) \mathrm{~GeV}^{2} \, . \end{aligned}$$
(17)

As shown in Eq. (16), the mass \(M_1\) of the state \(X_1\) depends on two free parameters, the Borel mass \(M_B\) and the threshold value \(s_0\). We investigate three aspects to find their proper working regions: (a) the convergence of OPE, (b) the sufficient amount of the pole contribution, and (c) the mass dependence on these two parameters.

Fig. 4
figure 4

CVG\(_{12}\) (short-dashed curve, defined in Eq. (18)), CVG\(_{10}\) (middle-dashed curve, defined in Eq. (19)), CVG\(_{8}\) (long-dashed curve, defined in Eq. (20)), and PC (solid curve, defined in Eq. (21)) as functions of the Borel mass \(M_B\). These curves are obtained using the current \(\eta ^1_{\alpha _1\alpha _2\alpha _3\alpha _4}\) when setting \(s_0 = 16.0\) GeV\(^2\)

Full size image
Fig. 5
figure 5

The mass \(M_1\) of the state \(X_1\) extracted from the current \(\eta ^1_{\alpha _1\alpha _2\alpha _3\alpha _4}\), with respect to a the threshold value \(s_0\) and b the Borel mass \(M_B\): a the short-dashed/solid/long-dashed curves are obtained by setting \(M_B^2 = 2.40/2.53/2.65\) GeV\(^2\), respectively; b the short-dashed/solid/long-dashed curves are obtained by setting \(s_0 = 15.0/16.0/17.0\) GeV\(^2\), respectively

Full size image
Table 1 QCD sum rule results for the fully-strange tetraquark states with the exotic quantum number \(J^{PC} = 4^{+-}\), extracted from the diquark–antidiquark currents \(\eta ^{1,2,3}_{\alpha _1\alpha _2\alpha _3\alpha _4}\) as well as their mixing currents \(J^{1,2,3}_{\alpha _1\alpha _2\alpha _3\alpha _4}\)
Full size table

Firstly, we investigate the convergence of OPE, which is the cornerstone for a reliable QCD sum rule analysis. We require the \(D=12\) terms (CVG\(_{12}\)) to be less than 5%, the \(D=10\) terms (CVG\(_{10}\)) to be less than 10%, and the \(D=8\) terms (CVG\(_{8}\)) to be less than 20%:

$$\begin{aligned} \text{ CVG}_{12}\equiv & {} \left| \frac{ \varPi _{11}^{D=12}(\infty , M_B^2) }{ \varPi _{11}(\infty , M_B^2) }\right| < 5\% \, , \end{aligned}$$
(18)
$$\begin{aligned} \text{ CVG}_{10}\equiv & {} \left| \frac{ \varPi _{11}^{D=10}(\infty , M_B^2) }{ \varPi _{11}(\infty , M_B^2) }\right| < 10\% \, , \end{aligned}$$
(19)
$$\begin{aligned} \text{ CVG}_8\equiv & {} \left| \frac{ \varPi _{11}^{D=8}(\infty , M_B^2) }{ \varPi _{11}(\infty , M_B^2) }\right| < 20\% \, . \end{aligned}$$
(20)

As depicted in Fig. 4 using the dashed curves, the lower bound of the Borel mass is determined to be \(M_B^2 > 2.40\) GeV\(^2\).

Secondly, we investigate the one-pole-dominance assumption by requiring the pole contribution (PC) to be larger than 40%:

$$\begin{aligned} \text{ PC } \equiv \left| \frac{ \varPi _{11}(s_0, M_B^2) }{ \varPi _{11}(\infty , M_B^2) }\right| > 40\% \, . \end{aligned}$$
(21)

As depicted in Fig. 4 using the solid curve, the upper bound of the Borel mass is determined to be \(M_B^2 < 2.65\) GeV\(^2\) when setting \(s_0 = 16.0\) GeV\(^2\). Altogether the Borel window is determined to be 2.40 GeV\(^2< M_B^2 < 2.65\) GeV\(^2\) for \(s_0 = 16.0\) GeV\(^2\). Redoing the same procedures, we find that there are non-vanishing Borel windows for \(s_0 > s_0^\mathrm{min} = 14.6\) GeV\(^2\). Accordingly, we choose \(s_0\) to be slightly larger, and determine its working region to be 13.0 GeV\(^2< s_0 < 19.0\) GeV\(^2\).

Thirdly, we show the mass \(M_1\) in Fig. 5, and investigate its dependence on \(M_B\) and \(s_0\). It is stable against \(M_B\) inside the Borel window 2.40 GeV\(^2< M_B^2 < 2.65\) GeV\(^2\), and its dependence on \(s_0\) is moderate insider the working region 13.0 GeV\(^2< s_0 < 19.0\) GeV\(^2\), where the mass is calculated to be

$$\begin{aligned} M_{1} = 3.50^{+0.21}_{-0.25}\mathrm{~GeV} \, . \end{aligned}$$
(22)

Its uncertainty is due to \(s_0\) and \(M_B\) as well as various QCD parameters listed in Eq. (17).

We repeat the same procedures to study the other two currents \(\eta ^2_{\alpha _1\alpha _2\alpha _3\alpha _4}\) and \(\eta ^3_{\alpha _1\alpha _2\alpha _3\alpha _4}\). The obtained results are summarized in Table 1.

5 Multi-channel analysis

To perform the multi-channel analysis, we take into account the off-diagonal correlation functions, which are actually non-zero, i.e., \(\rho _{ij}(s)|_{i \ne j} \ne 0\). It is interesting to see how large they are, so we choose \(s_0 = 11.0\) GeV\(^2\) and \(M_B^2 = 1.85\) GeV\(^2\) to obtain

$$\begin{aligned} \varPi _{ij}(s_0, M_B^2) = \left( \begin{array}{ccc} 2.77 &{} -0.04 &{} -3.83 \\ -0.04 &{} 0.98 &{} 0.46 \\ -3.83 &{} 0.46 &{} 2.38 \end{array}\right) \times 10^{-6} \mathrm{~GeV}^{14} .\nonumber \\ \end{aligned}$$
(23)

Hence, \(\eta ^{1}_{\cdots }\) and \(\eta ^{3}_{\cdots }\) are strongly correlated with each other, making the off-diagonal terms of \(\rho _{ij}(s)\) non-negligible, as depicted in Fig. 6 using the solid curve.

To diagonalize the \(3\times 3\) matrix \(\rho _{ij}(s)\), we construct three mixing currents \(J^{1,2,3}_{\alpha _1\alpha _2\alpha _3\alpha _4}\):

$$\begin{aligned} \left( \begin{array}{c} J^{1}_{\cdots } \\ J^{2}_{\cdots } \\ J^{3}_{\cdots } \end{array}\right) = \mathbb {T}_{3\times 3} \left( \begin{array}{c} \eta ^{1}_{\cdots } \\ \eta ^{2}_{\cdots } \\ \eta ^{3}_{\cdots } \end{array}\right) \, , \end{aligned}$$
(24)

with \(\mathbb {T}_{3\times 3}\) the transition matrix.

Fig. 6
figure 6

Off-diagonal terms, \(\left| \varPi _{13}/\sqrt{\varPi _{11}\varPi _{33}}\right| \) (solid) and \(\left| \varPi ^\prime _{13}/\sqrt{\varPi ^\prime _{11}\varPi ^\prime _{33}}\right| \) (dashed), as functions of the Borel mass \(M_B\). These curves are obtained by setting \(s_0 = 11.0\) GeV\(^2\)

Full size image
Fig. 7
figure 7

The mass \(M_1^\prime \) extracted from the mixing current \(J^1_{\alpha _1\alpha _2\alpha _3\alpha _4}\), with respect to a the threshold value \(s_0\) and b the Borel mass \(M_B\): a the short-dashed/solid/long-dashed curves are obtained by setting \(M_B^2 = 1.78/1.85/1.92\) GeV\(^2\), respectively; b the short-dashed/solid/long-dashed curves are obtained by setting \(s_0 = 10.0/11.0/12.0\) GeV\(^2\), respectively

Full size image

We apply the method of operator product expansion to extract the spectral densities \(\rho ^\prime _{ij}(s)\) from the mixing currents \(J^{1,2,3}_{\alpha _1\alpha _2\alpha _3\alpha _4}\). After choosing

$$\begin{aligned} \mathbb {T}_{3\times 3} = \left( \begin{array}{ccc} 0.72 &{} -0.06 &{} -0.69 \\ 0.14 &{} 0.99 &{} 0.05 \\ 0.68 &{} -0.13 &{} 0.72 \end{array}\right) \, , \end{aligned}$$
(25)

we obtain

$$\begin{aligned} \varPi ^\prime _{ij}(s_0, M_B^2) = \left( \begin{array}{ccc} 6.43 &{} 0 &{} 0 \\ 0 &{} 1.00 &{} 0 \\ 0 &{} 0 &{} -1.30 \end{array}\right) \times 10^{-6} \mathrm{~GeV}^{14} , \end{aligned}$$
(26)

at \(s_0 = 11.0\) GeV\(^2\) and \(M_B^2 = 1.85\) GeV\(^2\). Hence, the off-diagonal terms of \(\rho ^\prime _{ij}(s)\) are negligible around here, suggesting that the three mixing currents \(J^{1,2,3}_{\alpha _1\alpha _2\alpha _3\alpha _4}\) are nearly non-correlated around here, as depicted in Fig. 6 using the dashed curve. Moreover, Eq. (26) indicates that the QCD sum rule result from \(J^3_{\alpha _1\alpha _2\alpha _3\alpha _4}\) is non-physical around here due to its negative correlation function. Besides, Eq. (25) indicates that \(J^{2}_{\cdots }\) is almost the same as \(\eta ^{2}_{\cdots }\), while \(J^{1}_{\cdots }\) and \(J^{3}_{\cdots }\) are mainly from the recombination of \(\eta ^{1}_{\cdots }\) and \(\eta ^{3}_{\cdots }\).

We use the procedures previously applied on the diquark–antidiquark currents \(\eta ^{1,2,3}_{\alpha _1\alpha _2\alpha _3\alpha _4}\) to study their mixing currents \(J^{1,2,3}_{\alpha _1\alpha _2\alpha _3\alpha _4}\). The obtained results are also summarized in Table 1. Especially, the mass extracted from the current \(J^1_{\alpha _1\alpha _2\alpha _3\alpha _4}\) is significantly reduced to be

$$\begin{aligned} M^\prime _{1} = 2.85^{+0.19}_{-0.22} \mathrm{~GeV} \, . \end{aligned}$$
(27)

For completeness, we show it in Fig. 7 as a function of the threshold value \(s_0\) and the Borel mass \(M_B\).

6 Conclusion

In this paper we apply the method of QCD sum rules to study the fully-strange tetraquark states with the exotic quantum number \(J^{PC}=4^{+-}\). We work within the diquark–antidiquark picture and systematically construct their interpolating currents. We calculate both the diagonal and off-diagonal correlation functions. The obtained results are used to construct three mixing currents that are nearly non-correlated. We use the mixing current \(J^1_{\alpha _1\alpha _2\alpha _3\alpha _4}\) to evaluate the mass of the lowest-lying state to be \(2.85^{+0.19}_{-0.22}\) GeV.

In this paper we also systematically construct the fully-strange meson–meson currents of \(J^{PC}=4^{+-}\), and relate them to the diquark–antidiquark currents through the Fierz rearrangement. Especially, we can apply Eqs. (24) and (6) to transform the mixing current \(J^1_{\alpha _1\alpha _2\alpha _3\alpha _4}\) to be

$$\begin{aligned} J^1_{\cdots } = 4.3~\xi ^1_{\cdots } + 1.2~\xi ^2_{\cdots } - 1.3~\xi ^3_{\cdots } \, . \end{aligned}$$
(28)

This Fierz identity suggests that the lowest-lying state dominantly decays into the P-wave \(\phi (1020) f_2^\prime (1525)\) channel through the meson–meson current \(\xi ^1_{\alpha _1\alpha _2\alpha _3\alpha _4}\), given that the operator \(\bar{s}_b \gamma _{\alpha _2} s_b\) of \(I^GJ^{PC}=0^-1^{--}\) well couples to the vector meson \(\phi (1020)\) and the operator \(\mathcal {S}[\bar{s}_a \gamma _{\alpha _1} {\overset{\leftrightarrow }{D}}_{\alpha _3} s_a]\) of \(I^GJ^{PC}=0^+2^{++}\) well couples to the \(f_2^\prime (1525)\) meson. Accordingly, we propose to search for it in the \(X \rightarrow \phi (1020) f_2^\prime (1525) \rightarrow \phi K \bar{K}\) decay process in the future Belle-II, BESIII, COMPASS, GlueX, and PANDA experiments.

This is the first study on the exotic quantum number \(J^{PC}=4^{+-}\), and the above lowest-lying fully-strange tetraquark state of \(J^{PC}=4^{+-}\) is a purely exotic hadron to be potentially observed in future experiments. Its theoretical and experimental studies will continuously improve our understanding on the non-perturbative behaviors of the strong interaction in the low energy region.