Mass spectrum and strong decays of tetraquark ${\bar{c}}{\bar{s}} qq$ states

Abstract

We systematically study the mass spectrum and strong decays of the S-wave ${\bar{c}}{\bar{s}} q q$ states in the compact tetraquark scenario with the quark model. The key ingredients of the model are the Coulomb, the linear confinement, and the hyperfine interactions. The hyperfine potential leads to the mixing between different color configurations, and to the large mass splitting between the two ground states with $I(J^P)=0(0^+)$ and $I(J^P)=1(0^+)$. We calculate their strong decay amplitudes into the ${\bar{D}}^{(*)}K^{(*)}$ channels with the wave functions from the mass spectrum calculation and the quark-interchange method. We examine the interpretation of the recently observed $X_0(2900)$ as a tetraquark state. The mass and decay width of the $I(J^P)=1(0^+)$ state are $M=2941$ MeV and $\Gamma _X=26.6$ MeV, respectively, which indicates that it might be a good candidate for $X_0(2900)$. Meanwhile, we also obtain an isospin partner state $I(J^P)=0(0^+)$ with $M=2649$ MeV and $\Gamma _{X\rightarrow {\bar{D}} K}=48.1$ MeV, respectively. Future experimental search for X(2649) will be very helpful.

1 Introduction

Recently, the LHCb collaboration reported an enhancement on the $D^- K^+$ invariant mass distribution in the process $B^+\rightarrow D^+ D^- K^+$, which is parameterized as two Breit–Wigner resonances [1,2,3]:

$$\begin{aligned}&X_{0}:\\&M=2.866\pm 0.007\pm 0.002~\hbox {GeV},\,\Gamma =57\pm 12\pm 4~\hbox {MeV}, \\&X_{1}: \,\,\ \\&M=2.904 \pm 0.005 \pm 0.001~\hbox {GeV}, \,\Gamma =110 \pm 11 \pm 4~\hbox {MeV}, \end{aligned}$$

with $J^P=0^+$ and $J^P=1^-$, respectively. Since they were observed in the $D^- K^+$ channel, the minimal quark contents are ${\bar{c}} {\bar{s}} d u$. In 2016, another open-flavor exotic state X(5586) with the quark contents $su{\bar{b}}{\bar{d}}$ (or $sd{\bar{b}}{\bar{u}}$) was reported by the D0 collaboration. However, it was not confirmed by the LHCb [4], CMS [5], CDF [6] and ATLAS [7] collaborations. Thus, the X(2900) states might be the first open-flavor tetraquark states in experiment, which deserves a refined investigation on its existence and the inner dynamics. In the literature, there have been a couple of analyses of the ${\bar{c}} {\bar{s}} d u$ state in the molecular [8] and tetraquark [9,10,11,12] scenarios as the charmed partner state of X(5568) before the experimental observations. The recent experimental developments inspired extensive interest in the X(2900) states. So far, their inner structures and properties are still not clear. One explanation is that the enhancement might be solely from the rescattering effects of the ${\bar{D}}^*K^*\rightarrow {\bar{D}}K$ or ${\bar{D}}_1K^{(*)}\rightarrow {\bar{D}}K$ channels [13,14,15]. Another explanation is the genuine resonance [16,17,18,19,20,21,22,23,24,25,26,27,28,29,30], either the loosely bound molecular states or the compact tetraquark states.

In the hadronic molecular scheme, $X_0(2900)$ is explained as a ${\bar{D}}^* K^*$ molecule with $J ^P= 0^+$ in Refs. [16,17,18,19,20,21,22,23,24,25]. The molecular assignment of $X_1(2900)$ is ruled out in Refs. [17, 18] and it is explained as a virtual state with $I(J^P)=0(1^-)$ in Ref. [19]. Among these work, the isospin of $X_0(2900)$ is determined as $I=0$ in Refs. [16, 17, 20, 21], while in Ref. [19], its isospin is found to be $I=1$. The isospin of $X_0(2900)$ is not presented in the QCD sum rule calculation with the meson–meson interpolating current [23, 24].

Within the tetraquark scheme, $X_0(2900)$ is accommodated as the tetraquark state with $J^P=0^+$ [26,27,28,29], while the quark model study with dynamical calculation [31] does not favor it in view of the mass differences between the experimental mass of $X_0(2900)$ and the predicted masses (2675, 3065, 3152, 3396) MeV. $X_1(2900)$ is interpreted as the orbital excited tetraquark state with $J^P=1^-$ in Refs. [23, 23, 25, 29, 32].

The nature of the X(2900) states is still controversial. Most of the investigations mentioned above focus on the mass spectroscopy of X(2900), which is a major platform to probe the dynamics of the multi-quark system. However, compared with the conventional baryons and mesons, the tetraquark states are more complicated. For example, the tetraquark states contain much richer color configurations, i.e., ${\bar{3}}_c$–$3_c$ and $6_c$–${\bar{6}}_c$ components  [33]. Therefore, the quark models that succeed in the conventional mesons $({\bar{q}} q)$ and baryons qqq, might have large uncertainties in the multi-quark systems. The study of other properties such as production and decay patterns become essential, which are very sensitive to the inner structures of the multi-quark system. There are several theoretical studies about the decays and productions [15, 18, 22, 34, 35]. For instance, the authors in Ref. [35] discussed the productions and the decays of X(2900) in different physical scenarios, including the triangle diagrams, the molecules and the tetraquarks. The hadronic effects on X(2900) in heavy-ion collisions were investigated in Ref. [36].

In this paper, we study the four-quark state ${\bar{c}}{\bar{s}}q q$ in the tetraquark scenario and examine whether $X_0(2900)$ can be accommodated as a compact tetraquark. We first extend our previous work [33] to study the open-flavor system ${\bar{c}} {\bar{s}} q q$ spectrum within quark model considering the mixing effect of the two color configurations. Then we calculate the decay widths of the ${\bar{c}}{\bar{s}} qq$ system into the ${\bar{D}}^{(*)} K^{(*)}$ channels within the quark-interchange model [37,38,39,40,41,42]. In this model, the quark–quark interactions are described by the same quark model in the mass spectrum calculation.

The paper is arranged as follows. In Sect. 2, we introduce the Hamiltonian for the ${\bar{c}} {\bar{s}} q q$ system. With the quark model, we calculate the mass spectrum of the S-wave tetraquark states and present the results in Sect. 3. With the same quark–quark interaction, we investigate their strong decays into the ${\bar{D}}^{(*)} K^{(*)}$ channel using the quark-interchange model. The details are elaborated in Sect. 4. We give a summary in Sect. 5.

Table 1 The mass spectra of the mesons (in units of MeV) in the quark model. The experimental results are taken from Ref. [44]

2 Hamiltonian

In a tetraquark state, the four-quark Hamiltonian reads

$$\begin{aligned} H= & {} \sum _{i=1}^{4}\frac{p_{j}^{2}}{2m_{j}}-T_G+\sum ^4_{i<j=1}V_{ij}+\sum _{j}m_{j}, \end{aligned}$$

(1)

with $p_j$ and $m_j$ denoting the momentum and mass of the inner quark with index j, respectively. $T_G$ is the total kinematic energy of the system and it vanishes in the center-of-mass frame. The $V_{ij}$ is the quark–quark interaction between the quark pair (ij). In this work, we use the non-relativistic quark model proposed in Ref. [43] to describe the quark–quark interaction,

$$\begin{aligned}&V_{ij}(r_{ij})=-\frac{3}{16}\sum _{i<j}{\lambda }_{i}{\lambda }_{j}\Big (-\frac{\kappa (1-\hbox {exp}(-r_{ij}/r_{c}))}{r_{ij}}+b r_{ij}^{p}\nonumber \\&\quad -\Lambda +\frac{8\pi }{3m_{i}m_{j}}\kappa '(1-\hbox {exp}(-r_{ij}/r_{c}))\frac{\hbox {exp}(-r_{ij}^{2}/r_{0}^{2})}{\pi ^{3/2}r_{0}^{3}}{{\mathbf {s}}}_{i}\cdot {{\mathbf {s}}}_{j}\Big ),\nonumber \\ \end{aligned}$$

(2)

with

$$\begin{aligned}&r_0=A\left( \frac{2m_im_j}{m_i+m_j}\right) ^{-B}, \nonumber \\&A=1.6553~\hbox {GeV}^{B-1},\quad B=0.2204,\nonumber \\&r_{c}=0,\quad p=1,\quad \Lambda =0.8321~\hbox {GeV},\nonumber \\&\kappa =0.5069,\quad b=0.1653~\hbox {GeV}^{2},\quad \kappa '=1.8609,\nonumber \\&m_{c}=1.836~\hbox {GeV},\quad m_{q}=0.315~\hbox {GeV}, m_{s}=0.577~\hbox {GeV}, \nonumber \\ \end{aligned}$$

(3)

where $r_{ij}$ is the radius between the ith and jth quarks. The ${\lambda }_{i}$ ($-{\lambda }_i^T$) is the color generator for the quark (antiquark). The first two terms are the central parts of the model, the Coulomb and linear confinement potentials. The last term in $V_{ij}$ is the hyperfine interaction with the smearing effect parameterized by $r_0$, which is related to the reduced mass of the interacting quarks. The $\mathbf{s} _i$ is the spin operator of the ith quark. The hyperfine potential contains all the flavor information and is expected to play an important role for the mass spectrum. The values of the parameters are determined by fitting the mass spectra of the mesons in Table 1.

3 Mass spectrum

3.1 Wave function

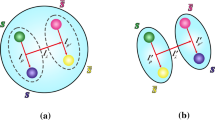
The spatial wave function of the four-body system can be described by three independent Jacobi coordinates. For the ${\bar{c}} {\bar{s}} q q$ state, there are two sets of Jacobi coordinates as presented in Fig. 1. In general, if we use one set of Jacobi coordinates with complete spatial bases and the complete color configurations, we can describe the four-quark system. In this work, we use the Jacobi coordinate in Fig. 1a to expand the wave function of the tetraquark state.

Fig. 1

The Jacobi coordinates in the tetraquark state ${\bar{c}}{\bar{s}} qq$

It reads

$$\begin{aligned}&\Psi ^{II_z}_{JJ_z}=\sum _{\alpha }A_{\alpha }\psi _{\alpha }(\mathbf { r_{12}},\mathbf { r_{34}},\mathbf {r}),\nonumber \\&\psi _{\alpha }=\phi _{n_al_a}({r}_{12},\beta _a)\phi _{n_bl_b} ({r}_{34},\beta _b)\phi _{n_{ab}l_{ab}}({r},\beta )\nonumber \\&\otimes \left[ [Y_{l_a}(\hat{\mathbf {r_{12}}})Y_{l_b}(\hat{\mathbf {r_{34}}})]_{\ell }Y_{l_{ab}}(\hat{\mathbf {r}})]_L\otimes [\chi _{s_{a}}(12)\chi _{s_{b}}(34)]_S\right] _{JJ_z} \nonumber \\&\otimes [\chi _c(12)\chi _c(34)]_{1_c} \otimes [\xi _f(12)\xi _f(34)]_{II_z}, \end{aligned}$$

(4)

where (1, 2, 3, 4) denote the four quarks $({\bar{c}}, {\bar{s}}, q,q )$, respectively. J $(J_z)$ and I $(I_z)$ are the total angular momentum and the isospin (the third component) of the tetraquark state. The $l_{a}$, $l_b$, and $l_{ab}$ represent the orbital angular momentum within the $({\bar{c}}{\bar{s}})$ cluster, the (qq) cluster and that between these two clusters, respectively. The $l_a$ and $l_b$ couples into the orbital angular momentum $\ell$. Then $\ell$ couples with $l_{ab}$ into the total orbital angular momentum L. The $s_a$ and $s_b$ are the spin of the $({\bar{c}}{\bar{s}})$ and (qq) clusters. They form the total spin of the tetraquark S. The $Y_{lm}$ is the spherical harmonics function. The sum of the script $\alpha$ represents the superposition of the four-body bases that satisfy the quantum number ($JJ_z,II_z$). $A_{\alpha }$ is the expanding coefficient for the corresponding basis. $\chi _{c}$, $\chi _s$, and $\xi$ are the wave functions in the color, spin and flavor space, respectively. The subscript $1_c$ denotes that the four quarks form a color singlet state. $\phi$ is the radial wave function in spatial space and reads

$$\begin{aligned} \phi _{n_a l_a}({\mathbf {r}}_{12},\beta _a)= & {} \left\{ \frac{2^{l_a+2}(2\nu _{n_a})^{l_a+3/2}}{\sqrt{\pi }(2l_a+1)!!}\right\} ^{1/2}r_{12}^{l_{a}} e^{-\nu _{n_a} r_{12}^{2}}, \end{aligned}$$

where $\nu _{n_a}$ is related to the oscillating parameter $\beta _a$ as follows:

$$\begin{aligned} \nu _{n_a}=\frac{n_a \beta ^2_a}{2},\quad (n_a=1,2,\ldots ,n^{\mathrm{max}}_a), \end{aligned}$$

(5)

$n_a$ is the radial quantum number. $n^{\mathrm{max}}_a$ is the number of the expanding bases along $r_a$. The spatial wave functions $\phi _{n_b l_b}(\mathbf {r}_{34},\beta _b)$ and $\phi _{n_{ab} l_{ab}}(\mathbf {r},\beta _{ab})$ have similar forms. In this work, we concentrate on the S-wave tetraquark state, which should be a superpositions of the states $|l_a=l_b=l=0\rangle$, $|l_a=l_b=1,l=0\rangle$, $|l_a=2,l_b=l=0\rangle$ etc. In conventional hadrons, the mass gap between the ground state and its first orbital excitation is about hundreds of MeV. The same pattern is expected in the compact multi-quark states. In addition, the high orbital excitations couple with the ground states through the tensor and spin-orbital potentials, which can be treated as perturbative compared with the Coulomb and linear confinement potentials. Thus, we only expand the tetraquark states by the ground spatial bases.

In the state ${\bar{c}}{\bar{s}}qq$, the color–spin–flavor wave configuration is constrained by Fermi statistics and the possible wave functions are listed in Table 2.

Table 2 The color–spin–flavor wave functions of the S-wave tetraquark states ${\bar{c}} {\bar{s}} q_1 q_2$ with different $J^P$ quantum numbers. The subscripts and superscripts denote the color representation and the spin, respectively. The symbol $\{q_1q_2\}$ and $[q_1q_2]$ represent that the two light quarks are symmetric and antisymmetric in the flavor space, respectively. The $(\beta _{a},\beta _{b},\beta _{ab})$ are the oscillating parameters in the spatial wave functions of the antidiquark ${\bar{c}}{\bar{s}}$, the diquark $q_1q_2$ and that between the two clusters

3.2 Results

By solving the Schrödinger equation with the variational method, we obtain the mass spectrum and present the results in Fig. 2. The explicit values of the mass spectrum and the oscillating parameters are summarized in Table 3. In Fig. 2, we find that the tetraquarks with the isospin $I=1$ are located higher than those with $I=0$. Especially, the ground $I(J^P)=1(0^+)$ state is about 300 MeV heavier than the $I(J^P)=0(0^+)$ one. This mass difference is about 200 MeV in Ref. [31]. As illustrated in Table 2, the $I(J^P)=0(0^+)$ and $I(J^P)=1(0^+)$ states contain the same color structures but different spin–flavor configurations. Thus, with the color interactions only, i.e., the Coulomb and linear confinement potentials, the mass spectra of the two states should be the same. The mass difference comes from the contribution of the hyperfine potential in view of different spin wave functions. The quark model which we adopted in this work successfully described the large mass splitting between the $\pi$ and $\rho$ mesons, which indicates that the hyperfine interaction should be very important for the light quarks. In the ${\bar{c}}{\bar{s}} qq$ system, the significant hyperfine potential for the diquark qq leads to the large mass splitting between the $I(J^P)=1(0^+)$ and $I(J^P)=0(0^+)$ states.

Fig. 2

The mass spectra of the S-wave tetraquark state ${\bar{c}}{\bar{s}} qq$. The dashing lines represent the mass thresholds of the ${\bar{D}}^{(*)}K^{(*)}$ states

Table 3 The mass spectra (in units of MeV) of the tetraquark states ${\bar{c}}{\bar{s}} qq$ with different $J^P$. The $\beta _{(a/b)}$, $\gamma _{(a/b)}$ and $\lambda _{(a/b)}$ are the oscillating parameters for different states as listed in Table 2. In this work, we use $N=2^3$ bases to expand the wave functions of the tetraquark state ${\bar{c}}{\bar{s}} qq$. Here, we list the results for the S-wave ground and the first radially excited states

Fig. 3

The mass spectrum of the $J^P=0^+$ ${\bar{c}}{\bar{s}} qq$ state without and with considering the mixing effects between the$[({\bar{c}}{\bar{s}})_{3_c} (qq)_{{\bar{3}}_c}]_{1_c}$ and $[({\bar{c}}{\bar{s}})_{6_c} (qq)_{ 6_c}]_{1_c}$ configurations

Table 4 The proportions of different color–spin configurations in the $J^P=0^+$ ${\bar{c}}{\bar{s}} qq$ system

Table 5 The proportions of different color configurations in the ${\bar{c}}{\bar{s}} qq$ states with $J^P=1^+$. The $\Psi _1$, $\Psi _2$, and $\Psi _3$ represent the color-flavor-spin configurations in Table 2

In Table 2, the $I(J^P)=0(0^+)$ and $I(J^P)=1(0^+)$ tetraquark states contain two color configurations $[({\bar{c}}{\bar{s}})_{3_c} (qq)_{{\bar{3}}_c}]_{1_c}$ and $[({\bar{c}}{\bar{s}})_{6_c} (qq)_{ 6_c}]_{1_c}$, respectively. We first discuss the mass spectra of the tetraquark states without considering the coupling between the $3_c$–${\bar{3}}_c$ and ${\bar{6}}_c$–$6_c$ states and display the results in Fig. 3. For the $I=1$ state, the ${\bar{6}}_c$–$6_c$ state is located higher than the ${ 3_c}-{\bar{3}}_c$ one, while the situation is reversed for the $I=0$ state.

With the mixing effect between the $3_c$–${\bar{3}}_c$ and ${\bar{6}}_c$–$6_c$ states, we obtain the mass spectrum and present them in the right panel of Fig. 3. The mixing effect comes from the quark-antiquark interactions between the diquark and the antiquark. With the quark model in Eq. (2), the coupling constants in the Coulomb and linear confinement interactions are flavor-independent. Thus the two interactions cancel with each other exactly and do not contribute to the color configuration mixing  [33]. Only the hyperfine interaction contributes. This interaction is inversely proportional to the masses of the interacting quarks. In Fig. 3, one finds that the mixing effects shift the masses at the order of 100 MeV, which is much larger than those in the fully heavy tetraquark states [33].

We also investigate the inner structures of the tetraquark states, including the proportions of different color configurations as listed in Tables 4, 5 and 6 and the root mean square radii between different interacting quarks in Table 7. The proportions show that the ground S-wave states contain important color configuration $[({\bar{c}} q)_{8_c}({\bar{s}} q)_{8_c}]_{1_c}$. As illustrated in Table 7, almost all of the root mean square radii are smaller than 1 fm, which indicates that the four quarks are compactly bound within the tetraquark states. One should be careful in identifying the states as the resonances. Since we have used the finite numbers of the bases to expand the tetraquark state, the eigenvectors may correspond to the bound or the resonance states, and the continuum in the finite space. To distinguish the resonance from the continuum, we may include their coupling and investigate whether the tetraquark states may remain as resonances or not by the real scaling method in the future [45, 46].

The mass of the $I(J^P)=1(0^+)$ state is 2941 MeV, which is 75 MeV larger than that of the $X_0(2900)$ state. Such a mass deviation is not very significant and conclusive if one considers the uncertainty of the quark model. One notices that the model parameters used in the mass spectrum calculation are obtained from the conventional hadrons. As a phenomenological model, the parameters may change for different systems. For instance, in Refs. [47,48,49], the authors studied the mass spectra of the mesons and the baryons in a unified relativized quark model. The overall constant term in the meson-based potential was $-340$ MeV , while the baryon-based one was selected as $-615$ MeV to obtain better solutions for the baryons qqq. When the meson-based quark model is applied to the multi-quark systems, a similar modification might also be essential. Furthermore, the confinement mechanisms in the multi-quark systems are still poorly understood. For example, because of the rich color configurations in the multi-quark system, the three-body interaction arising from the three-gluon vertex may also contribute, while it vanishes for the conventional hadrons. Considering the uncertainties of quark model, the X(2900) signal seems a candidate of the $I(J^P)=1(0^+)$ state. Besides X(2941), we also predict the other states such as the $I(J^P)=0(0^+)$ state with the mass around 2649 MeV.

4 Decay width

In this section, we calculate the strong decay widths of the tetraquark states ${\bar{c}}{\bar{s}}q q$. The dominant decay modes of tetraquark states ${\bar{c}}{\bar{s}}q q$ are $X\rightarrow {\bar{D}}^{(*)} K^{(*)}$ when the phase spaces are allowed. The tetraquarks may also decay into the ${\bar{D}} K^{(*)} \pi$ final state. The three-body decays are largely suppressed compared with the two-body decays due to the phase space suppression. Thus, we do not consider them in this work.

4.1 Quark-interchange model

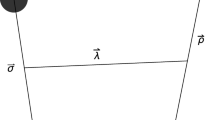
We first give a brief introduction to the quark-interchange model for the decay

$$\begin{aligned} {\bar{c}} {\bar{s}} q q\rightarrow B(c{\bar{q}})+C(s{\bar{q}}), \end{aligned}$$

(6)

where B and C are two color singlet mesons. The decay process occurs through interchanging the constituent quarks (antiquarks) as illustrated in Fig. 4, followed by hadronization into two mesons. This method has been applied to calculate the $I=3/2$ $K\pi$ scattering [50], the short-range NN interaction [51], the strong decays of the $Z_c$ states [52], X(3872) [53], and the pentaquark states [54]. In the decay, the interacting Hamiltonian reads

$$\begin{aligned} H_{ij}^I(r_{ij})=\sum _{i<j}V_{ij}(r_{ij}), \end{aligned}$$

(7)

where $V_{ij}$ is the potential as listed in Eq. (2). The T-matrix element is the sum of the four diagrams in Fig. 4, which are calculated as the overlaps of the wave functions with the Hamiltonian between the initial and final states. The wave functions of the initial tetraquark states and final mesons are obtained from the same quark model in Eq. (3). For each diagram, $T_{fi}$ is written as the product of factors (as defined in Ref. [52])

$$\begin{aligned} T_{fi}= & {} I_{\text{ flavor }}I_{\mathrm{color}} I_{\mathrm{spin-space}}. \end{aligned}$$

(8)

The element $I_{\text{ flavor }}$ is the overlap of wave functions in the flavor space. The color and the spin matrix elements are listed in Table 10 in the appendix. The calculation details of the spatial matrix element $I_{\text{ space }}$ are referred to Ref. [52].

The differential decay width is given by

$$\begin{aligned} \frac{{\mathrm{d}}\Gamma }{{\mathrm{d}}\Omega }=\frac{1}{2J+1}\frac{|{\vec p}_B|}{32\pi ^2M^2}|{\mathcal {M}} ({\bar{c}} {\bar{s}} q q\rightarrow B({\bar{c}}q)+C({\bar{s}}q) )|^2,\nonumber \\ \end{aligned}$$

(9)

where ${\vec p}_B$ is the momentum of the final state. M is the mass of the initial tetraquark state. The decay amplitude $\mathcal M$ is related to the T-matrix $T_{fi}$ by

$$\begin{aligned} {\mathcal {M}}({\bar{c}} {\bar{s}}{\bar{q}}{\bar{q}}\rightarrow B+C)=-(2\pi )^{3/2}\sqrt{2M}\sqrt{2E_B}\sqrt{2E_C}T_{fi},\nonumber \\ \end{aligned}$$

(10)

where $E_B$ and $E_C$ are the energies of the two mesons in the final state.

Table 6 The proportions of different color configurations in the $cs{\bar{q}} {\bar{q}}$ states with $J^P=2^+$

Table 7 The root mean square radii (in units of fm) between different interacting quarks in the $cs{\bar{q}} {\bar{q}}$ states with $J^P=0^+$, $J^P=1^+$ and $J^P=2^+$

4.2 Numerical results

We present the decay widths of the tetraquark states in Table 8. The $J^{P}=0^{+}$ states are of special interest because they might be the candidates for the recently observed $X_{0}(2900)$ in the LHCb collaboration. Two S-wave decay modes are available to the states, $\bar{D} {K}$ and $\bar{D}^{*}K^{*}$. For X(2941) and X(2649), we predict the partial decay widths into the $\bar{D}K$ channel as 20.1 MeV and 48.1 MeV, respectively. And the partial width ratio is

$$\begin{aligned} \frac{\Gamma _{DK}(X(2941))}{{\Gamma _{DK}}(X(2649))}=0.4. \end{aligned}$$

(11)

The X(2941) also decays into $\bar{D}^{*}K^{*}$ with a smaller decay width 6.5 MeV, while the mode is energetically forbidden for X(2649). In Sect. 3.2, the mass of X(2941) state is larger than the $X_0(2900)$ mass by 75 MeV. The predicted decay width 26.6 MeV is reasonably close to the experimental value of $57.2\pm 12.9$ MeV. If we regard X(2941) as the $X_0(2900)$ state and use the experimental value as the input mass in the decay, the $\bar{D}^{*}K^{*}$ decay mode is forbidden. It decays into the $\bar{D}K$ channel with the decay width 21.7 MeV. The partial width ratio is

$$\begin{aligned} \frac{{\Gamma _{\bar{D}K}}(X(2900))}{{\Gamma _{\bar{D}K}}(X(2649))}=0.5. \end{aligned}$$

(12)

The ratio indicates that, if $X_0(2900)$ is the $I(J^{P})=1(0^{+})$ state, the other $I(J^P)=0(0^+)$ state X(2649) in the $\bar{D}K$ channel might exist. More experimental study is expected in the future to test the tetraquark explanation for $X_0(2900)$.

For the $J^P=0^+$ states, the X(3222) and X(3013) states are promising to be observed in ${\bar{D}}^*K^*$ mode. The $\bar{D}K$ widths of the two states are much smaller than those of the ${\bar{D}}^*K^*$ ones, despite the larger phase spaces. The ${{\Gamma _{DK}}}(X(3222))$ is predicted to be 0.01 MeV, as it weekly couples with the $\bar{D}K$ channel. The $J^P=2^+$ states also decay into the ${\bar{D}}^*K^*$ mode. However, the partial decay widths are rather small and these tetraquark states may be difficult to observe in this mode.

The $J^{P}=1^{+}$ states may decay into the ${\bar{D}}^* K$, ${\bar{D}} K^*$ and ${\bar{D}}^* K^*$ channels. Most of the predicted widths are much smaller than those of the $J^{P}=0^{+}$ states except the X(2838) and X(2972). They both have large partial decay widths into ${\bar{D}}^* K$ and ${\bar{D}} K^*$, respectively.

Fig. 4

The diagrams for the tetraquark decaying into two mesons at the quark level. Here 1–4 denote the ${\bar{c}}$, ${\bar{s}}$, q, q quarks, respectively. The curve line denotes the quark–quark interactions

Table 8 The decay widths (in units of MeV) for the tetraquark states ${\bar{c}}{\bar{s}} qq$ decaying into ${\bar{D}}^{(*)}K^{(*)}$. The script “−” presents that the corresponding decay mode is forbidden by the phase space

5 Summary

In this work, we evaluate the mass spectrum and the decay widths of the system $cs{\bar{q}} {\bar{q}}$ with the quark model. We include the most important ingredients of the quark model, the Coulomb, the linear confinement, and the hyperfine interactions. With the results, we examine whether $X_0(2900)$ can be interpreted as a tetraquark state.

We first solve the Schrödinger equation with the variational method. We obtain the mass spectrum of the S-wave ${\bar{c}} {\bar{s}} qq$ states with $J^P=0^+$, $1^+$ and $2^+$. The $J^P=0^+$ and $1^+$ states are mixtures of different color–spin–flavor configurations. In the quark model, the color interaction does not mix different color–spin configurations. Only the hyperfine interactions contribute to their mixing effects. Since the ${\bar{c}}{\bar{s}} qq$ state contains the light quark, the mixing effect is larger than that in the fully heavy tetraquark state. With the Fierz transformation, we obtain the ratios of the $({\bar{c}} q)_{1_c}({\bar{s}} q)_{1_c}$ and $({\bar{c}} q)_{8_c}({\bar{s}} q)_{8_c}$ components. The ground state contains large color component $({\bar{c}} q)_{8_c}({\bar{s}} q)_{8_c}$. For the $J^P=0^+$ ${\bar{c}} {\bar{s}} qq$ system, the two isospin partner states have the same color configurations but different color–spin configurations. The mass splittings come from the hyperfine interactions.

With the obtained wave functions from the mass spectrum calculation, we study the strong decays for the tetraquarks ${\bar{c}}{\bar{s}}qq$ into the ${\bar{D}}^{(*)}K^{(*)}$ channels using the quark-interchange model. The partial decay widths might be helpful in the search for tetraquark states ${\bar{c}}{\bar{s}} qq$, as they suggest the golden channel to reconstruct the tetraquark states.

Table 9 The factor $\langle \frac{\mathbf \lambda _i}{2} \frac{\mathbf \lambda _j}{2}\mathbf{s}_i\cdot \mathbf{s}_j \rangle$ for the ${\bar{c}}{\bar{s}} q_1q_2$ state in the mass spectrum calculation. The subscripts of the “$\langle \dots \rangle$” correspond to the indice of the states $\Psi$ in Table 2

Combined the mass spectrum and decay width, X(2941) with the quantum number $I(J^P)=1(0^+)$ seems to be a good candidate for the $X_0(2900)$. Its mass and decay width are $M=2941$ MeV and $\Gamma =26.6$ MeV, respectively. The partial decay widths into the ${\bar{D}} K$ and ${\bar{D}}^* K^*$ modes are 20.1 and 6.5 MeV. If the X(2941) is treated as $X_0(2900)$, the ${\bar{D}}^* K^*$ mode is kinematically forbidden and the ${\bar{D}} K$ width is 21.7 MeV, which is close to the experimental data. Remarkably, we also find another state $I(J^P)=0(0^+)$ with $M=2649$ MeV and $\Gamma _{X\rightarrow DK}=48.1$ MeV at the same time. The decay width ratio $\Gamma (X(2941)\rightarrow DK)/\Gamma (X(2649)\rightarrow DK)=0.4$ indicates that if X(2941) is regarded as the X(2900), there might be another X(2649) state in the ${\bar{D}} K$ channel. In addition, one may also expect other states to be observed in the ${\bar{D}} ^*K$, ${\bar{D}}^* K$, and ${\bar{D}}^* K^*$ channels. The possible observation channels in experiments are related to their partial decay widths.

So far, we have evaluated the mass spectrum and the decay width with a meson-based quark model. The potentials in the multi-quark system might be different from the meson-based potentials. For instance, the parameters might change and the different confinement mechanisms might show up, which may bring uncertainties to our results and will be discussed lately. We expect more experimental measurements in the future to help test our results and improve the understanding of the interaction in the multi-quark system, especially the confinement mechanisms and dynamics in the strong decay.

Appendix

The hyperfine interaction plays an important role in the mass spectrum calculation, because it contributes to the mixing effects of different color–spin configurations, and induces the large mass splitting between the $I(J^P)=1(1^+)$ and $I(J^P)=0({0^+})$ ground states. We list the color–spin factor $\langle \frac{\mathbf \lambda _i}{2} \frac{\mathbf \lambda _j}{2}\mathbf{s}_i\cdot \mathbf{s}_j \rangle$ of the hyperfine interactions in the mass spectrum calculation in Table 9.

The values of the color matrix element $I_{\text{ color }}$ and the spin factor $I_{\mathrm{spin}}$ in the decay amplitudes are tabulated in Table 10.

Table 10 The color matrix element $I_{\text{ color }}=\langle \frac{{\lambda }_{i}}{2}\cdot \frac{{\lambda }_{j}}{2}\rangle$ and the spin factor $I_{\mathrm{spin}}=\langle [(cs)^{s_a}({\bar{q}}{\bar{q}})^{s_b}]^S| {\hat{V}}_s|[(c{\bar{q}})^{s_c}({s{\bar{q}}})^{s_d}]^S$ where ${\hat{V}}_s$ is taken as ${{{\mathbf {1}}}}$ for the Coulomb and linear confinement interactions, and ${{\mathbf {s}}}_{i}\cdot {{\mathbf {s}}}_{j}$ for the hyperfine potential. $s_a$ and $s_b$ are the spin of the diquark and antidiquark in the tetraquark state. $s_c$ and $s_d$ are those of the two mesons in the final state. The $3_c\otimes {\bar{3}}_c$ and ${\bar{6}}_c\otimes 6_c$ represent the color configurations $[({\bar{c}}{\bar{s}})_{3_c}(qq)_{{\bar{3}}_c}]_{1_c}$ and $[({\bar{c}}{\bar{s}})_{{\bar{6}}_c}(qq)_{{\bar{6}}_c}]_{1_c}$, respectively