Charmed $\Omega _c$ weak decays into $\Omega$ in the light-front quark model

Abstract

More than ten $\Omega _c^0$ weak decay modes have been measured with the branching fractions relative to that of $\Omega ^0_c\rightarrow \Omega ^-\pi ^+$. In order to extract the absolute branching fractions, the study of $\Omega ^0_c\rightarrow \Omega ^-\pi ^+$ is needed. In this work, we predict ${{\mathcal {B}}}_\pi \equiv {{\mathcal {B}}}(\Omega _c^0\rightarrow \Omega ^-\pi ^+)=(5.1\pm 0.7)\times 10^{-3}$ with the $\Omega _c^0\rightarrow \Omega ^-$ transition form factors calculated in the light-front quark model. We also predict ${{\mathcal {B}}}_\rho \equiv {{\mathcal {B}}}(\Omega _c^0\rightarrow \Omega ^-\rho ^+)=(14.4\pm 0.4)\times 10^{-3}$ and ${{\mathcal {B}}}_e\equiv {{\mathcal {B}}}(\Omega _c^0\rightarrow \Omega ^-e^+\nu _e)=(5.4\pm 0.2)\times 10^{-3}$. The previous values for ${{\mathcal {B}}}_\rho /{{\mathcal {B}}}_\pi$ have been found to deviate from the most recent observation. Nonetheless, our ${{\mathcal {B}}}_\rho /{{\mathcal {B}}}_\pi =2.8\pm 0.4$ is able to alleviate the deviation. Moreover, we obtain ${{\mathcal {B}}}_e/{{\mathcal {B}}}_\pi =1.1\pm 0.2$, which is consistent with the current data.

1 Introduction

The lowest-lying singly charmed baryons include the anti-triplet and sextet states $\mathbf{B}_c=(\Lambda _c^+,\Xi _c^0,\Xi _c^+)$ and $\mathbf{B}'_c=(\Sigma _c^{(0,+,++)},\Xi _c^{'(0,+)}, \Omega _c^0)$, respectively. The $\mathbf{B}_c$ and $\Omega _c^0$ baryons predominantly decay weakly [1,2,3,4,5], whereas the $\Sigma _c$ ($\Xi '_c$) decays are strong (electromagnetic) processes. There have been more accurate observations for the $\mathbf{B}_c$ weak decays in the recent years, which have helped to improve the theoretical understanding of the decay processes [6,7,8,9,10,11,12,13,14]. With the lower production cross section of $\sigma (e^+e^-\rightarrow \Omega _c^0X)$ [4], it is an uneasy task to measure $\Omega _c^0$ decays. Consequently, most of the $\Omega _c^0$ decays have not been reanalysized since 1990s [15,16,17,18,19,20,21,22,23], except for those in [24,25,26,27,28,29].

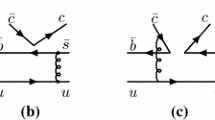
One still manages to measure more than ten $\Omega _c^0$ decays, such as $\Omega _c^0\rightarrow \Omega ^-\rho ^+$, $\Xi ^0{\bar{K}}^{(*)0}$ and $\Omega ^-\ell ^+ \nu _\ell$, but with the branching fractions relative to ${{\mathcal {B}}}(\Omega _c^0\rightarrow \Omega ^-\pi ^+)$ [5]. To extract the absolute branching fractions, the study of $\Omega _c^0\rightarrow \Omega ^-\pi ^+$ is crucial. Fortunately, the $\Omega _c^0\rightarrow \Omega ^-\pi ^+$ decay involves a simple topology, which benefits its theoretical exploration. In Fig. 1a, $\Omega _c^0\rightarrow \Omega ^-\pi ^+$ is depicted to proceed through the $\Omega _c^0\rightarrow \Omega ^-$ transition, while $\pi ^+$ is produced from the external W-boson emission. Since it is a Cabibbo-allowed process with $V_{cs}^* V_{ud}\simeq 1$, a larger branching fraction is promising for measurements. Furthermore, it can be seen that $\Omega _c^0\rightarrow \Omega ^-\pi ^+$ has a similar configuration to those of $\Omega _c^0\rightarrow \Omega ^-\rho ^+$ and $\Omega _c^0\rightarrow \Omega ^-\ell ^+ \nu _\ell$, as drawn in Fig. 1, indicating that the three $\Omega _c^0$ decays are all associated with the $\Omega _c^0\rightarrow \Omega ^-$ transition. While $\Omega$ is a decuplet baryon that consists of the totally symmetric identical quarks sss, behaving as a spin-3/2 particle, the form factors of the $\Omega _c^0\rightarrow \Omega ^-$ transition can be more complicated, which hinders the calculation for the decays. As a result, a careful investigation that relates $\Omega _c^0\rightarrow \Omega ^-\pi ^+,\Omega ^-\rho ^+$ and $\Omega _c^0\rightarrow \Omega ^-\ell ^+ \nu _\ell$ has not been given yet, despite the fact that the topology associates them together.

Based on the quark models, it is possible to study the $\Omega _c^0$ decays into $\Omega ^-$ with the $\Omega _c^0\rightarrow \Omega ^-$ transition form factors. However, the validity of theoretical approach needs to be tested, which depends on if the observations, given by

$$\begin{aligned} \frac{{{\mathcal {B}}}(\Omega _c^0\rightarrow \Omega ^-\rho ^+)}{{{\mathcal {B}}}(\Omega _c^0\rightarrow \Omega ^-\pi ^+)}= & {} 1.7\pm 0.3\,[4]\,(>1.3\,[5])\,, \nonumber \\ \frac{{{\mathcal {B}}}(\Omega _c^0\rightarrow \Omega ^-e^+\nu _e)}{{{\mathcal {B}}}(\Omega _c^0\rightarrow \Omega ^-\pi ^+)}= & {} 2.4\pm 1.2\,[5]\,, \end{aligned}$$

(1)

can be interpreted. Since the light-front quark model has been successfully applied to the heavy hadron decays [27, 30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46], in this report we will use it to study the $\Omega _c^0\rightarrow \Omega ^-$ transition form factors. Accordingly, we will be enabled to calculate the absolute branching fractions of $\Omega _c^0\rightarrow \Omega ^-\pi ^+(\rho ^+)$ and $\Omega _c^0\rightarrow \Omega ^- \ell ^+ \nu _\ell$, and check if the two ratios in Eq. (1) can be well explained.

Fig. 1

Feynman diagrams for a $\Omega _c^0\rightarrow \Omega ^-\pi ^+(\rho ^+)$ and b $\Omega _c^0\rightarrow \Omega ^-\ell ^+\nu _\ell$ with $\ell ^+=e^+$ or $\mu ^+$

2 Theoretical framework

2.1 General formalism

To start with, we present the effective weak Hamiltonians ${{\mathcal {H}}}_{H,L}$ for the hadronic and semileptonic charmed baryon decays, respectively [47]:

$$\begin{aligned} {{\mathcal {H}}}_H= & {} \frac{G_F}{\sqrt{2}} V_{cs}^*V_{ud} [c_1({\bar{u}} d)({\bar{s}} c)+c_2({\bar{s}} d)({\bar{u}} c)]\,,\nonumber \\ {{\mathcal {H}}}_L= & {} \frac{G_F}{\sqrt{2}}V_{cs}^*({\bar{s}}c)({\bar{u}}_\nu v_\ell )\,, \end{aligned}$$

(2)

where $G_F$ is the Fermi constant, $V_{ij}$ the Cabibbo–Kobayashi–Maskawa (CKM) matrix elements, $c_{1,2}$ the effective Wilson coefficients, $({\bar{q}}_1 q_2)\equiv {\bar{q}}_1\gamma _\mu (1-\gamma _5)q_2$ and $({\bar{u}}_\nu v_\ell )\equiv {\bar{u}}_\nu \gamma ^\mu (1-\gamma _5)v_\ell$. In terms of ${{\mathcal {H}}}_{H,L}$, we derive the amplitudes of $\Omega _c^0\rightarrow \Omega ^- \pi ^+(\rho ^+)$ and $\Omega _c^0\rightarrow \Omega ^- \ell ^+ \nu _\ell$ as [48, 49]

$$\begin{aligned} {{\mathcal {M}}}_h&\equiv {{\mathcal {M}}}(\Omega _c^0\rightarrow \Omega ^- h^+)\nonumber \\&=\frac{G_F}{\sqrt{2}}V^*_{cs}V_{ud}\,a_1 \langle \Omega ^-|({\bar{s}}c)|\Omega _c^0\rangle \langle h^+|({\bar{u}}d)|0 \rangle \,,\nonumber \\ {{\mathcal {M}}}_\ell&\equiv {{\mathcal {M}}}(\Omega _c^0\rightarrow \Omega ^- \ell ^+ \nu _\ell ) \nonumber \\&=\frac{G_F}{\sqrt{2}}V^*_{cs} \langle \Omega ^-|({\bar{s}}c)|\Omega _c^0 \rangle ({\bar{u}}_{\nu _\ell }v_\ell )\,, \end{aligned}$$

(3)

where $h=(\pi ,\rho )$, $\ell =(e,\mu )$, and $a_1=c_1+c_2/N_c$ results from the factorization [50], with $N_c$ the color number.

With $\mathbf{B}'_c\,(\mathbf{B}')$ denoting the charmed sextet (decuplet) baryon, the matrix elements of the $\mathbf{B}_c'\rightarrow \mathbf{B}'$ transition can be parameterized as [28, 45]

$$\begin{aligned} \langle T^\mu \rangle&\equiv \langle \mathbf{B}^{\prime }(P^{\,\prime },S',S_z^\prime )|{\bar{q}}\gamma ^\mu (1-\gamma _5)c|\mathbf{B}'_c(P,S,S_z)\rangle \nonumber \\&= \bar{u}_{\alpha }(P^{\,\prime },S_{z}^{\,\prime }) \left[ \frac{P^{\alpha }}{M}\left( \gamma ^{\mu }F^V_{1} +\frac{P^{\mu }}{M} F^V_{2} +\frac{P^{\,\prime \mu }}{M^{\prime }}F^V_{3}\right) \right. \nonumber \\&\quad \left. +g^{\alpha \mu }F^V_{4}\right] \gamma _{5}u(P,S_{z})\nonumber \\&\quad -\bar{u}_{\alpha }(P^{\,\prime },S_{z}^{\,\prime }) \left[ \frac{P^{\alpha }}{M}\left( \gamma ^{\mu }F^A_{1} +\frac{P^{\mu } }{M}F^A_{2} +\frac{P^{\,\prime \mu }}{M^{\prime }}F^A_{3}\right) \right. \nonumber \\&\quad \left. +g^{\alpha \mu }F^A_{4}\right] u(P,S_{z})\,, \end{aligned}$$

(4)

where $(M,M')$ and $(S,S')=(1/2,3/2)$ represent the masses and spins of $(\mathbf{B}'_c,\mathbf{B}')$, respectively, and $F^{V,A}_i$ ($i=1,2, \ldots ,4$) the form factors to be extracted in the light-front quark model. The matrix elements of the meson productions are defined as [5]

$$\begin{aligned}&\langle \pi (p) |({\bar{u}}d)|0 \rangle = if_\pi q^\mu \,,\nonumber \\&\langle \rho (\lambda ) |({\bar{u}}d)|0 \rangle =m_\rho f_\rho \epsilon _\lambda ^{\mu *}\,, \end{aligned}$$

(5)

where $f_{\pi (\rho )}$ is the decay constant, and $\epsilon _\lambda ^\mu$ is the polarization four-vector with $\lambda$ denoting the helicity state.

2.2 The light-front quark model

The baryon bound state $\mathbf{B}'_{(c)}$ contains three quarks $q_1$, $q_2$ and $q_3$, with the subscript c for $q_1=c$. Moreover, $q_2$ and $q_3$ are combined as a diquark state $q_{[2,3]}$, behaving as a scalar or axial-vector. Subsequently, the baryon bound state $|\mathbf{B}'_{(c)}(P,S,S_z)\rangle$ in the light-front quark model can be written as [31]

$$\begin{aligned}&|\mathbf{B}'_{(c)}(P,S,S_z)\rangle = \int \{d^{3}p_{1}\} \{d^{3}p_{2}\}2(2\pi )^{3}\delta ^{3}(\tilde{P}-\tilde{p}_{1}-\tilde{p}_{2})\nonumber \\&\quad \times \sum _{\lambda _{1},\lambda _{2}}\Psi ^{SS_{z}} (\tilde{p}_{1},\tilde{p}_{2},\lambda _{1},\lambda _{2})|q_1(p_1,\lambda _{1})q_{[2,3]} (p_{2},\lambda _{2})\rangle \,, \end{aligned}$$

(6)

where $\Psi ^{SS_{z}}$ is the momentum-space wave function, and $(p_i,\lambda _i)$ stand for momentum and helicity of the constituent (di)quark, with $i=1,2$ for $q_1$ and $q_{[2,3]}$, respectively. The tilde notations represent that the quantities are in the light-front frame, and one defines $P=(P^-,P^+,P_\bot )$ and ${\tilde{P}}=(P^+,P_\bot )$, with $P^\pm =P^0\pm P^3$ and $P_\bot =(P^1,P^2)$. Besides, $\tilde{p}_i$ are given by

$$\begin{aligned} {\tilde{p}}_i=(p_i^+, p_{i\bot })~, \quad p_{i\bot }= (p_i^1, p_i^2)~, \quad p_i^- = {m_i^2+p_{i\bot }^2\over p_i^+},\nonumber \\ \end{aligned}$$

(7)

with

$$\begin{aligned}&m_1=m_{q_1}, \quad m_2=m_{q_1}+m_{q_2},\nonumber \\&p^+_1=(1-x) P^+, \quad p^+_2=x P^+,\nonumber \\&p_{1\bot }=(1-x) P_\bot -k_\bot , \quad p_{2\bot }=xP_\bot +k_\bot \,, \end{aligned}$$

(8)

where x and $k_\perp$ are the light-front relative momentum variables with $k_\perp$ from $\vec {k}=(k_\perp ,k_z)$, ensuring that $P^{+}=p^+_1+p^+_2$ and $P_{\bot }=p_{1\bot }+p_{2\bot }$. According to $e_i\equiv \sqrt{m^2_{i}+{\vec {k}}^2}$ and $M_0\equiv e_1+e_2$ in the Melosh transformation [30], we obtain

$$\begin{aligned}&x=\frac{e_2-k_z}{e_1+e_2}\,,\quad 1-x=\frac{e_1+k_z}{e_1+e_2}\,,\quad k_z=\frac{xM_0}{2}-\frac{m^2_{2}+k^2_{\perp }}{2xM_0}\,,\nonumber \\&M_0^2={ m_{1}^2+k_\bot ^2\over 1-x}+{ m_{2}^2+k_\bot ^2\over x}\,. \end{aligned}$$

(9)

Consequently, $\Psi ^{SS_{z}}$ can be given in the following representation [41,42,43,44,45]:

$$\begin{aligned}&\Psi ^{SS_{z}}(\tilde{p}_{1},\tilde{p}_{2},\lambda _{1},\lambda _{2})\nonumber \\&\quad = \frac{A^{(\prime )}}{\sqrt{2(p_{1}\cdot \bar{P}+m_{1}M_{0})}}\bar{u}(p_{1},\lambda _{1}) \Gamma _{S,A}^{(\alpha )} u(\bar{P},S_{z})\phi (x,k_{\perp })\,,\nonumber \\ \end{aligned}$$

(10)

with

$$\begin{aligned} A&=\sqrt{\frac{3(m_{1}M_{0}+p_{1}\cdot \bar{P})}{3m_{1}M_{0}+p_{1}\cdot \bar{P}+ 2(p_{1}\cdot p_{2})(p_{2}\cdot \bar{P})/m_{2}^{2}}}\,,\\ \Gamma _S&=1,\;\; \Gamma _{A}=-\frac{1}{\sqrt{3}}\gamma _{5} \epsilon \! \! /^{*}(p_{2},\lambda _{2})\,, \end{aligned}$$

and

$$\begin{aligned}&A'=\sqrt{\frac{3m_{2}^{2}M_{0}^{2}}{2m_{2}^{2}M_{0}^{2}+(p_{2}\cdot \bar{P})^{2}}}\,,\;\; \Gamma _{A}^{\alpha }=\epsilon ^{*\alpha }(p_{2},\lambda _{2})\,, \end{aligned}$$

(11)

where the vertex function $\Gamma _{S(A)}$ is for the scalar (axial-vector) diquark in $\mathbf{B}'_c$, and $\Gamma _A^\alpha$ for the axial-vector diquark in $\mathbf{B}'$. We have used the variable ${\bar{P}}\equiv p_1+p_2$ to describe the internal motions of the constituent quarks in the baryon [32], which leads to $({\bar{P}}_\mu \gamma ^\mu -M_0)u(\bar{P},S_{z})=0$, different from $(P_\mu \gamma ^\mu -M)u(P,S_{z})=0$. For the momentum distribution, $\phi (x,k_{\perp })$ is presented as the Gaussian-type wave function, given by

$$\begin{aligned} \phi (x,k_{\perp })=4\left( \frac{\pi }{\beta ^{2}}\right) ^{3/4}\sqrt{\frac{e_{1}e_{2}}{x(1-x)M_{0}}}\exp \left( \frac{-{\vec {k}}^{2}}{2\beta ^{2}}\right) \,, \end{aligned}$$

(12)

where $\beta$ shapes the distribution.

Using $|\mathbf{B}'_c(P,S,S_z)\rangle$ and $|\mathbf{B}'(P,'S',S'_z)\rangle$ from Eq. (6) and their components in Eqs. (10), (11) and (12), we derive the matrix elements of the $\mathbf{B}'_c\rightarrow \mathbf{B}'$ transition in Eq. (4) as

$$\begin{aligned}&\langle {\bar{T}}^\mu \rangle \equiv \langle \mathbf{B}^{\prime }(P^{\,\prime },S',S_z^\prime )|{\bar{q}}\gamma ^\mu (1-\gamma _5)c|\mathbf{B}'_c(P,S,S_z)\rangle \nonumber \\&\quad = \int \{d^{3}p_{2}\}\frac{\phi ^{\prime }(x^{\prime },k_{\perp }^{\prime })\phi (x,k_{\perp })}{2\sqrt{p_{1}^{+}p_{1}^{\prime +}(p_{1}\cdot \bar{P}+m_{1}M_{0})(p_{1}^{\prime }\cdot \bar{P}^{\,\prime } +m_{1}^{\prime }M_{0}^{\prime })}}\nonumber \\&\qquad \times \sum _{\lambda _{2}}\bar{u}_{\alpha }(\bar{P}^{\,\prime },S_{z}^{\,\prime }) \left[ {\bar{\Gamma }}^{\,\prime \alpha }_{A}(p \! \! /_{1}^{\prime }+m_{1}^{\prime }) \right. \nonumber \\&\qquad \times \left. \gamma ^{\mu }(1-\gamma _{5})({p \! \! /}_{1}+m_{1})\Gamma _{A}\right] u(\bar{P},S_{z})\,, \end{aligned}$$

(13)

with $m_1=m_c$, $m'_1=m_q$ and ${{\bar{\Gamma }}}=\gamma ^0 \Gamma ^\dagger \gamma ^0$. We define $J_{5\,j}^{\mu }=\bar{u}(\Gamma _{5}^{\mu \beta })_{j}u_{\beta }$ and ${\bar{J}}_{5\,j}^{\mu }=\bar{u}({{\bar{\Gamma }}}_{5}^{\mu \beta })_{j}u_{\beta }$ with $j=1,2,...,4$, where

$$\begin{aligned} (\Gamma _{5}^{\mu \beta })_j= & {} \{\gamma ^{\mu }P^{\beta },P^{\,\prime \mu }P^{\beta },P^{\mu }P^{\beta },g^{\mu \beta }\}\gamma _{5}\,,\nonumber \\ ({\bar{\Gamma }}_{5}^{\mu \beta })_j= & {} \{\gamma ^{\mu }\bar{P}^{\beta },\bar{P}^{\,\prime \mu }\bar{P}^{\beta },\bar{P}^{\mu }\bar{P}^{\beta },g^{\mu \beta }\}\gamma _{5}\,. \end{aligned}$$

(14)

Then, we multiply $J_{5\,j}$ (${\bar{J}}_{5\,j}$) by $\langle T\rangle$ ($\langle {\bar{T}}\rangle$) as $F_{5\,j}\equiv J_{5\,j}\cdot \langle T\rangle$ and ${\bar{F}}_{5\,j}\equiv {\bar{J}}_{5\,j}\cdot \langle {\bar{T}}\rangle$ with $\langle T\rangle$ and $\langle {\bar{T}}\rangle$ in Eqs. (4) and (13), respectively, resulting in [45]

$$\begin{aligned}&F_{5\,j}=Tr\bigg \{ u_{\beta }\bar{u}_{\alpha } \left[ \frac{P^{\alpha }}{M}\left( \gamma ^{\mu }F^V_{1} +\frac{P^{\mu }}{M} F^V_{2} +\frac{P^{\,\prime \mu }}{M^{\prime }}F^V_{3}\right) \right. \nonumber \\&\quad \left. +g^{\alpha \mu }F^V_{4}\right] \gamma _{5}{\bar{u}}({\Gamma }_{5\mu }^{\beta })_j\bigg \}\,,\nonumber \\&{\bar{F}}_{5\,j}= \int \{d^{3}p_{2}\}\frac{\phi ^{\prime }(x^{\prime },k_{\perp }^{\prime })\phi (x,k_{\perp })}{2\sqrt{p_{1}^{+}p_{1}^{\prime +}(p_{1}\cdot \bar{P}+m_{1}M_{0})(p_{1}^{\prime }\cdot \bar{P}^{\,\prime } +m_{1}^{\prime }M_{0}^{\prime })}} \nonumber \\&\quad \times \sum _{\lambda _{2}} Tr\bigg \{u_{\beta }\bar{u}_{\alpha } \left[ {\bar{\Gamma }}^{\,\prime \alpha }_{A}(p \! \! /_{1}^{\prime }+m_{1}^{\prime }) \gamma ^{\mu }(p \! \! /_{1}+m_{1})\Gamma _{A}\right] u({\bar{\Gamma }}_{5\mu }^{\beta })_j\bigg \}\,.\nonumber \\ \end{aligned}$$

(15)

In the connection of $F_{5\,j}={\bar{F}}_{5\,j}$, we construct four equations. By solving the four equations, the four form factors $F^V_1$, $F^V_2$, $F^V_3$ and $F^V_4$ can be extracted. The form factors $F^A_i$ can be obtained in the same way.

2.3 Branching fractions in the helicity basis

One can present the amplitude of $\Omega _c^0\rightarrow \Omega ^- h^+(\Omega ^- \ell ^+\nu _\ell )$ in the helicity basis of $H_{\lambda _\Omega \lambda _{h(\ell )}}$ [28, 45], where $\lambda _\Omega =\pm 3/2,\pm 1/2$ represent the helicity states of the $\Omega ^-$ baryon, and $\lambda _{h,\ell }$ those of $h^+$ and $\ell ^+\nu _\ell$. Substituting the matrix elements in Eqs. (3) with those in Eqs. (4) and (5), the amplitudes in the helicity basis now read $\sqrt{2}{{\mathcal {M}}}_h= (i)\sum _{\lambda _\Omega ,\lambda _h}G_F V^*_{cs}V_{ud}\,a_1 m_h f_h H_{\lambda _\Omega \lambda _h}$ and $\sqrt{2}{{\mathcal {M}}}_\ell =\sum _{\lambda _\Omega ,\lambda _\ell }G_F V^*_{cs} H_{\lambda _\Omega \lambda _\ell }$, where $H_{\lambda _\Omega \lambda _f}=H^V_{\lambda _\Omega \lambda _f}-H^A_{\lambda _\Omega \lambda _f}$ with $f=(h,\ell )$. Explicitly, $H^{V(A)}_{\lambda _\Omega \lambda _f}$ is written as [28]

$$\begin{aligned} H^{V(A)}_{\lambda _\Omega \lambda _f} \equiv \langle \Omega ^-|{\bar{s}}\gamma _\mu (\gamma _5)c|\Omega _c^0\rangle \varepsilon ^\mu _f\,, \end{aligned}$$

(16)

with $\varepsilon ^\mu _h=(q^\mu /\sqrt{q^2},\epsilon _\lambda ^{\mu *})$ for $h=(\pi ,\rho )$. For the semi-leptonic decay, since the $\ell ^+\nu _\ell$ system behaves as a scalar or vector, $\varepsilon ^\mu _\ell =q^\mu /\sqrt{q^2}$ or $\epsilon _\lambda ^{\mu \,*}$. The $\pi$ meson only has a zero helicity state, denoted by $\lambda _\pi ={\bar{0}}$. On the other hand, the three helicity states of $\rho$ are denoted by $\lambda _\rho =(1,0,-1)$. For the lepton pair, we assign $\lambda _\ell =\lambda _\pi$ or $\lambda _\rho$. Subsequently, we expand $H^{V(A)}_{\lambda _\Omega \lambda _f}$ as

$$\begin{aligned}&H_{\frac{1}{2} {{\bar{0}}}}^{V(A)} =\sqrt{\frac{2}{3}\frac{Q^2_{\pm }}{q^2}} \left( \frac{Q^2_\mp }{2MM'}\right) (F_1^{V(A)} M_\pm \nonumber \\&\quad \mp F_2^{V(A)}{\bar{M}}_+ \mp F_3^{V(A)}{\bar{M}}'_- \mp F_4^{V(A)} M )\,, \end{aligned}$$

(17)

for $\varepsilon ^\mu _f=q^\mu /\sqrt{q^2}$, where $M_\pm = M\pm M'$, $Q^2_\pm = M_\pm ^2 - q^2$, and ${\bar{M}}_{\pm }^{(\prime )}=(M_+M_-\pm q^2)/(2M^{(\prime )})$. We also obtain

$$\begin{aligned}&H_{\frac{3}{2}1}^{V(A)} = \mp \sqrt{Q^2_\mp } \, F_4^{V(A)}\,,\nonumber \\&H_{\frac{1}{2}1}^{V(A)}=-\sqrt{\frac{Q^2_\mp }{3}} \left[ F_1^{V(A)} \left( \frac{Q^2_\pm }{M M'}\right) -F_4^{V(A)}\right] \,,\nonumber \\&H_{\frac{1}{2}0}^{V(A)}= \sqrt{\frac{2}{3}\frac{Q^2_\mp }{q^2}} \left[ F_1^{V(A)} \left( \frac{Q^2_\pm M_\mp }{2MM'}\right) \right. \nonumber \\&\quad \left. \mp \left( F_2^{V(A)}+F_3^{V(A)}\frac{M}{M'}\right) \left( \frac{|{\vec {P}}'|^2}{M'}\right) \mp F_4^{V(A)}{\bar{M}}'_- \right] \,, \end{aligned}$$

(18)

for $\varepsilon ^\mu _f=\epsilon _\lambda ^{\mu *}$, with $|{\vec {P}}'|=\sqrt{Q^2_+ Q^2_-}/(2M)$. Note that the expansions in Eqs. (17) and (18) have satisfied $\lambda _{\Omega _c}=\lambda _\Omega -\lambda _f$ for the helicity conservation, with $\lambda _{\Omega _c}=\pm 1/2$. The branching fractions then read

$$\begin{aligned} {{\mathcal {B}}}_h&\equiv {{\mathcal {B}}}(\Omega ^0_c\rightarrow \Omega ^- h^+)\nonumber \\&= \frac{\tau _{\Omega _c}G_F^2|{\vec {P}}'|}{32\pi m_{\Omega _c}^2} |V_{cs}V_{ud}^*|^2\,a_1^2 m_h^2 f_h^2 H_h^2\,,\nonumber \\ {{\mathcal {B}}}_\ell&\equiv {{\mathcal {B}}}(\Omega _c^0\rightarrow \Omega ^- \ell ^+\nu _\ell ) \nonumber \\&=\frac{\tau _{\Omega _c}G_F^2|V_{cs}|^2}{192\pi ^3 m_{\Omega _c}^2} \int ^{(m_{\Omega _c}-m_\Omega )^2}_{m_\ell ^2}dq^2 \left( \frac{|{\vec {P}}'|(q^2-m_\ell ^2)^2}{q^2}\right) H_\ell ^2\,,\nonumber \\ \end{aligned}$$

(19)

where

$$\begin{aligned} H_\pi ^2= & {} \left| H_{\frac{1}{2}{{\bar{0}}}}\right| ^2+\left| H_{{-\frac{1}{2}}{{\bar{0}}}}\right| ^2\,,\nonumber \\ H_\rho ^2= & {} \left| H_{\frac{3}{2}1}\right| ^2+\left| H_{\frac{1}{2}1}\right| ^2+\left| H_{\frac{1}{2}0}\right| ^2 +\left| H_{-\frac{1}{2}0}\right| ^2+\left| H_{-\frac{1}{2}-1}\right| ^2\nonumber \\&+\left| H_{-\frac{3}{2}-1}\right| ^2\,,\nonumber \\ H_\ell ^2= & {} \left( 1+\frac{m_\ell ^2}{2q^2}\right) H_\rho ^2+\frac{3m_\ell ^2}{2q^2}H_\pi ^2\,, \end{aligned}$$

(20)

with $\tau _{\Omega _c}$ the $\Omega _c^0$ lifetime.

3 Numerical analysis

In the Wolfenstein parameterization, the CKM matrix elements are adopted as $V_{cs}=V_{ud}=1-\lambda ^2/2$ with $\lambda =0.22453\pm 0.00044$ [5]. We take the lifetime and mass of the $\Omega _c^0$ baryon and the decay constants $(f_\pi ,f_\rho )=(132,216)$ MeV from the PDG [5]. With $(c_1,c_2)=(1.26,-0.51)$ at the $m_c$ scale [47], we determine $a_1$. In the generalized factorization, $N_c$ is taken as an effective color number with $N_c=(2,3,\infty )$ [28, 29, 46, 50], in order to estimate the non-factorizable effects. For the $\Omega _c^+(css)\rightarrow \Omega ^-(sss)$ transition form factors, the theoretical inputs of the quark masses and parameter $\beta$ in Eq. (15) are given by [34, 40]

$$\begin{aligned} m_{1}= & {} m_{c}=(1.35\pm 0.05)~\mathrm {GeV}\,,\quad m_{1}^{\prime }=m_{s}=0.38~\mathrm {GeV}\,,\quad \nonumber \\ m_{2}= & {} 2m_s=0.76~\mathrm {GeV}\,,\nonumber \\ \beta _c= & {} 0.60~\mathrm {GeV}\,, \quad \beta _s=0.46~\mathrm {GeV}\,, \end{aligned}$$

(21)

where $\beta _{c(s)}$ is to determine $\phi ^{(\prime )}(x^{(\prime )},k_{\perp }^{(\prime )})$ for $\Omega _c^0$ $(\Omega ^-)$. We hence extract $F^V_i$ and $F^A_i$ in Table 1. For the momentum dependence, we have used the double-pole parameterization:

$$\begin{aligned} F(q^2)=\frac{F(0)}{1-a\left( q^2/m_F^2\right) +b\left( q^4/m_F^4\right) }\,, \end{aligned}$$

(22)

with $m_F=1.86$ GeV.

Table 1 The $\Omega ^0_c\rightarrow \Omega ^-$ transition form factors with F(0) at $q^2=0$, where $\delta \equiv \delta m_c/m_c=\pm 0.04$ from Eq. (21)

Using the theoretical inputs, we calculate the branching fractions, whose results are given in Table 2.

4 Discussions and conclusions

Table 2 Branching fractions of (non-)leptonic $\Omega _c^0$ decays and their ratios, where ${{\mathcal {R}}}_{\rho (e)/\pi }\equiv {{\mathcal {B}}}_{\rho (e)}/{{\mathcal {B}}}_\pi$. The three numbers in the parenthesis correspond to $N_c=(2,3,\infty )$, and the errors come from the uncertainties of the form factors in Table 1

In Table 2, we present ${{\mathcal {B}}}_{\pi }$ and ${{\mathcal {B}}}_{\rho }$ with $N_c=(2,3,\infty )$. The errors come from the form factors in Table 1, of which the uncertainties are correlated with the charm quark mass. By comparison, ${{\mathcal {B}}}_\pi$ and ${{\mathcal {B}}}_\rho$ are compatible with the values in Ref. [28]; however, an order of magnitude smaller than those in Refs. [20, 22], whose values are obtained with the total decay widths $\Gamma _{\pi (\rho )}=2.09 a_1^2(11.34 a_1^2)\times 10^{11}$ s$^{-1}$ and $\Gamma _{\pi (\rho )}=1.33 a_1^2(4.68 a_1^2)\times 10^{11}$ s$^{-1}$, respectively. We also predict ${{\mathcal {B}}}_e=(5.4\pm 0.2)\times 10^{-3}$ as well as ${{\mathcal {B}}}_\mu \simeq {{\mathcal {B}}}_e$, which is much smaller than the value of $127\times 10^{-3}$ in [24]. Only the ratios ${{\mathcal {R}}}_{\rho /\pi }$ and ${{\mathcal {R}}}_{e/\pi }$ have been actually observed so far. In our work, ${{\mathcal {R}}}_{\rho /\pi }=2.8\pm 0.4$ is able to alleviate the inconsistency between the previous value and the most recent observation. We obtain ${{\mathcal {R}}}_{e/\pi }=1.1\pm 0.2$ with $N_c=2$ to be consistent with the data, which indicates that $({{\mathcal {B}}}_\pi ,{{\mathcal {B}}}_\rho )=(5.1\pm 0.7,14.4\pm 0.4)\times 10^{-3}$ with $N_c=2$ are more favorable.

The helicity amplitudes can be used to better understand how the form factors contribute to the branching fractions. With the identity $H^{V(A)}_{-\lambda _\Omega -\lambda _f} = \mp H^{V(A)}_{\lambda _\Omega \lambda _f}$ for the $\mathbf{B}'_c(J^P=1/2^+)$ to $\mathbf{B}'(J^P=3/2^+)$ transition [28], $H_\pi ^2$ in Eq. (20) can be rewritten as $H_\pi ^2=2(|H_{\frac{1}{2} {{\bar{0}}}}^V|^2 +|H_{\frac{1}{2} {{\bar{0}}}}^A|^2)$. From the pre-factors in Eq. (17), we estimate the ratio of $|H_{\frac{1}{2} {{\bar{0}}}}^V|^2/|H_{\frac{1}{2} {{\bar{0}}}}^A|^2\simeq 0.05$, which shows that $H_{\frac{1}{2} {{\bar{0}}}}^A$ dominates ${{\mathcal {B}}}_\pi$, instead of $H_{\frac{1}{2} {{\bar{0}}}}^V$. More specifically, it is the $F_4^A$ term in $H_{\frac{1}{2} {{\bar{0}}}}^A$ that gives the main contribution to the branching fraction. By contrast, the $F_{1,3}^A$ terms in $H_{\frac{1}{2} {{\bar{0}}}}^A$ largely cancel each other, which is caused by $F_1^A M_- \simeq F_3^A {\bar{M}}'_-$ and a minus sign between $F_1^A$ and $F_3^A$ (see Table 1); besides, the $F_2^A$ term with a small $F_2^A(0)$ is ignorable.

Likewise, we obtain $H_\rho ^2=2(|H_\rho ^V|^2+|H_\rho ^A|^2)$ for ${{\mathcal {B}}}_\rho$, where $|H_\rho ^{V(A)}|^2= |H_{\frac{3}{2}1}^{V(A)}|^2+|H_{\frac{1}{2}1}^{V(A)}|^2+|H_{\frac{1}{2}0}^{V(A)}|^2$. We find that $|H_\rho ^A|^2$ is ten times larger than $|H_\rho ^V|^2$. Moreover, $H_{\frac{1}{2}0}^A$ is similar to $H_{\frac{1}{2}{\bar{0}}}^A$, where the $F_{1,3}^A$ terms largely cancel each other, $F_2^A$ is ignorable, and $F_4^A$ gives the main contribution. While $F_1^A$ and $F_4^A$ in $H_{\frac{1}{2}1}^A$ have a positive interference, giving 20% of ${{\mathcal {B}}}_\rho$, $F_4^A$ in $H_{\frac{3}{2}1}^A$ singly contributes 35%. In Eq. (20), the factor of $m_\ell ^2/q^2$ with $m_\ell \simeq 0$ should be much suppressed, such that $H_\ell ^2\simeq H_\rho ^2$. Therefore, ${{\mathcal {B}}}_\ell$ receives the main contributions from the $F_4^A$ terms in $H_{\frac{1}{2}0}^A$, $H_{\frac{1}{2}1}^A$ and $H_{\frac{3}{2}1}^A$, which is similar to the analysis for ${{\mathcal {B}}}_\rho$.

In summary, we have studied the $\Omega ^0_c\rightarrow \Omega ^-\pi ^+,\Omega ^-\rho ^+$ and $\Omega ^0_c\rightarrow \Omega ^-\ell ^+\nu _\ell$ decays, which proceed through the $\Omega _c^0\rightarrow \Omega ^-$ transition and the formation of the meson $\pi ^+(\rho ^+)$ or lepton pair from the external W-boson emission. With the form factors of the $\Omega _c^0\rightarrow \Omega ^-$ transition, calculated in the light-front quark model, we have predicted ${{\mathcal {B}}}(\Omega _c^0\rightarrow \Omega ^-\pi ^+,\Omega ^-\rho ^+)=(5.1\pm 0.7,14.4\pm 0.4)\times 10^{-3}$ and ${{\mathcal {B}}}(\Omega _c^0\rightarrow \Omega ^- e^+\nu _e)=(5.4\pm 0.2)\times 10^{-3}$. While the previous studies have given the ${{\mathcal {R}}}_{\rho /\pi }$ values deviating from the most recent observation, we have presented ${{\mathcal {R}}}_{\rho /\pi }=2.8\pm 0.4$ to alleviate the deviation. Moreover, we have obtained ${{\mathcal {R}}}_{e/\pi }=1.1\pm 0.2$, consistent with the current data.