Study of the $K_1(1270)-K_1(1400)$ mixing in the decays $B\rightarrow J/\Psi K_1(1270), J/\Psi K_1(1400)$

Abstract

We study the B meson decays $B\rightarrow J/\Psi K_1(1270,1400)$ in the pQCD approach beyond the leading order. With the vertex corrections and the NLO Wilson coefficients included, the branching ratios of the considered decays are predicted as $Br(B^+\rightarrow J/\Psi K_1(1270)^+)=1.76^{+0.65}_{-0.69}\times 10^{-3}, Br(B^+\rightarrow J/\Psi K_1(1400)^+)=6.47^{+2.50}_{-2.34}\times 10^{-4}$, and $Br(B^0\rightarrow J/\Psi K_1(1270)^0)=(1.63^{+0.60}_{-0.64})\times 10^{-3}$ with the mixing angle $\theta _{K_1}=33^\circ$, which can agree well with the data or the present experimental upper limit within errors. So we support the opinion that $\theta _{K_1}\sim 33^\circ$ is much more favored than $58^{\circ }$. Furthermore, we also give the predictions of the polarization fractions, the direct CP violations, the relative phase angles for the considered decays with the mixing angle $\theta _{K_1}=33^\circ$ and $58^\circ$, respectively. The direct CP violations of the two charged decays $B^+\rightarrow J/\Psi K_1(1270,1400)^+$ are very small $(10^{-4}\sim 10^{-5})$, because the weak phase is very tiny. In order to check the dependence of the results on the nonperturbative input parameters, we also calculate them by using the harmonic-oscillator type wave functions for the $J/\Psi$ meson. These results can be tested at the running LHCb and forthcoming Super-B experiments.

1 Introduction

B meson exclusive decays into charmonia have been received a lot of attention for many years. They are regarded as the golden channels in researching CP violation and exploring new physics. At the same time, they play important roles in testing the unitarity of the Cabibbo–Kobayashi–Maskawa (CKM) triangle. Moreover, these decays are ideal modes to test the different factorization approaches. Compared with other factorization approaches, such as the naive factorization assumption (FA) [1, 2], the QCD-improved factorization (QCDF) [3, 4], the perturbtive QCD (pQCD) approach [5] has the unique advantage in solving the B meson charmed decays [6, 7]. The Sudakov factor induced by the $k_T$ resummation [8, 9] can eliminate the double logarithmic divergences. The jet function induced by the threshold resummation [10] can smear the end-point singularities. Without the divergences, one can evaluate all possible Feynman diagrams correctly, including the nonfactorizable emission diagrams and annihilation type diagrams. But it is difficult to calculate these two kinds of contributions by using other factorization approaches.

Some of the decays $B\rightarrow J/\Psi K_1(1270), J/\Psi K_1(1400)$ have been measured by Belle [11],

$$\begin{aligned}&Br(B^+\rightarrow J/\Psi K^+_1(1270)) =(1.80\pm 0.34\pm 0.39)\times 10^{-3},\nonumber \\ \end{aligned}$$

(1)

$$\begin{aligned}&Br(B^+\rightarrow J/\Psi K^+_1(1400))<5.4\times 10^{-4}, \end{aligned}$$

(2)

$$\begin{aligned}&Br(B^0\rightarrow J/\Psi K^0_1(1270)) =(1.30\pm 0.34\pm 0.31)\times 10^{-3},\nonumber \\ \end{aligned}$$

(3)

where the first uncertainties are statistical and the second are systematic.

As is well known, the physical mass eigenstates $K_1(1270)$ and $K_1(1400)$ are the mixing by the flavor eigenstates $K_{1A}$ and $K_{1B}$ through the following formula:

$$\begin{aligned} \left( \begin{matrix} |K_1(1270)\rangle \\ |K_1(1400)\rangle \end{matrix}\right) =\left( \begin{matrix}\sin \theta _{K_1} &{} \cos \theta _{K_1}\\ \cos \theta _{K_1} &{} -\sin \theta _{K_1}\end{matrix}\right) \left( \begin{matrix}|K_{1A}\rangle \\ |K_{1B}\rangle \end{matrix}\right) . \end{aligned}$$

(4)

Usually we combine $K_{1A}$ with $a_1(1260), f_1(1285), f_1(1420)$ to form the nonet $J^{PC}=1^{++}$, while combine $K_{1B}$ with $b_1(1235), h_1(1170), h_1(1380)$ to comprise the other nonet $J^{PC}=1^{+-}$. These two nonet mesons can also be denoted as $^3P_1$ and $^1P_1$ in terms of the spectroscopic notation $^{2S+1}L_{J}$. Various phenomenological studies indicate that the mixing angle $\theta _{K_1}$ is around either $33^\circ$ or $58^\circ$ [12,13,14,15,16,17,18,19].

In view of the above situation, we are motivated to set out to: (a) Proving whether the pQCD approach can be used in our considered decays by comparing with the data. Several earlier works on B decays into charmonia [6, 20, 21] show that this approach can give the results in agreement with data, which encourage our attempt. (b) Exploring the inner structure of the axial-vector mesons $K_1(1270, 1400)$, in other words, detecting which mixing angle shown in Eq. (4) is favored. (c) Studying of CP violation even new physics in these decays containing the charmonium state. Besides the full leading-order (LO) contributions, the next-to-leading-order (NLO) contributions are also included, which are mainly from the NLO Wilson coefficients and the vertex corrections to the hard kernel. Certainly, other NLO contributions, such as the quark loops and the magnetic penguin corrections, are also available in the literature [22, 23], while they will not contribute to the decays considered.

We review the LO order predictions for the decays $B\rightarrow J/\Psi K_1(1270),J/\Psi K_1(1400)$ including those for the main NLO contributions in Sect. 2. We perform the numerical study in Sect. 3, where the theoretical uncertainties are also considered. Section 4 is the conclusion.

2 The leading-order predictions and the main next-to-leading-order corrections

The weak effective Hamiltonian $H_\mathrm{eff}$ for the decays $B\rightarrow J/\Psi K_1(1270, 1400)$ can be written as

$$\begin{aligned}&{} H _\mathrm{eff}=\frac{G_F}{\sqrt{2}}\biggl [V^*_{cb}V_{cs}(C_1(\mu )O^c_1(\mu )+C_2(\mu )O^c_2(\mu ))\nonumber \\&\quad \quad \quad - V^{*}_{tb}V_{ts}\sum ^{10}_{i=3}C_i(\mu )O_i(\mu )\biggr ], \end{aligned}$$

(5)

where $C_i(\mu )$ are Wilson coefficients at the renormalization scale $\mu$, V represents for the Cabibbo–Kobayashi–Maskawa (CKM) matrix element, and the four fermion operators $O_i$ are given as

$$\begin{aligned} O^c_1= & {} (\bar{s}_{i}c_{j})_{V-A}(\bar{c}_{j}b_{i})_{V-A},\;\;\; O^c_2=(\bar{s}_{i}c_{i})_{V-A}(\bar{c}_{j}b_{j})_{V-A},\nonumber \\ \end{aligned}$$

(6)

$$\begin{aligned} O_3= & {} (\bar{s}_{i}b_{i})_{V-A}(\bar{q}_{j}q_{j})_{V-A},\;\;\; O_4=(\bar{s}_{i}b_{j})_{V-A}(\bar{q}_{j}q_{i})_{V-A}, \nonumber \\ \end{aligned}$$

(7)

$$\begin{aligned} O_5= & {} (\bar{s}_{i}b_{i})_{V-A}(\bar{q}_{j}q_{j})_{V+A},\;\;\; O_6=(\bar{s}_{i}b_{j})_{V-A}(\bar{q}_{j}q_{i})_{V+A}, \nonumber \\ \end{aligned}$$

(8)

$$\begin{aligned} O_7= & {} \frac{3}{2}(\bar{s}_{i}b_{i})_{V-A}\sum _{q}e_{q}(\bar{q}_{j}q_{j})_{V+A}, \nonumber \\ O_8= & {} \frac{3}{2}(\bar{s}_{i}b_{j})_{V-A}\sum _{q}e_{q}(\bar{q}_{j}q_{i})_{V+A}, \end{aligned}$$

(9)

$$\begin{aligned} O_9= & {} \frac{3}{2}(\bar{s}_{i}b_{i})_{V-A}\sum _{q}e_{q}(\bar{q}_{j}q_{j})_{V-A},\nonumber \\ O_{10}= & {} \frac{3}{2}(\bar{s}_{i}b_{j})_{V-A}\sum _{q}e_{q}(\bar{q}_{j}q_{i})_{V-A}, \end{aligned}$$

(10)

with i, j being the color indices.

Fig. 1

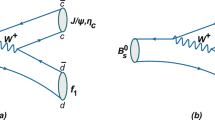
Feynman diagrams contributing to the decay $B^+\rightarrow J/\Psi K^+_{1A}$ at the leading order. The hard gluon connecting the four quark operator and the spectator quark is necessary to ensure the pQCD applicability. They are the same as those for $B^+\rightarrow J/\Psi K^+_{1B}$. If replacing the spectator u quark with d quark, we will obtain the Feynman diagrams for the decays $B^0\rightarrow J/\Psi K^0_{1A}, J/\Psi K^0_{1B}$

It is convenient to do the calculation in the rest frame of B meson because of the heavy b quark. Throughout this paper, we take the light-cone coordinate $(P^+,P^-,\mathbf P _T)$ to describe the meson’s momenta with $P^{\pm }=(p_0\pm p_3)/\sqrt{2}$ and $\mathbf P _T=(p_1,p_2)$. Then the momenta of mesons $B, J/\Psi$ and $K_1$ can be written as

$$\begin{aligned} P_1= & {} \frac{m_B}{\sqrt{2}}(1,1,\mathbf 0 _T), \;\;\;\;\;P_2=\frac{m_B}{\sqrt{2}}(1-r^2_3,r^2_2,\mathbf 0 _T),\nonumber \\ P_3= & {} \frac{m_B}{\sqrt{2}}(r^2_3,1-r^2_2,\mathbf 0 _T), \end{aligned}$$

(11)

respectively. The mass ratios $r_2=m_{J/\Psi }/m_B, r_3=m_{K_1}/m_B$. In the numerical calculation, the terms proportional to $r^2_3$ are neglected, as $r^2_3\sim 0.06$ is numerically small. Putting the (light) quark momenta in $B, J/\Psi , K_1$ mesons as $k_1, k_2, k_3$, respectively, we have

$$\begin{aligned} k_1= & {} (x_1P^+_1,0,\mathbf k _{1T}), \;\;\;\;k_2=x_2P_2+(0,0,\mathbf k _{2T}),\nonumber \\ k_3= & {} x_3P_3+(0,0,\mathbf k _{3T}). \end{aligned}$$

(12)

There are three kinds of polarizations of a vector or an axial-vector meson, namely longitudinal (L), normal (N) and transverse (T). So the amplitudes for the decay mode $B(P_1)\rightarrow V_2(P_2,\epsilon ^*_{2\mu }) +A_3(P_3,\epsilon ^*_{3\nu })$ are characterized by those polarization states, which can be decomposed as follows:

$$\begin{aligned} A^{(\sigma )}= & {} \epsilon ^*_{2\mu }(\sigma )\epsilon ^*_{3\nu }(\sigma )\left[ ag^{\mu \nu }+\frac{b}{M_2 M_3}P^\mu _1P^\nu _1\right. \nonumber \\&\quad \left. +\,i\frac{c}{M_2M_3}\epsilon ^{\mu \nu \alpha \beta }P_{2\alpha }P_{3\beta }\right] \nonumber \\&=\mathcal {M}^L+\mathcal {M}^N\epsilon ^*_2(\sigma =T)\cdot \epsilon ^*_3(\sigma =T)\nonumber \\&\quad +\,i\frac{\mathcal {M }^T}{M^2_B}\epsilon ^{\alpha \beta \gamma \rho }\epsilon ^*_{2\alpha }(\sigma ) \epsilon ^*_{3\beta }(\sigma )P_{2\gamma }P_{3\rho }, \end{aligned}$$

(13)

where $M_{2(3)}$ is the mass of the vector (axial-vector) meson $V_2(A_3)$. The definitions of the amplitudes $\mathcal {M}^j(j=L,N,T)$ in terms of the Lorentz-invariant amplitudes a, b and c are given as

$$\begin{aligned} \mathcal {M}^{L}= & {} a \epsilon ^*_{2}(L)\cdot \epsilon ^*_{3}(L)+\frac{b}{M_2M_3}\epsilon ^*_{2}(L)\cdot P_3 \epsilon ^*_{3}(L)\cdot P_2,\nonumber \\ \end{aligned}$$

(14)

$$\begin{aligned} \mathcal {M}^N= & {} a, \;\;\;\; \mathcal {M}^T=\frac{c}{r_2r_3}. \end{aligned}$$

(15)

It is noticed that the subscript $K_1$ refers to the flavor eigenstate $K_{1A}$ or $K_{1B}$. At the leading order, the relevant contributions are only from the factorizable and nonfactorizable emission diagrams, as shown in Fig. 1. We take the decay $B^+\rightarrow J/\Psi K_{1A(B)}^+$ as an example. The emission particle is the vector meson $J/\Psi$, and the amplitude for the factorizable emission diagrams. Figure 1a, b from the longitudinal polarization can be written as

$$\begin{aligned}&\mathcal {F}^{L}_{J/\Psi K_1}=8\pi C_F m^4_Bf_{J/\Psi }\int _0^1 \mathrm{d}x_1 \mathrm{d}x_3 \int _0^\infty \nonumber \\&\qquad \times b_1 db_1 b_3 db_3 \phi _B(x_1,b_1)(r^2_2-1)\nonumber \\&\qquad \times \{[(1+(1-r^2_2)x_3)\phi _{K_1}(x_3)\nonumber \\&\qquad +r_{3}(1-2x_3)(\phi ^s_{K_1}(x_3)+\phi ^t_{K_1}(x_3))] \nonumber \\&\qquad \times \alpha _s(t_a)E_e(t_a)h_e(x_1,x_3,b_1,b_3)S_t(x_3)\nonumber \\&\qquad +\alpha _s(t_b)E_e(t_b)h_e(x_3,x_1,b_3,b_1)\nonumber \\&\qquad \times S_t(x_1)2r_{3}\phi ^s_{K_1}(x_3) \}, \end{aligned}$$

(16)

where the color factor $C_F=4/3$. $\phi _{K_1}$ and $\phi ^{t,s}_{K_1}$ are the twist-2 and twist-3 distribution amplitudes for the axial-vector meson $K_{1A}$ or $K_{1B}$, which can be found in Appendix A. The evolution factors evolving the Sudakov factor, the hard function $h_{e}$ and the jet function $S_t(x)$ are given in Appendix B. Similarly, the normal and transverse polarization amplitudes are

$$\begin{aligned}&\mathcal {F}^{N}_{J/\Psi K_1}\nonumber \\&\quad =8\pi C_F m^4_Bf_{J/\Psi }\int _0^1 \mathrm{d}x_1 \mathrm{d}x_3\nonumber \\&\quad \times \int _0^\infty b_1 db_1 b_3 db_3 \phi _B(x_1,b_1)r_{2}\nonumber \\&\quad \times \{[r_{3}((r^2_2-1)x_3((r^2_2-1)\phi ^a_A(x_3)+\phi ^v_A(x_3))-2\phi ^v_A(x_3)) \nonumber \\&\quad +(r^2_2-1)\phi ^a_T(x_3) ] \alpha _s(t_a)E_e(t_a)h_e(x_1,x_3,b_1,b_3)S_t(x_3)\nonumber \\&\quad -r_{3}[(1-r^2_{2})\phi ^v_A(x_3)+(r^2_2-1)^2\phi ^a_A(x_3)]\alpha _s(t_b)E_e(t_b)\nonumber \\&\quad \times h_e(x_3,x_1,b_3,b_1)S_t(x_1) \}, \end{aligned}$$

(17)

$$\begin{aligned}&\mathcal {F}^{T}_{J/\Psi K_1}\nonumber \\&\quad =-16\pi C_F m^4_Bf_{J/\Psi }\int _0^1 \mathrm{d}x_1 \mathrm{d}x_3\nonumber \\&\quad \times \int _0^\infty b_1 db_1 b_3 db_3 \phi _B(x_1,b_1)r_2 \nonumber \\&\quad \times \{[r_{3}((r^2_2-1)x_3+2)\phi ^a_A(x_3)-r_{3}x_3\phi ^v_A(x_3)+\phi ^T_A(x_3)]\nonumber \\&\quad \times \alpha _s(t_a)E_e(t_a)h_e(x_1,x_3,b_1,b_3)S_t(x_3)\nonumber \\&\quad +r_{3}[(1-r^2_{2})\phi ^a_A(x_3)+\phi ^v_A(x_3)]\alpha _s(t_b)E_e(t_b)\nonumber \\&\quad \times h_e(x_3,x_1,b_3,b_1)S_t(x_1) \}. \end{aligned}$$

(18)

Fig. 2

NLO vertex corrections to the factorizable emission diagrams. Figure 1a, b for the decay $B^+\rightarrow J/\Psi K^+_{1A}$. Here the hard gluon is not shown for simplicity. It is the same as those for the decay $B^+\rightarrow J/\Psi K^+_{1B}$

The longitudinal polarization amplitude for the nonfactorizable spectator diagrams. Figure 1c, d is given as

$$\begin{aligned}&\mathcal {M}^{L}_{J/\Psi K_1} =\frac{32}{\sqrt{6}}\pi C_F m^4_B \int _0^1 \mathrm{d}x_1 \mathrm{d}x_2 \mathrm{d}x_3\nonumber \\&\quad \times \int _0^\infty b_1 db_1 b_2 db_2 \phi _B(x_1,b_1)(r^2_{2}-1)\nonumber \\&\quad \times (2r_{3}\phi _{K_1}^t(x_3)-\phi _{K_1}(x_3))[2r_cr_{2}\psi ^t(x_2)\nonumber \\&\quad +\,(r^2_2(x_3-2x_2)-x_3)\psi ^L(x_2)]\nonumber \\&\quad \times \alpha _s(t_d)E_{en}(t_d)h_d(x_1,x_2,x_3,b_1,b_2), \end{aligned}$$

(19)

where the twist-2 and twist-3 distribution amplitudes $\psi ^{L,t}(x_2)$ for the $J/\Psi$ meson (Type I) can be found in Appendix A. The other two polarization amplitudes are written as:

$$\begin{aligned}&\mathcal {M}^{N}_{J/\Psi K_1} =\frac{64}{\sqrt{6}}\pi C_F m^4_B \int _0^1 \mathrm{d}x_1 \mathrm{d}x_2 \mathrm{d}x_3\nonumber \\&\quad \times \int _0^\infty b_1 db_1 b_2 db_2 \phi _B(x_1,b_1)\nonumber \\&\quad \times \{r_2\psi ^v(x_2)[r_{3}(x_2(1+r_2^2)+x_3(1-r_2^2)) \phi _{K_1}^v(x_3)\nonumber \\&\quad -x_2(1-r_2^2)\phi ^T_{K_1}(x_3)]+r_c\psi ^T(x_2)[(1-r_2^2)\phi ^T_{K_1}(x_3)\nonumber \\&\quad -r_{3}(1{+}r_2^2)\phi _{K_1}^v(x_3)] \} \alpha _s(t_d)\nonumber \\&\quad E_{en}(t_d)h_d(x_1,x_2,x_3,b_1,b_2), \end{aligned}$$

(20)

$$\begin{aligned}&\mathcal {M}^{T}_{J/\Psi K_1}=\frac{128}{\sqrt{6}}\pi C_F m^4_B \int _0^1 \mathrm{d}x_1 \mathrm{d}x_2 \mathrm{d}x_3\nonumber \\&\quad \times \int _0^\infty b_1 db_1 b_2 db_2 \phi _B(x_1,b_1)\nonumber \\&\quad \times \{r_2\psi ^v(x_2)[r_{3}(x_2(1+r_2^2)+x_3(1-r_2^2)) \phi _{K_1}^a(x_3)\nonumber \\&\quad -x_2\phi ^T_{K_1}(x_3)]+r_c\psi ^T(x_2)[\phi ^T_{K_1}(x_3)\nonumber \\&\quad -r_{3}(1+r_2^2)\phi _{K_1}^a(x_3)] \}\nonumber \\&\quad \times \alpha _s(t_d)E_{en}(t_d)h_d(x_1,x_2,x_3,b_1,b_2). \end{aligned}$$

(21)

By combining these amplitudes from the different Feynman diagrams and Eq. (4), one can get the total decay amplitude for the decay $B^+\rightarrow J/\Psi K_{1}(1270)^+$:

$$\begin{aligned}&\mathcal {M}^{j}(B^+\rightarrow J/\Psi K_{1}(1270)^+)\nonumber \\&\quad =\mathcal {M}^{j}(B^+\rightarrow J/\Psi K^+_{1A})\sin \theta _{K_1}\nonumber \\&\qquad +\mathcal {M}^{j}(B^+\rightarrow J/\Psi K^+_{1B})\cos \theta _{K_1}\nonumber \\&\quad =(\mathcal {F}^{j}_{J/\Psi K_{1A}}\sin \theta _{K_1}+\mathcal {F}^{j}_{J/\Psi K_{1B}}\cos \theta _{K_1})\nonumber \\&\qquad \times [V^*_{cb}V_{cs}a_2-V^*_{tb}V_{ts}(a_3+a_5+a_7+a_9)]\nonumber \\&\qquad +(\mathcal {M}^{j}_{J/\Psi K_{1A}}\sin \theta _{K_1}+\mathcal {M}^{j}_{J/\Psi K_{1B}}\cos \theta _{K_1}) \nonumber \\&\qquad \times [V^*_{cb}V_{cs}C_2-V^*_{tb}V_{ts}(C_4-C_6-C_8+C_{10})], \end{aligned}$$

(22)

where $\mathcal {M}^{j}$ and $\mathcal {F}^{j}$ ($j=L,N,T$) refer to the different helicity amplitudes. The combinations of the Wilson coefficients $a_2=C_1+C_2/3, a_i=C_i+C_{i+1}/3$ with $i=3,5,7,9$. As for the decays $B^+\rightarrow J/\Psi K_{1}(1400)^+$, the total amplitude can be obtained by replacing $\sin \theta _{K_1}$ and $\cos \theta _{K_1}$ with $\cos \theta _{K_1}$ and $-\sin \theta _{K_1}$ in Eq. (22), respectively.

Here only the vertex corrections need to be considered in the NLO calculations for the decays $B^+\rightarrow J/\Psi K^+_{1A,B}$. Since the vertex corrections can reduce the dependence of the Wilson coefficients on the renormalization scale $\mu$, they usually play the important roles in the NLO analysis. It is well known that the nonfactorizable amplitude contributions are small [5], we concentrate only on the vertex corrections to the factorizable amplitudes, as shown in Fig. 2. Furthermore, the infrared divergences from the soft and the collinear gluons in these Feynman diagrams can be canceled each other. That is to say, these corrections are free from the end-point singularity in the collinear factorization theorem, so we can quote the QCDF expressions for the vertex corrections: their effects can be combined into the Wilson coefficients,

$$\begin{aligned} a^h_2\rightarrow & {} a_2+\frac{\alpha _s C_F}{4\pi N_c}C_2\left( -18+12\ln \frac{m_b}{\mu }+f^h_I\right) ,\end{aligned}$$

(23)

$$\begin{aligned} a^h_i\rightarrow & {} a_{i}+\frac{\alpha _s C_F}{4\pi N_c}C_{i+1}\nonumber \\&\times \left( -18+12\ln \frac{m_b}{\mu }+f^h_I\right) ,\quad (i=3,9),\end{aligned}$$

(24)

$$\begin{aligned} a^h_i\rightarrow & {} a_{i}+\frac{\alpha _s C_F}{4\pi N_c}C_{i+1}\nonumber \\&\times \left( 6-12\ln \frac{m_b}{\mu }-f^h_I\right) , \quad (i=5,6), \end{aligned}$$

(25)

with the function $f^h_I(h=0,\pm )$ defined as

$$\begin{aligned} f^0_I=f_I+g_I(1-r^2), \;\;\; f^{\pm }=f_I. \end{aligned}$$

(26)

As for the expressions of $f_I$ and $g_I$ are given in Appendix C. Certainly, the NLO Wilson coefficients will be used in the NLO calculations.

Fig. 3

The (blue) dashed curves correspond to the dependences of the branching ratio (left panel) and the direct CP violation (right panel) on the mixing angle for the decay $B^+\rightarrow J/\Psi K_1(1400)^+$, the (red) solid curves refer to the dependences of the branching ratio (left panel) and the direct CP violation (right panel) on the mixing angle for the decay $B^+\rightarrow J/\Psi K_1(1270)^+$. On the left panel, the shaded band shows the allowed region from the experiment and the (red) horizontal bisector is for the central experimental value $(1.8\pm 0.5)\times 10^{-3}$ of $Br(B^+\rightarrow J/\Psi K_1(1270)^+)$. The (blue) dashed line is the upper limit for the branching ratio of decay $B^+\rightarrow J/\Psi K_1(1400)^+$, $5.4\times 10^{-4}$

3 Numerical results and discussions

We use the following input parameters for the numerical calculations [24, 25]:

$$\begin{aligned} f_B= & {} 190\, \mathrm{MeV}, f_{K_{1A}}=0.250\pm 0.013\, \mathrm{GeV}, \nonumber \\ f_{K_{1B}}= & {} 0.190\pm 0.01\, \mathrm{GeV},\end{aligned}$$

(27)

$$\begin{aligned} M_B= & {} 5.28\, \mathrm{GeV}, M_{K_{1A}}=1.31\pm 0.06\, \mathrm{GeV}, \nonumber \\ M_{K_{1B}}= & {} 1.34\pm 0.08\, \mathrm{GeV}\end{aligned}$$

(28)

$$\begin{aligned} M_W= & {} 80.41\, \mathrm{GeV}, \tau _B^\pm =1.638\times 10^{-12}\, \mathrm{s}, \nonumber \\ \tau _{B^0}= & {} 1.519\times 10^{-12}\, \mathrm{s}. \end{aligned}$$

(29)

For the CKM matrix elements, we adopt the Wolfenstein parametrization and the values $A=0.814, \lambda =0.22537, \bar{\rho }=0.117\pm 0.021$, $\bar{\eta }=0.353\pm 0.013$ [24]. For the updated values, one can find in [26]. With the total amplitudes, one can write the decay width as

$$\begin{aligned}&\Gamma (B^+\rightarrow J/\Psi K_1(1270,1400)^+)\nonumber \\&\quad =\frac{G^2_F |\mathbf {P}_c|}{16\pi m^2_B}\sum _{\sigma =L,\parallel ,\perp }\mathcal {A}^\dagger _{\sigma }\mathcal {A}_{\sigma }, \end{aligned}$$

(30)

where $\mathbf {P}_c$ is the three momentum of either of the two final state mesons, and the three helicity amplitudes are defined as

$$\begin{aligned} \mathcal {A}_L= & {} \mathcal {M}_L,\;\;\;\;\; \mathcal {A}_\parallel =\sqrt{2}\mathcal {M}_N,\nonumber \\ \mathcal {A}_\perp= & {} r_{K_1}r_{J/\Psi }\sqrt{2(\kappa ^2-1)}\mathcal {M}_T, \end{aligned}$$

(31)

for the longitudinal, parallel, and perpendicular polarizations, respectively, and the ratio $\kappa {=}P_{J/\Psi }\cdot P_{K_1}\!/\!(M_{M_{J/\Psi }}M_{K_1})$. Then the polarization fractions $f_\sigma (\sigma =L,\parallel ,\perp )$ are written as

$$\begin{aligned} f_\sigma =\frac{|\mathcal {A}_\sigma |^2}{|\mathcal {A}_L|^2+|\mathcal {A}_\parallel |^2+|\mathcal {A}_\perp |^2}. \end{aligned}$$

(32)

With the above transversity amplitudes, one can defined the relative phases $\phi _{\parallel }$ and $\phi _{\perp }$ as

$$\begin{aligned} \phi _{\parallel }=arg\frac{\mathcal {A}_\parallel }{\mathcal {A}_L}, \;\;\; \phi _{\perp }=arg\frac{\mathcal {A}_\perp }{\mathcal {A}_L}. \end{aligned}$$

(33)

For the charged B meson decays, the direct CP violation $A^\mathrm{dir}_{CP}$ is written as

$$\begin{aligned} A^\mathrm{dir}_{CP}=\frac{|\mathcal {\bar{A}}_f|^2-|\mathcal {A}_f|^2}{|\mathcal {\bar{A}}_f|^2+|\mathcal {A}_f|^2}, \end{aligned}$$

(34)

where $\mathcal {A}_f$ is the total decay amplitude. If replacing $\mathcal {A}_f$ with the different polarization amplitudes $\mathcal {A}_L, \mathcal {A}_\parallel$ and $\mathcal {A}_\perp$, one can obtain different direct CP violations from the different polarization components, which are defined as $A^{\mathrm{dir},L}_{CP}, A^{\mathrm{dir},\parallel }_{CP}$ and $A^{\mathrm{dir},\perp }_{CP}$, respectively.

We can obtain the values of the branching ratios for decays $B^+\rightarrow J/\Psi K_1(1270)^+$ and $B^+\rightarrow J/\Psi K_1(1400)^+$ by combining the contributions from the flavor states $J/\Psi K_{1A}$ and $J/\Psi K_{1B}$ through Eq. (4):

$$\begin{aligned}&Br(B^+\rightarrow J/\Psi K_1(1270)^+)\nonumber \\&\quad ={\left\{ \begin{array}{ll}(1.76^{+0.42+0.14+0.47+0.02}_{-0.57-0.13-0.36-0.02})\times 10^{-3}, \text {for}\; \theta _{K_1}=33^\circ ,\\ (2.36^{+0.73+0.20+0.38+0.00}_{-0.54-0.20-0.32-0.01})\times 10^{-3}, \text {for} \;\;\theta _{K_1}=58^\circ , \end{array}\right. }\nonumber \\ \end{aligned}$$

(35)

$$\begin{aligned}&Br(B^+\rightarrow J/\Psi K_1(1400)^+)\nonumber \\&\quad ={\left\{ \begin{array}{ll}(6.47^{+1.73+1.01+1.49+0.15}_{-1.35-0.94-1.66-0.15})\times 10^{-4}, \text {for}\;\; \theta _{K_1}=33^\circ ,\\ (8.91^{+2.85+1.77+3.56+0.12}_{-2.19-1.42-3.31-0.06})\times 10^{-5}, \text {for} \;\;\theta _{K_1}=58^\circ , \end{array}\right. }\nonumber \\ \end{aligned}$$

(36)

where the first error comes from $\omega _b=0.4\pm 0.1$ GeV for B meson, the second error is from the decay constants $f_{K_{1A}}=0.250\pm 0.013$ GeV and $f_{K_{1B}}=0.190\pm 0.01$ GeV, the third error comes from the Gegenbauer momenta given in Appendix A, and the last one comes from the c quark mass $1.275\pm 0.025$ GeV.

When the mixing angle is taken as $\theta _{K_1}=33^\circ$, the pQCD prediction for the decay $B^+\rightarrow J/\Psi K_1(1270)^+$ can agree well with the experimental measurement $(1.80\pm 0.52)\times 10^{-3}$, at the same time, the result for the decay $B^+\rightarrow J/\Psi K_1(1400)^+$ is near the experimental upper limit $5.4\times 10^{-4}$. So we suggest our experimental colleagues to measure carefully the branching ratio of the decay $B^+\rightarrow J/\Psi K_1(1400)^+$ at LHCb. It is helpful to determine the mixing angle $\theta _{K_1}$ between $K_{1A}$ and $K_{1B}$ accurately. Considering that the difference of the branching ratios for the neutral and charged decay modes is mainly from the B meson lifetimes $\tau _{B^+}$ and $\tau _{B^0}$, one can obtain easily the branching ratios $Br(B^0\rightarrow J/\Psi K_1(1270)^0)=(1.63^{+0.60}_{-0.64})\times 10^{-3}$ and $Br(B^0\rightarrow J/\Psi K_1(1400)^0)=(6.52^{+2.50}_{-2.34})\times 10^{-4}$ for the mixing angle $\theta _{K_1}=33^\circ$. The former is consistent with the experimental value $(1.30\pm 0.46)\times 10^{-3}$ within errors, and the latter can be tested at the present LHCb experiment. So comparing our predictions and the present data, one can find that the mixing angle $\theta _{K_1}=33^\circ$ is much more favored than $58^\circ$. In Fig. 3a, we give the dependences of the branching ratios $Br(B^+\rightarrow J/\Psi K_1(1270)^+)$ and $Br(B^+\rightarrow J/\Psi K_1(1400)^+)$ on the mixing angle $\theta _{K_1}$. The predictions for the branching ratios of the decays $B^+\rightarrow J/\Psi K_1(1270)^+$ and $B^+\rightarrow J/\Psi K_1(1400)^+$ near the mixing angle $33^\circ$ can explain the data at the same time.

Table 1 Our LO and NLO predictions for each polarization amplitude (which is denoted as pol. amp.) for the decays $B^+\rightarrow J/\Psi K_{1A}^+$ and $B^+\rightarrow J/\Psi K_{1B}^+$, where only the central values are listed. The results in the brackets are the LO values, the other results are the NLO values

When comparing the LO and NLO results, one can find that the NLO corrections are necessary. The LO branching ratio for the decay $B^+\rightarrow J/\Psi K_1(1270)^+$ is about $3.42\times 10^{-3}$, which is almost two times of the experimental value. After including the NLO contributions, one can find that all of the real parts of the amplitudes decrease consistently (shown in Table 1). Furthermore, this downward trend is dominant by comparing with the changes of each imaginary part. So the NLO branching ratio for the decay $B^+\rightarrow J/\Psi K_1(1270)^+$ will decrease significantly and converge to the experimental value. Meanwhile the branching ratio of the decay $B^+\rightarrow J/\Psi K_1(1400)^+$ has a tiny increase compared with the LO result $6.38\times 10^{-4}$ with the mixing angle $\theta _{K_1}=33^\circ$.

Certainly, the mixing angle $\theta _{K_1}$ has also been checked in other B meson decays. For example, the charged decays $B^+\rightarrow \phi K_1(1270)^+$ and $B^+\rightarrow \phi K_1(1400)^+$ have been measured by BaBar Collaboration [27] with the branching ratio $(6.1\pm 1.9)\times 10^{-6}$ and an upper limit $3.2\times 10^{-6}$, respectively. In order to explaining these data, much work supports the smaller mixing angle ($\sim 33^\circ$) although suffering severe interference from the annihilation type contributions. The authors of Refs. [28, 29] found that the theoretical predictions for the decay $B^+\rightarrow \phi K_1(1270)^+$ could explain the data by taking $\theta _{K_1}\sim 33^\circ$, while the values of $Br(B^+\rightarrow \phi K_1(1400)^+)$ reached $10^{-5}$ order and would overshoot the upper limit greatly. In Ref. [30] the authors studied these two charged decays within the generalized factorization approach (GFA). With the annihilation type contributions turned off, their predictions about these two channels could agree with the data with $N^\mathrm{eff}_c=5$ being the effective color number containing the nonfactorizable effects. A similar situation also happened in the decays $B^+\rightarrow K_1(1270)^+\gamma$ and $B^+\rightarrow K_1(1400)^+\gamma$. In Ref. [31] the authors explained well the data $Br(B^+\rightarrow K_1(1270)^+\gamma )=(4.3\pm 1.3)\times 10^{-5}$ and $Br(B^+\rightarrow K_1(1400)^+\gamma )<1.5\times 10^{-5}$ with $\theta _{K_1}=(34\pm 13)^\circ$. Among these decays $B\rightarrow K_1(1270,1400)V$ (V refers to a vector meson or a photon), the branching ratios of decays $B\rightarrow K_1(1270)V$ are always larger than those of decays $B\rightarrow K_1(1400)V$, because of the constructive (destructive) interference between the modes $B\rightarrow K_{1A}V$ and $B\rightarrow K_{1B}V$ through Eq. (4) for the former (latter).

Table 2 The NLO predictions for the polarization fractions ($f_{L}, f_{\parallel }, f_{\perp }$), the direct CP violations from the different polarization components, and the relevant phase angles $(\phi _\parallel ,\phi _\perp )$ for the decays $B^+\rightarrow J/\Psi K_{1}(1270)^+$ with the mixing angle $\theta _{K_1}=33^\circ$ and $58^\circ$. The first uncertainty comes from the $\omega _b=0.4\pm 0.1$ for B meson, the second and the third uncertainties are from the decay constants $f_{K_{1A}}$ and $f_{K_{1B}}$ and the Gegenbauer momenta in the wave functions of $K_{1A}$ and $K_{1B}$. The last one comes from c quark mass $1.275\pm 0.025$ GeV

We also calculate the polarization fractions $f_{\sigma }(\sigma =L,\parallel ,\perp )$, the direct CP violations $A^{\mathrm{dir},L}_{CP}, A^{\mathrm{dir},\parallel }_{CP}, A^{\mathrm{dir},\perp }_{CP}$ from the different polarization components, and the relative phases $\phi _{\parallel ,\perp }$ defined in Eqs. (32)–(34), respectively. The results for the decay $B^+\rightarrow J/\Psi K_1(1270)^+$ are listed in Table 2 and for the decay $B^+\rightarrow J/\Psi K_1(1400)^+$ in Table 3. Comparing with the longitudinal polarization fractions for the decays $B^+\rightarrow J/\Psi K_1(1270)^+$ and $B^+\rightarrow J/\Psi K_1(1400)^+$, we find that the former decreases monotonically with the increase of the mixing angle $\theta _{K_1}$ from $0^\circ$ to $90^\circ$, while the latter decreases firstly and then increases in $\theta _{K_1}\in [0^\circ ,90^\circ ]$. The direct CP violation from the longitudinal component is much smaller than those from the two transverse components for the decay $B^+\rightarrow J/\Psi K_1(1270)^+$. As for the dependences of the total direct CP violations for these two charged decays on the mixing angle $\theta _{K_1}$ are shown in Fig. 3b. The total direct CP violation values corresponding to the mixing angle $\theta _{K_1}=33^\circ$ and $58^\circ$ are

$$\begin{aligned}&A^\mathrm{dir}_{CP}(B^+\rightarrow J/\Psi K_1(1270)^+)\nonumber \\&\quad ={\left\{ \begin{array}{ll}(1.12^{+0.27+0.00+0.10+0.01}_{-0.25-0.00-0.08-0.01})\times 10^{-4}, \text {for} \,\, \theta _{K_1}=33^\circ , \\ (1.06^{+0.26+0.01+0.05+0.00}_{-0.24-0.01-0.08-0.00})\times 10^{-4}, \text {for}\,\,\theta _{K_1}=58^\circ ,\end{array}\right. }\nonumber \\ \end{aligned}$$

(37)

$$\begin{aligned}&A^\mathrm{dir}_{CP}(B^+\rightarrow J/\Psi K_1(1400)^+)\nonumber \\&\quad ={\left\{ \begin{array}{ll}(8.11^{+1.82+0.17+1.46+0.27}_{-1.57-0.19-1.81-0.26})\times 10^{-5}, \text {for} \,\,\theta _{K_1}=33^\circ , \\ (3.22^{+1.15+0.42+4.72+0.74}_{-1.17-0.21-1.00-0.76})\times 10^{-5}, \text {for} \,\, \theta _{K_1}=58^\circ , \end{array}\right. }\nonumber \\ \end{aligned}$$

(38)

where the errors are the same as those in Eqs. (35) and (36). We adopt the Wolfenstein parametrization up to $\mathcal {O}(\lambda ^4)$ in our calculations. The weak phase will appear in the CKM matrix element $V_{cs}=-A\lambda ^2+\frac{1}{2}A\lambda ^4(1-2(\rho +i\eta ))$, where these Wolfenstein parameters are given at the start of this section. So such small CP asymmetries are in accordance with our expectation.

Table 3 Same as Table 2 but with the decay $B^+\rightarrow J/\Psi K_{1}(1400)^+$

Table 4 The NLO predictions for the branching ratios, the polarization fractions ($f_{L}, f_{\parallel }, f_{\perp }$), the direct CP violation, and the relevant phase angles $(\phi _\parallel ,\phi _\perp )$ for the decay $B^+\rightarrow J/\Psi K_{1}(1270)^+$ with the mixing angle $\theta _{K_1}=33^\circ$ (top) and $58^\circ$ (bottom), where the harmonic-oscillator type wave functions for the $J/\Psi$ meson are used

Table 5 Same as Table 4 but for the decay $B^+\rightarrow J/\Psi K_{1}(1400)^+$

In order to check whether the results are sensitive to the wave functions (WFs) of $J/\Psi$ meson, we also calculate them by using the harmonic-oscillator type wave functions for the $J/\Psi$ meson, which are listed in Appendix A. The results for the decays $B^+\rightarrow J/\Psi K_{1}(1270)^+$ and $B^+\rightarrow J/\Psi K_{1}(1400)^+$ are given in Tables 4 and 5, respectively. Through comparing these two sets of results corresponding to two type WFs of $J/\Psi$ meson, we can see that:

• The branching ratios will decease about $30\%$ by using the harmonic-oscillator type wave functions of $J/\Psi$ meson except for that of the decay $B^+\rightarrow J/\Psi K_1(1400)^+$ with mixing angle $\theta =58^\circ$, but anyway they keep in the same order by changing the wave functions for $J/\Psi$ meson.

• For the decay $B^+\rightarrow J/\Psi K_1(1400)^+$, the polarization fractions are sensitive to the wave functions of $J/\Psi$ meson. If taking the mixing angle $\theta =33^\circ$, the longitudinal component is less than the transverse components by using Type I WFs, but it is contrary in the case of using the harmonic-oscillator type WFs. If taking the mixing angle $\theta =58^\circ$, the longitudinal polarization fraction is close to the sum of other two transverse polarization fractions in Type I WFs, while the longitudinal polarization component is more dominant than the transverse ones in the harmonic-oscillator type WFs.

• In most cases, the values of these two relative strong phases are similar to each other in each decay mode. But for the case of the decay $B^+\rightarrow J/\Psi K_1(1400)^+$ with the mixing angle $\theta =58^\circ$, the relative strong phases $\phi _\parallel$ and $\phi _\perp$ are with opposite signs. It is valuable for us to determine the mixing angle by measuring these relative phases from the future experiments.

• In most cases, the values of the direct CP asymmetries are in the order of $10^{-4}$ by using both of these two type WFs of $J/\Psi$ meson. But still for the case of the decay $B^+\rightarrow J/\Psi K_1(1400)^+$ with the mixing angle $\theta =58^\circ$, there is a smaller direct CP violation value.

4 Summary

We study the B meson decays $B\rightarrow J/\Psi K_1(1270,1400)$ in the pQCD approach beyond the leading order. With the vertex corrections and the NLO Wilson coefficients included, the branching ratios of the considered decays are $Br(B^+\rightarrow J/\Psi K_1(1270)^+)=1.76^{+0.65}_{-0.69}\times 10^{-3}, Br(B^+\rightarrow J/\Psi K_1(1400)^+)=6.47^{+2.50}_{-2.34}\times 10^{-4}$, and $Br(B^0\rightarrow J/\Psi K_1(1270)^0)=(1.63^{+0.60}_{-0.64})\times 10^{-3}$ with the mixing angle $\theta _{K_1}=33^\circ$. These results can agree well with the data or the present experimental upper limit within errors. So we support the opinion that $\theta _{K_1}\sim 33^\circ$ is much more favored than $58^{\circ }$. We suggest our experimental colleagues to measure carefully the branching ratio of the decay $B^+\rightarrow J/\Psi K_1(1400)^+$ at LHCb. It is important to determine the mixing angle $\theta _{K_1}$ between $K_{1A}$ and $K_{1B}$ accurately. On the experimental side, we find that the branching ratios of the decays $B\rightarrow K_1(1270)V$ (V refers to a vector or a photon) are usually much larger than those of $B\rightarrow K_1(1400)V$. It is because of the constructive (destructive) interference between $B\rightarrow K_{1A}V$ and $B\rightarrow K_{1B}V$ for the former (latter). In order to check the dependence of our predictions on the wave functions of $J/\Psi$ meson, we also give the results by using the harmonic-oscillator type wave functions for the $J/\Psi$ meson, and find that these two type WFs can give the consistent results in most cases, while some values are sensitive to the type of wave functions of the $J/\Psi$ meson.

Appendices

Appendix A: Wave functions

For the B meson wave function, the popular parameterizations are written as [32]

$$\begin{aligned} \phi _B(x,b)=N_Bx^2(1-x)^2\exp \left[ -\frac{m^2_Bx^2}{2\omega ^2_b}-\frac{(\omega _bb)^2}{2}\right] ,\nonumber \\ \end{aligned}$$

(A1)

where the free parameter $\omega _b=0.40\pm 0.04$ GeV and the normalization factor $N_B=91.783$ corresponds to $\omega _b=0.40$ GeV.

For the $J/\Psi$ meson, the wave functions are given as

(A2)

(A3)

where the twist-2 $\psi ^L(x)$ and the twist-3 $\psi ^t(x)$ will give the contributions [33]

$$\begin{aligned}&\psi ^L(x)=\psi ^T(x)\nonumber \\&\quad =9.58\frac{f_{J/\Psi }}{2\sqrt{2N_c}}x(1-x)\left[ \frac{x(1-x)}{1-2.8x(1-x)}\right] ^{0.7}, \end{aligned}$$

(A4)

$$\begin{aligned}&\psi ^t(x)\nonumber \\&\quad =10.94\frac{f_{J/\Psi }}{2\sqrt{2N_c}}(1-2x)^2\left[ \frac{x(1-x)}{1-2.8x(1-x)}\right] ^{0.7},\end{aligned}$$

(A5)

$$\begin{aligned}&\psi ^v(x)\nonumber \\&\quad =1.67\frac{f_{J/\Psi }}{2\sqrt{2N_c}}(1+(2x-1)^2)\left[ \frac{x(1-x)}{1-2.8x(1-x)}\right] ^{0.7}.\nonumber \\ \end{aligned}$$

(A6)

Here x refers to the momentum fraction of the charm quark in the charmonium meson. We call the wave functions given in (A4)–(A6) Type I. Sometimes, the harmonic-oscillator type wave functions are often used [34]:

$$\begin{aligned}&\psi ^{L,T}(x,b)=\frac{f_{J/\Psi }N^{L,T}}{2\sqrt{2N_c}}x(1-x)\nonumber \\&\quad \exp \left\{ -\frac{m_c}{\omega }x(1-x)\left[ \left( \frac{1-2x}{2x(1-x)}\right) ^2+\omega ^2b^2\right] \right\} ,\;\;\;\;\;\;\;\; \end{aligned}$$

(A7)

$$\begin{aligned}&\psi ^t(x,b)=\frac{f_{J/\Psi }N^t}{2\sqrt{2N_c}}(1-2x)^2\nonumber \\&\quad \exp \left\{ -\frac{m_c}{\omega }x(1-x)\left[ \left( \frac{1-2x}{2x(1-x)}\right) ^2+\omega ^2b^2\right] \right\} , \end{aligned}$$

(A8)

$$\begin{aligned}&\psi ^v(x)=\frac{f_{J/\Psi }N^v}{2\sqrt{2N_c}}(1+(2x-1)^2)\nonumber \\&\quad \exp \left\{ -\frac{m_c}{\omega }x(1-x)\left[ \left( \frac{1-2x}{2x(1-x)}\right) ^2+\omega ^2b^2\right] \right\} , \end{aligned}$$

(A9)

where $N^{L,T,t}$ and $N^v$ are the normalization constants and b is the conjugate variable of the transverse momentum, $\omega =0.6\pm 0.1$ GeV.

For the wave functions of the axial-vector meson $K_{1A}$ or $K_{1B}$, we have [25]

(A10)

(A11)

where $K_1$ refers to the flavor state $K_{1A}$ or $K_{1B}$, and the corresponding distribution functions can be calculated by using the light-cone QCD sum rule:

$$\begin{aligned} {\left\{ \begin{array}{ll} \phi _{K_1}(x){=}\frac{f_{K_1}}{2\sqrt{2N_c}}6x(1{-}x)[a^{\parallel }_0{+}3a^{\parallel }_1t{+}\frac{3}{2}a^{\parallel }_2(5t^2-1)], \\ \phi ^t_{K_1}(x)=\frac{3f_{K_1}}{4\sqrt{2N_c}}[2a^\perp _0t^2+a^\perp _1t(3t^2-1)], \\ \phi ^s_{K_1}(x)=\frac{f_{K_1}}{4\sqrt{2N_c}}[2a^\perp _1x(1-x)-a^\perp _0t-a^\perp _1t^2]. \end{array}\right. } \end{aligned}$$

(A12)

The upper formulas are for the longitudinal polarization wave functions, and the transverse polarization ones are given as

$$\begin{aligned} {\left\{ \begin{array}{ll} \phi ^T_{K_1}(x){=}\frac{f_{K_1}}{2\sqrt{2N_c}}6x(1{-}x)[a^{\perp }_0{+}3a^{\parallel }_1t{+}\frac{3}{2}a^{\perp }_2(5t^2-1)], \\ \phi ^v_{K_1}(x)=\frac{3f_{K_1}}{8\sqrt{2N_c}}[a^\parallel _0(t^2+1)+2a^\parallel _1t^3], \\ \phi ^a_{K_1}(x)=\frac{3f_{K_1}}{4\sqrt{2N_c}}[2a^\parallel _1x(1-x)-a^\parallel _0t-a^\parallel _1t^2], \end{array}\right. } \end{aligned}$$

(A13)

where the Gegenbauer moments are given as [25, 35]

$$\begin{aligned} a^\parallel _0= & {} 1(-0.19\pm 0.07), a^\parallel _1=-0.30^{+0.00}_{-0.20}(-1.95\pm 0.45), \nonumber \\ a^\parallel _2= & {} -0.05\pm 0.03\left( 0.10^{+0.15}_{-0.19}\right) ,\end{aligned}$$

(A14)

$$\begin{aligned} a^{\perp }_0= & {} 0.27^{+0.03}_{-0.17}(1), a^{\perp }_1=-1.08\pm 0.48\left( 0.30^{+0.00}_{-0.33}\right) ,\nonumber \\ a^{\perp }_2= & {} 0.02\pm 0.21(-0.02\pm 0.22). \end{aligned}$$

(A15)

Appendix B: Hard functions, evolution factors and jet functions

The hard functions are the Fourier transformations from the propagators of the virtual quarks and gluons, which are

$$\begin{aligned}&h_e(x_1,x_3,b_1,b_3)=K_0\left( \sqrt{x_1x_3(1-r^2_2)}m_Bb_1\right) \nonumber \\&\quad \times \left[ \theta (b_1-b_3)K_0\left( \sqrt{x_3(1-r^2_2)}m_Bb_1\right) \right. \nonumber \\&\quad \times \left. I_0\left( \sqrt{x_3(1-r^2_2)}m_Bb_3\right) \right. \nonumber \\&\quad \left. +\theta (b_3-b_1)K_0\left( \sqrt{x_3(1-r^2_2)}m_Bb_3\right) \right. \nonumber \\&\quad \times \left. I_0\left( \sqrt{x_3(1-r^2_2)}m_Bb_1\right) \right] , \end{aligned}$$

(B1)

$$\begin{aligned}&h_{d}(x_1,x_2,x_3,b_1,b_2)\nonumber \\&=\left[ \theta (b_1-b_2)K_0\left( \sqrt{x_1x_3\left( 1-r^2_2\right) }m_Bb_1\right) \right. \nonumber \\&\quad \times \left. I_0\left( \sqrt{x_1x_3\left( 1-r^2_2\right) }m_Bb_2\right) \right. \nonumber \\&\quad +(b_1\leftrightarrow b_2)\Bigg ] \left( \begin{matrix}K_0(A_dm_Bb_2)&{} \text {for}\,\, A^2_d\ge 0\\ \frac{i\pi }{2}H^{(1)}_0\left( \sqrt{|A^2_d|}m_Bb_2\right) &{}\text {for}\,\, A^2_d\le 0\\ \end{matrix}\right) ,\nonumber \\ \end{aligned}$$

(B2)

with the variables $A^2_d$ being $A^2_d=r_c^2+(x_1-x_2)[(x_2-x_3)r^2_2+x_3]$. Here the formula for the propagator of the virtual gluons is given as $\frac{-1}{m_B^2x_1x_3(1-r^2_2)+(k_{3T}-k_{1T})^2}$.

The evolution factors are given by

$$\begin{aligned} E_e(t)= & {} \alpha _s(t)\exp [-S_B(t)-S_{K_1}(t)],\end{aligned}$$

(B3)

$$\begin{aligned} E_{en}(t)= & {} \alpha _s(t)\exp [-S_B(t)-S_{J/\Psi }(t)-S_{K_1}(t)|_{b_1=b_3}],\nonumber \\ \end{aligned}$$

(B4)

where the hard scales (t) are chosen as

$$\begin{aligned} t_a= & {} \max \left( \sqrt{x_3(1-r^2_2)}m_B,1/b_1,1/b_3\right) ,\end{aligned}$$

(B5)

$$\begin{aligned} t_b= & {} \max \left( \sqrt{x_1(1-r^2_2)}m_B,1/b_1,1/b_3\right) ,\end{aligned}$$

(B6)

$$\begin{aligned} t_{d}= & {} \max \left( \sqrt{x_1x_3(1-r_2^2)}m_B,\sqrt{|A^2_{d}|}m_B,1/b_1,1/b_2\right) .\nonumber \\ \end{aligned}$$

(B7)

The Sudakov exponents are defined as

$$\begin{aligned} S_B(t)= & {} s\left( x_1\frac{m_B}{\sqrt{2}},b_1\right) +\frac{5}{3}\int ^t_{1/b_1}\frac{\mathrm{d}\bar{\mu }}{\bar{\mu }}\gamma _q(\alpha _s(\bar{\mu })), \end{aligned}$$

(B8)

$$\begin{aligned} S_{J/\Psi }(t)= & {} s\left( x_2\frac{m_B}{\sqrt{2}},b_2\right) +s\left( (1-x_2)\frac{m_B}{\sqrt{2}},b_2\right) \nonumber \\&+\,2\int ^t_{1/b_2}\frac{\mathrm{d}\bar{\mu }}{\bar{\mu }}\gamma _q(\alpha _s(\bar{\mu })), \end{aligned}$$

(B9)

$$\begin{aligned} S_{K_1}(t)= & {} s\left( x_3\frac{m_B}{\sqrt{2}},b_3\right) +s\left( (1-x_3)\frac{m_B}{\sqrt{2}},b_3\right) \nonumber \\&+\,2\int ^t_{1/b_3}\frac{\mathrm{d}\bar{\mu }}{\bar{\mu }}\gamma _q(\alpha _s(\bar{\mu })), \end{aligned}$$

(B10)

where the quark anomalous dimension is $\gamma _q=-\alpha _s/\pi$, and the expression of the s(Q, b) in one-loop running coupling constant is

$$\begin{aligned} s(Q,b)= & {} \frac{A^{(1)}}{2\beta _1}\hat{q}\ln \left( \frac{\hat{q}}{\hat{b}}\right) -\frac{A^{(1)}}{2\beta _1}(\hat{q}-\hat{b}) +\frac{A^{(2)}}{4\beta ^2_1}\left( \frac{\hat{q}}{\hat{b}}-1\right) \nonumber \\&-\left[ \frac{A^{(2)}}{4\beta ^2_1}-\frac{A^{(1)}}{4\beta _1}\ln \left( \frac{\mathrm{e}^{2\gamma _E-1}}{2}\right) \right] \ln \left( \frac{\hat{q}}{\hat{b}}\right) , \end{aligned}$$

(B11)

here the variables are defined by $\hat{q}=\ln [Q/(\sqrt{2}\Lambda )], \hat{b}=\ln [1/(b\Lambda )]$ and the coefficients $A^{(1,2)}$ and $\beta _{1}$ are given as

$$\begin{aligned} \beta _1= & {} \frac{33-2n_f}{12},A^{(1)}=\frac{4}{3}, \end{aligned}$$

(B12)

$$\begin{aligned} A^{(2)}= & {} \frac{67}{9}-\frac{\pi ^2}{3} -\frac{10}{27}n_f+\frac{8}{3}\beta _1\ln \left( \frac{1}{2}\mathrm{e}^{\gamma _E}\right) , \end{aligned}$$

(B13)

where $n_f$ is the number of the quark flavors and $\gamma _E$ the Euler constant.

Appendix C: Vertex functions

The hard scattering functions $f_I$ and $g_I$ arising from the vertex corrections are given as [36, 37]

$$\begin{aligned}&f_I=\frac{2\sqrt{2N_C}}{f_{J/\Psi }}\left\{ \int ^1_0 \mathrm{d}x_2\psi ^{L}_{J/\Psi }(x_2)\left[ \frac{2r^2_2x_2}{1-r^2_2(1-x_2)} \right. \right. \nonumber \\&\qquad +(3-2x_2)\frac{\ln x_2}{1-x_2}+\left( -\frac{3}{1-r^2_2x_2}+\frac{1}{1-r^2_2(1-x_2)}\right. \nonumber \\&\left. \qquad -\frac{2r^2_2x_2}{[1-r^2_2(1-x_2)]^2}\right) r^2_2x_2\ln (r^2_2x_2)\nonumber \\&\qquad \left. \left. +\left( 3(1-r^2_2)+2r^2_2x_2+\frac{2r^4_2x^2_2}{1-r^2_2(1-x_2)}\right) \frac{\ln (1-r^2_2)-i\pi }{1-r^2_2(1-x_2)}\right] \right. \nonumber \\&\qquad \left. +\int ^1_0\mathrm{d}x_2\psi ^{T}_{J/\Psi }(x_2)\left[ \frac{-8x^2\ln x}{1-x}+\frac{8r^2_2x^2\ln (r^2_2x)}{1-r^2_2(1-x)}\right. \right. \nonumber \\&\qquad \left. \left. -8r^2_2x^2\frac{\ln (1-r^2_2)-i\pi }{1-r^2_2(1-x)}\right] \right\} ,\end{aligned}$$

(C1)

$$\begin{aligned}&g_I=\frac{2\sqrt{2N_c}}{f_{J/\Psi }}\left\{ \int ^1_0\mathrm{d}x\psi ^{L}_{J/\Psi }(x)\left[ \frac{-4x\ln x}{(1-r^2_2)(1-x)}\right. \right. \nonumber \\&\qquad +\frac{r^2_2x\ln (1-r^2_2)}{[1-r^2_2(1-x)]^2}+r^2_2x\ln (r^2_2x)\nonumber \\&\qquad \times \left( \frac{1}{(1-r^2_2x)^2}-\frac{1}{[1-r^2_2(1-x)]^2}+\frac{2(1+r^2_2-2r^2_2x)}{(1-r^2_2)(1-r^2_2x)^2}\right) \nonumber \\&\left. \qquad -\frac{i\pi r^2_2x}{[1-r^2_2(1-x)]^2}\right] \int ^1_0\psi ^{T}_{J/\Psi }(x)\left[ \frac{8x^2\ln x}{(1-r^2_2)(1-x)}\right. \nonumber \\&\qquad \left. \left. -\frac{8x^2r^2_2\ln (r^2_2x)}{(1-r^2_2)(1-r^2_2x)}\right] \right\} . \end{aligned}$$

(C2)