Thermodynamic consequences of well-known regular black holes under modified first law

Abstract

We modify the first law of thermodynamics of regular black hole of the non-minimal Einstein–Yang–Mill theory with gauge field of magnetic Wu–Yang type and a regular black hole which is associated with the cosmological constant by the surface tensions. The corresponding Smarr relations are also satisfied for them. We calculate the Gibbs free energy to discuss the global stability of the black holes. It is found that Gibbs free energy exhibits the positive behavior in most of the cases which leads to globally thermodynamically stability of both black holes.

1 Introduction

In modern theoretical physics, black hole (BH) is an interesting subject. At all times, BH is associated with a singularity inside it. Einstein’s theory of space, time and gravity empowers the existence of singularities. According to the General Relativity (GR), a singularity is a definite point in the space-time where explicit quantities even the curvature of space-time is infinite. The problem of singularities is one of the exceptional problems and GR made the prediction about the singularities in the interior of BHs. Firstly, it was anticipated that the both of these singularities does not naturally exist but occurs as a result of the preparative procedure of finding the harmony in the solutions. Penrose and Hawking’s theorems of singularities lead us to believe that they are inevitable [1,2,3,4,5,6]. As the initial exact BH solutions in GR predicts the singularity in the interior of an event horizon.

Sakharov [7, 8] and Gliner [9] proposed that for the sources like matter which have a de-Sitter core in the heart of the space-time its singularities could have been avoided and then Bardeen availed this theory to put forward the initial solution of the static spherically symmetric regular black hole (RBH), called “Bardeen BH”. Bronnikov and Melnikov particularize the detail of the many types of the RBH [10], explained the geometries of RBH in a nutshell and revealed the actuality of the black-universe (BU) solutions in GR in agreement with the minimally coupled phantom fields. By coupling the GR to non-linear electrodynamics (NED) many different kinds of RBH solutions have been derived [11,12,13,14,15]. It is mention here that RBHs asymptotically behave like an ordinary charged Reissner–Nordstrom BH solutions and all fields and curvature invariants are regular everywhere instead of usual singularities at their center. These solutions and singularity theorems have no contradiction at all between them.

Ayon-Beato and Garcia, in GR, introduced a proposal of exact nonsingular BH solution fulfilling the weak energy condition (WEC), which is produced by the new NED combined to gravity [11]. Bambi and Modesto proposed the solutions for the rotating RBH [16]. The spherically symmetric radiating and rotating solutions have been proposed by using the Newman–Janis algorithm [17]. Fan and Wang, in the gravity model composed those solutions of BHs which bear magnetic charge on them. Strategy of formulating the solutions of the electrically charged BHs has been illustrated and the thermodynamical possessions has been studied along with the formulation of the first law of thermodynamics. Also generalization of the construction of AdS BH solutions has been done [18].

Hawking and Penrose, during the late 1960s, put into practical a new complicated mathematical model which led to both proposing and proving the numerous theorems of singularity [3]. There is a parallelism between the ordinary 2nd law (OSL) of thermodynamics, which is stated as “the entropy of the closed system never decreases” and Hawking’s theorem, whose statement is that “the surface area of BH never decreases” [19, 20], and Bekenstein was the first to analyzed the resemblance between these two [21]. Then in the 1972, Hawking-Bekenstein debate started until 1974, when Hawking discovered the radiation of BH near event horizon produced by it’s quantum effects and named it, Hawking’s radiation [22].

The discovery about the area of the event horizon is irreducible lead towards a successful conclusions in GR and made up an essential demonstration that the BHs have thermodynamical properties. Thermodynamical properties of the space-times proved to be very important and grasped the worthwhile attentions [23]. They investigated the properties for the magnetically charged regular black hole (MCRBH). Phase transitions is another well-known phenomenon which is based on the fundamental principles of thermodynamics. In the succeeding work, the phase transitions and the thermodynamical stabilities has been studied for many different BHs [24].

Kastor, Ray and Traschen, for the anti de Sitter (AdS) BH, treated the cosmological constant associated with the pressure such as $P=-\frac{\Lambda }{8\pi }$, while treated its conjugate quantity as thermodynamic volume. The expanded first law of thermodynamics presented which has the new term in the format of effective volume times change in pressure, which indicates that the mass of AdS BH should be seen as the enthalpy of BH [25]. Kubiznak and Mann acquired this concept and investigated the thermodynamics of the charged AdS BH in the extended phase space [26]. In this way, the investigation on thermodynamics of the many BHs has been made and many significative critical phenomena were found in [15, 27,28,29,30,31,32,33,34,35,36,37,38,39,40,41, 43,44,45,46,47,48,49,50,51]. Hansen et al. modified the first law of thermodynamics by using the radial Einstein’s equation at the Kerr BH by the surface tension [52]. Chen and Zeng, modify the first law of thermodynamics of the Schwarzschild dS-BH at the BH horizon and the cosmological horizon. They have also derived the apparent horizon of the Friedmann–Robertson–Walker cosmology by the surface tension [53]. In recent work, for the dS and AdS space-times, Chen, Qingyu and Tao, modified the first law of thermodynamics by the surface tension at the BH horizon and cosmological horizon [54].

In this paper, our aim is to investigate the thermodynamics at the BH horizon of the two BHs (the non-minimal MCRBH and the RBH with cosmological constant in NED). In Sect. 2, we modify the first law of thermodynamics for the non-minimal MCRBH. We treat the cosmological constant to be fixed and drive the modified first law in the presence of the surface tension at the horizon. The correlated Smarr relation will be evaluated. Cosmological constant will be associated with the pressure as $P=-\frac{\Lambda }{8\pi }$ and get modified laws for non-minimal MCRBH in the stretched out phase space. In Sect. 3, we modify the first law of thermodynamics at the BH horizon treating the cosmological constant as fixed by the surface tension and as associated with the pressure ($P=\frac{-r_{+}^{2}\Lambda }{8\pi (q^{2}+r_{+}^{2})}$) of the RBH with cosmological constant in NED. Sect. 4 is devoted for conclusions.

2 Modification of First Law of Thermodynamics for non-minimal RBH

The establishment of the BH thermodynamics came into being in between the 1960’s to 1970’s. The discoveries of Bekenstein and Hawking break the grounds for BH thermodynamics [22] and [55]. Recently, Astorino examined the conserved charges and the thermodynamics of the accelerating (RN-BH), where he used the phase space technique for evaluating the mass which satisfies the standard first law of thermodynamics and the corresponding Smarr relation [56]. In the mean while, Chen, Qingyu and Tao make great efforts in modifying the first law of thermodynamics with fixed and varied cosmological constant $\Lambda$ for RN-AdS and dS BHs [54].

2.1 Fixed Cosmological Constant

Consider the line-element of non-minimal MCRBH whose new exact regular spherically symmetric solution was presented by Balakin, Lemos and Zayats [57], which is given by

$$\begin{aligned} ds^{2}=-\Delta dt^{2}+\frac{1}{\Delta }dr^{2}+r^{2}(d\theta ^{2}+\sin ^{2}d\Phi ^{2}), \end{aligned}$$

(1)

with the metric function $\Delta (r)$,

$$\begin{aligned} \Delta (r)=1+\left( \frac{r^{4}}{r^{4}+2Q_{m}^{2}\lambda } \right) \left( -\frac{2M}{r}+\frac{Q_{m}^{2}}{r^{2}}-\frac{\Lambda r^{2}}{3}\right) , \end{aligned}$$

(2)

where $\lambda$, $Q_{m}$, M, $\Lambda$ and r are non-minimal parameter of the theory, magnetic charge of the Wu–Yang gauge field, asymptotic mass of the object which appears to be the constant of integration, cosmological constant and radial variable of MCRBH, respectively. For our study, we consider $\lambda>0, ~\Lambda>0, ~\Lambda \le 0, Q_{m}^{2}>0$ and $M\ge 0$. The limiting case $\lambda =0$ gives the minimal coupled magnetized RN solution along with the cosmological constant as

$$\begin{aligned} \Delta (r)=1-\frac{2M}{r_+}+\frac{Q_{m}^{2}}{r_{+}^{2}}-\frac{\Lambda r_{+}^{2}}{3}. \end{aligned}$$

(3)

Since, there exist a curvature singularity at $r_+=0$ for this MCRBH solution. Also, for $\lambda <0$ at finite positive $r_+$, there exists space-time curvature singularity, therefore, we are only considering the case when $\lambda >0$.

Balakin, Lemos and Zayats, analyzed the horizons as functions of the parameters [57]. Equation (2) manifest explicitly a four parameter family of exact solutions, which contains solutions along with horizons, based on the corresponding values of these four parameters. Furthermore, for the horizons, all possible solutions depend on the value and sign of the $\Lambda$. Generally, Cauchy horizon, event horizon and cosmological horizon become apparent, in few cases these horizons can occur simultaneously with each other or three altogether.

Using Eq. (2), we can obtain the mass of the non-minimal MCRBH in horizon radius as follows

$$\begin{aligned} 2M=r_{+}+\frac{2Q_{m}^{2}\lambda }{r_{+}^{3}}+\frac{Q_{m}^{2}}{r_{+}}-\frac{\Lambda r_{+}^{3}}{3}, \end{aligned}$$

(4)

For $\Lambda >0$, which is the asymptotically dS, the MCRBH appears to have three horizons, Cauchy, event and cosmological horizons, based on the values above mentioned four parameters. In order to find the number of horizons, an auxiliary function $f(r_{+},\lambda ,\Lambda ,Q_{m})$ is introduced and Eq. (6) takes the form as,

$$\begin{aligned} 2M=f(r_{+},\lambda ,\Lambda ,Q_{m}), \end{aligned}$$

(5)

and

$$\begin{aligned} f(r_{+},\lambda ,\Lambda ,Q_{m})=r_{+}+\frac{2Q_{m}^{2}\lambda }{r_{+}^{3}}+\frac{Q_{m}^{2}}{r_{+}}-\frac{\Lambda r_{+}^{3}}{3} \end{aligned}$$

(6)

In [57], Fig. 1 illustrate four cases for the function $f(r_{+},\lambda ,\Lambda ,Q_{m})$, where the horizontal mass line $y=2M$ intersects with plot of function $f(r,\lambda ,\Lambda ,Q_{m})$ which implies that $\Delta (r_{+})$ takes zero values and represents the spheres $r_{+}$, which are the horizons of the MCRBH. Panels, (a) illustrate the model with one simple horizon, (b) illustrate the model with one or three simple horizons, or one simple and one double horizons depending on the values of mass M, (c) depicts the case in which only one horizon appears which is the triple one and (d) demonstrate zero, one double or two simple horizons in Fig. 1 of [57].

In [57], Eqs. (43) and (44) are the critical masses which come into the view of the analysis of horizons for eight different cases. The cases, when $M<M_{c1}$ and $M=0$, the cosmological horizon appears. When $M=M_{c1}$, there exists a double horizon which is the result of the Cauchy and event horizons. When $M_{c1}<M<M_{c2}$, there exists three individual, Cauchy, event and cosmological horizons. When $M>M_{c2}$ and $M_{c1}=M_{c2}$, Cauchy, event and cosmological horizons appear altogether, coinciding with one another.

For $\Lambda =0$, that is, when all space-times are asymptotically flat. In this case, cosmological horizon doesn’t exist, only Cauchy and event horizons become apparent. To sum it up, MCRBH solution can have three horizons, Cauchy, event and cosmological horizons for the positive values of cosmological constant and for $\Lambda =0$, only Cauchy and event horizons. Thus, we want to calculate the thermal quantities on the outer horizon and we refer it by $r_{+}$. The event horizon of the non-minimal MCRBH is obtained by setting $\Delta (r)=0$ in Eq. (2), which is located at the outer horizon $r_{+}$.

Fig. 1

Plot of temperature versus horizon radius at the fixed values of magnetic charge of the non-minimal MCRBH

In order to carry out the analysis of the thermodynamical properties of the non-minimal MCRBH, we use the definition of Misner–Sharp mass [58]. For the non-minimal MCRBH, the Misner–Sharp mass on the horizon can be obtained as $E=M-\frac{Q_{m}^{2}\lambda }{r_{+}^{3}}-\frac{Q_{m}^{2}}{2r_{+}}-\frac{r_{+}^{3}}{2l^{2}}$. By representing the mass M in E, we can find

$$\begin{aligned} E=\frac{r_{+}}{2}. \end{aligned}$$

(7)

The non-minimal MCRBH entropy and temperature are

$$\begin{aligned} S= & {} \frac{A}{4}=\pi r_{+}^{2}. \end{aligned}$$

(8)

$$\begin{aligned} T= & {} \frac{\Delta '(r_{+})}{4\pi }\nonumber \\= & {} \frac{-\Lambda r_{+}^{9}+3Mr_{+}^{6}+6Q_{m}^{4}qr_{+}^{2}-18MQ_{m}^{2}\lambda r_{+}^{2}-(6\lambda \Lambda +3)Q_{m}^{2}r_{+}^{5}}{6\pi (r_{+}^{4}+2Q_{m}^{2}\lambda )^{2}},\nonumber \\ \end{aligned}$$

(9)

respectively, where $\Delta '(r_{+})=\frac{\partial \Delta }{\partial r}|_{r=r_{+}}$. The value of T is determined by $r_{+}$, $Q_{m}$ and $\Lambda$. Figure 1 illustrates the behavior of the temperature T with respect to $r_{+}$ for specific values of $Q_{m}$ and $\Lambda$. The temperature shows the fluctuations between negative and positive values with the passage of horizon radius. For example, when $\Lambda =0.01$, the temperature exhibits the negative behavior for $0.55\le r_{+}\le 0.9$, however, it is positive and attains maximum value at $r_{+}=1.9$ while approaches to zero for higher values of horizon radius ($r_{+}\ge 1$). When $\Lambda =0$, the temperature is negative for the small values of horizon radius, positive for the higher values and approaches to $T=0.01$. For $\Lambda =-\,0.01$, the temperature approaches to $T=0.15$. We observe that the temperature is higher for positive cosmological constant as compare to the negative cosmological constant and $\Lambda =0$. From Eq. (9), we have the expression for physical mass as

$$\begin{aligned} M=\frac{-\Lambda r_{+}^{6}+3Q_{m}^{2}r_{+}^{2}+3r_{+}^{4}+6Q_{m}^{2}\lambda }{6r_{+}^{3}}. \end{aligned}$$

(10)

By using Eqs. (9) and (10), the temperature leads to

$$\begin{aligned} T=\frac{r_{+}^{4}-\Lambda r_{+}^{6}-Q_{m}^{2}r_{+}^{2}-6Q_{m}^{2}\lambda }{4\pi r_{+}(r_{+}^{4}+2Q_{m}^{2}\lambda )}. \end{aligned}$$

(11)

For obtaining real positive temperature, the restrictions are made to the other parameters and the conditions are as follows: (1) For $\Lambda >0, ~Q_{m}=1$ and $\lambda =0.1$, implies $r_{+}>0.9$. (2) $\Lambda =0, ~Q_{m}=2$ and $\lambda =0.1$, implies $r_{+}>1.4$. (3) $\Lambda <0, ~Q_{m}=3$ and $\lambda =0.1$, implies $r_{+}>1.9$.

The concept of horizon thermodynamics emerged from the discovery that Einstein’s equations on the BH horizon can be interpreted as a thermodynamical identity. The radial Einstein equation at the horizon is needed to be evaluated essentially in order to investigate the thermodynamics and the surface tension

$$\begin{aligned} G_{r}^{r}|_{r+}=8\pi T_{r}^{r}|_{r+}=\frac{r_{+}\Delta '(r_{+})-1}{r_{+}^{2}}. \end{aligned}$$

(12)

By inserting Eq. (12) into the Eq. (9), the non-minimal MCRBH temperature can be rewritten as follows

$$\begin{aligned} T=\frac{8\pi r_{+}^{2}T_{r}^{r}|r_{+}+1}{4\pi r_{+}}. \end{aligned}$$

(13)

Since the entropy of a non-minimal MCRBH which is related to the area of the BH horizon is $S=\pi r_{+}^{2}$. Furthermore, the partial derivative of S is $\delta S=2\pi r_{+}\delta r_{+}$. Multiplying the both sides of Eq. (16) by $\delta S$, we get

$$\begin{aligned} T\delta S=2r_{+}T|_{r}^{r}\delta S+\frac{\delta r_{+}}{2}. \end{aligned}$$

(14)

The first term on the R.H.S in above equation is depend on the matter while the second term can be identified as the differential form of the Misner–Sharp mass. $T_{r}^{r}|_{r+}$ can be obtained from the Eq. (13) as,

$$\begin{aligned} T_{r}^{r}|_{r+}=\frac{1}{8\pi r_{+}^{2}}\left[ \frac{(r_{+}^{4}-\Lambda r_{+}^{6}-Q_{m}^{2}r_{+}^{2}-6Q_{m}^{2}\lambda )}{r_{+}^{4}+2Q_{m}^{2}\lambda }-1\right] . \end{aligned}$$

(15)

Also, Eq. (14) can also be written as,

$$\begin{aligned} \delta E=T\delta S-\sigma \delta A. \end{aligned}$$

(16)

The above equation is the modified first law of thermodynamics at the non-minimal MCRBH horizon. Where $\sigma =\frac{r_{+}T_{r}^{r}|_{r+}}{2}=\frac{1}{16\pi r_{+}}[\frac{(r_{+}^{4}-\Lambda r_{+}^{6}-Q_{m}^{2}r_{+}^{2}-6Q_{m}^{2}\lambda )}{r_{+}^{4}+2Q_{m}^{2}\lambda }-1]$ describes the surface tension at the horizon and $\delta A$ can be identified as the differential form of the horizon area, whereas horizon area is $A=4S$. The surface tension $\sigma$ depends upon three factors such as magnetic charge $Q_{m}$, non-minimal parameter $\lambda$ and cosmological constant $\Lambda$. The surface tension approaches to zero for $r_{+}^{6}=-\frac{(r_{+}^{2}-8\lambda )Q_{m}}{\Lambda }$. If $r_{+}^{6}>-\frac{(r_{+}^{2}-8\lambda )Q_{m}^{2}}{\Lambda }$ then it yields positive surface tension and if $r_{+}^{6}<-\frac{(r_{+}^{2}-8\lambda )Q_{m}^{2}}{\Lambda }$ then the surface tension will be negative. The corresponding Smarr relation takes the following form

$$\begin{aligned} E=2TS-2\sigma A. \end{aligned}$$

(17)

It is found that this relation is satisfied for the values of E,  T,  S,  A. It is also mentioned here that the modified first law of thermodynamics in Eq. (16) is different from the Eq.(3.8) in [26]. Conventional thermodynamics analysis requires an application of the first law of thermodynamics, known as energy analysis. In Conventional thermodynamics, in accordance with the specifications of stable equilibrium, we calculate the thermodynamic variables, such as, the heat capacity at the constant pressure and volume and the Gibbs free energy in order to analyze the local and global thermodynamic stability of the BHs in GR. Moreover, the free energy in the grand canonical ensemble, also called Gibbs free energy. The expression for the Gibbs free energy is

$$\begin{aligned} G= & {} E-TS+\sigma A, \end{aligned}$$

(18)

$$\begin{aligned} G= & {} \frac{r_{+}}{2}-\left( \frac{r_{+}^{4}-\Lambda r_{+}^{6}-Q_{m}^{2}r_{+}^{2}-6Q_{m}^{2}\lambda }{4\pi r_{+}(r_{+}^{4}+2Q_{m}^{2}\lambda )}\right) \pi r_{+}^{2}+\sigma 4\pi r_{+}^{2}.\nonumber \\ \end{aligned}$$

(19)

We get $G=\frac{r_{+}}{4}$, using the expressions for $E,~T,~S,~\sigma$ and A. Carrying out the differential on the Gibbs free energy yields,

$$\begin{aligned} \delta G=-S\delta T+A\delta \sigma . \end{aligned}$$

(20)

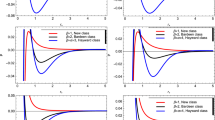
As the effective temperature represents the temperature of a black body that would emit the same total amount of radiation, consider the effective temperature be $T_{eff}=T-4\sigma =\frac{1}{4\pi r_{+}}$, and using the effective temperature in Eq. (19) which leads to $\delta E=T_{eff}\delta S$. The Gibbs free energy in terms of effective temperature will be $G_{eff}=E-T_{eff}S$ which behaves in accordance with $\delta G_{eff}=-S\delta T_{eff}$. In Fig. 2, for $-\,0.002\le \sigma \le 0.002$, we obtain the highest trajectory of the Gibbs free energy for positive cosmological constant. In Fig. 3, for the $\Lambda =0$, the Gibbs free energy increases for positive values of temperature. At $T=0.015$, the curve bounces back and the energies for $\sigma =0$ and $\sigma =0.002$ is positive but for $\sigma =-\,0.002$, the Gibbs free energy is negative. Figure 4 shows that the effective Gibbs free energy decreases with the increase of the effective temperature.

Fig. 2

Plot of Gibbs free energy versus temperature in the presence of surface tension for first case when cosmological constant is positive and $Q_{m}=1$ of the non-minimal MCRBH

Fig. 3

Plot of Gibbs free energy versus temperature in the presence of surface tension for second case when the cosmological constant is zero and $Q_{m}=2$ of the non-minimal MCRBH

Fig. 4

Plot of effective Gibbs free energy versus effective temperature

2.2 The Pressure

Here, we discuss the pressure at the horizon of MCRBH. Horizon thermodynamics takes a different approach to the problem of pressure in the BH thermodynamics. Since temperature with surface gravity yields $T=\frac{\kappa }{2\pi }=\frac{\Delta '(r_{+})}{4\pi }$, horizon thermodynamics is based upon the approach that the energy-momentum tensor on the horizon is interpreted as

$$\begin{aligned} P=T_{r}^{r}|_{r+}=\frac{1}{8\pi r_{+}^{2}}\left[ \left( \frac{r_{+}^{4}-\Lambda r_{+}^{6}-Q_{m}^{2}r_{+}^{2}-6Q_{m}^{2}\lambda }{r_{+}^{4}+2Q_{m}^{2}\lambda }\right) -1\right] . \end{aligned}$$

(21)

The area and the volume are inter-linked as $V=\frac{Ar_{+}}{3}$ which generates $\sigma \delta A=P\delta V$. By using Eq. (21), the modified law of thermodynamics in the presence of pressure can be written as follows

$$\begin{aligned} \delta E=T\delta S-P\delta V. \end{aligned}$$

(22)

The pressure and surface tensions are directly proportional to each other, thus if pressure is positive, negative or zero then it will be in accordance with positive, negative or zero surface tension, respectively. Using the pressure, $P=T_{r}^{r}|_{r+}$ in the Eq. (13), we get,

$$\begin{aligned} P=\frac{T}{2r_{+}}-\frac{1}{8\pi r_{+}^{2}}, \end{aligned}$$

(23)

which leads to

$$\begin{aligned} P=\frac{r_{+}^{4}-\Lambda r_{+}^{6}-Q_{m}^{2}r_{+}^{2}-6Q_{m}^{2}\lambda }{8\pi r_{+}^{2}(r_{+}^{4}+2Q_{m}^{2}\lambda )}-\frac{1}{8\pi r_{+}^{2}}. \end{aligned}$$

(24)

The Van der Waals equation correlate with state variables the pressure P, the volume V, the number of particles N and the temperature T, which can be written as

$$\begin{aligned} P=\frac{kT}{\nu -b}-\frac{a}{\nu ^{2}}, \end{aligned}$$

(25)

where k is the Boltzmann constant, $\nu$ is the specific volume, b is the size of molecules of the system and a is a constant which represents the attraction between the molecules of the system. By comparing the Eqs. (23) and (25), we get $a=\frac{1}{2\pi }$ , $b=0$ and $\nu =2r_{+}$. Hence the above expression of pressure takes the following form

$$\begin{aligned} P=\frac{T}{\nu }-\frac{1}{2\pi \nu ^{2}}. \end{aligned}$$

(26)

The Gibbs free energy is

$$\begin{aligned} G= & {} E-TS+PV=\frac{r_{+}}{2}\nonumber \\&\, -\,\left( \frac{r_{+}^{4}-\Lambda r_{+}^{6}-Q_{m}^{2}r_{+}^{2}-6Q_{m}^{2}\lambda }{4\pi r_{+}(r_{+}^{4} +2Q_{m}^{2}\lambda )}\right) \pi r_{+}^{2}\nonumber \\&+\,P \left( \frac{4\pi r^{3}}{3} \right) , \end{aligned}$$

(27)

which behave in accordance with

$$\begin{aligned} \delta G=-S\delta T+V\delta P, \end{aligned}$$

(28)

varying the horizon equation of state by treating the pressure P and temperature T as independent thermodynamics quantities then horizon equation of state established a new horizon first law in [59], which is same as Eq. (22) where temperature T, volume V and pressure P were specified and the horizon entropy S and the Gibbs free energy G were the derived concepts. By applying a degenerate Legendre transformation on Eq. (25), first law can be easily regained. This condition prevail over the mystery between the heat and the work terms. In Fig. 5, we observe the behavior of Gibbs free energy for different values of temperature and fixed values of pressure. For the first case, when the cosmological constant is positive, diagram illustrates that the Gibbs free energy values are lower for the high temperatures. As temperature decreases, the Gibbs free energy increases for all the fixed values of pressure. In Fig. 6, when $\Lambda =0$, the Gibbs free energy remains the same with the increase in temperature. When $T=0.016$, curves bounce back and Gibbs free energy increases for the lower values of temperature. For the negative value of pressure, the Gibbs free energy approaches to zero while for positive value of pressure and $P=0$, the Gibbs free energy increases.

Fig. 5

Plot of Gibbs free energy versus temperature for first case when $\Lambda =0.01, Q_{m}=1$ of the non-minimal MCRBH

Fig. 6

Plot of Gibbs free energy versus temperature for second case when $\Lambda =0, Q_{m}=2$ of the non-minimal MCRBH

In Eq. (14), the first term on the R.H.S can be rewritten as

$$\begin{aligned} 2r_{+}T_{r}^{r}|_{r+}\delta S=\left( -\frac{Q_{m}^{2}}{4\pi r_{+}^{3}}-\frac{Q_{m}^{2}\lambda }{\pi r_{+}^{5}}\right) \delta S+\left( -\frac{\Lambda r_{+}}{4\pi }\right) \delta S. \end{aligned}$$

(29)

By taking the differential on the entropy S, horizon area A and the volume V, we get,

$$\begin{aligned} 2r_{+}T_{r}^{r}|_{r+}\delta S=\left( -\frac{Q_{m}^{2}}{16\pi r_{+}^{3}}-\frac{Q_{m}^{2}\lambda }{4\pi r_{+}^{5}}\right) \delta A+\left( -\frac{\Lambda }{8\pi }\right) \delta V. \end{aligned}$$

(30)

which leads to

$$\begin{aligned} \delta E=T\delta S-\sigma _{eff}\delta A-P\delta V, \end{aligned}$$

(31)

here, the coefficient of $\delta A$ depends upon the magnetic charge $Q_{m}$, $P=-\frac{\Lambda }{8\pi }$ and $\sigma _{eff}=-\frac{Q_{m}^{2}}{16\pi r_{+}^{3}}-\frac{Q_{m}^{2}\lambda }{4\pi r_{+}^{5}}$ (effective surface tension). Moreover, one can get enthalpy ($E_{o}$) as follows

$$\begin{aligned} E_{o}=E+PV=M-\frac{Q_{m}^{2}}{2r_{+}}-\frac{Q_{m}^{2}\lambda }{r_{+}^{3}}. \end{aligned}$$

(32)

By using the transformation $P(\delta V)=\delta (PV)-V\delta P$ and differential of the Eq. (31), we obtain

$$\begin{aligned} \delta E_{o}=T\delta S-\sigma _{eff}\delta A+V\delta P. \end{aligned}$$

(33)

Thus, Eq. (33) is also the modified first law of thermodynamics of the non-minimal MCRBH. The corresponding Smarr relation leads to

$$\begin{aligned} E_{o}=2(TS-\sigma _{eff }A-PV). \end{aligned}$$

(34)

3 RBH with Cosmological Constant

3.1 Modifying Laws for RBH with Cosmological Constant

Mo Wen-Juan, Rong-Gen Cai and Su Ru-Keng [60] presented a new kind of RBH solution associated with the cosmological constant in NED. The $\Delta (r)$ of this metric has the following form

$$\begin{aligned} \Delta (r_{+})=1-2\left( \frac{\frac{Mr_{+}^{3}}{(r_{+}^{2}+q^{2})^{\frac{3}{2}}} -\frac{q^{2}r_{+}^{3}}{2(r_{+}^{2}+q^{2})^{2}}+\frac{\Lambda r_{+}^{3}}{6}}{r_{+}}\right) . \end{aligned}$$

(35)

By using $\Delta (r)=0$, we attain the BH horizon. The expression for mass M is ,

$$\begin{aligned} M=\frac{(r_{+}^{2}+q^{2})^{\frac{3}{2}}}{2r_{+}^{2}}+\frac{q^{2}}{2(r_{+}^{2}+q^{2})^{\frac{1}{2}}}-\frac{\Lambda (r_{+}^{2}+q^{2})^{\frac{3}{2}}}{6}. \end{aligned}$$

(36)

The q represent the electric charge of the given RBH. As we are considering the definition of the Misner–Sharp mass for investigating the thermodynamic properties of our RBH, therefore, the expression for mass is $E=\frac{Mr_{+}^{3}}{(r_{+}^{2}+q^{2})^{\frac{3}{2}}}-\frac{q^{2}r_{+}^{3}}{2(r+^{2}+q^{2})^{2}}+\frac{\Lambda r_{+}^{3}}{6}$. By using the expression of mass M from Eq. (36), we have get a very brief expression as $E=\frac{r_{+}}{2}$. The temperature of this RBH with cosmological constant is,

$$\begin{aligned} T=-\frac{2q^{6}+3q^{4}r_{+}^{2}+q^{2}r_{+}^{4}-r_{+}^{6}+r_{+}^{4}(q^{2}+r_{+}^{2})^{2}\Lambda }{4\pi r_{+}(q^{2}+r_{+}^{2})^{3}}. \end{aligned}$$

(37)

Fig. 7

Plot of T versus $r_{+}$

Figure 7 illustrates the behavior of the temperature and horizon radius at the fixed values of q and $\Lambda$. We have considered the three cases of $\Lambda$ in Fig. 7. For the positive cosmological constant, the temperature is increasing for $0.1\le r\le 0.4$ but it starts decreasing when $r\ge 0.4$. In the absence of cosmological constant, the temperature increases for $0.3\le r\le 0.5$ but when it reaches at $r=0.5$ it bounces back and starts decreasing. For negative cosmological constant, the temperature is increasing for the small values of horizon radius while it starts decreasing when $r\ge 1.0$. The temperatures almost approach to the same value when $r=2.0$ but not for $r\ge 2.0$.

When we rewrite Eq. (14) as Eq. (22), which is the modification of the first law of thermodynamics at horizon of the RBH with cosmological constant, the surface tension at the horizon becomes

$$\begin{aligned} \sigma =-\frac{3q^{6}+6q^{4}r_{+}^{2}+4q^{2}r_{+}^{4}+r_{+}^{4}(q^{2}+r_{+}^{2})^{2}\Lambda }{16\pi r_{+}(q^{2}+r_{+}^{2})^{3}}. \end{aligned}$$

(38)

The surface tension $\sigma$ depends on the electric charge q and the cosmological constant $\Lambda$. When $r_{+}^{4}=-\frac{(3q^{6}+6q^{4}r_{+}^{2}+4q^{2}r_{+}^{4})l^{2}}{\Lambda (q^{2}+r_{+}^{2})^{2}}$, the surface tension is zero, $r_{+}^{4}>-\frac{(3q^{6}+6q^{4}r_{+}^{2}+4q^{2}r_{+}^{4})l^{2}}{\Lambda (q^{2}+r_{+}^{2})^{2}}$, the surface tension is positive while negative surface tension is obtained for $r_{+}^{4}<-\frac{(3q^{6}+6q^{4}r_{+}^{2}+4q^{2}r_{+}^{4})l^{2}}{\Lambda (r_{+}^{2}+q^{2})^{2}}$. The corresponding Smarr relation is same as Eq. (17). The Gibbs free energy turns out to be

$$\begin{aligned} G= & {} E-T S+\sigma A\nonumber \\= & {} \frac{r_{+}}{2}+\left( 2q^{6}+3q^{4}r_{+}^{2}+q^{2}r_{+}^{4}-r_{+}^{6}+r_{+}^{4}(q^{2}+r_{+}^{2})^{2}\Lambda \right) \nonumber \\&\times \,\frac{\pi r_{+}^{2}}{4\pi r_{+}(q^{2}+r_{+}^{2})^{3}}+4\pi r_{+}^{2}\sigma . \end{aligned}$$

(39)

Fig. 8

Plot of G versus T of the RBH with cosmological constant in NED

Figure 8 represents the behavior of Gibbs free energy for the different values of surface tension, three cases will be discussed, i.e. the surface tension is positive, negative and zero. When the temperature is low, Gibbs free energy is increasing at slow rate. When $T=0.16$, the Gibbs free energy increasing rapidly and temperature bounces back for the $-\,0.02\le \sigma \le 0.02$. The effective temperature for the RBH with cosmological constant is also found to be $T_{eff}=T-4\sigma =\frac{1}{4\pi r_{+}}$. Now we will discuss the pressure for the RBH with cosmological constant at the horizon. Since the thermodynamic pressure is $P=T_{r}^{r}|r_{+}$, therefore, the expression for the pressure is evaluated as

$$\begin{aligned} P=-\frac{3q^{6}+6q^{4}r_{+}^{2}+4q^{2}r_{+}^{4}+r_{+}^{4}(q^{2}+r_{+}^{2})^{2}\Lambda }{8\pi r_{+}^{2}(q^{2}+r_{+}^{2})^{3}}. \end{aligned}$$

(40)

In the presence of pressure, the Gibbs free energy is,

$$\begin{aligned} G= & {} E-TS+PV\nonumber \\= & {} \frac{r_{+}}{2}+\left( 2q^{6}+3q^{4}r_{+}^{2}+q^{2}r_{+}^{4}-r_{+}^{6}+r_{+}^{4}(q^{2}+r_{+}^{2})^{2}\Lambda \right) \nonumber \\&\times \,\frac{\pi r_{+}^{2}}{4\pi r_{+}(q^{2}+r_{+}^{2})^{3}}+P \left( \frac{4\pi r^{3}}{3} \right) . \end{aligned}$$

(41)

Fig. 9

Plot of G versus T of the RBH with cosmological constant in NED

Figure 9 represents the behavior of the Gibbs free energy varying along with the temperature at the fixed values of pressures. We observe that when $P<0$, the Gibbs free energy increases for higher values of temperature, after certain value it bounces back and temperature decreases. Once the Gibbs free energy reaches its maximum value, it starts decreasing. Both red and green curves follows this behavior. But when $P\ge 0$, the Gibbs free energy increase for the different values of temperature.

Now, we will consider the cosmological constant, which is correlated with pressure and investigate the thermodynamics of the RBH with the cosmological constant. The first term on the R.H.S of Eq. (14) can be rewritten as

$$\begin{aligned} 2r_{+}T_{r}^{r}|_{r+}\delta S= & {} \left( -\frac{3q^{6}+6q^{4}r_{+}^{2}+4q^{2}r_{+}^{4}}{4\pi r_{+}(q^{2}+r_{+}^{2})^{3}} \right) \delta S\nonumber \\&+\,\frac{-r_{+}^{3}\Lambda }{4\pi (q^{2}+r_{+}^{2})}\delta S, \end{aligned}$$

(42)

$$\begin{aligned} 2r_{+}T_{r}^{r}|_{r+}\delta S= & {} \left( -\frac{3q^{6}+6q^{4}r_{+}^{2}+4q^{2}r_{+}^{4}}{16\pi r_{+}(q^{2}+r_{+}^{2})^{3}} \right) \delta A\nonumber \\&+\,\frac{-r_{+}^{2}\Lambda }{8\pi (q^{2}+r_{+}^{2})}\delta V. \end{aligned}$$

(43)

By using the relations between the entropy, horizon area and volume, we obtain the equal sign in the above equation. It is clear that the first term depends on the electric charge and second term depends on the cosmological constant. Let $\sigma _{eff }=-\frac{3q^{6}+6q^{4}r_{+}^{2}+4q^{2}r_{+}^{4}}{16\pi r_{+}(q^{2}+r_{+}^{2})^{3}}$ and $P=\frac{-r_{+}^{2}\Lambda }{8\pi (q^{2}+r_{+}^{2})}$, then also for RBH with cosmological constant, Eq. (14) takes the form of the Eq. (31), which further can be rewritten as Eq. (33). In these equations $E_{o}=E+PV$ is identified as the enthalpy and its expression is evaluated as

$$\begin{aligned}&E_{o}=\frac{Mr_{+}^{3}}{(r_{+}^{2}+q^{2})^{\frac{3}{2}}}\nonumber \\&\quad -\frac{r_{+} \left( 3q^{6}+9q^{4}r_{+}^{2}+7q^{2}r_{+}^{4} +r_{+}^{2}(q^{2}+r_{+}^{2})^{2}(2q^{2}+3r_{+}^{2})\Lambda \right) }{6(q^{2}+r_{+}^{2})^{3}}.\nonumber \\ \end{aligned}$$

(44)

After making analysis on the $E_{o}$, we have seen that it is the Misner–Sharp mass for the RBH with cosmological constant and by taking into account the expressions of $T, ~S, ~\sigma , ~A, ~P$ and V the corresponding Smarr relation is same as the Eq. (34), that we have obtained for the non-minimal RBH.

We obtain the expression for the corresponding Gibbs free energy as

$$\begin{aligned} G= & {} E-T S+\sigma _{eff }A+PV\nonumber \\= & {} \frac{r_{+}}{2}+ \left( \frac{2q^{6}+3q^{4}r_{+}^{2}+q^{2}r_{+}^{4}-r_{+}^{6}-8\pi r_{+}^{4}(q^{2}+r_{+}^{2})^{2}P}{4\pi r_{+}(q^{2}+r_{+}^{2})^{3}} \right) \nonumber \\&\times \,\pi r_{+}^{2}+4\pi r_{+}^{2}\sigma _{eff }+\frac{4\pi r_{+}^{3}P}{3}. \end{aligned}$$

(45)

In Fig. 10, we observe the behavior of Gibbs free energy at different temperatures and fixed values of $\sigma _{eff }$. When $0.01\le T\le 0.17$, the Gibbs free energy increases along with the increase in temperature and give us a characteristic cusp for the fixed values of surface tension. At $T=0.17$ the curves bounces back, and Gibbs free energy increases for the lower values of temperatures. For $\sigma _{eff }=-\,0.01$ the Gibbs free energy start decreasing for the certain value of temperature and becomes negative. When the surface tension $\sigma _{eff }\ge -\,0.0001$, the Gibbs free energy have higher values. Equations (35) and (36) are found to be same for the RBH with cosmological constant. Thus, for the lower negative values of surface tension, the Gibbs free energy have positive higher values. But $T_{o}$ is,

$$\begin{aligned} T_{o}= & {} T-4\sigma _{eff }\nonumber \\= & {} -\frac{5q^{6}+9q^{4}r_{+}^{2}+5q^{2}r_{+}^{4}-r_{+}^{6}+r_{+}^{4}(q^{2}+r_{+}^{2})^{2}\Lambda }{4\pi r_{+}(q^{2}+r_{+}^{2})^{3}}. \end{aligned}$$

(46)

The corresponding Gibbs free energy is evaluated as,

$$\begin{aligned} G= & {} E-T_{o}S+PV\nonumber \\= & {} \frac{r_{+}}{2}\nonumber \\&+\,\left( -\frac{5q^{6}+9q^{4}r_{+}^{2}+5q^{2}r_{+}^{4}-r_{+}^{6}-8\pi r_{+}^{4}(q^{2}+r_{+}^{2})^{2}P}{4\pi r_{+}(q^{2}+r_{+}^{2})^{3}} \right) \nonumber \\&\times \pi r_{+}^{2}+P \left( \frac{4\pi r_{+}^{3}}{3} \right) . \end{aligned}$$

(47)

Figure 11 illustrate the behavior of the Gibbs free energy at different values of $T_{o}$ and fixed pressure. When $T_{o}=0.112$, the curve bounces back and the Gibbs free energy increases along with the decrease in temperature at fixed values of pressure. When $P=0$, the Gibbs free energy increases. We conclude that when $0\le P\le 0.5$, the Gibbs free energy increase for the positive values of temperature.

Fig. 10

Plot of G versus T of the RBH with cosmological constant in NED

Fig. 11

Plot of G versus $T_{o}$ of the RBH with cosmological constant in NED

4 Conclusion

The radial Einstein’s equation at the BH event horizon and cosmological horizon has been used in this paper in which we have obtained the modified first laws of thermodynamics for two BHs: (1) The non-minimal MCRBH and (2) RBH with cosmological constant, for which all the correlated Smarr relations are also satisfied. We treated the cosmological constant $\Lambda$ in two ways, firstly it has been adopted as fixed and then secondly, as the variable which is correlated to the pressure. The surface tension $\sigma$ can be negative, zero and positive which value is ascertained by using the horizon radius $r_{+}$, magnetic charge $Q_{m}$, non-minimal parameter $\lambda$, electric charge q and the cosmological horizon $\Lambda$. The first law of thermodynamics has been modified in the presence of $\sigma$ for MCRBH. For $\Lambda >0$, plot of Gibbs free energy versus temperature in the presence of surface tension (for any value) shows that for the increasing values of temperature, the Gibbs free energy approaches to the same value, but for $\Lambda =0$ and negative surface tension, the Gibbs free energy and temperature, both are negative except for $\sigma \ge 0$, the Gibbs free energy increase with increasing temperature.

We have obtained the expression for effective Gibbs free energy by modifying the temperature into effective temperature, also analyzed that the effective Gibbs free energy decreases along with increasing effective temperature. We have also discussed pressure at horizon of MCRBH. For fixed values of pressure, negative, positive and zero, behavior of Gibbs free energy has been studied. For $\Lambda >0$, the Gibbs free energy decreases and approaches to the same value with increase in temperature for all fixed values of pressure. For $\Lambda =0$, we have analyzed that, the Gibbs free energy increases when $P=0$ and $p>0$, after bouncing back at $T=0.016$ but for $P<0$, it decrease to negative values.

• For RBH with cosmological constant, the first law of thermodynamics has also been modified as Eq. (22) in the presence of $\sigma$, which expression is given by Eq. (38). For $\Lambda =0.01$, we have analyzed that the Gibbs free energy increases for all, negative, zero and positive values of $\sigma$ along with the increase in temperature, after bouncing back at $T=0.16$. We have also obtained the expression for Gibbs free energy in the presence of pressure for RBH with cosmological constant. We have analyzed that for $\Lambda =0.01$, the Gibbs free energy decreases and approaches to negative values for negative pressure whereas, for positive pressure, the Gibbs free energy increases.

• We have obtained the modified temperature $T_{o}$ by using the relation between the Bekenstein entropy area relation. The first law of thermodynamics could have taken the possession of the differential form based on the above replacement for which the corresponding Smarr relation is not obeyed. This type of situation was also explained in [61]. When the surface effects of the curved surface are taken into the consideration then the pressures are generally unsteady. The cosmological constant has been treated as the thermodynamic pressure such as $P=-\frac{\Lambda }{8 \pi }$ which has been accounted for exploring the thermodynamics. To make further investigation for the RBH with cosmological constant $\Lambda$, we treated the cosmological constant as the pressure $P=\frac{-r_{+}^{2}\Lambda }{8\pi (q^{2}+r_{+}^{2})}$. For RBH with cosmological constant, we have analyzed that, when the $\Lambda$ is correlated with the pressure, the Gibbs free energy in the presence of effective surface tension increases for lower negative values of $\sigma _{eff }$. For positive fixed values of pressure, we have also analyzed that the Gibbs free energy increases for the increasing values of modified temperature, for the RBH with cosmological constant.