Spin-1 diquark contributing to the formation of tetraquarks in light mesons

Abstract

We apply a mixing framework to the light-meson systems and examine tetraquark possibility in the scalar channel. In the diquark–antidiquark model, a scalar diquark is a compact object when its color and flavor structures are in ($\bar{\mathbf {3}}_c$, $\bar{\mathbf {3}}_f$). Assuming that all the quarks are in an S-wave, the spin-0 tetraquark formed out of this scalar diquark has only one spin configuration, $|J,J_{12},J_{34}\rangle =|000\rangle$, where J is the spin of the tetraquark, $J_{12}$ the diquark spin, $J_{34}$ the antidiquark spin. In this construction of the scalar tetraquark, we notice that another compact diquark with spin-1 in ($\mathbf {6}_c$, $\bar{\mathbf {3}}_f$) can be used although it is less compact than the scalar diquark. The spin-0 tetraquark constructed from this vector diquark leads to the spin configuration $|J,J_{12},J_{34}\rangle =|011\rangle$. The two configurations, $|000\rangle$ and $|011\rangle$, are found to mix strongly through the color–spin interaction. The physical states can be identified with certain mixtures of the two configurations which diagonalize the hyperfine masses of the color–spin interaction. Matching these states to two scalar resonances $a_0(980), a_0(1450)$ or to $K^*_0(800), K^*_0(1430)$ depending on the isospin channel, we find that their mass splittings are qualitatively consistent with the hyperfine mass splittings, which can support their tetraquark structure. To test our mixing scheme further, we also construct the tetraquarks for $J=1,J=2$ with the spin configurations $|111\rangle$ and $|211\rangle$, and we discuss possible candidates in the physical spectrum.

1 Introduction

Recently, there has been a lot of progress in the study of the multiquark states which normally refer to hadrons containing four or higher number of quarks. Among multiquarks, tetraquarks are quite interesting as there have been several studies suggesting plausible evidence for their existence especially for hadrons containing heavy quarks. The hidden-charmed resonance, X(3872), measured in the B-meson decays [1,2,3,4] as well as the other resonances with similar masses, X(3823) [5], X(3900) [6], X(3940) [7], may be tetraquarks with the flavor structure $cq\bar{c}\bar{q}~ (q=u,d)$ [8,9,10,11]. Very recently, the LHCb collaboration [12, 13] reported X(4140), X(4274), X(4500), X(4700) measured in $J/\psi \phi$ structures from the decays $B^+\rightarrow J/\psi \phi K^+$. Among various interpretations for them, tetraquarks belong to the most promising scenarios to explain their nature.

The tetraquark possibility was also investigated in the D or B-meson excited states. In Ref. [14], we discussed how most of the D or B-meson excited states currently listed in particle data group (PDG) [15], especially as regards their mass spectrum, can be understood if they are viewed as tetraquarks with the diquark–antidiquark form, $cq{\bar{q}}{\bar{q}}, (q=u,d,s)$. Using the color–spin interaction, we reproduced the mass splittings of the resonances in the excited states of D and B mesons quite successfully. Also our model provides interesting phenomenology related to decays of spin-1 mesons, which seems to fit nicely with experimental observation. Based on its phenomenological success, we made some predictions for the D and B mesons to be found in future.

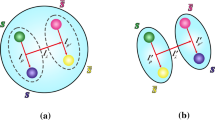
If the existence of the tetraquarks in heavy quark sector is confirmed, then it is likely that they can exist also in the light meson system composed of u, d, s quarks. This is because the binding among quarks in hadrons is governed by the color force which, in principle, does not discriminate against the quark flavors. Indeed, Jaffe proposed back in the 1970s that, based on the diquark–antidiquark picture, $a_0 (980)$, $f_0 (980)$, $\sigma (600)$, and $K^*_0 (800)$ may be tetraquarks forming a nonet in flavor space [16,17,18,19]. The main feature of this model starts from the fact that the spin-0 diquark belonging to a color and flavor antitriplet, ($\bar{\mathbf {3}}_c$, $\bar{\mathbf {3}}_f$), is the most compact object among all the possible diquarks. The spin-0 tetraquarks can be constructed by combining the spin-0 diquarks with the corresponding antidiquarks. This type of the four-quark picture is further supported by the other calculations [20, 21] even though it is still confronted with a two-quark picture involving a P-wave excitation [22].

What we want to emphasize in this work is that the above diquark with ($J=0$, $\bar{\mathbf {3}}_c$, $\bar{\mathbf {3}}_f$) is not a unique choice even though it is an optimal starting point in constructing tetraquarks in the diquark–antidiquark approach. An alternative way is to construct scalar tetraquarks by facilitating the spin-1 diquark with the color and flavor structures ($\mathbf {6}_c, \bar{\mathbf {3}}_f$). This spin-1 diquark is a less compact object than the spin-0 diquark but it is still the second most compact object among all the possible diquarks [19]. If we take this possibility into account, we then have two ways to construct tetraquarks with spin-0. These two tetraquarks are expected to mix, which may lead to interesting phenomena in the meson spectroscopy. Therefore, we explore possible consequences of the mixing between the two states in the spin-0 tetraquarks.

To make our investigation succinct, we focus on the isovector ($I=1$) and isodoublet ($I=1/2$) channels first of all. If the two states ought to mix, the physical states must be generated by the diagonalization among them, which should appear as doublets in the actual spectrum. The ones with lower masses can be identified by $a_0 (980)$ in the isovector channel, and by $K^*_0 (800)$ ¹ in the isodoublet channel. Then the others with higher masses must be found in the meson spectrum. Indeed, there are $a_0 (1450)$ in the isovector channel and $K^*_0 (1430)$ in the isodoublet channel, which can be identified as the candidates for this mixing scenario. As we will discuss below, the mixing is important to generate the huge mass splittings, about 500 and 740 MeV, from $a_0 (980)$ and $K^*_0 (800)$, respectively.

In fact, this type of the mixing was also discussed in Refs. [18, 23]. There, this mixing is used in a way to explain why the lowest lying states in $0^+$ channel have quite small masses below 1 GeV without investigating the other states with higher masses. Also Black et al. [24] discussed a different mixing scenario to explain $a_0 (1450)$ and $K^*_0 (1430)$. Their mixing is between a P-wave $q\bar{q}$ and $qq\bar{q}\bar{q}$. This is different from our approach where the mixing is introduced between the four-quark states with different color and spin configurations.

In addition, there are other approaches that can be found in the literature. Reference [25] proposed a model that $a_0(980)$ and $a_0(1450)$ can be dynamically generated from a single $\bar{q}q$ state. A kind of hybrid model was also proposed where $a_0 (1450)$ and $K^*_0 (1430)$ are viewed as the tetraquarks mixed with a glueball state [26].

Our approach based on spin-1 diquark should accompany two more spin states for the tetraquarks, namely $J=1,2$. Finding corresponding resonances in PDG can provide further supports of our model. Using the color–spin interactions, we also estimate the mass splittings of these members from the spin-0 tetraquarks and look for the candidates in PDG which can fit to our scheme.

This paper is organized as follows. In Sect. 2, we present tetraquark wave functions that could be relevant for the light-meson systems. The wave functions for flavor, color and spin spaces will be constructed using either the scalar or the vector diquark. In Sect. 3, we introduce the color–spin interaction as well as the color–electric interaction and provide formulas for the hyperfine masses and the color–electric masses. In Sect. 4, we present our results and discuss their implication in the light-meson spectroscopy. We summarize in Sect. 5.

Table 1 Here we collect all the isovector ($a_0,a_1,a_2$) and isodoublet ($K^*_0, K_1, K^{*}_2$) resonances with the positive parity from PDG and arrange them according to their spins $J=0,1,2$. We omit the other resonances like $f_0,f_1,f_2$ etc. as they are not our concern in the present work

2 Tetraquark wave functions

In this section, we construct the four-quark wave functions which might be relevant for the light mesons composed by u, d, s quarks. Our construction is based on the diquark–antidiquark picture with an assumption that all the quarks are in an S-wave state. This assumption constrains that the corresponding tetraquark candidates must be sought in the resonances with the positive parity to begin with. As possible candidates for them, we collect isovector and isodoublet resonances with $J^P=0^+,1^+,2^+$ in Table 1 from PDG. In this work, we do not discuss the isoscalar resonances for simplicity.

In constructing tetraquarks, the well-known approach, as advocated by Jaffe, is to facilitate the compact diquark, which is in $J=0$ with the color antitriplet $\bar{\mathbf {3}}_c$ and the flavor antitriplet $\bar{\mathbf {3}}_f$. It may be worth mentioning that, due to Pauli principle, the diquark must be in the spin state $J=0$ when its color and flavor structures are fixed to $\bar{\mathbf {3}}_c$ and $\bar{\mathbf {3}}_f$. The fact that this diquark is the most compact object among all the possible diquarks can be demonstrated straightforwardly by calculating the hyperfine mass of the color–spin interaction [19]. Likewise, the tight antidiquarks should be in $J=0$ with $\mathbf {3}_c$, $\mathbf {3}_f$.

Combining the diquarks with the antidiquarks leads to the tetraquarks forming a nonet in flavor, $\bar{\mathbf {3}}_f\otimes {\mathbf {3}}_f={\mathbf {8}}_f\oplus {\mathbf {1}}_f$. The flavor structure of the tetraquarks, by adopting the tensor notation for multiplets, can be expressed as

$$\begin{aligned}&[\mathbf{8}_f]^i_{j} = T_{j}\bar{T}^{i}-\frac{1}{3} \delta ^{i}_{j}T_{m}\bar{T}^{m}, \end{aligned}$$

(1)

$$\begin{aligned}&{} \mathbf{1}_f = \frac{1}{\sqrt{3}}T_{m}\bar{T}^{m}. \end{aligned}$$

(2)

Here the diquark ($T_i$) and the antidiquark ($\bar{T}^i$) are represented by the quark flavors as

$$\begin{aligned} T_i= & {} \frac{1}{\sqrt{2}}\epsilon _{ijk}q_j q_k\equiv [q_j q_k], \nonumber \\ \bar{T}^i= & {} \frac{1}{\sqrt{2}}\epsilon ^{ijk}\bar{q}^j \bar{q}^k \equiv [{\bar{q}}^j {\bar{q}}^k]. \end{aligned}$$

(3)

To avoid further complications coming from the mixing between the flavor octet and singlet among the isoscalar members, our discussion in this work focuses on the isovector and isodoublet members which can couple to $a_0$ and $K^*_0$. To be more precise, the charged octet members, $a_0^+$ and $K^{*+}_0$, will be considered as they are located at the boundary of the weight diagram where the multiplicity is just one. The flavor wave functions that can couple to $a_0^+$ and $K^{*+}_0$, respectively, are

$$\begin{aligned}{}[\mathbf{8}_f]^1_{2}=[su][\bar{d}\bar{s}]; \quad [\mathbf{8}_f]^1_{3}=[ud][\bar{d}\bar{s}] . \end{aligned}$$

(4)

With this four-quark approach, $a_0$ has the hidden strange component, $s\bar{s}$, while $K^*_0$ contains one strange quark. The experimental mass ordering, $M(a_0)\ge M(K^*_0)$, can be understood more easily from this tetraquark picture than from the two-quark picture.

As for the color part of the wave function, the diquark is in $\bar{\mathbf {3}}_c$, the antidiquark is in $\mathbf {3}_c$, and the four-quark state in total must be colorless. It means that, for each flavor combination involved in Eq. (4), if we call the first two quarks $q_1 q_2$, and the third and fourth antiquarks $\bar{q}^3 \bar{q}^4$, the four-quark system has the following color structure with the color normalization:

$$\begin{aligned} \frac{1}{\sqrt{12}} \varepsilon _{abd}^{} \ \varepsilon ^{aef} \Big (q_1^b q_2^d \Big ) \Big (\bar{q}^3_e \bar{q}^4_f \Big ). \end{aligned}$$

(5)

Here the Roman indices, a, b, d, e, f, denote the colors. Since the diquark spin $J_{12}$ and the antidiquark spin $J_{34}$ are zero, the total spin J must be zero. Then the spin structure for the tetraquarks of this type is restricted to

$$\begin{aligned} |J,J_{12},J_{34}\rangle =|000\rangle _{\bar{\mathbf {3}}_c,\mathbf {3}_c}. \end{aligned}$$

(6)

Here the subscripts denote the color structures for the diquark and antidiquark.

Alternatively, other types of diquark are also possible in constructing the tetraquarks. Considering only symmetry properties associated with the spin, color, flavor of the two-fermion system, it is possible to have other diquarks which have the structures ($J=1,\mathbf {6}_c, \bar{\mathbf {3}}_f$), ($J=1,\bar{\mathbf {3}}_c, \mathbf {6}_f$), ($J=0,\mathbf {6}_c, \mathbf {6}_f$). One can demonstrate through the color–spin interaction that the first one with ($J=1,\mathbf {6}_c, \bar{\mathbf {3}}_f$) is the most attractive configuration among these three [19]. In fact, other diquarks with the structures, ($J=1,\bar{\mathbf {3}}_c, \mathbf {6}_f$), ($J=0,\mathbf {6}_c, \mathbf {6}_f$), are not compact because the color–spin interaction for them are repulsive. Using the first one, one can construct another tetraquarks by combining the diquark with $(J=1,\mathbf {6}_c, \bar{\mathbf {3}}_f)$ and the antidiquark with $(J=1,\bar{\mathbf {6}}_c, \mathbf {3}_f)$.

The resulting tetraquarks form a nonet again in flavor. The octet members that can couple to $a^+_0, K^{*+}_0$, have the same flavor wave function as Eq. (4). But now the diquark is in $\mathbf {6}_c$ and the antidiquark is in $\bar{\mathbf {6}}_c$ so that they can be combined into a color singlet. Again, for each flavor combination involved in Eq. (4), calling the first two quarks as $q_1 q_2$ and the rest two antiquarks as $\bar{q}^3 \bar{q}^4$, the four-quark system has the following color structure:

$$\begin{aligned} \frac{1}{\sqrt{96}} \Big (q_1^a q_2^b+q_1^b q_2^a \Big ) \Big (\bar{q}^3_a \bar{q}^4_b+\bar{q}^3_b \bar{q}^4_a\Big ). \end{aligned}$$

(7)

Here again the Roman indices, a, b, denote the colors.

However, with this spin-1 diquark scenario, there are three possible spin states for tetraquarks. Namely, tetraquarks have the spins $J=0,1,2$ with the following configurations:

$$\begin{aligned} |011\rangle _{\mathbf {6}_c,\bar{\mathbf {6}}_c}; \quad |111\rangle _{\mathbf {6}_c,\bar{\mathbf {6}}_c}; \quad |211\rangle _{\mathbf {6}_c,\bar{\mathbf {6}}_c}. \end{aligned}$$

(8)

What is interesting is that the tetraquarks in the scalar channel, $|011\rangle _{\mathbf {6}_c,\bar{\mathbf {6}}_c}$, can mix with Eq. (6) through the color–spin interaction. The hyperfine masses, which are expectation values of the color–spin interaction, form a $2\times 2$ matrix in the basis, $|000\rangle ,|011\rangle$. A diagonalization is necessary in order to identify the physical states in this scalar channel. Therefore, if this framework is realized in the real world, there should be two resonances in the scalar mesons for each member in the octet, Eq. (4). Indeed, as shown in Table 1, there are two isovector resonances, $a_0(980)$ and $a_0(1450)$. Also, in the isodoublet channel, there are three resonances, $K^*_0(800), K^*_0(1430), K^*_0(1950)$, and two of them might be candidates fitting our framework. In this sense, the situation is quite promising and it is worth pursuing the consequences of this scenario further.

If our expectation works, additional resonances can be anticipated in the spin configurations, $|111\rangle _{\mathbf {6}_c,\bar{\mathbf {6}}_c}$, $|211\rangle _{\mathbf {6}_c,\bar{\mathbf {6}}_c}$. Alternatively, they can be hidden in the continuum of two-meson decays. Anyway, as one can see in Table 1, there are various resonances in $J=1,2$ and some of them might be possible candidates of this scenario. Therefore, it is also interesting to study which of them fits to this scheme.

3 Mass formulas

Normally a hadron mass can be calculated by adding constituent quark masses and the expectation value of the potential, V, generated by summing over all the pairs of quark–quark interaction. In this sense, the formula for a hadron mass ($M_H$) can be written schematically as

$$\begin{aligned} M_H=\sum _{i} m_i +\langle V \rangle , \end{aligned}$$

(9)

where $m_i^{}$ the constituent mass of the ith quark. The quark–quark interaction can have two different sources, one-gluon exchange potential [27,28,29,30] and the instanton-induced interaction [31, 32]. A common feature of the two sources is the color–spin interaction ($V_{\mathrm{CS}}$) which usually generates the mass splittings among hadrons with different spins but with the same flavor content. In particular, this interaction can explain the mass differences between the octet and decuplet baryons as well as between the spin-1 and spin-0 meson octets [10, 14, 33, 34]. The instanton-induced interaction further provides the color–electric term ($V_{{\mathrm{CE}}}$) and the constant shift [31, 32]. Taking the two sources into account, the potential can be effectively parameterized as

$$\begin{aligned} V = v_0 \sum _{i< j} \lambda _i \cdot \lambda _j \, \frac{J_i\cdot J_j}{m_i^{} m_j^{}} +v_1^{} \sum _{i < j} \frac{\lambda _i \cdot \lambda _j}{m_i^{} m_j^{}} + v_2. \end{aligned}$$

(10)

Here $\lambda _i$ denotes the Gell-Mann matrix for the color SU(3), $J_i$ the spin. The first and second terms are called color–spin and color–electric interactions and we denote them as

$$\begin{aligned} V_{\mathrm{CS}}= & {} v_0 \sum _{i < j} \lambda _i \cdot \lambda _j \, \frac{J_i\cdot J_j}{m_i^{} m_j^{}}, \end{aligned}$$

(11)

$$\begin{aligned} V_{{\mathrm{CE}}}= & {} v_1 \sum _{i < j} \frac{\lambda _i \cdot \lambda _j}{m_i^{} m_j^{}} . \end{aligned}$$

(12)

The parameters $v_0, v_1$ represent the strength of the color–spin and color–electric interactions which, in principle, need to be fitted from the hadron masses. The constant shift $v_2$ could be flavor-dependent in general.

The hadron masses of our concern can be formally calculated by Eq. (9) using the four states that we have introduced in Eqs. (6) and (8). As we have discussed in Ref. [10], fitting all the parameters $v_0,v_1,v_2$ with only the hadron masses of concern here may be questionable as to whether the same parameters can be used in other set of hadrons in general. To reduce the ambiguity coming from the parameters, we focus on the mass splittings among hadrons of concern.

Table 2 Formulas for the expectation values of $V_{\mathrm{CS}}$ and $V_{{\mathrm{CE}}}$ are presented for a specific flavor combination, $q_1 q_2 {\bar{q}}^3 {\bar{q}}^4$, with respect to the states indicated in the first column. Note that the diquark and antidiquark are in the color states, $\bar{\mathbf {3}}_c,\mathbf {3}_c$, for the spin configuration, $|000\rangle$, and they are in $\mathbf {6}_c,\bar{\mathbf {6}}_c$ for $|011\rangle , |111\rangle , |211\rangle$

Then one can approximate that the mass splittings are generated by the interactions, $V_{\mathrm{CS}}$ and $V_{{\mathrm{CE}}}$, through

$$\begin{aligned} \Delta M_H \approx \Delta \langle V_{\mathrm{CS}} \rangle + \Delta \langle V_{{\mathrm{CE}}} \rangle , \end{aligned}$$

(13)

if the differences are taken for the hadrons with the same flavor content. Here the expectation values are taken with respect to the states introduced in Eqs. (6), (8), and their differences constitute the right-hand side. It turns out that the right-hand side is dominated by the color–spin interaction, $V_{\mathrm{CS}}$. The color–electric interaction, $V_{{\mathrm{CE}}}$, although it contributes differently to the masses of $|000\rangle _{\bar{\mathbf {3}}_c,\mathbf {3}_c}$ and to the masses of the other category, $|011\rangle _{\mathbf {6}_c,\bar{\mathbf {6}}_c}$, $|111\rangle _{\mathbf {6}_c,\bar{\mathbf {6}}_c}$, $|011\rangle _{\mathbf {6}_c,\bar{\mathbf {6}}_c}$, its contribution to the mass splitting, $\Delta M_H$, is almost negligible as we will demonstrate below. In addition, since $V_{{\mathrm{CE}}}$ is independent of the spins, the mixing term between the two states in the scalar channel, $\langle 000 |V_{{\mathrm{CE}}}|011\rangle$, is zero by the orthogonality of the spin states.² The constant shift $v_2$ cancels in the differences.

The expectation values, $\langle V_{\mathrm{CS}} \rangle$ and $\langle V_{{\mathrm{CE}}} \rangle$, which we call hyperfine mass and color–electric mass respectively, can be calculated straightforwardly. We suggest the reader to refer Ref. [14] for the technical details. In Table 2, we present all the formulas for hyperfine and color–electric masses for the various spin configurations with one specific flavor combination, $q_1 q_2 {\bar{q}}^3 {\bar{q}}^4$. We also present the mixing term appearing in the scalar channel.

Note that the parameter $v_0$ has a negative value based on the analysis of the baryon spectroscopy [10, 14]. So from the formulas provided in the scalar channel, one can see that the color–spin interaction, $V_{\mathrm{CS}}$, provides a fair amount of binding. Of course, the actual binding from $V_{\mathrm{CS}}$ must take into account the mixing between the two states $|000\rangle$ and $|011\rangle$. In the spin-1 and spin-2 channel, one can also see that $|111\rangle$ is more bound than $|211\rangle$ as far as the color–spin interaction is concern. This makes the $|211\rangle$ state heavier than the $|111\rangle$ state which is consistent with the general hierarchy observed in the mass spectrum in hadrons. The contribution from the color–electric interaction is small due to the small strength $v_1$ as we will see below.

The final expressions for the hyperfine mass, $\langle V_{\mathrm{CS}}\rangle$, and the color–electric mass, $\langle V_{{\mathrm{CE}}}\rangle$, can be obtained by including various flavor combinations involved in Eq. (4). In particular, for the isovector channel which can couple to $a^+_0$, $a^+_1$ or $a^+_2$ depending on its spin, the hyperfine mass can be written schematically as

$$\begin{aligned} \langle V_{\mathrm{CS}} \rangle= & {} \frac{1}{4} \Big [ \langle V_{\mathrm{CS}} \rangle _{su{\bar{d}}{\bar{s}}} +\langle V_{\mathrm{CS}} \rangle _{su{\bar{s}}{\bar{d}}} \nonumber \\&+\;\langle V_{\mathrm{CS}} \rangle _{us{\bar{d}}{\bar{s}}} +\langle V_{\mathrm{CS}} \rangle _{us{\bar{s}}{\bar{d}}} \Big ], \end{aligned}$$

(14)

where the specified flavor combination in the subscripts and the normalization in front follow from Eq. (4). Since the flavor structures are the same for all the spin states, $J=0,1,2$, we have this type of flavor formula in common for the three spin states. The corresponding formula for the color–electric mass, $\langle V_{{\mathrm{CE}}} \rangle$, can be obtained simply by replacing the subscript $\mathrm{CS}\rightarrow {\mathrm{CE}}$.

For the isodoublet channel which can couple to $K^{*+}_0$, $K^+_1$ or $K^{*+}_2$ depending on its spin, we have a similar formula, but with different flavors,

$$\begin{aligned} \langle V_{\mathrm{CS}} \rangle= & {} \frac{1}{4} \Big [ \langle V_{\mathrm{CS}} \rangle _{ud{\bar{d}}{\bar{s}}} +\langle V_{\mathrm{CS}} \rangle _{ud{\bar{s}}{\bar{d}}} \nonumber \\&+\;\langle V_{\mathrm{CS}} \rangle _{du{\bar{d}}{\bar{s}}} +\langle V_{\mathrm{CS}} \rangle _{du{\bar{s}}{\bar{d}}}\Big ]. \end{aligned}$$

(15)

Again, the corresponding formula for the color–electric mass, $\langle V_{{\mathrm{CE}}} \rangle$, can be obtained by replacing the subscript $\mathrm{CS}\rightarrow {\mathrm{CE}}$ in this equation.

4 Results and discussion

Now we present and discuss the results for the mass splittings obtained from the expectation value of the color–spin and color–electric formulas provided in Table 2. For our numerical calculations, first we need to determine the input parameters appearing in Table 2. We take the standard values for the constituent quark masses $m_u = m_d = 330$ MeV, $m_s = 500$ MeV as in our previous work [10, 14]. For the strength $v_0$ of the color–spin interaction, we test two possible choices. One choice is to use the value determined from the D meson excited states studied within the tetraquark framework where $v_0$ is fixed from the mass spliting of $D_0^*(2318)$–$D_2^*(2463)$ [14]. This gives $v_0\sim (-192.9)^3$ MeV$^3$. The other choice is to use the value determined from $\Delta$–N mass difference, which gives a slightly different value: $v_0\sim (-199.6)^3$ MeV$^3$ [10, 14]. Since our results turn out to depend strongly on this parameter, we present the two results obtained by using the two values of this parameter. We call the first one as “Theory I” and the second one as “Theory II”. But for illustration purposes, we use mainly the results from “Theory I” but, in the final results, we will show both calculations.

For the color–electric interaction, the strength $v_1$ cannot be determined for example from the mass splittings of the baryon octet and decuplet as the two multiplets have the same color structure. For this purpose, we take the value determined by $N,\Delta ,\Lambda$ masses as inputs [10]. It gives $v_1 \sim (71.2)^3$ MeV$^3$. This value should be regarded as a qualitative estimate as it may depend on how it is extracted. Nevertheless, the contribution from the color–electric terms to our results are very small so that our results are not sensitive to this particular choice.

Table 3 The numerical values for $\langle V_{\mathrm{CS}}\rangle$ and $\langle V_{{\mathrm{CE}}}\rangle$ are presented here for the specified spin configurations. The $I=1$ channel can couple to $a_0$, $a_1$, $a_2$ and the $I=1/2$ isodoublet channel can couple to $K^*_0$, $K_1$, $K^*_2$. Here we present the results with “Theory I” which uses the color–spin interaction parameter as $v_0=(-192.9)^3$ MeV$^3$. All the numbers are given in MeV unit

Having set all the parameters involved, we now discuss the numerical values for the hyperfine masses and color–electric masses. Table 3 presents those masses calculated with respect to the specified spin configurations using $v_0=(-192.9)^3$ MeV$^3$ (“Theory I”). There are several interesting features to discuss as regards this result.

First, the hyperfine mass for $|011\rangle$ is more negative than the one for $|000\rangle$. It is quite different from the usual expectation that the tetraquarks involving the spin-0 diquark is more bound than the tetraquarks containing the spin-1 diquark. This interesting aspect can be understood if we examine carefully the formulas for $\langle 000|V_{\mathrm{CS}}|000 \rangle$ and $\langle 011|V_{\mathrm{CS}}|011 \rangle$ given in Table 2. The color–spin interaction in principle acts on all the pairs of quarks. For the $|000\rangle$ case, the calculated hyperfine mass is proportional to $\sim 1/m_1 m_2 + 1/m_3 m_4$ which means that the color–spin interaction is nonzero only for two quarks in the diquark or for two antiquarks in the antidiquark. There are no terms like $1/m_1 m_3$, $1/m_2 m_4$, indicating that the color–spin interaction acting on any quark–antiquark pair is zero for the $|000\rangle$ state. But for the $|011\rangle$ case, as one can see from the formula for $\langle 011|V_{\mathrm{CS}}|011 \rangle$ in Table 2, there are nonzero contributions coming from the quark–antiquark pairs in addition to those from two quarks in the diquark and two antiquarks in the antidiquark. This precisely makes the hyperfine mass of the $|011\rangle$ state more negative.

Secondly, we notice that the mixing term between the two states, $|000 \rangle$ and $|011 \rangle$, is quite large. The mixing term in the isovector channel for example is about $\langle 000|V_{\mathrm{CS}}|011 \rangle \sim -222$ MeV. Therefore, the two states, $|000 \rangle$ and $|011 \rangle$, must mix strongly in making the physical states.

An additional thing that can be seen from Table 3 is that the color–electric masses are quite small. Moreover, their magnitudes are essentially the same for all the spin configurations. The only exception is the element, $\langle 000|V_{{\mathrm{CE}}}|000 \rangle$, in the isovector channel but its value is different only slightly from other color–electric masses. Therefore, the color–electric masses almost cancel in the mass differences and our results below, based on the mass splittings, are almost independent of the color–electric interaction. That is, as long as our analysis focuses on the mass splittings, we can safely use the approximation

$$\begin{aligned} \Delta M_H \approx \Delta \langle V_{\mathrm{CS}} \rangle . \end{aligned}$$

(16)

4.1 Results on isovector channel

Let us begin with a discussion on the isovector channel ($I=1$) which can couple to $a_0$, $a_1$, $a_2$. Because of the mixing between the two states in spin-0, we have a $2\times 2$ matrix for the hyperfine masses $\langle V_{\mathrm{CS}}\rangle$ with respect to the states $|000 \rangle$ and $|011 \rangle$. This matrix needs to be diagonalized in order to get the physical hyperfine masses. For the isovector channel with spin-0, the hyperfine mass matrix whose elements collected from Table 3, and the matrix after the diagonalization are

$$\begin{aligned} \begin{array}{c|lr} &{} |000 \rangle &{} |011 \rangle \\ \hline |000 \rangle &{} -173.9 &{} -222.3\\ |011 \rangle &{} -222.3 &{} -331.5 \end{array} \quad\rightarrow & {} \quad \begin{array}{c|lr} &{} |0^{a_0}_A \rangle &{} |0^{a_0}_B \rangle \\ \hline |0^{a_0}_A \rangle &{} -16.8 &{} 0.0\\ |0^{a_0}_B \rangle &{} 0.0 &{} -488.5 \nonumber \end{array}. \end{aligned}$$

Here we denote the eigenstates as $|0^{a_0}_A \rangle$ and $|0^{a_0}_B \rangle$ with the superscript $a_0$ indicating the resonance that they can couple to. Note, the difference between the diagonal members, which is the key ingredient of our prediction, is amplified from 157.6 to 472 MeV. This shows that the mass splitting between the physical states $|0^{a_0}_A\rangle$, $|0^{a_0}_B\rangle$ is strongly driven by the mixing in the spin-0 channel. Note that the color–electric term $\langle V_{{\mathrm{CE}}}\rangle$ only shifts the diagonal masses by almost the same amount. Its contribution to the mass splittings therefore cancels and the gap, 472 MeV, is practically unchanged even with $\langle V_{{\mathrm{CE}}}\rangle$.

The eigenstates $|0^{a_0}_A\rangle , |0^{a_0}_B\rangle$ are related to the original spin configurations through

$$\begin{aligned} |0^{a_0}_A\rangle= & {} -0.817 \mid 000 \rangle + 0.577 \mid 011 \rangle , \nonumber \\ |0^{a_0}_B\rangle= & {} 0.577 \mid 000 \rangle + 0.817 \mid 011 \rangle . \end{aligned}$$

(17)

This result is to some measure consistent with Black et al. [23] where this mixing is used in a different context. Anyway, this indicates that the eigenstate $|0^{a_0}_A\rangle$ is in the state $|000 \rangle$ with the probability of 67% and in the $|011 \rangle$ state of 33%. It is interesting to see that the eigenstate with lower hyperfine mass, $|0^{a_0}_B\rangle$, are in the $|011 \rangle$ state with higher probability of 67%.

It may be worth mentioning that our tetraquarks have a meson–meson component which is either suppressed or enhanced, depending on the states given in Eq. (17). Our tetraquarks, schematically expressed by $q_1 q_2 {\bar{q}}^3 {\bar{q}}^4$, can have a component where $q_1{\bar{q}}^3$ and $q_2 {\bar{q}}^4$ are separately combined into a color singlet as well as the other component where those two pairs are separately combined into a color octet. The first component corresponds to the meson–meson component. One can work out this type of recombination from $|000\rangle$, $|011\rangle$ and demonstrate that the meson–meson component is suppressed for $|0^{a_0}_A\rangle$ and enhanced for $|0^{a_0}_B\rangle$. We expect that this aspect can provide an interesting phenomenology relating to the “fall-apart” decays of $|0^{a_0}_A\rangle$ and $|0^{a_0}_B\rangle$ [35].

According to Eq. (16), the mass difference between $|0^{a_0}_A\rangle$ and $|0^{a_0}_B\rangle$ can be written in terms of the hyperfine mass difference. By calling the masses of $|0^{a_0}_A\rangle$ and $|0^{a_0}_B\rangle$ $M_{0A}$ and $M_{0B}$ respectively, the calculated mass difference, which constitutes the result from “Theory I”, is $M_{0A}-M_{0B}=-16.8-(-488.5)= 471.7$ MeV,³ meaning that $|0^{a_0}_B\rangle$ has a lower mass than $|0^{a_0}_A\rangle$ by 472 MeV. This is indeed a huge separation in masses between the two states in spin-0. This observation clearly leads us to identify the states $|0^{a_0}_A\rangle$ and $|0^{a_0}_B\rangle$ with the physical resonances

$$\begin{aligned} |0^{a_0}_A\rangle =a_0 (1450); \quad |0^{a_0}_B\rangle =a_0 (980), \end{aligned}$$

(18)

because the experimental mass difference of these two states, $1474 - 980 =494$ MeV,⁴ is quite close to our result, only 20 MeV higher. Our calculation with the different parameter, $v_0=(-199.6)^3$ MeV$^3$, namely the “Theory II” result, gives $M_{0A}-M_{0B}=522.8$ MeV, which is about 29 MeV higher than the experimental mass splitting. Therefore, for $a_0 (1450)$ and $a_0 (980)$, our tetraquark formalism seems to work quite well.

To test our approach further, we look for a possible candidate which can fit to the $J=1$ resonance with the configuration, $|111\rangle$. As one can see in Table 1, there are two candidates in PDG with spin-1, $a_1(1260)$ and $a_1(1640)$. Or another possibility is that the $|111\rangle$ state might be hidden in the continuum of two-meson decays which is then too broad to be observed. The hyperfine mass of $|111\rangle$ is $-180.23$ MeV as shown in Table 3, which is higher than the hyperfine mass of $|0^{a_0}_B\rangle$, $-488.5$ MeV, but lower than that of $|0^{a_0}_A\rangle$, $-16.8$ MeV. Applying this hierarchy to the mass spectrum, we may identify the state $|111\rangle$ with $a_1 (1260)$. The other resonance, $a_1(1640)$, certainly does not fit into this hierarchy.

Denoting the mass of the state $|111\rangle$ as $M_1$, its mass splittings from the spin-0 members, $|0^{a_0}_A\rangle$, $|0^{a_0}_B\rangle$, are obtained from the hyperfine mass splittings,

$$\begin{aligned} M_{1}-M_{0B}= & {} -180.2-(-488.5)=308.3\,\mathrm{MeV},\\ M_{1}-M_{0A}= & {} -180.2-(-16.8)=-163.4\,\mathrm{MeV}. \end{aligned}$$

These values should be compared with the experimental mass splittings, 250 MeV between $a_1(1260)$ and $a_0 (980)$, and $-244$ MeV between $a_1(1260)$ and $a_0 (1450)$. The hyperfine mass splittings are off by $50\sim 80$ MeV from the experimental splittings. Although the agreement is not precise, the errors are within an acceptable range if one takes into account the broad decay width of $a_1(1260)$, $\Gamma =250 - 600$ MeV. Of course, this identification needs to be further examined in the future from other properties such as its decay modes and so on.

Table 4 The hyperfine mass splittings among the spin states are compared with the corresponding resonances in $a_0,a_1,a_2$ channel. Here, we identify $|0^{a_0}_B\rangle =a_0(980)$, $|0^{a_0}_A\rangle =a_0(1450)$, $|111\rangle =a_1(1260)$, $|211\rangle =a_2(1700)$. The column under the name “Theory I” [“Theory II”] is obtained with the strength $v_0=(-192.9)^3$ MeV$^3$ [$v_0=(-199.6)^3$ MeV$^3$]. See the text for the choice of this parameter

For the spin-2 case, there are two candidates in Table 1, $a_2(1320)$ and $a_2(1700)$, and one of them can be identified with $|211\rangle$. The hyperfine mass of $|211\rangle$ in Table 3 is 122.27 MeV, which is higher than any of the hyperfine masses for the states $|0^{a_0}_A\rangle$, $|0^{a_0}_B\rangle$, $|111\rangle$. Thus, the corresponding resonance to $|211\rangle$ must be heavier than those in spin-0 and spin-1. The resonance, $a_2(1700)$, fits into this criterion and it can be identified with $|211\rangle$. Denoting the mass for $|211\rangle$ by $M_2$, its mass splittings from the spin-0 and spin-1 states estimated from the hyperfine mass splittings are $M_2-M_{0B} = 611$ MeV, $M_2-M_{0A} = 138$ MeV, $M_2-M_1 = 303$ MeV. The corresponding mass splittings based on their experimental masses in Table 1 are 752 MeV, 258 MeV, 502 MeV, respectively. The mismatch is less than two hundred MeV or so. Again, although the agreement is not precise, the trend in mass differences seems to match more or less. Also taking into account the broad widths associated with the resonances involved, we can claim that the mismatch is not enough to rule out our four-quark scheme.

Our results for $a_0, a_1, a_2$ are summarized in Table 4. There, we present our results for “Theory I” and “Theory II” in comparison with the experimental mass splittings based on the identifications $|0^{a_0}_B\rangle =a_0(980)$, $|0^{a_0}_A\rangle =a_0(1450)$, $|111\rangle =a_1(1260)$, $|211\rangle =a_2(1700)$. Both results qualitatively agree with the experimental splittings. Based on these results, we may conclude that the spin-1 diquark seems to play an important role in the formation of the tetraquarks in light mesons.

4.2 Results on isodoublet channel

We now move to a discussion for the isodoublet ($I=1/2$) channels which can couple to $K^*_0$, $K_1$, $K^*_2$ resonances. Again in the spin-0 case, because of the mixing, we have a $2\times 2$ matrix for the hyperfine masses $\langle V_{\mathrm{CS}}\rangle$ with respect to the spin configurations $|000 \rangle$ and $|011 \rangle$. The diagonalization leads to

$$\begin{aligned} \begin{array}{c|lr} &{} |000 \rangle &{} |011 \rangle \\ \hline |000 \rangle &{} -218.7 &{} -267.8\\ |011 \rangle &{} -267.8 &{} -400.9 \end{array} \quad\rightarrow & {} \quad \begin{array}{c|lr} &{} |0^{K_0}_A \rangle &{} |0^{K_0}_B \rangle \\ \hline |0^{K_0}_A \rangle &{} -26.9 &{} 0.0\\ |0^{K_0}_B \rangle &{} 0.0 &{} -592.7 \end{array}. \end{aligned}$$

Here we have introduced the superscript $K_0$ in the eigenstates to indicate that the states can couple to $K^*_0$. The eigenstates $|0^{K_0}_A\rangle , |0^{K_0}_B\rangle$ are related to the original spin configurations through

$$\begin{aligned} |0^{K_0}_A\rangle= & {} -0.813 \mid 000 \rangle + 0.582 \mid 011 \rangle , \nonumber \\ |0^{K_0}_B\rangle= & {} 0.582 \mid 000 \rangle + 0.813 \mid 011 \rangle . \end{aligned}$$

(19)

The mixing parameters are not so different from the isovector case, Eq. (17).

We observe again that the mixing drives a huge separation of the diagonal hyperfine masses, about 565.8 MeV. The eigenstates $|0^{K_0}_A\rangle$ and $|0^{K_0}_B\rangle$ need to be identified with the physical resonances. Among three possible candidates with spin-0 in Table 1, $K^*_0(800)$, $K^*_0(1430)$, $K^*_0(1950)$, it may be appropriate to take the two states with lower masses, i.e.,

$$\begin{aligned} |0^{K_0}_A\rangle =K^*_0 (1430); \quad |0^{K_0}_B\rangle =K^*_0 (800). \end{aligned}$$

(20)

Using the experimental masses in PDG for $K^*_0 (1430)$ and $K^*_0 (800)$, their mass difference is $\Delta M_{H}=1425-682=743$ MeV, which is higher than the hyperfine mass splitting of 565.8 MeV. Considering the fact that the decay widths, respectively, of $K^*_0 (800)$ and $K^*_0 (1430)$ are 547, 270 MeV we may claim that our mixing scheme qualitatively works for this spin-0 isodoublet channel.

In the spin-1 case, there are three possible candidates in Table 1, $K_1 (1270)$, $K_1 (1400)$, $K_1 (1650)$ and one of them can be matched with our spin state $|111\rangle$. We choose one resonance by looking at the mass hierarchy generated from the hyperfine masses. The hyperfine mass for the state $|111\rangle$ is $-218.7$ MeV as can be seen in Table 3. Comparing this with the hyperfine masses for $|0^{K_0}_A\rangle$, $|0^{K_0}_B\rangle$, one can establish the mass hierarchy as $|0^{K_0}_A\rangle> |111\rangle > |0^{K_0}_B\rangle$. The resonance $K_1 (1270)$ fits to this hierarchy relatively well. The other candidate is $K_1(1400)$, although it barely fits to the hierarchy; its mass gap from $K^*_0 (1430)$ seems too narrow. With this identification, its mass splittings from the spin-0 resonances agree at least qualitatively with the hyperfine mass splittings as one can see in the second and third line from the top in Table 5.

A somewhat puzzling situation occurs for the spin-2 case. In Table 1, there are two candidates, $K^*_2(1430)$, $K^*_2(1980)$, that can be matched with the spin state, $|211\rangle$. According to Table 3, the hyperfine mass for $|211\rangle$ is 145.8 MeV, which is 502 MeV higher than the hyperfine mass of $|111\rangle$. With the identification with $|111\rangle =K_1 (1270)$, we need to have a spin-2 resonance with a mass around 1770 MeV. But the mass of $K^*_2(1430)$ is too small and the mass of $K^*_2(1980)$ is too large. We would rather hesitate to identify either of the resonances as $|211\rangle$ even if we take into account the broad width associated with the resonances. Nevertheless, by identifying $|211\rangle =K^*_2(1430)$, we obtain the experimental mass splittings, $M_2-M_{0B}= 743$ MeV, $M_2-M_{0A}= 0$ MeV, $M_2-M_{1}= 153$ MeV. The first number is consistent with our calculation but the second and third ones seems a little too far to fit our results given under “Theory I” and “Theory II” in Table 5. If we identify $|211\rangle =K^*_2(1980)$ instead, the experimental mass splittings associated with the spin-2 resonance become $M_2-M_{0B}= 1291$ MeV, $M_2-M_{0A}= 548$ MeV, $M_2-M_{1}= 701$ MeV, which do not fit our calculation also.

There could be various reasons for the disagreement in the spin-2 case. It is possible that the corresponding candidate may be hidden in two-meson continuum or has not be observed yet. Alternatively, there might be some other mechanisms, such as configuration mixing with different multiplets, to change the mass of the spin-2 resonance in the isodoublet. Anyway, it would be interesting to investigate this problem further in the future.

Table 5 The hyperfine mass splittings among the spin states are compared with the corresponding resonances in $K^*_0,K_1,K^*_2$ channel. Here, we identify $|0^{K_0}_B\rangle =K^*_0(800)$, $|0^{K_0}_A\rangle =K^*_0(1439)$, $|111\rangle =K_1(1270)$, $|211\rangle =K^*_2(1430)$. The spin-2 resonance seems not to fit our tetraquark framework. For the other explanations for this table, see the caption of Table 4

5 Summary

In this work, we have proposed two possible ways to construct tetraquarks in the light-meson system. The standard way is to facilitate the spin-0 diquark and spin-0 antidiquark to form a flavor nonet. In this approach, the color and flavor structures for the diquark are ($\bar{\mathbf {3}}_c$, $\bar{\mathbf {3}}_f$) and for the antidiquark, they are ($\mathbf {3}_c$, $\mathbf {3}_f$). The tetraquarks formed in this way have one spin configuration only, $|J,J_{12},J_{34}\rangle =|000\rangle$. The other way to construct tetraquarks is to facilitate the spin-1 diquark and antidiquark where the diquark is in ($\mathbf {6}_c$, $\bar{\mathbf {3}}_f$) and the antidiquark is in ($\bar{\mathbf {6}}_c$, $\mathbf {3}_f$). This construction is motivated by the fact that the spin-1 diquark with ($\mathbf {6}_c$, $\bar{\mathbf {3}}_f$) is the second most attractive among all the possible diquarks. With this approach, the tetraquarks can have three spin states with the configurations, $|011\rangle$, $|111\rangle$, $|211\rangle$.

Therefore, for spin-0 tetraquarks, there are two spin configurations, $|000\rangle$ and $|011\rangle$, and they are found to mix strongly through the color–spin interaction. We have found that the physical states obtained from the diagonalization of the hyperfine mass matrix match qualitatively well $[a_0(980), a_0(1450)]$ in the hidden strangeness channel and $[K^*_0(800), K^*_0(1430)]$ in the open strangeness channel.

To solidify our tetraquark framework, we have also looked for physical resonances that can be matched to the additional states $|111\rangle$ and $|211\rangle$. Our analysis from the mass splittings suggests that $a_1(1260)$ and $K_1(1270)$ may be the candidates for $|111\rangle$ and $a_2(1700)$ could be a candidate for $|211\rangle$. But there is one resonance seemingly missing in spin-2 with the open strangeness channel as neither of the existing resonances $K^*_2 (1430)$ and $K^*_2(1980)$ in that channel seems to fit our framework. Nevertheless, based on qualitative agreement in most spin channels, we believe that our tetraquark formalism may be realized in the light-meson system. Further studies such as their decay pattern and so on are necessary in order to establish this model.