1 Introduction

Recent development in a cosmological deep survey has clarified progressively the origin and distribution of matter and evolution of compact objects in the Universe. Some of their properties, such as masses, rotation frequencies and emission of radiation are measurable, whereas measurements of important parameters which determine the nature of compact stars still represent an observational challenge. The properties that are not directly linked to observations, such as the internal composition or masses and radii, require the development of theoretical models. On the theoretical side, the mass and the radius are determined by solving the hydrostatic equilibrium equation which expresses the equilibrium between gravitational and pressure forces. In the framework of general relativity the equilibrium of a spherical object is described by the Tolman–Oppenheimer–Volkoff (TOV) [1, 2] equations, and, for completeness, the equation of state is required. Very recently other theoretical advances in modelling of densely neutral gravitating objects in strong gravitational fields have generated much interest in last couple of decades. This is because of its importance in describing relativistic astrophysical objects such as neutron stars, quark stars, hybrid proto-neutron stars, bare quark stars etc.

The main theoretical routes have been used to study of stellar structure and evolution assuming that the interior of a star can be modelled as perfect fluid. The perfect fluid model necessarily requires the pressure in the interior of a star to be isotropic. Spacetime fuelled by a rotating anisotropic fluid has been used to model the interior of the star. One common source is a fluid with anisotropy in pressure. In particular at very high densities conventional celestial bodies are not composed purely of perfect fluids so that radial pressures are different from tangential pressures. The model of Bowers and Liang [3] is conceptually different from isotropic matter, but it possesses anisotropic matter in the study of general relativity. Mak and Harko [4] and Sharma et al. [5] suggest that anisotropy is a sufficient condition in the study of dense nuclear matter with a strange star. Some argument against the existence of anisotropy could be verifiable through the existence of a solid core or the presence of a type 3A fluid; see the work of Kippenhahn and Weigert [6]. On the other hand, this can arise from different kinds of phase transition and pion condensation as pointed out by Sokolov and Sawyer [7]. The structure of compact objects in general relativity will depend on several parameters, including fluid and magnetic stresses, entropy gradients, composition, heat flow and neutrino emission. However, we restrict our attention to the case of an anisotropic perfect fluid with equilibrium composition.

The theoretical investigation of compact objects has been done by several workers by using both analytical and numerical methods. However, emphasis has always been given on the importance of the local pressure anisotropy. This seems to be very reasonable explaining the matter distribution under a variety of circumstances. Also, this has been proved to be very useful to explore characteristics of relativistic compact objects [8–15]. In recent years, many exact solutions to the Einstein field equations have been generated by different approaches [16–22]. Therefore, the Einstein–Maxwell spacetime geometry for a compact object having a local anisotropic effect has attracted considerable attention in various physical investigations. However, the physical acceptability of the solution depends on the number of criteria which include the fulfillment of various energy conditions of general relativity.

Against this background we would like to mention that in one of the earlier works Maurya et al. [23] have proposed an algorithm of a charged anisotropic compact star while in the later works [24, 25] they have given a new approach for finding an anisotropic solution of Einstein’s field equations by using the metric potentials function. The present work is a sequel of the work done by Maurya et al. [26, 27], in which the authors have obtained the charged compact star and the structure of a relativistic electromagnetic mass model under the condition of a class one metric. It would be desirable to do a systematic stability analysis of our model based on anisotropic spacetime. In this work, we check the mass–radius relation, stability and surface redshift of our models and find their behaviour is well behaved.

The present article is organized as follows: Sect. 2 contains the spherically symmetric metric and the Einstein field equations. Also we find the metric function \(\lambda \) in terms of the metric function \(\nu \) by applying the class one condition. In Sect. 3, we obtain the interior structure of the anisotropic star under the class one condition. The values of the arbitrary constants and total mass of the compact star of radius R are obtained by using the boundary conditions in Sect. 4. In Sect. 5, we discuss several required physical conditions for anisotropic models along with the stability analysis which is vital one. Section 6 contains some concluding remarks on the anisotropic models.

2 Line element for class one metric and Einstein’s field equations

We consider the static spherically symmetric metric for describing the spacetime of the compact stellar configuration

$$\begin{aligned} \mathrm{d}s^{2} =-{e}^{\lambda } \mathrm{d}r^{2} -r^{2} (\mathrm{d}\theta ^{2} +\sin ^{2} \theta \, \mathrm{d}\phi ^{2} )+{e}^{\nu } \, \mathrm{d}t^{2}. \end{aligned}$$
(1)

The energy-momentum tensor of interior matter for a strange star may be expressed in the following standard form:

$$\begin{aligned} T_{ij}=\hbox {diag}(\rho , -p_\mathrm{r}, -p_\mathrm{t}, -p_\mathrm{t}), \end{aligned}$$
(2)

where \(\rho \), \(p_\mathrm{r}\) and \(p_\mathrm{t}\) correspond to the energy density, radial and tangential pressures, respectively, of the matter distribution.

The Einstein field equations can be written as

$$\begin{aligned} R_{ij}-\frac{1}{2}\,R\,g_{ij}=-8\pi \,T_{ij}. \end{aligned}$$
(3)

Here \(G = c = 1\) in geometrized relativistic units.

In view of the metric (1), Eq. (3) yields the following differential equations [28]:

$$\begin{aligned} p_\mathrm{r} =\frac{{e}^{-\lambda }}{8\pi }\left[ \frac{v'}{r} -\frac{({e}^{\lambda }-1)}{r^{2}} \right] , \end{aligned}$$
(4)
$$\begin{aligned} p_\mathrm{t} =\frac{{e}^{-\lambda }}{8\pi }\left[ \frac{v''}{2} -\frac{\lambda 'v'}{4} +\frac{v'^{2} }{4} +\frac{v'-\lambda '}{2r} \right] , \end{aligned}$$
(5)
$$\begin{aligned} \rho =\frac{{e}^{-\lambda }}{8\pi }\left[ \frac{\lambda '}{r} +\frac{({e}^{\lambda }-1 )}{r^{2}}\right] . \end{aligned}$$
(6)

The metric (1) may represent the spacetime of the embedding class one, if it satisfies the condition of Karmarker [29]. This condition gives the following relation between the metric potentials \(\nu \) and \(\lambda \) [24]:

$$\begin{aligned} e^{\lambda (r)}=1+C\,\nu '^{2}\,e^{\nu }. \end{aligned}$$
(7)

Here C is a positive constant quantity.

3 New anisotropic models for compact star

To find an interior solution of the anisotropic compact star in class one, we consider the pressure isotropy condition as given through the expression of the anisotropic factor as follows:

$$\begin{aligned}&\frac{e^{-\lambda }}{8\pi }\left[ \frac{v''}{2} -\frac{\lambda 'v'}{4} +\frac{v'^{2} }{4} -\frac{v'+\lambda '}{2r} +\frac{e^{\lambda }-1}{r^{2} } \right] \nonumber \\&\quad =\,(p_\mathrm{t} -\, p_\mathrm{r})=\Delta . \end{aligned}$$
(8)

For finding the non-zero expression for the anisotropic factor, we assume the metric potential to be in the form

$$\begin{aligned} e^{\nu }=B\,e^{2\,Ar^{2}}, \end{aligned}$$
(9)

where A and B are positive constants.

Hence from Eqs. (7) and (9), we get

$$\begin{aligned} e^{\lambda }=[\,1+D\,Ar^{2}\,e^{2Ar^{2}}\,], \end{aligned}$$
(10)

where

$$\begin{aligned} D=16\,A\,B\,C. \end{aligned}$$
(11)
Fig. 1
figure 1

Variation of metric potentials \(e^{\nu }\) and \(e^{\lambda }\) with the radial coordinate r / R for Her X-1 and RXJ 1856-37

Full size image

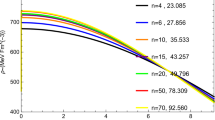
From Eqs. (9) and (10), we observe that \(e^{\lambda (0)}=1\) and \(e^{\nu (0)}=B\) at the centre, \(r=0\). This shows that metric potentials are singularity free and positive at the centre. Also both are monotonically increasing functions, which shows that these metric potential are physically valid [30]. These features can be observed from Fig. 1.

By plugging Eqs. (9) and (10) into Eq. (8), we get

$$\begin{aligned} \Delta =\,\frac{A^{2}r^{2}}{8\,\pi } \left[ \,\frac{-2+D\,e^{2Ar^{2}}}{1+D\,Ar^{2}\,e^{2Ar^{2}}}\right] ^2. \end{aligned}$$
(12)
Fig. 2
figure 2

Variation of anisotropic factor \(\Delta _i=\Delta /A\) with the radial coordinate r / R for Her X-1 and RXJ 1856-37

Full size image

We note from Fig. 2 that the anisotropy \(\Delta \) is zero at the centre \(r=0\) and is monotonically increasing with the increase of r. Also from Eq. (12), we observe that the anisotropic factor \(\Delta \) vanishes everywhere inside the compact star if and only if \(A=0\).

Equations (4), (5) and (6) give the expressions for the radial pressure \(p_\mathrm{r}\), the tangential pressure \(p_\mathrm{t}\) and the energy density \(\rho \):

$$\begin{aligned} p_\mathrm{r}=\frac{A}{8\,\pi }\,\left[ \frac{4-D\,e^{2Ar^{2}}}{1+D\,Ar^{2}\,e^{2Ar^{2}}}\right] , \end{aligned}$$
(13)
$$\begin{aligned} p_\mathrm{t}=\frac{A}{8\,\pi }\,\left[ \,\frac{4-D\,e^{2Ar^{2}}+4\,Ar^{2}}{(1+D\,Ar^{2}\,e^{2Ar^{2}})^{2}}\right] , \end{aligned}$$
(14)
$$\begin{aligned} \rho =\frac{A}{8\,\pi }\,\left[ \,\frac{\,D\,e^{2Ar^{2}}(3+4Ar^{2}+Ar^{2}D\,e^{2Ar^{2}})}{(1+D\,Ar^{2}\,e^{2Ar^{2}})^{2}}\right] . \end{aligned}$$
(15)

The radial and tangential pressures at the centre, \(r=0\), can be given by \(p_\mathrm{r}=A\,(4-D)/8\,\pi \) and \(p_\mathrm{t}=A\,(4-D)/8\,\pi \). Since A and D are positive and the pressure should be positive at the centre, this implies that \(D<4\). In a similar way, we can find the density at the centre, r=0, as \(\rho _{0}=(3\,A\,D/8\,\pi )\). Since the density should be positive at the centre, D is positive due to positivity of A. As D, A, B all are positive, C is also a positive quantity. The behaviour of \(p_r\) and \(p_t\) are shown in Figs. 3, 4.

Fig. 3
figure 3

Variation of radial pressure (left panel) and transverse pressure (right panel) with respect to the radial coordinate r / R with \(P_r = p_r/A\) and \(P_t = p_t/A\) for Her X-1 and RXJ 1856-37

Full size image

We suppose that the radial and tangential pressures of the star are related to the matter density by the parameters \(\omega _\mathrm{r}\) and \(\omega _\mathrm{t}\) as \(p_\mathrm{r}=\omega _\mathrm{r}\,\rho \) and \(p_\mathrm{t}=\omega _\mathrm{t}\,\rho \).

Then the expressions for the parameters \(\omega _\mathrm{r}\) and \(\omega _\mathrm{t}\) are given by

$$\begin{aligned} \omega _\mathrm{r}=\,\frac{(4-D\,e^{2Ar^{2}})(1+D\,Ar^{2}\,e^{2Ar^{2}})}{D\,e^{Ar^{2}}\,[3+4\,Ar^{2}+Ar^{2}De^{2Ar^{2}}]}, \end{aligned}$$
(16)
$$\begin{aligned} \omega _\mathrm{t}=\,\frac{4\,(1+Ar^{2})-D\,e^{2Ar^{2}}}{D\,e^{2Ar^{2}}\,[3+4\,Ar^{2}+Ar^{2}De^{2Ar^{2}}]}. \end{aligned}$$
(17)

From Fig. 5 it is clear that the ratios \(\omega _\mathrm{r}=p_\mathrm{r}/\rho \) and \(\omega _\mathrm{t}=p_\mathrm{t}/\rho \) are less than 1. This implies that the density dominates over the pressures throughout inside the star. However, this also implies that the underlying fluid distribution is non-exotic in nature [39].

4 Matching condition

For any physically acceptable anisotropic solution, the following boundary conditions must be satisfied:

  1. (i)

    At the surface of the compact star, the interior of metric (1) for anisotropic matter distribution match with the exterior of Schwarzschild solution [31], which is given by the metric

    $$\begin{aligned} \mathrm{d}s^{2}= & {} \left( 1-\frac{2M}{r} \right) \, \mathrm{d}t^{2} -r^{2} (\mathrm{d}\theta ^{2} +\sin ^{2} \theta \, \mathrm{d}\phi ^{2} )\nonumber \\&-\left( 1-\frac{2M}{r} \right) ^{-1} \mathrm{d}r^{2}, \end{aligned}$$
    (18)

    where M is a constant representing the total mass of the compact star at \(r=R\).

  2. (ii)

    The radial pressure \(p_\mathrm{r}\) must be finite and positive at the centre \(r=0\) and it must vanish at the surface \(r = R\) of the star [32]. The condition \(p_\mathrm{r}(R)=0\) gives

    $$\begin{aligned} D=16ABC=4e^{-2AR^2}. \end{aligned}$$
    (19)

    This readily yields the radius R of the compact star as

    $$\begin{aligned} R=\sqrt{\frac{1}{2A}\,\ln \left[ \frac{1}{4ABC}\right] }. \end{aligned}$$
    (20)

    Using the continuity of metric coefficients \(e^{\nu }\), \(e^{\lambda }\) and \(\frac{\partial g_{tt}}{\partial r}\) across the boundary of the star gives the following equations:

    $$\begin{aligned}&B\,e^{2AR^2}=1-\frac{2M}{R},\end{aligned}$$
    (21)
    $$\begin{aligned}&1+D\,AR^{2}\,e^{2AR^{2}}=\left[ 1-\frac{2M}{R}\,\right] ^{-1},\end{aligned}$$
    (22)
    $$\begin{aligned}&4\,B\,AR^2\,e^{2AR^2}=\frac{2M}{R}. \end{aligned}$$
    (23)

    The following equations with Eq. (19) give the value of the unknowns M, B and C as follows:

    $$\begin{aligned}&M=\frac{R}{2}\left[ \frac{4\,AR^{2}}{1+4\,AR^{2}}\right] ,\end{aligned}$$
    (24)
    $$\begin{aligned}&B=\frac{e^{-2AR^2}}{1+4AR^{2}},\end{aligned}$$
    (25)
    $$\begin{aligned}&C=\frac{1+4AR^{2}}{4\,A}. \end{aligned}$$
    (26)

    On the other hand, the value of the constant A can be determined by assuming the density at the surface of the star i.e. \(\rho _{s}\) at \(r=R\).

Fig. 4
figure 4

Variation of effective energy density (\(\tilde{\rho }=\rho /A\)) with respect to the radial coordinate r / R for Her X-1 and RXJ 1856-37

Full size image
Fig. 5
figure 5

Variation of parameters \(\omega _\mathrm{r}\) and \(\omega _\mathrm{t}\) with the radial coordinate r / R for Her X-1 and RXJ 1856-37

Full size image
Fig. 6
figure 6

Variation of sound speed with the radial coordinate r / R for the Her X-1 and RXJ 1856-37

Full size image
Fig. 7
figure 7

Variation of energy conditions with the radial coordinate r / R for Her X-1 (left panel) and RXJ 1856-37 (right panel)

Full size image

5 Physical features of the anisotropic models

5.1 Sound speed

The speed of sound should monotonically decrease throughout from the centre to the boundary of the star and it must be within the range \(0\le V_{i}=\sqrt{\mathrm{d}p_{i}/\mathrm{d}\rho }<1\). It is argued by Canuto [33] that the sound speed should decrease outwards for the EOS with an ultra-high distribution of matter. From Fig. 6, it is clear that the speed of sound is monotonically decreasing outwards.

5.2 Energy conditions

The anisotropic fluid must satisfy the following energy conditions: the Null energy condition (NEC), the Weak energy condition (WEC) and the Strong energy condition (SEC). Therefore, the following inequalities should hold simultaneously at each point inside the compact star corresponding to the above conditions (Fig. 7):

$$\begin{aligned}&\hbox {NEC}: \rho \ge 0,\end{aligned}$$
(27)
$$\begin{aligned}&\hbox {WEC}_\mathrm{r}: \rho -p_\mathrm{r} \ge 0,\end{aligned}$$
(28)
$$\begin{aligned}&\hbox {WEC}_\mathrm{t}: \rho -p_\mathrm{t} \ge 0,\end{aligned}$$
(29)
$$\begin{aligned}&\hbox {SEC}: \rho -p_\mathrm{r} - 2p_\mathrm{t} \ge 0. \end{aligned}$$
(30)

5.3 Tolman–Oppenheimer–Volkoff equation (TOV)

The generalized TOV equation for the anisotropic fluid distribution is given by [1, 2]

$$\begin{aligned} \frac{M_\mathrm{G} (\rho +p_\mathrm{r} )}{r^{2} } e^{\frac{\lambda -\nu }{2} } +\frac{\mathrm{d}p_\mathrm{r} }{\mathrm{d}r} +\frac{2}{r} (p_\mathrm{r} -p_\mathrm{t} )=0. \end{aligned}$$
(31)

We can write the above TOV equations as follows:

$$\begin{aligned} -\frac{1}{2}\,\nu '(\rho +p_\mathrm{r} )-\frac{\mathrm{d}p_\mathrm{r} }{\mathrm{d}r} +\frac{2}{r} (p_\mathrm{t} -p_\mathrm{r} )=0, \end{aligned}$$
(32)

where \(M_\mathrm{G}\) is the effective gravitational mass and it can be given by

$$\begin{aligned} M_\mathrm{G} (r)=\frac{1}{2} r^{2} e^{\frac{\nu -\lambda }{2} } \, \nu '. \end{aligned}$$
(33)

Equation (32) describes the equilibrium condition for an anisotropic fluid distribution subject to the gravitational (\(F_\mathrm{g}\)), the hydrostatic (\(F_\mathrm{h}\)) and the anisotropic stress (\(F_\mathrm{a}\)) so that

$$\begin{aligned} F_\mathrm{g} +F_\mathrm{h} +F_\mathrm{a} =0, \end{aligned}$$
(34)

where its components can be defined as

$$\begin{aligned} F_\mathrm{g} =-\frac{1}{2} \nu '\, (\rho +p_\mathrm{r}), \end{aligned}$$
(35)
$$\begin{aligned} F_\mathrm{h} =-\frac{\mathrm{d}p_\mathrm{r} }{\mathrm{d}r}, \end{aligned}$$
(36)
$$\begin{aligned} F_\mathrm{a} =\frac{2}{r} (p_\mathrm{t} -p_\mathrm{r}). \end{aligned}$$
(37)
Fig. 8
figure 8

Variation of different forces with the radial coordinate r / R for Her X-1 (left panel) and RXJ 1856-37 (right panel)

Full size image

The explicit form of the above forces can be expressed as (Fig. 8)

$$\begin{aligned} F_\mathrm{g}=-\frac{A^{2}r}{4\,\pi }\,\left[ \,\frac{4+2D\,e^{2Ar^{2}}\,(1+4Ar^{2})}{(1+D\,Ar^{2}\,e^{2Ar^{2}})^{2}}\right] , \end{aligned}$$
(38)
$$\begin{aligned} F_\mathrm{h}=-\frac{A^{2}r}{4\,\pi }\,\left[ \,\frac{D\,e^{2Ar^2}(-6+2D\,e^{2Ar^{2}}-8Ar^{2})}{(1+D\,Ar^{2}\,e^{2Ar^{2}})^{2}}\right] , \end{aligned}$$
(39)
$$\begin{aligned} F_\mathrm{a}=\frac{A^{2}r}{4\,\pi }\,\left[ \,\frac{-2+D\,e^{2Ar^{2}}}{(1+D\,Ar^{2}\,e^{2Ar^{2}})}\right] ^2. \end{aligned}$$
(40)

5.4 Stability of the models

5.4.1 Herrera cracking concept

We know that for physically acceptable anisotropic models, the radial and transverse speed of sound should lie between 0 and 1, i.e., \(0\le V_\mathrm{r} < 1\) and \(0\le V_\mathrm{t} < 1\). We observe from this inequality that the parameters also should satisfy the inequality \(0\le V^{2}_\mathrm{r} < 1\) and \(0\le V^{2}_\mathrm{t} < 1\). Now we define the expression for the square of the velocity of sound as

$$\begin{aligned}&V^{2}_\mathrm{r}=\frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}\rho }=\,\left[ \frac{(6-D\,e^{2Ar^{2}}+8Ar^{2})(1+D\,Ar^{2}\,e^{2Ar^{2}})}{D^{2}\,Ar^{2}\,e^{4Ar^{2}}-2\,(5+4Ar^{2})+D\,e^{2Ar^{2}}(5+6Ar^{2}+8A^{2}r^{4})}\right] ;\end{aligned}$$
(41)
$$\begin{aligned}&V^{2}_\mathrm{t}=\frac{\mathrm{d}p_\mathrm{t}}{\mathrm{d}\rho }=\,\left[ \frac{2[\,D\,e^{2Ar^{2}}\,(5+10Ar^{2}+8A^{2}r^{4})-2-D^{2} \,e^{4Ar^{2}}\,(1+Ar^{2})]}{D\,e^{2Ar^{2}}[D^{2}\,Ar^{2}\,e^{4Ar^{2}}-2\,(5+4Ar^{2})+D\,e^{2AR^{2}}(5+6Ar^{2}+8A^{2}r^{4})}\right] . \end{aligned}$$
(42)

From Fig. 9, we conclude that the square of the radial and transverse speeds of sound are within the range everywhere inside the stars. Therefore, \(0\le |{V^{2}_\mathrm{t}-V^{2}_\mathrm{r}}|<1 \). In order to examine the stability of the local anisotropic fluid distribution, we follow the cracking concept of Herrera and Aberu et al. [34, 35] which states that the region is potentially stable where the radial speed of sound is greater than the transverse speed of sound. This implies that there is no change in sign \( V^{2}_\mathrm{r}-V^{2}_\mathrm{t}\) and \( V^{2}_\mathrm{t}-V^{2}_\mathrm{r}\).

So we calculate the difference between the radial and transverse speeds of sound:

$$\begin{aligned} V^{2}_\mathrm{t}-V^{2}_\mathrm{r}=\left[ \frac{(2-D\,e^{2Ar^{2}})[2+\,D^{2}\,Ar^{2}\,e^{4AR^{2}}-D\,e^{2Ar^{2}} \,(1+6Ar^{2}+8A^{2}r^{4})]}{D\,e^{2Ar^{2}}[D^{2}\,Ar^{2}\,e^{4Ar^{2}}-2\,(5+4Ar^{2})+D\,e^{2Ar^{2}}(5+6Ar^{2}+8A^{2}r^{4})}\right] . \end{aligned}$$
(43)

We note from Fig. 10 that the radial speed of sound is always greater than the transverse speed of sound and also \(0\le |V^{2}_\mathrm{t}-V^{2}_\mathrm{r}|<1 \) everywhere inside the star. These features represent that the proposed physical models are stable.

5.4.2 Adiabatic index

In order to determine an equilibrium configuration, the matter must be stable against the collapse of local regions. This also requires Le Chatelier’s principle (known as the local or microscopic stability condition), stating that the radial pressure \(p_\mathrm{r}\) must be a monotonically non-decreasing function of \(\rho \) such that \(\frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}\rho }>0\) [36]. Heintzmann and Hillebrandt [37] also proposed that a neutron star with an anisotropic equation of state is stable for \(\gamma (=\frac{p_\mathrm{r}+\rho }{p_\mathrm{r}}\frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}\rho }) > 4/3\). From Fig. 11, it is clear that the adiabatic index (\(\gamma \)) is higher than 4 / 3 everywhere inside the star.

5.5 Effective mass–radius ratio

This section contains the maximum allowable mass–radius ratio for the above proposed anisotropic fluid models. As Buchdahl [38] has already discussed, the maximum limit of mass–radius ratio for a static spherically symmetric perfect fluid star should satisfy the upper bound \(2M/R<8/9\). Also Mak and Harko [4] have given the generalized expression for the same mass–radius ratio.

Fig. 9
figure 9

Variation of square of radial speed of sound and transverse speed of sound with radial coordinate r / R for Her X-1 and RXJ 1856-37

Full size image
Fig. 10
figure 10

Variation of difference between square of radial speed and transverse speed of sound with radial coordinate r / R for Her X-1 and RXJ 1856-37

Full size image

The effective mass of the anisotropic compact star is defined as

$$\begin{aligned} M_\mathrm{eff}= & {} 4\pi \int _{0}^{R}\rho \, r^{2} \mathrm{d}r=\frac{1}{2} R\, [1-e^{-\lambda (R)}]\nonumber \\= & {} \frac{R}{2}\left[ \frac{D\,AR^{2}e^{2AR^2}}{1+D\,AR^{2}e^{2AR^2}}\right] =\frac{R}{2}\left[ \frac{4\,AR^{2}}{1+4\,AR^{2}}\right] . \end{aligned}$$
(44)

However, the compactness u of the star can be expressed as

$$\begin{aligned} u=\frac{M_\mathrm{eff}}{R}=\frac{1}{2}\,\left[ \,\frac{4AR^{2}}{1+4AR^{2}}\right] . \end{aligned}$$
(45)

5.6 Surface redshift

The surface redshift (Z) corresponding to the above compactness (u) is given by the expression (Fig. 12)

$$\begin{aligned} Z=\frac{1-[\,1-2\,u]^{1/2}}{[\,1-2\,u]^{1/2}}=\,\sqrt{1+4\,AR^{2}}-1. \end{aligned}$$
(46)
Fig. 11
figure 11

Variation of adiabatic index (\(\gamma \)) with radial coordinate r / R for Her X-1 and RXJ 1856-37

Full size image
Fig. 12
figure 12

Variation of the redshift (Z) with the radial coordinate r / R for Her X-1 and RXJ 1856-37

Full size image
Table 1 Values of the model parameters mass (\(M_{\odot }\)), radius (R), D, A, B and C for different compact stars
Full size table
Table 2 The energy densities, the central pressure and \(AR^2\) for different compact star candidates for the above parameter values of Table 1
Full size table

6 Conclusions

In the present article, we have obtained new anisotropic compact star models of the embedding class one metric. Our models satisfy all the physical reality conditions. Some of the special features of the present model are as follows:

  1. 1.

    We used the boundary conditions by joining the Schwarzschild metric with a class one metric at the boundary of the star \(r=R\). Subsequently we obtained the arbitrary constants A, B, C along with the total mass of the compact star and the corresponding numerical values are provided in Table 1. All these values match the observed data of real compact stars.

  2. 2.

    The metric potentials are free from any singularity at the centre, and positive and finite inside the star (Fig. 1). Also the \(\rho \), \(p_\mathrm{r}\) and \(p_\mathrm{t}\) are positive, finite and monotonically decreasing away from the centre. However, the parameters \(\omega _\mathrm{r}\) and \(\omega _\mathrm{t}\) are within the range between 0 and 1 (Fig. 5).

  3. 3.

    The model is in static equilibrium. We observe from Fig. 8 that the gravitational force (\(F_\mathrm{g}\)) is dominating over the hydrostatic force (\(F_\mathrm{h}\)) and is counter balanced by the joint action of the hydrostatic force and the anisotropic stress.

  4. 4.

    The model has a density of the order \(10^{15}\,\mathrm{gm}/\mathrm{cm}^{3}\). The corresponding values for Her X-1 and RXJ 1856-37 are as follows:

    1. (i)

      at the centre \(\rho _{0}=1.8664\times {10^{15}}\,\mathrm{gm}/\mathrm{cm}^{3}\) and \(\rho _{0}=2.3968\times {10^{15}}\,\mathrm{gm}/\mathrm{cm}^{3}\),

    2. (ii)

      at the surface \(\rho _{s}=1.3273\times {10^{15}}\,\mathrm{gm}/\mathrm{cm}^{3}\) and \(\rho _{s}=1.6924\times {10^{15}}\,\mathrm{gm}/\mathrm{cm}^{3}\) (Table 2).

    This density profile shows that our models may represent a realistic anisotropic objects.

  5. (5)

    The redshift is monotonically decreasing and attains its maximum value at the centre of the compact star. The numerical values corresponding to the Her X-1 and RXJ 1856-37 are: (i) at the centre \(Z_{0}= 0.2669\) and \(Z_{0}= 0.2796\), (ii) at the surface \(Z_\mathrm{s}= 0.0474\) and \(Z_\mathrm{s}=0.0480\). As a final comment, an interesting and puzzling point about the anisotropic compact model is that its stability depends on the unavoidable anisotropic pressure and the TOV equations used to place a constraint on the anisotropic parameters. It would be interesting to propose a richer model in which consideration of the pressure anisotropy on the compact relativistic objects could lead to a more realistic model of the anisotropization mechanism as regards compact relativistic objects.