1 Introduction

Developed by Ovalle and collaborators [1,2,3,4,5,6,7,8,9,10,11,12], gravitational decoupling by minimal geometric deformation (MGD hereinafter) approach, has proved to be a novel and powerful tool in order to obtain analytic solutions to Einstein field equations described by an anisotropic fluid. Recently, several works available in the literature have proven the versatility of the method, using it in different contexts such as extending solutions of Einstein field equations described by perfect fluid to anisotropic domains [13,14,15,16,17], Einstein–Maxwell equations [18, 19], black holes [20,21,22], cloud of strings [23], Einstein–Klein–Gordon equations [24] and wi- thin the framework of theories in higher dimensions [25]. Originally, the method was developed to deform Schwarz- schild’s spacetime [1, 2] within the context of Randall-Sun- drum braneworld [26, 27]. However, it has been extended to another type of symmetry, specifically spacetime with cylindrical symmetry [28]. The main ingredient of this scheme is to add an extra source to the energy momentum tensor of a spherically symmetric and static spacetime through a dimensionless constant \(\beta \)

$$\begin{aligned} T^{m}_{n}=\tilde{T}^{m}_{n}+\beta \theta ^{m}_{n}, \end{aligned}$$
(1)

where \(\tilde{T}^{m}_{n}\) represents a perfect fluid matter distribution and \(\theta ^{m}_{n}\) is the extra source which encodes the anisotropy and can be formed by scalar, vector or tensor fields. It is worth mentioning that \(\tilde{T}^{m}_{n}\) does not necessarily should corresponds to a perfect fluid, in fact it can describes, for example, an anisotropic fluid, a charged fluid, etc. [18]. On the other hand it is well known that an astrophysical object not necessarily meet the isotropic condition at all i.e \(p_{r}= p_{t}\). Of course, a more realistic scenario has been shown that relaxing the isotropic condition i.e \(p_{r}\ne p_{t}\) leads to a better understanding of how compact structures like neutron stars, white dwarfs and black holes work. Theoretical researches in the past developed by Ruderman [29] Canuto [30,31,32] and Canuto et al. [33,34,35,36] revealed that anisotropies can be emerged when matter density is higher than the nuclear density one. These pioneering works established a new branch within the study of the influence of local anisotropies in general relativity [37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68]. Furthermore, over the last decade a lot of works available in the literature have considering the inclusion of anisotropic matter distribution in solving analytical models to Einstein field equations [69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109](and references contained therein). On the other hand as Mak and Harko have argued [63], anisotropy can arise in different contexts such as: the existence of a solid core or by the presence of type 3A superfluid [110], pion condensation [111] or different kinds of phase transitions [112]. Of course the presence of anisotropy introduces several and novel features in the matter distribution, e.g. in presence of a positive anisotropy factor \(\varDelta \equiv p_{t}-p_{r}>0\), the stellar configuration experiences a repulsive force (attractive in the case of negative anisotropy factor) that offsets the gravitational gradient. Therefore, we obtain a more compact and massive objects in distinction with the isotropic case [52, 60, 63]. Moreover, a positive anisotropy factor improves the stability and equilibrium of the system.

In the spirit of the above discussion we employ gravitational decoupling via MGD in order to extent the Maurya and Gupta [113] perfect fluid solution of Einstein field equations to an anisotropic scenario. To do so, we realize a geometric deformation on the radial metric component encode by a purely radial function g(r) and then we impose a suitable election on it, according with the physical and mathematical requirements, which leads us to know the contribution of the extra source \(\theta ^{m}_{n}\) to the material content. Of course, any solution to Einstein field equations must meet some basics criteria in order to be a well behaved and admissibly solution that can describes a realistic model [114]. So, the outline of the present work is as follows: Sect. 2 presents the mathematical formulation of Einstein field equations for anisotropic matter distribution in the framework of gravitational decoupling via MGD, Sect. 3 is devoted to the construction of the anisotropic version of the Maurya and Gupta perfect fluid solution. In Sect. 4 we match the obtained model with the exterior Schwarzschild spacetime in order to obtain the constant and physical parameters of the model, Sect. 5 analyzes all the basics criteria that an admissible solution to Einstein field equations must meet, such as regularity of the metric potentials and the thermodynamic observables within the stellar configuration, causality condition, energy conditions, equilibrium and stability conditions. In Sect. 6, we discuss the behavior and form of effective metric potentials at very large value of n i.e. n tends to infinity. Finally, Sect. 7 summarizes and concludes the work.

2 Mathematical structure of Einstein equations for gravitational decoupling

Let us consider the curvature coordinates to describe the ultradense spherically symmetric stellar system, by using the metric as follows [115],

$$\begin{aligned} {ds}^{2}={{e}^{\nu (r)}}{{dt}^{2}}-{{e}^{\lambda (r)}}{{dr}^{2}}-{r}^{2}\left( {{d\theta }^{2}}+{{sin}^{2}}\theta {{d\phi }^{2}}\right) , \end{aligned}$$
(2)

where \(\nu (r)\) and \(\lambda (r)\) are the metric potentials and function of the radial coordinate only. The energy-momentum tensor associated with the dimensionless coupling constant \(\beta \) can be read as,

$$\begin{aligned} T^{m}_{n} = \tilde{T}^{m}_{n} + \beta \,\theta ^{m}_{n} \end{aligned}$$
(3)

where the energy momentum tensor \(\tilde{T}^{m}_{n}\) corresponds to the perfect fluid solution for the metric (2) while the energy momentum tensor \(T^m_n\) corresponding to the anisotropic matter distribution is given as,

$$\begin{aligned} T^{m}_{n} =\left[ \rho +p_t)u^{m}u_{n}-p_t\delta ^{m}_{n} + (p_r-p_t)\upsilon ^{m}\upsilon _{n} \right] , \end{aligned}$$
(4)

By using Eqs. (2) and (4) together, we get the following equations

$$\begin{aligned}&{\mathrm{e}^{-\lambda }}\left( {\frac{\lambda ^{{\prime }}}{r}}-\frac{1}{r^2}\right) +\frac{1}{r^2}=8\pi \rho \end{aligned}$$
(5)
$$\begin{aligned}&{\mathrm{e}^{-\lambda }} \left( {\frac{\nu ^{{\prime }}}{r}}+\frac{1}{r^2}\right) -\frac{1}{r^2}=8\pi p_r \end{aligned}$$
(6)
$$\begin{aligned}&\frac{\mathrm{e}^{-\lambda }}{2} \left( \nu ^{{\prime \prime }}+\frac{{\nu ^{{\prime }}}^{2}}{2}+{\frac{\nu ^{{\prime }}-\lambda ^{{\prime }}}{r}}-\frac{\nu ^{{\prime }}\lambda ^{{\prime }}}{2} \right) = 8\pi p_t. \end{aligned}$$
(7)

The primes denote differentiation with respect to the radial coordinate r. However, \(\rho \), \(p_r\) and \(p_t\) represent the effective density, the effective radial pressure and the effective tangential pressure respectively, which are given by

$$\begin{aligned}&\rho =\tilde{\rho } + \beta \,\theta ^t_t, \end{aligned}$$
(8)
$$\begin{aligned}&p_r=\tilde{p} - \beta \,\theta ^r_r, \end{aligned}$$
(9)
$$\begin{aligned}&p_t=\tilde{p} - \beta \,\theta ^\varphi _\varphi , \end{aligned}$$
(10)

Here \(\tilde{\rho }\) and \(\tilde{p}\) represent the density and pressure for perfect fluid distribution. We note that the presence of term \(\theta \) clearly introduces an anisotropy if \(\theta ^r_r \ne \theta ^\varphi _\varphi \). Then the effective anisotropy is defined as,

$$\begin{aligned} \varDelta = p_t - p_r = \beta \, \left( \theta ^r_r - \theta ^\varphi _\varphi \right) . \end{aligned}$$
(11)

In order to solve Einstein’s equations we will introduce the gravitational decoupling via the MGD approach [12]. In this method, we transformed the metric potentials \(e^{\nu (r)}\) and \(e^{\lambda (r)}\) through a linear mapping which is given by,

$$\begin{aligned}&e^{\nu (r)} \longrightarrow e^{\tilde{\nu }(r)} + \beta \,f(r) \end{aligned}$$
(12)
$$\begin{aligned}&e^{-\lambda (r)} \longrightarrow e^{-\tilde{\lambda }(r)}+\beta \,g(r) \end{aligned}$$
(13)

Here \(e^{\tilde{\nu }(r)}\) and \(e^{\tilde{\lambda }(r)}\) are gravitational metric potentials corresponding to perfect fluid matter distribution while f(r) and g(r) are the corresponding deformations functions. It’s worth mentioning that the foregoing deformations are purely radial functions, this feature ensures the spherical symmetry of the solution. The so called MGD corresponds to set \(f(r)=0\) or \(g(r)=0\), in this case the deformation will be done only on the radial component, remaining the temporal one unchanged. Then the anisotropic sector \(\theta ^{m}_{n}\) is totally contained in the radial deformation (13). After replacing (13) into the system of Eqs. (5)–(7), it is decoupled in two systems of equations. The first one corresponds to \(\beta = 0\), it means perfect fluid matter distribution

$$\begin{aligned}&{\mathrm{e}^{-\tilde{\lambda } }}\left( {\frac{\tilde{\lambda }^{{\prime }}}{r}}-\frac{1}{r^2}\right) + \frac{1}{r^2}=8\pi \tilde{\rho } , \end{aligned}$$
(14)
$$\begin{aligned}&{\mathrm{e}^{-\tilde{\lambda }}} \left( {\frac{\tilde{\nu }^{{\prime }}}{r}}+\frac{1}{r^2}\right) -\frac{1}{r^2}=8\pi \tilde{p} \end{aligned}$$
(15)
$$\begin{aligned}&\frac{\mathrm{e}^{-\tilde{\lambda }}}{2} \left( \tilde{\nu }^{{\prime \prime }}+\frac{\tilde{\nu }^{{\prime \,2}}}{2}+{\frac{\tilde{\nu }^{{\prime }}-\tilde{\lambda }^{{\prime }}}{r}}-\frac{\tilde{\nu }^{{\prime }}\tilde{\lambda }^{{\prime }}}{2} \right) =8\pi \tilde{p}. \end{aligned}$$
(16)

The other set of equations corresponding to the factor \(\theta \) is given as,

$$\begin{aligned}&-\frac{g^\prime }{r}-\frac{g}{r^2}=8\,\pi \, \theta ^t_t , \end{aligned}$$
(17)
$$\begin{aligned}&-g \left( {\frac{\tilde{\nu }^{{\prime }}}{r}}+\frac{1}{r^2}\right) =8\pi \theta ^r_r \end{aligned}$$
(18)
$$\begin{aligned}&-\frac{g}{2} \left( \tilde{\nu }^{{\prime \prime }}+\frac{\tilde{\nu }^{{\prime \,2}}}{2}+{\frac{\tilde{\nu }^{{\prime }}}{r}}\right) -\frac{g^{\prime }}{2}\,\left( \frac{\tilde{\nu }^{{\prime }}}{2}+\frac{1}{r} \right) =8\pi \theta ^\varphi _\varphi . \end{aligned}$$
(19)

The set of Eqs. (14–16) and (17–19) satisfies the corresponding conservation equations,

$$\begin{aligned}&\frac{\tilde{\nu ^\prime }}{2}\,(\tilde{\rho }+\tilde{p})+\frac{d\tilde{p}}{dr}=0, \end{aligned}$$
(20)
$$\begin{aligned}&-\frac{\tilde{\nu ^\prime }}{2}\,(\theta ^t_t-\theta ^r_r)+\frac{d \theta ^r_r}{dr}-\frac{2}{r}\,(\theta ^\varphi _\varphi -\theta ^r_r)=0 \end{aligned}$$
(21)

We note that the linear combination of conservation Eqs.‘(20) and (21) via. coupling constant \(\beta \) provides the conservation equation for the energy momentum tensor \(T^m_n=\tilde{T}^m_n + \beta \,\theta ^m_n\), which is given as,

$$\begin{aligned}&-\frac{d\tilde{p}}{dr}-\beta \,\left[ \frac{\tilde{\nu ^\prime }}{2}\,(\theta ^t_t-\theta ^r_r)-\frac{d \theta ^r_r}{dr}+\frac{2}{r}\,(\theta ^\varphi _\varphi -\theta ^r_r)\right] \nonumber \\&\quad =\frac{\tilde{\nu ^\prime }}{2}\,(\tilde{\rho }+\tilde{p}).~~~~ \end{aligned}$$
(22)

3 Generalized anisotropic models for gravtational decoupling

Let us consider the Maurya and Gupta [113] perfect fluid solution of Einstein field equations for the Durgapal [116] type metric function,

$$\begin{aligned} ds^2= & {} B\,(1+Cr^2)^n \,dt^2 - \left[ \frac{-D_n\,Cr^2+2\,\psi _\lambda (r)}{2\,(1+Cr^2)^{n-2}} \right. \nonumber \\&+\frac{Cr^2\,[1+(n+1) Cr^2]\,h(r)}{(n+1)\,(1+Cr^2)^{n-2}} \nonumber \\&\left. +\frac{A\,Cr^2}{(1+Cr^2)^{n-2}\,[1+(n+1) Cr^2]^{2/(n+1)}}\right] ^{-1}dr^2\nonumber \\&-{r}^{2}({{d\theta }^{2}}+{{sin}^{2}}\theta {{d\phi }^{2}}), ~~~~ \end{aligned}$$
(23)

where, \(\psi _\lambda (r)=[1+(n+1) Cr^2]\),    \(D_n=\frac{(n-1) (n-2)}{2}-\frac{a_{n-4}}{n+1}+2n+2\), \(h(r)=\frac{A_{n-4}}{n+3}+\sum _{i=0}^{n-5}\frac{A_i\,(Cr^2)^{n-4-i}}{n^2-(i+2)n-(i+1)}\),    \(A_{i+1}=a_{i+1}-\frac{(n-4-i)\,A_i}{n^2-(i+2)n-(i+1)}\), \(a_{i+1}=\frac{(n-1)!}{(i+1)!\,(n-i-2)!}-\frac{a_i}{n+1}\),     \(A_0=a_0=1\) and \(A_{n-j}=a_{n-j}=0\) if \(n < j\). However A, B and C are arbitrary constants with dimension of C is \(length^{-2}\).

The metric (23) describes a static spherically symmetric configuration associated to an isotropic matter distribution which implies that radial and transverse pressures are equal i.e. \(p_r = p_t\). Therefore, the metric coefficients for perfect fluid distribution can be written as,

$$\begin{aligned} e^{\tilde{\nu }(r)}= & {} B\,(1+Cr^2)^n, \end{aligned}$$
(24)
$$\begin{aligned} e^{-\tilde{\lambda }(r)}= & {} \left[ \frac{-D_n\,Cr^2+2\,\psi _\lambda (r)}{2\,(1+Cr^2)^{n-2}} -\frac{Cr^2\,[1+(n+1) Cr^2]\,h(r)}{(n+1)\,(1+Cr^2)^{n-2}} \right. \nonumber \\&\left. +\frac{A\,Cr^2}{(1+Cr^2)^{n-2}\,[1+(n+1) Cr^2]^{2/(n+1)}}\right] .~~~~ \end{aligned}$$
(25)

Using Eqs. (24) and (25) together with Eqs. (14)–(16), we obtain the isotropic pressure and the energy density as,

$$\begin{aligned} \frac{8\,\pi \,\tilde{p}(r)}{C}= & {} \frac{[\,1 +(2n +1)Cr^2\,] }{(1+ Cr^2)}\left[ \frac{A\,(1+Cr^2)^{2-n}}{[1+(n+1) Cr^2]^{2/(n+1)}}\right. \nonumber \\&-\frac{[1+(n+1) Cr^2]\,h(r)}{(n+1)\,(1+Cr^2)^{n-2}}\nonumber \\&\left. -\frac{D_n}{2\,(1+Cr^2)^{n-2}} \right] +\frac{\psi _7(r)}{(1+Cr^2)^{n-1}},~~~~~ \end{aligned}$$
(26)
$$\begin{aligned} \frac{8\,\pi \,\tilde{\rho }(r)}{C}= & {} \left[ \frac{\psi _1(r)}{(1+Cr^2)^{n-1}}+\frac{D_n\,\psi _2(r)}{2\,(1+Cr^2)^{n-1}}\right. \nonumber \\&-\frac{A\,\psi _3(r)}{(1+Cr^2)^{n-1}\,\psi _4(r)} \nonumber \\&\left. +\frac{h(r)\,\psi _5(r)}{(n+1)\,(1+Cr^2)^{n-1}}+2\,\psi _6(r)\, \right] ,~~~~ \end{aligned}$$
(27)

where,

$$\begin{aligned} \psi _1(r)= & {} [\,\psi _8(r)-(n + 1)]\,(1 +Cr^2)\\&- 2[3+(3+2n-n^2)Cr^2\,],\\ \psi _2(r)= & {} [3+Cr^2+2(3-n)Cr^2], \\ \psi _3(r)= & {} [3+ (6+ n)Cr^2 + (3 +5n-2n^2)C^2r^4],\\ \psi _4(r)= & {} [1+ (n+ 1)Cr^2]^{(n+3)/(n+1)}, \\ \psi _5(r)= & {} [3+(3n+12) Cr^2 +(9 +7n- 2n^2) C^2r^4],\\ \psi _6(r)= & {} \frac{[1+(n+1)Cr^2]}{(n+1)\,(1+Cr^2)^{n-2}}\,\\&\times \sum \nolimits _{i=0}^{n-5} \frac{(n-4-i)\,A_i\,(Cr^2)^{n-4-i}}{n^2-(i+2)-(i+1)},\\ \psi _7(r)= & {} [(3n+ 2)-\psi _9(r) +(2n^2 +3n+1)Cr^2],\\ \psi _8(r)= & {} \sum \nolimits _{i=1}^{n-2} \frac{(n-2)!\,(Cr^2)^{i-1}}{i!\,(n-2-i)!},\\ \psi _9(r)= & {} \sum \nolimits _{i=1}^{n-1} \frac{(n-1)!\,(Cr^2)^{i-1}}{i!\,(n-1-i)!}. \end{aligned}$$

On the other hand, we want to obtain the components factors of \(\theta ^m_n\) by using the set of Eqs.  (17)–(19) which involves one extra unknown function g(r). For this purpose we take a suitable expression of this unknown function g(r) which has a form,

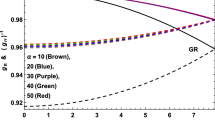
$$\begin{aligned} g(r)=\frac{n\,Cr^2}{\left[ 1+(n+1)Cr^2 \right] ^{2/(n+1)}}. \end{aligned}$$
(28)

Clearly, the above election of g(r) respects the physical and mathematical requirement regarding the behaviour of the metric potentials inside the stellar configuration, that is: positive, regular and increasing monotone functions with increasing radius within the compact object. Figure 1 shows the increasing behaviour of the deformation function g(r) with increasing radius.

Fig. 1
figure 1

Behaviour of g(r) vs. radial coordinate r / R with different values of n for \(LMC~X-4\)

Full size image

So, by inserting the Eqs. (24) and (28) into Eqs.  (17), (18) and (19) we get the components \(\theta ^m_n\) as,

$$\begin{aligned} \theta ^r_r= & {} - \frac{n\,C}{8\,\pi }\,\frac{[1 + (2\,n+1) C r^2]}{(1 + Cr^2)\,[\,1 + (n+1)Cr^2\,]^{2/(n+1)}}, \end{aligned}$$
(29)
$$\begin{aligned} \theta ^\varphi _\varphi= & {} - \frac{n\,C}{8\,\pi }\,\frac{[1+ 3\,n\,Cr^2 + (n^2+n-1)\,C^2r^4]}{(1 + Cr^2)^2\,[\,1 + (n+1)Cr^2\,]^{2/(n+1)}} \end{aligned}$$
(30)
$$\begin{aligned} \theta ^t_t= & {} - \frac{n\,C}{8\,\pi }\,\frac{[3 + (3\,n-1) C r^2]}{[1 + (n+1)Cr^2]^{(n+3)/(n+1)}}, \end{aligned}$$
(31)

Now, the anisotropic solution for the Maurya and Gupta [113] perfect fluid matter distribution can be described by the following gravitational potentials,

$$\begin{aligned}&e^{{\nu }(r)}=B\,(1+Cr^2)^n \end{aligned}$$
(32)
$$\begin{aligned}&e^{-{\lambda }(r)}=\left[ \phantom {\left. +\frac{n\,\beta \,Cr^2}{\left[ 1+(n+1)Cr^2 \right] ^{2/(n+1)}}\right] } \frac{-D_n\,Cr^2+2\,[1+(n+1) Cr^2]}{2\,(1+Cr^2)^{n-2}}\right. \nonumber \\&\qquad \qquad \quad -\frac{Cr^2\,[1+(n+1) Cr^2]\,h(r)}{(n+1)\,(1+Cr^2)^{n-2}} \nonumber \\&\qquad \qquad \quad +\frac{A\,Cr^2}{(1+Cr^2)^{n-2}\,[1+(n+1) Cr^2]^{2/(n+1)}}\nonumber \\&\qquad \qquad \quad \left. +\frac{n\,\beta \,Cr^2}{\left[ 1+(n+1)Cr^2 \right] ^{2/(n+1)}}\right] ,~~~ \end{aligned}$$
(33)

Hence, the expression for anisotropic pressures and density can be given as,

$$\begin{aligned} p_r(r;\beta )= & {} \tilde{p}(r)+ \frac{n\,\beta \,C}{8\,\pi }\,\nonumber \\&\times \frac{[1 + (2\,n+1) C r^2]}{(1 + Cr^2)\,[\,1 + (n+1)Cr^2\,]^{2/(n+1)}},\,\, \end{aligned}$$
(34)
$$\begin{aligned} p_t(r;\beta )= & {} \tilde{p}(r) + \frac{n\,\beta \,C}{8\,\pi }\,\nonumber \\&\times \frac{[1+ 3\,n\,Cr^2 + (n^2+n-1)\,C^2r^4]}{(1 + Cr^2)^2\,[\,1 + (n+1)Cr^2\,]^{2/(n+1)}},\,\, \end{aligned}$$
(35)
$$\begin{aligned} \rho (r;\beta )= & {} \tilde{\rho }(r)\nonumber \\&- \frac{n\,\beta \,C}{8\,\pi }\,\frac{[3 + (3\,n-1) C r^2]}{[1 + (1 + n)Cr^2]^{(n+3)/(n+1)}},\,\, \end{aligned}$$
(36)

where the \(\tilde{p}(r)\) and \(\tilde{\rho }(r)\) are given by the Eqs. (26) and (27). Using the Eqs. (29) and (30) the expression of anisotropy factor, \(\varDelta =\beta \, ( \theta ^r_r - \theta ^\varphi _\varphi )\), is given as,

$$\begin{aligned} \varDelta (r)=\frac{n\,\beta \,C}{8\,\pi }\,\left[ \frac{(n-2)[1+ (n+1)\,Cr^2]\,Cr^2}{(1 + Cr^2)^2\,[\,1 + (n+1)Cr^2\,]^{2/(n+1)}} \right] . \nonumber \\ \end{aligned}$$
(37)
Table 1 Physical parameters values of the compact star \(LMC ~X-4\) with mass \(M =1.29\left( M_\odot \right) \) and predicted radius \(R=8.831~(km)\), \(\beta =0.4\) for different values of n [120]
Full size table
Table 2 Numerical values of physical parameters for the compact stars for different values of n
Full size table

4 Junction conditions

To fix the values of the constants A, B and C, we need to ensure that the interior spacetime \(\mathscr {M^{-}}\) must match smoothly to the exterior spacetime \(\mathscr {M^{+}}\). In our case, the interior spacetime is given by the deformed metric given by (32)–(33), and since the exterior spacetime is empty, \(\mathscr {M^{+}}\) is taken to be the Schwarzschild solution [117]

$$\begin{aligned} ds^{2}= & {} \left( 1-\frac{2M}{r}\right) dt^{2}-\left( 1-\frac{2M}{r}\right) ^{-1}dr^{2} \nonumber \\&-r^{2}\bigg (d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}\bigg ). \end{aligned}$$
(38)

For this purpose we will use the Israel–Darmois junction conditions [118, 119]. These conditions require the continuity of the metric potentials \(e^{\nu (r)}\) and \(e^{\lambda (r)}\) across the surface \(\varSigma \) of the compact object defined by \(r=R\) (It is known as the first fundamental form). Then we have,

$$\begin{aligned}&e^{\nu (R)}=1-\frac{2M}{R}, \end{aligned}$$
(39)
$$\begin{aligned}&e^{-\lambda (R)}= 1-\frac{2M}{R}. \end{aligned}$$
(40)

On the other hand the effective radial pressure (34) vanishes at the surface star \((r=R)\), consequently

$$\begin{aligned} p_r(R;\beta )= \left( \tilde{p}-\beta \theta ^{r}_{r}\right) (R)=0. \end{aligned}$$
(41)

The above expression corresponds to the second fundamental form \([G_{\mu \nu }x^{\nu }]_{\varSigma }=0\), where \(x^{\nu }\) is a unit vector projected in the radial direction. Then the condition \(p_r(R;\beta )=0\) provides,

$$\begin{aligned} A= & {} [1 +(n+1)CR^2\,]^{\frac{2}{(n+1)}} \left[ \frac{[1+(n+1) CR^2]\,H(R)}{(n+1)}\right. \nonumber \\&\left. -\frac{\varPsi _7(R)}{[\,1 +(2n +1)CR^2\,]}\right] +\frac{D_n}{2}[1 +(n+1)CR^2\,]^{\frac{2}{(n+1)}} \nonumber \\&-n\,\beta \,(1 + CR^2)^{n-2}, ~~ \end{aligned}$$
(42)

and the condition \(e^{-\lambda (R)}= 1-\frac{2M}{R}\) leads to

$$\begin{aligned} M= & {} \frac{R}{2}\left[ 1+ \frac{D_n\,CR^2-2\,[\,1+(n+1) CR^2\,]}{2\,(1+CR^2)^{n-2}}\right. \nonumber \\&+\frac{CR^2\,[\,1+(n+1) CR^2\,]\,H(R)}{(n+1)\,(1+CR^2)^{n-2}}\nonumber \\&\left. -\frac{[\,A\,(1+CR^2)^{2-n}+n\,\beta \,]\, Cr^2}{[1+(n+1) CR^2]^{2/(n+1)}}\right] ,~~ \end{aligned}$$
(43)

while the condition \(e^{-\lambda (R)}=e^{\nu (R)}\) yields

$$\begin{aligned} B= & {} \left[ \frac{-D_n\,CR^2+2\,[1+(n+1) CR^2]}{2\,(1+CR^2)^{2n-2}}\right. \nonumber \\&-\frac{CR^2\,[1+(n+1) CR^2]\,H(R)}{(n+1)\,(1+CR^2)^{2n-2}} \nonumber \\&+\left. \phantom {\left[ \frac{-D_n\,CR^2+2\,[1+(n+1) CR^2]}{2\,(1+CR^2)^{2n-2}}\right. }\frac{[\,A\,(1+CR^2)^{2-2n}+n\,\beta \,]\, Cr^2}{[1+(n+1) CR^2]^{2/(n+1)}}\right] .~~~ \end{aligned}$$
(44)
Fig. 2
figure 2

Behaviour of gravitational potentials \(e^{\nu (r)}\) and \(e^{\lambda (r)}\) vs. radial coordinate r / R with different values of n for \(LMC~X-4\)

Full size image

So, Eqs. (42)–(44) are the necessary conditions in order to obtain the constant parameters. In addition, we have used the mass M and the radius R established on the obtained data for the strange star candidate \(LMC ~X-4\) [120]. In Table 1 are displaying the values of the constant parameters A, B and C for different n. Table 2 shows the same parameters to another two strange candidates 4U 1538-52 and SAX J1808.4-3658

5 Physical analysis

5.1 Regularity

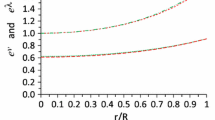
A physically acceptable solution of Einstein field equations, must be free of physical and geometrical singularities i.e the metric potentials must be regular from the center to the surface of the stellar configuration. So, from Eqs. (32) and (33) we can easily check that \(e^{\lambda }\) and \(e^{\nu }\) are completely regular, in fact

$$\begin{aligned} e^{\lambda (r)}|_{r=0}=1, \quad e^{\nu (r)}|_{r=0}=B. \end{aligned}$$
(45)

We can see from Eq. (45) that the constant parameter B must be positive. The features of the metric potentials are shown in Fig. 2. The profiles show that metric coefficients are regular and monotonic increasing functions of r inside the stellar interior.

On the other hand, we check the behavior of effective physical parameters \(\rho (r)\), \(p_r(r)\) and \(p_t(r)\) within the stellar configuration. All these parameters must be positive and monotonically decreasing as they tends to the boundary of compact object. The maximum values of above parameters must be attain at center of the star \(r=0\). The values of Eqs. (33)–(34) at the center \(r=0\) are given as,

$$\begin{aligned} \rho _0= & {} \frac{C}{8\,\pi }\,\left[ \,\frac{3\,A_{n-4}}{(n+1)\,(n+3)} \right. \nonumber \\&\left. + \frac{3\,a_{n-3}}{2}+(3\,n-6)-3\,A-3\,n\,\beta \,\right] ,~~~ \end{aligned}$$
(46)
$$\begin{aligned} p_{r0}= & {} p_{t0}=\frac{C}{8\,\pi }\left[ \frac{-A_{n-4}}{(n+1)\,(n+3)} \right. \nonumber \\&\left. \phantom {\left[ \frac{-A_{n-4}}{(n+1)\,(n+3)} \right. }-\frac{a_{n-3}}{2}+(n+2)+A+n\,\beta \right] .~~~~ \end{aligned}$$
(47)

Since \(p_{r0}\) and \(p_{t0}\) are positive then from Eq. (47) we obtain,

$$\begin{aligned} \left[ \,\frac{A_{n-4}}{(n+1)\,(n+3)}+\frac{a_{n-3}}{2}-(n+2)-n\,\beta \, \right] < A.~~~ \end{aligned}$$
(48)

Moreover, the solution should satisfy Zeldovich’s condition [121] at the interior of the star i.e. \(\frac{p_r}{\rho }\) much be \(\le 1\) at the center which give,

$$\begin{aligned} A \le \left[ \,\frac{A_{n-4}}{(n+1)\,(n+3)}+\frac{a_{n-3}}{2}-\frac{(n-4)}{2}-n\,\beta \, \right] . ~~~ \end{aligned}$$
(49)
Fig. 3
figure 3

Behaviour of radial pressure \(p_{r}(r)\) and tangential pressure \(p_{t}(r)\) vs. radial coordinate r / R with different values of n for \(LMC~X-4\)

Full size image
Fig. 4
figure 4

Behaviour of energy density \(\rho (r)\) (top) and pressure anisotropy \(\varDelta \) (bottom) vs. radial coordinate r / R with different values of n for \(LMC~X-4\)

Full size image

From the inequality (48) and (49) we get,

$$\begin{aligned}&\left[ \,\frac{A_{n-4}}{(n+1)\,(n+3)}+\frac{a_{n-3}}{2}-(n+2)-n\,\beta \, \right] \nonumber \\&\quad < A \le \left[ \,\frac{A_{n-4}}{(n+1)\,(n+3)}+\frac{a_{n-3}}{2}+\frac{(n-4)}{2}-n\,\beta \, \right] . ~~~ \nonumber \\ \end{aligned}$$
(50)

Figures 3 and 4 shows that all the above observables are well behaved inside the compact configuration. It is remarkable, that the present model exhibits a positive anisotropy factor \(\varDelta \), thus the object is subject to a repulsive force that counterbalances the gravitational gradient. Therefore, we have more compact and massive structures [52]. Figure 4 (bottom) shows the behaviour of the anisotropy factor \(\varDelta \). It is null at \(r=0\), because at the center the effective radial and transverse pressures are the same. Moreover, as the radius increases the values of these quantities drift apart, and therefore the anisotropy increases toward the surface of the object. Table 1 reports values corresponding to central and surface density, also the radial pressure is reported at the center of the star (we use the following notations in Table 1: sufarce redshift = \(z_s\), central density = \(\rho _c\), surface density = \(\rho _s\), central = \(p_c\)).

5.2 Causality condition

For an acceptable anisotropic solution of Einstein field equations via gravitational decoupling, the causality condition must satisfies inside the compact object i.e both the radial \(v_r\) and tangential \(v_t\) sound speeds are less than the speed of light c (in relativistic geometrized units the speed of light becomes \(c = 1\) ) i.e. the square of both radial (\(v^2_r\)) and tangential (\(v^2_t\)) speed of sounds should lie within interval [0, 1], which can be defined as,

$$\begin{aligned} v^2_r(r)= & {} \frac{dp_r(r;\beta )}{d\rho (r;\beta )} ~~\le 1~~~ \end{aligned}$$
(51)
$$\begin{aligned} v^2_t(r)= & {} \frac{dp_r(r;\beta )}{d\rho (r;\beta )}.~~\le 1 \end{aligned}$$
(52)

Figure 5 shows that the model fulfills both (51) and (52). Then the causality is preserved inside the star. From this figure it is also observed that the speed of sounds are decreasing towards the boundary of compact object. This decreasing feature of sound speed shows that our solution is well behaved [114]

Fig. 5
figure 5

Behaviour of radial velocity (\(v^2_r\)) and tangential velocity (\(v^2_t\)) vs. radial coordinate r / R with different values of n for \(LMC~X-4\)

Full size image
Fig. 6
figure 6

Behaviour of energy conditions vs. radial coordinate r / R with different values of n for \(LMC~X-4\)

Full size image

5.3 Energy condition

Within the framework of general relativity, models representing anisotropic fluids spheres must satisfy the energy conditions. There often exists a linear relationship between energy density and pressure of the matter obeying certain restrictions. For this purpose we examine (i) the null energy condition (NEC), (ii) weak energy condition (WEC), (iii) strong energy condition (SEC) and (iv) dominant energy conditions (DEC). More precisely, we have the following proposition: [122, 123],

$$\begin{aligned}&\mathrm{(i)}~ NEC: \rho (r;\beta ) \ge 0, \end{aligned}$$
(53)
$$\begin{aligned}&\mathrm{(ii)}~SEC: \rho (r;\beta )+p_r(r;\beta ) + 2\,p_t(r;\beta ) \ge 0 ,\end{aligned}$$
(54)
$$\begin{aligned}&\mathrm{(iii)}~ WEC: \rho (r;\beta )+p_r(r;\beta ) \ge 0,~\rho (r;\beta )\nonumber \\&\quad \;\;+p_t(r;\beta ) \ge 0,~~~~~~~ \end{aligned}$$
(55)
$$\begin{aligned}&\mathrm{(iv)}~DEC: \rho (r;\beta )-p_r(r;\beta ) \ge 0,~\rho (r;\beta )\nonumber \\&\quad \;-p_t(r;\beta ) \ge 0,~~~~~~~ \end{aligned}$$
(56)

The above inequalities should be satisfy inside the aniso- tropic compact star, implying that the energy momentum tensor is positive everywhere within the configuration. However, violations of the energy conditions have sometimes been presented as only being produced by unphysical stress energy tensors. Usually SEC is used as a fundamental guide will be extremely idealistic as SEC is violated in many cases, e.g. minimally coupled scalar field and curvature-coupled scalar field theories. On the other hand, SEC violation may or may not imply the violation of the more basic energy condition i.e. null energy condition and weak energy condition. Fortunately in our model all the energy conditions are well behaved, it is shown in Fig. 6, therefore the model has a positive and well behaved energy-momentum tensor.

5.4 Effective mass-radius ratio and redshift

In the study of static perfect fluid distribution for spherically symmetric line element, the upper limit of the mass-radius ratio must must satisfy the inequality \(\frac{M}{R} < \frac{4}{9}\) (where the units G = c = 1) [124]. However, this limit will be more general if the matter is anisotropic in nature [125]. This mass-radius ratio can be obtained through the effective mass which can be defined as [63],

$$\begin{aligned} M_{eff}= 4\,\pi \,\int ^R_0 {\rho (r)r^2\,dr}=\frac{R}{2}\,\left[ 1-e^{-\lambda (R)} \right] . \end{aligned}$$
(57)

The explicit form of effective mass can be written as,

$$\begin{aligned} M_{eff}= & {} \frac{R}{2}\left[ 1+ \frac{D_n\,CR^2-2\,[\,1+(n+1) CR^2\,]}{2\,(1+CR^2)^{n-2}} \right. \nonumber \\&+\frac{CR^2\,[\,1+(n+1) CR^2\,]\,H(R)}{(n+1)\,(1+CR^2)^{n-2}} \nonumber \\&\left. -\frac{[\,A\,(1+CR^2)^{2-n}+n\,\beta \,]\, Cr^2}{[1+(n+1) CR^2]^{2/(n+1)}}\right] .~~ \end{aligned}$$
(58)

Then the compactness factor \(\left( u=\frac{M_{eff}}{R}\right) \) becomes,

$$\begin{aligned} u= & {} \frac{1}{2}\left[ 1+ \frac{D_n\,CR^2-2\,[\,1+(n+1) CR^2\,]}{2\,(1+CR^2)^{n-2}}\right. \nonumber \\&+\frac{CR^2\,[\,1+(n+1) CR^2\,]\,H(R)}{(n+1)\, (1+CR^2)^{n-2}} \nonumber \\&\left. -\frac{[\,A\,(1+CR^2)^{2-n}+n\,\beta \,]\, Cr^2}{[1+(n+1) CR^2]^{2/(n+1)}}\right] .~~ \end{aligned}$$
(59)

The surface redshift can be obtained from the compactness u, which is given by (59)

$$\begin{aligned} Z_s=\sqrt{e^{-\lambda (R)}-1}=\frac{1-\sqrt{1-2u}}{\sqrt{1-2u}}. ~~ \end{aligned}$$
(60)
Fig. 7
figure 7

Behaviour of surface redshift (\(Z_{s}\)) vs. radial coordinate r / R with different values of n for \(LMC~X-4\)

Full size image

From the observational point of view, the surface gravitational redshift is an important ingredient, because it relates the mass M and the radius R of the astrophysical objects. As, was pointed out by Bowers and Liang [37] in the case of ultra dense object containing anisotropies, the surface redshift \(Z_{s}\) can be larger than its isotropic counterpart.

5.5 Equilibrium condition

Tolman–Oppenheimer–Volkoff (TOV) [126, 127] equation defines the equilibrium condition of the system. In the present situation the equilibrium of the anisotropic fluid models can be expressed by three different forces. These forces are gravitational force \(F_g\), hydrostatic force \(F_h\) and the anisotropic repulsive force \(F_a\). The anisotropic repulsive force \(F_a\) lies in the system due to presence of a positive anisotropy factor \(\varDelta \). It is fact that the gravitational force \(F_g\) is counterbalanced by joint action of the hydrostatic force \(F_h\) and the anisotropic repulsive force \(F_a\). Consequently, in distinction with the isotropic case where \(\varDelta =0\) the existence of point singularities due to a violent gravitational collapse, may be avoided. This is because, the equilibrium of the system is improved by the introduction of anisotropies inside the compact object.

Then the Tolman–Oppenheimer–Volkoff equation for an anisotropic matter distribution describing the equilibrium condition is given by

$$\begin{aligned} -\frac{\nu ^{\prime }}{2}\,\left[ \,\rho (r;\beta )+p_r(r;\beta )\,\right] - \frac{dp_r(r;\beta )}{dr}+\frac{2\,\varDelta }{r}=0, \end{aligned}$$
(61)

Now the explicit form these forces can be written as,

$$\begin{aligned} F_g= & {} -\frac{\nu ^{\prime }}{2}\,\left[ \,\rho (r;\beta )+p_r(r;\beta )\,\right] \nonumber \\= & {} -\frac{2\,B\,n\,Cr}{(1+Cr^2)}\,\left[ \phantom {\left. +\frac{2\,C\,n\,\beta }{8\,\pi }\,\frac{[-1 +(1 + n^2)\,C^2 r^4]}{(1 + C r^2)\,[1+(n+1)\,Cr^2]^{(n+3)/(n+1)}}\,\right] }\tilde{\rho }(r)+\tilde{p}(r)\right. \nonumber \\&\left. \quad +\frac{2\,C\,n\,\beta }{8\,\pi }\,\frac{[-1 +(1 + n^2)\,C^2 r^4]}{(1 + C r^2)\,[1+(n+1)\,Cr^2]^{(n+3)/(n+1)}}\,\right] ,~~ \end{aligned}$$
(62)
$$\begin{aligned} F_h= & {} -\frac{dp_r(r;\beta )}{dr}\nonumber \\&=-\frac{d\tilde{p}(r)}{dr}\nonumber \\&\quad -\frac{4n\, \beta \,C^2 r\,[-n^2\,Cr^2 + (1 + Cr^2)^2 + n\,(-1 + Cr^2 + 2\,C^2 r^4)]}{8\,\pi \,(1 + C r^2)^2\,[1+(n+1)\,Cr^2]^{(n+3)/(n+1)}}, \nonumber \\ \end{aligned}$$
(63)
$$\begin{aligned} F_a= & {} \frac{2\,\varDelta }{r}\nonumber \\= & {} \frac{2\,n\,\beta \,C^2r}{8\,\pi }\,\left[ \frac{(n-2)[1+ (n+1)\,Cr^2]}{(1 + Cr^2)^2\,[\,1 + (n+1)Cr^2\,]^{2/(n+1)}} \right] , \end{aligned}$$
(64)

where, \(\tilde{\rho }(r)\), \(\tilde{p}(r)\) and \(\frac{d\tilde{p(r)}}{dr}\) can be obtained from Eqs. (27) and (26).

Fig. 8
figure 8

Behaviour of different forces \(F_g\), \(F_h\) and \(F_a\) vs. radial coordinate r / R with different values of n for \(LMC~X-4\)

Full size image

Figure 8 displays the TOV equation, showing the equilibrium of the system under the three foregoing mentioned forces. Although the anisotropic force is small in comparison with the hydrostatic and gravitational forces, its presence considerably helps the balance of the system.

5.6 Stability conditions

5.6.1 Adiabatic index

Another significant features of the anisotropic fluid models is known as stability condition. In order to verify the stability of the present model we have to analyze adiabatic index \(\varGamma \) within the anisotropic compact object. It is well known that the average adiabatic index \(\varGamma \) is greater than 4/3 for a stable Newtonian isotropic fluid spheres and the collapsing condition correspond to \(\varGamma \le \frac{4}{3}\) . On the other hand, for isotropic fluid model, Knutsen [128] has shown analytically that the ratio of pressure and energy density monotonically decreases outwards corresponds to \(\varGamma \ge 1\), which implies that the temperature distribution is decreasing outwards. According to Herrera and his collaborators [48, 50] the collapsing condition corresponding to \(\varGamma \) for anisotropic fluid spheres is given by

$$\begin{aligned} \,\varGamma < \frac{4}{3}+\dfrac{4}{3}\left[ 2\pi \frac{\rho _0\,p_{r0}}{\left| p_{r0}^\prime \right| }r+\frac{(p_{t0}-p_{r0})}{\left| p_{r0}^\prime \right| r}\right] , \end{aligned}$$
(65)

where, \(p_{t0}\), \(p_{r0}\), and \(\rho _0\) are the initial tangential, radial, and energy density in static equilibrium stage which satisfies (61). The first term inside the brackets represents relativistic corrections to the Newtonian perfect fluid and the second term is anisotropic corrections. From Eq. (65) we observe that for a non-relativistic matter distribution by taking radial pressure \(p_r\) is equal to tangential pressure \(p_t\) i.e \(\varDelta =0\) which implies that the second term of the brackets vanishes and we achieve the collapsing Newtonian limit \(\varGamma < 4/3\) [129]. Heintzmann and Hillebrandt [38] also proposed that a relativistic compact star with an anisotropic equation of state in presence of positive and increasing anisotropy factor \(\varDelta =p_t-p_r > 0\) is stable for \(\varGamma > 4/3\). Since the positive anisotropic factor may slow down the growth of instability which implies that the gravitational collapse occurs in the radial direction. Therefore, it is enough to study about adiabatic index only in radial direction which is given by

$$\begin{aligned} \varGamma _r= \left( \frac{p_r+\rho }{p_r}\right) \,\frac{dp_r}{d\rho }. \end{aligned}$$
(66)

We can see from Fig. 9 the monotonically increasing behaviour of the adiabatic index. Moreover, it is in complete agreement with the condition \(\varGamma _{r}>4/3\), for compact object described by an anisotropic matter distribution. This fact shows that our model is stable.

Fig. 9
figure 9

Variation of adiabatic index \((\varGamma _r)\) vs. radial coordinate r / R with different values of n for \(LMC~X-4\)

Full size image

5.6.2 Herrera and Abreu’s criterion

Another way to check if the system is stable, is through the study of the subliminal sound speeds within the stellar configuration. For this purpose we use the well known Abreu’s criterion [68] (known as revised Herrera cracking concept [49]), which basically consists in explore the influence of density fluctuations and local anisotropy have on the stability of local and non-local anisotropic matter configurations. So, this criterion establishes,

$$\begin{aligned}&-1\le v^{2}_{t}-v^{2}_{r}\le 1 \nonumber \\&\quad = \left\{ \begin{array}{ll} -1\le v^{2}_{t}-v^{2}_{r}\le 0~~ &{} \mathrm {Potentially\ stable\ } \\ 0< v^{2}_{t}-v^{2}_{r}\le 1 ~~ &{} \mathrm {Potentially\ unstable\ } \end{array} \right. \end{aligned}$$
(67)
Fig. 10
figure 10

Variation of velocity difference \((v^2_t-v^2_r)\) and (\(v^2_r-v^2_t\)) vs. radial coordinate r / R with different values of n for \(LMC~X-4\)

Full size image

It means that the system is stable if the square of the radial sound speed is greater than the square of the tangential sound speed everywhere inside the star, then there is no change in sign \(-1\le v^{2}_{t}-v^{2}_{r}\le 0\) or equivalently the stability factor \(| v^{2}_{t}-v^{2}_{r}|\) lies between 0 and 1. We can observe from Fig. 5 that the square of the radial sound speed is always greater than the square of tangential sound speed and from Fig. 10 that there is no change in sign \(-1\le v^{2}_{t}-v^{2}_{r}\le 0\), then the present model is completely stable.

6 Behaviour of solution at very large value of n

In this article we have calculated our results upto \(n=3486\) due to computational limit. Since n is a positive integer so we wish to know that what will happen if n is very large i.e. tends to infinity. For this purpose we have plotted the graph of \(n\,C\) verses n which is shown in Fig. 11. From this figure it may observe an important result that the value of \(n\,C\) becomes approximately constant, say \(n\,C=K\) when \(n \ge 500\). This result will help us to write the expressions of our metric functions (\(e^{\nu (r)}\) and \(e^{\lambda (r)}\)) and deformation function g(r) which will take the following form,

$$\begin{aligned} e^{{\nu }(r)}= & {} B\,e^{K\,r^2} \end{aligned}$$
(68)
$$\begin{aligned} e^{\lambda (r)}= & {} 1+\frac{K\,r^2}{e^{K\,r^2/2}}\,\left[ D-\frac{1}{2\,e}\,Ei\left( 1+\frac{Cr^2}{2}\right) \right] \nonumber \\&+\beta \,K\,r^2 \end{aligned}$$
(69)
$$\begin{aligned} g(r)= & {} \beta \,K\,r^2, \end{aligned}$$
(70)

where:

$$\begin{aligned} Ei\left( 1+\frac{Cr^2}{2}\right) =\ln \left( 1+\frac{Cr^2}{2}\right) \,\sum _{n=1}^{\infty }\frac{\left( 1+\frac{Cr^2}{2}\right) }{n!\,n}. \end{aligned}$$

The above Eqs. (68)–(70) can provide the behavior of the solution at very large value of n.

Fig. 11
figure 11

Variation of \(n\,C\) vs. the integer values of n for \(LMC~X-4\)

Full size image

On the other hand, for sufficiently large values of n, the curves describing the observables such as radial and tangential pressure, energy density, redshift and other quantities as the anisotropy factor, energy conditions, subliminal sound speeds and adiabatic index tend to merge. This fact can be noticed from Figs. 3, 4, 5, 6, 7 and 9.

7 Concluding remarks

We have obtained an anisotropic extension of the Maurya-Gupta isotropic model [113] to Einstein field equations. To achieve it, we have employed the gravitational decoupling through the minimal geometric deformation approach, imposing an adequate form of the function g(r) in order to ensure the regularity of the metric potentials and all the physical parameters of the system within the stellar configuration. Once again, the minimal geometric deformation approach showed its versatility in this context, taking us an admissible solution to Einstein field equations. It is reflected in the graphical analysis, where from Figs. 2, 3 and 4 it is observed that the model is free from physical and geometrical singularities, moreover all the thermodynamic observables are finite, positive and monotone decreasing functions inside the star, and all of them attain their maximum value at the center of the compact object. Respect to the anisotropy factor (bottom panel Fig. 4), the system experiences a positive one, this is so because \(p_{t}>p_{r}\) everywhere within the star and as they get closer to the surface, they turn away. On the other hand, Fig. 5 shows that system is completely agree with causality i.e the subliminal radial and tangential sound speeds are less than the speed of light everywhere within the star, furthermore all the energy conditions are satisfied, it means that the model has a positive and well behaved energy-momentum tensor, as can be seen in Fig. 6. Respect to the equilibrium and the stability of the model, Fig. 8 shows that the object is in complete equilibrium under three different forces, the gravitational \(F_{g}\), the anisotropic \(F_{a}\) and the hydrostatic \(F_{h}\) force. Due to the fact that our model presents a positive anisotropy factor i.e \(\varDelta >0\), the anisotropic force \(F_{a}\) counterbalances the gravitational gradient, it helps to the system avoids the collapse to a point singularity during the gravitational collapse. In addition, a positive anisotropy factor not only enhances the equilibrium of the system also improves the stability. It is appreciate in Fig. 9 that the relativistic adiabatic index \(\varGamma _{r}\) is greater than 4 / 3 and is also increasing monotonically outward, it means that the system is stable. Finally, it is observed in Fig. 10 that the Abreu’s criteria is satisfied, this is so because the radial sound speed \(v^{2}_{r}\) is always greater than the transverse sound speed \(v^{2}_{t}\) everywhere within the star, besides there is no change in sign \(v^{2}_{t}-v^{2}_{r}\) and stability factor \(|v^{2}_{t}-v^{2}_{r}|\) lies between 0 and 1. Standing out that when n is large enough, the graphical analysis of many of these quantities shows that curves tend to merge. This happens because to \(n\ge 500\) the quantity \(n\,C\) remains constant.

On the other hand, in this work only radial deformations was reported, it may be interesting in a future work consider also temporal deformations. In addition, our model is representing the strange star candidates. LMC X-4, 4U 1538-52, SAX J1808.4-3658 where it is appreciated that all the numerical values of LMC X-4 presented in Table 1 for different values of n, associated with the central and surface density, central pressure and surface gravitational redshift are within the established ranges to describe ultra dense objects.

At this stage it is worth mentioning that despite its simplicity, gravitational decoupling by minimal geometric deformation, has proven to be a powerful tool in order to address the study that contemplate spherical and static configurations described by an anisotropic matter distributions within the framework of general relativity. Moreover, there is still much to be explored within this context and of course this novel method could provide clarifying and intriguing results.