Computation of $H\rightarrow gg$ in fdh and dred: renormalization, operator mixing, and explicit two-loop results

Abstract

The $H\rightarrow gg$ amplitude relevant for Higgs production via gluon fusion is computed in the four-dimensional helicity scheme (fdh) and in dimensional reduction (dred) at the two-loop level in the limit of heavy top quarks. The required renormalization is developed and described in detail, including the treatment of evanescent $\epsilon$-scalar contributions. In fdh and dred there are additional dimension-5 operators generating the H g g vertices, where g can either be a gluon or an $\epsilon$-scalar. An appropriate operator basis is given and the operator mixing through renormalization is described. The results of the present paper provide building blocks for further computations, and they allow one to complete the study of the infrared divergence structure of two-loop amplitudes in fdh and dred.

1 Introduction

Higgs production via gluon fusion is one of the most important LHC processes. Its computation at higher orders requires renormalization and factorization to cancel UV and IR divergences. Working in the limit of heavy top quarks, the required renormalization is less trivial than the one of standard QCD processes due to the required renormalization of non-renormalizable operators. The virtual corrections have been computed in conventional dimensional regularization (cdr) [1–5]; the required theory of operator renormalization in cdr has been developed in Ref. [6], based on general work in Refs. [7, 8].

In the past years, several alternative regularization schemes have been developed. Purely four-dimensional schemes such as implicit regularization [9, 10] and FDR [11] have been proposed and used to compute processes of practical interest such as $H\rightarrow \gamma \gamma$ [12, 13] and $H\rightarrow gg$ [14]. The present paper is devoted to regularization by dimensional reduction (dred) [15] and the related four-dimensional helicity (fdh) scheme [16]. Both schemes are actually the same regarding UV renormalization, but they differ in the treatment of external partons related to IR divergences.¹ There has been significant progress in the understanding of fdh and dred: the equivalence to cdr [20, 21], mathematical consistency and the quantum action principle [22], and infrared factorization [23, 24] have been established—these results solved several problems that had been reported earlier, related to violation of unitarity [25], Siegel’s inconsistency [26], and the factorization problem of [27, 28]. In addition, explicit multi-loop calculations have been carried out [29–34].

More recently, the multi-loop IR divergence structure of fdh and dred amplitudes has been studied in Ref. [35]. It has been shown that IR divergences in fdh and dred can be described by a generalization of the cdr formulas given in Refs. [36–41]. The description involves IR anomalous dimensions $\gamma ^i$ for each parton type i. In Ref. [35] they have been computed for the cases of quarks and gluons by comparing the general IR factorization formulas with explicit results for the quark and gluon form factor. In fdh and dred, however, the gluon can be decomposed into a D-dimensional gluon ${\hat{g}}$ and $(4-D)$ additional degrees of freedom, so-called $\epsilon$-scalars $\tilde{g}$. In dred, $\epsilon$-scalars also appear as external states.

The present paper is devoted to a detailed two-loop computation of the amplitude $H\rightarrow gg$ in fdh and dred. In dred, this involves the computations of $H\rightarrow {\hat{g}}{\hat{g}}$ and $H\rightarrow \tilde{g}\tilde{g}$, since the external gluons can either be gauge fields or $\epsilon$-scalars. The fdh result is identical to the one for $H\rightarrow {\hat{g}}{\hat{g}}$ and has already been given in Ref. [35], but we will provide further details here.

This detailed computation is of interest for two reasons: First, it provides the basis for obtaining the remaining IR anomalous dimension for $\epsilon$-scalars at the two-loop level. Second, it provides an example of the required renormalization in fdh and dred, including operator renormalization and operator mixing. The difficulty of renormalization in fdh and dred, particularly in connection with $H\rightarrow gg$, has been pointed out e.g. in Refs. [34, 42].

The outline of the paper is as follows: Sect. 2 gives a brief description of the regularization schemes and of the relevant Lagrangian and operators. It ends with a detailed list of the required ingredients of the calculation.

Apart from the actual two-loop computation and ordinary parameter and field renormalization that are described in Sects. 3 and 4, respectively, the main difficulty lies in the renormalization and mixing of the operators generating $H\rightarrow gg$. This is discussed in general in Sect. 5, and specific two-loop results are presented in Sect. 6. Section 7 then provides the final results for the on-shell amplitudes for $H\rightarrow {\hat{g}}{\hat{g}}$ and $H\rightarrow \tilde{g}\tilde{g}$. The appendix contains details on our projection operators and gives Feynman rules for the different operator insertions.

2 Regularization schemes and $H\rightarrow gg$

It is useful to distinguish the following regularization schemes [24]: conventional dimensional regularization (cdr), the ’t Hooft–Veltman (hv) scheme, the four-dimensional helicity (fdh) scheme, and dimensional reduction (dred). In all these schemes, momenta are treated in $D=4-2\epsilon$ dimensions (the associated space is denoted by QDS with metric tensor ${\hat{g}}^{\mu \nu }$). In order to define the schemes, one also needs an additional quasi-4-dimensional space (Q4S, metric $g^{\mu \nu }$) and the original 4-dimensional space (4S, metric ${\bar{g}}^{\mu \nu }$). The treatment of gluons in the four schemes is given in Table 1. In the table, “internal” gluons are defined as either virtual gluons that are part of a one-particle irreducible loop diagram or, for real correction diagrams, gluons in the initial or final state that are collinear or soft. “External gluons” are defined as all other gluons. For more details regarding this distinction, see e.g. Ref. [24].

Table 1 Treatment of internal and external gluons in the four different regularization schemes, i.e. prescriptions for which metric tensor has to be used in propagator numerators and polarization sums

Mathematical consistency and D-dimensional gauge invariance require that $Q4S\supset QDS\supset 4S$ and forbid to identify $g^{\mu \nu }$ and ${\bar{g}}^{\mu \nu }$. Details can be found in Refs. [22, 24, 35]. The most important relations for the present paper are

$$\begin{aligned} g^{\mu \nu }&={\hat{g}}^{\mu \nu }+\tilde{g}^{\mu \nu }, \quad {\hat{g}}^{\mu \rho }\tilde{g}_{\rho }{}^\nu =0, \quad {\hat{g}}^{\mu \rho }\bar{g}_{\rho }{}^\nu =\bar{g}^{\mu \nu },\nonumber \\&\quad {\hat{g}}^{\mu \nu }{\hat{g}}_{\mu \nu }=D, \quad \tilde{g}^{\mu \nu }\tilde{g}_{\mu \nu }=N_\epsilon , \nonumber \\ \gamma ^{\mu }&=\hat{\gamma }^{\mu }+\tilde{\gamma }^{\mu }, \quad \partial ^{\mu }=\hat{\partial }^{\mu }, \end{aligned}$$

(1)

where a complementary $2\epsilon$-dimensional metric tensor ${\tilde{g}}^{\mu \nu }$ has been introduced. With the metric tensors we can decompose a quasi-4-dimensional gluon field $A^\mu$ as

$$\begin{aligned} A^\mu&={\hat{g}}^{\mu \nu }A_\nu +\tilde{g}^{\mu \nu }A_\nu =\hat{A}^\mu +\tilde{A}^\mu \end{aligned}$$

(2)

into a D-dimensional gauge field $\hat{A}^\mu$ and an associated $\epsilon$-scalar field $\tilde{A}^\mu$ with multiplicity $N_\epsilon =2\epsilon$.² Correspondingly, there are two types of particles in the regularized theory: D-dimensional gluons ${\hat{g}}$ and $\epsilon$-scalars $\tilde{g}$. The unregularized external gluons $\bar{g}$ of fdh are a part of ${\hat{g}}$.

The regularized Lagrangian of massless QCD in fdh and dred is then obtained by applying relations (1) and (2) to the Lagrangian of ordinary QCD:

(3a)

(3b)

Here, ${\hat{F}}^{\mu \nu }$ and ${\hat{D}}^\mu =\partial ^\mu +ig_{s}{\hat{A}}^\mu$ denote the non-abelian field strength tensor and the covariant derivative in D dimensions; $\psi$ and c are the quark and ghost fields.

The resulting $\epsilon$-scalar Lagrangian $\mathcal {L}_\epsilon$ contains all standard interaction terms of scalar fields in the adjoint representation. Due to the Lorentz structure of the underlying vector space there is no $\epsilon$-scalar–ghost interaction in Eq. (3b). The coupling of $\epsilon$-scalars to (anti-)quarks is given by the evanescent Yukawa-like coupling $\ge$. This could in principle be set equal to the strong coupling $g_{s}$. But, since both couplings renormalize differently, this would only hold at tree level and for one particular renormalization scale [20]; the same is true for the quartic $\epsilon$-scalar coupling $g_{4\epsilon }$. In Eq. (3b) we introduce an abbreviation that includes the appearing Lorentz and color structure: $(g_{4\epsilon }^2)^{\alpha \beta \gamma \delta }_{abcd}\mathrel {\mathop :}=g_{4\epsilon }^2(f_{abe}f_{cde} {\tilde{g}}^{\alpha \gamma }{\tilde{g}}^{\beta \delta }+\text {perm.})$, where “perm.” denotes the five permutations arising from symmetrization in the multi-indices $(a,\alpha )\dots (c,\gamma )$. In the following we use all couplings in the form $\alpha _i=\frac{g_i^2}{4\pi }$ with $i = s, e, 4\epsilon$.

The process $H\rightarrow gg$ is generated by an effective Lagrangian which arises from integrating out the top quark in the Standard Model. In cdr it contains only the term $-\frac{1}{4}\lambda H {\hat{F}}^{\mu \nu }_a{\hat{F}}_{\mu \nu , a}$. In fdh and dred one again has to distinguish several gauge invariant structures containing either D-dimensional gluons or $\epsilon$-scalars. The effective Lagrangian can be written as

$$\begin{aligned} \mathcal{L}_{\text {eff}}= \lambda HO_1+\lambda _\epsilon H\tilde{O}_1+ \sum _i\lambda _{4\epsilon ,i}H\tilde{O}_{4\epsilon ,i}, \end{aligned}$$

(4)

with

$$\begin{aligned} O_1&=-\frac{1}{4} \hat{F}^{\mu \nu }_a \hat{F}_{\mu \nu ,a},\end{aligned}$$

(5a)

$$\begin{aligned} {\tilde{O}}_1&= -\frac{1}{2}(\hat{D}^\mu {\tilde{A}}^\nu )_a(\hat{D}_\mu {\tilde{A}}_\nu )_a. \end{aligned}$$

(5b)

${\tilde{O}}_{4\epsilon ,i}$ denote operators involving products of four $\epsilon$-scalars. Such operators are not important in the present paper and will not be given explicitly. Like for $\alpha _s,\alpha _e$ and $\alpha _{4\epsilon }$, the couplings $\lambda$ and $\lambda _\epsilon$ can be set equal at tree level, but they renormalize differently and have different $\beta$ functions.

Our final goal is the calculation of the two-loop form factors for gluons and $\epsilon$-scalars. This requires the on-shell calculation of the 3-point function $\Gamma _{H A^\mu A^\nu }(q,-p,-r)$. All momenta are defined as incoming, so $q=p+r$. The 3-point function can be separated into $\Gamma _{H {\hat{A}}^\mu {\hat{A}}^\nu }$ and $\Gamma _{H {\tilde{A}}^\mu {\tilde{A}}^\nu }$, corresponding to the amplitudes for $H\rightarrow {\hat{g}}{\hat{g}}$ and $H\rightarrow \tilde{g}\tilde{g}$, respectively.³ In dred, both on-shell amplitudes are needed according to Table 1. In fdh, only $H\rightarrow \bar{g}\bar{g}$ is needed, which, however, is identical to $H\rightarrow {\hat{g}}{\hat{g}}$ and will not be discussed separately.

The on-shell calculation requires the knowledge of the two-loop renormalization constants $\delta Z_\lambda ^{\mathrm{2L}}$ and $\delta Z_{\lambda _\epsilon }^{\mathrm{2L}}$. These in turn can be obtained from an off-shell calculation of $\Gamma _{H A^\mu A^\nu }$. Projectors extracting the required renormalization constants from the off-shell Green functions and precisely defining the gluon and $\epsilon$-scalar form factors are given in Appendix A.1.

We have now all ingredients to discuss the classes of Feynman diagrams that contribute to $\Gamma _{H A^\mu A^\nu }$ in fdh and dred:

• 1. Genuine two-loop diagrams $\Gamma _{H A^\mu A^\nu }^{\mathrm{2L}}$. Some remarks concerning the calculation are presented in Sect. 3.

• 2. Counterterm diagrams $\Gamma _{H A^\mu A^\nu }^{\mathrm{1LCT,a}}$ and $\Gamma _{H A^\mu A^\nu }^{\mathrm{2LCT,a}}$ arising from one- and two-loop renormalization of the fields, the gauge parameter $\xi$, and of the couplings $\alpha _s$, $\alpha _e$, and $\alpha _{4\epsilon }$. The required renormalization constants are presented in Sect. 4.

• 3. Counterterm diagrams $\Gamma _{H A^\mu A^\nu }^{\mathrm{1LCT,b}}$ arising from one-loop renormalization of the effective Lagrangian (4) at the one-loop level, which includes the renormalization of $\lambda$ and $\lambda _{\epsilon }$. This is a major complication and will be presented in Sect. 5.

• 4. Overall two-loop counterterm diagrams $\Gamma _{H A^\mu A^\nu }^{\mathrm{2LCT,b}}$ arising from the two-loop renormalization of the effective Lagrangian (4), equivalently from the renormalization constants $\delta Z_{\lambda }^{\mathrm{2L}}$ and $\delta Z_{\lambda _\epsilon }^{\mathrm{2L}}$. These renormalization constants are generally defined by the requirement that the appropriate off-shell Green functions are UV finite after renormalization. For the case of $\delta Z_\lambda$, an elegant alternative determination is possible [6], but that method fails for $\delta Z_{\lambda _\epsilon }$. The results for $\delta Z_{\lambda }^{\mathrm{2L}}$ and $\delta Z_{\lambda _\epsilon }^{\mathrm{2L}}$ are presented in Sect. 6.

3 Genuine two-loop diagrams

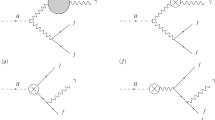
As mentioned above the Green function $\Gamma _{H A^\mu A^\nu }$ can be separated into $\Gamma _{H {\hat{A}}^\mu {\hat{A}}^\nu }$ and $\Gamma _{H {\tilde{A}}^\mu {\tilde{A}}^\nu }$, corresponding to $H\rightarrow {\hat{g}}{\hat{g}}$ and $H\rightarrow \tilde{g}\tilde{g}$. Examples for genuine two-loop diagrams with either external gluons or $\epsilon$-scalars are shown in Fig. 1.

Fig. 1

Sample two-loop diagrams for the process $H\rightarrow {\hat{g}}{\hat{g}}$ and $H\rightarrow \tilde{g}\tilde{g}$ in dred. $\epsilon$-scalars are denoted by dashed lines. The appearing coupling combinations from left to right are $\lambda \alpha _s^2$, $\lambda _\epsilon \alpha _e^2$, $\lambda _\epsilon \alpha _s^2$, $\lambda _\epsilon \alpha _{4\epsilon }^2$

All loop calculations have been performed using the following setup: the generation of diagrams and analytical expressions is done with the Mathematica package FeynArts [43]; to cope with the extended Lorentz structure in Q4S we use a modified version of TRACER [44]; all planar on-shell integrals are reduced and evaluated with an implementation of an in-house algorithm that is based on integration-by-parts methods and the Laporta-algorithm [45]; all non-planar and off-shell integrals are reduced and evaluated with the packages FIRE [46] and FIESTA [47].

4 Parameter and field renormalization in fdh and dred

We now consider the counterterm contributions $\Gamma _{H A^\mu A^\nu }^{\mathrm{1LCT,a}}$ and $\Gamma _{H A^\mu A^\nu }^{\mathrm{2LCT,a}}$. They are given by diagrams exemplified in Fig. 2, where the counterterm insertions are generated by the usual multiplicative QCD renormalization of the couplings and fields present in Eq. (3b). In the following we present the values of the required $\beta$ functions and anomalous dimensions, which govern the renormalization constants.

Fig. 2

Sample one-loop counterterm diagrams originating from the renormalization of the couplings $\alpha _s, \alpha _e$, $\alpha _{4\epsilon }$, and of the gauge parameter $\xi$, respectively

4.1 $\beta$ functions

The renormalization of the couplings $\alpha _s, \alpha _e$, and $\alpha _{4\epsilon }$ is done by replacing the bare couplings with the renormalized ones. As renormalization scheme we choose a modified version of the $\overline{\text {MS}}$ scheme: like in Ref. [35] we treat the multiplicity $N_\epsilon$ of the $\epsilon$-scalars as an initially arbitrary quantity and subtract divergences of the form $(\frac{N_\epsilon }{\epsilon })^n$. As a consequence, the corresponding $\beta$ functions depend on $N_\epsilon$: $\overline{\beta }^{i}\equiv \mu ^2\frac{\mathrm{d}}{\mathrm{d}\mu ^2}(\frac{\alpha _i}{4\pi })= \overline{\beta }^{i}(\alpha _s,\alpha _e,\alpha _{4\epsilon },N_\epsilon )$, with $i = s, e, 4\epsilon$. They are given in Refs. [34, 35] and read

$$\begin{aligned} \overline{\beta }^{s}&= -\Big (\frac{\alpha _s}{4\pi }\Big )^2 \Bigg [C_A \left( \frac{11}{3}-\frac{N_\epsilon }{6}\right) -\frac{2}{3}N_F\Bigg ]\nonumber \\&\quad -\Big (\frac{\alpha _s}{4\pi }\Big )^3 \Bigg [C_A^2 \left( \frac{34}{3}-\frac{7}{3}N_\epsilon \right) -\frac{10}{3}C_A N_F-2 C_F N_F\Bigg ]\nonumber \\&\quad -\Big (\frac{\alpha _s}{4\pi }\Big )^2 \Big (\frac{\alpha _e}{4\pi }\Big ) \Bigg [C_F N_FN_\epsilon \Bigg ]+\mathcal {O}(\alpha ^4), \end{aligned}$$

(6a)

$$\begin{aligned} \overline{\beta }^{e}&= -\Big (\frac{\alpha _s}{4\pi }\Big ) \Big (\frac{\alpha _e}{4\pi }\Big )\,6\,C_F -\Big (\frac{\alpha _e}{4\pi }\Big )^2 \nonumber \\&\quad \times \Bigg [C_A (2-N_\epsilon )+C_F (-4+N_\epsilon )-N_F\Bigg ] +\mathcal {O}(\alpha ^3). \end{aligned}$$

(6b)

The renormalization of the quartic coupling $(\alpha _{4\epsilon })^{\alpha \beta \gamma \delta }_{abcd}$ is more complicated since the tree-level color structure, $f_{abe}f_{cde}$, is not preserved under renormalization [20]. In the case of an SU(3) gauge group one therefore has to introduce three quartic couplings, $\alpha _{4\epsilon ,i}$ with $i=1,2,3$, each of them related to one specific color structure in a basis of color space. Examples for such a basis are given e.g. in Refs. [29, 30].

In the present case of $H\rightarrow g g$ the renormalization constant for $\alpha _{4\epsilon }$ only appears in diagrams like the third of Fig. 2. Hence, only the following contracted $\beta$ function is needed:

$$\begin{aligned}&(\overline{\beta }^{4\epsilon })^{\alpha \beta \gamma \delta }_{abcd}\, \delta _{ab}\, {\tilde{g}}_{\alpha \beta } \nonumber \\&\quad = \left\{ \left( \frac{\alpha _s}{4\pi }\right) ^2 C_A^2 (9\!+\!6\,N_\epsilon ) \!+\!\left( \frac{\alpha _s}{4\pi }\right) \left( \frac{\alpha _{4\epsilon }}{4\pi }\right) C_A^2\,(1\!-N_\epsilon )\,12 \right. \nonumber \\&\qquad + \left( \frac{\alpha _e}{4\pi }\right) ^2 [C_A N_F (4-2\,N_\epsilon )+C_F N_F(-8-4\,N_\epsilon )]\nonumber \\&\qquad + \left( \frac{\alpha _e}{4\pi }\right) \left( \frac{\alpha _{4\epsilon }}{4\pi }\right) C_A N_F\,(1-N_\epsilon )(-4)\nonumber \\&\qquad \left. + \left( \frac{\alpha _{4\epsilon }}{4\pi }\right) ^2 C_A^2\,(1\!-N_\epsilon )(-7-2\,N_\epsilon ) \right\} \,\delta _{cd}\,\tilde{g}^{\gamma \delta }\!+\!\mathcal {O}(\alpha ^3). \end{aligned}$$

(7)

This result is obtained from a direct off-shell calculation. It agrees with a general result from [48].

4.2 Anomalous dimensions

For the off-shell calculation of $\Gamma _{HA^\mu A^\nu }$ also renormalization of the fields and of the gauge parameter $\xi$ is needed. The renormalization of $\xi$ is fixed by the requirement that the gauge fixing term does not renormalize: $\xi \rightarrow Z_{{\hat{A}}}\xi$. The anomalous dimensions $\gamma _i=\mu ^2\frac{\mathrm{d}}{\mathrm{d}\mu ^2}\text {ln}\,Z_i$ of gluon and $\epsilon$-scalar fields are obtained from a direct off-shell calculation of the respective two-loop self energies. Their values up to two-loop level read

$$\begin{aligned} \gamma _{\hat{A}}&= -\Big (\frac{\alpha _s}{4\pi }\Big )\Bigg [C_A\left( \frac{13}{6}-\frac{\xi }{2}-\frac{N_\epsilon }{6}\right) -\frac{2}{3}N_F\Bigg ] \nonumber \\&\quad - \Big (\frac{\alpha _s}{4\pi }\Big )^2 \Bigg [C_A^2 \left( \frac{59}{8}-\frac{11}{8}\xi -\frac{\xi ^2}{4}-\frac{15}{8}N_\epsilon \right) \nonumber \\&\quad - \frac{5}{2} C_A N_F-2\, C_F N_F\Bigg ]\nonumber \\&\quad - \Big (\frac{\alpha _s}{4\pi }\Big ) \Big (\frac{\alpha _e}{4\pi }\Big ) C_F N_F N_\epsilon +\mathcal {O}(\alpha ^3), \end{aligned}$$

(8a)

$$\begin{aligned} \gamma _{{\tilde{A}}}&= -\Big (\frac{\alpha _s}{4\pi }\Big )C_A(3-\xi ) -\Big (\frac{\alpha _e}{4\pi }\Big )[-N_F] \nonumber \\&\quad - \Big (\frac{\alpha _s}{4\pi }\Big )^2 \Bigg [C_A^2 \left( \frac{61}{6}\!-\!2\xi \!-\!\frac{\xi ^2}{4}-\frac{11}{12}N_\epsilon \right) -\frac{5}{3} C_A N_F\Bigg ] \nonumber \\&\quad - \Big (\frac{\alpha _s}{4\pi }\Big ) \Big (\frac{\alpha _e}{4\pi }\Big )[-5\,C_F N_F] \nonumber \\&\quad - \Big (\frac{\alpha _e}{4\pi }\Big )^2 \Bigg [C_A N_F\left( -1\!+\!\frac{N_\epsilon }{2}\right) \!+\!C_F N_F\left( 2+\frac{N_\epsilon }{2}\right) \Bigg ]\nonumber \\&\quad - \Big (\frac{\alpha _{4\epsilon }}{4\pi }\Big )^2 C_A^2\,(1-N_\epsilon )\,\frac{3}{4}\nonumber \\&\quad + \mathcal {O}(\alpha ^3). \end{aligned}$$

(8b)

Setting $N_\epsilon$ and $\alpha _e$ to zero in Eq. (8a) yields the well-known gluon anomalous dimension in cdr; see e.g. [49]. The value of $\gamma _{\tilde{A}}$ agrees with the general result for the anomalous dimension of a scalar field [48], confirming the point of view that $\epsilon$-scalars behave like ordinary scalar fields with multiplicity $N_\epsilon$.

5 Operator renormalization and mixing in fdh and dred

The second type of counterterm contributions, denoted by $\Gamma _{H A^\mu A^\nu }^{\mathrm{1LCT,b}}$ and $\Gamma _{H A^\mu A^\nu }^{\mathrm{2lCT,b}}$, originates from the necessary renormalization of the effective Lagrangian (4), equivalently of the operators $O_1$ and ${\tilde{O}}_1$. One major difficulty is that multiplicative renormalization of the parameters $\lambda$ and $\lambda _\epsilon$ is not sufficient since the operators mix with further operators. We will show that the full operator mixing involving gauge non-invariant operators has to be taken into account. The renormalization constants cannot be predicted from known QCD renormalization constants but need to be determined from an off-shell calculation. The general theory of operator mixing in gauge theories and the classification of gauge invariant and gauge non-invariant operators has been developed long ago [7, 8, 50].

In the following we briefly describe operator mixing in the much simpler case of cdr and then explain the cases of fdh and dred, which involve further operators.

5.1 Operators in cdr

In cdr, a useful basis of scalar dimension-4 operators, which is closed under renormalization, is given in Ref. [6]:

$$\begin{aligned} O_1&= -\frac{1}{4} \hat{F}^{\mu \nu }_a \hat{F}_{\mu \nu , a} \end{aligned}$$

(9a)

$$\begin{aligned} O_2&= 0, \end{aligned}$$

(9b)

(9c)

(9d)

$$\begin{aligned} O_5&= (\hat{D}^\mu \partial _\mu \overline{c})_a c_{a}. \end{aligned}$$

(9e)

Operator $O_{1}$ is gauge invariant and related to coupling renormalization; $O_2=m\overline{\psi }\psi$ in Ref. [6] and corresponds to the fermion mass renormalization; we set $m=0$. All other operators are constrained by BRS invariance and Slavnov–Taylor identities [7, 8]; operators $O_4$ and $O_5$ are not gauge invariant. The basis is chosen such that $O_{3},O_{4}$, and $O_{5}$ are related to field renormalization of $\psi$, $\hat{A}^\mu$, and c, respectively. In particular, the first two terms of $O_4$ are generated by applying the functional derivative

$$\begin{aligned} {\hat{A}}_a^\nu (x)\frac{\delta }{\delta {\hat{A}}_a^\nu (x)} \end{aligned}$$

(10)

on the gauge invariant part of the QCD action; the remaining term is then required by BRS invariance and the non-renormalization of the gauge fixing term.⁴

The operators renormalize as

$$\begin{aligned} O_i \rightarrow \sum _{j}\,Z_{ij}\,O_{j,\mathrm{bare}}, \end{aligned}$$

(11)

where $O_{j,\mathrm{bare}}$ arises from $O_j$ by replacing all parameters and fields by the respective bare quantities. Following an elegant proof in Ref. [6] the nontrivial cdr renormalization matrix $Z_{ij}$ can be written in the form

$$\begin{aligned} Z_{ij} = \delta _{ij}+\mathbbm {D}_i\,\text {ln}\mathbbm {Z}_{j}. \end{aligned}$$

(12)

Here, $\mathbbm {D}_i$ are derivatives with respect to parameters and $\mathbbm {Z}_j$ are combinations of ordinary QCD renormalization constants. As a result, in particular the renormalization of $Z_{11}$ is given by

$$\begin{aligned} Z_{11} = 1+\alpha _s\,\frac{\partial }{\partial \alpha _s}\ln Z_{\alpha _s}, \end{aligned}$$

(13)

with the multiplicative renormalization constant of $\alpha _s$, $Z_{\alpha _s}$. In this way the renormalization of the parameter $\lambda$ in the cdr version of $\mathcal{L}_{\text {eff}}$ is related to the renormalization of $\alpha _s$.

5.2 Operators in fdh and dred

In fdh and dred, the basis of operators needs to contain additional terms involving $\epsilon$-scalars. We use a basis constructed analogously to Eqs. (9) from gauge invariant operators and operators corresponding to field renormalization. Then there are two kinds of changes: there are modifications of the operators $O_{3}$ and $O_4$, and there are additional basis elements. The new basis operators correspond to the $\epsilon$-scalar kinetic term, ${\tilde{O}}_1$, to the new parameters $\alpha _e$ and $\alpha _{4\epsilon }$, ${\tilde{O}}_3$, and ${\tilde{O}}_{4\epsilon ,i}$, and to the field renormalization of ${\tilde{A}}^\mu$, ${\tilde{O}}_4$. The notation is chosen such that in all cases $O_j$ and ${\tilde{O}}_j$ have a similar structure:

$$\begin{aligned}&O_1= -\frac{1}{4} \hat{F}^{\mu \nu }_a \hat{F}_{\mu \nu , a} , \end{aligned}$$

(14a)

$$\begin{aligned}&O_2= 0, \end{aligned}$$

(14b)

(14c)

(14d)

$$\begin{aligned}&O_5= ({\hat{D}}^\mu \partial _\mu \overline{c}_a)c_a, \end{aligned}$$

(14e)

(14f)

(14g)

(14h)

(14i)

Since we consider massless QCD there is no $\epsilon$-scalar mass term. Like in Eq. (4), operators involving four $\epsilon$-scalars are not needed explicitly.

This set of operators differs in a crucial way from the cdr case. The difference between operators ${\tilde{O}}_1$ and ${\tilde{O}}_4$ is related to the total derivative $\Box {\tilde{A}}^\mu {\tilde{A}}_\mu$. Hence, the basis for space-time integrated operators (zero-momentum insertions) does not coincide with the one for non-integrated operators (non-vanishing momentum insertions). As discussed by Spiridonov in Ref. [6], in such a case his method cannot be used. Therefore, in fdh and dred it is not possible to derive complete results for the operator mixing analogous to Eqs. (12) and (13).

This implies two difficulties: First, the two-loop renormalization of ${\tilde{O}}_1$ and the corresponding parameter $\lambda _\epsilon$ cannot be obtained from a priori known two-loop QCD renormalization constants but need to be determined from an explicit two-loop off-shell calculation. Second, the off-shell Green functions get contributions from unphysical, gauge non-invariant operators, so the full operator mixing needs to be taken into account.

We have carried out the explicit one-loop calculations to obtain all required one-loop results for $Z_{1j}$ and $Z_{\tilde{1}j}$. The results are

$$\begin{aligned} \delta Z_{11}^{\mathrm{1L}}&=\left( \frac{\alpha _s}{4\pi } \right) \left[ \Big (-\frac{11}{3}+\frac{N_\epsilon }{6}\,\Big )C_A+\frac{2}{3}N_F\right] \frac{1}{\epsilon }, \end{aligned}$$

(15a)

$$\begin{aligned} \delta Z_{\tilde{1}1}^{\mathrm{1L}}&= 0, \end{aligned}$$

(15b)

$$\begin{aligned} \delta Z_{1\tilde{1}}^{\mathrm{1L}}&= 0, \end{aligned}$$

(15c)

$$\begin{aligned} \delta Z_{\tilde{1}\tilde{1}}^{\mathrm{1L}}&=\bigg [ \Big (\frac{\alpha _s}{4\pi }\Big )(-3)C_A +\Big (\frac{\alpha _e}{4\pi }\Big ) N_F -\Big (\frac{\alpha _{4\epsilon }}{4\pi } \Big )(1-N_\epsilon )C_A \bigg ]\frac{1}{\epsilon }, \end{aligned}$$

(15d)

$$\begin{aligned} \delta Z_{13}^{\mathrm{1L}}&= 0, \end{aligned}$$

(15e)

$$\begin{aligned} \delta Z_{\tilde{1}3}^{\mathrm{1L}}&= \left( \frac{\alpha _e}{4\pi } \right) \frac{N_\epsilon }{2}C_F\frac{1}{\epsilon }, \end{aligned}$$

(15f)

$$\begin{aligned} \delta Z_{14}^{\mathrm{1L}}&= \left( \frac{\alpha _s}{4\pi } \right) \frac{3}{4}C_A\frac{1}{\epsilon }, \end{aligned}$$

(15g)

$$\begin{aligned} \delta Z_{\tilde{1}4}^{\mathrm{1L}}&= 0, \end{aligned}$$

(15h)

$$\begin{aligned} \delta Z_{1\tilde{4}}^{\mathrm{1L}}&= \left( \frac{\alpha _s}{4\pi } \right) \Big (-\frac{3}{2}\Big )C_A\frac{1}{\epsilon }, \end{aligned}$$

(15i)

$$\begin{aligned} \delta Z_{\tilde{1}\tilde{4}}^{\mathrm{1L}}&= \left( \frac{\alpha _s}{4\pi } \right) \frac{1}{2}(3-\xi )C_A\frac{1}{\epsilon }, \end{aligned}$$

(15j)

$$\begin{aligned} \delta Z_{15}^{\mathrm{1L}}&= 0, \end{aligned}$$

(15k)

$$\begin{aligned} \delta Z_{\tilde{1}5}^{\mathrm{1L}}&= 0. \end{aligned}$$

(15l)

Renormalization constants involving operators ${\tilde{O}}_3$ or ${\tilde{O}}_{4\epsilon ,i}$ are not needed for the calculations in the present paper. The renormalization constants (15a)–(15d) agree with those given in Ref. [35]. The only gauge-dependent quantity is $Z_{\tilde{1}\tilde{4}}^{\mathrm{1L}}$. This is due to the fact that operator ${\tilde{O}}_4$ is related to the field renormalization of the $\epsilon$-scalars. In all other renormalization constants related to field renormalization the gauge-dependent parts incidentally cancel out.

With these results the bare effective Lagrangian can be written as

$$\begin{aligned} \mathcal{L}_{\text {eff}}^{\mathrm{bare}} = H \sum _{j}( \lambda \, Z_{1j}O_{j,\mathrm{bare}} + \lambda _\epsilon \, Z_{\tilde{1}j}O_{j,\mathrm{bare}}), \end{aligned}$$

(16)

where the sum runs over all operators in Eqs. (14). Sometimes it is useful to write this using multiplicative renormalization constants for $\lambda$ and $\lambda _\epsilon$ as

$$\begin{aligned} \mathcal{L}_{\text {eff}}^{\mathrm{bare}} = Z_{\lambda } \lambda H O_{1,\mathrm{bare}} + Z_{\lambda _\epsilon } \lambda _\epsilon H O_{\tilde{1},\mathrm{bare}} +\cdots , \end{aligned}$$

(17)

suppressing operators not present at tree level, such that $\lambda Z_{\lambda } = \lambda Z_{11} + \lambda _\epsilon Z_{\tilde{1}1}$ and similarly for $Z_{\lambda _\epsilon }$.

The one-loop counterterm effective Lagrangian involving the renormalization constants of Eqs. (15) is then given by

$$\begin{aligned} \mathcal{L}_{\text {eff}}^{\mathrm{1LCT}} = H\sum _{j}\left( \lambda \,\delta Z_{1j}^{\mathrm{1L}}O_{j} + \lambda _{\epsilon }\,\delta Z_{\tilde{1}j}^{\mathrm{1L}} O_{j}\right) . \end{aligned}$$

(18)

We have now all ingredients for the one-loop counterterm diagrams $\Gamma _{H A^\mu A^\nu }^{\mathrm{1LCT,b}}$ relevant for the computation of $H\rightarrow gg$, where the gluons are either D-dimensional gauge fields or $\epsilon$-scalars. These counterterm contributions arise from one-loop counterterm diagrams with one insertion of $\mathcal{L}_{\text {eff}}^{\mathrm{1LCT}}$. Sample diagrams are given in Fig. 3. They show insertions of operators $O_3$, $O_4$, ${\tilde{O}}_4$, and $O_5$. The Feynman rules for operator insertions are given in Appendix A.2.

Fig. 3

Sample one-loop counterterm diagrams originating from operators $O_3$, $O_4$, ${\tilde{O}}_4$, and $O_5$

The calculation shows that all these operators generate non-vanishing contributions to $\Gamma _{H A^\mu A^\nu }^{\mathrm{1LCT,b}}$. However, in the extraction of the form factors and two-loop renormalization constants to be discussed in the next section there are cancelations, and $O_4$ is the only new operator which contributes.

6 Two-loop renormalization constants of $\lambda$ and $\lambda _\epsilon$

Putting together the results from the previous three sections it is possible to calculate the two-loop renormalization constants $\delta Z^{\mathrm{2L}}_{\lambda }$ and $\delta Z^{\mathrm{2L}}_{\lambda _{\epsilon }}$ appearing in Eq. (17). They can be obtained from a complete off-shell two-loop calculation and the requirement that the corresponding Green functions are UV finite after renormalization:

$$\begin{aligned}&\left[ \Gamma _{H A^\mu A^\nu }^{\mathrm{2L}} +\Gamma _{H A^\mu A^\nu }^{\mathrm{1LCT,a}} +\Gamma _{H A^\mu A^\nu }^{\mathrm{2LCT,a}} +\Gamma _{H A^\mu A^\nu }^{\mathrm{1LCT,b}}\right. \nonumber \\&\quad \left. +\Gamma _{H A^\mu A^\nu }^{\mathrm{2LCT,b}}\right] _{\mathrm{UV div.}}^{\mathrm{off-shell}}= 0. \end{aligned}$$

(19)

All ingredients except the last term are computed in the previous sections, and Eq. (19) is then used to extract $\delta Z^{\mathrm{2L}}_{\lambda }$ and $\delta Z^{\mathrm{2L}}_{\lambda _{\epsilon }}$. The result for $\delta Z^{\mathrm{2L}}_{\lambda }$ is

$$\begin{aligned} \delta Z^{\mathrm{2L}}_{\lambda }&= \Big (\frac{\alpha _s}{4\pi }\Big )^2 \Bigg \{ C_A^2 \Bigg [ \frac{\frac{121}{9}-\frac{11}{9}N_\epsilon +\frac{N_\epsilon ^2}{36}}{\epsilon ^2} +\frac{-\frac{34}{3}+\frac{7}{3}N_\epsilon }{\epsilon } \Bigg ] \nonumber \\&\quad + C_A N_F \Bigg [ \frac{-\frac{44}{9}+\frac{2}{9}N_\epsilon }{\epsilon ^2} \!+\!\frac{10}{3\epsilon }\!\Bigg ] \!+\!C_F N_F\frac{2}{\epsilon }+\!N_F^2\frac{4}{9 \epsilon ^2}\Bigg \}\nonumber \\&\quad + \Big (\frac{\alpha _s}{4\pi }\Big ) \Big (\frac{\alpha _e}{4\pi }\Big ) C_F N_F\frac{\left( -1-\frac{\lambda _{\epsilon }}{\lambda }\right) N_\epsilon }{2 \epsilon }. \end{aligned}$$

(20)

Since the off-shell calculations have been done numerically with the help of FIESTA [47] the analytical expressions have been obtained by rounding to a least common denominator. The numerical uncertainty is less than $\frac{1}{72}$ for the terms of the order $\mathcal {O}(\epsilon ^{-2})$ and $\frac{1}{6}$ for the terms of the order $\mathcal {O}(\epsilon ^{-1})$.

The result (20) is not new; it agrees with Ref. [35], where it has been obtained using Spiridonov’s method. The recalculation serves as a test of the setup and the results given in the previous sections. At the same time a comparison with Ref. [35] confirms that Eq. (20) is actually exactly correct, in spite of numerical uncertainties.

In the same way, we obtain the renormalization constant $\delta Z^{\mathrm{2L}}_{\lambda _{\epsilon }}$:

$$\begin{aligned}&\delta Z^{\mathrm{2L}}_{\lambda _{\epsilon }} = \Big (\frac{\alpha _s}{4\pi }\Big )^2\Bigg \{ C_A^2 \Bigg [ \frac{\frac{49}{4}+\frac{5}{4}N_\epsilon }{\epsilon ^2} +\frac{-\frac{113}{24}+\frac{71}{24}N_\epsilon +\frac{\lambda }{\lambda _{\epsilon }}\Big (2-\frac{N_\epsilon }{2}\Big )}{\epsilon } \Bigg ] \nonumber \\&\qquad + C_A N_F \Bigg [ -\frac{1}{\epsilon ^2} +\frac{\frac{5}{6}-2\frac{\lambda }{\lambda _{\epsilon }}}{\epsilon } \Bigg ] \Bigg \} \nonumber \\ \nonumber&\qquad + \Big (\frac{\alpha _s}{4\pi }\Big ) \Big (\frac{\alpha _e}{4\pi }\Big ) \Bigg \{ C_A N_F \Bigg [ -\frac{3}{\epsilon ^2} +\frac{\frac{3}{2}+3\frac{\lambda }{\lambda _{\epsilon }}}{\epsilon } \Bigg ]\\&\qquad + C_F N_F \Bigg [ -\frac{3}{\epsilon ^2} +\frac{\frac{5}{2}-3\frac{\lambda }{\lambda _{\epsilon }}}{\epsilon } \Bigg ]\Bigg \} \nonumber \\ \nonumber&\qquad + \Big (\frac{\alpha _s}{4\pi }\Big ) \Big (\frac{\alpha _{4\epsilon }}{4\pi }\Big ) C_A^2\,(1-N_\epsilon )\Bigg [ \frac{6}{\epsilon ^2} +\frac{-4-3\frac{\lambda }{\lambda _{\epsilon }}}{\epsilon } \Bigg ] \\ \nonumber&\qquad + \Big (\frac{\alpha _e}{4\pi }\Big )^2\Bigg \{ C_A N_F\frac{-\frac{3}{2}+\frac{3}{4}N_\epsilon }{\epsilon } \\ \nonumber&\qquad + C_F N_F \Bigg [ -\frac{3N_\epsilon }{2\,\epsilon ^2} +\frac{3-\frac{7}{4}N_\epsilon }{\epsilon } \Bigg ] +\frac{N_F^2}{ \epsilon ^2} \Bigg \} \\ \nonumber&\qquad + \Big (\frac{\alpha _e}{4\pi }\Big ) \Big (\frac{\alpha _{4\epsilon }}{4\pi }\Big ) C_A N_F\,(1-N_\epsilon )\Bigg [ -\frac{2}{\epsilon ^2} +\frac{3}{2\epsilon } \Bigg ] \\&\qquad + \Big (\frac{\alpha _{4\epsilon }}{4\pi }\Big )^2 C_A^2\,(1-N_\epsilon ) \Bigg [ \frac{-\frac{5}{4}-N_\epsilon }{\epsilon ^2} +\frac{15}{8\epsilon } \Bigg ]. \end{aligned}$$

(21)

Compared to Eq. (20) this result is more complicated and includes all combinations of the three couplings $\alpha _s, \alpha _e$, and $\alpha _{4\epsilon }$. This result is new; as described in Sect. 5 it cannot be obtained using Spiridonov’s method. The numerical uncertainty is less than $\frac{1}{48}$ for all terms. A forthcoming comparison with a prediction of the infrared structure of $H\rightarrow \tilde{g}\tilde{g}$ will confirm that expression (21) is exactly correct [51].

7 UV renormalized form factors of gluons and $\epsilon$-scalars

Now that all renormalization constants are known it is possible to calculate the two-loop form factors of gluons and $\epsilon$-scalars in the fdh and dred scheme. A proper definition of the form factors and the corresponding projection operators can be found in Appendix A.1.

We present the results in two ways: First, we give results with independent couplings needed to determine the IR anomalous dimensions of gluons and $\epsilon$-scalars; second, we give simplified results, where all couplings are set equal. These can be viewed as the final results for the UV renormalized but IR regularized form factors. We give them including higher orders in the $\epsilon$-expansion.

7.1 Results for independent couplings

The UV renormalized but IR divergent form factor for $H\rightarrow {\hat{g}}{\hat{g}}$ in dred is given at the one-loop and two-loop level by

$$\begin{aligned}&\nonumber \bar{F}^{\mathrm{1L}}_{{\hat{g}}} (\alpha _s,\lambda _{\epsilon }/\lambda ,N_\epsilon ) \\ \nonumber&\quad = \Big (\frac{\alpha _s}{4\pi }\Big ) \Bigg \{C_A \Bigg [ -\frac{2}{\epsilon ^2} +\frac{-\frac{11}{3}+\frac{N_\epsilon }{6}}{\epsilon } +\frac{\pi ^2}{6}+\frac{\lambda _{\epsilon }}{\lambda }N_\epsilon \\&\nonumber \qquad + \epsilon \Big (-2+\frac{14}{3}\zeta (3)+3\frac{\lambda _{\epsilon }}{\lambda }N_\epsilon \Big ) \Bigg ] +\frac{2 N_F}{3 \epsilon }\Bigg \} \\&\qquad + \mathcal {O}(\epsilon ^2), \end{aligned}$$

(22)

$$\begin{aligned}&\nonumber \bar{F}^{\mathrm{2L}}_{{\hat{g}}} (\alpha _s,\alpha _e,\lambda _{\epsilon }/\lambda ,N_\epsilon ) \\ \nonumber&\quad = \Big (\frac{\alpha _s}{4\pi }\Big )^2 \Bigg \{C_A^2 \Bigg [ \frac{2}{\epsilon ^4} +\frac{\frac{77}{6}-\frac{7}{12}N_\epsilon }{\epsilon ^3} \\ \nonumber&\qquad + \frac{\frac{175}{18}-\frac{\pi ^2}{6}-N_\epsilon \Big (1+2\frac{\lambda _{\epsilon }}{\lambda }\Big )+\frac{N_\epsilon ^2}{36}}{\epsilon ^2} \\ \nonumber&\qquad + \frac{\!-\frac{238}{27}-\frac{11}{36}\pi ^2-\frac{25}{3}\zeta (3) \!+N_\epsilon \Big (\frac{49}{27}\!+\frac{\pi ^2}{72}\!-\frac{29}{3}\frac{\lambda _{\epsilon }}{\lambda }\Big ) \!+\frac{1}{6}\frac{\lambda _{\epsilon }}{\lambda }N_\epsilon ^2}{\epsilon } \Bigg ] \\ \nonumber&\qquad + C_A N_F \Bigg [ -\frac{7}{3 \epsilon ^3} +\frac{-\frac{13}{3}+\frac{2}{9}N_\epsilon }{\epsilon ^2} +\frac{\frac{64}{27}+\frac{\pi ^2}{18}+\frac{2}{3}\frac{\lambda _{\epsilon }}{\lambda }N_\epsilon }{\epsilon } \Bigg ]\\&\qquad + C_F N_F \frac{1}{\epsilon } +\frac{4 N_F^2}{9 \epsilon ^2}\Bigg \} -\Big (\frac{\alpha _s}{4\pi }\Big )\Big (\frac{\alpha _e}{4\pi }\Big ) C_F N_F \frac{N_\epsilon }{2\epsilon } +\mathcal {O}(\epsilon ^0). \end{aligned}$$

(23)

As mentioned in the beginning the ${\hat{g}}$ form factor in dred is identical to the gluon form factor in fdh, and Eq. (23) agrees with the result given in Ref. [35].

Since there are no external $\epsilon$-scalars in diagrams related to the gluon form factor internal $\epsilon$-scalars have to be part of a closed $\epsilon$-scalar loop or have to couple to a closed fermion loop. Hence, the effective coupling $\lambda _{\epsilon }$ always appears together with at least one power of $N_\epsilon$ in Eqs. (22) and (23).

The $\epsilon$-scalar form factor for $H\rightarrow \tilde{g}\tilde{g}$ in dred is given by

$$\begin{aligned}&\nonumber \bar{F}^{\mathrm{1L}}_{\tilde{g}} (\alpha _s,\alpha _e,\alpha _{4\epsilon },\lambda /\lambda _{\epsilon },N_\epsilon ) \\ \nonumber&\quad = \Big (\frac{\alpha _s}{4\pi }\Big ) C_A \Bigg [ -\frac{2}{\epsilon ^2} -\frac{4}{\epsilon } -2+\frac{\pi ^2}{6}+2\frac{\lambda }{\lambda _{\epsilon }} \\&\qquad \nonumber +\epsilon \Big (-4+\frac{\pi ^2}{12}+\frac{14}{3}\zeta (3)+4\frac{\lambda }{\lambda _{\epsilon }}\Big ) \Bigg ]\\&\qquad + \Big (\frac{\alpha _e}{4\pi }\Big )\frac{N_F}{\epsilon } +\Big (\frac{\alpha _{4\epsilon }}{4\pi }\Big ) C_A\,(1-N_\epsilon ) \nonumber \\&\qquad \times \Bigg [ 2 +\epsilon \Big (4-\frac{\pi ^2}{12} \Big ) \Bigg ] +\mathcal {O}(\epsilon ^2), \end{aligned}$$

(24)

$$\begin{aligned} \nonumber&\bar{F}^{\mathrm{2L}}_{\tilde{g}} (\alpha _s,\alpha _e,\alpha _{4\epsilon },\lambda /\lambda _{\epsilon },N_\epsilon ) \\ \nonumber&\quad = \Big (\frac{\alpha _s}{4\pi }\Big )^2 \Bigg \{C_A^2 \Bigg [ \frac{2}{\epsilon ^4} +\frac{\frac{27}{2}-\frac{N_\epsilon }{4}}{\epsilon ^3} +\frac{\frac{281}{18}-\frac{\pi ^2}{6}-\frac{N_\epsilon }{9}-4\frac{\lambda }{\lambda _{\epsilon }}}{\epsilon ^2} \\ \nonumber&\qquad + \frac{\frac{469}{216}-\frac{5}{12}\pi ^2-\frac{25}{3}\zeta (3)+N_\epsilon \Big (\frac{233}{216}+\frac{\pi ^2}{24}\Big )-16\frac{\lambda }{\lambda _{\epsilon }}}{\epsilon } \Bigg ] \\ \nonumber&\qquad + C_A N_F \Bigg [ -\frac{1}{\epsilon ^3}-\frac{7}{9 \epsilon ^2} +\frac{\frac{113}{54}+\frac{\pi ^2}{6}}{\epsilon } \Bigg ]\Bigg \} \\ \nonumber&\qquad + \Big (\frac{\alpha _s}{4\pi }\Big )\Big (\frac{\alpha _e}{4\pi }\Big ) \Bigg \{C_A N_F \Bigg [ -\frac{2}{\epsilon ^3}\!-\!\frac{4}{\epsilon ^2} \!+\!\frac{-2\!-\!\frac{\pi ^2}{6}+2\frac{\lambda }{\lambda _{\epsilon }}}{\epsilon } \Bigg ]\\&\nonumber \qquad + C_F N_F \Bigg [ -\frac{3}{\epsilon ^2}+\frac{5}{2 \epsilon } \Bigg ]\Bigg \} \\ \nonumber&\qquad + \Big (\frac{\alpha _s}{4\pi }\Big )\Big (\frac{\alpha _{4\epsilon }}{4\pi }\Big ) C_A^2\,(1-N_\epsilon )\Bigg [ -\frac{4}{\epsilon ^2} +\frac{-16+\frac{\pi ^2}{6}}{\epsilon } \Bigg ] \\ \nonumber&\qquad + \Big (\frac{\alpha _e}{4\pi }\Big )^2 \Bigg \{C_A N_F \Bigg [ \frac{-1+\frac{N_\epsilon }{2}}{\epsilon ^2} +\frac{\frac{1}{2}-\frac{N_\epsilon }{4}}{\epsilon } \Bigg ] \\ \nonumber&\qquad + C_F N_F \Bigg [ \frac{2-\frac{N_\epsilon }{2}}{\epsilon ^2} +\frac{-1-\frac{N_\epsilon }{4}}{\epsilon } \Bigg ] +\frac{N_F^2}{\epsilon ^2}\Bigg \} \\ \nonumber&\qquad + \Big (\frac{\alpha _e}{4\pi }\Big )\Big (\frac{\alpha _{4\epsilon }}{4\pi }\Big )C_A N_F\,(1-N_\epsilon )\, \frac{2}{\epsilon }\\&\qquad + \Big (\frac{\alpha _{4\epsilon }}{4\pi }\Big )^2 C_A^2 (1-N_\epsilon )\frac{-3}{8\epsilon } +\mathcal {O}(\epsilon ^0). \end{aligned}$$

(25)

Compared to Eqs. (22) and (23) the result with external $\epsilon$-scalars is more complicated and includes all combinations of the couplings $\alpha _s, \alpha _e$, and $\alpha _{4\epsilon }$. In this result, like in all previous results, the evanescent coupling $\alpha _e$ appears always together with at least one power of $N_F$ and the quartic coupling $\alpha _{4\epsilon }$ is always accompanied by a factor $(1-N_\epsilon )$.

7.2 Results for equal couplings

During the renormalization process the couplings $\alpha _s$, $\alpha _e$, $\alpha _{4\epsilon }$, and $\lambda$, $\lambda _{\epsilon }$ have to be distinguished. After renormalization they can be set equal, giving a simpler form of the final result.⁵ The results for $N_\epsilon =2\epsilon$ at the one(two)-loop level up to order $\mathcal {O}(\epsilon ^4)$ ($\mathcal {O}(\epsilon ^2)$) then read

$$\begin{aligned} \nonumber \bar{F}^{\mathrm{1L}}_{{\hat{g}}}&= \Big (\frac{\alpha _s}{4\pi }\Big ) \Bigg \{ C_A \Bigg [ -\frac{2}{\epsilon ^2} -\frac{11}{3 \epsilon } +\frac{1}{3} +\frac{\pi ^2}{6} +\epsilon \frac{14}{3}\zeta (3) \\&\nonumber \quad +\epsilon ^2\frac{47}{720}\pi ^4+\epsilon ^3 \Big ( \frac{62}{5}\zeta (5) -\frac{7}{18}\pi ^2 \zeta (3) \Big ) \\&\quad +\epsilon ^4 \Big ( \frac{949}{60480}\pi ^6 -\frac{49}{9}\zeta (3)^2 \Big ) \Bigg ]+\frac{2 N_F}{3 \epsilon } \Bigg \} +\mathcal {O}(\epsilon ^5), \end{aligned}$$

(26)

$$\begin{aligned} \bar{F}^{\mathrm{2L}}_{{\hat{g}}}&= \Big (\frac{\alpha _s}{4\pi }\Big )^2 \Bigg \{ C_A^2\nonumber \\&\quad \times \Bigg [ \frac{2}{\epsilon ^4} +\frac{77}{6 \epsilon ^3} +\frac{ \frac{77}{9} -\frac{\pi ^2}{6} }{\epsilon ^2} +\frac{ -\frac{400}{27} -\frac{11}{36}\pi ^2 -\frac{25}{3}\zeta (3) }{\epsilon } \nonumber \\&\quad + \frac{5711}{162} +\frac{17}{9}\pi ^2 -33 \zeta (3) -\frac{7}{60}\pi ^4 \nonumber \\&\nonumber \quad + \epsilon \Bigg ( \frac{189767}{972} +\frac{65}{27}\pi ^2 -\frac{1058}{27}\zeta (3) -\frac{1111}{2160}\pi ^4 \nonumber \\&\nonumber \quad +\frac{71}{5}\zeta (5) +\frac{23}{18}\pi ^2 \zeta (3) \Bigg ) \\&\nonumber \quad + \epsilon ^2\Bigg ( \frac{4972715}{5832} -\frac{233}{324}\pi ^2 -\frac{26404}{81}\zeta (3) -\frac{307}{360}\pi ^4\nonumber \\&\nonumber \quad -\frac{341}{5}\zeta (5)+ \frac{257}{1680}\pi ^6 -\frac{11}{54}\pi ^2 \zeta (3) +\frac{901}{9}\zeta (3)^2 \Bigg ) \Bigg ] \\&\nonumber \quad + C_A N_F \Bigg [ -\frac{7}{3 \epsilon ^3} \!-\!\frac{13}{3 \epsilon ^2} \!+\!\frac{ \frac{76}{27}\! +\!\frac{\pi ^2}{18} }{\epsilon } -\frac{916}{81} \!-\!\frac{5}{18}\pi ^2 \!-\!2 \zeta (3) \\&\nonumber \quad + \epsilon \Bigg ( -\frac{14603}{243} -\frac{8}{27}\pi ^2 -\frac{604}{27}\zeta (3) -\frac{59}{1080}\pi ^4 \Bigg ) \\&\nonumber \quad + \epsilon ^2\Bigg ( -\frac{366023}{1458} +\frac{127}{162}\pi ^2 -\frac{4448}{81}\zeta (3) \\&\quad -\frac{257}{648}\pi ^4 -\frac{98}{5}\zeta (5) +\frac{61}{27}\pi ^2 \zeta (3) \Bigg ) \Bigg ] \nonumber \\&\nonumber \quad + C_F N_F \Bigg [ \frac{1}{\epsilon } -\frac{73}{6} +8 \zeta (3) \\&\quad + \epsilon \Bigg ( -\frac{2045}{36} +\frac{7}{18}\pi ^2 +\frac{92}{3}\zeta (3) +\frac{4}{27}\pi ^4 \Bigg ) \nonumber \\&\nonumber \quad + \epsilon ^2\Bigg ( -\frac{53269}{216} +\frac{263}{108}\pi ^2 +\frac{1232}{9}\zeta (3) +\frac{46}{81}\pi ^4 \\&\quad + 32 \zeta (5) -\frac{20}{9}\pi ^2 \zeta (3) \Bigg ) \Bigg ] + \frac{4 N_F^2}{9 \epsilon ^2} \Bigg \} +\mathcal {O}(\epsilon ^3), \end{aligned}$$

(27)

$$\begin{aligned} \nonumber \bar{F}^{\mathrm{1L}}_{\tilde{g}}&= \Big (\frac{\alpha _s}{4\pi }\Big )\Bigg \{ C_A \Bigg [ -\frac{2}{\epsilon ^2} -\frac{4}{\epsilon } +2 +\frac{\pi ^2}{6} +\epsilon \frac{14}{3}\zeta (3) \\&\, \nonumber \quad +\epsilon ^2\frac{47}{720}\pi ^4 +\epsilon ^3 \Big ( \frac{62}{5}\zeta (5) -\frac{7}{18}\pi ^2 \zeta (3) \Big ) \\&\quad +\epsilon ^4 \Big ( \frac{949}{60480}\pi ^6 -\frac{49}{9}\zeta (3)^2 \Big ) \Bigg ]+\frac{N_F}{\epsilon } \Bigg \} +\mathcal {O}(\epsilon ^5), \end{aligned}$$

(28)

$$\begin{aligned} \bar{F}^{\mathrm{2L}}_{\tilde{g}}&= \Big (\frac{\alpha _s}{4\pi }\Big )^2\Bigg \{ C_A^2 \Bigg [ \frac{2}{\epsilon ^4} +\frac{27}{2 \epsilon ^3} +\frac{ \frac{64}{9} -\frac{\pi ^2}{6} }{\epsilon ^2} \nonumber \\&\nonumber \quad \!+\! \frac{ -\frac{1211}{54} \!-\!\frac{\pi ^2}{4} -\frac{25}{3}\zeta (3) }{\epsilon } \!+\!\frac{6052}{81} \!+\!\frac{263}{108}\pi ^2 -\frac{323}{9}\zeta (3) \\&\quad -\frac{7}{60}\pi ^4 + \epsilon \Bigg ( \frac{263363}{972} +\frac{1489}{324}\pi ^2 -\frac{1655}{27}\zeta (3) \nonumber \\&\quad - \frac{67}{120}\pi ^4 +\frac{71}{5}\zeta (5) +\frac{23}{18}\pi ^2 \zeta (3) \Bigg ) \nonumber \\&\nonumber \quad + \epsilon ^2\Bigg ( \frac{6457043}{5832} \!+\!\frac{6803}{972}\pi ^2 \!-\!\frac{34459}{81}\zeta (3) \!-\!\frac{15221}{12960}\pi ^4\\&\nonumber \quad -\frac{235}{3}\zeta (5) + \frac{257}{1680}\pi ^6 -\frac{16}{27}\pi ^2 \zeta (3) +\frac{901}{9}\zeta (3)^2 \Bigg ) \Bigg ] \\&\nonumber \quad + C_A N_F \Bigg [ -\frac{3}{\epsilon ^3} -\frac{52}{9 \epsilon ^2} +\frac{151}{27 \epsilon } -\frac{1925}{162} -\frac{25}{54}\pi ^2 \\&\nonumber \quad -\frac{28}{9}\zeta (3) \!+\! \epsilon \Bigg ( -\frac{10538}{243} \!-\!\frac{46}{81}\pi ^2 \!-\!\frac{922}{27}\zeta (3) \!-\!\frac{61}{720}\pi ^4 \Bigg ) \\&\nonumber \quad + \epsilon ^2\Bigg ( -\frac{291065}{1458} +\frac{419}{486}\pi ^2 -\frac{8678}{81}\zeta (3) -\frac{3971}{6480}\pi ^4 \\&\nonumber \quad - \frac{382}{15}\zeta (5) +\frac{203}{54}\pi ^2 \zeta (3) \Bigg ) \Bigg ] \\&\nonumber \quad + C_F N_F \Bigg [ -\frac{1}{\epsilon ^2} +\frac{1}{2 \epsilon } -41 -\frac{\pi ^2}{3} +12 \zeta (3) \\&\nonumber \quad + \epsilon \Bigg ( -\frac{669}{4} -\frac{3}{2}\pi ^2 +\frac{196}{3}\zeta (3) +\frac{2}{9}\pi ^4 \Bigg ) \\&\nonumber \quad + \epsilon ^2\Bigg ( -\frac{4607}{8} -\frac{61}{12}\pi ^2 +\frac{868}{3}\zeta (3) +\frac{67}{60}\pi ^4\\&\quad + 48 \zeta (5) -\frac{10}{3}\pi ^2 \zeta (3) \Bigg ) \Bigg ] + \frac{N_F^2}{\epsilon ^2} \Bigg \} +\mathcal {O}(\epsilon ^3). \end{aligned}$$

(29)

8 Conclusions

We have computed the $H\rightarrow gg$ amplitudes at the two-loop level in the fdh and dred scheme and presented the $\overline{\text {MS}}$ renormalized on-shell results up to the order $\epsilon ^2$. In dred, this involves two different amplitudes for $H\rightarrow {\hat{g}}{\hat{g}}$ and $H\rightarrow \tilde{g}\tilde{g}$ with external gluons/$\epsilon$-scalars. The computation is motivated because it contains key elements which constitute important building blocks for further computations, and because it is essential for the complete understanding of the infrared divergence structure of fdh and dred amplitudes.

The renormalization procedure has been described in detail. It is less trivial than in many QCD calculations in cdr, since not only the strong coupling needs to be renormalized but also evanescent couplings of the $\epsilon$-scalar. The computation provides a further example of the well-known fact that regardless of whether fdh or dred is used, the evanescent couplings have to be renormalized independently.

Further, the renormalization of the effective dimension-5 operators involves mixing with new, $\epsilon$-scalar dependent operators. A suitable basis of operators has been provided. One unavoidable fact is that the extended operator space contains operators which are total derivatives. As a result the required operator mixing renormalization constants cannot be obtained in the same elegant way of Ref. [6] as in cdr. Instead, they had to be obtained from explicit one- and two-loop off-shell calculations.

The results for the UV renormalized but infrared divergent form factors can also be used to complete the study of the general infrared divergence structure of two-loop amplitudes in fdh and dred, begun in Ref. [34, 35]. From general principles it is known that all infrared divergences can be expressed in terms of cusp and parton anomalous dimensions. The results of the present paper allow one to extract the final missing two-loop anomalous dimension for external $\epsilon$-scalars. This extraction, together with further checks and results, will be presented in a forthcoming paper [51], where the infrared structure will also be investigated by a SCET approach.

Appendix A

1.1 A.1 Projectors and form factors of gluons and $\epsilon$-scalars

According to its Lorentz structure the on-shell Green function $\Gamma _{H{\hat{A}}^\mu {\hat{A}}^\nu }^{\mathrm{on}{\text {-}}\mathrm{shell}}$ can be represented as

$$\begin{aligned} \Gamma _{H{\hat{A}}^\mu {\hat{A}}^\nu }^{\mathrm{on}{\text {-}}\mathrm{shell}}&= a\,(p\cdot r)\,{\hat{g}}^{\mu \nu }+ b\,p^\nu r^\mu + c\,p^\mu r^\nu \nonumber \\&\quad + d\,p^\mu p^\nu + e\,r^\mu r^\nu , \end{aligned}$$

(30)

where the coefficients $a\ldots e$ are momentum-dependent quantities, and coefficient a is the gluon form factor. Due to QCD Ward-identities the relation $a=-b$ holds; see e.g. Ref. [1]. Accordingly, the on-shell Green function $\Gamma _{H{\tilde{A}}^\mu {\tilde{A}}^\nu }^{\mathrm{on}{\text {-}}\mathrm{shell}}$ with external $\epsilon$-scalars can be represented as

$$\begin{aligned} \Gamma _{{H\tilde{A}^{\mu } \tilde{A}^{\nu } }}^{\mathrm{on}{\text {-}}\mathrm{shell}} = f( {p \cdot r} )\tilde{g}^{{\mu \nu }}, \end{aligned}$$

(31)

where we refer to f as $\epsilon$-scalar form factor. All coefficients of the covariant decomposition can be extracted with appropriate projection operators, which are given below.

In the off-shell case the UV divergence structure of $\Gamma _{H{\hat{A}}^\mu {\hat{A}}^\nu }$ can be represented in a more specific way as

$$\begin{aligned} \Gamma _{H{\hat{A}}^\mu {\hat{A}}^\nu }\Big |^{\mathrm{off}{\text {-}}\mathrm{shell}}_{\mathrm{UV div.}}&= \left[ A+A'\,\frac{p^2+r^2}{(p\cdot r)}\right] (p\cdot r)\,{\hat{g}}^{\mu \nu } \nonumber \\&\quad + B\,p^\nu r^\mu \!+\! C\,p^\mu r^\nu \!+\! D\,p^\mu p^\nu \!+\! E\,r^\mu r^\nu , \end{aligned}$$

(32)

where the coefficients $A\dots E$ are now momentum-independent. Since these divergences can be absorbed by counterterms corresponding to operators $O_1$ and $O_4$ the relation $A=-B$ again holds; see e.g. the Feynman rules (35) and (38). Due to this there are two possibilities of extracting coefficient A, which corresponds to the desired renormalization constant $\delta Z^{\mathrm{2L}}_{\lambda }$: The first one is to extract the coefficient of $(p\cdot r)\,{\hat{g}}^{\mu \nu }$ and neglect terms $\propto p^2, r^2$; the second is to extract coefficient $-B$. We checked explicitly that the relations $a=-b$ and $A=-B$ hold throughout the paper.

Again, the covariant decomposition with external $\epsilon$-scalars is much simpler and reads

$$\begin{aligned} \Gamma _{H{\tilde{A}}^\mu {\tilde{A}}^\nu }\Big |^{\mathrm{off}{\text {-}}\mathrm{shell}}_{\mathrm{UV div.}} = \left[ F+F'\,\frac{p^2+r^2}{(p\cdot r)}\right] (p\cdot r)\,\tilde{g}^{\mu \nu }. \end{aligned}$$

(33)

The desired coefficient for the computation of $\delta Z^{\mathrm{2L}}_{\lambda _{\epsilon }}$ is F. Accordingly, we extract the coefficient of $(p\cdot r)\,\tilde{g}^{\mu \nu }$ and neglect terms $\propto p^2, r^2$.

The corresponding projection operators are

$$\begin{aligned} P^{\mu \nu }_{g,(p\cdot r){\hat{g}}^{\mu \nu }}&= \bigg \{ {\hat{g}}^{\mu \nu }[(p\cdot r)^2-p^2r^2]\nonumber \\&\quad - (p^\nu r^\mu +p^\mu r^\nu )(p\cdot r) \!+\! p^\mu p^\nu r^2\!+\!r^\mu r^\nu p^2\bigg \}\nonumber \\&\quad \times \frac{1}{(D-2)(p\cdot r)[(p\cdot r)^2-p^2r^2]}, \end{aligned}$$

(34a)

$$\begin{aligned} P^{\mu \nu }_{g,p^\nu r^\mu } \!&=\!\bigg \{ {\hat{g}}^{\mu \nu }\,(p\cdot r)[p^2 r^2-(p\cdot r)^2]+ p^\nu r^\mu [(p\cdot r)^2\nonumber \\&\quad +p^2 r^2 (D-2)] +p^\mu r^\nu \,(p\cdot r)^2\,(D-1)\nonumber \\&\quad + (p^\mu p^\nu r^2+r^\mu r^\nu p^2)(p\cdot r)(1-D)\bigg \} \nonumber \\&\quad \times \frac{1}{(D-2)[(p\cdot r)^2-p^2r^2]^2}, \end{aligned}$$

(34b)

$$\begin{aligned} P^{\mu \nu }_{\tilde{g},(p\cdot r){\tilde{g}}^{\mu \nu }}&= \frac{{\tilde{g}}^{\mu \nu }}{N_\epsilon (p\cdot r)}. \end{aligned}$$

(34c)

1.2 A.2 Feynman rules

In the following we give the Feynman rules according to operators $O_1, {\tilde{O}}_1, O_4$, and ${\tilde{O}}_4$, which are needed for the renormalization in the fdh and dred scheme. Feynman rules including four $\epsilon$-scalars are not relevant in this paper and are not given explicitly.

• Feynman rules according to the Lagrangian term $\lambda H O_1$:

  

  (35)
  

  (36)
  

  (37)

• Feynman rules according to the Lagrangian term $\lambda _{\epsilon }H {\tilde{O}}_1$

  

  (38)
  

  (39)
  

  (40)

• Feynman rules according to the Lagrangian term $H O_4$:

  

  (41)
  

  (42)
  

  (43)
  

  (44)
  

  (45)

• Feynman rules according to the Lagrangian term $H {\tilde{O}}_4$:

  

  (46)
  

  (47)