Abstract
We review the dispersion-theoretical analysis of the electromagnetic form factors of the nucleon. We emphasize in particular the role of unitarity and analyticity in the construction of the isoscalar and isovector spectral functions. We present new results on the extraction of the nucleon radii, the electric and magnetic form factors and the extraction of \(\omega \)-meson couplings. All this is supplemented by a detailed calculation of the theoretical uncertainties, using bootstrap and Bayesian methods to pin down the statistical errors, while systematic errors are determined from variations of the spectral functions. We also discuss the physics of the time-like form factors and point out further issues to be addressed in this framework.
Similar content being viewed by others
1 Introduction
Nucleons and electrons are the constituents of everyday matter with nucleons accounting for essentially all of its mass. The mass of the nucleon as a bound state of quarks and gluons, on the other hand, arises from the complicated strong interaction dynamics of quarks and gluons in Quantum Chromodynamics (QCD) [1]. The electromagnetic (em) form factors of the nucleon describe the structure of the nucleon as seen by an electromagnetic probe. As such, they provide a window on strong interaction dynamics over a large range of momentum, for recent reviews see, e.g. Refs. [2, 3]. Moreover, they are an important ingredient in the description of a wide range of observables ranging from the Lamb shift in atomic physics to the strangeness content of the nucleon [4, 5]. At small momentum transfers, they are sensitive to the gross properties of the nucleon like the charge and magnetic moment as well as the radii. At large momentum transfer, in contrast, they probe the quark substructure of the nucleon as described by QCD.
A new twist was recently added to this picture by measurements of the proton charge radius in muonic hydrogen. The proton charge radius was first indirectly measured in the Nobel prize winning electron scattering experiments by Hofstadter et al. [6, 7]. While electron scattering was the method of choice to refine the proton radius in the decades following these pioneering experiments, the Lamb shift in electronic hydrogen and muonic hydrogen is also sensitive to the proton radius [8]. The electronic Lamb shift measurements as well as most electron scattering experiments gave the so-called large radius, \(r_E^P\simeq 0.88\,\)fm, which was also the value given by CODATA [9].Footnote 1 It then came as a true surprise to most researchers when the first measurement of the muonic hydrogen Lamb shift, which has a larger sensitivity to \(r_E^P\) because of the much larger muon mass, led to the so-called small radius, \(r_E^P= 0.84184(67)\,\)fm, differing by 5\(\sigma \) from the CODATA value [10]. At about the same time, a high-precision electron-proton scattering experiment performed at the Mainz Microtron (MAMI) reinforced the large radius [11]. This glaring discrepancy in such a fundamental quantity, which was believed to be understood since long, became known as the “proton radius puzzle”. It led to much experimental and theoretical activity dedicated to uncover its cause, either physics beyond the Standard Model, or more mundane reasons, such as an underestimation of the experimental uncertainties. Recent experiments on the electronic Lamb shift [12,13,14] and a novel measurement of electron-proton scattering at unprecedented small momentum transfer [15] now point to the latter reason. With the exception of Ref. [13], all of these new determinations of \(r_p\) consistently give a small proton radius. Consequently, the newest edition of CODATA lists the proton charge radius as \(r_E^p = 0.8414(19)\,\)fm [16]. A short review of the current status is given in Ref. [17]. The important role of dispersion theory in solving this “puzzle” will be discussed below.
This paper is structured as follows: In Sect. 2, we briefly review earlier dispersion-theoretical analyses of the electromagnetic nucleon from factors. The complete formalism to perform such type of analysis is spelled out in Sect. 3, where all basic definitions are given and the various contributions to the spectral functions, the central objects of the dispersive method, are discussed in detail. Furthermore, constraints on the nucleon form factors and two-photon corrections to the electron-proton scattering cross section are presented. Finally, we discuss in detail methods to determine the theoretical uncertainties, both the statistical and the systematical ones. In Sect. 4, we display the results of our new dispersion-theoretical analysis of the electromagnetic form factors in the space-like region, including novel determinations of the various radii, form factors as well as the \(\omega \)-meson couplings. Then, we consider the extension of the form factors in the time-like region and discuss the physics encoded in these. We end with a brief summary and an outlook in Sect. 5. In the appendices, we give further details on the extraction of neutron form factors from light nuclei as well as on the construction of the continuum contributions to the spectral functions. We also collect the various parameters of our best fit discussed in the main text.
2 Short history of dispersive analyses of the nucleon form factors
Here, we briefly review earlier work using dispersion theory to analyze the electromagnetic structure of the nucleon. To be more precise, we only consider investigations that include explicitly the two-pion continuum, which generates the \(\rho \)-meson in the isovector part of the spectral function in addition to a very important uncorrelated two-pion contribution as first discussed by Frazer and Fulco [18,19,20]. For other work on dispersion relations applied to the nucleon electromagnetic from factors, we refer the reader to the review [21].
The first groundbreaking work was done by the Karlsruhe group in 1976 [22]. Here, electron-proton (ep) cross section data supplemented by neutron form factor data from elastic and quasi-elastic electron-deuteron scattering were fitted. Besides the two-pion continuum, the spectral functions contained the \(\omega \)-meson plus additional isoscalar and isovector poles and normalization constants for the data sets. It should be noted that the ep data base was pruned in the sense that in case of inconsistencies between data sets, only one was retained. A dozen of fits with varying number of vector mesons poles and excluding various subsets of data were performed. The best fit (fit 8.2) featured 8 resonance parameters. Theoretical errors were estimated from the variations in the different fits. The resulting proton radii are tabulated in Table 1 and the neutron radii in Table 2. The neutron magnetic radius could not be determined very precisely at that time. Also notable were the sizable \(\phi NN\) couplings, where N denotes the nucleon, at odd with expectations from the OZI rule [23,24,25].
In 1995, the Bonn-Mainz group (MMD) rejuvenated the dispersion-theoretical approach to the nucleon electromagnetic form factors, as many new form factor results had become available and perturbative QCD had firmly established the behavior of the form factors at large momentum transfer [26]. Fits were performed to the existing form factor data basis of the Bochum group (updated from Refs. [27, 28]). The two-pion continuum was still based on the Karlsruhe-Helsinki pion-nucleon (\(\pi N\)) partial wave amplitudes \(f_\pm ^1(t)\), but the \(\rho \)-\(\omega \) mixing visible in the pion vector form factor was included for the first time. The best fits where obtained with three additional isovector poles and one additional isoscalar one (besides the \(\omega \) and the \(\phi \)). It was found that the onset of perturbative QCD was not seen in these data and the radii and vector meson couplings were consistent with the findings of the Karlsruhe group, see Table 1 and Table 2. Remarkably, these dispersive fits could not be made consistent with the then existing best value for \(r_E^p\) from ep scattering, \(r_E^p = (0.862\pm 0.012)\,\)fm [29]. Further, the large deviation in the OZI rule of the \(\phi \) couplings was confirmed. One year later, the sparse and not very precise existing data on the proton and neutron form factors in the time-like region were included, which revealed some inconsistencies in the time-like data basis for the neutron [30].
In view of new data on the proton and neutron form factors, in particular the first polarization transfer measurements at Jefferson Lab at few \(\hbox {GeV}^2\) squared momentum transfer [31, 32], the MMD work was updated, with a particular emphasis on the magnetic radius of the proton and the neutron in [33]. In this work, no error analysis was performed.
A significant improvement of the dispersion relation (DR) analysis was performed in Ref. [34] (BHM). Not only was the data basis enlarged, but also the description of the isoscalar spectral function was improved by including the \(K{\bar{K}}\) [35, 36] and the \(\pi \rho \) [37] continua. Furthermore, the \(2\pi \) continuum was updated in view of new data for the pion vector form factor [38]. All data from the space-like and the time-like regions were included in the fit. In these fits, besides the mentioned continua, the isoscalar spectral function featured the \(\omega (782)\), the \(\phi (1020)\)Footnote 2 and two poles, where as the \(2\pi \) continuum was supplemented by 5 effective poles. The uncertainties were calculated by large scale Monte Carlo samplings of all solution with a \(\chi ^2/\)dof in the range \([\chi ^2_{\mathrm{min}},\chi ^2_{\mathrm{min}} +1.04]\), where \(\chi ^2_{\mathrm{min}}\) refers to the best fit, corresponding to the \(1\sigma \) coincidence in the p-value. Different to all earlier fits, the neutron charge radius squared was not included as a constraint. Nonetheless, the extracted value of \((r_E^n)^2\) came out consistent with determinations from low energy atom-neutron scattering, see Table 2. In that paper, it was stated that the then accepted proton charge radius determined from the Lamb shift in electronic hydrogen, \(r_E^p = 0.88 \ldots 0.90\,\)fm, see Ref. [39] (and references therein), was inconsistent with the dispersion analysis of the electron scattering data, thus previewing what was later called the “proton radius puzzle”. The various radii came out consistent with earlier DR determinations, see Table 1 and Table 2. The same spectral functions were also used to extract the strength of two-photon corrections from the difference of data obtained by Rosenbluth separation and direct polarization transfer measurements [40]. In more detail, the form factors were extracted from the polarization transfer data and the difference in the description of the cross section data was entirely attributed to two-photon exchange. The so determined two-photon corrections came out comparable to direct calculations available in the literature, such as Refs. [41,42,43].
The high-precision data with \(Q^2 \le 1\,\) \(\hbox {GeV}^2\) that emerged from MAMI-C in 2010 [11, 44] called for a further update of the DR analysis. A first DR analysis in Ref. [45] utilized the same continua as BHM with the \(\omega \), the \(\phi \) and three/five effective isoscalar/isovector poles. The fit was done to the reconstructed MAMI cross section data in the one-photon approximation and simultaneously to the neutron form factor data. The uncertainties were obtained by varying the continua within reasonable ranges, namely the \(2\pi \) continuum by 5% and the \(K{\bar{K}}\) and \(\pi \rho \) continua by 20%. Again, a small proton charge radius, \(r_E^p =0.84\,\)fm, emerged and the other radii were also agreeing with early DR determinations, very different to the values quoted in [11].
This work was further improved in various aspects in Ref. [46]. Here, only proton data were investigated, but two-photon exchange corrections to the cross section were calculated and systematically included to the MAMI-C data, overcoming some inconsistencies in older approaches to this problem. Furthermore, to extract the statistical error due to the fitting procedure, a bootstrap approach was implemented. The spectral function was the same as in [45], but in addition, normalization constants for the various data sets were included (in total 31 new parameters) and the \(\chi ^2\) definition was augmented by the correlation matrix. This method constituted an improvement over earlier error determinations. The uncertainties in the radii were somewhat increased compared to earlier determinations, see Tables 1 and 2. The measured proton form factor ratio data for \(Q^2 <1\,\) \(\hbox {GeV}^2\) [47, 48] were not included in the fits but well described.
The work of Ref. [46] was extended by including neutron space-like form factor data as well as then existing data for the proton and the neutron form factors in the time-like region in [49]. The emphasis of this work was to understand the structures seen by the BaBar collaboration [50] in the region between threshold up to highest measured center-of-mass energies. These structures (and similar but less pronounced ones in \(e^+e^-\rightarrow n{\bar{n}}\)) could be explained by including a \(\phi (2170)\) meson as well as the \(N{\bar{\varDelta }}\) and \(\varDelta {\bar{\varDelta }}\) thresholds.
A significant improvement of the isovector spectral functions was reported in Ref. [51], based on the high-precision analysis of pion-nucleon scattering in the framework of the so-called Roy-Steiner equations [52]. This work also featured a detailed investigations of the corresponding isospin breaking effects in the pion form factor and the pion-nucleon P-wave amplitudes. The spectral functions given there serve as input for any DR analysis.
The most recent DR analysis in [53] was triggered by the PRad data [15], that measured ep cross sections at extreme forward angles corresponding to unprecedented small momentum transfers. In Ref. [53], fits to the PRad as well as the PRad and MAMI-C data were performed. The best fit to the combined data featured 5 isoscalar and 5 isovector poles, while the PRad data could be well described with 2+2 poles only. Again, the low-\(Q^2\) data for \(\mu _p G_E^p/G_M^p\) were not included in the fit but could be well described. The error analysis was improved compared to earlier DR work, the bootstrap method was used to determine the “statistical” error, while the “systematic” error was obtained from varying the number of effective poles, e.g. in the combined analysis the range from (2+2) to (7+7) isoscalar + isovector poles was covered. This led to the very precise proton radii given in Table 1. It was pointed out that the statistical error in the PRad analysis is underestimated, consistent with the earlier findings of Ref. [54]. In Ref. [53], no uncertainties on the proton form factors were given and no neutron data were analyzed. In this review, we will fill this gap and present detailed results on these topics. Also, a Bayesian approach to calculate the statistical errors will be presented and compared to the bootstrap method.
It is remarkable how little fluctuations in the extracted values of the nucleon em radii based on dispersion relations have appeared with time, despite a dramatic improvement in the data base and a number of theoretical improvements, related in particular to the isoscalar and the isovector spectral functions and the calculation of the theoretical uncertainties.
There has also been some related work in the so-called dispersively improved chiral perturbation theory, see [55,56,57,58]. The extracted proton charge radius is consistent with our result, but as noted in Ref. [59], this approach is subject to uncertainties in the \(\rho \)-region, different from the exact representation used in the papers discussed above.
We end this section by noting that the so-called strangeness form factors of the nucleon can also be calculated (under certain assumptions) using the DR results for the isoscalar vector mesons, see e.g. Refs. [36, 60,61,62]. For more details on this interesting topic, see the reviews [4, 5].
3 Formalism
3.1 Definitions
The electromagnetic (em) structure of the nucleon is determined by the matrix element of the vector current operator
for the light quarks \(q=(u,d,s)^T\) with the charges \({{\mathcal {Q}}}= \mathrm{diag}(2,-1,-1)/3\) (in terms of the elementary charge), sandwiched between nucleon states as depicted in Fig. 1.
The nucleon matrix element of the electromagnetic current \(j_\mu ^{\mathrm{em}}\)
Denoting a nucleon state with four-momentum p as \(|p\rangle \) (for ease of notation, we do not display the corresponding spin or helicity index), with the help of Lorentz and gauge invariance and assuming CP invariance, this matrix element can be expressed in terms of two form factors,
where m is the nucleon mass (which can be either the neutron, the proton or the isospin averaged mass) and \(t=(p'-p)^2\) the four-momentum transfer squared. For the analysis of data in the space-like region, it is convenient to use the variable \(Q^2=-t>0\). The scalar functions \(F_1(t)\) and \(F_2(t)\) are the Dirac and Pauli form factors, respectively. They are normalized at \(t=0\) as
with \(\kappa _p=1.793\) and \(\kappa _n=-1.913\) the anomalous magnetic moment of the proton and the neutron, respectively, in units of the nuclear magneton, \(\mu _N = e/(2m_p)\). The magnetic moment of the proton and the neutron is thus given by \(\mu _{p} = 1 + \kappa _{p}\) and \(\mu _n=\kappa _n\), respectively.
For the theoretical analysis, it is often convenient to work in the isospin basis and to decompose the form factors into isoscalar (s) and isovector (v) parts,
where \(i = 1,2 \,\). The experimental data are usually given in terms of the Sachs form factors
where \(\tau = -t/(4 m^2)\). In the Breit frame, \(G_{E}\) and \(G_{M}\) may be interpreted as the Fourier transforms of the charge and magnetization distributions, respectively.
The nucleon root mean square radii (loosely called radii)
are defined via the low-t expansion of the form factors,
where F(t) is a generic form factor. In the case of the electric and Dirac form factors of the neutron, \(G_E^n\) and \(F_1^n\), the expansion starts with the term linear in t and the normalization factor F(0) is dropped. Note that the slopes of \(G_E^n\) and \(F_1^n\) are related via
with \(m_n\) the neutron mass. We remark that alternative information on the proton charge radius can be obtained from Lamb shift measurements in electronic as well as muonic hydrogen, see e.g. the reviews [63, 64].
In the space-like region with \(t<0\), the form factors are real valued quantities. This is different in the time-like region with \(t>0\). By their very definition, at the nucleon-antinucleon threshold, \(t_{\mathrm{thr}} = 4m^2\), they fulfill the relation
for both the proton and the neutron. In the physical region \(t>4m^2\) of \(e^+e^-\rightarrow {{\bar{N}}}N\), the FFs are complex valued quantities.
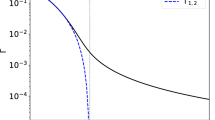
The form factor modulus \(|G_M^p(t)|\) for all possible momentum transfers based on a fit of space-like and time-like data around 1996 [30]. The colored area between the two dashed lines at \(t=0\) and \(t=4m^2\) is the unphysical region where the form factor cannot be observed
In Fig. 2, we sketch an exemplary form factor (here: \(G_M^p(t)\)) for all values of t. More precisely, the modulus of the form factor is depicted. For the space-like region, the threshold is located at \(t=0\), whereas the corresponding threshold in the time-like region is \(t=4m^2\). In between these two thresholds, the various vector meson poles (plus continua) build up the spectral function to be discussed in detail below. This region cannot be observed. We note that for the form factors in the time-like region, an additional complication arises due to the strong near-threshold nucleon-antinucleon interactions, which will be considered in Sect. 4.4.
3.2 Elementary cross section and polarization transfer
The form factors (FFs) can not be measured directly but are encoded in observables related to electron scattering. Consider for definiteness electron-proton (ep) scattering,
where the four-momenta \(p_i\) are subject to the constraint \(p_1+p_2 = p_3+p_4\). At first order in the electromagnetic fine-structure constant \(\alpha \), the Born-approximation, the differential cross section can be expressed through the Sachs FFs as
where
is the virtual photon polarization, \(\theta \) is the electron scattering angle in the laboratory frame, and \(({d\sigma }/{d\varOmega })_{\mathrm{Mott}}\) is the Mott cross section, which corresponds to scattering off a point-like particle,
where \(E_1\ (E_3)\) is the energy of the incoming (outgoing) electron, related via \(1/E_3= 1/E_1 +(2/m) \sin ^2(\theta /2)\). Two quantities out of the energies, momenta and angles suffice to determine this cross section and are related for such an elastic process. Specifically, in the laboratory frame with the initial nucleon at rest and neglecting the electron mass, we can write
In experiment, the differential cross section is usually given for a fixed total energy as a function of the scattering angle, so that a small scattering angle corresponds to a small momentum transfer. This is exactly the reason why a precise determination of the em radii is so difficult. At large momentum transfer, the contribution from the magnetic FF dominates the cross section. The contribution from the electric and the magnetic form factor can be read off form the reduced cross section \(\sigma _R\) defined in Eq. (11). The reduced cross section \(\sigma _R\) depends linearly on \(\epsilon \) for a given \(Q^2\), with slope \(G_E(Q^2)\) and intercept \(\tau G_M^2(Q^2)\). This is called the Rosenbluth separation [65]. Two-photon corrections to this cross section will be discussed in Sect. 3.11. Also, to investigate the neutron FFs, one measures electron scattering of a light nucleus like deuterium or \(^3\)He. This requires, however, some accurate few-body technique to disentangle the neutron contribution from the scattering cross section, as discussed briefly in App. A.
In early ep scattering experiments, it was found that the form factors could be well approximated by the dipole form, \(G_{\mathrm{dip}}(Q^2)\),
with \(G_E^n(Q^2)=0\) in this approximation. Employing these dipole FFs in the integrated cross section Eq. (11) defines the so-called dipole cross section, \(\sigma _{\mathrm{dip}}\). Often, the form factors or the measured cross sections are given relative to \(G_{\mathrm{dip}}(Q^2)\) and \(\sigma _{\mathrm{dip}}\), respectively.
A method to directly measure the form factor ratio \(G_E/G_M\) in polarized electron scattering off the proton, \(\overrightarrow{e}p\rightarrow \overrightarrow{e}p\) (or similarly for scattering off the deuteron or \(^3\)He), has been proposed in Refs. [66, 67]. A simultaneous measurement of the two recoil polarizations (longitudinal, \(P_l\), and transverse, \(P_t\)) allows one to measure directly the ratio
While this only determines the form factor ratio (and not the individual FFs), many systematic uncertainties cancel out and make this observable an important benchmark for any theoretical form factor calculation.
Let us briefly discuss the determination of the form factors in the time-like region. They can be extracted from the cross section data \(e^+e^- \leftrightarrow {\bar{p}}p\) and \(e^+e^-\rightarrow {\bar{n}}n\) for the proton and the neutron, respectively. As only very few differential cross section data exist in the time-like region, a separation of \(G_E\) and \(G_M\) is often not possible and one either makes an assumption like e.g. \(G_E = G_M\) in the analysis of the data or one extracts the effective form factor \(|G_{\mathrm{eff}}|\), discussed below. For a review on the nucleon em form factors in the time-like region, see Ref. [2].
We now consider the process,
in more detail. It is convenient to choose the center-of-mass (CM) frame, i.e., \(p_{1,2} = (E,\pm k_e)\) and \(p_{3,4} = (E,\pm k_p)\). The photon momentum q then determines the center-of-mass energy by \(q^2 = (p_1+p_2)^2=t = E_{\mathrm{CM}}^2 = (2E)^2\). In the metric used here, time-like q implies positive \(q^2\). The three-momenta \(k_e,k_p\) appear in the phase-space factor \(\beta = k_p/k_e\), which in the limit of neglecting the electron mass yields
the velocity of the proton, and \(m_p\) is the proton mass. We denote the emission angle of the proton by \(\theta \). The differential cross section in the one-photon-exchange approximation then is
in terms of the electric and magnetic Sachs form factors and \(C(q^2)\) is the Sommerfeld-Gamow factor that accounts for the Coulomb interaction between the final-state particles
Integrating over the full angular distribution gives the total cross section
This defines the effective form factor \(G_{\mathrm{eff}}\)
For neutrons, the formulas are equivalent except for the Sommerfeld-Gamow factor which is not present in that case. Beyond the Coulomb final-state interactions, higher order QED corrections are usually neglected. For the time-reversed process, the phase space factor is inverted, yielding
Taking into account the angular dependence of \(p{\bar{p}}\) production, one can express the differential cross section via the angular asymmetry \(\mathcal {A}\), see Ref. [68],
with
This can be determined from the FF ratio \(R = |G_E/G_M|\).
3.3 Dispersion relations and spectral decomposition
Dispersion relations (DRs) are based on unitarity and analyticity. Here, DRs relate the real and imaginary parts of the electromagnetic nucleon form factors. Let F(t) be a generic symbol for any one of the four independent nucleon form factors. We write down an unsubtracted dispersion relation of the form
where \(t_0\) is the threshold of the lowest cut of F(t) (see below) and the \(i\epsilon \) defines the integral for values of t on the cut. The convergence of an unsubtracted dispersion relation for the form factors has been assumed. For proofs of such a representation in perturbation theory, see Ref. [69] (and references therein). One could also use a once-subtracted dispersion relation, since the normalization of the form factors at \(t=0\) is known. However, in what follows, we will only employ the unsubtracted form give in Eq. (26). Most importantly, by Eq. (26) the electromagnetic structure of the nucleon can be related to its absorptive behavior. In Fig. 3 we display the analytic structure underlying the dispersion integral in Eq. (26). The various ingredients (continuum cuts, vector meson poles) will be discussed in detail below.
Analytic structure of a generic form factor in the complex-t plane. Shown are the lowest continuum cut at \(t_0\) and a number of vector meson poles at positive t (crosses). The dispersion integral is calculated for the space-like value of t also shown by a cross
The imaginary part \(\mathrm{Im}\, F\) entering Eq. (26) can be obtained from a spectral decomposition [70, 71]. For this purpose, consider the electromagnetic current matrix element in the time-like region (\(t>0\)), which is related to the space-like region (\(t<0\)) via crossing symmetry. This matrix element is given by
where \(p_3\) and \(p_4\) are the momenta of the nucleon and antinucleon created by the current \(j_\mu ^{\mathrm{em}}\), respectively. The four-momentum transfer squared in the time-like region is \(t=(p_3+p_4)^2\).
Using the LSZ reduction formalism, the imaginary part of the form factors is obtained by inserting a complete set of intermediate states as [70, 71]
where \({{\mathcal {N}}}\) is a nucleon spinor normalization factor, Z is the nucleon wave function renormalization, and \({\bar{J}}_N (x) = J_N^\dagger (x) \gamma _0\) with \(J_N(x)\) a nucleon source. This decomposition is illustrated in Fig. 4. It relates the spectral function to on-shell matrix elements of other processes, as detailed below.
The spectral decomposition of the nucleon matrix element of the electromagnetic current \(j_\mu ^{\mathrm{em}}\). \(| n \rangle \) denotes an hadronic intermediate state
The states \(|n\rangle \) are asymptotic (observable) states of momentum \(p_n\). They carry the same quantum numbers as the current \(j^{\mathrm{em}}_\mu \):
of the current \(j^{\mathrm{em}}_\mu \). Here, I and J denote the isospin \(I=0,1\) and the angular momentum \(J=1\) of the photon, whereas G, P and C give the G-parity, parity and charge conjugation quantum number, respectively. Furthermore, these currents have zero net baryon number. Because of G-parity, states with an odd number of pions only contribute to the isoscalar part, while states with an even number contribute to the isovector part. For the isoscalar part the lowest mass states are:
and for the isovector part they are:
Associated with each intermediate state is a cut starting at the corresponding threshold in t and running to infinity. As a consequence, the spectral function \(\mathrm{Im}\, F(t)\) is different from zero along the cut from \(t_0\) to \(\infty \), with \(t_0 = 4 \, (9) \, M_\pi ^2\) for the isovector (isoscalar) case.
The spectral functions are the central quantities in the dispersion-theoretical approach. Using Eqs. (27,28), they can in principle be obtained from experimental data. In practice, this program can only be carried out for the lightest two-particle intermediate states.
The longest-range, and therefore at low momentum transfer most important continuum contribution comes from the \(2\pi \) intermediate state which contributes to the isovector form factors [72]. A novel and very precise calculation of this contribution has recently been performed in Ref. [51] including the state-of-the-art pion-nucleon scattering amplitudes from dispersion theory, as detailed below. In the isoscalar channel, the inclusion of the \(K{\bar{K}}\) [35, 36] and \(\rho \pi \) continua [37] was first introduced in Ref. [34] in the dispersive analysis of the em form factors. For recent work on the isoscalar spectral functions in baryon chiral perturbation theory with explicit vector mesons, that strengthens the findings of these earlier works, see Ref. [73]. These important ingredients are discussed in more detail below. Apart from the continua, there are also single vector-meson pole contributions. As will become clear in the following, the contributions from the continua and the poles are sometimes strongly intertwined, e.g. the \(\rho \)-meson pole is indeed generated as part of the \(2\pi \)-continuum, as known since long [18,19,20].
3.4 Two-pion continuum
Two-pion cut contribution to the isovector form factors, given in terms of the pion vector form factor \(F_\pi ^V\) (represented by A) and the \(\pi \pi \rightarrow {{\bar{N}}} N\) P-waves \(f^1_\pm \) (represented by B). Solid, dashed, and wiggly lines denote nucleons, pions, and the external photon, respectively, while the dash-dotted line indicates the cutting of particle propagators
In the isovector channel, the lowest continuum contribution is given by the two-pion exchange as depicted in Fig. 5. Therefore, the unitarity relations for the nucleon form factors reads [20]
with \(q_t = \sqrt{t/4-M_\pi ^2}\), \(F_\pi ^V(t)\) is the vector form factor of the pion and the \(f_\pm ^1(t)\) are the P-wave \(\pi \pi \rightarrow {{\bar{N}}} N\) partial waves in the t-channel. Watson’s theorem ensures that the left-hand side of the equations stays real, as long as the same \(\pi \pi \) phase shift is used in the calculation of the pion form factor and the \(\pi \pi \rightarrow {{\bar{N}}} N\) partial waves. Therefore, in the most recent determination of the two-pion continuum, the same three variants of the phase shift \(\delta ^1_1\) in the data fits for \(F_\pi ^V(t)\) were used as in the Roy-Steiner analysis of pion-nucleon scattering [52]. The full consistency among all ingredients entering the unitarity relation that was achieved in Ref. [51] was a key improvement over earlier calculations, and thus the representation of the two-pion continuum given there will be discussed in what follows.
It is important to discuss the range of validity of the \(2\pi \) approximation to the unitarity relation. Strictly speaking, the \(4\pi \) threshold opens at \(\sqrt{t}=4M_\pi =0.56\) GeV, but it is well known from phenomenology that the \(4\pi \) contribution is completely negligible below the \(\omega \pi \) threshold at \(\sqrt{t}=0.92\) GeV, see e.g. [74], and only becomes sizable once the \(\rho '\), \(\rho ''\) resonances are excited. This can also be understood from chiral perturbation theory, where the \(4\pi \) contribution appears first at three loop order [75]. For this reason, the two-pion cut contribution to the isovector form factors is considered up to \(\sqrt{t} \simeq \sqrt{50} M_\pi \simeq 1\,\)GeV.
Let us now discuss in more detail the various ingredients entering the Eqs. (32). We start with the vector (em) form factor of the pion. It is given by
The \(\pi \pi \) intermediate states produce the unitarity relation
with the \(\pi \pi \) P-wave phase shift \(\delta ^1_1\). Eq. (34) reflects Watson’s final-state theorem [76], which states that the phase of \(F_\pi ^V\) has to coincide with the \(\pi \pi \) scattering phase shift (up to multiple integers of \(\pi \)). Neglecting higher intermediate states unitarity determines \(F_\pi ^V(t)\) up to a polynomial P(t) in terms of the Omnès factor \(\varOmega ^1_1(t)\) [77]
In fact, the representation (35) provides a very efficient and accurate parameterization of the experimental data, up to the distortions due to \(\rho \)–\(\omega \) mixing. This isospin-violating effect can be included via a modification of \(F_\pi ^V(t)\),
with the \(\omega \) mass \(M_\omega \) and width \(\varGamma _\omega \). The parameters \(\alpha \) and \(\epsilon \), where \(\epsilon \) parameterizes the strength of the \(\omega \)-\(\rho \) mixing, are fit to recent form factor data, see Refs. [78,79,80], below \(\sqrt{t}=1\,\)GeV using the same \(\pi \pi \) phase shifts as in the RS analysis [52]. The latter has been determined from Roy and Roy-like equations by the Bern [81] and the Madrid-Cracow group [82]. To get a better handle on the uncertainty estimate for the final spectral functions from the pion vector FF, in Ref. [51] a variant of the Bernese phase shift was also considered. It includes effects from the \(\rho '\) and the \(\rho ''\) in an elastic approximation [83].
Next, we discuss the t-channel partial waves \(f_\pm ^1(t)\), given by [19]
with the t-channel scattering angle \(z_t=(s-u)/(4p_tq_t)\), the \(P_J\) are the Legendre polynomials, and the momenta are \(q_t\) and \(p_t = \sqrt{t/4-m^2}\). Further, the standard decomposition of the \(\pi N\) scattering amplitude \(T(\pi ^a(q)+N(p)\rightarrow \pi ^b(q')+N(p'))\) in the isospin limit has been used,
where a, b are isospin indices, the \(\tau ^a\) are isospin Pauli matrices, \(I=\pm \) refers to isoscalar/isovector amplitudes and \(s=(p+q)^2\), \(t=(p'-p)^2\), \(u=(p-q')^2\) are the Mandelstam variables subject to the constraint \(s+t+u = 2(m^2 + M_\pi ^2)\). The best way to determine the pion-nucleon scattering amplitudes are undoubtedly dispersion relations, as they allow for a systematic continuation from the physical region into the unphysical ones and further make best use of the existing scattering data. The most modern and accurate investigations are based on the Roy-Steiner (RS) equation analysis of the Bonn group, developed and performed in Refs. [84,85,86,87] (for earlier work by the Karlsruhe-Helsinki group, see e.g. Refs. [88, 89]). The RS equations, originally developed in [90, 91] (and references therein), are hyperbolic DR integrating along a hyperbola in the Mandelstam plane,
which have a number of advantages compared to other formulations (like e.g. fixed-t DR). They combine all physical regions, display an explicit \(s \leftrightarrow u\) crossing, require the absorptive parts only in regions where the corresponding partial wave expansions converge, and, further, a judicious choice of the parameter a allows to increase the range of convergence. The RS equations have a limited range of validity, \(\sqrt{s}\le \sqrt{s_m} = 1.38\,\)GeV and \(\sqrt{t}\le \sqrt{t_m} = 2.00\,\)GeV, where \(\sqrt{s_m},\sqrt{t_m}\) denotes the so-called matching point for the s- and t-channel partial waves, respectively. The required inputs to solve the RS equations are the S- and P-waves above the matching point, the higher partial waves (D-, F-, \(\ldots \)) and the inelasticities. An important constraint are the pion-nucleon scattering lengths deduced from pionic hydrogen and pionic deuterium [92] (for a recent update, see [93]). The output of the RS equations are the so-called subthreshold parameters, which allow one to reconstruct the scattering amplitude in the unphysical region, such as the \(f_\pm ^1(t)\) in the pseudophysical region required for the isovector spectral functions. Some basic definitions of the \(\pi N\) scattering amplitude in the unphysical region are given in App. B. It should also be mentioned that the results of the RS analysis were given with theoretical uncertainties, which to our knowledge has been the first time that a dispersive analysis of pion-nucleon scattering provided these, for details see [52].
In Ref. [51], the isospin-violating effects beyond the \(\rho \)-\(\omega \) mixing in the pion form factor where also worked out, leading to an improved representation of the unitarity relations, Eq. (32), namely
For a more detailed discussion of this representation, the reader is referred to Ref. [51].
Weighted isovector spectral functions for \(G_E^v(t)/t^2\) and \(G_M^v(t)/t^2\). The black dashed line gives our central solution, the gray band the uncertainty estimate, and the red dashed line the result if \(\rho \)–\(\omega \) mixing is turned off. The insets magnify the region around the \(\rho \) peak
Putting pieces together, the isovector spectral functions divided by \(t^2\) based on Eq. (40) are shown in Fig. 6. These nicely exhibit the \(\rho \)-resonance at \(\sqrt{t}=0.77\,\)GeV as well as a remarkable enhancement on the left shoulder of the resonance. This shows that the \(\rho \) is indeed generated by unitarity [18] and thus no explicit \(\rho \)-meson is required in the isovector spectral function. The visible enhancement on the left shoulder of the \(\rho \) can be traced back to the fact that the partial wave amplitudes \(f_\pm ^1(t)\) have a singularity on the second Riemann sheet [89] (originating from the projection of the nucleon pole terms in the invariant pion-nucleon scattering amplitudes) located at
very close to the physical threshold at \(t_0 = 4M_\pi ^2\). The isovector form factors inherit this singularity (on the second sheet) and the closeness to the physical threshold leads to the pronounced enhancement between \(\sqrt{t} = 0.3-0.6\,\)GeV shown in Fig. 6. This issue will be taken up below. The uncertainties displayed in Fig. 6 originate from three different sources: 1) the subthreshold parameters \(b_{00}^-\), \(b_{01}^-\), \(a_{00}^-\) and \(a_{01}^-\) (as defined in App. B), 2) the pion-pion phase shift \(\delta _1^1(t)\) and 3) the data for the pion form factor \(F_\pi ^V(t)\). In fact, the uncertainty of the subthreshold parameters from the RS analysis is in fact the dominating effect below 1 GeV. We note that the effect of the \(\rho \)-\(\omega \) mixing is small, as the comparison of the black and red dashed lines in Fig. 6 shows. Note also that this consistent inclusion of isospin-breaking effects in the pion em form factor and the \(\pi N\) partial waves constitutes a major achievement compared to earlier analyses. The two-pion continuum contribution to the isovector form factors is displayed below in Fig. 8 .
Based on the DR, Eq. (26), it is straightforward to derive sum rules for the normalizations and radii of the isovector form factors. These were first considered in Ref. [72] for the various nucleon radii, see also [51],
where \(\mu ^v=(1+\kappa _p-\kappa _n)/2\simeq 2.353\) is the isovector magnetic moment of the nucleon. Note that the sum rules for the radii remain unchanged if a once-subtracted dispersion relation is used instead of the unsubtracted one. Cutting the integrals at \(\varLambda = 2m\), one finds
It is remarkable that just using a simple \(\rho \)-exchange using e.g. a Breit-Wigner or a Gounaris-Sakurai form [94], the corresponding isovector radii would be sizeably underestimated (by about 40%), as inspection of Fig. 6 reveals. Thus, any dispersive analysis that does not include the full two-pion continuum but only the \(\rho \)-resonance in the isovector spectral function below 1 GeV will simply miss important physics. We will come back later to these sum rules.
3.5 Three-pion continuum
The lowest isoscalar continuum is given by three-pion exchange as depicted in Fig. 7. There, A refers to the \(\gamma \rightarrow 3\pi \) transition amplitude, that is given at low energies by the anomalous Wess-Zumino-Witten Lagrangian [95, 96] and B corresponds to the \(3\pi \rightarrow {\bar{N}}N\) amplitude. An analysis based on unitarity alone of this contribution does not exist, but it has been shown in chiral perturbation theory at leading [97] and subleading [98] orders, that there is no enhancement on the left wing of the \(\omega \) resonance. This argument is outlined in App. C. Thus, the usual inclusion of the \(\omega \) as a vector meson pole is justified. In case of the \(\phi \), the situation is, however, more complicated as discussed next.
Three-pion cut contribution to the isoscalar form factors, given in terms of the \(\gamma \rightarrow 3\pi \) (represented by A) and the \(3\pi \rightarrow {{\bar{N}}} N\) (represented by B) transition amplitudes. Solid, dashed, and wiggly lines denote nucleons, pions, and the external photon, respectively, while the dash-dotted line indicates the cutting of particle propagators
3.6 \(K{\bar{K}}\) continuum
The first important continuum contribution to the isoscalar spectral function is the one from \(K{\bar{K}}\) states, as evaluated in Refs. [35, 36] from an analytic continuation of KN scattering data. The \(K{\bar{K}}\) contribution to the imaginary part of the isocalar form factors is given by [35, 36]
where \(p_t=\sqrt{t/4-m^2}\) and \(q_t=\sqrt{t/4-M_K^2}\), with \(M_K\) the charged kaon mass. Further, \(F_K^V (t)\) is the kaon form factor, defined via
whereas the \({b_1^{1/2,\,\pm 1/2}}(t)\) are the \(J=1\) partial wave amplitudes for \(K{\bar{K}}\rightarrow N{\bar{N}}\) [35, 36]. Having determined these imaginary parts, the contribution of the \(K{\bar{K}}\)-continuum to the form factors is obtained from the dispersion relation Eq. (26).
The \({b_1^{1/2,\,1/2}}(t)\) and \({b_1^{1/2,\,-1/2}}(t)\) in the above equations are the kaon-nucleon partial wave amplitudes with total angular momentum \(J=1\) (for definitions, see App. D). For \(t \ge 4m^2\) the partial waves are bounded by unitarity,
In the unphysical region \(4M_K^2 \le t \le 4m^2\), however, they are not constrained by unitarity. In Ref. [35], the amplitudes \({b_1^{1/2,\,\pm 1/2}}(t)\) in the unphysical region have been determined from an analytic continuation of KN-scattering amplitudes. The contribution of the physical region \(t\ge 4m^2\) in the dispersion integral (26) is suppressed for small momentum transfers and bounded because of Eq. (47). Using the analytically continued amplitudes in the unphysical region and the unitarity bound in the physical region, the contribution of the \(K{\bar{K}}\) continuum can therefore be calculated. Strictly speaking this calculation provides an upper bound on the spectral function since one replaces the amplitudes and the form factor in Eqs. (44,45) by their absolute values.
The striking feature in the spectral function is a clear \(\phi \) resonance structure just above the \(K{\bar{K}}\) threshold. The resonance emerges in the partial wave amplitude \(b_1^{1/2,\,1/2}\) as well as in the kaon form factor \(F_K\). In contrast to the \(2\pi \) continuum, there is no strong enhancement on the left wing of the \(\phi \) resonance which sits directly at the \(K{\bar{K}}\) threshold. This can be understood from the fact that the pole on the second Riemann sheet at \(t_c = 3.7\,M_K^2\) is too far from the threshold to induce such an enhancement.
The resulting contribution to the nucleon form factors can be parameterized by a pole term at the \(\phi \) mass [34]:
with \(a_1^{K{\bar{K}}}=0.1054\) \(\hbox {GeV}^2\) and \(a_2^{K{\bar{K}}}=0.2284\) \(\hbox {GeV}^2\). As a consequence, the contribution of the \(K{\bar{K}}\) continuum to the electromagnetic nucleon form factors can conveniently be included in the analysis via Eq. (48). The form factor contributions from Eq. (48) are also shown in Fig. 8.
The continuum contributions to the nucleon form factors \(F_1\) (left panel) and \(F_2\) (right panel) in the space-like region. The contribution of the \(2\pi \) continuum to the isovector form factors is given by the solid line, while the contribution of the \(K{\bar{K}}\) and \(\rho \pi \) continua to the isoscalar form factors are given by the dash-dotted and dashed lines, respectively
3.7 \(\rho \pi \) continuum
Another important contribution to the isoscalar spectral function is the correlated \(\rho \pi \) exchange, that was investigated in the Bonn-Jülich nucleon-nucleon interaction model in Ref. [99]. Since in that work cancellations between \(\phi \)-exchange contribution and this correlated \(\pi \rho \)-exchange was found, the \(\rho \pi \) contribution to the isoscalar spectral function was worked out in Ref. [37]. This continuum contribution was evaluated in terms of a dispersion integral which in turn can be represented by an effective pole term for a fictitious \(\omega '\) meson with a mass \(M_{\omega '} = 1.12\) GeV [37]:
with \(a_1^{\rho \pi }=-1.01\) \(\hbox {GeV}^2\) and \(a_2^{\rho \pi }=-0.04\) \(\hbox {GeV}^2\). In the form factor analysis, one uses this effective pole instead of the full spectral function.
There is very little sensitivity in the dispersive fits to \(a_{2}^{\rho \pi }\), which can vary between \(-0.04\) and \(-0.4\) without affecting the outcome of the fit. If the \(\omega ^{\prime }\) pole is treated as a real resonance, the latter value is consistent with \(f_{\omega ^{\prime }}\sim 10\) for \(a_{1}^{\rho \pi }=-1.01\) if the coupling constants \(g^i_{\omega ^{\prime }NN}\) (\(i=1,2\)) from Ref. [37] are used as input (for a precise definition of these couplings, see Sect. 3.8).
In Fig. 8, we show the contribution of the \(2\pi \), \(K{\bar{K}}\), and \(\rho \pi \) continua to the electromagnetic nucleon form factors \(F_1\) and \(F_2\). The \(2\pi \) contributes to the isovector form factors while the \(K{\bar{K}}\) and \(\rho \pi \) continua contribute to the isoscalar form factors. The \(K{\bar{K}}\) and \(\rho \pi \) contributions have opposite sign and partially cancel each other. The dominant contribution to \(F_1^s\) comes from the \(\rho \pi \) continuum while for \(F_2^s\) the \(K{\bar{K}}\) contribution is larger. While the \(K{\bar{K}}\) and \(\rho \pi \) contributions can be represented by simple pole terms, the expressions for the \(2\pi \) continuum Eq. (40) are more complicated. This is related to the strong enhancement close to the \(2\pi \) threshold on the left wing of the \(\rho \) resonance discussed above. Finally, note that these continuum contributions enter as an independent input in the dispersive analysis. They are not fitted to cross section or form factor data.
3.8 Vector meson poles
In the most simple picture, the photon couples to the nucleon through vector mesons only (i.e. there is no direct photon-nucleon coupling), the so-called vector meson dominance (VMD) picture, see e.g. [100,101,102,103], as depicted in Fig. 9.
Vector meson dominance: The photon only couples through vector mesons, \(V=\rho ,\omega ,\phi ,\ldots \), to the nucleon
In this picture, the form factors take the simple form
with
and the couplings \(f_V\) can be deduced from the leptonic decay widths \(V\rightarrow e^+e^-\),
Also, we have identified \(s_1,s_2\) with the \(\omega , \phi \) and \(v_1\) with the \(\rho \). Each such vector meson comes with two couplings, the vector coupling \(a_1^V\) and the tensor coupling \(a_2^V\). One also employs the ratio of the tensor to the vector coupling, \(\kappa _V\), defined via
While for some resonances these couplings can be deduced from nucleon-nucleon scattering data, in the dispersive analysis, they are considered as fit parameters (with the exception of the \(\rho \), which is completely determined from the \(2\pi \) continuum). In the pure VMD picture with only \(\rho \) and \(\omega \) vector mesons contributing, one can relate the tensor-to-vector coupling ratio to the isovector and isoscalar anomalous magnetic moments of the nucleon, such that
However, extracting \(\kappa _\rho \) from the two-pion continuum leads to a larger value, \(\kappa _\rho \simeq 6\), consistent with extractions from nucleon-nucleon scattering, see e.g. the discussion in [26].
The corresponding imaginary part, i.e. the contribution to the spectral function for any vector meson reads:
As already discussed in Sect. 3.4, the \(\rho \)-meson is entirely generated by the two-pion continuum, so that an explicit \(\rho \) will never appear in the spectral function. Different to that, the lowest isoscalar mesons are the \(\omega \) and the \(\phi \), which are explicitly taken into account. As noted before, the related \(3\pi \) continuum has a very small nonresonant contribution, that can be safely neglected [97], see also App. C. Also, in the isoscalar region around 1 GeV, we consider the \(K{\bar{K}}\) and \(\rho \pi \) continua, which tend to cancel, and an additional residual \(\phi \) pole. Because of the complicated structure of the isoscalar spectral function around 1 GeV, it is no longer possible to extract useful \(\phi NN\) couplings, as it was done in earlier works, where one just had the \(\phi \)-pole in this region. The large \(\phi \)-couplings found in these earlier studies are clearly an artifact of the simplified isoscalar spectral function assumed in this region.
3.9 Structure of the spectral functions
As discussed above, the spectral function can at present only be obtained from unitarity arguments and experimental data for the lightest two-particle intermediate states (\(2\pi \) and \(K{\bar{K}}\)). Furthermore, the \(\rho \pi \) continuum contribution has been calculated in the Bonn-Jülich NN model.
The remaining contributions to the spectral function can be parameterized by vector meson poles. On the one hand, the lower mass poles can be identified with physical vector mesons such as the \(\omega \) and the \(\phi \). The higher mass poles on the other hand, are simply an effective way to parameterize higher mass strength in the spectral function. These effective poles at higher momentum transfers appear in the isoscalar (\(s_1,s_2,\ldots \)) and isovector channels (\(v_1,v_2,\ldots \)) It should be noted that we are dealing with an ill-posed problem here [104, 105], that means increasing the number of poles will from some point on not improve the description of the data. Therefore, the strategy has always been to use as few poles as possible. We come back to this issue in Sect. 3.12.
Putting all pieces together, the spectral function has the general structure
For the light isoscalar vector mesons, the residua in the pole terms can be related to their couplings. Only rough estimates exist for these: \(0.5\,\text{ GeV}^2<a_{1}^\omega < 1\,\text{ GeV}^2\), \(|a_{2}^\omega | < 0.5\,\text{ GeV}^2\) [106] and \(|a_{1}^\phi | < 2\,\text{ GeV}^2\), \(|a_{2}^\phi | < 1\,\text{ GeV}^2\) [37]. Note that the dominant vector \(\omega NN\) coupling is taken to be positive, consistent with one-boson-exchange in the nucleon-nucleon interaction. These ranges are used as constraints in the fits. The masses of the effective poles (\(s_1, s_2, \ldots , v_1,v_2, \ldots \)) are fitted to the data. We remark that to ensure the stability of the fit [105], we demand that the residua of the vector meson poles are bounded, \(|a_i^V| < 5\,\) \(\hbox {GeV}^2\) (this can also be considered a naturalness argument for the couplings), and that no effective poles with masses below 1 GeV appear. Furthermore, the masses of these effective poles should also be smaller than 5 GeV. We generally do not include widths for the effective poles. However, if one wants to mimic the imaginary part of the form factors in the time-like region, one can e.g. allow for a large width for the highest mass effective pole (see, e.g., Ref. [34]). A cartoon of the resulting (isoscalar and isovector) spectral functions is shown in Fig. 10. The vertical dashed line separates the phenomonologically well-constrained low-mass region from the effective vector meson poles at higher masses.
Cartoon of the isoscalar (left) and isovector (right) spectral function in terms of continua and (effective) vector meson poles. The vertical dashed line separates the well-constrained low-mass region from the high-mass region which is parameterized by effective poles
3.10 Constraints
The number of parameters in the spectral function (i.e. the various meson couplings \(a_i^V\) (\(i=1,2\)) and the masses of the effective poles) is reduced by enforcing various constraints.
The first set of constraints concerns the low-t behavior of the form factors. We enforce the correct normalization of the form factors as given in Eq. (3). The nucleon radii, however, are not included as a constraint. The exception to this is the squared neutron charge radius, which in some dispersive fits has been constrained to the value from low-energy neutron-atom scattering experiments [107, 108]. In the new fits discussed later, we implement this constraint using the high-precision determination of the neutron charge radius squared based on a chiral effective field theory analysis of electron-deuteron scattering [109, 110],
Another set of constraints arises at large momentum transfers. Perturbative QCD (pQCD) constrains the behavior of the nucleon electromagnetic form factors for large momentum transfer. Brodsky and Lepage [111] worked out the behavior for \(Q^2 \rightarrow \infty \),
with
in terms of the leading order QCD \(\beta \)-function. The anomalous dimension \(\gamma \approx 2\) depends weakly on the number of flavors, \(N_f\) [111]. The power behavior of the form factors at large \(Q^2\) can be easily understood from perturbative gluon exchange. In order to distribute the momentum transfer from the virtual photon to all three quarks in the nucleon, at least two massless gluons have to be exchanged. Since each of the gluons has a propagator \(\sim 1/Q^2\), the form factor has to fall off as \(1/Q^4\). In the case of \(F_2\), there is additional suppression by \(1/Q^2\) since a quark spin has to be flipped. The analytic continuation of the logarithm in Eq. (59) to time-like momentum transfers \(-Q^2\equiv t>0\) yields an additional term, \(\ln (-t/\varLambda ^2) = \ln (t/\varLambda ^2) - i\pi \) for \(t> \varLambda ^2\). Employing the Phragmen-Lindeloef theorem [89], it follows that the imaginary part has to vanish in the asymptotic limit. Taking these facts into account, the proton effective FF can be described for large time-like momentum transfer t by [112]
with the parameters from a fit to data prior to the 2013 measurement by the BaBar collaboration [50], given as \(A=72\,\) \(\hbox {GeV}^{-4}\) and \(\varLambda =0.52\,\)GeV.
The power behavior of the form factors leads to superconvergence relations of the form
with \(n=0\) for \(F_{1}\) and \(n=0,1\) for \(F_{2}\). These will be employed in the current analysis. In earlier DR analyses, modifications of the superconvergence relations were used including e.g. some higher order corrections. These should be, however, abandoned as the data are simply not sensitive to such corrections. We note that these superconvergence relations have already been used in Ref. [22], i.e. before the pQCD analysis.
Consequently, the number of effective poles in Eqs. (56, 57) is determined by the stability criterion mentioned before, that is, we take the minimum number of poles necessary to fit the data. The number of free parameters is then strongly reduced by the various constraints (unitarity, normalizations, superconvergence relations). These constraints can be implemented as what is called “hard constraints” or “soft constraints”, respectively. In the former case, one solves a system of algebraic equations relating the various parameters (couplings, masses), thus reducing the number of free parameters in the fit (for an explicit representation, see e.g. [26]). In the latter case, the \(\chi ^2\) is augmented by a Lagrange multiplier enforcing the corresponding constraints, see Sect. 3.12. Both options are viable and have been used.
It is straightforward to enumerate the number of fit parameters, which is given by the couplings and masses of the vector meson, \(N_V = 4 + 3N_s +3N_v\), with \(N_s (N_v)\) the number of the effective isoscalar (isovector) poles and the 4 represents the \(\omega \) and \(\phi \) couplings, minus the number of constraints, given by \(N_C = 4 + 6 + 1\), referring to the low-t, the high-t constraints and the neutron charge radius squared, respectively. If the latter in not included, \(N_C =10\). Putting pieces together, we have in total \(N_F = N_V - N_C = 3(N_s+N_v) - 7\) or \(N_F = 3(N_s+N_v) - 6\) fit parameters (including or excluding the \((r_E^n)^2\)-constraint).
3.11 Two-photon effects
The interest in two-photon corrections was triggered by the high precision measurements of the form factor ratio \(G_{E}/G_{M}\) using the polarization transfer method reported in Refs. [31, 32]. These results were found to be in striking disagreement with the world data based on the Rosenbluth separation. Even after removing inconsistencies from the Rosenbluth data base [113], this discrepancy remained, triggering a flurry of works on two-photon corrections beyond the work of Refs. [114,115,116], which neglected, however, the effects of the structure of the nucleon in the calculation of the two-photon box and crossed-box diagrams, see Fig. 11. These diagrams were calculated in various approaches, like in hadronic models, using generalized parton distributions or using dispersive methods, see e.g. Refs. [117, 118] for reviews and very recent work in Ref. [119]. Here, we concentrate on the work presented in [46], because the two-photon corrections given there are applied in the DR analyses since then.
The two-photon exchange box and crossed box graphs. The thin solid line denotes electron, the wiggly line photons, the soild line represents nucleons in the incoming and outgoing states and the fat grey line denotes the nucleon or the \(\varDelta \)-resonance in the intermediate state
The corrections to the electron-proton cross sections at order \(\alpha ^3\) are given by the interference of the one-photon-exchange amplitude \(\mathcal {M}_{1\gamma }\) and the amplitudes from vacuum polarization, vertex corrections, self-energy corrections and the two-photon-exchange amplitude \(\mathcal {M}_{2\gamma }\) and additionally the contribution from Bremsstrahlung. The main data set that are considered in the DR analyses already contains a set of calculations of such corrections by Maximon and Tjon [116]. This calculation contains improvements towards earlier works by Mo and Tsai [115] but still uses a soft-photon approximation, particularly relevant for the two-photon exchange (TPE) contribution. This contribution to the corrected cross section can be expressed through a factor of \((1 + \delta _{2\gamma })\) as
so that
We briefly discuss the soft-photon approximation by Maximon and Tjon since only the difference between any new evaluation of the \(2\gamma \) corrections and this approximation is required for the purification of the ep scattering data. Ref. [116] separates the IR-divergent part of the TPE-amplitude by considering the poles in the photon propagators, i.e. one vanishing photon momentum. The resulting factor is
where \(\lambda \) is an infinitesimal photon mass and \(E_1~(E_3)\) the incoming (outgoing) electron energy. The logarithmic infrared singularity in \(\lambda \) is canceled by a term in the Bremsstrahlung correction, so that the complete cross section is \(\lambda \)-independent. The same cancellation takes place, if both \(\delta _{2\gamma , \text {IR}}\) and the Bremsstrahlung correction are calculated in the older approximation scheme by Mo and Tsai.
In Ref. [46], the interference between the \(1\gamma \)-amplitude
and the \(2\gamma \)-amplitude
was calculated. In this notation, the metric tensor from the photon propagator has already been contracted. Then, \(\mathcal {M}_{1\gamma }\) is given in terms of the conventional lepton spinors u(p) and the elastic nucleon-vertex \(\varGamma ^\nu (q)\) from Eq. (2). The \(2\gamma \)-amplitude contains the lepton tensor
whereas the hadronic tensor for nucleon or \(\varDelta \) intermediate states are
respectively. Here, \(\varGamma _{\gamma \varDelta \rightarrow N}^{\mu \alpha }(p,k)\) is the transition vertex
in terms of the Raita-Schwinger spinor field \(\varPsi _{\mu }^{(a)}(p)\) [120]. Various parameterizations of this transition matrix element exist, see e.g. Refs. [121, 122]. The corresponding electric \(G_E\), magnetic \(G_M\) and Coulomb \(G_C\) transition form factors can be related to the helicity amplitudes measured in pion electroproduction off the nucleon, see e.g. Ref. [123]. Accounting for this momentum dependence also in the \(\varDelta N \gamma \) vertices in the box and crossed box diagrams was the main improvement in Ref. [46] compared to some earlier calculations. Further, in the denominator of the photon propagator for the pure nucleon graph, one includes an infinitesimal photon mass \(\lambda \)
to regulate the infrared divergences. The loop containing the \(\varDelta \) is not IR divergent because of the larger mass of the \(\varDelta \). The \(S_F\) and \(S_{\alpha \beta } \) in Eqs. (68,69) are the conventional spin-1/2 and spin-3/2 propagators, respectively. The calculation of the crossed box graph proceeds accordingly.
In Fig. 12, the \(\epsilon \)-dependence at \(Q^2\) = 3 \(\hbox {GeV}^2\) is shown, which allows for a comparison to previous calculations such as [42]. In this case, the dependence on the nucleon FF parameterization largely cancels out. The use of the pole fit parameterization from Ref. [42] indeed reproduces their result. Lowering the \(Q^2\)-value in the calculation decreases the nucleon-TPE correction.
Dependence of the TPE with nucleon intermediate state on the nucleon form factors at \(Q^2\) = 3 \(\hbox {GeV}^2\). The correction factor \(\delta _{2\gamma ,N}\) is calculated once with dipole Sachs FFs (green dashed line) and once with the simplified pole fit from Ref. [42] (red solid line). Displayed is the difference of the calculation in [46] to the soft-photon approximation by Maximon and Tjon [116]
Dependence of the TPE with \(\varDelta \) intermediate state on the nucleon form factors at \(Q^2\) = 3 \(\hbox {GeV}^2\) with the \(N\varDelta \gamma \)-vertex directly matched to helicity amplitudes from electroproduction of nucleon resonances. The red solid, green dashed and blue dotted lines refer to the calculation with the FFs from the dispersive approach, Sachs dipole FFs and Sachs monopole FFs, respectively. Note that the result based on monopole FFs is only shown because they have been used in some earlier analyses. For more details, see Ref. [46]
For the intermediate \(\varDelta \), the situation is different, one finds a stronger dependence on the FF parameterizations. In Fig. 13 the results of the calculation that employs the helicity amplitudes obtained from data on electroproduction of nucleon resonances [124] are displayed. These corrections can be parameterized conveniently by a set of FFs, determined in Ref. [123] and used in Ref. [125] for a similar calculation albeit without realistic NFFs. This form of the \(\gamma N\varDelta \)-vertex does not deviate significantly from recent data and is numerically well-treatable. These results are similar to the ones of Ref. [126], where different transition form factors are employed.
As stated before, the sum of \(\delta _{2\gamma , N}\) and \(\delta _{2\gamma , \varDelta }\) from Ref. [46] constitute the two-photon corrections employed in the DR analysis of the Bonn-Darmstadt group. Their effect on the high-precision data from Mainz [11] is displayed in Fig. 14. Note that the original data contain the McKinley-Feshbach approximation of the two-photon correction given by [127].
where Z is the nuclear charge (here, \(Z=1\)). As pointed out in Ref. [128], this approximation is only valid as \(Q^2\rightarrow 0\) and has the wrong sign for some kinematical regions. Thus, this contribution is subtracted from the data and the two-photon corrections from Ref. [46] are added. The differences are quite visible. The corrections from Ref. [46] will be also employed in the calculations presented in the next section. Nevertheless, an updated calculation of these corrections would be welcome.
The impact of TPE-corrections on the electron-proton scattering cross sections from Ref. [11]. From the original data, the McKinely-Feshbach approximation is subtracted and the corrections from Ref. [46] are added. Shown are the cross section data divided by that one calculated by dipole Sachs FFs to make the deviations clearer. Blue lines: McKinley-Feshbach–approximation, red crosses: TPE with intermediate nucleon states only, black crosses: TPE with intermediate nucleons and \(\varDelta \) resonances
3.12 Fit strategies and error analysis
In this section, we briefly describe how the fits of the spectral functions to data are performed and how the statistical and systematic errors can be determined.
First, we discuss the quality of the fits, which is measured in terms of the total (traditional) \(\chi ^2\),
where \(C_i\) are the cross section data at the points \(Q^2_i,\theta _i\) and \(C(Q^2_i,\theta _i,\mathbf{p}\,)\) are the cross sections for a given FF parameterization for the parameter values contained in \(\mathbf{p}\). Moreover, the \(n_k\) are normalization coefficients for the various data sets (labeled by the integer k), while \(\sigma _i\) and \(\nu _i\) are their statistical and systematical errors, respectively. A more refined definition of the \(\chi ^2\) is given by [46]
in terms of the covariance matrix \(V_{ij} = \sigma _i\sigma _j\delta _{ij} + \nu _i\nu _j\). This latter definition accounts for the correlation between the various fit parameters. A fit to form factor data uses the same definitions, except for the absence of the normalization factors.
One also considers the reduced \(\chi ^2\), which is given by:
with \(N_D\) the number of fitted data points and \(N_F\) the number of independent fit parameters, see Sect. 3.10.
As noted in Sect. 3.10 the various constraints on the form factors can be implemented algebraically (hard constraints) or by modifying the \(\chi ^2\) (soft constraints). The latter type of constraints are implemented as additive terms to the total \(\chi ^2\) in the following form
where \(\langle x\rangle \) is the desired value and p is a strength parameter, which regulates the steepness of the exponential well and helps to stabilize the fits [34, 129].
The bootstrap procedure exemplified on the example of the proton charge radius extraction from the PRad data. See text for more details
Prior distributions used for the various couplings and masses in the analysis of the PRad data. Upper/lower panel: Normal/uniform distribution
One method to estimate the fit (statistical) errors is the bootstrap procedure, see e.g. Ref. [130]. One simulates a large number of data sets compared to the number of data points by randomly varying the points in the original set within the given errors assuming their normal distribution. Let us consider the radius extraction. In that case, one fits to each of these data sets separately, extracts the radius from each fit and consider the distribution of these radius values, which is sometimes denoted as bootstrap distribution. The artificial data sets represent many real samples. Therefore, this radius distribution represents the probability distribution that one would get from fits to data from a high number of measurements. The precondition for using this method are independent and identically distributed data points which is fulfilled when the \(\chi ^2\) sum does not depend on the sequential order of the contributing points. For n simulated data sets, the errors thus scale with \(1/\sqrt{n}\). However, to get a more realistic uncertainty, we exclude one percent of the data points from the sample and can so determine the lowest and highest value of the extracted radius. The same procedure can, of course, also be applied to the full form factors. In Fig. 15, we again use the 71 PRad data points to show the bootstrap extraction of the proton charge radius and its statistical uncertainty based on 1000 samples. The extracted error thus reads (a similar plot is obtained for the magnetic radius) [53]
We note that the bootstrap error for \(r_M^p\) for the PRad data given in [53] is corrected here.
Another statistical tool to estimate the error intervals of our model parameters is the Bayesian approach, see e.g. Ref. [131] (and references therein). In contrast to the interpretation of probabilities in the classical (also called frequentist) approach, where the probability is the frequency of an event to occur over a large number of repeated trials, the Bayesian method uses probabilities to express the current state of knowledge about the unknown parameters, which allows one to estimate the uncertainty as a statement about the parameters. The key ingredients to a Bayesian analysis are the prior distribution, which quantifies what is known about the model parameters prior to data being observed, and the likelihood function, which describes information about the parameters contained in the data. The prior distribution and likelihood can be combined to derive the posterior distribution by means of Bayes’ theorem:
where “paras” denotes the parameters and P(a|b) is the conditional probability that a happens given b.
It is the main goal of a Bayesian statistical analysis to obtain the posterior distribution of the model parameters. The posterior distribution contains the total knowledge about the model parameters after the data have been observed. From a Bayesian perspective, any statistical inference of interest can be obtained through an appropriate analysis of the posterior distribution. For example, point estimates of parameters are commonly computed as the mean of the posterior distribution and interval estimates can be calculated by producing the end points of an interval that correspond with specified percentiles of the posterior distribution. A powerful and easy-to-implement method to access posterior distribution is Markov Chain Monte Carlo (MCMC) algorithm. A systematic illustration of Bayesian analysis applications can be found in Ref. [132].
As an example, we implement a Bayesian analysis for the fit to PRad data where the \(2s+2v\) configuration of the spectral function is used. The likelihood function is given by
with the \(\chi ^2\) objective function defined in Eq. (74). Here, \(\mathbf{p}\) contains the model parameters and \(D=\{d_i\}\) denotes the PRad data points, and N is a normalization constant. Two different prior distributions shown in Fig. 16 are considered to test the stability of the obtained statistical outputs from our Bayesian analysis. We apply a particular MCMC sampling algorithm called ParaMonte [133] to acquire a Monte Carlo sample from the posterior distribution. The obtained posteriors of the parameters \(m^V_1\) and \(a_1^\omega \) are taken as an example to show the equivalence of normal and uniform priors we used as shown in Fig. 17. The statistical estimates of form factor and radius errors from our Bayesian analysis are discussed in next section.
Posterior distributions of \(m_1^V\)(upper panel) and \(a_1^\omega \) (lower panel) from the Bayesian analysis of the fits to the PRad data. Blue/Red lines: Normal/uniform prior
Next, we discuss the extraction of the systematic uncertainties, which is always the most difficult task. Our strategy is similar to what was already done in Ref. [22], namely to vary the number of isoscalar and isovector poles around the values corresponding to the best solution, where the total \(\chi ^2\) does not change by more than 1%. An example of this is given in Table 3 taken from Ref. [53]. Here, only the PRad data [15] are considered. The best fit corresponds to 2 isoscalar and 2 isovector poles, so we can read off the systematic errors in this case as [53]
We note that while the absolute \(\chi ^2\) does not change, the reduced one worsens as the number of fit parameter increases. As expected, the systematic error is larger for the magnetic radius as at low \(Q^2\), the electric FF dominates. More detailed results will be given below.
4 Physics results
In this section, we display a number of physics results, in particular we discuss fits including proton polarization transfer and neutron form factor data, and present new uncertainty analyses, thus extending and deepening the work of Ref. [53]. We also discuss the inclusion of data for the time-like form factors and the related physics. First, however, we want to sharpen and validate our toolbox to pin down the errors on the example of the PRad data.
4.1 Detailed analysis of the PRad data
The PRad data [15] are given at two beam energies, \(E=1.1, 2.2\,\) GeV, covering squared momentum transfers in the range \(Q^2 = 2\cdot 10^{-4}-6\cdot 10^{-2}\,\) \(\hbox {GeV}^2\), in total 71 differential cross section data points. Using this data set, we will make a detailed comparison of the bootstrap and the Bayesian methods to extract the statistical uncertainty. The extraction of the systematic uncertainty for these data was already discussed in Sect. 3.12.
Before continuing, it is worth noting that from the proton data alone, the isospin of a given pole is not determined. One can, however, simply assign a given number of isoscalar and isovector poles besides the continuum contributions, which have a given isospin, as well as the \(\omega \) and \(\phi \) mesons. This ambiguity will be resolved once neutron data are also fitted, see Sect. 4.2.
We consider first the Bayesian analysis described in Sect. 3.12. We assume two sets of priors, the normal and the uniform distributions depicted in Fig. 16. In both cases, the constraints on the various couplings and masses discussed in Sect. 3.10 are already included. Note further that in case of the uniform distribution, the prior for the unknown mass \(m_1^v\) is biased towards smaller values. The resulting proton em radii are equal within 3 significant digits for these two different prior distributions, see Table 4. Note that the systematic errors of these data have already been discussed in Sect. 3.12.
Next, we compare the radius extraction from the Bayesian and the bootstrap method, which are shown in Fig. 18 for the proton charge radius.
Distributions of \(r_E^p\) from the PRad data using the bootstrap approach (left, orange points) and from the Bayesian method (right, blue points)
Electric (open panel) and magnetic (lower panel) form factor extracted from the PRad data with the uncertainties determined from the Bayesian method (normal prior distribution) (red area) and from the bootstrap approach (blue area). Both form factors are normalized to the dipole FF and systematic uncertainties are not shown
As can be read off from this figure and also seen in Table 4, the results are very similar, with the bootstrap having slightly larger errors, which is due to our conservative choice considering the 99% quantile. The resulting normalized form factors \(G_E(Q^2)/G_{\mathrm{dip}}(Q^2)\) and \(G_M(Q^2)/(\mu _p G_{\mathrm{dip}}(Q^2))\) as well as their uncertainties for the two methods are shown in Fig. 19. The differences are negligible. The form factor ratio \(\mu _p G_E^p/G_M^p\) measured below \(Q^2 =1\,\)GeV [47, 48] is also well described, as already displayed in Fig. 2 of Ref. [53]. Note also that the magnetic form factor does not display any bump-dip structure below \(Q^2<1\) \(\hbox {GeV}^2\) as found in the MAMI analysis [44].
Having shown the equivalence of both methods here, in what follows we will stick to the bootstrap procedure, which is easier to implement in case of large data sets with a larger number of fit parameters.
4.2 Fits to proton and neutron data
We are now in the position to analyze the full data set. To be more precise, for the proton we fit to the cross section data from PRad [15] and from MAMI-C [44] as well as to the polarization transfer data from Jefferson Lab [134,135,136,137] above \(Q^2 = 1\,\) \(\hbox {GeV}^2\) (note that the data from Refs. [31, 32] are updated in Refs. [134, 137], respectively, and thus do not appear in the data base) together with the neutron form factor world data base already used in [45]. The size of the data base and the \(Q^2\)-ranges we are fitting is provided in Table 5.
We also include the constraint on the neutron charge radius squared, updated to the latest value given in Eq. (58) from Ref. [109]. Ultimately, we need to reassess the neutron data base by performing chiral EFT analyses of electron scattering of the deuteron and (polarized) \(^3\)He. This, however, goes beyond the scope of the present work.
Before showing the results of the best fit and the corresponding statistical and systematic uncertainties, it is worth pointing out that we made extensive searches for solutions with altogther 36 combinations of isoscalar (is) and isovector (iv) poles, ranging from \(3+3\) to \(8+8\) is+iv poles, with the reduced \(\chi ^2\) varying by less than 5%, in most cases even by less than 1%. We notice that the fits with a larger number of is than iv poles turned out to be slightly better.
The best solution has \(6+4\) is+iv poles, and the fits to the ep cross section data with \(Q^2<1\,\) \(\hbox {GeV}^2\), the proton form factor ratio with \(Q^2>1\,\) \(\hbox {GeV}^2\), the electric form factor of the neutron and the magnetic form factor of the neutron are shown in Figs. 20, 21, 22, 23, respectively.
Best fit (solid red line ) to the ep cross section data from PRad (upper panel) and MAMI (lower panel) including the two-photon corrections discussed in Sect. 3.11. The red bands give the uncertainty due to the bootstrap procedure. Systematical uncertainties are not shown
Best fit to the proton form factor ratio data from JLab. Note that the blue data (also shown for \(Q^2<0.7\,\) \(\hbox {GeV}^2\) in the inset) are not fitted. For notations, see Fig. 20
Best fit to the neutron electric form factor data. For notations, see Fig. 20
Best fit to the neutron magnetic form factor data. For notations, see Fig. 20
The corresponding central values for the various vector mesons masses, vector meson couplings and the normalization constants of the MAMI and PRad data are collected in Table 6 in App. E. It is remarkable that while the isoscalar spectral functions requires a number of high mass effective poles, the effective isovector poles all have masses below 2.3 GeV. We note that the vector coupling of the residual \(\phi \) comes out small, consistent with expectations from the OZI rule. The tensor coupling is, however, quite large, but the next effective isoscalar pole has a comparable tensor coupling of opposite sign, see also the discussion in Sect. 4.3. We also note that the various normalization factors are deviating from one by less than 1%.
Let us now discuss the predictions of and physics related to these fits. First, we extract the various radii from these fits,
where the first error is statistical (based on the bootstrap procedure explained in Sect. 3.12) and the second one is systematic, based on the variations in the spectral functions discussed before. The values for the radii are completely consistent with earlier determination, cf. Tables 1,2, but with a much improved uncertainty estimation. Clearly, given the data set we fitted, the systematic uncertainty is largest for the neutron magnetic radius. The statistical uncertainty is small for all three radii.
It is also interesting to give the radii of the Dirac and Pauli from factors in the isospin basis, in particular for the comparison with lattice QCD results. The reason for this is that the contribution of the so-called disconnected diagrams to the isoscalar FFs, which are notoriously difficult to calculate. These radii are given by:
Similarly, the electric and magnetic radii in the isospin basis are (using the conventions given in Eqs. (6,7))
We note that the central values in Eq. (83) lead to the squared isovector radii, of \((1/2)(r_E^v)^2= 0.405\,\) \(\hbox {fm}^2\) and \(\mu ^v(r_M^v)^2 = 1.72\,\) \(\hbox {fm}^2\), which are perfectly consistent with the sum rule estimates in Eq. (43) but have, of course, much smaller uncertainties. It is also interesting to compare the values for the squared isovector radii with a recent state-of-the-art lattice QCD calculation at physical pion masses [138]. These are given by,
While the value of the isovector charge radius is consistent with ours, the lattice value for the isovector magnetic radius is smaller than ours, that is there is some tension. It remains to be seen what future lattice calculations will give.
As in earlier fits [46, 53], the data for the proton form factor ratio \(\mu _PG_E^p/G_M^p\) for \(Q^2<1\,\) \(\hbox {GeV}^2\), which do not participate in the fit, are well described, see the inset in Fig. 21. This points towards consistency between the two-photon corrected cross section data and the ratio data, that are not affected by such corrections. The situation is, however, different for larger momentum transfers. In Figs. 24,25 we display \(G_E^p(Q^2)\) and \(G_M^p(Q^2)\), that did not participate in the fits. Because the proton form factor ratio tends to zero at \(Q^2 \simeq 8\,\) \(\hbox {GeV}^2\), marked deviations from the dipole form are observed. Only at very large momentum transfer, the fall-off required by pQCD is observed. More precisely, we find that \(Q^4 F^{p,n}_1(Q^2)\) starts to level off beyond \(30\,\) \(\hbox {GeV}^2\), whereas that is not the case yet for \(Q^6 F^{p,n}_2(Q^2)\). Clearly, in this region of momentum transfer, more data are needed to pin down the form factors more precisely and to eventually see the onset of perturbative QCD. This is entirely consistent with earlier findings, see e.g. Refs. [26, 34].
Proton electric form factor divided by the dipole FF from the best fit (red solid line) with the bootstrap uncertainties displayed by the light red band
Proton magnetic form factor divided by the dipole FF from the best fit (red solid line) with the bootstrap uncertainties displayed by the light red band
Note that the long-range part of the Breit-frame charge and magnetization distributions that follows from the Sachs form factors can be interpreted in terms of a “pion cloud” and some additional short-range contributions from the \(\rho \) and other short-ranged physics. However, we emphasize that this separation is scale-dependent and thus not unique. A general discussion of the pion cloud can be found in Refs. [139, 140].
4.3 Vector meson couplings
As noted before, in the earlier DR analyses, in the isoscalar spectral function below 1 GeV, only the \(\omega \) and the \(\phi \) mesons were retained and thus using Eq. (51), one was able to extract the vector and the tensor couplings of these mesons. However, we have shown that in the region of the \(\phi \), the isoscalar spectral function is much more complicated, preventing one from extracting \(\phi \)-meson couplings. In what follows, we will thus only consider the \(\omega \)-meson. In this case, we have
with
The earlier fits, which had no restrictions on the residua led to a large vector and a small tensor coupling,
from Ref. [22] and Ref. [26], respectively. This vector coupling is sizeably larger than from the determination using forward dispersion relations in nucleon-nucleon scattering, \(g_1^{\omega NN} = 10.1\pm 0.9\) [106]. This smaller value is, however, inconsistent with the approximate dipole behavior of \(F^s_1(Q^2)\) [141]. Note further that in one-boson-exchange models of the NN interaction, one typically finds values of \(g_1^{\omega NN}(M_\omega ^2) \simeq 20\) which for typical strong form factors translates to \(g_1^{\omega NN}(0) \simeq 10\) [142].
Starting with the work of BHM [34], the isoscalar spectral function was considerably improved. In that work, the vector coupling was still large, but the tensor coupling could not be pinned down so precisely,
Values within this range where also found in the analysis of the MAMI-C data combined with the proton form factor data for \(Q^2>1\,\) \(\hbox {GeV}^2\) and the neutron FF data base [45]
where only central values were given. Finally, the analyses that concentrated mostly on the high-precision ep data from MAMI-C and PRad, the \(\omega \) couplings took the values
from Ref. [46] and Ref. [53], respectively. Finally, we present the results of our new fits, including the statistical and the systematical uncertainty:
For the central values, the tensor-to-vector coupling ratio is small, \(\kappa _\omega = 0.06\). We note that the uncertainties on the vector coupling are modest, they are much larger for the suppressed tensor coupling. Similar to the findings in BHM, the sign of the tensor coupling is not determined and the range of allowed values is sizeable.
4.4 Time-like form factors and final-state interactions
Upper panel: Cross section for \(e^+e^-\rightarrow p{\bar{p}}\) in the threshold region. The data are from BESIII [143] (blue circles), BaBar [50] (black square), CMD-3 [144] (green diamonds), DM1 [145] (maroon crosses) and FENICE [146] (violet triangles). The dashed black line denote the phase space, normalized to the data at 50 MeV excess energy. Lower panel: Cross section for \(e^+e^-\rightarrow p{\bar{p}}\) for invariant masses below 3 GeV. The blue circles/black squares represent the data from BESIII [143]/BaBar [50]. In both panels, the vertical red dashed line marks the \(p{\bar{p}}\) threshold
Before discussing the DR fits including the data from the time-like region, it is worth noting two very intriguing experimental findings related to the cross section \(\sigma (e^+e^-\rightarrow p{\bar{p}})\) (and the reversed reaction) and the corresponding effective form factor \(|G_{\mathrm{eff}}^p|\). First, as shown in the upper panel of Fig. 26, there is a strong enhancement in the close-to-threshold region, as comparison with the phase space behavior (normalized to the data at about 50 MeV excess energy) clearly reveals. Note also that due to the Coulomb interaction between the proton and the antiproton, the cross section does not start at zero. No such effects are seen in \(\sigma (e^+e^-\rightarrow n{\bar{n}})\). We note that such threshold enhancements are also observed in other processes like e.g. \(J/\varPsi \rightarrow xp{\bar{p}}\), \(\varPsi '(3686)\rightarrow xp{\bar{p}}\) with \((x = \gamma , \omega , \rho , \pi , \eta )\) and \(B^+\rightarrow K^+p{\bar{p}}\), see e.g. Refs. [147,148,149]. Second, extending further out in momentum transfer, the BaBar data [50] and also the BESIII data [143] exhibit some oscillating structures, most pronounced for invariant masses \(M_{p{\bar{p}}}\) below 2.5 GeV, see the lower panel in Fig. 26. The corresponding neutron data from FENICE [146] and SND [150] are less precise than the proton data, but show a similar behavior for \(q^2 \lesssim 4\,\) \(\hbox {GeV}^2\). For recent fits to the time-like proton effective FF accounting for these structures, see [151].
DR fits including space- and time-like data were performed in Refs. [30, 34, 49]. Here, we focus on the work done in the latest paper. Though that work investigated some issues related to FSI in an exploratory way, it provides the most detailed information on the physics contained in the time-like FFs. In this work, the spectral functions was enlarged to account for the coupling to the newly established \(\phi (2170)\) vector meson, as well as baryonic triangle graphs with virtual \(NN\pi \), \(N\varDelta \pi \) and \(\varDelta \varDelta \pi \) particles, the first of these giving a simple representation of the strong final-state interactions (FSI), see the discussion below.
Simultaneous fits to proton and neutron FFs for space- and time-like momenta including the \(\phi (2170)\) were performed in Ref. [49]. More precisely, the differential cross sections and the ratio \(G_E/G_M\) from polarization observables on the scattering side in addition to the effective FF and \(|G_E/G_M|\) on the production side were included for the proton. In case of the neutron, \(G_E\) and \(G_M\) from scattering data and again the effective FF on the production side were considered. The spectral function included the the \(2\pi \), \(K{\bar{K}}\) and \(\rho \pi \)-continuum, the \(\omega \)- and \(\phi \)-contribution and three/five isoscalar/isovector poles restricted in the mass range \(M_V = 1\ldots 1.8\,\)GeV. In addition, the new vector resonance was taken at a mass of 2.125 GeV and its width was determined in the fit, which turned out to be \(\varGamma = 0.088\) GeV. Good agreement with the existing data, as shown in Fig. 27 for the proton and neutron effective form factors and in Fig. 28 for the proton form factor ratio in the space-like and the time-like region, was obtained. In particular, the SND data for the neutron effective FF show a very similar behavior to the proton effective FF over a large range, which can be well described in this approach. However, the range around the \(\phi (2170)\) calls for further neutron measurements to allow for a determination of the isospin of the structures in \(G_{\mathrm{eff}}^p\).
Let us now discuss the various threshold effects in the time-like data, in particular the strong enhancement at the \(p{\bar{p}}\) threshold. This was first observed at LEAR in the inverse reaction \(p{\bar{p}}\rightarrow e^+e^-\) [153] and substantiated by the BaBar collaboration [154], which provided data for \( e^+e^-\rightarrow p{\bar{p}}\) down to the threshold region. As noted before, this threshold enhancement was also observed in a number of other production reactions such as \(J/\psi \) and B decays. Several explanations involving unobserved meson resonances or scenarios that involve \(N{\bar{N}}\) bound states (baryonium) have been put forward, see e.g. Ref. [147]. More conventional but plausible interpretations of this phenomenon were given in terms of the FSI between the proton and the antiproton, employing either a Migdal-Watson approximation or meson-exchange models of various levels of sophistication to describe the \(p{\bar{p}}\) interaction, see e.g. the earlier works Refs. [155,156,157,158,159,160]. The latest and arguably most sophisticated approach to this phenomenon employs simple point-like form factors, whose energy dependence is entirely given by the proton-antiproton FSI (or the \(p{\bar{p}}\) initial state interactions in the annihilation process) [161]. The nucleon-antinucleon interaction is based on chiral effective field theory at NLO [162] and NNLO [163]. In this approach, the steep rise of the effective FF for energies close to the \(p{\bar{p}}\) threshold is explained solely in terms of the \(p{\bar{p}}\) interactions, cf. Fig. 29, consistent with the findings in Refs. [160, 164,165,166,167,168,169,170,171,172]. Also existing experimental information (differential cross sections, form factor ratio) is quantitatively described in this approach. In addition, predictions for various spin-dependent observables, that can be tested in the future with \(\overline{\mathrm{P}}\)ANDA at FAIR, are also given in that work. Note, however, that this framework is only applicable to the threshold region, that is up excess energies of about 100 MeV.
Effective proton form factor as a function of the excess energy. The data are from the DM1 [145] (triangles), FENICE [146] (squares), and BaBar [154] (empty circles), [50] (filled squares) collaborations. The green/red band refers to the calculation of the \(p{\bar{p}}\) interaction within chiral EFT at NLO/NNLO. Figure courtesy of Johann Haidenbauer
Triangle graphs with virtual \(N{\bar{\varDelta }}\pi \) and \(\varDelta {\bar{\varDelta }}\pi \) states were also considered in Ref. [49], picking up an idea of Rosner [173], in order to approximate possible cusp effects. However, the vertices are not well known for these kinematics, so the calculation was reduced to the scalar loop integral parameterized in terms of fitted strength parameter \(f_{N\varDelta /\varDelta \varDelta }\sim {{\mathcal {O}}}(1)\) multiplying each loop structure. The explicit momentum dependence of the vertices was accounted for in terms of overall form factors,
with \(\varLambda _{N\varDelta /\varDelta \varDelta }\) the respective fitted cut-off parameter. Interestingly, performing fits with these structures instead of the explicit poles discussed before leads to an equally good description of the proton effective FF, very similar to what is shown in Fig. 27 (upper panel).
Furthermore, in Ref. [49] the nucleon FFs were also discussed in region of \(t_0 = 4M_{\pi }^2< t < t_{\mathrm{thr}} = 4m_p^2\) which is not accessible by direct measurements, but by analytic continuation in \(t = q^2 = -Q^2\). In fact, an additional particle emission from the initial state proton can lower the energy of the (virtual proton) to reach below the threshold, as discussed in Ref. [174] for the process \(p{\bar{p}}\rightarrow e^+e^-\pi ^0\). To get insight into the unphysical region, it is instructive to use a DR for the logarithm, see e.g. Refs. [175,176,177,178,179]. In principle, this also allows for a separation of the FF phase \(\delta (t)\) and modulus in the representation \(G(t) = |G(t)|e^{i\delta (t)}\). A once-subtracted DR for the function \(\ln [G(t)/G(0)]/(t\sqrt{t_0 - t})\) takes the form (\(t<0\))
where the first term vanishes due to the normalization \(G_E(0) = G_M(0)/\mu _p = 1\). Experimental information on this integral equation (93) is available in the space-like region \(t<0\) on G(t) and in the time-like region for \(t>t_{\mathrm{thr}}\) on the modulus |G(t)|. The solution of this integral equation is not straightforward, it requires additional information to be included (as the problem is ill-conditioned). One possible solution was proposed in Refs. [177, 178], namely to consider the integral contributions to the logarithm \(\ln |G(t)|\) in the space-like region, using definite values for the known part above \(t_{\mathrm{thr}}\)
In Ref. [49], as input for the left-hand-side of Eq. (94), the discretized result of a simultaneous fit to data in all accessible regions were used. A typical result for the modulus of \(G_E^p(t)\) is shown in Fig. 30. The enhancement just below the production threshold could signal the appearance of a broad baryonium state, but clearly more precise data on the time-like nucleon FFs are required to come to a definite conclusion here.
An exemplary result for the modulus of electric form factor obtained from the logarithmic integral Eq. (93). The form factors for \(t<0\) are considered via the differential cross sections, therefore they are not displayed here
5 Summary and outlook
This paper served two purposes. First, we have reviewed the dispersion-theoretical approach to the electromagnetic form factors of the nucleon, with particular emphasis on the constraints posed by unitarity and analyticity on the spectral functions. Second, we have performed new fits including recent high-precision data on electron-proton scattering for squared momentum transfers \(Q^2<1\,\) \(\hbox {GeV}^2\), the proton form factor ratio in the range \(Q^2 \simeq 1\cdots 8.5\,\) \(\hbox {GeV}^2\) and the world data basis on the neutron electric and magnetic form factors, including the recent accurate extraction of the neutron charge radius squared from chiral nuclear EFT. We also have sharpened the toolbox to determine the statistical and systematical uncertainties. This led to a number of new results concerning the various nucleon electromagnetic radii, the form factors and the \(\omega NN\) couplings. We would like to stress again that DRs have always found a small proton charge radius, \(r_E^p \simeq 0.84\,\)fm, with a slightly larger proton magnetic radius, \(r_M^p \simeq 0.85\,\)fm. As before, we find that the neutron magnetic radius is the largest, \(r_M^n \simeq 0.87\,\)fm. Consistent with earlier analyses, the onset of pQCD is not seen in the existing form factor data. We have also discussed our present understanding of the physics in the time-like region, where a strong enhancement of the cross section for \(e^+e^-\rightarrow p {\bar{p}}\) (and in its reversed process \(p{\bar{p}}\rightarrow e^+e^-\)) is observed, that can be understood in terms of proton-antiproton final-state interactions (or initial-state interactions for the reserved process). Furthermore, there are interesting oscillating structures in the cross section that require additional poles and/or thresholds.
Clearly, there are a number of issues that require more data and/or further investigations:
-
For the neutron data basis, a thorough analysis of the existing electron-deuteron and electron-\(^3\)He scattering data based on chiral effective field theory and including two-photon corrections should be performed. This would allow to consistently analyze the proton and neutron form factors based on the dispersive approach applied directly to cross section data.
-
A new combined analysis of the space-like data (as done here) with the time-like data should be performed, including the improved knowledge of the \(p{\bar{p}}\) final-state interactions obtained in the last decade. This would also sharpen the predictions for future measurements with \(\overline{\mathrm{P}}\)ANDA at the FAIR facility.
-
Data on ep scattering or the polarization transfer at \(Q^2 \gg 10\,\) \(\hbox {GeV}^2\) are urgently needed to investigate the onset of perturbative QCD. It will also be interesting to find out whether the form factor ratio really crosses zero as the present data seem to indicate.
-
It would also be useful to improve our understanding of the spectral functions in the unphysical region, see Figs. 2 and 30. This requires more work based on logarithmic dispersion relations such as Eq. (93).
Finally, let us point out that the dispersion-theoretical approach to the nucleons electromagnetic form factors has matured and become a precision tool to analyze electron scattering and form factor ratio data. In the future, it will also be extended to analyze the upcoming muon-proton scattering data from the MUSE [180] and AMBER [181] experiments.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Author’s comment: The results on the form factors can be obtained from the corresponding author.]
Notes
Note, however, that dispersion-theoretical analyses of the same data always gave a smaller radius as will be discussed in detail below.
As discussed later, this is indeed a residual \(\phi \).
References
F. Wilczek, Cent. Eur. J. Phys. 10, 1021 (2012). arXiv:1206.7114 [hep-ph]
A. Denig, G. Salme, Prog. Part. Nucl. Phys. 68, 113–157 (2013). arXiv:1210.4689 [hep-ex]
V. Punjabi, C.F. Perdrisat, M.K. Jones, E.J. Brash, C.E. Carlson, Eur. Phys. J. A 51, 79 (2015). arXiv:1503.01452 [nucl-ex]
D.S. Armstrong, R.D. McKeown, Annu. Rev. Nucl. Part. Sci. 62, 337–359 (2012). arXiv:1207.5238 [nucl-ex]
F.E. Maas, K.D. Paschke, Prog. Part. Nucl. Phys. 95, 209–244 (2017)
R.W. McAllister, R. Hofstadter, Phys. Rev. 102, 851 (1956)
R. Hofstadter, Annu. Rev. Nucl. Part. Sci. 7, 231 (1957)
R. Karplus, A. Klein, J. Schwinger, Phys. Rev. 86, 288 (1952)
P.J. Mohr, B.N. Taylor, D.B. Newell, Rev. Mod. Phys. 80, 633 (2008). arXiv:0801.0028 [physics.atom-ph]
R. Pohl et al., Nature 466, 213 (2010)
J.C. Bernauer et al., [A1 Collaboration]. Phys. Rev. Lett. 105, 242001 (2010). arXiv:1007.5076 [nucl-ex]
A. Beyer et al., Science 358, 79 (2017)
H. Fleurbaey et al., Phys. Rev. Lett. 120, 183001 (2018). arXiv:1801.08816 [physics.atom-ph]
N. Bezginov, T. Valdez, M. Horbatsch, A. Marsman, A.C. Vutha, E.A. Hessels, Science 365, 1007 (2019)
W. Xiong, A. Gasparian, H. Gao, D. Dutta, M. Khandaker, N. Liyanage, E. Pasyuk, C. Peng, X. Bai, L. Ye et al., Nature 575(7781), 147–150 (2019)
H.-W. Hammer, U.-G. Meißner, Sci. Bull. 65, 257–258 (2020). arXiv:1912.03881 [hep-ph]
W.R. Frazer, J.R. Fulco, Phys. Rev. Lett. 2, 365 (1959)
W.R. Frazer, J.R. Fulco, Phys. Rev. 117, 1603–1609 (1960)
W.R. Frazer, J.R. Fulco, Phys. Rev. 117, 1609–1614 (1960)
S. Pacetti, R. Baldini Ferroli, E. Tomasi-Gustafsson, Phys. Rep. 550–551, 1–103 (2015)
G. Höhler, E. Pietarinen, I. Sabba Stefanescu, F. Borkowski, G.G. Simon, V.H. Walther, R.D. Wendling, Nucl. Phys. B 114, 505–534 (1976)
S. Okubo, Phys. Lett. 5, 165–168 (1963)
G. Zweig, CERN-TH-412 (1964)
J. Iizuka, Prog. Theor. Phys. Suppl. 37, 21–34 (1966)
P. Mergell, U.-G. Meißner, D. Drechsel, Nucl. Phys. A 596, 367–396 (1996). arXiv:hep-ph/9506375 [hep-ph]
M. Gari, W. Krümpelmann, Z. Phys. A 322, 689–693 (1985)
M. Gari, W. Krümpelmann, Phys. Lett. B 173, 10–14 (1986)
G. G. Simon, C. Schmitt, F. Borkowski, V. H. Walther, Nucl. Phys. A 333, 381-391
H.-W. Hammer, U.-G. Meißner, D. Drechsel, Phys. Lett. B 385, 343–347 (1996). arXiv:hep-ph/9604294 [hep-ph]
M. K. Jones et al., [Jefferson Lab Hall A], Phys. Rev. Lett. 84, 1398-1402 (2000) arXiv:nucl-ex/9910005 [nucl-ex]
O. Gayou et al., [Jefferson Lab Hall A], Phys. Rev. Lett. 88, 092301 (2002) arXiv:nucl-ex/0111010 [nucl-ex]
H.-W. Hammer, U.-G. Meißner, Eur. Phys. J. A 20(3), 469–473 (2004). arXiv:hep-ph/0312081 [hep-ph]
M.A. Belushkin, H.-W. Hammer, U.-G. Meißner, Phys. Rev. C 75, 035202 (2007). arXiv:hep-ph/0608337 [hep-ph]
H.-W. Hammer, M.J. Ramsey-Musolf, Phys. Rev. C 60, 045205 (1999) [Erratum-ibid. C 62, 049903 (2000)] arXiv:hep-ph/9812261
H.-W. Hammer, M.J. Ramsey-Musolf, Phys. Rev. C 60, 045204 (1999) [Erratum-ibid. C 62, 049902 (2000)] arXiv:hep-ph/9903367
U.-G. Meißner, V. Mull, J. Speth, J.W. van Orden, Phys. Lett. B 408, 381 (1997). arXiv:hep-ph/9701296
M.A. Belushkin, H.-W. Hammer, U.-G. Meißner, Phys. Lett. B 633, 507–511 (2006). arXiv:hep-ph/0510382 [hep-ph]
K. Melnikov, T. van Ritbergen, Phys. Rev. Lett. 84, 1673–1676 (2000). arXiv:hep-ph/9911277 [hep-ph]
M.A. Belushkin, H.-W. Hammer, U.-G. Meißner, Phys. Lett. B 658, 138–142 (2008). arXiv:0705.3385 [hep-ph]
P.G. Blunden, W. Melnitchouk, J.A. Tjon, Phys. Rev. Lett. 91, 142304 (2003). arXiv:nucl-th/0306076 [nucl-th]
P.G. Blunden, W. Melnitchouk, J.A. Tjon, Phys. Rev. C 72, 034612 (2005). arXiv:nucl-th/0506039 [nucl-th]
S. Kondratyuk, P.G. Blunden, W. Melnitchouk, J.A. Tjon, Phys. Rev. Lett. 95, 172503 (2005). https://doi.org/10.1103/PhysRevLett.95.172503. arXiv:nucl-th/0506026 [nucl-th]
J. C. Bernauer et al., [A1], Phys. Rev. C 90, no.1, 015206 (2014) https://doi.org/10.1103/PhysRevC.90.015206, arXiv:1307.6227 [nucl-ex]
I.T. Lorenz, H.-W. Hammer, U.-G. Meißner, Eur. Phys. J. A 48, 151 (2012). arXiv:1205.6628 [hep-ph]
I.T. Lorenz, U.-G. Meißner, H.-W. Hammer, Y.B. Dong, Phys. Rev. D 91(1), 014023 (2015). arXiv:1411.1704 [hep-ph]
G. Ron et al., Jefferson Lab Hall A. Phys. Rev. C 84, 055204 (2011). arXiv:1103.5784 [nucl-ex]
X. Zhan, K. Allada, D.S. Armstrong, J. Arrington, W. Bertozzi, W. Boeglin, J.P. Chen, K. Chirapatpimol, S. Choi, E. Chudakov et al., Phys. Lett. B 705, 59–64 (2011). arXiv:1102.0318 [nucl-ex]
I.T. Lorenz, H.-W. Hammer, U.-G. Meißner, Phys. Rev. D 92(3), 034018 (2015). arXiv:1506.02282 [hep-ph]
J. P. Lees et al., [BaBar], Phys. Rev. D 87(9) , 092005 (2013) arXiv:1302.0055 [hep-ex]
M. Hoferichter, B. Kubis, J. Ruiz de Elvira, H.-W. Hammer, U.-G. Meißner, Eur. Phys. J. A 52(11), 331 (2016). arXiv:1609.06722 [hep-ph]
M. Hoferichter, J. Ruiz de Elvira, B. Kubis, U.-G. Meißner, Phys. Rept. 625, 1–88 (2016). arXiv:1510.06039 [hep-ph]
Y.H. Lin, H.-W. Hammer, U.-G. Meißner, Phys. Lett. B 816, 136254 (2021). arXiv:2102.11642 [hep-ph]
G. Paz, Mod. Phys. Lett. A 36, 2150143 (2021)
J.M. Alarcón, C. Weiss, Phys. Rev. C 97(5), 055203 (2018). arXiv:1710.06430 [hep-ph]
J.M. Alarcón, C. Weiss, Phys. Lett. B 784, 373–377 (2018). arXiv:1803.09748 [hep-ph]
J.M. Alarcón, D.W. Higinbotham, C. Weiss, Z. Ye, Phys. Rev. C 99(4), 044303 (2019). arXiv:1809.06373 [hep-ph]
J.M. Alarcón, D.W. Higinbotham, C. Weiss, Phys. Rev. C 102(3), 035203 arXiv:2002.05167 [hep-ph] (2020)
S. Leupold, Eur. Phys. J. A 54(1), 1 (2018). arXiv:1707.09210 [hep-ph]
R.L. Jaffe, Phys. Lett. B 229, 275–279 (1989)
H.-W. Hammer, U.-G. Meißner, D. Drechsel, Phys. Lett. B 367, 323–328 (1996). arXiv:hep-ph/9509393 [hep-ph]
H. Forkel, Phys. Rev. C 56, 510–525 (1997). arXiv:hep-ph/9607452 [hep-ph]
R. Pohl, R. Gilman, G.A. Miller, K. Pachucki, Ann. Rev. Nucl. Part. Sci. 63, 175–204 (2013). arXiv:1301.0905 [physics.atom-ph]
J.P. Karr, D. Marchand, E. Voutier, Nat. Rev. Phys. 2(11), 601–614 (2020)
M.N. Rosenbluth, Phys. Rev. 79, 615–619 (1950)
A.I. Akhiezer, M.P. Rekalo, Sov. Phys. Dokl. 13, 572 (1968)
R.G. Arnold, C.E. Carlson, F. Gross, Phys. Rev. C 23, 363 (1981)
E. Tomasi-Gustafsson, M.P. Rekalo, Phys. Lett. B 504, 291–295 (2001)
S.D. Drell, F. Zachariasen, Electromagnetic Structure of Nucleons (Oxford University Press, London, 1965)
G.F. Chew, R. Karplus, S. Gasiorowicz, F. Zachariasen, Phys. Rev. 110(1), 265 (1958)
P. Federbush, M.L. Goldberger, S.B. Treiman, Phys. Rev. 112, 642–665 (1958)
G. Höhler, E. Pietarinen, Phys. Lett. B 53, 471–475 (1975)
Y. Ünal, U.-G. Meißner, Phys. Lett. B 794, 103–108 (2019). arXiv:1902.03143 [hep-ph]
S. Eidelman, L. Lukaszuk, Phys. Lett. B 582, 27 (2004). arXiv:hep-ph/0311366
J. Gasser, U.-G. Meißner, Nucl. Phys. B 357, 90–128 (1991)
K.M. Watson, Phys. Rev. 95, 228–236 (1954)
R. Omnes, Nuovo Cim. 8, 316–326 (1958)
B. Aubert et al., [BaBar]. Phys. Rev. Lett. 103, 231801 (2009). arXiv:0908.3589 [hep-ex]
D. Babusci et al., [KLOE]. Phys. Lett. B 720, 336–343 (2013). arXiv:1212.4524 [hep-ex]
M. Ablikim et al., [BESIII], Phys. Lett. B 753, 629-638 (2016) [erratum: Phys. Lett. B 812, 135982 (2021)], arXiv:1507.08188 [hep-ex]
I. Caprini, G. Colangelo, H. Leutwyler, Eur. Phys. J. C 72, 1860 (2012). arXiv:1111.7160 [hep-ph]
R. Garcia-Martin, R. Kaminski, J.R. Pelaez, J. Ruiz de Elvira, F.J. Yndurain, Phys. Rev. D 83, 074004 (2011). arXiv:1102.2183 [hep-ph]
S.P. Schneider, B. Kubis, F. Niecknig, Phys. Rev. D 86, 054013 (2012). arXiv:1206.3098 [hep-ph]
C. Ditsche, M. Hoferichter, B. Kubis, U.-G. Meißner, JHEP 06, 043 (2012). arXiv:1203.4758 [hep-ph]
M. Hoferichter, C. Ditsche, B. Kubis, U.-G. Meißner, JHEP 06, 063 (2012). arXiv:1204.6251 [hep-ph]
M. Hoferichter, J. Ruiz de Elvira, B. Kubis, U.G. Meißner, Phys. Rev. Lett. 115, 092301 (2015). arXiv:1506.04142 [hep-ph]
J Ruiz de Elvira, M. Hoferichter, B. Kubis, U.-G. Meißner, J. Phys. G 45(2), 024001 (2018). arXiv:1706.01465 [hep-ph]
R. Koch, E. Pietarinen, Nucl. Phys. A 336, 331–346 (1980)
G. Höhler, Pion-Nukleon-Streuung: Methoden und Ergebnisse, in Landolt-Börnstein, 9b2. ed. by H. Schopper (Springer Verlag, Berlin, 1983)
F. Steiner, PhD thesis, University of Karlsruhe, (1968)
G.E. Hite, F. Steiner, Nuovo Cim. A 18, 237–270 (1973)
V. Baru, C. Hanhart, M. Hoferichter, B. Kubis, A. Nogga, D.R. Phillips, Nucl. Phys. A 872, 69–116 (2011). arXiv:1107.5509 [nucl-th]
A. Hirtl, D.F. Anagnostopoulos, D.S. Covita, H. Fuhrmann, H. Gorke, D. Gotta, A. Gruber, M. Hennebach, P. Indelicato, T.S. Jensen et al., Eur. Phys. J. A 57(2), 70 (2021)
G.J. Gounaris, J.J. Sakurai, Phys. Rev. Lett. 21, 244–247 (1968)
J. Wess, B. Zumino, Phys. Lett. B 37, 95–97 (1971)
E. Witten, Nucl. Phys. B 223, 422–432 (1983)
V. Bernard, N. Kaiser, U.-G. Meißner, Nucl. Phys. A 611, 429–441 (1996). arXiv:hep-ph/9607428 [hep-ph]
N. Kaiser, E. Passemar, Eur. Phys. J. A 55(2), 16 (2019). arXiv:1901.02865 [nucl-th]
G. Janssen, K. Holinde, J. Speth, Phys. Rev. C 54, 2218–2234 (1996)
J.J. Sakurai, Ann. Phys. 11, 1–48 (1960)
N.M. Kroll, T.D. Lee, B. Zumino, Phys. Rev. 157, 1376–1399 (1967)
M. Bando, T. Kugo, K. Yamawaki, Phys. Rep. 164, 217–314 (1988)
U.-G. Meißner, Phys. Rep. 161, 213 (1988)
S. Ciulli, C. Pomponiu, I. Sabba-Stefanescu, Phys. Rep. 17, 133 (1975)
I. Sabba Stefanescu, J. Math. Phys. 21, 175 (1980)
W. Grein, P. Kroll, Nucl. Phys. B 137, 173–188 (1978)
S. Kopecky, P. Riehs, J.A. Harvey, N.W. Hill, Phys. Rev. Lett. 74, 2427–2430 (1995)
S. Kopecky, M. Krenn, P. Riehs, S. Steiner, J.A. Harvey, N.W. Hill, M. Pernicka, Phys. Rev. C 56, 2229–2237 (1997)
A.A. Filin, V. Baru, E. Epelbaum, H. Krebs, D. Möller, P. Reinert, Phys. Rev. Lett. 124(8), 082501 (2020). arXiv:1911.04877 [nucl-th]
A.A. Filin, D. Möller, V. Baru, E. Epelbaum, H. Krebs, P. Reinert, Phys. Rev. C 103(2), 024313 [arXiv:2009.08911 [nucl-th]] (2021)
G.P. Lepage, S.J. Brodsky, Phys. Rev. D 22, 2157 (1980)
A. Bianconi, E. Tomasi-Gustafsson, Phys. Rev. Lett. 114(23), 232301 (2015). arXiv:1503.02140 [nucl-th]
J. Arrington, Phys. Rev. C 68, 034325 (2003). arXiv:nucl-ex/0305009 [nucl-ex]
N. Meister, D.R. Yennie, Phys. Rev. 130, 1210–1229 (1963)
L.W. Mo, Y.S. Tsai, Rev. Mod. Phys. 41, 205–235 (1969)
L.C. Maximon, J.A. Tjon, Phys. Rev. C 62, 054320 (2000). arXiv:nucl-th/0002058 [nucl-th]
J. Arrington, P.G. Blunden, W. Melnitchouk, Prog. Part. Nucl. Phys. 66, 782–833 (2011). arXiv:1105.0951 [nucl-th]
A. Afanasev, P.G. Blunden, D. Hasell, B.A. Raue, Prog. Part. Nucl. Phys. 95, 245–278 (2017). arXiv:1703.03874 [nucl-ex]
J. Ahmed, P.G. Blunden, W. Melnitchouk, Phys. Rev. C 102(4), 045205 (2020). arXiv:2006.12543 [nucl-th]
W. Rarita, J. Schwinger, Phys. Rev. 60, 61 (1941)
H.F. Jones, M.D. Scadron, Ann. Phys. 81, 1–14 (1973)
S. Kondratyuk, O. Scholten, Phys. Rev. C 64, 024005 (2001). arXiv:nucl-th/0103006 [nucl-th]
O. Lalakulich, E.A. Paschos, G. Piranishvili, Phys. Rev. D 74, 014009 (2006). arXiv:hep-ph/0602210 [hep-ph]
L. Tiator, D. Drechsel, S. Kamalov, M.M. Giannini, E. Santopinto, A. Vassallo, Eur. Phys. J. A 19, 55–60 (2004). arXiv:nucl-th/0310041 [nucl-th]
K.M. Graczyk, Phys. Rev. C 88, 065205 (2013). arXiv:1306.5991 [hep-ph]
H.Q. Zhou, S.N. Yang, Eur. Phys. J. A 51(8), 105 (2015). arXiv:1407.2711 [nucl-th]
W.A. McKinley, H. Feshbach, Phys. Rev. 74, 1759–1763 (1948)
J. Arrington, Phys. Rev. Lett. 107, 119101 (2011). arXiv:1108.3058 [nucl-ex]
H.-W. Hammer, Eur. Phys. J. A 28, 49–57 (2006). arXiv:hep-ph/0602121 [hep-ph]
B. Efron, R. Tibshirani, Stat. Sci. 57(1), 54–75 (1986)
M. R. Schindler, D. R. Phillips, Annals Phys. 324 (2009), 682-708 [erratum: Ann. Phys. 324 (2009), 2051-2055]
S. Wesolowski, N. Klco, R.J. Furnstahl, D.R. Phillips, A. Thapaliya, J. Phys. G 43(7), 074001 (2016). arXiv:1511.03618 [nucl-th]
A. Shahmoradi, F. Bagheri, arXiv:2009.14229 [cs.MS]
V. Punjabi, C. F. Perdrisat, K. A. Aniol, F. T. Baker, J. Berthot, P. Y. Bertin, W. Bertozzi, A. Besson, L. Bimbot, W. U. Boeglin, et al. Phys. Rev. C 71, 055202 (2005), [erratum: Phys. Rev. C 71, 069902 (2005)], arXiv:nucl-ex/0501018 [nucl-ex]
A.J.R. Puckett, E.J. Brash, M.K. Jones, W. Luo, M. Meziane, L. Pentchev, C.F. Perdrisat, V. Punjabi, F.R. Wesselmann, A. Ahmidouch et al., Phys. Rev. Lett. 104, 242301 (2010). arXiv:1005.3419 [nucl-ex]
M. Meziane et al., GEp2gamma. Phys. Rev. Lett. 106, 132501 (2011). arXiv:1012.0339 [nucl-ex]
A.J.R. Puckett, E.J. Brash, O. Gayou, M.K. Jones, L. Pentchev, C.F. Perdrisat, V. Punjabi, K.A. Aniol, T. Averett, F. Benmokhtar et al., Phys. Rev. C 85, 045203 (2012). arXiv:1102.5737 [nucl-ex]
D. Djukanovic, T. Harris, G. von Hippel, P.M. Junnarkar, H.B. Meyer, D. Mohler, K. Ottnad, T. Schulz, J. Wilhelm, H. Wittig, Phys. Rev. D 103, 094522 (2021). arXiv:2102.07460 [hep-lat]
H.-W. Hammer, D. Drechsel, U.-G. Meißner, Phys. Lett. B 586, 291–296 (2004). arXiv:hep-ph/0310240 [hep-ph]
U.-G. Meißner, A.I.P. Conf, Proc. 904(1), 142–150 (2007). arXiv:nucl-th/0701094 [nucl-th]
G. Höhler, PiN Newslett. 1993(9), 1–36 (1993)
T.E.O. Ericson, W. Weise, Int. Ser. Monogr. Phys. 74(1988)
M. Ablikim et al., [BESIII]. Phys. Lett. B 817, 136328 (2021). arXiv:2102.10337 [hep-ex]
R.R. Akhmetshin et al., [CMD-3]. Phys. Lett. B 794, 64–68 (2019). arXiv:1808.00145 [hep-ex]
B. Delcourt, I. Derado, J.L. Bertrand, D. Bisello, J.C. Bizot, J. Buon, A. Cordier, P. Eschstruth, L. Fayard, J. Jeanjean et al., Phys. Lett. B 86, 395–398 (1979)
A. Antonelli, R. Baldini, P. Benasi, M. Bertani, M.E. Biagini, V. Bidoli, C. Bini, T. Bressani, R. Calabrese, R. Cardarelli et al., Nucl. Phys. B 517, 3–35 (1998)
J.Z. Bai et al., [BES]. Phys. Rev. Lett. 91, 022001 (2003). arXiv:hep-ex/0303006 [hep-ex]
B. Aubert et al., [BaBar]. Phys. Rev. D 72, 051101 (2005). arXiv:hep-ex/0507012 [hep-ex]
M. Ablikim et al., [BESIII]. Phys. Rev. Lett. 108, 112003 (2012). arXiv:1112.0942 [hep-ex]
M.N. Achasov, A.Y. Barnyakov, K.I. Beloborodov, A.V. Berdyugin, D.E. Berkaev, A.G. Bogdanchikov, A.A. Botov, T.V. Dimova, V.P. Druzhinin, V.B. Golubev et al., Phys. Rev. D 90(11), 112007 (2014). arXiv:1410.3188 [hep-ex]
E. Tomasi-Gustafsson, A. Bianconi, S. Pacetti, Phys. Rev. C 103(3), 035203 [arXiv:2012.14656 [hep-ph]] (2021). arXiv:2012.14656
J. P. Lees et al., [BaBar], Phys. Rev. D 88(7) , 072009 (2013) arXiv:1308.1795 [hep-ex]
G. Bardin, G. Burgun, R. Calabrese, G. Capon, R. Carlin, P. Dalpiaz, P.F. Dalpiaz, J. Derré, U. Dosselli, J. Duclos et al., Nucl. Phys. B 411, 3–32 (1994)
B. Aubert et al., [BaBar]. Phys. Rev. D 73, 012005 (2006). arXiv:hep-ex/0512023 [hep-ex]
B.S. Zou, H.C. Chiang, Phys. Rev. D 69, 034004 (2004). arXiv:hep-ph/0309273 [hep-ph]
B. Kerbikov, A. Stavinsky, V. Fedotov, Phys. Rev. C 69, 055205 (2004). arXiv:hep-ph/0402054 [hep-ph]
D. V. Bugg, Phys. Lett. B 598 (2004), 8-14 arXiv:hep-ph/0406293 [hep-ph]
A. Sibirtsev, J. Haidenbauer, S. Krewald, U.-G. Meißner, A.W. Thomas, Phys. Rev. D 71, 054010 (2005). arXiv:hep-ph/0411386 [hep-ph]
B. Loiseau, S. Wycech, Phys. Rev. C 72, 011001 (2005). arXiv:hep-ph/0501112 [hep-ph]
J. Haidenbauer, H.-W. Hammer, U.-G. Meißner, A. Sibirtsev, Phys. Lett. B 643, 29–32 (2006). arXiv:hep-ph/0606064 [hep-ph]
J. Haidenbauer, X.W. Kang, U.-G. Meißner, Nucl. Phys. A 929, 102[arXiv:1405.1628 [nucl-th]]-118 (2014). arXiv:1405.1628 [nucl-th]
X.W. Kang, J. Haidenbauer, U.-G. Meißner, JHEP 02, 113 (2014). arXiv:1311.1658 [hep-ph]
L.Y. Dai, J. Haidenbauer, U.-G. Meißner, JHEP 07, 078 (2017). arXiv:1702.02065 [nucl-th]
V.F. Dmitriev, A.I. Milstein, Phys. Lett. B 658, 13–16 (2007)
G.Y. Chen, H.R. Dong, J.P. Ma, Phys. Rev. D 78, 054022 (2008). arXiv:0806.4661 [hep-ph]
G.Y. Chen, H.R. Dong, J.P. Ma, Phys. Lett. B 692, 136–142 (2010). arXiv:1004.5174 [hep-ph]
O.D. Dalkarov, P.A. Khakhulin, A.Y. Voronin, Nucl. Phys. A 833, 104–118 (2010). arXiv:0906.0266 [nucl-th]
A.E. Bondar, V.F. Dmitriev, A.I. Milstein, V.M. Strakhovenko, Phys. Lett. B 697, 159–163 (2011). arXiv:1012.4638 [hep-ph]
J. Haidenbauer, U.-G. Meißner, Phys. Rev. D 86, 077503 (2012). arXiv:1208.3343 [hep-ph]
V.F. Dmitriev, A.I. Milstein, Phys. Lett. B 722, 83–85 (2013). arXiv:1303.0653 [hep-ph]
V.F. Dmitriev, A.I. Milstein, S.G. Salnikov, Phys. Atom. Nucl. 77(9), 1173–1177 (2014). arXiv:1307.0936 [hep-ph]
D.R. Entem, F. Fernandez, Phys. Rev. D 75, 014004 (2007)
J.L. Rosner, Phys. Rev. D 74, 076006 (2006). arXiv:hep-ph/0608102 [hep-ph]
J. Guttmann, M. Vanderhaeghen, Phys. Lett. B 719, 136–142 (2013). arXiv:1210.3290 [hep-ph]
M. Gourdin, Phys. Rep. 11, 29 (1974)
B.V. Geshkenbein, B.L. Ioffe, M.A. Shifman, Yad. Fiz. 20, 128–136 (1974)
R. Baldini, S. Dubnicka, P. Gauzzi, S. Pacetti, E. Pasqualucci, Y. Srivastava, Eur. Phys. J. C 11, 709–715 (1999)
S. Pacetti, Eur. Phys. J. A 32(4), 421–427 (2007)
S. Pacetti, Chin. Phys. C 34, 874–876 (2010). arXiv:1012.1232 [hep-ph]
E. J. Downie, [MUSE], EPJ Web Conf. 73, 07005 (2014)
B. Adams, C. A. Aidala, R. Akhunzyanov, G. D. Alexeev, M. G. Alexeev, A. Amoroso, V. Andrieux, N. V. Anfimov, V. Anosov, A. Antoshkin, et al.,arXiv:1808.00848 [hep-ex]
M. Garcon, J.W. Van Orden, Adv. Nucl. Phys. 26, 293 (2001). arXiv:nucl-th/0102049 [nucl-th]
H. Krebs, Eur. Phys. J. A 56(9), 234 (2020). arXiv:2008.00974 [nucl-th]
R. Navarro Pérez, J.E. Amaro, E. Ruiz Arriola, Phys. Rev. C 95(6), 064001 (2017). arXiv:1606.00592 [nucl-th]
P. Reinert, H. Krebs, E. Epelbaum, Phys. Rev. Lett. 126(9), 092501 (2021). arXiv:2006.15360 [nucl-th]
V. Bernard, N. Kaiser, U.-G. Meißner, Int. J. Mod. Phys. E 4, 193–346 (1995). arXiv:hep-ph/9501384 [hep-ph]
R.J. Eden, P.V. Landshoff, D.I. Olive, J.C. Polkinghorne, The Analytic S-Matrix (Cambridge University Press, Cambridge, 1966)
M. Jacob, G.C. Wick, Ann. Phys. 7, 404–428 (1959)
M. J. Musolf, H.-W. Hammer, D. Drechsel, Phys. Rev. D 55, 2741 (1997),[erratum: Phys. Rev. D 62, 079901 (2000)], arXiv:hep-ph/9610402 [hep-ph]
Acknowledgements
We are grateful to our (former) collaborators a for helping us to sharpen our view on the issues discussed. We acknowledge useful conversations with Jürgen Dölz on uncertainty quantifications. We thank Johann Haidenbauer and Bernard Metsch with help to prepare some of the figures. This work of UGM and YHL is supported in part by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) and the NSFC through the funds provided to the Sino-German Collaborative Research Center TRR 110 “Symmetries and the Emergence of Structure in QCD” (DFG Project-ID 196253076 - TRR 110, NSFC Grant No. 12070131001), by the Chinese Academy of Sciences (CAS) through a President’s International Fellowship Initiative (PIFI) (Grant No. 2018DM0034), by the VolkswagenStiftung (Grant No. 93562), and by the EU Horizon 2020 research and innovation programme, STRONG-2020 project under grant agreement No. 824093. HWH was supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Projektnummer 279384907 – CRC 1245 and by the German Federal Ministry of Education and Research (BMBF) (Grant No. 05P18RDFN1).
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Nicolas Alamanos.
Appendices
Neutron form factors from light nuclei
As there are no free neutron targets, the neutron form factors must be extracted from electron scattering off light nuclei. In this appendix, we briefly outline how this can be achieved in case of the simplest nucleus, the deuteron. The extension to systems with 3 or 4 nucleons is similar but more complicated.
The deuteron is a spin-1 particle. Using Lorentz invariance, time-reversal invariance as well as parity and current conservation, the matrix element of the deuteron em currents takes the form, see e.g. [67, 182] (as usual, in units of the elementary charge e)
where \(p',p\) are the deuteron four-momenta, \(\lambda ',\lambda \) the corresponding helicities, \(m_d = 1.8756\,\)GeV is the deuteron mass and \(Q^2 \equiv -k_\mu k^\mu = -(p'-p)^2\ge 0\). Furthermore, the polarization four-vectors \(\xi _\mu \) are subject to the constraints \(\xi _\mu (p,\lambda )p^\mu = 0\) and \(\xi ^*_\mu (p',\lambda ')p'^\mu =0\). Instead of the scalar functions \(G_i(Q^2)\, (i=1,2,3)\), one often uses the deuteron charge (\(G_C\)), magnetic (\(G_M\)) and quadrupole (\(G_Q\)) form factors given by
with \(\eta = Q^2/(4m_d^2)\). These form factors are subject to the normalizations:
in terms of the deuteron magnetic moment, \(\mu _d = 0.857\, \mu _N\), and the deuteron quadrupole moment, \(Q_d = 0.286\,\) \(\hbox {fm}^2\).
In the one-photon exchange approximation, the unpolarized elastic electron-deuteron (ed) scattering cross section in the laboratory (lab) frame is given by
with E the energy of the incoming electron, \(\theta \) the electron scattering angle in the lab frame and \(Q^2\ge 0\) is the squared momentum transfer. The structure functions \(A(Q^2)\) and \(B(Q^2)\) are related to the three form factors of the deuteron via
As can be seen, from the unpolarized cross section one can not disentangle the charge and the quadrupole form factors. This can be achieved by considering polarization data, e.g. the tensor analyzing power \(T_{20}(Q^2,\theta )\) is sensitive to a different combination of the three deuteron FFs.
Electromagnetic response of the deuteron. Diagram a depicts the IA, that is sensitive to the nucleon em FFs (black circle) whereas diagram b denotes the so-called two-body corrections (depicted by the shaded box) as explained in the text. The hatched triangles denote a deuteron wave function and solid (wiggly) lines represent nucleons (photons)
Using a chiral expansion (or a meson-exchange model in older times), these deuteron FFs can now be related to the single nucleon form factors as depicted in Fig. 31. The so-called impulse approximation (IA), where the photon couples to one nucleon, is depicted in graph a). This contribution is evidently sensitive to the single nucleon em FFs. To be precise, one takes the proton FFs as given and is then entirely sensitive to \(G_E^n\) and \(G_M^n\), see below. There are, however, a number of corrections as displayed by graph b) in Fig. 31. This include one- and two-pion exchange currents as well as photon–four-nucleon vertices (or heavy meson exchanges in the older language). The status of the nuclear currents based on a systematic evaluation of the few-body wave functions and the current operators is given in Ref. [183]. Consider for example the charge density that generates the charge form factor. As the deuteron is an isoscalar, its em response is entirely sensitive to the isoscalar form factors. Modulo higher order corrections, at leading order in the chiral expansion, the charge density gives rise to the form factors:
where one works in the Breit frame with \(\mathbf{k}^2 = Q^2\), the direction of the photon momentum is taken along the positive z-axis and \(k = |\mathbf{k}|\). Also, u(r) and w(r) are the deuteron S- and D-wave wave functions, normalized to one, see e.g. [142], and \(j_0(x),j_2(x)\) are the spherical Bessel functions. Corrections to this leading order results can be worked out straightforwardly, these are given for a chiral EFT approach in Ref. [110] (and references therein).
Pion-nucleon scattering in the unphysical region
Here, we briefly discuss the subthreshold expansion of the \(\pi N\) amplitudes, which proceeds in terms of the variables \(\nu =(s-u)/(4m)\) and t around \(\nu =t=0\) ,
where the upper/lower entry corresponds to \(I=\pm \), and the \(a_{mn}^\pm , b_{mn}^\pm \) are the subthreshold parameters. The \({\bar{A}}, {\bar{B}}\) are the Born-term-subtracted amplitudes, defined as
with
Here, the subscript ‘pv’ refers to the pseudovector \(\pi N\) coupling as required from chiral symmetry and g denotes the \(\pi N\) coupling constant, to be identified later with \(g_c\) for the charged-pion vertex. In the RS analysis of \(\pi N\) scattering, the value \(g_c^2/(4\pi )=13.7(0.2)\) [92] has been used. This value is in line with the most recent determination from nucleon–nucleon scattering [184, 185]. More details on the subthreshold expansion of the \(\pi N\) scattering amplitude is given in Refs. [52, 89].
Analysis of the three-pion contribution
Here, we briefly review the arguments of Ref. [97] that there is no strong enhancement on the left shoulder of the \(\omega \) resonance, the lowest vector meson in the three-pion channel (for a recent update, see Ref. [98]). The imaginary parts of the isoscalar electromagnetic form factors open at the three-pion threshold \(t_0 = 9M_\pi ^2\). The three-pion cut contribution is given by
where the symbol ’A’ refers to the \(\gamma \rightarrow 3\pi \) and ’B’ to the \(3\pi \rightarrow {{\bar{N}}} N\) transition, respectively, and \(d\varGamma _3\) is the measure on the invariant three-body phase space. This can be explicitly worked out in baryon chiral perturbation theory [186], where to leading order in the small parameter p, namely at order \({{\mathcal {O}}}(p^7)\), the two-loop diagrams shown in Fig. 32 can contribute to the isoscalar imaginary parts, however, graph (d) vanishes because of an isospin factor zero.
Two-loop diagrams contributing to the imaginary parts of the isoscalar electromagnetic nucleon form factors. Wiggly, dashed and solid lines represent photons, pions and nucleons, in order
The isoscalar imaginary parts in the heavy nucleon limit \(m\rightarrow \infty \) can be given in compact form (note that this corresponds to switching off all higher order corrections starting at \({{\mathcal {O}}}(p^8)\))
with
and in terms of the kinematical variables of the two independent pions (the third one can be expressed in terms of these and the nucleon momenta),
The behavior near threshold \(t_0 = 9M_\pi ^2\) of the imaginary parts for finite pion mass, Eqs. (105,106), is given by
which corresponds to a stronger growth than pure phase space
This feature indicates (as in the isovector case) that in the heavy nucleon mass limit \(m \rightarrow \infty \) normal and anomalous thresholds coincide. In order to find these singularities for finite nucleon mass m an investigation of the Landau equations is necessary [187]. By using standard techniques [187] one finds one anomalous threshold of diagrams (a) and (b) at
which is very near to the (normal) threshold \(t_0=9M_\pi ^2\) and indeed coalesces with \(t_0\) in the infinite nucleon mass limit. Note that diagram (d) does not possess this anomalous threshold, but only the normal one.
Spectral distribution of the isoscalar electric and magnetic nucleon form factors weighted with \(1/t^2\) in the heavy nucleon limit. Shown are Im \(G_M^S (t)/t^2\) (solid line) and Im \(G_E^S (t)/t^2\) (dashed line)
The resulting spectral distributions weighted with \(1/t^2\) are shown in Fig. 33. Very different to the isovector spectral functions discussed in Sect. 3.4, they show a smooth rise and are two orders of magnitude smaller than the corresponding isovector ones, cf. Fig. 6. There is indeed no enhancement of the isoscalar electromagnetic spectral function near threshold. We note that the corrections calculated in Ref. [98] further reduce these spectral functions considerably in magnitude. Even though the isoscalar and isovector electromagnetic form factors behave formally very similar concerning the existence of anomalous thresholds \(t_c\) very close to the normal thresholds \(t_0\), the influence of these on the physical spectral functions is rather different for the two cases. Only in the isovector case a strong enhancement is visible. This is presumably due to the different phase space factors, which are \((t-t_0)^{3/2}\) and \((t-t_0)^4\) for the isovector and isoscalar case, respectively. In the latter case, the anomalous threshold at \(t_c = 8.9M_\pi ^2\) is thus effectively masked. This justifies the standard DR approach of only taking the \(\omega \)-meson as the lowest pole in isoscalar spectral function.
\(K{\bar{K}}\rightarrow N{\bar{N}}\) partial wave amplitudes
We seek the partial wave expansion of the \(K{\bar{K}}\rightarrow N{\bar{N}}\) amplitude. This allows one to impose the constraints of unitarity in a straightforward way. Here, we utilize the helicity amplitude formalism of Jacob and Wick [188]. Denoting with \(\lambda \) and \({\bar{\lambda }}\) the nucleon and antinucleon helicities, the corresponding S-matrix element takes the form
where \(t=P^2=(p+{{\bar{p}}})^2\) and \(M_K\) is the kaon mass. The partial wave expansion of the pertinent matrix element \({\langle \theta , \phi , \lambda , {\bar{\lambda }}\vert }{{{\hat{S}}}}(P){\vert 00\rangle }\) is given by [188, 189]
where \({{\mathcal {D}}}_{\nu \, \nu '}^J(\alpha , \beta , \gamma )\) denotes a Wigner rotation matrix with \(\mu =\lambda -{\bar{\lambda }}\). Further, the \(b_J^{\lambda \, {\bar{\lambda }}}\) define partial waves of angular momentum J. Because of the quantum numbers of the isoscalar em current, only the \(J=1\) partial waves contribute to the spectral functions. Moreover, because of parity invariance only two of the four partial waves are independent. In Ref. [35], the \({b_1^{1/2,\,1/2}}\) and \({b_1^{1/2,\,-1/2}}\) were chosen. These fulfill the threshold relation [189]
Using the above definitions, unitarity of the S-matrix, \(S^{\dag } S = 1\), requires that
for \(t\ge 4{m^2}\). Thus, unitarity gives model-independent bounds on the contribution of the physical region (\(t\ge 4{m^2}\)) to the imaginary part. In the unphysical region, that is for \(4{M_{{\scriptscriptstyle K}}^2}\le t \le 4{m^2}\), the partial waves are not bounded by unitarity. Therefore, one must rely upon an analytic continuation of KN scattering amplitudes, which is not entirely straightforward. This is discussed in detail in Ref. [35].
Fit parameters of the best fit
We collect the various vector meson masses and couplings that appear in the spectral functions and the normalization constants of the various data sets in Table 6.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lin, YH., Hammer, HW. & Meißner, UG. Dispersion-theoretical analysis of the electromagnetic form factors of the nucleon: Past, present and future. Eur. Phys. J. A 57, 255 (2021). https://doi.org/10.1140/epja/s10050-021-00562-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epja/s10050-021-00562-0