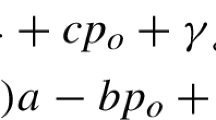Joint order and pricing decisions for fresh produce with put option contracts

Abstract

This paper investigates a newsvendor problem for fresh produce with put option contracts, in which the stochastic demand is price sensitive. The newsvendor can obtain products by ordering from a firm and return unsold products by purchasing and exercising put options. The fresh produce incurs a circulation loss in quantity during its transportation. The optimal joint order and pricing decisions for the newsvendor are analytically derived in the presence of put option contracts and circulation loss. Moreover, combined with numerical analysis, the optimal order quantity and selling price of the newsvendor are found to decrease with option price, but increase with exercise price and circulation loss, whereas the maximum expected profit is found to decrease with option price and circulation loss, but increase with exercise price. Furthermore, the newsvendor with put option contracts can deal with the risks that caused by demand uncertainty and high circulation loss of fresh produce.

Appendices

Appendix: Proof of Lemma 1

When $p_{0}$ is given, $E\left[ {\pi \left( {z_{0} } \right)} \right] = \left[ {p_{0} \left( {1 - \beta } \right) - w_{1} } \right]\frac{{y\left( {p_{0} } \right) + \mu }}{1 - \beta } - w_{1} \frac{{\varLambda \left( {z_{0} } \right)}}{1 - \beta } - \left[ {\left( {p_{0} + g} \right)\left( {1 - \beta } \right) - w_{1} } \right]\frac{{\varTheta \left( {z_{0} } \right)}}{1 - \beta }$. As $\frac{{{\text{d}}E\left[ {\pi \left( {z_{0} } \right)} \right]}}{{{\text{d}}z_{0} }} = - w_{1} + (p_{0} + g)\left( {1 - \beta } \right)\left\{ {1 - F\left[ {z_{0} \left( {1 - \beta } \right)} \right]} \right\}$ and $\frac{{{\text{d}}^{2} E\left[ {\pi \left( {z_{0} } \right)} \right]}}{{{\text{d}}z_{0}^{2} }} = - \left( {p_{0} + g} \right)\left( {1 - \beta } \right)^{2} f\left[ {z_{0} \left( {1 - \beta } \right)} \right] < 0$, $E\left[ {\pi \left( {z_{0} } \right)} \right]$ is concave in $z_{0}$. Thus, the unique optimal $z_{0}^{*}$ is set by $\frac{{{\text{d}}E\left[ {\pi \left( {z_{0} } \right)} \right]}}{{{\text{d}}z_{0} }} = 0$, that is, $z_{0}^{*}$ is the unique $z_{0}$ in the region $\left[ {A,B} \right]$ that satisfies $\left( {p_{0} + g} \right)\left( {1 - \beta } \right)\left\{ {1 - F\left[ {z_{0} \left( {1 - \beta } \right)} \right]} \right\} = w_{1}$, and $q_{0}^{*} = \frac{{y\left( {p_{0} } \right)}}{1 - \beta } + z_{0}^{*}$.

When $z_{0}$ is given, $E\left[ {\pi \left( {p_{0} } \right)} \right] = \left[ {p_{0} \left( {1 - \beta } \right) - w_{1} } \right]\frac{{y\left( {p_{0} } \right) + \mu }}{1 - \beta } - w_{1} \frac{{\varLambda \left( {z_{0} } \right)}}{1 - \beta } - \left[ {\left( {p_{0} + g} \right)\left( {1 - \beta } \right) - w_{1} } \right]\frac{{\varTheta \left( {z_{0} } \right)}}{1 - \beta }$. As $\frac{{{\text{d}}E\left[ {\pi \left( {p_{0} } \right)} \right]}}{{{\text{d}}p_{0} }} = 2b\left( {\bar{p}_{0} - p_{0} } \right) - \varTheta \left( {z_{0} } \right)$ and $\frac{{{\text{d}}^{2} E\left[ {\pi \left( {p_{0} } \right)} \right]}}{{{\text{d}}p_{0}^{2} }} = - 2b < 0$, $E\left[ {\pi \left( {p_{0} } \right)} \right]$ is concave in $p_{0}$. Thus, the optimal $p_{0}^{*}$ is set by $\frac{{{\text{d}}E\left[ {\pi \left( {p_{0} } \right)} \right]}}{{{\text{d}}p_{0} }} = 0$. We then have $p_{0}^{*} = \bar{p}_{0} - \frac{{\varTheta \left( {z_{0} } \right)}}{2b}$, where $\bar{p}_{0} = \frac{{a + \frac{{bw_{1} }}{1 - \beta } + \mu }}{2b}$.

Proof of Proposition 1

We obtain $\frac{{{\text{dE}}\left[ {\pi (z_{0} ,p_{0} (z_{0} ))} \right]}}{{{\text{d}}z_{0} }} = - w_{1} + \left( {\bar{p}_{0} - \frac{{\varTheta \left( {z_{0} } \right)}}{2b} + g} \right)\left( {1 - \beta } \right)\left\{ {1 - F\left[ {z_{0} \left( {1 - \beta } \right)} \right]} \right\}$ by substituting $p_{0}^{*} \equiv p_{0} \left( {z_{0} } \right)$ into $E\left[ {\pi (z_{0} ,p_{0} )} \right]$. Let $R\left( {z_{0} } \right) = \frac{{{\text{dE}}\left[ {\pi (z_{0} ,p_{0} (z_{0} ))} \right]}}{{{\text{d}}z_{0} }}$. Then, $\frac{{{\text{d}}R\left( {z_{0} } \right)}}{{{\text{d}}z_{0} }} = - \left( {1 - \beta } \right)^{2} \frac{{f\left[ {z_{0} \left( {1 - \beta } \right)} \right]}}{2b}\left\{ {2b\left( {\bar{p}_{0} + g} \right) - \varTheta \left( {z_{0} } \right) - \frac{{1 - F\left[ {z_{0} \left( {1 - \beta } \right)} \right]}}{{r\left[ {z_{0} \left( {1 - \beta } \right)} \right]}}} \right\}$ and $\frac{{{\text{d}}^{2} R\left( {z_{0} } \right)}}{{{\text{d}}z_{0}^{2} }} = \frac{{{\text{d}}R\left( {z_{0} } \right)/{\text{d}}z_{0} }}{{f\left[ {z_{0} \left( {1 - \beta } \right)} \right]}} \cdot \frac{{{\text{d}}f\left[ {z_{0} \left( {1 - \beta } \right)} \right]}}{{{\text{d}}z_{0} }} - \left( {1 - \beta } \right)^{3} \frac{{f\left[ {z_{0} \left( {1 - \beta } \right)} \right]\left\{ {1 - F\left[ {z_{0} \left( {1 - \beta } \right)} \right]} \right\}}}{{2br\left[ {z_{0} \left( {1 - \beta } \right)} \right]^{2} }}\left\{ {2r\left[ {z_{0} \left( {1 - \beta } \right)} \right]^{2} + r^{'} \left[ {z_{0} \left( {1 - \beta } \right)} \right]} \right\}$. Thus, we have $\left. {\frac{{{\text{d}}^{2} R\left( {z_{0} } \right)}}{{{\text{d}}z_{0}^{2} }}} \right|_{{\frac{{{\text{d}}R\left( {z_{0} } \right)}}{{{\text{d}}z_{0} }} = 0}} = - \left( {1 - \beta } \right)^{3} \frac{{f\left[ {z_{0} \left( {1 - \beta } \right)} \right]\left\{ {1 - F\left[ {z_{0} \left( {1 - \beta } \right)} \right]} \right\}}}{{2br\left[ {z_{0} \left( {1 - \beta } \right)} \right]^{2} }}\left\{ {2r\left[ {z_{0} \left( {1 - \beta } \right)} \right]^{2} + r^{'} \left[ {z_{0} \left( {1 - \beta } \right)} \right]} \right\}$.

As $F\left( \cdot \right)$ has an increasing failure rate, $2r\left[ {z_{0} \left( {1 - \beta } \right)} \right]^{2} + r^{'} \left[ {z_{0} \left( {1 - \beta } \right)} \right] > 0$; then, $\left. {\frac{{{\text{d}}^{2} R\left( {z_{0} } \right)}}{{{\text{d}}z_{0}^{2} }}} \right|_{{\frac{{{\text{d}}R\left( {z_{0} } \right)}}{{{\text{d}}z_{0} }} = 0}} < 0$. Therefore, $R\left( {z_{0} } \right)$ obtains its maximum when $\frac{{{\text{d}}R\left( {z_{0} } \right)}}{{{\text{d}}z_{0} }} = 0$. Thus, $R\left( {z_{0} } \right)$ either is monotone or unimodal. Then, $R\left( {z_{0} } \right) = 0$ has at most two roots. Furthermore, $R\left( B \right) = - w_{1} < 0$. Thus, $R\left( {z_{0} } \right) = 0$ has only one root if $R\left( A \right) > 0$, which indicates $a - b\left( {\frac{{w_{1} }}{1 - \beta } - 2g} \right) + A\left( {1 - \beta } \right) > 0$.

Proof of Proposition 2

Following the implicit function rule, $\frac{{{\text{d}}z_{0}^{*} }}{{{\text{d}}w_{1} }} = - \left( {\frac{{\partial R\left( {z_{0}^{*} } \right)}}{{\partial w_{1} }}} \right)/\left( {\frac{{\partial R\left( {z_{0}^{*} } \right)}}{{\partial z_{0}^{*} }}} \right)$. We obtain $\frac{{\partial R\left( {z_{0}^{*} } \right)}}{{\partial w_{1} }} = - \frac{1}{2}\left\{ {1 + F\left[ {z_{0}^{*} \left( {1 - \beta } \right)} \right]} \right\} < 0$. As $z_{0}^{*}$ is the largest $z_{0}$ in the region $\left[ {A,B} \right]$ that satisfies $\frac{{{\text{d}}E\left[ {\pi (z_{0} ,p_{0} (z_{0} ))} \right]}}{{{\text{d}}z_{0} }} = 0$, and $R\left( B \right) < 0$, we obtain $\frac{{\partial R\left( {z_{0}^{*} } \right)}}{{\partial z_{0}^{*} }} < 0$. Thus, $\frac{{{\text{d}}z_{0}^{*} }}{{{\text{d}}w_{1} }} < 0$. The first part of the proof is completed.

Next, $\frac{{{\text{d}}p_{0}^{*} }}{{{\text{d}}w_{1} }} = \frac{{\partial p_{0}^{*} }}{{\partial w_{1} }} + \frac{{\partial p_{0}^{*} }}{{\partial z_{0}^{*} }}\frac{{{\text{d}}z_{0}^{*} }}{{{\text{d}}w_{1} }} = \frac{{1 - br\left[ {z_{0}^{*} \left( {1 - \beta } \right)} \right]\left[ {\bar{p}_{0} - \frac{{\varTheta \left( {z_{0}^{*} } \right)}}{2b} + g} \right]}}{{\left( {1 - \beta } \right)\left\{ {1 - F\left[ {z_{0}^{*} \left( {1 - \beta } \right)} \right] - 2br\left[ {z_{0}^{*} \left( {1 - \beta } \right)} \right]\left( {\bar{p}_{0} - \frac{{\varTheta \left( {z_{0}^{*} } \right)}}{2b} + g} \right)} \right\}}}$. Given that $\frac{{\partial R\left( {z_{0}^{*} } \right)}}{{\partial z_{0}^{*} }} < 0$, we have $1 - F\left[ {z_{0}^{*} \left( {1 - \beta } \right)} \right] - 2br\left[ {z_{0}^{*} \left( {1 - \beta } \right)} \right]\left( {\bar{p}_{0} - \frac{{\varTheta \left( {z_{0}^{*} } \right)}}{2b} + g} \right) < 0$. Thus, if $br\left[ {z_{0}^{*} \left( {1 - \beta } \right)} \right]\left[ {\bar{p}_{0} - \frac{{\varTheta \left( {z_{0}^{*} } \right)}}{2b} + g} \right] \le 1$, $\frac{{{\text{d}}p_{0}^{*} }}{{{\text{d}}w_{1} }} \le 0$; otherwise, $\frac{{{\text{d}}p_{0}^{*} }}{{{\text{d}}w_{1} }} > 0$.

Proof of Lemma 2

When $p$ is given, $\begin{aligned} E\left[ {\pi \left( {q_{2} ,z} \right)} \right] & = \left[ {p\left( {1 - \beta } \right) - w_{1} } \right]\frac{y\left( p \right) + \mu }{1 - \beta } - w_{1} \frac{{\Lambda \left( {q_{2} ,z} \right)}}{1 - \beta } \\ & \quad - \left[ {w_{2} \left( {1 - \beta } \right) - w_{1} } \right]\frac{{\Omega \left( {q_{2} ,z} \right)}}{1 - \beta } - \left[ {\left( {p + g} \right)\left( {1 - \beta } \right) - w_{1} } \right]\frac{{\Theta \left( z \right)}}{1 - \beta } \\ & \quad - \left[ {w_{0} + w_{1} - w_{2} \left( {1 - \beta } \right)} \right]q_{2} \mathop \smallint \limits_{A}^{{z\left( {1 - \beta } \right)}} f\left( x \right){\text{d}}x - w_{0} q_{2} \mathop \smallint \limits_{{z\left( {1 - \beta } \right)}}^{B} f\left( x \right){\text{d}}x \\ \end{aligned}$. $\frac{{\partial E\left[ {\pi \left( {q_{2} ,z} \right)} \right]}}{{\partial q_{2} }} = w_{2} \left( {1 - \beta } \right)F\left[ {\left( {z - q_{2} } \right)\left( {1 - \beta } \right)} \right] - w_{0}$, $\frac{{\partial^{2} E\left[ {\pi \left( {q_{2} ,z} \right)} \right]}}{{\partial q_{2}^{2} }} = - w_{2} \left( {1 - \beta } \right)^{2} f\left[ {\left( {z - q_{2} } \right)\left( {1 - \beta } \right)} \right]$, $\frac{{\partial E\left[ {\pi \left( {q_{2} ,z} \right)} \right]}}{\partial z} = \left[ {\left( {p + g} \right)\left( {1 - \beta } \right) - w_{1} } \right] - w_{2} \left( {1 - \beta } \right)F\left[ {\left( {z - q_{2} } \right)\left( {1 - \beta } \right)} \right] - \left( {p + g - w_{2} } \right)\left( {1 - \beta } \right)F\left[ {z\left( {1 - \beta } \right)} \right]$, $\frac{{\partial^{2} E\left[ {\pi \left( {q_{2} ,z} \right)} \right]}}{{\partial z^{2} }} = - w_{2} \left( {1 - \beta } \right)^{2} f\left[ {\left( {z - q_{2} } \right)\left( {1 - \beta } \right)} \right] - \left( {p + g - w_{2} } \right)\left( {1 - \beta } \right)^{2} f\left[ {z\left( {1 - \beta } \right)} \right]$, and $\frac{{\partial^{2} E\left[ {\pi \left( {q_{2} ,z} \right)} \right]}}{{\partial q_{2} \partial z}} = \frac{{\partial^{2} E\left[ {\pi \left( {q_{2} ,z} \right)} \right]}}{{\partial z\partial q_{2} }} = w_{2} \left( {1 - \beta } \right)^{2} f\left[ {\left( {z - q_{2} } \right)\left( {1 - \beta } \right)} \right]$. As $\frac{{\partial^{2} E\left[ {\pi \left( {q_{2} ,z} \right)} \right]}}{{\partial q_{2}^{2} }} = - w_{2} \left( {1 - \beta } \right)^{2} f\left[ {\left( {z - q_{2} } \right)\left( {1 - \beta } \right)} \right] < 0$ and $\left| {\begin{array}{*{20}c} {\frac{{\partial^{2} E\left[ {\pi \left( {q_{2} ,z} \right)} \right]}}{{\partial q_{2}^{2} }}} & {\frac{{\partial^{2} E\left[ {\pi \left( {q_{2} ,z} \right)} \right]}}{{\partial q_{2} \partial z}}} \\ {\frac{{\partial^{2} E\left[ {\pi \left( {q_{2} ,z} \right)} \right]}}{{\partial z\partial q_{2} }}} & {\frac{{\partial^{2} E\left[ {\pi \left( {q_{2} ,z} \right)} \right]}}{{\partial z^{2} }}} \\ \end{array} } \right| = \left( {p + g - w_{2} } \right)w_{2} \left( {1 - \beta } \right)^{4} f\left[ {z\left( {1 - \beta } \right)} \right]f\left[ {\left( {z - q_{2} } \right)\left( {1 - \beta } \right)} \right] > 0,$ the Hessian matrix of $E\left[ {\pi \left( {q_{2} ,z} \right)} \right]$ is negative definite. Thus, $E\left[ {\pi \left( {q_{2} ,z} \right)} \right]$ is jointly concave in $q_{2}$ and $z$, that is, the unique optimal $q_{2}^{*}$ and unique optimal $z^{*}$ are set by $\frac{{\partial E\left[ {\pi \left( {q_{2} ,z} \right)} \right]}}{{\partial q_{2} }} = 0$ and $\frac{{\partial E\left[ {\pi \left( {q_{2} ,z} \right)} \right]}}{\partial z} = 0$, respectively.

When $q_{2}$ and $z$ are given, $\begin{aligned} E\left[ {\pi \left( p \right)} \right] & = \left[ {p\left( {1 - \beta } \right) - w_{1} } \right]\frac{y\left( p \right) + \mu }{1 - \beta } - w_{1} \frac{{\Lambda \left( {q_{2} ,z} \right)}}{1 - \beta } - \left[ {w_{2} \left( {1 - \beta } \right) - w_{1} } \right]\frac{{\Omega \left( {q_{2} ,z} \right)}}{1 - \beta } \\ & \quad - \left[ {\left( {p + g} \right)\left( {1 - \beta } \right) - w_{1} } \right]\frac{{\Theta \left( z \right)}}{1 - \beta } - \left[ {w_{0} + w_{1} - w_{2} \left( {1 - \beta } \right)} \right]q_{2} \mathop \smallint \limits_{A}^{{z\left( {1 - \beta } \right)}} f\left( x \right)dx \\ & \quad - w_{0} q_{2} \mathop \smallint \limits_{z(1 - \beta )}^{B} f\left( x \right)dx \\ \end{aligned}$. As $\frac{{{\text{d}}E\left[ {\pi \left( p \right)} \right]}}{{{\text{d}}p}} = 2b\left( {\bar{p} - p} \right) - \varTheta \left( z \right)$ and $\frac{{{\text{d}}^{2} E\left[ {\pi \left( p \right)} \right]}}{{{\text{d}}p^{2} }} = - 2b < 0$, $E\left[ {\pi \left( p \right)} \right]$ is concave in $p$. Thus, the unique optimal $p^{*}$ is set by $\frac{{{\text{d}}E\left[ {\pi \left( p \right)} \right]}}{{{\text{d}}p}} = 0$.

Proof of Proposition 3

By substituting $p^{*} = p\left( z \right)$ into $E\left[ {\pi \left( {q_{2} ,z,p} \right)} \right]$, we obtain $\frac{{\partial E\left[ {\pi \left( {q_{2} ,z,p(z)} \right)} \right]}}{{\partial q_{2} }} = w_{2} \left( {1 - \beta } \right)F\left[ {\left( {z - q_{2} } \right)\left( {1 - \beta } \right)} \right] - w_{0}$ and $\frac{{\partial E\left[ {\pi \left( {q_{2} ,z,p(z)} \right)} \right]}}{\partial z} = w_{2} \left( {1 - \beta } \right) - w_{1} - w_{2} \left( {1 - \beta } \right)F\left[ {\left( {z - q_{2} } \right)\left( {1 - \beta } \right)} \right] + \left[ {\bar{p} - \frac{\varTheta \left( z \right)}{2b} + g - w_{2} } \right]\left( {1 - \beta } \right)\left\{ {1 - F\left[ {z\left( {1 - \beta } \right)} \right]} \right\}$. From Lemma 2, let $\frac{{\partial E\left[ {\pi \left( {q_{2} ,z,p(z)} \right)} \right]}}{{\partial q_{2} }} = 0$, we obtain $F\left[ {\left( {z - q_{2} } \right)\left( {1 - \beta } \right)} \right] = \frac{{w_{0} }}{{w_{2} \left( {1 - \beta } \right)}}$. Let $\frac{{\partial E\left[ {\pi \left( {q_{2} ,z,p(z)} \right)} \right]}}{\partial z} = 0$, we derive $\left[ {\bar{p} - \frac{\varTheta \left( z \right)}{2b} + g - w_{2} } \right] \cdot \left\{ {1 - F\left[ {z\left( {1 - \beta } \right)} \right]} \right\} = \frac{{w_{0} + w_{1} }}{1 - \beta } - w_{2}$. Therefore, $z^{*}$ is the unique $z$ in the region $\left[ {A,B} \right]$ that satisfies $\left[ {\bar{p} - \frac{\varTheta \left( z \right)}{2b} + g - w_{2} } \right] \cdot \left\{ {1 - F\left[ {z\left( {1 - \beta } \right)} \right]} \right\} = \frac{{w_{0} + w_{1} }}{1 - \beta } - w_{2}$. Given that $F\left[ {\left( {z - q_{2} } \right)\left( {1 - \beta } \right)} \right] = \frac{{w_{0} }}{{w_{2} \left( {1 - \beta } \right)}}$, $q_{2}^{*} = z^{*} - \frac{1}{1 - \beta }F^{ - 1} \left[ {\frac{{w_{0} }}{{w_{{2}} \left( {1 - \beta } \right)}}} \right]$.

Proof of Proposition 4

Let $R\left( z \right) = \frac{{{\text{d}}E\left[ {\pi \left( {q_{2} ,z,p(z)} \right)} \right]}}{{{\text{d}}z}}$. Similar to the proof of Proposition 2, $\frac{{{\text{d}}z^{*} }}{{{\text{d}}w_{0} }} = - \left( {\frac{{\partial R\left( {z^{*} } \right)}}{{\partial w_{0} }}} \right)/\left( {\frac{{\partial R\left( {z^{*} } \right)}}{{\partial z^{*} }}} \right)$. We obtain $\frac{{\partial R\left( {z^{*} } \right)}}{{\partial w_{0} }} = - 1 < 0$. As $z^{*}$ is the largest $z$ in the region [A, B] that satisfies $\frac{{dE\left[ {\pi \left( {q_{2} ,z,p(z)} \right)} \right]}}{dz} = 0$, and $R\left( B \right) = - \left[ {w_{0} + w_{1} - w_{2} \left( {1 - \beta } \right)} \right] < 0$, we derive $\frac{{\partial R\left( {z^{*} } \right)}}{{\partial z^{*} }} < 0$. Thus, $\frac{{dz^{*} }}{{dw_{0} }} < 0$. Similarly, we obtain $\frac{{\partial R\left( {z^{*} } \right)}}{{\partial w_{2} }} = F\left[ {z^{*} \left( {1 - \beta } \right)} \right]\left( {1 - \beta } \right) > 0$, and $\frac{{{\text{d}}z^{*} }}{{{\text{d}}w_{2} }} = - \left( {\frac{{\partial R\left( {z^{*} } \right)}}{{\partial w_{2} }}} \right)/\left( {\frac{{\partial R\left( {z^{*} } \right)}}{{\partial z^{*} }}} \right) > 0$.

Next, we have $\frac{{dp^{*} }}{{dw_{0} }} = \frac{{\partial p^{*} }}{{\partial z^{*} }}\frac{{{\text{d}}z^{*} }}{{{\text{d}}w_{0} }}$. Given that $\frac{{\partial p^{*} }}{{\partial z^{*} }} = \frac{{\left( {1 - \beta } \right)\left\{ {1 - F\left[ {z^{*} \left( {1 - \beta } \right)} \right]} \right\}}}{2b} > 0$ combined with $\frac{{{\text{d}}z^{*} }}{{{\text{d}}w_{0} }} < 0$, we obtain $\frac{{{\text{d}}p^{*} }}{{{\text{d}}w_{0} }} < 0$. Similarly, we have $\frac{{{\text{d}}p^{*} }}{{{\text{d}}w_{2} }} = \frac{{\partial p^{*} }}{{\partial z^{*} }}\frac{{{\text{d}}z^{*} }}{{{\text{d}}w_{2} }}$. As $\frac{{\partial p^{*} }}{{\partial z^{*} }} > 0$, combined with $\frac{{{\text{d}}z^{*} }}{{{\text{d}}w_{2} }} > 0$, we obtain $\frac{{{\text{d}}p^{*} }}{{{\text{d}}w_{2} }} > 0$.

Proof of Proposition 5

From Proposition 3, we have $q_{2}^{*} = z^{*} - \frac{1}{1 - \beta }F^{ - 1} \left[ {\frac{{w_{0} }}{{w_{{2}}\left( {1 - \beta } \right) }}} \right]$. Let $x = \frac{{w_{0} }}{{w_{{2}}\left( {1 - \beta } \right) }}$. Thus, $x$ increases with $w_{0}$. Given that $F^{ - 1} \left[ x \right]$ increases with $x$, $F^{ - 1} \left[ x \right]$ increases with $w_{0}$. In Proposition 4, $z^{*}$ decreases with $w_{0}$. Thus, $q_{2}^{*}$ decreases with $w_{0}$. Similarly, $x$ decreases with $w_{2}$. Given that $F^{ - 1} \left[ x \right]$ increases with $x$, $F^{ - 1} \left[ x \right]$ decreases with $w_{2}$. In Proposition 4, $z^{*}$ increases with $w_{2}$. Thus, $q_{2}^{*}$ increases with $w_{2}$.