Pricing strategy with quality improvement in a dual collection channel closed-loop supply chain under return uncertainty

Abstract

A closed-loop supply chain (CLSC) is the process of restoring the used product to useful life. The quantity of returned products has environmental and economic impacts on the CLSC. But, for the implementation of CLSC, one of the major barriers is the uncertain quantity of returned products. Therefore, we examine a two-period CLSC model with a dual collection channel under uncertainty in return quantity. In the model, a third party and a manufacturer compete to collect used products based on the acquisition prices offered to consumers in the second period. During the first period, the manufacturer relies solely on raw materials to produce a new product. In the second period, the manufacturer produces an improved product using both raw materials and used products. Because an improved new version of the product is now available, some consumers decide to return their first-period purchases for the improved product. The problem is formulated as a two-period newsvendor model and solved using the backward induction approach. It is shown that the acquisition price and transfer price offered by the manufacturer increase the quantity of the returned product. The acquisition price offered by the third party first increases and then decreases if the competition between the collectors is low, but the acquisition price increases when the competition is high.

Appendices

Appendix A

Proof of Proposition 1

2.1 The second period

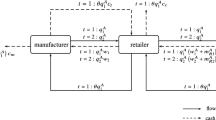
In the second period, the decision is made by the manufacturer first, then by the retailer, and finally by the third party. Based on the former choices made by the manufacturer and retailer, we determine the third party's reaction. After that, given the manufacturer's prior choices, the retailer's optimal reaction is determined. Finally, the manufacturer's second-period response is calculated.

The third party determines the optimal acquisition price ${p}_{t}$ by optimising its expected profit during the second period $E\left[{\pi }_{t}\left({p}_{t}\right)\right]$ in Eq. (9), the first derivative of $E\left[{\pi }_{t}\left({p}_{t}\right)\right]$ w.r.t. ${p}_{t}$ is obtained as

$$\frac{\partial E\left[{\pi }_{t}\left({p}_{t}\right)\right]}{\partial {p}_{t}}= -q-Q\gamma +\beta {p}_{m}+\alpha \left({b}_{t}-{p}_{t}\right)-\alpha {p}_{t}-{\mu }_{t}.$$

(21)

Since $E\left[{\pi }_{t}\left({p}_{t}\right)\right]$ is concave in ${p}_{t}$ for $\alpha >0$ as

$\frac{{\partial }^{2}E\left[{\pi }_{t}\left({p}_{t}\right)\right]}{\partial {p}_{t}^{2}}= -2\alpha <0.$

Hence, by setting $\frac{\partial E\left[{\pi }_{t}\left({p}_{t}\right)\right]}{\partial {p}_{t}}=0$, we get

$${p}_{t}\left({b}_{t},{p}_{m},Q\right)=\frac{-q-Q\gamma +\alpha {b}_{t}+\beta {p}_{m}-{\mu }_{t}}{2\alpha }.$$

(22)

The retailer decides the optimal price ${p}_{2}$ by maximising its expected profit in the second period,

$E\left[{\pi }_{r,2}\left({p}_{2}\right)\right]=\left({p}_{2}-{w}_{2}\right)\left(a-b{p}_{2}+\upsilon Q\right).$

The first derivative of $E\left[{\pi }_{r,2}\left({p}_{2}\right)\right]$ w.r.t. ${p}_{2}$ can be written as

$$\frac{\partial E\left[{\pi }_{r,2}\left({p}_{2}\right)\right]}{\partial {p}_{2}}=a+Q\upsilon -b{p}_{2}-b\left({p}_{2}-{w}_{2}\right),$$

(23)

and $E\left[{\pi }_{r,2}\left({p}_{2}\right)\right]$ is concave in ${p}_{2}$ for $b>0$ since $\frac{{\partial }^{2}E\left[{\pi }_{r,2}\left({p}_{2}\right)\right]}{\partial {p}_{2}^{2}}=-2b<0.$

Hence, by setting $\frac{\partial E\left[{\pi }_{r,2}\left({p}_{2}\right)\right]}{\partial {p}_{2}}=0$, the retailer’s best reaction is obtained as

$${p}_{2}\left({w}_{2},Q\right)=\frac{a+Q\upsilon +b{w}_{2}}{2b}.$$

(24)

Finally, the manufacturer maximises its second-period expected profit in Eq. (4), considering the reactions of the third-party collector and retailer to obtain the optimal response. Therefore, using Eq. (4), the partial derivatives of $E\left[{\pi }_{m,2}\right]$ w.r.t. ${w}_{2}, {p}_{m},{b}_{t},Q$ and $z$ can be obtained, respectively, as

$$\frac{\partial E\left[{\pi }_{m,2}\left({{w}_{2},p}_{m},{b}_{t},Q,z\right)\right]}{\partial {w}_{2}}=\frac{1}{2}\left(a+Q\upsilon +b{c}_{m}-2b{w}_{2}\right),$$

(25)

$$\frac{\partial E\left[{\pi }_{m,2}\left({{w}_{2},p}_{m},{b}_{t},Q,z\right)\right]}{\partial {p}_{m}}=\frac{2\alpha \beta {b}_{t}-\left(2\alpha +\beta \right)\left[q+Q\gamma -\left(\alpha -\beta \right)\tau \Delta \right]-\left(4{\alpha }^{2}-2{\beta }^{2}\right){p}_{m}-2\alpha {\mu }_{m}-\beta {\mu }_{t}}{2\alpha },$$

(26)

$$\frac{\partial E\left[{\pi }_{m,2}\left({{w}_{2},p}_{m},{b}_{t},Q,z\right)\right]}{\partial {b}_{t}}= \frac{\left(\alpha -\beta \right)\tau \Delta -2\alpha {b}_{t}+2\beta {p}_{m}-{\mu }_{t}-q-Q\gamma }{2},$$

(27)

$$\frac{\partial E\left[{\pi }_{m,2}\left({{w}_{2},p}_{m},{b}_{t},Q,z\right)\right]}{\partial Q}=\frac{\left(3\alpha +\beta \right)\gamma \tau \Delta -2Q\alpha \delta -\alpha \gamma {b}_{t}-\alpha \upsilon {c}_{m}-\left(2\alpha +\beta \right)\gamma {p}_{m}+\alpha \upsilon {w}_{2}}{2\alpha }$$

(28)

and

$$\frac{\partial E\left[{\pi }_{m,2}\left({{w}_{2},p}_{m},{b}_{t},Q,z\right)\right]}{\partial z}=-\tau s+\tau \left(\Delta +s+h\right)\left(1-F\left(z\right)\right).$$

(29)

It can be demonstrated that the Hessian matrix provided below is negative definite if $\delta >\frac{b\left(3\alpha +\beta \right){\gamma }^{2}+\alpha \left(\alpha -\beta \right){\upsilon }^{2}}{4b\alpha \left(\alpha -\beta \right)}$.

$${H}_{m,2}=\left[\begin{array}{ccccc}-b& 0& 0& \frac{\upsilon }{2}& 0\\ 0& -2\alpha +\frac{{\beta }^{2}}{\alpha }& \beta & -\frac{\left(2\alpha +\beta \right)\gamma }{2\alpha }& 0\\ 0& \beta & -\alpha & -\frac{\gamma }{2}& 0\\ \frac{\upsilon }{2}& -\frac{\left(2\alpha +\beta \right)\gamma }{2\alpha }& -\frac{\gamma }{2}& -\delta & 0\\ 0& 0& 0& 0& -\tau \left(\Delta +s+h\right)f\left(z\right)\end{array} \right].$$

By setting the first-order derivatives in Eqs. (25)–(29) to zero and solving them simultaneously to obtain the manufacturer's second-period best reaction, we get

$${w}_{2}\left(Q\right)=\frac{a+Q\upsilon +b{c}_{m}}{2b},$$

(30)

$${p}_{m}\left(Q\right)=\frac{\left(\alpha +\beta \right)\left(\left(\alpha -\beta \right)\tau \Delta -q-Q\gamma \right)-\alpha {\mu }_{m}-\beta {\mu }_{t}}{2({\alpha }^{2}-{\beta }^{2})},$$

(31)

$${b}_{t}\left(Q\right)=\frac{\left(\alpha +\beta \right)\left(\left(\alpha -\beta \right)\tau \Delta -q-Q\gamma \right)-\alpha {\mu }_{m}-\beta {\mu }_{t}}{2({\alpha }^{2}-{\beta }^{2})},$$

(32)

$$Q=\frac{b\left(3\alpha +\beta \right)\left(q+\left(\alpha -\beta \right)\tau \Delta \right)\gamma +\alpha \left(\alpha -\beta \right)\left(a-b{c}_{m}\right)\upsilon +2b\alpha \gamma {\mu }_{m}+b\left(\alpha +\beta \right)\gamma {\mu }_{t}}{\left[\alpha \left(\alpha -\beta \right)\left(4b\delta -{\upsilon }^{2}\right)-b\left(3\alpha +\beta \right){\gamma }^{2}\right]}$$

(33)

and

$$z={F}^{-1}\left(\frac{\Delta +h}{\Delta +h+s}\right).$$

(34)

The first period

Based on all members' second-period reactions and the manufacturer's first-period decision, we calculate the retailer's best first-period reaction. The retailer sets ${p}_{1}$ to maximise the expected profit. Thus, the total expected profit of the retailer in Eq. (7) is expressed as a function of ${p}_{1}$ and ${w}_{1}$ using Eqs. (22), (24) and (30)–(34), and then differentiating $E\left[{\pi }_{r}\right]$ w.r.t. ${p}_{1}$, we get

$$\frac{\partial E\left[{\pi }_{r}\right]}{ \partial {p}_{1}}=a-b{p}_{1}-b\left({p}_{1}-{w}_{1}\right),$$

(35)

and again differentiating $E\left[{\pi }_{r}\right]$ w.r.t. ${p}_{1}$, we obtain.

$\frac{{\partial }^{2}E\left[{\pi }_{r}\right]}{ \partial {p}_{1}^{2}}=-2b\le 0.$

By setting $\frac{\partial E\left[{\pi }_{r}\right]}{ \partial {p}_{1}}$ to zero and solving for ${p}_{1}$, the retailer’s optimal first-period reaction is obtained as

$${p}_{1}\left({w}_{1}\right)=\frac{a+b{w}_{1}}{2b}.$$

(36)

Based on the best first-period response of the retailer, the manufacturer will maximise its total expected profit in Eq. (5) by optimising the wholesale price ${w}_{1}$, which is subjected to a constraint that the return quantity in the second period should not exceed the demand in the first period, i.e.

$2q+\left(\alpha -\beta \right)\left({p}_{m}+{p}_{t}\right)+2\gamma Q+\epsilon \le a-b{p}_{1}.$

On substituting the second-period responses of all members from Eqs. (22), (24), (30) to (34) and the retailer's reaction from Eq. (36) into Eq. (5), and applying the KKT conditions, we obtain

$$\frac{\partial E\left[{\pi }_{m}\left({w}_{1}\right)\right]}{\partial {w}_{1}}=a+\frac{b\lambda }{2}-\frac{1}{2}b\left({w}_{1}-{c}_{m}\right)-\frac{1}{2}\left(a+b{w}_{1}\right)=0$$

(37)

and

$$\lambda \left[\left(2q+\left(\alpha -\beta \right)\left({p}_{m}+{p}_{t}\right)+2\gamma Q+\epsilon \right)-\left(a-b{p}_{1}\right)\right]=0.$$

(38)

Again differentiating $E\left[{\pi }_{m}\left({w}_{1}\right)\right]$ w.r.t. ${w}_{1}$, we get

$\frac{{\partial }^{2}E\left[{\pi }_{m}\left({w}_{1}\right)\right]}{\partial {w}_{1}^{2}}= -b<0.$

By solving Eqs. (37) and (38) for ${w}_{1}$, the manufacturer's first-period optimal wholesale price is obtained as

$${w}_{1}=\frac{a+b{c}_{m}}{2b}.$$

(39)

Also, to satisfy the non-negativity requirement of the decision variables, the conditions are obtained as.

$q\le \left(\alpha -\beta \right)\tau \Delta -{Q}^{*}\gamma$ and $q\le \frac{\left({\alpha }^{2}-{\beta }^{2}\right)\tau \Delta }{3\alpha -\beta }-{Q}^{*}\gamma$.

Here, both the above conditions will be satisfied if

$q\le \frac{\left({\alpha }^{2}-{\beta }^{2}\right)\tau \Delta }{3\alpha -\beta }-{Q}^{*}\gamma.$

Therefore, on substituting the expression of ${Q}^{*}$ from Eq. (14) in the above condition, we get

$$q\le \frac{\left({\alpha }^{2}-{\beta }^{2}\right)\tau\Delta }{3\alpha -\beta }\left(1-\frac{b\left(3\alpha +\beta \right){\gamma }^{2}}{\alpha \left(\alpha -\beta \right)\left(4b\delta -{\upsilon }^{2}\right)}\right)-\frac{b\left(\alpha -\beta \right)\left(3\alpha +\beta \right){\gamma }^{2}\tau\Delta +\alpha \left(a-b{c}_{m}\right)\left(\alpha -\beta \right)\upsilon \gamma +2\alpha b\gamma {\mu }_{m}+b\left(\alpha +\beta \right)\gamma {\mu }_{t}}{\alpha \left(\alpha -\beta \right)\left(4b\delta -{\upsilon }^{2}\right)}$$

(40)

Hence, in order to obtain a unique optimal solution, $q$ should satisfy constraint (40) along with constraint (5).

Appendix B

Proof of comparison between single collection channel and dual collection channel

5.1 Proof of Corollary

For the dual collection channel, differentiating Eq. (14) w.r.t. $\alpha$, $\beta$, $b$ and $\tau$, we get

$$\frac{\partial {Q}^{*}}{\partial \alpha }=-b\gamma \left(\left(3\alpha -\beta \right)\left(\alpha +\beta \right)\left(4b\updelta q+\upsilon \left(\left(a-b{c}_{m}\right)\gamma -q\upsilon \right)\right)+\tau \left(b{\left(3\alpha +\beta \right)}^{2}{\gamma }^{2}+{\left(\alpha -\beta \right)}^{2}\beta \left(4b\delta -{\upsilon }^{2}\right)\right)\Delta +2\left(b\beta {\gamma }^{2}+4b{\alpha }^{2}\delta -{\alpha }^{2}{\upsilon }^{2}\right){\mu }_{m}+\left(4b{\alpha }^{2}\delta -2b\beta \left({\gamma }^{2}-4\alpha \delta +2\beta \delta \right)-\left({\alpha }^{2}+2\alpha \beta -{\beta }^{2}\right){\upsilon }^{2}\right){\mu }_{t}\right)<0,$$

(41)

$$\frac{\partial {Q}^{*}}{\partial \beta }=b\gamma \left(16bq{\alpha }^{2}\delta +b\left({\left(3\alpha +\beta \right)}^{2}{\gamma }^{2}+4\alpha {\left(\alpha -\beta \right)}^{2}\delta \right)\tau \Delta -\alpha \upsilon \left(4\alpha \left(q\upsilon -a\gamma +b{\gamma c}_{m}\right)+{\upsilon \left(\alpha -\beta \right)}^{2}\tau \Delta \right)+2\alpha \left(\left(b{\gamma }^{2}+4b\alpha \delta -\alpha {\upsilon }^{2}\right){\mu }_{m}-\left(b{\gamma }^{2}-4b\alpha \delta +\alpha {\upsilon }^{2}\right){\mu }_{t}\right)\right)>0,$$

(42)

$$\frac{\partial {Q}^{*}}{\partial b}=-\alpha \left(\alpha -\beta \right)\upsilon \left[4a\alpha \left(\alpha -\beta \right)\delta -a\left(3\alpha +\beta \right){\gamma }^{2}+\left(3\alpha +\beta \right)\gamma \left(q+\left(\alpha -\beta \right)\tau \Delta \right)\upsilon +\alpha \upsilon \left(2\gamma {\mu }_{m}-\left(\alpha -\beta \right)\upsilon {c}_{m}\right)+\left(\alpha +\beta \right)\gamma \upsilon {\mu }_{t}\right]<0$$

(43)

and

$$\frac{\partial {Q}^{*}}{\partial \tau }=\frac{b\left(\alpha -\beta \right)\left(3\alpha +\beta \right)\gamma \Delta }{4b\alpha \left(\alpha -\beta \right)\delta -b\left(3\alpha +\beta \right){\gamma }^{2}-\alpha \left(\alpha -\beta \right){\upsilon }^{2}}>0.$$

(44)

For the single collection channel with the manufacturer as the collector and the conditions $\beta =0, {\mu }_{t}=0$, the first hand derivative of Eq. (14) w.r.t. $\alpha$, $b$ and $\tau$, are obtained as

$$\frac{\partial {Q}^{*}}{\partial \alpha }=-\frac{4b\gamma \left(8bq\delta +8b{\gamma }^{2}\tau \Delta +\left(4b\delta -{\upsilon }^{2}\right){\mu }_{m}+2a\gamma \upsilon -2q{\upsilon }^{2}-2b\gamma \upsilon {c}_{m}\right)}{{\left(8b{\gamma }^{2}-4b\alpha \delta +\alpha {\upsilon }^{2}\right)}^{2}}<0,$$

(45)

$$\frac{\partial {Q}^{*}}{\partial b}=-\frac{\alpha \upsilon \left(4\left(a\alpha \delta +2q\gamma \upsilon +\alpha \gamma \tau \Delta \upsilon +\gamma \upsilon {\mu }_{m}-2a{\gamma }^{2}\right)-\alpha {\upsilon }^{2}{c}_{m}\right)}{{\left(8b{\gamma }^{2}-4b\alpha \delta +\alpha {\upsilon }^{2}\right)}^{2}}<0$$

(46)

and

$$\frac{\partial {Q}^{*}}{\partial \tau }=\frac{4b\alpha \gamma \Delta }{4b\alpha \delta -8b{\gamma }^{2}-\alpha {\upsilon }^{2}}>0.$$

(47)

For the single collection channel with the third party as the collector and the conditions $\beta =0, {\mu }_{m}=0$, on differentiating Eq. (14) w.r.t $\alpha$, $b$ and $\tau$, we obtain

$$\frac{\partial {Q}^{*}}{\partial \alpha }=-\frac{3b\gamma \left(3\left(4bq\delta +3b{\gamma }^{2}\tau \Delta +a\gamma \upsilon -q{\upsilon }^{2}\right)-3b\gamma \upsilon {c}_{m}+\left(4b\delta -{\upsilon }^{2}\right){\mu }_{t}\right)}{{\left(9b{\gamma }^{2}-4b\alpha \delta +\alpha {\upsilon }^{2}\right)}^{2}}<0,$$

(48)

$$\frac{\partial {Q}^{*}}{\partial b}=-\frac{\alpha \upsilon \left(4a\alpha \delta +9q\gamma \upsilon +3\alpha \gamma \tau \Delta \upsilon +3\gamma \upsilon {\mu }_{t}-9a{\gamma }^{2}-\alpha {\upsilon }^{2}{c}_{m}\right)}{{\left(9b{\gamma }^{2}-4b\alpha \delta +\alpha {\upsilon }^{2}\right)}^{2}}<0$$

(49)

and

$$\frac{\partial {Q}^{*}}{\partial \tau }=\frac{3b\alpha \gamma \Delta }{4b\alpha \delta -9b{\gamma }^{2}-\alpha {\upsilon }^{2}}>0.$$

(50)

Proof of Proposition 2

For the comparison between the single collection channel with the third party as the collector and the dual collection channel with no collection competition, we get equivalent return quantity as ${\widehat{q}}_{t}=2q+\alpha {p}_{t}+2\gamma Q+{\epsilon }_{t}$ and $\beta =0$ in Eqs. (10)–(18) and obtain.

if $a\ge \frac{3b\alpha \gamma \upsilon {c}_{m}+\left(4b\alpha \delta -9b{\gamma }^{2}-\alpha {\upsilon }^{2}\right){\mu }_{m}-\alpha \left(\left(3q+{\mu }_{t}\right)\left(4b\delta -{\upsilon }^{2}\right)+9b{\gamma }^{2}\tau \Delta \right)}{3\alpha \gamma \upsilon }$, then

$${Q}^{D*}-{Q}^{S*}=\frac{2b\gamma \left[\left(4b\alpha \delta -9b{\gamma }^{2}-\alpha {\upsilon }^{2}\right){\mu }_{m}-\alpha \left(\left(3q+{\mu }_{t}\right)\left(4b\delta -{\upsilon }^{2}\right)+9b{\gamma }^{2}\tau \Delta \right)-\left(a-b{c}_{m}\right)3\alpha \gamma \upsilon \right]}{\left(4b\alpha \delta -3b{\gamma }^{2}-\alpha {\upsilon }^{2}\right)\left(4b\alpha \delta -9b{\gamma }^{2}-\alpha {\upsilon }^{2}\right)}\le 0,$$

(51)

$${p}_{2}^{D*}-{p}_{2}^{S*}=\frac{3\gamma \upsilon \left[3\alpha \left(q\left(4b\delta -{\upsilon }^{2}\right)+3b{\gamma }^{2}\tau \Delta +\left(a-b{c}_{m}\right)\gamma \upsilon \right)-\left(4b\alpha \delta -9b{\gamma }^{2}-\alpha {\upsilon }^{2}\right){\mu }_{m}+\alpha \left(4b\delta -{\upsilon }^{2}\right){\mu }_{t}\right]}{2\left(4b\alpha \delta -3b{\gamma }^{2}-\alpha {\upsilon }^{2}\right)\left(4b\alpha \delta -9b{\gamma }^{2}-\alpha {\upsilon }^{2}\right)}\le 0,$$

(52)

$${w}_{2}^{D*}-{w}_{2}^{S*}=\frac{\alpha \left[q\left(4b\delta -{\upsilon }^{2}\right)+3b{\gamma }^{2}\tau \Delta +\left(a-b{c}_{m}\right)\gamma \upsilon \right]\left(3b{\gamma }^{2}+8b\alpha \delta -2\alpha {\upsilon }^{2}\right)}{2\alpha \left(4b\alpha \delta -9b{\gamma }^{2}-\alpha {\upsilon }^{2}\right)\left(4b\alpha \delta -3b{\gamma }^{2}-\alpha {\upsilon }^{2}\right)}+\frac{b\gamma \left[9\gamma \left(4b\alpha \delta -2b{\gamma }^{2}-\alpha {\upsilon }^{2}\right){\mu }_{t}-3\gamma \left(4b\alpha \delta -9b{\gamma }^{2}-\alpha {\upsilon }^{2}\right){\mu }_{m}\right]}{2\alpha \left(4b\alpha \delta -9b{\gamma }^{2}-\alpha {\upsilon }^{2}\right)\left(4b\alpha \delta -3b{\gamma }^{2}-\alpha {\upsilon }^{2}\right)}\le 0$$

(53)

and

$${p}_{t}^{D*}-{p}_{t}^{S*}=\frac{\left(4b{\alpha }^{2}\delta -30b\alpha {\gamma }^{2}-{\alpha }^{2}{\upsilon }^{2}\right)\tau \Delta -7q\alpha \left(4b\delta -{\upsilon }^{2}\right)-7\alpha \gamma \upsilon \left(a-b{c}_{m}\right)+3\left(2b{\gamma }^{2}-4b\alpha \delta +\alpha {\upsilon }^{2}\right){\mu }_{t}}{4\alpha \left(9b{\gamma }^{2}-4b\alpha \delta +\alpha {\upsilon }^{2}\right)}-\frac{3\alpha \left(q\left(4b\delta -{\upsilon }^{2}\right)+\left(a-b{c}_{m}\right)\gamma \upsilon \right)+\alpha \left(12b{\gamma }^{2}-4b\alpha \delta +\alpha {\upsilon }^{2}\right)\tau \Delta +6b{\gamma }^{2}{\mu }_{m}+\left(12b\alpha \delta -6b{\gamma }^{2}-3\alpha {\upsilon }^{2}\right){\mu }_{t}}{4\alpha \left(4b\alpha \delta -3b{\gamma }^{2}-\alpha {\upsilon }^{2}\right)}\le 0,$$

(54)

Based on above results, $E\left[{\pi }_{t}^{D*}\right]-E\left[{\pi }_{t}^{S*}\right]\le 0$,$E\left[{\pi }_{r}^{D*}\right]-E\left[{\pi }_{r}^{S*}\right]\ge 0$ and $E\left[{\pi }_{m}^{D*}\right]-E\left[{\pi }_{m}^{S*}\right]\ge 0$.

Hence, Proposition 2 is proved.

Proof of Proposition 3

For the comparison between the single collection channel with the manufacturer as the collector and the dual collection channel with no collection competition, we get equivalent return quantity as ${\widehat{q}}_{m}=2q+\alpha {p}_{t}+2\gamma Q+{\epsilon }_{m}$ and $\beta =0$ in Eqs. (10)–(18) and obtain.

If $a\ge \frac{\alpha \left(5q+\alpha \tau \Delta \right){\upsilon }^{2}+5b\alpha \gamma \upsilon {c}_{m}+\left(4b\alpha \delta -8b{\gamma }^{2}-\alpha {\upsilon }^{2}\right){\mu }_{t}-4b\alpha \left(5q\delta +\left(3{\gamma }^{2}+\alpha \delta \right)\tau \Delta \right)-\left(4b\left({\gamma }^{2}+2\alpha \delta \right)-2\alpha {\upsilon }^{2}\right){\mu }_{m}}{5\alpha \gamma \upsilon }$, then

$${Q}^{D*}-{Q}^{S*}=\frac{3b\gamma \left(q+\alpha \tau \Delta \right)+\left(a-b{c}_{m}\right)\alpha \upsilon +b\gamma \left(2{\mu }_{m}+{\mu }_{t}\right)}{4b\alpha \delta -3b{\gamma }^{2}-\alpha {\upsilon }^{2}}-\frac{4b\gamma \left(2q+\alpha \tau \Delta \right)+\left(a-b{c}_{m}\right)\alpha \upsilon +4b\gamma {\mu }_{m}}{4b\alpha \delta -8b{\gamma }^{2}-\alpha {\upsilon }^{2}}\ge 0,$$

(55)

$${p}_{2}^{D*}-{p}_{2}^{S*}=\frac{\left(3b{\gamma }^{2}-4b\alpha \delta +4\alpha {\upsilon }^{2}\right){c}_{m}-3\left(a\left(4\alpha \delta -3{\gamma }^{2}\right)+3\gamma \left(q+\alpha \Delta \tau \right)\upsilon +\gamma \upsilon \left(2{\mu }_{m}+{\mu }_{t}\right)\right)}{4\left(3b{\gamma }^{2}-4b\alpha \delta +\alpha {\upsilon }^{2}\right)}-\frac{\left(9b{\gamma }^{2}-4b\alpha \delta +4\alpha {\upsilon }^{2}\right){c}_{m}-3\left(4a\alpha \delta +3\left(3q+\alpha \tau \Delta +{\mu }_{t}\right)\gamma \upsilon -9a{\gamma }^{2}\right)}{4\left(9b{\gamma }^{2}-4b\alpha \delta +\alpha {\upsilon }^{2}\right)}\ge 0,$$

(56)

$${w}_{2}^{D*}-{w}_{2}^{S*}=\frac{a\left(3{\gamma }^{2}-4\alpha \delta \right)-3\gamma \left(q+\alpha \tau \Delta \right)\upsilon +\left(3b{\gamma }^{2}-4b\alpha \delta +2\alpha {\upsilon }^{2}\right){c}_{m}-\gamma \upsilon \left(2{\mu }_{m}+{\mu }_{t}\right)}{2\left(3b{\gamma }^{2}-4b\alpha \delta +\alpha {\upsilon }^{2}\right)}-\frac{\left(4b{\gamma }^{2}-2b\alpha \delta +\alpha {\upsilon }^{2}\right){c}_{m}-2\left[\left(2q+\alpha \tau \Delta +{\mu }_{m}\right)\gamma \upsilon -2a{\gamma }^{2}+a\alpha \delta \right]}{8b{\gamma }^{2}-4b\alpha \delta +\alpha {\upsilon }^{2}}\ge 0$$

(57)

and

$${p}_{m}^{D*}-{p}_{m}^{S*}=\frac{q\alpha \left(4b\delta -{\upsilon }^{2}\right)+\left(6b\alpha {\gamma }^{2}-4b{\alpha }^{2}\delta +{\alpha }^{2}{\upsilon }^{2}\right)\tau \Delta +\left(a-b{c}_{m}\right)\alpha \gamma \upsilon +b{\gamma }^{2}{\mu }_{t}-\left(b{\gamma }^{2}-4b\alpha \delta +\alpha {\upsilon }^{2}\right){\mu }_{m}}{2\alpha \left(4b\alpha \delta -3b{\gamma }^{2}-\alpha {\upsilon }^{2}\right)}-\frac{2\left(a-b{c}_{m}\right)\gamma \upsilon +2\left(4b\delta -{\upsilon }^{2}\right)q+\left(4b\delta -{\upsilon }^{2}\right){\mu }_{m}-\left(4b\alpha \delta -16b{\gamma }^{2}-\alpha {\upsilon }^{2}\right)\tau \Delta }{2\left(4b\alpha \delta -8b{\gamma }^{2}-\alpha {\upsilon }^{2}\right)}\ge 0.$$

(58)

Based on above results, $E\left[{\pi }_{r}^{D*}\right]-E\left[{\pi }_{r}^{S*}\right]\le 0$ and $E\left[{\pi }_{m}^{D*}\right]-E\left[{\pi }_{m}^{S*}\right]\le 0$.

Hence, Proposition 3 is proved.

Proof of Proposition 4

For the comparison between two single collection channels with the manufacturer as the collector and the third party as the collector, we get equivalent return quantity as ${\widehat{q}}_{t}=2q+\alpha {p}_{t}+2\gamma Q+{\epsilon }_{t}$ and ${\widehat{q}}_{m}=2q+\alpha {p}_{t}+2\gamma Q+{\epsilon }_{m}$ and obtain.

If $a\ge \frac{4\left(4b\alpha \delta -9b{\gamma }^{2}-\alpha {\upsilon }^{2}\right){\mu }_{m}+\alpha \left(4b\delta -{\upsilon }^{2}\right)\left(\alpha \tau \Delta -q\right)-3\left(4b\alpha \delta -8b{\gamma }^{2}-\alpha {\upsilon }^{2}\right){\mu }_{t}-\left(12\gamma \tau \Delta -\upsilon {c}_{m}\right)b\alpha \gamma }{\alpha \gamma \upsilon }$, then

$${Q}^{m*}-{Q}^{t*}=\frac{9bq\gamma +3b\alpha \gamma \tau \Delta +\left(a-b{c}_{m}\right)\alpha \upsilon +3b\gamma {\mu }_{t}}{9b{\gamma }^{2}-4b\alpha \delta +\alpha {\upsilon }^{2}} -\frac{8bq\gamma +4b\alpha \gamma \tau \Delta +\left(a-b{c}_{m}\right)\alpha \upsilon +4b\gamma {\mu }_{m}}{8b{\gamma }^{2}-4b\alpha \delta +\alpha {\upsilon }^{2}}\ge 0,$$

(59)

$${p}_{2}^{m*}-{p}_{2}^{t*}=\frac{\left(2b{\gamma }^{2}-b\alpha \delta +\alpha {\upsilon }^{2}\right){c}_{m}-3\left(a\alpha \delta +\left(2q+\alpha \tau \Delta +{\mu }_{m}\right)\gamma \upsilon -2a{\gamma }^{2}\right)}{8b{\gamma }^{2}-4b\alpha \delta +\alpha {\upsilon }^{2}}-\frac{\left(9b{\gamma }^{2}-4b\alpha \delta +4\alpha {\upsilon }^{2}\right){c}_{m}-3\left(4a\alpha \delta +3\left(3q+\alpha \tau \Delta +{\mu }_{t}\right)\gamma \upsilon -9a{\gamma }^{2}\right)}{4\left(9b{\gamma }^{2}-4b\alpha \delta +\alpha {\upsilon }^{2}\right)}\ge 0$$

(60)

and

$${w}_{2}^{m*}-{w}_{2}^{t*}=\frac{\left(4b{\gamma }^{2}-2b\alpha \delta +\alpha {\upsilon }^{2}\right){c}_{m}-2\left(a\alpha \delta +\left(2q+\alpha \tau \Delta +{\mu }_{m}\right)\gamma \upsilon -2a{\gamma }^{2}\right)}{8b{\gamma }^{2}-4b\alpha \delta +\alpha {\upsilon }^{2}}-\frac{\left(9b{\gamma }^{2}-4b\alpha \delta +4\alpha {\upsilon }^{2}\right){c}_{m}-3\left(4a\alpha \delta +3\left(3q+\alpha \tau \Delta +{\mu }_{t}\right)\gamma \upsilon -9a{\gamma }^{2}\right)}{2\left(9b{\gamma }^{2}-4b\alpha \delta +\alpha {\upsilon }^{2}\right)}\ge 0.$$

(61)

Based on the above results, $E\left[{\pi }_{r}^{m*}\right]-E\left[{\pi }_{r}^{t*}\right]\ge 0$ and $E\left[{\pi }_{m}^{m*}\right]-E\left[{\pi }_{m}^{t*}\right]\ge 0$.

Hence, Proposition 4 is proved.