1 Introduction

Rapid economic development and ongoing industrialization has led to enormous energy consumption. Energy demand prediction has become increasingly important when devising development plans for a country, and particularly for developing countries (Pi et al, 2010), such as China. Meanwhile, energy management is an important issue for future economic prosperity and environmental security (Suganthi and Samuel, 2012). China has become increasingly influential in energy production and consumption (Liu, 2015). China energy has been mainly provided by coal and crude oil, comprising 2/3 (66 %) and 18 %, respectively, of total energy consumed (National Bureau of Statistics of China, 2014). In the past decade, annual energy consumption increases were larger than energy production increases, and China faces not only inevitable environmental impacts, but also the challenge of devising an energy policy forecasting energy demand. Also, energy demand forecasting for China has been an interesting issue (Suganthi and Samuel, 2012).

Grey prediction models are capable of characterizing an unknown system using small data sets (Deng, 1982), without requiring conformance with statistical assumptions. Only few sample data points are required to achieve reliable and acceptable prediction accuracy (Wen, 2004; Wang and Hsu, 2008) and have been widely applied to management, economics, and engineering (e.g. Feng et al, 2012; Chang et al, 2015; Pi et al, 2010; Lee and Tong, 2011; Mao and Chirwa, 2006; Zeng et al, 2016; Chang et al, 2015; Tsaur and Liao, 2007; Wen, 2004; Cui et al, 2013; Wei et al, 2015). Grey prediction systems are particularly appropriate for energy demand forecasting, because energy consumption data are often few and/or do not conform to the usual statistical assumptions, such as normal distribution (Lee and Tong, 2011; Suganthi and Samuel, 2012). Wu et al, (2013) also used practical numerical examples to demonstrate that the small sample usually has more accuracy than the large sample for setting up a grey prediction model. Artificial intelligence techniques, multivariate regression, and time series models (e.g. Ediger and Akar, 2007; Gonzalez and Zamarreno, 2005; Tutun et al, 2015; Lauret et al, 2008; Duran, 2009; Xia et al, 2010) require large sample sizes to achieve reasonable forecasting accuracy (Wang and Hsu, 2008; Feng et al, 2012; Chang et al, 2015; Pi et al, 2010), which is impractical for energy demand forecasting.

The GM(1,1) model is one of the most frequently used grey prediction models for time series forecasting (Liu and Lin, 2006). To improve prediction accuracy of the original GM(1,1) model, several improved versions have been proposed, such as a discrete forecasting model (Xie and Liu, 2009), a grey Lotka–Volterra model (Wu et al, 2012), a new model with the fractional order accumulation (Wu et al, 2013), a novel BGM(1,1) using a box plot to analyse data features (Chang et al, 2015), an improved grey model with convolution integral GMC(1, n) (Wang and Hao, 2016), and a self-adaptive intelligence model (Zeng et al, 2016). Besides, the residual model has been eye-catching and played an important role in grey prediction (Liu and Lin, 2006; Deng, 1982). The residual modification model thus becomes the focus of this study.

When the corresponding residual model is established, predicted values from the original model can be adjusted by those from the residual model. The two models comprise a grey residual modification model, and both models are usually constructed in the same way as the traditional GM(1,1) model. However, the background value has an important role for the traditional model, but is not easily determined. This leads to some well-known prediction models using the traditional GM(1,1) model, developed for residual sign estimation to improve the prediction accuracy of the residual modification model, which also encounter the difficulty in determining background value, for example the MLP-GM(1,1) model based on multi-layer perceptron (MLP) (Hsu and Chen, 2003) and the GP-GM(1,1) model based on genetic programming (GP; Lee and Tong, 2011). The neural-network-based GM(1,1) (NN-GM(1,1)) model is free of the dependency on the background value (Hu et al, 2001) and performs well in comparison with the traditional GM(1,1) model. Therefore, it is interesting to investigate the impact on prediction accuracy of the proposed neural-network-based residual modification models on energy demand forecasting for China by using the NN-GM(1,1) model rather than the traditional GM(1,1) model.

The remainder of the paper is organized as follows. Section 2 introduces the traditional grey residual modification model, and Section 3 introduces the NN-GM(1,1) model and the proposed neural-network-based residual modification model. On the basis of the MLP-GM(1,1) and GP-GM(1,1) models, Section 4 examines the forecasting performances of the proposed prediction models using real cases of power and energy demand. Section 5 discusses the outcomes and presents conclusions.

2 Traditional grey residual modification model

2.1 Traditional GM(1,1) model

The computational steps to construct a traditional GM(1,1) model are as follows:

Step 1:

Present an original and nonnegative data sequence \( {\mathbf{x}}^{(0)} = \left( {x_{1}^{(0)} ,x_{2}^{(0)} , \ldots ,x_{n}^{(0)} } \right), \) provided by one system and consisting of n samples.

Step 2:

Perform the accumulated generating operation (AGO).

Identify the potential regularity hidden in \( {\mathbf{x}}_{{}}^{(0)} \) using AGO (Liu and Lin, 2006; Duran, 2009) to generate a new sequence, \( {\mathbf{x}}^{(1)} = \left( {x_{1}^{(1)} ,x_{2}^{(1)} , \ldots ,x_{n}^{(1)} } \right), \)

$$ x_{k}^{(1)} = \sum\limits_{j = 1}^{k} {x_{k}^{(0)} } ,\quad k = 1,2, \ldots ,n $$
(1)

and \( x_{1}^{(1)} ,x_{2}^{(1)} , \ldots ,x_{n}^{(1)} \) can be then approximated by a first-order differential equation,

$$ \frac{{d{\mathbf{x}}^{(1)} }}{dt} + ax^{(1)} = b $$
(2)

where a and b are the developing coefficient and control variable, respectively. The predicted value, \( \hat{x}_{k}^{(1)} \), for \( x_{k}^{(1)} \) can be obtained by solving the differential equation with initial condition \( x_{1}^{(1)} = x_{1}^{(0)} \):

$$ \hat{x}_{k}^{(1)} = \left( {x_{1}^{(0)} - \frac{b}{a}} \right)e^{{{-}a(k - 1)}} + \frac{b}{a} $$
(3)
Step 3:

Determine the developing coefficient and control variable.

a and b can be obtained using the ordinary least-squares method:

$$ \left[ {a,b} \right]^{T} = \left( {{\mathbf{B}}^{T} {\mathbf{B}}} \right)^{ - 1} {\mathbf{B}}^{T} {\mathbf{y}} $$
(4)

where

$$ {\mathbf{B}} = \left[ {\begin{array}{*{20}c} { - z_{2}^{(1)} } & 1 \\ { - z_{3}^{(1)} } & 1 \\ \vdots & \vdots \\ { - z_{n}^{(1)} } & 1 \\ \end{array} } \right] $$
(5)
$$ z_{k}^{(1)} = \alpha x_{k}^{(1)} + (1 - \alpha )x_{k}^{(1)} $$
(6)
$$ {\mathbf{y}} = \left[ {x_{2}^{(0)} ,x_{3}^{(0)} , \ldots x_{n}^{(0)} } \right]^{T} $$
(7)

where \( z_{k}^{(1)} \) is the background value. α is usually specified as 0.5 for convenience, but this is not an optimal setting. Thus, a and b are fully dependent on \( z_{k}^{(1)} \), which is not easily determined.

Step 4:

Perform the inverse accumulated generating operation (IAGO).

Using the IAGO, the predicted value of \( x_{k}^{(0)} \) is

$$ \hat{x}_{k}^{(0)} = \hat{x}_{k}^{(1)} - \hat{x}_{k - 1}^{(1)} ,\quad k = 2,3, \ldots ,n $$
(8)

Therefore,

$$ \hat{x}_{k}^{(0)} = (1{-}e^{a} )\left( {x_{1}^{(0)} - \frac{b}{a}} \right)e^{{{-}a(k - 1)}} ,\quad k = 2,3, \ldots ,n $$
(9)

and note that \( \hat{x}_{1}^{(1)} = \hat{x}_{1}^{(0)} \) holds.

2.2 Residual modification using traditional GM(1,1) models

A residual modification model is usually established using traditional GM(1,1) models. The computational steps of constructing a traditional residual modification model are as follows:

Step 1:

Establish a traditional GM(1,1) model for \( {\mathbf{x}}_{{}}^{(0)} \).

Step 2:

Generate the sequence of absolute residual values, \( {\varvec{\upvarepsilon}}^{(0)} = \left( {\varepsilon_{2}^{(0)} ,\varepsilon_{3}^{(0)} , \ldots ,\varepsilon_{n}^{(0)} } \right), \) where

$$ \varepsilon_{k}^{(0)} = \left| {x_{k}^{(0)} - \hat{x}_{k}^{(0)} } \right|,\quad k = 2,3, \ldots ,n $$
(10)
Step 3:

Establish a residual model.

A residual model is established as a traditional GM(1,1) model for \( {\varvec{\upvarepsilon}}_{{}}^{(0)} \). Similar to \( \hat{x}_{k}^{(0)} \), the predicted residual of \( \varepsilon_{k}^{(0)} \) is

$$ \hat{\varepsilon }_{k}^{(0)} = \left( {1 - e^{{a_{\varepsilon } }} } \right)\left( {\varepsilon_{2}^{(0)} - \frac{{b_{\varepsilon } }}{{a_{\varepsilon } }}} \right)e^{{ - a_{\varepsilon } (k - 1)}} ,\quad k = 3,4, \ldots ,n $$
(11)

where a ɛ and b ɛ are the developing coefficient and the control variable, respectively, and are also fully dependent on the background value.

Step 4:

Perform residual modification.

A predicted value \( \hat{x}_{{k^{tr} }}^{(0)} \) can be obtained by adding or subtracting \( \hat{\varepsilon }_{k}^{(0)} \) from original \( \hat{x}_{k}^{(0)} \) (Hsu and Wen, 1998).

$$ \hat{x}_{{k^{tr} }}^{(0)} = \hat{x}_{k}^{(0)} + s_{k} \hat{\varepsilon }_{k}^{(0)} ,\quad k = 2,3, \ldots ,n $$
(12)

where s k denotes the positive or negative sign for \( \hat{\varepsilon }_{k}^{(0)} \). The determination of s k can be dependent on the mechanism of sign estimation provided by other residual modification models, for instance the MLP-GM(1,1) and GP-GM(1,1) models. For simplicity, the sign estimation methods of those two prediction models are omitted.

3 Neural-network-based grey residual modification model

3.1 NN-GM(1,1) model

Because \( z_{k}^{(1)} \) is not easily determined, it is quite reasonable to consider finding a and b without requiring \( z_{k}^{(1)} \). A cost function E(a, b),

$$ E(a,b) = \frac{1}{2}\sum\limits_{k} {\left( {x_{k}^{(0)} - \hat{x}_{k}^{(0)} } \right)^{2} } ,\quad k = 2,3, \ldots ,n $$
(13)

was built for the NN-GM(1,1) model, where a and b are the connection weights. The model itself was a widely used single-layer perceptron (SLP). Similar to the back-propagation algorithm (BP; Smith and Gupta, 2002), the computational steps to constructing such a model are as follows:

Step 1:

Present a randomly selected sequence (k, 1, 1) (k = 2, 3,…, n) with \( x_{k}^{(0)} \) as its desired output to NN-GM(1,1).

Step 2:

Calculate the actual output \( \hat{x}_{k}^{(0)} \) of NN-GM(1,1).

Step 3:

Adjust the connection weights. For (k, 1, 1), a and b are adjusted to a + ∆a and b + ∆b, respectively. Then ∆a and ∆b can be derived by the gradient descent method on the cost function, and

$$ \Delta a = \eta \left( {x_{k}^{(0)} - \hat{x}_{k}^{(0)} } \right)V_{ak} $$
(14)
$$ \Delta b = \eta (x_{k}^{(0)} - \hat{x}_{k}^{(0)} )V_{bk} $$
(15)

where

$$ V_{ak} = \left[ {({-}e^{a} )\left( {x_{1}^{(0)} - \frac{b}{a}} \right)e^{{{-}a(k - 1)}} + (1{-}e^{a} )\left( {\frac{b}{{a^{2} }}} \right)e^{{{-}a(k - 1)}} + (1{-}e^{a} )\left( {x_{1}^{(0)} - \frac{b}{a}} \right)({-}k + 1)e^{{{-}a(k - 1)}} } \right] $$
(16)
$$ V_{bk} = \left[ {(1 \, {-}e^{a} )\left( { - \frac{1}{a}} \right)e^{{{-}a(k - 1)}} } \right] $$
(17)
Step 4:

Terminate when a pre-specified number of iterations have been performed; otherwise, return to Step 1.

3.2 Residual modification using NN-GM(1,1) models

In the proposed neural-network-based model, traditional GM(1,1) models are no longer used; rather, NN-GM(1,1) models considered. The construction of the proposed grey prediction model is described as follows:

Step 1:

Establish a NN-GM(1,1) model for \( {\mathbf{x}}_{{}}^{(0)} \).

Step 2:

For \( {\mathbf{x}}_{{}}^{(0)} \), generate the sequence of absolute residual values, \( {\varvec{\upvarepsilon}}^{(0)} = \left( {\varepsilon_{2}^{(0)} ,\varepsilon_{3}^{(0)} , \ldots ,\varepsilon_{n}^{(0)} } \right) \).

Step 3:

Establish a residual NN-GM(1,1) model.

A residual NN-GM(1,1) model, using all sequences of absolute residual values, is established where a ɛ and b ɛ are connection weights of a SLP for processing residuals. ∆a ɛ and ∆b ɛ may be derived with respect to a ɛ and b ɛ , respectively, by defining a cost function

$$ E\left( {a_{\varepsilon } ,b_{\varepsilon } } \right) = \frac{1}{2}\sum\limits_{k} {\left( {\varepsilon_{k}^{(0)} - \hat{\varepsilon }_{k}^{(0)} } \right)^{2} ,} \quad k = 3,4, \ldots ,n $$
(18)

Similar to a and b, a ɛ and b ɛ can be adjusted to a ɛ  + ∆a ɛ and b ɛ  + ∆b ɛ , respectively, after presenting a randomly selected sequence (k, 1, 1) (k = 3, 4,…, n) with desired output \( \varepsilon_{k}^{(0)} \) to the SLP related to, where

$$ \Delta a_{\varepsilon } = \eta\left( {\varepsilon_{k}^{(0)} - \hat{\varepsilon }_{k}^{(0)} } \right)V_{ak} $$
(19)
$$ \Delta b_{\varepsilon } = \eta\left( {\varepsilon_{k}^{(0)} - \hat{\varepsilon }_{k}^{(0)} } \right)V_{bk} $$
(20)

and

$$ V_{ak} = ({-}e^{a} )\left( {\varepsilon_{2}^{(0)} - \frac{b}{a}} \right)e^{{{-}a(k - 1)}} + (1{-}e^{a} )\left( {\frac{b}{{a^{2} }}} \right)e^{{{-}a(k - 1)}} + (1{-}e^{a} )\left( {\varepsilon_{2}^{(0)} - \frac{b}{a}} \right)({-}k + 1)e^{{{-}a(k - 1)}} $$
(21)
$$ V_{bk} = (1 \, {-}e^{a} )\left( {{-}\frac{1}{a}} \right)e^{{{-}a(k - 1)}} $$
(22)
Step 4:

Perform residual modification.

A predicted value \( \hat{x}_{{k^{nnr} }}^{(0)} \) is produced by adding or subtracting \( \hat{\varepsilon }_{k}^{(0)} \) from the original \( \hat{x}_{k}^{(0)} \),

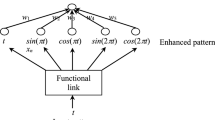
$$ \hat{x}_{{k^{nnr} }}^{(0)} = \hat{x}_{k}^{(0)} + s_{k} \hat{\varepsilon }_{k}^{(0)} ,\quad k = 2,3, \ldots ,n $$
(23)

As demonstrated in Figure 1, two independent SLPs were employed to establish the proposed neural-network-based grey residual modification model: one each for the original and residual sequences. The MLP-GM(1,1) and GP-GM(1,1) models used two traditional GM(1,1) models, independently, and artificial intelligence tools were applied to effectively determine s k . The flow chart of the proposed residual modification model is illustrated in Figure 2.

Figure 1
figure 1

A neural-network-based residual modification model

Full size image
Figure 2
figure 2

Flow chart of the proposed residual modification model

Full size image

When the NN-GM(1,1) models were incorporated into the MLP-GM(1,1) and GP-GM(1,1) models, rather traditional GM(1,1) models, two new prediction models, NN-MLP-GM(1,1) and NN-GP-GM(1,1), were able to remove the requirement of determining background values.

4 Empirical results

Empirical studies were conducted using real data sets to compare energy demand forecasting ability of the proposed NN-MLP-GM(1,1) and NN-GP-GM(1,1) models against original GM(1,1), NN-GM(1,1), MLP-GM(1,1), and NN-GP-GM(1,1) models. Mean absolute percentage error (MAPE) was employed to measure prediction performance, as this can be treated as the benchmark and is more stable than the commonly used mean absolute error and root mean square error (Makridakis, 1993; Lee and Shih, 2011). MAPE with respect to \( x_{k}^{(0)} \) is

$$ {\text{MAPE}} = \sum\limits_{k \in T} {\frac{{e_{k} }}{\left| T \right|}} $$
(24)

where T denotes the set of training or test data, whereas e k is the absolute percentage error (APE) with respect to \( x_{k}^{(0)} \),

$$ e_{k} = \frac{{\left| {x_{k}^{(0)} - \hat{x}_{{k^{p} }}^{(0)} } \right|}}{{x_{k}^{(0)} }} \times 100\,\% $$
(25)

where \( \hat{x}_{{k^{p} }}^{(0)} \) is a predicted value (e.g. \( \hat{x}_{k}^{(0)} \), \( \hat{x}_{{k^{tr} }}^{(0)} \), \( \hat{x}_{{k^{nnr} }}^{(0)} \)) with respect to \( x_{k}^{(0)} \). Lewis (1982) proposed MAPE criteria for evaluating a forecasting model, where MAPE ≤ 10, 10 < MAPE ≤ 20, 20 < MAPE ≤ 50, and MAPE > 50 correspond to high, good, reasonable, and weak forecasting models, respectively.

4.1 Applications to energy demand forecasting

4.1.1 Case I

An experiment was conducted on the historical annual power demand of Taiwan from 1985 to 2000. As in Hsu and Chen (2003), data from 1985 to 1998 were reserved for the model-fitting, and data from 1999 to 2000 were used for ex post testing. Table 1 summarizes forecasting results, reported by Hsu and Chen (2003), of original GM(1,1) and MLP-GM(1,1) models, along with the corresponding details for the proposed NN-MLP-GM(1,1) model. From Table 1, we can see that the MAPE of the original GM(1,1), the MLP-GM(1,1), and the NN-MLP-GM(1,1) models for model-fitting was 1.54, 0.57, and 1.56 %, respectively. And for ex post testing, the MAPE was 3.88, 1.29, and 0.78 %, respectively.

Table 1 Prediction accuracy obtained by different forecasting models for power demand (unit: 103 Wh)
Full size table

It is noteworthy that, although the NN-MLP-GM(1,1) model is slightly inferior to the original GM(1,1) and the MLP-GM(1,1) models for model-fitting, it is superior to the original GM(1,1) and the MLP-GM(1,1) models for ex post testing. Actually, when evaluating a prediction model, more emphasis should be placed on generalization rather than model-fitting (Luo et al, 2013). In this case, the MLP-GM(1,1) model seems to suffer from over-fitting. Figure 3 demonstrates the superiority of the generalization ability of the proposed NN-MLP-GM(1,1) model over the original GM(1,1) and the MLP-GM(1,1) models.

Figure 3
figure 3

Absolute percentage errors by different prediction models for Case I

Full size image

4.1.2 Case II

The second experiment was conducted on the historical annual energy demand of China, collected from 1990 to 2007. Same as Lee and Tong (2011), data from 1990 to 2003 were used for the model-fitting, and data from 2004 to 2007 were used for ex post testing. Forecasting results from Lee and Tong (2011) obtained by original GM(1,1), MLP-GM(1,1) and GP-GM(1,1) models are summarized in Table 2, along with the corresponding details for the proposed NN-MLP-GM(1,1) and NN-GP-GM(1,1) models. Table 2 shows that the MAPE of the original GM(1,1), the MLP-GM(1,1), the GP-GM(1,1), the NN-GM(1,1), the NN-MLP-GM(1,1), and the NN-GP-GM(1,1) models for model-fitting was 4.13, 3.61, 2.59, 3.81, 4.15, and 2.80 %, respectively. And for ex post testing, the MAPE was 26.21, 20.23, 20.23, 28.71, 14.81, and 14.81 %, respectively. Since a change on an epic scale happened to 2004, this can explain why results of the ex post testing is not as good as those of the model-fitting.

Table 2 Prediction accuracy obtained by different forecasting models for energy demand (unit: 104 tons of SCE)
Full size table

Similar to Case I, although MAPE obtained by NN-MLP-GM(1,1) and NN-GP-GM(1,1) models is slightly inferior to that from MLP-GM(1,1) and GP-GM(1,1), respectively, for model-fitting, they are superior to MLP-GM(1,1) and GP-GM(1,1), respectively, for ex post testing. In this case, it seems that both MLP-GM(1,1) and GP-GM(1,1) models suffer from over-fitting. The predicted values obtained by different forecasting models are illustrated in Figure 4. The proposed NN-MLP-GM(1,1) and NN-GP-GM(1,1) models show “good” generalization ability, whereas the other prediction models have only “reasonable” forecasting ability for testing data. The generalization ability of the NN-MLP-GM(1,1) and the NN-GP-GM(1,1) models are conspicuous.

Figure 4
figure 4

Predicted values obtained by different prediction models

Full size image

4.1.3 Case III

The third experiment was conducted on historical annual electricity demand of China, collected from China Statistical Yearbook (National Bureau of Statistics of China, 2014), 1981–2002. Following (Zhou et al, 2006), data from 1981 to 1998 were used for model-fitting, and from 1999 to 2002 for ex post testing. The forecasting results obtained from the different forecasting models are summarized in Table 3. All the models have “high” forecasting ability on the training and test data.

Table 3 Prediction accuracy obtained by different forecasting models for electricity demand (unit: 100 million kWh)
Full size table

Table 3 shows that results obtained by the proposed NN-MLP-GM(1,1) and NN-GP-GM(1,1) models are satisfactory. The MAPE of the original GM(1,1), the MLP-GM(1,1), the GP-GM(1,1), the NN-GM(1,1), the NN-MLP-GM(1,1), and the NN-GP-GM(1,1) models for model-fitting was 2.28, 2.03, 1.44, 1.84, 1.84, and 1.28 %, respectively. And for ex post testing, the MAPE was 7.24, 3.90, 3.90, 10.35, 3.34, and 3.34 %, respectively. The proposed NN-MLP-GM(1,1) and NN-GP-GM(1,1) models have superior fitting and generalization ability compared to MLP-GM(1,1) and GP-GM(1,1) models, respectively. Figure 5 also demonstrates the superiority of the generalization ability of NN-MLP-GM(1,1) and NN-GP-GM(1,1) models over the other prediction models.

Figure 5
figure 5

Absolute percentage errors by different prediction models for Case III

Full size image

5 Discussion and conclusions

Energy demand forecasting can be regarded as a grey system problem (Pi et al, 2010; Suganthi and Samuel, 2012) because several factors, such as income and population, influence energy demand but the precise relationships are not clear. That is, although relationships exist between input factors and dependent variable in the real problems, but it is not distinct about what these relationships are (Hu, 2016; Hu et al, 2015). Energy demand data are often limited and do not conform to the usual statistical assumptions, such as normal distribution. The GM(1,1) model is the most frequently used grey prediction model and has played an important role in energy demand prediction because it requires only limited samples to construct a prediction model without statistical assumptions. However, the traditional residual modification model has suffered from determination of the background value, as does the traditional GM(1,1) model, whereas the NN-GM(1,1) model is able to directly determine the developing coefficient and control variable using a SLP without requiring the background value. The NN-GM(1,1) model is also simple to implement as a computer program. Therefore, it is reasonable to replace the traditional GM(1,1) model with the NN-GM(1,1) model for a grey residual modification model. It is noted that, unlike the traditional SLP, the NN-GM(1,1) model does not use the sigmoid function as its activation function.

Some improved residual modification models, such as MLP-GM(1,1) and GP-GM(1,1), focused on residual sign estimation, but they retain the drawback of the traditional GM(1,1) model. On the other hand, the proposed NN-MLP-GM(1,1) and NN-GP-GM(1,1) models were developed from MLP-GM(1,1) and GP-GM(1,1) models, respectively, by substituting NN-GM(1,1) for traditional GM(1,1) models. Therefore, the proposed residual modification model can estimate residual signs effectively and is free from the drawback of the traditional GM(1,1) model.

Real cases of energy demand data from China were used to evaluate the forecasting performances of the proposed NN-MLP-GM(1,1) and NN-GP-GM(1,1) models. The outcomes verified that the proposed forecasting models perform well. Zhou et al (2006) showed that for Case III, MAPE for an autoregressive integrated moving average (ARIMA) and trigonometric grey prediction model was 3.25 and 2.12 %, for model-fitting, respectively, which are inferior to the proposed NN-MLP-GM(1,1) and NN-GP-GM(1,1) models. For Cases II and III, it is interesting to note that the NN-GM(1,1) model is superior to the traditional GM(1,1) model for model-fitting, but inferior for ex post testing. In other words, the NN-GM(1,1) model appears to be over-fitting. Experimental results show that the generalization ability of NN-MLP-GM(1,1) and NN-GP-GM(1,1) models are superior to the MLP-GM(1,1) and GP-GM(1,1) models. Thus, the generalization ability of a residual modification model could be improved by incorporating NN-GM(1,1) models.

The SLP in this study was trained on the basis of the BP using gradient descent. The learning is continued until a convergent condition is reached. It is known that one drawback of using BP is that a local minimum (Weiss and Kulikowski, 1991) is likely to be stuck during the learning process. Therefore, other optimization techniques such as genetic algorithm (GA; Goldberg, 1989; Man et al, 1999) could be applied to automatically determine the connection weights. In parenthesis, in comparison with the BP, an advantage of using GA is that a local minimum is unlikely to be stuck (Rooij et al, 1996; Vonkj et al, 1997; Hu, 2010). Additionally, the MLP-GM(1,1), the NN-GP-GM(1,1), and the proposed models have something in common. It is evident that they are grey residual modification models and developed for residual sign estimation to improve the prediction accuracy of the residual modification model. However, it is interesting to estimate not only the sign but the extent to which \( \hat{x}_{k}^{(0)} \) obtained from the original GM(1,1) model can be modified by \( \hat{\varepsilon }_{k}^{(0)} \) (k = 2, 3,…, n). This remains for the future work.