1 Introduction

Over the past few decades, continuous economic development and population increase worldwide have led to rapid growth in electricity demand. The average annual growth rate of global electricity demand was 2.6% for 1990–2000 and 3.3% for 2000–2010. It is expected to reach 2.8% for 2010–2020 (Liu, 2015). Electricity plays a very important role among energy sources. Therefore, electricity consumption is important for every national authority when making energy policy. An energy policy has a great impact on industrial development in a country, especially for developing countries.

Many forecasting methods, such as computational intelligence methods, multivariate regression and time-series analysis, have been frequently used for electricity consumption prediction (Nogales et al, 2002; Costa et al, 2011; Tutun et al, 2015; Abdoos et al, 2015). A large number of samples are required for multivariate regression and time-series analysis (Wang and Hsu, 2008). The performance of computational intelligence methods can be significantly affected by the number of training patterns (Pi et al, 2010). Beyond this, statistical methods usually require that the data conform to statistical assumptions, such as having a normal distribution (Lee and Tong, 2011). However, using long-term data to build electricity consumption prediction models may be impractical because the average annual growth rate of electricity consumption is high and unstable. In addition, the data collected on energy consumption often do not conform to statistical assumptions (Lee and Tong, 2011). Therefore, to construct an electricity consumption prediction model, a forecasting method is needed that works well with small samples and without making any statistical assumptions (Feng et al, 2012; Li et al, 2012).

The grey system theory proposed by Deng (1982) was developed to avoid the inherent defects of statistical methods and requires only a limited amount of data to estimate the behaviour of an uncertain system (Wen, 2004). The GM(1,1) model, which is a primary time-series forecasting model in grey theory, is one approach that has the merit of effectively constructing a prediction model for short-term problems (Liu and Lin, 2006). In addition, it only needs four recent data points to achieve reliable and acceptable accuracy for future prediction (Wang and Hsu, 2008; Wang et al, 2008). The GM(1,1) has been widely used in many fields such as management, economics and engineering, and the related models have been developed (Feng et al, 2012; Li et al, 2012; Pi et al, 2010; Lee and Tong, 2011; Mao and Chirwa, 2006; Hu et al, 2015; Hu, 2013; Tsaur and Liao, 2007; Chang et al, 2015, 2016; Wang and Hao, 2016; Lu et al, 2016; Mao et al, 2016; Yuan et al, 2016). Moreover, grey prediction has been gaining in popularity in the past decade because of its simplicity and ability to characterize unknown systems by a few data points (Suganthi and Samuel, 2012).

Traditional GM(1,1) model uses the least square method to obtain the developing coefficient and the control variable using grey difference equations. However, these equations can be affected by the background value that is not easy to be determined. Hu et al (2001) thus presented a novel neural-network-based GM(1,1) model called NNGM(1,1) to resolve such a troublesome problem. This study contributes to verify the usefulness and applicability of the NNGM(1,1) by applying this grey prediction model to electricity consumption forecasting. The experimental results indicate that NNGM(1,1) performs well compared to other variants of GM(1,1).

The remainder of the paper is organized as follows. Section 2 introduces traditional GM(1,1) and NNGM(1,1). Section 3 examines the electricity consumption forecasting performance of NNGM(1,1) by means of two experiments on real-world data. Section 4 includes a discussion and conclusions.

2 Neural-Network-Based GM(1,1)

From the perspective of grey system theory, the original data provided by most systems are finite, insufficient and chaotic, but the potential regularity hidden in these data sequences can be identified by generating new sequences through the accumulated generating operation (AGO) (Liu and Lin, 2006; Deng, 1982). Let \( {\mathbf{x}}^{(0)} = (x_{1}^{(0)} ,x_{2}^{(0)} , \ldots ,x_{n}^{(0)} ) \) consisting of n samples denote an original sequence. A new sequence \( {\mathbf{x}}^{(1)} = (x_{1}^{(1)} ,x_{2}^{(1)} , \ldots ,x_{n}^{(1)} ) \) can be generated from x (0) by AGO as follows:

$$ x_{k}^{(1)} = \sum\limits_{j = 1}^{k} {x_{j}^{(0)} } ,\quad k = 1,2, \ldots ,n $$
(1)

\( x_{1}^{(1)} ,x_{2}^{(1)} , \ldots ,x_{n}^{(1)} \) can be approximated by an exponential function, which is a first-order differential equation.

$$ \frac{{{\text{d}}{\mathbf{x}}^{(1)} }}{{{\text{d}}t}} + ax^{(1)} = b $$
(2)

where a and b are the developing coefficient and the control variable, respectively. The predicted value, \( \hat{x}_{k}^{(1)} \), for \( x_{k}^{(1)} \) can be obtained by solving the differential equation with initial condition \( x_{1}^{(1)} \) = \( x_{1}^{(0)} \):

$$ \hat{x}_{k}^{(1)} = \left( {x_{1}^{(0)} - \frac{b}{a}} \right)e^{{{-}a\left( {k - 1} \right)}} + \frac{b}{a} $$
(3)

As for a and b, both parameters can be estimated by means of a grey difference equation:

$$ x_{k}^{(0)} + az_{k}^{(1)} = b $$
(4)

where the background value \( z_{k}^{(1)} \) can be formulated as follows:

$$ z_{k}^{(1)} = \alpha x_{k}^{(1)} + (1{-}\alpha )x_{k - 1}^{(1)} $$
(5)

α is usually specified as 0.5 for convenience. Traditional GM(1,1) uses the least square method to obtain a and b using n − 1 grey difference equations (k = 2, 3,…, n). This means that the determinations of both developing coefficient and control variable are fully dependent on the background value. Finally, by means of the inverse accumulated generating operation (IAGO), the predicted value, \( \hat{x}_{k}^{(0)} \), of \( x_{k}^{(0)} \) can be generated as follows:

$$ \hat{x}_{k}^{(0)} = \hat{x}_{k}^{(1)} - \hat{x}_{k - 1}^{(1)} ,\quad k = 2,3, \ldots ,n $$
(6)

Therefore,

$$ \hat{x}_{k}^{(0)} = (1{-}e^{a} )\left( {x_{1}^{(0)} - \frac{b}{a}} \right)e^{{{-}a(k - 1)}} ,\quad k = 2,3, \ldots ,n $$
(7)

Note that \( \hat{x}_{1}^{(1)} = \hat{x}_{1}^{(0)} \) holds.

Because \( z_{k}^{(1)} \) is not easily determined, it is quite reasonable to find a and b without the interference coming from \( z_{k}^{(1)} \) (Hu et al, 2001). A cost function E(a, b) of NNGM(1,1) was built on this argument.

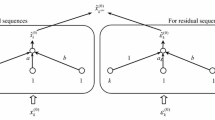
$$ E(a,b) = \frac{1}{2}\sum\limits_{k} {\left( {x_{k}^{(0)} - \hat{x}_{k}^{(0)} } \right)^{2} ,\quad k = \, 2, \, 3, \ldots ,n} $$
(8)

As shown in Figure 1, NNGM(1,1) is established by a well-known neural network, namely a single-layer perceptron (SLP), in which a and b are connection weights. The learning rules Δa and Δb with respect to a and b, respectively, can be easily obtained by implementing the gradient descent method on the cost function (Hertz et al, 1991):

$$ \Delta a = {-}\eta \frac{\partial E[a,b]}{\partial a} = \eta \sum\limits_{k} {\left( {x_{k}^{(0)} - \hat{x}_{k}^{(0)} } \right)} V_{ak} $$
(9)
$$ \Delta b = {-}\eta \frac{\partial E[a,b]}{\partial b} = \eta \sum\limits_{k} {\left( {x_{k}^{(0)} - \hat{x}_{k}^{(0)} } \right)} V_{bk} $$
(10)

where η is the learning rate. V ak and V bk are derived as follows:

$$ V_{ak} = \left[ {\left( {{-}e^{a} } \right)\left( {x_{1}^{(0)} - \frac{b}{a}} \right)e^{{{-}a(k - 1)}} + \left( {1{-}e^{a} } \right)\left( {\frac{b}{{a^{2} }}} \right)e^{{{-}a(k - 1)}} + \left( {1{-}e^{a} } \right)\left( {x^{(0)} (1){-}\frac{b}{a}} \right)\left( {{-}k + 1} \right)e^{{{-}a(k - 1)}} } \right] $$
(11)
$$ V_{bk} = \left[ {1{-}e^{a} \left( { - \frac{1}{a}} \right)e^{{{-}a(k - 1)}} } \right] $$
(12)

It is obvious that the determinations of a and b are dependent on Δa and Δb instead of on \( z_{k}^{(1)} \). The steps for establishing NNGM(1,1) can be described as follows:

Figure 1
figure 1

Single-layer perceptron for NNGM(1,1)

Full size image
  1. 1.

    Present a randomly selected sequence (k, 1, 1) (k = 2, 3,…, n) with \( x_{k}^{(0)} \) as its desired output to NNGM(1,1).

  2. 2.

    Calculate the actual output \( \hat{x}_{k}^{(0)} \) of NNGM(1,1).

  3. 3.

    Adjust the connection weights only for (k, 1, 1) so that a and b can be adjusted to be a + Δa and b + Δb, respectively. The modifications of Δa and Δb below are performed for (k, 1, 1):

    $$ \Delta a = \eta \left( {x_{k}^{(0)} - \hat{x}_{k}^{(0)} } \right)V_{ak} $$
    (13)
    $$ \Delta b = \eta \left( {x_{k}^{(0)} - \hat{x}_{k}^{(0)} } \right)V_{bk} $$
    (14)
  4. 4.

    Repeat the above steps until a pre-specified number of iterations have been performed.

Figure 2 illustrates the flow chart of constructing NNGM(1,1).

Figure 2
figure 2

Flow chart of construction of NNGM(1,1)

Full size image

3 Computer simulations

To examine the electricity consumption forecasting ability of NNGM(1,1), the first experiment involved comparing its results with those from GM(1,1) with rolling mechanism (GPRM) as described in Akay and Atak (2007) on a data set collected from 1970 to 2004 and obtained from the Turkish Ministry of Energy and Natural Resources (MENR). The second experiment involved comparing the results with those from the adaptive GM(1,1) (AGM(1,1)) proposed by Li et al (2009) on a sample of twenty-one countries in the Asia–Pacific region from 2000 to 2007, which was obtained from the Asia–Pacific Economic Cooperation (APEC) energy database. Details of these data sets can be obtained from the relevant publications.

As for parameter specifications for training NNGM(1,1), because η should be specified as a small value to avoid generating excessive perturbations of Δa and Δb, η was initially specified as 10−2. Next, the initial values of a and b were randomly given. Considering the available computing time, the maximum number of iterations was set to 5000. Although these parameter specifications are somewhat subjective, the experimental results show that they are acceptable.

3.1 Application to Turkish MENR data

GM(1,1) can use only recent data with small sample size to increase forecasting accuracy in future prediction in case of having chaotic data. The rolling mechanism can implement concretely this unique characteristic of GM(1,1). The mechanism works as follows: \( \hat{x}_{k}^{(0)} \) is obtained by using \( x_{1}^{(0)} ,x_{2}^{(0)} , \ldots ,x_{k - 1}^{(0)} \) corresponding to 1970, 1971, …, 1970 + (k − 2), respectively, to construct a forecasting model, whereas \( \hat{x}_{k + 1}^{(0)} \) is obtained from \( x_{2}^{(0)} ,x_{3}^{(0)} , \ldots ,x_{k}^{(0)} \) corresponding to 1971, 1972, …, 1970 + (k − 1), respectively, and so on. In other words, as the prediction model develops further, the significance of the older data is reduced (Liu and Lin, 2006). The term GPRM refers to a traditional GM(1,1) using the rolling mechanism.

As in Akay and Atak (2007), this study applied NNGM(1,1) separately to total and industrial sector electricity consumption for Turkey and used the rolling mechanism to build NNGM(1,1). Four samples were used as the training data, and the incoming datum was predicted. For instance, \( \hat{x}_{5}^{(0)} \) can be produced by the model build using \( x_{1}^{(0)} \), \( x_{2}^{(0)} \), \( x_{3}^{(0)} \), \( x_{4}^{(0)} \), whereas \( x_{2}^{(0)} \), \( x_{3}^{(0)} \), \( x_{4}^{(0)} \), \( x_{5}^{(0)} \) are used to obtain \( \hat{x}_{6}^{(0)} \). The mean absolute percentage error (MAPE) used to measure the prediction performance with respect to \( x_{k}^{(0)} \) (k = 5, 6, …, 35) can be calculated as follows:

$$ {\text{MAPE}} = \sum\limits_{k = 5}^{35} {\frac{{\left| {x_{k}^{(0)} - \hat{x}_{k}^{(0)} } \right|}}{{31 \times x_{k}^{(0)} }}} \times 100\% $$
(15)

The MAPE values obtained by NNGM(1,1) for total and industrial electricity consumptions were 3.41 and 4.76%, respectively, whereas those obtained by GPRM for total and industrial electricity consumptions were 3.69 and 5.70%, respectively.

Besides, the forecasting results obtained by two well-known neural networks, a multi-layer perceptron using back-propagation training (i.e. BP network, BPN) and a radial basis function network (RBFN), are included. To train the neural networks, for instance, the inputs with respect to the desired outputs \( x_{1}^{(0)} \), \( x_{2}^{(0)} \), \( x_{3}^{(0)} \) and \( x_{4}^{(0)} \) are 1, 2, 3 and 4, respectively. Then, an actual output \( \hat{x}_{5}^{(0)} \) for \( x_{5}^{(0)} \) can be obtained by using 5 as an input. A two-layer perceptron with one input node, two hidden nodes and a single output for total and industrial electricity consumptions was 4.48 and 7.26%, respectively, whereas that obtained by a RBFN with one receptive field unit, two hidden nodes and a single output for total and industrial electricity consumptions was 7.91 and 7.68%, respectively. Therefore, the prediction accuracy of NNGM(1,1) is superior to that of GPRM, BPN and RBFN.

Additionally, MENR has used the Model of Analysis of the Energy Demand (MAED) to carry out energy forecasting studies (Akay and Atak, 2007). The forecasting results reported by MENR for 1994–2004 for total and industrial electricity consumptions are summarized in Tables 1 and 2, respectively. It is obvious that NNGM(1,1) performs well and outperforms MAED, GPRM and RBFN. Furthermore, GPRM, NNGM(1,1), BPN and RBFN show much better prediction accuracy than MAED.

Table 1 Absolute percentage errors obtained by different methods for total electricity consumption
Full size table
Table 2 Absolute percentage errors obtained by different methods for industrial electricity consumption
Full size table

3.2 Application to APEC Data

Li et al (2012) explored the forecasting performance of a novel adaptive GM(1,1) called AGM(1,1) using electricity consumption data from the Asia–Pacific Economic Cooperation (APEC) energy database. Similarly to Akay and Atak (2007), AGM(1,1) and NNGM(1,1) were built by the rolling mechanism and by selecting 4 years of recent data \( x_{k - 4}^{(0)} \), \( x_{k - 3}^{(0)} \), \( x_{k - 2}^{(0)} \), \( x_{k - 1}^{(0)} \) to predict \( \hat{x}_{k}^{(0)} \) (k ≥ 5) for each country. For instance, for Australia, a forecasting model was constructed using data from 2000 to 2003 to predict a value for 2004, whereas the predicted value for 2005 was obtained using data from 2001 to 2004, and so on. The forecasting results measured using MAPE, including a two-layer BPN and support vector regression (SVR) as reported in Li et al (2012), are summarized in Table 3. It is apparent that NNGM(1,1) gives satisfactory performance compared to the other forecasting methods considered.

Table 3 Absolute percentage errors obtained by different methods for electricity consumption of countries in the Asia–Pacific region
Full size table

4 Discussion and conclusions

Electricity consumption forecasting plays an important role in making energy policy. Either overestimation or underestimation of electricity demand will lead to excessive operating costs (Nogales et al, 2002). GM(1,1) is an appropriate approach for electricity demand prediction because it can use a limited number of samples to construct a prediction model without statistical assumptions. This study has applied NNGM(1,1) to electricity consumption. Compared to traditional GM(1,1), NNGM(1,1) has the convenience of determining directly the developing coefficient and the control variable using a SLP without using the background value. Besides, one merit of NNGM(1,1) is that it is simple enough to implement as a computer program. Note that although Wang and Hsu (2008) proposed a genetic-algorithm-based GM(1,1) to determine the developing coefficient and the control variable, it should be stressed that NNGM(1,1) is the first approach to use an optimization technique to obtain these two parameters in grey prediction. Note also how to optimize the related parameters of grey forecasting models to increase prediction accuracy using different computational intelligence tools has become an important issue. For instance, Hsu (2009) used a genetic algorithm to determine the development coefficient and the grey input coefficients for GM(1,N). Hsu and Chen (2003) used neural networks to estimate the signs for residual models. Similarly, Lee and Tong (2011) incorporated genetic programming into residual GM(1,1) for energy demand forecasting.

In this study, two data sets were used to examine the forecasting performance of NNGM(1,1). The experimental results show that NNGM(1,1) outperformed GPRM on the Turkish energy data for total and industrial electricity consumptions. NNGM(1,1) also outperformed AGM(1,1), BPN and SVR on the Asia–Pacific energy data by the average MAPE. It can be seen that BPN and SVR are inferior to AGM(1,1) and NNGM(1,1) because the training sample size has a significant impact on the forecasting performance of computational intelligence methods. Their forecasting performance would be improved by increasing the amount of training data. This demonstrates the usefulness of NNGM(1,1) for electricity forecasting problems. It should be noted that the SLP in this study was trained on the basis of the BP using gradient descent. The learning is continued until a convergent condition is reached. It is known that one disadvantage of using BP is that a local minimum [41] is likely to be stuck during the learning process. However, it seemed not to be a serious problem for NNGM(1,1) in view of the forecasting performance on electricity consumption.

Energy demand forecasting can be regarded as a grey system problem (Pi et al, 2010; Suganthi and Samuel, 2012) because a few factors such as income and population have influence on energy demand, but how exactly these factors affect energy demand is not clear. Therefore, on the basis of the remarkable forecasting performance of NNGM(1,1) for electricity consumption, it would be interesting to explore the applicability of NNGM(1,1) to other energy forecasting problems such as total energy production in certain developing countries. Moreover, it is known that the prediction accuracy of the traditional GM(1,1) can be improved by the residual GM(1,1) (Liu and Lin, 2006; Deng, 1982). The two models comprise a grey residual modification model, and both models are usually constructed in the same way as the traditional GM(1,1) model. To further improve the prediction accuracy of a residual modification model, how NNGM(1,1) can combine with the residual GM(1,1) becomes an interesting issue for energy demand forecasting. These remain for the future work.