1 Introduction

With the people's growing demand for energy and increasing awareness of environmental protection, the development and use of clean and green energy have attracted more and more attention. As the most common vibration source, machine vibration widely exists in nature. Collecting the original disusing vibration energy effectively, turning it into electricity to turn waste into treasure, will provide electricity for low power electronic sensors without needing batteries or mains so that the sensors realize clean, green, and wireless use. With the deep research on vibration energy harvesting (VEH) technology, some novel design schemes have been proposed and improved, which can be classified into three types according to their conversion mechanisms: electromagnetic induction [1], electrostatic induction [2], and piezoelectric effect [3]. Therein, piezoelectric VEH has become a research hotspot in VEH technology areas because of its high energy conversion efficiency, no need for an external power supply, and application of MEMS technology.

The sources of vibration in the environment are rather complex, and the single frequency vibration is rare [4, 5]. Due to most of the vibration sources containing multiple frequency components coexist, and their strength being different, the frequencies of the VEH device should be distributed over a wide frequency bandwidth to ensure efficient capture of vibration energy. Therefore, VEH devices with different nonlinear structures are designed, for example, monostable [6], bistable [7], and multistable [8]. Then some preloaded clamped–clamped structures are also proposed to achieve the mechanical nonlinearity structure, which can realize the frequency tuning with preload configuration, and it does not need an external system [9,10,11]. Recently, some more complex VEH systems have been further proposed and analyzed their harvesting performance, such as the bistable L-shaped beam [12], the structure of phononic crystal beam [13], crank-connecting rod [14], pressure fluctuation energy harvester [15] and so on. However, the nonlinear VEH system at work was affected by stochastic loads inevitably. As is well known, noise is widespread, and many studies have testified that stochastic excitation makes the already complex dynamics phenomenon of nonlinear systems more abundant and changeable, like stochastic bifurcation [16,17,18,19], stochastic transition [20], stochastic resonance [21], etc. In particular, the harvesting performance changes inevitably in the nonlinear VEH system driven by noise. To better understand the change rules of harvesting performance, many stochastic methods have been developed to analyze the correlation between the model structure of the system and the harvesting performance. For example, the effect of stochastic VEH system parameters with different design structures on the mean square voltage was investigated using the stochastic averaging method [22,23,24,25,26]. The harmonic balance method [27] and the multiple scale technique [28], two other analysis techniques, were used to obtain the vibration response of forced VEH systems. In addition, as another effective analytical tool of the stochastic system, the path integration procedure was also developed to analyze the probabilistic solution of nonlinear VEH systems [29,30,31]. In addition, Wang et al. [32] obtained the probability density functions (PDFs) of asymmetric multi-stable energy harvesters by the principle of detailed balance that found the design of the asymmetric structure is more conducive to improving the energy harvesting performance relative to the symmetric case. From the above research results, it is not hard to see that those theoretical analysis methods are all established based on all the information of the stochastic model.

Shannon entropy is established based on the statistical theory of random events and reflecting information uncertainty. Jaynes [33] systematically introduced the maximum entropy principle, which relates mathematical problems to maximum information entropy. The maximum entropy method can infer the unknown distributions when the partial information is known, and it has been widely used in various fields due to its advanced predictive power [34, 35]. During this period, the combination of information theory and stochastic dynamics has attracted great interest in the research field, such as predicting the dynamic behavior of stochastic systems through partial information. In earlier studies, Spencer [36, 37] studied the failure probabilities of linear systems excited by the Gaussian white noise by the maximum entropy method based on the moment information of the system. Subsequently, Sobczyk [38,39,40] proposed an improved entropy method to predict the probability distribution of a class of nonlinear stochastic systems based on partial moment information. On this basis, Ricciardi [41] used the entropy principles, which combined the maximum entropy method with the stochastic linearization method to seek the approximate PDF from a nonlinear stochastic differential equation. Xu et al. [42] analyzed the efficient reliability of the limit state function of the stochastic structure by the maximum entropy method based on the fractional moments. Recently, Tian et al. [43] proposed a data-driven method to derive the approximate expression of the stationary PDF of a nonlinear random vibrating system based on the principle of maximum entropy. However, there is little research considering the response and performance prediction of the symmetric and asymmetric VEH system under Gaussian white noise by the method of maximum entropy when only knowing the partial information of the nonlinear system, such as the moment information.

This work aims to predict the stochastic responses and analyze the harvesting performance of nonlinear VEH systems based on partial information. This paper is organized as follows: The mathematical model of the stochastic VEH system is described in Sect. 2. Section 3, introduced the cumulant truncation method to obtain the moment information of the nonlinear stochastic system. In Sect. 4, combined with the known moment information, the maximum entropy method and the intelligent optimization algorithm are used to predict the stationary PDF of the system. Section 5 discussed the PDF of response, the average output power, and the power conversion efficiency of VEH systems on different nonlinear geometric structures. Some conclusions are given in the last section.

2 Problem Formulation

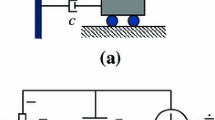
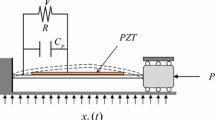
Considering a class of the electromechanical coupled VEH model, which can be configured by a mechanical oscillator coupled to an electric circuit through electromechanical energy conversion. The more common type of them is piezoelectric, see Fig. 1, the equations of motion can be described as the following forms:

$$\begin{aligned} m\ddot{\bar{X}} + c\dot{\bar{X}} + \frac{{d\bar{U}\left( {\bar{X}} \right)}}{{d\bar{X}}} + \theta \bar{V} & = - m\ddot{\bar{X}}_{b} \\ C_{p} \dot{\bar{V}} + \frac{1}{R}\bar{V} & = \theta \dot{\bar{X}}, \\ \end{aligned}$$
(1)

where \(\overline{X}\) is the relative displacement of an inertial mass \(m\), the dot denotes a derivative with respect to time \(t\); \(c\) denotes the linear viscous damping coefficient of the VEH system; The function \(\overline{U}(\overline{X})\) denotes the linear and nonlinear potential function of the mechanical oscillator. \(\theta\) represents a linear electromechanical coupling coefficient. \(\overline{V}\) is the induced voltage in capacitive harvesters, which is measured across an equivalent resistive load \(R\). \(C_{{{p}}}\) is the piezoelectric capacitance. \(\ddot{\overline{X}}_{{{b}}}\) stands for the random environmental disturbance.

Fig. 1
figure 1

Schematic of a piezoelectric VEH model

Full size image

For being convenient to study, the following dimensionless quantities will be introduced.

$$X = \frac{{\bar{X}}}{{l_{L} }},\quad V = \frac{{C_{p} }}{{\theta l_{L} }},\quad \frac{{dU\left( X \right)}}{{dX}} = \frac{{d\bar{U}\left( {\bar{X}} \right)}}{{ml_{L} \,d\bar{X}}},\quad c = \frac{c}{m},\quad \beta = \frac{{\theta ^{2} }}{{C_{p} }},\quad \alpha = \frac{1}{{RC_{p} }},\quad \xi (t) = - \frac{1}{{l_{L} }}\ddot{\bar{X}}_{b} ,$$

where \(l_{L}\) is a length scale. One can obtain the following dimensionless model for a couple of nonlinear VEH system:

$$\ddot{X} + c\dot{X} + \frac{{dU\left( X \right)}}{{dX}} + \beta V = \xi \left( t \right),$$
(2a)
$$\dot{V} + \alpha V = \dot{X},$$
(2b)

where the random environmental excitation \(\xi (t)\) is the Gaussian white noise, which has zero mean, \(E\left[ {\xi \left( t \right)} \right] = 0\), and autocorrelation function noise \(E\left[ {\xi \left( t \right)\xi \left( {t + \tau } \right)} \right] = 2D\delta \left( \tau \right)\).

3 The Moments Information is Derived by Cumulant Truncation

This section describes a theoretical method for obtaining moment information. Let \(Y = \dot{X}\), the system (2) can be rewritten as the following first order Itô stochastic differential equations:

$$\begin{aligned} dX & = Y\,dt, \\ dY & = \left[ { - cY - \frac{{dU(X)}}{{dX}} - \beta V} \right]dt + 2D\,dW(t), \\ dV & = \left[ {Y - \alpha V} \right]dt, \\ \end{aligned}$$
(3)

in which \(W(t)\) is the standard Weiner process.

According to the Itô differential rule and the theory of moment differential equations, one can obtain the following first-order moments equations are

$$\begin{aligned} \frac{d}{{dt}}\mu _{{X,Y,V}}^{{1,0,0}} & = \frac{d}{{dt}}E\left[ X \right] = E\left[ Y \right], \\ \frac{d}{{dt}}\mu _{{X,Y,V}}^{{0,1,0}} & = \frac{d}{{dt}}E\left[ Y \right] = - cE\left[ Y \right] - E\left[ {\frac{{dU\left( X \right)}}{{dX}}} \right] - \beta E\left[ V \right], \\ \frac{d}{{dt}}\mu _{{X,Y,V}}^{{0,0,1}} & = \frac{d}{{dt}}E\left[ V \right] = E\left[ Y \right] - \alpha E\left[ V \right], \\ \end{aligned}$$
(4)

and the \(M\,{{th}}\;\left( {M \ge 2} \right)\) order moments equation are

$$\begin{aligned} \frac{d}{{dt}}\mu _{{X,Y,V}}^{{k_{1} ,k_{2} ,k_{3} }} & = \frac{d}{{dt}}E\left[ {X^{{k_{1} }} Y^{{k_{2} }} V^{{k_{3} }} } \right] \\ & = E\left[ {k_{1} X^{{k_{1} - 1}} Y^{{k_{2} + 1}} V^{{k_{3} }} - k_{2} \beta X^{{k_{1} }} Y^{{k_{2} - 1}} V^{{k_{3} + 1}} - \left( {ck_{2} + \alpha k_{3} } \right)X^{{k_{1} }} Y^{{k_{2} }} V^{{k_{3} }} } \right] \\ & + E\left[ {k_{3} X^{{k_{1} }} Y^{{k_{2} + 1}} V^{{k_{3} - 1}} - k_{2} X^{{k_{1} }} Y^{{k_{2} - 1}} V^{{k_{3} }} \frac{{dU\left( X \right)}}{{dX}} + 2k_{2} \left( {k_{2} - 1} \right)D^{2} X^{{k_{1} }} Y^{{k_{2} - 2}} V^{{k_{3} }} } \right]\;, \\ \end{aligned}$$
(5)

in which \(M = \sum\nolimits_{i = 1}^{3} {k_{i} } \ge 2\) and \(k_{i}\) is a positive integer. It can be seen that the nonlinear potential function \(U\left( X \right)\) will lead to the order of the moment \(E\left[ {X^{{k_{1} }} Y^{{k_{2} - 1}} V^{{k_{3} }} {\text{d}}U\left( X \right)/{\text{d}}X} \right]\) higher than \(M\), which will lead to the number of equations less than the variable. Then the moment of an order higher than \(M\) will be expressed in those moments of order \(M\) and lower than \(M\) by the technique of cumulant truncation. The following shows the relationship between moments and cumulants \(k\left[ \cdot \right]\):

$$\begin{aligned} E\left[ {X_{1} } \right] & = k_{1} \left[ {X_{1} } \right], \\ E\left[ {X_{1} X_{2} } \right] & = k_{2} \left[ {X_{1} ,X_{2} } \right] + k_{1} \left[ {X_{1} } \right]k_{1} \left[ {X_{2} } \right], \\ E\left[ {X_{1} X_{2} X_{3} } \right] & = k_{3} \left[ {X_{1} ,X_{2} ,X_{3} } \right] + \left\{ {k_{1} \left[ {X_{1} } \right]k_{2} \left[ {X_{2} ,X_{3} } \right]} \right\}_{s\left( 3 \right)} + k_{1} \left[ {X_{1} } \right]k_{1} \left[ {X_{2} } \right]k_{1} \left[ {X_{3} } \right], \\ E\left[ {X_{1} X_{2} X_{3} X_{4} } \right] & = k_{4} \left[ {X_{1} ,X_{2} ,X_{3} ,X_{4} } \right] + \left\{ {k_{2} \left[ {X_{1} ,X_{2} } \right]k_{2} \left[ {X_{3} ,X_{4} } \right]} \right\}_{s\left( 3 \right)} + \left\{ {k_{1} \left[ {X_{1} } \right]k_{3} \left[ {X_{2} ,X_{3} ,X_{4} } \right]} \right\}_{s\left( 4 \right)} \\ & + \left\{ {k_{1} \left[ {X_{1} } \right]k_{1} \left[ {X_{2} } \right]k_{2} \left[ {X_{3} ,X_{4} } \right]} \right\}_{s\left( 6 \right)} + k_{1} \left[ {X_{1} } \right]k_{1} \left[ {X_{2} } \right]k_{1} \left[ {X_{3} } \right]k_{1} \left[ {X_{4} } \right], \\ \end{aligned}$$
$$\begin{aligned} E\left[ {X_{1} X_{2} X_{3} X_{4} X_{5} } \right] & = k_{5} \left[ {X_{1} ,X_{2} ,X_{3} ,X_{4} ,X_{5} } \right] + \left\{ {k_{1} \left[ {X_{1} } \right]k_{4} \left[ {X_{2} ,X_{3} ,X_{4} ,X_{5} } \right]} \right\}_{s\left( 5 \right)} \\ & + \left\{ {k_{3} \left[ {X_{1} ,X_{2} ,X_{3} } \right]k_{2} \left[ {X_{4} ,X_{5} } \right]} \right\}_{{s\left( {10} \right)}} + \left\{ {k_{3} \left[ {X_{1} ,X_{2} ,X_{3} } \right]k_{1} \left[ {X_{4} } \right]k_{1} \left[ {X_{5} } \right]} \right\}_{{s\left( {10} \right)}} \\ & + \left\{ {k_{2} \left[ {X_{1} ,X_{2} } \right]k_{2} \left[ {X_{3} ,X_{4} } \right]k_{1} \left[ {X_{5} } \right]} \right\}_{{s\left( {15} \right)}} + \left\{ {k_{2} \left[ {X_{1} ,X_{2} } \right]k_{1} \left[ {X_{3} } \right]k_{1} \left[ {X_{4} } \right]k_{1} \left[ {X_{5} } \right]} \right\}_{{s\left( {20} \right)}} \\ & + k_{1} \left[ {X_{1} } \right]k_{1} \left[ {X_{2} } \right]k_{1} \left[ {X_{3} } \right]k_{1} \left[ {X_{4} } \right]k_{1} \left[ {X_{5} } \right], \\ E\left[ {X_{1} X_{2} X_{3} X_{4} X_{5} X_{6} } \right] & = k_{6} \left[ {X_{1} ,X_{2} ,X_{3} ,X_{4} ,X_{5} ,X_{6} } \right] + \left\{ {k_{5} \left[ {X_{1} ,X_{2} ,X_{3} ,X_{4} ,X_{5} } \right]k_{1} \left[ {X_{6} } \right]} \right\}_{s\left( 6 \right)} \\ & + \left\{ {k_{4} \left[ {X_{1} ,X_{2} ,X_{3} ,X_{4} } \right]k_{2} \left[ {X_{5} ,X_{6} } \right]} \right\}_{{s\left( {15} \right)}} + \left\{ {k_{3} \left[ {X_{1} ,X_{2} ,X_{3} } \right]k_{3} \left[ {X_{4} ,X_{5} ,X_{6} } \right]} \right\}_{{s\left( {10} \right)}} \\ & + \left\{ {k_{4} \left[ {X_{1} ,X_{2} ,X_{3} ,X_{4} } \right]k_{1} \left[ {X_{5} } \right]k_{1} \left[ {X_{6} } \right]} \right\}_{{s\left( {15} \right)}} \\ & { + }\left\{ {k_{3} \left[ {X_{1} ,X_{2} ,X_{3} } \right]k_{2} \left[ {X_{4} ,X_{5} } \right]k_{1} \left[ {X_{6} } \right]} \right\}_{{s\left( {60} \right)}} \\ & + \left\{ {k_{3} \left[ {X_{1} ,X_{2} ,X_{3} } \right]k_{1} \left[ {X_{4} } \right]k_{1} \left[ {X_{5} } \right]k_{1} \left[ {X_{6} } \right]} \right\}_{{s\left( {20} \right)}} \\ & { + }\left\{ {k_{2} \left[ {X_{1} ,X_{2} } \right]k_{2} \left[ {X_{3} ,X_{4} } \right]k_{1} \left[ {X_{5} } \right]k_{1} \left[ {X_{6} } \right]} \right\}_{{s\left( {45} \right)}} \\ & + \left\{ {k_{2} \left[ {X_{1} ,X_{2} } \right]k_{1} \left[ {X_{3} } \right]k_{1} \left[ {X_{4} } \right]k_{1} \left[ {X_{5} } \right]k_{1} \left[ {X_{6} } \right]} \right\}_{{s\left( {15} \right)}} \\ & { + }\left\{ {k_{2} \left[ {X_{1} ,X_{2} } \right]k_{2} \left[ {X_{3} ,X_{4} } \right]k_{2} \left[ {X_{5} ,X_{6} } \right]} \right\}_{{s\left( {15} \right)}} \\ & + k_{1} \left[ {X_{1} } \right]k_{1} \left[ {X_{2} } \right]k_{1} \left[ {X_{3} } \right]k_{1} \left[ {X_{4} } \right]k_{1} \left[ {X_{5} } \right]k_{1} \left[ {X_{6} } \right], \\ & \cdots \cdots \cdots \cdots \cdots \cdots \quad \cdots \cdots \cdots \cdots \cdots \cdots \quad \cdots \cdots \cdots \cdots \cdots \cdots \\ \end{aligned}$$

where \(X_{i}\) represents any of the three variables \(X,\;Y\) and \(\;V\). The symbol \(\left\{ \cdot \right\}_{s\left( n \right)}\) denotes the rotation symmetric sum, and \(s\left( n \right)\) is the number of sum terms. For example, under the constraint of moment equations Eq. (5), if the truncation level is set at \(M = 4\), then the moments of order higher than the fourth can be expressed as

$$\begin{aligned} E\left[ {X_{1} X_{2} X_{3} X_{4} X_{5} } \right] & = \left\{ {E\left[ {X_{1} X_{2} } \right]E\left[ {X_{3} X_{4} X_{5} } \right]} \right\}_{{s\left( {10} \right)}} , \\ E\left[ {X_{1} X_{2} X_{3} X_{4} X_{5} X_{6} } \right] & = \left\{ {E\left[ {X_{1} X_{2} } \right]E\left[ {X_{3} X_{4} X_{5} X_{6} } \right]} \right\}_{{s\left( {15} \right)}} + \left\{ {E\left[ {X_{1} X_{2} X_{3} } \right]E\left[ {X_{4} X_{5} X_{6} } \right]} \right\}_{{s\left( {10} \right)}} \\ & - 2\left\{ {E\left[ {X_{1} X_{2} } \right]E\left[ {X_{3} X_{4} } \right]E\left[ {X_{5} X_{6} } \right]} \right\}_{{s\left( {15} \right)}} , \\ & \cdots \cdots \cdots \cdots \cdots \cdots \quad \cdots \cdots \cdots \cdots \cdots \cdots \quad \cdots \cdots \cdots \cdots \cdots \cdots \\ \end{aligned}$$
(6)

Substituting Eq. (6) into Eqs. (4) and (5), combined with the conditions of stationary response \({\text{d}}E\left[ {X^{i} Y^{j} V^{k} } \right]/{\text{d}}t = 0\), the following moment equations can be derived

$$\left( {E\left[ {G\left( {X^{i} ,Y^{j} ,V^{k} } \right)} \right]} \right)_{M \times 1} = 0,\quad 0 < i + j + k \le M{\kern 1pt} \quad {{and}}\quad i,j,k \ge 0,$$
(7)

where \(G\left( {X^{i} ,Y^{j} ,V^{k} } \right)\) is a function that depends on the variables \(X,\;Y\) and \(\;V\). As should be obvious, these is algebraic equations about the moment variables \(E\left[ {G\left( {X^{i} ,Y^{j} ,V^{k} } \right)} \right]\). Then the moments from first to fourth order are obtained by solving the Eqs. (7), and substituting those results into Eq. (6), the moment of order higher than \(M = 4\) will be further obtained.

4 The Prediction of the Stationary PDF by the Moment Information

In this subsection, without depending on the model information, the maximum entropy method will be introduced to determine a PDF from a set of information about moments, which has been acquired in the previous section.

Without loss of generality, let's suppose that the function \(p\left( {\tilde{x}} \right)\) denotes the PDF for the random object variable \(\tilde{x}\), where the object variable can be replaced by the variables \(X,\;Y,V\) and their function. The corresponding \(K\)th order moment \(\mu_{{\tilde{x}}}^{K}\) of variables \(\tilde{x}\) can be obtained by

$$\mu _{{\tilde{x}}}^{K} = E\left[ {\tilde{x}^{K} } \right] = \int_{{\left( {\tilde{x}} \right)}} {\tilde{x}^{K} p\left( {\tilde{x}} \right)} d\tilde{x},\quad \quad K = 0,1,2, \ldots ,M,$$
(8)

where \(\tilde{x}^{K} = X^{{k_{1} }} Y^{{k_{2} }} V^{{k_{3} }} ,\;\;K = \sum\nolimits_{i = 1}^{3} {k_{i} } ,\,\;k_{i} \ge 0\). \(\mu_{{\tilde{x}}}^{0} = 1\) is the normalization of PDF \(p\left( {\tilde{x}} \right)\).This meant that the moment information obtained from solving Eq. (5) can also be determined by Eq. (7). In the context of information theory [34], the Boltzmann-Shannon entropy function of \(p\left( {\tilde{x}} \right)\) is given by the following integral

$$H = - \int_{{\left( {\tilde{x}} \right)}} {p\left( {\tilde{x}} \right)\left[ {\ln p\left( {\tilde{x}} \right)} \right]} d\tilde{x}.$$
(9)

The maximum entropy estimation of the function \(p\left( {\tilde{x}} \right)\) is obtained by maximizing the entropy \(H\) associated to \(p\left( {\tilde{x}} \right)\) under the constraint of moment information, where the moment has been given by solving the Eqs. (4) and (5).

Applying the Lagrange multipliers method, introducing the following Lagrange multipliers to seek maximization of the entropy function

$$\tilde{H}\left( {p\left( {\tilde{x}} \right)} \right) = - \int_{{\left( {\tilde{x}} \right)}} {p\left( {\tilde{x}} \right)\left[ {\ln p\left( {\tilde{x}} \right)} \right]} d\tilde{x} - \sum\limits_{{K = 0}}^{M} {\tilde{\lambda }_{K} \left[ {\int_{{\left( {\tilde{x}} \right)}} {p\left( {\tilde{x}} \right)} d\tilde{x} - \mu _{{\tilde{x}}}^{K} } \right]} ,$$
(10)

where \(\tilde{\lambda }_{{\tilde{x}}}^{0} ,\;\;\tilde{\lambda }_{{\tilde{x}}}^{1} ,\;\;\tilde{\lambda }_{{\tilde{x}}}^{2} ,\; \ldots \;,\;\;\tilde{\lambda }_{{\tilde{x}}}^{M}\) are unknown Lagrange multipliers. Under the conditions that existence of an extremum of function \(\tilde{H}\left( p \right)\), that is \({{\delta \tilde{H}} \mathord{\left/ {\vphantom {{\delta \tilde{H}} {\delta p}}} \right. \kern-\nulldelimiterspace} {\delta p}} = 0\), then the maximum entropy distribution can be expressed as

$$p\left( {\tilde{x}} \right) = p\left( {X,Y,V} \right) = C\exp \left\{ { - \sum\limits_{K = 1}^{M} {\tilde{\lambda }_{{\tilde{x}}}^{K} \tilde{x}^{K} } } \right\} = C\exp \left\{ { - \sum\limits_{K = 1}^{M} {\tilde{\lambda }_{{\tilde{x}}}^{K} X^{{k_{1} }} Y^{{k_{2} }} V^{{k_{3} }} } } \right\},\quad \sum\limits_{i = 1}^{3} {k_{i} } = K,$$
(11)

where \(\tilde{\lambda }_{K} = \lambda_{X,Y,V}^{{k_{1} ,k_{2} ,k_{3} }}\). Now the PDF prediction problem of the system (2) is converted into identifying the Lagrange multiplier \(\tilde{\lambda } = \left( {\tilde{\lambda }_{1} ,\tilde{\lambda }_{2} , \ldots ,\tilde{\lambda }_{M} } \right)\).The Lagrange multiplier can be solved by the constrained nonlinear optimization problem based on the moment information. For this optimization problem, we define the following objective function

$$R\left( {\tilde{\lambda }} \right) = R\left( {\tilde{\lambda }_{0} ,\tilde{\lambda }_{1} , \ldots ,\tilde{\lambda }_{M} } \right) = \sum\limits_{{K = 0}}^{M} {\left[ {\int\limits_{X} {\int\limits_{Y} {\int\limits_{V} {X^{{k_{1} }} Y^{{k_{2} }} V^{{k_{3} }} p\left( {X,Y,V} \right)} } } dXdYdV - \mu _{{X,Y,V}}^{{k_{1} ,k_{2} ,k_{3} }} } \right]^{2} } .$$
(12)

Next, the effective intelligent optimization algorithms will be used to calculate the Lagrange multiplier \(\tilde{\lambda }\) to meet \(\tilde{\lambda }^{{{{op}}}} = \arg \mathop {\min }\limits_{{\tilde{\lambda }}} R\left( {\tilde{\lambda }} \right)\), in which the design of the procedure as follows:

Step 1: Initialization: First, let's assume that the population number of particles is \(N_{{{{pop}}}}\) and the range of the maximum speed. We are defining the random initialization speed \(V^{0} = \left( {V_{1}^{0} ,V_{2}^{0} , \ldots ,V_{M}^{0} } \right)\) and random initialization position \(\tilde{\lambda }^{0} = \left( {\tilde{\lambda }_{1}^{0} ,\tilde{\lambda }_{2}^{0} , \ldots ,\tilde{\lambda }_{M}^{0} } \right)\).

Step 2: Individual extremum and global optimal solution \(\tilde{\lambda }^{{{{op}}}}\): The individual extremum is the optimal solution found for each particle, and a global solution is found from these optimal solutions, which is called the global optimal solution. By comparing with the historical global optimum, the best solution \(\tilde{\lambda }^{{{{op}}}}\) will be chosen as the current historical optimal.

Step 3: The \(i\)-th particles are manipulated according to the following equation

$$\begin{aligned} V_{d}^{i} & = \omega V_{d}^{i} + C_{1} \cdot r_{1} \cdot \left( {P_{id} - \tilde{\lambda }_{d}^{i} } \right) + C_{2} \cdot r_{2} \cdot \left( {P_{gd} - \tilde{\lambda }_{d}^{i} } \right) \\ \tilde{\lambda }_{d}^{i} & = \tilde{\lambda }_{d}^{i} + V_{d}^{i} , \\ \end{aligned}$$

where \(\omega\) is the inertia weight.\(C_{1}\) and \(C_{2}\) are two positive constants.\(r_{1}\) and \(r_{2}\) are two random numbers within the \(\left[ {0,1} \right]\). \(P_{i} = \left( {P_{i1} ,P_{i2} , \ldots ,P_{iM} } \right)\) represents the best previous position of the \(i\)-th particles. \(P_{g} = \left( {P_{g1} ,P_{g2} , \ldots ,P_{gM} } \right)\) denotes the best particle among all the particles.

Step 4: The program ends when the iterative number achieves the maximum number \(N_{\max }\) of iterations, and outputs the optimum selection \(\tilde{\lambda }^{op}\).

Similarly, the PDF of variables \(X,\;Y\) and \(\;V\) are also written as

$$\begin{aligned} p\left( {X,Y} \right) & = C\exp \left\{ { - \sum\limits_{\begin{subarray}{l} k_{1} + k_{2} = 1 \\ k_{1} ,k_{2} \ge 0 \end{subarray} }^{M} {\lambda_{X,Y,V}^{{k_{1} ,k_{2} ,0}} X^{{k_{1} }} Y^{{k_{2} }} } } \right\},\quad p\left( X \right) = C\exp \left\{ { - \sum\limits_{{k_{1} = 1}}^{M} {\lambda_{X,Y,V}^{{k_{1} ,0,0}} X^{{k_{1} }} } } \right\}, \\ p\left( Y \right) & = C\exp \left\{ { - \sum\limits_{{k_{2} = 1}}^{M} {\lambda_{X,Y,V}^{{0,k_{2} ,0}} Y^{{k_{2} }} } } \right\},\quad p\left( V \right) = C\exp \left\{ { - \sum\limits_{{k_{3} = 1}}^{M} {\lambda_{X,Y,V}^{{0,0,k_{3} }} V^{{k_{3} }} } } \right\}, \\ \end{aligned}$$
(13)

where \(C\) is a normalization constant, and then applying the intelligent optimization method, the expressions of PDF \(p\left( X \right)\), \(p\left( Y \right)\) and \(p\left( V \right)\) will be determined. In addition, based on the linear relationship between the mean square output voltage and the average output power, we can obtain the expression for the average output power of the system (2) as

$$E\left[ P \right] = \alpha \beta E\left[ {V^{2} } \right] = \alpha \beta \int_{V} {v^{2} p\left( v \right)} dv = \alpha \beta C\int_{V} {v^{2} \exp \left\{ { - \sum\limits_{{k_{3} = 1}}^{M} {\lambda _{{X,Y,V}}^{{0,0,k_{3} }} v^{{k_{3} }} } } \right\}} dv.$$
(14)

5 Examples of Nonlinear VEH Systems with Different Geometric Structure

In this section, we consider the potential energy function of the nonlinear VEH system with the following general form

$$U(X) = \frac{1}{2}X^{2} + \frac{1}{3}K_{2} X^{3} + \frac{1}{4}K_{3} X^{4} ,$$
(15)

where \(K_{3} > 0\) and \(- 2\sqrt {K_{3} } < K_{2} < 2\sqrt {K_{3} }\). In this case, the potential energy function has a stationary point \(x = 0\) and shows the shape characteristics of nonlinear monostable. When \(- 2\sqrt {K_{3} } < K_{2} < 0\), the potential function shows an asymmetry around the equilibrium. As \(K_{2}\) increased to 0, the potential function remains monostable, but the shape characteristics from asymmetry to symmetry, that is the potential function is symmetry for \(K_{2} = 0\). Subsequently, as the continuing increase of \(K_{2}\), the potential function loses its symmetry again and shows a new asymmetry. Contrary to the previous asymmetry results, this means that the potential function is also asymmetry for \(0 < K_{2} < 2\sqrt {K_{3} }\), and corresponding some results are shown in Fig. 2.

Fig. 2
figure 2

Different potential energy functions of nonlinear VEH system in the parameter \(K_{2} \in \left( { - 2\sqrt {K_{3} } ,\;2\sqrt {K_{3} } } \right)\)

Full size image

Next, the PDF and the average output power will be predicted for different shapes characteristic of the potential energy function by the proposed method in Sect. 5.

5.1 The Nonlinear Symmetrical VEH System

In the investigation into nonlinear VHE with symmetrical harvesting, the parameters of the potential function are defined as \(K_{2} = 0\) and \(K_{3} = 1\). Then the moments all before \(M\)th order can be calculated by moment Eqs. (4) and (5), and the part results of the moment before the eighth order for variables \(X,\;Y\) and \(\;V\) are given in Table 1.

Table 1 The vibration information of symmetrical VEH system about each moment
Full size table

Then start applying the first eight moment information to objective function (12) and combined with the intelligent optimization algorithm, the Lagrange multiplier \(\lambda_{X,Y,V}^{{k_{1} ,k_{2} ,k_{3} }}\) of the maximum entropy distribution in Eq. (13) will be estimated. In this case, the convergence curve of the objective function for symmetrical harvesting will be calculated using the intelligent optimization algorithm, shown in Fig. 3. Then the joint PDF and marginal PDFs of state variables \(X\) and \(\;Y\) can be expressed as

$$\begin{aligned} p\left( {X,Y} \right) & = C\exp \left\{ {0.019998X - 0.012986Y + 0.02XY - 1.665987X^{2} - 0.993884Y^{2} } \right. \\ & + 0.02X^{3} - 0.013646X^{2} Y + 0.02XY^{2} - 0.019892Y^{3} - 0.27635X^{4} \\ & + \left. {0.006204X^{3} Y + 0.003133X^{2} Y^{2} + 0.02XY^{3} - 0.02Y^{4} } \right\}, \\ \end{aligned}$$
(16)

and

$$\begin{aligned} p\left( X \right) & = C\exp \left\{ { - 0.00988X - 1.797621X^{2} - 0.02X^{3} - 0.246403X^{4} + 0.017764X^{5} } \right. \\ & - {\kern 1pt} \left. {0.01984X^{6} - 0.02X^{7} - 0.004597X^{8} } \right\}, \\ p\left( Y \right) & = C\exp \left\{ { - 0.002869Y - 1.076595Y^{2} - 0.008448Y^{3} - 0.009972Y^{4} + 0.007532Y^{5} } \right. \\ & + {\kern 1pt} \left. {0.001843Y^{6} - 0.000359Y^{7} - 0.00181Y^{8} } \right\}, \\ \end{aligned}$$
(17)
Fig. 3
figure 3

Convergence curve of intelligent optimization algorithm under symmetrical harvesting

Full size image

the PDF of induced voltage \(V\) is

$$\begin{aligned} p\left( V \right) & = C\exp \left\{ {0.005874V - 1.927013V^{2} - 0.005727V^{3} - 0.017541V^{4} + 0.007372V^{5} } \right. \\ & - \left. {0.011285V^{6} - 0.016027V^{7} - 0.002368V^{8} } \right\}. \\ \end{aligned}$$
(18)

To test estimated results (16), (17), and (18), direct Monte Carlo methods are used to verify the correctness of those analytical results. In detail, Fig. 4a, b illustrate analytical results and numerical results for joint PDFs of displacement and velocity response of the nonlinear symmetrical VEH system under white noise. Furthermore, the comparison of numerical and analytical marginal PDFs of displacement, velocity, and the induced voltage are shown in Figs. 5. Those results indicate that the response of the nonlinear harvester is symmetrical around the stationary point, and numerical results are in good agreement with the estimation results.

Fig. 4
figure 4

Joint PDF for displacement and velocity. a Analytical results; b direct Monte Carlo results

Full size image
Fig. 5
figure 5

Comparison of analytical results (blue line) and direct Monte Carlo results (red asterisk) for PDFs of state variables. a Displacement \(X\), b velocity \(Y\), c induced voltage \(V\)

Full size image

Finally, we analyzed the average output power based on the moment information of the nonlinear symmetrical VEH system, and direct Monte Carlo simulations were conducted to verify the conclusions. Figure 6 shows the comparative results of the numerical and analytical with various physical variables. Figure 6a illustrates the influence of noise density on the output performance of the symmetrical VEH system. The results show that with the increase in noise density, the average output power of the symmetric VEH system increases.

Fig. 6
figure 6

Relationship between mean output power with related physical parameters. a Noise density \(D\), b electromechanical coupling coefficient \(\beta\), c time constant ratio \(\alpha\)

Full size image

However, as we mentioned earlier in this section, the changes in the physical parameter \(K_{2}\) will cause changes in the shape of the potential energy function. That is, the phenomenon of asymmetrical right-skewed for the potential energy function will happen when \(- 2\sqrt {K_{3} } < K_{2} < 0\), or the phenomenon of asymmetrical left-skewed for the potential energy function will occur in \(K_{2} \in \left( {0,\;2\sqrt {K_{3} } } \right)\). The changes in the shape of the potential energy function will trigger the dynamic response of VEH system change.

5.2 The Asymmetrical Right-Skewed VEH System

To further detailed study the harvesting performance of the nonlinear VEH system with asymmetrical potential energy function, the case of asymmetrical right-skewed will firstly be considered, without loss of generality, that we assume the parameters \(K_{2} = - 1.5\) and \(K_{3} = 1\). The moments all before \(M\)th order can also be calculated by moment Eqs. (4) and (5) in this situation, and the part results of the moment before the eighth order for variables \(X,\;Y\) and \(\;V\) are given in Table 2.

Table 2 The vibration information of asymmetrical right-skewed VEH system about each moment
Full size table

Then start substituting all the first eight moments information into the objective function (12) and combined with the intelligent optimization algorithm, the Lagrange multiplier \(\lambda_{X,Y,V}^{{k_{1} ,k_{2} ,k_{3} }}\) of the maximum entropy distribution in Eq. (13) will be estimated, and correspondingly the joint PDF and marginal PDFs of state variables \(X\) and \(\;Y\) can be expressed as

$$\begin{aligned} p(X,Y) & = C\exp \left\{ {{0}{{.000588}}X - {0}{{.003556}}Y + {0}{{.014916}}XY - {1}{{.095065}}X^{2} - {1}{{.204689}}Y^{2} } \right. \\ & + {0}{{.663233}}X^{3} { + 0}{{.000385}}X^{2} Y + {0}{{.005155}}XY^{2} + { - 0}{{.000865}}Y^{3} - {0}{{.399085}}X^{4} \\ & + \left. {{0}{{.001207}}X^{3} Y - {0}{{.001427}}X^{2} Y^{2} + 0.02XY^{3} - 0.006825Y^{4} } \right\}. \\ \end{aligned}$$
(19)

and

$$\begin{aligned} p(X) & = C\exp \left\{ {{0}{{.016725}}X - {1}{{.779613}}X^{2} + {0}{{.441330}}X^{3} - {0}{{.058091}}X^{4} - {0}{{.004692}}X^{5} } \right. \\ & { + }\left. {{0}{{.007144}}X^{6} - {0}{{.014531}}X^{7} - {0}{{.003714}}X^{8} } \right\}, \\ p(Y) & = C\exp \left\{ { - {0}{{.013938}}Y - {1}{{.236557}}Y^{2} - {0}{{.016703}}Y^{3} - {0}{{.01465}}Y^{4} - {0}{{.009041}}Y^{5} } \right. \\ & - \left. {{0}{{.019961}}Y^{6} + {0}{{.007320}}Y^{7} - {0}{{.00012}}Y^{8} } \right\}. \\ \end{aligned}$$
(20)

The PDF of induced voltage \(V\) is

$$\begin{aligned} p(V) & = C\exp \left\{ {{0}{{.009883}}V - {1}{{.83168}}V^{2} - {0}{{.007253}}V^{3} - {0}{{.011771}}V^{4} + 0.02V^{5} } \right. \\ & + \left. {0.013832V^{6} + 0.02V^{7} - 0.010081V^{8} } \right\}. \\ \end{aligned}$$
(21)

To verify that we're getting the expected results (19)–(21), the direct Monte Carlo methods are used to provide conclusion comparisons. Under the circumstance of potential energy function with asymmetrical right-skewed, the joint PDF of displacement and velocity response obtained by Eq. (19) is shown in Fig. 7a, and the corresponding results of the direct Monte Carlo method are shown in Fig. 7b. Later, the marginal PDFs of displacement, velocity, and the induced voltage of analytical results Eqs. (20) and (21) are shown in Fig. 8, and it has shown that analytical results and direct Monte Carlo results have a good consistency. These results suggest that the asymmetrical right-skewed of potential energy function will cause the asymmetric of the PDF of the displacement variable and the trailing phenomenon that occurs in the right of the stationary point \(x = 0\). Next, the change of energy harvesting performance is carefully considered for the physical variables such as noise density \(D\), electromechanical coupling coefficient \(\beta\), and the time constant ratio \(\alpha\) change, as shown in Fig. 9. We can see that these three physical parameters are proportional to the average output power. Consequently, they can greatly enhance the energy harvesting performance for the asymmetrical right-skewed VEH system.

Fig. 7
figure 7

Asymmetrical joint PDF for displacement and velocity. a: Analytical results; b direct Monte Carlo results

Full size image
Fig. 8
figure 8

Comparison of analytical results (blue line) and direct Monte Carlo results (red asterisk) for PDFs of state variables. a Displacement \(X\); b velocity \(Y\); c induced voltage \(V\)

Full size image
Fig. 9
figure 9

Relationship between mean output power with related physical parameters. a Noise density \(D\); b electromechanical coupling coefficient \(\beta\); c the time constant ratio \(\alpha\)

Full size image

5.3 The Asymmetrical Left-Skewed VEH System

Different from the previous two cases, we will further research the dynamic response of the VEH system with asymmetrical left-skewed of the potential energy function in this subsection. In this case, we will assume the parameters \(K_{2} = 1.5\) and \(K_{3} = 1\) of the potential energy function. Then the moments all before \(M\)th order can also be calculated by moment Eqs. (4) and (5), and the part results of the moment before the eighth order for variables \(X,\;Y\) and \(\;V\) are given in Table 3.

Table 3 The vibration information of asymmetrical left-skewed VEH system about each moment
Full size table

Substituting all the first eight moments information into the objective function (12), the Lagrange multiplier \(\lambda_{X,Y,V}^{{k_{1} ,k_{2} ,k_{3} }}\) of the maximum entropy distribution in Eq. (13) will be estimated by the intelligent optimization algorithm, the joint PDF and marginal PDFs of state variables \(X\) and \(\;Y\) can be expressed as

$$\begin{aligned} p(X,Y) & = C\exp \left\{ { - 0.007073X^{2} Y - 0.02XY^{2} - 0.02Y^{3} - 0.493872X^{4} - 0.02X^{3} Y\,} \right. \\ & + \left. {0.009693X^{2} Y^{2} + 0.017192XY^{3} + 0.008156Y^{4} } \right\}, \\ \end{aligned}$$
(22)

and

$$\begin{aligned} p\left( X \right) & = C\exp \left\{ { - 0.002144X - 1.961921X^{2} - 1.197422X^{3} - 0.368664X^{4} {\kern 1pt} + 0.016263X^{5} } \right. \\ & - \left. {0.001277X^{6} + 0.007987X^{7} - 0.00371X^{8} } \right\}, \\ p\left( Y \right) & = C\exp \left\{ { - 0.006586Y - 1.307708Y^{2} - 0.008479Y^{3} - 0.019721Y^{4} - 0.018295Y^{5} } \right. \\ & - \,\left. {0.018889Y^{6} + 0.002326Y^{7} + 0.001948Y^{8} } \right\}. \\ \end{aligned}$$
(23)

The PDF of induced voltage \(V\) is

$$\begin{aligned} p\left( V \right) & = C\exp \left\{ { - 0.016486V - 1.813805V^{2} + 0.015569V^{3} - 0.018442V^{4} - 0.018829V^{5} } \right. \\ & - \left. {0.019339V^{6} + 0.008795V^{7} + 0.000019V^{8} } \right\}. \\ \end{aligned}$$
(24)

Likewise, in this case, the theoretical results of the joint PDF are determined by Eq. (22) shown in Fig. 10a, and the corresponding numerical results by direct Monte Carlo method from original Eq. (2) are shown in Fig. 10b to verify the precision of the proposed method. Figure 11 shows the marginal PDF of the system displacement, velocity, and induced voltage calculated by Eqs. (23) and (24). All these results are compared with the direct Monte Carlo simulation method, where solid lines denote the theoretical results and circle symbols represent direct Monte Carlo method results. It can be found that those theoretical results agree with direct Monte Carlo results well. Figure 11a shows that the asymmetrical left-skewed of potential energy function causes the asymmetric of the PDFs about the displacement variable, then the trailing phenomenon that occurs in the left of the stationary point \(x = 0\). In addition, when physical variables such as noise density \(D\), electromechanical coupling coefficient \(\beta\), and time constant ratio \(\alpha\) change, the changes of harvesting performance are also carefully considered. The changes results of those physical variables are shown in Fig. 12. One can see that increasing those three physical parameters can promote the output of the averaging output power. Consequently, they can enhance the energy harvesting performance for the asymmetrical left-skewed VEH system.

Fig. 10
figure 10

Asymmetrical joint PDF for displacement and velocity. a Analytical results; b direct monte Carlo results

Full size image
Fig. 11
figure 11

Comparison of analytical results (blue line) and direct Monte Carlo results (red asterisk) for PDFs of state variables. a Displacement \(X\); b velocity \(Y\); c induced voltage \(V\)

Full size image
Fig. 12
figure 12

Relationship between mean output power with related physical parameters. a Noise density \(D\); b electromechanical coupling coefficient \(\beta\); c time constant ratio \(\alpha\)

Full size image

5.4 Advantage Analysis of Symmetric and asymmetric VEH Systems

In this subsection, an evaluation index, named power conversion efficiency \(\rho \%\) will be introduced in subsequent studies to assess the electrical power conversion efficiency of the VEH system (2). It is defined as [44]

$$\rho \% = \frac{{\left\langle {P_{{{{Elec}}}} } \right\rangle_{t} }}{{\left\langle {P_{{{{Mech}}}} } \right\rangle_{t} }}100\% ,$$
(25)

where \(\left\langle \cdot \right\rangle\) is the average in time.\(P_{{{{Elec}}}}\) is the capture electrical power harvested, which comes from VEH.\(P_{{{{Mech}}}}\) is the input power, which is generated by stochastic perturbation.

The dimensionless coupled stochastic VEH system (2) under the potential energy function (15) can be subtly rewritten to the following forms:

$$\frac{d}{{dt}}\left( {\frac{1}{2}\dot{X}^{2} + \frac{1}{2}X^{2} + \frac{1}{3}K_{2} X^{3} + \frac{1}{4}K_{3} X^{4} } \right) + c\dot{X}^{2} + \beta V\dot{X} = \dot{X}\xi \left( t \right)$$
(26a)
$$\frac{d}{{dt}}V^{2} = V\dot{X} - \alpha V^{2} .$$
(26b)

Consider the steady state balance of Eq. (26b), that is \({{dV^{2} } \mathord{\left/ {\vphantom {{dV^{2} } {dt}}} \right. \kern-\nulldelimiterspace} {dt}} = 0\), then substitute the corresponding results into Eq. (26a), one can obtain the following equation:

$$\frac{d}{{dt}}\left( {\frac{1}{2}\dot{X}^{2} + \frac{1}{2}X^{2} + \frac{1}{3}K_{2} X^{3} + \frac{1}{4}K_{3} X^{4} } \right) + c\dot{X}^{2} + \alpha \beta V^{2} = \dot{X}\xi \left( t \right).$$
(27)

Then the \(P_{Elec}\) and \(P_{Mech}\) can be expressed as

$$P_{{{{Elec}}}} = \alpha \beta V^{2}$$
(28)
$$P_{{{{Mech}}}} = \dot{X}\xi \left( t \right) = c\dot{X}^{2} + \alpha \beta V^{2} = cY^{2} + \alpha \beta V^{2} .$$
(29)

Substitute Eqs. (28) and (29) into Eq. (25), the power conversion efficiency can be written as

$$\rho \% = \frac{{\left\langle {\alpha \beta V^{2} } \right\rangle }}{{\left\langle {\dot{X}\xi \left( t \right)} \right\rangle }}100\% = \frac{{\alpha \beta \left\langle {V^{2} } \right\rangle }}{{c\left\langle {Y^{2} } \right\rangle + \alpha \beta \left\langle {V^{2} } \right\rangle }}100\% = \frac{E\left[ P \right]}{{cE\left[ {Y^{2} } \right] + E\left[ P \right]}}100\% .$$
(30)

Next, applying Eq. (30), the effects of the noise intensity \(D\), electromechanical coupling coefficient \(\beta\), and the time constant ratio \(\alpha\) on the power conversion efficiency were studied under the three different nonlinear structures, including symmetrical, asymmetrical left-skewed, and asymmetrical right-skewed, as shown in Fig. 13. One can see that in different nonlinear structures, the power conversion efficiency decreases with the increase of noise density from 0.1 to 0.2, as shown in Fig. 13a. Comprehensive comparison of the power conversion efficiency in Fig. 13, the power conversion efficiency of asymmetrical structures is higher than the symmetrical case, but two different asymmetrical skewed were only slightly different when parameters \(K_{2}\) as the opposite. On the contrary, increasing the electromechanical coupling coefficient or time constant ratio will significantly improve the power conversion efficiency under the three different structures. Meanwhile, the power conversion efficiency \(\rho {{\% }}\) under the asymmetric case is higher than the symmetric case, as shown in Fig. 13b, c. The results show that the asymmetric VEH system can convert more mechanical energy into harvester electric than the symmetric system.

Fig. 13
figure 13

Comparison of power conversion efficiency with related physical parameters. a Noise density \(D\); b electromechanical coupling coefficient \(\beta\); c time constant ratio \(\alpha\)

Full size image

6 Conclusions

This paper theoretically studies the prediction of the dynamic behavior and analyses the harvesting performance of the nonlinear VEH system when only partial information of the system is known, such as the moment information. Firstly, the cumulant truncation method is used to obtain the moment equation of the nonlinear stochastic VEH system, and then the corresponding higher-order moments of the system are obtained. Secondly, without assuming that the geometric structure of the nonlinear VEH system, using the principle of maximum entropy, the PDF of the stationary response is expressed as an exponential form, which has some unknown parameters that need to be determined. On this basis, the appropriate objective function is established by combining the obtained moment information and using the intelligent optimization algorithm to find the optimal solution to minimize the objective function, thereby determining all the unknown parameters of the PDF. Subsequently, taking the moment information of three different nonlinear geometry VEH systems, including symmetric, asymmetric left-biased, and asymmetric as the examples, obtain the PDF expressions of each response variable of the corresponding stochastic VEH system by using the proposed method. The effects of the noise intensity, electromechanical coupling coefficient, and time constant ratio on the harvesting performance are also discussed. And the results show that the increase of these physical parameters has a positive effect on improving the average output power under the three different nonlinear geometries. Finally, the power conversion efficiency is introduced in subsequent studies to assess the electrical power conversion efficiency of the stochastic VEH system under three differential nonlinear geometry structures. The results show that asymmetric geometry structure relative to the symmetric structure has a higher power conversion efficiency. However, when the two geometric structure parameters \(K_{2}\) are the contrary, the power conversion efficiency of the two asymmetric deflections is only slightly different.