1 Introduction

In the last decade, vibration energy harvesting was often researched for its great potential application and market in powering low-power wireless sensor networks, portable electronic mobile devices and embedded devices applied to monitor structural health and vibration control [1,2,3,4,5,6]. Different kinds of energy harvesters were designed to efficiently harvest energy from flow induced vibration, base vibration, and human bodies, etc. [7,8,9,10,11,12]. Especially, nonlinear vibration energy harvesters were designed and experimentally tested to enhance broadband energy harvesting [13,14,15,16,17,18,19,20].

Erturk and Inman [21, 22] designed a Duffing-typed bistable energy harvester to efficiently harvest energy from base harmonic excitations, and they found the high-energy interwell orbits. Cottone et al. [23] and later Litak et al. [24, 25] respectively designed nonlinear piezoelectric energy harvesters through exploring the dynamical characteristics of nonlinear oscillators under random excitations. Zhou et al. [26, 27] numerically and experimentally investigated the energy harvesting performance of tristable energy harvesters under harmonic excitations, and then they deduced the analytical solutions. It is found that nonlinear energy harvesters are very sensitive to the system parameters and external excitation conditions [28, 29]. In addition, during the designing and production of nonlinear energy harvesters, their structural and electrical parameters are uncertain due to the errors in the manufacturing process. These uncertain parameters have a significant impact on the output voltage. To quantify this influence, two kinds of uncertain analysis methods are developed: non-probabilistic and probabilistic approaches [30].

For the probabilistic method, many samples and data are required to properly determine the probability density functions of uncertainties (for example, Monte Carlo Simulation) [31]. In fact, it is difficult to get enough samples to satisfy statistical requirements. Therefore, the non-probabilistic approaches were developed, in which we just need to know the bounds of uncertain parameters and can use the interval number to define these uncertainties. Researchers developed several interval analysis method, such as the general interval analysis [31,32,33], the Parameterized Interval Analysis (PIA) [34, 35]which has the optimization and anti-optimization problems [33]. Among interval analysis methods, the Taylor Expansion [36,37,38,39,40] is popular since it is not required to alter the governing functions of system dynamics. Especially, there is a nonlinear relation between the output response of the system and uncertainties. Recently, the uncertainties in the nonlinear vibrational energy harvester have been investigated. Nanda et al. [41] used the method of Quadratures and the Maximum Entropy principle to study the influence of uncertainties on the mean power output of piezoelectric based energy harvesters. Liu et al. [42] carried out the probabilistic response analysis of a nonlinear energy harvester under Gaussian colored noise excitations. Li et al. [43] studied the influence of the uncertain external excitation on the output voltage of nonlinear monostable energy harvesters using an improved interval extension approach based on the 2nd order Taylor series. Meanwhile, some optimization researches are conducted to improve the performance of piezoelectric energy harvesters [44].

In above works, uncertain parameters are not taken into consideration, but these uncertainties can make the objective function apart from the optimal value and harm the gain of the optimization. In this case, a stable design in which the influence of uncertainties on the objective function is small, is urgently needed. This means that the robust design optimization (RDO) [45] should be conducted. The RDO can simulate different uncertain parameters in engineering optimization and reduce the sensitivity of the objective function to uncertain variables. Therefore, such an approach can minimize the mean and variation of the objective function simultaneously.

This paper presents a robust design optimization method based on the improved interval extension to obtain a robust design of the nonlinear monostable energy harvester (NMEH) with uncertain design variables (mass, capacitance, electromechanical coupling coefficient). These uncertain design variables are described by interval number. The central point value and deviation of output voltage are calculated by the improved interval extension based on the 2nd order Taylor series. Then, a robust design optimization is constructed by maximizing the central point value of output voltage and minimizing the deviation of output voltage. This double objective optimization issue is converted into a single objective optimization issue by the penalty function approach, and finally this unconstraint optimization problem is solved.

2 Theoretical solutions of the NMEH

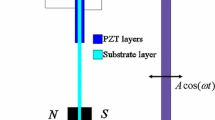
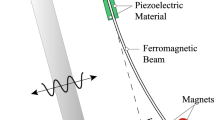
Figure 1 describes the sketch diagram of the magnetic coupled NMEH. As shown in Fig. 1, the magnetic force can be produced by the endmost magnet and two external magnets. Under the excitation \({x}_{b}\left(t\right)\), the NMEH can be governed by the following equations [43, 46]:

$$M\ddot{x}\left(t\right)+C\dot{x}\left(t\right)+{F}_{r}-\theta V\left(t\right)=-nM{\ddot{x}}_{b}\left(t\right)$$
(1)
$${C}_{p}\dot{V}\left(t\right)+V\left(t\right){\left(R\right)}^{-1}+\theta \dot{x}\left(t\right)=0$$
(2)

where \(x\left(t\right)\) presents the tip displacement. \(M\), \(C\) and \({F}_{r}={K}_{1}x\left(t\right)+{K}_{3}{x}^{3}\left(t\right)\) are respectively the equivalent mass, damping, nonlinear restoring force. \({C}_{p}\), \(\theta\) and R are respectively the equivalent capacitance, electromechanical coupling coefficient, load resistance. \(V\left(t\right)\) is the output voltage. n is the amplitude-wise correction factor [46].

Fig. 1
figure 1

The NMEH with magnetic coupling.

Full size image

Under the base acceleration excitation \(Acos\left(\omega t\right)\) (\(A\) stands for the base acceleration excitation amplitude), the governing equations of the NMEH can be re-written as follows [43, 47]:

$$\ddot{x}\left(t\right)+\stackrel{-}{C}\dot{x}\left(t\right)+{\stackrel{-}{K}}_{1}x\left(t\right)+{\stackrel{-}{K}}_{3}{x}^{3}\left(t\right)-\stackrel{-}{\theta }V\left(t\right)=nAcos\left(\omega t\right)$$
(3)
$${C}_{p}\dot{V}\left(t\right)+V\left(t\right){\left(R\right)}^{-1}+\theta \dot{x}\left(t\right)=0$$
(4)

where \(\stackrel{-}{C}=C/M\), \({\stackrel{-}{K}}_{1}={K}_{1}/M\), \({\stackrel{-}{K}}_{3}={K}_{3}/M\) and \(\stackrel{-}{\theta }=\theta /M\).

The steady-state displacement and voltage solutions of the harvester can be obtained via the lower order harmonic balance method [43, 46]:

$${\left(\frac{3}{4}{\stackrel{-}{K}}_{3}{r}^{2}-{\omega }^{2}+{\stackrel{-}{K}}_{1}+\text{S}{C}_{p}{\upomega }\right)}^{2}{r}^{2}+{\left(\omega \stackrel{-}{c}+\frac{S}{R}\right)}^{2}{r}^{2}=(n{A)}^{2}$$
(5)
$$V=\left|\left.\frac{\theta \omega }{\sqrt{\frac{1}{{R}^{2}}+{\left({C}_{p}\omega \right)}^{2}}}\right|\right.r$$
(6)

where r is the amplitude of the response displacement\(,\)V is the amplitude of the response voltage, and \(S=\frac{\stackrel{-}{\theta }\theta \omega }{\frac{1}{{R}^{2}}+{\left({C}_{p}\omega \right)}^{2}}\).

3 Uncertain analysis and robust optimization

To output high-level voltage, these parameters of the NMEH may be tuned but the better choice is to optimize output voltage maximization. However, the objective function (output voltage) is a random variable due to uncertain parameters in the NMEH. To reduce this effect, the sensitivities of objective function to these uncertainties should be limited during maximizing the output voltage, and robust optimization should be conducted.

In this paper, M, \({C}_{p}\) and \(\theta\) are assumed to be uncertain parameters. Here, we use interval numbers to define them, and their corresponding central values and deviations are listed in Table 1. Other parameters of the NMEH are given in Table 2. Acceleration and amplitude of excitation are set as 0.5 g and 15 Hz, respectively.

Table 1 Uncertain parameters of the NMEH
Full size table
Table 2 Determined (fixed) parameters of the NMEH
Full size table

Firstly, the improved interval extension based on the 2nd order Taylor series is employed to take effect of uncertainties listed in Table 1 and achieve the deviation of the objective function (output voltage). For the interval analysis, the uncertainties are defined by the interval variables [43]:

$${x}^{I}=\left[\underset{\_}{x}, \overline{x}\right]$$
(7)

where \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x}\) and \(\overline{x}\) are respectively the lower and upper bounds of interval. The central value (\({x}_{c}\)) and deviation (\(\Delta x\)) are shown as:

$${x}_{c}=\frac{ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} +\overline{x}}{2}$$
(8)
$$\Delta x=\frac{\overline{x}-\underset{\_}{x}}{2}$$
(9)

Alternatively, an interval \({x}^{I}\) can be rewritten by using the PIA [43]:

$${x}^{I}={x}_{c}+\Delta xsin\alpha$$
(10)
$$\alpha \in \left[-\frac{\pi }{2},\frac{\pi }{2}\right]$$
(11)

The 2nd order Taylor expansion of the output voltage \(V\left({X}^{I}\right)\) around the central value \({X}_{c}\) is [43]:

$$V\left({X}^{I}\right)\approx V\left({X}_{c}\right)+\sum _{i=1}^{n}\frac{\partial V\left({X}_{c}\right)}{\partial {x}_{i}}\left({x}_{i}^{I}-{x}_{ic}\right)+\frac{1}{2!}\sum _{i=1}^{n}\sum _{j=1}^{n}\frac{{\partial }^{2}V\left({X}_{c}\right)}{\partial {x}_{i}\partial {x}_{j}}\left({x}_{i}^{I}-{x}_{ic}\right)\left({x}_{j}^{I}-{x}_{jc}\right)$$
(12)

where \({X}^{I}=\left[{M}^{I}, {C}_{p}^{I}, {\theta }^{I} \right] \,\text{ and }\, {X}_{c}={[M}_{c}, {C}_{Pc}, {\theta }_{c}\)].

In the 2nd order Taylor expansion, \(V\left({X}_{c}\right)\) is the output voltage when the interval variables equal to their central values. \(\frac{\partial V\left({X}_{c}\right)}{\partial {x}_{i}}\) and \(\frac{{\partial }^{2}V\left({X}_{c}\right)}{\partial {x}_{i}\partial {x}_{j}}\) are respectively the 1st order and the 2nd order sensitivities of the output voltage with respect to these intervals.

Equations (10) and (11) are substituted into Eq. (12) to construct a continuous function with the 2nd order independent variables [43]:

$$V\left({X}^{I}\right)\approx V\left({\alpha }_{k}\right)=V\left({X}_{c}\right)+\sum _{i=1}^{n}\frac{\partial V\left({X}_{c}\right)}{\partial {x}_{i}}\left[\Delta {x}_{i}sin{\alpha }_{k}\right]$$
$$\begin{aligned} V\left( {X^{I} } \right) & \approx V\left( {\alpha _{k} } \right) = V\left( {X_{c} } \right) + \mathop \sum \limits_{{i = 1}}^{n} \frac{{\partial V\left( {X_{c} } \right)}}{{\partial x_{i} }}\left[ {\Delta x_{i} sin\alpha _{k} } \right] \\ & \quad + ~\frac{1}{{2!}}\mathop \sum \limits_{{i = 1}}^{n} \mathop \sum \limits_{{j = 1}}^{n} \frac{{\partial ^{2} V\left( {X_{c} } \right)}}{{\partial x_{i} \partial x_{j} }}\left[ {\Delta x_{i} \Delta x_{j} \left( {sin\alpha _{k} } \right)^{2} } \right] \\ \end{aligned}$$
(13)

Eq. (13) can be rewritten as:

$$V\left({X}^{I}\right)\approx V\left({\alpha }_{k}\right)=V\left({X}_{c}\right)+V\left({\alpha }_{k}\right)$$
(14)
$$V\left({\alpha }_{k}\right)=\sum _{i=1}^{n}\frac{\partial V\left({X}_{c}\right)}{\partial {x}_{i}}[\Delta {x}_{i}sin{\alpha }_{k}]+\frac{1}{2!}\sum _{i=1}^{n}\sum _{j=1}^{n}\frac{{\partial }^{2}V\left({X}_{c}\right)}{\partial {x}_{i}\partial {x}_{j}}[\Delta {x}_{i}\Delta {x}_{j}{\left(sin{\alpha }_{k}\right)}^{2}]$$
(15)

where \(k\) is the number of categories of uncertainties, and the same type of uncertain variables is expressed by a single \(\alpha\). There are two kinds of variables: a structural parameter (\({M}^{I}\)), and electrical parameters (\({C}_{p}^{I}, {\theta }^{I}\)). Therefore, \(k\) equals 2 and the bounds of function \(V\left({X}^{I}\right)\) can be calculated by minimizing and maximizing the continuous function \(G\left({\alpha }_{k}\right)\), as shown in Eqs. (16) and (17):

$$\underset{\_}{V\left({X}^{I}\right)}=V\left({X}_{c}\right)+minimum\left(G\left({\alpha }_{k}\right)\right)$$
(16)
$$\overline{V\left({X}^{I}\right)}=V\left({X}_{c}\right)+maximum\left(G\left({\alpha }_{k}\right)\right)$$
(17)

Considering the efficiency of the numerical calculation in the practical energy harvestings, we ignore the cross partial derivatives. Meanwhile, the 1st order and the remaining 2nd order sensitivities are retained. The finite difference approach is used to calculate the sensitivities, and the equations are given as:

$${V}^{\prime}\left(x\right)=\frac{V\left(x+h\right)-V(x-h)}{2h}$$
(18)
$${V}^{\prime\prime}\left(x\right)=\frac{V\left(x+h\right)-2V\left(x\right)+V(x-h)}{{h}^{2}}$$
(19)

where \(h\) is the finite-difference interval.

According to Eqs. 9, 16 and 17, the deviation of the output voltage is computed as:

$$\Delta V\left({X}^{I}\right)=\frac{\overline{V\left({X}^{I}\right)}-\underset{\_}{V\left({X}^{I}\right)}}{2}=\frac{maximum\left(G\left({\alpha }_{k}\right)\right)-minimum\left(G\left({\alpha }_{k}\right)\right)}{2}$$
(20)

Secondly, the improved interval extension method is employed to build the robust design optimization issue. Compared with the deterministic optimization problem of the NMEH given in Table 3, uncertain parameters can be simulated and the robust design of the NMEH can be obtained by maximizing the central value of output voltage (\(V\left({X}_{c}\right)\)) and minimizing the deviation of output voltage (\(\Delta V\left({X}^{I}\right)\) in Eq. 20) to limit the effect of these uncertainties on the objective function. As a result, the deterministic optimization with a single objective function is transformed into the robust design optimization with the double objective function (Table 4).

Table 3 Deterministic optimization of the NMEH
Full size table
Table 4 Robust optimization of the NMEH
Full size table

The double objective optimization model listed in Table 4 is further transformed into the following unconstrained optimization model \({Min}f\left({X}^{I}\right)\)based on the penalty function method [45, 48]:

$$f\left({X}^{I}\right)=\frac{{e}_{1}\left(-V\left({X}_{c}\right)+{e}_{2}\right)}{{e}_{3}}+\frac{\left(1-{e}_{1}\right)\left(\Delta V\left({X}^{I}\right)+{e}_{2}\right)}{{e}_{4}}$$
(21)

where the negative sign in front of \(V\left({X}_{c}\right)\) converts finding the maximum of objective function into searching for the minimum. \({e}_{1}\in \left[\text{0,1}\right]\) is the weighting factor whose different values illustrate the different minimization of the central value of minus output voltage (\(-V\left({X}_{c}\right)\)) and the deviation of output voltage (\(\Delta V\left({X}^{I}\right)\)). This means, a stronger robust design can be obtained by reducing \({e}_{1}\). The parameter \({e}_{2}\) is used to keep the non-negativity of \(\left(-V\left({X}_{c}\right)+{e}_{2}\right)\) and \(\left(\Delta V\left({X}^{I}\right)+{e}_{2}\right)\). The parameters \({e}_{3}\) and \({e}_{4}\) are normalization factors to guarantee that the polynomial with a central value pertain to the same order of magnitude as the one with deviation. The optimization problem (Eq. 21) with uncertain design variables and constraint listed in Table 4 can be solved by the nonlinear programming method [49].

The above works can be summarized as one process shown in Fig. 2 according to which three cases are optimized; the first is the deterministic optimization given in Table 3, the other two are both the robust design optimizations listed in Table 4. In the robust design optimizations, we alter the parameter \({e}_{1}\) to obtain optimal designs with different robustness (\({e}_{1}=0.9 \,\text{ and }\, 0.1\)). The results will be given in the following section.

Fig. 2
figure 2

Flow chart of building robust design optimization.

Full size image

4 Results and discussion

The design variables in the three cases are mass, capacitance and electromechanical coupling coefficient, bounds of which are given in Table 5. These design variables are uncertain especially in the last two cases (robust optimization), and their deviations are listed in Table 1.

Table 5 The design variables
Full size table

In the first case, the deterministic optimization problem defined in Table 3 is carried out, and a stopping criteria is set to determine the convergence of optimization. In this algorithm, if the change in the value of the objective function is smaller than tolerance, \(\left|f\left({x}_{i}\right)-f\left({x}_{i+1}\right)\right|<\delta\), the iterations end. Here, the tolerance (\(\delta\)) is set as \(1\times {10}^{-16}\). Starting from nominal design values after 12 interactive calculations, the output voltage converges to 16.7940 V, as shown in Fig. 3. At the same time, \(M\) increases and the other two design variables (\({C}_{p}\), \(\theta\)) drop, shown in Figs. 4, 5 and 6.

Fig. 3
figure 3

Optimization history of the output voltage in deterministic optimization.

Full size image
Fig. 4
figure 4

Optimization history of the mass in deterministic optimization.

Full size image
Fig. 5
figure 5

Optimization history of the capacitance in deterministic optimization.

Full size image
Fig. 6
figure 6

Optimization history of the electromechanical coupling coefficient in deterministic optimization.

Full size image

In the second case, the robust design optimization problem defined in Table 4 is calculated, and \({e}_{1}\) equals 0.9. It means that we look forward to obtaining as high output voltage as possible, even if the robustness decreases. After interactive computing, the alteration of the objective function is smaller than the tolerance. The central value of output voltage converges to 16.7942 V, and its deviation is 2.3 V, as shown in Figs. 7 and 8. The optimization processes of design variables are given in Figs. 9, 10 and 11.

Fig. 7
figure 7

Optimization history of the central value of the output voltage in robust optimization (\({e}_{1}=0.9\)).

Full size image
Fig. 8
figure 8

Optimization history of the deviation of the output voltage in robust optimization (\({e}_{1}=0.9\)).

Full size image
Fig. 9
figure 9

Optimization history of the mass in robust optimization (\({e}_{1}=0.9\)).

Full size image
Fig. 10
figure 10

Optimization history of the capacitance in robust optimization (\({e}_{1}=0.9\)).

Full size image
Fig. 11
figure 11

Optimization history of the electromechanical coupling coefficient in robust optimization (\({e}_{1}=0.9\)).

Full size image

In the last case, parameter \({e}_{1}\) is set as 0.1 to obtain optimal design with better robustness, and the robust design optimization problem defined in Table 4 is calculated again. After interactive computing, the objective function tolerance of change is satisfied, and the central value of output voltage converges to a smaller value (14.3232 V) than the one in the second case. However, the deviation decreases from 2.3 to 1.8572 V, as shown in Figs. 12 and 13. Finally, the deviation of output voltage is smaller. This means that the optimal design has better robustness than that obtained in the second case. The histories of design variables iterations are shown in Figs. 14, 15 and 16.

Fig. 12
figure 12

Optimization history of the central value of output voltage in robust optimization (\({e}_{1}=0.1\)).

Full size image
Fig. 13
figure 13

Optimization history of the deviation of output voltage in robust optimization (\({e}_{1}=0.1\)).

Full size image
Fig. 14
figure 14

Optimization history of the mass in robust optimization (\({e}_{1}=0.1\)).

Full size image
Fig. 15
figure 15

Optimization history of the capacitance in robust optimization (\({e}_{1}=0.1\)).

Full size image
Fig. 16
figure 16

Optimization history of the electromechanical coupling coefficient in robust optimization (\({e}_{1}=0.1\)).

Full size image

5 Conclusion

This paper presents a robust design optimization method for nonlinear monostable energy harvesters with structural uncertainties from the improved interval extension. Due to the 2nd order items in the extension formula of the objective function (output voltage), this robust design optimization method is suitable for nonlinear systems. Having made a robust design of the NMEH, it is illustrated that the high central value and the small deviation of output voltage can be obtained by this robust design optimization method. More importantly, the robustness of the NMEH can be increased based on this method. It can be also used for bistable/tristable/multistable energy harvesters thanks to the non-intrusive features of the improved interval extension in this paper.