Introduction

The way in which firms and workers bargain over wages and sometimes over employment probably is one of the most important institutional features underlying the determination of labour market outcomes (cf. Nickell 1997; Nickell and Layard 1999; Blanchard and Wolfers 2000). According to the backers of this view, actual labour markets are far from competitive and are fairly described instead by a scheme of bilateral monopoly where firms and workers stand on opposite sides. Consequently, the prevailing rules according to which the value of produced output—or the total surplus—is split among the two bargaining parties are an essential determinant of wages and employment and they also deeply contribute to shape the evolution of these variables over time (cf. Lockwood and Manning 1989; Manning 1991, 1993; de la Croix et al. 1996).

In this paper, given the production technology available to firms and the preferences of workers, we aim at contributing to the normative literature on dynamic wage bargaining by exploring how different negotiation settings may affect labour market fluctuations in an intertemporal setting without time discontinuities similar to the ones usually employed in differential games of bargaining (e.g., Leitman 1973; Petrosyan and Yeung 2014). Specifically, under the assumption that the economy is continuously hit by stochastic disturbances to the effectiveness of labour, we show how the way in which firms and workers—or unions—bargain over the wage contributes to determine the dynamics of output, employment, and wages. In detail, relying on the optimal control frameworks originally put forward by Guerrazzi (2011, 2021), we make such a theoretical exploration by developing non-deterministic dynamic versions of the right to manage, the monopoly union, and the efficient bargaining models in which the wage is always taken as the control variable, whereas the evolution of employment—taken as the state variable on a par with productivity shocks—is assumed to be constrained by different adjustment mechanisms. In other words, we assume that employment may alternatively adjust itself with some attrition towards the demand schedule of the firms or the contract curve of the two parties and we make the hypothesis that the actual positions of such equilibrium relationships are affected by the erratic realizations of productivity shocks. Thereafter, calibrating and simulating each versions of the mentioned dynamic bargaining models by targeting the observed volatility of GDP, we try to assess which is the theoretical negotiation setting that better replicates the available empirical evidence on employment and wage fluctuations in the US at the aggregate level. To the best of our knowledge, this is the first contribution in which dynamic wage bargaining is framed within a stochastic optimal control setting by testing its ability to reproduce actual data on labour market oscillations.

The central finding of our analysis is that the interaction between the preferences of the two bargainers and the rules that define the employment adjustments underlying the wage bargaining process are crucial in determining the cyclical properties of the dynamic model economy. Specifically, on the basis of our numerical simulations, we find that with a quadratic production function and risk averse workers, wage bargaining outcomes whose employment adjustments go in the direction of the downward-sloping labour demand schedule of the representative firm—like the ones implied by the right to manage and the monopoly union models—match the cyclical behaviour of the involved economic variables but fail to replicate the observed real wage rigidity (cf. McDonald and Solow 1981; MaCurdy and Pencavel 1986). By contrast, we find that wage bargaining outcomes whose employment adjustments target the upward-sloping contract curve of two negotiating parties—like the ones implied by the efficient bargaining model—not only replicate the co-movement of the economic variables taken into consideration but are also able to deliver a strong degree of wage stickiness that is missing when employment adjustments target an inefficient locus (cf. Thomas 1988; Asheim and Strand 1991).

The paper is arranged as follows. Section 2 provides the theoretical framework of the numerical analysis. Section 3 shows the results of the numerical simulations of the different versions of the bargaining settings under scrutiny. Finally, Sect. 4 concludes by providing some directions for further developments.

Theoretical framework

We consider a dynamic model economy hit by stochastic disturbances that affect the production possibilities of entrepreneurs in which time is continuous and labour is the only tunable productive factor. Within this stylized economy, a risk neutral representative firm and a unionized group of risk averse workers bargain over the wage under the supervision of an omniscient and infinitely lived mediator—or arbitrator—that counterbalances the instantaneous objective functions of the two parties over an infinite horizon. Since the instantaneous solution of the bargaining process is assumed to have an influence on future bargaining opportunities, in what follows we explicitly consider the intertemporal features of the negotiation activities in which the firm and the union are supposed to be permanently involved (cf. Raiffa 1953).

On the productive side, we make the hypothesis that the production function is given by the following quadratic expression:

$$\begin{aligned} Y\left( t\right) =\alpha _{1}\left( t\right) L\left( t\right) -\alpha _{2}\left( t\right) \left( L\left( t\right) \right) ^{2}, \end{aligned}$$
(1)

where \(Y\left( t\right)\) is the instantaneous output of the representative firm, and \(L\left( t\right)\) is the number of employed workers, whereas \(\alpha _{1}\left( t\right)\) and \(\alpha _{2}\left( t\right)\) are random positive shocks that affect, respectively, the intercept and the slope of the instantaneous marginal productivity of labour; indeed, the suggested expression for \(Y\left( t\right)\) implies that \(\partial Y\left( t\right) /\partial L\left( t\right) =\alpha _{1}\left( t\right) -2\alpha _{2}\left( t\right) L\left( t\right)\).Footnote 1

Following Guerrazzi (2011, 2021), we assume that in each instant, \(\alpha _{1}\left( t\right)\) is defined as:

$$\begin{aligned} \alpha _{1}\left( t\right) \equiv 1+2\alpha _{2}\left( t\right) . \end{aligned}$$
(2)

The normalization of the two shocks conveyed by Eq. (2) has two important implications. First, an increase (decrease) in \(\alpha _{2}\left( t\right)\) increases (decreases) the intercept and the absolute value of the slope of the instantaneous marginal productivity of labour. Consistently with the implicit hypothesis that on the background, there exists a fixed factor in addition to labour, this means that a technological improvement (worsening) increases (decreases) the level of the marginal productivity, but it also accelerates (delays) labour saturation. Moreover, normalizing to 1 the membership of the workers’ union, Eq. (2) implies that the level of the marginal productivity of labour achieved when all the members of the union are employed is equal to 1, as well. Therefore, \(w_{0}\equiv 1\) can be taken as the fall-back level of the wage for the union that is sitting at the bargaining table together with the firm and 1 is also the competitive wage bill.

In the remainder of the paper, we also make the hypothesis that the motion of \(\alpha _{2}\) over time is described by an Ornstein–Uhlenbeck process, so that

$$\begin{aligned} \overset{\cdot }{\alpha _{2}}\left( t\right) =\kappa \left( \mu _{\alpha }-\alpha _{2}\left( t\right) \right) +\sigma _{\alpha }\overset{\cdot }{x}\left( t\right) , \end{aligned}$$
(3)

where \(\mu _{\alpha }>0\) is the long-run mean of the process, \(\kappa >0\) is its speed of mean reversion, and \(\sigma _{\alpha }>0\) is its instantaneous standard deviation, whereas \(\overset{\cdot }{x}\left( t\right)\) is a standard Brownian motion with zero drift and unit variance (cf. Cox and Miller 1967).

The expression in Eq. (3) reveals that in each instant, the value of \(\alpha _{2}\) tends to fluctuate around \(\mu _{\alpha }\) that represents its expected long-run value. Moreover, it also shows that the amplitude of short-run fluctuations directly depends on the magnitude of \(\sigma _{\alpha }\) whereas—outside the long-run equilibrium of the process—the speed of convergence towards \(\mu _{\alpha }\) is an increasing function of the parameter \(\kappa\).

The building blocks fixed above allow us to derive the objective function of the firm as well as the preferences of the union. On one hand, given the production function in Eq. (1) and the normalization of the two shocks in Eq. (2), the profit of the firm can be written as

$$\begin{aligned} \Pi \left( L\left( t\right) ,w\left( t\right) \right) =\left( 1+2\alpha _{2}\left( t\right) -w\left( t\right) \right) L\left( t\right) -\alpha _{2}\left( t\right) \left( L\left( t\right) \right) ^{2}, \end{aligned}$$
(4)

where \(w\left( t\right)\) is the real wage paid to employed workers in instant t.

In a competitive market for goods, the profit of the firm will be inexorably driven to zero. As a consequence, consistently with the non-Walrasian features of the model economy under scrutiny recalled above, such a critical threshold is taken as the fall-back level of profit in the bargaining process. In other words, the firm is assumed to leave the bargaining table whenever its profits become negative.Footnote 2

On the other hand, recalling that 1 is the level of the wage that fully employs all the union members, the union utility is assumed to be given by the following ordinal objective function:

$$\begin{aligned} U\left( L\left( t\right) ,w\left( t\right) \right) =L\left( t\right) \left( \left( w\left( t\right) \right) ^{\beta }-1\right) , \end{aligned}$$
(5)

where \(0<\beta <1\) is a parameter that measures the degree of risk aversion of unionized workers.

As argued by Manning (1991), Eq. (5) implies that union members get utility from the wage paid by the firm according to the concave function \(\left( w\left( t\right) \right) ^{\beta }\). Specifically, they are assumed to care about the excess of such an expression over the level of utility that they could get if they leave the bargaining table and took their chances in the open labour market which offers the competitive wage and a corresponding utility level equal to 1. Moreover, the decreasing curvature of the wage utility implied by the values in which the parameter \(\beta\) is allowed to vary reveals the risk attitude of unionized workers; indeed, a concave specification of the utility derived from the wage implies that regarding fluctuations in labour earnings union members are risk averse. Since unions tend to discourage firms from firing and offer income support to its rank and file in case of dismissal, there is massive evidence that risk averse individuals find profitable to join or create such organizations (cf. Colombier et al. 2008; Goerke and Pannenberg 2012).

Following Guerrazzi (2011, 2021), in this paper, we model wage bargaining as an optimal control problem solved by the mediator mentioned above and we consider a right to manage, a monopoly union, as well as an efficient bargaining setting that differ from one another for the rules underlying the sluggish employment adjustments. According to such a theoretical proposal, the evolution of employment over time as well as the one of labour effectiveness are taken as dynamic accumulation constraints affecting the size of the future surpluses of the two bargaining parties (cf. Muthoo 1999, Section 10.3).

In the dynamic right to manage and monopoly union cases, the omniscient and infinitely lived mediator sets the wage by considering that in each instant, employment tends to adjust itself with some exogenous attrition towards the level that maximizes the instantaneous profits of the firm, an allocation that—given the effectiveness of labour and the bargained wage—corresponds to the labour demand schedule implied by the productive technology (cf. Nickell and Andrews 1983). Consequently, considering the expression in Eq. (4), in the dynamic right to manage and the monopoly union frameworks, employment dynamics is described by

$$\begin{aligned} \overset{\cdot }{L}\left( t\right) =\theta \left( \frac{1+2\alpha _{2}\left( t\right) -w\left( t\right) }{2\alpha _{2}\left( t\right) }-L\left( t\right) \right) , \end{aligned}$$
(6)

where \(\theta >0\) is a parameter that measures the attrition between actual and desired employment as well as the instantaneous employment out-flows.

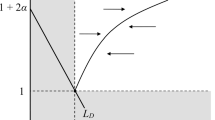
Given the realization of the stochastic process \(\alpha _{2}\) and the bargained wage set by the mediator, the differential equation in (6) reveals that in each instant, employment tends to adjust itself in the direction of the downward-sloping line \((L_{D})\) depicted in Fig. 1. Since the union will never accept a wage rate below 1 and employment goes towards the \(L_{D}\) line, the gray area denotes the unfeasible allocations.

Fig. 1
figure 1

Employment adjustments in the dynamic right to manage and monopoly union models

Full size image

Employment adjustments that go in the direction of the labour demand schedule of the firm like the ones indicated by the arrows in Fig. 1 are usually rationalized with the observation that the level of employment is almost never the subject of collective wage bargaining (cf. Oswald 1993). Consequently, when an agreement on the wage is achieved by the two bargainers, the firm has an incentive to adjust employment towards the level that maximizes its profits and—by hypothesis—the mediator will accommodate this tendency; indeed, as argued by Manning (1987) in a sequential bargaining framework, both the right to manage and the monopoly model describe a situation in which the union has no power in the determination of employment. Of course, whenever the bargained wage converges to a value above 1, some members of the union will be unemployment. As argued by MaCurdy and Pencavel (1986), such an employment rationing can be achieved by long apprenticeship programs, high entrance fees requested by the union, and some form of nepotism in the hiring process. Furthermore, the diagram in Fig. 1 shows that a positive (negative) productivity shock leads the employment–wage pairs, such that employment is stable to rotate in a clockwise (counter-clockwise) direction by pivoting on the outside option of the union.

In the dynamic efficient bargaining case, the mediator is instead assumed to set the wage by considering that employment tends to adjust itself—again with some attrition—in the direction of the contract curve implied by the preferences of the firm and the ones of the union (cf. Leontief 1946). Therefore, considering the expressions in Eqs. (4) and (5) and recalling that the contract curve is given by the employment–wage pairs in which the isoprofit curves of the firm are tangent to the indifferent curves of the union, in an intertemporal efficient bargaining framework employment dynamics is described by

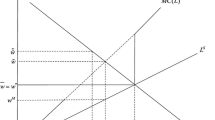
$$\begin{aligned} \overset{\cdot }{L}\left( t\right) =\theta \left( \frac{\beta \left( 1+2\alpha _{2}\left( t\right) \right) +\left( 1-\beta \right) w\left( t\right) -\left( w\left( t\right) \right) ^{1-\beta }}{2\alpha _{2}\left( t\right) \beta }-L\left( t\right) \right) . \end{aligned}$$
(7)

Symmetrically, given the realization of \(\alpha _{2}\) and the wage, the differential equation in (7) reveals that employment tends to adjust itself in the direction of the upward-sloping contract curve (CC) depicted in Fig. 2. Again, since the union will never accept a wage lower than 1 and employment goes towards the CC curve, the gray area denotes the unfeasible allocations.

Fig. 2
figure 2

Employment adjustments in the dynamic efficient bargaining model

Full size image

The employment adjustments illustrated by the arrows in Fig. 2 describe a situation in which the wage bargaining process going on between the risk neutral firm and the utilitarian union made by risk averse workers over an infinite time-horizon has a concern also for the level of employment; indeed, assuming that the wage is set before the employment level (or vice versa), Manning (1987) argues that the efficient bargaining model describes a situation in which the union and the firm have the same power in determining the wage–employment pair. There are a number of reasons why the mediator may accommodate this kind of tendency that leads necessarily to over-employment, i.e., a bargained value of L higher than 1.Footnote 3 For example, Pohjola (1987) argues that the wage–employment pairs on the contract curve can be actually achieved when there is bargaining over profit sharing, with the firm fixing employment. Moreover, Johnson (1990) states that a concern for employment may endogenously arise when labour–management negotiations have as a subject the number of workers assigned to each machine and/or the amount of work intensity that each worker is required to provide on the job. Under these circumstances, bargained employment can go well above the level of union membership leading the mediator to comply with this kind of out-of-equilibrium dynamics. Furthermore, similarly to what we observed before, even in the case depicted in Fig. 2, a positive (negative) productivity shock leads the employment–wage pairs, such that employment is stable to rotate in a clockwise (counter-clockwise) direction.

The dynamic right to manage and monopoly union models

As argued by Guerrazzi (2011), when the wage is bargained in a right-to-manage manner the infinitely lived mediator maximizes a weighted average of the profit of the firm and the utility of the union by taking into account the employment dynamics conveyed by Eq. (6) and the evolution of the productivity parameter described in Eq. (3). Consequently, the stochastic-dynamic problem of the forward-looking mediator becomes the following:

$$\begin{aligned} V\left( \alpha _{0,}L_{0}\right)=\; & {} \underset{\left\{ w\left( t\right) \right\} _{t=0}^{\infty }}{\max }\text { }E_{0}\left[ {\displaystyle \int \limits _{0}^{\infty }} \exp \left( -\rho t\right) \left( \gamma \Pi \left( L\left( t\right) ,w\left( t\right) \right) +\left( 1-\gamma \right) U\left( L\left( t\right) ,w\left( t\right) \right) \right) dt\right] \nonumber \\&\text {s.to}\nonumber \\ \overset{\cdot }{L}\left( t\right)=\; & {} \theta \left( \frac{1+2\alpha _{2}\left( t\right) -w\left( t\right) }{2\alpha _{2}\left( t\right) }-L\left( t\right) \right) \nonumber \\ \overset{\cdot }{\alpha _{2}}\left( t\right)=\; & {} \kappa \left( \mu _{\alpha }-\alpha _{2}\left( t\right) \right) +\sigma _{\alpha }\overset{\cdot }{x}\left( t\right) \nonumber \\ L\left( 0\right)=\; & {} L_{0}\text {, }\alpha _{2}\left( 0\right) =\alpha _{0}, \end{aligned}$$
(8)

where \(V\left( \cdot \right)\) is the value function, \(E\left[ \cdot \right]\) is the expectation operator, \(\gamma \geqslant 0\) is a parameter that measures the weight assigned by the mediator to firm’s profits, and \(\rho >0\) is its discount rate, whereas \(L_{0}>0\) and \(\alpha _{0}>0\) are, respectively, the initial level of employment and the initial value of the stochastic process that hits labour productivity.

The linear bargaining solution implemented in the maximandum of the problem in (8) is appealing and analytically tractable in a deterministic setting, but it may lead to some unpleasant inconsistencies. Specifically, taking values of \(\gamma\) in the closed interval \(\left[ 0,1\right]\) as is commonly done with the generalized Nash solution, it may drive the outcomes of the dynamic bargaining process towards meaningless allocations for the firm and/or the union (cf. Lockwood and Manning 1989). However, as shown by Guerrazzi (2011, 2021), these inconsistencies may be easily bypassed by allowing the parameter \(\gamma\) to vary in a given interval—say \(\left[ \gamma _{\min },\gamma _{\max }\right]\)—where \(\gamma _{\min }\) is not necessarily equal to zero and \(\gamma _{\max }\) instead is strictly lower than 1.

To be precise, for the dynamic right to manage model, Guerrazzi (2011) shows that the required limiting values for the weight attached by the mediator to firm’s profits are, respectively, \(\gamma _{\min }=0\) and \(\gamma _{\max } =\beta /\left( 1+\beta \right) <1\); indeed, straightforward differentiation of the linear maximandum in (8) reveals that taking values of \(\gamma\) within the interval \(\left[ 0,\beta /\left( 1+\beta \right) \right]\), the instantaneous marginal evaluation of a wage variation is never negative for the mediator. Consequently, when \(\gamma =\gamma _{\max }\) the bargained employment–wage pair is (1, 1). Moreover, when \(\gamma =\gamma _{\min }=0\), i.e., when the mediator gives no importance to firm’s profits, the problem in (8) describes a dynamic version of the monopoly union model, so that the bargained employment–wage pair is \(\left( w_{\max }^{\text {MU} },L_{\min }^{\text {MU}}\right)\), where \(w_{\max }^{\text {MU}}>1\) and \(L_{\min }^{\text {MU}}\equiv \left( 1+2\alpha _{2}-w_{\max }^{\text {MU}}\right) /2\alpha _{2}<1\) fix a point on the labour demand schedule (cf. Hoel 1991; Booth and Schiantarelli 1987; Oswald 1982; Lindblom 1948).

Allowing \(\gamma\) to vary in the closed interval \([0,\gamma _{\max }]\) and taking values of the state L belonging to \([L_{\min }^{\text {MU}},1]\) together with values of the control w belonging to \([1,w_{\max }^{\text {MU} }]\), the Hamilton–Jacobi–Bellman (HJB) equation for the mediator problem can be written as follows:

$$\begin{aligned} \rho V(\alpha _{0,}L_{0})= & {} \underset{w\in [1,w_{\max }^{\text {MU}}]}{\max }\left\{ \gamma \Pi \left( L,w\right) +\left( 1-\gamma \right) U\left( L,w\right) \right. \nonumber \\&+\theta \left( \frac{1+2\alpha _{2}-w}{2\alpha _{2}}-L\right) \frac{\partial V(\alpha _{0,}L_{0})}{\partial L}+\kappa \left( \mu _{\alpha }-\alpha _{2}\right) \frac{\partial V(\alpha _{0,}L_{0})}{\partial \alpha _{2} }\nonumber \\&\left. +\;\frac{1}{2}\sigma _{\alpha }^{2}\frac{\partial ^{2}V(\alpha _{0,}L_{0} )}{\partial \alpha _{2}^{2}}\right\} , \end{aligned}$$
(9)

where \(\gamma \Pi \left( L,w\right) +\left( 1-\gamma \right) U\left( L,w\right)\) is a function defined in \((L_{\min }^{\text {MU}},1)\times\) \(\left( 1,w_{\max }^{\text {MU}}\right)\) that returns non-negative values.

Given the expressions in Eqs. (4) and (5), the first-order condition (FOC) for w requires that along the optimal path, it must hold that

$$\begin{aligned} \frac{\partial V(\alpha _{0,}L_{0})}{\partial L}=\frac{2\alpha _{2}L\left( \left( 1-\gamma \right) \beta w^{\beta -1}-\gamma \right) }{\theta }. \end{aligned}$$
(10)

Moreover, the envelope condition for L is given by

$$\begin{aligned} \left( \rho +\theta \right) \frac{\partial V\left( \alpha _{0,}L_{0}\right) }{\partial L}=\; & {} \theta \left( \frac{1+2\alpha _{2}-w}{2\alpha _{2}}-L\right) \frac{\partial ^{2}V\left( \alpha _{0,}L_{0}\right) }{\partial L^{2}}\nonumber \\&+\kappa \left( \mu _{A}-\alpha _{2}\right) \frac{\partial ^{2}V\left( \alpha _{0,}L_{0}\right) }{\partial \alpha _{2}\partial L}+\frac{1}{2} \sigma _{\alpha }^{2}\frac{\partial ^{3}V\left( \alpha _{0,}L_{0}\right) }{\partial \alpha _{2}^{2}\partial L}\nonumber \\&+\sigma _{\alpha }^{2}\frac{\partial ^{2}V\left( \alpha _{0,}L_{0}\right) }{\partial \alpha _{2}^{2}}. \end{aligned}$$
(11)

The dynamic efficient bargaining model

When the wage is bargained in an efficient manner, the mediator maximizes the same integral collected in problem (8) under the same dynamic constraint for the evolution of \(\alpha _{2}\). However, as argued by Guerrazzi (2011, 2021), it takes into consideration that employment follows the adjustment process described by Eq. (7). Consequently, the stochastic-dynamic problem of the mediator becomes the following:

$$\begin{aligned} V(\alpha _{0,}L_{0})=\; & {} \underset{\left\{ w\left( t\right) \right\} _{t=0}^{\infty }}{\max }\text { }E_{0}\left[ {\displaystyle \int \limits _{0}^{\infty }} \exp \left( -\rho t\right) \left( \gamma \Pi \left( L\left( t\right) ,w\left( t\right) \right) +\left( 1-\gamma \right) U\left( L\left( t\right) ,w\left( t\right) \right) \right) dt\right] \nonumber \\&\text {s.to}\nonumber \\ \overset{\cdot }{L}\left( t\right)=\; & {} \theta \left( \frac{\beta \left( 1+2\alpha _{2}\left( t\right) \right) +\left( 1-\beta \right) w\left( t\right) -\left( w\left( t\right) \right) ^{1-\beta }}{2\alpha _{2}\left( t\right) \beta }-L\left( t\right) \right) \nonumber \\ \overset{\cdot }{\alpha _{2}}\left( t\right)=\; & {} \kappa \left( \mu _{\alpha }-\alpha _{2}\left( t\right) \right) +\sigma _{\alpha }\overset{\cdot }{x}\left( t\right) \nonumber \\ L\left( 0\right)=\; & {} L_{0}\text {, }\alpha _{2}\left( 0\right) =\alpha _{0}. \end{aligned}$$
(12)

In this case, as shown by Guerrazzi (2021), the value of \(\gamma _{\max }\) for which the linear maximandum deliver meaningful solutions is the same of the dynamic right to manage model, i.e. \(\beta /\left( 1+\beta \right)\), whereas the value of \(\gamma _{\min }\) is not zero, but is given instead by the value of \(\gamma\), such that the bargained wage leads to zero profits.Footnote 4 That value of the wage is the one at which the contract curve illustrated in Fig. 2 intersects the zero-profit line of the firm and it coincides with the unique root of the non-linear function given by \(f\left( w\right) \equiv w^{\beta -1}\left( \left( 1+\beta \right) w-\beta \left( 1+2\alpha _{2}\right) \right) -1\). Plugging the root of this function—say \(w_{\max }^{\text {EB}}\)—into the contract curve conveys the maximum level of bargained (over)employment achievable in the efficient bargaining setting, that is \(L_{\max }^{\text {EB}}\equiv \left( \beta \left( 1+2\alpha _{2}\right) +\left( 1-\beta \right) w_{\max }^{\text {EB}}-\left( w_{\max }^{\text {EB}}\right) ^{1-\beta }\right) /2\alpha _{2}\beta >1\).

Allowing \(\gamma\) to vary in the closed interval \(\left[ \gamma _{\min } ,\gamma _{\max }\right]\) and taking values of the state L belonging to \([1,L_{\max }^{\text {EB}}]\) together with values of w belonging to \([1,w_{\max }^{\text {EB}}]\), the HJB equation for the mediator problem can now be written as

$$\begin{aligned} \rho V(\alpha _{0,}L_{0})= & {} \underset{w\in [1,w_{\max }^{\text {EB}}]}{\max }\left\{ \gamma \Pi \left( L\ ,w\right) +\left( 1-\gamma \right) U\left( L,w\right) \right. \nonumber \\&+\theta \left( \frac{\beta \left( 1+2\alpha _{2}\right) +\left( 1-\beta \right) w-w^{1-\beta }}{2\alpha _{2}\beta }-L\right) \frac{\partial V(\alpha _{0,}L_{0})}{\partial L}\nonumber \\&\left. +\;\kappa \left( \mu _{\alpha }-\alpha _{2}\right) \frac{\partial V(\alpha _{0,}L_{0})}{\partial \alpha _{2}}+\frac{1}{2}\sigma _{\alpha }^{2} \frac{\partial ^{2}V(\alpha _{0,}L_{0})}{\partial \alpha _{2}^{2}}\right\} . \end{aligned}$$
(13)

In this case, \(\gamma \Pi \left( L\ ,w\right) +\left( 1-\gamma \right) U\left( L,w\right)\) is defined in \([1,L_{\max }^{\text {EB}}]\times [1,w_{\max }^{\text {EB}}]\), but—as it happens for the HJB equation in \(\left( 9\right)\)—it always returns non-negative values.

The FOC for w requires that

$$\begin{aligned} \frac{\partial V(\alpha _{0,}L_{0})}{\partial L}=\frac{2\alpha _{2}\beta w^{\beta }L\left( \left( 1-\gamma \right) \beta w^{\beta -1}-\gamma \right) }{\theta \left( 1-\beta \right) \left( 1-w^{\beta }\right) }. \end{aligned}$$
(14)

Moreover, the envelope condition for L is given by

$$\begin{aligned} \left( \rho +\theta \right) \frac{\partial V\left( \alpha _{0,}L_{0}\right) }{\partial L}=\; & {} \theta \left( \frac{\beta \left( 1+2\alpha _{2}\right) +\left( 1-\beta \right) w-w^{1-\beta }}{2\alpha _{2}\beta }-L\right) \frac{\partial ^{2}V\left( \alpha _{0,}L_{0}\right) }{\partial L^{2}}\nonumber \\&+\kappa \left( \mu _{A}-\alpha _{2}\right) \frac{\partial ^{2}V\left( \alpha _{0,}L_{0}\right) }{\partial \alpha _{2}\partial L}+\frac{1}{2} \sigma _{\alpha }^{2}\frac{\partial ^{3}V\left( \alpha _{0,}L_{0}\right) }{\partial \alpha _{2}^{2}\partial L}\nonumber \\&+\sigma _{\alpha }^{2}\frac{\partial ^{2}V\left( \alpha _{0,}L_{0}\right) }{\partial \alpha _{2}^{2}}. \end{aligned}$$
(15)

Numerical simulations

Despite the elementary features of the stochastic process exploited to describe the evolution of labour effectiveness over time, analytical results for the endogenous dynamics of employment and wages may be difficult to derive. Nevertheless, after a careful calibration, the solutions of our stochastic models can be retrieved by relying on numerical techniques aimed at approximating the value functions in (9) and (13) over a given grid (cf. Kushner and Dupuis 1992). Following Krawczyk and Windsor (1997), we simulate the different dynamic bargaining models developed above by means of a Markov decision chain approximation.Footnote 5

Calibration

The model economy is discretized and calibrated on a quarterly basis by taking as reference the US economy according to the following strategy. First, the values of the parameters that represent the fundamentals of the model, i.e., the attrition of bargained employment, the preferences of the workers, the degree of impatience of the mediator, and the mean effectiveness of the firm’s technology, are chosen in accordance with the available evidence on these factors. Specifically, the attrition of employment \(\left( \theta \right)\) is set according to the estimations carried out by Abowd and Zellner (1985) who derive estimates of employment out-flows using data retrieved from the US Current Population Survey. The discount rate of the mediator \(\left( \rho \right)\) is taken in the neighbourhood of the figures of the real interest rates prevailing in the period before the Great Recession of 2008–2009 (cf. Alvarez and Shimer 2011). The measure of the degree of risk aversion of workers \(\left( \beta \right)\) is calibrated as in Guerrazzi (2011, 2021) who extrapolates the figures of the curvature of the utility function for wages from the estimates of Goerke and Pannenberg (2012). Moreover, recalling that in our setting, the competitive wage bill is normalized to 1, the long-run mean of the technology parameter \(\left( \mu _{\alpha }\right)\) is calibrated in order to deliver a competitive share of profit, i.e., \(\mu _{\alpha }/(1+\mu _{\alpha })\), which is consistent with the conventional estimates of the US capital share that—as it is well-known—suggest a figure around one-third (cf. Kydland and Prescott 1982).

Second, given the fixed values of the fundamental parameters explained above, the weight assigned by the mediator to each party in the right to manage and in the efficient bargaining versions of the model economy is set to meet the efficiency criterion of matching models proposed inter alia by Shimer (2004) (cf. Hosios 1990). In detail, we fix the value of the weight assigned by the mediator to firm’s profits \(\left( \gamma \right)\) with the aim of achieving a deterministic stationary solution—denoted with asterisked variables—in which the total surplus produced in the model economy is equally split between the firm and unionized workers (cf. Guerrazzi 2021). In other words, in the dynamic right to manage model and in the dynamic efficient bargaining model, the parameter \(\gamma\) is set to be consistent with the following equality:

$$\begin{aligned} \frac{\Pi \left( L^{*},w^{*}\right) }{\Pi \left( L^{*},w^{*}\right) +U\left( L^{*},w^{*}\right) }=\frac{1}{2}. \end{aligned}$$
(16)

In our setting, the LHS of Eq. (16) provides the ‘conventional’ measure of the bargaining power of the firm; indeed, when \(\gamma =\gamma _{\max }\), the equilibrium wage coincides with the outside option of unionized workers, so that \(U\left( L^{*},w^{*}\right)\) is equal to zero and the firm appropriates the whole surplus (cf. Nash 1950).

Thereafter, we also consider the monopolistic-union version of the model in which employment is assumed to adjust in the direction of the labour demand schedule implied by the production technology and firm’s profits are not taken into account by the mediator \(\left( \gamma =0\right)\).Footnote 6 Moreover, for the resulting three model specifications, the speed of mean reversion of the effectiveness of production \((\kappa )\) is set at the value of the convergent root implied by the deterministic version of each model under examination, whereas its volatility \((\sigma _{\alpha })\) is tuned to replicate the observed value of the standard deviation of real output as reported by Ravn and Simonelli (2007) (cf. Guerrazzi and Giribone 2019). On one hand, the choice of the value of \(\kappa\) leads productivity shocks to have the same speed of convergence of w and L in the respective deterministic version of each model. On the other hand, the choice of the value of \(\sigma _{\alpha }\) keeps the realized values of \(\alpha _{2}\) on meaningful positive magnitudes and allows us to make a comparison between the simulated dynamics of w and L and their observed counterparts.

The whole set of fixed fundamental parameters, their description, and the respective values are collected in Table 1. The values of the remaining parameters will be given when the point numerical results of each model specification will be presented.

Table 1 Calibration of the fundamental parameters
Full size table

The parameters’ values in Table 1 have two important implications that is worth mentioning before giving the output of simulations. First, given the arguments put forward in Sect. 2, the maximum weight attachable to firm’s profits, i.e., \(\gamma _{\max }\) is given by \(0.80/(1+0.80)=0.4444\). Moreover, the maximum wage achievable by the union in the dynamic efficient bargaining model coincides with the unique solution of \(\left( w_{\max }^{\text {EB} }\right) ^{0.80-1}\left( \left( 1+0.80\right) w_{\max }^{\text {EB} }-1.60\right) -1=0\) which is given by 1.4906. Such a value of the bargained wage implies that for the dynamic efficient bargaining model, the value of \(\gamma _{\min }\) is equal to 0.4020 that is strictly lower than \(\gamma _{\max }\) (cf. Guerrazzi 2021).

Numerical results

After having completed the calibration of each version of the three dynamic bargaining models by supplementing the structural parameter values in Table 1 with the proper figures for \(\gamma\), \(\kappa\), and \(\sigma _{\alpha }\), the theoretical values of output, employment, and wages are obtained by replicating the typical steps followed in business cycles contributions (cf. Shimer 2004). Specifically, we first generate 1200 theoretical observations. Throwing away the first 1000 to mitigate the possible butterfly effect, we remain with 200 observations that represent the corresponding quarterly figures of the typical 50-year horizon covered by business cycle analyses. For each variable of interest, we take the standard deviation and the correlation matrix of the log deviations from the corresponding deterministic long-run reference. Thereafter, such a procedure is repeated for 10, 000 times and theoretical values are obtained by averaging the outcomes of each replication.

Defining \({\overline{x}}\) as \(\ln x-\ln x^{*}\), where \(x^{*}\) is the deterministic stationary solution for the generic variable x, the simulation results for output, wages, and employment as well as the values of the model parameters omitted in Table 1 are collected in Tables 2, 3, and 4 (observed values in parenthesis).

Table 2 The dynamic right to manage model (\(L^{*}=0.6072\), \(w^{*}=1.3928\))
Full size table
Table 3 The dynamic monopoly union model (\(L^{*}=L_{\min }^{\text {MU}}=0.4449\), \(w^{*}=w_{\max }^{\text {MU}}=1.5551\))
Full size table
Table 4 The dynamic efficient bargaining model (\(L^{*}=1.0067\), \(w^{*}=1.2790\))
Full size table

Looking first at the figures in Table 2, we immediately realize that in the dynamic right to manage model, the bargaining power of the firm increases at increasing rates with respect to the variations of the weight attached by the mediator to firm’s profit; indeed, an equal division of the surplus between the two bargainers is actually achieved with a value of \(\gamma\) higher than the half of the implied value for \(\gamma _{\max }\). Moreover, the present version of the dynamic bargaining model matches the positive correlation of employment and wages to output, and it fairly replicates the standard deviation of employment. However, it deeply overstates the volatility of wages. This feature of the theoretical model presented in the first part of Sect. 2 is due to the specification of the production possibilities of the firm. In fact, according to the production function in Eq. (1) and the normalization adopted in Eq. (2), the elasticity of the labour demand schedule is not constant, but it is given instead by \(w\left( t\right) /(1+2\alpha _{2}\left( t\right) -w\left( t\right) )\) and such an expression—given the bargained wage—is a decreasing function of productivity shocks. Consequently, when the model economy is hit by a positive (negative) productivity shock, labour demand becomes more (less) rigid by making the firm (union) more willing to accept a wage increase (reduction) for any given level of employment (cf. McDonald and Solow 1981; Layard and Nickell 1990). Obviously, as it is illustrated in Fig. 3 that tracks a sample of typical trajectories of L, w, and \(\alpha _{2}\), this pattern will tend to exacerbate the volatility of wages with respect to the one of employment.

Fig. 3
figure 3

Stochastic trajectories of the dynamic right to manage model

Full size image

Switching to Table 3, we notice that the dynamic monopoly union model, i.e., the model specification in which \(\gamma\) is equal to zero, so that the wage pressure is at its maximum level at the expense of the employment level; indeed, \(w^{*}>w_{\max }^{\text {EB}}\), confirms the cyclical properties of the right to manage framework, but it leads to a reduction of the volatility of employment and wages. Nevertheless, the simulated standard deviation of wages remains far above its observed counterpart. The lower standard deviation of employment and wages retrieved in this case is due to the fact that in the monopoly union model, the mediator determines the wage instant by instant by giving full power to the risk averse unionized workers that dislike fluctuations in labour earnings. Consequently, since the preferences of the risk neutral firm are completely neglected in the maximization process, its choices will tend to smooth the path of employment and wages over time. However, as it is illustrated by the sample trajectories of Fig. 4, such a smoothing effect driven by the preferences of unionized workers does not counterbalance in a significant manner the amplification mechanism of productivity disturbances induced by the aforementioned counter-cyclical elasticity of labour demand implied by the production technology adopted by the firm.

Fig. 4
figure 4

Stochastic trajectories of the dynamic monopoly union model

Full size image

Finally, focusing on the results disclosed in Table 4, we realize that the shape of the curvature of the relationship between the bargaining power of the firm and \(\gamma\) is the opposite with respect to the one that holds in the dynamic right to manage model; indeed, the value of the weight attached by the mediator to firm’s profits to split equally the surplus between the two parties is lower than \((\gamma _{\min }+\gamma _{\max })/2=0.4232\). Obviously, as explicitly recognized by Guerrazzi (2021), this means that in this case, the bargaining power of the firm increases at decreasing rates with respect to \(\gamma\). Moreover, it clearly emerges that the dynamic efficient bargaining model preserves the pro-cyclical pattern of employment and wages and—at the same time—the model economy starts to display a quite strong degree of real-wage rigidity that is missing in the bargaining settings analyzed before that brings the numerical results closer to empirical evidence on wage fluctuations.

Using different strategies, several scholars who analyzed the US labour market argued in favour of the stronger reliability of the efficient bargaining model over models in which employment adjusts itself towards the labour demand of firms. For instance, estimating the effect of alternative and paid wages on the labour productivity of firms operating in the US newspaper industry, MaCurdy and Pencavel (1986) show that adjustments towards the labour demand are inconsistent with data.Footnote 7 Furthermore, using data on publicly traded US companies, Abowd (1989) finds that unexpected changes in collectively bargained labour costs tend to move shareholders’ wealth in the opposite direction by the same amount as predicted by the hypothesis of adjustments in the direction of the contract curve of the bargaining parties. Nonetheless, our dynamic cooperative bargaining model deeply underestimates the volatility of employment and wages as it usually happens in labour contracts that cannot be reneged by a risk neutral firm that employs risk averse workers (cf. Thomas 1988; Asheim and Strand 1991). As argued by McDonald and Solow (1981), the smooth dynamics of wages reveals that in the theoretical model presented in the second part of Sect. 2, a positive (negative) productivity shock leads the contract curve to rotate in clockwise (counter-clockwise) direction and the equity locus that splits the total surplus between the firm and the union to shift to the right (left). As illustrated in the sample trajectories in Fig. 5, where on the left-hand (right-hand) side scale, we find steady-state deviations of \(\alpha _{2}\) (L and w), these two distinct movements tend to offset almost perfectly the wage impact of productivity disturbances whose final effect will fall mainly on parallel employment adjustments.

Fig. 5
figure 5

Stochastic trajectories of the dynamic efficient bargaining model

Full size image

The values of the elasticity of the labour demand schedule implied by the numerical results in Tables 2, 3, and 4 are certainly too high with respect to the available empirical evidence. Actually, Hamermesh (1993) and, more recently, Hijzen and Swaim (2010) reports values between 0.15 and 0.70. On a very different scale, our framework implies instead an average value of 3.4953 for the monopoly union model, a value of 2.2938 for the right to manage model, and a value of 1.7739 for the efficient bargaining model. These high figures of the reactivity of the labour demand with respect to wages suggest that even if wage negotiations proceed by targeting the contract curve of the firm and the union, then the observed volatility of employment—in comparison with the one of wages—is too low with respect of what will be generated by the optimal wage choices of an omniscient mediator that continuously supervises the bargaining process by counterbalancing the objective functions of the two players in an optimal manner. This finding can be easily rationalized by referring to the wide literature on employment adjustment costs whose presence on the side of firms tends to delay both hiring and firing; indeed, such costs are not considered in our specification of the profit function in Eq. (4) (cf. Foster 1999).

Concluding remarks

In this paper, we explored the way in which different bargaining settings affect the shape of labour market fluctuations given the production technology available to firms and the preferences of unionized workers. Specifically, after having developed non-deterministic versions of the dynamic bargaining models set forth originally by Guerrazzi (2011, 2021), we showed how productivity disturbances affect the path of output, employment, and wages by making different hypothesis about the instantaneous out-of-equilibrium adjustments of employment underlying the wage negotiation process. In detail, we developed a set of stochastic dynamic models where an omniscient infinitely lived mediator supervises the bargaining process going on between a representative firm an a pool of unionized workers. Our theoretical settings can be considered as useful normative devices to analyze the dynamics of the main involved economic variables when they are hit by productivity shocks.

On one hand, assuming that employment adjustments are constrained towards the labour demand schedule of the representative firm as it happens in the right to manage and in the monopoly union models of wage bargaining, we showed that with a quadratic production function and risk averse workers, our theoretical framework reproduces the pro-cyclical pattern of wages and employment, but it cannot mimic the observed rigidity of wages (cf. McDonald and Solow 1981; MaCurdy and Pencavel 1986). This pattern is due to the anti-cyclical behaviour of the labour demand elasticity implied by the productive technology taken into consideration. On the other hand, assuming that employment adjustments go in the direction of the contract curve of the two bargainers, our model economy displays a strong degree of wage stickiness that is typical of wage contracts that cannot be reneged (cf. Thomas 1988; Asheim and Strand 1991). This result can be attributed to the fact that productivity shocks lead the contract curve and the equity locus underlying the determination of bargained wages to move in a way that offset wage variations (cf. McDonald and Solow 1981).

Since wage stickiness is a robust feature of business cycle contributions focused on labour market fluctuations (e.g., Shimer 2004; Ravn and Simonelli 2007), our numerical findings tend to offer some support for the empirical validity of bargaining models whose asymptotic outcomes represent efficient allocations for the involved parties (cf. Abowd 1989). On the ground of desirable labour market policies, such a characterization of actual wage negotiations implies that interventions aimed at weakening trade unions and reducing workers’ power—like the ones driven by the recent trends of labour market deregulation—would not lead to more efficient outcomes but merely to a redistribution of income from workers to entrepreneurs and to an increase in unemployment (cf. Brown and Ashenfelter 1986).

The theoretical analysis carried out in this paper could be extended in different directions. For instance, as argued by Huizinga and Schiantarelli (1992), we could consider the effects on output, wage, and employment driven by variation in the outside option of the union. This would provide a dynamic general equilibrium model of bargaining (cf. Layard and Nickell 1990). In addition, some refinements should be done in the definition of the union’ preferences, an issue on which labour economists are still debating without reaching a firm agreement (cf. Farber 1986; Gahan 2002; Kaufman 2002). The implied extensions are left to further developments.