1 Introduction

In his influential paper on wage contracting, Leontief (1946) argued that a monopolistic wage setter who sells labour services to a set of buyers that can freely choose the corresponding quantity to purchase would always achieve an inefficient allocation in terms of wage and employment outcomes. On the contrary, he showed that when the monopolistic wage setter combines wage-fixing with employment-fixing by means of an all-or-none offer there may be an efficient redistribution of labour income that improves the welfare of the seller as well as the one of the buyers (cf. Fellner 1947). That was the seminal intuition from which originated the theory of efficient—or cooperative—wage bargaining that in the labour economics literature is usually opposed to the theory of non-cooperative negotiations encapsulated in the right-to-manage and the monopoly union models (cf. Booth 1995).

From a theoretical point of view, the achievement of efficiency in the wage negotiation process that involves workers—or trade unions—and productive firms and its labour market implications have been explored in several directions. For instance, McDonald and Solow (1981) argue that the efficiency gains described by Leontief (1946) can be approximately achieved by a bargaining process that involves wages and the capital–labour ratio (cf. Johnson 1990). Moreover, Espinoza and Rhee (1989) as well as Strand (1989) derive the conditions under which efficient outcomes emerge from the repeated bargaining between a labour union and a firm carried out by means of alternate wage proposals from the two parties. Petrakis and Vlassis (2000) show that when the bargaining power of the union is sufficiently low, the firm can find profitable to commit itself to a given employment level because this would allow it to become a Stackelberg leader in the output market by creating the incentives to achieve Pareto-optimal solutions. More recently, Dobbelaere and Luttens (2016) show that in a model economy with concave production and risk-neutral agents where bargaining proceeds as a finite sequence of sessions between a firm and a union of variable size, the resulting equilibrium is equivalent to the efficient bargaining outcome (cf. Stole and Zwiebel 1996).

In this paper, drawing on ideas originally sketched by Guerrazzi (2011) in a companion work, I aim at further contributing to the theoretical literature on cooperative wage negotiations by deriving and solving a dynamic version of the efficient bargaining model grounded on the Pontryagin’s Maximum Principle. Specifically, following a normative perspective, I develop an inter-temporal optimizing framework with continuous time in which an omniscient and infinitely lived mediator—or an arbitrator—is assumed to set the real wage by maximizing a weighted average between the profit of a risk-neutral firm and the sum of the utilities of a group of risk-averse unionized workers by taking into account that the stock of employed workers tends to adjust smoothly in the direction of the upward-sloping contract curve implied by the objective functions of the two bargaining parties (cf. Raiffa 1953; Muthoo 1999, Section 10.3). To the best of my knowledge, completing the analysis set forth by Guerrazzi (2011), the present contribution is the first attempt to frame the efficient bargaining model in an optimal control setting in which time is assumed to evolve without discontinuities as it usually happens in differential games of bargaining (cf. Ambrus et al. 2015; Castaner et al. 2018).

The results of this theoretical exploration reveal that the typical findings retrieved in a companion right-to-manage framework in which employment is assumed to adjust itself in the direction of the downward-sloping labour demand schedule of the firm are completely overturned. In detail, I demonstrate that increases in the bargaining power of the firm push the equilibrium outcomes of the dynamic negotiation process in the direction of the allocation in which the wage equals the marginal productivity of employed labour by accelerating the speed of convergence towards the stationary solution of the model (cf. Lockwood and Manning 1989; Guerrazzi 2011). Furthermore, since the mediator of the bargaining process is assumed to consider the effects of its wage-setting behaviour on employment dynamics, I show that the inter-temporal negotiation of wages tends to penalize unionized workers and favour the firm with respect to the bargaining outcomes of a similar wage-setting framework in which the time dimension is omitted (cf. de la Croix et al. 1996).

The paper is arranged as follows. Section 2 sets out the model and derives its analytical solution. Section 3 explores its numerical properties. Section 4 compares the outcomes of the dynamic efficient bargaining model with the ones of a similar timeless framework. Finally, Sect. 5 concludes by providing suggestions for further developments.

2 Efficient Bargaining as an optimal control problem

2.1 The model

Assuming that time is continuous, Guerrazzi (2011) models the dynamic wage-bargaining process going on between a risk-neutral firm and a union of risk-averse workers whose total membership is normalized to 1. On the one hand, the firm is assumed to be endowed with a quadratic production function that leads to the following expression for realized profits:

$$\begin{aligned} \Pi \left( w\left( t\right) ,L\left( t\right) \right) \equiv \left( 1+2\alpha -w\left( t\right) \right) L\left( t\right) -\alpha \left( L\left( t\right) \right) ^{2} \end{aligned}$$
(1)

where \(w\left( t\right) \) is the wage prevailing in instant t, \(L\left( t\right) \) is the corresponding number of workers employed by the firm, whereas \(\alpha >0\) is a parameter that affects the slope and the intercept of the production function.

An interesting feature of the profit function in Eq. (1) is that \(\left. \partial \Pi \left( w\left( t\right) ,L\left( t\right) \right) /\partial L\left( t\right) \right| _{L\left( t\right) =1}=0\) if and only if \(w\left( t\right) =1\). Therefore, 1 is also the value of the profit-maximizing wage that prevails when all the unionized workers are actually employed by the representative firm, i.e. the level of the prevailing wage when \(L\left( t\right) =1\).

On the other hand, obeying a utilitarian criterion, the union of workers is assumed to maximize the sum of the surplus of employed workers. Consequently, the utility function of the union can be written as

$$\begin{aligned} U\left( w\left( t\right) ,L\left( t\right) \right) \equiv L\left( t\right) \left( \left( w\left( t\right) \right) ^{\beta }-1\right) \end{aligned}$$
(2)

where \(0<\beta <1\) is a measure of the degree of risk aversion of unionized workers.

The dynamic version of the efficient bargaining model sketched by Guerrazzi (2011) is built by assuming that in each instant an infinitely lived mediator chooses the wage by maximizing a weighted average of the objective functions of the firm and the union by considering that—in each instant—the level of employment tends to adjust itself with some attrition in the direction of the contract curve implied by the preferences of each party. Consistently with the idea that bargaining problems can be viewed as arbitration schemes constrained by a dynamic accumulation law for some relevant variables, this setting captures the idea that the forward-looking mediator is called in to settle in an optimal way a continuous stream of bargaining conflicts whose point solution affects future negotiation opportunities through the dynamics of employment (cf. Raiffa 1953; Muthoo 1999, Section 10.3). As a consequence, taking into account the expressions in (1) and (2) and recalling that in this case the contract curve is given by the wage–employment pairs such that the slope of isoprofit curves of the firm equals the one of union’s indifference curves, the dynamic problem of the mediator is given by

$$\begin{aligned} \underset{w\left( \cdot \right) \in {\mathscr {A}}_{0}\left( \overline{L}\right) }{\max \text { }} {\displaystyle \int \limits _{t=0}^{\infty }} \exp \left( -\rho t\right) \left( \gamma \Pi \left( w\left( t\right) ,L\left( t\right) \right) +\left( 1-\gamma \right) U\left( w\left( t\right) ,L\left( t\right) \right) \right) \hbox {d}t \end{aligned}$$
(3)

subject to

$$\begin{aligned} \overset{\cdot }{L}\left( t\right) =\theta \left( \frac{\beta \left( 1+2\alpha \right) +\left( 1-\beta \right) w\left( t\right) -\left( w\left( t\right) \right) ^{1-\beta }}{2\alpha \beta }-L\left( t\right) \right) \ \ \ \ \ \ L\left( 0\right) ={\overline{L}} \end{aligned}$$
(4)

where \(\rho >0\) is the discount rate of the mediator, \(\gamma >0\) is a measure of the weight attached to firm’s profits, \(\theta >0\) is a parameter that measures the attrition between desired and actual employment, whereas \({\overline{L}}>0\) is the initial level of employment.

In order to have economically meaningful trajectories, the set of all admissible control strategies \(w\left( \cdot \right) \) starting from the initial couple \(\left\{ 0,{\overline{L}}\right\} \) is defined as

$$\begin{aligned} {\mathscr {A}}_{0}\left( {\overline{L}}\right) := {\mathbb {L}} _{\mathbf{loc }}^{1}\left\{ w\left( \cdot \right) \in \left( {\mathbb {R}}_{+}; {\mathbb {R}} _{+}\right) :L_{0}\left( t;{\overline{L}},w\left( \cdot \right) \right) >0 \ \ \forall t\in {\mathbb {R}} _{+}\right\} \end{aligned}$$
(5)

According to the definition in (5), \(w\left( \cdot \right) \) belongs to the set of locally integrable (or summable) functions such that the wage and the employment levels are positive all over the relevant time horizon.

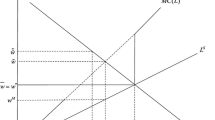
The upward-sloping contract curve towards which employment is assumed to gradually adjust itself in each instant in the course of the never-ending wage bargaining process as well as the downward-sloping labour demand implied by the profit function in Eq. (1)—denoted by \(L_{D}\)—is illustrated in Fig. 1. Since the union will never accept a wage rate lower than 1 and employment moves towards the contrast curve, the area in grey indicates the unfeasible allocations for the union.

Fig. 1
figure 1

Employment adjustments

Full size image

The employment adjustments indicated by the arrows in Fig. 1 describe a situation in which the wage negotiation process that involves the firm and the union has a concern not only for the wage but also for the level of employment. Without any loss of generality, the omniscient mediator may accommodate this kind of tendency for several reasons. For instance, Pohjola (1987) shows that the wage–employment pairs on the contract curve can be actually achieved when there is bargaining over profit sharing, with the firm fixing employment. Moreover, Johnson (1990) argues that a concern for employment may endogenously arise when labour–management negotiations have as a subject the number of workers assigned to each working machine and/or the amount of work intensity that each worker is required to provide on the job. Under these circumstances, respecting the limit of the available labour supply that—by assumption—is never binding, employment can go well beyond unity, i.e. the size of union membership.

At this stage, some remarks are due for the instantaneous objective function of the mediator; indeed, the linear component of the integral in (3) looks appealing and it is certainly useful to preserve the analytical tractability of the model. However, as argued by Lockwood and Manning (1989), the range of values for \(\gamma \) that deliver meaningful solutions for the bargaining process is not necessarily constrained in the \(\left( 0,1\right) \) interval as it happens instead when the generalized Nash maximandum is applied (cf. Binmore and Rubinstein 1986).Footnote 1

In the present context, the highest eligible value for the weight attached to the firm’s profits—say \(\gamma _{\max }\)—is the value of \(\gamma \) such that the instantaneous marginal value of a wage variation for the mediator evaluated in the outside option of the union becomes equal to zero. Consequently, given the expressions in Eqs. (1) and (2), \(\gamma _{\max }\) is equal to \(\beta /\left( 1+\beta \right) \) and for such a value of \(\gamma \) all the union members will be employed at a wage that coincides with their marginal productivity in the stationary equilibrium of the bargaining process (cf. Guerrazzi 2011). Thereafter, for values of \(\gamma \) lower than \(\gamma _{\max }\), bargained wage–employment pairs start to climb indefinitely on the upward-sloping contract curve depicted in Fig. 1 by increasing the utility of the union and reducing the profits of the firm. Along that rising path, it becomes possible to find the lowest eligible value of \(\gamma \)—say \(\gamma _{\min }\). Specifically, \(\gamma _{\min }\) will be the value of \(\gamma \) such that the bargained wage–employment pair leads the profits of the firm to be equal to zero, i.e. the value that conveys the outside option of the entrepreneur. Therefore, given the expressions in (1) and (2), \(\gamma _{\min }\) will be equal to the point value of \(\gamma \) such that the bargained wage coincides with the solution of the following nonlinear equation:

$$\begin{aligned} W\left( w\right) =1 \end{aligned}$$
(6)

where \(W\left( w\right) \equiv w^{\beta -1}\left( \left( 1+\beta \right) w-\beta \left( 1+2\alpha \right) \right) \).

As illustrated in the diagram on the left-hand-side panel of Fig. 2, given that \(\partial W\left( \cdot \right) /\partial w>0\) and \(W\left( 1\right) =1-2\alpha \beta <1\), the expression in Eq. (6) admits a unique solution higher than 1—say \(w_{\max }\)—which represents the maximum value of the bargained wage that can be attributed by the mediation to unionized workers by avoiding that the firm leaves the bargaining table. Geometrically speaking—as argued by McDonald and Solow (1981)—the point \(\left( L_{\max },w_{\max }\right) \), where \(L_{\max }\equiv \left( \beta \left( 1+2\alpha \right) +\left( 1-\beta \right) w_{\max }-\left( w_{\max }\right) ^{1-\beta }\right) /2\alpha \beta \), singles out the point at which the contract curve intersects the zero-isoprofit curve of the firm. In the present case, as illustrated in the diagram on the right-hand-side panel of Fig. 2, such an isoprofit curve \((\Pi =0)\) is simply a line with the same intercept of the labour demand schedule but with a halved slope. Interestingly, in the case under scrutiny, higher (lower) firm’s productivity, i.e. higher values of \(\alpha \) and/or lower (higher) workers’ risk aversion, i.e. higher (lower) values of \(\beta \), lead to higher (lower) values of \(w_{\max }\).

Fig. 2
figure 2

The bargained wage that leads firm’s profits to zero

Full size image

The usual way to assess the actual bargaining power of an agent involved in a negotiation process is to measure the fraction of the total surplus assigned by the mediator to that agent (Nash 1950, 1953). Consequently, for values of \(\gamma \) belonging to the closed interval \([\gamma _{\min },\gamma _{\max }]\), in each instant of the negotiation process the point bargaining power of the firm—say \(\gamma _{A}\left( t\right) \)—will be measured by the ratio between its profits and the sum of the net gains of the two bargainers. Formally speaking, it holds that

$$\begin{aligned} \gamma _{A}\left( t\right) \equiv \frac{\Pi \left( w\left( t\right) ,L\left( t\right) \right) }{\Pi \left( w\left( t\right) ,L\left( t\right) \right) +U\left( w\left( t\right) ,L\left( t\right) \right) } \end{aligned}$$
(7)

Obviously, \(1-\gamma _{A}\left( t\right) \) will represent the time-varying bargaining power of the union.

The first-order conditions (FOCs) of the dynamic problem described in (3) and (4) are given by

$$\begin{aligned}&L\left( t\right) \left( \left( 1-\gamma \right) \beta \left( w\left( t\right) \right) ^{\beta -1}-\gamma \right) +\frac{\theta \left( 1-\beta \right) \Lambda \left( t\right) \left( \left( w\left( t\right) \right) ^{\beta }-1\right) }{2\alpha \beta \left( w\left( t\right) \right) ^{\beta }}=0 \end{aligned}$$
(8)
$$\begin{aligned}&\overset{\cdot }{\Lambda }\left( t\right) =\left( \rho +\theta \right) \Lambda \left( t\right) -\gamma \left( 1+2\alpha \left( 1-L\left( t\right) \right) -w\left( t\right) \right) -\left( 1-\gamma \right) \left( \left( w\left( t\right) \right) ^{\beta }-1\right) \nonumber \\\end{aligned}$$
(9)
$$\begin{aligned}&\underset{t\rightarrow \infty }{\lim }\exp \left( -\rho t\right) \Lambda \left( t\right) L\left( t\right) =0 \end{aligned}$$
(10)

where \(\Lambda \left( t\right) \) is the costate variable associated to \(L\left( t\right) \).

Equation (8) is the FOC with respect to \(w\left( t\right) \), the differential equation in (9) describes the optimal path of \(\Lambda (t)\), whereas (10) is the required transversality condition.

Differentiating Eq. (8) with respect to time and exploiting the expression in (9) allows us to derive the implied dynamics of the bargained wage rate. Formally speaking, the differential equation for w(t) can be written as

$$\begin{aligned} \overset{\cdot }{w}\left( t\right) =\Phi \left( w\left( t\right) \right) \frac{\overset{\cdot }{L}\left( t\right) }{L\left( t\right) }+\frac{\theta \left( 1-\beta \right) }{2\alpha \beta }\Psi \left( w\left( t\right) \right) \frac{\overset{\cdot }{\Lambda }\left( t\right) }{L\left( t\right) } \end{aligned}$$
(11)

where \(\Phi \left( w\left( t\right) \right) \) and \(\Psi \left( w\left( t\right) \right) \) are given respectively by

$$\begin{aligned}&\Phi \left( w\left( t\right) \right) \equiv \frac{\left( \left( w\left( t\right) \right) ^{\beta }-1\right) w\left( t\right) \left( \left( 1-\gamma \right) \beta \left( w\left( t\right) \right) ^{\beta -1} -\gamma \right) }{\left( \left( 1-\gamma \right) \left( w\left( t\right) \right) ^{\beta -1}\left( \left( 1-\beta \right) \left( \left( w\left( t\right) \right) ^{\beta }-1\right) +\beta \right) -\gamma \right) \beta } \nonumber \\&\Psi \left( w\left( t\right) \right) \equiv \frac{\left( w\left( t\right) ^{\beta }-1\right) ^{2}}{\left( \left( 1-\gamma \right) \left( w\left( t\right) \right) ^{\beta -1}\left( \left( 1-\beta \right) \left( \left( w\left( t\right) \right) ^{\beta }-1\right) +\beta \right) -\gamma \right) \beta \left( w\left( t\right) \right) ^{\beta -1}}\nonumber \\ \end{aligned}$$
(12)

The pairs \(\left\{ w,L\right\} \in {\mathbb {R}} _{+}^{2}\) such that \(\overset{\cdot }{w}\left( t\right) =0\) define the ‘equity’—or the ‘power’—locus whose intersection with the contract curve depicted in Fig. 1 returns the stationary solution of the efficient bargaining process singled out by the dynamic problem in (3) and (4) (cf. McDonald and Solow 1981). Outside that stationary solution, the expression in Eq. (11) shows that the dynamics of bargained wages is proportional to the dynamics of employment and to the one of the costate variable according to the two coefficients defined in (12). In this respect, the sign of \(\Phi \left( w\left( t\right) \right) \) is very important because it determines the cyclical behaviour of negotiated wages. Specifically, whenever \(\Phi \left( w\left( t\right) \right) \) is positive (negative), wages are pro-cyclical (counter-cyclical) since they move in the same (opposite) direction of employment and output.

2.2 Steady state

Reasoning in terms of the control and the state variable of the problem in (3) and (4), steady-state allocations are defined as the set of couples \({\mathscr {S}}:=\left\{ w^{*},L^{*}\right\} \in {\mathbb {R}} _{+}^{2}\) such that \(\overset{\cdot }{w}\left( w^{*},L^{*}\right) =\overset{\cdot }{L}\left( w^{*},L^{*}\right) =0\). In case of asymptotical stability of the wage–employment trajectories implied by the dynamic efficient bargaining model developed above, some elements of that set will be also characterized by the fact that \(\lim _{t\rightarrow \infty }w\left( t\right) =w^{*}\) \(\wedge \) \(\lim _{t\rightarrow \infty }L\left( t\right) =L^{*}\). A straightforward way to find the unique component of \({\mathscr {S}}\) is the following. First, find the value of \(L\left( t\right) \) such that the expression for \(\overset{\cdot }{L}\left( t\right) \) in (4) is equal to zero. Specifically,

$$\begin{aligned} L^{*}=\frac{\beta \left( 1+2\alpha \right) +\left( 1-\beta \right) w^{*}-\left( w^{*}\right) ^{1-\beta }}{2\alpha \beta }\geqslant 1 \end{aligned}$$
(13)

The expression in (13) reveals that the slope of the contract curve, as well as the one of the stationary locus for bargained employment, depends on the risk attitude of the workforce. Risk-averse workers are ex post better off being employed than being unemployed. Consequently, efficient bargaining outcomes may be associated with the over-employment of the unionized labour pool (cf. McDonald and Solow 1981). As argued by Oswald (1985), in a model economy where there is no way for the union to provide insurance against the risk of unemployment, a level of employment above the competitive one is the optimal way to reduce workers’ risk at the expense of the productive efficiency.

Second, plugging Eq. (13) into Eq. (8) and solving for \(\Lambda \left( t\right) \) leads us to

$$\begin{aligned} \Lambda ^{*}=\frac{\left( \left( 1+2\alpha \right) \beta \left( w^{*}\right) ^{\beta -1}+\left( 1-\beta \right) \left( w^{*}\right) ^{\beta }-1\right) \left( \gamma -\left( 1-\gamma \right) \beta \left( w^{*}\right) ^{\beta -1}\right) }{\theta \left( 1-\beta \right) \left( w^{*}\right) ^{\beta -2}\left( \left( w^{*}\right) ^{\beta }-1\right) }\nonumber \\ \end{aligned}$$
(14)

where \(\Lambda ^{*}\) is the steady-state value of the costate variable.

Finally, setting the differential equation in (9) to zero and exploiting the expressions in Eqs. (13) and (14) allows us to find the steady-state value of the bargained wage as the solution of the following equation:

$$\begin{aligned} \Gamma \left( w^{*}\right) =\frac{\gamma \left( \left( w^{*}\right) ^{\beta }\left( 1-2\beta \right) -1\right) }{\beta \left( w^{*}\right) ^{\beta -1}}+\left( 1-\gamma \right) \left( \left( w^{*}\right) ^{\beta }-1\right) \end{aligned}$$
(15)

where \(\Gamma \left( w^{*}\right) \equiv \frac{\left( \rho +\theta \right) \left( \beta \left( w^{*}\right) ^{\beta -1}\left( 1+2\alpha \right) +\left( w^{*}\right) ^{\beta }\left( 1-\beta \right) -1\right) \left( \gamma w^{*}-\left( 1-\gamma \right) \beta \left( w^{*}\right) ^{\beta }\right) }{\theta \left( 1-\beta \right) \left( \left( w^{*}\right) ^{\beta }-1\right) }\).

Given the unique positive value of \(w^{*}\) that fulfils Eq. (15) and considering the expression for \(\Gamma \left( w^{*}\right) \) defined above, the steady-state solution of \(L\left( t\right) \) follows immediately from Eq. (13) and this allows us to pin down the singleton set \({\mathscr {S}}\) previously detailed.

2.3 Local dynamics

The local dynamics of \(w\left( t\right) \) and \(L\left( t\right) \) around the stationary bargaining solution is conveyed by the following linear system:

$$\begin{aligned} \left( \begin{array}[c]{c} \overset{\cdot }{w}\left( t\right) \\ \overset{\cdot }{L}\left( t\right) \end{array} \right) =\left[ \begin{array}[c]{cc} J_{1}+J_{2}\left( J_{3}+J_{4}+J_{5}\right) &{} \quad J_{6}+J_{7}\\ \frac{\theta \left( 1-\beta \right) \left( \left( w^{*}\right) ^{\beta }-1\right) }{2\alpha \beta \left( w^{*}\right) ^{\beta }} &{} \quad -\theta \end{array} \right] \left( \begin{array}[c]{c} w\left( t\right) -w^{*}\\ L\left( t\right) -L^{*} \end{array} \right) \end{aligned}$$
(16)

where the \(J_{i}\) factors, with \(\left\{ i=1,..,7\right\} \), are defined below as

$$\begin{aligned}&J_{1}\equiv \frac{\Phi \left( w^{*}\right) \theta \left( 1-\beta \right) \left( \left( w^{*}\right) ^{\beta }-1\right) }{2\alpha \beta L^{*}\left( w^{*}\right) ^{\beta }}\nonumber \\&J_{2}\equiv \frac{\theta \left( 1-\beta \right) \Psi \left( w^{*}\right) }{2\alpha \beta }\nonumber \\&J_{3}\equiv \frac{2\alpha \beta \left( \rho +\theta \right) \left( \gamma \beta \left( w^{*}\right) ^{\beta -1}-\left( 1-\gamma \right) \beta \left( 2\beta -1\right) \left( w^{*}\right) ^{2\left( \beta -1\right) }\right) \left( \left( w^{*}\right) ^{\beta }-1\right) }{\theta \left( 1-\beta \right) \left( \left( w^{*}\right) ^{\beta }-1\right) ^{2}}\nonumber \\&J_{4}\equiv \frac{2\alpha \beta \left( \rho +\theta \right) \left( \left( 1-\gamma \right) \beta ^{2}\left( w^{*}\right) ^{3\beta -2}-\gamma \beta \left( w^{*}\right) ^{2\beta -1}\right) }{\theta \left( 1-\beta \right) \left( \left( w^{*}\right) ^{\beta }-1\right) ^{2}}\nonumber \\&J_{5}\equiv \frac{\gamma -\left( 1-\gamma \right) \beta \left( w^{*}\right) ^{\beta -1}}{L^{*}}\nonumber \\&J_{6}\equiv \frac{\Phi \left( w^{*}\right) \gamma \left( w^{*} -1-2\alpha \right) }{\left( L^{*}\right) ^{2}}\nonumber \\&J_{7}\equiv \frac{\theta \left( 1-\beta \right) \Psi \left( w^{*}\right) \left( \gamma \left( 2\alpha -w^{*}+1\right) +\left( 1-\gamma \right) \left( \left( w^{*}\right) ^{\beta }-1\right) \right) }{2\alpha \beta \left( L^{*}\right) ^{2}} \end{aligned}$$
(17)

An interesting feature of the J’s factors in (17) is that whenever \(L^{*}=w^{*}=1\), i.e. whenever \({\mathscr {S}}\) consists of the full employment allocation, the Jacobian matrix of the linear system in (16) collapses simply to

$$\begin{aligned} \left[ \begin{array}[c]{cc} \rho +\theta &{} \quad 0\\ 0 &{} \quad -\theta \end{array} \right] \end{aligned}$$
(18)

Given that all the model’s parameters are positive, the \(2\times 2\) matrix in (18) reveals that when the stationary solution of the dynamic bargaining process is the one in which all the unionized workers are employed by the firm at their marginal productivity, the dynamic system has two real eigenvalues—say \(r_{1}\) and \(r_{2}\)—of opposite sign. Specifically, \(r_{1}=\rho +\theta >0\) and \(r_{2}=-\theta <0\). Obviously, this means that \(L^{*} =w^{*}=1\) is a saddle point so that the local dynamics of the model economy is determined and the unique element of \({\mathscr {S}}\) is locally asymptotically stable. In other words, taking an initial employment level, say L(0), there is a unique value of w(0) in the neighbourhood of \(w^{*}=1\) that generates an employment–wage trajectory converging to (1, 1) as t goes to infinity. The corresponding level of w(0) should be selected to satisfy the transversality condition in (10), and it will place the system on the stable branch of the saddle point (1, 1) (cf. Guerrazzi 2011).

3 Numerical properties

With the exception of the competitive stationary solution denoted by the pair \(L^{*}=w^{*}=1\), the analytical results derived above are not that manageable and do not allow to state general conclusions. Consequently, in order to have a deeper appraisal of the theoretical framework developed in the previous section, I resort to some numerical simulations aimed at finding a larger set of stationary solutions and the corresponding properties of their local dynamics.Footnote 2 The baseline calibration exploited for these computations draws on Guerrazzi (2011) and is reported in Table 1.

Table 1 Calibration
Full size table

The adopted set of parameter’s values straightforwardly implies that \(\gamma _{\max }\) is equal to 0.4444, whereas—by means of the numerical solution of Eq. (5)—\(w_{\max }\) achieves the value of 1.4906. Plugging this value of the wage into Eq. (14) returns the maximum level of (over)employment achievable through bargaining that in the present context is equal to 1.0188.

Given the baseline calibration described in Table 1, Table 2 collects the implied figures for the stationary solution, the corresponding values of the coefficient \(\Phi \left( w^{*}\right) \) and the two eigenvalues of the linearized system in (16) retrieved for different eligible values of the equilibrium bargaining power of the firm, i.e. for the different eligible values of \(\gamma _{A}\)—as defined by Eq. (7)—implied by different levels of \(\gamma \).

Table 2 Numerical solutions
Full size table

The figures in Table 2 reveal a number of interesting findings. First, consistently with the outcomes of a standard efficient bargaining framework in which unionized workers are risk averse, the higher (lower) the bargaining power of the firm, the lower (higher) the equilibrium levels of the wage and the employment prevailing in the model economy. In this respect, it is worth noting that according to the taxonomy introduced in Sect. 2\(\gamma _{\min }\), i.e. the value of \(\gamma \) that leads firm’s profit to zero, is equal to 0.4020. Second, the relationship between the weight attached to firm’s profits \((\gamma )\) and its actual bargaining power \((\gamma _{A}^{*})\) is concave; indeed, the value of \(\gamma \) that splits equally the surplus between the firm and the union is lower than the average between the minimum and the maximum of its eligible references. Third, given the positive values of the \(\Phi \)’s terms, wages are always pro-cyclical during the adjustment process towards the steady state and the magnitude of the spillover of employment dynamics into the dynamics of wages is a decreasing function of the bargaining power of the firm. Fourth, given that the two eigenvalues are always real and have opposite sign, the stationary solution of the model is a saddle point even outside \(L^{*}=w^{*}=1\). In other words, all the eligible stationary solutions are locally asymptotically stable. Moreover, the modulus of the converging root of the dynamic system in (16), i.e. \(r_{2}\), is an increasing function of the bargaining power of the firm. Obviously, this implies that the higher (lower) the bargaining power of the firm, the faster (slower) the convergence towards the stationary solution.

As anticipated in the introduction, the positive relation between the speed of convergence towards the stationary solution and the bargaining power of the firm is at odds with respect to the result obtained by means of a companion right-to-manage dynamic model in which, on the contrary, increasing union power speeds up the adjustment process towards the stationary solution (cf. Guerrazzi 2011; Lockwood and Manning 1989). The rationale for this opposite finding is that a mediator whose employment adjustments are constrained towards an efficiency locus, i.e. towards the contract curve, tends to resolve faster the bargaining disputes in which the equilibrium wage is closer to the marginal productivity of labour. In fact, the results in Table 1 show that—given the initial level of employment—the allocation towards which convergence is faster is exactly the one in which it holds the standard condition for an efficient allocation of labour, i.e. the allocation in which the equilibrium real wage coincides with the marginal productivity of labour employed by the firm so that the bargaining is “strongly efficient” (cf. Layard and Nickell 1990). By contrast, convergence becomes slower when the steady-state values of the wage and employment moves away from the full employment allocation.Footnote 3

Fixing the bargaining power of the firm according to the efficiency criterion implemented inter alia by Shimer (2004), i.e. fixing the value of \(\gamma \) that leads to \(\gamma _{A}^{*}=0.5\), and using the remaining parameter values in Table 1, the out-of-equilibrium dynamics of employment, wages and the bargaining power of the firm are illustrated in the two panels of Fig. 3. Specifically, on the left-hand side there are the out-of-equilibrium adjustments retrieved when \(L_{0}\) is \(1\%\) above its steady-state reference, whereas on the right-hand side is reported the case in which \(L_{0}\) is \(1\%\) below that threshold.

Fig. 3
figure 3

Out-of-equilibrium adjustments of L, w and \(\gamma _{A}\)

Full size image

The plots of the two diagrams in Fig. 3 show that when the initial level employment overshoots (undershoots) its stationary value of \(1\%\), the wage does the same but to a lower extent—about \(0.5\%\)—whereas the bargaining power of the firm undershoots (overshoots) its equilibrium value of about \(4\%\). This pattern reveals two intriguing features of the dynamics underlying the model economy. First, the counter-cyclical behaviour of the bargaining power of the firm is the factor that leads to the convergence of w and L when their values are out of the stationary equilibrium; indeed, increases (reductions) of \(\gamma _{A}\) lead to a reduction (an increase) of the bargained values for employment and wages. Moreover, during the whole adjustment process, the sequence of bargained wages displays a lower deviation from their long-run mean with respect to employment and—together with the already mentioned pro-cyclicality of w(t)—this is consistent with the available empirical business cycle evidence that suggests the wages are less volatile than (un)employment (cf. Ravn and Simonelli 2007; Shimer 2004).

4 The dynamic versus the static problem

In a timeless environment with the same fundamental features of the dynamic model developed in Sect. 2, the mediator will maximize the instantaneous component of the linear maximandum in (3) with respect to the wage by considering that bargained employment is pinned down by the contract curve implied by the preferences of the two bargainers. Consequently, using the expressions for firm’s profits and union utility conveyed, respectively, by Eqs. (1) and (2), the static counterpart of the dynamic problem in (3) and (4) is simply the following:

$$\begin{aligned} \underset{w}{\max \text { }}\gamma \left( \left( 1+2\alpha -w\right) L-\alpha L^{2}\right) +\left( 1-\gamma \right) L\left( w^{\beta }-1\right) \end{aligned}$$
(19)

subject to

$$\begin{aligned} L=\frac{\beta \left( 1+2\alpha \right) +\left( 1-\beta \right) w-w^{1-\beta } }{2\alpha \beta } \end{aligned}$$
(20)

The FOC for w of the static problem described by (18) and (19) can be written as

$$\begin{aligned} \Omega \left( w_{s}\right) +\Xi \left( w_{s}\right) =0 \end{aligned}$$
(21)

where \(\Omega \left( w_{s}\right) \) and \(\Xi \left( w_{s}\right) \) are respectively defined by

$$\begin{aligned}&\Omega \left( w_{s}\right) \equiv \frac{\left( 1-\beta \right) \left( w_{s}^{\beta }-1\right) }{2\alpha \beta w_{s}^{\beta }}\left( \gamma \left( \frac{\left( 1+2\alpha \right) \beta w_{s}^{\beta -1}+\left( 1-3\beta \right) w_{s}^{\beta }-1}{2\beta w_{s}^{\beta -1}}\right) \right. \nonumber \\&\quad \left. +\left( 1-\gamma \right) \left( w_{s}^{\beta }-1\right) \right) \nonumber \\&\Xi \left( w_{s}\right) \equiv \frac{\left( 1+2\alpha \right) \beta w_{s}^{\beta -1}+\left( 1-\beta \right) w_{s}^{\beta }-1}{2\alpha \beta w_{s}^{\beta -1}}\left( \gamma \left( \frac{\left( 1-\beta \right) \left( w_{s}^{\beta }-1\right) -2\beta w_{s}^{\beta }}{2\beta w_{s}^{\beta } }\right) \right. \nonumber \\&\quad \left. +\left( 1-\gamma \right) \beta w_{s}^{\beta -1}\right) \end{aligned}$$
(22)

Obviously, plugging the value of \(w_{s}\) that fulfils Eq. (21) into Eq. (20) and considering the two expressions defined in (21) allows us to derive the equilibrium level of employment in the static model—say \(L_{s}\).

Taking into account the required parameter values in Table 1, Fig. 4 offers a visual comparison between the employment solutions of the static model in (19) and (20) and the corresponding stationary levels of employment of the dynamic framework in (3) and (4) both retrieved for the same values of the bargaining power of the firm implied by the eligible values of \(\gamma \).

Fig. 4
figure 4

Employment in the static and the dynamic model

Full size image

The plot of Fig. 4 shows that the static model always delivers a higher level of employment with respect to the stationary employment solution of the dynamic one and that the distance between the two references is an increasing function of the bargaining power of the union. Given the positive slope of the contract curve implied by the risk attitude of unionized workers, this means that even the wage is higher in the static setting than in the dynamic one. In the same direction of the finding about the convergent roots discussed above, this pattern is at odds with the one retrieved by comparing a static and a dynamic right-to-manage framework and it suggests that for any given value of \(\gamma \) a mediator that sets the wage in a static environment gives a larger portion of the surplus to workers and a smaller one to the firm with respect of the corresponding allocations assigned by the same mediator that sets the wage in a dynamic economy (cf. Guerrazzi 2011).

The reason for such an additional divergent outcome is that in the dynamic bargaining model developed in Sect. 2 the mediator’s marginal evaluation of an employment variation is always negative, i.e. the values taken by \(\Lambda \left( t\right) \) are systematically lower than zero. In other words, given the positive slope of the contract curve towards which employment is assumed to adjust itself, a mediator that sets the wage in a forward-looking manner anticipates that a positive (negative) employment variation—being associated to higher (lower) wages—will tend to benefit the union (firm) at the expense of the firm (union) (cf. de la Croix et al. 1996). Consequently, everything else being equal, a mediator that operates its tasks in a dynamic environment will strive to counterbalance that tendency by setting a lower wage with respect to the one set by a mediator that works instead in a static framework for which—by definition—the marginal evaluation of an employment variation is equal to zero.

5 Concluding remarks

In this paper, I derived a dynamic version of the efficient bargaining model grounded on the maximum principle with the aim of addressing the out-of-equilibrium dynamics of negotiated wages and employment. Specifically, drawing on Guerrazzi (2011), I developed an inter-temporal model with continuous time in which an infinitely lived arbitrator set the wage by considering that employment tends to adjust smoothly in the direction of the upward-sloping contract curve implied by the preferences of a risk-neutral firm and a pool of risk-averse unionized workers. Such a theoretical setting is an useful device to analyse the dynamics of wages and employment from a normative perspective.

The striking feature of the analysis carried out in this work is that its analytical and numerical findings are at odds with respect to the ones achieved by analysing a companion right-to-manage model in which employment is assumed to adjust itself in the direction of the downward-sloping labour demand curve of the representative firm with some attrition. In detail, I showed that increases in the bargaining power of the firm (union) enhance (delay) the convergence towards the steady state, whereas the dynamic negotiation of the wage penalize unionized workers and favour the firm with respect to the bargaining outcomes achieved in a similar static wage-setting framework (cf. Lockwood and Manning 1989; de la Croix et al. 1996). Moreover, an additional interesting pattern that characterizes the dynamic efficient bargaining model developed in this paper is that its out-of-equilibrium adjustments displayed a certain degree of wage rigidity that is consistent with circumstantial evidence on business cycles (cf. Ravn and Simonelli 2007; Shimer 2004).

The analysis summarized above could be developed in different directions. On the one hand, it could be interesting to consider how productivity shocks affect the evolution of wages and employment over time. Specifically, after the definition of a stochastic process for the productivity parameter that enters the profit function of the firm, the dynamic efficient bargaining model—as well as its right-to-manage version—could be augmented by an additional dynamic constraint in order to analyse the transmission mechanism of productivity disturbances generated by the inter-temporal negotiation of wages. As it holds in this model, i.e. when the bargaining process is carried out in an efficient manner and the deviations of wages from their long-run mean displayed during the adjustment process are smaller than the ones displayed by employment, such an extension may be particularly promising for the possible generation of a sound degree of wage rigidity that usually holds in wage contracts that cannot be reneged (cf. Thomas and Worrall 1988). In this direction, McDonald and Solow (1981) argue that in a static efficient bargaining model the contract curve and the equity locus for wages move in a way that tends to offset the wage effect of productivity disturbances. On the other hand, even the outside option of the union could be considered as a time-varying factor in order to explore how the model economy reacts to modifications in labour supply (cf. Gerber and Upmann 2006). The implied extensions are left to further developments.