Lebesgue points of $\ell _1$-Cesàro summability of d-dimensional Fourier series

Abstract

We generalize the classical Lebesgue’s theorem and prove that the $\ell _1$-Cesàro means of the Fourier series of the multi-dimensional function $f\in L_1({{\mathbb {T}}}^d)$ converge to f at each strong $\omega$-Lebesgue point.

1 Introduction

In 1905, Lebesgue [13] proved in his famous result that the so called Fejér means

$$\begin{aligned}\sigma _n f(x) := \sum _{k=-n}^n \left( 1-\frac{|k|}{n} \right) {\widehat{f}}(k) e^{\imath kx} \end{aligned}$$

of the trigonometric Fourier series of a one-dimensional integrable function f converge to f(x) at each Lebesgue point, thus almost everywhere. Here $\widehat{f}(k)$ denotes the kth Fourier coefficient. Some years later Riesz [17] generalized this theorem for the Cesàro means of one-dimensional integrable functions. The Cesàro summability was investigated in several papers (see e.g. Gát [5,6,7], Goginava [8,9,10], Simon [18, 19], Nagy et al. [15, 16], Weisz [22, 23] and Zygmund [27]).

In this paper, we will generalize this result to the Cesàro summability of multi-dimensional functions. More exactly, we investigate the $\ell _1$-Fejér means

$$\begin{aligned}\sigma _n f(x) := \sum _{k\in {{\mathbb {Z}}}^d, \, |k|\le n} \left( 1-\frac{|k|}{n} \right) {\widehat{f}}(k) e^{\imath k \cdot x} \end{aligned}$$

and their generalization, the $\ell _1$-Cesàro means of d-dimensional functions, where $|k|=|k_1|+\cdots +|k_d|$. These means were investigated e.g. in Berens et al. [1, 2, 14, 26], Szili and Vértesi [20]. Recently, using Hardy spaces, we [21, 22] proved that $\sigma _nf\rightarrow f$ almost everywhere if $f \in L_1({{\mathbb {T}}}^{d})$.

Here we partly characterize the set of this convergence. We generalize the Lebesgue points and introduce a new type Lebesgue points, the so called strong $\omega$-Lebesgue points. In [24], we verified that almost every point is a strong $\omega$-Lebesgue point of $f\in L_1({{\mathbb {T}}}^d)$. Our main result reads as follows. If the Hardy–Littlewood maximal function $\mathcal {M}^{\omega }f(x)$ is finite and x is a strong $\omega$-Lebesgue point of $f\in L_1({{\mathbb {T}}}^d)$, then

$$\begin{aligned}\lim _{n\rightarrow \infty }\sigma _n^{\alpha } f(x) = f(x), \end{aligned}$$

where $\sigma _n^{\alpha } f$ denotes the nth $\ell _1$-Cesàro mean of the Fourier series of f. A similar result was shown for the $\ell _1$-$\theta$-means of Fourier transforms in [25]. However, the $\theta$-summability does not contain the Cesàro summability and in this paper we consider Fourier series. So in the present proof, we have to use new ideas and the parts that are similar to [25] are omitted.

2 Hardy–Littlewood maximal function and strong $\omega$-Lebesgue points

Let us fix $d \ge 3$, $d\in {{\mathbb {N}}}$. For a set ${{{\mathbb {Y}}}}\ne \emptyset$, let ${{{\mathbb {Y}}}}^d$ be its Cartesian product ${{{\mathbb {Y}}}} \times \cdots \times {{{\mathbb {Y}}}}$ taken with itself d times. We briefly write $L_p({{\mathbb {T}}}^d)$ instead of the $L_p({{\mathbb {T}}}^d,\lambda )$ space equipped with the norm

$$\begin{aligned} \Vert f\Vert _p:=\left( \int _{{{\mathbb {T}}}^d}|f|^p \, \mathrm{d}\lambda \right) ^{1/p} \qquad (1\le p<\infty ), \end{aligned}$$

with the usual modification for $p=\infty$, where $\lambda$ is the Lebesgue measure. We identify the torus ${{\mathbb {T}}}$ with $[- \pi ,\pi ]$.

By a diagonal, we understand any diagonal of the two-dimensional faces of the cube $[0,\pi ]^d$. Let us denote by $P_{2^{i_1}h,\ldots ,2^{i_d}h}$ a parallelepiped, whose center is the origin and whose sides are parallel to the axes and/or to the diagonals and whose kth side length is $2^{i_k+1}h$ if the kth side is parallel to an axis and $\sqrt{2} 2^{i_k+1}h$ if the kth side is parallel to a diagonal $(i\in {{\mathbb {N}}}^d,h>0,k=1,\ldots ,d)$. In [24], we introduced the next Hardy–Littlewood maximal function. For some $\omega >0$ and $f\in L_1({{\mathbb {T}}}^d)$, let

$$\begin{aligned} \mathcal {M}^\omega f(x)&:= \sup _{P_{2^{i_1}h,\ldots ,2^{i_d}h},i\in {{\mathbb {N}}}^d,h>0} 2^{-\omega |i|} \\&\qquad \times \frac{1}{\left| P_{2^{i_1}h,\ldots ,2^{i_d}h}\right| } \int _{P_{2^{i_1}h,\ldots ,2^{i_d}h}} |f(x-t)| \, \mathrm{d}t, \end{aligned}$$

where the supremum is taken over all parallelepipeds $P_{2^{i_1}h,\ldots ,2^{i_d}h}$ $(i\in {{\mathbb {N}}}^d,h>0)$ just defined. Taking the supremum over all parallelepipeds whose sides are parallel to the axes and $\omega =0$, we obtain the strong Hardy–Littlewood maximal function, and, if in addition $i_1=\cdots =i_d$, the usual Hardy–Littlewood maximal function (for more about these maximal functions see e.g. Feichtinger and Weisz [4] and the references therein). We have proved in [24] that

$$\begin{aligned} \sup _{\rho>0} \rho \lambda (\mathcal {M}^\omega f > \rho ) \le C \Vert f\Vert _1 \qquad (f \in L_1({{\mathbb {T}}}^d)) \end{aligned}$$

(2.1)

and, for $1<p \le \infty$,

$$\begin{aligned} \left\| \mathcal {M}^\omega f \right\| _p\le C_p \Vert f\Vert _p \qquad (f \in L_p({{\mathbb {T}}}^d)). \end{aligned}$$

In this paper the constants C and $C_p$ may vary from line to line.

Based on the Hardy–Littlewood maximal function $\mathcal {M}^{\omega }$, we introduced the following type of Lebesgue points in [25]. Let

$$\begin{aligned} U_{r}^{\omega }f(x)&:= \sup _{\begin{array}{c} P_{2^{i_1}h,\ldots ,2^{i_d}h},i\in {{\mathbb {N}}}^d,h>0 \\ 2^{i_k}h<r,k=1,\ldots d \end{array}} 2^{-\omega \left| i\right| } \\&\qquad \times \frac{1}{\left| P_{2^{i_1}h,\ldots ,2^{i_d}h}\right| } \int _{P_{2^{i_1}h,\ldots ,2^{i_d}h}} |f(x-t)-f(x)| \, \mathrm{d}t, \end{aligned}$$

where the supremum is taken over all parallelepipeds mentioned above. For $\omega >0$, a point $x\in {{\mathbb {T}}}^d$ is called a strong $\omega$-Lebesgue point of $f\in L_1({{\mathbb {T}}}^d)$ if

$$\begin{aligned} \lim _{r\rightarrow 0} U_{r}^{\omega }f(x) =0. \end{aligned}$$

Taking the supremum in $U_{r}^{\omega }f$ over all parallelepipeds whose sides are parallel to the axes and $\omega =0$, we obtain the strong Lebesgue points. Moreover, if in addition $i_1=\cdots =i_d$, then we get the usual Lebesgue points, i.e.,

$$\begin{aligned} \lim _{h\rightarrow 0} \frac{1}{(2h)^d}\int _{-h}^{h} \cdots \int _{-h}^{h} |f(x-t)-f(x)| \,\mathrm{d}t=0. \end{aligned}$$

Note that every strong $\omega _2$-Lebesgue point is a strong $\omega _1$-Lebesgue point $(0<\omega _2<\omega _1<\infty )$, because of $U_{r}^{\omega _1} f\le U_{r}^{\omega _2} f$. If f is continuous at x, then x is a strong $\omega$-Lebesgue point of f. The next theorem was proved in [25].

Theorem 1

For $\omega >0$, almost every point $x\in {{\mathbb {T}}}^d$ is a strong $\omega$-Lebesgue point of $f\in L_1({{\mathbb {T}}}^d)$.

3 The kernel functions

For $x=(x_1,\ldots ,x_d)\in {{\mathbb {R}}}^d$ and $u=(u_1,\ldots ,u_d)\in {{\mathbb {R}}}^d$ set $u\cdot x := \sum _{k=1}^d u_k x_k$ and $|x|:= \sum _{k=1}^d |x_k|$. The kth Fourier coefficient of a d-dimensional integrable function $f\in L_1({{\mathbb {T}}}^d)$ is defined by

$$\begin{aligned} {\widehat{f}}(k) = \frac{1}{(2\pi )^d} \int _{{{\mathbb {T}}}^d} f(x) e^{-\imath k\cdot x} \, \mathrm{d}x \qquad (k\in {{\mathbb {Z}}}^d). \end{aligned}$$

For $f\in L_1({{\mathbb {T}}}^d)$ and $n \in {{\mathbb {N}}}$, the nth $\ell _1$-partial sum $s_nf$ of the Fourier series of f and the nth $\ell _1$-Dirichlet kernel $D_n$ are given by

$$\begin{aligned} s_{n} f(x) := \sum _{k\in {{\mathbb {Z}}}^d,\, |k| \le n} {\widehat{f}}(k) e^{\imath k \cdot x} \end{aligned}$$

and

$$\begin{aligned} D_{n}(t) := \sum _{k\in {{\mathbb {Z}}}^d, \, |k| \le n} e^{\imath k \cdot t}, \end{aligned}$$

respectively. It is known (see e.g. Grafakos [11] or Weisz [23]) that for $f\in L_p({{\mathbb {T}}}^d)$, $1<p<\infty$,

$$\begin{aligned} \lim _{n\rightarrow \infty } s_{n} f = f \qquad \text{ in } \text{ the } L_p({{\mathbb {T}}}^d)\text{-norm } \text{ and } \text{ a.e. } \end{aligned}$$

Since this convergence does not hold for $p=1$, we consider the Cesàro summation.

For $\alpha \ne -1,-2,\ldots$ and $n \in {{\mathbb {N}}}$, let

$$\begin{aligned} A_{n}^{\alpha } := \left( {\begin{array}{c}n+\alpha \\ n\end{array}}\right) = \frac{(\alpha +1)(\alpha +2)\cdots (\alpha +n)}{n!}. \end{aligned}$$

Then $A_0^{\alpha }=1$, $A_n^{0}=1$ and $A_n^{1}=n+1$ $(n \in {{\mathbb {N}}})$. Let $f\in L_1({{\mathbb {T}}}^{d})$, $n \in {{\mathbb {N}}}$ and $\alpha \ge 0$. The nth $\ell _1$-Cesàro means $\sigma _n^{\alpha }f$ of the Fourier series of f are introduced by

$$\begin{aligned} \sigma _n^{\alpha } f(x) := \frac{1}{A_{n-1}^{\alpha }} \sum _{k\in {{\mathbb {Z}}}^d, \, |k|\le n} A_{n-1-|k|}^{\alpha } {\widehat{f}}(k) e^{\imath k \cdot x}. \end{aligned}$$

If $\alpha =0$, we get $s_nf$, if $\alpha =1$, then the $\ell _1$-Fejér means

$$\begin{aligned} \sigma _n^{1} f(x) := \sum _{k\in {{\mathbb {Z}}}^d, \, |k|\le n} \left( 1-\frac{|k|}{n} \right) {\widehat{f}}(k) e^{\imath k \cdot x}. \end{aligned}$$

It is easy to see that

$$\begin{aligned} \sigma _n^{\alpha }f(x)=\frac{1}{(2\pi )^{d}}\int _{{{\mathbb {T}}}^d} f(x-t) K_n^{\alpha }(t) \, \mathrm{d}t, \end{aligned}$$

where the $\ell _1$-Cesàro kernel is given by

$$\begin{aligned} K_n^{\alpha }(t)&:= \frac{1}{A_{n-1}^{\alpha }} \sum _{k\in {{\mathbb {Z}}}^d, \, |k|\le n} A_{n-1-|k|}^{\alpha } e^{\imath k \cdot t} = \frac{1}{A_{n-1}^{\alpha }} \sum _{j=0}^{n-1} A_{n-1-j}^{\alpha -1} D_j(t). \end{aligned}$$

(3.1)

It is clear that

$$\begin{aligned} |D_{n}(t)|\le C n^d, \qquad |K_n^{\alpha }(t)|\le Cn^d \qquad (t \in {{\mathbb {T}}}^{d}). \end{aligned}$$

(3.2)

The next two lemmas can be found in Zygmund [27].

Lemma 1

For $0<\alpha \le 1$, $n \ge 1$, $m \in {{\mathbb {N}}}$ and $t \in {{\mathbb {T}}}$, $t\ne 0$,

$$\begin{aligned} \left| \sum _{k=0}^{n-1} k^{m} A_{n-1-k}^{\alpha -1} \sin ((k+1/2)t) \right| \le \frac{Cn^{m}}{|\sin (t/2)|^\alpha } + \frac{Cn^{\alpha +m-1}}{|\sin (t/2)|} \end{aligned}$$

and

$$\begin{aligned} \left| \sum _{k=0}^{n-1} k^{m} A_{n-1-k}^{\alpha -1} \cos ((k+1/2)t) \right| \le \frac{Cn^{m}}{|\sin (t/2)|^\alpha } + \frac{Cn^{\alpha +m-1}}{|\sin (t/2)|}. \end{aligned}$$

Lemma 2

For $\alpha >-1$ and $h>0$, we have

$$\begin{aligned} \sigma _n^{\alpha +h}f = \frac{1}{A_{n-1}^{\alpha +h}} \sum _{k=1}^{n} A_{n-k}^{h-1} A_{k-1}^{\alpha } \sigma _{k}^{\alpha } f. \end{aligned}$$

Lemma 3 was proved in Weisz [21, 22].

Lemma 3

If $0<\alpha \le 1$, then

$$\begin{aligned} \sup _{n \in {{\mathbb {N}}}} \int _{{{\mathbb {T}}}^d} \left| K_n^{\alpha }\right| \, d\lambda \le C. \end{aligned}$$

We define the nth divided difference of a function f at the pairwise distinct knots $x_1,\ldots ,x_n\in {{\mathbb {R}}}$ by

$$\begin{aligned} {[}x_1]f:=f(x_1), \qquad [x_1,\ldots ,x_n]f:=\frac{[x_1,\ldots ,x_{n-1}]f-[x_2,\ldots ,x_n]f}{x_1-x_n}. \end{aligned}$$

It is known (see e.g. DeVore and Lorentz [3, p. 120]) that if f is $(n-1)$-times continuously differentiable on [a, b] and $x_1,\ldots ,x_n\in [a,b]$, then there exists $\xi \in [a,b]$ such that

$$\begin{aligned} {[}x_1,\ldots ,x_n]f=\frac{f^{(n-1)}(\xi )}{(n-1)!}. \end{aligned}$$

(3.3)

Herriot [12] and Berens and Xu [1, 26] proved that the $\ell _1$-Dirichlet kernels can be expressed as

$$\begin{aligned} D_n(x) = [\cos x_1,\ldots ,\cos x_d]G_n \qquad (x\in {{\mathbb {T}}}^d), \end{aligned}$$

(3.4)

where

$$\begin{aligned} G_n(\cos x):=(-1)^{[(d-1)/2]}2 \cos (x/2) (\sin x)^{d-2} \mathrm{soc \, }((n+1/2)x) \end{aligned}$$

and

$$\begin{aligned} \mathrm{soc \, }x:= \left\{ \begin{array}{ll} \cos x, &{} \hbox {if } d \hbox { is even;} \\ \sin x, &{} \hbox {if } d \hbox { is odd.} \end{array} \right. \end{aligned}$$

A sequence $(i_l,j_l)_{l}=(i_l,j_l)_{l=1}^{d-1}$ is called a proper index sequence, if

• $i_1=1$, $j_1=d$,

• for any $l=1,\ldots ,d-2$ we have that either $i_{l+1}=i_l$ and $j_{l+1}=j_l-1$ or $i_{l+1}=i_l+1$ and $j_{l+1}=j_l$.

Let us denote by $\mathcal {I}(1,\ldots ,d)$ the set of all proper index sequences. Then $(i_l)_l$ is non-decreasing and $(j_l)_l$ is non-increasing. Moreover, $i_l<j_l$ for all $l=1,\ldots ,d-1$ and $j_l-i_l=d-l$ $(l=1,\ldots ,d-1)$. For $(i_l,j_l)_{l=1}^{d-1}\in \mathcal {I}(1,\ldots ,d)$, we say that the first k term of the sequence, i.e. $(i_l,j_l)_{l=1}^{k}$ is in $\mathcal {I}^{{(k)}}(1,\ldots ,d)$. Then $\mathcal {I}^{{(d-1)}}(1,\ldots ,d)$=$\mathcal {I}(1,\ldots ,d)$.

Using (3.4), we can easily prove the next lemma by induction (see also [21, 25]). For $k=0$ the equation is the same as (3.4).

Lemma 4

For $k=0,1,\ldots ,d-2$, we have

$$\begin{aligned} D_n(x)&= \sum _{(i_l,j_l)_{l=1}^{k+1}\in \mathcal {I}^{{(k+1)}}(1,\ldots ,d)} (-1)^{i_{k+1}-1} \\&\qquad \times \left( \prod _{l=1}^{k}(\cos x_{i_l}- \cos x_{j_l})^{-1}\right) [\cos x_{i_{k+1}},\ldots ,\cos x_{j_{k+1}}]G_n. \end{aligned}$$

We estimate the Cesàro kernel $K_{n}^{\alpha }$ as follows.

Lemma 5

If $0<\alpha \le 1$, $\pi>x_1>x_2>\ldots>x_d>0$, $1<n_1<\cdots<n_m<d$ and $m=0,\ldots ,d-2$, then

$$\begin{aligned} |K_{n}^{\alpha }(x)|&\le C n^{m} \sum _{(i_l,j_l)_l\in \mathcal {I}(\{1,\ldots ,d\}{\setminus }\{n_1,\ldots ,n_m\})} x_{i_1}^{-1} \nonumber \\&\quad \times \prod _{l=1}^{d-1-m}(x_{i_l}-x_{j_l})^{-1} 1_{\{x_{j_{d-1}}\le \pi /2\}} \nonumber \\&\quad + C n^{m} \sum _{(i_l,j_l)_l\in \mathcal {I}(\{1,\ldots ,d\}{\setminus }\{n_1,\ldots ,n_m\})} \left( \pi -x_{j_1}\right) ^{-1} \nonumber \\&\quad \times \prod _{l=1}^{d-1-m}(x_{i_l}-x_{j_l})^{-1} 1_{\{x_{j_{d-1}}>\pi /2\}}. \end{aligned}$$

(3.5)

Proof

In this proof we use the notation $D_n^d(x):=D_n(x)$, where d denotes the dimension. We apply Lemma 4 with $k=d-2$ to get that

$$\begin{aligned} \left| D_n^d(x)\right|&\le \sum _{(i_l,j_l)_l\in \mathcal {I}(1,\ldots ,d)} \left| \prod _{l=1}^{d-1}(\cos x_{i_l}- \cos x_{j_l})^{-1}\right| \\&\qquad \times \left| G_n(\cos x_{i_{d-1}})-G_n(\cos x_{j_{d-1}})\right| \nonumber \\&\le C \sum _{(i_l,j_l)_l\in \mathcal {I}(1,\ldots ,d)}\left| \prod _{l=1}^{d-1}(\cos x_{i_l}- \cos x_{j_l})^{-1}\right| \\&\qquad \times \left( \sin ^{d-2}x_{i_{d-1}} + \sin ^{d-2}x_{j_{d-1}}\right) . \end{aligned}$$

We use the trigonometric identity

$$\begin{aligned} \cos a - \cos b = -2 \sin ((a-b)/2) \sin ((a+b)/2) \end{aligned}$$

(3.6)

and the estimations

$$\begin{aligned} \sin (a\pm b)/2\sim a\pm b \quad \text{ if } \quad 0 \le b\le \pi /2, b<a \le \pi \end{aligned}$$

(3.7)

and

$$\begin{aligned} \sin (a-b)/2\sim a-b,\quad \sin (a+b)/2\sim 2\pi -a-b \end{aligned}$$

(3.8)

if $0 \le b<a\le \pi , \pi /2<a$. Then

$$\begin{aligned} \left| D_n^d(x)\right|&\le C \sum _{(i_l,j_l)_l\in \mathcal {I}(1,\ldots ,d)} \left( \prod _{l=1}^{d-1}(x_{i_l}-x_{j_l})^{-1}\right) \left( \prod _{l=1}^{d-1}(x_{i_l}+x_{j_l})^{-1}\right) \\&\quad \times \left( \sin ^{d-2}x_{i_{d-1}} + \sin ^{d-2}x_{j_{d-1}}\right) 1_{\{x_{j_{d-1}}\le \pi /2\}} \\&\quad + C \sum _{(i_l,j_l)_l\in \mathcal {I}(1,\ldots ,d)} \left( \prod _{l=1}^{d-1}(x_{i_l}-x_{j_l})^{-1}\right) \left( \prod _{l=1}^{d-1}(2 \pi -x_{i_l}-x_{j_l})^{-1}\right) \\&\quad \times \left( \sin ^{d-2}x_{i_{d-1}} + \sin ^{d-2}x_{j_{d-1}}\right) 1_{\{x_{j_{d-1}}>\pi /2\}}. \end{aligned}$$

Since $x_{i_1}+x_{j_1}\ge x_{i_{1}}$, $2 \pi -x_{i_1}-x_{j_1}>\pi -x_{j_l}$, $x_{i_l}+x_{j_l}\ge x_{i_{d-1}}$ and $2 \pi -x_{i_l}-x_{j_l}>\pi -x_{j_{d-1}}$ for $l=2,\ldots ,d-1$, we have

$$\begin{aligned} \left| D_n^d(x)\right|&\le C \sum _{(i_l,j_l)_l\in \mathcal {I}(1,\ldots ,d)} x_{i_1}^{-1} \left( \prod _{l=1}^{d-1}(x_{i_l}-x_{j_l})^{-1}\right) \nonumber \\&\quad \times \left( \prod _{l=2}^{d-1}(x_{i_l}+x_{j_l})^{-1}\right) x^{d-2}_{i_{d-1}} 1_{\{x_{j_{d-1}}\le \pi /2\}} \nonumber \\&\quad + C \sum _{(i_l,j_l)_l\in \mathcal {I}(1,\ldots ,d)} (\pi -x_{j_1})^{-1} \left( \prod _{l=1}^{d-1}(x_{i_l}-x_{j_l})^{-1}\right) \nonumber \\&\quad \times \left( \prod _{l=2}^{d-1}(2 \pi -x_{i_l}-x_{j_l})^{-1}\right) (\pi -x_{j_{d-1}})^{d-2} 1_{\{x_{j_{d-1}}>\pi /2\}} \nonumber \\&\le C \sum _{(i_l,j_l)_l\in \mathcal {I}(1,\ldots ,d)} x_{i_1}^{-1} \left( \prod _{l=1}^{d-1}(x_{i_l}-x_{j_l})^{-1}\right) 1_{\{x_{j_{d-1}}\le \pi /2\}} \nonumber \\&\quad + C \sum _{(i_l,j_l)_l\in \mathcal {I}(1,\ldots ,d)} (\pi -x_{j_1})^{-1} \left( \prod _{l=1}^{d-1}(x_{i_l}-x_{j_l})^{-1}\right) 1_{\{x_{j_{d-1}}>\pi /2\}}. \end{aligned}$$

(3.9)

Then (3.5) with $m=0$ follows from (3.1).

We may suppose that $n_1=2$. Observe that

$$\begin{aligned} D_{n}^{d}(x)&= \sum _{k\in {{\mathbb {Z}}}^d, \, |k| \le n} e^{\imath k \cdot x} \\&= \sum _{k_2=-n}^{n} e^{\imath k_2 x_2} \sum _{k_1=-n+|k_2|}^{n-|k_2|} \\&\quad \times \sum _{k_3=-n+|k_1|+|k_2|}^{n-|k_1|-|k_2|} \cdots \sum _{k_d=-n+|k_1|+\ldots +|k_{d-1}|}^{n-|k_1|-\ldots -|k_{d-1}|} e^{\imath (k_1 x_1+k_3x_3+\ldots +k_dx_d)}\\&= \sum _{k_2=-n}^{n} e^{\imath k_2 x_2} D_{n-|k_2|}^{d-1}(x_1,x_3,\ldots ,x_{d}). \end{aligned}$$

We apply (3.9) for the $(d-1)$-dimensional Dirichlet kernel $D_{n-|k_2|}^{d-1}(x_1,x_3,\ldots ,x_{d})$ and get that

$$\begin{aligned} \left| D_n^d(x)\right|&\le C n \sum _{(i_l,j_l)_l\in \mathcal {I}(1,3,\ldots ,d)} x_{i_1}^{-1} \left( \prod _{l=1}^{d-2}(x_{i_l}-x_{j_l})^{-1}\right) 1_{\{x_{j_{d-1}}\le \pi /2\}} \nonumber \\&\quad + C n \sum _{(i_l,j_l)_l\in \mathcal {I}(1,3,\ldots ,d)} (\pi -x_{j_1})^{-1} \left( \prod _{l=1}^{d-2}(x_{i_l}-x_{j_l})^{-1}\right) 1_{\{x_{j_{d-1}}>\pi /2\}}. \end{aligned}$$

Hence (3.1) implies (3.5) with $m=1$. The proof can be finished in the same way. $\square$

Lemma 6

Suppose that $0<\alpha \le 1$ and $\pi -1/n>x_1>x_2>\ldots>x_d>1/n$. Then

$$\begin{aligned} |K_{n}^{\alpha }(x)|&\le C n^{- \alpha } \sum _{(i_l,j_l)_l\in \mathcal {I}(1,\ldots ,d)} x_{i_1}^{-1} x_{j_1}^{-\alpha } \prod _{l=1}^{d-1}(x_{i_l}-x_{j_l})^{-1} 1_{\{x_{j_{d-1}}\le \pi /2\}} \nonumber \\&\quad + C n^{- \alpha } \sum _{(i_l,j_l)_l\in \mathcal {I}(1,\ldots ,d)} \left( \pi -x_{j_1}\right) ^{-1} (\pi -x_{i_1}^{-1})^{-\alpha } \nonumber \\&\quad \times \prod _{l=1}^{d-1}(x_{i_l}-x_{j_l})^{-1} 1_{\{x_{j_{d-1}}>\pi /2\}}. \end{aligned}$$

(3.10)

If $m=1,\ldots ,d-2$, then

$$\begin{aligned} |K_{n}^{\alpha }(x)|&\le C n^{m- \alpha } \sum _{(i_l,j_l)_l\in \mathcal {I}(1,\ldots ,d)} x_{i_1}^{-1} x_{j_1}^{-\alpha } \nonumber \\&\qquad \qquad \prod _{l=1}^{d-1-m}(x_{i_l}-x_{j_l})^{-1} 1_{\{x_{j_{d-m}}\le \pi /2\}} \nonumber \\&\quad + C n^{m- \alpha } \sum _{(i_l,j_l)_l\in \mathcal {I}(1,\ldots ,d)} \left( \pi -x_{j_1}\right) ^{-1} (\pi -x_{i_1}^{-1})^{-\alpha } \nonumber \\&\quad \times \prod _{l=1}^{d-1-m}(x_{i_l}-x_{j_l})^{-1} 1_{\{x_{i_{d-m}}>\pi /2\}}. \end{aligned}$$

(3.11)

Moreover,

$$\begin{aligned} |K_{n}^{\alpha }(x)| \le C n^{d-1-\alpha } x_{j_1}^{-1-\alpha } 1_{\{x_{j_{1}}\le \pi /2\}}+ C n^{d-1-\alpha } (\pi -x_{i_1})^{-1-\alpha } 1_{\{x_{i_{1}}>\pi /2\}}. \end{aligned}$$

Proof

We use Lemma 4 with $k=d-2$ and (3.1) to obtain

$$\begin{aligned} |K_n^{\alpha }(x)|&= \frac{1}{A_{n-1}^{\alpha }} \Bigg | \sum _{j=0}^{n-1} A_{n-1-j}^{\alpha -1} \sum _{(i_l,j_l)\in \mathcal {I}} (-1)^{i_{d-1}-1} \\&\quad \times \left( \prod _{l=1}^{d-2}(\cos x_{i_l}- \cos x_{j_l})^{-1}\right) [\cos x_{i_{d-1}},\cos x_{j_{d-1}}]G_j \Bigg | \\&\le \frac{1}{A_{n-1}^{\alpha }}\sum _{(i_l,j_l)\in \mathcal {I}} \left| \prod _{l=1}^{d-1}(\cos x_{i_l}- \cos x_{j_l})^{-1}\right| \\&\quad \times \left| \sum _{j=0}^{n-1} A_{n-1-j}^{\alpha -1} \Big (G_j(x_{i_{d-1}})-G_j(\cos x_{j_{d-1}}) \Big )\right| . \end{aligned}$$

Taking into account Lemma 1 and the definition of $G_n$,

$$\begin{aligned} |K_n^{\alpha }(x)|&\le \frac{C}{A_{n-1}^{\alpha }} \sum _{(i_l,j_l)\in \mathcal {I}} \left| \prod _{l=1}^{d-1}(\cos x_{i_l}- \cos x_{j_l})^{-1}\right| \\&\quad \times \Bigg (\sin ^{d-2}(x_{i_{d-1}})\sin ^{-\alpha }(x_{i_{d-1}}/2) \\&\quad \quad + Cn^{\alpha -1}\sin ^{d-2}(x_{i_{d-1}})\sin ^{-1}(x_{i_{d-1}}/2)\\&\quad \quad +\sin ^{d-2}(x_{j_{d-1}})\sin ^{-\alpha }(x_{j_{d-1}}/2) \\&\quad \quad + Cn^{\alpha -1}\sin ^{d-2}(x_{j_{d-1}})\sin ^{-1}(x_{j_{d-1}}/2) \Bigg ). \end{aligned}$$

Now we use again (3.6), (3.7) and (3.8) and conlude

$$\begin{aligned} |K_n^{\alpha }(x)|&\le C n^{-\alpha } \sum _{(i_l,j_l)\in \mathcal {I}} \left( \prod _{l=1}^{d-1}(x_{i_l}-x_{j_l})^{-1}\right) \left( \prod _{l=1}^{d-1}(x_{i_l}+x_{j_l})^{-1}\right) \\&\quad \times \Big (x_{i_{d-1}}^{d-2-\alpha } + Cn^{\alpha -1}x_{i_{d-1}}^{d-3} + x_{j_{d-1}}^{d-2-\alpha } + Cn^{\alpha -1}x_{j_{d-1}}^{d-3} \Big ) 1_{\{x_{j_{d-1}}\le \pi /2\}} \\&\quad + C n^{-\alpha } \sum _{(i_l,j_l)\in \mathcal {I}} \left( \prod _{l=1}^{d-1}(x_{i_l}-x_{j_l})^{-1}\right) \left( \prod _{l=1}^{d-1}(2 \pi -x_{i_l}-x_{j_l})^{-1}\right) \\&\quad \times \Big ( (\pi -x_{i_{d-1}})^{d-2-\alpha } + Cn^{\alpha -1} (\pi -x_{i_{d-1}})^{d-3} \\&\qquad \qquad + (\pi -x_{j_{d-1}})^{d-2-\alpha } + Cn^{\alpha -1} (\pi -x_{j_{d-1}})^{d-3} \Big ) 1_{\{x_{j_{d-1}}>\pi /2\}}. \end{aligned}$$

Since $\pi -1/n>x_1>x_2>\cdots>x_d>1/n$, we have

$$\begin{aligned} |K_n^{\alpha }(x)|&\le C n^{-\alpha } \sum _{(i_l,j_l)\in \mathcal {I}} x_{i_1}^{-1} \left( \prod _{l=1}^{d-1}(x_{i_l}-x_{j_l})^{-1}\right) \left( \prod _{l=2}^{d-1}(x_{i_l}+x_{j_l})^{-1}\right) \\&\quad \times \Big (x_{i_{d-1}}^{d-2-\alpha } + x_{j_{d-1}}^{d-2-\alpha } \Big ) 1_{\{x_{j_{d-1}}\le \pi /2\}} \\&\quad + C n^{-\alpha } \sum _{(i_l,j_l)\in \mathcal {I}} (\pi -x_{j_1})^{-1} \\&\quad \times \left( \prod _{l=1}^{d-1}(x_{i_l}-x_{j_l})^{-1}\right) \left( \prod _{l=2}^{d-1}(2 \pi -x_{i_l}-x_{j_l})^{-1}\right) \\&\quad \times \Big ( (\pi -x_{i_{d-1}})^{d-2-\alpha } + (\pi -x_{j_{d-1}})^{d-2-\alpha } \Big ) 1_{\{x_{j_{d-1}}>\pi /2\}} \\&\le C n^{-\alpha } \sum _{(i_l,j_l)\in \mathcal {I}} x_{i_1}^{-1} x_{j_{1}}^{-\alpha } \left( \prod _{l=1}^{d-1}(x_{i_l}-x_{j_l})^{-1}\right) 1_{\{x_{j_{d-1}}\le \pi /2\}} \\&\quad + C n^{-\alpha } \sum _{(i_l,j_l)\in \mathcal {I}} (\pi -x_{j_1})^{-1} (\pi -x_{i_{1}})^{-\alpha } \\&\quad \times \left( \prod _{l=1}^{d-1}(x_{i_l}-x_{j_l})^{-1}\right) 1_{\{x_{j_{d-1}}>\pi /2\}}, \end{aligned}$$

which shows (3.10).

After some basic calculation, we can see that

$$\begin{aligned} G_n^{(m)}(y)&= C \sum _{r_1=0}^{m} \sum _{k_1=1}^{r_1} \sum _{l_1=(r_1-k_1)/2}^{r_1-k_1} \cos ^{(k_1)}\left( \frac{\arccos y}{2}\right) \\&\qquad \times (1-y^{2})^{-k_1/2-l_1} y^{l_1-(r_1-k_1-l_1)} \\&\qquad \times \sum _{r_2=0}^{m-r_1} \sum _{k_2=1}^{\min (r_2,d-2)} \sum _{l_2=\max (r_2/2-k_2,0)}^{r_2-k_2} \sin ^{d-2-k_2}(\arccos y) \\&\qquad \times (1-y^{2})^{-k_2/2-l_2} y^{k_2+l_2-(r_2-k_2-l_2)} \\&\qquad \times \sum _{k_3=1}^{r_3} \sum _{l_3=(r_3-k_3)/2}^{r_3-k_3} (n+1/2)^{k_3} \mathrm{soc \, }^{(k_3)} ((n+1/2)\arccos y) \\&\qquad \times (1-y^{2})^{-k_3/2-l_3} y^{l_3-(r_3-k_3-l_3)}, \end{aligned}$$

where $r_1+r_2+r_3=m$ and

$$\begin{aligned} G_n(y):=(-1)^{[(d-1)/2]}2 \cos \left( \frac{\arccos y}{2}\right) \sin ^{d-2}(\arccos y) \mathrm{soc \, }((n+1/2)\arccos y). \end{aligned}$$

This implies for $y=\cos \xi$ that

$$\begin{aligned}&G_n^{(m)}(\cos \xi ) \\&= C \sum _{r_1=0}^{m} \sum _{k_1=1}^{r_1} \sum _{l_1=(r_1-k_1)/2}^{r_1-k_1} \sum _{r_2=0}^{m-r_1} \sum _{k_2=1}^{\min (r_2,d-2)} \sum _{l_2=\max (r_2/2-k_2,0)}^{r_2-k_2} \sum _{k_3=1}^{r_3} \sum _{l_3=(r_3-k_3)/2}^{r_3-k_3} \\&\quad \times \cos ^{(k_1)}(\xi /2) \cos ^{\beta }(\xi ) \sin ^{d-2-m}(\xi ) \sin ^{- \beta }(\xi ) (n+1/2)^{k_3} \mathrm{soc \, }^{(k_3)} ((n+1/2) \xi ), \end{aligned}$$

where

$$\begin{aligned} \beta&=k_1+2l_1+2k_2+2l_2+k_3+2l_3-r_1-r_2-r_3 \\&=k_1+2l_1+2k_2+2l_2+k_3+2l_3-m \end{aligned}$$

and

$$\begin{aligned} 0 \le \beta \le m-k_3. \end{aligned}$$

Using this formula as well as (3.1) and Lemma 4 for $k=d-1-m$ $(m=1,\ldots ,d-1)$, we conclude

$$\begin{aligned} |K_n^{\alpha }(x)|&= \frac{1}{A_{n-1}^{\alpha }} \Bigg | \sum _{j=0}^{n-1} A_{n-1-j}^{\alpha -1} \sum _{(i_l,j_l)_{l=1}^{d-m}\in \mathcal {I}^{{(d-m)}}(1,\ldots ,d)} (-1)^{i_{d-m}-1} \\&\qquad \times \left( \prod _{l=1}^{d-1-m}(\cos x_{i_l}- \cos x_{j_l})^{-1}\right) [\cos x_{i_{d-m}},\ldots ,\cos x_{j_{d-m}}]G_j \Bigg | \\&= \frac{1}{A_{n-1}^{\alpha }} \Bigg | \sum _{(i_l,j_l)_{l=1}^{d-m}\in \mathcal {I}^{{(d-m)}}(1,\ldots ,d)} (-1)^{i_{d-m}-1} \left( \prod _{l=1}^{d-1-m}(\cos x_{i_l}- \cos x_{j_l})^{-1}\right) \\&\qquad \times [\cos x_{i_{d-m}},\ldots ,\cos x_{j_{d-m}}] \left( \sum _{j=0}^{n-1} A_{n-1-j}^{\alpha -1}G_j\right) \Bigg |. \end{aligned}$$

Taking into account (3.3), we deduce

$$\begin{aligned} |K_n^{\alpha }(x)|&\le \frac{1}{A_{n-1}^{\alpha }} \sum _{(i_l,j_l)_{l=1}^{d-m}\in \mathcal {I}^{{(d-m)}}(1,\ldots ,d)} \left| \prod _{l=1}^{d-1-m}(\cos x_{i_l}- \cos x_{j_l})^{-1}\right| \\&\qquad \times \left| \sum _{j=0}^{n-1} A_{n-1-j}^{\alpha -1} \frac{G^{(m)}_j(\cos \xi )}{m!}\right| \\&= \frac{C}{A_{n-1}^{\alpha }} \sum _{(i_l,j_l)_{l=1}^{d-m}\in \mathcal {I}^{{(d-m)}}(1,\ldots ,d)} \left| \prod _{l=1}^{d-1-m}(\cos x_{i_l}- \cos x_{j_l})^{-1}\right| \\&\qquad \times \Bigg |\sum \cos ^{(k_1)}(\xi /2) \cos ^{\beta }(\xi ) \sin ^{d-2-m}(\xi ) \sin ^{- \beta }(\xi ) \\&\qquad \quad \times \sum _{j=0}^{n-1} A_{n-1-j}^{\alpha -1} (j+1/2)^{k_3} \mathrm{soc \, }^{(k_3)} ((j+1/2) \xi )\Bigg |, \end{aligned}$$

where $x_{j_{d-m}}^2 \le \xi =\xi _{(i_l,j_l)_l} \le x_{i_{d-m}}^2$. By Lemma 1, (3.6), (3.7) and (3.8),

$$\begin{aligned} |K_n^{\alpha }(x)|&\le \frac{C}{A_{n-1}^{\alpha }} \sum \sum _{(i_l,j_l)_{l=1}^{d-m}\in \mathcal {I}^{{(d-m)}}(1,\ldots ,d)} \left| \prod _{l=1}^{d-1-m}(\cos x_{i_l}- \cos x_{j_l})^{-1}\right| \\&\qquad \times \sin ^{d-2-m}(\xi ) \sin ^{- \beta }(\xi ) \Big (n^{k_3}\sin (\xi /2)^{-\alpha } + n^{\alpha +k_3-1} \sin (\xi /2)^{-1}\Big )\\&\le C n^{- \alpha } \sum \sum _{(i_l,j_l)_{l=1}^{d-m}\in \mathcal {I}^{{(d-m)}}(1,\ldots ,d)} \left( \prod _{l=1}^{d-1-m}(x_{i_l}-x_{j_l})^{-1}\right) \\&\qquad \times \left( \prod _{l=1}^{d-1-m}(x_{i_l}+x_{j_l})^{-1}\right) \xi ^{d-2-m- \beta } \\&\qquad \times \Big (n^{k_3}\xi ^{-\alpha } + n^{\alpha +k_3-1} \xi ^{-1}\Big ) 1_{\{\xi \le \pi /2\}}\\&\quad +C n^{- \alpha } \sum \sum _{(i_l,j_l)_{l=1}^{d-m}\in \mathcal {I}^{{(d-m)}}(1,\ldots ,d)} \\&\qquad \times \left( \prod _{l=1}^{d-1-m}(x_{i_l}-x_{j_l})^{-1}\right) \left( \prod _{l=1}^{d-1-m}(2 \pi -x_{i_l}-x_{j_l})^{-1}\right) \\&\qquad \times (\pi -\xi )^{d-2-m- \beta } \Big (n^{k_3}(\pi -\xi )^{-\alpha } + n^{\alpha +k_3-1} (\pi -\xi )^{-1}\Big ) 1_{\{\xi >\pi /2\}}. \end{aligned}$$

Since $1/n<\xi <\pi -1/n$,

$$\begin{aligned} |K_n^{\alpha }(x)|&\le C n^{- \alpha } \sum \sum _{(i_l,j_l)_{l=1}^{d-m}\in \mathcal {I}^{{(d-m)}}(1,\ldots ,d)} x_{i_1}^{-1} \left( \prod _{l=1}^{d-1-m}(x_{i_l}-x_{j_l})^{-1}\right) \\&\quad \times \left( \prod _{l=1}^{d-2-m}(x_{i_l}+x_{j_l})^{-1}\right) n^{k_3}\xi ^{d-2-m- \beta -\alpha } 1_{\{x_{j_{d-m}}\le \pi /2\}}\\&\quad +C n^{- \alpha } \sum \sum _{(i_l,j_l)_{l=1}^{d-m}\in \mathcal {I}^{{(d-m)}}(1,\ldots ,d)} (\pi -x_{j_1})^{-1}\left( \prod _{l=1}^{d-1-m}(x_{i_l}-x_{j_l})^{-1}\right) \\&\quad \times \left( \prod _{l=1}^{d-2-m}(2 \pi -x_{i_l}-x_{j_l})^{-1}\right) n^{k_3}(\pi -\xi )^{d-2-m- \beta -\alpha } 1_{\{x_{i_{d-m}}>\pi /2\}} \end{aligned}$$

and

$$\begin{aligned} |K_n^{\alpha }(x)|&\le C \sum n^{k_3- \alpha } \sum _{(i_l,j_l)_{l=1}^{d-m}\in \mathcal {I}^{{(d-m)}}(1,\ldots ,d)} x_{i_1}^{-1} \left( \prod _{l=1}^{d-1-m}(x_{i_l}-x_{j_l})^{-1}\right) \\&\quad \times \xi ^{- \beta -\alpha } 1_{\{x_{j_{d-m}}\le \pi /2\}}\\&\quad +C \sum n^{k_3- \alpha } \sum _{(i_l,j_l)_{l=1}^{d-m}\in \mathcal {I}^{{(d-m)}}(1,\ldots ,d)} (\pi -x_{j_1})^{-1}\left( \prod _{l=1}^{d-1-m}(x_{i_l}-x_{j_l})^{-1}\right) \\&\quad \times (\pi -\xi )^{- \beta -\alpha } 1_{\{x_{i_{d-m}}>\pi /2\}}. \end{aligned}$$

Furthermore,

$$\begin{aligned} |K_n^{\alpha }(x)|&\le C n^{m- \alpha } \sum _{(i_l,j_l)_{l=1}^{d-m}\in \mathcal {I}^{{(d-m)}}(1,\ldots ,d)} x_{i_1}^{-1} x_{j_1}^{-\alpha } \\&\quad \times \left( \prod _{l=1}^{d-1-m}(x_{i_l}-x_{j_l})^{-1}\right) 1_{\{x_{j_{d-m}}\le \pi /2\}}\\&\quad +C n^{m- \alpha } \sum _{(i_l,j_l)_{l=1}^{d-m}\in \mathcal {I}^{{(d-m)}}(1,\ldots ,d)} (\pi -x_{j_1})^{-1} (\pi -x_{i_1})^{- \alpha } \\&\quad \times \left( \prod _{l=1}^{d-1-m}(x_{i_l}-x_{j_l})^{-1}\right) 1_{\{x_{i_{d-m}}>\pi /2\}}. \end{aligned}$$

which proves (3.11). $\square$

4 Convergence at strong $\omega$-Lebesgue points

Now we are ready to prove our main theorem.

Theorem 2

Suppose that $0<\alpha <\infty$, $0<\omega <\min (\alpha ,1)/d$ and $\mathcal {M}^{\omega }f(x)$ is finite. If $f\in L_1({{\mathbb {T}}}^d)$ is periodic with respect to $\pi$ and x is a strong $\omega$-Lebesgue point of f, then

$$\begin{aligned} \lim _{n\rightarrow \infty }\sigma _n^{\alpha } f(x) = f(x). \end{aligned}$$

Proof

By Lemma 2, it is enough to prove the theorem for $0<\alpha \le 1$. Since

$$\begin{aligned} \frac{1}{(2\pi )^{d/2}}\int _{{{\mathbb {T}}}^d} K_n^{\alpha }(t) \, \mathrm{d}t =1, \end{aligned}$$

we have

$$\begin{aligned} \left| \sigma _n^{\alpha }f(x)-f(x)\right| \le \frac{1}{(2\pi )^{d/2}} \int _{{{\mathbb {T}}}^d} \left| f(x-t)-f(x)\right| \left| K_n^{\alpha }(t)\right| \, \mathrm{d}t. \end{aligned}$$

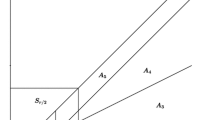
It is enough to integrate on the set

$$\begin{aligned} S:=\left\{ t \in {{\mathbb {T}}}^{d}:\pi>t_1>\cdots>t_d>0\right\} . \end{aligned}$$

We introduce the sets

$$\begin{aligned} A_{0}&:= \left\{ t: 8/n> t_1>\cdots> t_d>0\right\} \cup \left\{ t: \pi> t_1>\cdots> t_d>\pi -8/n\right\} ,\\ A_{1}&:= \left\{ t: \pi> t_1>\cdots>t_d>0,t_k-t_{k+1}>2/n,k=1,\ldots ,d-1\right\} {{\setminus }} A_0,\\ A_{i}&:= \left\{ t: \pi> t_1>\cdots>t_d>0,t_k-t_{k+i}>2/n,k=1,\ldots ,d-i \right. \\&\left. \text{ and } \text{ there } \text{ exists } \ 1\le j \le d-i+1 \ \text{ such } \text{ that }\ t_j-t_{j+i-1}\le 2/n\right\} {\setminus } A_0 \end{aligned}$$

for $i=2,\ldots ,d-1$,

$$\begin{aligned} A_{d}:= \left\{ t: \pi> t_1>\ldots>t_d>0,t_1-t_{d}\le 2/n\right\} {{\setminus }} A_0 \end{aligned}$$

and

$$\begin{aligned} B_1:=\left\{ t: 0<t_d\le 1/n\right\} , \qquad B_2:= \left\{ t: \pi >t_1 \ge \pi -1/n\right\} . \end{aligned}$$

Since x is a strong $\omega$-Lebesgue point of f, we can fix a number $r<\pi /2$ such that $U_r^\omega f(x)<\epsilon$. Let us introduce the cubes

$$\begin{aligned} S_{r/2}:=\left[ -\frac{r}{2},\frac{r}{2}\right] ^{d}, \qquad T_{r/2}:=\left[ \pi -\frac{r}{2},\pi +\frac{r}{2}\right] ^{d} \end{aligned}$$

and suppose that $8/n<r/2$. Instead of S, we will integrate on the sets $A_0$ and

$$\begin{aligned} \bigcup _{j=1}^{d} \bigcup _{k_1=0}^{1} \bigcup _{k_2=0}^{1} \bigcup _{k_3=0}^{1} \bigcup _{k_4=0}^{1} (A_j\cap B_1^{k_1} \cap B_2^{k_2} \cap S_{r/2}^{k_3} \cap T_{r/2}^{k_3}), \end{aligned}$$

where $H^{0}:=H$ and $H^{1}:=H^c$ denotes the complement of the set H.

Since $A_0\subset S_{r/2}\cup T_{r/2}$, (3.2) and the periodicity of f imply

$$\begin{aligned}&\int _{A_0} \left| f(x-t)-f(x)\right| \left| K_n^{\alpha }(t)\right| \, \mathrm{d}t \\&\quad \le Cn^d \int _{0}^{8/n} \cdots \int _{0}^{8/n} \left| f(x-t)-f(x)\right| \, \mathrm{d}t \\&\qquad + Cn^d \int _{\pi -8/n}^{\pi } \cdots \int _{\pi -8/n}^{\pi } \left| f(x-t)-f(x)\right| \, \mathrm{d}t \\&\quad \le C U_r^\omega f(x)< C\epsilon . \end{aligned}$$

Note that $A_d\cap B_1 = A_d\cap B_2 = \emptyset$, $S_{r/2} \cap T_{r/2}= \emptyset$, $B_1 \cap T_{r/2}= \emptyset$ and $B_2 \cap S_{r/2}=\emptyset$. Let us start with the integral on $A_j\cap B_1^{c} \cap B_2 \cap S_{r/2}^{c} \cap T_{r/2}$. If $t \in T_{r/2}$, then each $t_k>\pi /2$, hence we have to use only the second summand of (3.5). Henceforth, for $j=1,\ldots ,d-1$,

$$\begin{aligned}&\int _{A_j\cap B_1^{c} \cap B_2 \cap S_{r/2}^{c} \cap T_{r/2}} \left| f(x-t)-f(x)\right| \left| K_n^{\alpha }(t)\right| \, \mathrm{d}t \nonumber \\&\qquad \le \int _{A_j \cap B_2 \cap T_{r/2}} \left| f(x-t)-f(x)\right| \left| K_n^{\alpha }(t)\right| \, \mathrm{d}t \nonumber \\&\qquad \le C n^{m} \int _{A_j \cap B_2 \cap T_{r/2}} \left| f(x-t)-f(x)\right| \nonumber \\&\qquad \qquad \times \sum _{(i_l,j_l)_l\in \mathcal {I}(\{1,\ldots ,d\}{\setminus }\{n_1,\ldots ,n_m\})} \left( \pi -t_{j_1}\right) ^{-1} \prod _{l=1}^{d-1-m}(t_{i_l}-t_{j_l})^{-1} \, \mathrm{d}t. \end{aligned}$$

(4.1)

For $j=1$, we use this estimation with $m=0$. On $B_2 {{\setminus }} A_0$, we have $\pi -t_d>2(\pi -t_1)$ and so $t_1-t_d > (\pi -t_d)/2$. This implies

$$\begin{aligned}&\int _{A_1\cap B_1^{c} \cap B_2 \cap S_{r/2}^{c} \cap T_{r/2}} \left| f(x-t)-f(x)\right| \left| K_n^{\alpha }(t)\right| \, \mathrm{d}t \nonumber \\&\quad \le C \sum _{(i_l,j_l)_l\in \mathcal {I}(1,\ldots ,d)} \int _{A_1\cap B_2 \cap T_{r/2}} \left| f(x-t)-f(x)\right| \left( \pi -t_{j_1}\right) ^{-1} \prod _{l=1}^{d-1}(t_{i_l}-t_{j_l})^{-1} \, \mathrm{d}t \nonumber \\&\quad \le C \sum _{(i_l,j_l)_l\in \mathcal {I}(1,\ldots ,d)} \int _{A_1\cap B_2 \cap T_{r/2}} \left| f(x-t)-f(x)\right| \left( \pi -t_{j_1}\right) ^{-2} \prod _{l=2}^{d-1}(t_{i_l}-t_{j_l})^{-1} \, \mathrm{d}t. \end{aligned}$$

(4.2)

For a given proper index sequence $(i_l,j_l)_l\in \mathcal {I}(1,\ldots ,d)$, we introduce a permutation $i_1',\ldots ,i_d'$ of $1,\ldots ,d$ and then we integrate with respect to $t_{i_d'}, t_{i_{d-1}'}, \ldots , t_{i_1'}$, in this order. Let $i'_{1}=j_1=d$ and compute the integral

$$\begin{aligned} \sum _{k_1=3}^{r_0} \int ^{\pi -2^{k_1}/n}_{\pi -2^{k_1+1}/n}\cdots \left( \pi -t_{j_1}\right) ^{-2}\,\mathrm{d}t_{i_1'}, \end{aligned}$$

where $r_0$ denotes the natural number i, for which $r/2\le 2^{i+1}/n<r$. Next let $i_2'=i_1=1$ and compute the integral

$$\begin{aligned} \int ^{\pi }_{\pi -1/n}\cdots \,\mathrm{d}t_{i_2'}. \end{aligned}$$

Let us continue with the next two cases. If $i_2=i_1$ and $j_2=j_1-1$, then let $i_3'=j_2$ and consider the integral

$$\begin{aligned} \sum _{k_2=0}^{k_1} \int _{t_{i_2}-2^{k_2+1}/n}^{t_{i_2}-2^{k_2}/n}\cdots (t_{i_2}-t_{j_2})^{-1}\,\mathrm{d}t_{i_3'}. \end{aligned}$$

If $i_2=i_1+1$ and $j_2=j_1$, then let $i_3'=i_2$ and consider the integral

$$\begin{aligned} \sum _{k_2=0}^{k_1} \int _{t_{j_2}+2^{k_2}/n}^{t_{j_2}+2^{k_2+1}/n}\cdots (t_{i_2}-t_{j_2})^{-1}\,\mathrm{d}t_{i_3'}. \end{aligned}$$

Continuing this process and substituting $t_j=u_j+ \pi$, we get the integrals

$$\begin{aligned} \sum _{k_1=3}^{r_0} \int ^{-2^{k_1}/n}_{-2^{k_1+1}/n}\cdots t_{j_1}^{-2}\,\mathrm{d}t_{i_1'}, \qquad \int ^{0}_{-1/n}\cdots \,\mathrm{d}t_{i_2'} \end{aligned}$$

and

$$\begin{aligned} \sum _{k_2=0}^{k_1} \int _{t_{i_2}-2^{k_2+1}/n}^{t_{i_2}-2^{k_2}/n}\cdots (t_{i_2}-t_{j_2})^{-1}\,\mathrm{d}t_{i_3'} \end{aligned}$$

or

$$\begin{aligned} \sum _{k_2=0}^{k_1} \int _{t_{j_2}+2^{k_2}/n}^{t_{j_2}+2^{k_2+1}/n}\cdots (t_{i_2}-t_{j_2})^{-1}\,\mathrm{d}t_{i_3'}. \end{aligned}$$

Consequently, we integrate over a parallelepiped $P_{2^{k_1}/n,\ldots ,2^{k_{d}}/n}$, with $k_d=0$ and obtain

$$\begin{aligned}&\int _{A_1\cap B_1^{c} \cap B_2 \cap S_{r/2}^{c} \cap T_{r/2}} \left| f(x-t)-f(x)\right| \left| K_n^{\alpha }(t)\right| \, \mathrm{d}t \nonumber \\&\quad \le C \sum _{(i_l,j_l)_l\in \mathcal {I}(1,\ldots ,d)} \sum _{k_1=3}^{r_0} \sum _{k_2=0}^{k_1} \cdots \sum _{k_{d-1}=0}^{k_1} \left( \frac{2^{k_1}}{T}\right) ^{-2} \prod _{l=2}^{d-1} \left( \frac{2^{k_l}}{T}\right) ^{-1} \nonumber \\&\qquad \times \int _{P_{2^{k_1}/n,\ldots ,2^{k_{d}}/n}} \left| f(x-t)-f(x)\right| \, \mathrm{d}t \nonumber \\&\quad \le C \sum _{(i_l,j_l)_l\in \mathcal {I}(1,\ldots ,d)} \sum _{k_1=3}^{r_0} \sum _{k_2=0}^{k_1} \cdots \sum _{k_{d-1}=0}^{k_1} 2^{(\omega -1/(d-1)) \left| k\right| } \\&\qquad \times 2^{-\omega |k|} \frac{1}{\left| P_{2^{k_1}/n,\ldots ,2^{k_{d}}/n}\right| } \int _{P_{2^{k_1}/n,\ldots ,2^{k_{d}}/n}} \left| f(x-t)-f(x)\right| \, \mathrm{d}t\\&\quad \le C \sum _{(i_l,j_l)_l\in \mathcal {I}(1,\ldots ,d)} \sum _{k_1=3}^{r_0} \sum _{k_2=0}^{k_1} \cdots \sum _{k_{d-1}=0}^{k_1} 2^{(\omega -1/(d-1)) \left| k\right| } U_r^\omega f(x)< C\epsilon . \end{aligned}$$

It is easy to see that $t_1>(\pi -t_d)/2$ on $B_2$. By (3.5),

$$\begin{aligned}&\int _{A_1\cap B_1^{k_1} \cap B_2 \cap S_{r/2}^{c} \cap T_{r/2}^{c}} \left| f(x-t)-f(x)\right| \left| K_n^{\alpha }(t)\right| \, \mathrm{d}t \nonumber \\&\qquad \le C n^{m} \int _{A_j \cap B_2 \cap T_{r/2}^{c}} \left| f(x-t)-f(x)\right| \nonumber \\&\qquad \qquad \times \sum _{(i_l,j_l)_l\in \mathcal {I}(\{1,\ldots ,d\}{\setminus }\{n_1,\ldots ,n_m\})} \left( \pi -t_{j_1}\right) ^{-1} \prod _{l=1}^{d-1-m}(t_{i_l}-t_{j_l})^{-1} \, \mathrm{d}t \end{aligned}$$

for $k_1=0,1$. Similarly as above,

$$\begin{aligned}&{\int _{A_1\cap B_1^{k_1} \cap B_2 \cap S_{r/2}^{c} \cap T_{r/2}^{c}} \left| f(x-t)-f(x)\right| \left| K_n^{\alpha }(t)\right| \, \mathrm{d}t } \\&\quad \le C \sum _{(i_l,j_l)_l\in \mathcal {I}(1,\ldots ,d)} \sum _{k_1=r_0}^{\infty } \sum _{k_2=0}^{k_1} \cdots \sum _{k_{d-1}=0}^{k_1} \left( \frac{2^{k_1}}{T}\right) ^{-2} \prod _{l=2}^{d-1} \left( \frac{2^{k_l}}{T}\right) ^{-1} \\&\quad \quad \times \int _{P_{2^{k_1}/n,\ldots ,2^{k_{d}}/n}} \left| f(x-t)-f(x)\right| \, \mathrm{d}t\\&\le C \sum _{(i_l,j_l)_l\in \mathcal {I}(1,\ldots ,d)} \sum _{k_1=r_0}^{\infty } \sum _{k_2=0}^{k_1} \cdots \sum _{k_{d-1}=0}^{k_1} 2^{(\omega -1/(d-1)) \left| k\right| } \\&\quad \quad \times 2^{-\omega |k|} \frac{1}{\left| P_{2^{k_1}/n,\ldots ,2^{k_{d}}/n}\right| } \int _{P_{2^{k_1}/n,\ldots ,2^{k_{d}}/n}} \left| f(x-t)-f(x)\right| \, \mathrm{d}t\\&\le C \sum _{(i_l,j_l)_l\in \mathcal {I}(1,\ldots ,d)} \sum _{k_1=r_0}^{\infty } \sum _{k_2=0}^{k_1} \cdots \sum _{k_{d-1}=0}^{k_1} 2^{(\omega -1/(d-1)) \left| k\right| } \mathcal {M}^\omega f(x) \\&\quad \quad + C \sum _{(i_l,j_l)_l\in \mathcal {I}(1,\ldots ,d)} \sum _{k_1=r_0}^{\infty } \sum _{k_2=0}^{k_1} \cdots \sum _{k_{d-1}=0}^{k_1} 2^{-|k|/(d-1)}|f(x)| \\&\le C \sum _{k_1=r_0}^{\infty } 2^{(\omega -1/(d-1)) k_1} \mathcal {M}^\omega f(x) + C \sum _{k_1=r_0}^{\infty } 2^{-k_1/(d-1)}|f(x)|\\&\le C 2^{(\omega -1/(d-1))r_0} \mathcal {M}^\omega f(x) + C 2^{-r_0/(d-1)}|f(x)| \\&\le C (nr)^{\omega -1/(d-1)} \mathcal {M}^\omega f(x) + C (nr)^{-1/(d-1)}|f(x)| \rightarrow 0 \end{aligned}$$

as $n\rightarrow \infty$.

To integrate on $A_2$, we introduce the sets $A_2^{\alpha _1,\ldots ,\alpha _m}$ $(1 \le \alpha _1<\cdots <\alpha _m \le d-1,1 \le m \le d-1)$ containing all $t \in A_2$ for which $t_{\alpha _j}-t_{\alpha _j+1}\le 2/n$ $(j=1, \ldots ,m)$ and $t_k-t_{k+2}>2/n$ for all $k=1,\ldots ,d-2$. Instead of $A_2$, we will integrate on $A_2^{\alpha _1,\ldots ,\alpha _m}$. If $m=d-1$, then the integrals on $A_2^{\alpha _1,\ldots ,\alpha _m}\cap B_1^{c} \cap B_2 \cap S_{r/2}^{c} \cap T_{r/2}$ and $A_2^{\alpha _1,\ldots ,\alpha _m}\cap B_1^{k_1} \cap B_2 \cap S_{r/2}^{c} \cap T_{r/2}^{c}$ are similar to the integrals above. Suppose that $1 \le m \le d-2$ and $\alpha _m+1<d$. Then let $n_j=\alpha _j+1$, $j=1,\ldots ,m$ and by (4.1) and (4.2),

$$\begin{aligned}&\int _{A_2^{\alpha _1,\ldots ,\alpha _m}\cap B_1^{c} \cap B_2 \cap S_{r/2}^{c} \cap T_{r/2}} \left| f(x-t)-f(x)\right| \left| K_n^{\alpha }(t)\right| \, \mathrm{d}t \nonumber \\&\quad \le C n^{m} \sum _{(i_l,j_l)_l\in \mathcal {I}(\{1,\ldots ,d\}{\setminus }\{n_1,\ldots ,n_m\})} \nonumber \\&\qquad \times \int _{A_2^{\alpha _1,\ldots ,\alpha _m} \cap B_2 \cap T_{r/2}} \left| f(x-t)-f(x)\right| (\pi -t_{i_1})^{-2} \prod _{l=2}^{d-1-m}(t_{i_l}-t_{j_l})^{-1} \, \mathrm{d}t. \end{aligned}$$

Here, we integrate first as follows:

$$\begin{aligned} \int _{t_{n_{m}-1}-2/n}^{t_{n_{m}-1}} \cdots \mathrm{d}t_{n_m}, \quad \int _{t_{n_{m-1}-1}-2/n}^{t_{n_{m-1}-1}} \cdots \mathrm{d}t_{n_{m-1}}, \quad \ldots , \quad \int _{t_{n_{1}-1}-2/n}^{t_{n_{1}-1}} \cdots \mathrm{d}t_{n_1}. \end{aligned}$$

Then we continue with the integrals as before in (4.2) with $\mathcal {I}(\{1,\ldots ,d\}{\setminus }\{n_1,\ldots ,n_m\})$ instead of $\mathcal {I}(\{1,\ldots ,d\})$. This means that we integrate over a parallelepiped $P_{2^{k_1}/n,\ldots ,2^{k_{d}}/n}$ with $k_{n_1}=\ldots =k_{n_m}=1$, $k_d=0$ and get that

$$\begin{aligned}&\int _{A_2^{\alpha _1,\ldots ,\alpha _m}\cap B_1^{c} \cap B_2 \cap S_{r/2}^{c} \cap T_{r/2}} \left| f(x-t)-f(x)\right| \left| K_n^{\alpha }(t)\right| \, \mathrm{d}t \nonumber \\&\quad \le C n^{m} \sum _{(i_l,j_l)_l\in \mathcal {I}(\{1,\ldots ,d\}{\setminus }\{n_1,\ldots ,n_m\})} \\&\qquad \times \sum _{k_1=3}^{r_0} \sum _{k_{\beta _2}=0}^{k_1} \cdots \sum _{k_{\beta _{d-1-m}}=0}^{k_1} \left( \frac{2^{k_1}}{T}\right) ^{-2} \prod _{l=2}^{d-1-m} \left( \frac{2^{k_{\beta _l}}}{T}\right) ^{-1} \\&\qquad \times \int _{P_{2^{k_1}/n,\ldots ,2^{k_{d}}/n}} \left| f(x-t)-f(x)\right| \, \mathrm{d}t\\&\quad \le C \sum _{(i_l,j_l)_l\in \mathcal {I}(\{1,\ldots ,d\}{\setminus }\{n_1,\ldots ,n_m\})} \sum _{k_1=3}^{r_0} \sum _{k_{\beta _2}=0}^{k_1} \cdots \sum _{k_{\beta _{d-1-m}}=0}^{k_1} 2^{(\omega -1/(d-1-m)) \left| k\right| } \\&\qquad \times 2^{-\omega |k|} \frac{1}{\left| P_{2^{k_1}/n,\ldots ,2^{k_{d}}/n}\right| } \int _{P_{2^{k_1}/n,\ldots ,2^{k_{d}}/n}} \left| f(x-t)-f(x)\right| \, \mathrm{d}t\\&\quad \le C \sum _{(i_l,j_l)_l\in \mathcal {I}(\{1,\ldots ,d\}{\setminus }\{n_1,\ldots ,n_m\})} \\&\qquad \times \sum _{k_1=3}^{r_0} \sum _{k_{\beta _2}=0}^{k_1} \cdots \sum _{k_{\beta _{d-1-m}}=0}^{k_1} 2^{(\omega -1/(d-1-m)) \left| k\right| } U_r^\omega f(x)< C\epsilon , \end{aligned}$$

where the indices $1<\beta _2<\cdots<\beta _{d-1-m}<d$ are all different from $n_1,\ldots ,n_m$. It is easy to see that if $\alpha _m+1=d$, then we can also choose $1<n_1<\cdots<n_m<d$ such that $n_j=\alpha _j$ or $n_j=\alpha _j+1$, $j=1,\ldots ,m$ and the estimation of the integral is the same. The integrals on the sets $A_2^{\alpha _1,\ldots ,\alpha _m}\cap B_1^{k_1} \cap B_2 \cap S_{r/2}^{c} \cap T_{r/2}^{c}$, $A_j\cap B_1^{c} \cap B_2 \cap S_{r/2}^{c} \cap T_{r/2}$ and on $A_j\cap B_1^{k_1} \cap B_2 \cap S_{r/2}^{c} \cap T_{r/2}^{c}$ $(j=3,\ldots ,d-1,k_0=0,1)$ can be handled similarly.

We estimate the integrals on $A_j\cap B_1 \cap B_2^{c} \cap S_{r/2} \cap T_{r/2}^{c}$ and $A_j\cap B_1 \cap B_2^{k_2} \cap S_{r/2}^{c} \cap T_{r/2}^{c}$ $(j=1,\ldots ,d-1,k_0=0,1)$ with the integrals on $A_j\cap B_1 \cap S_{r/2}$ and $A_j\cap B_1 \cap S_{r/2}^{c}$ and these integrals can be found in Weisz [25]. Here we use the first summand of (3.5).

Next, we integrate on $A_j\cap B_1^{c} \cap B_2^{c} \cap S_{r/2}^{c} \cap T_{r/2}$ and introduce the set

$$\begin{aligned} F:= \{t: (\pi -t_d)/2>t_1-t_d\}= \{t: \pi -t_1>(\pi -t_d)/2\}. \end{aligned}$$

For $j=1$, we use inequality (3.10) to obtain

$$\begin{aligned}&\int _{A_1\cap B_1^{c} \cap B_2^{c} \cap S_{r/2}^{c} \cap T_{r/2} \cap F} \left| f(x-t)-f(x)\right| \left| K_n^{\alpha }(t)\right| \, \mathrm{d}t \nonumber \\&\quad \le C n^{-\alpha } \sum _{(i_l,j_l)_l\in \mathcal {I}(1,\ldots ,d)} \int _{A_1\cap B_1^{c} \cap B_2^{c} \cap S_{r/2}^{c} \cap T_{r/2} \cap F} \left| f(x-t)-f(x)\right| \nonumber \\&\qquad \quad \times (\pi -t_{j_1})^{-1} (\pi -t_{i_1})^{-\alpha } \prod _{l=1}^{d-1}(t_{i_l}-t_{j_l})^{-1} \, \mathrm{d}t \nonumber \\&\quad \le C n^{-\alpha } \sum _{(i_l,j_l)_l\in \mathcal {I}(1,\ldots ,d)} \int _{A_1 \cap B_2^{c} \cap T_{r/2}} \left| f(x-t)-f(x)\right| \\&\qquad \quad \times (\pi -t_{j_1})^{-1-\alpha } \prod _{l=1}^{d-1}(t_{i_l}-t_{j_l})^{-1} \, \mathrm{d}t. \end{aligned}$$

We can integrate as in (4.2) with the only difference that, with respect to $t_{i_2'}$, we consider the integral $\sum _{k_d=0}^{k_1} \int _{t_{j_1}+2^{k_d}/n}^{t_{j_1}+2^{k_d+1}/n}\cdots (t_{i_1}-t_{j_1})^{-1}\,\mathrm{d}t_{i_2'}$. Thus

$$\begin{aligned}&\int _{A_1\cap B_1^{c} \cap B_2^{c} \cap S_{r/2}^{c} \cap T_{r/2} \cap F} \left| f(x-t)-f(x)\right| \left| K_n^{\alpha }(t)\right| \, \mathrm{d}t \nonumber \\&\quad \le C n^{-\alpha }\sum _{(i_l,j_l)_l\in \mathcal {I}(1,\ldots ,d)} \sum _{k_1=3}^{r_0} \sum _{k_2=0}^{k_1} \cdots \sum _{k_{d}=0}^{k_1} \left( \frac{2^{k_1}}{T}\right) ^{-1- \alpha } \prod _{l=2}^{d} \left( \frac{2^{k_l}}{T}\right) ^{-1} \nonumber \\&\qquad \times \int _{P_{2^{k_1}/n,\ldots ,2^{k_{d}}/n}} \left| f(x-t)-f(x)\right| \, \mathrm{d}t \nonumber \\&\le C \sum _{(i_l,j_l)_l\in \mathcal {I}(1,\ldots ,d)} \sum _{k_1=3}^{r_0} \sum _{k_2=0}^{k_1} \cdots \sum _{k_{d}=0}^{k_1} 2^{(\omega - \alpha /d) \left| k\right| } \nonumber \\&\qquad \times 2^{-\omega |k|} \frac{1}{\left| P_{2^{k_1}/n,\ldots ,2^{k_{d}}/n}\right| } \int _{P_{2^{k_1}/n,\ldots ,2^{k_{d}}/n}} \left| f(x-t)-f(x)\right| \, \mathrm{d}t \nonumber \\&\quad \le C \sum _{(i_l,j_l)_l\in \mathcal {I}(1,\ldots ,d)} \sum _{k_1=3}^{r_0} \sum _{k_2=0}^{k_1} \cdots \sum _{k_{d}=0}^{k_1} 2^{(\omega - \alpha /d) \left| k\right| } U_r^\omega f(x)< C\epsilon . \end{aligned}$$

(4.3)

Moreover, on the set $F^{c}$, we have

$$\begin{aligned}&\int _{A_1\cap B_1^{c} \cap B_2^{c} \cap S_{r/2}^{c} \cap T_{r/2} \cap F^{c}} \left| f(x-t)-f(x)\right| \left| K_n^{\alpha }(t)\right| \, \mathrm{d}t \nonumber \\&\quad \le C n^{-\alpha } \sum _{(i_l,j_l)_l\in \mathcal {I}(1,\ldots ,d)} \int _{A_1\cap B_1^{c} \cap B_2^{c} \cap S_{r/2}^{c} \cap T_{r/2} \cap F^{c}} \left| f(x-t)-f(x)\right| \\&\qquad \times (\pi -t_{j_1})^{-2} (\pi -t_{i_1})^{-\alpha } \prod _{l=2}^{d-1}(t_{i_l}-t_{j_l})^{-1} \, \mathrm{d}t \nonumber \\&\quad \le C n^{-\alpha } \sum _{(i_l,j_l)_l\in \mathcal {I}(1,\ldots ,d)} \int _{A_1 \cap B_2^{c} \cap T_{r/2}} \left| f(x-t)-f(x)\right| \\&\qquad \times (\pi -t_{j_1})^{-1-\alpha } (\pi -t_{i_1})^{-1} \prod _{l=2}^{d-1}(t_{i_l}-t_{j_l})^{-1} \, \mathrm{d}t. \end{aligned}$$

We can use the same order as in (4.2) and we compute the integral

$$\begin{aligned} \sum _{k_d=0}^{k_1} \int _{\pi -2^{k_d+1}/n}^{\pi -2^{k_d}/n}\cdots (\pi -t_{i_1})^{-1}\,\mathrm{d}t_{i_2'}. \end{aligned}$$

Similarly to (4.3),

$$\begin{aligned}&\int _{A_1\cap B_1^{c} \cap B_2^{c} \cap S_{r/2}^{c} \cap T_{r/2} \cap F^{c}} \left| f(x-t)-f(x)\right| \left| K_n^{\alpha }(t)\right| \, \mathrm{d}t \nonumber \\&\quad \le C n^{-\alpha }\sum _{(i_l,j_l)_l\in \mathcal {I}(1,\ldots ,d)} \sum _{k_1=3}^{r_0} \sum _{k_2=0}^{k_1} \cdots \sum _{k_{d}=0}^{k_1} \left( \frac{2^{k_1}}{T}\right) ^{-1- \alpha } \prod _{l=2}^{d} \left( \frac{2^{k_l}}{T}\right) ^{-1} \nonumber \\&\qquad \times \int _{P_{2^{k_1}/n,\ldots ,2^{k_{d}}/n}} \left| f(x-t)-f(x)\right| \, \mathrm{d}t \nonumber \\&\quad \le C \sum _{(i_l,j_l)_l\in \mathcal {I}(1,\ldots ,d)} \sum _{k_1=3}^{r_0} \sum _{k_2=0}^{k_1} \cdots \sum _{k_{d}=0}^{k_1} 2^{(\omega - \alpha /d) \left| k\right| } U_r^\omega f(x)< C\epsilon . \end{aligned}$$

On the set $A_j\cap B_1^{c} \cap B_2^{c} \cap S_{r/2}^{c} \cap T_{r/2}$, we use the inequality (3.11) with $m=j-1$. We omit the details because they are similar to those above and to those in [25]. We estimate the integrals on $A_j\cap B_1^{c} \cap B_2^{c} \cap S_{r/2} \cap T_{r/2}^{c}$ with the integrals on $A_j\cap B_1^{c} \cap S_{r/2}$ $(j=1,\ldots ,d)$. The latter integrals can be found in Weisz [25].

Finally, by (3.10),

$$\begin{aligned}&\int _{A_1\cap B_1^{c} \cap B_2^{c} \cap S_{r/2}^{c} \cap T_{r/2}^{c}} \left| f(x-t)-f(x)\right| \left| K_n^{\alpha }(t)\right| \, \mathrm{d}t \nonumber \\&\quad \le C n^{-\alpha } \sum _{(i_l,j_l)_l\in \mathcal {I}(1,\ldots ,d)} \int _{A_1\cap B_1^{c} \cap B_2^{c} \cap S_{r/2}^{c} \cap T_{r/2}^{c}} \left| f(x-t)-f(x)\right| \\&\quad \quad \times t_{i_1}^{-1} t_{j_1}^{-\alpha } \prod _{l=1}^{d-1}(t_{i_l}-t_{j_l})^{-1} 1_{\{t_{j_{d-1}}\le \pi /2\}} \, \mathrm{d}t \nonumber \\&\quad \quad + C n^{-\alpha } \sum _{(i_l,j_l)_l\in \mathcal {I}(1,\ldots ,d)} \int _{A_1\cap B_1^{c} \cap B_2^{c} \cap S_{r/2}^{c} \cap T_{r/2}^{c}} \left| f(x-t)-f(x)\right| \\&\quad \quad \times (\pi -t_{j_1})^{-1} (\pi -t_{i_1})^{-\alpha } \prod _{l=1}^{d-1}(t_{i_l}-t_{j_l})^{-1}1_{\{x_{j_{d-1}}>\pi /2\}} \, \mathrm{d}t \nonumber \\&\quad \le C n^{-\alpha } \sum _{(i_l,j_l)_l\in \mathcal {I}(1,\ldots ,d)} \int _{A_1\cap B_1^{c} \cap S_{r/2}^{c}} \left| f(x-t)-f(x)\right| \\&\quad \quad \times t_{i_1}^{-1} t_{j_1}^{-\alpha } \prod _{l=1}^{d-1}(t_{i_l}-t_{j_l})^{-1} 1_{\{t_{j_{d-1}}\le \pi /2\}} \, \mathrm{d}t \nonumber \\&\quad \quad + C n^{-\alpha } \sum _{(i_l,j_l)_l\in \mathcal {I}(1,\ldots ,d)} \int _{A_1\cap B_2^{c} \cap T_{r/2}^{c}} \left| f(x-t)-f(x)\right| \\&\quad \quad \times (\pi -t_{j_1})^{-1} (\pi -t_{i_1})^{-\alpha } \prod _{l=1}^{d-1}(t_{i_l}-t_{j_l})^{-1}1_{\{x_{j_{d-1}}>\pi /2\}} \, \mathrm{d}t. \end{aligned}$$

These integrals as well as the integral on $A_j\cap B_1^{c} \cap B_2^{c} \cap S_{r/2}^{c} \cap T_{r/2}^{c}$ $(j=1,\ldots ,d)$ can be estimated as above. The details are left to the reader. This completes the proof of the theorem. $\square$

Theorems 1, 2 and (2.1) imply the next corollary, which was shown in Weisz [22].

Corollary 1

If $0<\alpha <\infty$ and $f\in L_1({{\mathbb {T}}}^d)$ is periodic with respect to $\pi$, then

$$\begin{aligned} \lim _{n\rightarrow \infty }\sigma _n^{\alpha } f = f \qquad \text{ a.e. } \end{aligned}$$