1 Introduction

Adhesive-bonded joints are widely accepted as potential substitute to mechanical joints in modern industries (marine, oil, sports, packaging, automotive, electronics, aeronautical, construction and so on) for different applications [1, 2]. The adhesive-bonded joint offers significant technical advantages over conventional joining methods, namely ease of fabrication, uniform stress distribution, design flexibility, reduced structure weight, economical, better fatigue resistance, damage tolerance, excellent surface contours and high strength-to-weight ratio [1,2,3]. Adhesive-bonded composite joints for structural parts are increasingly used in most of the aforementioned applications from the past two decades [1, 4]. In recent years, researchers all around the globe pay much attention to replace the metal parts with the adhesive-bonded fiber-reinforced composite joints [3, 5,6,7]. High specific strength, corrosion resistance, uniform stress distribution, light weight, economical and greater design flexibility characteristics make the potential candidate for replacing the metal parts [3, 6]. The significant benefits of adhesive-bonded joints must be balanced with their associated drawbacks during assembly task [8]. Mechanical joints (i.e., bolts, rivets and fasteners) used in composite structures for assembly operations enable breaking of reinforcing fibers while making a hole. This results in higher stress concentration around the fastener holes which leads to creation of either micro- or macro-damages at the composite laminate and often weakens the strength of the whole structure [3, 8]. Therefore, significant attention is required to study and analyze the failure mechanisms of adhesively bonded composite joints with a focus on damage control.

Critical analysis of interlaminar bonding strength and detailed insight of mechanics of composite laminates are essential for damage control of adhesive-bonded joints [9]. Till date, classical engineering experimental approach (i.e., varying one factor at once and keeping rest at fixed values) and analytical and numerical modeling studies are carried out for the analysis of failure mechanisms of laminates [10,11,12,13,14,15,16,17,18,19,20]. Determining solutions with analytical methods are often difficult due to the requirement of incorporation of material nonlinearity and geometry in analysis [12]. Although mechanical tests can be conducted for such cases and stresses can be estimated, which is often expensive and time-consuming due to many influencing parameters [12], numerical methods such as finite element analysis FEA can estimate the stresses of any complex geometry subjected to tensile load [12]. The effects of adhesive thickness, adherend widths and thickness and scarf angles were studied to know the stress distributions in scarf adhesive single-lap joints using numerical finite element methods [13,14,15]. However, numerical methods often analyze and determine solutions based on many assumptions which are impractical to attain in real experiments. The following few assumptions are discussed in estimating the solutions, viz., finite element analysis such as [21, 22], (1) adhesives behave pure shear state during shear loading (in practical, the adhesive behaves linear at the joint or thickness of adhesives and nonlinear at the lap ends). (2) Maximum adhesive peel stress is also influenced with the assumptions considered such as plane stress or plain strain analysis with or without considering the shear deformation of adherends and so on. Therefore, experimental analysis is more reliant to offer precise analysis and gives detailed insight of failure mechanisms by limiting the models that rely on assumptions. Classical experimental approaches are used to know the performances of bonded structure of composites by considering different variables such as geometrical parameters (fillet, adhesive thickness, overlap length, ply angle, etc.), materials (adhesive and adherend types, and properties), surface treatment, environment (temperature and humidity), loading rate, bonding methods and so on [1, 17, 18, 22,23,24,25]. The major disadvantages of classical experimental approaches are [26, 27] (1) increase in influencing variables increases the number of experiments (i.e., large experimental trials are essential with increase in control variables). (2) Fail to estimate the interaction factor effects and their contribution toward output. (3) Generates sub-optimal solutions. (4) Time-consuming approach, each parameter is analyzed individually. (5) This approach does not derive empirical relations, and hence, predictions cannot be possible. To limit the said disadvantages of above methods, the multivariate statistical methods are of paramount importance for precise analysis and perform optimization.

Design of experiments (DOE) is a statistical technique, wherein the multiple variables are studied simultaneously by conducting minimum experiments which offer precise analysis and derive optimal solutions [27, 28]. Taguchi-based design of experiments is used to study the influence of composite–adhesive interfacial adhesion and the adhesive strength on the performance of carbon fiber-reinforced composite joint strength [29]. Taguchi experimental design is used to study the variables (adhesive toughness and thickness, overlap length, surface preparation and adherend thickness) on the performances of single-lap joint made up of carbon steel [30]. However, the derived predictive equation resulted in a maximum error of 56.2% and greater than 20% error for more than five experiments (out of 12). This error might be due to the output data of failure load collected partly from the finite element analysis rather than experiments. Adhesive thickness resulted in significant influence on the fracture behavior subjected to loading [31]. The effect of adhesive thickness and adhesive types on the single-lap joints are studied using the Taguchi method [32]. High-strength steel is used as adherend material, and FEA analysis is used to detail the insight of lap shear strength. The numerical method offers approximate solutions but requires complex mathematical computations and often difficult to implement and interpret the obtained results by engineers working in industries. The Taguchi method is an excellent tool which can be applied by practice engineers (as it solves the problem with simple computational steps) to analyze and determine the optimal levels for a process. However, the Taguchi method fails to perform prediction (for both single and multiple outputs) without the requirement of practical experiments. Industry personnel are more interested to develop the tools such that the predictions can be done for multiple outputs with simple steps at reduced computation time, effort and cost.

In recent times, the use of artificial neural networks (ANNs) for prediction of output values has increased in research. The experimental works are costlier, time dependent and involves complexity in understanding the response behavior. In order to overcome these experimental difficulties, researchers use various modeling techniques. ANNs is one of the most widely used modeling techniques for predictions. ANNs learn from experimental data possessing inherent characteristics with good generalization capabilities to handle nonlinear behavior of data patterns [33]. ANNs are used to develop mathematical models that could predict the wear behavior of carbon fiber-reinforced epoxy composites [34]. Levenberg–Marquardt (LM) algorithm showed better wear prediction compared to other seven variants of backpropagation algorithms [34]. ANNs predict the failure load of pultruded composite samples for the set of bonding angle, patching type and patching structure [35]. It is important to note that LM algorithm of ANNs outperformed other six algorithms in predicting the failure load of composites. ANNs and multiple linear regression (MLR) models are used to predict the bonding strength of wood for the set of moisture content and assembly time both open and close before the joint preparation [36]. ANNs predict the wood bonding strength of the joints better than the MLR model. Failure load corresponds to single-lap adhesive joints (i.e., adherend: aluminum alloy and adhesive: DP460) is predicted by varying two variables overlap length and width of adherend using ANNs trained with LM algorithm [37]. Note that, although the output data collected with neural networks are capable to predict close to the target values. From the above literature, ANNs with LM algorithm is capable to predict the outputs with good accuracy corresponding to target (i.e., experimental) values. In addition, not much experimental studies are carried out to study the factor effects on the strength of the glass fiber-reinforced composites of adhesive-bonded SLJs.

The present research work is carried out to experimentally study the effects of two input factors, namely adhesive thickness and overlap length on the performance of shear strength and failure of adhesive-bonded SLJs. Taguchi experimental design is used not only to limit the conduction of the large number of practical experiments, but also to perform statistical analysis (i.e., to determine factor effects and optimal levels for shear strength and failure load). Multiple linear regression equations are derived for both the responses (FL and SS) expressed as mathematical function of input variables. ANNs trained with LM algorithm are employed to predict the multiple outputs for the different combinations of adhesive thickness and overlap length. The practicality of usefulness of the developed models (ANNs and Taguchi methods) for adhesive-bonded SLJs is discussed in detail. The frame work of the proposed research work of modeling, and analysis and prediction of adhesive-bonded joint strength are shown in Fig. 1.

Fig. 1
figure 1

Framework adopted for modeling, analysis and prediction of adhesive-bonded joint strength

Full size image

2 Selection of factors, materials and experimentation

2.1 Selection of factors influencing the performance of bonded joints

The strength of the bonded joints or structure is dependent on the appropriate choice of the parameters such as adhesive thickness, overlap length, adherend thickness and surface preparation [1, 2]. Surface preparation of composites is paramount importance and is carried out with 150-grit sand paper that could help to roughen the surface and allow the mixture (gel composed of epoxy resin and hardener) to penetrate deeply into the crevices and pores. The cavities thus formed on the composites during roughening provide a larger surface area, wherein the gel mixture goes deeply inside the adherends (top and bottom) and enable strong chemical reaction that increases the strength of adhesive-bonded joints. The surface roughness of the adherends should not be too high, as it weakens the adherend strengths, since increased surface roughness weakens the interlaminar bonding forces. Therefore, for the present work the surface roughness of the adherends is maintained to a fixed average value of 2 ± 0.1 µm. The adhesive joint strengths are proportional to the overlap length [25]. Increased values of overlap length make the composite stiffer, but beyond the critical value the joint strength remains unaltered or even few times drops [11, 38]. True overlap length is dependent on adhesive thickness for the particular adherends [38]. Increased values of adhesive thickness result in thick bonding lines which create more defects in the form of voids and micro-cracks [1, 2, 18]. The joint strength is influenced mainly by many parameters, and appropriate choice of parameters could result in strong joint [29, 30]. The operating levels of overlap length and the adhesive thickness are selected after conducting some pilot experiments and consulting literatures [11, 12, 18, 20, 29, 30].

2.2 Materials and fabrication

The hand layup method is used to prepare the glass fiber epoxy composite. 250 GSM E-glass fiber is used as the reinforcement material for preparing composites which possess a density of 2.48 g/cm3 supplied by Mactech India Pvt. Ltd, Bengaluru. Epoxy resin [i.e., LAPOX L-12 (3202)] is used as a matrix material to prepare the composites. Triethylenetetramine (K-6) hardener possessing a density of 954 kg/m3 supplied by Atul India Pvt. Ltd is used. Note that, curing has been carried out at room temperature. The viscosity of the hardener is less than that of the epoxy resin. The epoxy resin-to-hardener ratio is maintained at 10:1 during composite preparation. The gel time of a mixture (hardener and epoxy resin) is allowed for 20 min for proper mixing. Thus, the prepared composite laminates are hard pressed to squeeze out the excess mixture and allowed to set for a period of 24 h. The glass fabric–reinforced epoxy composite panels are prepared for a dimension (width × breadth × thickness: 300 × 300 × 3 mm) with the help of hand layup process.

2.3 Specimen preparation

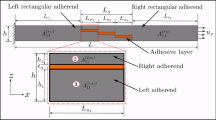
After the composite materials are cured, the specimens for tensile testing are cut by a diamond-tipped cutter to attain the desired dimensions according to ASTM D5868 (refer Fig. 2). The samples are cleaned with acetone to remove the traces of oil or grease, present if any. The 150-grit sand paper is used to prepare the surface of a composite for the desired surface roughness. Later, the inner- and outer-adherend regions of a joint are covered with adhesive mixture (i.e., epoxy resin and hardener). The present work aims at studying the shear strength and failure load behavior of the specimens prepared with three different overlap lengths (15, 25 and 35 mm) and adhesive thickness (0.2, 0.3 and 0.5 mm). In order to maintain the desired dimensions of an adhesive thickness, the steel plate with (0.2, 0.3 and 0.5 mm) is positioned between the adherends placed at the edges of composites. In order to spread the adhesive uniformly across the bonding area, the two adherends are gently pressed that will help to obtain the desired dimension by squeezing out the excess adhesives. Then, the joints are allowed to cure at room temperature about 2 h.

Fig. 2
figure 2

a Single-lap joint specimen geometry, b SLJs with uniform adhesive thickness maintained by steel plates

Full size image

2.4 Tensile test on joint

The specimen for strength testing has been prepared according to ASTM D5868, and the testing has been carried out using universal testing machine (UTM) Instron 3366 of 1 Ton capacity. The specimens are held between the grippers while testing the strength using UTM. The grippers are connected to both movable and fixed arms of the testing device. During testing, the grippers are aligned effectively with the load assigned. The tensile loading test was performed at the controlled rate of 13 mm/min for each of the joints, as per the ASTM standard D5868 for testing of FRP-bonded joints. As reported by many researchers, rate of loading will also influence the load bearing capacity of the joint. In the experimental trials, the specimen elongates parallel to the direction of applied load. The load is utilized by effectively gripping reverse ends of the specimen as well as paralleling it aside. Failure load as well as deflection of the specimens is determined by pulling the specimens at their ends. The failure position is of great interest, and it is normally called the breaking load or failure load.

3 The Taguchi procedure

Dr. Genechi Taguchi introduced the parametric design concept for the design of parameter levels and to develop the correlations toward excellence in characteristics with least variations. The Taguchi method not only minimizes the experimental trials, but also details the insight of influencing variables on different responses. Compared to classical engineering experimental approach, The Taguchi method reveals precisely the interplay between the parameters on the responses. In this study, there are two factors operating at three levels, which influence the strength of adhesively bonded composite joints, and hence, L9 orthogonal array experimental trials are used for planning the experiments, analysis and determine optimal levels for a process. Table 1 provides the details of input variables (adhesive thickness and overlap length) and their operating levels. Table 2 shows the experimental design of L9 orthogonal array.

Table 1 Influencing factors and levels of adhesive bonding process
Full size table
Table 2 L9 orthogonal array of input–output details of adhesive-bonded SLJs
Full size table

4 ANN approach

Neural networks (NN) are the simplified models of network of neurons which are naturally available in our biological nervous system (i.e., animal brain). Neural networks contain the large number of interconnected assemblies of processing element referred as neurons. The human brain consists of 1011 neurons, wherein each neuron can connect up to 20 × 104 neurons and approximately 103 to 104 connections are available. The neurons are arranged in a connected pattern with weights to form a layer, which refers to network architecture. In neural networks, the weights act as a connecting strength which carries the information about the input signal [33]. The performance of neural networks is dependent on the appropriate choice of hidden neurons and training the algorithm employed [39,40,41,42,43].

4.1 Levenberg–Marquardt algorithm

Kenneth Levenberg and Donald Marquardt are credited for the development of LM algorithm [44]. LM algorithm was developed to limit the disadvantages of error-backpropagation algorithm, namely slow convergence and getting trapped at local solutions. Note that, error-backpropagation algorithm possesses excellent generalization capability from the data patterns during network training. Gaussian–Newton method speeds up the training process when error-backpropagation algorithm trapped at local minima. LM algorithm combines the desirable features of error-backpropagation algorithm and Gauss–Newton method that offers fast and stable convergence. Training with LM algorithm uses error-backpropagation algorithm where solutions are searched at large area till they get trapped at local minima and switch to Gauss–Newton method, wherein it helps to jump from local minima and speed up the training process toward faster convergence.

LM algorithm training includes the following steps,

  • Step 1 Calculation of Jacobian Matrix.

  • Step 2 Design the training process.

The steps involved in calculation of Jacobian matrix include both forward and backward computations [44],

Forward pass computation involves:

  1. 1.

    Determine the net values (\({\text{net}}_{j}^{1}\)), slope (\(S_{j}^{1}\)) and network outputs (\(Y_{j}^{1}\)) of all the neurons lying in the input (i.e., first) layer [refer Eqs. (1)–(3)].

    $${\text{net}}_{j}^{1} = \sum\limits_{i \, = \, 1}^{ni} {I_{i} \, W_{j, \, i}^{1} + } \, W_{j, \, o}^{1} \,$$
    (1)
    $$Y_{j}^{1} = f_{j}^{1} \left( {{\text{net}}_{j}^{1} } \right)$$
    (2)
    $$S_{j}^{1} = \frac{{\partial f_{j}^{1} \, }}{{\partial {\text{net}}_{j}^{1} }}$$
    (3)

    Terms \(f_{j}^{1}\) refer to the transfer or activation function of jth neuron, \({\text{net}}_{j}^{1}\) be the sum of weighted input units of neuron j, \(W_{j, \, i}^{1}\) be the weighted ith input unit of neuron j, \(W_{j, \, o}^{1}\) refers to bias weight of the neuron j, Ii corresponds to network inputs and j refers to the index neurons lying in the first layer.

  2. 2.

    The neurons output of input layer is treated as the inputs of all neurons lying in the hidden (i.e., second) layer. The calculations correspond to second-layer neurons of net values, slopes and network outputs are done using Eqs. (4)–(6).

    $${\text{net}}_{j}^{2} = \sum\limits_{i \, = \, 1}^{n1} {Y_{i}^{1} \, W_{j, \, i}^{2} + } \, W_{j, \, o}^{2}$$
    (4)
    $$Y_{j}^{2} = f_{j}^{2} \left( {{\text{net}}_{j}^{2} } \right)$$
    (5)
    $$S_{j}^{2} = \frac{{\partial f_{j}^{2} \, }}{{\partial {\text{net}}_{\text{j}}^{ 2} }}$$
    (6)
  3. 3.

    The output (third) layer of the net values, slopes and outputs is computed with the outputs of the second-layer neurons using Eqs. (7)–(9).

    $${\text{net}}_{j}^{3} = \sum\limits_{i \, = \, 1}^{n2} {Y_{i}^{2} \, W_{j, \, i}^{3} + } \, W_{j, \, o}^{3}$$
    (7)
    $$O_{j} = f_{j}^{3} \left( {{\text{net}}_{j}^{3} } \right)$$
    (8)
    $$S_{j}^{3} = \frac{{\partial f_{j}^{3} \, }}{{\partial {\text{net}}_{j}^{3} }}$$
    (9)

    The backward pass computation is performed with the results of forward pass calculations to update and optimize the network weights that could result in minimum error.

  4. 4.

    Determine network error (i.e., difference of neural network predictions of forward pass calculation and target values) at output j and initial slope of output j (refer Eq. 10).

    $${\text{Error}}\;(e) = {\text{target}}\;{\text{output}} - {\text{network}}\;{\text{output}} = d_{j} - O_{j}$$
    (10)
    $$\delta_{j,j}^{3} = {\text{Self-backpropagation }} = \, S_{j}^{3}$$
    (11)
    $$\delta_{j, \, k}^{3} = {\text{Backpropagation}}\;{\text{from}}\;{\text{other}}\;{\text{neurons}}\;{\text{lying}}\;{\text{in}}\;{\text{the}}\;{\text{output}}\;{\text{layer }} = { 0}$$
    (12)
  5. 5.

    To update weights, backpropagate δ from the output layer inputs to the outputs of the hidden layer (refer Eq. 13).

    $$\delta_{j, \, k}^{2} = W_{j, \, k}^{3} \times \delta_{j, \, k}^{3}$$
    (13)

    Term, k, refers to the index of neurons lying in the hidden layer from 1 to n2.

  6. 6.

    To update the slope, backpropagate δ from the outputs to inputs of the hidden layer (refer Eq. 14).

    $$\delta_{j, \, k}^{2} = \delta_{j, \, k}^{2} \times S_{ \, k}^{2}$$
    (14)
  7. 7.

    To update slope, backpropagate δ from the inputs of the hidden layer to input of input layer outputs (refer Eq. 15).

    $$\delta_{j, \, k}^{1} = \delta_{j, \, k}^{1} \times S_{ \, k}^{1}$$
    (15)

    Term k refers to the index of neurons lying in the hidden layer, from 1 to n1.

    Step 4–7 is repeated for computation of other outputs.

  8. 8.

    The Jacobian Matrix (J) is obtained by calculating the forward and backward computation which generates the array of whole δ and y matrix for the given inputs.

4.2 Training process design

The training process is designed with the defined rule of LM algorithm, and the computation of Jacobian matrix is carried out using Eq. (16). During training, if the resulted error of the current iteration is smaller than the previous error, then it works with quadratic approximation and the μ (i.e., combination coefficient) value could be changed to low values that reduce the effect of the gradient descent method (error-backpropagation). Contrary, if current iteration resulted in higher error values than the previous one, then it follows the error-backpropagation algorithm till to obtain the appropriate curvature for quadratic approximation and for this situation, μ should be increased. Note that, if µ value is very small (say near to zero) then the Gauss–Newton method is used [refer Eq. (17)]. However, if µ value is very large then the error-backpropagation method is used [refer Eq. (18)], where α (learning rate) = 1/µ, \(e_{k}\) be the error vector and N and k refer to the number of weights and iterations, respectively. Note that, the weights are continuously updated till it reaches the set target error.

$$W_{k + 1} = W_{k} - \left( {J_{k}^{T} J_{k} + \mu I} \right)^{ - 1} J_{k} \times e_{k}$$
(16)
$$W_{k + 1} = W_{k} - \left( {J_{k}^{T} J_{k} } \right)^{ - 1} J_{k} \times e_{k}$$
(17)
$$W_{k + 1} = W_{k} - \alpha \times g_{k}$$
(18)
$${\text{Gradient}}\;{\text{vector}}, \, g_{k} = \left[ {\frac{\partial E}{{\partial w_{1} }}\frac{\partial E}{{\partial w_{2} }}\frac{\partial E}{{\partial w_{3} }} - - - - \frac{\partial E}{{\partial w_{N} }}} \right]^{\text{T}}$$
(19)

5 Results and discussion

In this section, the Taguchi experimental results were analyzed by identifying the significant parameters both individual and interaction for failure load and shear strength of the joints using analysis of variance. MLR and NN models are developed for prediction purpose. In addition, the predicted results of failure load and shear strengths of adhesive-bonded joints are tested for the ten random experimental cases by the two developed models (MLR and NN).

5.1 Taguchi method experimental results

The experimental input–output data correspond to adhesive-bonded single-lap composite joints are presented in Table 2. Three replicates are taken for each experimental trials, and the corresponding average values of failure load and shear strengths of adhesive-bonded composite SLJs are presented. Table 2 shows the experimental design of L9 orthogonal array and outputs of the SLJs of composites.

5.2 Tensile test investigation

The tensile test determines the behavior of material subjected to tension with the application of load. During tensile tests, the specimens (adhesive-bonded GFRP composite-lap joints) held in a gripper such that effective loading is carried out in a controlled manner till the joints undergo fracture to determine the failure load and shear strength of SLJs of composite.

5.2.1 The plots of load versus displacement for single-lap joints (SLJ’s)

Figure 3a–c shows the load versus displacement plots for different overlap lengths (15, 25 and 35 mm) at constant adhesive thickness of 0.2, 0.3 and 0.5 mm, respectively. The minimum and maximum failure load occurred for the overlap length is found equal to 15 mm and 35 mm, respectively. The results showed that the deformation at the joint increases linearly till the failure of adhesive-bonded lap joints. Increase in overlap length of adhesive-bonded composite joint from 15 to 35 mm results in increase in failure load in the ranges between 3250.2 and 6096.1 N, 2879.8 and 5813.16 N, and 2250.6 and 4036.88 N for 0.2, 0.3 and 0.5 mm of adhesive thickness, respectively. This occurs due to increase in bonding area. It is worth mentioning that increased values of overlap length from 15 to 35 mm resulted in 1.87, 2.02 and 1.79 times increment to that of failure load for 0.2, 0.3 and 0.5 mm of adhesive thickness, respectively. This could be attributed to the substantial increase in adhesive bonding area which tends to receive increased proportion of total load carried out at the composite joints.

Fig. 3
figure 3

Load versus displacement plot for different overlap lengths (15, 25 and 35 mm) at a constant adhesive thickness: a 0.2 mm, b 0.3 mm and c 0.5 mm

Full size image

5.3 Multiple regression analysis

Multiple linear regression technique is applied to determine the relationship between the adhesive-bonded joint strengths and the two influencing variables such as overlap length and adhesive thickness. The experimental input–output data of adhesive-bonded joints presented in Table 2 were used to derive the response equations and determine significant contributions. The derived response equation for failure load and shear strength expressed as a mathematical function of input variables are presented in Eqs. (20) and (21).

$${\text{FL}} = 1485 + 190.2A - 2016B - 192AB$$
(20)
$${\text{SS}} = 19.5 + 2.497A - 26.4B - 2.53AB$$
(21)

5.4 Analysis of variance (ANOVA)

The Taguchi method alone could not detail the factor effects and optimal levels on any process. Therefore, Ronald A Fisher, a British statistician, was credited for the development of ANOVA. In general, ANOVA is performed to interpret the data collected from a series of experiments and determine optimal parameter levels for a process. In the present work, ANOVA is used to determine the significance of both individual factors such as overlap length, adhesive thickness and their interaction effects on the responses (FL and SS). Minitab software of ANOVA module is used to know the factor effects on responses. The ANOVA test results for failure load and shear strength are presented in Table 3.

Table 3 ANOVA results of adhesive-bonded composite SLJs for the responses (FL and SS)
Full size table

ANOVA table consists of degrees of freedom (DF), adjusted sum of squares (Adj. SS) and mean square (Adj. MS), Fisher (F value) and preset confidence (P value) value. The significance of parameters is determined for the preset confidence level of 95% (i.e., P value < 0.05). For the responses (i.e., FL and SS), both the main effect factors (i.e., overlap length A and adhesive thickness B) are found to be significant as their corresponding P values are less than 0.05. However, the interplay of adhesive thickness and overlap length are not significant and also inclusion of the term AB does not contribute much toward both the responses (refer Table 3). Figure 4a, b shows the surface plots of responses (FL and SS) with overlap length and adhesive thickness. Increase in overlap length tends to increase both FL and SS, whereas decreasing trend of FL and SS was observed with increased values of adhesive thickness. This might be due to the fact that as the overlap length increases, the bonding area improves that helps to sustain higher loads, whereas increase in adhesive thickness results in thick bonding lines coupled with the formation of voids and micro-cracks. It is also clear from the surface plots that higher and lower values correspond to overlap length and adhesive thickness could produce higher failure load and shear strength (refer Fig. 4a, b). The results of the surface plots are in good agreement with the statistical values correspond to optimal levels determined for FL and SS (refer Table 4). From Fig. 4a, b, it is clearly showed that the impact of overlap length is more compared to that of adhesive thickness for both the responses. Table 4 shows the statistical values of impact (rank) of adhesive thickness and overlap length and the optimal levels for FL and SS.

Fig. 4
figure 4

Surface plots of responses: a FL with overlap length and adhesive thickness and b SS with overlap length and adhesive thickness

Full size image
Table 4 Optimal parameter levels for failure load and shear strength
Full size table

The models developed for failure load and shear strength of adhesive-bonded single-lap composite joints are tested for statistical adequacy by estimating multiple correlation coefficients. For all terms (significant and insignificant), the multiple correlation coefficient values correspond to failure load and shear strengths are found equal to 0.9217 and 0.9223, respectively. The correlation coefficient values with inclusion of all terms are found close to unity, indicating that the models are statistically capable for their practical usefulness. Noteworthy that correlation coefficient values by neglecting noncontributory terms [i.e., AB shown in Table 5 and Eqs. (20) and (21)] resulted in 0.8747 for FL and 0.8754 for SS. It is important to note that removing insignificant terms from the regression equations not only reduces the prediction accuracy (because the calculated F values generate more than that of Table F values), but also results in imprecise input–output relationships. From the above discussions, the models developed for both responses are statistically adequate and can be used for practical usefulness in industries.

Table 5 Coefficient of multiple correlations, significance and nonsignificant terms for FL and shear Strength
Full size table

5.5 Artificial neural networks

ANNs learn with examples (input–output data) and predict the performances based on their learned or training experiences. Therefore, collecting an appropriate set of quality data and quantity of training data is of paramount importance. Neural networks train with low data (say less than 20) may find it difficult to estimate the fitting parameters, and even if does, they are not mathematically logical due to number of network connections which found to be greater than that of the data available for training [45]. The mathematically derived response equations through experiments were used to generate artificially [random sets of 91 inputs are generated and outputs are predicted with Eqs. (20) and (21)] huge input–output data for training. Note that, the training data consist of both artificial and experimental data whose value corresponds to 91 and 9, respectively.

LM algorithm is used to train the three-layered neural network architecture developed for prediction of failure load and shear strength. Two neurons in the input layer represent the overlap length and adhesive thickness, whereas failure load and shear strengths are treated as output neurons lying in the output layer. The hidden neurons lying in their respective layer is determined after conducting many trials with a goal corresponding to minimum error or better correlation coefficient (i.e., R value). There exists a perfect correlation between experimental and predicted values when R = 1, while R = 0 indicates there is no correlation. A total of 100 input–output data sets are treated with 80% for training and 20% for validation. A set of total ten experimental cases are used for testing the trained neural network (refer Table 6). To avoid numerical overflows, the training and testing data were normalized between the ranges of 0 and 1. Training has been carried out to optimize the network architecture (i.e., weights and hidden neurons). During training, the activation functions correspond to the hidden layer was log-sigmoid function, whereas linear activation function is used for both input and output layers. After many trials (i.e., different neurons varied in the hidden layer from 3 to 10), the neurons of hidden layer are kept fixed to 6, as their corresponding R value was found better than that of other neurons tested for hidden layer. Therefore, the final network architecture corresponds to better correlation coefficient was found equal to 2–6–2 (i.e., neurons of input–hidden–output layers) and obtained at 45 iterations.

Table 6 Input–output data of ten random experimental cases
Full size table

Regression plots give the relationships between network outputs and the defined targets, which are used to validate the performance of NN. Figure 5 show the regression plots correspond to training and validation of neural networks. The R value is 0.99995 for training and 0.9998 for validation, which indicates the values of experimental outputs (i.e., FL and SS) are close to the target values. Since the R values of network training and validation are close to unity, the models are ideal to make predictions for random test (i.e., experimental) cases.

Fig. 5
figure 5

Regression plots correspond to optimal network architecture (2–6–2) for training and testing

Full size image

5.5.1 Summary results of MLR and NN predictions

NN and MLR models are examined for the prediction performances of adhesive-bonded joints (i.e., FL and SS) of composites. The prediction performances are evaluated with two indices such as mean absolute percent error (MAPE) and correlation coefficients (R).

Figure 6a–d shows the model comparison for failure load and shear strength predictions with experimental failure load and shear strengths for ten experimental cases. Note that, the experimental cases generated at random are to know their practical usefulness of the developed models. Although R values obtained for NN model in predicting the experimental cases are found close to unity, they are slightly inferior compared to that of training and validation (refer Figs. 5 and 6). This occurs because the experimental cases used for testing are different from those data used for training and validation for efficient model development. The R values of NN are found better than MLR in predicting both the responses (i.e., FL and SS). The percent deviation in predictions of FL is found to vary in the ranges of − 2.74 to + 1.75% for NN, and − 4.20 to + 1.59% for MLR, respectively (refer Fig. 7a). For shear strength, the range of percent deviation in predictions is found to be − 8.72 to + 3.29% for NN, and − 9.31 to + 4.31% for MLR, respectively (Fig. 7b). The FL and SS data points are predicted on both positive and negative sides from the reference zero line and follow the identical path for both the models. Note that, most of the data points representing the percent deviations are close to reference zero line for NN model compared to MLR (refer Fig. 7). The MAPE obtained for FL is 1.5% for NN, 1.69% for MLR, and for SS is 3.03% for NN, and 4.56% for MLR, respectively. Considering both the outputs, the average absolute percent deviation in predictions is found equal to 2.27% for NN and 3.12% for MLR. Neural network predictions are found better, might be due to the inherent ability to capture the process nonlinearity. Simultaneous prediction of multiple outputs by the neural networks is useful for online monitoring of a process.

Fig. 6
figure 6

Experimental- versus model-predicted values: a FL of NN model, b FL of MLR model, c SS of NN model and d SS of MLR model

Full size image
Fig. 7
figure 7

Percent deviation in prediction of two models for different responses: a failure load and b shear strength

Full size image

6 Conclusion

Systematic experimental analysis for the development of predictive models and determining optimal levels are carried out for adhesive-bonded joining process to limit the several theories used in past, which are developed based on assumptions. The following conclusions are drawn as discussed below,

  1. 1.

    The Taguchi method is used to collect the experimental input–output data correspond to adhesive-bonded single-lap composite joints. Overlap length and adhesive thickness are statistically significant, whereas the corresponding interaction terms are statistically insignificant. The overlap length contributions are more compared to adhesive thickness for both the FL and SS. Coefficient of multiple correlation is found equal to 0.9217 for FL and 0.9223 for SS, respectively. A3B1 is the optimal levels for adhesive-bonded single-lap composite joints, which results in high values of 6096.1 N for FL and 80 MPa for SS.

  2. 2.

    As the overlap length increases from 15 to 35 mm, it results in 1.87, 2.02 and 1.79 times increment in failure load for the constant adhesive thickness of 0.2, 0.3 and 0.5 mm. This occurs because increased proportion of adhesive bonding area helps to sustain maximum total load at the composite joints.

  3. 3.

    LM algorithm-trained artificial neural networks with 100 data sets (experimental and artificially generated data with response equations) resulted with R value close to 1 for both training and validation. Ten experimental cases were used to test the prediction accuracy of adhesive-bonded composite single-lap joint strengths (i.e., FL and SS) resulted with the mean absolute percent error found equal to 2.27% for NN, and 3.12% for MLR, respectively. Multiple output predictions of NN not only capture the dependency among the outputs, but also are used for online monitoring of adhesive-bonded joints strengths.

  4. 4.

    The models (Taguchi, NN and MLR) developed for adhesive-bonded single-lap composite joints are capable for predictions and determine optimal levels that could result in higher strengths accurately. Therefore, the developed models can readily be used in industries for adhesive bonding joining process.