Modeling the Response of Tensile Steel Bars by Means of Incremental Energy Minimization

Abstract

A non-local variational model for the evolution of plastic deformation and fracture in tensile bars is proposed. The model is based on an energy functional, sum of an elastic bulk energy, a non-convex dissipative inelastic energy, and a quadratic non-local gradient term, as in (Del Piero et al. in J. Mech. Mater. Struct. 8(2–4):109–151, 2013). The non-local energy is enriched, by assuming a dependence on both the inelastic deformation and its gradient, in order to improve the description of fracture, and bars with varying cross-section are considered, to accurately reproduce the geometry of samples which are commonly used in tensile tests. The evolution of the deformation is described by a two-field incremental minimization problem, where the longitudinal displacement and the plastic part of the deformation are assumed as independent variables. The problem is discretized by finite elements, and the resulting sequence of constrained quadratic programming problems is solved numerically.

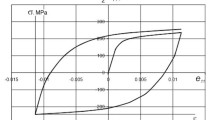
Different simulations are proposed, reproducing the results of experiments on smooth and notched bone-shaped steel samples. The numerical tests provide accurate response curves, and they capture the distinct phases of the evolution observed in experiments: from the initial yielding phase, in which inelastic deformations form, and propagate as slow plastic waves, to the final rupture, which constitutes the ending stage of a strain-localization process.

Appendices

Appendix A: Finite Elements Discretization

In the finite element discretization, two-points linear elements are considered for γ, and three-points quadratic elements for u. This allows to approximate both u′ and γ with linear functions, within each element. In the arbitrary e-th element (x _e ,x _e+1), the approximated solution is

$$\begin{aligned} u_t(x)=\boldsymbol {\varphi}^e(x)\cdot{ \mathbf{u}}^e_t,\qquad\gamma _t(x)=\boldsymbol { \psi}^e(x)\cdot{ \boldsymbol {\gamma}}^e_t, \end{aligned}$$

(56)

where $\mathbf{u}^{e}_{t}=[u_{t}(x_{e}),u_{t}((x_{e}+x_{e+1})/2),u_{t}(x_{e+1})]^{T}$, and $\boldsymbol {\gamma}^{e}_{t}=[\gamma_{t}(x_{e}),\gamma_{t}(x_{e+1})]^{T}$ are the nodal vectors of displacement and inelastic deformation, respectively, and $\boldsymbol {\varphi}^{e}(x)=[\varphi^{e}_{1}(x),\varphi^{e}_{2}(x),\varphi ^{e}_{3}(x)]^{T}$ and $\boldsymbol {\psi}^{e}(x)=[\psi^{e}_{1}(x),\psi^{e}_{2}(x)]^{T}$ are the vectors of the quadratic and linear shape functions, respectively. Substituting (56) in the functional (21), restricted to the e-th element, we obtain the discrete quadratic form

$$\begin{aligned} \mathcal{F}^e\bigl(u_t, \gamma_t; \dot{\mathbf{u}}_t^e, \dot{\boldsymbol { \gamma }}_t^e\bigr)=\frac{1}{2}\tau^2 \left [ \begin{array}{c@{\quad }c} {\mathbf{H}}^e_{11} & \mathbf{H}^e_{12} \\ \mathbf{H}_{12}^{eT} & \mathbf{H}^e_{22}(\gamma_t) \end{array} \right ]\left [ \begin{array}{c} \dot{\mathbf{u}}^e \\ \dot{\boldsymbol {\gamma}}^e \end{array} \right ]\cdot \left [ \begin{array}{c} \dot{\mathbf{u}}^e \\ \dot{\boldsymbol {\gamma}}^e \end{array} \right ]+ \tau \left [ \begin{array}{c} {\mathbf{f}}_1^e \\ \mathbf{f}_2^e(u_t,\gamma_t) \end{array} \right ]\cdot \left [ \begin{array}{c} \dot{\mathbf{u}}^e \\ \dot{\boldsymbol {\gamma}}^e \end{array} \right ], \end{aligned}$$

(57)

where $u_{t}=\boldsymbol {\varphi}^{e}\cdot{\mathbf{u}}_{t}^{e}$ and $\gamma =\boldsymbol {\psi}^{e}\cdot{ \boldsymbol {\gamma}}_{t}^{e}$, and

$$\begin{aligned} &\mathbf{H}^e_{11}=\int_{x_e}^{x_{e+1}}AE \boldsymbol {\varphi}'^e\otimes{ \boldsymbol {\varphi}}'^e \,dx,\qquad \mathbf{H}^e_{12}={\mathbf{H}^e_{21}}^T=- \int_{x_e}^{x_{e+1}}AE\boldsymbol {\varphi}'^e \otimes{ \boldsymbol {\psi}}^e\,dx, \\ &\begin{aligned}[b] {\mathbf{H}}^e_{22}(\gamma_t)&= \displaystyle \int_{x_e}^{x_{e+1}}A \biggl[ \biggl(E+\theta''+ \frac{1}{2}\alpha_t'' \gamma_t'^2 \biggr)\boldsymbol {\psi }^e\otimes{ \boldsymbol {\psi}}^e\\ &\quad {}+ \displaystyle \alpha_t\boldsymbol {\psi}'^e\otimes{ \boldsymbol { \psi}}'^e+ 2\alpha_t' \gamma_t'\,\mathrm{sym}\bigl(\boldsymbol {\psi}^e \otimes{ \boldsymbol {\psi }}'^e\bigr) \biggr]\,dx, \end{aligned} \\ &{\mathbf{f}}^e_1=\int _{x_e}^{x_{e+1}}EA\boldsymbol {\varphi }'^e \,dx, \\ &\mathbf{f}^e_2(u_t, \gamma_t)=\int_{x_e}^{x_{e+1}}A \biggl[ \biggl( \theta _t'-E\bigl(u_t'- \gamma_t\bigr)+\frac{1}{2}\alpha_t' \gamma_t'^2 \biggr)\boldsymbol {\psi }^e+\alpha_t\gamma_t'{\boldsymbol {\psi}}'^e \biggr]\,dx. \end{aligned}$$

(58)

Integrals are evaluated by means of two-point Gaussian quadrature. The dimension of the discretized problem is 3n _e +2, with n _e the number of elements.

Appendix B: Coefficients c _h and c _s of Formula (46)

Case θ″>0.

$$\begin{aligned} c_h(kl,hl)=\frac{(kl)^2}{(kl)^2+(hl)^2 (1-\frac{2}{kl}\tanh \frac {kl}{2} )},\qquad c_s(kl,hl)= \frac{(kl)^2}{(kl)^2+(hl)^2}. \end{aligned}$$

(59)

Case θ″=0.

$$\begin{aligned} c_h(kl,hl)=\frac{12}{12+(hl)^2},\qquad c_s(kl,hl)=0. \end{aligned}$$

(60)

Case θ″<0.

$$\begin{aligned} \begin{aligned}[c] &c_h(kl,hl)= \left \{ \begin{array}{l@{\quad }l} \frac{(kl)^2}{(kl)^2-(hl)^2 (1-\frac{2}{kl}\tan \frac {kl}{2} )}, & \mbox{if }kl\leq2\pi; \\ \frac{(kl)^2}{(kl)^2-\frac{2\pi}{kl}(hl)^2}, & \mbox{if }kl> 2\pi; \end{array} \right . \\ &c_s(kl,hl)= \left \{ \begin{array}{l@{\quad }l} \frac{(kl)^2}{(kl)^2-(hl)^2},& \mbox{if } kl\leq\pi; \\ \frac{(kl)^2}{(kl)^2-\frac{\pi}{kl}(hl)^2}, & \mbox{if }kl> \pi. \end{array} \right . \end{aligned} \end{aligned}$$

(61)