Largest nearest-neighbour link and connectivity threshold in a polytopal random sample

Abstract

Let $X_1,X_2, \ldots$ be independent identically distributed random points in a convex polytopal domain $A \subset \mathbb {R}^d$. Define the largest nearest-neighbour link $L_n$ to be the smallest r such that every point of $\mathscr {X}_n:=\{X_1,\ldots ,X_n\}$ has another such point within distance r. We obtain a strong law of large numbers for $L_n$ in the large-n limit. A related threshold, the connectivity threshold $M_n$, is the smallest r such that the random geometric graph $G(\mathscr {X}_n, r)$ is connected (so $L_n \le M_n$). We show that as $n \rightarrow \infty$, almost surely $nL_n^d/\log n$ tends to a limit that depends on the geometry of A, and $nM_n^d/\log n$ tends to the same limit. We derive these results via asymptotic lower bounds for $L_n$ and upper bounds for $M_n$ that are applicable in a larger class of metric spaces satisfying certain regularity conditions.

1 Introduction

This paper is primarily concerned with the connectivity threshold and largest nearest-neighbour link for a random sample $\mathscr {X}_n$ of n points in a specified compact region A in a d-dimensional Euclidean space.

The connectivity threshold, here denoted $M_n$, is defined to be the smallest r such that the random geometric graph $G(\mathscr {X}_n,r)$ is connected. For any finite $\mathscr {X}\subset \mathbb {R}^d$ the graph $G(\mathscr {X},r)$ is defined to have vertex set $\mathscr {X}$ with edges between those pairs of vertices x, y such that $\Vert x - y\Vert \le r$, where $\Vert \cdot \Vert$ is the Euclidean norm. More generally, for $k\in \mathbb {N}$, the k-connectivity threshold $M_{n,k}$ is the smallest r such that $G(\mathscr {X}_n,r)$ is k-connected (see the definition in Sect. 2).

The largest nearest-neighbour link, here denoted $L_n$, is defined to be the smallest r such that every vertex in $G(\mathscr {X}_n,r)$ has degree at least 1.

More generally, for $k \in \mathbb {N}$ with $k < n$, the largest k-nearest neighbour link $L_{n,k}$ is the smallest r such that every vertex in $G(\mathscr {X}_n,r)$ has degree at least k. These thresholds are random variables, because the locations of the centres are random. We investigate their probabilistic behaviour as n becomes large.

We shall derive strong laws of large numbers showing that $nL_{n,k}^d/\log n$ converges almost surely (as $n \rightarrow \infty$) to a finite positive limit, and establishing the value of the limit. Moreover we show that $nM_{n,k}^d/\log n$ converges to the same limit. These strong laws carry over to more general cases where k may vary with n, and the distribution of points may be non-uniform. We give results of this type for A a convex polytope.

Previous results of this type (both for $L_{n,k}$ and for $M_{n,k}$) were obtained for A having a smooth boundary, and for A a d-dimensional hypercube; see Penrose (2003). It is perhaps not obvious from the earlier results, however, how the limiting constant depends on the geometry of $\partial A$, the topological boundary of A, for general polytopal A, which is quite subtle.

It turns out, for example, that when $d=3$ and the points are uniformly distributed over a polyhedron, the limiting behaviour of $L_n$ is determined by the angle of the sharpest edge if this angle is less than $\pi /2$ (the angle of an edge is the angle between the two faces meeting at that edge). We believe (but do not formally prove here) that if this angle exceeds $\pi /2$ then the point of $\mathscr {X}_n$ furthest from the rest of $\mathscr {X}_n$ is asymptotically uniformly distributed over $\partial A$, but if this angle is less than $\pi /2$ the location of this point is asymptotically uniformly distributed over the union of those edges which are sharpest.

Our motivation for this study is twofold. First, understanding the connectivity threshold in dimension two is vital in telecommunications, for example, in 5 G wireless network design, with the nodes of $\mathscr {X}_n$ representing mobile transceivers [see for example Baccelli and Błaszczyszyn (2009)]. Second, detecting connectivity is a fundamental step for detecting all other higher-dimensional topological features in modern topological data analysis (TDA), where the dimension of the ambient space may be very high. See Bobrowski (2022), Bobrowski and Kahle (2018) for discussion of issues related to the one considered here, in relation to TDA. General motivation for considering random geometric graphs is discussed in Penrose (2003).

While our main results are presented (in Sect. 2) in the concrete setting of a polytopal sample in $\mathbb {R}^d$, our proofs proceed via general lower and upper bounds (Propositions 3.3 and 3.7) that are presented in the more general setting of a random sample of points in a metric space satisfying certain regularity conditions. This could be useful in possible future work dealing with similar problems for random samples in, for example, a Riemannian manifold with boundary, a setting of importance in TDA.

Mathematically, one contribution of this paper is to extend the range of problems amenable to the technique of granulation, whereby $\mathbb {R}^d$ is discretized into cubes of equal side length that is a small constant times $r_n$, where $(r_n)$ is a sequence of proposed upper or lower bounds for $M_n$ or $L_n$. We use different sizes of cubes for different kinds of regions within A (corresponding to the various faces of A). This technique was already used to obtain SLLNs for the coverage threshold in Penrose (2023) and is here also used for the largest nearest-neighbour link and connectivity threshold. It enables us to reduce the problems of understanding these thresholds to determining the asymptotic covering and packing numbers of different regions within that domain of interest, by small balls, given knowledge about how the measure of the balls decays with the radius (this rate of decay depends on on how cornered the region is).

We shall use this method to provide asymptotic lower bounds for $L_n$ in Proposition 3.3 and upper bounds for $M_n$ in Proposition 3.7, both of which are stated not only for $\mathbb {R}^d$ but in a more general class of metric spaces having a ‘measure doubling’ property (not required for the lower bounds). These asymptotic lower and upper bounds turn out to be sharp in the special case of a polytope that we are interested in here.

2 Statement of results

Throughout this paper, we work within the following mathematical framework. Let $d \in \mathbb {N}$. Suppose we have the following ingredients:

• A finite compact convex polytope $A \subset \mathbb {R}^d$ (i.e., one with finitely many faces).

• A Borel probability measure $\mu$ on $\mathbb {R}^d$ with probability density function f, supported by A (so $f \equiv 0$ on $\mathbb {R}^d \setminus A$).

• On a common probability space $(\mathbb {S},{{\mathscr {F}}},\mathbb {P})$, a sequence $X_1,X_2,\ldots$ of independent identically distributed random d-vectors with common probability distribution $\mu$.

For $n \in \mathbb {N}$, let $\mathscr {X}_n:= \{X_1,\ldots ,X_n\}$ (we use $:=$ to denote definition). This is the point process that concerns us here.

For $x \in \mathbb {R}^d$ and $r>0$ set $B(x,r):= \{y \in \mathbb {R}^d:\Vert y-x\Vert \le r\}$. Let $A^o$ denote the interior of A, and for $r>0$, let $A^{(r)}:=\{ x \in A: B(x,r) \subset A^o\}$, the ‘r-interior’ of A.

For any point set $\mathscr {X}\subset \mathbb {R}^d$ and any $D \subset \mathbb {R}^d$ we write $\mathscr {X}(D)$ for the number of points of $\mathscr {X}$ in D, and we use below the convention $\inf (\varnothing ):= +\infty$.

Given $n, k \in \mathbb {N}$, and $t \in (0,\infty )$, define the largest k-nearest neighbour link $L_{n,k}$ by

$$\begin{aligned} L_{n,k}: = \inf ( \left\{ r >0: \mathscr {X}_n (B(x,r)) \ge k+1 ~~~~ \forall x \in \mathscr {X}_n \right\} ). \end{aligned}$$

(2.1)

Set $L_n: = L_{n,1}$. Then $L_n$ is the largest nearest-neighbour link.

We are chiefly interested in the asymptotic behaviour of $L_n$ for large n. More generally, we consider $L_{n,k}$ where k may vary with n.

Let $\theta _d:= \pi ^{d/2}/\Gamma (1 + d/2)$, the volume of the unit ball in $\mathbb {R}^d$. Given $x,y \in \mathbb {R}^d$, we denote by [x, y] the line segment from x to y, that is, the convex hull of the set $\{x,y\}$.

Given $m \in \mathbb {N}$ and functions $g: \mathbb {N}\cap [m,\infty ) \rightarrow \mathbb {R}$ and $h: \mathbb {N}\cap [m,\infty ) \rightarrow (0,\infty )$, we write $g(n) = O(h(n))$ as $n \rightarrow \infty$, if $\limsup _{n \rightarrow \infty }|g(n)|/h(n) < \infty$.

We write $g(n) = \Omega (h(n))$ as $n \rightarrow \infty$ if $\liminf _{n \rightarrow \infty } (g(n)/h(n) ) >0$.

Given $s >0$ and functions $g: (0,s) \rightarrow \mathbb {R}$ and $h:(0,s) \rightarrow (0,\infty )$, we write $g(r) = O(h(r))$ as $r \downarrow 0$ if $\limsup _{r \downarrow 0} |g(r) |/h(r) < \infty$. We write $g(r) = \Omega (h(r))$ as $r \downarrow 0$, if $\liminf _{r \downarrow 0} (g(r) /h(r)) >0$.

Throughout this section, assume we are given a constant $\beta \in [0,\infty ]$ and a sequence $k: \mathbb {N}\rightarrow \mathbb {N}$ with

$$\begin{aligned} \lim _{n \rightarrow \infty } \left( k(n)/\log n \right) = \beta ; ~~~~~ \lim _{n \rightarrow \infty } \left( k(n)/n \right) = 0. \end{aligned}$$

(2.2)

We make use of the following notation throughout:

$$\begin{aligned} f_0:= & {} \mathrm{ess~inf}_{x \in A} f(x); ~~~~~~~ f_1:= \inf _{x \in \partial A} f(x); \end{aligned}$$

(2.3)

$$\begin{aligned} H(t):= & {} {\left\{ \begin{array}{ll} 1-t + t \log t, ~~~ &{} \textrm{if} ~ t >0 \\ 1, &{} \textrm{if} ~ t =0. \end{array}\right. } \end{aligned}$$

(2.4)

Observe that $-H(\cdot )$ is unimodal with a maximum value of 0 at $t=1$. Given $a \in [0,\infty )$, we define the function $\hat{H}_a: [0,\infty ) \rightarrow [a,\infty )$ by

$$\begin{aligned} y = \hat{H}_a(x) \Longleftrightarrow y H(a/y) =x,~ y \ge a, \end{aligned}$$

with $\hat{H}_0(0):=0$. Note that $\hat{H}_a(x)$ is increasing in x, and that $\hat{H}_0(x)=x$ and $\hat{H}_a(0)=a$.

Throughout this paper, the phrase ‘almost surely’ or ‘a.s.’ means ‘except on a set of $\mathbb {P}$-measure zero’. For $n \in \mathbb {N}$, we use [n] to denote $\{1,2,\ldots ,n\}$. We write $f|_A$ for the restriction of f to A.

Let $\Phi (A)$ denote the set of all faces of the polytope A (of all dimensions up to $d-1$). Also, let $\Phi ^*(A):= \Phi (A) \cup \{A\}$; it is sometimes useful for us to think of A itself as a face, of dimension d.

Given a face $\varphi \in \Phi ^*(A)$, denote the dimension of this face by $D(\varphi )$. Then $0 \le D(\varphi ) \le d$, and $\varphi$ is a $D(\varphi )$-dimensional polytope embedded in $\mathbb {R}^d$. Let $\varphi ^o$ denote the relative interior of $\varphi$, and set $\partial \varphi := \varphi \setminus \varphi ^o$ (if $D(\varphi )=0$ we take $\varphi ^o:= \varphi$). If $D(\varphi ) < d$ then set $f_\varphi := \inf _{x \in \varphi }f(x)$, and if $\varphi =A$ then set $f_\varphi := f_0$.

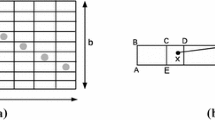
Given $\varphi$, we claim (and prove later as Lemma 3.1, and illustrate in Fig. 1) that there is a unique cone $\mathscr {K}_\varphi$ in $\mathbb {R}^d$ such that every $x \in \varphi ^o$ has a neighbourhood $U_x$ such that $A \cap U_x = (x+ \mathscr {K}_\varphi ) \cap U_x$. (Recall that a cone in $\mathbb {R}^d$ is a set that is closed under nonnegative scalar multiplication.) Define the angular volume $\rho _\varphi$ of $\varphi$ to be the d-dimensional Lebesgue measure of $\mathscr {K}_\varphi \cap B(o,1)$.

For example, if $\varphi = A$ then $\rho _\varphi = \theta _d$. If $D(\varphi )=d-1$ then $\rho _\varphi = \theta _d/2$. If $D(\varphi ) = 0$ then $\varphi = \{v\}$ for some vertex $v \in \partial A$, and $\rho _\varphi$ equals the volume of $B(v,r) \cap A$, divided by $r^d$, for all sufficiently small r. If $d=2$, $D(\varphi )=0$ and $\omega _\varphi$ denotes the angle subtended by A at the vertex $\varphi$, then $\rho _{\varphi } = \omega _\varphi /2$ (see Fig. 1 for an example). If $d=3$ and $D(\varphi )=1$, and $\alpha _\varphi$ denotes the angle subtended by A at the edge $\varphi$ [which is the angle between the two faces of A meeting at $\varphi$; see e.g. Penrose (2023) for a more detailed definition], then $\rho _{\varphi } = 2 \alpha _\varphi /3$ (e.g., for a cube in $\mathbb {R}^3$, each 1-dimensional edge $\varphi$ has $\alpha _\varphi = \pi /2$ and $\rho _\varphi = \pi /3$).

Fig. 1

Illustration of the cone $\mathcal{K}_\varphi$, when $d=2$ and A is the lightly shaded polygon shown, and $\varphi$ is the 0-dimensional face $\{v\}$, where v is the vertex shown. The cone ${{\mathscr {K}}}_\varphi$ is the thickly shaded sector between two half-lines drawn from the origin o as shown, extended to infinity. The angle $\omega _\varphi$ is $\pi /4$ and for r small the area of $B(x,r) \cap A$ is $\pi r^2/8$, so $\rho _\varphi = \pi /8$

Theorem 2.1

Suppose A is a compact convex finite polytope in $\mathbb {R}^d$. Assume that $f|_A$ is continuous at x for all $x \in \partial A$, and that $f_0>0$. Assume $k(\cdot )$ satisfies (2.2). Then, almost surely,

$$\begin{aligned} \lim _{n \rightarrow \infty } nL_{n,k(n)}^d/ k( n)&= \max _{\varphi \in \Phi ^*(A)} \left( \frac{1}{f_\varphi \rho _\varphi } \right)&\textrm{if} ~\beta = \infty ; \end{aligned}$$

(2.5)

$$\begin{aligned} \lim _{n \rightarrow \infty } nL_{n,k(n)}^d/ \log n&= \max _{\varphi \in \Phi ^*(A)} \left( \frac{ \hat{H}_\beta ( D(\varphi )/d) }{ f_\varphi \rho _\varphi } \right)&\textrm{if} ~\beta < \infty . \end{aligned}$$

(2.6)

In the next three results, we spell out some special cases of Theorem 2.1.

Corollary 2.2

Suppose that $d=2$, A is a convex polygon and $f|_A$ is continuous at x for all $x \in \partial A$. Let V denote the set of vertices of A, and for $v \in V$ let $\omega _v$ denote the angle subtended by A at vertex v. Assume (2.2) holds with $\beta < \infty$. Then, almost surely,

$$\begin{aligned} \lim _{n \rightarrow \infty } \left( \frac{ n L_{n,k(n)}^2}{\log n}\right) = \max \left( \frac{\hat{H}_\beta (1)}{\pi f_0}, \frac{2 \hat{H}_\beta (1/2)}{\pi f_1}, \max _{v \in V} \left( \frac{2 \beta }{ \omega _{v} f(v) } \right) \right) . \end{aligned}$$

(2.7)

In particular, for any constant $k \in \mathbb {N}$, $\lim _{n \rightarrow \infty } \left( \frac{ n \pi L_{n,k}^2}{\log n}\right) = \frac{1}{f_0}.$

Corollary 2.3

Suppose $d=3$ (so $\theta _d = 4\pi /3$), A is a convex polyhedron and $f|_A$ is continuous at x for all $x \in \partial A$. Let V denote the set of vertices of A, and E the set of edges of A. For $e\in E$, let $\alpha _e$ denote the angle subtended by A at edge e, and $f_e$ the infimum of f over e. For $v \in V$ let $\rho _v$ denote the angular volume of vertex v. Suppose (2.2) holds with $\beta < \infty$. Then, almost surely,

$$\begin{aligned} \lim _{n \rightarrow \infty } \left( \frac{ n L_{n,k(n)}^3}{\log n}\right) = \max \left( \frac{\hat{H}_\beta (1)}{\theta _3 f_0}, \frac{2 \hat{H}_\beta (2/3)}{\theta _3 f_1}, \frac{3 \hat{H}_\beta (1/3) }{ 2 \min _{e \in E} (\alpha _e f_e ) }, \max _{v \in V} \left( \frac{\beta }{ \rho _{v} f(v) } \right) \right) . \end{aligned}$$

In particular, if $\beta =0$ the above limit comes to $\max \left( \frac{3}{ 4 \pi f_0}, \frac{1}{\pi f_1}, \max _{e \in E} \left( \frac{1 }{2 \alpha _e f_e } \right) \right)$.

Corollary 2.4

(Penrose 2003) Suppose $A = [0,1]^d$, and $f|_A$ is continuous at x for all $x \in \partial A$. For $1 \le j \le d$ let $\partial _j$ denote the union of all $(d-j)$-dimensional faces of A, and let $f_j$ denote the infimum of f over $\partial _j$. Assume (2.2) with $\beta < \infty$. Then

$$\begin{aligned} \lim _{n \rightarrow \infty } \left( \frac{ n L_{n,k(n)}^d}{\log n}\right) = \max _{0 \le j \le d} \left( \frac{2^j \hat{H}_\beta (1-j/d) }{ \theta _d f_j } \right) , ~~~~~ a.s. \end{aligned}$$

(2.8)

It is perhaps worth spelling out what the preceding results mean in the special case where $\beta =0$ (for example, if k(n) is a constant) and also $\mu$ is the uniform distribution on A (i.e., $f(x) \equiv f_0$ on A). In this case, the right hand side of (2.6) comes to $\max _{\varphi \in \Phi ^*(A)} \frac{D(\varphi )}{(d f_0 \rho _\varphi )}$. The limit in (2.7) comes to $1/(\pi f_0)$, while the limit in Corollary 2.3 comes to $f_0^{-1} \max [ 1/\pi , \max _e (1 /(2 \alpha _e))]$.

So far we have only presented results for the largest k-nearest neighbor link. A closely related threshold is the k-connectivity threshold defined by

$$\begin{aligned} M_{n,k}:= \inf \{r>0: G(\mathscr {X}_n,r) \text{ is } k \text{-connected } \}, \end{aligned}$$

where a graph G of order n is said to be k-connected ($k<n$) if G cannot be disconnected by the removal of at most $k-1$ vertices. Set $M_{n,1}=M_n$. Then $M_n$ is the connectivity threshold.

Notice that for all k, n with $k<n$ we have

$$\begin{aligned} L_{n,k}\le M_{n,k}. \end{aligned}$$

(2.9)

Indeed, if $r<L_{n,k}$, then there exists $i\in [n]$ such that $\deg X_i <k$ in $G(\mathscr {X}_n,r)$. Then the removal of all vertices adjacent to $X_i$ disconnects $G(\mathscr {X}_n,r)$, implying that $r< M_{n,k}$. This proves the claim.

Our second main result shows that $(M_{n,k}/L_{n,k}) \rightarrow 1$ almost surely as $n \rightarrow \infty$. For this result we need $d \ge 2$.

Theorem 2.5

Suppose $d \ge 2$. Suppose A is a compact convex finite polytope in $\mathbb {R}^d$. Assume that $f|_A$ is continuous at x for all $x \in \partial A$, and that $f_0>0$. Assume $k(\cdot )$ satisfies (2.2). Then, almost surely,

$$\begin{aligned} \lim _{n \rightarrow \infty } n M_{n,k(n)}^d/ k( n)&= \max _{\varphi \in \Phi ^*(A)} \left( \frac{1}{f_\varphi \rho _\varphi } \right)&\textrm{if} ~\beta = \infty ; \end{aligned}$$

(2.10)

$$\begin{aligned} \lim _{n \rightarrow \infty } n M_{n,k(n)}^d/ \log n&= \max _{\varphi \in \Phi ^*(A)} \left( \frac{ \hat{H}_\beta ( D(\varphi )/d) }{ f_\varphi \rho _\varphi } \right)&\textrm{if} ~\beta < \infty . \end{aligned}$$

(2.11)

Remark 2.6

One can spell out consequences of Theorem 2.5 in dimensions $d=2,3$ and the case of $[0,1]^d$ with exactly the same statement as in Corollaries 2.2–2.4.

Remark 2.7

Theorems 2.1 and 2.5 extend earlier work found in Penrose (2003) on the case where A is the unit cube, to more general polytopal regions. The case where A has a smooth boundary is also considered in Penrose (2003) (in this case with also $k(n)=$ const., the result was first given in Penrose (1999a) for $L_{n,k}$ and in Penrose (1999b) for $M_{n,k}$).

Remark 2.8

In Penrose (2023), similar results are given for the k-coverage threshold $R_{n,k}$, which is given by

$$\begin{aligned} R_{n,k}: = \inf \left\{ r >0: \mathscr {X}_n (B(x,r)) \ge k ~~~~ \forall x \in A \right\} ; ~~~ n,k \in \mathbb {N}. \end{aligned}$$

(2.12)

Our results here, together with Penrose (2023, Theorem 4.2), show that both $L_{n,k(n)}$ and $M_{n,k(n)}$ are asymptotic to $R_{n,k(n)}$ almost surely, as $n \rightarrow \infty$.

Remark 2.9

In Fig. 2 we illustrate our results with some plots against n of simulated values of $nL_n^d/\log n$ and $nM_n^d/\log n$, for uniformly distributed points over a square in $\mathbb {R}^2$, a tetrahedron or dodecahedron in $\mathbb {R}^3$, or a simplex in $\mathbb {R}^4$. Our simulations suggest that $L_n=M_n$ for large n. A result of this sort is proved for uniformly distributed points in $[0,1]^d$, in Penrose (2003, Theorem 13.17), but we do not prove such a result for general polytopes here. We hope to come back to this issue in future work.

Fig. 2

Four plots of $\frac{n L_n^d}{\log n}$ and $\frac{n M_n^d}{\log n}$ against n. The domains are: the square $[0,1]^2$ (top left), a regular tetrahedron (top right), a regular dodecahedron (bottom left), and the 4-dimensional simplex $\{ x \in \mathbb {R}^d: \sum _{i=1}^4 x_i \le 1 \text { and } x_i \ge 0 \text { for all } i \in \{1, 2, 3, 4\} \}$ (bottom right). Where $L_n = M_n$, only the red line is visible. The limit on the right-hand side of (2.6) is indicated by the blue dashed line. For the 4-dimensional simplex, we confirmed using numerical experiments that the maximum on the right-hand side of (2.6) is attained when $\varphi$ is one of the edges of the form $\{ x \in \mathbb {R}^4: x_i = x_j = 0, x_l + x_m = 1\}$ for distinct $i, j, k, l \in \{1,2,3,4\}$, and we estimated its angular volume numerically. For the other three shapes the limit is known exactly

3 Proofs

In this section we prove the results stated in Sect. 2. Throughout this section we are assuming we are given a constant $\beta \in [0,\infty ]$ and a sequence $(k(n))_{n \in \mathbb {N}}$ satisfying (2.2). Recall that $\mu$ denotes the distribution of $X_1$, and this has a density f with support A, and that $L_{n,k}$ is defined at (2.1). Recall that $\hat{H}_\beta (x)$ is defined to be the $y \ge \beta$ such that $y H(\beta /y) =x$, where $H(\cdot )$ was defined at (2.4).

We start by justifying the claim in Sect. 2 concerning the cone $\mathscr {K}_\varphi$ associated with each face $\varphi$.

Lemma 3.1

Suppose $\varphi \in \Phi ^*(A)$ is a face of A. Then there is a unique cone $\mathscr {K}_\varphi$ such that every $x \in \varphi ^o$ has a neighbourhood $U_x$ such that $A \cap U_x = (x+ \mathscr {K}_\varphi ) \cap U_x$.

Proof

If $\varphi = A$, we clearly take $\mathscr {K}_\varphi = \mathbb {R}^d$, so it suffices to consider the case with $D(\varphi ) < d$. Since A is assumed to be a finite compact convex polytope, it is the intersection of a finite collection of half-spaces $\mathbb {H}_1,\ldots ,\mathbb {H}_m$. For each $i \in [m]:= \{1,\ldots ,m\}$, let $\pi _i$ denote the boundary of $\mathbb {H}_i$, which is an affine hyperplane in $\mathbb {R}^d$.

Given $\varphi$, let I be the set of $i \in [m]$ such that $\varphi \subset \pi _i$. For each $i \in I$ let $\mathbb {H}'_i$ be the translate of $\mathbb {H}_i$ that has the origin on its boundary, and let

$$\begin{aligned} \mathscr {K}_\varphi = \cap _{i\in I} \mathbb {H}'_i. \end{aligned}$$

Then $\mathbb {H}'_i$ is a cone for each $i \in I$, so that $\mathscr {K}_\varphi$ is a cone.

Given $x \in \varphi ^o$ and $j \in [m ] {\setminus } I$, we claim that $x \notin \pi _j$. Indeed, if $D(\varphi )=0$ then if $x \in \pi _j$ we would have $\varphi = \{x\} \subset \pi _j$, contradicting the assumption $j\notin I$. If $D(\varphi ) >0$ and $x \in \pi _j$, since $j \notin I$ we could find $y \in \varphi {\setminus } \pi _j$. Then since $x \in \varphi ^o$ we could find $\delta >0$ such that $z:= x +\delta (x-y) \in \varphi$. But then z and y would lie on opposite sides of the hyperplane $\pi _j$, and since $y \in \mathbb {H}_j$ we would have $z \notin \mathbb {H}_j$, and hence $z \notin A$, so $z \notin \varphi$, which is a contradiction. Hence the claim.

Let $x \in \varphi ^o$. By the preceding claim we can and do choose $r >0$ so that $U_x: = B(x,r)$ satisfies $U_x \cap \pi _j = \varnothing$ for all $j \in [m] \setminus I$. Then $U_x \subset \cap _{i \in [m ] \setminus I} \mathbb {H}_i$. Also for all $i \in I$, we have $x \in \pi _i$ so that $(-x) + \mathbb {H}_i = \mathbb {H}'_i$ and $x + \mathbb {H}'_i = \mathbb {H}_i$. Therefore

$$\begin{aligned} A \cap U_x = \left( \cap _{i \in I} \mathbb {H}_i \right) \cap U_x = \left( \cap _{i \in I} (x + \mathbb {H}'_i) \right) \cap U_x = (x+ \mathscr {K}_\varphi ) \cap U_x. \end{aligned}$$

For any other cone $\mathscr {K}' \ne \mathscr {K}_\varphi$, and any neighbourhood U of x, we have $(x+\mathscr {K}') \cap U \ne (x + \mathscr {K}_\varphi ) \cap U$, and the uniqueness follows from this. $\square$

For $n \in \mathbb {N}$ and $p \in [0,1]$ let $\textrm{Bin}(n,p)$ denote a binomial random variable with parameters n, p.

Given $t>0$, let $Z_t$ be a Poisson(t) variable.

The proofs in this section rely heavily on the following lemma.

Lemma 3.2

(Chernoff bounds) Suppose $n \in \mathbb {N}$, $p \in (0,1)$, $t >0$ and $0 \le k < n$.

(a) If $k \ge np$ then $\mathbb {P}[ \textrm{Bin}(n,p) \ge k ] \le \exp \left( - np H(k/(np) ) \right)$.

(b) If $k \le np$ then $\mathbb {P}[ \textrm{Bin}(n,p) \le k ] \le \exp \left( - np H(k/(np)) \right)$.

(c) If $k \ge e^2 np$ then $\mathbb {P}[ \textrm{Bin}(n,p) \ge k ] \le \exp \left( - (k/2) \log (k/(np))\right) \le e^{-k}$.

(d) If $k < t$ then $\mathbb {P}[Z_t \le k ] \le \exp (- t H(k/t))$.

(e) If $k \in \mathbb {N}$ then $\mathbb {P}[Z_t = k ] \ge (2 \pi k)^{-1/2}e^{-1/(12k)}\exp (- t H(k/t))$.

Proof

See e.g. Penrose (2003, Lemmas 1.1, 1.2 and 1.3). $\square$

3.1 A general lower bound

In this subsection we present an asymptotic lower bound on $L_{n,k(n)}$, not requiring any extra assumptions on A. In fact, A here can be any metric space endowed with a Borel probability measure $\mu$ which satisfies the following for some $\varepsilon ' >0$ and some $d>0$:

$$\begin{aligned} \mu (B(x,r))\ge \varepsilon ' r^d, \quad \forall ~ r\in (0,1), x\in A. \end{aligned}$$

(3.1)

The definition of $L_{n,k}$ at (2.1) carries over in an obvious way to this general setting.

Later, we shall derive the results stated in Sect. 2 by applying the results of this subsection to the different regions within A (namely interior, boundary, and lower-dimensional faces).

Given $r>0, a>0$, define the ‘packing number’ $\nu (r,a)$ to be the largest number m such that there exists a collection of m disjoint closed balls of radius r centred on points of A, each with $\mu$-measure at most a.

Proposition 3.3

(General lower bound) Assume (3.1) with $d,\varepsilon '>0$. Let $a >0, b \ge 0$. Suppose $\nu (r,a r^d) = \Omega (r^{-b})$ as $r \downarrow 0$. Assume (2.2).

(a) If $\beta = \infty$ then $\liminf _{n \rightarrow \infty } \left( n L_{n,k(n)}^d/k(n) \right) \ge 1/a$, almost surely.

(b) If $\beta < \infty$ then $\liminf _{n \rightarrow \infty } \left( n L_{n,k(n)}^d/\log n \right) \ge a^{-1} \hat{H}_\beta (b/d)$, almost surely.

Proof

First suppose $\beta = \infty$. Let $u\in (0,1/a )$. Set $r_n:= \left( uk(n)/n \right) ^{1/d}$, $n \in \mathbb {N}$. By (2.2), $r_n \rightarrow 0$ as $n \rightarrow \infty$. Then, given n sufficiently large, we have $\nu (r_n,ar_n^d ) >0$ so we can find $y_n \in A$ such that $\mu (B(y_n,r_n)) \le a r_n^d$, and hence $n \mu (B(y_n,r_n)) \le a uk(n)$. If $k(n) \le e^2 n \mu (B(y_n,r_n))$ (and hence $n \mu (B(y_n,r_n)) \ge e^{-2} k(n)$), then since $\mathscr {X}_n(B(y_n,r_n))$ is binomial with parameters n and $\mu (B(y_n,r_n))$, by Lemma 3.2(a) we have that

$$\begin{aligned} \mathbb {P}[ \mathscr {X}_n(B(y_n,r_n) ) \ge k(n) ]\le & {} \exp \left( - n \mu (B(y_n,r_n)) H \left( \frac{k(n)}{n \mu ( B(y_n,r_n))} \right) \right) \\\le & {} \exp \left( - e^{-2} k(n) H \left( (a u)^{-1} \right) \right) , \end{aligned}$$

while if $k (n) > e^2 n \mu (B(y_n,r_n))$ then by Lemma 3.2(c), $\mathbb {P}[\mathscr {X}_n (B(y_n,r_n)) \ge k(n)] \le e^{-k(n)}$. Therefore $\mathbb {P}[\mathscr {X}_n (B(y_n,r_n)) \ge k(n)]$ is summable in n because $k(n)/\log n \rightarrow \infty$ as $n \rightarrow \infty$ by (2.2).

Let $\delta _0 \in (0,1)$. By (3.1) $\mu (B(y_n,\delta _0 r_n)) \ge \varepsilon ' \delta _0^d u k(n)/n$. Therefore by Lemma 3.2(b), $\mathbb {P}[\mathscr {X}_n(B(y_n,\delta _0 r_n)) =0] \le \exp (-\varepsilon ' \delta _0^d u k(n))$, which is summable in n.

Thus by the Borel-Cantelli lemma, almost surely the event

$$\begin{aligned} F_n:= \{\mathscr {X}_n (B(y_n,r_n)) < k(n) \} \cap \{\mathscr {X}_n(B(y_n,\delta _0 r_n)) >0\} \end{aligned}$$

occurs for all but finitely many n. But if $F_n$ occurs then $L_{n,k(n)} \ge (1-\delta _0) r_n$ so that $n L_{n,k(n)}^d/k(n) \ge (1-\delta _0)^d u$. This gives the result for $\beta = \infty$.

Now suppose instead that $\beta < \infty$. Suppose first that $b=0$, so that $\hat{H}_\beta (b/d) = \beta$. Assume that $\beta >0$ (otherwise the result is trivial). Choose $\beta ' \in (0, \beta )$. Let $\delta > 0$ with $\beta ' < \beta - 2\delta$ and with $\beta ' H \left( \frac{ \beta - 2 \delta }{\beta ' } \right) > \delta .$ This is possible because $H(\beta /\beta ')>0$ and $H(\cdot )$ is continuous. For $n \in \mathbb {N}$, set $r_n:= ( (\beta ' \log n)/ (a n) )^{1/d}$. Also set $k'(n)= \lceil (\beta - \delta ) \log n \rceil$, and $k''(n)= \lceil (\beta - 2 \delta ) \log n \rceil$. By assumption $\nu (r_n,a r_n^d) = \Omega (1)$, so for all n large enough, we can (and do) choose $x_n \in A$ such that $n \mu (B(x_{n},r_n)) \le n a r_n^d = \beta ' \log n.$ Then by a simple coupling, and Lemma 3.2(a),

$$\begin{aligned} \mathbb {P}[ \mathscr {X}_{n} ( B(x_{n},r_n) ) \ge k''(n) ]\le & {} \mathbb {P}\left[ \textrm{Bin}\left( n, (\beta ' \log n)/n) \right) \ge k''(n) \right] \\\le & {} \exp \left( - \left( \beta ' \log n \right) H \left( \frac{\beta - 2 \delta }{\beta ' } \right) \right) \le n^{- \delta }. \end{aligned}$$

Let $\delta ' \in (0,1)$. By (3.1), for n large enough and all $x \in A$,

$$\begin{aligned} n \mu (B(x, \delta ' r_n)) \ge n \varepsilon ' (\delta ' r_n)^d = \varepsilon ' (\delta ')^d (\beta '/a) \log n \end{aligned}$$

so that by Lemma 3.2(b), $\mathbb {P}[\mathscr {X}_n(B(x,\delta ' r_n)) =0] \le n^{-\varepsilon '(\delta ')^d\beta '/a}$.

Now choose $K \in \mathbb {N}$ such that $\delta K >1$ and $K\varepsilon ' (\delta ')^d \beta '/a >1$. For $n \in \mathbb {N}$ set $z(n):=n^K$. For all large enough n we have $k'(z(n)) \ge k''(z(n+1))$, so by the preceding estimates,

$$\begin{aligned} \mathbb {P}[\mathscr {X}_{z(n+1)}(B(x_{z(n+1)},r_{z(n+1)})) \ge k'(z(n))] \\ \le \mathbb {P}[\mathscr {X}_{z(n+1)}(B(x_{z(n+1)},r_{z(n+1)})) \ge k''(z(n+1))] \le (n+1)^{-\delta K}, \end{aligned}$$

and since $x_{z(n+1)} \in A$, also $\mathbb {P}[ \mathscr {X}_{z(n)}(B(x_{z(n+1)},\delta ' r_{z(n)})) =0] \le n^{- \varepsilon ' (\delta ')^d \beta ' K/a}$. Both of these upper bounds are summable in n, so by the Borel-Cantelli lemma, almost surely for all large enough n the event

$$\begin{aligned} \{\mathscr {X}_{z(n+1)}(B(x_{z(n+1)},r_{z(n+1)})) < k'(z(n))\} \cap \{\mathscr {X}_{z(n)}(B(x_{z(n+1)},\delta ' r_{z(n)})) >0 \} \end{aligned}$$

occurs. Suppose the above event occurs and suppose $m \in \mathbb {N}$ with $z(n ) \le m \le z(n+1)$. Note that $r_{z(n+1)}/r_{z(n)}\rightarrow 1$ as $n\rightarrow \infty$. Then, provided n is large enough,

$$\begin{aligned} L_{m,k'(z(n))} \ge r_{z(n+1)}- \delta ' r_{z(n)} \ge (1-\delta ')^2 r_{m}, \end{aligned}$$

and moreover $k'(z(n)) \le k(m)$ so that $L_{m,k(m)} \ge (1- \delta ')^2 r_m$. Hence it is almost surely the case that

$$\begin{aligned} \liminf _{m \rightarrow \infty } (m L_{m,k(m)}^d/\log m) \ge (1- \delta ')^{2d} \liminf _{m \rightarrow \infty } (m r_{m}^d/ \log m) = (1-\delta ')^{2d} a^{-1}\beta ', \end{aligned}$$

and this yields the result for this case.

Now suppose instead that $\beta < \infty$ and $b > 0$. Let $u\in ( a^{-1}\beta , a^{-1} \hat{H}_\beta (b/d))$; note that this implies $ua H(\beta /(ua)) < b/d$. Choose $\varepsilon >0$ such that $(1+ \varepsilon ) ua H(\beta /(ua)) < (b/d)-9 \varepsilon$. Also let $\delta ' \in (0,1)$.

Assume for now that the underlying probability space $(\mathbb {S},{{\mathscr {F}}},\mathbb {P})$ is rich enough to support, as well as the sequence $(X_1,X_2,\ldots )$, a unit rate Poisson counting process $(Z_t,t\ge 0)$, independent of $(X_1,X_2,\ldots )$ (so $Z_t$ is Poisson distributed with mean t for each $t >0$). For each $t >0$, let $\mathscr {P}_t:= \{X_1,\ldots ,X_{Z_t}\}$. Observe that $\mathscr {P}_t$ is a Poisson point process in $\mathbb {R}^d$ with intensity measure $t \mu$ [see e.g. Last and Penrose (2018)].

For each $n \in \mathbb {N}$ set $r_n= (u(\log n)/n)^{1/d}$. Let $m_n:= \nu (r_n,a r_n^d)$, and choose $x_{n,1},\ldots ,$ $x_{n,m_n} \in A$ such that the balls $B(x_{n,1},r_n),\ldots ,B(x_{n,m_n},r_n)$ are pairwise disjoint and each have $\mu$-measure at most $ar_n^d$.

Set $\lambda (n):= n+ n^{3/4}$ and $\lambda ^-(n):= n- n^{3/4}$. For $1 \le i \le m_n$, if $k(n) \ge 1$ then by a simple coupling, and Lemma 3.2(e),

$$\begin{aligned}{} & {} \mathbb {P}[ \mathscr {P}_{\lambda (n)}( B(x_{n,i},r_n) ) \le k(n) ] \ge \mathbb {P}[ Z_{\lambda (n) ar_n^d} \le k(n)] \\{} & {} \quad \ge \left( \frac{e^{-1/(12k(n))}}{ \sqrt{2 \pi k(n)}} \right) \exp \left( - \lambda (n) a r_n^d H \left( \frac{k(n)}{\lambda (n) a r_n^d} \right) \right) . \end{aligned}$$

Now $\lambda (n)r_n^d/\log n \rightarrow u$ so by (2.2), $k(n)/(\lambda (n) a r_n^d) \rightarrow \beta /(ua)$ as $n \rightarrow \infty$. Thus by the continuity of $H(\cdot )$, provided n is large enough, for $1 \le i \le m_{n}$,

$$\begin{aligned} \mathbb {P}[\mathscr {P}_{\lambda (n)}(B(x_{n,i},r_n)) \le k(n)] \nonumber \\ \ge \left( \frac{e^{-1/12} }{\sqrt{2 \pi (\beta +1 ) \log n }} \right) \exp \left( - (1+ \varepsilon ) a uH \left( \frac{\beta }{a u} \right) \log n \right) . \end{aligned}$$

Hence, by our choice of $\varepsilon$, there is a constant $c >0$ such that for all large enough n and all $i \in [m_n]$ we have

$$\begin{aligned} \mathbb {P}[\mathscr {P}_{\lambda (n)}(B(x_{n,i},r_n)) \le k(n)] \ge c (\log n)^{-1/2} n^{ 9 \varepsilon - b/d } \ge n^{8\varepsilon -b/d}. \end{aligned}$$

(3.2)

Since $x_{n,i} \in A$, by (3.1), for n large enough and $1 \le i \le m_n$ we have $\mu (B(x_{n,i}, \delta ' r_n)) \ge \varepsilon ' (\delta ' r_n)^d$ (as well as $\mu (B(x_{n,i}, r_n)) \le a r_n^d$). Thus, given the value of $\mathscr {P}_{\lambda (n)}(B(x_{n,i},r_n))$, the value of $\mathscr {P}_{\lambda ^-(n)} (B(x_{n,i},\delta 'r_n))$ is binomially distributed with probability parameter bounded away from zero. Also $\min _{1\le i \le m_n} \mathbb {E}[\mathscr {P}_{\lambda (n)} (B(x_{n,i},r_n))]$ tends to infinity as $n \rightarrow \infty$, so in particular

$$\begin{aligned} \liminf _{n \rightarrow \infty } \left( \min _{1 \le i \le m_n} \mathbb {P}[ \mathscr {P}_{\lambda (n)} (B(x_{n,i},r_n) ) \ge 1 | \mathscr {P}_{\lambda (n)} (B(x_{n,i},r_n) ) \le k] \right) >0. \end{aligned}$$

Therefore there exists $\eta >0$ such that for all large enough n, defining the event

$$\begin{aligned} E_{n,i}:= \{\mathscr {P}_{\lambda (n)} (B(x_{n,i},r_n)) \le k(n) \} \cap \{ \mathscr {P}_{\lambda ^-(n)}(B(x_{n,i},\delta ' r_n)) \ge 1 \}, \end{aligned}$$

we have for all large enough n that

$$\begin{aligned} \inf _{1 \le i \le m_n} \mathbb {P}[E_{n,i}|\mathscr {P}_{\lambda (n)}(B(x_{n,i},r_n)) \le k(n)] \ge \eta . \end{aligned}$$

Hence, setting $E_n:= \cup _{i=1}^{m_n} E_{n,i}$, for all large enough n we have

$$\begin{aligned} \mathbb {P}[E_n^c] \le ( 1- \eta n^{8\varepsilon -b/d})^{m_n} \le \exp ( - \eta m_n n^{8\varepsilon -b/d} ). \end{aligned}$$

By assumption $m_n = \nu (r_n, a r_n^d) = \Omega (r_n^{-b})$ so that for large enough n we have $m_n \ge n^{(b/d) - \varepsilon }$, and therefore $\mathbb {P}[E^c_n]$ is summable in n.

By Lemma 3.2(d), and Taylor expansion of H(x) about $x=1$ (see the print version of Penrose (2003, Lemma 1.4) for details; there may be a typo in the electronic version), for all n large enough $\mathbb {P}[Z_{\lambda (n)} < n] \le \exp ( - \frac{1}{9} n^{1/2})$. Similarly $\mathbb {P}[Z_{\lambda ^-(n)} > n] \le \exp ( - \frac{1}{9} n^{1/2})$. If $E_n$ occurs, and $Z_{\lambda ^-(n)} \le n$, and $Z_{\lambda (n)} \ge n$, then for some $i \le m_n$ there is at least one point of $\mathscr {X}_n$ in $B(x_{n,i},\delta ' r_n)$ and at most k(n) points of $\mathscr {X}_n$ in $B(x_{n,i},r_n)$, and hence $L_{n,k(n)} > (1- \delta ')r_n$. Hence by the union bound

$$\begin{aligned} \mathbb {P}[L_{n,k(n)} \le r_n(1- \delta ')] \le \mathbb {P}[E_n^c] + \mathbb {P}[ Z_{\lambda (n)} < n] + \mathbb {P}[ Z_{\lambda ^-(n)} > n] , \end{aligned}$$

(3.3)

which is summable in n by the preceding estimates (also the event on the left in (3.3) does not depend on the Poissonization so its probability is the same regardless of whether or not the underlying probability space supports an independent Poisson process.) Therefore by the Borel-Cantelli lemma,

$$\begin{aligned} \mathbb {P}[ \liminf ( n L_{n,k(n)}^d /\log n) \ge u(1-\delta ')^d ] =1, ~~~~~ u< a^{-1} \hat{H}_\beta (b/d), \delta ' \in (0,1), \end{aligned}$$

so the result follows for this case too. $\square$

3.2 Proof of Theorem 2.1

In this subsection we assume, as in Theorem 2.1, that A is a compact convex finite polytope in $\mathbb {R}^d$. We also assume that the probability measure $\mu$ has density f with respect to Lebesgue measure on $\mathbb {R}^d$, and that $f|_A$ is continuous at x for all $x \in \partial A$, and that $f_0 >0$, recalling from (2.3) that $f_0: = \mathrm{ess~inf}_{x \in A} f(x)$. Also we let k(n) satisfy (2.2) for some $\beta \in [0,\infty ]$. Let $\textrm{Vol}$ denote d-dimensional Lebesgue measure.

Lemma 3.4

There exists $\varepsilon ' >0$ depending only on $f_0$ and A, such that (3.1) holds.

Proof

Let $B_0$ be a (fixed) ball contained in A, and let b denote the radius of $B_0$. For $x \in A$, let $S_x$ denote the convex hull of $B_0 \cup \{x\}$. Then $S_x \subset A$ since A is convex. If $x \notin B_0$, then for $r < b$ the set $B(x,r) \cap S_x$ is the intersection of B(x, r) with a set of the form $x+ \tilde{\mathscr {K}}_x$, where $\tilde{\mathscr {K}}_x$ is a convex cone, and since A is bounded the angular volume of the cone $\tilde{\mathscr {K}}_x$ is bounded away from zero, uniformly over $x \in A \setminus B_0$. Therefore $r^{-d} \textrm{Vol}(B(x,r) \cap A)$ is bounded away from zero uniformly over $r \in (0,b)$ and $x \in A {\setminus } B_0$ (and hence over $x \in A$). Since we assume $f_0 >0$, (3.1) follows. $\square$

Recall that $\nu (r,a)$ was defined just before Proposition 3.3. Recall that for each face $\varphi \in \Phi ^*(A)$ we denote the angular volume of A at $\varphi$ by $\rho _{\varphi }$, and set $f_\varphi := \inf _{x \in \varphi } f(x)$ (if $\varphi \in \Phi (A)$) or $f_\varphi := f_0$ (if $\varphi =A$).

Lemma 3.5

Let $\varphi \in \Phi ^*(A)$. Assume $f|_A$ is continuous at x for all $x \in \varphi$. Then, almost surely:

$$\begin{aligned} \liminf _{n \rightarrow \infty } \left( n L^d_{n,k(n)}/ k(n) \right)&\ge ( \rho _\varphi f_\varphi )^{-1} ~~~&\textrm{if} ~ \beta = \infty ; \end{aligned}$$

(3.4)

$$\begin{aligned} \liminf _{n \rightarrow \infty } \left( n L^d_{n,k(n)}/ \log n \right)&\ge (\rho _\varphi f_{\varphi } )^{-1} \hat{H}_\beta (D(\varphi )/d) ~~~&\textrm{if} ~ \beta < \infty . \end{aligned}$$

(3.5)

Proof

Let $a > f_{\varphi }$. Take $x_0 \in \varphi$ such that $f (x_0) <a$. If $D(\varphi ) >0$, assume also that $x_0 \in \varphi ^o$. By the assumed continuity of $f|_A$ at $x_0$, for all small enough $r >0$ we have $\mu (B(x_0,r)) \le a \rho _\varphi r^d$, so that $\nu (r,a \rho _\varphi r^d) = \Omega (1)$ as $r \downarrow 0$. By Lemma 3.4, there exists $\varepsilon ' >0$ such that (3.1) holds. Hence, we can apply Proposition 3.3 (taking $b=0$). By that result, if $\beta = \infty$ then almost surely $\liminf _{n \rightarrow \infty } n L_{n,k(n)}^d/k(n) \ge 1/(a \rho _\varphi )$, and (3.4) follows.

If $\beta < \infty$ and if $D(\varphi ) =0$, then by Proposition 3.3 (with $b=0$), almost surely $\liminf _{n \rightarrow \infty } (n L_{n,k(n)}^d/\log n) \ge \hat{H}_\beta (0)/(a \rho _\varphi )$, and hence (3.5) in this case.

Now suppose $\beta < \infty$ and $D(\varphi )>0$. Take $\delta >0$ such that $f(x) < a$ for all $x \in B(x_0, 2 \delta ) \cap A$, and such that moreover $B(x_0,2 \delta ) \cap A = B(x_0,2 \delta ) \cap (x_0+ \mathscr {K}_\varphi )$ (the cone $\mathscr {K}_\varphi$ was defined in Sect. 2). Then for all $x \in B(x_0,\delta ) \cap \varphi$ and all $r \in (0,\delta )$, we have $\mu (B(x,r)) \le a \rho _\varphi r^d$.

There is a constant $c >0$ such that for small enough $r >0$ we can find at least $cr^{-D(\varphi )}$ points $x_i \in B(x_0,\delta ) \cap \varphi$ that are all at a distance more than 2r from each other, and therefore $\nu ( r,a \rho _\varphi r^d ) = \Omega ( r^{-D(\varphi )})$ as $r \downarrow 0$. Thus by Proposition 3.3 we have

$$\begin{aligned} \liminf _{n \rightarrow \infty } \left( nL_{n,k(n)}^d/k(n) \right) \ge ( a \rho _\varphi )^{-1} \hat{H}_{\beta }(D(\varphi )/d), \end{aligned}$$

almost surely, and (3.5) follows. $\square$

If we assumed $f|_A$ to be continuous on all of A, we would not need the next lemma because we could instead use Lemma 3.5 for $\varphi =A$ as well as for lower-dimensional faces. However, in Theorem 2.1 we make the weaker assumption that $f|_A$ is continuous at x only for $x \in \partial A$. In this situation, we also require the following lemma to deal with $\varphi = A$.

Lemma 3.6

It is the case that

$$\begin{aligned} \mathbb {P}[ \liminf (n L_{n,k(n)}^d/k(n) )&\ge 1 /(\theta _d f_0)]=1&\textrm{if} ~\beta = \infty ; \end{aligned}$$

(3.6)

$$\begin{aligned} \mathbb {P}[ \liminf _{n\rightarrow \infty } ( n L_{n,k(n)}^d /\log n)&\ge \hat{H}_\beta (1)/(\theta _df_0)] =1&\textrm{if} ~\beta < \infty . \end{aligned}$$

(3.7)

Proof

Let $\alpha > f_0$. Then by taking $B=A$ in Penrose (2023, Lemma 6.4),

$$\begin{aligned} \liminf _{r \downarrow 0} r^d \nu (r, \alpha \theta _d r^d) > 0. \end{aligned}$$

(3.8)

If $\beta = \infty$, then by (3.8) we can apply Proposition 3.3 (taking $a= \alpha \theta _d$ and $b=d$) to deduce that $\liminf _{n \rightarrow \infty } nL_{n,k(n)}^d/k(n) \ge (\theta _d \alpha )^{-1}$, almost surely, and (3.6) follows.

Suppose instead that $\beta < \infty$. By (3.8), $\nu (r, \alpha \theta _d r^{d}) = \Omega (r^{-d})$ as $r \downarrow 0$. Hence by Proposition 3.3, almost surely $\liminf _{n \rightarrow \infty } \left( n L_{n,k(n)}^d /\log n \right) \ge (\alpha \theta _d)^{-1} \hat{H}_\beta (1)$. The result follows by letting $\alpha \downarrow f_0$. $\square$

Proof of Theorem 2.1

First suppose $\beta < \infty$.

It is clear from (2.1) and (2.12) that $L_{n,k} \le R_{n,k+1}$ for all n, k. Also by (2.2) we have $(k(n)+1)/\log n \rightarrow \beta$ as $n \rightarrow \infty$. Therefore using Penrose (2023, Theorem 4.2) for the second inequality below, we obtain almost surely that

$$\begin{aligned} \limsup _{n\rightarrow \infty } \left( \frac{n L_{n,k(n)}^d}{\log n} \right) \le \limsup _{n\rightarrow \infty } \left( \frac{n R_{n,k(n)+1}^d}{ \log n} \right) \le \max _{\varphi \in \Phi ^*(A)} \left( \frac{ \hat{H}_\beta (D(\varphi )/d)}{ f_\varphi \rho _\varphi } \right) . \qquad \end{aligned}$$

(3.9)

Alternatively, this upper bound could be derived using (2.9) and the asymptotic upper bound on $M_n$ that we shall derive in the next section for the proof of Theorem 2.5.

By Lemmas 3.6 and 3.5, we have a.s. that

$$\begin{aligned} \liminf _{n\rightarrow \infty } \left( n L_{n,k(n)}^d/\log n \right) \ge \max _{\varphi \in \Phi ^*(A)} \left( \frac{ \hat{H}_\beta (D(\varphi )/d) }{ f_\varphi \rho _\varphi } \right) , \end{aligned}$$

(3.10)

and combining this with (3.9) yields (2.6).

Now suppose $\beta = \infty$. In this case, again using the inequality $L_{n,k} \le R_{n,k+1}$ and Penrose (2023, Theorem 4.2), we obtain instead of (3.9) that a.s.

$$\begin{aligned} \limsup _{n\rightarrow \infty } \left( n L_{n,k(n)}^d/k(n) \right) \le \max _{\varphi \in \Phi ^*(A)} \left( \frac{ 1}{ f_\varphi \rho _\varphi } \right) . \end{aligned}$$

(3.11)

Also by Lemmas 3.6 and 3.5, instead of (3.10) we have a.s. that

$$\begin{aligned} \liminf _{n\rightarrow \infty } \left( n L_{n,k(n)}^d/k(n) \right) \ge \max _{\varphi \in \Phi ^*(A)} \left( \frac{ 1 }{ f_\varphi \rho _\varphi } \right) , \end{aligned}$$

and combining this with (3.11) yields (2.5). $\square$

3.3 A general upper bound

In this subsection we present an asymptotic upper bound for $M_{n,k(n)}$. As we did for the lower bound in Sect. 3.1, we shall give our result (Proposition 3.7 below) in a more general setting; we assume that A is a general metric space endowed with two Borel measures $\mu$ and $\mu _*$ (possibly the same measure, possibly not). Assume that $\mu$ is a probability measure and that $\mu _*$ is a doubling measure, meaning that there is a finite constant $c_*$ (called a doubling constant for $\mu _*$) such that $\mu _*(B(x,2r))\le c_* \mu _*(B(x,r))$ for all $x \in A$ and $r >0$. Assume moreover that $\mu _* (B(x,r)) < \infty$ for some $x \in A, r >0$ (and hence for all such x, r). We shall require further conditions on A: a condition on balls (B), a topological condition (T) and a geometrical condition (G) as follows:

• Condition (B): For all $x \in A$ and $r>0$, the ball B(x, r) is connected.

• Condition (T): The space A is connected and unicoherent. (A is said to be unicoherent if for any two closed connected sets $A_1, A_2 \subset A$ with $A_1 \cup A_2 = A$, the set $A_1 \cap A_2$ is also connected. If A is simply connected, it is unicoherent; see Penrose (2003, Section 9.1).)

• Condition (G): There exists $\delta _1>0$, and $K_0 \in (1,\infty )$, such that for all $r< \delta _1$ and any $x\in A$, the number of components of $A\setminus B(x,r)$ is at most two, and if there are two components, at least one of these components has diameter at most $K_0 r$.

For an example where Condition (G) fails, consider a triangle in $\mathbb {R}^2$ with vertices at (0, 0), (1, 0) and (1, 1) but where the edge from (0, 0) to (1, 1), instead of being a straight line segment, is given by the curve $\{(x,x^2): 0 \le x \le 1\}$ (but the other two edges are straight line segments). For this space, for r small one can use a disk of radius r to cut off a region that has diameter that is $O(r^{1/2})$.

Given $D \subset A$ and $r >0$, we write $D_r$ for $\{y \in A: \,\textrm{dist}(y,D) \le r\}$. Also, let $\kappa (D,r)$ be the r-covering number of D, that is, the minimal $m\in \mathbb {N}$ such that D can be covered by m balls centred in D with radius r.

As before, given $\mu$ we assume $X_1,X_2,\ldots$ to be independent $\mu$-distributed random elements of A with the k-connectivity threshold $M_{n,k}$ defined to be the minimal r such that $G(\mathscr {X}_n,r)$ is k-connected, with $\mathscr {X}_n:= \{X_1,\ldots ,X_n\}$.

Proposition 3.7

(General upper bound) Suppose that $(A,\mu ,\mu _*)$ are as described above and A satisfies Conditions (B), (T) and (G). Let $\ell \in \mathbb {N}$ and let $d >0$. For each $j \in [\ell ]$ let $a_j >0, b_j\ge 0$. Suppose that there exists $r_0 >0$ such that for all $r\in (0,r_0)$, there is a partition $\{T(j,r), j\in [\ell ]\}$ of A with the following two properties. Firstly, for each fixed $j\in [\ell ]$, we have

$$\begin{aligned} \kappa (T(j,r),r)=O(r^{-b_j}) ~~~\textrm{as} ~~ r\downarrow 0, \end{aligned}$$

(3.12)

and secondly, for all $K \in \mathbb {N}$, there exists $r_0(K) >0$ such that for all $j \in [\ell ]$, $r \in (0,r_0(K))$ and any $G \subset A$ intersecting T(j, 2Kr) with $\textrm{diam}(G )\le K r$, we have

$$\begin{aligned} \mu (G _r\setminus G ) \ge a_j r^d. \end{aligned}$$

(3.13)

Assume (2.2). Then, almost surely,

$$\begin{aligned} \limsup _{n\rightarrow \infty } \big ( n M^d_{n,k(n)}/k(n) \big )&\le \max _{j \in [\ell ]} (a_j^{-1})&\textrm{if} ~\beta = \infty ; \\ \limsup _{n\rightarrow \infty } \big ( n M_{n,k(n)}^d/\log n \big )&\le \max _{j\in [\ell ]} (a_j^{-1} {\hat{H}}_\beta (b_j/d))&\textrm{if} ~\beta <\infty . \end{aligned}$$

There is a kind of duality between the packing condition in Proposition 3.3, and the covering condition in Proposition 3.7. Indeed, the condition for Proposition 3.3 requires that we can pack $\Omega (r^{-b})$ balls of radius r and measure at most $ar^d$. The conditions (3.12) and (3.13) (taking G to be a singleton) in Proposition 3.3 imply that we can cover T(j, r) by $O(r^{-b_j})$ balls of radius r and measure at least $a_j r^d$.

Later we shall use Proposition 3.7 in the case where A is a convex polytope in $\mathbb {R}^d$ to prove Theorem 2.5, taking $\mu$ to be the measure with density f and taking $\mu _*$ to be the restriction of Lebesgue measure to A (in fact, if f is bounded from above then we could take $\mu _*= \mu$ instead). The sets in the partition each represent a region near to a particular face $\varphi \in \Phi ^*(A)$ (if $\varphi = A$ the corresponding set in the partition is an interior region). In this case, the coefficients $a_j$ in the measure lower bound (3.13) depend heavily on the geometry of the determining cone near a particular face.

As a first step towards proving Proposition 3.7, we spell out some useful consequences of the measure doubling property. In this result (and again later) we use $|\cdot |$ to denote the cardinality (number of elements) of a set.

Lemma 3.8

Let $\mu _*$ be a doubling measure on the metric space A, with doubling constant $c_*$. We have the following.

• (i) For any $\varepsilon \in (0,1)$, there exists $\rho (\varepsilon )\in \mathbb {N}$ such that $\kappa (B(x,r), \varepsilon r) \le \rho (\varepsilon )$ for all $x\in A, r\in (0,\infty )$.

• (ii) For all $r \in (0,1)$ and all $D \subset A$, we can find ${\mathscr {L}}\subset D$ with $|{\mathscr {L}}| \le \kappa (D,r/5)$, such that $D \subset \cup _{x \in {\mathscr {L}}} B(x,r)$, and moreover the balls B(x, r/5), $x \in {\mathscr {L}}$, are disjoint.

Proof

To prove (i), let $x \in A, r >0$. By the Vitali covering lemma, we can find a set ${\mathscr {U}} \subset B(x,r)$ such that balls $B(y,\varepsilon r/5),$ $y \in {\mathscr {U}}$ are disjoint and that $B(x,r) \subset \cup _{y\in {\mathscr {U}}} B(y,\varepsilon r)$. Set $\rho (\varepsilon ):= \lceil c_*^{\lceil \log _2 (15/\varepsilon ) \rceil }\rceil$. Then by using the doubling property of $\mu _*$ repeatedly, we have $\mu _*(B(y,3r)) \le \rho (\varepsilon ) \mu _*(B(y,r/5))$ for all $y \in A$. Moreover, by the triangle inequality and the condition ${\mathscr {U}} \subset B(x,r)$, we have $B(x,2r)\subset B(y,3r)$ for all $y\in {\mathscr {U}}$. Also $\cup _{y\in {\mathscr {U}}} B(y,\varepsilon r/5) \subset B(x, 2r)$ and the union is disjoint. Thus

$$\begin{aligned}&| {\mathscr {U}}| \mu _*(B(x,2r)) \le \sum _{y\in {\mathscr {U}}} \mu _*(B(y,3r))\\&\le \rho (\varepsilon ) \sum _{y\in {\mathscr {U}}} \mu _*(B(y,\varepsilon r/5)) \le \rho (\varepsilon ) \mu _*(B(x,2r)), \end{aligned}$$

and therefore $|{\mathscr {U}}|\le \rho (\varepsilon )$; the claim about $\kappa (B(x,r), \varepsilon r)$ follows.

Now we prove (ii). Let ${\mathscr {L}}^0 \subset D$ with $|{\mathscr {L}}^0| = \kappa (D,r/5)$ and with $D \subset \cup _{x \in {\mathscr {L}}^0} B(x,r/5)$. By the Vitali covering lemma, we can find ${\mathscr {L}}\subset {\mathscr {L}}^0$ such that $D\subset \cup _{x \in {\mathscr {L}}} B(x,r)$ and the balls $B(x,r/5), x \in {\mathscr {L}},$ are disjoint, and (ii) follows. $\square$

Given countable $\sigma \subset A$, $r >0$ and $k \in \mathbb {N}$, we say that $\sigma$ is (r, k)-connected if the geometric graph $G(\sigma , r)$ is k-connected. Assuming Condition (B) holds, we see that $\sigma$ is (r, 1) connected if and only if $\sigma _{r/2}$ is a connected subset of A.

Lemma 3.9

(Peierls argument) Let $\ell \in \mathbb {N}$, $a \in [1,\infty )$. Let $r \in (0,1/a)$ and $n \in \mathbb {N}$. Let ${\mathscr {L}} \subset A$ with the property that $|{\mathscr {L}}\cap B(x,r)| \le \ell$ for all $x \in A$, and let $x_0 \in {\mathscr {L}}_r$. Then the number of (ar, 1)-connected subsets of ${\mathscr {L}}$ containing $x_0$ with cardinality n is at most $c^n$, where c depends only on $\ell$, a and $c_*$.

Proof

First we claim that $|{\mathscr {L}}\cap B(x,ar) | \le \ell \rho (1/a)$ for all $x \in A$, where $\rho (1/a)$ is as given in Lemma 3.8-(i). Indeed, we can cover B(x, ar) by $\rho (1/a)$ balls of radius r, and each of these balls contains at most $\ell$ points of ${\mathscr {L}}$.

The result then follows by applying (Kesten 1982, Lemma 5.1, eqn (5.22)) to the graph $G({\mathscr {L}},ar)$. For the reader’s convenience we sketch the argument from there. Fix $p \in (0,1)$ and perform Bernoulli site percolation on $G({\mathscr {L}},ar)$. Let $\mathscr {C}_{x_0}$ be the resulting cluster at $x_0$. All sites in $\mathscr {C}_{x_0}$ must be open and all sites adjacent to $\mathscr {C}_{x_0}$ must be closed. By our upper bound on degrees in this graph, with $a_n$ denoting the number of possibilities for $\mathscr {C}_{x_0}$,

$$\begin{aligned} { 1 \ge \mathbb {P}[|\mathscr {C}_{x_0}| =n ] \ge a_n p^n(1-p)^{n \ell \rho (1/a)}, } \end{aligned}$$

and the result follows with $c= p^{-1}(1-p)^{-\ell \rho (1/a)}$. $\square$

Preparing for a proof of Proposition 3.7, we recall a condition that is equivalent to k-connectedness of a graph G. We say that non-empty sets $U,W\subset V$ in a graph G with vertex set V form a k-separating pair if (i) the subgraph of G induced by U is connected, and likewise for W; (ii) no element of U is adjacent to any element of W; (iii) the number of vertices of $V\setminus (U\cup W)$ lying adjacent to $U\cup W$ is at most k. We say that U is a k-separating set for G if (i) the subgraph of G induced by U is connected, and (ii) at most k vertices of $V \setminus U$ lie adjacent to U. The relevance of these definitions is presented in the following lemma.

Lemma 3.10

(Penrose 2003, Lemma 13.1) Let G be a graph with more than $k+1$ vertices. Then G is either $(k+1)$-connected, or it has k separating pair, but not both.

By Lemma 3.10, for Proposition 3.7 it suffices to prove, for arbitrary $u> \max _j a_j^{-1} {\hat{H}}_\beta (b_j/d)$, the non-existence of $(k(n)-1)$-separating pairs in $G(\mathscr {X}_n,r_n)$ with $r_n = (u\log n/n)^{1/d}$, as $n\rightarrow \infty$. Notice that, for any fixed $K\in \mathbb {N}$, if (U, W) is a $(k-1)$-separating pair, then either both U and W have diameter at least $K r_n$, or one of them, say U, is a $(k-1)$-separating set of diameter at most $Kr_n$. Here by the diameter of a non-empty set $U \subset A$ we mean the number $\textrm{diam}(U):= \sup _{u,v \in U}\,\textrm{dist}(u,v)$.

The goal is to prove that neither outcome is possible when $n\rightarrow \infty$. Let us first eliminate the existence of a small separating set.

Lemma 3.11

Suppose the assumptions of Proposition 3.7 hold. If $\beta =\infty$, let $u>\max _j a_j^{-1}$ and for $n\in \mathbb {N}$, set $r_n = (u k(n)/n)^{1/d}$. If $\beta <\infty$, let $u> \max _{j\in [\ell ]} a_j^{-1} {\hat{H}}_\beta (b_j/d)$, and for $n \in \mathbb {N}$ set $r_n = (u (\log n)/n)^{1/d}$. For $K \in \mathbb {N}$, let $E_n(K,u)$ be the event that there exists a $(k(n)-1)$-separating set for $G(\mathscr {X}_n,r_n)$ of diameter at most $K r_n$. Then, given any $K \in \mathbb {N}$, almost surely $E_n(K,u)$ occurs for only finitely many n.

Proof

For $j \in [\ell ]$, $r \in (0,r_0)$ let T(j, r) be as in the assumptions of Proposition 3.7. For $j \in [\ell ]$, $K \in \mathbb {N}$ we claim that $\kappa (T(j,2Kr_n),\varepsilon r_n/5) = O(r_n^{-b_j})$ as $n \rightarrow \infty$. Indeed,

$$\begin{aligned} \kappa (T(j,2K r_n),\varepsilon r_n/5)&\le \kappa (T(j,2Kr_n),2Kr_n)\sup _{x\in A}\kappa (B(x,2Kr_n), \varepsilon r_n/5) \\&\le \rho \kappa (T(j,2Kr_n),2Kr_n), \end{aligned}$$

where $\rho = \rho (\varepsilon /(10K))$ is the constant in Lemma 3.8-(i). The claim follows from the assumption at (3.12).

Choose $n_0 \in \mathbb {N}$ such that $r_n < r_0$ for all $n \in \mathbb {N}$ with $n \ge n_0$. By Lemma 3.8-(ii), for each $j \in [\ell ]$ and $n \in \mathbb {N}$ we can find a set ${\mathscr {L}}_{n}^{j} \subset T(j,2 Kr_n)$, with $|{\mathscr {L}}_n^j| \le \kappa ( T(j,2Kr_n),\varepsilon r_n/5) = O(r_n^{-b_j})$, such that $T(j,2K r_n) \subset \cup _{x \in {\mathscr {L}}_n^j} B(x, \varepsilon r_n)$ and that the balls $B(x, r_n \varepsilon /5)$, $x \in {\mathscr {L}}_n^j$, are disjoint. Set

$$\begin{aligned} {\mathscr {L}}_n := \cup _{i=1}^\ell {\mathscr {L}}^j_n. \end{aligned}$$

(3.14)

For $n \ge n_0, j \in [\ell ]$ let ${\mathscr {T}}_n^j=\{\sigma \subset {\mathscr {L}}_n: \textrm{diam}(\sigma )\le 2K r_n, \sigma \cap T(j,2K r_n)\ne \varnothing \}$. We claim that as $n \rightarrow \infty$, the cardinality of ${\mathscr {T}}^j_n$, $|{\mathscr {T}}^j_n|$, satisfies

$$\begin{aligned} |{\mathscr {T}}^j_n| = O(|{\mathscr {L}}_n^j|)=O(r_n^{-b_j}). \end{aligned}$$

(3.15)

Indeed, $\sigma \cap T(j,2K r_n) \ne \varnothing$ means $\sigma \cap {\mathscr {L}}^j_n\ne \varnothing$. Moreover, as explained below,

$$\begin{aligned} \limsup _{n \rightarrow \infty } \sup _{x \in {\mathscr {L}}_n} |B(x,2Kr_n) \cap {\mathscr {L}}_n| < \infty , \end{aligned}$$

(3.16)

and $\textrm{diam}(\sigma )\le 2Kr_n$. The claim about cardinality follows from this.

Now we show (3.16). By Lemma 3.8-(i), for n large and for all $x \in A$, we can cover $B(x,2Kr_n)$ by $\rho (\varepsilon /(10K))$ balls of radius $r_n \varepsilon /5$, and each of these balls contains at most $\ell$ points of ${\mathscr {L}}_n$.

Now assume $\beta <\infty$. The condition on u implies that $ua_j > \beta$ and $ua_j H(\beta /(ua_j)) > b_j/d$, for each $j \in [\ell ]$. Then we can and do choose $\beta ' > \beta$ and $\varepsilon \in (0,1/4)$ such that for each $j \in [\ell ]$, $(1- 3 \varepsilon )^du a_j > \beta '$ and

$$\begin{aligned} (1-3\varepsilon )^d ua_j H\Big (\frac{\beta '}{(1-3\varepsilon )^d ua_j}\Big )>\frac{b_j}{d} +\varepsilon . \end{aligned}$$

For $n \in \mathbb {N}$ define $k'(n)=\lceil \beta ' \log n\rceil$.

For $n \ge n_0$ and $\sigma \subset {\mathscr {L}}_n$, set

$$\begin{aligned} D_{\sigma ,n} := \sigma _{(1-2 \varepsilon ) r_n} \setminus \sigma _{\varepsilon r_n}. \end{aligned}$$

(3.17)

Let $J \in \mathbb {N}$ with $J >1/\varepsilon$. For $m \in \mathbb {N}$, define $z(m):=m^J$. For $\sigma \subset {\mathscr {L}}_{z(m)}$, define

$$\begin{aligned} F_m(\sigma ) = \{ \mathscr {X}_{z(m)}( D_{\sigma , z(m)})< k'(z(m)) \}. \end{aligned}$$

Now let $n \in \mathbb {N}$ and choose $m= m(n)$ such that $z(m ) \le n < z(m+1)$. Assume $z(m) \ge n_0$. Suppose that $E_n(K,u)$ occurs and let U be a $(k(n)-1)$-separating set of $G(\mathscr {X}_n,r_n)$ with $\textrm{diam}(U)\le Kr_n$. We define its ‘pixel version’ $\sigma (U):= {\mathscr {L}}_{z(m(n))} \cap U_{\varepsilon r_{z(m(n))}}$.

Since $\sigma (U)\subset A$, there exists $j\in [\ell ]$ such that $\sigma (U)\cap T(j,2 K r_{z(m(n))}) \ne \varnothing$. By our choice of $\varepsilon$, provided n is large enough we have $\textrm{diam}(\sigma (U))\le 2Kr_{z(m(n))}$. Therefore $\sigma (U) \in \cup _{j=1}^{[\ell ]} {\mathscr {T}}^j_{z(m(n))}$.

Since U is $(k(n)-1)$-separating for $G(\mathscr {X}_n,r_n)$, we have $\mathscr {X}_n( U_{r_n} \setminus U )< k(n)$. We claim that $\mathscr {X}_n(D_{\sigma (U),z(m(n))})<k(n)$ provided n is large enough. Indeed, by the triangle inequality $\sigma (U)_{(1-2 \varepsilon )r_{z(m(n))}} \subset U_{(1-\varepsilon )r_{z(m(n))}} \subset U_{r_n}$ (for n large), while $U \subset \sigma (U)_{\varepsilon r_{z(n(m))}}$. Thus $D_{\sigma (U), z(m(n))} \subset U_{r_n} \setminus U$, and the claim follows. Also, provided n is large enough, we have $k(n)\le k'(z(m(n)))$. Thus we have the event inclusions

$$\begin{aligned} E_n(K,u)&\subset \cup _{j=1}^{\ell } \cup _{\sigma \in \mathscr {T}^j_{z(m(n))}} \{ \mathscr {X}_n(D_{\sigma ,z(m(n))})< k(n)\} \\&\subset \cup _{j=1}^{\ell } \cup _{\sigma \in {\mathscr {T}}^j_{z(m(n))}} F_{ m(n)}(\sigma ). \end{aligned}$$

By (3.17), for any $n \in \mathbb {N}$ and $\sigma \subset \mathscr {L}_n$ we have $D_{\sigma ,n} \supset (\sigma _{\varepsilon r_n})_{(1-3 \varepsilon )r_n} {\setminus } \sigma _{\varepsilon r_n}$. Hence by (3.13), for all large enough n and all $\sigma \in \cup _{j\in [\ell ]} {\mathscr {T}}_{n}^j$ we have $\mu (D_{\sigma ,n}) \ge a_j (1-3\varepsilon )^d r_n^d$. A simple coupling shows that, provided m is large, we have

$$\begin{aligned} \mathbb {P}[\cup _{j\in [\ell ]}\cup _{\sigma \in {\mathscr {T}}^j_{z(m)}} F_m(\sigma )]= \sum _{j=1}^{\ell } O(r_{z(m)}^{-b_j})\mathbb {P}[ \textrm{Bin}(z(m), (1-3\varepsilon )^d a_j r_{z(m)}^d) < k'(z(m))]. \end{aligned}$$

By Lemma 3.2(b) and our choice of $r_n$ and $\varepsilon$, provided m is large, we have

$$\begin{aligned}&\mathbb {P}[\cup _{j\in [\ell ]}\cup _{\sigma \in {\mathscr {T}}^j_{z(m)}} F_m(\sigma )]\\&=O(1) \sum _{j=1}^{\ell } \exp \Big ( (b_j/d)\log z(m) - (1-3\varepsilon )^d u a_j H\big (\frac{\beta '}{(1-3\varepsilon )^d ua_j}\big )\log z(m) \Big ) \\&= O(m^{-J\varepsilon }), \end{aligned}$$

which is summable in m.

It follows from the Borel-Cantelli lemma that almost surely $\cup _{j\in [\ell ]}\cup _{\sigma \in {\mathscr {T}}^j_{z(m)}} F_m(\sigma )$ occurs only for finitely many m which implies that $E_n(K,u)$ occurs for only finitely many n. This completes the proof of the case $\beta <\infty$.

Now assume $\beta =\infty$ instead. For the rest of the proof assume also that $\varepsilon \in (0,1)$ is such that $ua_j(1-\varepsilon )^d>1$ for all $j \in [\ell ]$. We do not have to go through the subsequence argument as before because the growth of k(n) is super-logarithmic. Now redefine $F_n(\sigma ):= \{\mathscr {X}_n (D_{\sigma , n})< k(n)\}$, with $D_{\sigma ,n}$ still defined by (3.17) but now using our new choice of $\varepsilon$. If $E_n(K,u)$ happens then we now redefine the pixel version of the separating set U as

$$\begin{aligned} \sigma (U):= {\mathscr {L}}_n \cap U_{\varepsilon r_n}, \end{aligned}$$

and enumerate the possible shapes $\sigma$ of the pixel version. Thus we have

$$\begin{aligned} E_n(K,u) \subset \cup _{j=1}^\ell \cup _{\sigma \in {\mathscr {T}}^j_n} F_n(\sigma ). \end{aligned}$$

Using the estimate of $|{\mathscr {T}}^j_n|$ at (3.15), we have

$$\begin{aligned} \mathbb {P}[E_n(K,u)] = \sum _{j=1}^\ell O(r_n^{-b_j}) \mathbb {P}[\textrm{Bin}(n, (1-3\varepsilon )^d a_j r_n^d )<k(n)]. \end{aligned}$$

Noticing $r_n^{-1}=O(n^{1/d})$, and applying Lemma 3.2-(b) leads to

$$\begin{aligned} \mathbb {P}[E_n(K,u)] = O(n^{b_j/d}) \sum _{j=1}^\ell \exp \Big ( - (1-3\varepsilon )^d a_j u k(n) H\big (\frac{k(n)}{ (1-3\varepsilon )^d a_j u k(n)}\big ) \Big ) \end{aligned}$$

which is summable in n, and the claim follows by the Borel-Cantelli lemma. $\square$

The following lemma eliminates the existence of a $(k(n)-1)$-separating pair with both diameters larger than $Kr_n$.

Lemma 3.12

Let the assumptions of Proposition 3.7 hold. If $\beta =\infty$, let $u>\max _j a_j^{-1}$ and for $n\in \mathbb {N}$, set $r_n = (u k(n)/n)^{1/d}$. If $\beta <\infty$, let $u> \max _{j\in [\ell ]} a_j^{-1} {\hat{H}}_\beta (b_j/d)$, and for $n \in \mathbb {N}$ set $r_n = (u (\log n)/n)^{1/d}$. For $K \in \mathbb {N}$ let $H_n(K,u)$ denote the event that there exists a $(k(n)-1)$-separating pair (U, W) in $G(\mathscr {X}_n,r_n)$ such that $\min (\textrm{diam}(U),\textrm{diam}(W))\ge K r_n$. Then there exists $K_1 \in \mathbb {N}$ such that (i) $\mathbb {P}[H_n(K_1,u)] = O(n^{-2})$ as $n \rightarrow \infty$, and (ii) almost surely $H_n(K_1,u)$ occurs for only finitely many n.

Proof

Suppose $H_n(K,u)$ holds. Then $U_{r_n/2}$ and $W_{r_n/2}$ are disjoint and connected in A. One of the components of $A{\setminus } U_{r_n/2}$ contains W; denote this component by $W'$. Set $U'= A\setminus W'$. Then $U\subset U'$, $W\subset W'$ and $A= W'\cup U'$. Let $\partial _W U:= \overline{W'}\cap \overline{U'}$. Then $\partial _WU$ is connected by the unicoherence of A. Moreover, any continuous path in A connecting U and W must pass through $\partial _W U$.

Recall $\delta _1$ and $K_0$ in Condition (G). We claim (and show in the next few paragraphs) that

$$\begin{aligned} \textrm{diam}(\partial _W U) \ge \frac{1}{2K_0+2} \min (\delta _1/3, \textrm{diam}(W)/3, \textrm{diam}(U)/3). \end{aligned}$$

(3.18)

Suppose the opposite. Setting $b=\textrm{diam}(\partial _W U)$, we can find $x\in A$ such that $\partial _W U\subset B(x,b)$, and we can find $X\in U\setminus B(x,b), Y\in W\setminus B(x,b)$. Since $b< \delta _1/3$, the number of components of $A{\setminus } B(x,b)$ is at most two. There have to be two components because otherwise X and Y can be connected by a path in A disjoint from $\partial U$, which is a contradiction.

Suppose that X lies in the component of $A \setminus B(x,b)$ having diameter at most $K_0 b$, denoted by $Q_X$, and Y lies in the other component, denoted by $Q_Y$ (if it is the other way round we reverse the roles of X and Y in the rest of this argument). We claim that there exists $X'\in U$ such that $\,\textrm{dist}(X,X')>(2K_0+2)b$. If not, then for any $X_1, X_2\in U$, we have by triangle inequality that $\,\textrm{dist}(X_1, X_2)\le 2(2K_0+2)b$, yielding that $\textrm{diam}(U)\le 2(2K_0+2)b$, contradicting $\textrm{diam}(U)>3(2K_0+2)b$ by the negation of (3.18).

We claim that $\,\textrm{dist}(X,B(x,b)) \le K_0b$. To see this, using the assumed connectivity of A, take a continuous path in A from X to Y. The first exit point of this path from $Q_X$ lies in B(x, b) (else it would not be an exit point from $Q_X$) but also in the closure of $Q_X$, and hence in $B(X,K_0b)$. This yields the latest claim.

We show that $X'$ and Y have to be in the same component of $A {\setminus } B(x,b)$. To this end, notice first that $X'$ cannot be in $Q_X$, because for any $z\in Q_X$,

$$\begin{aligned} \,\textrm{dist}(X,z)\le K_0 b < (2K_0+2) b. \end{aligned}$$

Secondly, $X'$ cannot be in B(x, b) either because for any $z\in B(x,b)$, we have

$$\begin{aligned} \,\textrm{dist}(z,X)\le \,\textrm{dist}(X,B(x,b)) + 2b \le (K_0 +2)b < (2K_0+2) b. \end{aligned}$$

Therefore, $X'$ has to be in $Q_Y$, and we reach again to a contradiction that $X'$ and Y can be connected by a path in A disjoint from $\partial U$. We have thus proved (3.18).

Let $\varepsilon \in (0,1/9)$ and let ${\mathscr {L}}_n$ be as defined at (3.14), with ${\mathscr {L}}_n^j$ as defined just before (3.14) (the $\varepsilon$ does not have to be the same as it was there). Recall that ${\mathscr {L}}_n$ has the covering property that for every $x \in A$ we have $\mathcal{L}_n \cap B(x,r_n \varepsilon ) \ne \varnothing$ and the spacing property that $|\mathcal{L}_n \cap B(x,r_n \varepsilon /3)| \le \ell$ for all such x.

Define $D_WU = \{ x\in {\mathscr {L}}_n: B(x,\varepsilon r_n)\cap \partial _WU \ne \varnothing \}$. Then by the covering property of ${\mathscr {L}}_n$, $(D_WU)_{\varepsilon r_n}$ is connected and covers $\partial _WU$. That is, $D_WU$, as a subset of the metric space A, is $(2\varepsilon r_n,1)$-connected.

By (3.18) and the occurrence of $H_n(K,u)$, we have

$$\begin{aligned} 2\varepsilon r_n |D_WU| \ge \textrm{diam}(\partial _W U) \ge \min (\delta _1/3, Kr_n/3)/(2K_0+2). \end{aligned}$$

Therefore, provided n is large, we have $|D_WU|\ge K/(6\varepsilon (2K_0+2))$.

We claim that there is a constant $c \in (0,\infty )$, independent of n, such that for all $q \in \mathbb {N}$, if $|D_WU|=q$ then $D_WU$ can take at most $O(r_n^{-\max (b_j)} c^q)$ possible ’shapes’. Indeed, given $x_0 \in \mathcal{L}_n$, set

$$\begin{aligned} {\mathscr {U}}_{n,q}(x_0):=\{\sigma \subset {\mathscr {L}}_n: |\sigma |=q, \sigma \text{ is }\, (2\varepsilon r_n,1)\,\text{-connected }, x_0\in \sigma \}. \end{aligned}$$

Then $D_W U \in \cup _{j\in [\ell ]} \cup _{x_0\in {{\mathscr {L}}_n^j}} {\mathscr {U}}_{n,q}(x_0).$ By Lemma 3.9, we have $|{\mathscr {U}}_{n,q}(x_0)|\le c^{q}$ for some finite constant c. Recall from the proof of Lemma 3.11 that ${|{\mathscr {L}}_n^j|} = O(r_n^{-b_j})$. The claim follows.

For all $n \in \mathbb {N}$, if $x \in \partial _WU$ then $\,\textrm{dist}(x,U) = r_n/2$. Therefore by the triangle inequality, $(D_WU)_{\varepsilon r_n/5} \subset U_r$, while $U\cap (D_WU)_{\varepsilon r_n/5} =\varnothing$; hence $\mathscr {X}_n \cap (D_W U)_{\varepsilon r_n/5} =\varnothing$. This, together with the the union bound, yields that

$$\begin{aligned} \mathbb {P}[ H_n(K,u)]\le \sum _{q\ge K/(6\varepsilon (2K_0+2))} \sum _{\sigma } \mathbb {P}[ \mathscr {X}_n(\sigma _{\varepsilon r_n/5}) < k(n) ], \end{aligned}$$

(3.19)

where the second sum is over all possible shapes $\sigma \subset {\mathscr {L}}_n$ of cardinality q that are $(2 \varepsilon r_n,1)$-connected. Since every point in A is covered at most $\ell$ times, by (3.13) (with $G=\{z\}$), there exists $\varepsilon _1\in (0,1)$ such that

$$\begin{aligned} \mu (\sigma _{\varepsilon r_n/5}) \ge (1/\ell ) \sum _{z\in \sigma }\mu (B(z,\varepsilon r_n/5)) \ge (q/\ell ) \varepsilon _1 (\varepsilon r_n/5)^d. \end{aligned}$$

Suppose $\beta <\infty$. Set $\varepsilon _2:= (\varepsilon _1/\ell ) (\varepsilon /5)^d$. By (3.19) and Lemma 3.2(b), provided n is large,

$$\begin{aligned} \mathbb {P}[H_n(K,u)]\le \sum _{q\ge K/(6\varepsilon (2K_0+2))} O(r_n^{-\max (b_j)} c^q) \mathbb {P}[\textrm{Bin}(n, \varepsilon _2q r_n^d)< (\beta +1) \log n] \\ =O(1) \sum _{q\ge K/(6\varepsilon (2K_0+2))} c^q \exp \Big ( (\max (b_j)/d) \log n - \varepsilon _2 q u H\big (\frac{\beta +1}{\varepsilon _2 q u}\big ) \log n\Big ). \end{aligned}$$

By the continuity of $H(\cdot )$ and the fact that $H(0)=1$, there exists $q_0>16 /(\varepsilon _2 u)$ such that for any $q>q_0$, we have $H\big (\frac{\beta +1}{q \varepsilon _2 u}\big )>1/2$ and $q u \varepsilon _2 >4 \max (b_j)/d$. Choosing $K = 6\varepsilon (2K_0+2)q_0$ so that $q\ge q_0$ in the sum, we see that the exponent of the exponential is bounded from above by

$$\begin{aligned} (\max (b_j)/d) \log n - q \varepsilon _2 (u/2) \log n \le -(qu \varepsilon _2/4) \log n. \end{aligned}$$

Therefore, we have for n large that

$$\begin{aligned} \mathbb {P}[H_n(K,u)]&= O(1) \sum _{q\ge q_0} c^q \exp ( - q u(\varepsilon _2/4) \log n) \\&= O(1) \sum _{q\ge q_0} \exp ( - q u(\varepsilon _2/8) \log n) = O(\exp ( - q_0 u(\varepsilon _2/8) \log n)) =O(n^{-2}). \end{aligned}$$

Now suppose $\beta =\infty$. By (3.19) and the estimates of $|\cup _j\cup _{x_0}{\mathscr {U}}_{n,q}(x_0)|$ as previously, we have

$$\begin{aligned} \mathbb {P}[H_n(K,u)]\le \sum _{q\ge K/(6\varepsilon (2K_0+2))} O(r_n^{-\max (b_j)} c^q) \mathbb {P}[\textrm{Bin}(n, (q/\ell ) \varepsilon _1 (\varepsilon r_n/5)^d)< k(n)]. \end{aligned}$$

We have $r_n^{-\max (b_j)} = O(n^{\max (b_j)/d})$, and by Lemma 3.2-(b),

$$\begin{aligned} \mathbb {P}[H_n(K,u)] \le \sum _{q\ge K/(6\varepsilon (2K_0+2))} c^q \exp \Big ( (\max (b_j)/d) \log n - q \varepsilon _2 u k(n) H(\frac{k(n)}{q \varepsilon _2 u k(n)}) \Big ). \end{aligned}$$

As before, we can choose $K=K_1$ (large) so that the $H(\cdot )$ term in every summand is bounded from below by 1/2. By the super-logarithmic growth of k(n), we conclude that $\mathbb {P}[H_n(K,u)]\le n^{-2}$ provided n is large, completing the proof of Part (i). Part (ii) then follows from Part (i), by applying the Borel-Cantelli lemma. $\square$

Proof of Proposition 3.7

If $\beta = \infty$ then let $u > \max _{j \in [\ell ]}(a_j^{-1})$ and set $r(n):= u (k(n)/n)^{1/d}$. If $\beta < \infty$ then let $u> \max _{j \in [\ell ]}( a_j^{-1} {\hat{H}}_\beta (b_j/d))$ and set $r_n:= (u(\log n)/n)^{1/d}$. By Lemmas 3.11 and 3.12, there exists $K \in \mathbb {N}$ such that almost surely, $E_n(K,u)\cup H_n(K,u)$ occurs for at most finitely many n. By Lemma 3.10, if $M_{n,k} > r_n$ then $E_n(K,u) \cup H_n(K,u)$ occurs. Therefore $M_{n,k(n)}\le r_n$ for all large enough n, almost surely, and the result follows. $\square$

3.4 Proof of Theorem 2.5

In this subsection we go back to the mathematical framework in Sect. 2; that is, we make the assumptions in the statement of Theorem 2.5. In particular we return to assuming A is a convex polytope in $\mathbb {R}^d$ with $d \ge 2$, and the probability measure $\mu$ has a density f. We shall check the conditions required in order to apply Proposition 3.7.

To check these conditions, we shall use the following lemma and notation.

Lemma 3.13

(Penrose 2023, Lemma 6.12) Suppose $\varphi , \varphi '$ are faces of A with $D(\varphi )>0$ and $D(\varphi ')=d-1$, and with $\varphi \setminus \varphi '\ne \varnothing$. Then $\varphi ^o\cap \varphi '=\varnothing$ and $K(\varphi ,\varphi ')<\infty$, where we set

$$\begin{aligned} K(\varphi ,\varphi '):= \sup _{x\in \varphi ^o} \frac{\,\textrm{dist}(x,\partial \varphi )}{\,\textrm{dist}(x,\varphi ')}. \end{aligned}$$

(3.20)

Now define

$$\begin{aligned} K(A) := \max \{K(\varphi , \varphi '): \varphi , \varphi ' \in \Phi (A), D(\varphi ) >0, D(\varphi ') = d-1, \varphi \setminus \varphi ' \ne \varnothing \}. \end{aligned}$$

(3.21)

Then $K(A)<\infty$ since A is a finite polytope.

For $j \in \{0,1,\ldots ,d\}$ let $\Phi _j(A)$ denote the collection of j-dimensional faces of A. For any $D\subset A$ and $r>0$ set $D_r = \{x\in A: B(x,r)\cap D\ne \varnothing \}$.

Lemma 3.14

The restriction of Lebesgue measure to A has the doubling property. Moreover Conditions (B), (T) and (G) are satisfied.

Proof

First we verify the doubling property. By the proof of Lemma 3.4, there exists $b >0$ such that $\inf _{x \in A,r \in (0,b]}r^{-d} \textrm{Vol}(B(x,r) \cap A) >0$. Since $\textrm{Vol}(B(x,2r) \cap A)$ is at most $2^d\theta _d r^d$ for $r \le b$, and is at most $\textrm{Vol}(A)$ for all r, the doubling property follows.

Since A is convex, for all $x \in A$ and $r >0$ the set $B(x,r) \cap A$ is convex and hence connected, implying (B). All convex polytopes are simply connected, and therefore unicoherent (Penrose 2003, Lemma 9.1), hence (T). Condition (G) follows immediately from Proposition 3.15, which we prove below. $\square$

Proposition 3.15

Let A be a convex finite polytope in $\mathbb {R}^d$. Let $N(\cdot )$ denote the number of components of a set. There exists $\delta _1>0$ such that for any $x \in A$ any $r \in (0,\delta _1)$, we have $N(A\setminus B(x,r)) \le 2$. Moreover, in the case that $N(A\setminus B(x,r))=2$, the diameter of the smaller component is at most cr, where c is a constant depending only on A.

Proof of Proposition 3.15

Write B for B(x, r). Our first observation is that if $y \in A {\setminus } B$, then there is at least one vertex $v \in \Phi _0(A)$ such that the line segment [y, v] is contained in $A \setminus B$. Indeed, if this failed then for each $v \in \Phi _0(A)$ there would exist a point $u(v) \in [y,v] \cap B$. But then since A is convex, y would lie in the convex hull of $\{v:v \in \Phi _0(A) \}$, and therefore also in the convex hull of $\{u(v):v \in \Phi _0(A) \}$. Indeed, there exist $\alpha _v\ge 0$ with $\sum _{v\in \Phi _0(A)} \alpha _v=1$ such that $y=\sum _{v\in \Phi _0(A)} \alpha _v v$, and there exists $\beta _v\in [0,1]$ such that $u(v)= \beta _v y + (1-\beta _v) v$. Substituting v by u(v) and rearranging terms shows that $y= \sum _{v} \alpha '_v u(v)$ with some nonnegative $\alpha '_v$ and $\sum _v \alpha '_v=1$, thus the claim. But then since B is convex we would have $y \in B$, a contradiction.

We refer to the one-dimensional faces $\varphi \in \Phi _1(A)$ as edges of A. Our second observation is that if the number of edges of A that intersect B is at most 1, then $A \setminus B$ is connected. Indeed, in this case, for any distinct $v,v' \in \Phi _0(A)$ there is a path along edges of A from v to $v'$ that avoids B. For example, if $v,v'$ lie in the same two-dimensional face $\varphi$ of A then since B intersects at most one edge of the polygon $\varphi$, there is a path from v to $v'$ along the edges of $\varphi$ avoiding B. Therefore all $v \in \Phi _0(A)$ lie in the same component of $A \setminus B$, so using the first observation we deduce that $A \setminus B$ is connected.

Recall the definition of K(A) at (3.21). Our third observation is that if $\,\textrm{dist}(v,B) \ge 3r K(A)$ for all $v \in \Phi _0(A)$ then $A {\setminus } B$ is connected. Indeed, suppose $\,\textrm{dist}(v,B) \ge 3rK(A)$ for all $v \in \Phi _0(A)$. Suppose $\varphi ,\varphi '$ are distinct edges of A with $B \cap \varphi \ne \varnothing$, and pick $y \in B \cap \varphi$. Then $\,\textrm{dist}(y,\partial \varphi ) \ge 3r K(A)$ so that by (3.20), $\,\textrm{dist}(y,\varphi ') \ge 3 r K(A)/K(\varphi ,\varphi ') \ge 3r$. Hence by the triangle inequality $\,\textrm{dist}(B,\varphi ') \ge 3r -2r = r$, so that $B \cap \varphi ' = \varnothing$. Hence B intersects at most one edge of A, and by our second observation $A \setminus B$ is connected.

Suppose $\,\textrm{dist}(v,B) \le 3rK(A)$ for some $v \in \Phi _0(A)$. Provided r is small enough, this cannot happen for more than one $v \in \Phi _0(A)$. If $u,u' \in \Phi _0(A) {\setminus } \{v\}$, then $v \notin [u,u']$ so $\,\textrm{dist}(v,[u,u']) > 0$. Therefore provided r is small enough, $[u,u'] \subset A \setminus B$.

Thus provided r is small enough, all vertices $u \in \Phi _0(A) {\setminus } \{v\}$ lie in the same component of $A \setminus B$. If also v lies in this component, then (by our first observation) $A {\setminus } B$ is connected.

Thus $A \setminus B$ is disconnected only if v lies in a different component of $A \setminus B$ than all the other vertices. In that case, for $y \in A {\setminus } B$, if $[y,v] \subset A {\setminus } B$ then y is in the same component as v; otherwise (by our first observation) y lies in the same component as all of the other vertices, and thus $A \setminus B$ has exactly two components.

If $A \setminus B$ has two components, and $y \in A \setminus B$ with $\Vert y-v\Vert > (3K(A)+2)r$, then we claim $[y,v] \cap B \ne \varnothing$. Indeed, for each $u \in \Phi _0(A) {\setminus } \{v\}$ the ray from v in the direction of u passes through B. But then by an argument based on the convexity of both A and B, the ray from v in the direction of y must also pass through B. Since $\,\textrm{dist}(v,B) \le 3rK(A)$ and $\textrm{diam}(B) = 2r$, this ray must pass through B at a distance at most $(3K(A)+2)r$ from v, i.e. before it reaches y, and the claim follows. Therefore y lies in the component of $A \setminus B$ that does not contain v, and thus the component containing v has diameter at most $(3K(A)+2)r$. $\square$

To apply Proposition 3.7, we need to define a partition of A for each small $r>0$, then estimate the corresponding covering numbers and $\mu$-measures in (3.13).

Taking into account a variety of boundary effects near $\partial A$, one should consider separately regions near different faces of A. It is however not trivial to construct this partition in such a way that we can obtain tight $\mu$-measure estimates in (3.13). The matter is complicated by the fact that the set G in (3.13) that intersects a region near $\varphi$ is potentially close to a lower dimensional face lying inside $\partial \varphi$. We can avoid the boundary complications by constructing inductively from regions near to the highest dimensional face to the lowest, with increasing ’thickness’. The partition made of $T(\varphi ,r)$’s defined below and the left-over interior region is defined for this purpose.

Let $(K_j)_{j\in \mathbb {N}}$ be an increasing sequence with $K_1=1$, and with $K_{j+1}> (2K(A) +1) K_j$ for each $j \in \mathbb {N}$. For instance, we could take $K_{j}= (2K(A)+2)^{j-1}$.

Now for each $r>0$ and $\varphi \in \Phi (A)$, define the set

$$\begin{aligned} T(\varphi ,r): = \varphi _{r K_{d- D(\varphi )} } \setminus \cup _{\varphi ' \in \Phi (A): \varphi ' \subsetneq \varphi } (\varphi ')_{r K_{d-D(\varphi ')}}, \end{aligned}$$

where the T stands for ‘territory’. Also define $T(A,r):= A {\setminus } \cup _{\varphi \in \Phi (A)} \varphi _{r K_{d-D(\varphi )}}$. For each $\varphi \in \Phi ^*(A)$, we have $T(\varphi ,r)\ne \varnothing$ for all r sufficiently small. Hence, there exists $r_0>0$ such that for all $\varphi$ and all $r<r_0$, $T(\varphi ,r)\ne \varnothing$. Moreover, territories of distinct faces are disjoint, as we show in the following lemma.

Lemma 3.16

There exists $r_0 >0$ such that for all $r \in (0,r_0)$, and any distinct $\varphi ,\varphi '\in \Phi ^*(A)$, it holds that $T(\varphi ,r)\cap T(\varphi ',r)=\varnothing$. Moreover, if $\varphi , \varphi '\in \Phi (A)$ with $\varphi {\setminus } \varphi '\ne \varnothing$, and $y\in T(\varphi ,r)$, then B(y, r) does not intersect $\varphi '$.

Proof

We can (and do) assume without loss of generality that $\varphi {\setminus } \varphi '\ne \varnothing$ and $\varphi '{\setminus } \varphi \ne \varnothing$. Indeed, if $\varphi \subset \varphi '$, then by construction $T(\varphi ',r)\cap T(\varphi ,r)=\varnothing$.

If $\varphi$ is a vertex, then $\,\textrm{dist}(\varphi , \varphi ') >0$ so that $T(\varphi ,r)\cap T(\varphi ',r)=\varnothing$ for all r small. So it suffices to consider the case where $D(\varphi )>0$ and $D(\varphi ')>0$.

Let $j:= d-D(\varphi )$ and $j':= d-D(\varphi ')$. We can and do assume $j'\le j\le d-1$.

If there exists $x\in T(\varphi ,r)\cap T(\varphi ',r)$, then we can find $z\in \varphi , z'\in \varphi '$ such that $\Vert x-z\Vert \le r K_j$ and $\Vert x-z'\Vert \le r K_{j'}$. Therefore $\,\textrm{dist}(z,\varphi ')\le r(K_j + K_{j'})\le 2rK_{j}$.

On the other hand, since $x \in T(\varphi ,r)$, $\,\textrm{dist}(x,\partial \varphi )\ge rK_{j+1}$, and so by the triangle inequality, $r K_{j+1} - rK_{j} \le \,\textrm{dist}(z,\partial \varphi )\le K(A)\,\textrm{dist}(z,\varphi ')$, where the last inequality comes from (3.20). Combining the estimates leads to $K_{j+1}\le (2K(A)+1)K_{j}$, which is a contradiction. The first claim follows.

Moving to the second claim, let $\varphi , \varphi ' \in \Phi (A)$ with $\varphi {\setminus } \varphi ' \ne \varnothing$. Suppose $y \in \varphi '_r$. Set

$$\begin{aligned} \tilde{\Phi }:= \{ \psi \in \Phi (A): \psi \subsetneq \varphi ', y \in \psi _{K_{D-d(\psi )}} \}. \end{aligned}$$

If $\tilde{\Phi } = \varnothing$ then $y \in T(\varphi ',r)$. Otherwise, choose $\psi \in \tilde{\Phi }$ of minimal dimension. Then $y \in T(\psi ,r)$. Either way, $y \notin T(\varphi ,r)$ by the first claim. Therefore $T(\varphi ,r) \cap \varphi '_r = \varnothing$. $\square$

As a last ingredient for applying Proposition 3.7, for each $J>1$ and $r\in (0,1)$, we construct a partition of A and show (3.13) for all G with diameter at most Jr. The coefficients $a_j$ depend on the location of G in relation to faces of A.

Lemma 3.17

Let $J\in \mathbb {N}$ and $\varepsilon >0$. Then the following hold:

• (i) For each $\varphi \in \Phi (A)$ we have $\kappa ( T(\varphi ,r), r)=O(r^{-D(\varphi )})$ as $r \downarrow 0$. Moreover we have $\kappa ( A {\setminus } \cup _{\varphi \in \Phi (A)} T(\varphi ,r),r)=O(r^{-d})$ as $r \downarrow 0$.

• (ii) For all small $r>0$ and any $G \subset A$ with $\textrm{diam}(G)\le J r$, if G intersects $T(\varphi ,2Jr)$ for some $\varphi \in \Phi ^*(A)$, then

  $$\begin{aligned} \mu (G_r\setminus G)\ge (1-\varepsilon ) f_\varphi \rho _\varphi r^d. \end{aligned}$$

  (3.22)

Proof

Item (i) follows by the definition of $T(\varphi , r)$. Indeed, $\varphi$ is contained in a bounded region within a $D(\varphi )$-dimensional affine space, and therefore can be covered by $O(r^{-D(\varphi )})$ balls of radius r. If we then take balls of radius $r(1+ K_{d-D(\varphi )})$ with the same centres, they will cover $T(\varphi ,r)$, and one can then cover each of the larger balls with a fixed number of balls of radius r.

For (ii), let $G \subset A$ with $\textrm{diam}(G)\le Jr$. Suppose first that $G\cap T(\varphi ,2Jr)\ne \varnothing$ for some $\varphi \in \Phi (A)$. Let $x_0\in G\cap T(\varphi ,2Jr)$. Then $G_r \subset B(x_0,2Jr)$. By Lemma 3.16, we see that $B(x_0, 2Jr)$ does not intersect any $\varphi '\in \Phi (A)$ with $\varphi \setminus \varphi '\ne \varnothing$. It follows that

$$\begin{aligned} B(x_0, 2Jr)\cap A = B(x_0,2Jr)\cap (z_0 + {\mathscr {K}}_\varphi ), \end{aligned}$$

(3.23)

where ${\mathscr {K}}_\varphi$ is the cone determined by $\varphi$ as in Lemma 3.1, and $z_0$ is the point of $\varphi$ closest to $x_0$.

Set $D(x,r):= B(x,r)\cap (x + {\mathscr {K}}_\varphi )$. We claim that for any $x\in G$, we have $D(x,r)\subset A$. Indeed, given $y\in D(x,r)$, we can write $y=z_0 + (x-z_0) + (y-x)=: z_0 + \theta _1 + \theta _2$. Here $\theta _1, \theta _2\in {\mathscr {K}}_\varphi$. By convexity and scale invariance of ${\mathscr {K}}_\varphi$, we have $\theta _1+\theta _2 \in {\mathscr {K}}_\varphi$ so $y \in z_0+ \mathscr {K}_\varphi$. Also $\Vert y-x_0\Vert \le \Vert y-x\Vert + \Vert x-x_0\Vert \le 2Jr$, and hence $y\in A$ by (3.23), as claimed.

It follows that (with $\oplus$ denoting Minkowski addition)

$$\begin{aligned} \mu (G_r \setminus G) \ge \mu ((G\oplus D(o,r)) \setminus G) \ge \textrm{Vol}((G\oplus D(o,r)) \setminus G) \inf _{x \in G\oplus D(o,r)} f(x). \end{aligned}$$

By the Brunn–Minkowski inequality (Penrose 2003, Section 5.3), we have $\textrm{Vol}(G\oplus D(o,r)) \ge \textrm{Vol}(G) + \textrm{Vol}(D(o,r)) = \textrm{Vol}(G) + \rho _\varphi r^d$. The claim (3.22) follows by the continuity of f on $\partial A$.

As for the case $\varphi =A$, suppose now that $G \cap T(A,2Jr) \ne \varnothing .$ Taking $x \in G \cap T(A,2Jr)$ we have $\,\textrm{dist}(x,\partial A) \ge 2Jr$, and hence $\,\textrm{dist}(G, \partial A) \ge 2Jr - Jr =Jr$. Therefore

$G_r\subset A$, so by the Brunn–Minkowski inequality

$$\begin{aligned} \mu (G_r \setminus G) \ge f_0 \textrm{Vol}((G \oplus B(o,r)) \setminus G) \ge f_0 \theta _d r^d. \end{aligned}$$

In this case $f_\varphi =f_0$ and $\rho _\varphi = \theta _d$, and the claim (3.22) follows in this case too, completing the proof of (ii). $\square$

Proof of Theorem 2.5

By (2.9), and Theorem 2.1, it suffices to prove the upper bound. We shall do this by applying Proposition 3.7 in the situation of Theorem 2.5.

By Lemma 3.14, the restriction to A of Lebesgue measure has the doubling property, and Conditions (B), (T) and (G) are satisfied.

To apply Proposition 3.7, we need to define (for each $r \in (0,r_0)$) a finite partition $\{T(j,r)\}$. For this we take the sets $T(\varphi ,r), \varphi \in \Phi ^*(A)$. By Lemma 3.16, and the definitions of $T(\varphi ,r)$, $\varphi \in \Phi ^*(A)$, there exists $r_0 >0$ such that for $r \in (0,r_0)$ the sets $T(\varphi ,r),$ $\varphi \in \Phi ^*(A)$, do indeed partition A.

For each $\varphi \in \Phi ^*(A)$, using Lemma 3.17-(i) we have the condition (3.12) in Proposition 3.7, where the constant denoted $b_j$ there is equal to $D(\varphi )$.

Also, using Lemma 3.17-(ii) we have the condition (3.13) in proposition 3.7, where the constant denoted $a_j$ there is equal to $(1-\varepsilon ) f_\varphi \rho _\varphi$.

Suppose $\beta <\infty$. By applying Proposition 3.7 in the manner described above we see that for $\varepsilon >0$, we have

$$\begin{aligned} \limsup _{n\rightarrow \infty } n (M_{n,k(n)})^d/\log n \le \max _{\varphi \in \Phi ^*(A)} \Big ( \frac{{\hat{H}}_\beta (D(\varphi )/d)}{(1-\varepsilon )f_\varphi \rho _\varphi } \Big ), \end{aligned}$$

and the result follows. If $\beta =\infty$, using corresponding part of Proposition 3.7 gives the result in this case too. $\square$