A mathematical model to study the COVID-19 pandemic in India

Abstract

In this paper, a compartmental model is proposed to study the dynamics of COVID-19 pandemic caused by the coronavirus SARS-CoV-2 and the role of media in controlling this ongoing infection. Model includes implementation of media awareness as a control measure to mitigate the spread of the disease. In the proposed model, we have divided the total human population into four sub-classes, namely susceptibles, asymtomatic infectives, aware susceptibles and symptomatic infectives (or Isolated infectives which are under treatment/hospitalized) incorporating classes representing cumulative density of virus and media alert. The important mathematical features of the model are thoroughly investigated. The endemic equilibrium is found to be locally asymptotically stable as well as non-linearly asymptotically stable with certain conditions. Numerical simulations are also carried out in support of the analytical results and to show the effects of certain key parameters.

Introduction

In present time, the coronavirus infection is the most common infection escalated worldwide with alarming rate. The spread of coronavirus disease 2019 (COVID-19) is threatening people’s physical and mental health and even life safety. Almost every country is facing the impact of this dreaded disease. To contain the spread of the disease, countrywide or local lockdown was imposed which itself is enough to describe the seriousness of the pandemic. Globally, till 30 May 2021, there have been 169,597,415 confirmed cases of COVID-19, including 3,530,582 deaths, reported to WHO. As of 26 May 2021, a total of 1,546,316,352 vaccine doses have been administered (Corona virus fact sheet by WHO 2021). Figures of COVID-19 cases clearly indicate the huge impact of the disease on human population. Therefore, it is essential to pay the attention to study the dynamics of this disease and suggest the ways to stop further its spreading.

This recent spread of COVID-19 disease has led to many theoretical investigations suggesting various non-pharmaceutical interventions (Aldila et al. 2020; Almomani and AlQuran 2020; Agaba 2020; Cai et al. 2020; Chen et al. 2020; Chekol and Melesse 2020; Contreras et al. 2020; Cooper et al. 2020; Corbet et al. 2021; Cui et al. 2008a, b; Dubey et al. 2016; Fredj and Cherif 2020; Gao et al. 2020; Hu et al. 2020; Khan and Atangana 2020; Krishna and Prakash 2020; Misra et al. 2015; Mitchel 2020; Naresh et al. 2009, 2011a; Kumar and Somani 2020; Pai et al. 2020; Panovska-Griiths 2020; Pandey et al. 2020; Sarkar et al. 2020; Shereen et al. 2020; Wang et al. 2020; Wiah et al. 2020; Zeb et al. 2020; Zehra et al.2020). In particular, Aldila et al. (2020) formulated a modified susceptible, exposed, infectious, recovered compartmental model considering asymptomatic individuals. They used the incidence data from the city of Jakarta, Indonesia and observed that the strict social distancing is very much helpful is delaying the outbreak of the disease. However, if the strict social distancing policy is relaxed, a massive rapid-test intervention should be conducted to avoid a large-scale outbreak in future. Contreras et al. (2020) developed a general multi-group SEIRA model for representing the spread of COVID-19 among a heterogeneous population. Cooper et al. (2020) studied the effectiveness of the modeling approach on the pandemic due to the spreading of the novel COVID-19 disease and developed a susceptible-infected-removed (SIR) model that provides a theoretical framework to investigate its spread within a community. Liu et al. (2020) developed models to account for latency period and evaluated the role of the exposed or latency period on the dynamics of a COVID-19. Sarkar et al. (2020) proposed a compartmental model that predicts the dynamics of COVID-19 in 17 provinces of India and the overall India. Almomani and AlQuran (2020) observed that with the spread of the coronavirus globally, the negative effects increased at all levels especially in the economic and social sectors. Their study shows that the situation further worsened by the spread of rumors and false information about the disease circulated through social media and online platforms. Cai et al. (2020) observed in their study, the impact on mental health, resilience and social support of health care workers due to continuously being in close vicinity with persons affected with COVID-19. Chen et al. (2020) proposed a reservoir-people transmission network model for calculating the transmissibility of SARS-CoV-2. Fredj and Cherif (2020) proposed a deterministic compartmental model based on the clinical progression of the disease, the epidemiological state of the individuals and the intervention for the dynamics of COVID-19 infection. Khan and Atangana (2020) proposed a mathematical model by assuming interaction among the bats and unknown hosts, then among the peoples and the infection reservoir (seafood market). The seafood markets, considered to be the main source of infection, where bats and the unknown hosts (may be wild animals) leave the infection for further transmission. Krishna and Prakash (2020) developed a phase-based mathematical model for COVID-19 and concluded that the spreading of COVID-19 capacity is superior than MERS into the Middle East nationals.

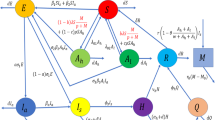
The disease spread is faster in closed population groups through small droplets emanated from the nose or mouth via coughing, sneezing or exhalation of a COVID-19-affected person. These droplets may deposit on objects and surfaces around the person or remain airborne for some time. The susceptibles may get exposed to COVID-19 infection upon touching their eyes, nose or mouth after coming in contact with these objects or surfaces or if they breathe in droplets from a person with COVID-19 who coughs out or exhales droplets. From the above studies, it may be noted that these investigations ignore a very important prevention strategy, i.e. media awareness campaign. Though the vaccine has been developed but it may take years to reach the entire population. Thus, it would be very effective and helpful to educate the people about the COVID-19, its causes and preventive measures in the form of non-pharmaceutical intervention strategies like face cover/mask wearing, social distancing, etc. through media awareness campaigns. Media awareness campaigns not only play a very crucial role in creating awareness to reduce the spread of any infectious disease, but also induce the behavioral change in general population which ultimately changes the pattern of disease spread (Cui et al. 2008a, b; Misra et al. 2011, 2015; Naresh et al. 2011a, b; Tripathi et al. 2007; Tripathi and Naresh 2019). The transmission dynamics of Corona virus is given in Fig. 1.

Fig. 1

Schematic diagram of transmission dynamics of Corona virus (Shereen et al. 2020)

Formulation of mathematical model

We consider the population of size N(t) at time t with constant immigration rate A. The population size N(t) is divided into four subclasses of susceptibles X(t), asymptomatic infectives Y(t) (also assumed to be infectious), aware susceptibles (who are staying home/isolated) $X_M(t)$ and symptomatic infectives $Y_i(t)$ (who are isolated for treatment/hospitalized). The variable V(t) be the cumulative density of virus and the variable M(t) denotes the cumulative density representing media alert to make the population aware of the disease (Misra et al. 2011). With these considerations, the mathematical model is proposed as follows,

$$\begin{aligned} \frac{{\mathrm{d}}X}{{\mathrm{d}}t}= &\, {} A-\beta \frac{XY}{N}-\lambda V X - \nu \frac{XM}{1+\gamma M} \nonumber \\&-{\mathrm{d}}X + \lambda _{11}X_M+\beta _{11}Y_i +\alpha Y \end{aligned}$$

(1)

$$\begin{aligned} \frac{{\mathrm{d}}Y}{{\mathrm{d}}t}= &\, {} \beta \frac{XY}{N}+\lambda V X - {\mathrm{d}}Y - \alpha Y -\beta _1Y \end{aligned}$$

(2)

$$\begin{aligned} \frac{{\mathrm{d}}X_M}{{\mathrm{d}}t}= &\, {} \nu \frac{XM}{1+\gamma M}-{\mathrm{d}}X_M - \lambda _{11}X_M \end{aligned}$$

(3)

$$\begin{aligned} \frac{{\mathrm{d}}Y_i}{{\mathrm{d}}t}= &\, {} \beta _1 Y -{\mathrm{d}}Y_i- \alpha _1 Y_i - \beta _{11} Y_i \end{aligned}$$

(4)

$$\begin{aligned} \frac{{\mathrm{d}}V}{{\mathrm{d}}t}= &\, {} \theta Y - \theta _0 V \end{aligned}$$

(5)

$$\begin{aligned} \frac{{\mathrm{d}}M}{{\mathrm{d}}t}= &\, {} \mu Y - \sigma M \end{aligned}$$

(6)

where d is the natural mortality rate constant, $\alpha _1$ is disease-induced death rate constant. The constant $\beta$ represents the transmission rate by which susceptible individuals X(t) come into contact with asymptomatic infectives Y(t) directly and become infective. The constant $\lambda$ represents the transmission rate by which susceptible individuals X(t) become infected by directly coming in contact with virus V(t) deposited on surfaces/objects or airborne droplets. Some of the aware susceptibles may again become susceptible with a rate $\lambda _{11}$ due to fading of the effect of media awareness campaigns. The term $\frac{\nu M}{1+\gamma M}$ denotes the effect of media coverage on susceptible population where $\nu$ can be thought of as the dissemination rate of awareness programs among susceptibles and $\gamma$ limits the effect of awareness programs on susceptibles, $\frac{\nu }{\gamma }$ is the maximum effect that media can put on susceptibles (Dubey et al. 2016). The constant $\alpha$ is the rate by which mild infectives from asymptomatic class are cured but remain vulnerable to join the susceptible class and $\beta _1$ is the rate of appearance of symptoms by which asymptomatic infectives join the symptomatic (hospitalized/isolated) class. The constant $\beta _{11}$ represents the recovery rate coefficient of symptomatic (hospitalized/isolated) individulas who again become susceptible after recovery. The viral density V(t) is assumed to be directly proportional to the asymptomatic infectives where $\theta$ is the rate of increase of V. The constant $\theta _0$ is the rate by which viral density declines due to control/preventive measures. The constant $\mu$ represents the rate by which awareness programs are being implemented and are assumed to be directly proportional to the asymptomatic infective population. The constant $\sigma$ represents the depletion rate of these programs due to ineffectiveness, social problems in the population, etc.

Since $N(t)=X(t)+Y(t)+X_M(t)+Y_i(t)$, the model system (1)–(6) can be rewritten as,

$$\begin{aligned} \frac{{\mathrm{d}}N}{{\mathrm{d}}t}= &\, {} A-{\mathrm{d}}N-\alpha _1 Y_i \end{aligned}$$

(7)

$$\begin{aligned} \frac{{\mathrm{d}}Y}{{\mathrm{d}}t}= &\, {} \beta \frac{(N-Y-X_M -Y_i)Y}{N}\nonumber \\&+\lambda V (N-Y-X_M -Y_i) - (d+ \alpha +\beta _1)Y \end{aligned}$$

(8)

$$\begin{aligned} \frac{{\mathrm{d}}X_M}{{\mathrm{d}}t}= &\, {} \nu \frac{(N-Y-X_M -Y_i)M}{1+\gamma M} -{\mathrm{d}}X_M - \lambda _{11}X_M \end{aligned}$$

(9)

$$\begin{aligned} \frac{{\mathrm{d}}Y_i}{{\mathrm{d}}t}= &\, {} \beta _1 Y -(d+\alpha _1+\beta _{11})Y_i \end{aligned}$$

(10)

$$\begin{aligned} \frac{{\mathrm{d}}V}{{\mathrm{d}}t}= &\, {} \theta Y - \theta _0 V \end{aligned}$$

(11)

$$\begin{aligned} \frac{{\mathrm{d}}M}{{\mathrm{d}}t}= &\, {} \mu Y - \sigma M \end{aligned}$$

(12)

with initial conditions, $N(0)=N_0 >0, Y(0)=Y_0\ge 0, X_M(0)=X_{M0}\ge 0,Y_i(0)=Y_{i0}\ge 0,V(0)=V_0\ge 0,$ and $M(0)=M_0\ge 0$

Invariant region

To study the stability of equilibrium points, we need the bounds of dependent variables of the model system (7)–(12). For this, we find the invariant region in the form of following lemma, stated without proof.

Lemma The closed set $D= \{ (N, Y, X_M, Y_i, V, M)\in R_6^+: \frac{A}{\alpha _1+d}<N<\frac{A}{d}, 0<Y+X_M+Y_i\le N, 0\le V \le \frac{\theta }{\theta _0}\frac{A}{d}, 0\le M \le \frac{\mu }{\sigma }\frac{A}{d} \}$

Existence of equilibria

The system (7)–(12) exhibits two equilibria, namely

• (i) $E_0 (\frac{A}{d}, 0, 0, 0, 0, 0)$, the disease-free equilibrium, which is obvious.

• (ii) $E^*(N^*, Y^*, X_M^*, Y_i^*, V^*, M^*)$, the endemic equilibrium,

where $N^*, Y^*, X_M^*, Y_i^*, V^*\,$ and $M^*$ are the positive solutions which we get on solving the following system of algebraic equations obtained by putting right-hand side of model equations (7)–(12) to zero,

$$\begin{aligned}&A-{\mathrm{d}}N-\alpha _1 Y_i = 0 \end{aligned}$$

(13)

$$\begin{aligned}&\left( \frac{\beta Y}{N}+\lambda V\right) \left( N-Y-X_M -Y_i\right) \nonumber \\&\quad -(d+ \alpha +\beta _1)Y = 0 \end{aligned}$$

(14)

$$\begin{aligned}&\nu \frac{(N-Y-X_M -Y_i)M}{1+\gamma M} -{\mathrm{d}}X_M - \lambda _{11}X_M = 0 \end{aligned}$$

(15)

$$\begin{aligned}&\beta _1 Y -(d+\alpha _1+\beta _{11})Y_i = 0 \end{aligned}$$

(16)

$$\begin{aligned}&\theta Y - \theta _0 V = 0 \end{aligned}$$

(17)

$$\begin{aligned}&\mu Y - \sigma M = 0 \end{aligned}$$

(18)

From Eqs.  (13), (17) and (18) we get, respectively,

$$\begin{aligned}&Y_i = \frac{A-{\mathrm{d}}N}{\alpha _1} = f(N)(say) > 0 \end{aligned}$$

(19)

$$\begin{aligned}&V = \frac{\theta }{\theta _0}Y > 0 \end{aligned}$$

(20)

$$\begin{aligned}&M = \frac{\mu }{\sigma }Y > 0 \end{aligned}$$

(21)

$$\begin{aligned}&Y = \frac{(A-{\mathrm{d}}N)(d+\alpha _1+\beta _{11})}{\alpha _1 \beta _1} = uf(N)> 0 \end{aligned}$$

(22)

here, $u=\frac{(d+\alpha _1+\beta _{11})}{\beta _1}$, and from Eq.  (15) we get,

$$\begin{aligned} X_M = \frac{\nu \left[ N-uf(N)-f(N)\right] }{\nu +(\lambda _{11}+d)\left[ 1+\gamma \frac{\mu }{\sigma }uf(N)\right] } = g(N) (say) \end{aligned}$$

(23)

Now on substituting all the values in Eq. (14) we get,

$$\begin{aligned} F(N)= &\, {} (\beta +\lambda \frac{\theta }{\theta _0}N)[N-uf(N)-g(N)-f(N)]\nonumber \\&-(\alpha +d+\beta _1)N=0 \end{aligned}$$

(24)

It would be sufficient if we show that the Eq. (24) has one and only one positive root between $\frac{A}{\alpha _1+d}$ and $\frac{A}{d}$. To prove this, from Eq. (24) we have,

$$\begin{aligned} F\left( \frac{A}{\alpha _1+d}\right)= &\, {} -\frac{A}{\alpha _1+d}\left( \beta +\lambda \frac{\theta }{\theta _0}\frac{A}{\alpha _1+d}\right) \nonumber \\&\left[ u\frac{(\lambda _{11}+d)\left[ 1+\gamma \frac{\mu }{\sigma }u\frac{A}{\alpha _1+d}\right] }{\nu +(\lambda _{11}+d) \left[ 1+\gamma \frac{\mu }{\sigma }u\frac{A}{\alpha _1+d}\right] }\right] \nonumber \\&-(\alpha +d+\beta _1)\frac{A}{\alpha _1+d}<0 \end{aligned}$$

(25)

$$\begin{aligned} F\left( \frac{A}{d}\right)= &\, {} \frac{A}{d}(d+\alpha +\beta _1)\left[ R_0 \frac{\lambda _{11}+d}{\nu +\lambda _{11}+d}-1\right] >0 \end{aligned}$$

(26)

provided $R_0 (\frac{\lambda _{11}+d}{\nu +\lambda _{11}+d})>1$. Here, $R_0$ represents the reproductive number, given as $R_0=\frac{(\beta +\lambda \frac{\theta }{\theta _0}\frac{A}{d})}{(\alpha +d+\beta _1)}$.

Also, from Eq. (24) and after some algebraic manipulation,

$$\begin{aligned} F'(N) = 2\beta +\lambda \frac{\theta }{\theta _0}N+\lambda \frac{\theta }{\theta _0}[N-uf(N)-g(N)-f(N)] -2(\alpha +d+\beta _1) \end{aligned}$$

(27)

since, $N-Y-X_M-Y_i=X$, therefore,

$$\begin{aligned} F'(N)=2\beta +\lambda \frac{\theta }{\theta _0}(N+X)-2(\alpha +d+\beta _1)>0 \end{aligned}$$

(28)

provided

$$\begin{aligned} 2\beta +\lambda \frac{\theta }{\theta _0}(N+X)>2(\alpha +d+\beta _1) \end{aligned}$$

(29)

This shows that $F(N)=0$ has exactly one root(say $N^*$) between $\frac{A}{\alpha _1+d}$ and $\frac{A}{d}.$ Using $N^*$, the values of $Y^*, X_M^*$, $Y_i^*$, $V^*$ and $M^*$ can be found easily.

Stability of equilibria

In this section, we carry out the stability analysis of the equilibrium points. For this, the following theorems are proposed.

Theorem 4.1

The disease-free equilibrium $E_0$ is locally asymptotically stable if $R_0<1$ so that the infection does not persist in the population and under this condition the endemic equilibrium $E^*$ does not exist. It is unstable for $R_0 > 1$ and endemic equilibrium $E^*$ appears.

Theorem 4.2

The endemic equilibrium $E^*$ is locally asymptotically stable under the following conditions,

$$\begin{aligned}&20ar <q(a+\lambda _{11}+d) \end{aligned}$$

(30)

$$\begin{aligned}&5s\theta < r\theta _0 \end{aligned}$$

(31)

$$\begin{aligned}&\frac{9}{4}\frac{\alpha _1^2}{d(\alpha _1+d+\beta _{11})} <\frac{4}{15}\frac{dqr}{p^2\beta _1} \end{aligned}$$

(32)

See Appendix 1 for proof of Theorems 4.1and 4.2.

Theorem 4.3

The endemic equilibrium $E^*$ is non-linearly asymptotically stable under the following conditions,

$$\begin{aligned}&20a <(a+\lambda _{11}+d) \end{aligned}$$

(33)

$$\begin{aligned}&5\theta \lambda \frac{A}{d}<r\theta _0 \end{aligned}$$

(34)

$$\begin{aligned}&\frac{9}{4}\frac{\alpha _1^2}{d(\alpha _1+d+\beta _{11})} <\frac{4}{15}\frac{dr^2}{Y^{*2}\beta _1\phi } \end{aligned}$$

(35)

See Appendix 2 for proof of Theorem 4.3.

The symbols used in Theorems 4.2 and 4.3 are defined as follows:

$p=\frac{\beta (Y^*+X_M^*+Y_i^*)Y^*}{N^*2}+\lambda V^* >0$, $q=\frac{\beta Y^*}{N^*}+\frac{\lambda V^*(N^*-X_M^*-Y_i^*)}{Y^*}>0$, $r=\frac{\beta Y^*}{N^*}+\lambda V^* > 0$, $s= \lambda (N^*-Y^*-X_M^*-Y_i^*)>0$, $a=\frac{\nu M^*}{1+\gamma M^*} >0$, $b=\frac{\nu (N^*-Y^*-X_M^*-Y_i^*)}{(1+\gamma M^*)^2}>0$, $\phi =\left[ \frac{(\alpha _1+d)}{d}\frac{\beta }{N^*}+\frac{\lambda V^*}{Y^*}\right] ^2>0$

Numerical analysis and discussion

In this section, we perform some numerical simulations for the model system (7)–(12). For this, we integrate the system by fourth-order Runge–Kutta method using MATLAB. Most of the parameter values used in simulation are adopted from previously published articles, while others are estimated intuitively. The unit of parameters is in per day. We use initial values for simulation as stated below (Sarkar et al. 2020; Tripathi and Naresh 2019).

$$\begin{aligned} N(0)=1300000000, Y(0)=0, X_M(0)=0, Y_i(0)=1, V(0)=1, M(0)=0 \end{aligned}$$

In Table 2, the reported corona-positive cases (confirmed infectives) in India are depicted during first wave of pandemic for the months January to August 2020. Till 18 September 2020, Indian government declared the total 5,214,677 corona-positive cases, in which 4,112,551 were cured/discharged and 8472 deaths were due to this disease. The active cases of corona were 1,017,754. According to government of India, the recovery rate was 78.8% and death rate was 2.25% (Corona virus statistics by India 2020).

The parameters used in the model are given in Table 1.

Table 1 Parameters of the model

Table 2 Reported corona positive cases during first wave of pandemic by months Jan. to Aug. 2020 (Corona virus statistics by India 2020)

Fig. 2

Validation of model with Indian data

From Fig. 2, we can see the trend of data as reported in Table 2 and the curve represented by the model for corona cases using the above parameters. It is noted that the number of confirmed infected persons (symptomatic/isolated) estimated by the model for the above set of parameter values is closer to the reported Indian data (Table 2).

The results of numerical simulation are displayed graphically in Figs. 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 and 14. In Figs. 3 and 4, the behaviour of asymptomatic infectives and symptomatic infectives is shown with time for different values of the transmission rate $\lambda$ due to direct contact of susceptibles with virus. It is seen from these figures that the number of asymptomatic infectives increases with increase in the transmission rate $\lambda$ due to direct contact of susceptibles with virus, (Fig. 3). Consequently, the number of symptomatic infectives also increases and remains endemic with higher viral load, (Fig. 4). This indicates that if the transmission rate is curtailed by way of face cover/mask wearing, social distancing, avoidance of crowded places etc., the number of asymptomatic infectives and consequently the symptomatic infectives can be decreased due to non-exposure with virus. In Fig. 5, we have shown the variation of aware susceptible population with time for different values of $\lambda$, the transmission rate due to direct contact of susceptibles with virus. It is noted from this figure that the aware susceptible population declines as the transmission rate $\lambda$ due to direct contact of susceptibles with virus increases.

In Figs. 6 and 7, the variation of aware susceptible population and symptomatic infectives is shown with time for different values of $\nu$, the dissemination rate of media awareness programs. It is observed that the aware susceptible population increases with increase in the dissemination rate of media awareness programs, (Fig. 6) and consequently the symptomatic infectives population decreases, (Fig. 7). This highlights the importance of media awareness campaigns as a result of which more and more susceptible persons become aware of disease escalation. The resulting behavioral change helps in reducing the spread of COVID-19 infection and hence the symptomatic population decreases.

In Fig. 8, the variation of asymptomatic infectives with time t is shown for different values the recovery rate of symptomatic (hospitalized/isolated) infectives $\beta _{11}$. It is seen that the population of asymptomatic infectives increases in the long run with increase in the recovery rate of symptomatic infectives. These recovered symptomatic infectives remain susceptible to increase the susceptible population which in turn increases the asymptomatic infective population. The increase in the recovery rate of symptomatic (hospitalized/isolated) individuals $\beta _{11}$ decreases the population of symptomatic class, (Fig. 9). This recovered population of symptomatic individuals who are discharged from hospitals increases the susceptible population which makes the aware susceptible population to increase, (Fig. 10).

In Figs. 11 and 12, the variation of aware susceptible population and symptomatic (hospitalized/isolated) infective population with time t is shown for different values of $\lambda _{11}$, the rate at which aware susceptibles lose the effect of awareness and become susceptible again due to fading of the effect of media programs. It is seen from these figures that as the effect of media awareness programs fades away, the aware susceptible population declines, (Fig. 11) and consequently the symptomatic infectives population increases, (Fig. 12). Thus, if aware susceptible population loses the impact of media awareness campaigns, the symptomatic population continues to grow and hence the infection will be maintained in the population.

In Figs. 13 and 14, the variation of virus density and symptomatic (hospitalized/isolated) infective population with time t is shown for different values of $\theta$, the growth rate of viral density which is directly proportional to the asymptomatic infectives. It is seen from these figures that as the growth rate of viral density, which is proportional to the asymptomatic infectives, increases, the load of virus increases in the atmosphere (Fig. 13) and hence the symptomatic infectives population also increases (Fig. 14). Since the virus is directly emitted by the asymptomatic infective population and is deposited on surfaces/objects or remain airborne for some time, it increases the load of virus which ultimately results in increasing the symptomatic population. This suggests that if people are educated through media awareness campaigns to wear face cover/masks and avoid touching the infected surfaces/objects and maintain social distancing, the viral density in the atmosphere would decline. This decreased viral density will consequently make the symptomatic infectives population diminish. Thus, media awareness campaigns can be of vital importance to reduce the spreading of COVID-19 infection.

Fig. 3

Variation of asymptomatic Infectives Y with time t for different values of $\lambda$

Fig. 4

Variation of symptomatic infectives $Y_i$ with time t for different values of $\lambda$

Fig. 5

Variation of aware susceptibles $X_M$ with time t for different values of $\lambda$

Fig. 6

Variation of aware susceptibles $X_M$ with time t for different values of $\nu$

Fig. 7

Variation of symptomatic infectives $Y_i$ with time t for different values of $\nu$

Fig. 8

Variation of asymptomatic Infectives Y with time t for different values of $\beta _{11}$

Fig. 9

Variation of symptomatic infectives $Y_i$ with time t for different values of $\beta _{11}$

Fig. 10

Variation of aware susceptibles $X_M$ with time t for different values of $\beta _{11}$

Fig. 11

Variation of aware susceptibles $X_M$ with time t for different values of $\lambda _{11}$

Fig. 12

Variation of symptomatic infectives $Y_i$ with time t for different values of $\lambda _{11}$

Fig. 13

Variation of virus density V with time t for different values of $\theta$

Fig. 14

Variation of symptomatic infectives $Y_i$ with time t for different values of $\theta$

Conclusion

In this paper, a non-linear mathematical model is proposed and analyzed to study the effect of media awareness campaigns on the transmission dynamics of COVID-19 pandemic caused by the coronavirus SARS-CoV-2 in a population with variable size structure. It is assumed that the susceptibles become infected by direct contacts with asymptomatic infectives as well as by coming in contacts with virus deposited on surfaces and /or droplets which are airborne for some time due to coughing, sneezing, exhalation of symptomatic infectives, etc. In the proposed model, the total human population is divided into four sub-classes, namely susceptibles, asymptomatic infectives, aware susceptibles and symptomatic infectives (hospitalized/ isolated), incorporating classes representing cumulative density of virus and media alert. The model is analyzed using stability theory of differential equations and numerical simulation. Some inferences have been drawn regarding the spread of the disease by way of establishing local and global stability results. It is found that with increase in the dissemination of media awareness programs, the aware susceptible population increases and consequently the symptomatic infectives population decreases. Thus, if more and more susceptible persons become aware of disease escalation, the resulting behavioral change helps in reducing the spread of COVID-19 infection.

Appendices

Appendix 1

Proof of Theorem 4.1. To prove this theorem, we have the following Jacobian matrix evaluated at $E_0$.

$$\begin{aligned}&J(E_0)= \\&\quad \left[ \begin{array}{cccccc} -d &{} 0 &{} 0 &{} -\alpha _1 &{} 0 &{} 0 \\ 0 &{} [\beta -(\alpha +d+\beta _1)] &{} 0 &{} 0 &{} \lambda \frac{A}{d} &{} 0 \\ 0 &{} 0 &{} -(\lambda _{11}+d) &{} 0 &{} 0 &{} 0 \\ 0 &{} \beta _1 &{} 0 &{} -(\alpha _1+d+\beta _{11}) &{} 0 &{} 0\\ 0 &{} \theta &{} 0 &{} 0 &{} -\theta _0 &{} 0 \\ 0 &{} \mu &{} 0 &{} 0 &{} 0 &{} -\sigma \\ \end{array} \right] \end{aligned}$$

The characteristic equation is

$$\begin{aligned} g(x)= &\, {} (\lambda _{11}+d+x)(\alpha _1+d+\beta _{11}+x)\nonumber \\&(\sigma +x)(x^3+l_1x^2+l_2x+l_3)=0 \end{aligned}$$

(36)

From Eq. (36) it is clear that the three eigen values are negative and remaining three can be checked by cubic equation, $(x^3+l_1x^2+l_2x+l_3)=0,$ using Routh Hurwitz criteria

where, $l_1=d+\theta _0-[\beta -(\alpha +d+\beta _1)]$

$l_2=d\theta _0-[\beta -(\alpha +d+\beta _1)](d+\theta _0)$

$l_3=-[\beta -(\alpha +d+\beta _1)]d\theta _0-\lambda \frac{A}{d}\theta$

It can be easily seen that $l_1$ and $l_2$ are positive for $\beta <(\alpha +d+\beta _1)$, while $l_3$ is positive when $\beta +\lambda \frac{A\theta }{d\theta _0}<(\alpha +d+\beta _1)$. Therefore, only for a condition $\beta +\lambda \frac{A\theta }{d\theta _0}<(\alpha +d+\beta _1)$ the term $l_1, l_2$ and $l_3$ are positive and also satisfying $l_1l_2-l_3>0$. Which fulfills all the conditions of Routh Hurwitz criteria. Thus, the disease free equilibrium is locally asymptotically stable if $\beta +\lambda \frac{A\theta }{d\theta _0}<(\alpha +d+\beta _1)$ i.e $R_0<1$.

Proof of Theorem 4.2. Now to establish the local stability of the endemic equilibrium $E^*$, we linearize the system using small perturbations n, y, $x_m$, $y_i$, v and m as follows,

$N = N^*+n, Y = Y^*+y, X_M = X_M^*+x_m, Y_i = Y_i^*, V=V^*+v, M = M^*+m$

Let us consider the following positive definite function,

$$\begin{aligned} U= &\, {} k_1 \frac{1}{2}n^2 + k_2\frac{1}{2}y^2 + k_3\frac{1}{2}x_m^2\nonumber \\&+k_4\frac{1}{2}y_i^2+k_5\frac{1}{2}v^2+k_6\frac{1}{2}m^2 \end{aligned}$$

(37)

where $k_1$, $k_2$, $k_3$, $k_4$, $k_5$ and $k_6$ are positive constants to be chosen appropriately.

On differentiating U with respect to t

$$\begin{aligned} \frac{{\mathrm{d}}U}{{\mathrm{d}}t}= &\, {} k_1 n \frac{{\mathrm{d}}n}{{\mathrm{d}}t}+ k_2 y \frac{{\mathrm{d}}y}{{\mathrm{d}}t}+k_3 x_m\frac{{\mathrm{d}}x_m}{{\mathrm{d}}t}\nonumber \\&+k_4 y_i \frac{{\mathrm{d}}y_i}{{\mathrm{d}}t}+k_5 v \frac{{\mathrm{d}}v}{{\mathrm{d}}t}+k_6 m\frac{{\mathrm{d}}m}{{\mathrm{d}}t} \end{aligned}$$

(38)

Now using the linearized system of (7)–(12) and after some algebraic manipulations, we get

$$\begin{aligned} \frac{{\mathrm{d}}U}{{\mathrm{d}}t}= &\, {} -k_1 d n^2 -k_2 q y^2 - k_3 (a+\lambda _{11}+d)\nonumber \\&x_m^2-k_4 (\alpha _1+d+\beta _{11}) y_i^2-k_5\theta _0 v^2-k_6\sigma m^2\nonumber \\&+ k_2 p ny +k_3 a nx_m - k_1 \alpha _1 ny_i-(k_2r+k_3a)yx_m+\nonumber \\&(k_4\beta _1- k_2 r)yy_i \nonumber \\&+(k_5\theta + k_2 s)yv+k_6\mu y m-k_3 a x_m y_i+ k_3 b x_m m \end{aligned}$$

(39)

Choosing, $k_1 =1$, and after algebraic manipulation we obtain $k_2 < \frac{4}{15}\frac{dq}{p^2}$, $k_3< {\mathrm{min.}}(\phi _1, \phi _2, \phi _3, \phi _4)$, $\frac{9}{4}\frac{\alpha _1^2}{d(\alpha _1+d+\beta _{11})}<k_4 <\frac{4}{15}\frac{dqr}{p^2\beta _1}$, $k_5<\frac{4}{15}\frac{dqs}{p^2\theta }$ and $k_6<\frac{8}{75}\frac{dq^2\sigma }{p^2\mu ^2}$.

Here $\phi _1=\frac{1}{3}\frac{d(a+\lambda _{11}+d)}{a^2}$, $\phi _2=\frac{4}{15}\frac{dqr}{p^2 a}$, $\phi _3= \frac{4}{75}\frac{dq^2\sigma ^2(a+\lambda _{11}+d)}{p^2 \mu ^2 b^2}$ , $\phi _4=\frac{1}{3}k_4\frac{(a+\lambda _{11}+d)(\alpha _1+d+\beta _{11})}{a^2}$ we get $\frac{{\mathrm{d}}U}{{\mathrm{d}}t}$ to be negative definite for the conditions given in the theorem.

Appendix 2

Proof of Theorem 4.3. To prove this theorem, we consider the following positive definite function,

$$\begin{aligned} W= &\, {} \frac{1}{2}p_1(N-N^*)^2 + p_2\left(Y-Y^*-Y^*ln\frac{Y}{Y^*}\right) \nonumber \\&+ \frac{1}{2}p_3 (X_M-X_M^*)^2 \nonumber \\&+\frac{1}{2}p_4(Y_i-Y_i^*)^2 \nonumber \\&+\frac{1}{2}p_5(V-V^*)^2 +\frac{1}{2}p_6(M-M^*)^2 \end{aligned}$$

(40)

Differentiating W with respect to t, we get

$$\begin{aligned} \frac{{\mathrm{d}} W}{{\mathrm{d}}t}= &\, {} p_1(N-N^*)\frac{{\mathrm{d}} N}{{\mathrm{d}}t} + p_2 \frac{(Y-Y^*)}{Y} \frac{{\mathrm{d}} Y}{{\mathrm{d}}t} \nonumber \\&+ p_3 (X_M-X_M^*)\frac{{\mathrm{d}} X_M}{{\mathrm{d}}t} \nonumber \\&+p_4 (Y_i-Y_i^*) \frac{{\mathrm{d}} Y_i}{{\mathrm{d}}t}+ p_5 (V-V^*) \nonumber \\&\frac{{\mathrm{d}} V}{{\mathrm{d}}t}+ p_6 (M-M^*)\frac{{\mathrm{d}} M}{{\mathrm{d}}t} \end{aligned}$$

(41)

where $p_i (i = 1, 2, 3, 4, 5, 6)$ are positive constants, to be chosen appropriately.

After some algebraic manipulations,$\frac{{\mathrm{d}}W}{{\mathrm{d}}t}$ can be written as

$$\begin{aligned} \frac{{\mathrm{d}} W}{{\mathrm{d}}t}= &\, {} -p_1 d (N-N^*)^2- p_2\nonumber \\&\left[ \frac{r}{Y^*}+\lambda \frac{(N-Y-X_M-Y_i)V}{Y^*Y}\right] (Y-Y^*)^2 \nonumber \\&-p_3(a+\lambda _{11}+d) (X_M - X_M^*)^2 -p_4(\alpha _1+d+\beta _{11})(Y_i-Y_i^*)^2\nonumber \\&-p_5\theta _0(V-V*)^2-p_6\sigma (M-M^*)^2 +p_3 a (N-N^*)(X_M-X_M^*)\nonumber \\&+p_2\left[ \frac{\beta (Y+X_M+Y_i)}{NN^*}+\lambda \frac{V^*}{Y^*}\right] \nonumber \\&(N-N^*)(Y-Y^*)- p_1\alpha _1 (N-N^*)(Y_i-Y_i^*)\nonumber \\&-\left( p_2\frac{r}{Y^*}+p_3a\right) (Y-Y^*)(X_M-X_M^*)\nonumber \\&+\left( p_4\beta _1 - p_2\frac{r}{Y^*}\right) (Y-Y^*)(Y_i-Y_i^*) \nonumber \\&+p_6\mu (Y-Y^*)(M-M^*)+p_3\frac{\nu (N - Y - X_M - Y_i)}{(1+\gamma M) (1+\gamma M^*)}\nonumber \\&(X_M-X_M^*)(M-M^*)\nonumber \\&+\left[ p_2\frac{\lambda (N - Y - X_M - Y_i)}{Y^*}+p_5\theta \right] (Y-Y^*)(V-V^*)\nonumber \\&-p_3a(X_M-X_M^*)(Y_i-Y_i^*) \end{aligned}$$

(42)

The Eq. (42) can be rewritten as,

$$\begin{aligned} \frac{{\mathrm{d}} W}{{\mathrm{d}}t}\le & {} -p_1 d (N-N^*)^2- p_2 \nonumber \\&\frac{r}{Y^*}(Y-Y^*)^2-p_3(a+\lambda _{11}+d) (X_M - X_M^*)^2\nonumber \\&-p_4(\alpha _1+d+\beta _{11})(Y_i-Y_i^*)^2-p_5\theta _0(V-V*)^2-p_6\sigma (M-M^*)^2\nonumber \\&+p_2\left[ \frac{\beta }{N^*}\frac{(\alpha _1+d)}{d}+\lambda \frac{V^*}{Y^*}\right] \nonumber \\&(N-N^*)(Y-Y^*)+p_3 a (N-N^*)(X_M-X_M^*)\nonumber \\&- p_1\alpha _1 (N-N^*)(Y_i-Y_i^*)-\left( p_2\frac{r}{Y^*}+p_3a\right) (Y-Y^*)(X_M-X_M^*)\nonumber \\&+\left( p_4\beta _1 - p_2\frac{r}{Y^*}\right) (Y-Y^*)(Y_i-Y_i^*)-p_3a(X_M-X_M^*)(Y_i-Y_i^*) \nonumber \\&+\left[ p_2\frac{\lambda \left( \frac{A}{d}\right) }{Y^*}+p_5\theta \right] (Y-Y^*)(V-V^*) +p_6\mu (Y-Y^*)(M-M^*)\nonumber \\&+p_3\frac{\nu \left( \frac{A}{d}\right) }{(1+\gamma M^*)} (X_M-X_M^*)(M-M^*) \end{aligned}$$

(43)

Choosing, $p_1=1$, and after algebraic manipulation we obtain $p_2 < \frac{4}{15}\frac{dr}{Y^*\phi }$, $p_3< {\mathrm{min.}} (\phi _1,\frac{4}{15}\frac{dr^2}{aY^{*2}\phi } ,\frac{4}{75}\frac{dr^2\sigma ^2(a+\lambda _{11}+d)}{Y^{*2}\mu ^2\phi \frac{\nu \left( \frac{A}{d}\right) }{(1+\gamma M^*)}} ,\phi _4)$, $\frac{9}{4}\frac{\alpha _1^2}{d(\alpha _1+d+\beta _{11})}<p_4 <\frac{4}{15}\frac{dr^2}{Y^{*2}\beta _1\phi }$, $p_5<\frac{4}{15}\frac{\lambda A r}{Y^{*2}\theta \phi }$ and $p_6<\frac{8}{75}\frac{d\sigma r^2}{Y^{*2}\mu ^2\phi }$. we get $\frac{{\mathrm{d}}W}{{\mathrm{d}}t}$ to be negative definite for the conditions given in the theorem. Here p, q, r, s, a, b and $\phi$ used in the Theorems 4.2 and 4.3 are defined as follows,

$p=\frac{\beta (Y^*+X_M^*+Y_i^*)Y^*}{N^{*2}}+\lambda V^* >0$, $q=r+\frac{\lambda V^*(N^*-X_M^*-Y_i^*)}{Y^*}>0$,

$r=\frac{\beta Y^*}{N^*}+\lambda V^* > 0$, $s= \lambda (N^*-Y^*-X_M^*-Y_i^*)>0$,

$a=\frac{\nu M^*}{1+\gamma M^*} >0$, $b=\frac{\nu (N^*-Y^*-X_M^*-Y_i^*)}{(1+\gamma M^*)^2}>0$, $\phi =\frac{(\alpha _1+d)}{d}\frac{\beta }{N^*}+\frac{\lambda V^*}{Y^*}>0$.